- Учителю
- Программа спецкурса по математике Избранные вопросы математики (9 класс)
Программа спецкурса по математике Избранные вопросы математики (9 класс)
Министерство образования Республики Марий Эл
Муниципальное общеобразовательное учреждение «Средняя общеобразовательная школа № 3 г. Козьмодемьянска»
Спецкурс в 9 классе
«Избранные вопросы математики»
Разработала: учитель математики
высшей квалификационной категории
Авдеева Галина Николаевна
г. Козьмодемьянск
2015
Пояснительная записка
В современном мире математическое образование занимает одно из ведущих мест. Поэтому основная задача обучения математики в школе - обеспечить прочное, сознательное усвоение учащимися математических знаний и умений, необходимых в повседневной жизни и трудовой деятельности каждого человека, достаточных для изучения смежных дисциплин и продолжения образования.
Экзамен по математике является обязательным как в 9-м, так и в 11-м классе. Среди заданий ОГЭ и ЕГЭ (профильный уровень) встречаются не только задачи, направленные на проверку базовых знаний учащихся, но и задачи повышенного уровня сложности, требующие умения решать нестандартные задачи.
Данный спецкурс направлен на восполнение недостающих знаний, углубление и расширение круга математических вопросов, не изучаемых на уроках. Спецкурс рассчитан на учащихся 9-ых классов. Данный спецкурс предусматривает формирование у учащихся устойчивого интереса к предмету, выявление математических способностей, возможность выбора профильного обучения в 10 - 11 классах.
Спецкурс рассчитан на 34 часа. Он включает в себя важные разделы алгебры, а также задачи по планиметрии, решение которых требует знания дополнительного теоретического материала по геометрии.
Цели курса:
• развивать математическую культуру учащихся;
• развивать познавательную деятельность учащихся;
• развивать интерес школьников к предмету.
Задачи курса:
• расширить представления учащихся по некоторым темам, изучаемым в
основном курсе;
• познакомить учащихся с различными методами решения задач;
• развивать логическое мышление, умение аргументировать ответы.
Ожидаемые результаты:
• умение учащихся решать задачи различными методами;
• применение полученных знаний для успешной сдачи ОГЭ и ЕГЭ;
• определение склонностей ученика при выборе профильного обучения.
Виды деятельности на занятиях:
• лекция, практикум, беседа.
Учебно-тематическое планирование
-
Тема
Количество
часов
1.
Уравнения высших степеней
6
2.
Уравнения с модулями
5
3.
Иррациональные уравнения
4
4.
Уравнения с параметрами
9
5.
Задачи по планиметрии
10
Содержание спецкурса
1. Уравнения высших степеней (6 ч)
Решение уравнений высших степеней следующими методами: метод введения новой переменной; метод разложения на множители; раскрытие скобок парами; раскрытие скобок парами и деление обеих частей уравнения; использование основного свойства дроби; возвратные уравнения; уравнения, содержащие взаимно обратные выражения.
2. Уравнения с модулями (5 ч)
Решение уравнений вида 
; 
; 
. Решение уравнений методом введения новой переменной и методом
промежутков.
3. Иррациональные уравнения (4 ч)
Решение уравнений вида 
; 
; 
. Решение уравнений методом введения новой переменной. Решение
других видов иррациональных уравнений.
4. Уравнения с параметрами (9 ч)
Линейные и простейшие дробно-рациональные уравнения с параметрами. Квадратные уравнения с параметрами. Теорема Виета. Расположение корней квадратного трехчлена.
5. Задачи по планиметрии (10 ч)
Решение задач, предлагавшихся в тестах ОГЭ: на выбор правильного ответа, задачи из второй части на 2, 3 и 4 балла.
Приложение
1. Уравнения высших степеней (6 ч)
Лекция по теме «Уравнения высших степеней»
• 1. Метод введения новой переменной.
1. 
;
2. 
;
3. 
;
4. 
;
5. 
;
6. 
;
7. 
;
8. 
;
9. 
;
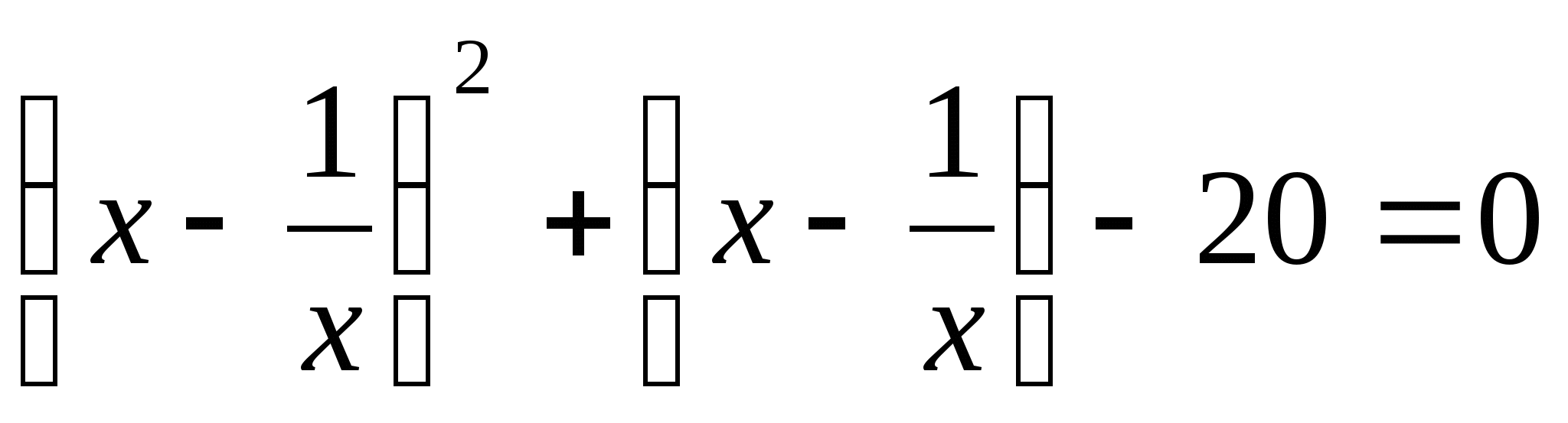10. 
;
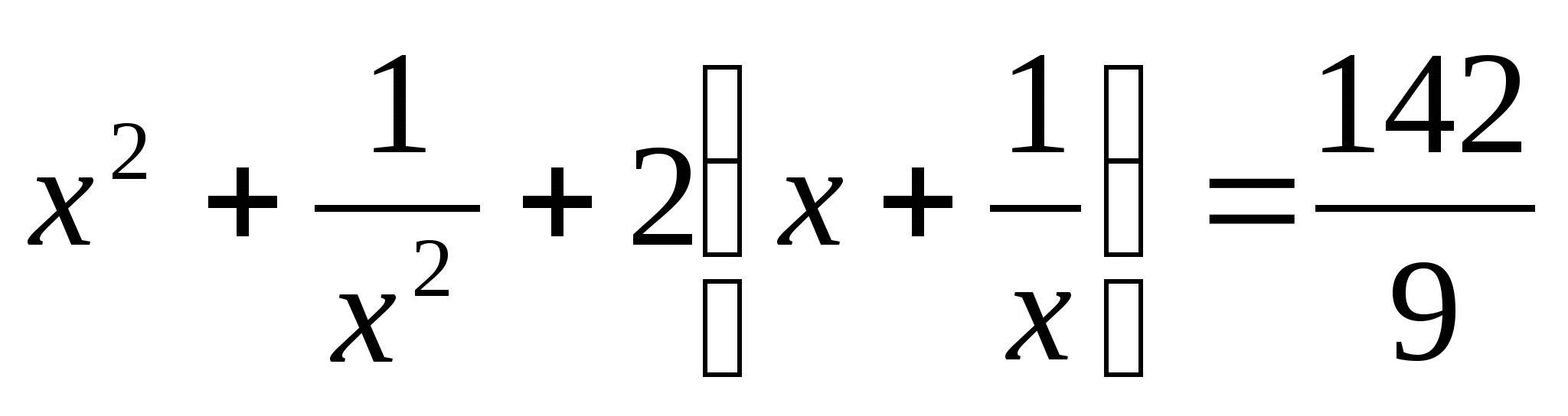11. 
.
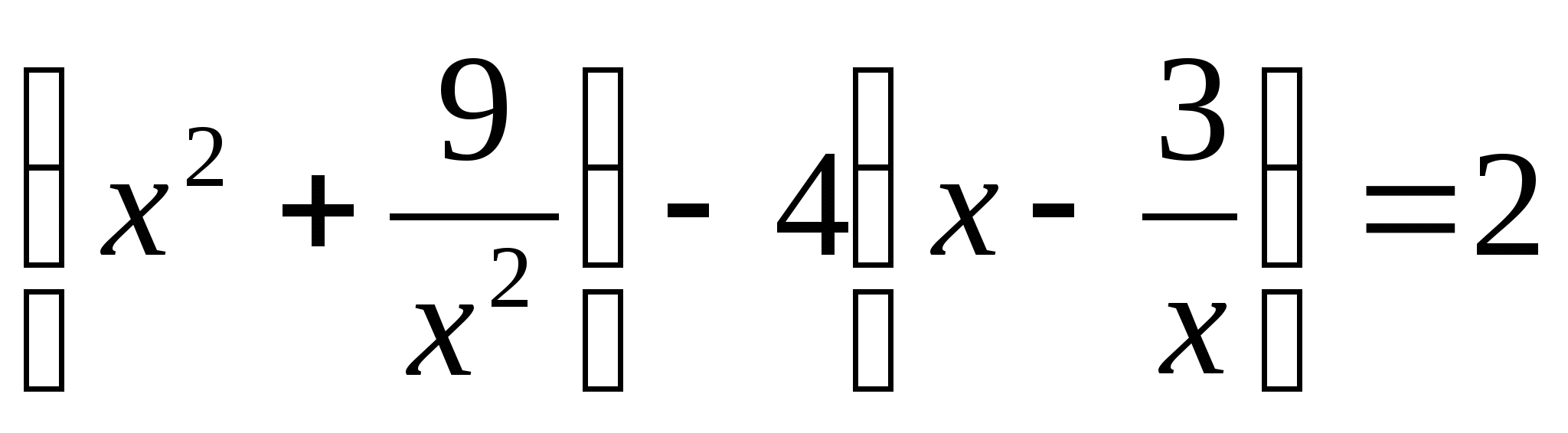• 2. Метод разложения на множители.
1. 
;
2. 
;
3. 
;
4. 
;
5.* 
.
• 3. Раскрытие скобок парами.
1. 
;
2. 
;
3. 
;
4. 
;
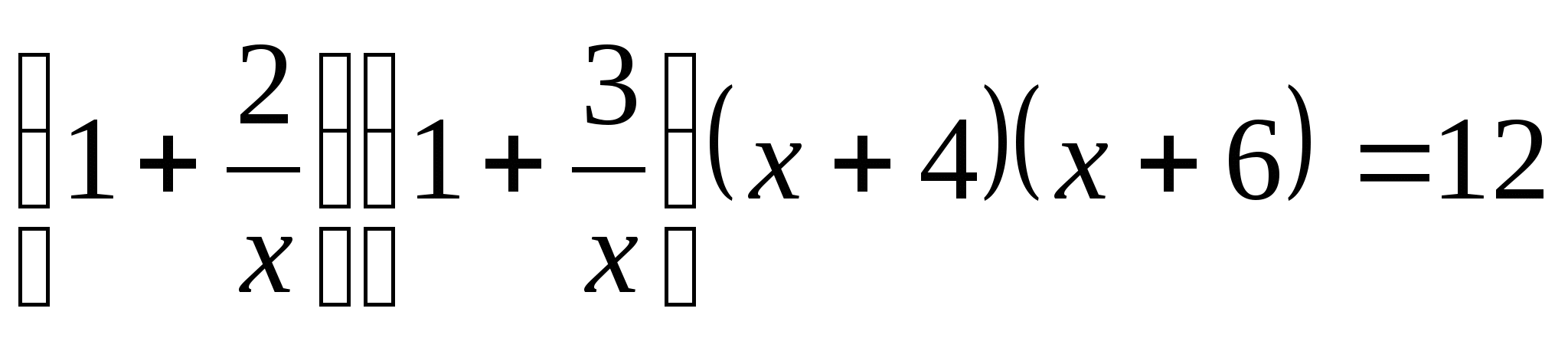5. 
.
• 4. Раскрытие скобок парами и деление обеих частей уравнения.
1. 
;
2. 
.
• 5. Использование основного свойства дроби.
1. 
;
2. 
;
3. 
.
• 6. Возвратные уравнения.
Определение. Возвратным уравнением называют уравнение, в котором
равноудаленные от концов уравнения коэффициенты равны.
1. 
;
2. 
.
• 7. Уравнения, содержащие взаимно обратные выражения.
1. 
;
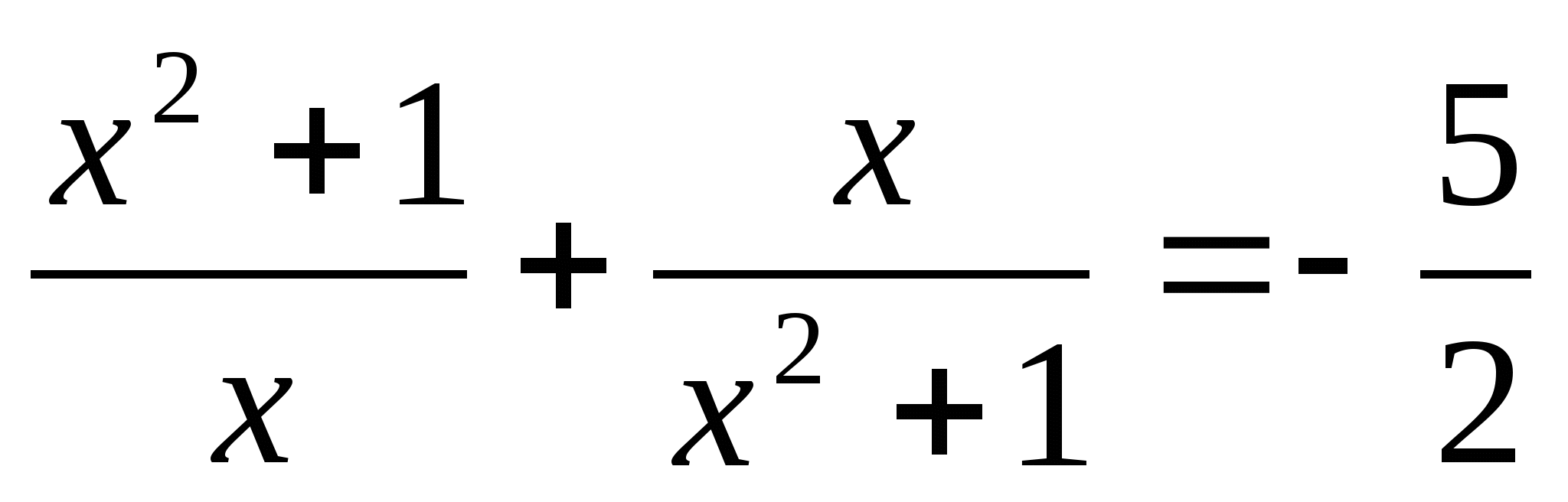2. 
.
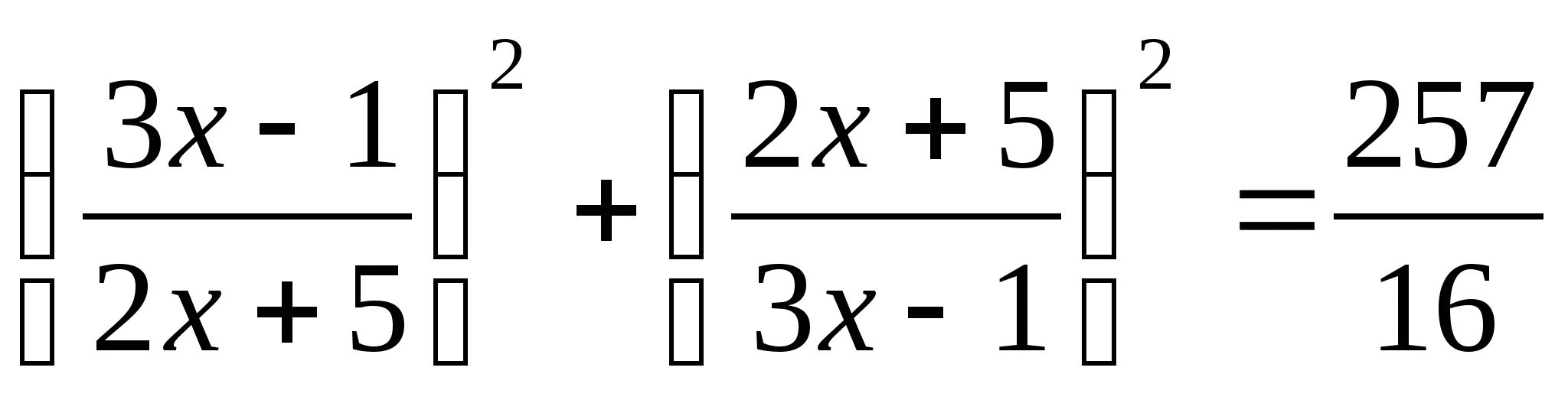Практикум по теме «Уравнения высших степеней»
1. 
;
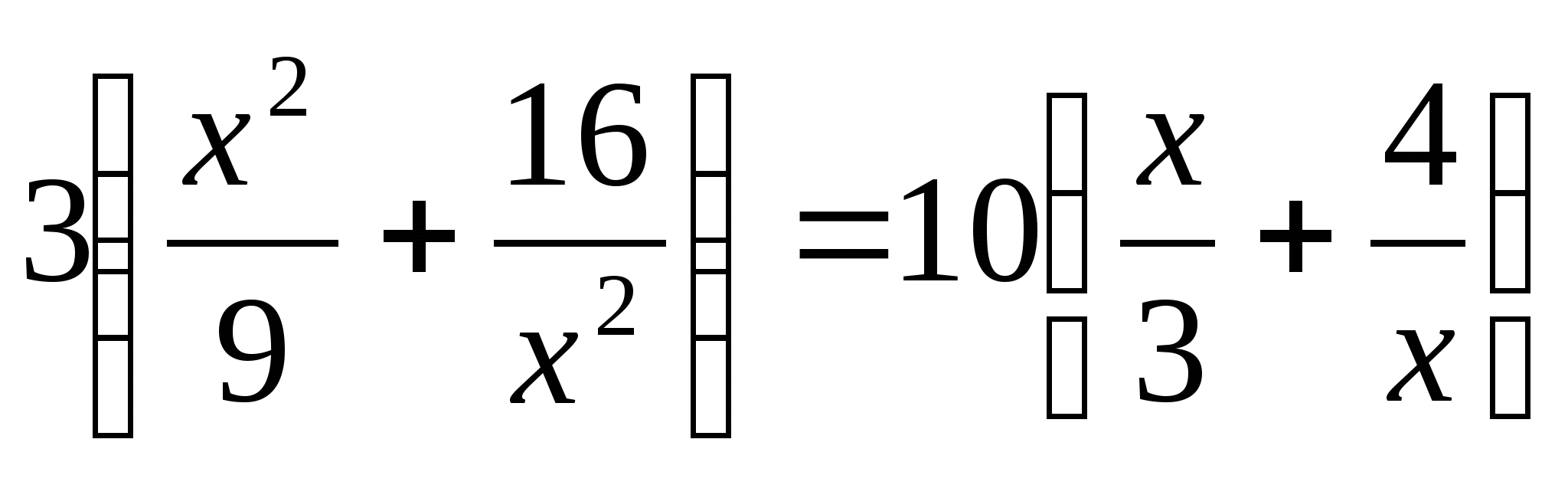2. 
;
3. 
;
4. 
;
5. 
;
6. 
;
7. 
;
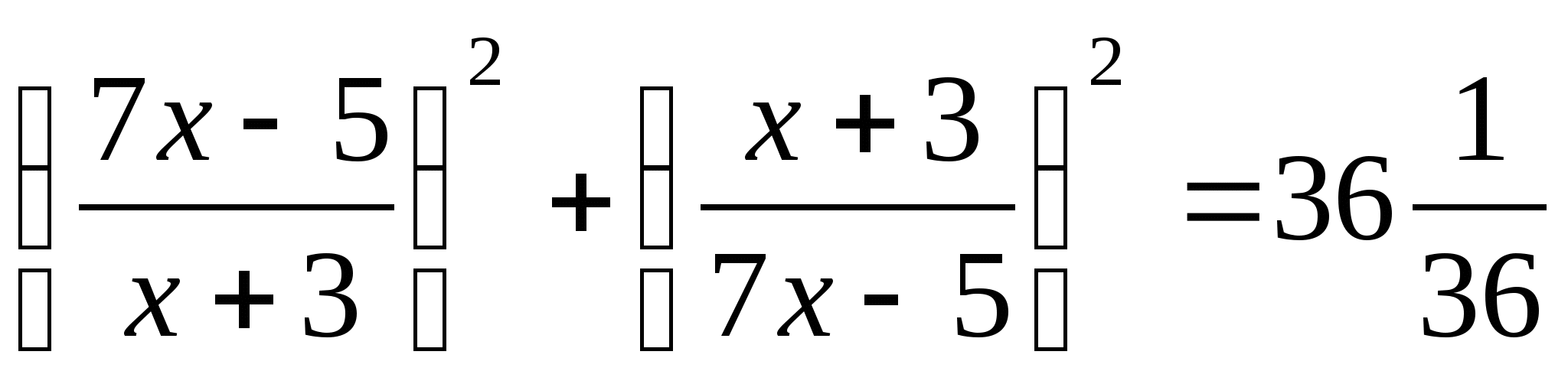8. 
;
9. 
;
10. 
;
11. 
;
12.* 
.
2. Уравнения с модулями (5 ч)
Лекция по теме «Уравнения с модулями»
• 1. Уравнения вида
.
;
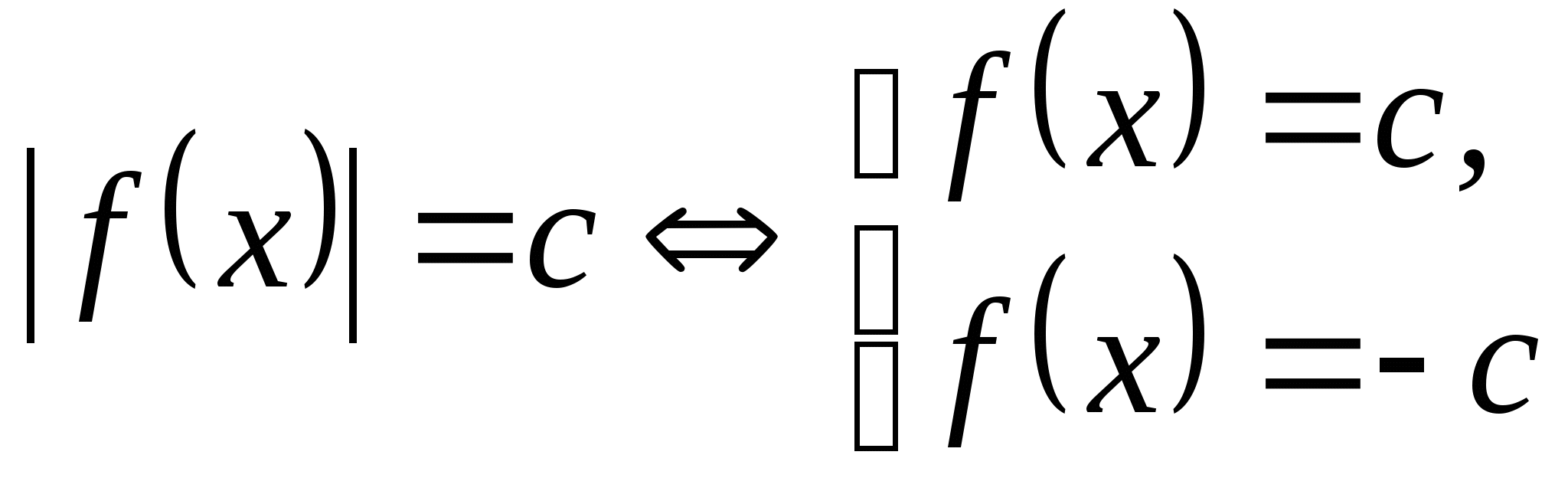где с > 0.
1. 
;
2. 
;
3. 
.
• 2. Уравнения вида
.
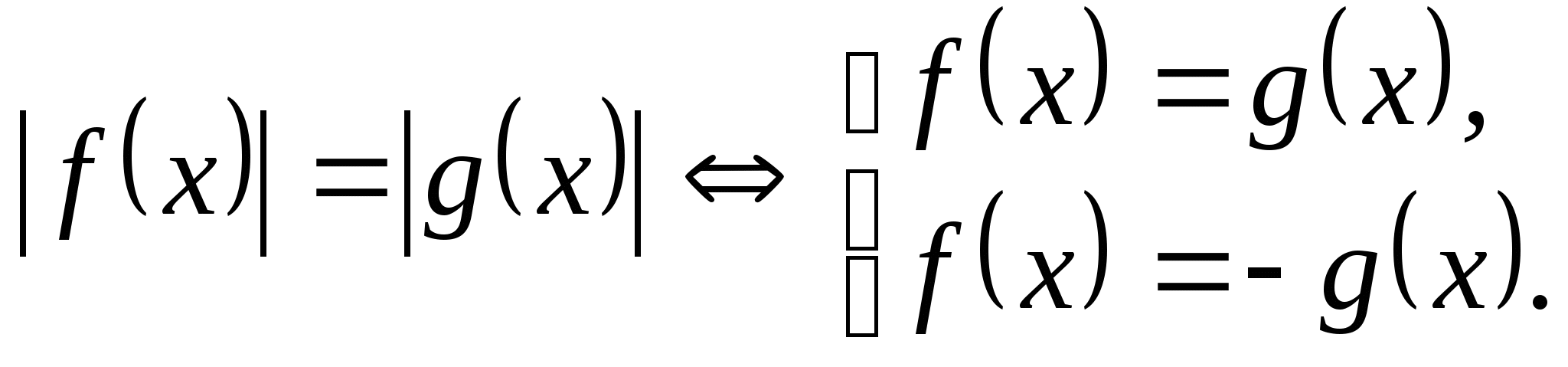
1. 
;
2. 
;
3. 
.
• 3. Уравнения вида
.
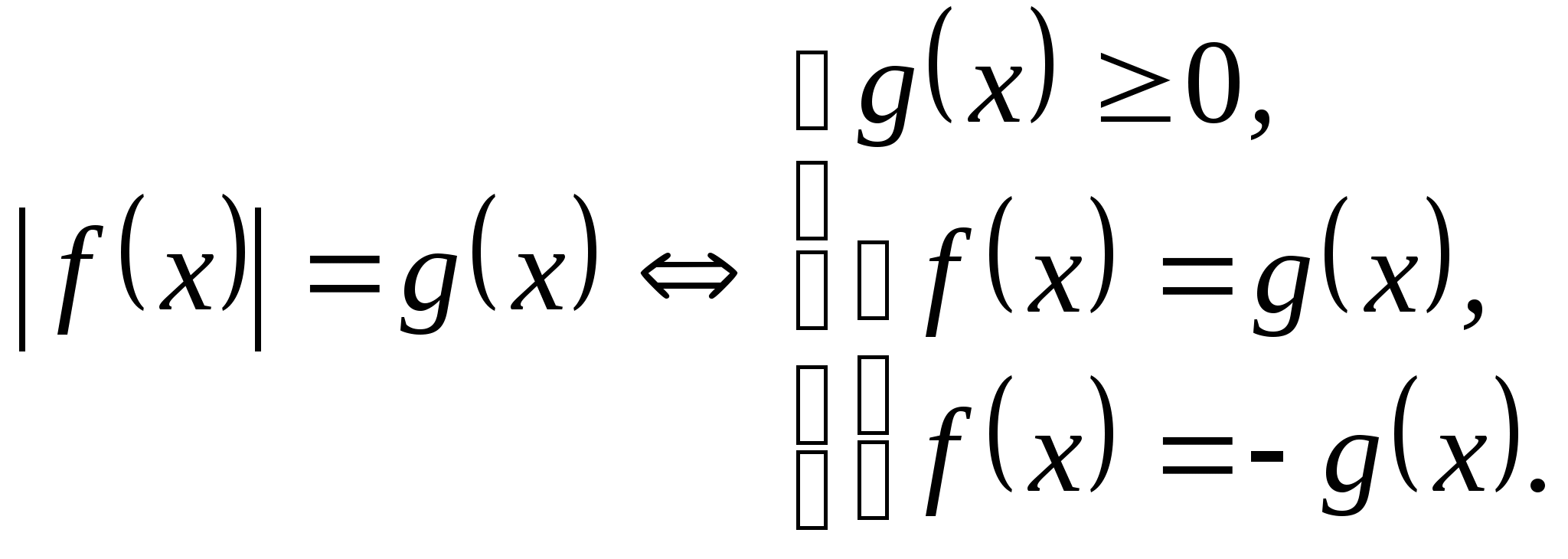
1. 
;
2. 
;
3. 
.
• 4. Метод введения новой переменной.
1. 
;
2. 
;
3. 
.
• 5. Метод промежутков.
1. 
;
2. 
;
3. 
.
Практикум по теме «Уравнения с модулями»
1. 
;
2. 
;
3. 
;
4. 
;
5. 
;
6. 
;
7. 
;
8. 
;
9. 
;
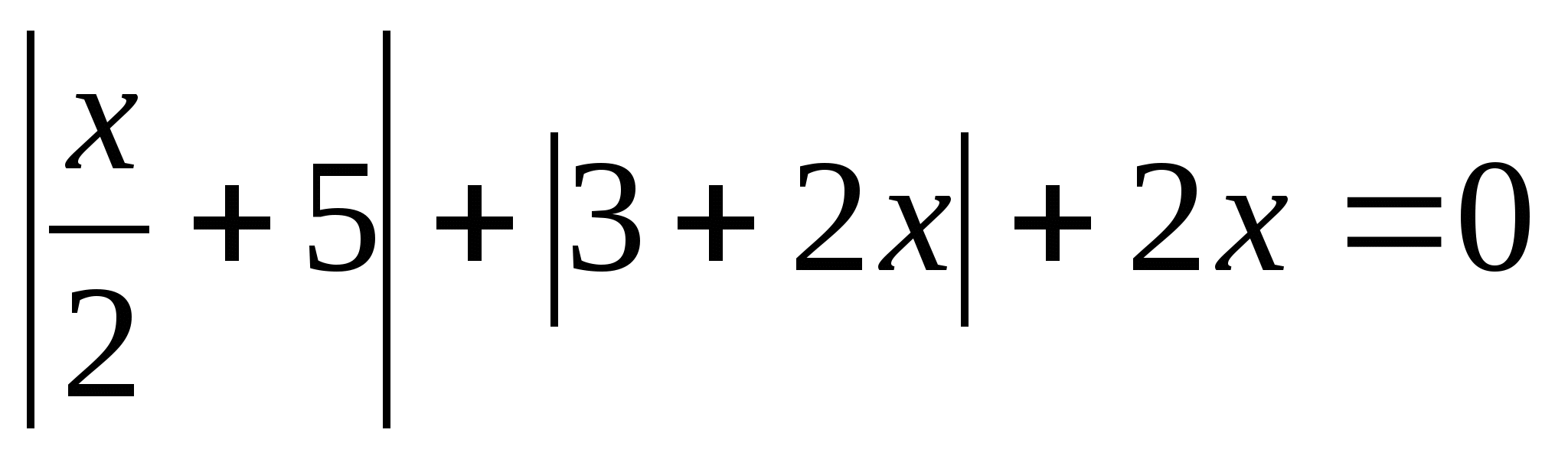10. 
.
3. Иррациональные уравнения (4 ч)
Определение. Уравнение, в котором переменная содержится под знаком радикала,
называется иррациональным уравнением.
• 1. Уравнения вида
, с > 0.
1. 
; 2.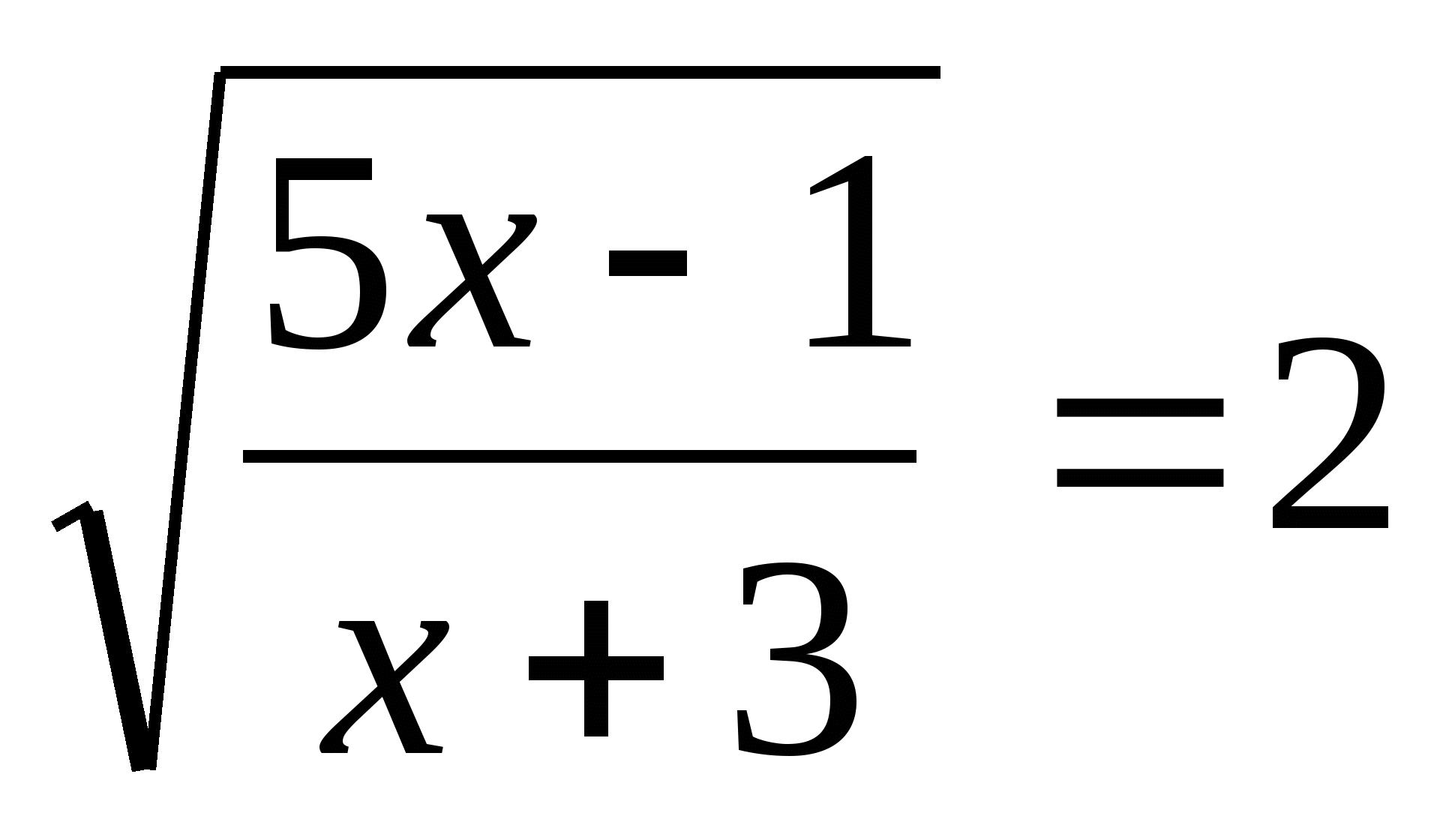 
.
• 2. Уравнения вида
.
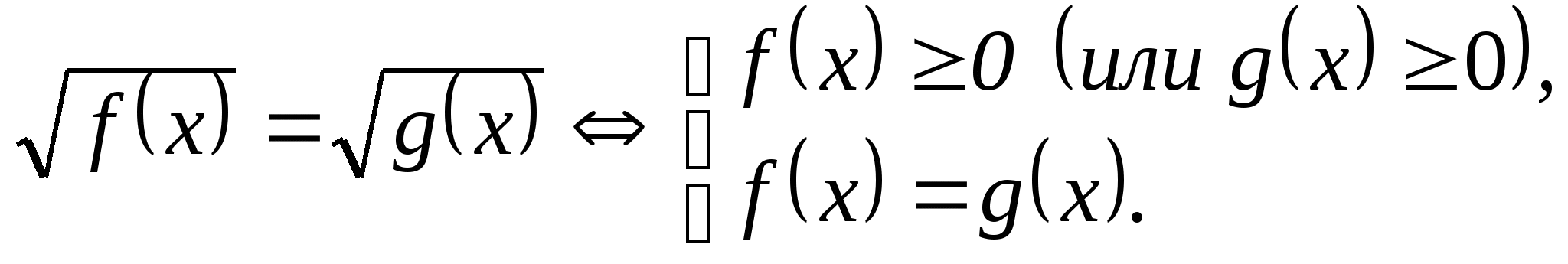
1. 
;
2. 
;
3. 
;
4. 
.
• 3. Уравнения вида
.
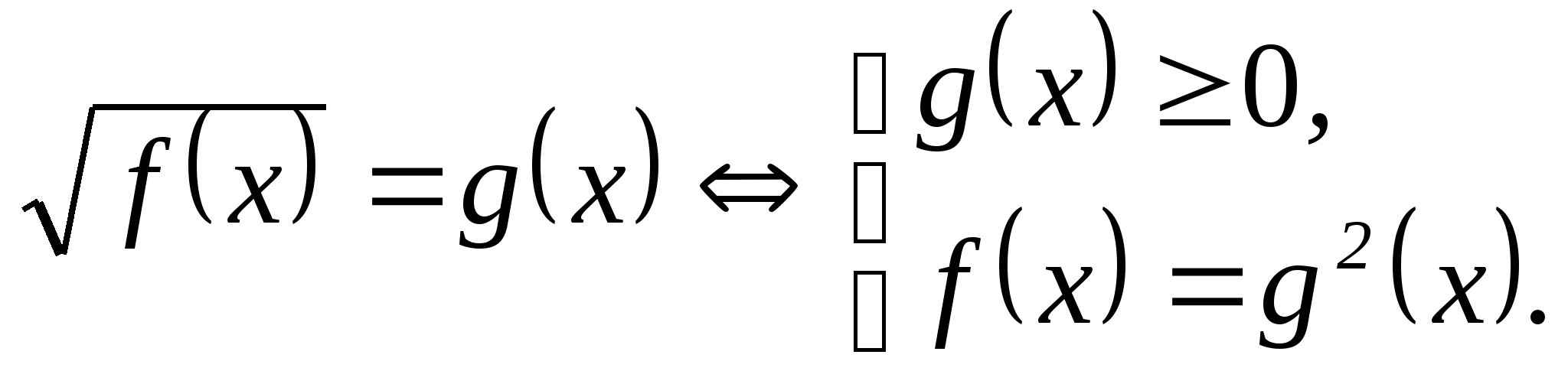
1. 
;
2. 
;
3. 
.
• 4. Метод введения новой переменной.
1. 
;
2. 
;
3. 
;
4. 
;
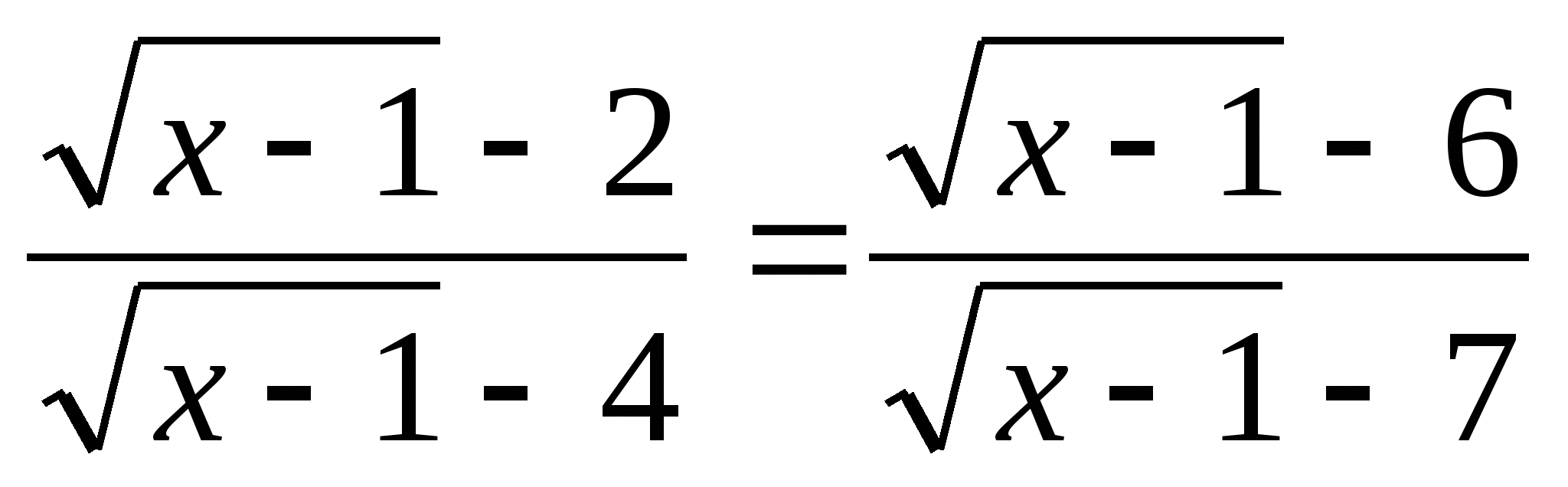5. 
;
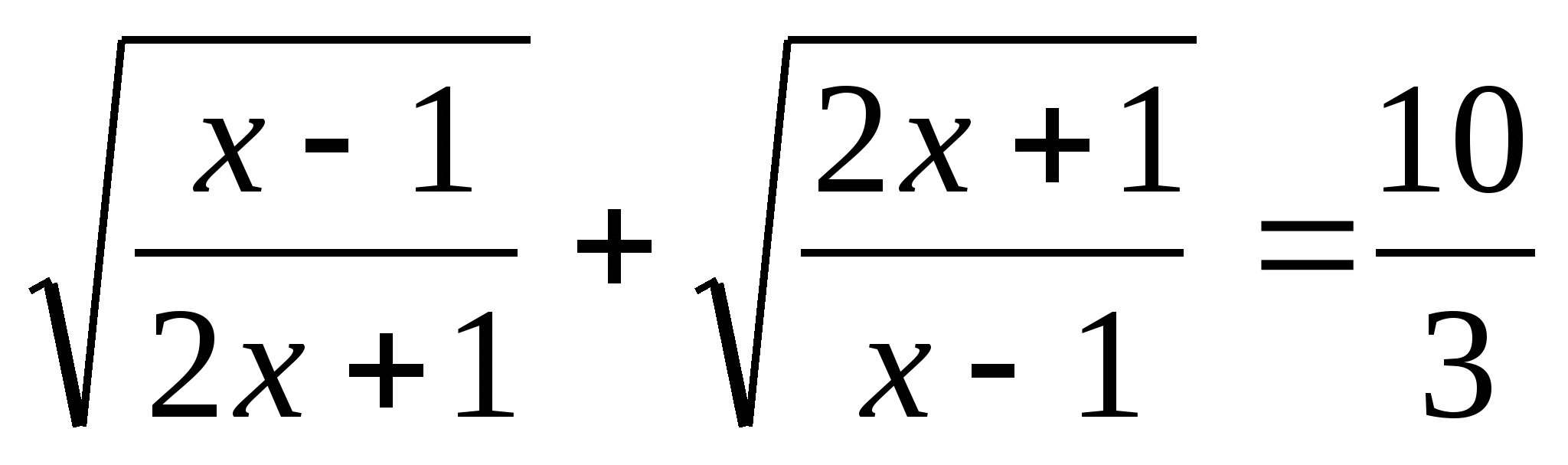6. 
.
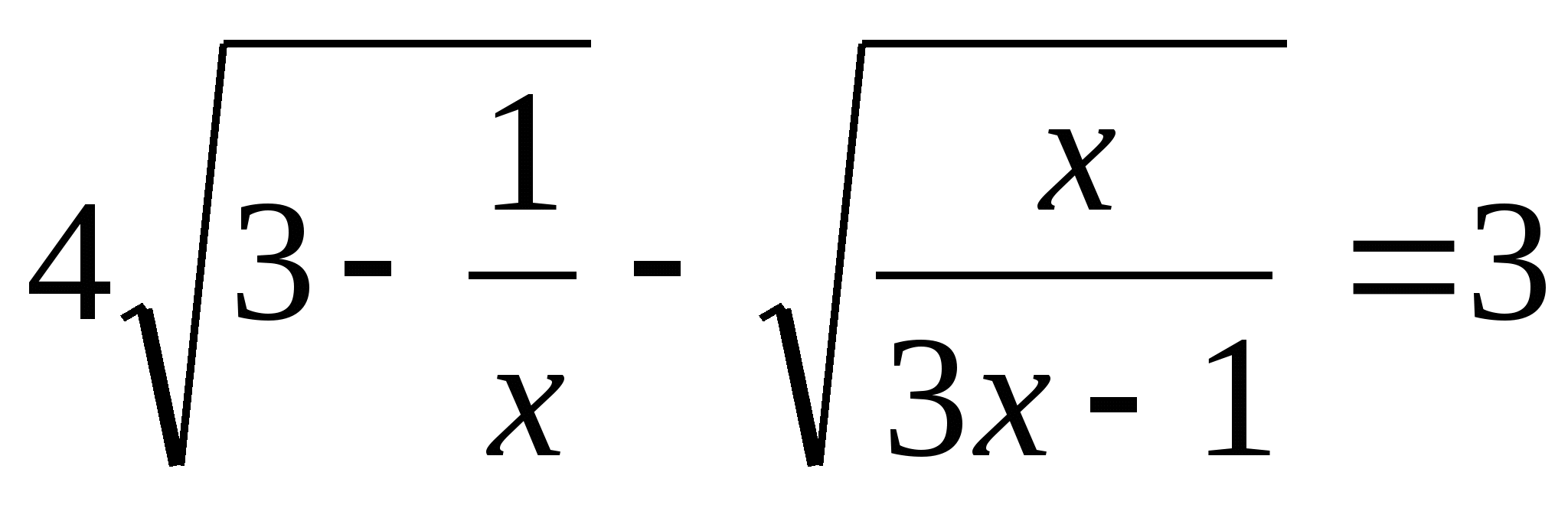• 5. Разные уравнения.
1. 
;
2. 
;
3. 
;
4. 
;
5. 
.
4. Уравнения с параметрами (9 ч)
Если дано уравнение 
, которое надо решить относительно переменной х, и в котором буквой
а обозначено произвольное число, то говорят, что задано уравнение с
параметром.
Решить уравнение с параметром - значит, для всех значений параметра найти множество всех корней заданного уравнения.
• 1. Линейные и простейшие дробно-рациональные уравнения.
1. 
;
2. 
;
3. 
;
4. 
;
5. 
;
6. 
;
7. 
.
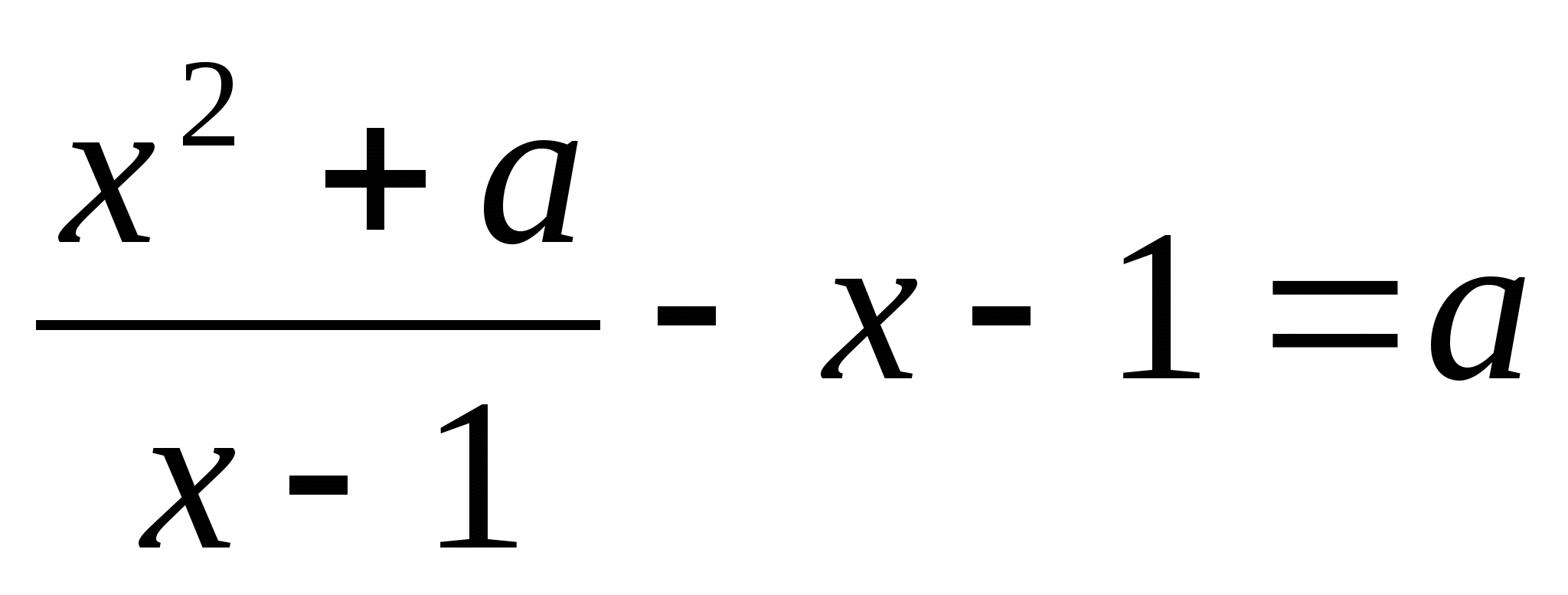8. При каких значениях параметра а среди корней уравнения
есть
корни, большие 1?
9. Найдите значения параметра а, при каждом из которых уравнение
имеет
положительный корень.
10. Найдите все значения параметра а, при которых уравнение
имеет
только один корень.
• 2. Квадратные уравнения.
1. 
;
2. 
;
3. 
.
4. При каких значениях параметра а уравнение 
имеет единственный корень?
5. При каких значениях параметра а уравнение 
не имеет решений?
6. Для всех значений параметра а решите уравнение 
.
7. Для всех значений параметра а решите уравнение 
.
8. Для каждого значения т решите уравнение: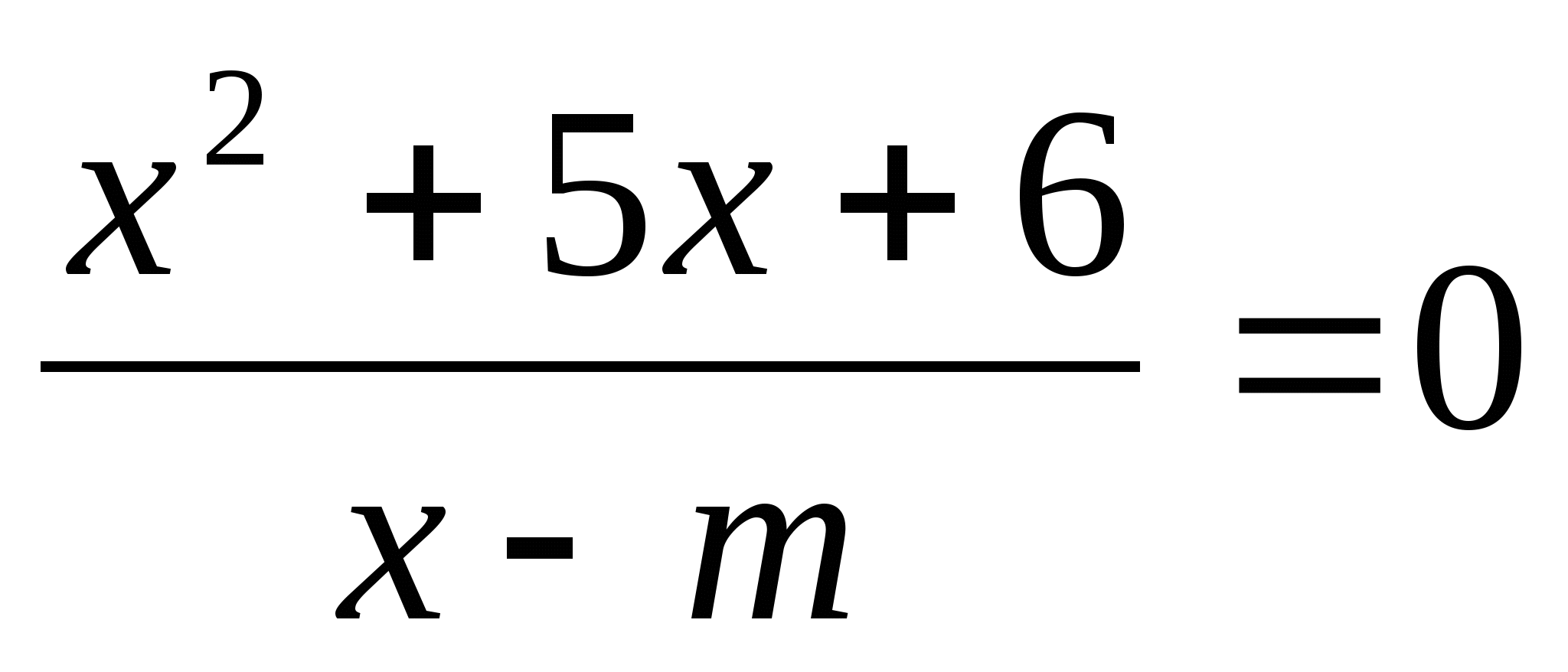 
.
9. Для каждого значения т решите уравнение: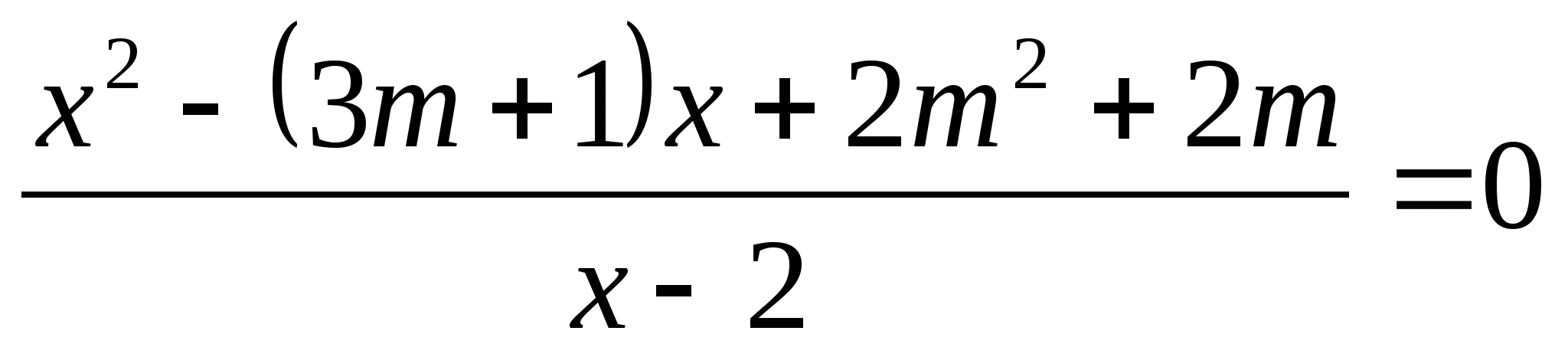 
.
10. Найдите значения k, при которых прямая у = kх - 8 и парабола у = х2 + 5х - k
имеют ровно одну общую точку.
• 3. Теорема Виета.
1. При каких значениях параметра а уравнение 
имеет действительные корни, сумма квадратов которых равна 4.
2. При каких значениях параметра а уравнение 
имеет действительные корни, произведение которых меньше 1.
3. При каких значениях параметра а уравнение 
имеет: а) корни разных знаков; б) корни одного знака; в) положительные
корни.
4. Дано уравнение 
. Известно, что сумма его корней
равна 4. Найдите произведение его корней и число р.
• 4. Расположение корней квадратного трехчлена
1. Найти все значения параметра а, при которых корни уравнения
имеют
разные знаки.
2. Найти все значения параметра b, при которых корни уравнения
меньше
1.
3. При каких значениях параметра а корни уравнения
положительны?
4. При каких значениях параметра а корни уравнения
заключены
в интервале (1; 3)?
5. При каких значениях параметра т корни уравнения
заключены
между числами -2 и 4?
6. При каких значениях параметра а уравнение 
имеет корни, удовлетворяющие неравенствам х1 < 1, х2 ≥ 2?
7. При каких значениях параметра а корни уравнения
лежат
на луче (−2; +∞)?
8. Найти все значения параметра а, при которых корни квадратного трехчлена
различны
и не больше а.
9. При каких значениях параметра а корни уравнения 
расположены по разные стороны от точки х = 1?
10. При каких значениях параметра а уравнение
имеет
различные корни х1 и х2 ,
удовлетворяющие неравенствам х1 ≤ 2 и х2 > 2?
11. При каких значениях параметра а уравнение 
имеет хотя бы один корень на луче (−∞; 2]?
• 5. Графический метод решения уравнений с параметрами
1. Сколько корней имеет уравнение 
а в зависимости от параметра а?
2. Сколько корней имеет уравнение 
а в зависимости
от параметра а?
3. Найти сумму значений параметра р, при которых уравнение
имеет
ровно 3 корня.
4. При каких значениях параметра а уравнение 
имеет более трех корней?
5. Задачи по планиметрии (10 ч)
• 1. Модуль «Геометрия». Анализ геометрических высказываний
1. Какие из следующих утверждений верны?
1) Если два угла одного треугольника равны двум углам другого треугольника, то
равны и третьи углы.
2) Тангенс любого острого угла меньше единицы.
3) У любой трапеции основания параллельны.
Ответ: 1 и 3.
2. Какие из следующих утверждений верны?
1) Площадь трапеции равна половине высоты, умноженной на разность
оснований.
2) Две окружности пересекаются, если радиус одной окружности больше
радиуса другой окружности.
3) Существует прямоугольник, диагонали которого взаимно перпендикулярны.
Ответ: 3.
3. Какие из следующих утверждений верны?
1) Любой прямоугольник можно вписать в окружность.
2) Отношение площадей подобных треугольников равно коэффициенту подобия.
3) Средняя линия трапеции равна сумме её оснований.
Ответ: 1.
4. Какие из следующих утверждений верны?
1) Площадь параллелограмма равна половине произведения его диагоналей.
2) Для точки, лежащей на окружности, расстояние до центра окружности равно
радиусу.
3) Сумма углов прямоугольного треугольника равна 90°.
Ответ: 2.
5. Какие из следующих утверждений верны?
1) Точка, равноудалённая от всех вершин треугольника, является центром
окружности, вписанной в этот треугольник.
2) Одна из высот прямоугольного треугольника всегда делит его на два
подобных треугольника.
3) Если основания трапеции равны 2 и 8, то средняя линия этой трапеции равна 5.
Ответ: 2 и 3.
6. Какие из следующих утверждений верны?
1) В любой ромб можно вписать окружность.
2) Угол, вписанный в окружность, равен соответствующему центральному углу,
опирающемуся на ту же дугу.
3) Смежные углы равны.
Ответ: 1.
7. Какие из следующих утверждений верны?
1) Через заданную точку плоскости можно провести единственную прямую.
2) Если диагонали выпуклого четырёхугольника равны и перпендикулярны, то
то это квадрат.
3) Две прямые, перпендикулярные третьей прямой, параллельны друг другу.
Ответ: 3.
8. Какие из следующих утверждений верны?
1) Биссектрисы треугольника пересекаются в центре вписанной в него
окружности.
2) Площадь ромба равна половине произведения его диагоналей.
3) В прямоугольном треугольнике гипотенуза равна сумме катетов.
Ответ: 1 и 2.
• 2. Задачи на 2 балла
1. Биссектрисы углов А и D параллелограмма АВСD пересекаются в точке,
лежащей на стороне ВС. Найдите ВС, если АВ = 30.
2. Окружность с центром на стороне АС треугольника АВС проходит через
вершину С и касается прямой АВ в точке В. Найдите диаметр окружности,
если АВ = 6, АС = 10.
3. Отрезки АВ и DC лежат на параллельных прямых, а отрезки АС и BD
пересекаются в точке М. Найдите МС, если АВ = 11, DC = 22, АС = 27.
4. Высота АН ромба АВСD делит сторону СD на отрезки DН = 15 и СН = 2.
Найдите высоту ромба.
5. Вершины треугольника делят описанную около него окружность на три дуги,
длины которых относятся как 1 : 2 : 3. Найдите радиус окружности, если
меньшая из сторон треугольника равна 17.
6. Точка Н является основанием высоты, проведенной из вершины прямого угла
В треугольника АВС к гипотенузе АС. Найдите АВ, если АН = 5, АС = 20.
7. Найдите боковую сторону АВ трапеции АВСD, если углы АВС и ВСD равны
соответственно 45° и 150°, а СD = 26.
8. Биссектрисы углов А и В при боковой стороне АВ трапеции АВСD
пересекаются в точке F. Найдите АВ, если АF = 24, ВF = 10.
9. Отрезки АВ и СD являются хордами окружности. Найдите расстояние от
центра окружности до хорды СD, если АВ = 18, СD = 24, а расстояние от
центра окружности до хорды АВ равно 12.
10. Окружность пересекает стороны АВ и АС треугольника АВС в точках К и
Р соответственно и проходит через вершины В и С. Найдите длину отрезка
КР, если АК = 14, а сторона АС в 2 раза больше стороны ВС.
11. Окружность, вписанная в треугольник АВС, касается его сторон в точках М,
К и Р. Найдите углы треугольника АВС, если углы треугольника МКР равны
42°, 62° и 76°.
• 3. Задачи на 3 балла
1. Известно, что около четырехугольника АВСD можно описать окружность и
что продолжения сторон АВ и СD четырехугольника пересекаются в точке
М. Докажите, что треугольники МВС и МDА подобны.
2. Основания ВС и АD трапеции АВСD равны соответственно 7 и 28, ВD = 14.
Докажите, что треугольники СВD и АDВ подобны.
3. Докажите, что отрезок, соединяющий середины оснований трапеции, делит её
на две равные по площади части.
4. Сторона АВ параллелограмма АВСD вдвое больше стороны ВС. Точка N -
середина стороны АВ. Докажите, что CN - биссектриса угла ВСD.
5. В выпуклом четырехугольнике АВСD углы DАС и DВС равны. Докажите, что
углы СDВ и САВ также равны.
6. В трапеции АВСD с основаниями АD и ВС диагонали пересекаются в точке
Р. Докажите, что площади треугольников АРВ и СРD равны.
7. Биссектрисы углов В и С трапеции АВСD пересекаются в точке О, лежащей
на стороне АD. Докажите, что точка О равноудалена от прямых АВ, ВС и СD.
8. Окружности с центрами в точках М и N пересекаются в точках S и Т, причем
точки М и N лежат по одну сторону от прямой SТ. Докажите, что МN
SТ.
9. Внутри параллелограмма АВСD выбрали произвольную точку Е. Докажите,
что сумма площадей треугольников ВЕС и АЕD равна половине площади
параллелограмма.
10. Высоты АА1 и СС1 остроугольного треугольника АВС пересекаются в точке
Е. Докажите, что углы АА1С1 и АСС1 равны.
• 4. Задачи на 4 балла
1. Биссектриса СМ треугольника АВС делит сторону АВ на отрезки АМ = 8 и
МВ = 13. Касательная к описанной окружности треугольника АВС, проходящая
через точку С, пересекает прямую АВ в точке D. Найдите СD.
2. Вершины ромба расположены на сторонах параллелограмма, а стороны ромба
параллельны диагоналям параллелограмма. Найдите отношение площадей ром-
ба и параллелограмма, если отношение диагоналей параллелограмма равно 44.
3. Две касающиеся внешним образом в точке К окружности, радиусы которых
равны 16 и 20, касаются сторон угла с вершиной А. Общая касательная к этим
окружностям, проходящая через точку К, пересекает стороны угла в точках В
и С. Найдите радиус окружности, описанной около треугольника АВС.
4. На стороне ВС остроугольного треугольника АВС (АВ ≠ АС) как на диаметре
построена полуокружность, пересекающая высоту АD в точке М, АD = 32,
МD = 24, Н - точка пересечения высот треугольника АВС. Найдите АН.
5. В равнобедренном треугольнике АВС стороны АВ = ВС = 10,
cosАВС = 
.
Найдите радиус окружности, вписанной в треугольник.
6. В равнобедренную трапецию с верхним основанием, равным 2, вписана
окружность радиуса 2. Найдите нижнее основание трапеции.
Список литературы
1. А.Г. Мордкович. Алгебра - 8 . Часть 1. Учебник. Мнемозина, 2013 год.
2. А.Г. Мордкович и др. Алгебра - 8. Часть 2. Задачник. Мнемозина, 2013 год
3. А.Г. Мордкович, Н.П. Николаев. Алгебра - 8. Учебник для классов с
углублённым изучением математики. Мнемозина, 2010 год.
4. Л.И. Звавич, А.Р. Рязановский. Алгебра - 8. Задачник для классов с
углублённым изучением математики. Мнемозина, 2010 год.
5. А.Г. Мордкович. Алгебра - 9 . Часть 1. Учебник. Мнемозина, 2013 год.
6. А.Г. Мордкович и др. Алгебра - 9. Часть 2. Задачник. Мнемозина, 2013 год
7. А.Г. Мордкович, Н.П. Николаев. Алгебра - 9. Учебник для классов с
углублённым изучением математики. Мнемозина, 2009 год.
8. Л.И. Звавич, А.Р. Рязановский, П.В. Семёнов. Алгебра - 9. Задачник для
классов с углублённым изучением математики. Мнемозина, 2009 год.
9. М.Л.Галицкий, А.М.Гольдман, Л.И.Звавич. Сборник задач по алгебре. 8 - 9
классы. М.: Просвещение, 2010 год.
10. Л.С. Атанасян и др. Геометрия. 7 - 9. Просвещение, 2010 год.
11. Л.С. Атанасян и др. Геометрия. Дополнительные главы к учебнику
8 класса. Пособие для классов с углублённым изучением математики.
Москва, «Вита - Пресс», 2010 год.
12. Л.С.Атанасян и др. Геометрия. Дополнительные главы к учебнику
9 класса. Пособие для классов с углублённым изучением математики.
Москва, «Вита - Пресс», 2010 год.
13. Математика. 9 класс. Подготовка к ОГЭ-2015. Учебно-тренировочные тесты
по новой демоверсии. / Под ред. Ф.Ф.Лысенко, С.Ю.Кулабухова. - Ростов-на-
-Дону: Легион, 2015.
14. Е.Г.Коннова. Математика. 9 класс. Подготовка к ГИА. Задания с параметром:
теория, методика, упражнения и задачи. / Под редакцией Ф.Ф.Лысенко,
С.Ю.Кулабухова. Ростов-на-Дону, Легион, 2014.