Разработка Один из способов доказательства первого признака подобия треугольников в рамках учебника «Геометрия 7- 9» А.В. Погорелова для 8 класса (8 класс)

_{Один из способов доказательства первого признака подобия треугольников в рамках учебника «Геометрия 7- 9» А.В. Погорелова для 8 класса}

_{Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники подобны.}

_{Доказательство. I этап. Пусть у и имеются два равных угла: и. По теореме о сумме углов треугольника: . Таким образом, мы получили, что , и . Для доказательства подобия осталось установить, что .}

_{II этап. Положим, что является наибольшим в . Это мы можем сделать всегда, обозначив вершину наибольшего угла треугольника буквой С. Правда, может оказаться, либо , тогда для определённости мы всё равно выбираем .}

_{Опустим из вершины С высоту СМ. Тогда разбивается на и . Они прямоугольные, так как , поскольку СМ является высотой.}

_{Так как , то является наибольшим в . Опустим из вершины высоту . Тогда разбивается на и . Они прямоугольные, так как , поскольку является высотой.}

_{Почему мы опускали высоту из вершины наибольшего угла? А потому, что только в этом случае высота будет находится внутри треугольника, а не снаружи, и, следовательно, будет разбивать треугольник на два прямоугольных.}

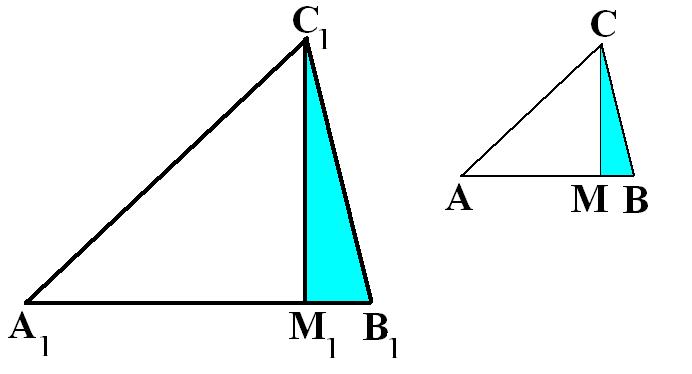
_{III этап. Рассмотрим и . По определению косинуса угла в прямоугольном треугольнике:}

_{и и}

_{Заметим, что . Из теоремы о сумме углов треугольника заключаем, что}

_{По теореме - косинус угла зависит только от градусной меры угла и не зависит от расположения треугольника и его линейных размеров - получаем}

_{Рассмотрим и . По определению косинуса угла в прямоугольном треугольнике:}

_{и и}

_{Заметим, что . Из теоремы о сумме углов треугольника заключаем, что}

_{По той же теореме получаем}

_{IV этап. В итоге получаем четыре равенства}

₁₎₃₎

₂₎₄₎

_{Перемножим левые и правые части равенств 1) и 2) соответственно}

_{т. е. Разделим обе части на : Умножим теперь обе части этого равенства на :т. е.}

_{Умножив обе части равенств 3) на и 4) на соответственно, получим равенства и Отсюда следует, что и Складывая левые и правые части этих равенств почленно, получим . Так как и , тогда , и следовательно,}

_{Таким образом, . Что и требовалось доказать.}

3