Теория по применению производной для исследования функции

Теория по применению производной для исследования функции

Всегда применяем формулу k = tga = f'().

1 тип задач. Дан график функции и касательная, проведенная к нему в точке .

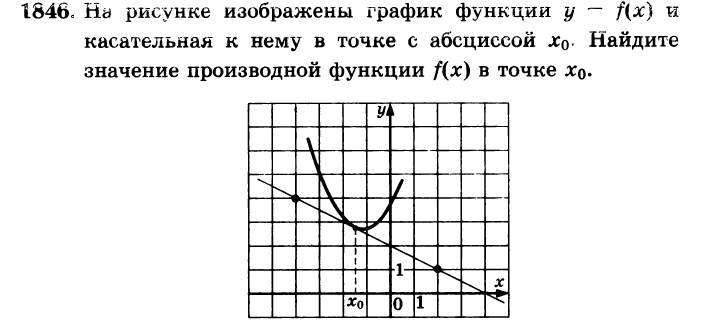
Алгоритм решения

1. На графике находим прямоугольный треугольник, в котором касательная является гипотенузой.

2. Определяем вид угла (острый или тупой) между касательной и положительным направлением оси Ох (если угол острый, то тангенс - положительный, если угол тупой, то тангенс - отрицательный).

3. Вычисляем тангенс этого угла (тангенс - это отношение противолежащего катета к прилежащему катету).

4. Это и есть значение производной в данной точке.

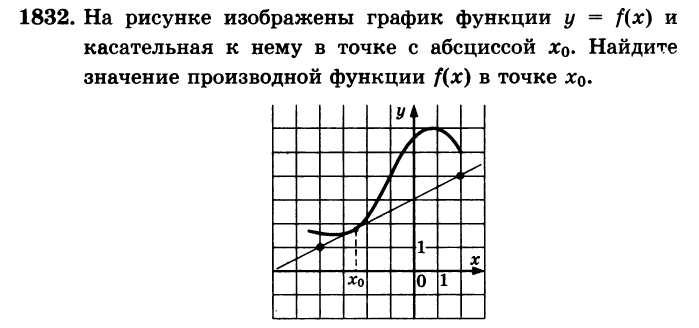
2 тип задач. Дан график функции.

Всегда применяем формулу k = tga = f'().

Алгоритм решения

1. Касательная параллельна прямой у = 0х - 5, значит их угловые коэффициенты равны к = 0, tgα = 0, α = 0, касательная параллельна оси Ох в точках максимума и минимума функции.

2. Находим количество этих точек. Их 7.

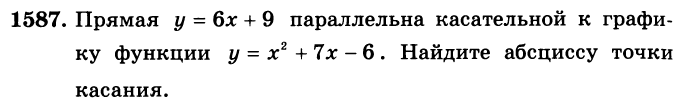
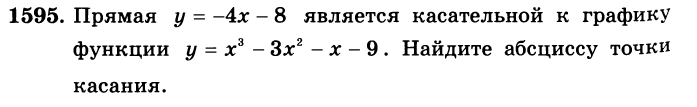
Алгоритм решения

1. Прямая параллельна касательной у=6х+9, значит их угловые коэффициенты равны к = 6.

2. Находим производную у'.

3. Решаем уравнение у'= 6.

4. Решение этого уравнения и будет ответом.

3 тип задач. Дан график производной.

Всегда применяем формулу k = tga = ƭ'().

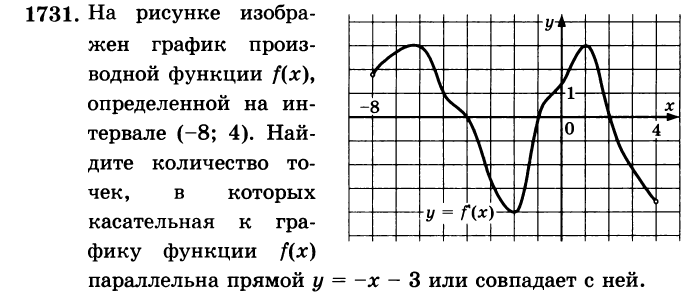
Алгоритм решения

1. Касательная параллельна прямой у = -х - 3, значит их угловые коэффициенты равны к = -1.

2. Строим прямую у = -1, пересекающую график производной.

3. Находим количество точек их пересечения. Их 3.

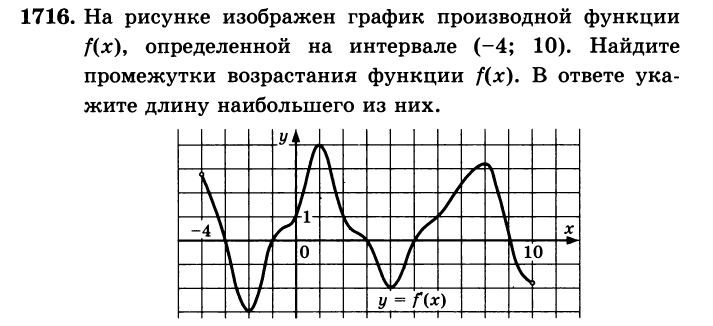
Алгоритм решения

1. Если f' > 0 на [а;в], то f(x) возрастает, если f'< 0 на[а;в], то f(x) убывает на этом отрезке.

2. f(x) возрастает на (-4;-3], [-1;3], [5;9]. Находим их длины (количество клеток).

3. Ответ: 4.

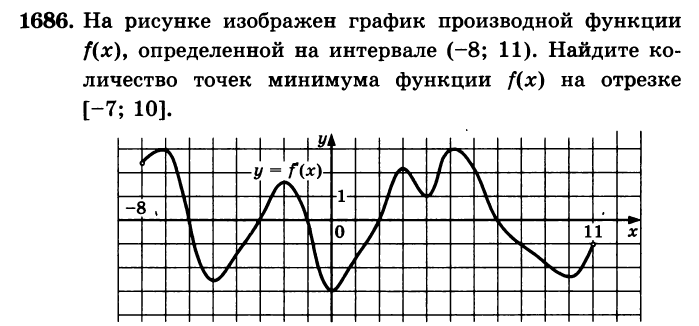
Алгоритм решения

1. На графике производной точки минимума и максимума расположены на оси Ох.

2. Если производная меняет знак с (-) на (+), то это точка минимума, если производная меняет знак с (+) на (-), то это точка максимума.

3. Это -3, 2. Их количество 2.

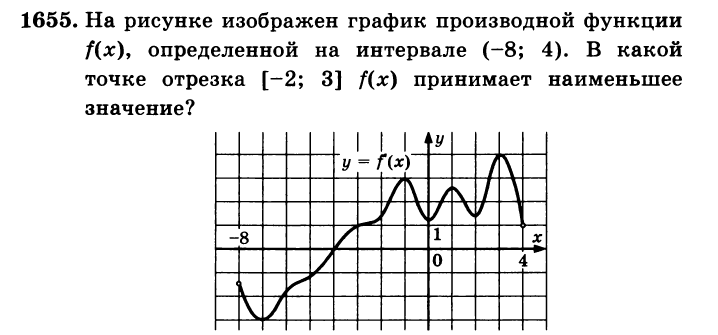
Алгоритм решения

1. На [-2;3] f'(х) > 0, значит f(х) возрастает и поэтому свое наименьшее значение она принимает в левом конце отрезка при х = -2.

2. Ответ: - 2.

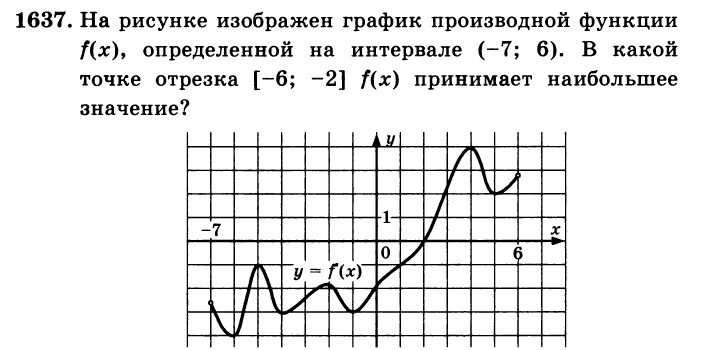
Алгоритм решения

1. На [-6;-2] f'(х)0, значит f(х) убывает и поэтому свое наибольшее значение она принимает в левом конце отрезка при х = -6.

2. </<font face="Times New Roman, serif">Ответ: - 6.