- Учителю
- 'Преобразование тригонометрических выражений' урок в 9 классе
'Преобразование тригонометрических выражений' урок в 9 классе
Алгебра- 9 класс
Учитель Бабаченко Лидия Петровна
Тема : Преобразование тригонометрических выражений
Информационная карта урока :
Цель :
1)Обучающая : Систематизировать и обобщить знания о тригонометрических выражениях
2)Развивающая : Развивать вычислительные навыки, развитие нестандартного и творческого мышления
3) Воспитательная : содействовать повышению интереса к уроку, формировать навыки самоконтроля и взаимоконтроля, повышать уровень коммуникативной компетенции
Тип: обобщение
Вид урока : практикум
Конструирование урока : на основе модульной технологии
Технология: элементы уровневой дифференциации, критического мышления, личностно-ориентированного обучения, элементы технологии тестового контроля.
Методы: частично - поисковый, исследовательский, практический, самостоятельная работа.
Форма контроля: самоконтроль, взаимоконтроль, контроль со стороны учителя
ТСО: интерактивное оборудование
Пояснительная записка.
Место урока в образовательной области и предмете:
- урок по алгебре в 9-м классе,
Профиль школы, класса. Урок разработан для обучающихся общеобразовательной школы.
Принцип отбора содержания учебного материала: содержание отобрано в соответствии с возрастными и психологическими особенностями обучающихся.
Материально-техническое обеспечение урока.
-
компьютер;
-
интерактивная доска;
Структура урока :
I. Организационный момент- 3мин
-
Мотивация учебной деятельности через осознание учащимися практической значимости применяемых знаний и умений , сообщение темы урока, цели и задач урока. Актуализация знаний учащихся -10 мин
-
Осмысление содержания практических и самостоятельных действий при выполнении заданий на уроке -16 мин
-
Самостоятельное выполнение заданий - тест/ 8 мин
-
Систематизирование , обобщение и подведение итогов выполненных самостоятельных заданий -3 мин
-
Подведение итога урока и инструктаж домашнего задания -5 мин
-
Резерв
Ход урока
-
Организационный момент
Временный интервал 3 мин
-
Проверяется подготовленность учащихся к уроку. Приветствие
-
Мотивация
ІІ. Здравствуйте! Озвучивается тема, цель и задачи урока.
-
Тема урока « Преобразования тригонометрических выражений » Мы с вами сегодня свой урок начнем с « Путешествия по Казахстану» .....
1) Блиц-опрос . Хочу обратить ваше внимание, ребята,
все факты, связанные с тригонометрией не нужно запоминать наизусть, а достаточно понимать, где искать их на числовой окружности
Вопрос №1:
Назовите формулы перевода градусной меры угла в радианную и радианной меры угла в градусую
Ответ : ![]() -градусная мера
-градусная мера ![]() , а- радианная мера
, а- радианная мера ![]()
Задание №2:
Установите соответсвие между частями фраз, стоящих в левой и правой колонках , чтобы получилось определение.
Синусом угла ![]() называется
называется
Косинусом угла ![]() называется
называется
Тангенсом угла ![]() называется
называется
Котангенсом угла ![]() называется
называется
Отношение ординаты точки А к ее абсциссе
Отношение ординаты точки В к длине ее радиуса
Отношение абсциссы точки В к ее ординате
Отношение абсциссы точки В к длине ее радиуса
Ответ :
Синусом угла ![]() называется
называется
Косинусом угла ![]() называется
называется
Тангенсам угла ![]() называется
называется
Котангенсом угла ![]() называется
называется
Отношение ординаты точки А к ее абсциссе
Отношение ординаты точки В к длине ее радиуса
Отношение абсциссы точки В к ее ординате




Отношение абсциссы точки В к длине ее радиуса
Вопрос №3
Назовите область определения и область значения функции У= sin ![]()
Ответ :
Область определения от ![]() ,а область значения
,а область значения ![]()
Задание №4
Укажите стрелками какой четверти принадлежит угол ![]() , если:
, если:
І четверть
![]()
![]()
ІІ четверть
![]()
ІІІ четверть
![]()
ІV четверть
![]()
Ответ :
І четверть
ІІ четверть
ІІІ четверть
ІV четверть
![]()
![]()
![]()
![]()
![]()


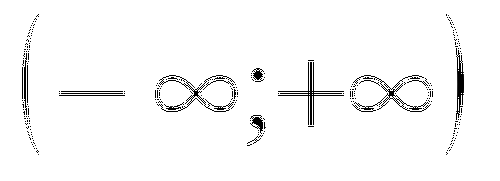
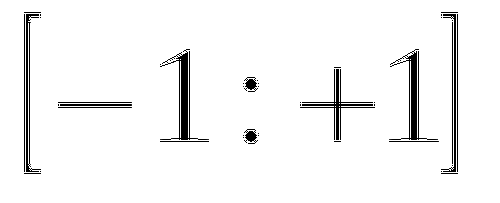

Вопрос №5
Какие тригонометрические функции являются четными и нечетными
Ответ :
Четная функция - косинус, а нечетные функции :синус, тангенс, котангенс
Задание №6
Допишите основные тригонометрические тождества :
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Ответ :
![]()
![]()
![]()
![]() 1+
1+![]()
![]()
![]()
![]() 1
1
![]()
![]()
Ш . Решение задач
№1 задача
Упростить выражение:
1) ![]()
Ответ :
1) ![]()
![]() =
=
![]()
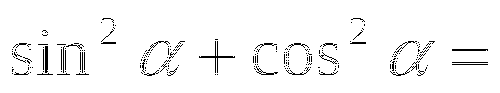
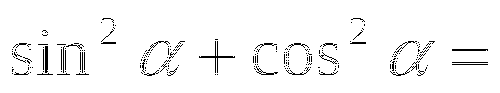
Задача №2
Упростить выражение:
1) ![]()
О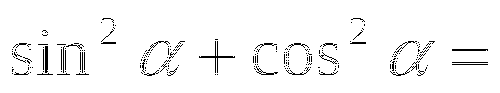
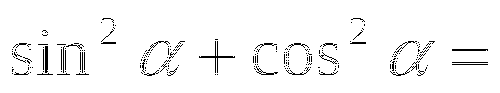
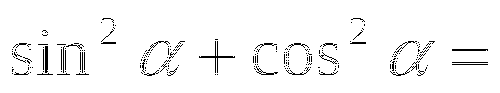
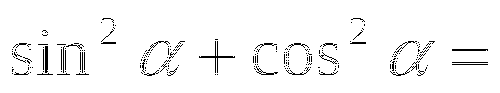 твет
твет
1) ![]()
![]()
-Спасибо ! Молодцы!
Задача №3
![]() , если
, если ![]() наити
наити ![]() f(x)-
f(x)-
Ответ :
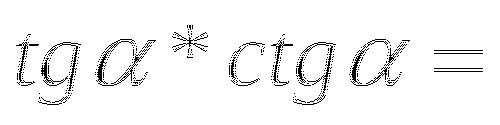
Задача №4
Упростить выражение: ![]()
Ответ :
![]()
![]()
Задача №5
![]() ,
,![]() . Найти значения
. Найти значения ![]()
Ответ : По условию задачи угол ![]() принадлежит к ІІ четверти , значит знак косинуса (-).
принадлежит к ІІ четверти , значит знак косинуса (-).
По ( 1) формуле находим
![]() -
-
![]()
2) ![]()
Ребята, для решения некоторых тригонометрических примеров вовсе не обязательно пользоваться формулами . Можно использовать прямоугольный треугольник и четко знать определения синуса, косинуса, тангеса, котангенса.
Например:
1. tg ![]() =
=![]() ,
, ![]()
Sin ![]() -?
-?
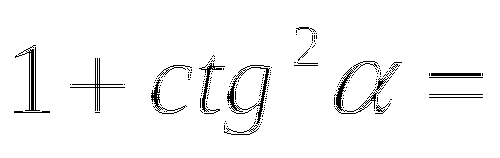 Используем определение синуса острого угла
Используем определение синуса острого угла
17 прямоуголь ного треугольника , что это есть
8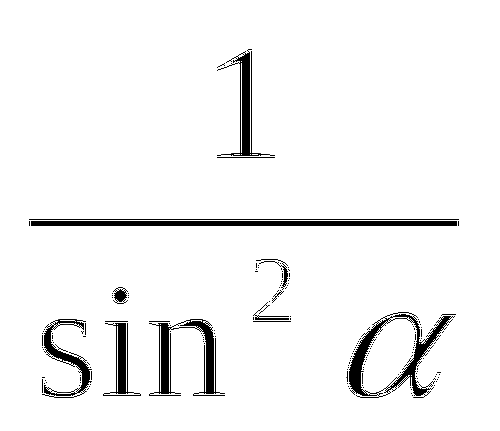 отношение противолежащего катета
отношение противолежащего катета
к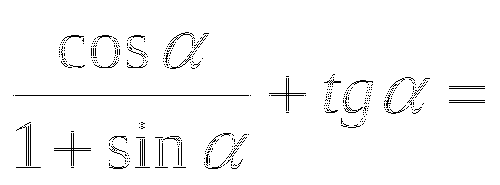 гипотенузе, а так же ,
гипотенузе, а так же ,
15 α что синус в третьей четверти
отрицательный, получим:
, Sin ![]()
![]()
I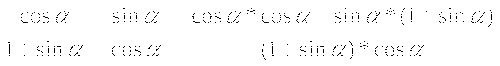 V . Самостоятельное выполнение учащимися заданий под контролем учителя
V . Самостоятельное выполнение учащимися заданий под контролем учителя
Учитель : -Сейчас вам ,ребята, будут заданы тестовые задания. И отвечая на каждый ответ, вам еще предстоит отметить задания)
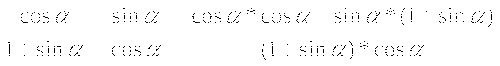 ( -не требует повторения ,знаю хорошо)
( -не требует повторения ,знаю хорошо)
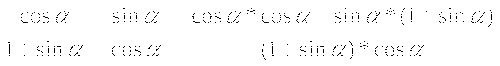
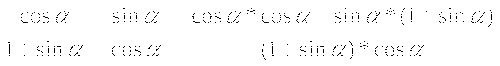 ( ) -нужно напомнить на следующем уроке способ деятельности, еще раз обсудить)
( ) -нужно напомнить на следующем уроке способ деятельности, еще раз обсудить)
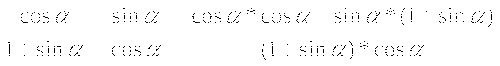
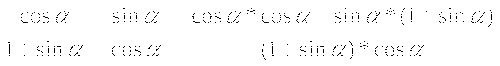
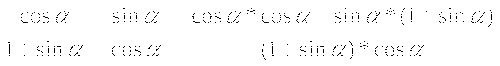 ( -трудно, хочу решить подобную задачу в классе)
( -трудно, хочу решить подобную задачу в классе)
Тест
№
Задания
Ответы
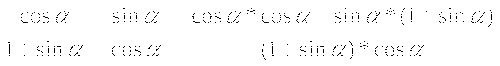
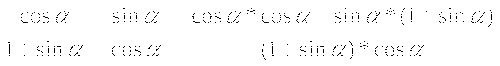
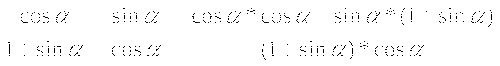
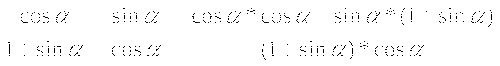
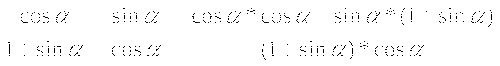
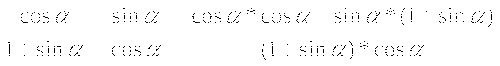
1
800 какой четверти относится
А) I B)II C)III D)IV
2
Значение Cos 600
А) ![]() B)
B)![]() C)
C)![]() D)
D)![]()
3
Какая из чисел больше нуля
А) sin1500B)cos 1200 C) sin 600 D)cos 500
4
Если ![]() ,
,![]() то найти
то найти ![]()
А) ![]() B)
B)![]() C)0 D)1
C)0 D)1
5
Упростить выражение: ![]()
А) ![]() B)0 C)
B)0 C) ![]() D) 2
D) 2
V. Обобщение и систематизация выполненных заданий
Учитель: -Ребята при выполнении таких упражнений, как вы видите, вам нужно не только запомнить определения, или же знаки тригонометрических функций , но и использовать формулы при преобразовании тригонометрических выражений.
Всем известно ,что через 2 года вы все будете сдавать ЕНТ. Оказывается, значения синусов и косинусов углов « находятся» на ладони .
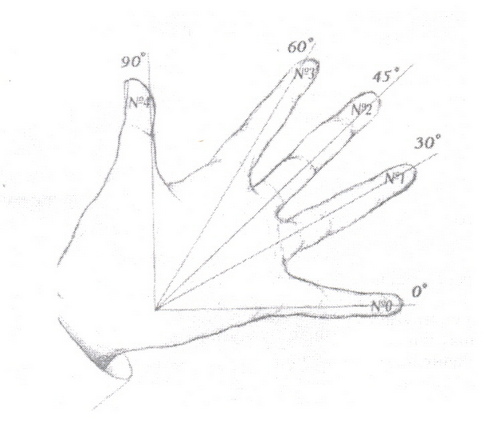
Рассмотрим правило нахождения синусов:
На пересечений мизинца и большого пальца находится бугор Луны. Измерим углы между пальцами ( пальцы развести как можно сильнее). Угол между мизинцем и безымянным пальцем - 300, угол меджу мизинцем и средним пальцем- 450, угол между мизинцем и указательным пальцем- 600, угол между мизинцем и большим пальцем-900 и это у всех людей без исключения. Если пальцы считать лучами, исходящими из бугра Луны на ладони, то, если совместить пальцы с мизинцем, угол между лучами будет 00 т.е. можно считать, что направление мизинца соответствует началу отсчета углов, т.е. 00. Введем нумерацию пальцев:
Мизинец-№0 соответствует 00
Безымянный -№1 соответствует 300
Средний-№2 соответствует 450
Указательный -№3 соответствует 600
Большой- №4 соответствует 900
Нужно запомнить формулу :
![]() половина квадратного корня из номера (n)пальца
половина квадратного корня из номера (n)пальца
/А, для косинуса берем обратное/
правильные ответы
№
Ответы
1
А
2
А
3
В
4
А
5
С
VI. Подведение итогов урока и инструктаж домашнего задания
-Учитель : А теперь, запишите задание, которое вы сами опираясь на те знания и навыки ,которые вы сегодня получили на уроке
Выполните дома :
1. Повторение теоретического материала/ определении, формулы/
2. А №301
В № 304
С №328
Вопрос учителя: - Ребята, какое у вас сложилось мнение об уроке и что еще вы хотели бы узнать в последующих уроках?
Ответ: /Рассказ учащихся о работе в классе, группы и своей деятельности/