Решение систем уравнений с двумя неизвестными как математические модели реальных ситуаций 9 класс

Долхонова В.В. МБОУ «Еланцынская СОШ»

Урок по алгебре

Класс: 9

Тема: «Решение систем уравнений как математические модели реальных ситуаций»

Цели урока:

Обучающие:

1. Продолжать работу по формированию навыков решения задач с помощью систем уравнений второй степени.

2. Закрепить знания решения систем уравнений второй степени аналитическим способом (способ подстановки)в ходе решения задач.

3. решать задания, которые наиболее часто встречаются на «ГИА».

Развивающие:

1. использование для достижения поставленной задачи уже полученные знания;

2. умение обосновывать свои рассуждения;

Воспитательные:

1. выработка желания и потребности обобщать полученные факты;

2. воспитание настойчивости и терпения при выполнении заданий.

3. Побуждать учеников к самоконтролю, воспитывать интерес к математике.

Оборудование: проектор, ПК

Прогнозируемый результат:

1. Знать способы и методы решения систем уравнений второй степени.

2. Уметь правильно отбирать способы решения систем уравнений второй степени для решения задач с помощью систем уравнений.

Эпиграф:

1.Китайская мудрость: « Я слышу - я забываю, я вижу - запоминаю,

я делаю - я усваиваю».

2. «Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их!»

Д. Пойа

План урока:

1. Организационный момент.

2. Математический диктант.

3. Объяснение материала

4. Закрепление материала

5. Подведение итога урока.

6. Домашняя работа

Ход занятия

1. Организационный момент

1. Проверка подготовленности учащихся к занятию.

2. Приветствие учителя и учащихся.

3. Постановка целей и задач занятия.

Прочитайте высказывание математика Д. Пойа. Какой совет дает ученый нам? Мудрость высказывания математика Д.Пойа объедините с предыдущей темой и сформулируйте тему урока.

Сегодня мы познакомимся с задачами, решение которых сводится к

системам уравнений. Запишем тему урока. Назовите цель урока.

Мотивация (самоопределение) к учебной деятельности.

- Работать сегодня мы будем коллективно, в парах и индивидуально.

Вспомните правила работы в парах. (Прислушиваться к мнению соседа, работать дружно, помогать друг другу). В конце урока каждый из вас оценит свою работу и работу партнёра.

2.Математический диктант

Перед вами лежат задания математического диктанта, выполните его.

1вариант.

Составьте уравнение с двумя переменными, если:

1. Сумма двух натуральных чисел равна 16.

2. Периметр прямоугольника равен 12 см.

3. Одна сторона прямоугольника на 8 см больше другой.

4. Произведение двух натуральных чисел равно 28.

5. Диагональ прямоугольника равна 5 см.

2 вариант

Составьте уравнение с двумя переменными, если:

1. Разность двух натуральных чисел равна 14.

2. Площадь прямоугольника равна 26 см².

3. Катет прямоугольного треугольника на 5 см больше другого.

4. Сумма квадратов двух натуральных чисел равна 30.

5. Гипотенуза прямоугольного треугольника равна 8 см.

На экране проецируются ответы и критерии оценивания.

Ребятам в парах предлагается проверить и оценить работу друг друга.

Объяснение материала

При решении задач с помощью системы уравнений придерживаемся следующего алгоритма: (слайд)

I. Составление математической модели:

1. Внимательно изучить условие задачи:

2. Какой процесс описывается в задаче?

3. Какими величинами характеризуется этот процесс?

4. Как связаны между собой эти величины?

5. Значения, каких величин требуется найти?

6. Обозначить буквами искомые величины;

7. Выразить искомые величины через данные;

8. Составить уравнения и из них соответствующую систему;

II. Работа с математической моделью:

Найти решение системы;

III. Ответ на вопрос задачи:

Проверить, какие из решений системы удовлетворяют условиям задачи.

Алгоритм решения задачи дать каждому ученику.

Задача 1. Прямоугольный газон обнесен изгородью, длина которого 40 м. Площадь газона 96 . Найдите длины сторон газона.

I этап:

Составим выражения по данным задачи, пусть a и b -длины сторон, тогда 2(a+b)=40 будет периметр газона, площадь газона выразим как . По данным выражениям составим систему уравнений и найдем решения данной системы.

II этап:

III этап: обе пары чисел удовлетворяют условию задачи.

Ответ: 12 м и 8м

После решения задачи необходимо ещё раз объяснить ход решения и поинтересоваться у учащихся, понятно ли им данное решение. Так же необходимо заметить, что в некоторых случаях целесообразно создавать геометрические модели для лучшего восприятия условия задачи. Чаще всего такие модели составляются к задачам на движение, которые нам еще предстоит решать.

2. Закрепление материала

Выполнение заданий на карточках:

Задача 2. Гипотенуза прямоугольного треугольника равна 13 см. Один из катетов на 7 см больше другого. Найдите катеты прямоугольного треугольника.

I этап:

Пусть катеты равны x и y, составляем 1 уравнение. По теореме Пифагора составляем 2 уравнение. Методом подстановки:

II этап:

III этап : По смыслу задачи пара чисел -5 и -12 не могут быть решением системы

Ответ: 12 см и 5 см.

Взаимопроверка решения задачи в парах. После этого решение проецируется на экран.

Задача 3. Произведение двух положительных чисел равно 96. Одно из них на 4 больше другого. Найдите эти числа.

I этап:

Пусть 1 число - x, 2 число - у.

x>0 и y>0

II этап:

III этап: По смыслу задачи исключаем числа - 8 и - 12

Ответ: 12 и 8.

Также взаимопроверка в парах.

Теперь решим задачу №7.2 коллективно.

Расстояние между двумя пунктами по реке составляет 14 км. Лодка проходит этот путь по течению за 2 часа, против течения - за 2 часа 48 минут. Найдите скорость лодки в стоячей воде и скорость течения реки.

Решение:

I этап:

Вспомним уравнение прямолинейного равномерного движения:

S - расстояние,

V - скорость,

T - время.

Переведем 2 часа 48 минут в часы, это составит

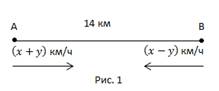
Пусть x км/ч - скорость лодки в стоячей воде, y км/ч - скорость течения реки. Вспоминаем движение по течению и против течения реки. Составим математическую модель.

Составим таблицу:.

S, км

V, км/ч

T, ч

По течению

14

Против течения

14

II этап:

Решим полученную систему.

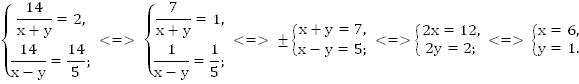
III этап:

Ответ: 6 км/ч; 1 км/ч.

Подведение итогов занятия

1.Обсуждение успешности достижения целей занятия.

2.Оценивание работы учащихся

</ Разъяснение дом. задания - №№ 7.6 и 7.12