Открытый урок по теме:Способы решения квадратных уравнений.

Тема урока: «Способы решения квадратных уравнений».

1.Организационный момент.

Цели для учащихся определяются вместе с учителем.

- Здравствуйте, ребята, садитесь. Начинаем наш урок с организационного момента. Приводим в порядок свое рабочее место и настраиваемся на рациональную и плодотворную работу.

Тема нашего урока: «Способы решения квадратных уравнений». Сегодня на уроке мы вспомним различные способы и методы решения квадратных уравнений, научимся рационально их использовать. Достаточно часто перед вами будут вставать вопросы:

- Как выбрать способ решения квадратного уравнения?

- Какой из способов решения квадратных уравнений наиболее рациональный? - на эти и другие вопросы мы сегодня попробуем дать ответы.

Цели и задачи организационного момента:

ПУУД: подготовка учащихся к восприятию темы урока,

РУУД: создание условий для освоения регулятивных универсальных учебных действий: воспитание внимания, развитие навыков ответственного отношения к собственной деятельности, уважение к старшим и друг к другу.

Методы организации работы учащихся на начальном этапе урока:

- беседа, нацеливающая на подготовку рабочего места и самоорганизацию учащихся;

- постановка проблемных вопросов;

Мотивация настроя учеников на учебную деятельность:

- объяснение роли организационного этапа урока;

- постановка цели перед классом на этот этап урока;

- нацеленность на осмысленный результат самоорганизации в начале урока.

Мотивация настроя на предмет и тему урока:

- актуализация знаний;

- объяснение, зачем следует научиться решать квадратные уравнения рациональными способами.

2. Актуализация знаний (проверка домашнего задания).

Учитель:

- Переходим к следующему этапу урока - актуализации знаний. Какие цели стоят перед каждым из Вас на этом этапе урока?

Ответы восьмиклассников:

- повторить основные понятия, способы и методы решения квадратных уравнений;

- продемонстрировать свои знания по данной теме.

Цели, которые учитель ставит перед собой на данном этапе урока:

Предметные цели: выяснить степень усвоения обучающимися изучаемого материала.

Для достижения предметной цели необходимо решить соответствующие задачи:

- повторить основные понятия, связанные с квадратными уравнениями;

- познакомиться с историей развития квадратных уравнений.

- проверить знание теоретического материала, умение решать квадратные уравнения стандартными способами.

Метапредметные цели и задачи:

ПУУД: создать условия для развития навыков самостоятельной познавательной деятельности;

РУУД: научить детей контролировать, корректировать свои действия;

ЛУУД: научиться выражать собственное мнение

I. Вопросы и задания для фронтального опроса:

1. Дайте определение квадратного уравнения.

2. Какие вы знаете виды квадратных уравнений?

3. Какое уравнение называют неполным квадратным уравнением?

4. Какое уравнение называют приведённым квадратным уравнением?

5. Сколько корней может иметь квадратное уравнение?

6. Отчего зависит количество корней полного квадратного уравнения?

7. Даны квадратные уравнения:

1) х²-6х-16=0; 4) х²-2х-24=0;

2) х²-2х+24=0; 5) х²+6х-16=0;

3) х²-10х+25=0; 6) х²-6х=0.

Назовите, уравнение, в котором:

а) сумма корней равна 6, а произведение равно -16;

б) один из корней равен 6;

в) корни равны.

II.Тест с элементами поисково-творческого задания (каждому правильному ответу соответствует определенная буква, поэтому правильное выполнение теста поможет найти ключевое слово урока):

6) Найдите разность наибольшего и наименьшего из корней уравнения .

а)

б)

т)

к) 0

е) 8

м) -8

2) Выберите лишнее:

7) Какое из уравнений рационально решать, используя теорему Виета:

а)

б)

в)

г)

м)

н)

с)

3) Решите уравнение: .

8) Какое уравнение является дробно-рациональным:

и)

к)

о)

в)

т)

д)

4) Реши уравнение: .

9) Найдите область допустимых значений (ОДЗ):

р) 0 и -3

ё) 2 и 6

ж) 3 и -2

в)

к)

л)

5) Найдите произведение корней (или корень, если он единственный) уравнения .

10) Найдите корни уравнения:

ч) -9

п) 9

р) 0

о) 2 и 5

п) корней нет

я) -2 и -5

-Ребята, выполнив тест, выпишите в одну строку все буквы, соответствующие правильному ответу. Какое слово вы получили?

Учащиеся выполняют задание и читают получившееся слово:

- ТВОРЧЕСТВО.

- Как вы думаете, почему именно это слово является ключевым к нашему уроку?

- Наверное, потому, что нам нужно будет учиться творчески подходить к решению квадратных уравнений.

- Совершенно верно! Итак, творчество и сотрудничество - девиз нашего урока.

Методы, способствующие решению поставленных целей и задач:

- фронтальный опрос-беседа по теоретическому материалу;

- выполнение теста с последующей проверкой;

- деление класса на группы на предыдущем уроке, предложение творческих заданий;

- распределение обязанностей в группе.

Критерии достижения целей и задач данного этапа урока:

- освоение теоретического материала подтверждают правильные ответы на вопросы учителя и выполнение теста (получение ключевого слова «творчество»).

3. Обобщение и систематизация знаний.

- Переходим к следующему этапу урока - обобщение и систематизация знаний.

Постановка конкретной учебной цели перед учащимися выполняется совместно с учителем.

Учитель:

- На прошлом уроке класс был разделен на несколько групп. Каждая группа получила домашнее задание:

Историки: собрать материал об истории возникновения и способах решения квадратных уравнений;

Теоретики: собрать материал о видах и способах решения квадратных уравнений;

Практики: показать практическое применение различных методов решения квадратных уравнений;

Исследователи: провести сравнительный анализ изученных способов решения.

- Ребята, как вы думаете, какая цель стоит перед Вами на данном этапе урока?

- Познакомиться с результатами деятельности творческих групп.

- Обсудить услышанные сообщения…

- Повторить различные способы и методы решения квадратных уравнений…

- Систематизировать и обобщить их.

- Какой, по вашему мнению, результат должен быть достигнут Вами на данном этапе урока?

- Повторить способы и методы решения квадратных уравнений, научиться выбирать наиболее рациональный способ.

Цели и задачи, которых учитель планирует достичь на данном этапе урока:

Предметные цели: выяснить степень усвоения изучаемого материала, умение анализировать, систематизировать полученные знания.

Для достижения предметной цели необходимо решить соответствующие задачи: проверить выполнение творческих заданий и обсудить их с учащимися (презентации); показать многообразие методов решения квадратного уравнения и их рационального использования.

Метапредметные цели и задачи

ЛУУД: освоение навыков самореализации (для тех, кто приготовил сообщения); воспитание творческого отношения обучающихся к тем видам деятельности, которые они выполняют;

РУУД: научить детей ставить перед собой учебную цель, планировать свои действия;

ПУУД: научить анализировать и систематизировать полученные знания; осуществлять поиск и отбор учебного материала; ориентироваться в информационном пространстве;

КУУД: уметь работать в команде, планировать деятельность, вести диалог; воспитывать уважение к одноклассникам - умение слушать.

Методы, способствующие решению поставленных целей и задач:

-презентации творческих работ;

- учебный диалог.

Критерии достижения предметных целей:

- восьмиклассники подготовили и представили в виде презентаций интересный материал по изучаемой теме.

Методы стимулирования и мотивации:

- создание ситуации успеха;

- словесные поощрения;

- получение баллов в оценочный лист.

Сообщения учащихся о результатах работы в группах (презентации).

1. Сообщение первой группы - историков.

Первые упоминания о способах решения уравнений, которые мы сейчас называем квадратными, относятся ко второму тысячелетию до н.э. - это эпоха расцвета Вавилонии и Древнего Египта. В IX веке узбекский математик Аль-Хорезми в трактате "Алгебра" классифицирует квадратные уравнения. Все это время отличные по записи уравнения считались различными. Не было единого подхода к их решению. И только в XVI веке французский юрист, тайный советник короля Франции и математик Франсуа Виет впервые вводит в обращение буквенные обозначения не только для неизвестных величин, но и для данных, то есть коэффициентов уравнения. Тем самым он заложил основы буквенной алгебры. Общее правило решения квадратных уравнений, приведенных к единому каноническому виду +вх+с=0, было сформулировано в Европе лишь в 1544г. Штифелем. В древней Индии были распространены публичные соревнования в решении трудных задач. В одной из старинных индийских книг говорится по поводу таких соревнований следующее: «Как солнце блеском своим затмевает звезды, так ученый человек затмит славу другого в народных собраниях, предлагая и решая алгебраические задачи». Задачи часто облекались в стихотворную форму. Задача знаменитого индийского математика XII века Бхаскары звучит так:

Обезьянок резвых стая, всласть поевши, развлекалась.

Их в квадрате часть восьмая на полянке забавлялась.

А двенадцать по лианам стали прыгать, повисая.

Сколько ж было обезьянок, ты скажи мне, в этой стае?

Ответить на этот вопрос и на многие другие нам помогут квадратные уравнения. «Уравнение - это золотой ключ, открывающий все математические сезамы».

Решение задачи Бхаскары:

Пусть было x обезьянок, тогда на поляне их забавлялось - .

Уравнение:

+ 12 = х; - 64х = - 768, - 64х += - 768 + , = 256,

(х-32)=16 или (х-32)=-16

=48, =16.

2. Выступление теоретиков. Методы решения квадратных уравнений.

1.Неполные квадратные уравнения:

2. Общая формула решение квадратного уравнения, записанного в стандартном виде.

Выражение вида D=b²-4ac называют дискриминантом квадратного уравнения.

если D>0, то уравнение имеет два корня;

если D=0, то уравнение имеет один корень;

если D<0, то уравнение не имеет корней.

Формулы корней квадратного уравнения: ;

3.Формула решения квадратного уравнения с четным вторым коэффициентом: ax²+2кx+с=0; .

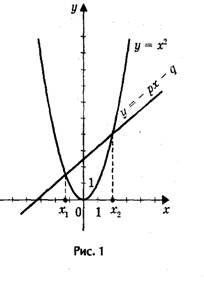
4.Графическое решение квадратного уравнения:

Если в уравнении x²+px+q=0 перенести второй и третий члены в правую часть, то получим: x²= -px-q.

Построим графики зависимости у =x² и у = - px - q. Абсциссы точек пересечения графиков функций являются корнями уравнения.

5. Метод выделения полного квадрата.

Пример:

х² + 2х - 48 = 0;

(х + 1)² - 49 = 0; (х + 1)² = 49;

х + 1 = 7 или х + 1 = -7

6, = -8.

6. Метод разложения на множители.

+ 10х - 24 = 0.

+ 10х - 24 = + 12х - 2х - 24 = х(х + 12) - 2(х + 12) = (х + 12)(х - 2).

Следовательно, уравнение можно переписать так:

(х + 12)(х - 2) = 0

Левая часть уравнения обращается в нуль при х = 2, а также при х = - 12. Это означает, что числа 2 и - 12 являются корнями уравнения + 10х - 24 = 0.

3. Результаты работы исследователей. Зависимость между коэффициентами и корнями квадратного уравнения.

Устные способы решения квадратных уравнений:

1.Теорема Виета: сумма корней приведённого квадратного уравнения x²+px+q=0, + = -p, а произведение корней = q - свободному члену уравнения. В общем случае, то есть для не приведённого квадратного уравнения: ax²+вx+с=0+=, =.

Используя эту теорему, можно решать некоторые квадратные уравнения устно.

2.Если в квадратном уравнении a+b+c=0,то один из корней равен 1, а второй по теореме Виета равен с/а.

2х² + 5х - 7 = 0: а+b+с= 0, =1. == -3,5.

3.Если в квадратном уравнении a+c=b,то один из корней равен -1,

а второй по теореме Виета равен - с/а.

2х² +5х +3 = 0: а-b+с=0, =-1. ==-1,5.

4.Метод «переброски» старшего коэффициента:

Суть метода состоит в то, что корни квадратных уравнений

ax² + bx + c = 0 и y²+by+ac=0 связаны соотношениями:х₁= у₁/а и х₂ = у₂/а. В некоторых случаях удобно решать сначала не данное уравнение

ax² + bx + c = 0, а приведенное y²+by+ac=0,которое получается из данного "переброской" коэффициента а, а затем разделить найденные корни на а для нахождения корней исходного уравнения.

Рассмотрим квадратное уравнение: аx² + bх + с = 0, где а ≠0. Умножая обе его части на а, получаем уравнение: x²+ аbх + ас = 0. Пусть ах = у, откуда х = у/а; тогда приходим к уравнению y²+by+ac=0, равносильно данному. Его корни у₁и у₂ найдем с помощью теоремы Виета. Окончательно получаем:

х₁= у₁/а и х₂ = у₂/а. При этом способе коэффициент а умножается на свободный член, как бы «перебрасывается» к нему, поэтому его называют способом «переброски». Этот способ применяют, когда можно легко найти корни уравнения, используя теорему Виета и, что самое важное, когда дискриминант есть точный квадрат.

Пример: решите уравнение: 2х²-9х-5=0. Заменим приведенным квадратным уравнением с "переброской" коэффициента а: у²-9у-10=0, по теореме, обратной теореме Виета, подбором найдем корни: у₁ =10 и у₂ =-1,

вернемся к корням исходного уравнения: х₁= у₁/а и х₂ = у₂/а,

х₁= 10/2=5 и х₂ = -1/2=-0,5. Ответ: 5; -0,5.

4.Исследовав знаки приведенного квадратного уравнения, мы пришли к следующим выводам:

Знаки коэффициентов Знаки корней

a > 0, b>0, c<0 Разные: больший по абсолютной

величине - отрицательный;

a > 0, b<0, c<0 Разные: больший по абсолютной

величине - положительный.

a > 0, b>0, c > 0 Одинаковые: оба отрицательные.

a> 0, b < 0, c > 0 Одинаковые: оба положительные.

Обсуждение прослушанных сообщений:

- Ребята, Вам понравились выступления одноклассников?

- Что Вы узнали нового?

- Мы достигли поставленных целей? Вы вспомнили все способы решения квадратных уравнений?

- Какой из них Вам показался наиболее интересным?

- Вспомните, каким способом решена задача знаменитого индийского математика XII века Бхаскары?

4. Закрепление.

Учитель:

- Переходим к следующему этапу урока - применение знаний и умений в новой ситуации.

Постановка конкретной учебной цели перед учащимися выполняется совместно с учителем.

- Ребята, как вы думаете, какая цель стоит перед вами на этом этапе урока?

- Научиться правильно решать квадратные уравнения различными способами.

- Какой результат должен быть достигнут вами на данном этапе урока?

- Научиться выбирать наиболее рациональные способы решения.

Цели и задачи, которые ставит перед собой учитель на данном этапе урока.

Предметные цели и задачи:

-научить решать уравнение разными способами;

- научить выбирать наиболее рациональный способ решения;

- применять полученные знания на практике.

Метапредметные цели и задачи:

- освоение умений анализировать, сравнивать, обобщать, делать выводы;

-развивать внимание, грамотную математическую речь;

- уметь работать в команде, планировать деятельность, вести диалог.

Личностные УУД:

- развивать навыки ответственного отношения при работе в группе;

- воспитывать чувство толерантности.

Формы организации учебной работы: групповая, индивидуальная.

Методы деятельности:

- словесные методы: беседа, учебный диалог;

- игровые методы;

- работа в группах.

Критерии определения уровня внимания и интереса:

- учащиеся заинтересованно и активно работают в группах;

- обсуждают учебные вопросы;

- проявляют взаимоуважение;

- охотно участвуют в презентации ответа.

Методы мотивации учебно-познавательной деятельности:

- выполнение интересных заданий;

-игра;

- создание условий для сотрудничества;

- взаимное выставление оценок, повышение собственного статуса;

- создание ситуации успеха, педагогической поддержки, похвалы, поощрения;

- возможность набрать баллы и получить хорошую оценку.

Методы оценивания: оценочный лист.

Критерии оценивания:

за каждый правильный ответ в тесте 1 балл (максимум 10 б.);

за каждый правильный ответ по обсуждаемым вопросам 1 балл (макс. 10 б.)

за участие в творческом отчете (презентация) 6 баллов;

за решение квадратного уравнения одним способом 1 балл (макс. 8 баллов);

за победу в игре 1 балл.

Дальнейшая работа проводится в группах, однако каждый член группы выбирает свой способ решения, затем идет взаимопроверка и совместное выставление оценок в оценочный лист.

Последующее обсуждение способов решения уравнений проводится у доски и завершается выбором наиболее рационального.

Задание 1. Для каждого уравнения выбрать наиболее рациональный способ решения (свой выбор обосновать):

1. х² - 12х = 0; 4) 313х² + 326х + 13 = 0;

2. 15х² - 22х - 37 = 0; 5) 4х² + 20х + 25 = 0;

3. 3х² +11х +6 = 0; 6) 3х²- 18х + 15 = 0.

Учащиеся, выбравшие наиболее рациональный способ, демонстрируют его применение на доске.

Задание 2. Девизом к следующему виду работы пусть послужат слова великого математика У. Сойера: «Человеку, изучающему алгебру, часто полезнее решить одну и ту же задачу тремя различными способами, чем решить три-четыре различные задачи. Решая одну задачу различными методами, можно путем сравнений выяснить, какой из них короче и эффективнее. Так вырабатывается опыт».

Решить уравнение: х² +4х - 5 = 0:

1. методом выделения полного квадрата;

2. методом разложения на множители;

3. по общей формуле;

4. графически;

5. по теореме обратной теореме Виета;

6. по сумме коэффициентов.

Задание 3. Игра «Домино». Каждая команда получает пять карточек. Выигрывает та из них, которая первой сложит их в правильном порядке. Каждый член победившей команды получает дополнительный балл в оценочный лист.

После выполнения заданий восьмиклассники приступают к заполнению оценочного листа с учетом критериев оценивания.

«5» 24- 35 баллов; «3» 8- 15 баллов;

«4» 16 - 23 баллов; «2» менее 8 баллов.

Подсчитывают набранные баллы и ставят оценки за урок.

Учитель:

- Итак, подведем итог сегодняшнего урока. Что нового Вы сегодня узнали на уроке?

- Ответы учащихся.

- Какие открытия для себя сделали?

-…

- Какие методы решения квадратных уравнений Вы запомнили?

- …

- Достигли ли Вы поставленной цели? - Да, достигли.

- Подводя итог уроку, я прошу вас заполнить анкету:

1. На уроке я работал активно/пассивно

2. Своей работой на уроке я доволен/не доволен

3. Урок мне показался коротким/длинным

4. За урок я не устал/устал

5. Моё настроение стало лучше/стало хуже

6. Материал урока мне был понятен/ не понятен

полезен/бесполезен

интересен/скучен

Задание на дом:

Цели, которые учитель ставит перед учащимися:

- развивать навыки саморегуляции, умения организовать самостоятельную учебную деятельность в домашних условиях;

- развивать творческое отношение к выполняемой деятельности, стремление сделать работу рационально и эффективно.

Цели и задачи, которые ставит перед собой учитель на данном этапе урока:

- развивать умение обучающихся анализировать свои решения, намечать перспективу на будущее; способность дать оценку успешности достижения цели;

- создать условия для развития навыков рефлексии - способности осознавать и оценивать свои мысли и действия, соотносить результат деятельности с поставленной целью, определять своё знание и незнание.

1. Решить квадратное уравнение х²-2х-8=0 различными способами (не менее пяти - шести). Указать наиболее рациональный способ.

Оценочные листы и анкеты учащиеся сдают учителю.

Оценочный лист

Учени__ 8_____класса

________________________________________

Максимальный

балл

Баллы

учащегося

1.

Ответы на обсуждаемые вопросы

10

2.

Тест

10

3.

Презентация

6

4.

Решение уравнений

8

5.

Игра

1

Итого

35

Оценка: «5» - 24- 35 баллов; «4» - 16 - 23 баллов; «3» - 8- 15 баллов;

«2» менее 8 баллов.