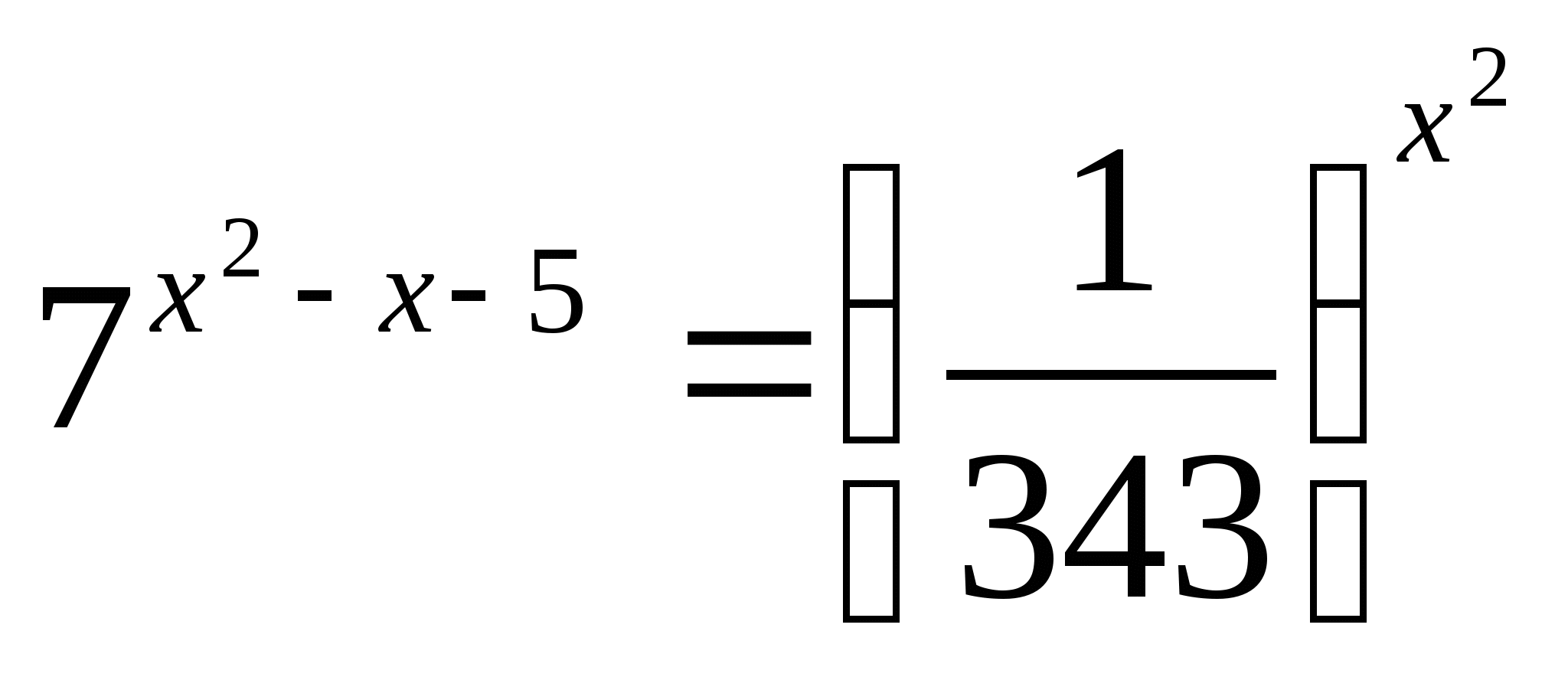7


  • Учителю
  • Урок по теме Решение показательных уравнений и неравенств

Урок по теме Решение показательных уравнений и неравенств

Автор публикации:
Дата публикации:
Краткое описание:
предварительный просмотр материала





Тема: Решение показательных уравнений



Цели урока:

  • Обобщение и систематизация знаний и умений учащихся по теме «Решение показательных уравнений»; формирование умения применять полученные знания при решении задач; создание условий для осознанного усвоения темы, применения полученных знаний на практике.

  • Воспитывать аккуратность, внимательность чувство гордости за свои успехи в математике. Уверенность в своих силах.

  • Развитие самостоятельности при выполнении конкретных заданий, развитие навыков работы в группе.



Тип урока: урок обобщения и систематизации знаний и умений учащихся.

Форма проведения урока: урок практикум.

Формы работы на уроке: устная работа, самостоятельная работа, групповая работа.

Оборудование: доска, проектор, компьютер, карточки с заданиями.



План поведения урока:



  1. организационный этап 1мин.

  2. подготовительный этап 7 мин.

  3. основной этап 26 мин.

    1. Выполнение теста 8 мин.

    2. Работа в группах 11 мин.

    3. Защита заданий у доски 7 мин

  4. итог урока 6 мин.





Ход урока:

I этап: организационный этап.

Цель этапа: создать благоприятную обстановку в классе. Психологически подготовить учеников к предстоящему уроку.



Деятельность



Кто сегодня отсутствует? (отметить отсутствующих)

- Здравствуйте.



II этап: подготовительный этап.

Цель этапа: организовать и целенаправить познавательную деятельность учащихся через актуализацию знаний по данной теме, мотивацию учащихся на работу на уроке

Деятельность



- Верно. Сегодня на уроке мы так же продолжим изучать данную тему. Откройте тетради, запишите в тетрадях число и тему урока «Решение показательных уравнений»

- Попробуйте сформулировать основные цели, стоящие перед нами на сегодняшнем уроке.





- Правильно. Действительно, сегодня на уроке мы будем продолжать учиться решать показательные уравнения и определять по виду уравнения способ его решения.

- И наш урок я хотела бы начать со следующих слов:

Развитие и образование ни одному

человеку не могут быть даны или сообщены.

Всякий, кто желает к ним приобщиться,

должен достигнуть этого собственной

деятельностью, собственными силами,

собственным напряжением.

А. Дистервег (на слайде 2)



- Прежде, чем начинать решать уравнения, давайте с вами немного повторим. (На слайдах вопросы - затем ответы).

1) Какая функция называется показательной?

2) Назовите промежутки монотонности показательной функции.

3) Что называется уравнением?

4) Что значит решить уравнение?

5) Что называется корнем уравнения?

6) Какое уравнение называется показательным?

7) Перечислите основные способы решения показательных уравнений.



- Молодцы.





- Решение показательных уравнений.

- записывают в тетради число и тему урока.

- Закрепит умение решать различные виды показательных уравнений, используя уже известные алгоритмы.



























1.Функция, содержащая переменную в показателе степени, называется показательной.

2. При основании a>1 функция возрастает, а при 0<a<1 функция убывает.

3. Уравнение - это равенство, содержащее неизвестную величину, значение которой нужно найти.

4.Решит уравнение - это значит найти его корни или доказать, что их нет.

5. Корень уравнения - это значение неизвестной величины, при котором равенство не теряет смысл.

6. Уравнение, содержащее переменную в показателе степени, называется показательным

7. Графический, вынесение общего множителя за скобки, введение новой переменной, сведение к одному основанию.













III этап: основной.

Цель этапа: формирование умения применять полученные знания при решении показательных уравнения, формирования умения работать в группе..



Вариант 1

  1. Показательной является функция:

А) y=x; Б) Урок по теме Решение показательных уравнений и неравенств; В) Урок по теме Решение показательных уравнений и неравенств

Г) среди предложенных вариантов нет верных.



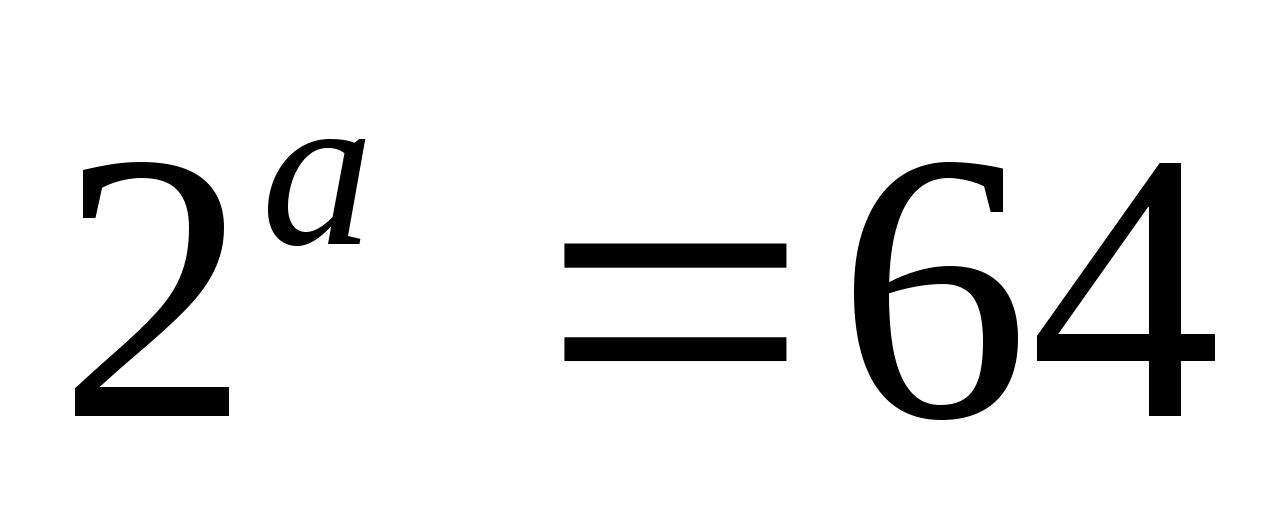  1. Корнем уравнения Урок по теме Решение показательных уравнений и неравенств является число…

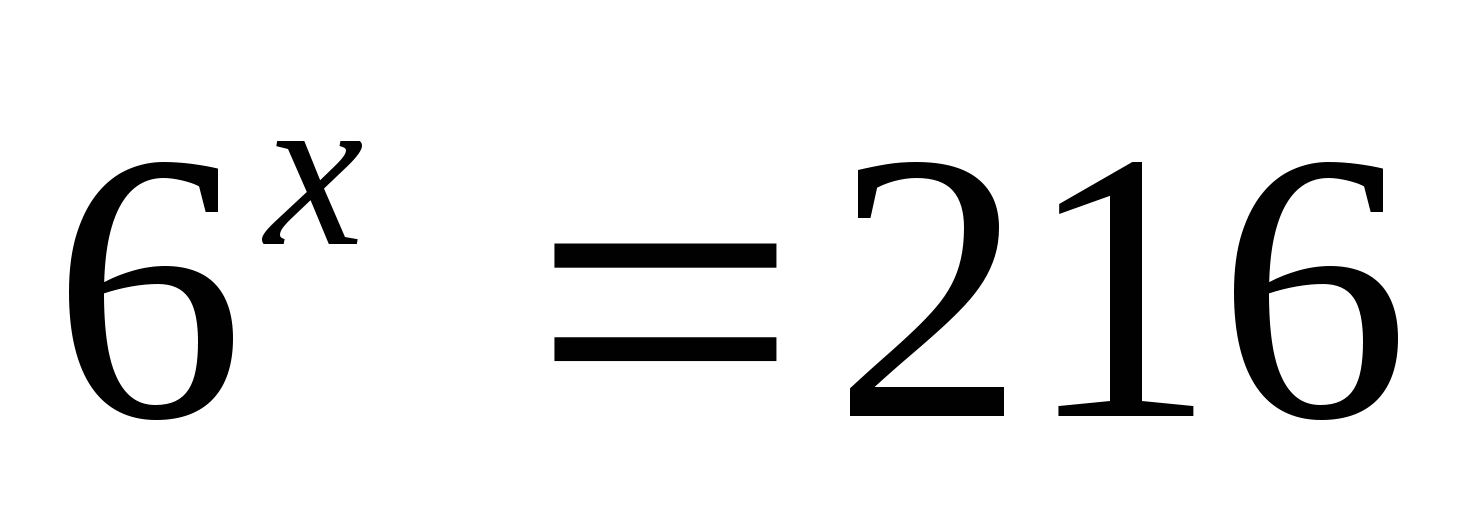  2. Корнем уравнения Урок по теме Решение показательных уравнений и неравенств является число …

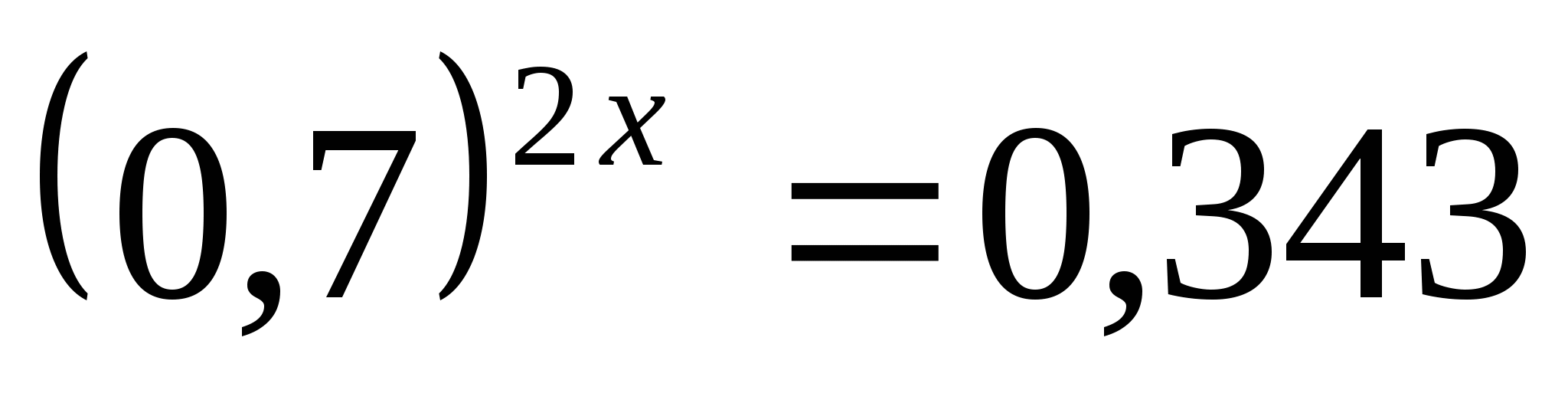  3. Корнем уравнения Урок по теме Решение показательных уравнений и неравенств является число …

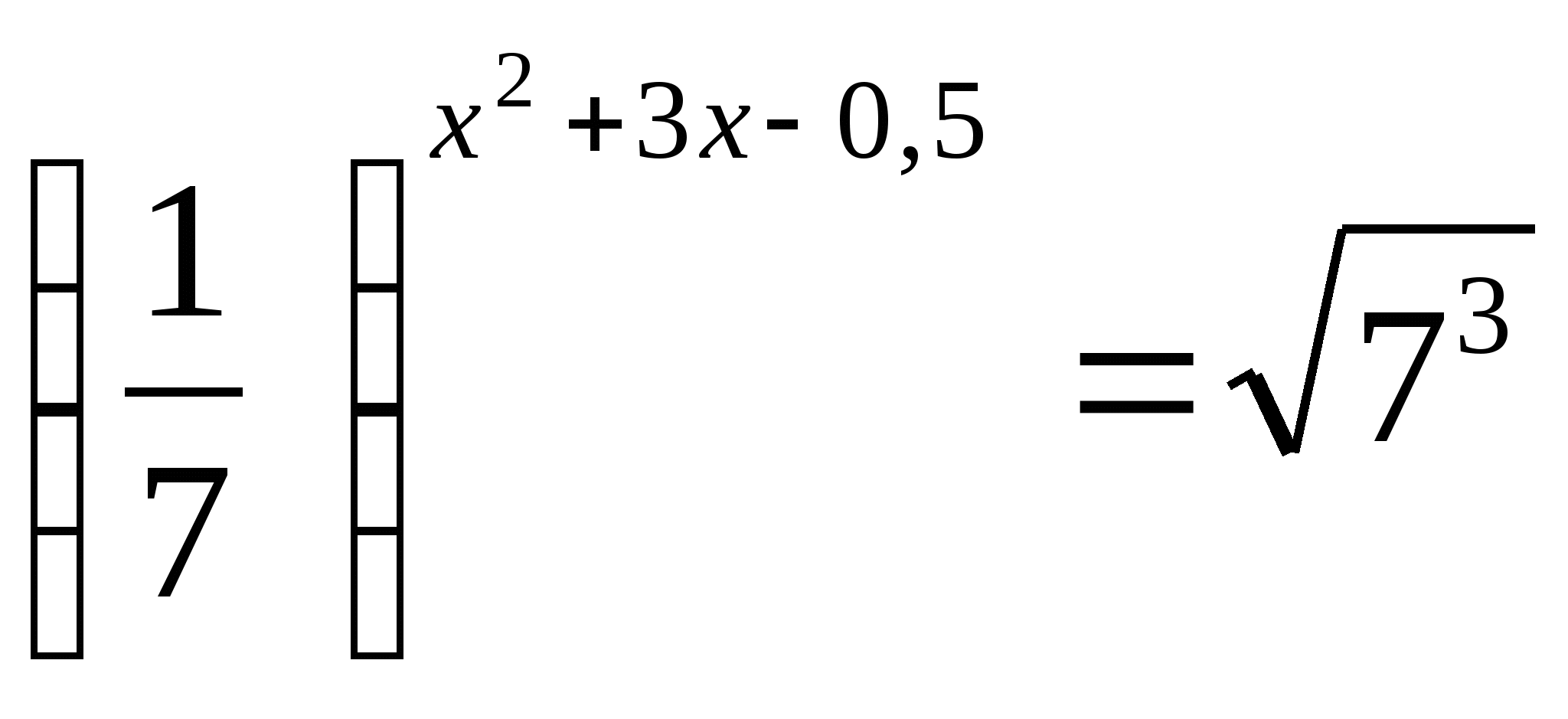  4. Корнем уравнения Урок по теме Решение показательных уравнений и неравенств является число …

6. Функция Урок по теме Решение показательных уравнений и неравенств при Урок по теме Решение показательных уравнений и неравенств является

а) не убывающей

б) убывающей

в) не возрастающей

г) возрастающей

Вариант 2

  1. Показательной является функция:

А) y=x; Б) Урок по теме Решение показательных уравнений и неравенств; В) Урок по теме Решение показательных уравнений и неравенств

Г) среди предложенных вариантов нет верных.



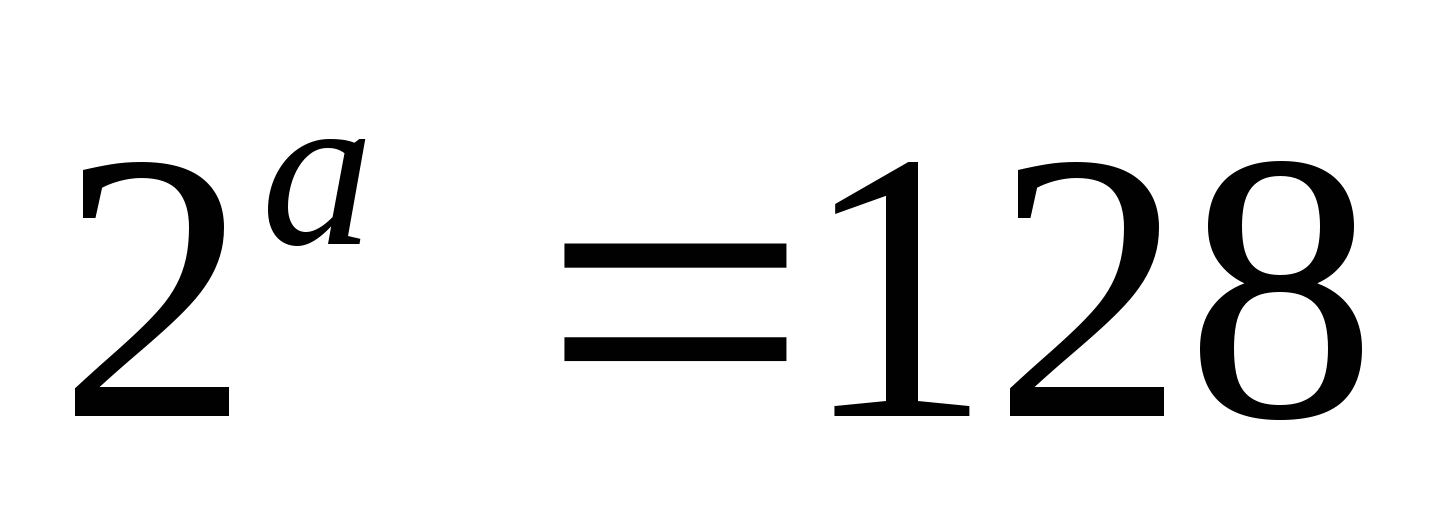  1. Корнем уравнения Урок по теме Решение показательных уравнений и неравенств является число…

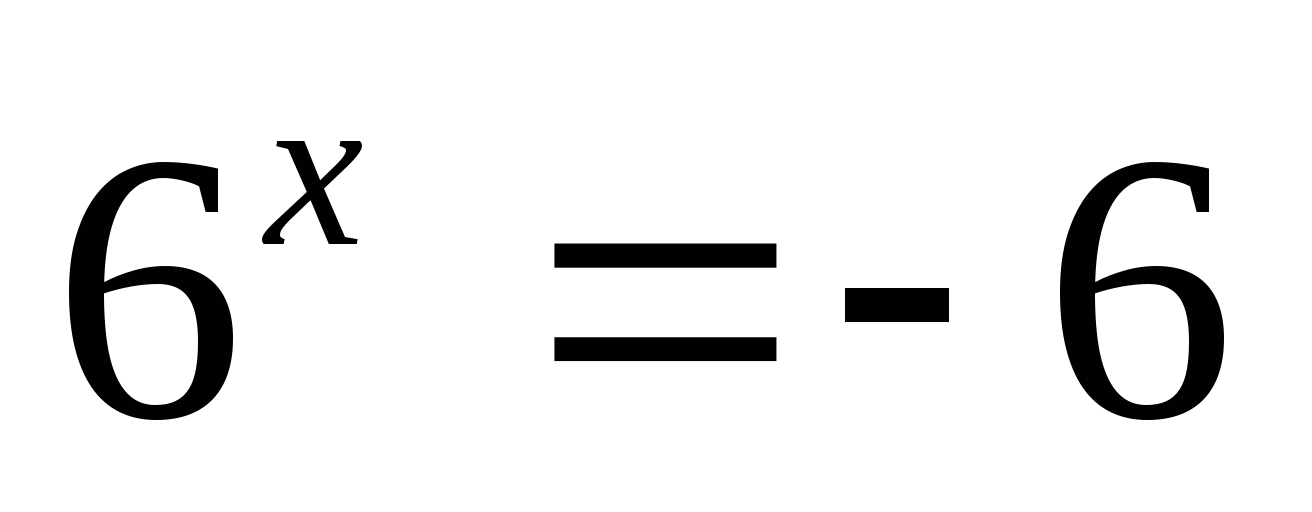  2. Корнем уравнения Урок по теме Решение показательных уравнений и неравенств является число …

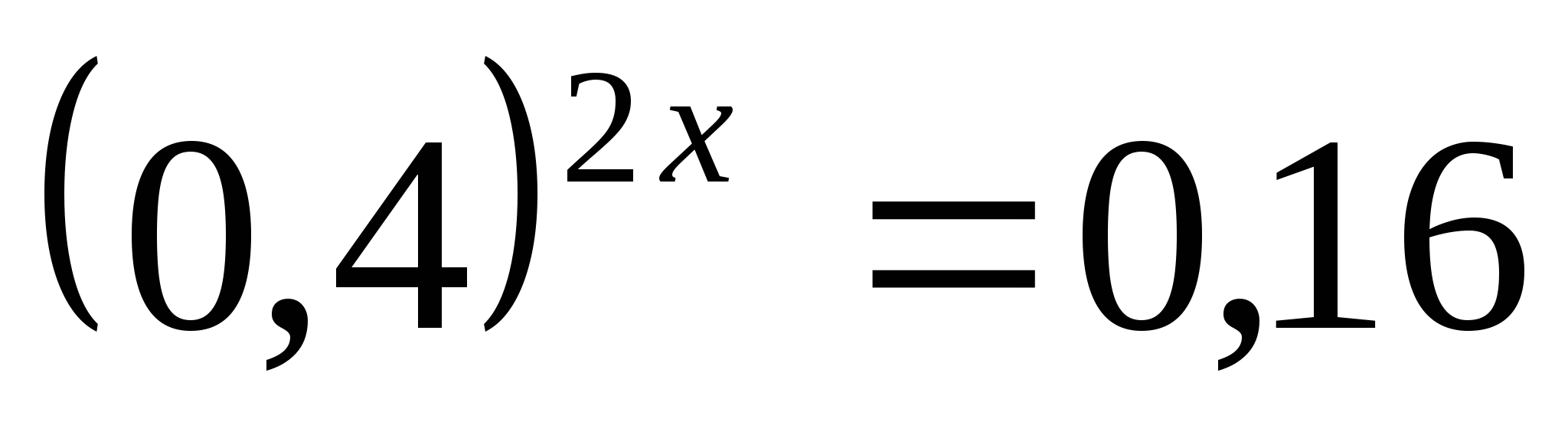  3. Корнем уравнения Урок по теме Решение показательных уравнений и неравенств является число …

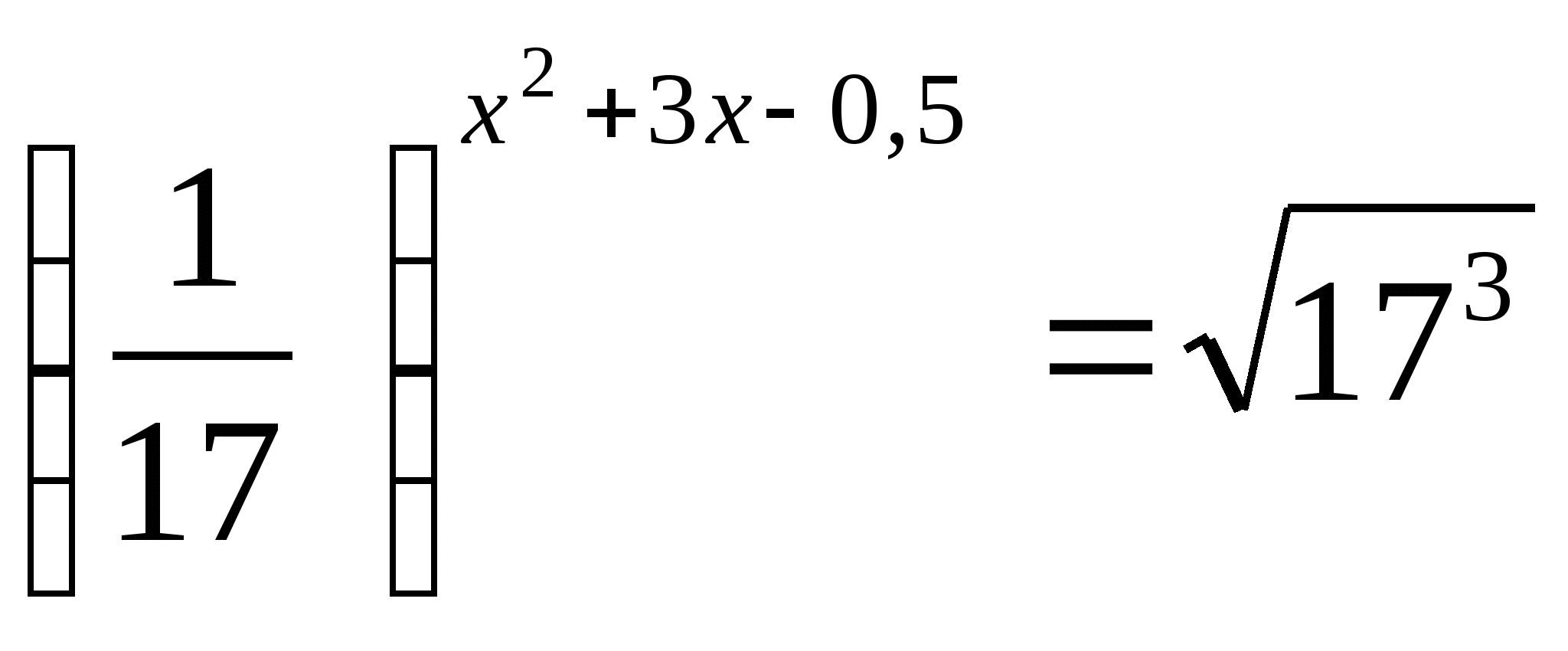  4. Корнем уравнения Урок по теме Решение показательных уравнений и неравенств является число…

6. Функция Урок по теме Решение показательных уравнений и неравенств при Урок по теме Решение показательных уравнений и неравенств является

а) не убывающей

б) убывающей

в) не возрастающей

г) возрастающей

- В конце урока вы сдадите листы с выполненным тестом и листом работы в группе, по итогам этих двух работ каждый получит оценку за работу на уроке.

- Далее мы переходим к следующему этапу работы на уроке - работе в группах.

У каждой группы на солее лежит карточка с заданиями. В каждой карточке по пять показательных уравнений, которые вы должны выполнить за 10 минут. Одно из уравнений, оно выделено красным цветом, группа защищает у доски. Предлагаю вам сразу же распределить каждому участнику группы по уравнению, а затем начинать работу. Работа каждой группы будет оцениваться по следующим параметрам:

- Количество решенных уравнений;

- Правильность решения уравнений;

- Защита задания у доски.

В помощь вам на экран будет выведена уже известная таблица соотнесения вида показательного уравнения и способа его решения.

- Какие у вас есть вопросы по организации групповой работы?



К доске сразу же выходят представители групп, которые будут защищать отмеченные задания и начинают оформлять их на доске.

После 10 минут работы в группах начинается защита заданий у доски.

- выполняют тестовые задания, с последующей проверкой с помощью ключа.



1 вариант: 1)в; 2)6; 3)3; 4) 1,5; 5) 1 и -4; 6) Б

2 вариант: 1)в; 2)7; 3)корней нет; 4) 1; 5) 1 и -4; 6) Г

















































































































К доске сразу же выходят представители групп, которые будут защищать отмеченные задания и начинают оформлять их на доске.



























Защищают задания у доски





IVэтап: итог урока.

Цель этапа: обобщить полученные знания. Проверить уровень усвоения темы.



Деятельность



- На дом вы получите подборку уравнений, которые встречаются в заданиях типа С1 и С3 ЕГЭ.

Содержание домашнего задания

Решите уравнения:

1. Урок по теме Решение показательных уравнений и неравенств

2. Урок по теме Решение показательных уравнений и неравенств

3. Урок по теме Решение показательных уравнений и неравенств

4. Урок по теме Решение показательных уравнений и неравенств

5. Урок по теме Решение показательных уравнений и неравенств



На оценку «3» - 3 правильно решенных уравнения

На оценку «4» - 4 правильно решенных уравнения

На оценку «5» - 5 правильно решенных уравнения

- Все сдайте тест и результаты групповой работы

- Всем спасибо за работу на уроке. До свидания!

Сдают работы



















До свидания!





















































Алгоритм решения показательного уравнения

  1. Определить, можно ли свести уравнение к одному основанию степени

+ -

  1. Определить вид уравнения и способ решения



Вид уравнения:

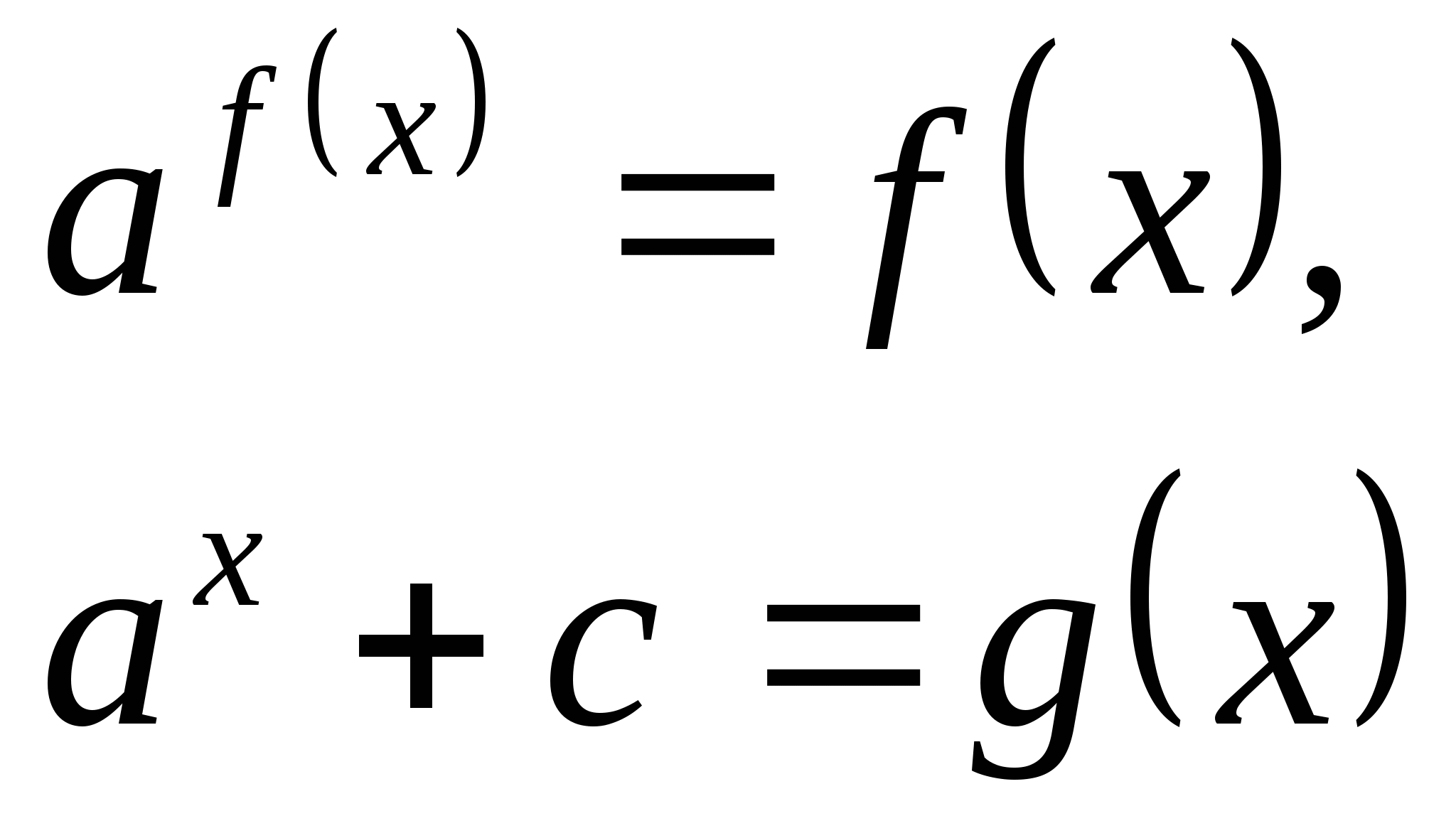
Урок по теме Решение показательных уравнений и неравенств

Урок по теме Решение показательных уравнений и неравенств

Представить с в виде степени с основанием а



Метод решения: Функционально- графический

Урок по теме Решение показательных уравнений и неравенств

Разделить обе части уравнения на Урок по теме Решение показательных уравнений и неравенств>0 или Урок по теме Решение показательных уравнений и неравенств>0



Урок по теме Решение показательных уравнений и неравенств, где c=b d

Разделить обе части уравнения на

Урок по теме Решение показательных уравнений и неравенств или

Урок по теме Решение показательных уравнений и неравенств



Урок по теме Решение показательных уравнений и неравенств

Вынести за скобки общий множитель Урок по теме Решение показательных уравнений и неравенств, где Урок по теме Решение показательных уравнений и неравенств- наименьший из Урок по теме Решение показательных уравнений и неравенств



Урок по теме Решение показательных уравнений и неравенств

(приводимое к квадратному)

Ввести новую переменную

Урок по теме Решение показательных уравнений и неравенств



















Тест







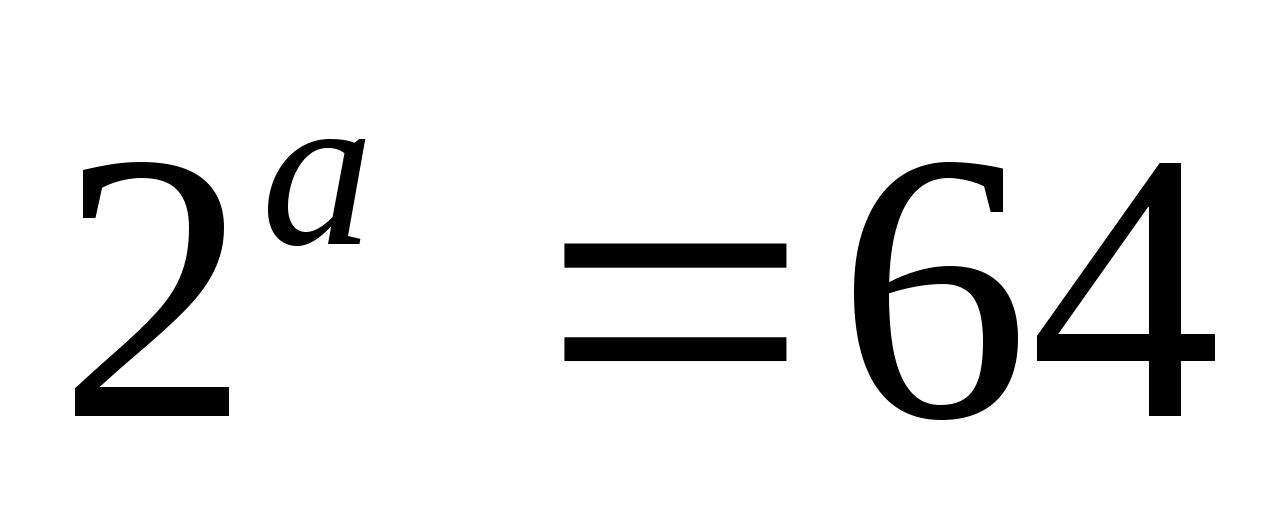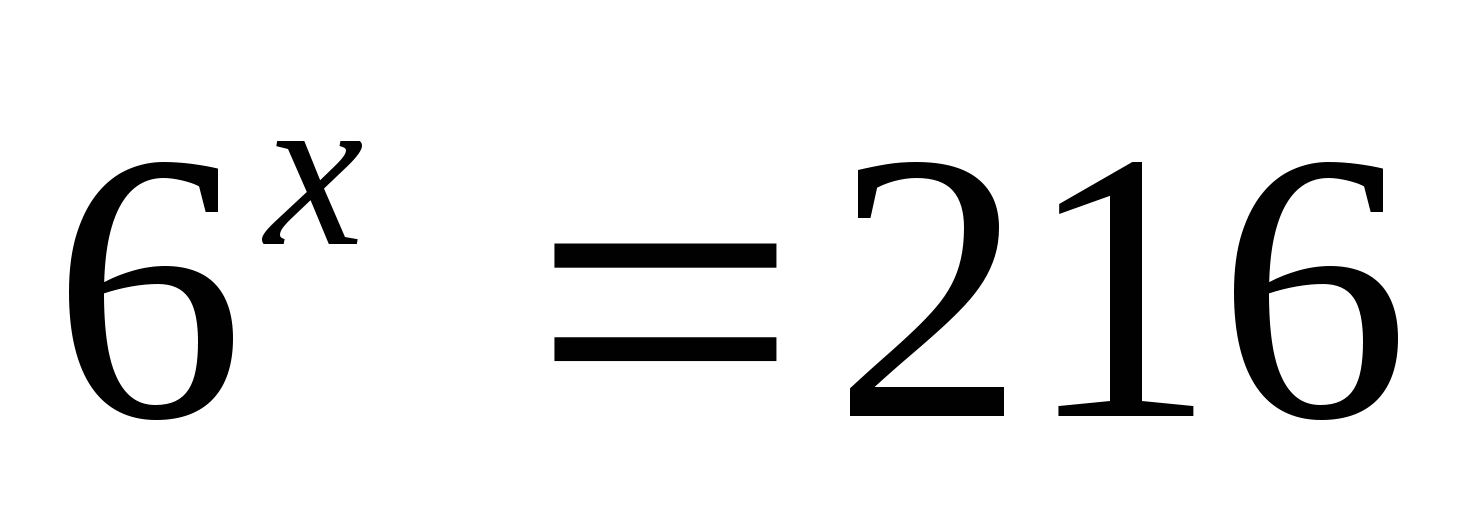А) y=x; Б) Урок по теме Решение показательных уравнений и неравенств; В) Урок по теме Решение показательных уравнений и неравенств

Г) среди предложенных вариантов нет верных.



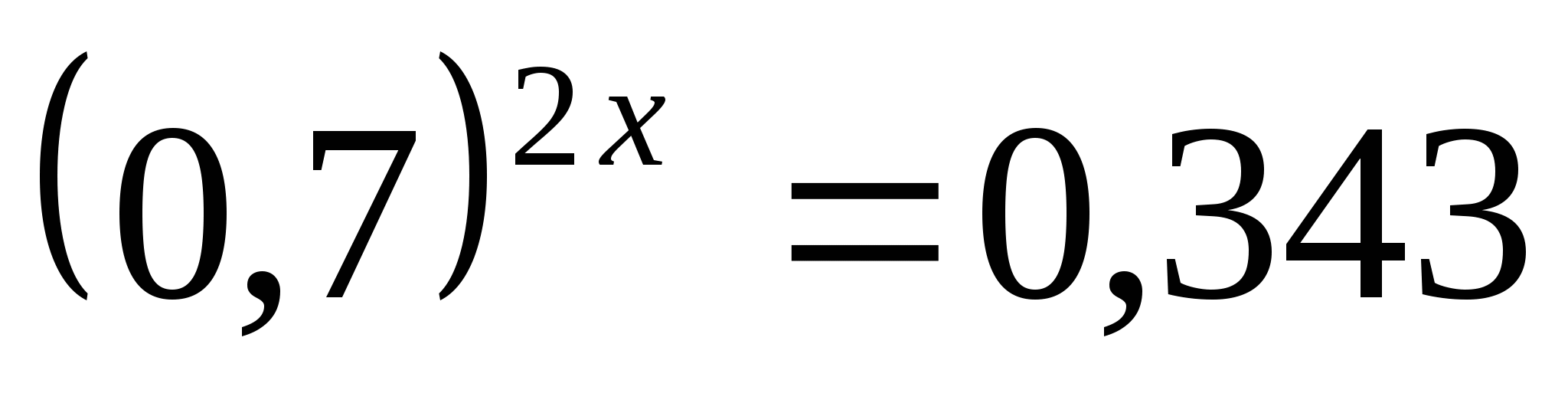  1. Корнем уравнения Урок по теме Решение показательных уравнений и неравенств является число…

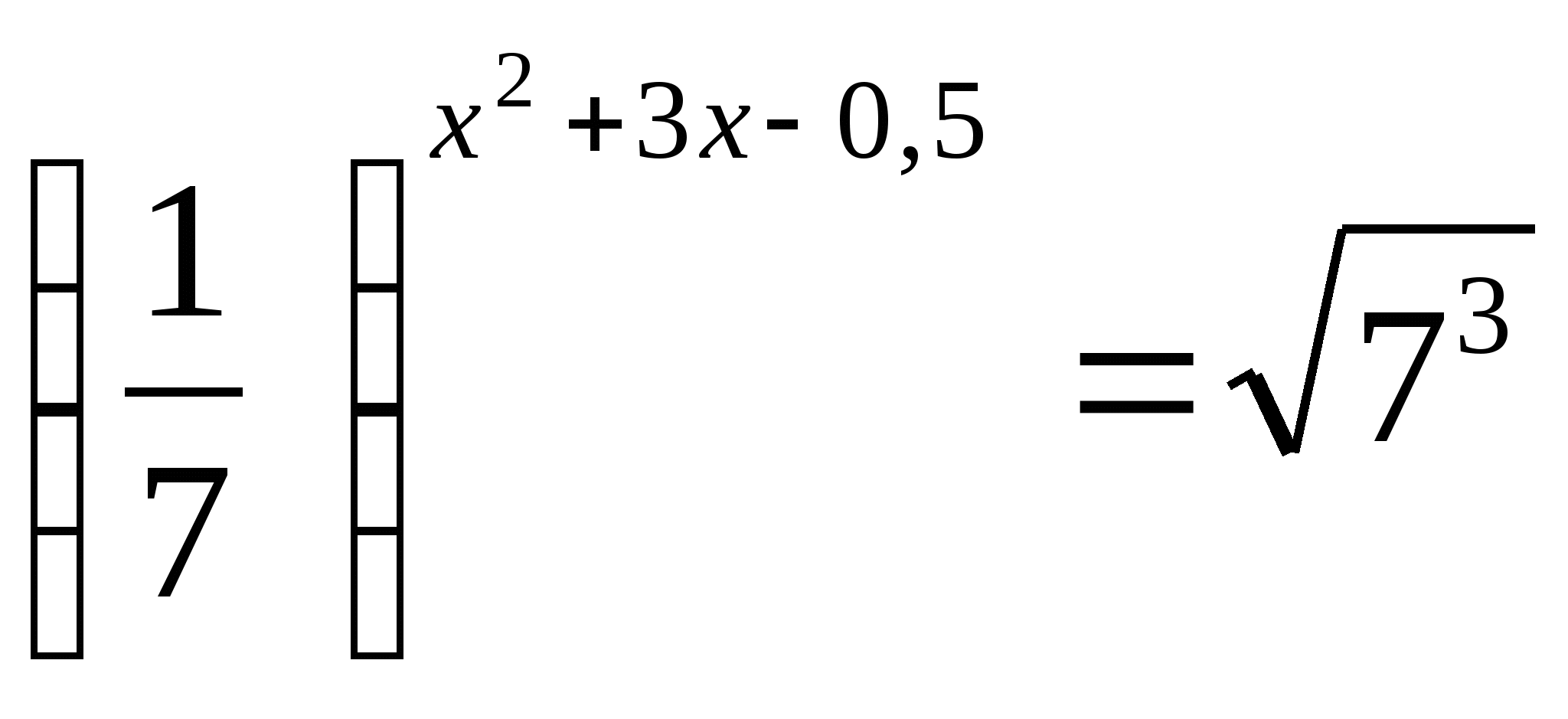  2. Корнем уравнения Урок по теме Решение показательных уравнений и неравенств является число …

  3. Корнем уравнения Урок по теме Решение показательных уравнений и неравенств является число …

  4. Корнем уравнения Урок по теме Решение показательных уравнений и неравенств является число …

6. Функция Урок по теме Решение показательных уравнений и неравенств при Урок по теме Решение показательных уравнений и неравенств является

а) не убывающей

б) убывающей

в) не возрастающей

г) возрастающей

  1. Показательной является функция:

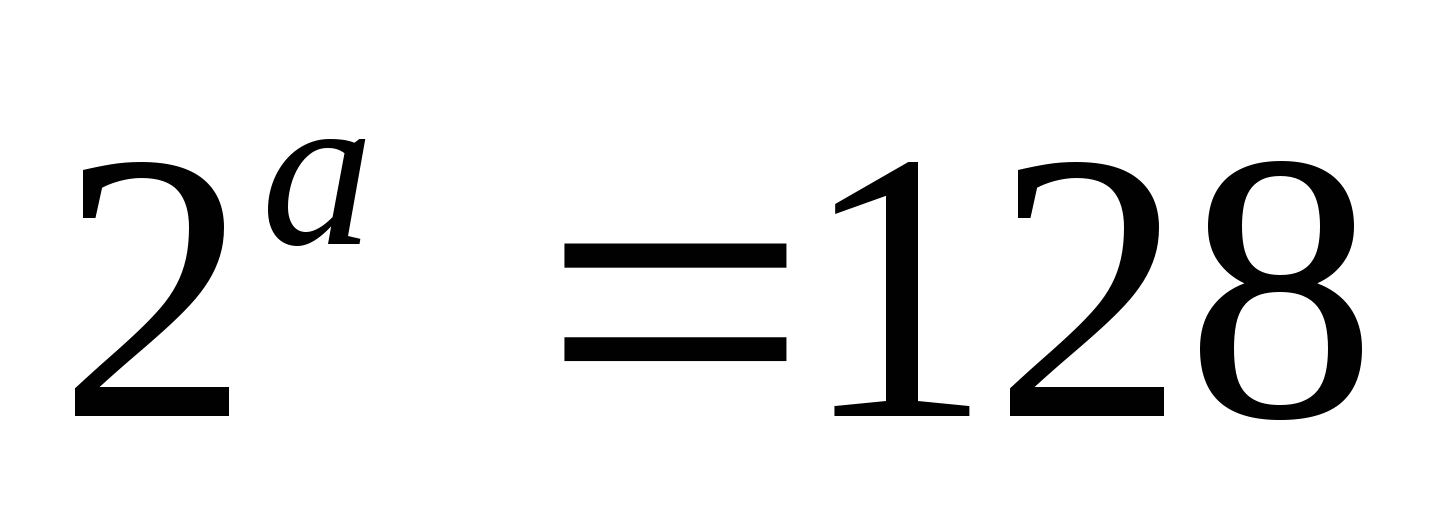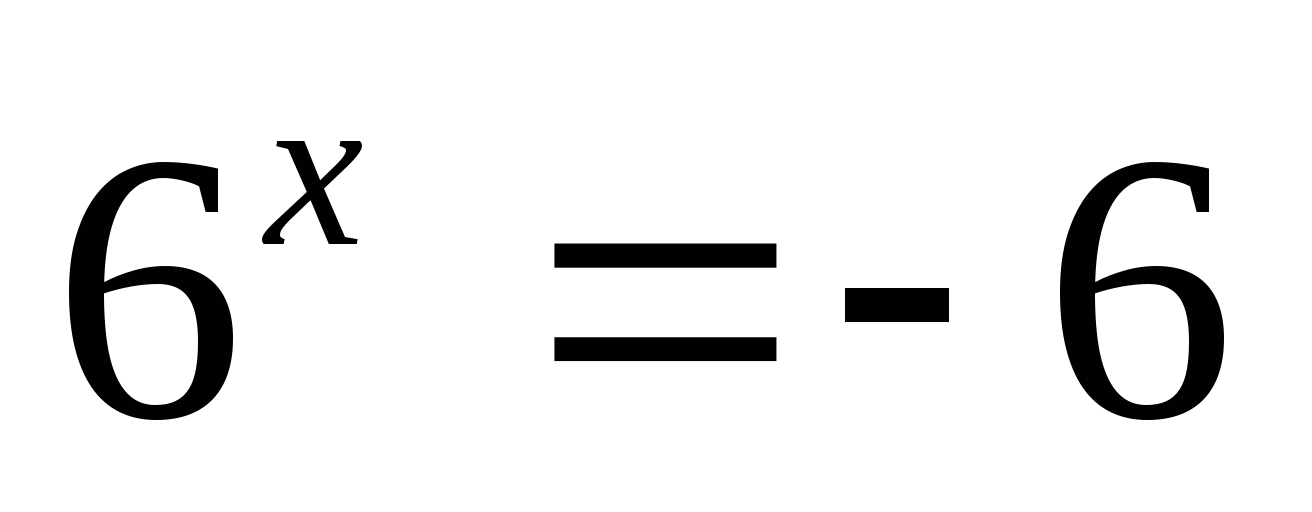А) y=x; Б) Урок по теме Решение показательных уравнений и неравенств; В) Урок по теме Решение показательных уравнений и неравенств

Г) среди предложенных вариантов нет верных.



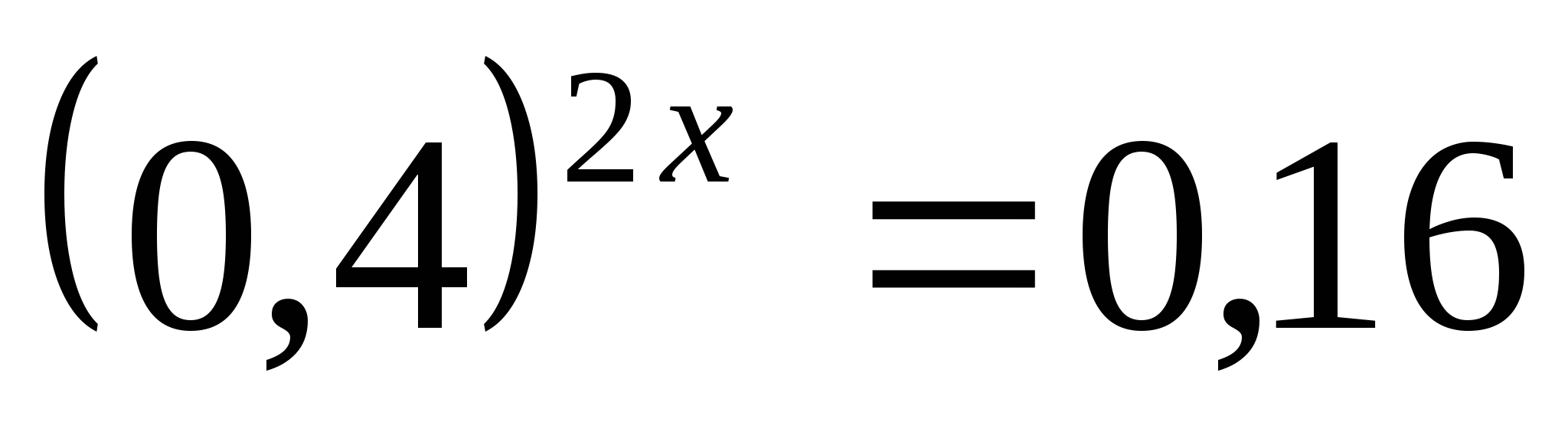  1. Корнем уравнения Урок по теме Решение показательных уравнений и неравенств является число…

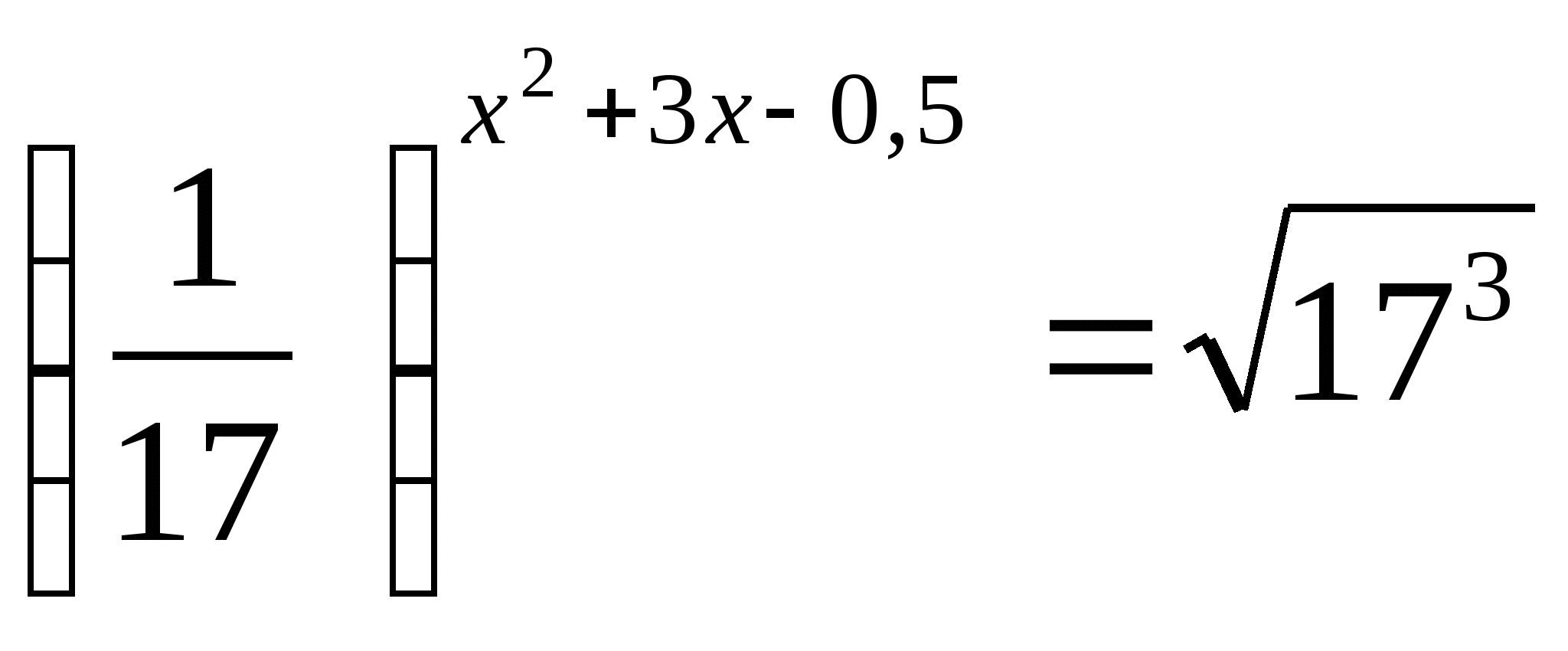  2. Корнем уравнения Урок по теме Решение показательных уравнений и неравенств является число …

  3. Корнем уравнения Урок по теме Решение показательных уравнений и неравенств является число …

  4. Корнем уравнения Урок по теме Решение показательных уравнений и неравенств является число…

6. Функция Урок по теме Решение показательных уравнений и неравенств при Урок по теме Решение показательных уравнений и неравенств является

а) не убывающей

б) убывающей

в) не возрастающей

г) возрастающей















































Задания для работы в группах



1 группа



Решите уравнение.

  1. Урок по теме Решение показательных уравнений и неравенств

  2. Урок по теме Решение показательных уравнений и неравенств

  3. Урок по теме Решение показательных уравнений и неравенств

  4. Урок по теме Решение показательных уравнений и неравенств

  5. Урок по теме Решение показательных уравнений и неравенств

2 группа



Решите уравнение.

  1. Урок по теме Решение показательных уравнений и неравенств

  2. Урок по теме Решение показательных уравнений и неравенств

  3. Урок по теме Решение показательных уравнений и неравенств

  4. Урок по теме Решение показательных уравнений и неравенств

  5. Урок по теме Решение показательных уравнений и неравенств



3 группа



Решите уравнение.

  1. Урок по теме Решение показательных уравнений и неравенствУрок по теме Решение показательных уравнений и неравенств

  2. Урок по теме Решение показательных уравнений и неравенств

  3. Урок по теме Решение показательных уравнений и неравенств

  4. Урок по теме Решение показательных уравнений и неравенств

  5. Урок по теме Решение показательных уравнений и неравенств

4 группа



Решите уравнение.

  1. Урок по теме Решение показательных уравнений и неравенств

  2. Урок по теме Решение показательных уравнений и неравенств

  3. Урок по теме Решение показательных уравнений и неравенств

  4. Урок по теме Решение показательных уравнений и неравенств

  5. Урок по теме Решение показательных уравнений и неравенств

5 группа



Решите уравнение

  1. Урок по теме Решение показательных уравнений и неравенств

  2. Урок по теме Решение показательных уравнений и неравенств

  3. Урок по теме Решение показательных уравнений и неравенств

  4. Урок по теме Решение показательных уравнений и неравенств

  5. Урок по теме Решение показательных уравнений и неравенств





Содержание презентации



12

⇧
⇩
скачать материал


 
 
X

Чтобы скачать данный файл, порекомендуйте его своим друзьям в любой соц. сети.

После этого кнопка ЗАГРУЗКИ станет активной!

Кнопки рекомендации:

загрузить материал