Рабочая программа по геометрии для 8 класса. Л.С.Атанасян.

I. Пояснительная записка.

Нормативные и учебно-методические документы, определяющие содержание программы:

Рабочая программа по геометрии в 8 классе составлена на основании следующих нормативно-правовых документов:

• Федерального базисного учебного плана, утвержденного приказом Министерства образования РФ «Об утверждении федерального базисного учебного плана и примерных учебных планов для образовательных учреждений Российской Федерации, реализующих программы общего образования» от 09.03.2004 №1312;

• Федерального компонента государственного стандарта основного общего образования, примерной программы основного общего образования по математике (утверждена приказом Министерства образования РФ от 09.03.04 №1312).

• Алгебра. Сборник рабочих программ 7-9 классы: пособие для учителей общеобразоват. организаций/сост. Т.А.Бурмистрова - М:Просвещение 2011, 96с.

• Примерные программы по алгебре и геометрии (письмо Департамента государственной политики в образовании Минобрнауки России от 07.07.2005г. № 03-1263

• «Временных требований к минимуму содержания основного общего образования» (приказ МО РФ от 19.05.98. № 1236)

• Геометрия. Сборник рабочих программ 7-9 классы: пособие для учителей общеобразоват. организаций/сост. Т.А.Бурмистрова - 2-е изд., дораб-М:Просвещение 2014,95с.

Цели

Изучение математики на ступени основного общего образования направлено на достижение следующих целей:

• овладение системой математических знаний и умений, необходимых для применения в практической деятельности,

• изучения смежных дисциплин, продолжения образования;

• интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;

• формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;

• воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии.

Общеучебные умения, навыки и способы деятельности.

В ходе преподавания математики в основной школе, работы над формированием у учащихся перечисленных в программе знаний и умений, следует обращать внимание на то, чтобы они овладевали умениями общеучебного характера, разнообразными способами деятельности, приобретали опыт:

• планирования и осуществления алгоритмической деятельности,

• выполнения заданных и конструирования новых алгоритмов;

• решения разнообразных классов задач из различных разделов курса, в том числе задач, требующих поиска пути и способов решения;

• исследовательской деятельности, развития идей, проведения экспериментов, обобщения, постановки и формулирования новых задач;

• ясного, точного, грамотного изложения своих мыслей в устной и письменной речи, использования различных языков математики (словесного, символического, графического), свободного перехода с одного языка на другой для иллюстрации, интерпретации, аргументации и доказательства;

• проведения доказательных рассуждений, аргументации, выдвижения гипотез и их обоснования;

• поиска, систематизации, анализа и классификации информации, использования разнообразных информационных источников, включая учебную и справочную литературу, современные информационные технологии.

II. Общая характеристика учебного предмета.

Математическое образование в 8 классе складывается из следующих содержательных компонентов: алгебра; геометрия; элементы комбинаторики, теории вероятностей, статистики и логики. В своей совокупности они отражают богатый опыт обучения математике в нашей стране, учитывают современные тенденции отечественной и зарубежной школы и позволяют реализовать поставленные перед школьным образованием цели на информационно емком и практически значимом материале. Эти содержательные компоненты, развиваясь на протяжении всех лет обучения, естественным образом переплетаются и взаимодействуют в учебных курсах.

Геометрия - один из важнейших компонентов математического образования, необходимая для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математической культуры, для эстетического воспитания учащихся. Изучение геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства.

III. Место учебного предмета в учебном плане.

На изучение учебного предмета геометрия в 7 классе в инвариантной части учебного плана выделяется 2 учебных часа в неделю. При 35 учебных неделях - 70 часов в год.

IV. Содержание учебного предмета.

Повторение курса геометрии 7 класса

Четырехугольники.

Понятия многоугольника, выпуклого многоугольника. Параллелограмм и его признаки и свойства. Трапеция. Прямоугольник, ромб, квадрат и их свойства. Осевая и центральная симметрии.

Площади фигур.

Понятие площади многоугольника. Площади прямоугольника, параллелограмма, треугольника, трапеции. Теорема Пифагора.

Подобные треугольники.

Подобные треугольники. Признаки подобия треугольников. Применение подобия к доказательствам теорем и решению задач. Соотношения между сторонами и углами прямоугольного треугольника.

Окружность.

Взаимное расположение прямой и окружности. Касательная к окружности и ее свойства и признак. Центральные и вписанные углы. [Четыре замечательные точки треугольника.] Вписанная и описанная окружности.

Итоговое повторение.

V. Тематическое планирование.Основное содержание по темам

Количество часов

Требования к результату

Повторение курса геометрии 7 класса

4

Актуализация знаний за курс геометрии 7 класса

Четырехугольники.

14

Знать определение многоугольника, выпуклого многоугольника, четырехугольника как частного вида выпуклого четырехугольника, теоремы о сумме углов выпуклого многоугольника, определение параллелограмма, его свойства и признаки; определения трапеции и ее элементов, равнобедренной и прямоугольной трапеции, свойства равнобедренной трапеции; теорему Фалеса; определение прямоугольника и его свойства; определения, свойства и признаки прямоугольника, ромба и квадрата; определения и свойства осевой и центральной симметрии.

Уметь решать задачи по теме

Площади фигур.

14

Знать понятие площади, основные свойства площадей, формулу для вычисления площади квадрата; формулу площади прямоугольника, параллелограмма, треугольника, трапеции; теорему Пифагора; теорему, обратную теореме Пифагора.

Уметь решать задачи по теме

Подобные треугольники.

20

Знать определение подобных треугольников, понятие пропорциональных отрезков, свойство биссектрисы угла, теорему об отношении площадей подобных треугольников, признаки подобия треугольников; понятия синуса, косинуса и тангенса острого угла прямоугольного треугольника, основные геометрические тождества; значения синуса, косинуса и тангенса для углов, равных 30, 45, 60

Уметь решать задачи по теме, применять теорию о подобных треугольниках при измерительных работах на местности.

Окружность.

15

Знать различные случаи расположения прямой и окружности; понятия касательной, точки касания, отрезков касательных, проведенных из одной точки; свойство касательной и ее признак; свойства отрезков касательных, проведенных из одной точки; понятия градусной меры дуги окружности, центрального и вписанного угла, теорему о вписанном угле и ее следствия; теорему об отрезках пересекающихся хорд; свойство биссектрисы угла и его следствия; понятие серединного перпендикуляра; теорему о серединном перпендикуляре; теорему о точке пересечения высот треугольника; понятия вписанной и описанной окружностей; свойство описанного и вписанного четырехугольника;

Уметь решать задачи по теме

Итоговое повторение

3

Знать основные определения и теоремы по темам

Уметь решать задачи по темам

ИТОГО

70

VI. Календарно-тематическое планирование№ п/п

Дата

Тема

Кол-во часов

Оборудование

Основные виды учебной деятельности

Вид контроля

I четверть

1 - 3

Повторение курса геометрии 7 класса.

3

4

Входная контрольная работа.

1

Демонстрация знаний, умений и навыков

Контрольная работа

1. Четырехугольники.

5 - 6

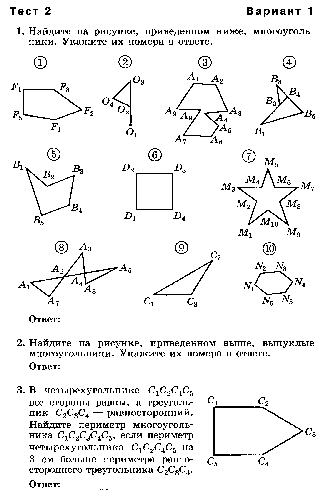
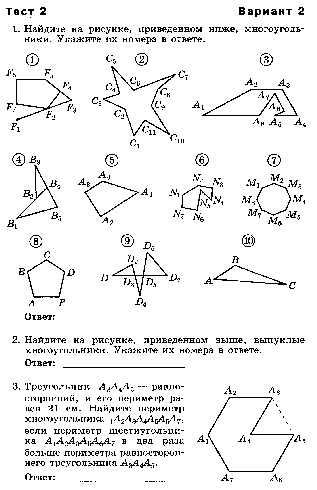
Многоугольники

2

Таблица3.4.Свойства многоугольников

Объяснять, что такое многоугольник, его вершины, смежные стороны, диагонали, изображать четырехугольники на чертежах; изображать и распознавать многоугольники на чертежах. Показывать элементы многоугольника, его внутреннюю и внешнюю области; формулировать определение выпуклого многоугольника; изображать и распознавать выпуклые и невыпуклые многоугольники. Формулировать и доказывать утверждение о сумме углов выпуклого многоугольника. Объяснять, какие стороны(вершины) называются противоположными.

Тест№2 «Многоугольники»

7

Параллелограмм. Свойства параллелограмма.

1

Таблица3.1.Свойства параллелограммов

Формулировать определения параллелограмма, трапеции, равнобедренной и прямоугольной трапеций, прямоугольника, ромба, квадрата; распознавать и изображать эти четырехугольники. Формулировать и доказывать утверждения о свойствах и признаках указанных четырехугольников. Решать задачи на вычисление, доказательство и построение, связанные с этими видами четырехугольников. Объяснять, какие две точки называются симметричными относительно прямой(точки), в каком случае фигура называется симметричной относительно прямой(точки) и что такое ось(центр) симметрии фигуры. Приводить примеры фигур, обладающих осевой(центральной) симметрией, а также приводить примеры осевой и центральной симметрии в окружающей нас обстановке.

Самостоятельная работа №1 «Свойства параллелограмма»

8

Признаки параллелограмма.

1

Таблица3.3.Признаки параллелограмма и его виды

9

Решение задач по теме «Параллелограмм»

1

10

Трапеция

1

Таблица3.2. Трапеция

Самостоятельная работа №2 «Трапеция

11

Решение задач по теме «Параллелограмм и трапеция».

1

CD4-61 «Признаки параллелограмма. Трапеция»

12

Трапеция. Задачи на построение.

1

13

Прямоугольник.

1

Тест№5 «Прямоугольник»

14

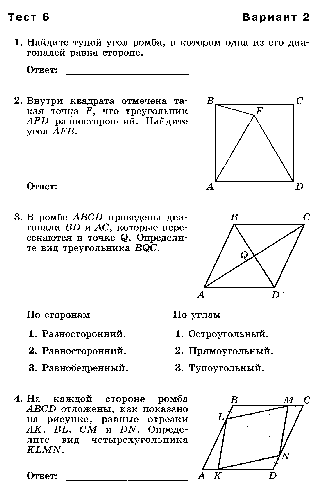
Ромб. Квадрат

1

Тест№6 «Ромб. Квадрат»

15

Решение задач по теме «Ромб. Квадрат»

1

16

Осевая и центральная симметрия»

1

Самостоятельная работа №3 «Прямоугольник, ромб, квадрат. Осевая и центральная симметрия»

17

Решение задач по теме «Прямоугольник. Ромб. Квадрат».

1

CD4-61 Тестирование «Ромб. Квадрат»

18

Контрольная работа №1 по теме "Многоугольники"

1

Демонстрация знаний, умений и навыков

Контрольная работа

II четверть

2. Площадь.

19 - 20

Площадь многоугольника.

2

Презентация по теме «Площади многоугольников»

Объяснять, как производится измерение площадей многоугольников; формулировать основные свойства площадей. Выводить формулы площадей параллелограмма, треугольника, трапеции, с помощью формул площадей прямоугольника и квадрата. Формулировать и доказывать теорему об отношении площадей треугольников, имеющих по равному углу.

21

Площадь параллелограмма.

1

Таблица3.8. Площадь многоугольника (1)

Таблица3.10. Площадь многоугольника (2)

22-23

Площадь треугольника.

2

Самостоятельная работа №5 «Площадь параллелограмма, треугольника»

24

Площадь трапеции.

1

Самостоятельная работа №6 «Площадь трапеции»

25-26

Решение задач на вычисление площадей фигур.

2

Тес№8 «Площади параллелограмма, треугольника и трапеции»

27

Теорема Пифагора.

1

Таблица2.6. Прямоугольный треугольник

Таблица2.7. Теорема Пифагора

Формулировать и доказывать теорему Пифагора и обратную ей. Выводить формулу Герона для площади треугольника. Решать задачи на вычисление, доказательство и построение, связанные с формулами площадей и теоремой Пифагора.

28

Теорема, обратная теореме Пифагора.

1

Самостоятельная работа №7 «Теорема Пифагора»

29

Решение задач на применение теоремы Пифагора

1

Презентация «Теорема Пифагора. Решение задач»

30 - 31

Формула Герона. Решение задач.

1

31

Решение задач по теме «Площади многоугольников»

1

Матемаический дикант «Площади многоугольников»

32

Контрольная работа №2 по теме "Площади многоугольников"

1

Демонстрация знаний, умений и навыков

Контрольная работа

III четверть

3. Подобные треугольники.

33

Пропорциональные отрезки. Определение подобных треугольников.

1

Таблица2.9.Подобие треугольников

Объяснять понятие пропорциональности отрезков. Формулировать определения подобных треугольников и коэффициента подобия

Тест№10 «Определение подбных треугольников»

34

Отношение площадей подобных треугольников.

1

CD4-61 «Отношение площадей треугольников, имеющих по равному углу»

Формулировать и доказывать теоремы: об отношении площадей подобных треугольников, о признаках подобия треугольников.

Самостоятельная работа №8 «Определение подобных треугольников. Свойство биссектрисы угла треугольника»

35

Первый признак подобия треугольников.

1

36

Первый признак подобия треугольников. Решение задач.

1

37

Второй и третий признак подобия треугольников.

1

38-39

Решение задач на применение признаков подобия треугольников.

2

CD4-61 «Признаки подобия треугольников»

Самостоятельная работа №9 «Признаки подобия треугольников»

40

Контрольная работа №3 по теме "Подобные треугольники"

1

Демонстрация знаний, умений и навыков

Контрольная работа

41 - 42

Средняя линия треугольника

2

Презентация «Применение подобия к решению задач»

Формулировать и доказывать теоремы: о средней линии треугольника, о пересечении медиан треугольника, о пропорциональных отрезках в прямоугольном треугольнике.

Самостоятельная работа №10 «Средняя линия треугольника»

43-44

Пропорциональные отрезки в прямоугольном треугольнике.

2

45

Измерительные работы на местности.

1

Объяснять, как можно использовать свойства подобных треугольников в измерительных работах на местности.

46-47

Задачи на построение методом подобия

2

48

Синус, косинус и тангенс острого угла прямоугольного треугольника.

1

Талица2.8. Синус, косинус, тангенс острого угла прямоугольного треугольника

Формулировать определения и иллюстрировать понятия синуса, косинуса и тангенса острого угла прямоугольного треугольника. Выводить основное тригонометрическое тождество и значения синуса, косинуса, тангенса углов 30⁰,45⁰,60⁰. Решать задачи, связанные с подобием треугольников и нахождением неизвестных элементов прямоугольного треугольника. Для вычисления значений тригонометрических функций использовать компьютерные программы.

Математический диктант «Соотношения в прямоугольном треугольнике»

49

Значения синуса, косинуса и тангенса для углов 30, 45 и 60.

1

Презентация «Соотношения между сторонами и углами прямугольного треугольника»

50

Соотношение между сторонами и углами прямоугольного треугольника.

1

Самостоятельная работа №12 «Соотношения между сторонами и углами прямоугольного треугольника»

51

Контрольная работа №4 по теме "Подобные треугольники"

1

Демонстрация знаний, умений и навыков

Контрольная работа

4. Окружность

52-53

Касательная к окружности.

2

Таблица4.1. Окружность. Хорды и касательные

IV четверть

54

Касательная к окружности. Решение задач.

1

Исследовать взаимное расположение прямой и окружности. Формулировать определение касательной к окружности.

Самостоятельная работа №13 «Касательная к окружности»

55

Градусная мера дуги окружности.

1

Таблица4.5. Центральные и вписанные углы

Формулировать и доказывать теоремы: о свойстве касательной, об отрезках касательных, проведенных из одной точки. Формулировать понятия центрального угла и градусной меры дуги окружности. Формулировать и доказывать теоремы: о вписанном угле, о произведении отрезков хорд,.

56

Теорема о вписанном угле.

1

57

Теорема об отрезках пересекающихся хорд.

1

58

Решение задач по теме «Центральные и вписанные углы»

1

Самостоятельная работа №14 «Центральные и вписанные углы»

59

Свойство биссектрисы угла.

1

CD4-61 «Точка пересечения биссектрис к сторонам треугольника»

Формулировать и доказывать теоремы, связанные с замечательными точками треугольника: о биссектрисе угла и, как следствие, о пересечении биссектрис треугольника; о серединном перпендикуляре к отрезку и, как следствие, о пересечении серединных перпендикулярах к сторонам треугольника; о пересечении высот треугольника

60

Серединный перпендикуляр

1

61

Теорема о точке пересечения высот треугольника.

1

Самостоятельная работа №15 «Четыре замечательные точки трегольника»

62

Свойство описанного четырехугольника.

1

Формулировать определения окружностей, вписанной в многоугольник и описанной около многоугольника. Формулировать и доказывать теоремы: об окружности, вписанной в треугольник, об окружности, описанной около треугольника, об окружности, описанной около треугольника, о свойстве сторон описанного четырехугольника, о свойстве углов вписанного четырехугольника. Решать задачи на вычисление, доказательство, построение, связанные с окружностью, вписанными и описанными треугольниками и четырехугольниками. Исследовать свойства конфигураций, связанных с окружностью, с помощью компьютерных программ.

63

Описанная окружность

1

64

Свойство вписанного четырехугольника.

1

Самостоятельная работа №16 «Вписанная и описанная окружность»

65-66

Решение задач по теме «Окружность»

2

Таблица4.2. Окружность, описанная около треугольника

67

Контрольная работа №5 по теме "Окружность"

1

Демонстрация знаний, умений и навыков

Контрольная работа

68

Повторение по теме «Многоугольники»

1

69

Повторение по теме «Подобные треугольники»

1

70

Итоговая контрольная работа

1

Демонстрация знаний, умений и навыков

Контрольная работа

ИТОГО

70

VII. Учебно-методическое и материально-техническое обеспечение образовательного процесса.Перечень используемых учебников и учебных пособий

Основная литература:

1. Геометрия. 8 кл: поурочные планы по учебнику Л.С.Атанасяна, В.Б.Бутузова, С.Б.Кадомцева и др. / авт.-сост. Т.Л.Афонасьева, Л.А.Тапилина. - Волгоград: Учитель, 2006.

2. Л.С. Атанасян, В.Б.Бутузов, С.Б.Кадомцев и др. «Геометрия 7-9 кл.» - М.: Просвещение, 2008

3. Изучение геометрии в 7-9 классах: Метод. Рекомендации к учеб.: Кн. для учителя / Л.С. Атана-сян, В.Б.Бутузов, Ю.А.Глазков и др. - М.: Просвещение, 1999

4. Рабинович Е.М. Задачи и упражнения на готовых чертежах. 7-9 классы. Геометрия. - М.: Илек-са, Харьков: Гимназия, 1999

5. Г.Г. Левитас. Карточки для коррекции знаний по геометрии для 8-9 классов. - М.: Илекса, 2003

6. Зив Б.Г., Мейлер В.М. Дидактические материалы по геометрии для 8 класса.- М.: Просвещение, 1992

7. Мищенко Т.М. Геомерия. Тематические тесты, 8 класс/ _ М.:Просвещение,2011.- 128 с.

8. Журавлев. Контрольные и самостоятельные работы по алгебре и геометрии6 8 класс: к учебникам Ю.Н.Макарычева и др. «Алгебра. 8 класс». А.Г.Мордковича «Алгебра. 8 класс», С.М.Никольского и др. «Алгебра. 8 класс», Л.С.Атанасяна и др. «Геометрия. 7-9 кл.», А.В.Погорелова «Геометрия. 7-9 кл.». ФГОС (к новому учебнику)/ С.Г.Журавлев, С.А.Изотова, С.В.Киреева. - М.: Издательство «Экзамен», 2015 - 239 с.

Дополнительная литература:

9. Тесты для промежуточной аттестации 7-8 классы, Ф.Ф. Лысенко, 2015

10. ГИА 3000 задач. математика, Семенов, Ященко

Дидактико-технологическое обеспечение

Комплект таблиц по алгебре

Печатные, электронные,

экранно - звуковые учебные изданияВся элементарная математика: Средняя математическая интернет-школа

www.bymath.net

2. Задачник для подготовки к олимпиадам по математике

tasks.ceemat.ru

3. Занимательная математика - школьникам (олимпиады, игры, конкурсы по математике)

www.math-on-line.com

4. Интернет-проект «Задачи»

www.problems.ru

5. Математические этюды

www.etudes.ru

6. Математические олимпиады и олимпиадные задачи

www.zaba.ru

7. Международный математический конкурс «Кенгуру»

www.kenguru.sp.ru

8. Методика преподавания математики

methmath.chat.ru

9. Газета «Математика» Издательского дома «Первое сентября»

mat.1september.ru

10. Математика в Открытом колледже

www.mathematics.ru

11. Math.ru: Математика и образование

www.math.ru

12. Московский центр непрерывного математического образования (МЦНМО)

www.mccme.ru

13. Allmath.ru - вся математика в одном месте

www.allmath.ru

14. Exponenta.ru: образовательный математический сайт

www.exponenta.ru

15. Образовательные ресурсы

fcior.edu.ru/

Технические средства обучения (средства ИКТ)

Компьютер, мультимедийный проектор, интерактивная доска

Учебно-практическое и учебно-лабораторное оборудование

-

Натуральные объекты

-

Демонстрационные пособия

-

Музыкальные инструменты

-

VIII. Результаты освоения учебного предмета геометрия и система их оценки.

Планируемые результаты

В результате изучения курса учащиеся 8 класса должны:

Знать:

• существо понятия математического доказательства; приводить примеры доказательств;

• существо понятия алгоритма; приводить примеры алгоритмов;

• как используются математические формулы; примеры их применения для решения математических и практических задач;

• каким образом геометрия возникла из практических задач землемерия; примеры геометрических объектов и утверждений о них, важных для практики;

• смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации.

• Теорема Фалеса. Средняя линия треугольника и ее свойства.

• Теорема Пифагора. Решение прямоугольных треугольников. Метрические соотношения между элементами прямоугольного треугольника.

• Подобие треугольников. Признаки подобия треугольников.

• Четырехугольники. Параллелограмм. Прямоугольник, ромб, квадрат. Трапеция. Свойства.

• Площади четырехугольников.

• Многоугольники. Сумма углов выпуклого многоугольника.

• Окружность и круг. Касательная к окружности и ее свойства. Центральные и вписанные углы.

• Осевая симметрия. Центральная симметрия.

Уметь:

• пользоваться геометрическим языком для описания предметов окружающего мира;

• распознавать геометрические фигуры, различать их взаимное расположение;

• изображать геометрические фигуры, выполнять чертежи по условию задач, осуществлять преобразования фигур;

• решать задачи на вычисление геометрических величин, применяя изученные свойства фигур и формулы;

• вычислять значения геометрических величин (длин, площадей), в том числе: для углов от 30, 45, 60 определять значения тригонометрических функций по заданным значениям углов; находить значения тригонометрических функций по значению одной из них,

• находить стороны и площади треугольников, дуг окружности, площадей основных геометрических фигур и фигур, составленных из них;

• решать геометрические задачи, опираясь на изученные свойства фигур и отношений между ними и применяя дополнительные построения, алгебраический аппарат и соображения симметрии;

• проводить доказательные рассуждения при решении задач, используя известные теоремы и обнаруживая возможности для их использования;

• решать простейшие планиметрические задачи в пространстве;

• </ владеть алгоритмами решения основных задач на построение;

Использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:

• описания реальных ситуаций на языке геометрии;

• решения практических задач, связанных с нахождением геометрических величин (используя при необходимости справочники и технические средства);

• построений геометрическими инструментами (линейка, угольник, циркуль, транспортир);

• владения практическими навыками использования геометрических инструментов для

• изображения фигур, а также нахождения длин отрезков и величин углов.

Виды и формы контроляВиды контроля:

• входной;

• контроль итоговый.

• устный (фронтальный опрос, развернутый ответ, устный счет);

• письменный (индивидуальное задание, математический диктант, самостоятельная работа, тестирование, практическая работа, контрольная работа)

Текущий контроль (проводится в течение всего обучения, на каждом уроке, причем почти на каждом его этапе)

1. Индивидуальная форма контроля (каждый школьник получает свое задание, которое он должен выполнять без посторонней помощи - применяется, если требуется выяснить индивидуальные знания, способности и возможности отдельных учащихся)

2. Групповая форма контроля (класс делится на несколько групп от 2 до 10 учащихся и каждой группе дается проверочное задание - применяют при повторении с целью обобщения и систематизации учебного материала, при выделении приемов и методов решения задач, при акцентировании внимания учащихся на наиболее рациональных способах выполнения заданий, на лучшем из вариантов доказательства теоремы и т. п.).

3. Фронтальная форма контроля (задания предлагаются всему классу - изучается правильность восприятия и понимания учебного материала, качество словесного, графического предметного оформления, степень закрепления в памяти).

4. Тематический контроль (осуществляется периодически, после изучения темы или нового раздела и имеет целью систематизацию знаний учащихся - осуществляется на повторительно-обобщающих уроках и способствует подготовке к контрольным мероприятиям: устных и письменных зачетов).

5. Итоговый контроль (проводится в форме экзаменов или годовых контрольных работ - проверяются знания по важнейшим разделам и темам курса или курсу в целом).

6. Математический диктант (для усвоения текущего материала, для обобщения пройденного)

7. Тест (задания, состоящие из ряда вопросов и нескольких вариантов ответа - проверить большой объем изученного материала малыми порциями, быстро диагностировать овладение учебным материалом большим массивом учащихся)

Перечень контрольных работ

Критерии и нормы оценки знаний, умений и навыков обучающихся по математике.

Оценка письменных контрольных и самостоятельных работ обучающихся по математике.

Ответ оценивается отметкой «5», если:

• работа выполнена полностью;

• в логических рассуждениях и обосновании решения нет пробелов и ошибок;

• в решении нет математических ошибок (возможна одна неточность, описка, которая не является следствием незнания или непонимания учебного материала).

Отметка «4» ставится в следующих случаях:

• работа выполнена полностью, но обоснования шагов решения недостаточны (если умение обосновывать рассуждения не являлось специальным объектом проверки);

• допущены одна ошибка или есть два - три недочёта в выкладках, рисунках, чертежах или графиках (если эти виды работ не являлись специальным объектом проверки).

Отметка «3» ставится, если:

• допущено более одной ошибки или более двух - трех недочетов в выкладках, чертежах или графиках, но обучающийся обладает обязательными умениями по проверяемой теме.

Отметка «2» ставится, если:

• допущены существенные ошибки, показавшие, что обучающийся не обладает обязательными умениями по данной теме в полной мере.

Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.

Оценка устных ответов обучающихся по математике

Ответ оценивается отметкой «5», если ученик:

• полно раскрыл содержание материала в объеме, предусмотренном программой и учебником;

• изложил материал грамотным языком, точно используя математическую терминологию и символику, в определенной логической последовательности;

• правильно выполнил рисунки, чертежи, графики, сопутствующие ответу;

• показал умение иллюстрировать теорию конкретными примерами, применять ее в новой ситуации при выполнении практического задания;

• продемонстрировал знание теории ранее изученных сопутствующих тем, сформированность и устойчивость используемых при ответе умений и навыков;

• отвечал самостоятельно, без наводящих вопросов учителя;

• возможны одна - две неточности при освещение второстепенных вопросов или в выкладках, которые ученик легко исправил после замечания учителя.

Ответ оценивается отметкой «4», если удовлетворяет в основном требованиям на оценку «5», но при этом имеет один из недостатков:

• в изложении допущены небольшие пробелы, не исказившее математическое содержание ответа;

• допущены один - два недочета при освещении основного содержания ответа, исправленные после замечания учителя;

• допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные после замечания учителя.

Отметка «3» ставится в следующих случаях:

• неполно раскрыто содержание материала (содержание изложено фрагментарно, не всегда последовательно), но показано общее понимание вопроса и продемонстрированы умения, достаточные для усвоения программного материала (определены «Требованиями к математической подготовке обучающихся» в настоящей программе по математике);

• имелись затруднения или допущены ошибки в определении математической терминологии, чертежах, выкладках, исправленные после нескольких наводящих вопросов учителя;

• ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме;

• при достаточном знании теоретического материала выявлена недостаточная сформированность основных умений и навыков.

Отметка «2» ставится в следующих случаях:

• не раскрыто основное содержание учебного материала;

• обнаружено незнание учеником большей или наиболее важной части учебного материала;

• допущены ошибки в определении понятий, при использовании математической терминологии, в рисунках, чертежах или графиках, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.

Оценка математического диктанта и тестовой работы обучающихся по математике

• «5» - 90-100%

• «4» - 75-80%

• «3» - 60-70%

• «2» - 50% и менее.

Контрольно-измерительный материалКонтрольная работа № 1

Вариант 1

1^о. Диагонали прямоугольника CDEF пересекаются в точке О. Найдите угол между диагоналями, если СDO = 40⁰.

2^о. Найдите боковую сторону равнобедренной трапеции, основания которой равны 12см и 6см, а один из углов равен 60⁰.

3^о. На продолжении диагонали АС прямоугольника ABCD отложены равные отрезки АМ и СN. Докажите: а) что треугольники MAD и NCB равны; б) что четырехугольник MBND параллелограмм.

Контрольная работа № 1

Вариант 2

1^о. Диагонали ромба ABCD пересекаются в точке О. Найдите углы треугольника АОВ, если между диагоналями, если ВСD = 75⁰.

2^о. Найдите меньшую боковую сторону прямоугольной трапеции, основания которой равны 10см и 6см, а один из углов равен 45⁰.

3^о. На диагонали NK прямоугольника MNPK отложены равные отрезки NА и KE. Докажите: а) что треугольники ANP и EKM равны; б) что четырехугольник APEM параллелограмм.

Контрольная работа № 2

Вариант 1

1^о. Смежные стороны параллелограмма равны 12см и 20см, а один из его углов равен 30⁰. Найдите площадь параллелограмма.

2^о. Найдите периметр прямоугольника, если его диагональ равна 15см, а одна из сторон - 9см.

3^о. Площадь прямоугольной трапеции равна 120см², а ее высота равна 8см. Найти все стороны трапеции, если одно из оснований больше другого на 6см.

Контрольная работа № 2

Вариант 2

1^о. Высота BD треугольника АВС делит основание АС на отрезки: AD = 8см, DC = 12см, а угол А при основании равен 45⁰. Найдите площадь этого треугольника.

2^о. Найдите периметр прямоугольного треугольника, если его катеты равны 12см и 16см.

3^о. Найти площадь трапеции CDEF c основаниями CF и DE, если CD = 12см, DE = 14cм, CF = 30см, D = 150⁰.

Контрольная работа № 3

Вариант 1

1^о. Высота CD прямоугольного треугольника АВС делит гипотенузу АВ на части AD = 16см и BD = 9см. Докажите, что ∆ ACD ∞ ∆ CBD.

2^о. АВ || CD. Найдите АВ, если OD = 15см, OB = 9см, CD = 25см.

Контрольная работа № 3

Вариант 2

1^о. Высота CD прямоугольного треугольника АВС отсекает от гипотенузы АВ, равной 9см, отрезок AD = 4см. Докажите, что ∆ AВC ∞ ∆ АCD.

2^о. MN || DF. Найдите MN, если DM = 6см, EM = 8см, DF = 21см.

Контрольная работа № 4

Вариант 1

1^о. Площадь ромба равна 48см². Найти площадь четырехугольника, вершинами которого являются середины сторон данного ромба.

2. В равнобедренной трапеции меньшее основание равно 4см, боковая сторона равна 6см, а один из углов равен 120⁰. Найти площадь трапеции.

3. В прямоугольном треугольнике АВС А = 90⁰, АВ = 20см, высота AD = 12см. Найти АС и cos C.

Контрольная работа № 4

Вариант 2

1^о. Площадь прямоугольника равна 36см². Найти площадь четырехугольника, вершинами которого являются середины сторон данного прямоугольника.

2. В прямоугольной трапеции меньшее основание равно 3см, большая боковая сторона равна 4см, а один из углов равен 150⁰. Найти площадь трапеции.

3. Высота BD прямоугольного треугольника АВС равна 24см и отсекает от гипотенузы АС отрезок DC, равный 18см. Найти АВ и cos А.

Контрольная работа № 5

Вариант 1

1^о. Диагонали ромба АВСD пересекаются в точке О. Докажите, что прямая BD касается окружности с центром А и радиусом, равным ОС.

2^о. Центр описанной окружности лежит на высоте равнобедренного треугольника и делит высоту на отрезки, равные 5см и 13см. Найти площадь этого треугольника.

3^о. Основание равнобедренного треугольника равно 18см, а боковая сторона равна 15см. Найти радиусы вписанной в треугольник и описанной около треугольника окружностей.

Контрольная работа № 5

Вариант 2

1^о. В равнобедренном треугольнике АВС с основанием АС проведена медиана BD. Докажите, что прямая BD касается окружности с центром С и радиусом, равным AD.

2^о. Меньший из отрезков, на которые центр описанной около равнобедренного треугольника окружности делит его высоту , равен 8см, а основание треугольника равно 12см. Найти площадь этого треугольника.

3^о. Высота, проведенная к основанию равнобедренного треугольника, равно 9см, а само основание равно 24см. Найти радиусы вписанной в треугольник и описанной около треугольника окружностей.