7


  • Учителю
  • Презентация по математике Решение простейших тригонометрических уравнений

Презентация по математике Решение простейших тригонометрических уравнений

Автор публикации:
Дата публикации:
Краткое описание:
предварительный просмотр материала



МОСКОВСКИЙ ГУМАНИТАРНЫЙ УНИВЕРСИТЕТ

Колледж



































Решение простейших тригонометрических уравнений



Методическая разработка занятия по дисциплине «Математика»

Для специальности 43.02.11 Гостиничный сервис

I курс





















Составил преподаватель: Мухамметжанова Р.К.











2015





Тема «Решение простейших тригонометрических уравнений»



Цели занятия:



Образовательная:

  • Вывести формулы решения простейших тригонометрических уравнений.

  • Сформировать у студентов первичные умения и навыки решения простейших тригонометрических уравнений.

Развивающая:

  • Развивать математическое мышление.

  • Умение наблюдать, сравнивать, обобщать и анализировать математические ситуации.

Воспитательная:

  • Воспитывать активность, самостоятельность, упорство и достижение цели.

Формируемые ОК:

  • ОК.3. Принимать решения в стандартных и нестандартных ситуациях, и нести за них ответственность.

  • ОК.4. Осуществлять поиск и использование информации, необходимой для эффективного выполнения профессиональных задач, профессионального и личностного развития;

  • ОК.5. Владеть информационной культурой, анализировать и оценивать информацию с использованием информационно-коммуникационных технологий.

  • ОК.6. Работать в коллективе и команде, эффективно общаться с коллегами, руководством, потребителями.



Знания и умения:

уметь:

У.5. уметь определять основные свойства функций и строить графики изученных функций

У.7. уметь преобразовывать простейшие тригонометрические выражения

У.9. уметь решать иррациональные, логарифмические и тригонометрические уравнения



знать:

З.1. Знать значение математической науки для решения теоретических и практических задач;

З.3. знать способы решения различных алгебраических уравнений

З.4. знать основные определения и формулы тригонометрии



Тип занятия: комбинированный.



Обеспечение занятия:

Наглядные пособия: таблицы значений тригонометрических функций, сводные таблицы решения тригонометрических уравнений, тригонометрический круг.

ТСО: компьютер, диапроектор.

Оснащение ТСО: программа Microsoft office PowerPoint.

Вычислительные средства: микрокалькуляторы, таблицы значений тригонометрических функций, тригонометрический круг.





Ход занятия:

  1. Организационный момент:

    1. Проверка отсутствующих, заполнение журнала.

    2. Постановка темы и целей урока.

  2. Проверка знаний:

    1. Фронтальный опрос (устные вопросы)

    2. 1. Тригонометрический круг (слайд №2)

2. Сформулируйте определение арксинуса числа.

3.Чему равен Презентация по математике Решение простейших тригонометрических уравнений ?

4.Сформулируйте определение арккосинуса числа.

5.Чему равен Презентация по математике Решение простейших тригонометрических уравнений ?

6.Сформулируйте определение арктангенса.

7.Чему равен Презентация по математике Решение простейших тригонометрических уравнений ?

8.Дайте определение арккотангенса числа.

9.Чему равен Презентация по математике Решение простейших тригонометрических уравнений ?



Устный счет по таблицам значения тригонометрических функций: (слайд №3, 4)

Презентация по математике Решение простейших тригонометрических уравнений; Презентация по математике Решение простейших тригонометрических уравнений ; Презентация по математике Решение простейших тригонометрических уравнений ; Презентация по математике Решение простейших тригонометрических уравнений ; Презентация по математике Решение простейших тригонометрических уравнений ;

Презентация по математике Решение простейших тригонометрических уравнений; Презентация по математике Решение простейших тригонометрических уравнений ; Презентация по математике Решение простейших тригонометрических уравнений .Презентация по математике Решение простейших тригонометрических уравнений



  1. Объяснение нового материала:



Актуализация опорных знаний:

Обратные тригонометрические функции необходимы нам для изучения новой темы «Решение простейших тригонометрических уравнений»,

так как они используются при решении тригонометрических уравнений.

В курсе алгебры вы уже встречались с различными видами уравнений. Давайте вспомним какие это уравнения?

Предполагаемый ответ: линейные, квадратные, кубические, логарифмические, показательные, иррациональные.

Сегодня мы с вами познакомимся с тригонометрическими уравнениями.

Это не последние уравнения в математике, например, на втором курсе мы начнем решать дифференциальные уравнения.



3.1 (Слайд № 5: Определение и виды простейших тригонометрических уравнений)



Давайте запишем определение тригонометрического уравнения.

Тригонометрическим называется уравнение, содержащее переменную под знаком тригонометрической функции.



Сегодня мы рассмотрим решение простейших из них:

Презентация по математике Решение простейших тригонометрических уравнений; Презентация по математике Решение простейших тригонометрических уравнений ; Презентация по математике Решение простейших тригонометрических уравнений ; Презентация по математике Решение простейших тригонометрических уравнений , где Презентация по математике Решение простейших тригонометрических уравнений

Решить тригонометрическое уравнение - это значит найти все его корни.

Корнем тригонометрического уравнения называется такое значение входящей в него переменной, которая удовлетворяет этому уравнению.



3.2 (Слайд № 6: Частные случаи уравнения Презентация по математике Решение простейших тригонометрических уравнений . )

При а=1 уравнение Презентация по математике Решение простейших тригонометрических уравнений имеет решения Презентация по математике Решение простейших тригонометрических уравнений , Презентация по математике Решение простейших тригонометрических уравнений .

При а=-1 уравнение Презентация по математике Решение простейших тригонометрических уравнений имеет решения Презентация по математике Решение простейших тригонометрических уравнений , Презентация по математике Решение простейших тригонометрических уравнений

При а=0 уравнение Презентация по математике Решение простейших тригонометрических уравнений имеет решения Презентация по математике Решение простейших тригонометрических уравнений , Презентация по математике Решение простейших тригонометрических уравнений .



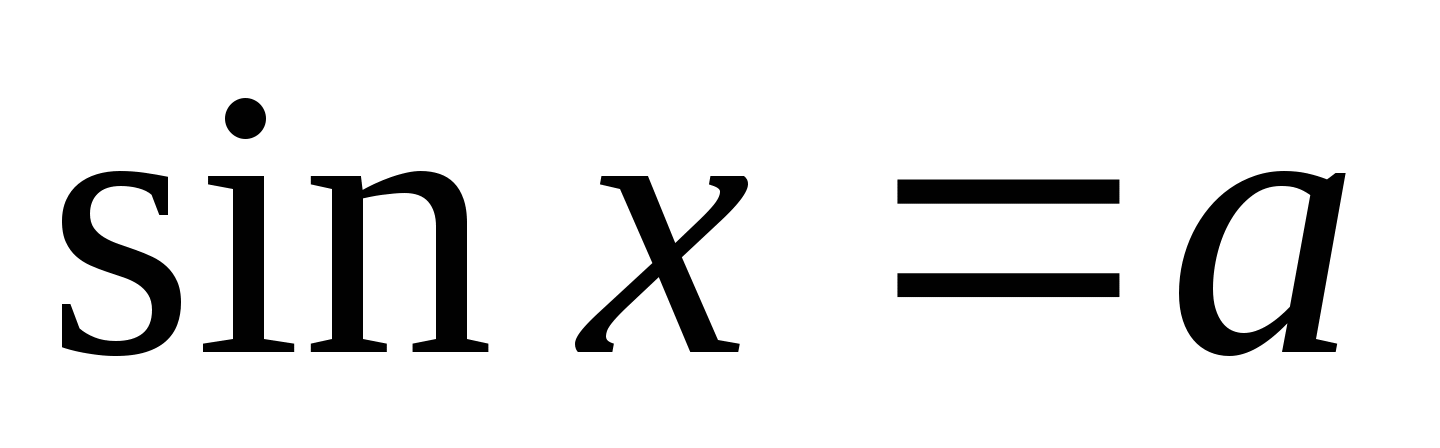  1. (Слайд №7,8,9: Уравнение вида Презентация по математике Решение простейших тригонометрических уравнений )



Рассмотрим уравнение вида Презентация по математике Решение простейших тригонометрических уравнений .

Так как Презентация по математике Решение простейших тригонометрических уравнений , то уравнение Презентация по математике Решение простейших тригонометрических уравнений при Презентация по математике Решение простейших тригонометрических уравнений и Презентация по математике Решение простейших тригонометрических уравнений не имеет решений.



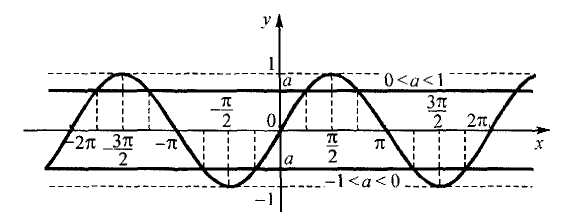
Период синуса равен Презентация по математике Решение простейших тригонометрических уравнений , поэтому достаточно найти все решения этого уравнения на любом отрезке длины Презентация по математике Решение простейших тригонометрических уравнений . Из рисунка видно что, что на отрезке Презентация по математике Решение простейших тригонометрических уравнений синус возрастает и принимает каждое свое значение один раз. Следовательно, на этом отрезке Презентация по математике Решение простейших тригонометрических уравнений . На отрезке Презентация по математике Решение простейших тригонометрических уравнений синус убывает и принимает каждое свое значение тоже один раз. Чтобы найти решение на этом отрезке, вспомним что Презентация по математике Решение простейших тригонометрических уравнений . Если Презентация по математике Решение простейших тригонометрических уравнений , то

Презентация по математике Решение простейших тригонометрических уравнений, и поэтому решением уравнения Презентация по математике Решение простейших тригонометрических уравнений на отрезке Презентация по математике Решение простейших тригонометрических уравнений будет Презентация по математике Решение простейших тригонометрических уравнений .

Для получения всех решений уравнения Презентация по математике Решение простейших тригонометрических уравнений к каждому из двух полученных решений прибавим числа вида Презентация по математике Решение простейших тригонометрических уравнений где Презентация по математике Решение простейших тригонометрических уравнений .Следовательно,

Презентация по математике Решение простейших тригонометрических уравнений(1)

Презентация по математике Решение простейших тригонометрических уравнений. (2)

Обе серии решений можно объединить:

Презентация по математике Решение простейших тригонометрических уравнений, Презентация по математике Решение простейших тригонометрических уравнений (3)

Презентация по математике Решение простейших тригонометрических уравненийназывают параметром, при к четном получается формула (1), при к нечетном получается формула (2)



Презентация по математике Решение простейших тригонометрических уравнений



















  1. (Слайд№10: Решите уравнение(закрепление))



3.5(Слайд №11: Частные случаи уравнения Презентация по математике Решение простейших тригонометрических уравнений )



При а=1 уравнение Презентация по математике Решение простейших тригонометрических уравнений имеет решения Презентация по математике Решение простейших тригонометрических уравнений , Презентация по математике Решение простейших тригонометрических уравнений .

При а= -1 уравнение Презентация по математике Решение простейших тригонометрических уравнений имеет решения Презентация по математике Решение простейших тригонометрических уравнений , Презентация по математике Решение простейших тригонометрических уравнений

При а=0 уравнение Презентация по математике Решение простейших тригонометрических уравнений имеет решения Презентация по математике Решение простейших тригонометрических уравнений , Презентация по математике Решение простейших тригонометрических уравнений .



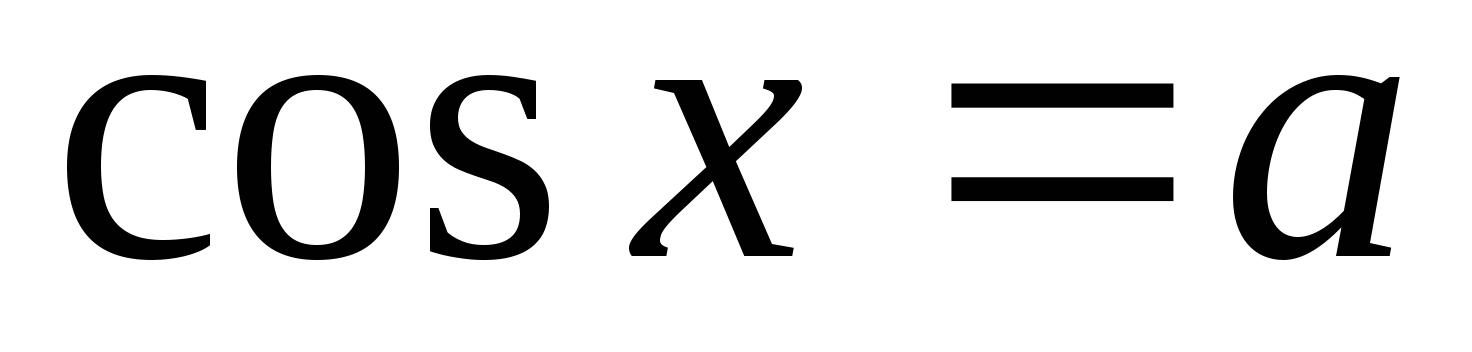  1. (Слайд №12,13,14: уравнение вида: Презентация по математике Решение простейших тригонометрических уравнений )

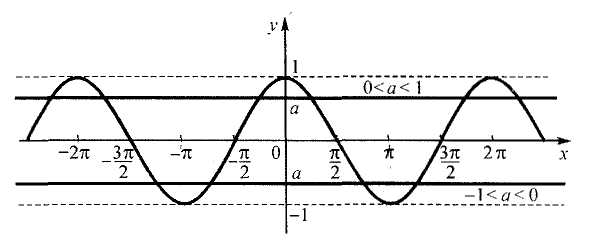
Рассмотрим уравнение Презентация по математике Решение простейших тригонометрических уравнений . При Презентация по математике Решение простейших тригонометрических уравнений и Презентация по математике Решение простейших тригонометрических уравнений уравнение Презентация по математике Решение простейших тригонометрических уравнений не имеет решений, так как Презентация по математике Решение простейших тригонометрических уравнений .

Презентация по математике Решение простейших тригонометрических уравнений











Так как период косинуса равен Презентация по математике Решение простейших тригонометрических уравнений , то при Презентация по математике Решение простейших тригонометрических уравнений для нахождения всех решений достаточно рассмотреть отрезок длины Презентация по математике Решение простейших тригонометрических уравнений . Удобнее всего выбрать отрезок Презентация по математике Решение простейших тригонометрических уравнений . Очевидно, что уравнение Презентация по математике Решение простейших тригонометрических уравнений на отрезке Презентация по математике Решение простейших тригонометрических уравнений имеет решение Презентация по математике Решение простейших тригонометрических уравнений , а на отрезке Презентация по математике Решение простейших тригонометрических уравнений - решение Презентация по математике Решение простейших тригонометрических уравнений так как функция косинус четная. Таким образом на отрезке Презентация по математике Решение простейших тригонометрических уравнений уравнение Презентация по математике Решение простейших тригонометрических уравнений имеет решения

Презентация по математике Решение простейших тригонометрических уравнений.

Чтобы записать все решения уравнения необходимо, учитывая периодичность косинуса, прибавить к каждому из найденных значений по Презентация по математике Решение простейших тригонометрических уравнений , где Презентация по математике Решение простейших тригонометрических уравнений . В итоге получим бесконечное множество решений

Презентация по математике Решение простейших тригонометрических уравнений, Презентация по математике Решение простейших тригонометрических уравнений .



3.7 (Слайд №15: Решите уравнение (закрепление))



3.8 (Слайд №16,17: уравнения вида: Презентация по математике Решение простейших тригонометрических уравнений , Презентация по математике Решение простейших тригонометрических уравнений : )

Так как период тангенса равен Презентация по математике Решение простейших тригонометрических уравнений , то для того чтобы найти все решения уравнения Презентация по математике Решение простейших тригонометрических уравнений , достаточно найти все его решения на любом отрезке длины Презентация по математике Решение простейших тригонометрических уравнений . По определению арктангенса решение уравнения на промежутке Презентация по математике Решение простейших тригонометрических уравнений есть Презентация по математике Решение простейших тригонометрических уравнений .

Для того чтобы получить все решения уравнения нужно к решению, полученному на отрезке длины Презентация по математике Решение простейших тригонометрических уравнений , прибавить Презентация по математике Решение простейших тригонометрических уравнений . Следовательно,



Презентация по математике Решение простейших тригонометрических уравнений, Презентация по математике Решение простейших тригонометрических уравнений

И решение уравнения Презентация по математике Решение простейших тригонометрических уравнений

Презентация по математике Решение простейших тригонометрических уравнений, Презентация по математике Решение простейших тригонометрических уравнений



3.9 (Слайд №18: Решите уравнение(закрепление))



3.10(Слайд № 19: Сводная таблица решения простейших тригонометрических уравнений)



Сводная таблица решения простейших тригонометрических уравнений,

Презентация по математике Решение простейших тригонометрических уравнений

Презентация по математике Решение простейших тригонометрических уравнений,

Презентация по математике Решение простейших тригонометрических уравнений

Презентация по математике Решение простейших тригонометрических уравнений,

Презентация по математике Решение простейших тригонометрических уравнений

Презентация по математике Решение простейших тригонометрических уравнений,

Презентация по математике Решение простейших тригонометрических уравнений

Презентация по математике Решение простейших тригонометрических уравнений, Презентация по математике Решение простейших тригонометрических уравнений

Презентация по математике Решение простейших тригонометрических уравнений,

Презентация по математике Решение простейших тригонометрических уравнений

Презентация по математике Решение простейших тригонометрических уравнений,

Презентация по математике Решение простейших тригонометрических уравнений

Презентация по математике Решение простейших тригонометрических уравнений,

Презентация по математике Решение простейших тригонометрических уравнений

Презентация по математике Решение простейших тригонометрических уравнений,

Презентация по математике Решение простейших тригонометрических уравнений

Презентация по математике Решение простейших тригонометрических уравнений

Презентация по математике Решение простейших тригонометрических уравнений,

Презентация по математике Решение простейших тригонометрических уравнений

Презентация по математике Решение простейших тригонометрических уравнений

Презентация по математике Решение простейших тригонометрических уравнений

Презентация по математике Решение простейших тригонометрических уравнений,

Презентация по математике Решение простейших тригонометрических уравнений

Презентация по математике Решение простейших тригонометрических уравнений,

Презентация по математике Решение простейших тригонометрических уравнений

Презентация по математике Решение простейших тригонометрических уравнений

Презентация по математике Решение простейших тригонометрических уравнений,

Презентация по математике Решение простейших тригонометрических уравнений

Презентация по математике Решение простейших тригонометрических уравнений,

Презентация по математике Решение простейших тригонометрических уравнений

Презентация по математике Решение простейших тригонометрических уравнений,

Презентация по математике Решение простейших тригонометрических уравнений

Презентация по математике Решение простейших тригонометрических уравнений,

Презентация по математике Решение простейших тригонометрических уравнений

Студенты заполняют сводную таблицу по ходу объяснения материала.





3.11 (Слайд №20, 21: Примеры решения уравнений).



  1. Самостоятельное решение уравнений трех уровней. Ребята, вы сейчас постараетесь решить уравнения по карточкам. Те из вас, кто быстро сможет решить 1-2 уравнение 1 уровня, переходите на следующий. Задания 1 уровня решить всем. Кто не успеет выполнить, будет решать эти уравнения дома.



I уровень II уровень III уровень





соsх = Презентация по математике Решение простейших тригонометрических уравнений соs2х = Презентация по математике Решение простейших тригонометрических уравнений соs(2хПрезентация по математике Решение простейших тригонометрических уравнений )=Презентация по математике Решение простейших тригонометрических уравнений

sin х= - Презентация по математике Решение простейших тригонометрических уравнений sin3 х=Презентация по математике Решение простейших тригонометрических уравненийsin (хПрезентация по математике Решение простейших тригонометрических уравнений)­= Презентация по математике Решение простейших тригонометрических уравнений

соsх= 0 соs5х=1 2 sin(3хПрезентация по математике Решение простейших тригонометрических уравнений)= 1

tgх= Презентация по математике Решение простейших тригонометрических уравнений Презентация по математике Решение простейших тригонометрических уравнений+ 2соsх=0 соs(хПрезентация по математике Решение простейших тригонометрических уравнений )= - 1

сtgх= -2



  1. (Слайд№22: Подведение итогов занятия).



Продолжите фразу :

Сегодня на занятии я повторил …

Сегодня на занятии я узнал …

Сегодня на занятии я научился …

На следующем занятии мы рассмотрим более сложные тригонометрические уравнения и познакомимся с методами их решения.



Активным студентам выставление оценок.

6. (Слайд№23: домашнее задание).

(2) §33-35, решить примеры.



Литература:





  • 1.Математика для техникумов. Алгебра и начала анализа: Учебник. Ч.1/ Под ред. Г.Н. Яковлева - М.: Наука, 1987 - 464с.

  • Н.В. Богомолов Практические занятия по математике: Учеб. Пособие для средних спец. Заведений / Н.В. Богомолов - М.: Высшая школа, 2003-495с.Презентация по математике Решение простейших тригонометрических уравнений

  • 3. Ш.А. Алимов Алгебра и начала анализа 10 - 11 Москва Просвещение 2016г.

  • А.Г. Мордкович Алгебра и начала анализа 10 - 11 «Мнемозина» 2012г.

  • В.С. Шипачев Задачи по высшей математике «Легион Ростов на Дону» 2015г.



































8



⇧
⇩
скачать материал


 
 
X

Чтобы скачать данный файл, порекомендуйте его своим друзьям в любой соц. сети.

После этого кнопка ЗАГРУЗКИ станет активной!

Кнопки рекомендации:

загрузить материал