Содержание

4

Предмет и объект оценивания ………………………………….

6

Организация контроля и оценки освоения программы учебной дисциплины «Математика» …………………………..

7

2

КОМПЛЕКТ ОЦЕНОЧНЫХ СРЕДСТВ

2.1

Структура индивидуального варианта …………………………

8

2.2

Задания для обучающихся для подготовки к экзамену ……….

9

2.3

Критерии оценивания заданий …………………………………

23

3

ПЕРЕЧЕНЬ РЕКОМЕНДУЕМЫХ ИНФОРМАЦИОННЫХ ИСТОЧНИКОВ ДЛЯ ПОДГОТОВКИ ………………………..

25

1. ПАСПОРТ КОМПЛЕКТА КОНТРОЛЬНО-ОЦЕНОЧНЫХ СРЕДСТВ

   1. Контроль и оценка результатов освоения учебной дисциплины «Математика».

1. 2. Предмет и объект оценивания.

Объект оценивания

З1 - З3

Вопрос 1. ТЕОРЕТИЧЕСКИЙ

У1 - У7, У12 - У17, У26, У27, У29 - У31

Вопрос 2. ПРАКТИЧЕСКОЕ ЗАДАНИЕ

(уровень А)

У1 - У7, У12 - У17, У26, У27, У29 - У31

Вопрос 3. ПРАКТИЧЕСКОЕ ЗАДАНИЕ

(уровень В)

1. 2. Организация контроля и оценки освоения программы учебной дисциплины «Математика».

итогового контроля

Критерии положительной аттестации

1 семестр

Экзамен

Условием допуска к промежуточной аттестации является положительная текущая аттестация. Экзаменационная отметка выставляется исходя из демонстрации освоенных умений, знаний и компетенций по контролируемым показателям.

2 семестр

Экзамен

Условием допуска к промежуточной аттестации является положительная текущая аттестация. Экзаменационная отметка выставляется исходя из демонстрации освоенных умений, знаний и компетенций по контролируемым показателям.

2. КОМПЛЕКТ ОЦЕНОЧНЫХ СРЕДСТВ

2.1. Структура индивидуального варианта

• ЦЕЛЬ: проверить уровень сформированности образовательных результатов обучающихся

• ПРОВЕРЯЕМЫЕ ОБРАЗОВАТЕЛЬНЫЕ РЕЗУЛЬТАТЫ:

У1 - У7, У12 - У17, У26, У27, У29 - У31, З1 - З3

• СТРУКТУРА ИНДИВИДУАЛЬНОГО БИЛЕТА

Наименование дидактических единиц

К-во

Формируются

из №№ заданий

1 вопрос - ТЕОРЕТИЧЕСКИЙ (на 30 баллов)

I

1.1

Развитие понятия числа.

1

1.1.1 - 1.1.4

1.2

Уравнения и системы.

1

1.2.1 - 1.2.4

II

1.3

Функции. Основные понятия. График функции.

1

1.3.1 - 1.3.5

1.4

Свойства функций.

1

1.4.1 - 1.4.3

1.5

Предел функции. Вычисление пределов.

1

1.5.1 - 1.5.8

III

1.6

Степени и корни.

1

1.6.1 - 1.6.2

1.7

Логарифмы.

1

1.7.1 - 1.7.6

1.8

Степенная, показательная и логарифмическая функция.

1

1.8.1 - 1.8.3

1.9

Иррациональные, показательные и логарифмические уравнения и неравенства.

1

1.9.1 - 1.9.4

IV

1.10

Комбинаторика, статистика и теория вероятностей.

1

1.10.1 - 1.10.4

2 Вопрос - ПРАКТИЧЕСКОЕ ЗАДАНИЕ, уровень А (на 50 баллов)

I

2.1

Работа над формулами

1

2.1.1 - 2.1.12

2.2

Уравнения и системы

1

2.2.1 - 2.2.12

II

2.3

Функция. Основные понятия и определения. График функции.

1

2.3.1 - 2.3.12

2.4

Исследование функций.

1

2.4.1 - 2.4.12

2.5

Предел функции. Вычисление пределов.

1

2.5.1 - 2.5.12

III

2.6

Степени и корни.

1

2.6.1 - 2.6.12

2.7

Логарифмы.

1

2.7.1 - 2.7.12

2.8

Показательные уравнения и неравенства.

1

2.8.1-2.8.12

2.9

Логарифмические уравнения и неравенства.

1

2.9.1 - 2.9.12

IV

2.10

Комбинаторика.

1

2.10.1 - 2.10.12

3 Вопрос - ПРАКТИЧЕСКОЕ ЗАДАНИЕ, уровень В (на 30 баллов)

I

3.1

Уравнения и системы.

1

3.1.1 - 3.1.12

II

3.2

Функции. Пределы. Непрерывность.

1

3.2.1 - 3.2.12

III

3.3

Степенная, показательная и логарифмическая функции.

1

3.3.1 - 3.3.12

• Исходные материалы: двойной лист в клетку, ручка, МК, Краткий справочник по математике.

• Время выполнения: 180 мин.

• Формирование билета: 1ВОПРОС = 10 теор. вопросов, 2 ВОПРОС = 10 практических задания уровня А, 3 ВОПРОС = 3 практических задания уровня В.

• Оценивание заданий: Вопрос № 1 - 10 вопросов по 3 балла; вопрос №2 - 10 заданий по 5 баллов; вопрос № 3 - 3 задания по 10 баллов.

• Отметка «5»  81 % правильных ответов

«4» = 61- 80 % правильных ответов

«3» = 39 - 60 % правильных ответов

«2» < 39 % правильных ответов

ПРИМЕЧАНИЕ: 1 Не разрешается выходить из аудитории

2. Отметка ставится только на основании правильных за ошибочные ответы баллы не снижаются.

2.2. Задания для обучающихся для подготовки к экзамену

ВОПРОС 1 ТЕОРЕТИЧЕСКИЙ

Вопрос 1. 1 РаЗВИТИЕ понятия числа.

1) Развитие понятия числа

• определения:  натуральных чисел

 целых чисел

 рациональных чисел

 иррациональных чисел

 действительных чисел

2) Основное свойство пропорции.

3) Формулы сокращенного умножения

(a + b)²

a² + b²

(a + b)³

a³ + b³

(a - b)²

a² - b²

(a - b)³

a³ - b³

4) Формула разложения квадратного трехчлена на линейные множители при Д > 0 и Д = 0.

Вопрос 1. 2 Уравнения И системы.

1) Линейные уравнения, неравенства, системы

• определения:  линейного уравнения и неравенства

 дробно-линейного уравнения и неравенства

 дробно-рационального уравнения и неравенства

 о.д.з уравнения

 равносильных уравнений

2) Решение уравнений: и

3) Квадратные уравнения

• определение:  полного квадратного уравнения

 неполного квадратного уравнения

 приведенного квадратного уравнения

• формула нахождения корней квадратного уравнения;

• виды неполных квадратных уравнений;

• теорема Виета

4) Алгоритмы решений:

• квадратных неравенств

• метод интервалов;

• системы двух линейных уравнений с двумя переменными;

• систем.

Вопрос 1.3 ФУНКЦИИ. ОСНОВНЫЕ ПОНЯТИЯ. ГРАФИК ФУНКЦИИ.

1. Функция. Основные понятия

• определение функции и символическое обозначение функции;

• определение и обозначение области определения функции;

• определение и обозначение множества значений функции;

• определение значения функции в точке х₀.

2. Числовая функция

• определение;

• область определения числовой функции;

• основные правила нахождения области определения числовой функции.

3. График функции. Простейшие преобразования графика функции

• определение графика функции;

• графики основных элементарных функций:

• правила преобразования графиков функций:

4. Обратная функция

• определение обратимой функции;

• алгоритм нахождения

 формулы для функции, обратной данной;

 построения графика функции, обратной данной;

5. Сложная функция

• определение.

Вопрос 1.4 СВОЙСТВА ФУНКЦИЙ.

1. Определения:

• монотонность функции;

• промежутки знакопостоянства функции;

• четность и нечетность;

• нули функции;

• ограниченность;

• периодичность;

• непрерывность;

• наибольшее и наименьшее значения функции.

2. Исследование функций аналитически. Как по формуле находится?

• область определения числовой функции;

• множество значений функции;

• нули функции;

• четность и нечетность функции.

3. Исследование функций по графику. Как по графику определить?

• область определения;

• множество значений;

• нули (корни) функции;

• монотонность;

• промежутки знакопостоянства;

• четность и нечетность;

• обратимость;

• непрерывность;

• наибольшие и наименьшие значения;

• ограниченность;

• периодичность.

Вопрос 1.5 ПРЕДЕЛ ФУНКЦИИ. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ.

1. Предел функции

• определение предела функции в точке и на бесконечности;

• определение окрестности точки;

• теорема о единственности предела.

2. Односторонние пределы: определение и обозначение.

3. Основные теоремы о пределах.

4. Табличные пределы: .

5. Замечательные пределы.

6. Правила вычисления пределов

• виды неопределенностей;

• правила раскрытия неопределенностей вида: ; , зависящие от иррациональности, .

7. Непрерывность функции

• определение функции, непрерывной в точке и на промежутке;

• условия непрерывности функции в точке;

• свойства непрерывности функции.

8. Точки разрыва функции

• определение точек разрыва функции;

• классификация точек разрыва.

Вопрос 1.6 СТЕПЕНИ И КОРНИ.

1. Степени

• определение степени  с натуральным показателем;

 с рациональным показателем;

 с действительным показателем;

• виды степеней;

• свойства степеней с рациональными показателями.

2. Корни

• свойства;

• свойства арифметических корней n-й степени.

Вопрос 1.7 ЛОГАРИФМЫ.

1) определение логарифма и его краткая запись;

2) основное логарифмическое тождество;

3) свойства логарифмов;

4) определение и правила логарифмирования и потенцирования;

5) формула перехода от одного основания логарифма к другому;

6) обозначение десятичного и натурального логарифмов.

Вопрос 1.8 СТЕПЕННАЯ, ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИЯ

1. Степенная функция

• определение;

• виды степенных функций; их графики и свойства.

1. Показательная функция

• определение;

• виды; их графики и свойства.

1. Логарифмическая функция

• определение;

• связь между показательной и логарифмической функциями;

• виды; их графики и свойства.

Вопрос 1.9 ИРРАЦИОНАЛЬНЫЕ, ПОКАЗАТЕЛЬНЫЕ И ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА.

1. Иррациональные уравнения и неравенства

• определения и алгоритмы решений.

2. Степенные уравнения и неравенства

• решение уравнений вида: ;

• решение неравенств вида:

при х₁ < х₂, при а > 1 и 0 < a < 1.

3. Показательные уравнения и неравенства

• определения;

• основное свойство;

• решение уравнений вида:

• методы решения показательных уравнений.

• решение неравенств вида: при а > 1 и 0<a <1.

4. Логарифмические уравнения и неравенства

• определения;

• решение уравнений вида:

.

• методы решения логарифмических уравнений.

• решение неравенств вида:

при а > 1 и 0 < a < 1.

Вопрос 1.10 КОМБИНАТОРИКА,

СТАТИСТИКА И ТЕОРИЯ ВЕРОЯТНОСТЕЙ.

1. Понятия комбинаторики

определения : комбинаторики; соединений; п - факториала.

2. Основные виды соединений

• • • Перестановки: определение обозначение, формула

    • Размещения: определение; обозначение; формулы, свойства

    • Сочетания: определение; обозначение формула свойства

3. Основные понятия события.Определения:

   • теории вероятностей,

   • испытания

   • случайного события

   • искомого события

   • равновозможных событий

   • достоверного события

   • невозможного события

   • полной системы событий

   • противоположных событий

4. Вероятность события

• Классическое определение;

• формула;

• свойства:

ВОПРОС 2 ПРАКТИЧЕСКОЕ ЗАДАНИЕ (уровень А)

2. 1. РАБОТА НАД ФОРМУЛАМИ

1)

, Ок - ? 7) , Н₁ - ?

2)

, Ин - ? 8) , m_ред - ?

3)

, Лн - ? 9) , Т - ?

4)

, Пв - ? 10) , l - ?

5)

, N - ? 11) , р₂ - ?

6)

, h - ? 12) , С_обр - ?

2. 2. УРАВНЕНИЯ И СИСТЕМЫ

Упростить: .

2)

Найти сумму корней уравнения .

• Решить уравнение

3)

4)

5)

Если (х₀; у₀) - решение системы, то сумма х₀ + у₀ равна

6)

Решить неравенство: .

7)

Решить систему неравенств

• Решить неравенства

8)

11)

9)

12)

10

2. 3. ФУНКЦИЯ. ОСНОВНЫЕ ПОНЯТИЯ И ОПРЕДЕЛЕНИЯ. ГРАФИК ФУНКЦИИ.

Найти значение аргумента, если значение функции равно 13.

• Найти область определения числовой функции

2)

3)

• Построить графики функций

4)

7)

5)

8)

6)

9)

10)

Найти функцию, обратную данной: а) б)

• Дана функция

11)

Найти сумму значений функций в указанных точках: .

12)

Построить график функции.

2. 4. ИССЛЕДОВАНИЕ ФУНКЦИЙ.

Найти нули функции: .

2)

Найти область определения функции: .

3)

Определить четность функции: а) ; б) .

4)

Определить промежутки, на которых функция отрицательна.

• По графику функции определить:

5)

… область определения функции

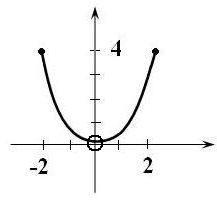
6)

… область значения функции

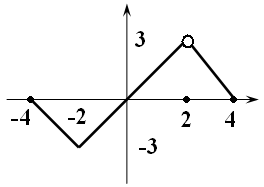
7)

… нули функции

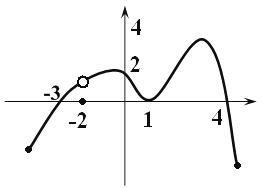
8)

… все значения х, при которых график функции возрастает

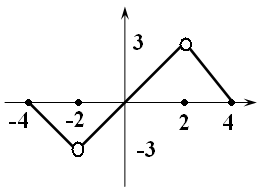
9)

… все значения х, при которых график функции принимает положительные значения

10)

все значения х, при которых функция принимает наибольшие значения

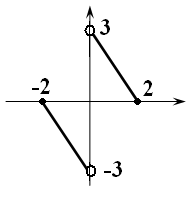
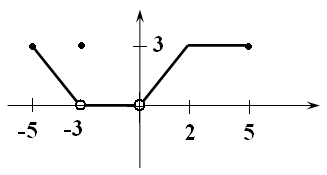
11)

… обратимые функции

а) б) в) г)

12)

… четные функции

а) б) в) г)

2. 5. ПРЕДЕЛ ФУНКЦИИ. ВЫЧИСЛЕНИЕ ПРЕДЕЛОВ.

1)

7)

2)

8)

3)

9)

4)

10)

5)

11)

6)

12)

2. 6. СТЕПЕНИ И КОРНИ.

1)

2)

• Вычислить:

3)

6)

4)

4² 4^-3 + 1,5⁰ - 2:2²

7)

5)

8)

• Упростить:

9)

11)

Упростить:

10)

12)

Освободится от знака корня в знаменатели дроби

2. 7. ЛОГАРИФМЫ.

1)

2)

• Вычислить:

3)

5)

4)

6)

• Вычислить:

7)

9)

8)

10)

11)

Найти х, если

12)

Из данных выражений выбрать те, которые имеют смысл

а) в)

б) г)

2. 8. ПОКАЗАТЕЛЬНЫЕ УРАВНЕНИЯ И НЕРАВЕНСТВА.

1)

4 2^х = 1

4)

2)

4 ^х-1 = 1

5)

3)

6 ^{3х - 1} = 6 ^{1 - 2х}

6)

• Решить неравенство:

7)

10)

8)

11)

9)

12)

2. 9. ЛОГАРИФМИЧЕСКИЕ УРАВНЕНИЯ И НЕРАВЕНСТВА.

1)

4)

2)

5)

3)

,

где a, b - const

6)

• Решить уравнение:

7)

10)

8)

11)

9)

12)

Найти область определения функции

2. 10. КОМБИНАТОРИКА

Сколькими способами могут разместиться 6 человек вокруг круглого стола?

2)

Сколькими способами 5 человек, избранные в студсовет, могут распределить между собой пять различных обязанностей.

3)

Вычислить:

а) б)

5)

а) б)

4)

а) б)

6)

7)

На станции 10 запасных путей. Сколькими способами можно расставить 6 поездов?

8)

Перед выпуском группа студентов в 30 человек обменялась фотографиями. Сколько всего было роздано фотокарточек?

9)

Сколькими способами можно заполнить лотерейный билет 5 из 36?

10)

Из 10 кандидатов нужно выбрать 3 человека на конференцию. Сколькими различными способами это можно сделать?

11)

Из 7 кандидатов в студсовет необходимо выбрать трех человек. Сколькими способами это можно сделать.

12)

В урне 12 шаров: 3 белых, 4 черных и 5 красных. Какова вероятность вынуть из урны черный шар?

ВОПРОС 3 ПРАКТИЧЕСКОЕ ЗАДАНИЕ (уровень В)

3.1. УРАВНЕНИЯ И СИСТЕМЫ.

• Решить уравнение:

1)

2)

3)

Решить систему уравнений

• Решить уравнения:

4)

6)

5)

(5х + 1)² + 6 (5х + 1) - 7 = 0

7)

х³ - 2х² - 3х + 6 = 0

• Решить неравенства:

8)

9)

• Решить неравенства:

10)

12)

11)

3.2. ФУНКЦИИ. ПРЕДЕЛЫ. НЕПРЕРЫВНОСТЬ.Построить график функции:

1)

2)

• По графику, изображенному на рисунке, укажите:

3)

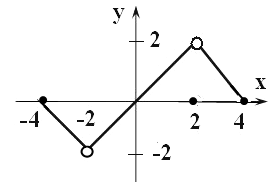
а)

область определения;

б)

область значения;

в)

обратимость;

г)

промежутки знакопостоянства;

д)

четность и нечетность

4)

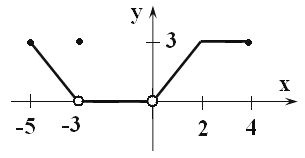
а)

область определения;

б)

множество значений;

в)

точки, в которых функция обращается в ноль;

г)

промежутки возрастания и убывания функции;

д)

наибольшее и наименьшее значения

5)

Дана функция:

а) построить ее график;

б) найти значение функций

у(- 2), у( 1), у( 3), у( - 4)

6)

Найти область определения функции

• Найти пределы:

7)

10)

8)

11)

9)

12)

3.3. СТЕПЕННАЯ, ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ.

1)

• Решить уравнения:

2)

3)

• Решить неравенство

4)

5)

• Решить уравнения:

6)

8)

7)

• Решить неравенство

9)

.

10)

• Построить график функции

11)

12)

.

2.3. Критерии оценивания заданий

ВОПРОС 1 ТЕОРЕТИЧЕСКИЙ

ВОПРОС 1 состоит из 10 теоретических вопросов.

Правильное выполнение любого задания ВОПРОСА 1 оценивается в 3 балла. За неверный ответ или его отсутствие ставится 0 баллов.

ВОПРОС 2 ПРАКТИЧЕСКОЕ ЗАДАНИЕ (уровень А)

ВОПРОС 2 состоит из 10 практических задач уровня А.

Правильное выполнение любого задания ВОПРОСА 2 оценивается в 5 баллов. За каждое практическое задание уровня А ставится:

• 5 баллов ставится если студент:

• полностью выполнил все требования индивидуального задания;

• отвечал самостоятельно без наводящих вопросов преподавателя. Возможны одна - две неточности при освещении второстепенных вопросов или в выкладках, которые студент легко исправил по замечанию преподавателя.

• 3-4 балла ставится если ответ удовлетворяет основным требованиям, но при этом имеет один из недостатков:

• в выполнении допущены небольшие неточности, не исказившие решение задания;

• допущены один - два недочета при освещении основного содержания ответа, исправленные по замечанию преподавателя;

• допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные по замечанию преподавателя.

• 1-2 балла ставится в следующих случаях:

• допущены неточности в выполнении индивидуального задания, но показано общее понимание вопроса;

• имелись затруднения или допущены ошибки в выполнении индивидуального задания, но осуществлены значительные исправления после нескольких наводящих вопросов преподавателя;

• 0 баллов ставится в следующих случаях:

• не в полном объеме решена поставленная задача;

• обнаружено значительные отклонения в выполнении индивидуального задания;

• после нескольких замечаний преподавателя не исправлены неточности в выполнении индивидуального задания.

ВОПРОС 3 ПРАКТИЧЕСКОЕ ЗАДАНИЕ (уровень В)

ВОПРОС 3 состоит из 3 практических задач уровня В.

Правильное выполнение любого задания ВОПРОСА 3 оценивается в 10 баллов. За каждое практическое задание уровня В ставится:

• 9-10 баллов ставится если студент:

• полностью выполнил все требования индивидуального задания;

• отвечал самостоятельно без наводящих вопросов преподавателя. Возможны одна - две неточности при освещении второстепенных вопросов или в выкладках, которые студент легко исправил по замечанию преподавателя.

• 6-8 баллов ставится если ответ удовлетворяет основным требованиям, но при этом имеет один из недостатков:

• в выполнении допущены небольшие неточности, не исказившие решение задания;

• допущены один - два недочета при освещении основного содержания ответа, исправленные по замечанию преподавателя;

• допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные по замечанию преподавателя.

• 3-5 баллов ставится в следующих случаях:

• допущены неточности в выполнении индивидуального задания, но показано общее понимание вопроса;

• имелись затруднения или допущены ошибки в выполнении индивидуального задания, но осуществлены значительные исправления после нескольких наводящих вопросов преподавателя;

• 1-2 балла ставится в следующих случаях:

• не в полном объеме решена поставленная задача;

• обнаружено значительные отклонения в выполнении индивидуального задания;

• после нескольких замечаний преподавателя не исправлены неточности в выполнении индивидуального задания.

• 0 баллов ставится, если:

• студент обнаружил полное незнание и непонимание изучаемого учебного материала или не смог выполнить задание.

Баллы, полученные за все выполненные теоретические и практические задания, суммируются. По конечной сумме выставляется отметка в зачетную книжку студента:

Отметка «5»  91 балла;

«4» = 74-90 баллов;

«3» = 60-73 баллов;

«2» < 60 баллов.

ПЕРЕЧЕНЬ РЕКОМЕНДУЕМЫХ ИНФОРМАЦИОННЫХ

ИСТОЧНИКОВ ДЛЯ ПОДГОТОВКИ

ОСНОВНЫЕ ИСТОЧНИКИ:

1. Башмаков М. И. Математика. Задачник : Учебное пособие, изд. 3-е / М. И. Башмаков. - М.: Академия, 2014.

2. Башмаков М. И. Математика : Учебник для учреждений начального и среднего профессионального образования / М. И. Башмаков. - М.: Академия, 2011.

3. Богомолов Н. В. Математика. Среднее профессиональное образование, 7-е изд., стереотипное / Н. В. Богомолов, П. Самойленко. - М.: Дрофа, 2010.

4. Богомолов Н. В. Сборник дидактических заданий по математике: учебное пособие для Ссузов, 3-е изд., стереотипное / Н. В. Богомолов. - М.: Дрофа, 2011.

5. Дадаян А. А. Сборник задач по математике : Учебное пособие. Гриф МО РФ / А. А Дадаян. - М.: Форум, 2013.

6. Колягин Ю. М. Математика. Книга 1: Учебник. Среднее профессиональное образование / Ю. М. Колягин, Г. Л. Луканкин, Г. Яковлев. - М.: ОНИКС 21 век, 2009.

7. Пехлецкий И. Д. Математика : Учебник для студентов образовательных учреждений среднего профессионального образования. Гриф МО РФ / И. Д. Пехлецкий. - М.: Академия, 2013.

ДОПОЛНИТЕЛЬНЫЕ ИСТОЧНИКИ:

8. Гмурман В. Е. Руководство к решению задач по теории вероятностей и математической статистике: учеб.пособие / В. Е. Гмурман- М.: Высш. шк., 2010.

9. Гмурман В. Е. Теория вероятностей и математическая статистика:учеб.пособие / - В. Е. Гмурман. - М.: Высшая школа ,2008

10. Майсеня Л.И. Справочник по математике. Основные понятия и формулы / Л. И. Майсеня. - М.: Вышейшая школа, 2012.

11. Райбул С. В. Алгебра и геометрия в таблицах и схемах / С. В. Райбул. - Ростов на/Д.: Феникс, 2013.

ИНТЕРНЕТ-РЕСУРСЫ:

12. Средняя математическая интернет-школа. Вся элементарная математика. Режим доступа: www.bymath.net/index.html

13. Виртуальная школа Юного математика. Режим доступа: www.math.md/school/indexr.html

14. Репетитор по математике. Справочные материалы. Режим доступа: ege-ok.ru/spravochnyie-materialyi/

15. Портал ЯКласс. Образовательный интернет-портал. Режим доступа: www.shkola.lv/index.php?mode=newlsn&lsnid=0

16. Прикладная математика. Справочник математических формул. Режим доступа: www.pm298.ru/menu.php</