- Учителю
- Проект 'Рабочий словарь по алгебре' к УМК А. Г. Мордковича 7 класс
Проект 'Рабочий словарь по алгебре' к УМК А. Г. Мордковича 7 класс
Рабочий словарь- справочник по алгебре
для УМК А. Г. Мордковича 7 класс
Паспорт проекта
Название проекта
Рабочий словарь- справочник по алгебре
(7 класс, к УМК А. Г. Мордковича)
Целевая аудитория
Учащиеся 7 класса
Автор проекта
Пирогова Татьяна Николаевна
Тип проекта
По числу учащихся - индивидуальный и групповой.
По доминирующему методу - информационный и творческий.
По предметной области - математика.
По продолжительности - длительный (учебный год).
Основные цели и задачи проекта
Стимулировать интерес учеников к изучению математического языка, формировать их самостоятельность, инициативность в решении задач.
Работа со словарями и справочниками по математике, с учебником А. Г. Мордковича Алгебра 7 класс.
Создание своего словарика-справочника по математике.
Сравнение своей работы с другими и обобщение полученных результатов.
Результаты
Коллективно создан краткий словарь-справочник по алгебре 7 класса. В него вошли определения математических терминов, изученных в курсе алгебры 7 класса.
Также словарь содержит 8 теорем, 9 правил, 10 различных алгоритмов, сравнительные таблицы, формулы, свойства и основные степени чисел.
Период и этапы реализации
Систематически на уроках и дома в течении всего учебного года.
Заключение
Данный проект учащихся - это дидактическое средство активизации познавательной деятельности, развитие креативности и одновременно формирование определѐнных личностных качеств, которые ФГОС определяет как результат освоения основной
образовательной программы среднего общего образования.
Предложенное направления проектной деятельности позволяет школьникам среднего звена углубиться в изучение математики, а также повысить им уровень ее понимания. Но кроме этого, оно предоставляет учащимся дополнительные возможности самореализации, помогает стать успешными в изучении математики.
Данный проект способствует эффективному формированию всех ключевых компетенций (информационной, коммуникативной, социальной, умения учиться и жить вместе).
Я уверена, что учитель математики обязательно должен следит за правильностью и точностью речи учащихся - верным употреблением терминов.
Предмет математика - сложный, наиболее трудоёмкий предмет. Для сознательного усвоения знаний по математике учащемуся необходимо умение логически мыслить, грамотно рассуждать, анализировать. Но в первую очередь он должен ясно, точно, кратко излагать свои мысли, правильно строить предложения.
Именно на уроках математики учащийся должен привыкать к краткой, чёткой, логически обоснованной речи.
К видам работы по коррекции речи на уроках математики можно отнести следующее:
1. ведение словарей, где записывают новые термины (работа с математическим словарём)
2. использование «памяток»
3. написание словарных диктантов
4. придумывание историй, сказок, написание стихотворений и составление кроссвордов с использованием математических терминов.
В интернете есть множество готовых справочников и таблиц по математике, есть различные словари от 1 класса до ВУЗа, но я считаю, что словарь, составленный лично учащимися при работе с учебником, намного полезнее.
Мне близка концепция учебника автора А. Г. Мордковича рассматривать математику, как гуманитарный предмет, который позволяет субъекту правильно ориентироваться в окружающей действительности, «ум в порядок приводит» и оказывает существенное влияние на развитие речи обучаемых». Действительно, математика описывает реальные процессы на математическом языке в виде математических моделей. Поэтому математический язык и математическая модель - ключевые слова курса, его идейный стержень.
Изучая новый материал на уроке с учителем, учащиеся узнают новые понятия и новые слова. Дома, опираясь на работу со словарями, справочниками по математике и учебником, учащиеся продолжают работу с ними. Используя знаки-символы, изображенные на полях учебника, ученики прекрасно ориентируется в том, что надо запомнить и записать в свой рабочий словарь- справочник.
Системно-деятельностный подход к обучению предполагает:
• наличие у детей познавательного мотива (желания узнать, открыть, научиться) и конкретной учебной цели (понимания того, что именно нужно выяснить, освоить);
• выполнение учениками определённых действий для приобретения недостающих знаний;
• выявление и освоение учащимися способа действия, позволяющего осознанно применять приобретённые знания;
• формирование у школьников умения контролировать свои действия - как после их завершения, так и по ходу;
• включение содержания обучения в контекст решения значимых жизненных задач.
Ведение учащимися рабочего словаря по алгебре полностью соответствует реализации системно-деятельностного подхода в обучении.
Термин
Определение
числовое выражение
Числовым выражением называют всякую запись, составленную из чисел и знаков арифметических действий.
алгебраическое выражение
Алгебраическим выражением называют всякую запись, составленную из чисел, букв и знаков арифметических действий.
значение числового выражения
Число, которое получается в результате упрощений числового выражения, называют значением числового выражения.
значение алгебраического выражения
Число, которое получается в результате упрощений и вычислений алгебраического выражения, при конкретных значениях входящих в него букв, называют значением алгебраического выражения.
допустимые значения переменной
Конкретные значения переменных называют допустимыми значениями, если при них алгебраическое выражение имеет числовое значение.
недопустимые значения переменной
Конкретные значения переменных называют недопустимыми, если при них алгебраическое выражение не имеет смысла.
математическая модель
Математическая модель - описание различных реальных ситуаций на математическом языке, используя разные правила, свойства, законы.
словесная модель
Математическая модель, которая описывает реальные ситуации словами, называется словесной моделью.
алгебраическая модель
Математическая модель, которая описывает реальные ситуации алгебраически, называется алгебраической или аналитической моделью.
графическая модель
Математическая модель, которая описывает реальные ситуации графически, называется графической или геометрической моделью.
уравнение
Равенство, содержащее переменные
корень уравнения
Значения переменной, при каждом из которых уравнение обращается в верное числовое равенство - называется корнем уравнения.
решить уравнение
Решить уравнение - это значит найти все его корни или установить, что их нет.
линейным уравнением с одной переменной
Линейным уравнением с одной переменной х называют уравнение вида
ах + в = 0.
коэффициент
Числа а и в в уравнении ах + в = 0 называются коэффициентами.
алгоритм
Определенная программа действий, определенный порядок ходов - в математике называется алгоритмом
координатная прямая или координатная ось
Прямую, на которой выбрана начальная точка (начало отсчета), масштаб (единичный отрезок, т. е. отрезок, длина которого считается равной 1) и положительное направление, называют координатной прямой или координатной осью
координата точки
Каждому числу соответствует единственная точка координатной прямой, эти числа называют координатами соответствующих точек.
открытый луч
Множество точек, которые лежат на прямой правее точки а, называют открытым лучом и обозначают (а; +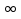 ), множество точек, которые лежат на прямой левее точки в также называют открытым лучом и обозначают (-
), множество точек, которые лежат на прямой левее точки в также называют открытым лучом и обозначают (-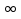 ; в)
; в)
луч
Множество точек, которые лежат на прямой правее точки а, включая точку а, называют лучом и обозначают [а; +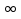 ), множество точек, которые лежат на прямой левее точки в, включая точку в. также называют лучом и обозначают (-
), множество точек, которые лежат на прямой левее точки в, включая точку в. также называют лучом и обозначают (-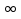 ; в]
; в]
интервал
Множество точек, которые лежат правее точки а, но левее точки в - называют интервалом и обозначают (а; в).
отрезок
Если к интервалу (а; в) добавить его концы, т. е. точки а и в, то получится отрезок [а; в]
полуинтервал
Если к интервалу (а; в) добавить только один конец - только точку а
или только точку в, получится полуинтервал, который в первом
случае обозначают [а; в), а во втором - (а; в].
числовой промежуток
Луч, открытый луч, интервал, отрезок, полуинтервал множества точек координатной прямой - общий термин: числовые промежутки.
прямоугольная система координат
Если проведены две взаимно перпендикулярные координатные прямые и считается началом отсчета на обеих прямых точка их пересечения, то говорят, что на плоскости задана прямоугольная система координат.
координатная плоскость
Если на плоскости задана прямоугольная система координат, то плоскость называют координатной.
начало координат
Точка пересечения двух взаимно перпендикулярных координатных прямых, которая считается началом отсчета на обеих прямых, называется началом координат.
координатные углы
Координатные прямые (ось х и ось у) называют осями координат, а прямые углы, образованные осями координат, называют координатными углами.
ось абсцисс
Горизонтальную координатную прямую называют осью абсцисс или осью х.
ось ординат
Вертикальную координатную прямую называют осью ординат или осью у.
линейное уравнение с двумя переменными
ах + by + с = О,
где а, в, с - числа (коэффициенты) - линейное уравнение с двумя
переменными х и у (или с двумя неизвестными х и у).
Решение уравнения
ах + ву + с = 0
Решением уравнения ах + ву + с = 0 называют всякую пару чисел (х; у), которая удовлетворяет этому уравнению, т. е. обращает равенство с переменными ах + by + с = 0 в верное числовое равенство.
линейная функция
y = kx + m, где k, m - числа (коэффициенты - называется линейной функцией).
Независимая переменная (аргумент)
х - независимая переменная (или аргумент),
зависимая переменная
у - зависимая переменная.
график линейной
функции
Графиком линейной функции у = kх +т - является прямая.
наибольшее значение
линейной функции
Самая большая ордината у точек, принадлежащих [а; в], - это наибольшее значение линейной функции на отрезке [а; в], запись: унаиб.
наименьшее значение
линейной функции
Самая меньшая ордината у точек, принадлежащих [а; в], - это наименьшее значение линейной функции на отрезке [а; в],запись: унаим.
возрастание
Если при движении по графику слева направо, ординаты точек графика все время увеличиваются, то говорят о возрастании:
если k > 0, то линейная функция y = kx + m возрастает.
убывание
Если при движении по графику слева направо, ординаты точек графика все время уменьшаются, то говорят об убывании:
если k < 0, mo линейная функция y = kx + m убывает.
угловой коэффициент
Коэффициент k в записи у = kx и y = kx + m называют угловым коэффициентом.
Если k > 0, то прямая y = kx + m образует с положительным направлением оси х острый угол , а если k < 0, - тупой угол.
система уравнений
Вообще, если даны два линейных уравнения с двумя переменными х и у: а1х + в1у + с1 = 0 и а2х + в2у + с2 = 0, - и поставлена задача найти такие пары значений (х; у), которые одновременно удовлетворяют и тому, и другому уравнению, то говорят, что заданные уравнения образуют систему уравнений.
решение системы уравнений
Пару значении (х; у), которая одновременно является решением и первого, и второго уравнения, называют решением системы.
решить систему
Решить систему - это значит найти все ее решения или установить, что их нет.
графический метод
решения системы уравнений
Построение графиков уравнений системы в одной системе координат и определение абсциссы и ординаты точки пересечения графиков - называют графическим методом решения системы уравнений.
несовместная система
Если система не имеет решений, то говорят также, что система несовместна.
неопределенная система
Если система имеет бесконечно много решений, то говорят
также, что система неопределенна.
метод
подстановки
Метод решения системы двух уравнений с двумя переменными путем выражения у через х из одного уравнения системы и подставки полученного выражения вместо у в другое уравнение системы, решение полученного уравнение относительно х и подставка найденного значения х в выражение у через х.
метод алгебраического
сложения
Метод решения системы двух уравнений с двумя переменными путем исключения одной переменной, складывая оба уравнения системы, умноженные на дополнительные множители.
степень
основание степени
показатель степени
Под ап, где п = 2, 3, 4, 5, ..., понимают произведение п одинаковых
множителей, каждым из которых является число а. Выражение ап называют степенью, число а - основанием степени, число п показателем степени.
возведение в степень
Операцию отыскания степени ап называют возведением в степень.
степень с нулевым
показателем
Если а ≠ 0, то а0 = 1.
одночлен
Одночленом называют алгебраическое выражение, которое представляет собой произведение чисел и переменных, возведенных в степень с натуральными показателями.
стандартный вид одночлена
Вид одночлена называется стандартным, если все числовые множители перемножены, и их произведение поставлено на первое место и перемножены все имеющиеся степени с одинаковым буквенным основанием.
коэффициент одночлена
Числовой множитель одночлена, записанного в стандартном виде, называют коэффициентом одночлена.
подобные одночленами.
Два одночлена, состоящие из одних и тех же переменных, каждая из которых входит в оба одночлена в одинаковых степенях (т. е. с равными показателями степеней), называют подобными одночленами.
метод введения новой
переменной
Метод замены одинакового выражения новой переменной.
многочлен
Многочленом называют сумму одночленов.
члены многочлена двучлен
трехчлен
Слагаемые (одночлены), из которых состоит многочлен, называют членами многочлена: если их два, то говорят, что дан двучлен, если их три, то говорят, что дан трехчлен.
приведение подобных членов
Подобные одночлены в многочлене одинаково подчеркивают, а потом складывают - эту процедуру называют приведением подобных членов.
стандартный вид многочлена
Если в многочлене все члены записаны в стандартном виде и
приведены подобные члены, то говорят, что многочлен приведен
к стандартному виду.
квадрат суммы
(а + b)2 = а2 + 2ав + в2 квадрат суммы двух выражений равен сумме их квадратов плюс их удвоенное произведение.
квадрат разности
(а - b)2 = а2 - 2ав + в2 квадрат разности двух выражений равен сумме их квадратов минус их удвоенное произведение.
разность квадратов
а2- в2= (а + в)(а-в ) разность квадратов двух выражений равна произведению суммы этих выражений на их разность.
полный квадрат суммы
(разности)
Каждое из выражений а2 + 2ав + в2 и а2 - 2ав + в2 называют полным квадратом (суммы или разности).
неполный квадрат суммы (разности)
Каждое из выражений а2 + ав + в2 и а2 - aв + в2 называют неполным квадратом (суммы или разности).
разность кубов
а3 - в3 = (а - в) (а2 + ав + в2) разность кубов двух выражений равна
произведению разности этих выражений на неполный квадрат их суммы.
сумма кубов
а3 + в3= (а+ в) (а2 - ав + в2) сумма кубов двух выражений равна
произведению суммы этих выражений на неполный квадрат их разности.
разложение многочлена на множители
Если многочлен представлен в виде произведения более простых многочленов, то говорят, что многочлен удалось разложить на множители.
вынесение общего множителя за скобки
Способ разложения на множители многочлена, используя распределительное свойство при вынесении общего множителя нескольких одночленов за скобки.
способ группировки
Если члены многочлена можно сгруппировать так,
что в каждой группе после вынесения общих множителей в скобках остается один и тот же многочлен, который, в свою очередь,
может быть вынесен за скобки как общий множитель, то говорят, что разложение многочлена на множители осуществлено способом группировки.
метод выделения
полного квадрата
Прибавив к заданному многочлену то, что нужно и тут же это вычтя: группируют три члена так, что выделится полный квадрат.
алгебраическая дробь
Алгебраической дробью называют отношение двух многочленов Р и Q. При этом используют запись 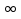 , где Р - числитель, Q - знаменатель
, где Р - числитель, Q - знаменатель
тождественно равные
выражения
Равенства верные при любых значениях входящих в их состав переменных в алгебре называют тождествами. Левую и правую части тождества называют выражениями, тождественно равными друг другу
тождественное преобразование
Всякую замену одного выражения другим, тождественно равным
ему, называют тождественным преобразованием выражения.
тождество
Тождество - это равенство, верное при любых допустимых значениях входящих в его состав переменных.
парабола
Линия - график функции у = х2
ось симметрии параболы
ветви параболы
вершина параболы
Ось у является осью симметрии параболы у = х2 или что парабола симметрична относительно оси у.
Ось симметрии как бы разрезает параболу на две части, которые обычно называют ветвями параболы.
Особая точка параболы, в которой смыкаются обе ветви и которая лежит на оси симметрии параболы - точка (0; 0), ей присвоили специальное название - вершина параболы.
кусочная функция
Функции, которые заданы разными моделями на разных числовых промежутках, называют кусочными функциями. Её график воспроизводится «по кусочкам» входящих в неё графиков функций.
чтение графика
Описание с помощью построенного графика некоторых свойств функции у = f(x) -называют чтением графика. Чтение графика - это своеобразный переход от геометрической модели к словесной, а построение графика - это переход от аналитической модели к геометрической.
область определения функции
Все значения, которые «пробегает» независимая переменная х
- область определения функции. Для каждого такого значения х можно вычислить значение функции f(x).
непрерывная функция
Если функция не имеет точек разрыва, то ее называют непрерывной.
точка разрыва
Если функция y = f(x) претерпевает разрыв, то абсцисса этой точки
называется точка разрыва.
3 этапа решения задачи:
Первый этап. Составление математической модели.
Второй этап. Работа с математической моделью.
Третий этап. Ответ на вопрос задачи.
![]() расстояние между точками на координатной прямой
расстояние между точками на координатной прямой
Теорема 1.
Если хотя бы один из коэффициентов а, в линейного уравнения ах + ву + с = О отличен от нуля, то графиком уравнения служит прямая линия.
Теорема 2.
Графиком линейной функции у = kх +т - является прямая.
Теорема 3.
Графиком линейной функции у = kx является прямая, проходящая через начало координат.
Теорема 4.
Прямая, служащая графиком линейной функции у = kx + m, параллельна прямой, служащей графиком линейной функции у = kx.
Теорема 5.
Пусть даны две линейные функции у = k1x + т1 и у = k2x + т2. Прямые, служащие графиками заданных линейных функций:
1) параллельны, если k1 =k2, m1 ≠ т2;
2) совпадают, если k1 = k2, т1 = т2;
3) пересекаются, если k1 ≠ k2.
Теорема 6.
Если а -любое число а n,k - натуральные числа, то справедливо равенство ап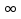 ак = а п + к.
ак = а п + к.
Теорема 7.
Если а - любое число а n,k - натуральные числа, то справедливо равенство ап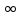 ак = а п - к.
ак = а п - к.
Теорема 8.
Для любого числа а и любых натуральных чисел п и к справедливо равенство (an)k = ank.

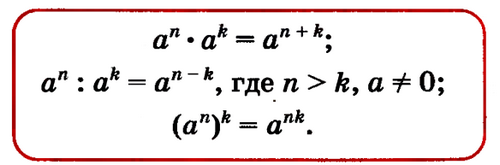

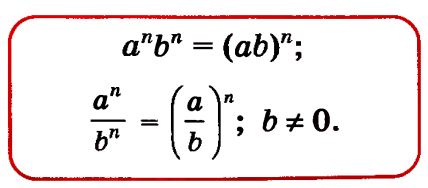



 123
123
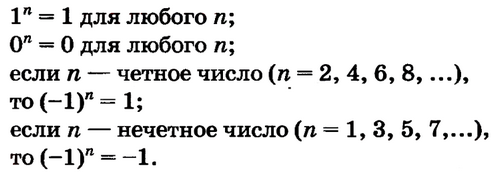
![]()




1. Алгоритм решения линейного уравнения ах + в = 0 в случае, когда а ≠0. 
1. Преобразовать уравнение к виду ах = - в.
2. Записать корень уравнения в виде х = 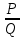 ,
,
2. Алгоритм решения уравнения ах + в = сх + d (a ≠ с)
1. Перенести все члены уравнения из правой части в левую с противоположными знаками.
2. Привести в левой части подобные слагаемые, в результате чего получится уравнение вида
kx + т = 0, где k ≠ 0.
3. Преобразовать уравнение к виду kx = - т и записать его корень: х =  .
.
3. Алгоритм отыскания координат точки М, заданной в системе координат х0у
1. Провести через точку М прямую, параллельную оси у, и найти координату точки пересечения этой прямой с осью х - это будет абсцисса точки М.
2. Провести через точку М прямую, параллельную оси х, и найти координату точки пересечения этой прямой с осью у - это будет ордината точки М.
4. Алгоритм построения точки М(а; в) в прямоугольной системе координат х0у
1. Построить прямую х = а.
2. Построить прямую у = в.
3. Найти точку пересечения построенных прямых - это и будет точка М(а; в).
5. Алгоритм построения графика уравнения ах + ву + с = 0, где а  0, в
0, в  0
0
1. Придать переменной х конкретное значение х = х1, найти из уравнения ах1 + by + с = 0 соответствующее значение у = y1
2. Придать переменной х другое значение х = х2, найти из уравнения ах2 + by + с = 0 соответствующее значение у = у2
3. Построить на координатной плоскости х0у точки (х1; у1) и (х2; у2)
4. Провести через эти две точки прямую -она и будет графиком уравнения ах + by + с = 0.
6. Алгоритм решения системы двух уравнений с двумя переменными методом подстановки
1. Выразить у через х из первого уравнения системы.
2. Подставить полученное на первом шаге выражение вместо у во второе уравнение системы.
3. Решить полученное на втором шаге уравнение относительно х.
4. Подставить найденное на третьем шаге значение х в выражение у через х, полученное на первом шаге.
5. Записать ответ в виде пары значений (х; у), которые были найдены соответственно на третьем и четвертом шагах.
7. Алгоритм приведения одночлена к стандартному виду.
1) перемножить все числовые множители и поставить их произведение на первое место;
2) перемножить все имеющиеся степени с одним буквенным основанием;
3) перемножить все имеющиеся степени с другим буквенным основанием и т. д.
8. Алгоритм сложения одночленов
1. Привести все одночлены к стандартному виду.
2. Убедиться, что все одночлены подобны; если же они неподобны, то алгоритм далее не применяется.
3. Найти сумму коэффициентов подобных одночленов.
4. Записать ответ: одночлен, подобный данным, с коэффициентом, полученным на третьем шаге.
9. Алгоритм отыскания общего множителя нескольких одночленов
1. Найти наибольший общий делитель коэффициентов всех одночленов, входящих в многочлен, - он и будет общим числовым множителем (разумеется, это относится только к случаю целочисленных коэффициентов).
2. Найти переменные, которые входят в каждый член многочлена, и выбрать для каждой из них наименьший (из имеющихся) показатель степени.
3. Произведение коэффициента, найденного на первом шаге, и степеней, найденных на втором шаге, является общим множителем, который целесообразно вынести за скобки.
10. Алгоритм графического решения уравнения вида ḟ (х) = g (x).
1. Ввести в рассмотрение функции у= ḟ (х) и у= g (x). .
2. Построить в одной системе координат их графики.
3. Найти точки пересечения графиков.
4. Найти абсциссы точек пересечения - это и есть корни уравнения.