Урок-консультация по алгебре в 10 классе 'Решение тригонометрических уравнений с модулем'

Класс: 10 класс

Тема: Решение тригонометрических уравнений с модулем

Тип урока по цели: изучение

Тип урока по форме проведения: урок-консультация.

Форма работы с учащимися: общая, групповая и индивидуальная.

Эпиграф Сухомлинский считал, что «Чувство удивления- могучий источник желания знать; от удивления к знаниям - один шаг».

Давайте вместе сегодня сделаем этот шаг к определению способов решения тригонометрических уравнений с модулем.

Цели урока:

• дидактическая:

1. повторить методы решения тригонометрических уравнений,

2. изучить способы раскрытия модуля по определению и с помощью формулы

3. рассмотреть комбинированные методы решения тригонометрических уравнений с модулем;

4. рассмотреть тригонометрические уравнения, модуль в которых появляется в ходе их решения

• развивающая:

5. развивать навыки самостоятельной работы, прививать умение выслушивать других учащихся, дополнять их ответы

6. развивать математическую речь (используя грамотно математические термины);

7. развивать логическое мышление, память, познавательный интерес,

8. вырабатывать умение анализировать и сравнивать.

• воспитательная:

9. формировать опыт самостоятельной деятельности и личной ответственности.

10. показывать, что математические понятия не изолированы друг от друга, а представляют определенную систему знаний, все звенья которой находятся во взаимной связи,

11. формировать эстетические навыки при оформлении записей, навыки контроля и самоконтроля.

Средства наглядности: макеты единичной окружности, сборник подготовки к ЕГЭ, раздаточный материал: лист-конспект (рабочая тетрадь, копирка), видео-консультация, мультимедийный проектор, компьютеры, карточки для магнитной доски, магниты.

Карта урока:

этап

Деятельность учителя

Деятельность учеников

время

Организационный

момент

Говорят, алгебра держится на четырех китах: это уравнение, число, тождество, функция. Сегодня мы продолжаем изучение тригонометрических уравнений.

1

Подготовка учащихся к активному и сознательному усвоению нового материала

Устно:

1. Блиц-опрос.

Показываем таблички с простейшими тригонометрическими уравнениями.

Ученики решают

Решите уравнение

• sin x=-1

• cos x=1/2

• tg x=-1

• sin 2x=-1/2

• cos x=2

• tg 2x=4

• sin x=-0

По цепочке

1

Устно:

2. фронтальный опрос

• определение модуля действительного числа

• Какие способы решения уравнений мы используем ?

• назовите виды тригонометрических уравнений

• о чем надо помнить при решении тригонометрических уравнений

1

Устно:

Работа у магнитной доски группы из 2 учеников

Перед вами уравнения, распределите уравнения по известным вам методам (алгоритмам) решения в таблицу.

Объясните свой выбор.

Простейшее

тригон-ское

Замена переменной

Разложение на множители

Однородные

Триг 1 степени

Однородные

Триг 2 степени

1) 2sinx cos 5x - cos 5x =0;

2) sin (π+x)=0

3)3tg ² x + 2tg x -1=0

4) 2 cos² x + 9cos x +14=0

5) sin 2х = -1

6)2sinx - 3cosx = 0

7) cos 3x = 0

8) cos (х - π/4) = ½

sin²x - 3sinx cosx + 2cos²x = 0

9) sin (x/2+ π /3)= -1/2.

10) 3sin²x - 4sinx cosx + cos²x = 0

11)√3tg2x + 1 = 0

12) 3cos²x - sinx - 1 =0

13) 2cos(π/3 + 3x) - √3 = 0

14)

Распределяют уравнениями по колонкам таблицы

1

Усвоение новых знаний

Сухомлинский считал, что «Чувство удивления- могучий источник желания знать; от удивления к знаниям - один шаг».

Давайте вместе сегодня сделаем этот шаг к определению способов решения тригонометрических уравнений с модулем.

Тема урока

Учитель называет вид уравнений, оставшихся на магнитной доске, объявляет тему урока.

В лист конспект вписывают фамилию и класс

1

Актуализация знаний

Уравнения широко представлены в экзаменационном материале. А тригонометрические уравнения, содержащие модуль входят в задание 15.

1. вспомним определение модуля действительного числа.

2. Рассмотрим способы раскрытия модуля:

• Как раскрыть модуль по определению, используя формулу и с учетом ОДЗ

• Как раскрыть модуль используя метод оценки левой и правой части уравнения.

3. Комбинированные методы решения тригонометрических уравнений с модулем и уравнений, модуль в которых будет появляться в ходе их решения

4. Как не потерять корни уравнения, выполняя преобразования

5. Решение уравнений задания 15

1. В чем недостаток графического способа?

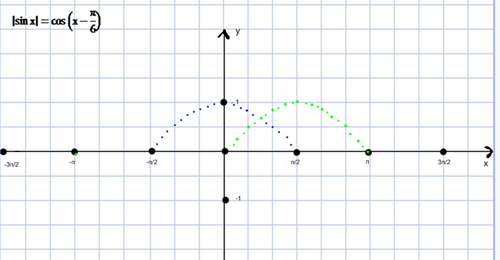
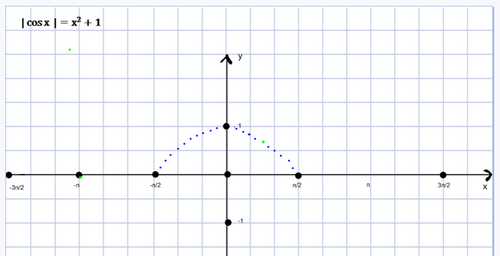
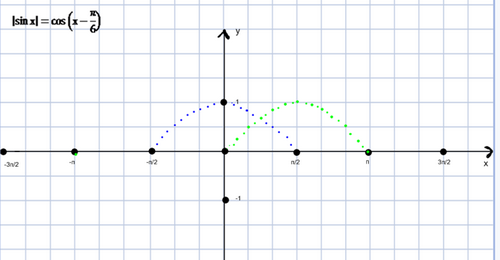
Рассмотрим Графический способ решения уравнений

У доски работает 1 человек:

-Построить в одной системе координат два графика функции

-убедиться, что они имеют общую точку

-абсцисса точки-корень уравнения

Ребята выполняют задание в конспекте, сверяют с доской, делают необходимые пометки на свое усмотрение.

2

2. Рассмотрим комбинированные методы решения тригонометрических уравнений с модулем и уравнений, модуль в которых будет появляться в ходе их решения

Работа у доски: 6 ученика

1.Раскрытие модуля по определению -2ученика

2.Метод оценки левой и правой части уравнения-1

3.Раскрытие модуля по определению и учетом ОДЗ-1

4.Появление модуля в ходе решения уравнения-1

5.Раскрытие модуля по формуле:-1

Ребята выполняют задание в конспекте, сверяют с доской, делают необходимые пометки на свое усмотрение.

15

3. интернет-консультация

Использование интернет ресурса - видео урок

Смотрят, внимательно слушают

3

4. Историческая справка

Доклад о применении тригонометрических функций, уравнений в физике, медицине, музыке…

Работа с презентацией

2

Проверка понимания учащимися нового материала.

Устно: выяснить, усвоен ли учащимися способ решения уравнений с модулем

• Раскрывая модуль по определению сколько систем получаем?

• Когда удобно раскрывать модуль по формуле?

Отвечают на вопросы

1

Закрепление и проверка усвоения нового материала.

проверить у учащихся знания и умения, которые они получили на уроке.

Учитель предлагает учащимся решить самостоятельно по вариантам 1 уравнение

Решают под копирку, второй лист сдают учителю

Самопроверка.Сверяют с образцом на компьютере, обменявшись работой друг с другом.

10

Рефлексия: Думаем, все согласятся, что - математика замечательный предмет для удивления.

Ответь на вопросы (да «+», нет «-», не совсем «?»):

Я понял(а), в каких случаях раскрывать модуль по определению____

Я понял(а), в каких случаях раскрывать модуль по формуле ____

Я понял(а), в каком случае использовать метод оценки левой и правой части уравнения____

Я могу решать тригонометрические уравнения с модулем___

Я ставлю себе за работу на уроке оценку « ____»

1

Итог урока

Выставление оценок

1

Думаем, научившись бороться с трудностями при решении ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ с модулем, вы сможете преодолевать любые преграды в жизни.

Ход урока

1. Оргмомент:

- Здравствуйте ребята. Садитесь.

2. Постановка цели:

Говорят, алгебра держится на четырех китах: это уравнение, число, тождество, функция. Сегодня мы продолжаем изучение тригонометрических уравнений.

3. Устная работа:

Блиц-опрос. Решите уравнения( учитель показывает таблички с простейшими тригонометрическими уравнениями. Ученики говорят решения по цепочке).

sin x=-1

cos x=1/2

tg x=-1

sin 2x=-1/2

cos x=2

Нет решения

tg 2x=4

sin x=-0

фронтальный опрос. Ответьте на вопросы

• определение модуля действительного числа

• Какие способы решения уравнений мы используем ?

• назовите виды тригонометрических уравнений

• о чем надо помнить при решении тригонометрических уравнений

Работа у магнитной доски (группа из 2 учеников).

Простейшее

Замена переменной

Разложение на множители

Однородные

1 степени

Однородные

2 степени

sin 2х = -1

sin (π+x)=0

2sinx cos 5x - cos 5x =0;

2sinx - 3cosx = 0

sin²x - 3sinx cosx + 2cos²x = 0

cos 3x = 0

3tg ² x + 2tg x -1=0

3sin²x - 4sinx cosx + cos²x = 0

√3tg2x + 1 = 0

2 cos² x + 9cos x +14=0

cos (х - π/4) = ½

3cos²x - sinx - 1 =0

sin (x/2+ π /3)= -1/2.

2cos(π/3 + 3x) - √3 = 0

Изучение нового материала:

ИТОГ: Учитель называет вид уравнений, оставшихся на магнитной доске, объявляет тему урока: Решение тригонометрических уравнений с модулем.

Сухомлинский считал, что «Чувство удивления- могучий источник желания знать; от удивления к знаниям - один шаг».

- Давайте вместе сегодня сделаем этот шаг к определению способов решения тригонометрических уравнений с модулем.

Цель урока:

1. Изучить способы раскрытия модуля:

2. Выяснить, как раскрыть модуль по определению; используя формулу; с учетом ОДЗ.

3. Ответить на вопрос: Как раскрыть модуль используя метод оценки левой и правой части уравнения?

4. Рассмотреть комбинированные методы решения тригонометрических уравнений с модулем. И уравнений, модуль в которых будет появляться в ходе их решения уравнений.

5. Повторить, как не потерять корни уравнения, выполняя преобразования.

6. Решить уравнения из ЕГЭ,задания 15.

Вопрос

1. Назовите определение модуля действительного числа.

2. В чем недостаток графического способа перед аналитическим?

1. Рассмотрим графический способ решения уравнений (у доски работает ученик, все в листе-конспекте выполняют задания и сравнивают свое решение).

Повторяем алгоритм графического решения тригонометрических уравнений с модулем:

• Построить в одной системе координат два графика функции

• -убедиться, что они имеют общую точку

• -абсцисса точки-корень уравнения

2. Рассмотрим комбинированные методы решения тригонометрических уравнений с модулем и уравнений, модуль в которых будет появляться в ходе их решения (у доски работают 6 учеников, поочередно решая свои уравнения, комментируя решения. Класс делает запись в конспекте).

• Раскрыть модуль по определению:

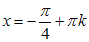
• Раскрыть модуль по определению(под знаком модуля не триг.функ.):

Решение. Раскрывая знак модуля, получаем системы:

• Метод оценки частей уравнения

Решение. Правая часть уравнения неотрицательна, значит, неотрицательна и левая часть, поэтому, раскрывая знак модуля, получим только одну систему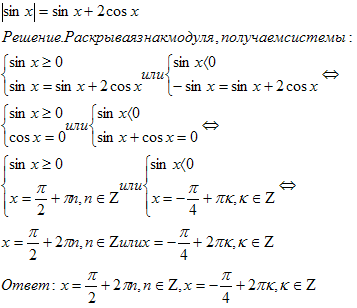

• Появление модуля в ходе решения уравнения

Физминутка: Ребята закройте глаза, положите голову на руки. Подумайте о!!!!!!!!!!

• Раскрытие модуля по формуле:

,

• Раскрытие модуля с учетом ОДЗ

Решение. ОДЗ:

Раскрывая знак модуля, получаем системы:

ИТОГ: Когда для раскрытия модуля используем определение? Почему составляем строгое неравенство при раскрытии модуля как в последнем случае?

-Все методы описаны у вас в конспекте. Подсказки при подготовке дом.заданий обеспечены.

Интернет-КОНСУЛЬТАЦИЯ .

- Внимательно посмотрим на решение уравнения из ЕГЭ (видео).

При поступлении в вуз необходимо знать чуть больше чем другие абитуриенты, чтобы набрать больше баллов и составить конкуренцию.

- Решение можно попробовать записать самостоятельно. Кто затрудняется, может взять подсказку (на рабочем столе).

- Где и как можно использовать знания, полученные при изучении тригонометрических уравнений? Узнаем из исторической справки.

Презентация. Доклад о применении тригонометрических функций, уравнений в физике, медицине, музыке…

ИТОГ:- Дополнительную информацию можно посмотреть в Интернете.

Самостоятельная работа:

-Учитель предлагает учащимся решить самостоятельно по вариантам 1 уравнение.

(Решают под копирку, второй лист сдают учителю. Обмениваются работами, проверяют их, используя образец на компьютере).

-Кто справился полностью с работой?

Рефлексия:

-Возьмите опросник и ответьте на вопросы (собрать листочки).

Кто оценил свою работу:

на 5?

на 4?

на 3?

У кого остались вопросы?

Домашнее задание из ЕГЭ.

-Так как на одном уроке невозможно ответить и решить все уравнения. Мы продолжим отвечать на вопросы на следующем уроке. Сегодня вы активно поработали. Оценки получили .Молодцы ребята! Думаем, все согласятся, что - математика замечательный предмет для удивления.Спасибо за урок.

Лист-конспект: Решение тригонометрических уравнений с модулем Ф. И.______________________, класс__

Аналитический способ

1.Раскрытие модуля по определению

2.Метод оценки левой и правой части уравнения

3.Раскрытие модуля по определению и учетом ОДЗ

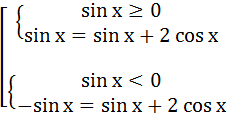
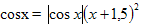
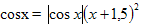
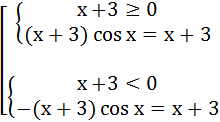
n

корень

Да/нет

n= -1

n=0

n=1

m= -1

m=0

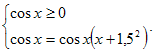
одз

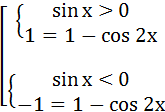
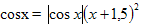
Графический способ

4.Появление модуля в ходе решения уравнения

5.Раскрытие модуля по формуле:

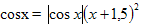
ИНТЕРНЕТ-консультация

Полезные ссылки:

2. ()

4. http://учительский.сайт/Заболотнева-Наталья-Викторовна

5. http://учительский.сайт/Лобанова-Фаина-Александровна

Домашнее задание (Д.А.Мальцев Математика ЕГЭ 2015.книга 2 Профильный уровень) ТЕСТ 31 задание15

найти все корни этого уравнения, принадлежащие промежутку

Самостоятельная работа

1 вариант

2 вариант

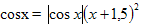
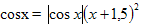
Ответь на вопросы (да «+», нет «-», не совсем «?»):

2. Я понял(а), в каких случаях раскрывать модуль по определению____

3. Я понял(а), в каких случаях раскрывать модуль по формуле ____

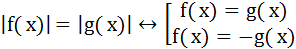4. Я понял(а), в каком случае использовать метод оценки левой и правой части уравнения____

5. Я могу решать тригонометрические уравнения с модулем___

6. Я ставлю себе за работу на уроке оценку « ____»

Думаем, научившись бороться с трудностями при решении ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ с модулем, вы сможете преодолевать любые преграды в жизни.

Самое важное отличие тригонометрических уравнений от алгебраических состоит в том, что в алгебраических уравнениях конечное число корней, а в тригонометрических --- бесконечное, что сильно усложняет отбор корней. Еще одной спецификой тригонометрических уравнений является неединственность формы записи ответа.