- Учителю
- Материал для конференции учащихся
Материал для конференции учащихся
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БАШКОРТОСТАН
ОТДЕЛ ОБРАЗОВАНИЯ АДМИНИСТРАЦИИ
ГОРОДСКОГО ОКРУГА г. СТЕРЛИТАМАК
МОУ «СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА № 12 с
углубленным изучением отдельных предметов»
Фракталы и их применнения
научно - исследовательская работа
по математике
ученика
Щербанева Дмитрия
Научный руководитель:
Гайдукова Н.Н.
Оглавление
Введение 3
I. Понятие фрактала и его разновидности 4
§1 Б.Мандельброт - основоположник фракталов 4
§ 2 Понятие фрактала 4
§ 3 Разновидности фракталов 5
§ 4 Геометрические фракталы 5
§ 5 Алгебраические фракталы 6
§ 6 Стохастические фракталы 6
II. Применение фракталов 7
§1 Фракталы в цифровой технике 7
§ 2 Фракталы как элементы визуализации и спецэффектов 7
§ 3 Фракталы в физике и астрономии 8
§ 4 Фракталы в биологии 8
§ 5 Фракталы в медицине 9
§ 6 Фракталы в метеорологии 11
§ 7 Фракталы в географии 11
§ 8 Фракталы в экономике 12
§ 9 Фрактальные принципы в литературных текстах 12
§ 10 Фракталы в искусстве 13
§ 11 Фракталы в дизайне мебели 15
Заключение 16
Библиографический список 17
Введение
Данная тема сегодня очень актуальна, поскольку в современной математике развивается новый раздел - фрактальная геометрия. Фракталы успели занять полноправное место не только в математике, но и в других областях науки, а красивые рисунки, выполненные с помощью компьютерной графики, привлекают к ним даже людей, далёких от науки. Области применения фракталов:
-
Компьютерные системы (фрактальное сжатие данных)
-
Децентрализованные сети
-
Радиотехника (фрактальные антенны)
-
Естественные науки (физика, биология, телекоммуникации, медицина).
-
Экономика и финансы (анализ биржевых котировок).
-
Компьютерная графика (построение изображений природных объектов)
-
Живопись, музыка, литература.
В своей работе я рассмотрел понятие фрактала и автоподобных фигур, а также об их роли в современной математике, других областях науки и искусстве. Задачи:
-
узнать, что такое «фракталы»;
-
изучить историю возникновения и развития фрактальной геометрии;
-
ознакомиться с биографией создателя фракталов - Б.Мандельброта;
-
рассмотреть область применения фракталов
Методы исследования: изучение и анализ источников информации. Для достижения поставленных целей была найдена и проработана литература, интернет-ресурсы. Сейчас существует большое количество как научно-популярных книг, так и монографий, посвященных фракталам и фрактальной геометрии. Например, сведения о них встречаются в книгах: «БЭС: математический словарь», «Энциклопедия Аванта+. Математика», «Наглядная топология» В. Г. Болтянского и В. А. Ефремовича.
I. Понятие фрактала и его разновидности
§1 Б.Мандельброт - основоположник фракталов
Основоположником фракталов является Бенуа Мандельброт. Окончив университет, Мандельброт сначала стал «чистым математиком». Но, получив докторскую степень, он ушел от академической науки.
Работал над задачами теории игр, экономики, географии, астрономии, физики. Ему нравилось бросаться от одной темы к другой: он искал. Исследуя экономику, Мандельброт обнаружил, что произвольные, на первый взгляд, колебания цены могу следовать скрытому математическому порядку.
Сегодня Бенуа Мандельброт - профессор Йельского университета, член американской Академии искусств и наук США. Он удостоен многочисленных почётных степеней и наград. Его последняя важная награда - премия Вольфа по физике.
§ 2 Понятие фрактала
Понятия фрактал и фрактальная геометрия, появившиеся в конце 70-х, с середины 80-х прочно вошли в обиход математиков и программистов. Слово фрактал образовано от латинского «fractus» и в переводе означает состоящий из фрагментов. Оно было предложено Бенуа Мандельбротом в 1975 году для обозначения нерегулярных, но самоподобных структур, которыми он занимался. Рождение фрактальной геометрии принято связывать с выходом в 1977 году книги Мандельброта `The Fractal Geometry of Nature'. В его работах использованы научные результаты других ученых, работавших в период 1875-1925 годов в той же области (Пуанкаре, Фату, Жюлиа, Кантор, Хаусдорф). Но только в наше время удалось объединить их работы в единую систему.
Фрактал - это бесконечно самоподобная геометрическая фигура, каждый фрагмент которой повторяется при уменьшении масштаба, это геометрические объекты с удивительными свойствами: любая часть фрактала содержит его уменьшенное изображение. То есть, сколько фрактал не увеличивай, из любой его части на вас будет смотреть его маленькая копия.
§ 3 Разновидности фракталов
Существует несколько разновидностей фракталов, которые отличаются друг от друга не только способами построения, но и областями использования и самой сущностью этих фракталов.
Самые большие группы это:
-
геометрические фракталы
-
алгебраические фракталы
-
системы итерируемых функций
-
стохастические фракталы
§ 4 Геометрические фракталы
История фракталов началась с геометрических фракталов, которые исследовались математиками в XIX веке. Этот тип фракталов получается путем простых геометрических построений. При построении этих фракталов обычно берется набор отрезков, на основании которых будет строиться фрактал. Далее к этому набору применяют набор правил, который преобразует их в какую-либо геометрическую фигуру. Далее к каждой части этой фигуры применяют опять тот же набор правил. С каждым шагом фигура будет становиться все сложнее и сложнее, и если представить бесконечное количество подобных операций, получается геометрических фрактал. Примерами геометрических фракталов также служат: кривая дракона; кривая Коха; кривая Леви; кривая Минковского.
На рисунке приведены три первых шага процедуры построения для кривой Коха:
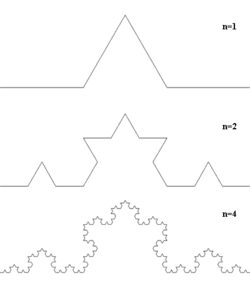
§ 5 Алгебраические фракталы
Самой обширной группой фракталов являются алгебраические фракталы.
Алгебраические фракталы появились гораздо позже геометрических, а их изображения ученые научились получать лишь после создания ЭВМ.
Их построение ведется на основе алгебраических формул.

§ 6 Стохастические фракталы
Типичный представитель данного класса фракталов "Плазма". Для ее построения возьмем прямоугольник и для каждого его угла определим цвет. Далее находим центральную точку прямоугольника и раскрашиваем ее в цвет равный среднему арифметическому цветов по углам прямоугольника плюс некоторое случайное число. Чем больше случайное число - тем более "рваным" будет рисунок.

II. Применение фракталов
§1 Фракталы в цифровой технике
Фрактальная геометрия внесла неоценимый вклад в разработку новых технологий в области цифровой музыки, а так же сделала возможной сжатие цифровых изображений. Существующие фрактальные алгоритмы сжатия изображения основаны на принципе хранения сжимающего изображения вместо самой цифровой картинки. Для сжимающего изображения основная картинка остаётся неподвижной точкой. Фирма «Microsoft» использовала один из вариантов данного алгоритма при издании своей энциклопедии, но по тем или иным причинам широкого распространения эта идея не получила.
Во многих фантастических фильмах используются фракталы для создания инопланетных ландшафтов. Эти техники очень эффективны, и их можно найти в книге Мандельброта «Фрактальная геометрия природы». Существует большое количество прикладных программных средств, предназначенных для работы с фрактальной графики.
§ 2 Фракталы как элементы визуализации и спецэффектов.
Фракталы очень часто используют для создания различного рода создания спецэффектов в компьютерной графике и т.д.
Сегодня в очень многих играх (самый яркий пример Minecraft), где присутствуют разного рода природные ландшафты, так или иначе используются фрактальные алгоритмы.
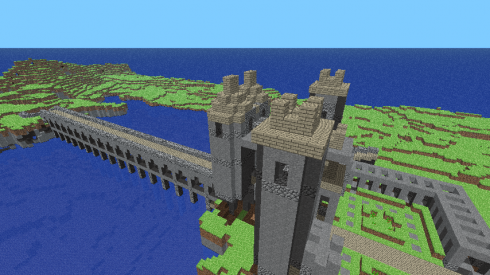
Фрактальная геометрия позволяет художникам по спецэфффектам без труда создавать такие объекты как облака, дым, пламя, звёздное небо и т.д.
§ 3 Фракталы в физике и астрономии
В физике фракталы естественным образом возникают при моделировании нелинейных процессов таких, как турбулентное течение жидкости, пламя, облака и т. п. При помощи фракталов можно смоделировать языки пламени. Пористые материалы хорошо представляются в фрактальной форме в связи с тем, что они имеют очень сложную геометрию.
Звезды формируют галактики, галактики - галактические кластеры, а последние - сверхгалактические скопления. В настоящее время основополагающей для космической модели является теория Эйнштейна, согласно которой материя во Вселенной распределяется однородно, даже в случае столь крупных масштабов. Если предположение о том, что материя в нашей вселенной распределяется в виде фрактала, подтвердится, ученым придется пересматривать традиционные модели Вселенной.

§ 4 Фракталы в биологии
Моделирование популяций; биосенсорные взаимодействия; процессы внутри организма, например, биение сердца.


Осьминог - морское придонное животное из отряда
головоногих.
Взглянув на эту фотографию, мне стало очевидно фрактальное строение
его тела и присосок на всех восьми щупальцах этого животного. Это
родственник улиток, брюхоногий голожаберный моллюск Главк.


Фрактальные формы обнаруживаются в организации живых организмов,
как одноклеточных, так и многоклеточных. Особенно сильно заметна
фрактальная структура: у животных - системы органов; у растений -
построение соцветий, разветвление главной оси - стебля.


§ 5 Фракталы в медицине
Фракталы в будущем возможно помогут описывать клеточное строение человека, излечить многие вирусы и многое другое, неподвластному нашему пониманию сейчас. В человеческом организме множество фракталоподобных образований - в структуре кровеносных сосудов и различных протоков, а также в нервной системе. Сам по себе человеческий организм состоит из множества фракталоподобных структур: кровеносная система, мышцы, бронхи и т.д. Примеры фракталоподобных структур в организме человека: бронхи, сосуды, мышцы.
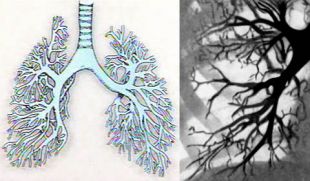
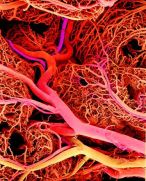
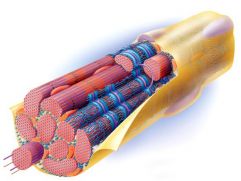
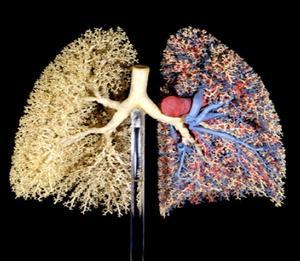
Поэтому учёные задумались можно ли применять фрактальные алгоритмы для диагностики или лечения каких-либо заболеваний? Оказывается возможно.
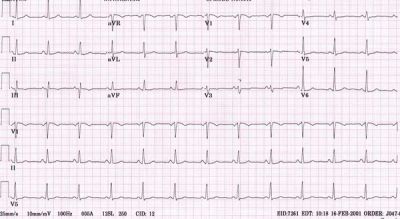 Пример кардиограммы.
Пример кардиограммы.
Сравнивая фрактальные размерности сложных сигналов, энцефалограмм или шумов в сердце, медики могут диагностировать некоторые тяжелые заболевания на ранней стадии, когда больному еще можно помочь.
§ 6 Фракталы в метеорологии
Метеорологи научились определять по фрактальной размерности изображения на экране радара скорость восходящих потоков в облаках, что позволяет с большим упреждением выдавать морякам и летчикам штормовые предупреждения.

Также фрактальный анализ помогает в поиске и разработке месторождений полезных ископаемых, распределение которых очень часто происходит по фрактальному механизму. Исследование разломной тектоники и сейсмичности порой тоже исследуется с помощью фрактальных алгоритмов. Геофизика использует фракталы и фрактальный анализ для исследования аномалий магнитного поля, для изучения распространение волн и колебаний в упругих средах, для исследования климата и многих других вещей.
§ 7 Фракталы в географии
Береговая линия представляет собой фрактал. Например, побережье Норвегии изрезано большими и малыми фьордами.
Покрывая карту сеткой из квадратных ячеек можно определить фрактальную размерность Хаусдорфа - Безиковича побережья для Норвегии равную 1,52, а для сравнительно гладкого южного побережья Африки - 1,3.С помощью этой размерности можно определить длину побережья. Но чем меньше ячейки, тем больше будет величина фрактальной размерности и следовательно длина побережья.

§ 8 Фракталы в экономике
В середине века двадцатого, когда весь научный мир увлекался только что появившейся теорией фракталов, известный американский финансист Ральф Эллиот предложил свою теорию поведения цен на акции, которая была основана на использовании теории фракталов.
В конце XIX века американский финансист Чарльз Доу обратил внимание, что цены на акции подвержены циклическим колебаниям: за ростом следует падение, потом снова рост и падение и т.д. Через полвека Ральф Эллиот пришёл к выводу, что каждый пик цены может быть представлен совокупностью более мелких подобных же пиков, для которых исходный пик является трендом. Таким образом, колебания носят фрактальный характер.
§ 9 Фрактальные принципы в литературных текстах
Среди литературных произведений находят такие, которые обладают текстуальной, структурной или семантической фрактальной природой («У попа была собака…», «Притча о философе, которому снится, что он бабочка, которой снится, что она философ, которому снится), неразветвляющиеся бесконечные тексты с вариациями («У Пегги был веселый гусь…») и тексты с наращениями («Дом, который построил Джек»).
§ 10 Фракталы в искусстве
Фракталы встречаются в народном творчестве. Присмотревшись внимательней к матрешке, с уверенностью можно сказать, что эта игрушка-сувенир - типичный фрактал. Принцип фрактальности очевиден, когда все фигурки деревянной игрушки выстроены в ряд, а не вложены друг в друга.

Луис Уэйн (1860-1939) - английский художник, известный тем, что рисовал кошек. Его работы этого периода характеризуются яркими оттенками и цветами, сложными абстрактными узорами, хотя основная его тема - кошки - долгое время оставалась неизменной, пока не была окончательно вытеснена фракталоподобными узорами.

Без преувеличения можно сказать, что соавтором открытия Мандельброта явился компьютер. Чтобы нарисовать фрактал, нужно произвести большое количество вычислений, а найденные точки изобразить на графике. Если раньше ученым приходилось иметь дело, в основном, с числами и формулами, то теперь их работа стала гораздо интереснее. С помощью компьютеров ученые могут рисовать большие красивые картинки изучаемых явлений. Некоторые из ученых так увлеклись этим, что стали художниками, и сегодня простая любопытность математиков, коей являлись фракталы еще в начале 80-х, превратилась в уважаемый вид искусства. Выставки фрактальных изображений проходят в музеях всего мира, большое количество конкурсов проводится в компьютерной сети Internet и в офлайне.


Казалось бы, какое отношение могут иметь фракталы, и вообще математика к музыке? А оказывается самое непосредственное! Считается, что в музыкальном плане наиболее интересными являются стохастические фракталы. В основе исследований использование фракталов в музыкальном искусстве лежит теория Ричарда Восса, который установил, что любой звук имеет фрактальные свойства. Современные исследователи на основе предложенных методов пытаются осознать музыку как абстрактное искусство, а также выявить некие универсальные законы создания музыкального произведения.
§ 11 Фракталы в дизайне мебели
Принцип фрактальности использовал японский дизайнер Такеши Миякава. Именно его фрактальная тумбочка стала первым примером использования фракталов в реальном мире, а не только в виртуальном. Наверное, дизайнер Такеши Миякава (Takeshi Miyakawa) в детстве мечтал стать математиком.

И его тоже занимала мысль о практическом использовании фракталов. Иначе как объяснить этот предмет мебели: тумбочка Fractal 23 содержит 23 ящика самых разных размеров и пропорций, которые как-то ухитряются уживаться между собой внутри кубического корпуса, заполняя почти всё доступное им пространство.
Ни для кого не секрет, что японцы по жизни сильно ограничены в пространстве, в связи с чем, им приходится всячески изощряться в эффективном его использовании. Этот пример использования фракталов в реальной жизни, применительно к дизайну мебели показал мне, что фракталы реальны не только на бумаге в математических формулах и компьютерных программах.
Заключение
Таким образом, выяснилось, что фракталы окружают людей в их повседневной жизни постоянно. Фрактальная графика может применяться во многих областях естественных наук. Фракталы помогают геофизикам определять и предсказывать форму и характер растрескиваний земной коры, а астрономам - характер рассеивания лучей и космической пыли. В математике активно развивается новое направление - фрактальная геометрия, изучающая свойства автоподобных фигур. Возможно, во фрактальной геометрии со временем будут появляться новые результаты: будут открыты новые типы самоподобных множеств, фракталов и автоподобных фигур, будут обнаружены какие-либо их новые свойства. Возможно, будет найдена новая область применения автоподобных фигур.
Лично для меня изучение темы «Фракталы и их примение» оказалось очень интересным и необычным. В процессе исследования я сам для себя сделал массу новых открытий, связанных не только с темой проекта, но и с окружающим миров в целом. Я испытываю огромный интерес к этой теме, и поэтому данная работа оказала исключительно положительное влияние на мое представление о современной науке. Но я убедился, что тем, кто занимается фракталами, открывается прекрасный, удивительный мир, в котором царят математика, природа и искусство.
Думаю, что после знакомства с моей работой, вы, как и я, убедились в том, что математика прекрасна и удивительна. Планирую продолжить исследование выбранной темы.
Библиографический список
-
Азевич А.И. Фракталы: геометрия и искусство.// Математика в школе. - № 5. - 2005. - с.76-78
-
Диков А.В. Команды на LOGO конструируют фракталы. // Математика в школе № 4. - 2005. - с. 76-80
-
Харитонова О.В. 3D Studio MAX на уроке стереометрии. // Математика в школе» № 8. - 2006. - с. 61-65
-
Мандельброт Б.Б. «Фрактальная геометрия природы» - М.: «Институт компьютерных исследований», 2002, - 666 с.
-
Пайтген Х.-О., Рихтер П.Х. Красота фракталов - М.: Мир, 1993, 206 с.
-
Попов К.А. Векторы, фракталы и компьютерное моделирование.// Математика в школе. - № 6. - 2006. - с.56-61.
Сайты в Интернете:
-
ru.wikipedia.org/wiki
-
sworm.narod.ru/
-
www.codenet.ru/progr/fract/Fractals-Around/
-
www.fractals.narod.ru/tips.htm
-
www.fractals.nsu.ru
-
www.ghcube.com/fractals
-
www.realcoding.net/articles/geometricheskie-fraktaly.html</</font>