План -конспект урока 7 класс на тему ' Решение систем линейных уравнений'

РАЗРАБОТКА УРОКА

С ПРИМЕНЕНИЕМ ТЕХНОЛОГИИ РАЗВИТИЯ КРИТИЧЕСКОГО МЫШЛЕНИЯ

Автор - Васильева Эльвира Леонтьевна, учитель математики коммунального государственного учреждения « Надеждинская средняя школа» района Магжана Жумабаева Северо-Казахстанской области

Предмет: алгебра

Класс: 7

Тема урока: «Решение систем линейных уравнений»

Тип урока: систематизации и обобщения изученного.

Цели урока:

• Обобщить изученный материал по теме;

• Проконтролировать степень усвоения знаний и умений по изученной теме;

• Показать рациональность применения различных способов решения для конкретной системы

• способствовать формированию у учащихся приёмов критического мышления, анализа и синтеза;

• воспитывать у учащихся способность работать в группе

• повышать познавательный интерес учащихся к предмету.

Ресурсы урока:

• для каждого ученика: учебник по алгебре для 7 класса общеобразовательных учреждений, рабочая тетрадь по предмету, индивидуальные листы оценивания , тексты, карточки устного счета для деления на группы ,стикеры, плакат « Дерево Познания» для ЗХУ

• презентация к уроку

• мультимедийное оборудование

Ход урока

Организационный момент, создание положительной мотивации (2 мин.) Слайд 1

Учитель и ученики встают в круг, приветствуют друг друга с пожеланием достижения новых учебных целей, зачитывается девиз урока:

« Деятельность - это единственный путь к достижению знаний» Бернард Шоу

Деление класса на 3 группы по 4 человека. Карточки на отработку устного счета действий с рациональными числами. ( Приложение 1)

Постановка темы урока. (3мин)

Учитель предлагает группам вспомнить материал прошлых уроков и в совместной деятельности сформулировать свои знания по пройденной теме.

Ученики совещаются, на стикерах пишут, то, что они знают по теме « Решение систем линейных уравнений». ( заполнение « Дерева познания» по стратегии ЗХУ- ЗНАЮ).

Постановка цели урока. (3 мин) Слайд 2

Учитель и учащиеся обобщают знания, умения по теме. Далее выдвигается идея, о том ,что необходимо расширить знания по теме. Работа в группах, обсуждение новых целей урока, пишут на стикерах « Что я хочу узнать» ( заполнение « Дерева познания» по стратегии ЗХУ- ХОЧУ УЗНАТЬ).

Актуализация знаний (5 мин.) Стратегия « Верю. Не верю» Слайд 3

Учитель: Мы с вами продолжаем заниматься решением систем двух линейных уравнений с двумя переменными различными способами. Перед вами карточки с вопросами. Если вы считаете высказывание верным, то отмечаете в столбце « Верю», если высказывание неверное, то отметка ставиться в столбце «Не верю».

Работа самостоятельная, индивидуальная. ( Примечание: система линейных уравнений далее СЛУ).

1.Уравнения вида ах+ву=с -является линейным уравнением с двумя неизвестными

2.Все уравнения являются линейными

3.Решением СЛУ является пара чисел, обращающих в верное равенство хотя бы одно из уравнений

4.СЛУ может иметь бесконечно много решений

5.Решить СЛУ можно способом умножения

6.Существует только три способа решения СЛУ

7.Достоинство графического метода-наглядность.

8.СЛУ имеет одно решение, если коэффициенты К1=К2

9. Способ сложения предполагает исключение одной переменной.

10.Решить систему способом подстановки, это значить выразить только переменную у через х

Учащиеся работают в индивидуальных карточках с данными вопросами. Предполагается взаимопроверка, на доске правильные ответы. Слайд 3 .

Предлагается оценить работу товарища по критериям оценивания. Слайд 4

Практическое применение всех способов решения (15 мин.) Групповая работа.

Учитель: Что значить решить СЛУ?

Задание1 (3 мин): Проверить, является ли пара чисел (-1,-3) решением СЛУ? Слайд 5а)

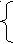13х - 8у = 11 1 балл

-8х + 15у = 37

З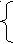адание 2: ( 4 мин) По виду системы определить, сколько решений имеет каждая система уравнений? Слайд 6. Слайд 7

а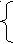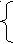) 2х - 2у = 1 -4х+2у = 8 2х + у = -3

6х - 6у = 3 -2х + у = 1 3х + у = 1

1 балл 1 балл 1 балл

Задание 3: (8 мин) Решить эти системы уравн ений рациональным способом для данной системы, но не забудем отметить достоинства остальных методов. 5 баллов

У доски по одному представителю от каждой группы решают заданную систему своим способом, который определен с помощью жеребьевки (отрывают лепестки от ромашки, на которых написаны названия способов решения). Группы решают на местах в рабочих тетрадях, помогая своему представителю. Обсуждение правильности решения, оценивание.

Критерии оценивания: правильность выполнения, объяснение хода решения, достоинства и недостатки метода.

Оценивание по итогам выполнения трех заданий

8-9 баллов -«5»

6-7 баллов- «4»

4-5 баллов- «3»

Меньше 4 - «2»

Работа с текстом. ( 5 мин). Техника « Инсерт» Слайд 8

Учащимся предлагается текст, для самостоятельного чтения. Приложение 2. Анализ текста. Учащиеся обсуждают, пишут на стикерах, что они узнали нового о СЛУ и способах решения. (Заполнение « Дерева познания» по стратегии ЗХУ- УЗНАЛ).

Этап рефлексии. (5 мин). Подведем итог нашей работы.

• Как вы оцениваете свою работу на уроке?

• Какие знания и навыки вам помогли успешно справиться с заданиями, что помешало?

• Перечислите все известные вам методы решения СЛУ?

• Назовите преимущества и недостатки каждого из методов решения СЛУ?

• Было ли вам комфортно работать в группе?

Подведение итогов урока. (4мин)

Суммативное оценивание по листам оценивания.

Домашнее задание: (3 мин) (разноуровневое) . Уровень А - решить систему удобным способом. Уровень В - решить задачу с применением СЛУ. Уровень С-придумать системы уравнений на каждый способ решения. Написать ессе « Чем мне интересны системы линейных уравнений» Слайд 9

« Чтобы переваривать знания, надо поглощать их с аппетитом»

Анатоль Франц. Французский писатель 19 в. Слайд 10

Текст для техники Инсерт

Уравнение вида ах+вх=с , называется линейным уравнением с двумя неизвестными.

Система линейных уравнений с двумя неизвестными содержит два и более уравнений. Решить систему, значить найти пару чисел (х,у), которая после подстановки в каждое уравнение обращает его в верное равенство Методы решения простейших линейных уравнений были известны еще во 2 тысячелетие до нашей эры, о чем свидетельствуют древнеегипетские папирусы. Более сложные задачи умели решать и в Древнем Вавилоне. В найденных глиняных пластинках, относящихся к 2 тысячелетию до нашей эры, приведены методы решения систем уравнений с двумя неизвестными. Решением уравнений занимались математики Древней Греции, Индии. Диофант Александрийский-древнегреческий математик, живший в 3 веке нашей эры, в своем сборнике « Арифметика» отразил уравнения, решения которых можно было найти на множестве целых чисел. Такие уравнения получили название «диофантовы уравнения». В 5 веке центром математических становятся страны Ближнего Востока, Средней Азии, Китая, Индии. В Китае разработали метод последовательного исключения неизвестных для решения систем линейных уравнений, в Индии ввели отрицательные величины, усовершенствовали буквенную символику. В 9 веке появляется трактат «Китаб аль-джебр вальмукабала», выдающегося узбекского математика и астронома Мухаммеда Аль-Хорезми. Слово «аль-джебр» означает перенос отрицательных членов уравнения из одной части в другую с изменением знака. От слова «аль-джебр»-(восстановление) получила название алгебра. Сейчас существует большое количество методов, для решения систем линейных уравнений с двумя неизвестными, наиболее известные и распространенные: графический, способ сложения, способ подстановки, метод подбора, формулы Крамера и другие…