- Учителю
- Контроль теоретического материала за курс геометрии 7 класса
Контроль теоретического материала за курс геометрии 7 класса
Лист опроса № 1
-
Геометрия.
-
Аксиома.
-
3 аксиомы планиметрии о взаимном расположении точек и прямых.
-
IV аксиома планиметрии о трех точках прямой.
-
V аксиома планиметрии о точке прямой.
-
VI аксиома планиметрии о прямой на плоскости.
-
Отрезок.
-
Луч.
-
Угол.
-
Развернутый угол.
-
Равные фигуры.
-
Середина отрезка.
-
Биссектриса угла.
-
Измерение отрезков.
-
Свойства измерения отрезков.
-
Измерение углов.
-
Свойства измерения углов.
-
Прямой угол.
-
Острый угол.
-
Тупой угол.
-
Смежные углы.
-
Свойство смежных углов.
-
Вертикальные углы.
-
Свойство вертикальных углов.
-
Перпендикулярные прямые.
-
Свойство перпендикулярных прямых.
-
Треугольник.
-
Периметр треугольника.
-
Равные треугольники.
-
Теорема, доказательство теоремы.
-
Первый признак равенства треугольников.
-
Второй признак равенства треугольников.
-
Третий признак равенства треугольников.
-
Теорема о единственности опущенного перпендикуляра.
-
Медиана треугольника.
-
Биссектриса треугольника.
-
Высота треугольника.
-
Свойство о пересечении медиан, биссектрис и высот треугольников.
-
Равнобедренный треугольник.
-
Равносторонний треугольник.
-
Свойства равнобедренного треугольника.
-
Определение.
-
Определение окружности.
-
Хорда окружности.
-
Диаметр окружности.
-
Дуга окружности.
-
Круг.
-
Определение параллельных прямых.
-
Параллельные отрезки.
-
Секущая.
-
Углы при параллельных прямых и секущей.
-
3 признака параллельности двух прямых.
-
Аксиома параллельных прямых.
-
2 следствия из аксиомы параллельных прямых.
-
Обратная теорема.
-
Свойства параллельных прямых.
-
Свойство прямой, перпендикулярной к одной из двух параллельных прямых.
-
Сумма углов треугольника.
-
Внешний угол треугольника.
-
Свойства внешнего угла треугольника.
-
Виды треугольников.
-
Элементы прямоугольного треугольника.
-
Теорема о соотношениях между сторонами и углами треугольника.
-
2 следствия из теоремы о соотношениях между сторонами и углами треугольника.
-
Неравенства треугольника.
-
Свойства прямоугольных треугольников.
-
Признаки равенства прямоугольных треугольников.
-
Свойство двух параллельных прямых о равноудаленности точек.
-
Расстояние между параллельными прямыми.
-
Замечательные точки треугольника.
Ответы к листу опроса № 1
-
Геометрия - это наука, занимающаяся изучением геометрических фигур. Школьный курс геометрии делится на планиметрию и стереометрию. В планиметрии рассматриваются свойства фигур на плоскости, в стереометрии - свойства фигур в пространстве.
-
Аксиома - основные утверждения геометрии, не требующие доказательства.
-
А1: Каждой прямой принадлежат, по крайней мере, две точки.
А2: Имеются по крайней мере 3 точки, не лежащие на одной прямой.
А3: Через любые 2 точки проходит прямая, и притом только одна.
-
А4: Из трех точек прямой одна и только одна лежит между двумя другими.
-
А5: Каждая точка О прямой разделяет её на 2 части (два луча) так, что любые две точки одного и того же луча лежат по одну сторону от точки О, а любые две точки разных лучей лежат по разные стороны от точки О.
-
А6: Каждая прямая а разделяет плоскость на две части (две полуплоскости) так, что любые две точки одной и той же полуплоскости лежат по одну сторону от прямой а, а любые две точки разных полуплоскостей лежат по разные стороны от прямой а.
-
Отрезок - это часть прямой, ограниченная двумя точками. Точки, ограничивающие отрезок, называются его концами. Отрезок обозначается двумя заглавными латинскими буквами. Например, АВ или ВА.
-
Луч - это часть прямой, ограниченная одной точкой. Эта точка называется началом луча. Луч обозначается двумя заглавными латинскими буквами или одной строчной латинской буквой. Например, луч АВ или луч m.
-
Угол - это геометрическая фигура, которая состоит из точки и двух лучей, исходящих из этой точки. Лучи называются сторонами угла, а их общее начало - вершиной угла. Угол обозначается тремя заглавными латинскими буквами или одной заглавной латинской буквой или двумя строчными латинскими буквами. Например,
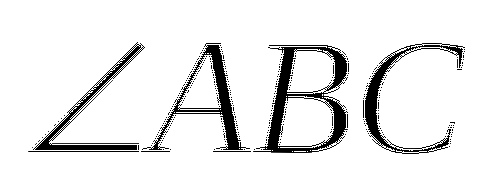 или
или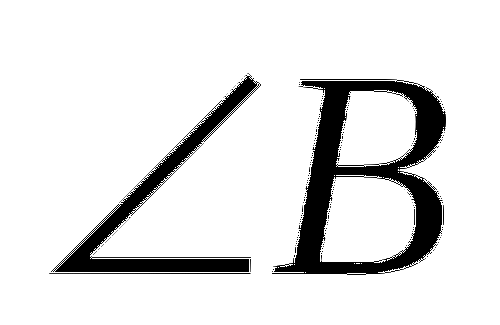 или
или 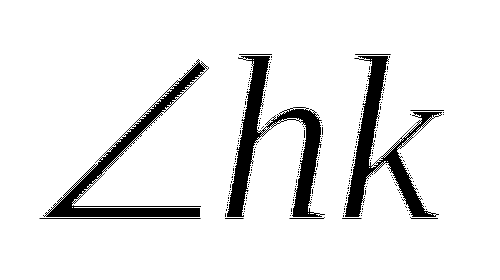 .
. -
Угол называется развернутым, если обе его стороны лежат на одной прямой.
-
Две геометрические фигуры называются равными, если их можно совместить наложением.
-
Середина отрезка - это точка отрезка, делящая его пополам, т.е. на два равных отрезка.
-
Биссектриса угла - это луч, исходящий из вершины угла и делящий его на два равных угла.
-
Измерение отрезков. Выбрав единицу измерения, можно измерить любой отрезок, т.е. выразить его длину некоторым положительным числом.
-
Свойства измерения отрезков. 1) Равные отрезки имеют равные длины. 3) Меньший отрезок имеет меньшую длину. 3) Когда точка делит отрезок на два отрезка, длина всего отрезка равна сумме длин этих двух отрезков.
-
Измерение углов. Градусной мерой угла называется положительное число, которое показывает, сколько раз градус и его части укладываются в данном угле.
-
Свойства измерения углов. 1) Равные углы имеют равные градусные меры.2) Меньший угол имеет меньшую градусную меру. 3) Развернутый угол равен 180 градусам. 4Неразвернутый угол меньше 180 градусов. 5) Когда луч делит угол на два угла, градусная мера всего угла равна сумме градусных мер этих углов.
-
Прямой угол - угол, градусная мера которого равна 90 градусов.
-
Острый угол - угол, градусная мера которого меньше 90 градусов.
-
Тупой угол - угол, градусная мера которого больше 90 градусов, но меньше 180 градусов.
-
Смежные углы - два угла, у которых одна сторона общая, а две другие являются продолжениями одна другой.
-
Свойство смежных углов. Сумма смежных углов равна 180 градусов.
-
Вертикальные углы. Два угла называются вертикальными, если стороны одного угла являются продолжениями сторон другого.
-
Свойство вертикальных углов. Вертикальные углы равны.
-
Перпендикулярные прямые. Две пересекающиеся прямые называются перпендикулярными, если они образуют четыре прямых угла.
-
Свойство перпендикулярных прямых. Две прямые, перпендикулярные к третьей, не пересекаются.
-
Треугольник - геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой, соединенных отрезками. Три точки называются вершинами, а отрезки - сторонами треугольника.
-
Периметр треугольника - это сумма длин трех сторон треугольника.
-
Равные треугольники - треугольники, которые при наложении совмещаются. Если два треугольника равны, то элементы одного треугольника соответственно равны элементам другого треугольника.
-
Теорема, доказательство теоремы. Утверждение, справедливость которого устанавливается путем рассуждения, называется теоремой, а сами рассуждения называются доказательством теоремы.
-
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
-
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
-
Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.
-
Из точки, не лежащей на прямой, можно провести перпендикуляр к этой прямой, и притом только один.
-
Отрезок, соединяющий вершину треугольника с серединой противоположной стороны, называется медианой треугольника.
-
Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника.
-
Перпендикуляр, проведённый из вершины треугольника к прямой, содержащей противоположную сторону, называется высотой треугольника.
-
В любом треугольнике медианы пересекаются в одной точке, биссектрисы пересекаются в одной точке, высоты или их продолжения также пересекаются в одной точке.
-
Треугольник называется равнобедренным, если его две стороны равны. Эти стороны называются боковыми, а третья - основанием.
-
Треугольник, все стороны которого равны, называется равносторонним.
-
В равнобедренном треугольнике углы при основании равны. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
-
Предложение, в котором разъясняется смысл того или иного выражения или названия, называется определением.
-
Окружностью называется геометрическая фигура, состоящая из всех точек, расположенных на заданном расстоянии от данной точки. Данная точка называется центром окружности, а отрезок, соединяющий центр с какой-либо точкой окружности, - радиусом окружности.
-
Отрезок, соединяющий две точки окружности, называется её хордой.
-
Хорда, проходящая через центр окружности, называется диаметром.
-
Часть окружности, ограниченная двумя точками, называется дугой окружности.
-
Часть плоскости, ограниченная окружностью, называется кругом.
-
Две прямые на плоскости называются параллельными, если они не пересекаются.
-
Два отрезка называются параллельными, если они лежат на параллельных прямых.
-
Прямая с называется секущей по отношению к прямым a и b, если она пересекает их в двух точках.
-
Углы при параллельных прямых и секущей:
-
накрест лежащие углы;
-
односторонние углы;
-
соответственные углы.
-
3 признака параллельности двух прямых:
-
Если при пересечении двух прямых секущей накрест лежащие углы равны, то прямые параллельны.
-
Если при пересечении двух прямых секущей соответственные углы равны, то прямые параллельны.
-
Если при пересечении двух прямых секущей сумма односторонних углов равна 1800, то прямые параллельны.
-
Через точку, не лежащую на данной прямой, проходит только одна прямая, параллельная данной.
-
1) Если прямая пересекает одну из двух параллельных прямых, то она пересекает и другую.
2)Если две прямые параллельны третьей прямой, то они параллельны.
-
Теоремой, обратной данной, называется такая теорема, в которой условием является заключение данной теоремы, а заключением - условие данной теоремы.
-
Свойства параллельных прямых:
-
Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
-
Если две параллельные прямые пересечены секущей, то соответственные углы равны.
-
Если две параллельные прямые пересечены секущей, то сумма односторонних углов равна 1800.
-
-
Если прямая перпендикулярна к одной из двух параллельных прямых, то она перпендикулярна и к другой.
-
Сумма углов треугольника равна 1800.
-
Внешним углом треугольника называется угол, смежный с каким-нибудь углом этого треугольника.
-
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
-
Виды треугольников:
-
остроугольный
-
тупоугольный
-
прямоугольный
-
-
Сторона прямоугольного треугольника, лежащая против прямого угла, называется гипотенузой, а две другие стороны - катетами.
-
В треугольнике: 1) против большей стороны лежит больший угол;
2) обратно, против большего угла лежит большая сторона.
-
2 следствия из теоремы о соотношениях между сторонами и углами треугольника:
-
В прямоугольном треугольнике гипотенуза больше катета.
-
Если два угла треугольника равны, то треугольник равнобедренный (признак равнобедренного треугольника)
-
-
Каждая сторона треугольника меньше суммы двух других сторон.
-
Свойства прямоугольных треугольников:
-
Сумма двух острых углов прямоугольного треугольника равна 900.
-
Катет прямоугольного треугольника, лежащий против угла в 300, равен половине гипотенузы.
-
Если катет прямоугольного треугольника равен половине гипотенузы, то угол, лежащий против этого катета, равен 300.
-
-
Признаки равенства прямоугольных треугольников:
-
По двум катетам: Если катеты одного прямоугольного треугольника соответственно равны катетам другого прямоугольного треугольника, то такие треугольники равны.
-
По катету и прилежащему острому углу: Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему к нему острому углу другого прямоугольного треугольника, то такие треугольники равны.
-
По гипотенузе и острому углу: Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
-
По гипотенузе и катету: Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.
-
-
Все точки каждой из двух параллельных прямых равноудалены от другой прямой.
-
Расстояние от произвольной точки одной из параллельных прямых до другой прямой называется расстоянием между этими прямыми.
-
Замечательные точки треугольника:
-
Три высоты треугольника всегда пересекаются в одной точке, называемой ортоцентром треугольника. Ортоцентр остроугольного треугольника (рис.26) расположен внутри треугольника, а ортоцентр тупоугольного треугольника (рис.27) - снаружи; ортоцентр прямоугольного треугольника совпадает с вершиной прямого угла.
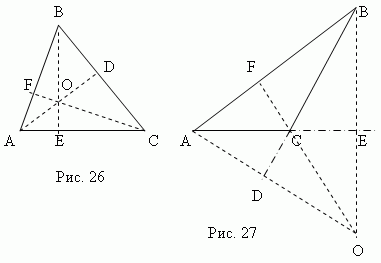
-
Три медианы треугольника (рис.28) пересекаются в одной точке, всегда лежащей внутри треугольника и являющейся его центром тяжести. Эта точка делит каждую медиану в отношении 2:1, считая от вершины.
-
Т
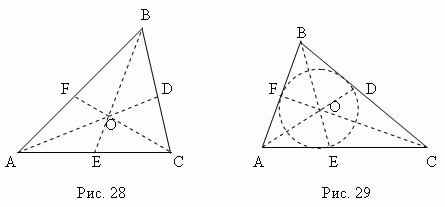 ри биссектрисы треугольника (рис.29) пересекаются в одной точке, всегда лежащей внутри треугольника и являющейся центром вписанной окружности. Биссектриса делит противоположную сторону на части, пропорциональные прилегающим сторонам; например, на рис.29 AE : CE = AB : BC .
ри биссектрисы треугольника (рис.29) пересекаются в одной точке, всегда лежащей внутри треугольника и являющейся центром вписанной окружности. Биссектриса делит противоположную сторону на части, пропорциональные прилегающим сторонам; например, на рис.29 AE : CE = AB : BC .
-
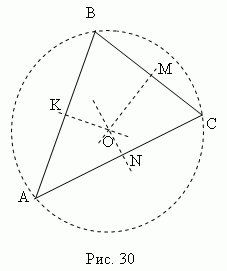
Три срединных перпендикуляра треугольника (рис.30) пересекаются в одной точке, являющейся центром описанной окружности. В остроугольном треугольнике эта точка лежит внутри треугольника; в тупоугольном - снаружи; в прямоугольном в середине гипотенузы.
-
Ортоцентр, центр тяжести, центр описанного и центр вписанного круга совпадают только в равностороннем треугольнике.