Урок- игра по математике в 6-х классах

(математический марафон)

ПОД ДЕВИЗОМ: «УЧЕНЬЕ С УВЛЕЧЕНЬЕМ»

«Учиться можно только весело…

чтобы переваривать знания, надо

поглощать их с аппетитом»

Анатоль Франс.

Цель: развитие познавательных и творческих способностей учащихся.

Задачи: Образовательные:

• овладение учащимися знаний по теме координатная плоскость;

• повторение понятий и терминов математики.

Развивающие:

• развитие пространственного воображения, логики и мышления;

• использование математики в практической деятельности людей.

Воспитательные:

• формирование интереса к предмету, развитие внимания, навыков самостоятельной работы при выполнении различных заданий на уроке.

Тип урока: обобщающий урок с элементами математического модулирования

Форма: урок - игра

Методы обучения: иллюстративно-наглядные, развивающие, проблемно-поисковые.

Форма работы: индивидуальная, работа в парах, самостоятельная работа.

Оборудование: компьютер, проектор, карточки с заданиями.

Ход урока

1. Организационный момент (сообщение темы, цели и задачи урока).

2. Игровой момент с творческим заданием (лист Мёбиуса)

3. Игровой момент (кроссворд, игра «поймай рыбку», игра «Лучший художник»)

4. Рефлексия. Подведение итогов.

I. Игровой момент (кроссворд, изобрази фигуру)

1. Кроссворд

Вставить слова в кроссворд: параллелепипед, тонна, круг, сотка, алгебра, сантиметр, километр, квадрат, грамм, метр.

Математика - наука о величинах и количествах; всё что можно выразить цифрой, принадлежит математике(из толкового словаря В.И. Даля)

2. Кроссвордк

у

б

х

о

р

д

а

у

р

а

в

н

е

н

и

е

р

а

д

и

у

с

л

и

н

е

й

к

а

п

р

о

ц

е

н

т

в

ы

ч

и

т

а

н

и

е

ч

и

с

л

и

т

е

л

ь

ц

и

р

к

у

л

ь

м

а

с

ш

т

а

б

т

ы

с

я

ч

а

1. Объёмное тело, каждая грань которого является квадратом.

2. Отрезок, соединяющий две любые точки окружности.

3. Равенство, где есть неизвестное число.

4. Отрезок, соединяющий центр окружности с любой её точкой.

5. Инструмент для измерения длины отрезка.

6. Сотая часть числа.

7. Действие, с помощью которого по сумме и одному из слагаемых находят другое слагаемое.

8. Число в записи дроби.

9. Инструмент для построения окружности.

10. Отношение длины отрезка на карте к длине соответствующего отрезка на местности.

11. Сто десятков - это сколько?

Слайд про С.В. Ковалевскую

3. Игра «Поймай рыбку»

(игра на компьютере)

4. Игра «Лучший художник»

Дети работают индивидуально по карточкам, рисуя животного в координатной плоскости по заданным точкам.

Утенок

1) (3; 0), (1; 2), (-1; 2), (3; 5), (1; 7), (-3; 6),

(-5; 7), (-3; 4), (-6; 3), (-3; 3), (-5; 2), (-5; -2),

(-2; -3), (-4; -4), (1; -4), (3; -3), (6; 1), (3; 0)

2) Глаз (-1; 5).

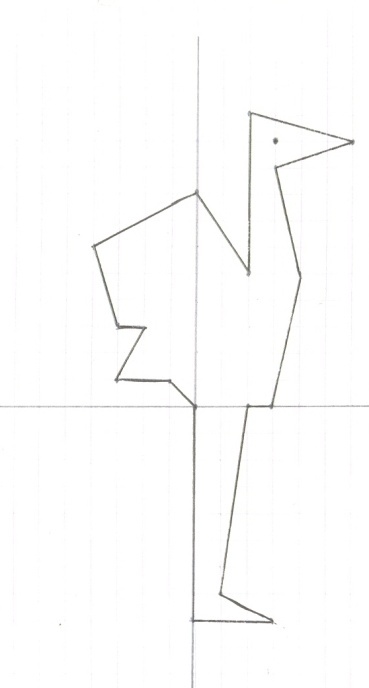
Страус

1. (0; 0), (- 1; 1), (- 3; 1), (- 2; 3), (- 3; 3), (- 4; 6), (0; 8), (2; 5), (2; 11), (6; 10), (3; 9), (4; 5), (3; 0), (2; 0),

(1; - 7), (3; - 8), (0; - 8), (0; 0).

2) Глаз: (3; 10).

2. Игровой момент с творческим заданием ( лист Мёбиуса)

Ведущий: Найдите фамилию немецкого математика, решив примеры. Ответ и соответствующую букву запишите в таблицу и вы прочитаете фамилию ученого.

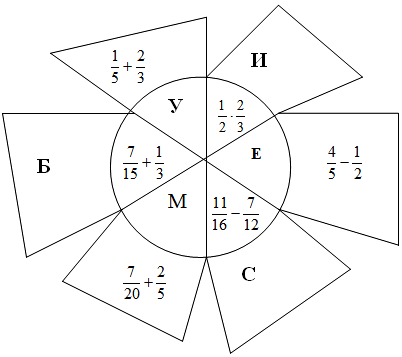
Ответы заносятся в таблицу.

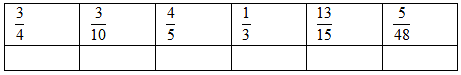
Если команда правильно решила примеры и правильно заполнила таблицу, то получили фамилию немецкого ученого МЁБИУС.

Лист Мёбиуса, лента Мёбиуса - топологический объект, простейшая односторонняя поверхность с краем. Попасть из одной точки этой поверхности в любую другую можно, не пересекая края. Лента Мёбиуса была обнаружена независимо немецкими математиками Августом Фердинандом Мёбиусом и Иоганном Бенедиктом Листингом в 1858 году. Модель ленты Мёбиуса может легко быть сделана. Для этого надо взять достаточно вытянутую бумажную полоску и соединить концы полоски, предварительно перевернув один из них. (делаем модель Мёбиуса с детьми)

• Лента Мёбиуса обладает любопытными свойствами. Если попробовать разрезать ленту вдоль по линии, равноудалённой от краёв, вместо двух лент Мёбиуса получится одна длинная двухсторонняя (вдвое больше закрученная, чем лента Мёбиуса) лента, которую фокусники называют «афганская лента». (делаем с детьми)

• Если теперь эту ленту разрезать вдоль посередине, получаются две ленты намотанные друг на друга. Если же разрезать ленту Мёбиуса, отступая от края приблизительно на треть её ширины, то получаются две ленты, одна - более тонкая лента Мёбиуса, другая - длинная лента с двумя полуоборотами (Афганская лента). (делаем с детьми)

Девочки 8 класса Носкова Ирина и Волоскова Марина рассказывают с помощью презентации о свойствах и применении листа Мёбиуса.

5. Рефлексия. Подведение итогов.

Выводы:

вспомнили основные математические термины, решая кроссворд;

закрепили знания по теме координатная плоскость;

узнали много нового и интересного о математическом объекте лист Мёбиуса.