Внеурочное мероприятие для 7 класса по теме: «СОСТАВЛЕНИЕ И РАСПРОСТРАНЕНИЕ УЗОРОВ НА ПЛОСКОСТИ С ПОМОЩЬЮ ГЕОМЕТРИЧЕСКИХ ФИГУР»

Внеурочное мероприятие для 7 класса по теме:

«СОСТАВЛЕНИЕ И РАСПРОСТРАНЕНИЕ УЗОРОВ НА ПЛОСКОСТИ С ПОМОЩЬЮ ГЕОМЕТРИЧЕСКИХ ФИГУР»

Подготовила и провела учитель математики:

Азаматова Ленура Рустемовна,

МОУ «Майская школа с крымскотатарским

языком обучения»

2015г

ТЕМА: «СОСТАВЛЕНИЕ И РАСПРОСТРАНЕНИЕ УЗОРОВ НА ПЛОСКОСТИ С ПОМОЩЬЮ ГЕОМЕТРИЧЕСКИХ ФИГУР»

Цель:

Научиться рисовать на клетчатой, треугольной и круговой сетках;

установление факта заполняемости плоскости равными треугольниками, четырёхугольниками, и шестиугольниками с попарно параллельными и равными сторонами;

использовать свойства углов многоугольников и симметрии;

развивать пространственное и логическое мышление;

уметь решать геометрические задачи с помощью алгебры.

Оборудование: интерактивная доска.

Наглядность: презентация.

Ход мероприятия:

1. При решении геометрических задач очень важно так называемое «геометрическое зрение» - умение видеть на чертеже не только то, что бросается в глаза, но и все то, что на нем вообще есть.

Такие задачи развивают пространственное воображение, что помогает нам мыслить и уметь изображать свою точку зрения на чертеже.

Рассмотрим и научимся строить различные виды сеток для будущего составления орнамента.

Составление и распространение узоров на клетчатой бумаге

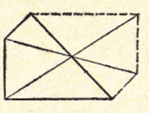
Выделяю ячейку в 1 см² на клетчатой бумаге, наношу внутри нее произвольный рисунок и распространяю на весь листок, применяя преобразование осевой симметрии, принимая за оси симметрии стороны первоначального и вновь образующихся квадратов.

Составление и распространение узоров на треугольной сетке.

Узор на треугольной сетке строю так: намечаю элементы узора в одной из ячеек сетки, распространяю его, применив преобразование осевой симметрии.

Треугольную сетку, состоящую из равносторонних треугольников, расчерчиваю на листе бумаги из ученической тетради в линейку с помощью масштабной линейки, специально изготовленной для этой цели из бумаги, взятой из той же тетради. Такую линейку сделать просто. Из середины тетради вынимаю двойной лист, перегибаю пополам (вдоль направления линий разлиновки), распрямляю и снова перегибаю. Линия перегиба, разделённая на одинаковые части - служит такой линейкой.

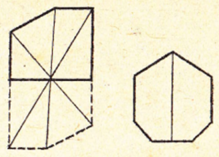
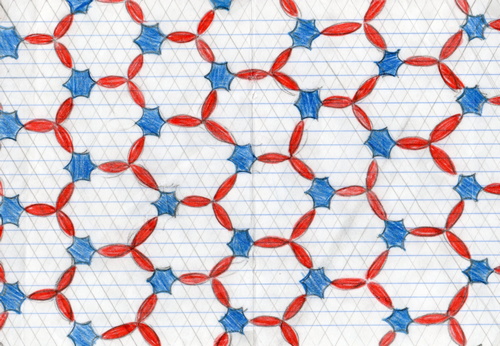
Составление узоров на круговой сетке.

Для того, чтобы составить рисунок, необходим чертёжный лист бумаги, циркуль и цветные карандаши.

Сначала заполняю листок контурным узором. На основе деления окружности на шесть равных частей строю контурный узор (сетка), состоящий из одних только окружностей и представляющий собой как бы канву для нанесения всевозможных узоров. Радиус окружности 2 см. Узор составляю, выделяя в определенной системе «круговые луночки» соответствующей раскраски. Выбор рисунка узора и его раскраски - дело вкуса. Цвет усиливает эмоциональное восприятие красоты геометрических форм. Несмотря на то, что контурный узор остаётся неизменным, возможности получить различные узоры путём выбора и раскраски «луночек» очень большие.

2.Практическая работа

Важным шагом в изучении этого вопроса являлось установление факта заполняемости плоскости равными треугольниками, четырёхугольниками, и шестиугольниками с попарно параллельными и равными сторонами.(смотреть презентацию)

Это свойство шестиугольника было выявлено, так же как и свойство четырехугольника центрально-симметричным преобразованием фигур. После этого, уже в порядке следствий, были высказаны следующие предложения:

1. Выпуклыми четырехугольниками произвольного вида можно заполнить плоскость. Действительно, два центрально-симметричных четырехугольника составляют шестиугольник с попарно равными и параллельными сторонами;

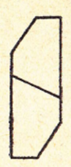
2. Выпуклыми пятиугольниками с двумя параллельными сторонами можно заполнить плоскость. Действительно, два центрально-симметричных пятиугольника с центром симметрии в середине стороны, соединяющей параллельные стороны, составляют шестиугольник с попарно параллельными и равными сторонами.

Затем я попыталась заполнить плоскость выпуклыми семиугольниками, восьмиугольниками и т.д. Все попытки оказались безуспешными. Но заметила любопытную вещь: выпуклыми семиугольниками заполнить плоскость нельзя, а вот «половинками» семиугольника некоторого вида, оказывается можно , если из двух половинок такого семиугольника сложить шестиугольник с попарно параллельными сторонами (при допущении поворота фигур в пространстве).

На основании проведенного эксперимента была высказана следующая гипотеза: никакого вида равными выпуклыми n-угольниками при n>6 нельзя заполнить плоскость без просветов и перекрытий. Однако доказать это предложение нам не удалось.

4. А теперь пригласим одноклассников, которые проводили исследовательскую работу, продолжающую нашу тему.

Выступление учеников.

Мы попытались установить связь между суммой всех углов, прилегающих с внешней стороны к периметру данного многоугольника, и способом распространения этой фигуры в плоскости. Эта идея, постепенно развиваемая и углубляемая нами, вылилась в целый ряд математических предложений, смысл которых заключается в следующем.

Пусть дан выпуклый n-угольник с углами вида а , а , ……, а и пусть сумма всех углов, прилегающих к его периметру с внешней стороны, равна Р.

Если можно заполнить многоугольниками данного вида плоскость, то смежные многоугольники (равные данному), очевидно, будут иметь те же углы а₁, а₂,……., а_К , что и данный.

Следовательно, и углы, непосредственно прилегающие к периметру данного многоугольника , будут принадлежать этому же множеству. Однако число каждого вида таких углов из этой совокупности неизвестно. Можно составить неопределенное уравнение.

х₁a₁₊х₂а_2+……+х_ка_{к =}Р_,

_где х_1, х_2,….,x_к-неизвестное число углов каждого вида.

Если многоугольниками данного вида можно заполнить плоскость, то среди целочисленных решений этого уравнения будут и такие, которые удовлетворят геометрическим требованиям задачи.

A это значит, что некоторые полученные комбинации углов будут соответствовать возможным расположениям многоугольников в плоскости и, следовательно, в какой-то мере будут ориентировать на способ распространения данной фигуры в плоскости.

Действительно, пусть дан шестиугольник с двумя углами по 45⁰ и остальными -по 157,5⁰. Сумма всех углов, прилегающих к его периметру, Р=360⁰*6-180⁰*4=1440⁰.

Составим уравнение: 45х+1575у=1440, после упрощения получим:2х+7у=64. Целочисленными положительными решения его будут:1) х=4, у=8; 2)х=11, у=6; 3)х=18, у=4; 4)х=25, у=2.

Первые два решения уравнения приводят нас к способам заполнения плоскости шестиугольниками данного вида. Третий и четвертый варианты не являются решениями задачи, так как не поддаются геометрической интерпретации, удовлетворяющей условию задачи.

Рассмотрим еще пример. Пусть дан пятиугольник с двумя углами по 90⁰ и тремя по 120⁰; Р=360⁰*5-180⁰*3=1260⁰.

Составим уравнение:90х+120у=1260, после упрощения получим:3х+4у=42. Целочисленными положительными решениями его будут:1) х=2, у=9; 2)х=6, у=6; 3)х=10, у=3.

Первое и третье решение не поддаются геометрической интерпретации в желательном для нас смысле. Второе же решение уравнения приводит нас к двум возможным комбинациям в расположении равных пятиугольников с двумя углами по 90⁰ и тремя-по 120⁰.

Пусть теперь дан семиугольник с одним углом 90 и остальными-по 135⁰. Тогда Р =360⁰*7-180⁰*5=1620⁰,и уравнение 90х+135у=1620, составленное из этих данных, будет иметь следующие целочисленные положительные решения:1)х=3, у=10; 2)х=6, у=8; 3) х=9, у=6; 4)х=12, у=4; 5) х=15, у=2.

Ни одно из этих решений не дает способа заполнения плоскости равными семиугольниками данного вида.

Итак, разрешимость уравнения х₁а₁+х₂а₂+…..+х_ка_к=Р в целых положительных числах -необходимо условие заполняемости плоскости выпуклыми равными многоугольниками данного вида.

5. Получением этих результатов мы завершили с вами наши исследования, направленные на решение проблемы заполнения плоскости равными фигурами.

Решить проблему полностью так мне не удалось.

6.Домашнее задание: попробуйте заполнить плоскость помощью пятиугольников (пентагонов). Соберите материал и докажите, если это возможно или нет.

7. Подведение итогов: Составьте свое заключение- итог урока.

Распространение узоров на плоскости с помощью шестиугольников с двумя углами по 45⁰ и остальными -по 157,5⁰.

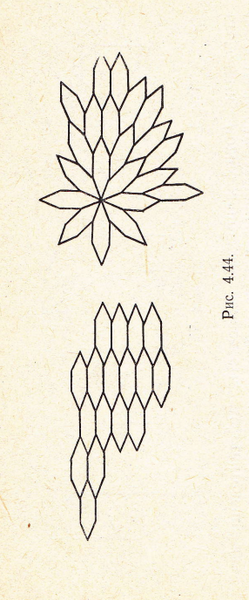
Распространение узоров на плоскости с помощью пятиугольников с двумя углами по 90⁰ и тремя по 120⁰

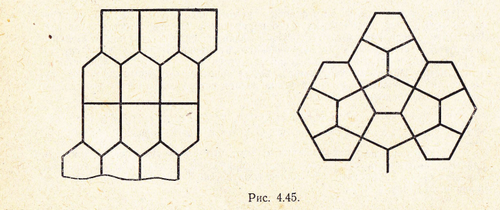
На клетчатой сетке

На треугольной сетке

На круговой сетке