- Учителю
- Урок + презентация по геометрии для 9 класса по теме «Площади подобных фигур»
Урок + презентация по геометрии для 9 класса по теме «Площади подобных фигур»
Урок геометрии в 9 классе по теме « Площади подобных фигур»
Тип урока: продуктивно - познавательный
Цель урока:
Рассмотреть зависимость отношения площадей подобных фигур от отношения их линейных размеров.
Задачи:
-выработать у учащихся умение находить отношения площадей подобных фигур по известным длинам пары соответствующих элементов этих фигур
-развивать мышление, умение анализировать, обобщать, систематизировать, ставить и разрешать проблемы
-формировать развитие аккуратности, трудолюбия, усердия, проявлять добросовестное отношение к работе
Актуализация опорных знаний учащихся:
-
Вспомнить какое преобразование называется преобразованием подобия.
-
Повторить свойства подобных фигур ( в частности подобие треугольников), обратить внимание учащихся на то, что у подобных фигур не только пропорциональны соответствующие стороны, но и высоты, медианы ( проведенные к соответствующим сторонам), периметры и др.
Постановка проблемы:
Верно ли такое же утверждение для площади? Предложить учащимся решить задачи и сравнить отношение линейных размеров с отношение площадей данных подобных фигур.
1. Треугольник АВС подобен треугольнику А1В1С1. Угол А = углу А1 = 30 . АВ=4, А1В1=8,АС=5, А1С1=10. Найти отношение линейных размеров , отношение площадей.
. АВ=4, А1В1=8,АС=5, А1С1=10. Найти отношение линейных размеров , отношение площадей.
2. Параллелограмм АВСD подобен параллелограмму А1В1С1D1. АD=3, А1D1=9, высота ВН = 4, В1Н1=12. Найти отношение линейных размеров , отношение площадей.
3. Трапеция АВСD подобна трапеции А1В1С1D1. Средняя линия трапеции АВСD равна 20, высота 8, а средняя линия трапеции А1В1С1D1=5, а высота 2. Найти отношение линейных размеров , отношение площадей.
1. 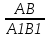 =
=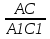 =
=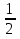
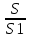 =
= 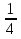 2.
2. 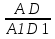 =
=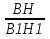 =
=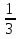
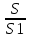 =
=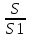 3.
3. 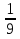 =
=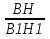 = 4
= 4 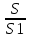 = 16
= 16
Учащиеся выдвигают гипотезу: отношение площадей подобных фигур равно квадрату отношений их линейных размеров (квадрату коэффициента подобия).
Если F ̴ F′, то S:S1=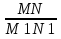
Докажем, что это утверждение справедливо для всех простых многоугольников.
Изучение нового материала:
Теорема: Площади подобных фигур относятся как квадраты их линейных размеров.
( доказательство излагается в устной форме по заранее заготовленным записям).
Закрепление нового материала:
Разберем несколько примеров, где применяется данная теорема.
Устно:
-
Треугольник АВС подобен треугольнику РОТ, к=
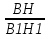 . Найти отношение площадей.
. Найти отношение площадей. -
Треугольник АВС подобен треугольнику РОТ. АВ = 2 см, РО = 6 см. Найти отношение площадей.
-
Отношение площадей равно 4:9. Найти отношение периметров.
Письменно:
-
Треугольник АВС подобен треугольнику МТР. Площадь треугольника АВС равна 500
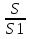 , а площадь треугольника МТР равна 125
, а площадь треугольника МТР равна 125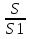 . АС = 18 см. Найти МР.
. АС = 18 см. Найти МР. -
В треугольнике АВС проведена прямая параллельная стороне АС , которая делит другие стороны треугольника пополам. Площадь треугольника АВС равна 12
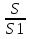 . Найти площадь полученного треугольника.
. Найти площадь полученного треугольника.
Проверка усвоения материала ( с проверкой в классе)
1 вариант
-
Найти отношения площадей подобных квадратов, если отношения соответствующих сторон этих квадратов равно 2:3.
-
Как относятся стороны двух подобных квадратов, если отношения площадей этих квадратов равно
9:2?
-
Периметры двух подобных многоугольников равны 90см и 60 см. Найти отношение их площадей.
-
Площадь большего из двух подобных многоугольников равна 45
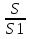 . Найдите площадь второго многоугольника, если их соответствующие стороны равны 15 см и 10см.
. Найдите площадь второго многоугольника, если их соответствующие стороны равны 15 см и 10см. -
Сторона АВ треугольника АВС, разделена на три равных отрезка точками К и Р ( начиная от А). Через точку К проведена прямая параллельно АС, через точку Р проведена прямая параллельно СВ, точка М- их точка пересечения. Определить площадь треугольника КМР, если площадь треугольника АВС равна 36.
2 вариант
-
Найти отношения площадей подобных квадратов, если отношения соответствующих сторон этих квадратов равно 1:1,5.
-
Как относятся стороны двух подобных квадратов, если отношения площадей этих квадратов равно 3:4?
-
Высоты двух равносторонних треугольников равны 6 см и 7 см. Найти отношение их площадей.
-
Площадь меньшего из двух подобных многоугольников равна 36
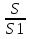 . Найдите площадь второго многоугольника, если их периметры равны 27 см и 45 см.
. Найдите площадь второго многоугольника, если их периметры равны 27 см и 45 см. -
Сторона АВ треугольника АВС, разделена на три равных отрезка точками К и Р ( начиная от точки А). Через точку К и Р проведены прямые КМ и РН параллельные СА. Найти отношение площадей треугольника АВС и треугольника ВНР, если площадь треугольника ВНР равна 3.
Собрать работы учащихся, а затем рассмотреть решения задач по заготовкам.
Итог урока:
1.Вспомнили свойства подобия фигур.
2. Сформулировали и доказали теорему о площадях многоугольников.
3. Рассмотрели примеры, иллюстрирующие эту теорему.
4. Самостоятельно решали задачи по данной теме урока.
Домашнее задание:
П. 128 в.7 № 50, 52