- Учителю
- Конспект урока по математике на тему: Решение текстовых задач (элективный курс, 10-11 класс)
Конспект урока по математике на тему: Решение текстовых задач (элективный курс, 10-11 класс)
МБОУ «Кармалинская СОШ»
Конспект урока по теме «Решение текстовых задач»
(элективный курс)
Ермилова Елена Алексеевна
Предмет: Математика.
Тип урока: урок применения знаний и умений.
Тема урока: Решение текстовых задач (элективный курс).
Продолжительность: 45 мин.
Класс: 10-11 класс.
Цель урока:
Образовательная:
Формировать умение решать задачи на движение, содействовать развитию практических навыков работы с величинами.
Развивающая:
Развивать интерес к дальнейшему учебному процессу, аккуратность, математическую грамотность.
Воспитательная:
Воспитание стремления детей к успеху в учебе, умения адекватно оценивать свой труд.
Медиа продукт: презентация к уроку
Средства обучения: компьютер, мультимедийный проектор, презентация PowerPoint.
План урока:
1) Организационная часть (приветствие, объявление темы и цели занятия) - 3 мин.
2) Основная часть (Решение текстовых задач на движение)- 40 мин.
3) Заключительная часть (Запись домашнего задания, подведение итогов) - 2 мин.Ссылка на слайд в презентации
Предполагаемые
действия учащихся
1
ОРГАНИЗАЦИОННАЯ ЧАСТЬ
Приветствие. Объявление темы и цели урока.
Здравствуйте, ребята! Сегодня у нас не совсем обычное занятие, вместе собрались и 10 и 11 класс. Давайте для начала решим небольшую задачу:
-
Школьный автобус, привозя детей из с. Городище в с. Кармалы, преодолевает расстояние в 4 км за 5 минут. С какой скоростью едет автобус? Получит ли он штраф, если максимально разрешенная скорость равна 60 км/ч?
(Решение: 4: 1/14=56 км/ч, нет)
-
Скорость распространения света самая большая в природе - 300000 км/с. На Солнце произошла вспышка. Через какое время ее увидят на Земле, если расстояние от Земли до Солнца равно 150000000 км?
(Решение: 150000000/300000=500 с)
</ - Что это за задачи?
- Что объединяет эти задачи?
- Что в них общего?
- Где мы сталкивались с такими задачами?
- Какой это номер в ЕГЭ?
- Что нужно знать, чтобы решить такие задачи?
- Вы умеете решать эти задачи?
- Чем мы с вами будем заниматься сегодня на уроке?
Текстовые задачи являются традиционным разделом на ЕГЭ. Как правило, основная трудность при решении текстовой задачи состоит в переводе её условий на математический язык уравнений. Общего способа такого перевода не существует. Однако многие задачи достаточно типичны.
Слайд №1
Слайд № 2-3
Решают задачи
Отвечают на вопросы
2
ПОДГОТОВКА К РЕШЕНИЮ ЗАДАЧ НА ДВИЖЕНИЕ
- Как вы думаете, из каких этапов состоит решение текстовой задачи?
Этапы решения текстовых задач:
1. Анализ содержания задачи.
2. Поиск пути решения задачи и составление плана ее решения.
3. Осуществление плана решения задачи.
4. Проверка решения задачи.
Слайд № 4
Записывают в тетради этапы решения задач.
Стандартная схема решения таких задач включает в себя:
1.Выбор и обозначение неизвестных.
2.Составление уравнений (возможно неравенств) с использованием неизвестных и всех условий задачи.
3.Решение полученных уравнений (неравенств).
4.Отбор решений по смыслу задачи.
Слайд № 5
- Каким способом легче всего решать текстовые задачи?
Подходы к решению текстовых задач
Наиболее распространенный, довольно эффективный способ использования таблиц. В зависимости от типа решаемой задачи столбики в таблице будут иметь разные названия
Слайд № 6
- С какими задачами вы встречались? (Задачи на работу, смеси, проценты, сплавы, прогрессии)
- А с какими задачами именно на движение?
Основными типами задач на движение являются:
-задачи на движение по прямой (навстречу и вдогонку);
-задачи на движение по замкнутой трассе;
-задачи на движение по воде;
-задачи на среднюю скорость;
-задачи на движение протяжённых тел.
Слайд № 7
При решении этих задач принимают следующие допущения:
Если нет специальных оговорок, то движение считают равномерным.
Скорость считается величиной положительной.
Всякие переходы на новый режим движения, на новое направление движения считают происходящим мгновенно.
Слайд № 8
- Какие обозначения используются в задачах на движение?
(В задачах на движение используются
S- пройденное расстояние,
V- cкорость равномерного движения,
t - время движения.)
- Как найти v, если известно S, t? (V=S/t)
- Как найти t? (t=S/V)
При составлении уравнений в таких задачах часто бывает удобно прибегнуть к геометрической иллюстрации процесса движения: путь изображается в виде отрезка прямой, место встречи движущихся с разных сторон объектов точкой на отрезке и т.д.
Часто для усложнения задачи её условие формулируется в различных единицах измерения (метры, километры, часы, минуты и т.д.). В этом случае при выписывании уравнений необходимо пересчитывать все данные задачи в одинаковых единицах измерения.
Слайд № 9
Слайд № 10
3
РЕШЕНИЕ И ПОДРОБНЫЙ РАЗБОР НЕКОТОРЫХ ЗАДАЧ НА ДВИЖЕНИЕ
- Какие виды задач на движение по прямой вы встречали?
Встречное движение
Движение в противоположных направлениях их одного пункта
Движение в противоположных направлениях их двух пунктов
Движение вдогонку
Движение с одного пункта с отставанием
Движение из двух пунктов с отставанием
-Давайте мы с вами раздерем сегодня именно задачи на движение по прямой.
Слайд № 11-16
Разбирают схемы по раздаточному материалу
-
Из городов А и В, расстояние между которыми равно 330 км, навстречу друг другу одновременно выехали два автомобиля и встретились через 3 часа на расстоянии 180 км от города В. Найдите скорость автомобиля, выехавшего из города А. Ответ дайте в км/ч.
Решение:
V, км/ч
S, км
t, ч
1 автомобиль
?
330-180=150
3
2 автомобиль
180
3
Один ученик у доски, остальные в тетради решают задачу
-
Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью 24 км/ч, а вторую половину пути - со скоростью, на 16 км/ч большей скорости первого, в результате чего прибыл в пункт B одновременно с первым автомобилем. Найдите скорость первого автомобиля. Ответ дайте в км/ч.
Решение:
V, км/ч
S, км
t, ч
1 автомобиль
х
1
2 автомобиль
24
Х+16
1
Один ученик у доски, остальные в тетради решают задачу
-
Задача:
Из городов A и B навстречу друг другу выехали мотоциклист и велосипедист. Мотоциклист приехал в B на 3 часа раньше, чем велосипедист приехал в A, а встретились они через 48 минут после выезда. Сколько часов затратил на путь из B в A велосипедист?
Решение:
V, км/ч
S, км
t, ч
мотоциклист
1
велосипедист
1
х
Примем расстояние между городами 1. Пусть время движения велосипедиста равно х ч, тогда время движения мотоциклиста равно х-3 ч. К моменту встречи они находились в пути 48 минут и в сумме преодолели всё расстояние между городами, поэтому
Один ученик у доски, остальные в тетради решают задачу
Физкультминутка для глаз
Слайд № 17
Выполняют физкультминутку для глаз, наблюдают за движущимися фиурами
Работа в парах
Два велосипедиста одновременно отправились в 240-километровый пробег. Первый ехал со скоростью, на 1 км/ч большей, чем скорость второго, и прибыл к финишу на 1 час раньше второго. Найти скорость велосипедиста, пришедшего к финишу первым. Ответ дайте в км/ч.
Решение:
V, км/ч
S, км
t, ч
1 велосипедист
х+1
240
2 велосипедист
х
240
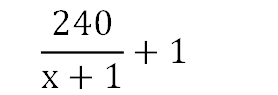
Ответ: 16 км/ч
Слайд № 18
Решают в парах
Самостоятельная работа
Автомобиль выехал с постоянной скоростью 75 км/ч из города А в город В, расстояние между которыми равно 275 км. Одновременно с ним из города С в город В, расстояние между которыми равно 255 км, с постоянной скоростью выехал мотоциклист. По дороге он сделал остановку на 50 минут. В результате автомобиль и мотоцикл прибыли в город В одновременно. Найдите скорость мотоциклиста. Ответ дайте в км/ч
V, км/ч
S, км
t, ч
автомобиль
75
275
275:75
мотоцикл
х
255
255:х
Решение:
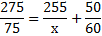
Ответ: 90 км/ч
Слайд № 19
Решают самостоятельно
4
ИТОГИ УРОКА,
Рефлексия, запись домашнего задания.
- Какие цели мы сегодня поставили?
- Достигли поставленные цели или нет?
- Чему научились?
- Что вам понравилось?
- Что вызвало наибольшие трудности?
- Какую бы оценку за урок вы бы себе поставили?
Домашнее задание:
Из сборников ЕГЭ посмотрите любые 3 задачи на движение и решите их.
Записывают д/з. в дневник.