Исследовательская работа по математике Многогранники

‌‌Vl‌ l‌ районная научно-практическая конференция исследовательских, проектных и творческих работ учащихся «Первые шаги в науке»

Тема

Многогранники вокруг нас

Выполнила: ученица 7 класса Щербакова Ольга

Руководитель: Тремаскина В.С.

Содержание.

Введение.

1.Основная часть.

1.1. Общая информация о многогранниках.

1.2. История многогранников.

1.3. Классификация многогранников.

1.3.1. Платоновы тела.

1.3.2. Тела Архимеда.

1.3.3. Тела Кеплера-Пуансо.

1.4. Многогранники вокруг нас.

1.4.1. Многогранники в химии.

1.4.2. Многогранники в географии.

1.4.3. Многогранники в биологии.

1.4.4. Многогранники в медицине.

1.4.5. Многогранники в быту.

1.4.5. Многогранники в природе

1.4.6. Многогранники в живописи и искусстве.

1.4.7. Многогранники в архитектуре.

1.5. Практическая часть.

Вывод.

Список литературы.

Приложение.

Введение

С многогранниками мы знакомы с детских лет. О них напоминают окружающие нас предметы: спичечная коробка, камушки, буханка хлеба.

Многогранники имеют не только значение при геометрических исследованиях по геометрии, но и для практических приложений в других разделах математики. Формы многогранников находят широкое применение в конструировании сложных и красивых многогранных поверхностей, которые используются в реальных архитектурных проектах. Идёт это с глубокой древности. Для лучшей эксплуатации и моделирования зданий нужно изучить свойства многогранников. Поэтому мне захотелось, чтобы мы больше узнали о многогранниках, научились изготавливать их различные модели и выявляли их роль в окружающем мире.

Возникла проблема: что такое многогранники и где их можно встретить в окружающем мире.

Цель исследования: познакомиться с понятием многогранника и яркими примерами применения многогранников в окружающем мире, научиться изготовлять модели многогранников.

Задачи исследования:

- изучить необходимую литературу по данной теме;

- доказать, что многогранники встречаются в жизни;

- определить и рассмотреть использование многогранников в неживой и живой природе;

-сделать многогранник.

Объект исследования: многогранники.

Предмет исследования: многогранники вокруг нас.

Гипотеза: если изучу тему «Многогранники», проанализирую информацию по этой теме, то смогу ответить на возникшие вопросы и использовать полученные знания в дальнейшем.

Методы исследования:

- работа с литературой;

- работа с интернет ресурсами;

- беседа с преподавателем;

- наблюдение.

Актуальность: данная работа является актуальной, потому что

при изучении темы «Многогранники», недостаточно говорится

о их практическом применении в сфере человеческой жизни. Звездчатые многогранники очень декоративны, что позволяет широко применять их в ювелирной промышленности при изготовлении всевозможных украшений. Применяются они и в архитектуре. Многие формы звездчатых многогранников подсказывает сама природа. Снежинки - это звездчатые многогранники. С древности люди пытались описать все возможные типы снежинок, составляли специальные атласы. Сейчас известно несколько тысяч различных типов снежинок.

Практическая значимость: использовать на уроках геометрии,

изобразительного искусства, МХК. Знания о формах многогранников находят широкое применение в конструировании сложных и красивых многогранных поверхностей, которые используются в реальных архитектурных проектах.

1.Основная часть.

1.1. Общая информация о многогранниках.

Многогранником называется тело, граница которого является объединением конечного числа многоугольников.

М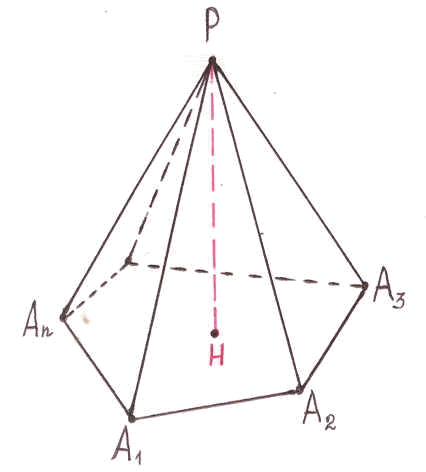ногоугольники из которых составлен многогранник называются его гранями. Стороны граней - ребрами.

Концы ребер - вершинами многогранника.

Отрезок соединяющий две вершины не принадлежащий

одной грани называются диагональю.

Многогранники имеют красивые формы, они обладают богатой историей, которая связана с именами таких ученых, как Пифагор, Евклид, Архимед. Многогранники выделяются необычными свойствами, самое яркое из которых формулируется в теореме Эйлера о числе граней, вершин и ребер выпуклого многогранника: для любого выпуклого многогранника справедливо соотношение Г+В-Р=2, где Г-число граней, В-число вершин, Р-число ребер данного многогранника.

1.2. История многогранников.

Правильные многогранники известны с древнейших времён. Их орнаментные модели можно найти на резных каменных шарах, созданных в период позднего неолита, в Шотландии, как минимум за 1000 лет до Платона. В костях, которыми люди играли на заре цивилизации, уже угадываются формы правильных многогранников.Начиная с 7 века до нашей эры в Древней Греции создаются философские школы. Большое значение в этих школах приобретают рассуждения, с помощью которых удалось получать новые геометрические свойства.

1.3.Классификация многогранников

Многогранники

Выпуклые Невыпуклые

Правильные Звездчатые

Многогранник называется выпуклым, если он лежит по одну сторону от плоскости любой из его граней.

М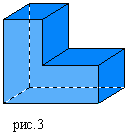ногогранник называется невыпуклым, если он лежит по разные стороны от плоскости любой из его граней

Выпуклый Невыпуклый

1.3.1. Платоновы тела.

С древнейших времен наши представления о красоте связаны с симметрией. Наверное, этим объясняется интерес человека к многогранникам - удивительным символам симметрии, привлекавшим внимание выдающихся мыслителей. Пифагорейцы считали правильные многогранники божественными фигурами и использовали в своих философских сочинениях. Позже учение пифагорейцев о правильных многогранниках изложил в своих трудах другой древнегреческий ученый, философ - идеалист Платон. С тех пор правильные многогранники стали называться платоновыми телами.

Платон Афинский, настоящее Имя Аристокл, Сын Аристона и Периктионы

(род. 27 мая 427, Афины - ум. 347 до Р. X., там же) - древнегреч. Философ

Правильным многогранником называется такой выпуклый многогранник, все грани которого являются одинаковыми правильными многоугольниками и все двугранные углы попарно равны.

1.3.2. Тела Архимеда.

Но есть и такие многогранники, у которых все многогранные углы равны, а грани - правильные, но разноименные правильные многоугольники. Многогранники такого типа называются равноугольно-полуправильными многогранниками. Впервые многогранники такого типа открыл Архимед. Им подробно описаны 13 многогранников, которые позже в честь великого ученого были названы телами Архимеда.

Множество архимедовых тел можно разбить на пять групп.

П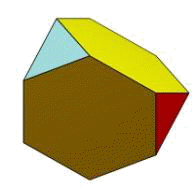ервую группу составляют пять многогранников, которые получаются из пяти платоновых тел в результате их усечения:

усеченный тетраэдр,

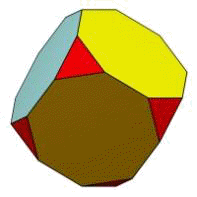
усеченный куб,

усеченный додекаэдр

усеченный икосаэдр

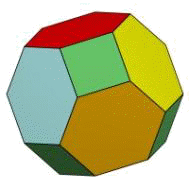
усеченный октаэдр

Вторую группу составляют два тела, называемых квазиправильными многогранниками. Это название означает, что гранями этого многогранника являются правильные многоугольники всего двух типов, причем каждая грань одного типа окружена гранями другого типа. Эти два тела называются

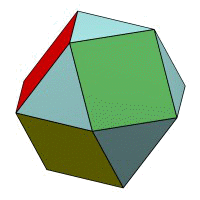кубоктаэдр икосододекаэдр.

В третью группу входят ромбокубоктаэдр, который иногда называют малым ромбокубоктаэдром и ромбоикосододекаэдр, называемый также малым ромбоикосододекаэдром. В эту же группу входят ромбоусеченный кубоктаэдр, иногда называемый большим ромбокубоктаэдром и ромбоусеченный икосододекаэдр, называемый также большим ромбоикосододекаэдром, которые получаются из кубоктаэдра и икосододекаэдра при другом варианте усечения

В четвертую группу входят две курносые модификации - курносый куб и курносый додекаэдр.

Для них характерно несколько повернутое положение граней. В результате эти многогранники, в отличие от предыдущих, не имеют плоскостей симметрии, но имеют оси симметрии. Так как плоскостей симметрии нет, то зеркальное отражение такого тела не совпадает с исходным телом, и поэтому существуют по две формы каждого из них - "правая" и "левая", отличающиеся так же, как правая и левая руки.

Пятая группа Архимедовых тел состоит из одного многогранника: Псевдоромбокубооктаэдр

Вот они все.

Полуправильные многогранники называют также равноугольно полуправильными многогранниками, из-за того, что все их многогранные углы равны. Рассмотрим многогранники, двойственные к полуправильным многогранникам. Их центры граней являются вершинами полуправильных многогранников. Они образуют класс, так называемых равногранно полуправильных многогранников.

1.3.3. Тела Кеплера-Пуансо.

Кроме полуправильных многогранников из правильных многогранников - Платоновых тел, можно получить так называемые правильные звездчатые многогранники. Их всего четыре, они называются также телами Кеплера-Пуансо. Кеплер открыл малый додекаэдр, названный им колючим или ежом, и большой додекаэдр. Пуансо открыл два других правильных звездчатых многогранника, двойственных соответственно первым двум: большой звездчатый додекаэдр и большой икосаэдр.

Пуансо (Louis Poinsot, 1777-1859) -

французский математик

Иоганн Кеплер

(1571 - 1630 гг.)

ТЕЛА ПУАНСО-КЕПЛЕРА

звездчатые многогранники (правильные невыпуклые многогранники).

БОЛЬШОЙ ИКОСАЭДР

• Грани большого икосаэдра - пересекающиеся треугольники.

• Вершины большого икосаэдра совпадают с вершинами описанного икосаэдра.

• Большой икосаэдр был впервые описан Луи Пуансо в 1809 г.

МАЛЫЙ ЗВЕЗДЧАТЫЙ ДОДЕКАЭДР

• Грани малого звездчатого додекаэдра - пентаграммы, как и у большого звездчатого додекаэдра. У каждой вершины соединяются пять граней. Вершины малого звездчатого додекаэдра совпадают с вершинами описанного икосаэдра.

• Малый звездчатый додекаэдр был впервые описан Кеплером в 1619 г.

БОЛЬШОЙ ДОДЕКАЭДР

• Грани большого додекаэдра - пересекающиеся пятиугольники.

• Вершины большого додекаэдра совпадают с вершинами описанного икосаэдра.

• Большой додекаэдр был впервые описан Луи Пуансо в 1809 г.

БОЛЬШОЙ ЗВЕЗДЧАТЫЙ ДОДЕКАЭДР

• Грани большого звездчатого додекаэдра - пентаграммы, как и у малого звездчатого додекаэдра. У каждой вершины соединяются три грани.

• Вершины большого звездчатого додекаэдра совпадают с вершинами описанного додекаэдра.

• Большой звездчатый додекаэдр был впервые описан Кеплером в 1619 г.

1.4. Многогранники вокруг нас.

1.4.1. Многогранники в химии.

Правильные многогранники - самые выгодные фигуры. Кристаллы некоторых знакомых нам веществ имеют форму правильных многогранников. Так, куб передает форму кристаллов поваренной соли NaCl, монокристалл алюминиево-калиевых квасцов (KAlSO4)2 12Н2О имеет форму октаэдра, кристалл сернистого колчедана FeS имеет форму додекаэдра, сурьмянистый сернокислый натрий - тетраэдра, бор - икосаэдра. Правильные многогранники определяют форму кристаллических решеток некоторых химических веществ.

1.4.2. Многогранники в географии.

В географии - многогранники занимают важное место в исследовании залежей полезных ископаемых, которые тянутся вдоль икосаэдровододекаэдровой сетки .

1.4.3. Многогранники в биологии.

Интересно, что именно икосаэдр оказался в центре внимания биологов в их спорах относительно формы вирусов. Чтобы установить форму вируса, брали различные многогранники, направляли на них свет под теми же углами, что и поток атомов на вирус. Оказалось, что только один многогранник дает точно такую же тень - икосаэдр . Его геометрические свойства, о которых говорилось выше, позволяют экономить генетическую информацию.

Вирус полиомиелита имеет также форму додекаэдра. Живет, и размножаться только в клетках человека и приматов

1.4.4. Многогранники в медицине.

Усечённый октаэдр нейтрализует энергетическое воздействие извне, повышает уровень энергетики головного мозга, помогает в работе на интуитивном уровне и очищает энергетическую структуру места в радиусе 500 м;

икосаэдр со стороной 5 см устраняет психологические зависимости, восстанавливает биоструктуру, гармонизирует личность, очищает структуру места в радиусе 100 м;

десятигранная пирамида защищает от излучений техногенного свойства, активизирует саморегуляцию организма, восстанавливает энергообмен человека, усиливает энергетику человека, повышает энергетический уровень места (70 м), восстанавливает эндокринную систему человека, нейтрализует геомагнитные излучения, гармонизирует взаимоотношения между людьми.

Своеобразная форма многогранников позволяет накапливать энергию и передавать ее владельцу. Положительно влияет в основном на психику и поведение.

1.4.5. Многогранники в быту.

Усеченный икосаэдр

(футбольный мяч)

Пирамида Мефферта

Кубик-рубик

1.4.5. Многогранники в природе

Математики считают, что пчёлы

строили свои шестиугольные соты

задолго до появления человека. Пчёлы - удивительные создания.

Пчелиные соты представляют собой пространственный паркет и заполняют пространство так, что не остается просветов. Как не согласиться с мнением пчелы из сказки «Тысяча и одна ночь»: «Мой дом построен по законам самой строгой архитектуры. Сам Эвклид мог бы поучиться, познавая геометрию сот».

</</p>

1.4.6. Многогранники в живописи и искусстве.