- Учителю
- Рабочая программа элективного курса Параметры (10 класс)
Рабочая программа элективного курса Параметры (10 класс)
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА.
Задачи с параметрами встречаются во всех вариантах ЕГЭ, поскольку на них наиболее ярко выявляются глубина и не формальность знаний выпускника. Известно, что в программах по математике для общеобразовательных школ этим задачам отводится незначительное место. Однако они играют важную роль в формировании логического мышления и математической культуры у школьников. Каждое уравнение и неравенство с параметрами представляет собой целый класс обычных уравнений и неравенств, для каждого из которых должно быть получено решение. Трудности при решении задач с параметрами обусловлены тем, что наличие параметра заставляет решать задачу не по шаблону, а рассматривать различные случаи, при каждом из которых методы решения существенно отличаются друг от друга. Так же необходимо хорошо знать свойства функций и выделять те, которые нужно применять в конкретном случае.
Цели программы:
- овладение аналитическим и графическими способами решения задач с
параметром;
- приобретение исследовательских навыков в решении задач с параметрами;
- развитие логического мышления.
Задачи программы:
- познакомиться с понятиями «параметр», «уравнение с параметром», «неравенство
с параметром», «система уравнений с параметром», «система неравенств с
параметром»;
- различать условия параметрических задач;
- научиться решать уравнения, неравенства, системы уравнений и неравенств с
параметром аналитическим и графическим способами;
- научиться математически грамотно оформлять решение задач с параметром.
Данный элективный курс предназначен для учащихся 10 класса.
При проведении занятий на первое место выходят следующие формы организации работы: лекционно-семинарская, групповая и индивидуальная. Рекомендуемые методы работы: исследовательский и частично-поисковый.
Освоение элективного курса завершается итоговым тестированием. В данной программе представлены приложения в виде теоретических, практических, контрольно - измерительных материалов.
Содержание курса.
Программа содержит вводное занятие, 4 основных блока, практикум и итоговое занятие. Для достижения наилучшего результата необходимо сохранить последовательность и целостность содержания этих блоков.
Вводное занятие (1ч.) предназначено для знакомства учащихся с целями и задачами данного элективного курса, организацией занятий, требованиями к усвоению курса. На нем проводится входная диагностика по решению линейных и квадратных уравнений с последующим разбором решений.
Блок I (4ч). На занятиях рассматривается влияние параметра на расположение графиков линейной и квадратичной функций, формируются умения анализировать графики для выбора ответа.
Блок II (8ч). Предназначен для изучения основных приёмов решения уравнений с параметром I степени с одним неизвестным и уравнений, приводимых к линейным, содержащим параметр, а также для формирования умений решать задачи с выполнением условий на расположение корней. На занятиях формируются умения определять число решений систем линейных уравнений с параметром и решать системы линейных уравнений. Учащиеся изучают способы решения линейных неравенств с параметром и неравенств, приводимых к ним.
Блок III (8ч). Направлен на изучение аналитического и функционально-графического способов решений квадратных уравнений с параметром и уравнений, сводящимся к ним.
Блок IV (5ч). Предназначен для овладения способами решения квадратных уравнений и систем квадратных уравнений с параметром, а также квадратных неравенств с параметром и систем квадратных неравенств.
Практикум (4 ч.) Направлен на обобщение и систематизацию знаний и умений учащихся по темам элективного курса, на отработку навыков решения уравнений, неравенств и систем уравнений и неравенств с параметром.
Итоговые занятия (2ч.) Предусматривают проведение итогового теста и обсуждение его результатов.
Один час резерва учитель использует по своему усмотрению.
Примерное распределение часов по темам (34 часа)
Тема
Количество
часов
1.
Вводное занятие.
Что такое параметр?
1
1
I.
2.
Функциональный и графический методы решения уравнений с параметрами.
4
II.
3.
4.
5.
Линейные уравнения с параметром и уравнения, сводящиеся к ним.
Системы линейных уравнений с параметром.
Линейные неравенства с параметром.
2
3
3
III.
6.
Квадратные уравнения с параметром и уравнения, сводящиеся к ним.
8
IV.
7.
8.
Квадратные неравенства с параметром.
Системы квадратных уравнений и неравенств с параметром.
3
2
9.
Практикум.
Итоговые занятия.
Резерв.
4
2
1
Методические рекомендации
После освоения курса учащийся должен иметь представление
о параметрических уравнениях, неравенствах, системах уравнений и неравенств.
Учащийся должен знать:
- понятие параметра,
- что значит решить уравнение с параметром, неравенство с параметром, систему
уравнений и неравенств с параметром;
- основные способы решения различных уравнений, неравенств и систем уравнений
и неравенств с параметром (линейных и квадратных).
Учащийся должен уметь:
- определять вид уравнения (неравенства) с параметром;
- выполнять равносильные преобразования;
- применять аналитический или функционально-графический способы для решения задач с параметром;
- выбирать и записывать ответ.
Учащийся должен владеть:
- анализом и самоконтролем;
- исследованием ситуаций, в которых результат принимает те или иные количественные или качественные формы.
Программа элективного курса считается усвоенной учеником, если он положительно выполнил промежуточный и итоговый контроль, посетил не менее 80% занятий.
При подготовке к проведению занятий по каждой теме учитель может воспользоваться приведённым ниже теоретическим и дидактическим материалом, а также может видоизменять или дополнять его.
Примерное планирование занятий элективного курса.
Вводное занятие: 1) знакомство с целями и задачами курса;
2) вводная диагностика понятий «Функция», «уравнение и его
корни», «неравенство и его решение» для определения уровня
готовности к усвоению курса и анализ её результатов.
ТЕМА 1. Рассматривается понятие параметра, форма записи ответа в уравнениях в зависимости от значений параметра. Итогом занятия является выполнение разноуровневого теста.
ТЕМА 2.
Занятия 1,2. Рассматриваются функциональный и графический методы решения линейных, квадратных уравнений с параметрами, влияние параметров на расположение графиков функций; анализируются рисунки, содержащие графики функций. В конце каждого занятия предложен набор заданий для практикума.
Занятия 3,4. Предназначены для знакомства с особенностями координатно-параметрического метода решение линейных и квадратных уравнений с параметрами; отработки умений преобразовывать заданное уравнение к виду, используемому в данном методе и выбору ответа.
ТЕМА 3.
Занятие 1,2. Повторяется алгоритм решения уравнений I степени и уравнений, сводимых к линейным, с параметром, на корни которых наложены дополнительные условия. Для закрепления знаний предлагается широкий круг заданий. В конце второго занятия проводится самостоятельная работа.
ТЕМА 4.
Занятие 1,2. Повторяются условия, при которых система линейных уравнений имеет единственное решение, бесконечное множество решений, не имеет решений. На конкретных примерах формируются умения определять число решений систем линейных уравнений с параметрами.
Занятие 3 посвящено контролю усвоения знаний по данной теме (тест).
ТЕМА 5.
Занятие 1,2,3. Посвящены формированию умений решать линейные неравенства, содержащие параметр, и неравенства с параметром, приводимые к линейным. На занятиях обеспечиваются благоприятные условия для дифференцированного обучения, создаются условия для самостоятельной и творческой работы учащихся (разноуровневый тест).
ТЕМА 6.
Занятие 1,2,3,4. Способствуют формированию умений решать квадратные уравнения с параметрами аналитическим способом. Обобщаются и углубляются знания школьников по изучаемой теме, устанавливается связь между коэффициентами квадратного уравнения, его корнями через графическую интерпретацию.
Занятие 5,6,7,8. Систематизируются, обобщаются знания и умения учащихся по применению предыдущего материала при решении уравнений, приводимых к квадратным. Проводятся промежуточный и итоговый контроль.
ТЕМА 7.
Занятие 1,2,3. На занятиях повторяются графический и аналитический методы решения квадратных неравенств. Формируются умения и навыки решения
квадратных неравенств с параметром.
ТЕМА 8.
Занятие 1,2. Формируются умения и навыки различными способами решать системы квадратных уравнений и квадратных неравенств с параметрами.
ТЕМА 9.
Занятие 1,2,3,4.На занятиях обобщаются и систематизируются знания и умения учащихся по всем темам курса. Предлагается набор обязательных и дополнительных заданий.
Итоговые занятия.
Занятие 1. Итоговый тест по теме «Решение линейных уравнений и неравенств с параметром» и его обсуждение.
Занятие 2. Итоговый тест по теме «Решение квадратных уравнений, неравенств с параметром и их систем» и его обсуждение.
Библиография.
А.И. Азаров, С.А. Барвенов, В.С. Федосеенко. Методы решения задач с параметрами. Минск: Аверсэв, 2003.
М.И Башмаков, Т.А. Братусь и др. Алгебра и начала анализа 10-11. Дидактические материалы. М.: Дрофа, 2003.
А.В. Белошистая. Математика: тематическое планирование уроков подготовки к экзамену. М.: Экзамен, 2005.
В.И. Голубев, А.М. Гольдман, Г.В. Дорофеев. О параметрах с самого начала.// Репетитор, 1991, №2.
П. И. Горнштейн, В. Б. Полонский, М.С. Якир. Задачи с параметрами. Москва- Харьков: Илекса, Гимназия, 2002.
П.И. Горнштейн, А.Г. Мерзляк, В.Б. Полонский. Подводные рифы конкурсного экзамена по математике. Киев: Евроиндекс ЛТД, 1994.
Г.В. Дорофеев. Квадратный трехчлен в задачах. Львов, 1991.
Л.И. Звавич, Л.Я. Шляпочник. Контрольные и проверочные работы по алгебре 10-11. Методическое пособие. М.: Дрофа, 1997.
В.К. Марков. Метод координат и задачи с параметрами. М.: Московский университет, 1970.
В.В. Локоть. Задачи с параметрами. Показательные и логарифмические уравнения, неравенства, системы. М.: АРКТИ, 2005.
В.П. Моденов. Задачи с параметрами. М.: Экзамен, 2006.
А.Г. Мордкович. Беседы с учителями математики. М.: Школа-Пресс, 1995.
Математика 8-9 классы: сборник элективных курсов. Авт.-сост. В.Н. Студенецкая, Л.С. Сагателова. Волгоград: Учитель, 2006.
514 задач с параметрами. Под ред. С.А. Тынянкина. Волгоград, 1991.
Е.М. Родионов. Математика. Решение задач с параметрами. Пососбие для поступающих в ВУЗы. М.: НЦ ЭНАС, 2006.
Г.А. Ястребинецкий. Задачи с параметрами. М.: Просвещение, 1986.
Приложение.
Вводное занятие.
Входная диагностика.
Вариант I.
1. Решите уравнение mx + 2 = -1 относительно х.
а) х= -![]() при
m≠0, б) 1) при m=0 корней нет, в) 1) при m=0 корней нет,
при
m≠0, б) 1) при m=0 корней нет, в) 1) при m=0 корней нет,
2) при m≠0 х=![]() ; 2) при
m≠0 х=-
; 2) при
m≠0 х=- ![]() .
.
2. Решите уравнение k(х-4) + 2(х+1) = 1 относительно х.
а) б) в)
1) при k = -2 корней нет, 1) при k = -2 корней нет, 1) при k=0 корней нет,
2) при k≠ -2 х=![]() ; 2) при
k=
; 2) при
k=![]() х=0; 2)
при k≠ -2 х=
х=0; 2)
при k≠ -2 х=![]() ;
;
3) при k≠ -2, k=![]() х=
х=![]() .
.
3. Решите уравнение 2а(а-2)x =а2-5а+6 относительно х.
а) 1) при а=2 хєR, б) 1) при а=2 хєR,
2) при а=0 корней нет; 2) при а=0 корней нет;
3) при а≠0 и а≠2 х=![]() ; 3) при
а≠0 и а≠2 х=
; 3) при
а≠0 и а≠2 х=![]() ;
;
в) 1) при а=2 хєR,
2) при а=0 корней нет;
3) при а=3 х=0;
4) при а≠2, а≠0, а≠3 х=![]() .
.
4. При каких значениях b уравнение 1 + 2х - bх = 4 + х имеет отрицательное решение?
а) при b<1, б) при b>1; в) при b< -2.
5. При каких значениях а парабола у = ах2 - 2х + 25 касается оси Ох?
а) при а=25, б) при а=0 и а=0,04; в) при а=0,04.
6. Найдите наименьшее целое значение k, при котором уравнение 3х2 + 5х - k = 0 имеет два различных корня?
а) k=-2![]() , б)
k= -2; в) k= -3.
, б)
k= -2; в) k= -3.
7. При каких значениях а произведение корней уравнения х2 - 4х + а2 - 3а + 2 = 0 равно нулю?
а) при а= -1, а= -2; б) при а=1, а=2; в) при а=2, а=4.
8. При каких значениях k уравнение (k-2)x2 - (4-2k)х + 3 = 0 имеет единственное решение?
а) при k = -5, k = -2 ; б) при k = 5; в) при k =2, k = 5.
9*. Решите уравнение (а-2)х2 + (4-2а)х + 3 = 0 относительно х.
а) 1) при ає(2; 5) корней нет,
2) при а=5 х=1;
3) при ає(-∞; 2)U(5; +∞) х1=![]() ,
х2=
,
х2=![]() ;
;
б) 1) при ає[2; 5) корней нет,
2) при а=5 х=1;
3) при ає(-∞; 2)U(5; +∞) х1=![]() ,
х2=
,
х2=![]() ;
;
в) 1) при а=2 и ає(2; 5) корней нет,
2) при а=5 х=1;
3) при а=2 х=0;
4) при ає(-∞; 2)U(5; +∞) х1=![]() ,
х2=
,
х2=![]() .
.
10. При каком значении b сумма квадратов корней уравнения х2 - (b+2)х + b - 3 = 0 принимает наименьшее значение?
а) таких значений b нет, б) при b=9; в) при b= -1.
Вариант II.
1. Решите уравнение nx - 7 = -3 относительно х.
а) 1) х= -![]() при
n≠0, б) 1) при n=0 корней нет, в) х=
при
n≠0, б) 1) при n=0 корней нет, в) х= ![]() .
.
2) при n=0 корней нет, 2) при n≠0 х=![]() ;
;
2. Решите уравнение 2х(а+1) = 3а(х+1) + 7 относительно х.
а) б) в)
1) при а = 2 корней нет, 1) при а = 2 корней нет, 1) при а=0 корней нет,
2) при а≠ 2 х=![]() ; 2) при
а=-
; 2) при
а=-![]() х=0; 2) при а≠ 0 х=
х=0; 2) при а≠ 0 х=![]() ;
;
3) при а≠ 2, а≠-![]() х=
х=![]() .
.
3. Решите уравнение (а2-81)х=а2+7а-18 относительно х.
а) 1) при а=-9 хєR, б) 1) при а=-9 хєR,
2) при а=9 корней нет; 2) при а=9 хєR,
3) при а≠-9 и а≠9 х=![]() ; 3) при
а≠-9 и а≠9 х=
; 3) при
а≠-9 и а≠9 х=![]() ;
;
в) 1) при а=9 корней нет ,
2) при а=-9 хєR;
3) при а=2 х=0;
4) при а≠-9, а≠9, а=2 х=![]() .
.
4. При каких значениях b уравнение 2+4х-bх = 3 + х имеет отрицательное решение?
а) при b<3, б) при b<2; в) при b>3.
5. При каких значениях а уравнение х2 -(2а - 6)х +3а+9= 0 имеет корни разных
знаков?
а) при ає(-∞; -3], б) при ає(-∞; -3), в) при ає(-3; +∞).
6. Найдите наибольшее целое значение k, при котором уравнение 2х2 + 4х - k = 0
не имеет действительных корней?
а) k=-1, б) k= -2; в) k= -3.
7. При каких значениях а произведение корней уравнения х2 - 7х + 3а2 - 8а + 6 = 0
равно 1?
а) при а= 3, а= 5; б) при а=-1,
а=-![]() ; в)
при а=1, а=
; в)
при а=1, а=![]() .
.
8. При каких значениях а уравнение аx2 - 6х + а = 0 имеет два различных корня?
а) при а є(-3; 0) U(0; 3) б) при а є(-3; 3) ; в) при а є (-∞; -3) U(3; +∞).
9*. Решите уравнение (а-1)х2 + 2(2а+1)х =-4а-3.
а) 1) при ає(-∞; -0,8) корней нет, 2) при а=-0,8
х=-![]() ;
;
3) при ає(-0,8; 1)U(1; +∞) х1=![]() ,
х2=
,
х2=![]() ;
;
б) 1) при ає(-∞; -0,8) корней нет, 2) при а==-0,8
х=-![]() ; 3) при
а=1 х=-
; 3) при
а=1 х=-![]()
4) при ає(-0,8; +∞) х1=![]() ,
х2=
,
х2=![]() ;
;
в) 1) при ає(-∞; -0,8) корней нет, 2) при а=-0,8
х=-![]() ; 3) при
а=1 х=-
; 3) при
а=1 х=-![]() ;
;
4) при ає(-0,8; 1)U(1; +∞) х1=![]() ,
х2=
,
х2=![]() .
.
10*. При каких значениях b сумма квадратов корней уравнения х2 - (b+4)х + b - 2 = 0
принимает наименьшее значение?
а) при b = 11 б) при b = -3; в) при b = 3.
Ключ ответов:
На усмотрение учителя, задания в каждом из вариантов можно оценить в баллах:
Тема 1. Что такое параметр.
Цели занятия: - знать, что такое параметр,
- знать, что значит решить уравнение с параметром;
- уметь отличать в уравнениях параметр от неизвестных;
- уметь выбирать и записывать ответ в простейших уравнениях
с параметрами.
Ход занятия:
І. Организационный момент.
ІІ. Теоретический материал.
Задача. Внук - восьмиклассник возвращается из школы:
- Дедушка, мы всем классом к Новому году решили обменяться фотоснимками.
- Это хорошо. Память будет. Но это ж сколько карточек надо?
- А мы уже сосчитали -650. Нас в классе…
- Подожди, не говори. Я сам сосчитаю. Так сколько же учеников в классе?
Решение. Пусть учеников - х. Тогда каждый должен
отдать (х-1) фотографию. Составляем уравнение х(х-1)=650, решая
которое получаем х![]() =26,
х
=26,
х![]() =-25. По
смы-слу задачи число учеников не может быть отрицательным, тогда
ответом будет 26.
=-25. По
смы-слу задачи число учеников не может быть отрицательным, тогда
ответом будет 26.
Каким числом может быть число фотографий, чтобы задача всегда имела решение?
Ответ: 2·1=2, 3 ·2=6, 4· 3=12, 5· 4=20,……30 ·29=870,…
Общий вид уравнения, при помощи которого решается эта задача х(х-1)=а, где а=2, 6, 12, 20,..., 870,... Буквой а обозначено заранее известное в задаче число (параметр), при определённых значениях которого задача имеет решение.
Решить уравнение с параметром - это значит найти все те и только те значения параметра, при которых задача имеет решения.
Условимся считать, что параметры в уравнениях принимают действительные значения, в задачах с параметрами отыскиваются действительные решения.
Другими примерами равенств с параметрами могут служить общие виды функций, изучаемых в основной школе:
- линейная функция y=kx+b, (k, b - параметры, x, y- переменные);
- квадратичная функция y= ax²+bx+c, где а≠0 (a, b, c-параметры, x, y -переменные).
Задачи с параметрами мы встречаем и в геометрии.
Уравнение окружности с центром в начале координат имеет вид
![]() , где x,
y- координаты точек - переменные, r- радиус окружности - параметр.
, где x,
y- координаты точек - переменные, r- радиус окружности - параметр.
Моделируя различного вида задачи, можно получить различного вида уравнения, для которых нужно уметь выбирать ответы.
Например, х-а=0, ответ: при
а![]() х=а;
х=а;
5х=а, ответ: при а![]() х=а:5;
х=а:5;
х:2=а, ответ: при а![]() х=2а;
х=2а;
|х|=|а|, ответ: при а![]() х=
х=![]() ;
;
х![]() ответ:
при а
ответ:
при а![]() х=
х=![]() .
.
Не всегда значения параметра могут быть любыми действительными числами.
Например, 1) уравнение ах=1 ответом имеет
множество х=![]() при
а
при
а![]() или
или
ає(-![]() )
)![]() ; при
а=0 уравнение корней не имеет.
; при
а=0 уравнение корней не имеет.
2) 0·х=а. Ответ: при а=0 х- любое
действительное число, при а![]() 0 корней
нет.
0 корней
нет.
3) х=![]() . Ответ:
при а<0 корней нет, при а
. Ответ:
при а<0 корней нет, при а![]() 0
х=а².
0
х=а².![]()
4) |х|=а. Ответ: при а<0 корней
нет, при а=0 х=0, при а>0 х =![]() а.
а.
5) Sin²x+Cos²x=a. Ответ: при |а|>1
корней нет, при а=1 х - любое действительное число, при
|а|![]() уравнение имеет единственное решение, которое можно найти
специальными способами, изучаемыми в курсе 10 класса.
уравнение имеет единственное решение, которое можно найти
специальными способами, изучаемыми в курсе 10 класса.
6) 2x²=ax. Ответ: при а=0 х=0 -
единственный корень, при а![]() два
корня х1=0 и х2=а.
два
корня х1=0 и х2=а.
III. Тренировочный тест.
1.Найти параметр в уравнении:
a) 2х- 4 =2b.
1) b; 2) х; 3) 2; 4) Нет параметра.
b) ![]() .
.
1) х; 2) а; 3) Нет параметра; 4) 5.
c) a![]() .
.
1) а; 2) Нет параметра; 3) -4; 4) 5.
d)![]() .
.
1) Нет параметра; 2) а; 3) a и b; 4) b.
2. Решить уравнение с параметром:
a) 2x-a=4;
b) x: (a-1)=5;
c) |x-a| =3;
d) |x-2|=b;
e)![]()
f)![]()
g)![]()
3)Составьте уравнение с параметром, чтобы:
a) каждому значению параметра соответствовало единственное значение переменной х;
b) при любом значении параметра оно не имело корней;
c) которое не имеет корней при всех а<0;
d) которое не имело корней при каком-то одном значении параметра, а при всех остальных его значениях имело бы корни;
e) которое имело бы корни при одном значении параметра, а при всех остальных его значениях не имело бы корней.
Ответы.
1.а) 1; b) 2; c) 2; d) 3.
2.a) x=![]() при
любом значении параметра a;
при
любом значении параметра a;
b) при a=1 корней нет, при ![]() х=5(а-1);
х=5(а-1);
c) при любом значении а х1=а+3, х2=а-3;
d) при b<0 корней нет, при b![]() х1=2+b, x2=2-b;
х1=2+b, x2=2-b;
e) при a<0 корней нет, при а![]() х=а²-5;
х=а²-5;
f) при m>3 корней нет, при m![]() x=(3-m)²;
x=(3-m)²;
g) при любом значении n х=(n+2)![]() +1.
+1.
3.a) x=a, 2x+1=1, a²x=a-x;
b) ![]() ,
x²+a²+1=0, Sin ax=
,
x²+a²+1=0, Sin ax=![]() ;
;
c) |x|=a, x²=a, ![]() , при
а<0;
, при
а<0;
d)![]() ,
,
![]() .
.
e) Cos²x+Sin²x=a, (1+x)²=1+2x+a.
ІV. Итоги занятия.
Блок I. Тема 2. Функциональный и графический методы решения
уравнений с параметрами. Занятие 1. Функциональный и графический методы решения линейных
уравнений с параметрами.
Цели занятия:
- знать как влияют параметры на расположение графика линейной функции;
- уметь анализировать рисунки, содержащие график линейной функции;
-уметь выбирать ответ, исходя из анализа графика.
Ход занятия:
І. Организационный момент.
ІІ. Теоретический материал.
Линейная функция задаётся формулой y= kx+b, где x,y- переменные, k и b- параметры.
Графиком линейной функции является прямая линия, расположение которой зависит от параметров k и b. Угловой коэффициент k определяет угол наклона к положительному направлению оси абсцисс. При k>0 этот угол острый, при k<0 этот угол тупой. Коэффициент b определяет сдвиг прямой вдоль оси Оy. При b>0 вверх, при b<0 вниз (см. рис. а и б).
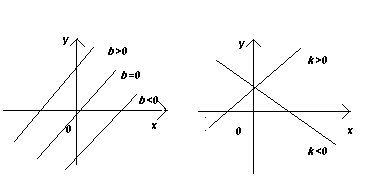
(рис. а) (рис. б)
Свойства функции.
1)Область определения - х - любое действительное число.
2) Множество значений - у - любое действительное число.![]()
3) Функция монотонно возрастает при k>0.
4) Функция монотонно убывает при k<0 .
5) Нули функции (точки пересечения с осью абсцисс при у=0) х=
-![]()
6) Чётность и нечётность.
Функция у=f(x) называется чётной, если для любых её значений х и -х из области её определения выполняется равенство f(-x)=f(x). График чётной функции симметричен относительно оси ординат.
Функция у=f(x) называется нечётной, если для любых её значений х и-х из области её определения выполняется равенство f(-x)=-f(x). График нечётной функции симметричен относительно начала координат.
Пример. При каких значениях параметра ![]() функция
функция
![]()
а) является чётной;
б) монотонно возрастает;
в) пересекает ось абсцисс в точке х=1
Ответ: а) при а=2;
б) при а>2;
в) при a=-1.
ІІІ. Практикум по решению задач.
Задание 1. При каких значениях параметра a функция ![]()
а) пересекает ось абсцисс в точке х=5;
б) монотонно убывает;
в) является нечётной?
Задание 2. Найдите значение а, при котором прямые у=ax-5 и у=7х+4 не имеют общих точек.
Задание 3. Найдите все значения параметра а, при котором
точка пересечения прямых ![]() и
и
![]() лежит ниже прямой
лежит ниже прямой ![]()
Задание 4.Для каждого действительного значения a решить уравнение
![]() =
=![]() .
.
Задание 5.Сколько корней в зависимости от параметра a имеет уравнение
ax-x-1=0?
(Графиком функции, содержащей модуль, является ломаная, точка излома (0;1)).
Ответы: 1) а)![]() б)
б)
![]() <-3;
в)
<-3;
в) ![]()
2) a=7.
3) ![]() .
.
4) при ![]() корней
нет;
корней
нет;
при ![]() х-
любое действительное число,
х-
любое действительное число,
при ![]() х=
х=![]()
5) при ![]() уравнение имеет единственный корень, при
уравнение имеет единственный корень, при ![]() <0
уравнение имеет два корня.
<0
уравнение имеет два корня.
IV. Итог занятия.
Занятие 2. Квадратные уравнения с параметрами.
(функционально-графический метод решения)
Цели занятия:
-знать как влияют параметры на расположение графика функции;
-уметь анализировать рисунки, содержащие график квадратичной функции;
-уметь выбирать ответ с помощью рисунка графика.
Ход занятия:
I. Организационный момент.
II. Теоретический материал (работа по таблице).
Квадратичная функция задаётся формулой
y=ax²+bx+c, где![]() параметры,
x и y- переменные. Графиком квадратичной функции является парабола.
параметры,
x и y- переменные. Графиком квадратичной функции является парабола.
Коэффициент a определяет направление ветвей параболы. Если а >0 , то они направлены вверх, если а<0, то направлены вниз. Дискриминант квадратного трёхчлена D=b²-4ac определяет наличие и количество общих точек с осью Ох. Если D<0, то парабола не пересекает ось абсцисс. Если D=0, то парабола и ось имеют одну общую точку. Если D>0, то общих точек две.
Графический способ решения задач с параметрами является универсальным, а значит (обратная сторона любой универсальности), есть конкретные случаи, когда задачу можно решить несколько проще.
Пусть для функции y=ax²+bx+c, где![]() параметры,
x и y - переменные. Числа
параметры,
x и y - переменные. Числа ![]() и
и
![]() -
нули функции, D = b
-
нули функции, D = b![]() -
4ac, D > 0,
-
4ac, D > 0, ![]()
![]()
![]() ,
,
![]() =
-
=
-![]() -
абсцисса вершины параболы. В этих задачах, как правило, требуется
определить те значения параметра, при которых выполняется некоторое
условие для расположения корней.
-
абсцисса вершины параболы. В этих задачах, как правило, требуется
определить те значения параметра, при которых выполняется некоторое
условие для расположения корней.
Перечислим основные условия:
1) оба корня меньше некоторого числа А ![]()
![]()
![]() <А;
<А;
2) число А лежит между корнями ![]() <А<
<А<![]() ;
;
3) оба корня больше некоторого числа А А< ![]()
![]()
![]() ;
;
4) оба корня лежат между числами А и В А< ![]()
![]()
![]() <В;
<В;
5) только больший корень принадлежит промежутку (А;В) ![]() < А,
А<
< А,
А< ![]() <В;
<В;
6) только меньший корень принадлежит промежутку (А;В) А<
![]() <В,
В<
<В,
В< ![]() ;
;
7) оба корня лежат по обе стороны от промежутка (А;В) ![]() < А,
< А,
![]() >В.
>В.
В таблице приведены условия, необходимые и достаточные для
выполнения перечисленных условий. Понятно, что запомнить их
все-задача весьма непростая, но это и не требуется. Покажем, что
означает то или иное неравенство в условиях, начав с первого
случая: 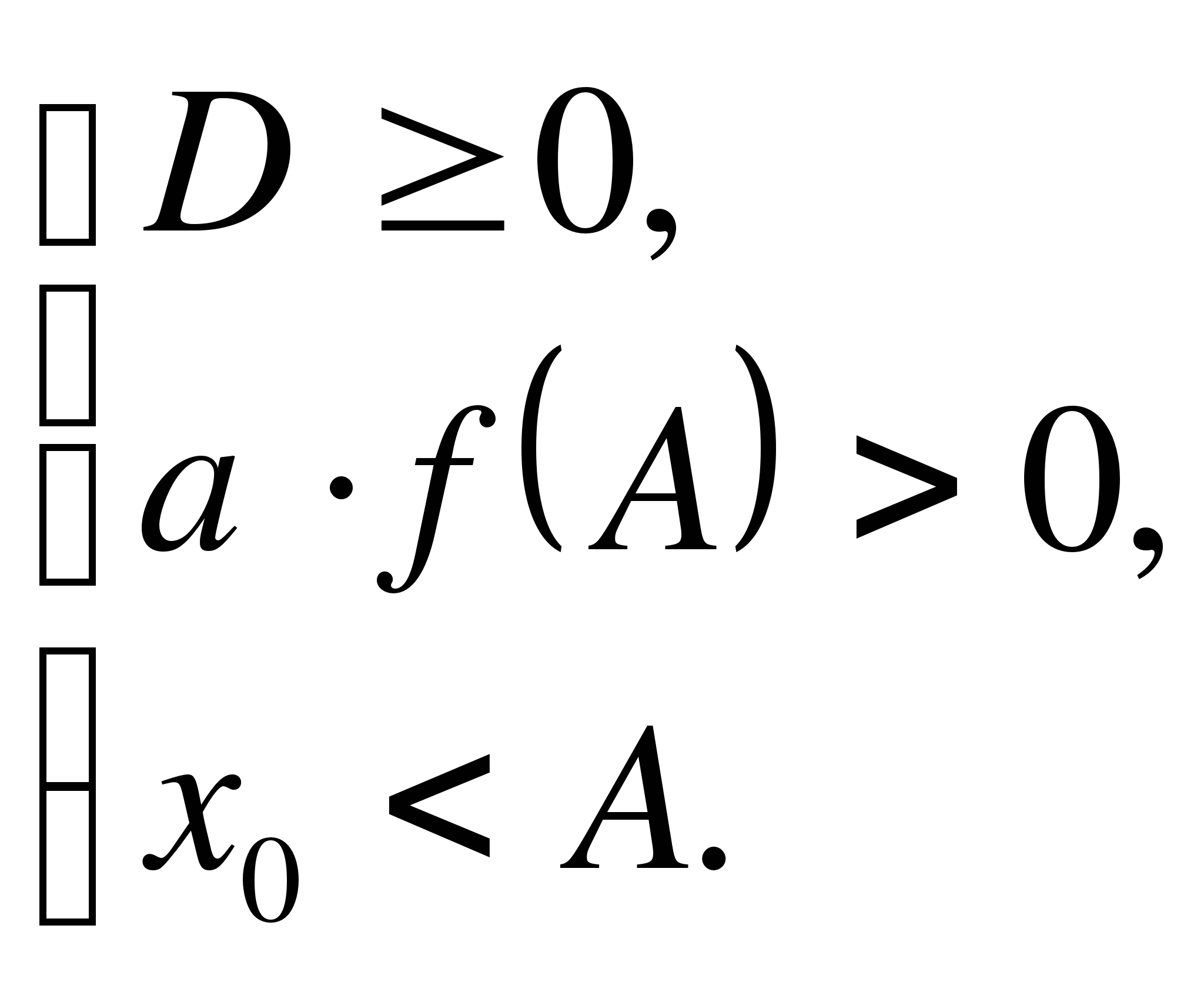 Самое
простое требование - не отрицательность дискриминанта квадратного
трёхчлена- корни должны существовать. А вот второе неравенство
системы совсем неочевидно.
Самое
простое требование - не отрицательность дискриминанта квадратного
трёхчлена- корни должны существовать. А вот второе неравенство
системы совсем неочевидно.
Если мы знаем знак выражения![]() , то
всегда можем определить где лежит число А (между корнями или нет).
Если a>0, то график квадратного трёхчлена «растёт» вверх. Тогда
, то
всегда можем определить где лежит число А (между корнями или нет).
Если a>0, то график квадратного трёхчлена «растёт» вверх. Тогда
![]() , меньше
нуля. Когда число А не находится между корнями, то
, меньше
нуля. Когда число А не находится между корнями, то ![]() больше
нуля.
больше
нуля.
Если а<0,то график квадратного трёхчлена «растёт
вниз». При этом значение ![]() наоборот, меньше нуля, когда число А находится между корнями.
Однако выражение
наоборот, меньше нуля, когда число А находится между корнями.
Однако выражение ![]() снова
отрицательно. Аналогично, это выражение положительно при А
снова
отрицательно. Аналогично, это выражение положительно при А![]() (
(![]() ;
;![]() ).
).
Итак, если ![]() <0,
то А
<0,
то А![]() (
(![]() ;
;
![]() ),
если
),
если ![]() >0,
то А
>0,
то А![]() (
(![]() ;
;
![]() ).вернёмся
к условиям
).вернёмся
к условиям 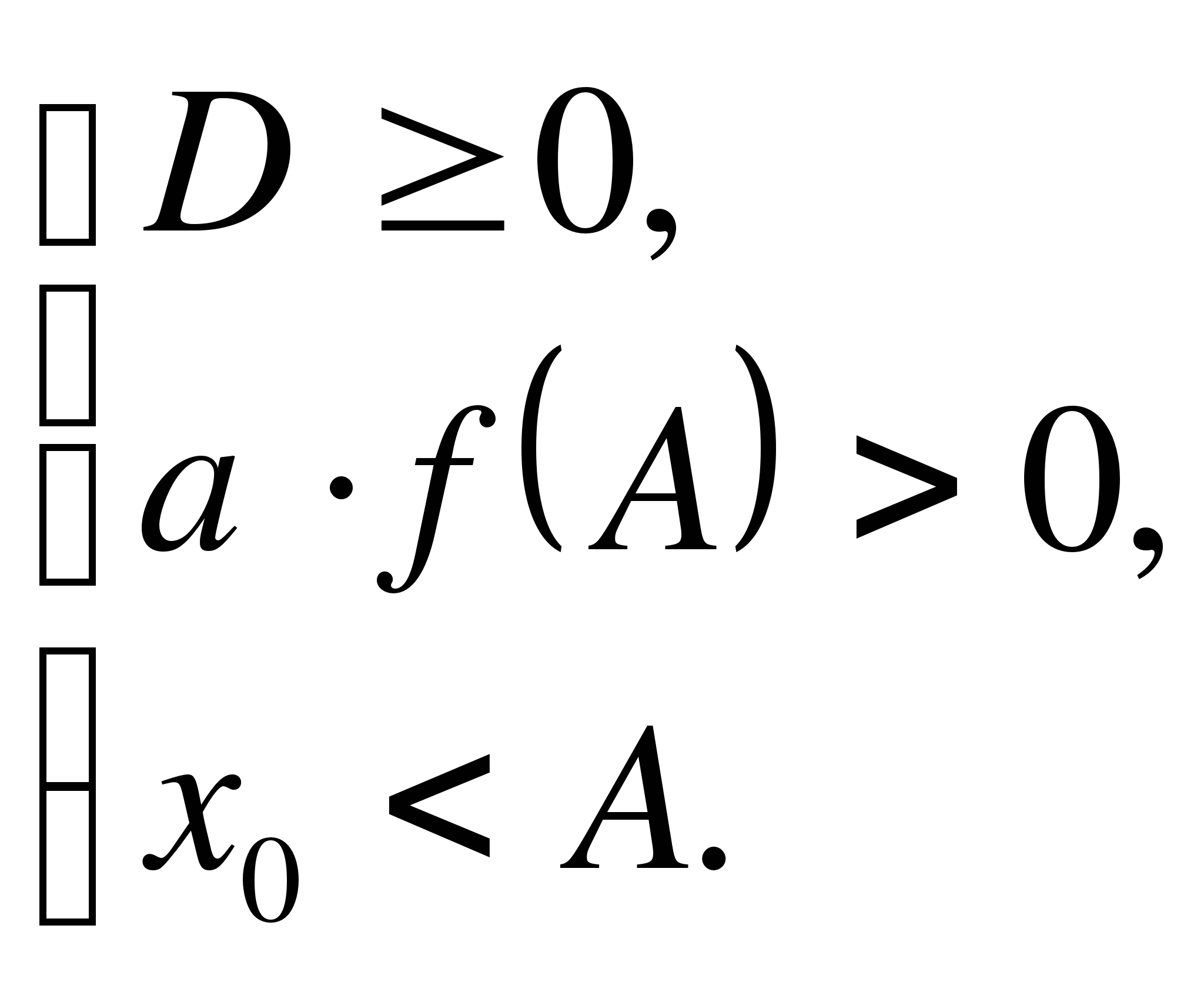 не
отрицательность дискриминанта даёт существование корней,
положительность выражения
не
отрицательность дискриминанта даёт существование корней,
положительность выражения ![]() соответствует тому, что А
соответствует тому, что А![]() (
(![]() ;
;![]() ), а
последнее неравенство устанавливает расположение обоих корней слева
от А, ведь абсцисса вершины параболы - середина отрезка
), а
последнее неравенство устанавливает расположение обоих корней слева
от А, ведь абсцисса вершины параболы - середина отрезка ![]() -находится
слева. Выбор абсциссы вершины объясняется тем, что работать с
формулой
-находится
слева. Выбор абсциссы вершины объясняется тем, что работать с
формулой ![]() =
-
=
-![]() в
общем случае проще, чем с формулами корней квадратного трёхчлена.
Условия в третьем случае аналогичны предыдущим.
в
общем случае проще, чем с формулами корней квадратного трёхчлена.
Условия в третьем случае аналогичны предыдущим.
Для существования второго расположения корней относительно
данного числа А достаточно, чтобы выполнялось неравенство ![]() <0.
Это же неравенство даёт нам условие существования корней, если их
нет, то выражение
<0.
Это же неравенство даёт нам условие существования корней, если их
нет, то выражение ![]() всегда
положительно.
всегда
положительно.
Условия для случаев 4-7 следуют из уже рассмотренных нами случаев.
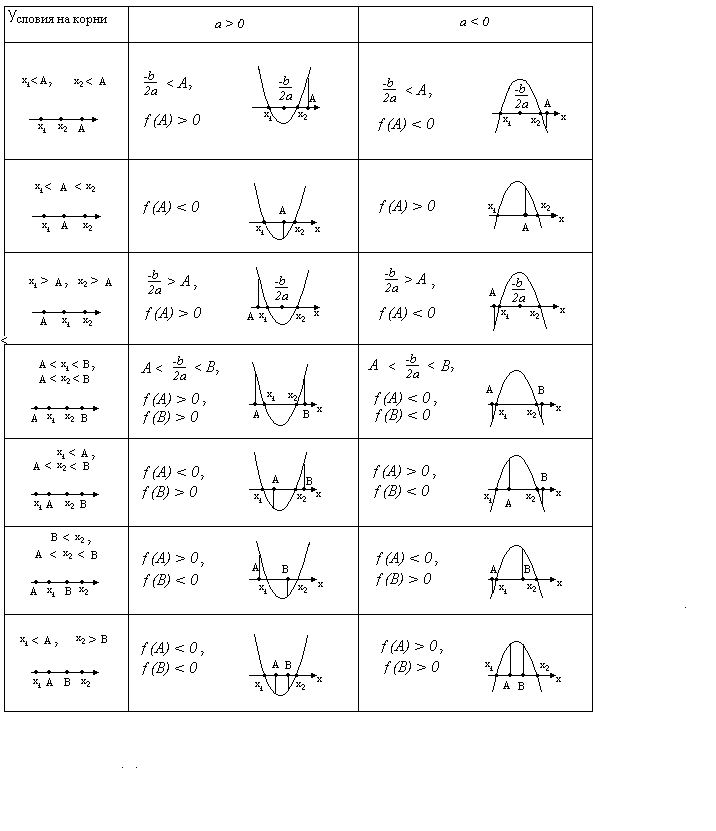
III. Практикум по решению задач с использованием таблицы.
Пример 1. Найти все значения параметра а, при которых корни уравнения
(а-2)х![]() -3(а+3)х+а+1=0
имеют разные знаки?
-3(а+3)х+а+1=0
имеют разные знаки?
Решение.
Пусть ![]() (а-2)х
(а-2)х![]() -3(а+3)х+а+1,
-3(а+3)х+а+1,
![]() -корни
-корни
![]() причём,
причём,
![]()
![]()
![]() .
.
Условие того, что уравнение ![]() =0 имеет
корни разных знаков, равнозначно условию расположения числа 0 между
нулями квадратичной функции у =
=0 имеет
корни разных знаков, равнозначно условию расположения числа 0 между
нулями квадратичной функции у =![]() .
.
Необходимым и достаточным условием этого является следующее неравенство
(см. второй случай в таблице) (а-2)(а+1)<0, где
а второй коэффициент при х![]() квадратного
трёхчлена; f(0) = а+1 - значение квадратного трёхчлена при
х=0.
квадратного
трёхчлена; f(0) = а+1 - значение квадратного трёхчлена при
х=0.
Решив неравенство (а-2)(а+1)<0, получим -1<а<2.
Ответ.(-1;2)
Пример 2. Найти все значения параметра b, при которых корни уравнения
(b+1)x²+2x-3b-1=0 меньше 1.
Ответ:![]()
Пример 3. Найти все значения а, при которых корни уравнения
(а+1)x²-(а²+2а)x-а-1=0 принадлежат отрезку
![]()
Ответ: ![]()
Указания: рассмотреть случаи, когда старший коэффициент при x² равен нулю и когда он не равен нулю, во втором случае найти абсциссу вершины параболы, значение квадратного трёхчлена в точке х=1, дискриминант. С помощью таблицы составить систему неравенств, преобразовать её в простейшую и выбрать ответ из двух случаев.
IV. Итог занятия.
Занятие 3. Координатно - параметрический метод решения уравнений с параметрами.
Цели занятия:
- знать особенности координатно- параметрический метода;
- уметь преобразовывать заданное уравнение к виду, используемому в данном методе;
- уметь выбирать ответ, используя графическую интерпретацию уравнений с модулем. Ход занятия:
I. Организационный момент
II. Теоретический материал
Пусть даны на плоскости две взаимно перпендикулярные прямые с общим началом числовые оси. Одну из них (Ох) назовём координатной; другую (Оа)
-параметрической, а плоскость хОа или аОх- координатно- параметрической.
Метод решения задач с параметрами, использующий такую плоскость называется координатно- параметрическим. Он основан на нахождении всех точек плоскости, значение координаты х и параметра а каждой из которых удовлетворяют заданному в условиях задачи условию (соотношению).
Решение уравнений с параметрами.
Пусть задано уравнение F(x;a)=0 *, где F(x;a)- некоторая функция переменной х и числового параметра а. Пусть на координатно- параметрической плоскости найдено множество всех точек, значения координаты х и параметра а каждой из которых удовлетворяют рассматриваемому уравнению.
Может оказаться, что при любом допустимом значении параметра
уравнение решений не имеет х![]() ,
либо для некоторых значений параметра х
,
либо для некоторых значений параметра х![]()
или уравнение имеет конечное число решений, или бесконечное.
или уравнение имеет конечное число решений, или бесконечное.
Записывая ответ, поставим в соответствие каждому допустимому фикси-рованному значению параметра а значение искомой величины х - координаты соответствующих точек найденного множества.
Частные случаи.
1) Координата х есть функция параметра а:
х=f(a),неявно заданная уравнением ![]() . На
плоскости хОа с горизонтальной параметрической осью
Оа множество всех точек, значения координаты х и параметра
а каждой из которых удовлетворяют уравнению, представляет
собой график функции, где роль аргумента играет параметр.
. На
плоскости хОа с горизонтальной параметрической осью
Оа множество всех точек, значения координаты х и параметра
а каждой из которых удовлетворяют уравнению, представляет
собой график функции, где роль аргумента играет параметр.
2) Параметр а есть функция координаты х: а=f(x)
неявно заданная уравнением![]() .В этом
случае можно рассматривать плоскость аОх с вертикальной
параметрической осью Оа и интерпретировать множество всех
точек, значения координаты и параметра каждой из которых
удовлетворяют уравнению графика функции, где роль аргумента функции
играет координата х.
.В этом
случае можно рассматривать плоскость аОх с вертикальной
параметрической осью Оа и интерпретировать множество всех
точек, значения координаты и параметра каждой из которых
удовлетворяют уравнению графика функции, где роль аргумента функции
играет координата х.
Центральное место в этом методе занимает нахождение всех точек
плоскости, определяемых уравнением![]() .
Наиболее просто дело обстоит, когда левой частью уравнения являются
многочлены первой или второй степеней. Например, уравнение
.
Наиболее просто дело обстоит, когда левой частью уравнения являются
многочлены первой или второй степеней. Например, уравнение
![]() определяет
окружность, уравнение ха-1=0 определяет гиперболу,
уравнение
определяет
окружность, уравнение ха-1=0 определяет гиперболу,
уравнение![]()
![]() параболу,
а уравнение
параболу,
а уравнение ![]() пару
пересекающихся (взаимно перпендикулярных) прямых х+а=0 и
х-а=0. Для построения этих графиков используются знакомые из
алгебры способы: табличный, способ сдвига, симметричного
отображения относительно начала или осей координат.
пару
пересекающихся (взаимно перпендикулярных) прямых х+а=0 и
х-а=0. Для построения этих графиков используются знакомые из
алгебры способы: табличный, способ сдвига, симметричного
отображения относительно начала или осей координат.
Пример 1.Для каждого значения параметра решить уравнение х-|a|=0.
Решение.
Перейдём от неявного к явному заданию функции, воспользовавшись определением модуля числа, заменим уравнение равносильной ему совокупностью смешанных систем:
x=|a| ![]()

На координатно-параметрической плоскости хОа с горизонтальной параметрической осью Оа множество всех точек (х;а), значения координаты и параметра каждой из которых удовлетворяют полученной совокупности смешанных систем, представляют собой изображённый на рисунке график функции х=|a|, аргументом которой является параметр а.
Каждому значению параметра а соответствует одно единственное значение координаты х, а именно, если а<0, то х= -а, если а=0, то х=0, если а>0, то х=а.
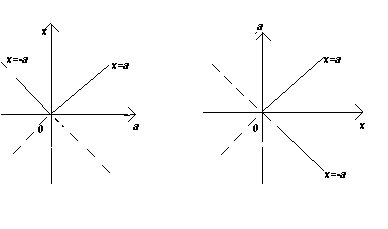
На втором рисунке то же множество изображено на плоскости аОх
с вертикальной параметрической осью Оа. Каждая из прямых семейства а=const пересекает изображённое множество в точке с координатой х, определяющей решение исходного уравнения, а именно, если а=const<0, то х=-а, если а=const=0, то х=0, если а=const>0, то х=а, то есть получаем тот же результат, что и в первом случае.
Ответ. Если а<0, то х=-а,
если а=0, то х=0,
если а>0, то х=а.
Пример 2. На координатно-параметрической плоскости хОа
изобразить множество решений уравнения ![]()
Решение.
По определению модуля имеем 
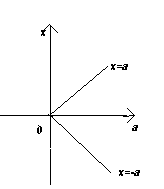
Ответ. На рисунке линией изображено рассматриваемое множество точек.
Пример3. Для каждого значения параметра а решить
уравнение![]()
Решение.
Изобразим на плоскости хОа множество точек (х;а), значения координаты и параметра каждой из которых удовлетворяют заданному уравнению.
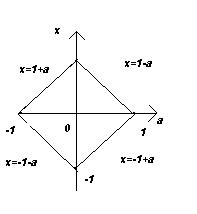 В первой
четверти при х
В первой
четверти при х![]() уравнение принимает вид х+а=1.Значит множество в первой
четверти изображается прямой х=1-а, а следовательно в силу
симметрии относительно осей Ох и Оа искомое множество
представляет собой контур квадрата.
уравнение принимает вид х+а=1.Значит множество в первой
четверти изображается прямой х=1-а, а следовательно в силу
симметрии относительно осей Ох и Оа искомое множество
представляет собой контур квадрата.
Ответ. Если а<-1, то х ![]() , если
а = -1, то х=0,
, если
а = -1, то х=0,
если -1<а<0, то х = -1-а, х=1+а;
если 0<a<1, то х = -1+а, х=1-а;
если а=1, то х=0; если а>1, то ![]() х
х![]() .
.
Для решения уравнений, содержащих линейно зависимый аргумент или параметр,
можно применять замену переменных.
III. Задания для практической работы в парах.
Пример 1. Для каждого значения параметра решить уравнение
![]()


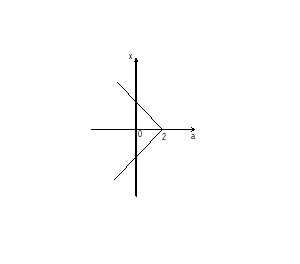
Пример №2. Решить уравнение ![]()
Решение.

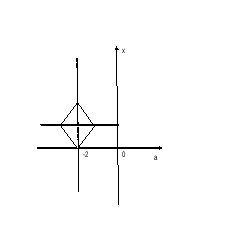
Ответ: при а<-3, a>-1; при а=-3,а=-1,х=1;
при -3<a<-2 x = a+4, x= -a-2; при -2<a<-1 x= -a, x =a+2.
Для дополнительной работы можно использовать следующее
задание:![]()
![]()
Ответы: Если a<-1, то ![]() ;
;
если ![]() то
то
![]() ;
;
если -1<a<1, то х=-1, х=1;
если a=1, то ![]() ;
;
если a>1, то ![]() .
.
IV. Итог занятия.
Занятие 4. Координатно - параметрический метод решения квадратных уравнений с параметрами.
Цели занятия:
- знать особенности координатно- параметрического метода;
- уметь преобразовывать заданное уравнение к виду используемому в данном методе;
-уметь выбирать ответ, используя графическую интерпретацию квадратных уравнений.
Ход занятия:
I. Организационный момент
II. Повторение теоретического материала.
1) Что называют К-П плоскостью?
2) В чём заключается К-П метод?
3) Какие линии в К-П плоскости надо уметь строить для решения уравнений с параметрами?
III. Примеры решения заданий.
Пример 1. Найти все значения параметра ![]() , при
которых уравнение
, при
которых уравнение ![]() имеет
два различных неотрицательных корня.
имеет
два различных неотрицательных корня.
Решение.
На К-П плоскости ![]() множество всех точек
множество всех точек ![]() ,
значение координаты х и параметра а каждой из которых
удовлетворяют данному уравнению, представляют собой параболу. Её
уравнение
,
значение координаты х и параметра а каждой из которых
удовлетворяют данному уравнению, представляют собой параболу. Её
уравнение ![]() .
.
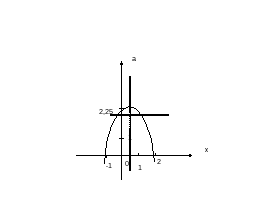
Парабола пересекает ось Ох в точках х = -1, а=0, х=2, а=0. Вершина параболы
х=-0,5; а=2,25. В ней оба корня совпадают. При ![]() <2,25
оба корня неотрицательны.
<2,25
оба корня неотрицательны.
Ответ. ![]() <2,25
<2,25
Пример 2. Найти значение параметра а, при которых
уравнение ![]()
имеет хотя бы один корень больший 0,5.
Решение.
На К-П плоскости ![]() множество
всех точек
множество
всех точек ![]() ,
координата x и параметр a каждой из которых удовлетворяют уравнению
и представляет собой график функции
,
координата x и параметр a каждой из которых удовлетворяют уравнению
и представляет собой график функции![]() ,то есть
параболу. Эта парабола пересекает ось
,то есть
параболу. Эта парабола пересекает ось ![]() в точках
в точках
![]() =0,
x=1. Вершиной параболы является точка
=0,
x=1. Вершиной параболы является точка ![]() .
Неравенству
.
Неравенству ![]() x>0,5
удовлетворяют точки полуплоскости без границы
x>0,5
удовлетворяют точки полуплоскости без границы ![]() =0.5.
См. рис.
=0.5.
См. рис.
Ответ. ![]() > -
0,25.
> -
0,25.
 a
a


0 x

- 0,25- 1
Пример 3. Решить уравнение ![]()
Решение.
По определению модуля имеем:
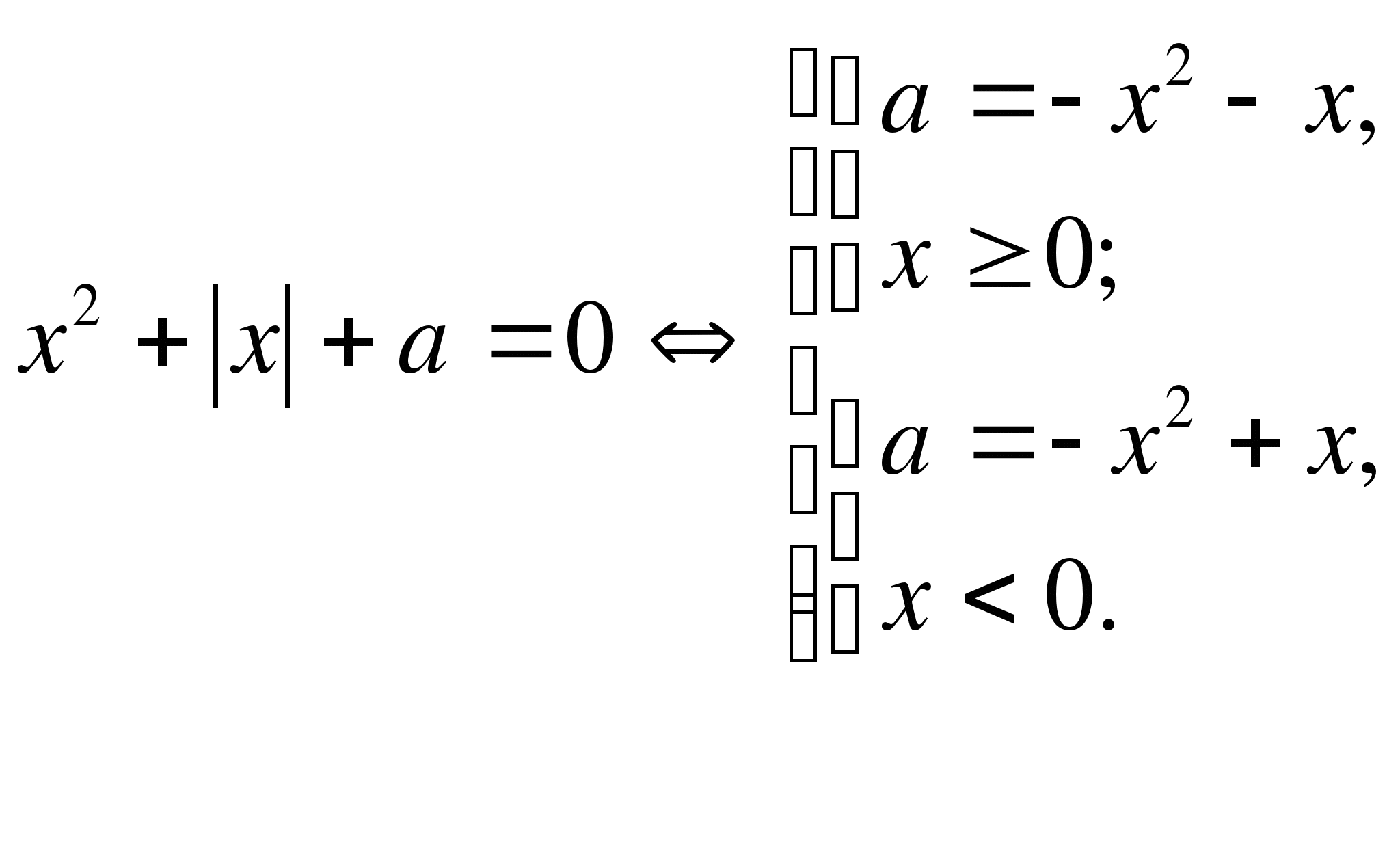
1) Тогда на К-П плоскости ![]() множество точек
множество точек ![]() ,
значение координаты и параметра которых удовлетворяют первой
смешанной системе совокупности, представляет собой часть параболы
,
значение координаты и параметра которых удовлетворяют первой
смешанной системе совокупности, представляет собой часть параболы
![]() расположенной
в полуплоскости
расположенной
в полуплоскости ![]() . 2)
Множеством точек
. 2)
Множеством точек ![]() ,
значения координаты и параметра которых удовлетворяют второй
смешанной системе совокупности, является часть параболы
,
значения координаты и параметра которых удовлетворяют второй
смешанной системе совокупности, является часть параболы ![]() расположенной
в левой полуплоскости
расположенной
в левой полуплоскости ![]() без
границы.
без
границы. ![]()
Зная уравнения ветвей парабол, запишем ответ.
Ответ. Если ![]() то
то![]()
![]() , если
, если
![]() то
то![]()
если ![]() ,
то
,
то .
.
III. Упражнения для самостоятельного решения.
1) При каких значениях параметра а уравнение ![]() имеет
ровно три корня?
имеет
ровно три корня?
Ответ.![]()
2) Для каждого значения ![]() определить
число корней уравнения
определить
число корней уравнения![]() .
.
Ответ. ![]() то ;
то ;
![]() то
два корня;
то
два корня;
![]() то
четыре корня;
то
четыре корня;
![]() =4,
то три корня.
=4,
то три корня.
IV. Итог занятия.
Блок II. Тема 3. Линейные уравнения с параметром и уравнения, сводящиеся к ним.
Цель занятия:
- повторить алгоритм решения уравнений I степени с параметром, на корни которых
накладываются дополнительные условия;
- продолжить развитие интеллектуальных (выделять главное, сравнивать, обобщать,
делать выводы, определять и объяснять понятия) и познавательных умений,
познавательного интереса в процессе решения уравнений 1-й степени с одним
неизвестным и уравнений, приводимых к линейным.
Занятие 1: «Решение уравнений с параметром 1-й степени с одним
неизвестным».
Ход занятия:
-
Этап повторения (актуализация знаний).
В некоторых задачах требуется определить те значения параметра, при которых выполняются некоторые условия на расположение корней.
1. При каких значениях параметра а среди корней уравнения
2ах - 4х -а2 + 4а - 4 = 0 есть корни больше 1?
Решение: 2ах - 4х = а2 - 4а + 4,
(2а - 4)х = (а - 2)2 ,
2(а - 2)х = (а - 2)2 .
1) Если а = 2, то решением уравнения 0х = 0 будет любое число, в том числе и больше 1.
2) Если а ≠ 2, то ![]() .
.
По условию х > 1, т.е. ![]() > 1,
а > 4.
> 1,
а > 4.
Ответ: при а = 2 и а > 4.
2. При каких значениях параметра а корни уравнения ![]() = 2
будут меньше -1?
= 2
будут меньше -1?
Решение: При х ≠ -а уравнение равносильно уравнению
ах + а = 2х + 2а,
ах - 2х = 2а - а,
(а - 2)х = а.
1) Если а = 2, то уравнение 0х = 2 не имеет решений.
2) Если а ≠ 2, то х = ![]() .
.
3) Если х = -а, то ![]() =
-а,
=
-а,
а = -а2 + 2а,
а2 - а = 0,
а(а - 1) = 0,
а = 0 или а = 1. (1).
По условию х > -1, т.е. ![]() ≥ -1
≥ -1
![]()
![]() +1 ≥ 0
+1 ≥ 0
![]()
![]() ≥ 0.
≥ 0.

а ![]() (-
∞; 1]
(-
∞; 1] ![]() (2;
+∞).
(2;
+∞).
Учитывая условие 1 а ![]() (- ∞;
0)
(- ∞;
0) ![]() (0; 1)
(0; 1)
![]() (2;
+∞).
(2;
+∞).
Ответ: а ![]() (- ∞;
0)
(- ∞;
0) ![]() (0; 1)
(0; 1)
![]() (2;
+∞).
(2;
+∞).
-
Этап закрепления знаний (самостоятельная работа в группах).
1. Найти значения а, при каждом из которых уравнение а(3х - а) = 6х - 4 имеет положительный корень.
Решение: 3ах - а2 = 6х - 4,
(3а - 6)х = а2- 4,
3(а - 2)х = (а - 2)(а + 2).
-
Если а - 2 = 0, а = 2, то решением уравнения 0х = 0 будет любое число, в том числе и положительный корень.
-
Если а + 2 = 0, а = -2, то уравнение -12х = 0 имеет решение х = 0, 0 - не положительное число.
-
Если а ≠ 2, а ≠ -2, то х =
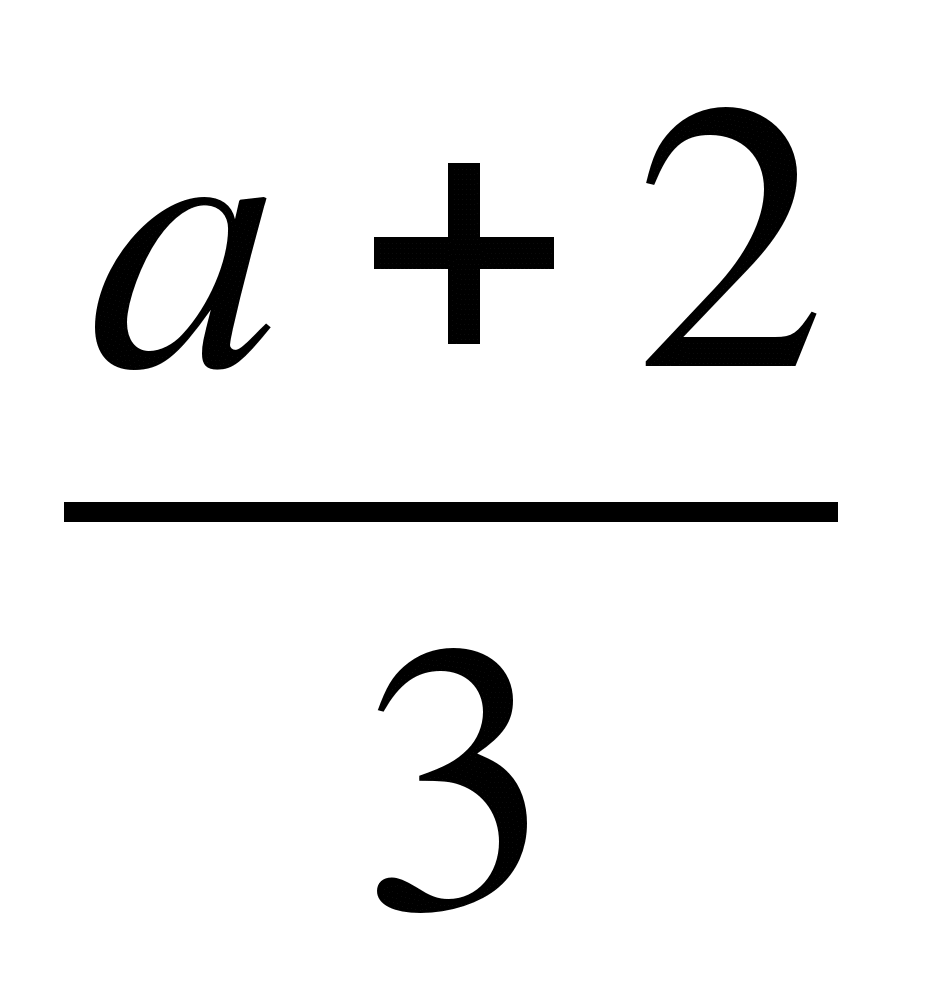 будет иметь положительный корень
будет иметь положительный корень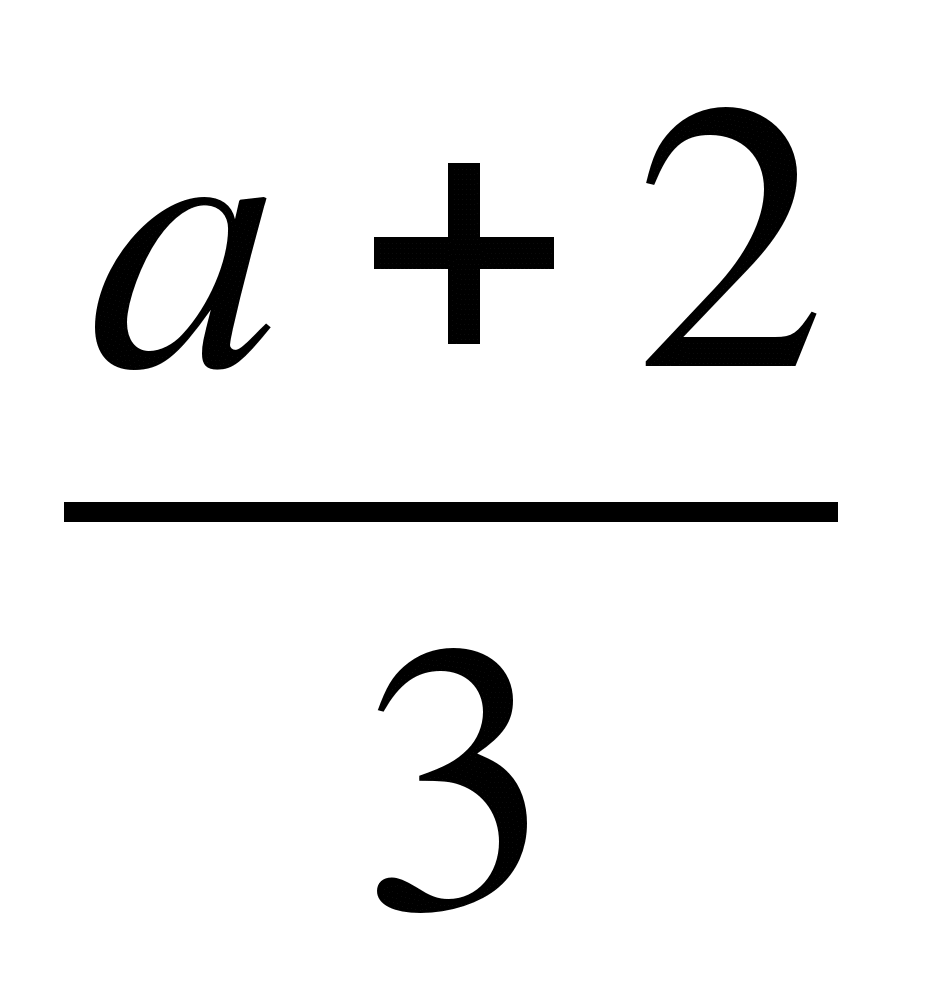 > 0
> 0
при а +2 > 0, а >-2.
Учитывая условия 1) и 2) имеем что уравнение имеет положительный корень при а >-2.
Ответ: а >-2.
2. При каких значениях а корень уравнения 6 - 3а + 4ах = 4а + 12х меньше 1?
Решение: 4ах - 12х = 4а + 3а - 6,
(4а -12 )х = 7а - 6,
4(а - 3)х = 7а - 6.
-
Если а - 3 = 0, а = 3, то 0х = 15 не имеет решений.
-
Если а ≠ 3, то х=
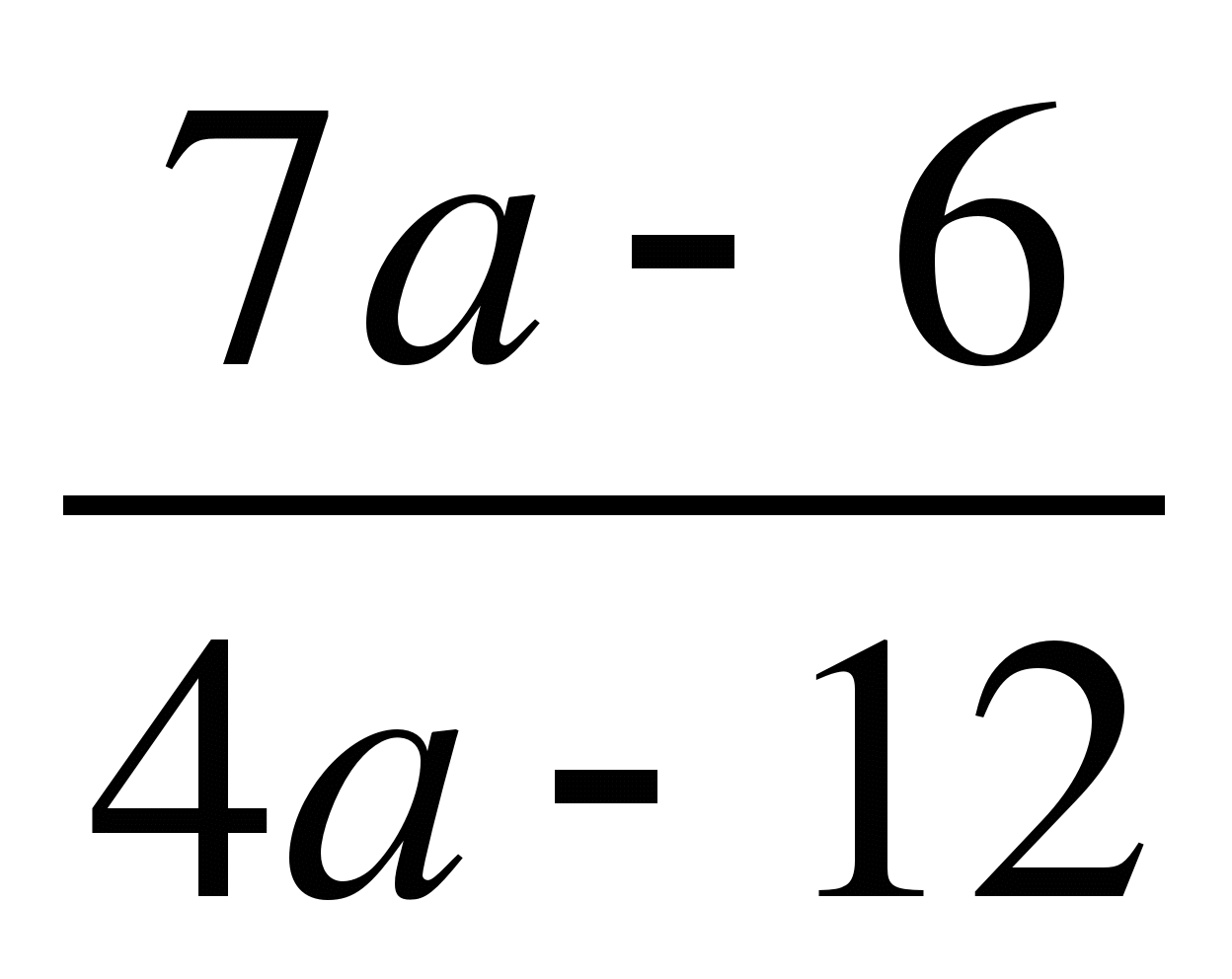 .
.
По условию ![]() < 1
< 1 ![]()
![]() < 0
< 0
![]()
![]() < 0.
< 0.

-2 < а < 3.
Ответ: а ![]() (-2;
3).
(-2;
3).
-
Этап рефлексии.
-
Дополнительные задания: При каких значениях а среди корней уравнения
х - ах + а2 - 1 = 0 есть корни больше 1?
Занятие 2: «Решение уравнений с параметрами, приводимых к линейным.»
Ход занятия:
-
Этап повторения (актуализация знаний).
-
При каких значениях параметра а корни уравнения
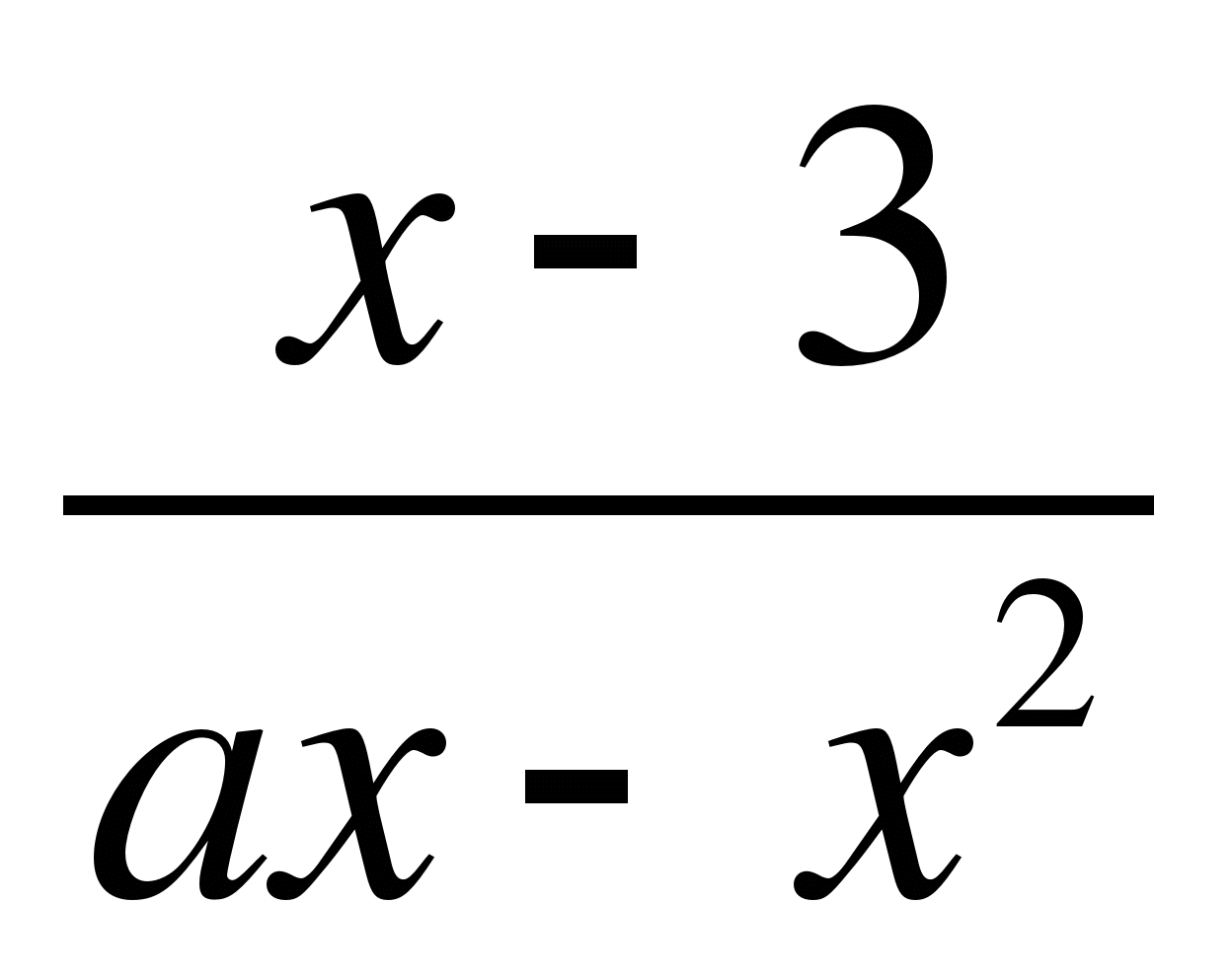 -
-
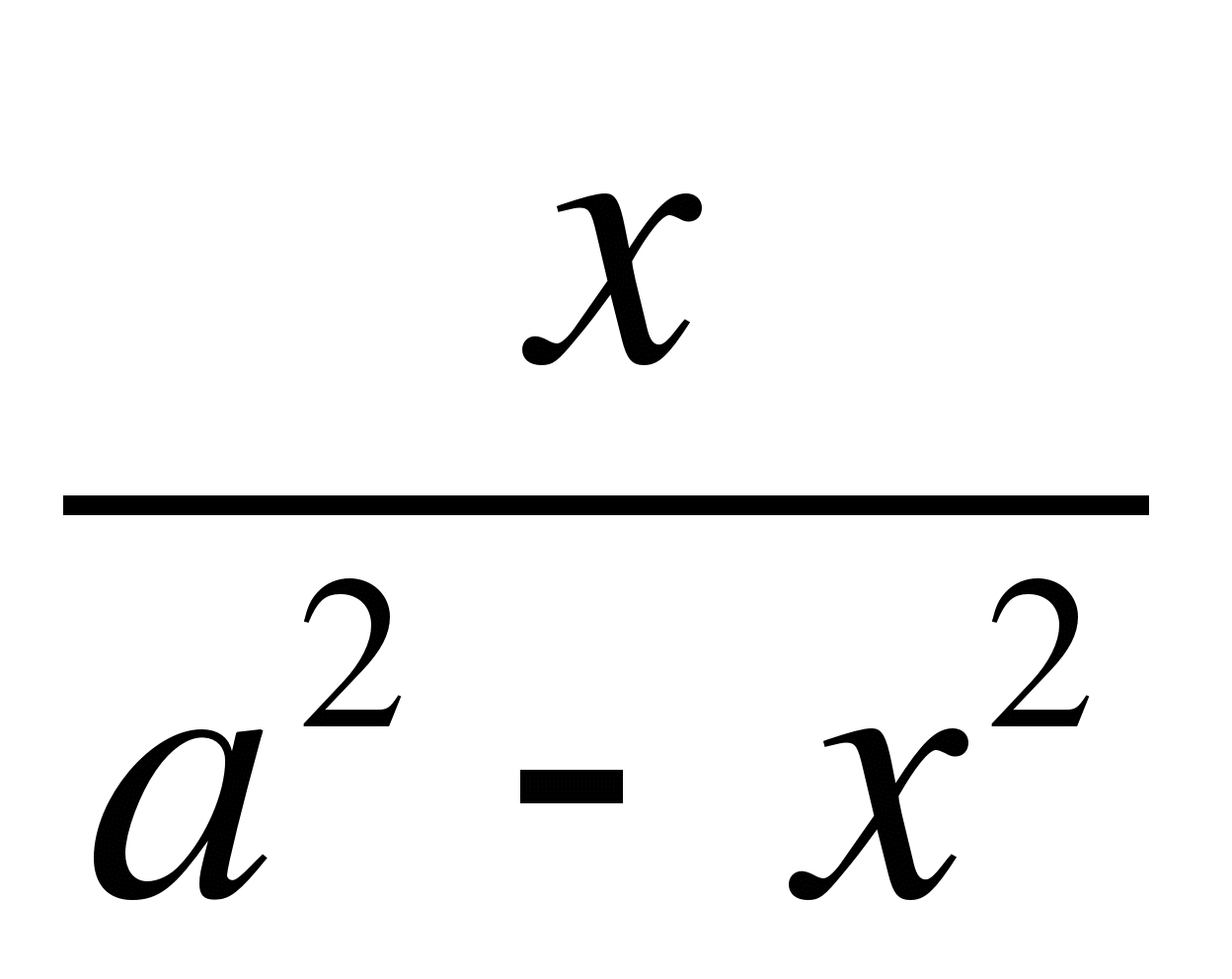 =
=
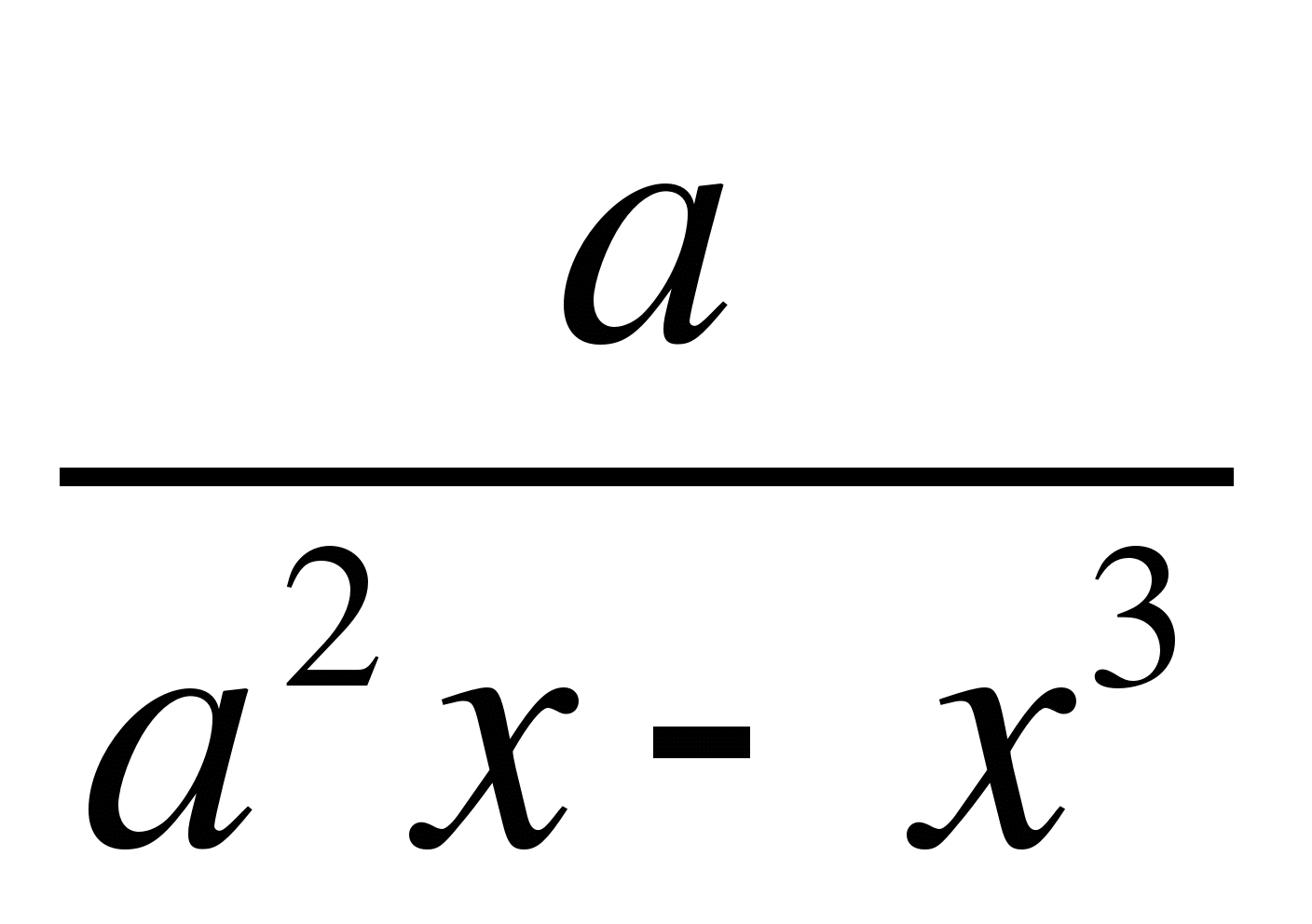 принадлежит отрезку [-2;1].
принадлежит отрезку [-2;1].
Решение: ![]() -
-
![]() =
=
![]() . О.О.У:
. О.О.У:
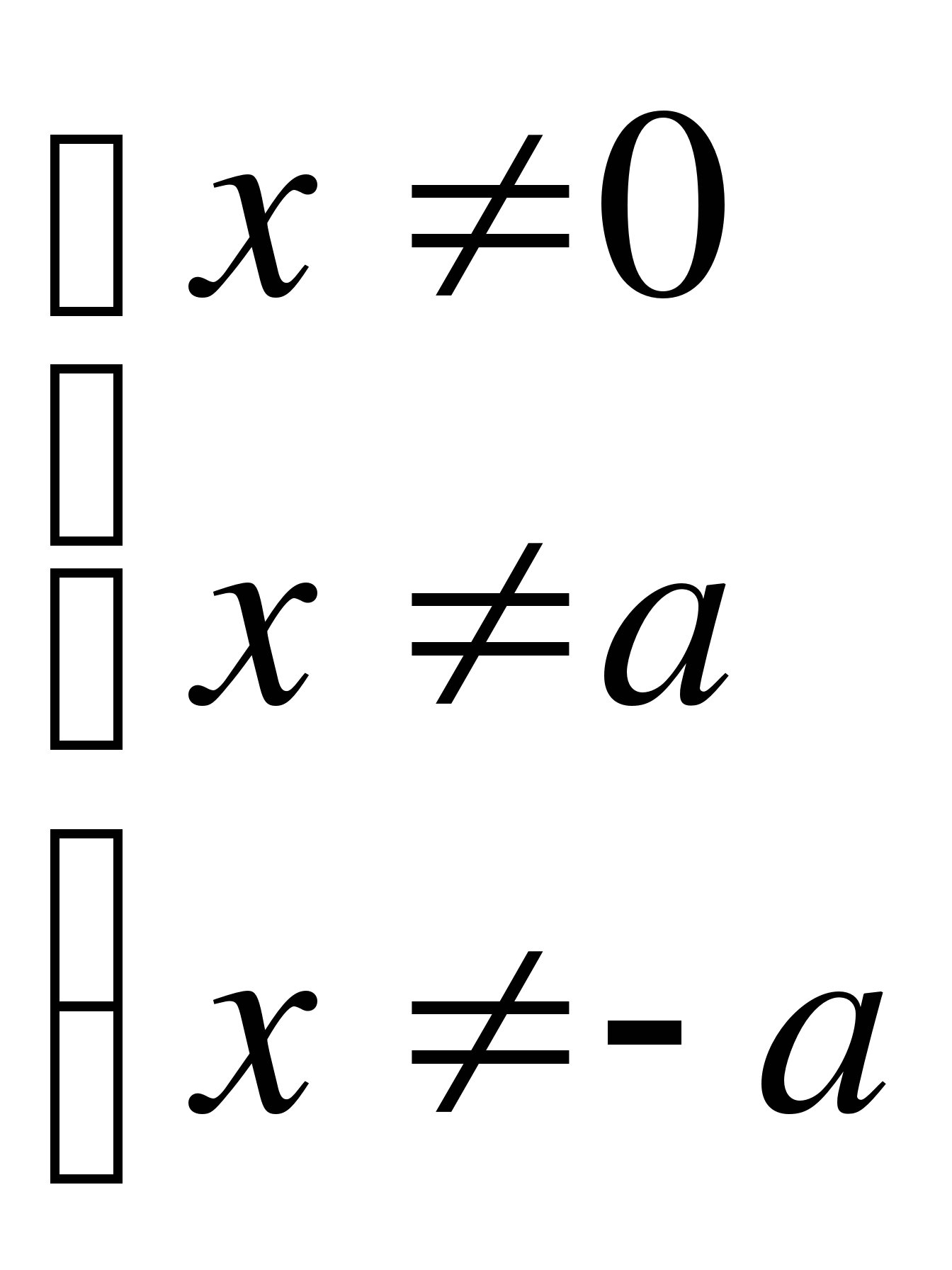 .
.
Умножим обе части уравнения на общий знаменатель
(х - 3)(а + х) - хх = а,
ах - 3а + х2 - 3х - х2- а = 0,
(а - 3)х = 4а.
1) Если а - 3 = 0, а = 3, то уравнение 0х = 12 не имеет корней.
2) Если а ≠ 3, то х = ![]() .
.
Найдем а, при которых х = 0, х = а, х = -а.
а) х = 0, то ![]() = 0,
а = 0.
= 0,
а = 0.
б) х = а, то ![]() =
а, а2 - 3а - 4а = 0,
а2 - 7а = 0, а(а - 7) = 0,
а = 0 или а = 7.
=
а, а2 - 3а - 4а = 0,
а2 - 7а = 0, а(а - 7) = 0,
а = 0 или а = 7.
в) х = -а, то ![]() =
-а, -а2 + 3а - 4а = 0,
а2 + а = 0, а(а + 1) = 0,
а = 0 или а = -1.
=
-а, -а2 + 3а - 4а = 0,
а2 + а = 0, а(а + 1) = 0,
а = 0 или а = -1.
При а ≠ -1, а ≠ 0, а ≠ 3, а ≠ 7, х =
![]() .
.
По условию -2 ≤ х ≤ 1
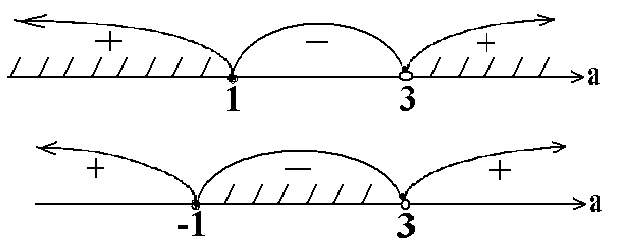 -2 ≤
-2 ≤
![]() ≤ 1.
≤ 1.
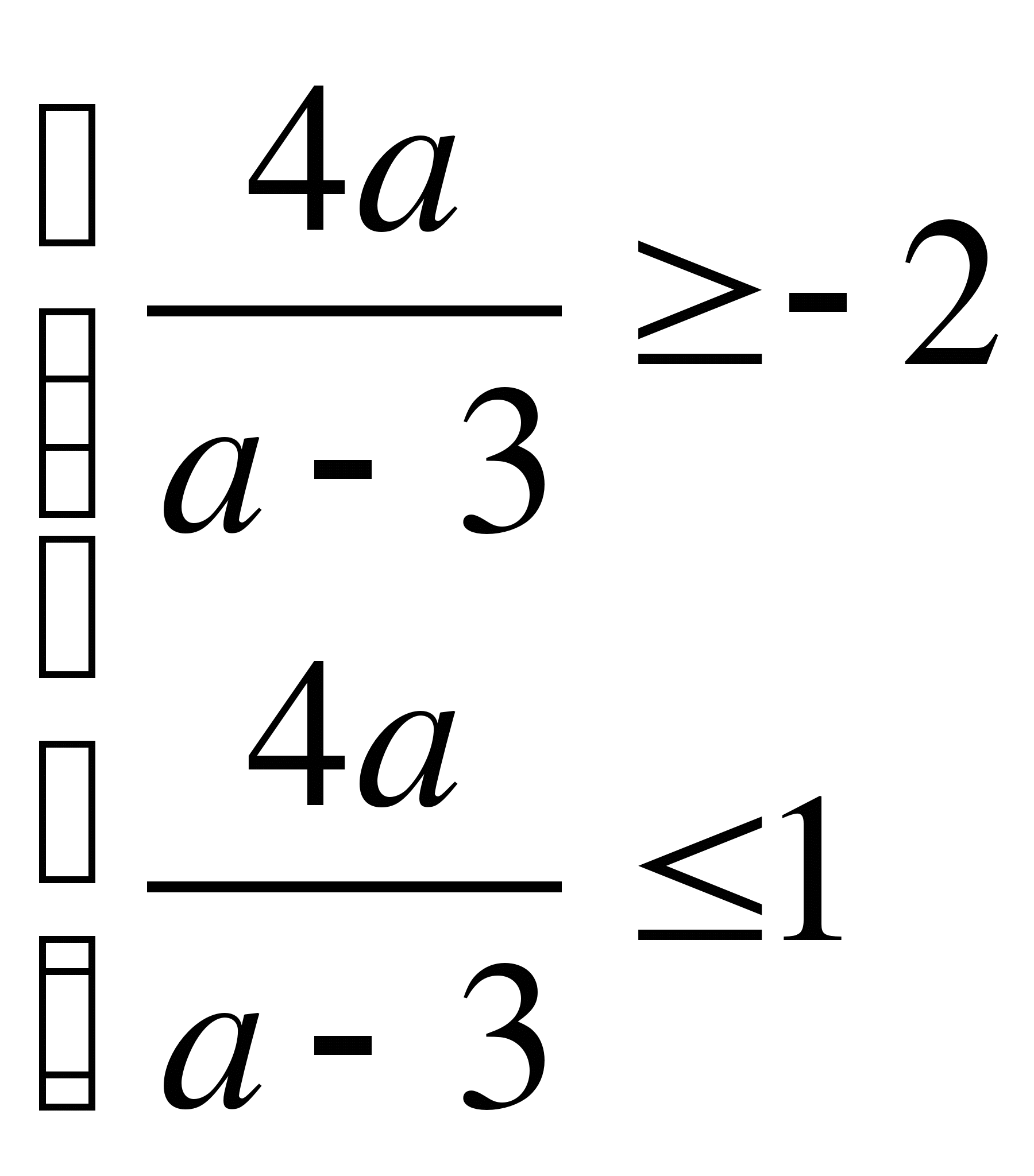
![]()
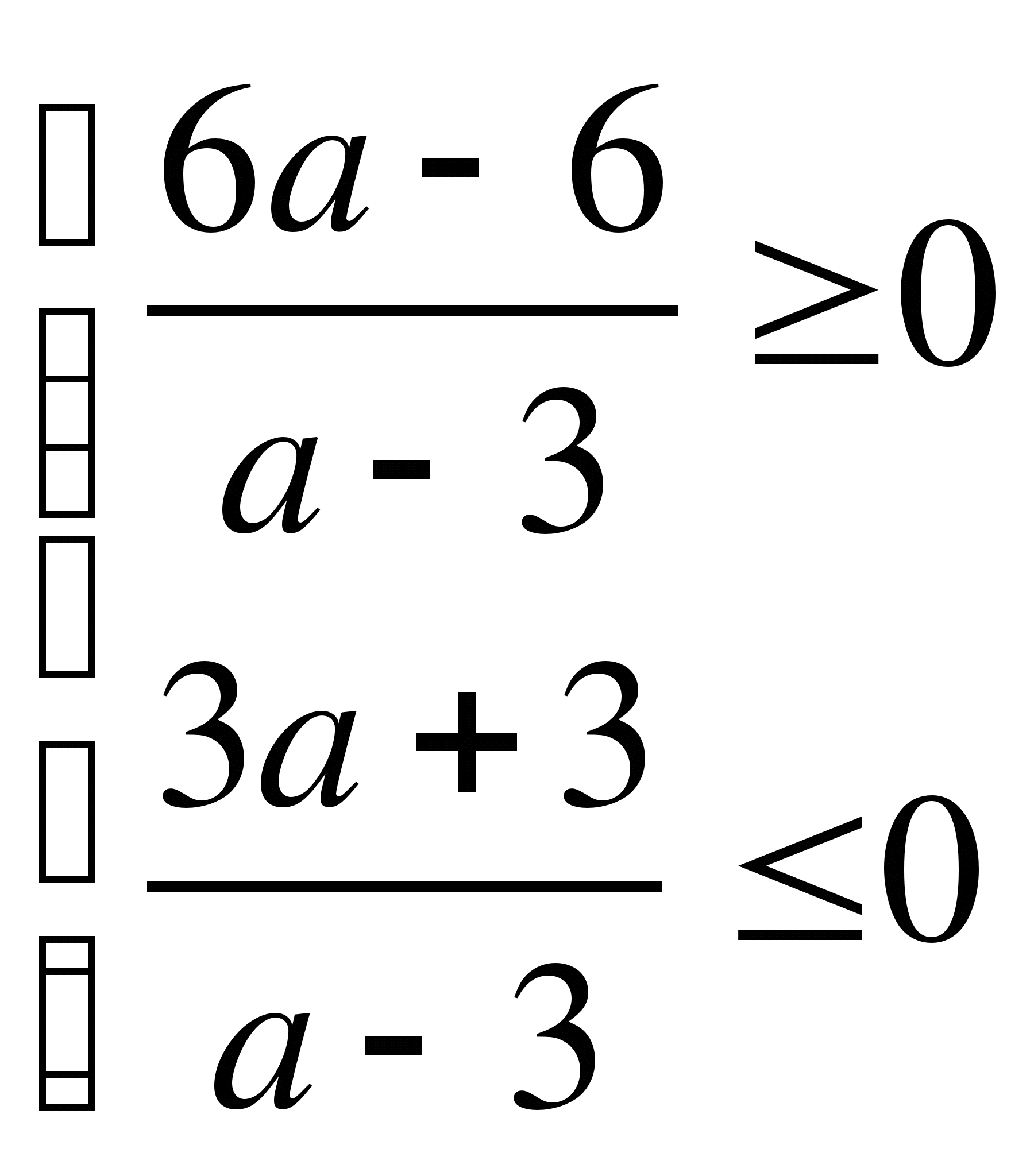
![]()
![]() -1 ≤
а ≤ 1.
-1 ≤
а ≤ 1.
Учитывая, что а ≠ -1, а ≠ 0, а ≠ 3,
а ≠ 7, получим, что а ![]() (-1; 0)
(-1; 0)
![]() (0; 1].
(0; 1].
Ответ: а ![]() (-1; 0)
(-1; 0)
![]() (0; 1].
(0; 1].
2. Найти все значения параметра а, при каждом из которых число 7 является единственным корнем уравнения х - 7 = ах - 7а2 (1).
Решение. Если для некоторого значения параметра а число 7 является корнем уравнения, то для этого значения а справедливо равенство 7 - 7 = 7а - 7а2,
а(а - 1) = 0, а = 0 или а = 1.
Требуется, чтобы этот корень был единственным, поэтому еще нужно проверить, является ли число 7 единственным корнем при а = 0 или а = 1.
Если а = 0, то уравнение (1) перепишем в виде х -7 = 0, х =7. При а = 0 число 7 является единственным корнем уравнения (1).
Если а = 1, то уравнение (1) имеет вид х -7 = х - 7, т.е. любое действительное число является корнем уравнения (1), значит число 7 не является единственным корнем уравнения (1).
Ответ: а = 0.
-
Этап закрепления знаний (самостоятельная работа - в группах).
1. Найти значение параметра а, при которых корни
уравнения ![]() принадлежит отрезку
принадлежит отрезку
[-1;4].
Решение: ![]() .
О.О.У.: ах - 1 ≠ 0, ах ≠ 1, х ≠
.
О.О.У.: ах - 1 ≠ 0, ах ≠ 1, х ≠ ![]() при
а ≠ 0.
при
а ≠ 0.
2а - ах = ах - 1,
2ах = 2а + 1;
-
если а = 0, то х =
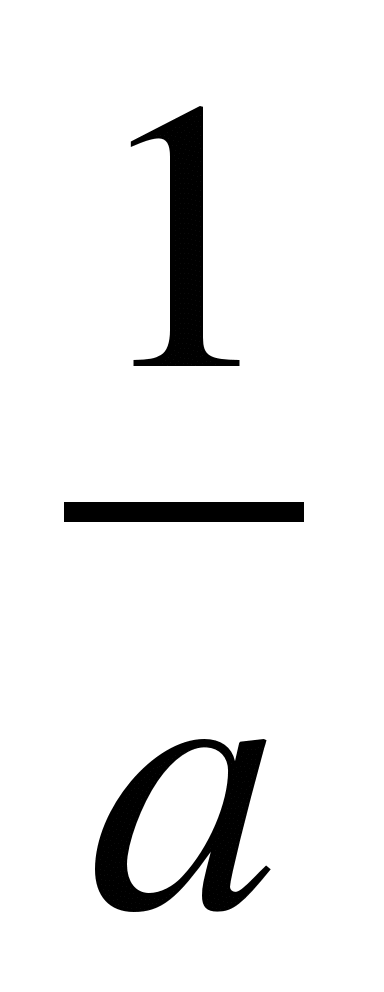 ,то
уравнение не имеет решений.
,то
уравнение не имеет решений.
-
если а ≠ 0, то х =
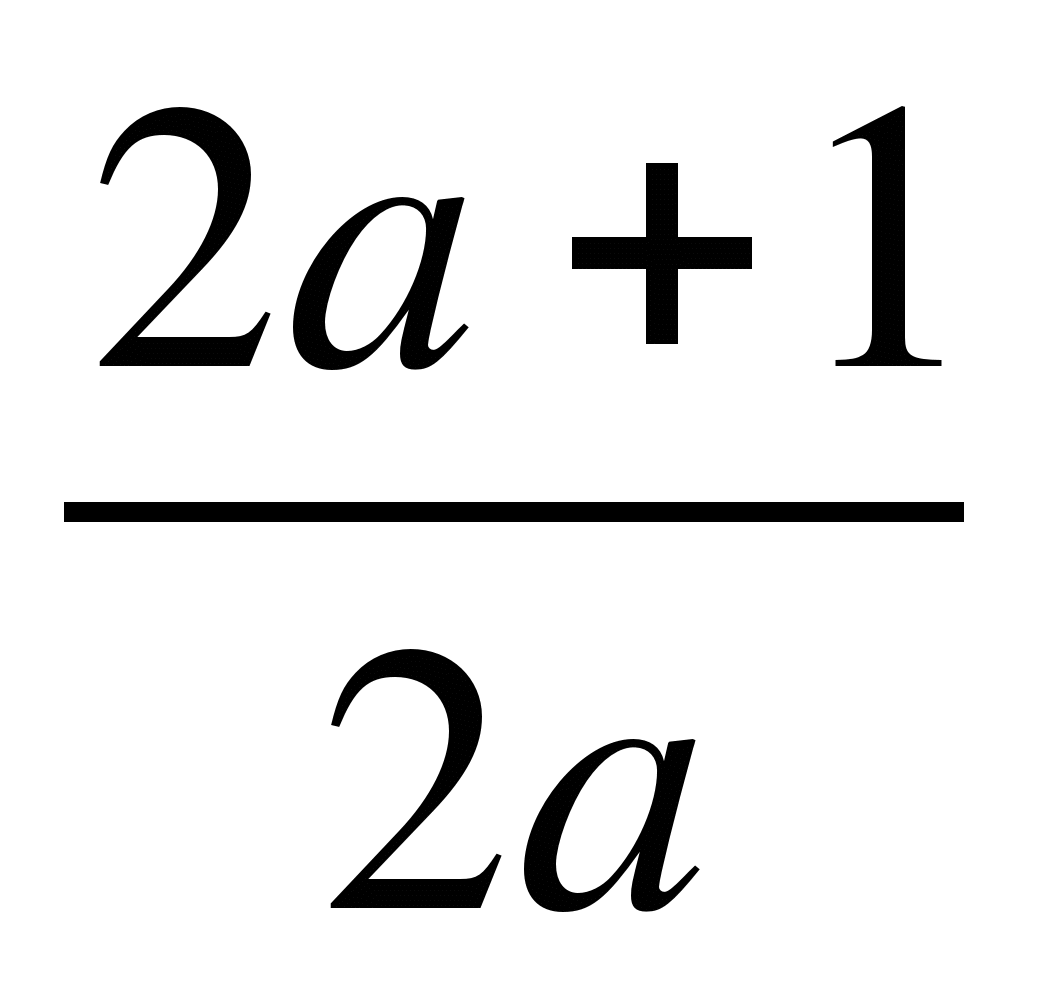 .
Найдем а, при которых х =
.
Найдем а, при которых х = 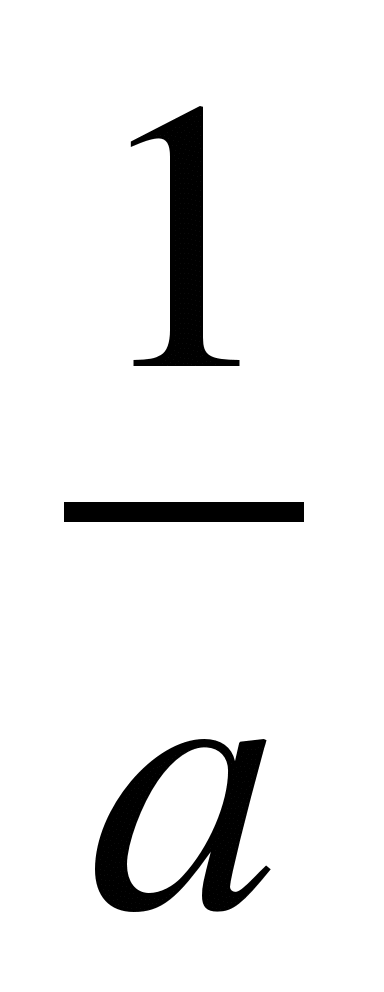 ,
,
![]() =
=
![]() ,
2а = 2а2 +а, а(2а -1)
= 0, а ≠ 0 или а =
,
2а = 2а2 +а, а(2а -1)
= 0, а ≠ 0 или а = ![]() .
.
При а ≠ 0, а ≠![]() , х =
, х =
![]() .
.
П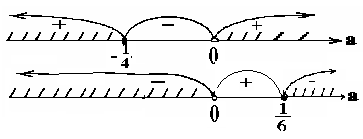 о
условию -1 ≤
о
условию -1 ≤![]() ≤ 4
≤ 4
![]()
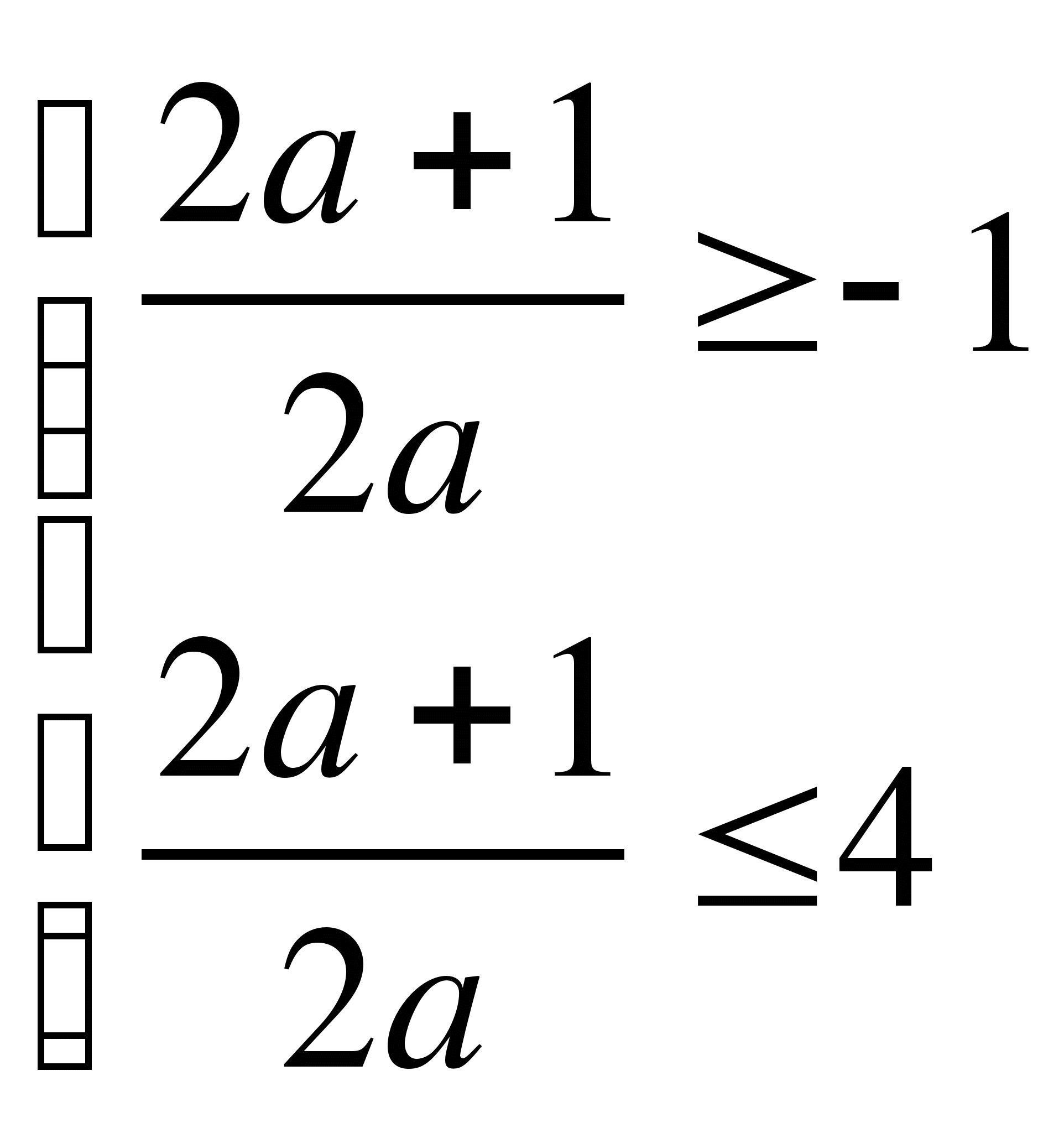
![]()
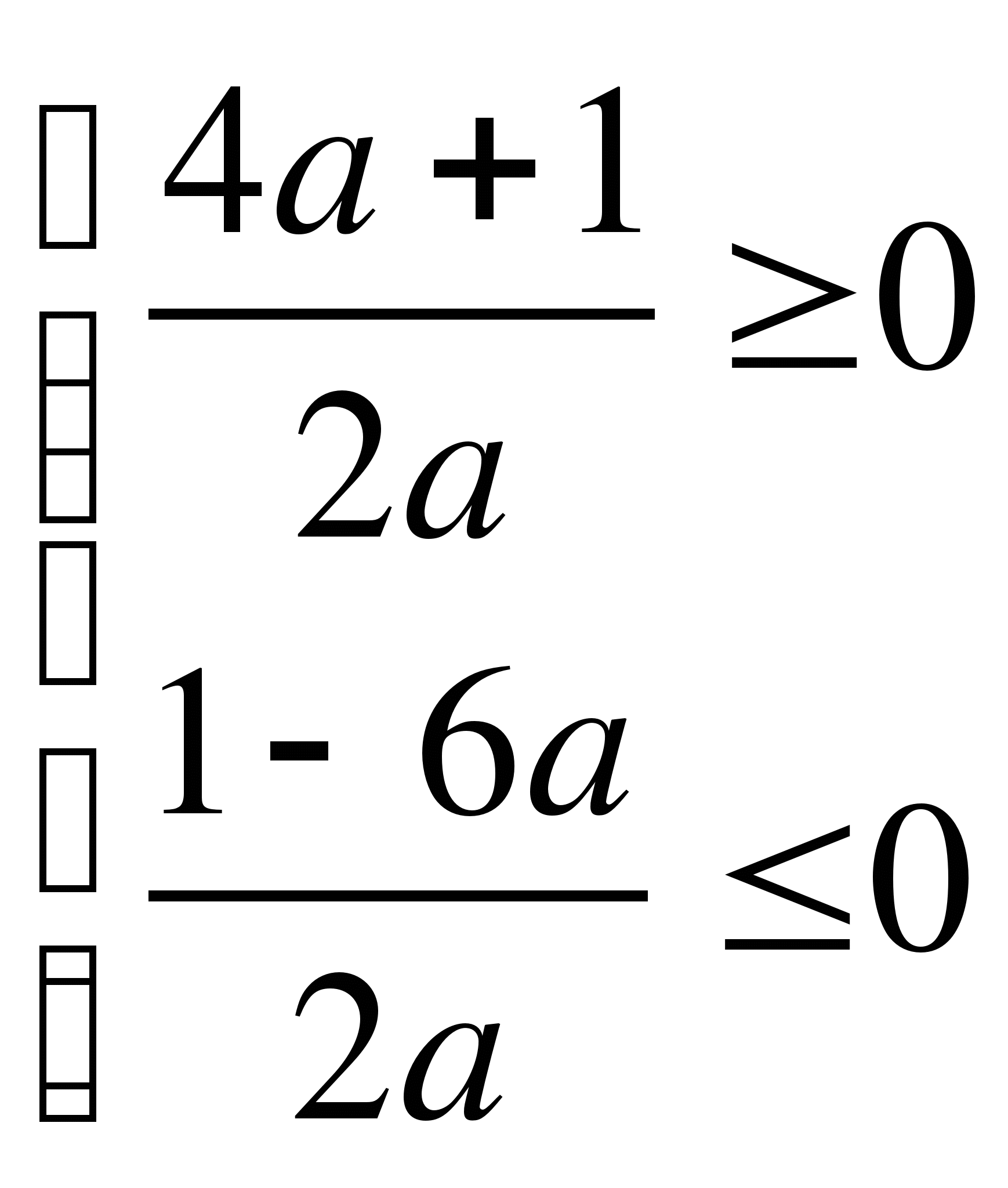
а ![]() (-∞;-
(-∞;-![]() ]
]
![]() [
[
![]() ; +∞).
; +∞).
Учитывая, что а ≠ 0, а ≠![]() а
а
![]() (-∞;-
(-∞;-![]() ]
]
![]() [
[
![]() ;
;
![]() ).
).![]() (
(
![]() ; +∞).
; +∞).
Ответ: а ![]() (-∞;-
(-∞;-![]() ]
]
![]() [
[
![]() ;
;
![]() ).
).![]() (
(
![]() ; +∞).
; +∞).
-
Этап рефлексии.
-
Дополнительные задания: Найти все значения параметра а, при каждом из которых уравнения ах - 5 = х + а и ах2 - 3 = х + а2 имеют общий корень.
Занятие 3. «Линейные уравнения с параметром».
Цель:
- развитие навыков самоконтроля при решении линейных уравнений с параметрами;
- проверить уровень усвоения темы с помощью самостоятельной работы (тест).
Ход занятия.
I. Этап подготовки учащихся к самоконтролю знаний
Учитель: Как записывается линейное уравнение в общем виде?
Ученик: Ах=В (1)
Учитель: Как решается линейное уравнение (1)?
Ученик: При решении уравнения (1) следует рассмотреть три случая:
-
Если А≠ 0, то
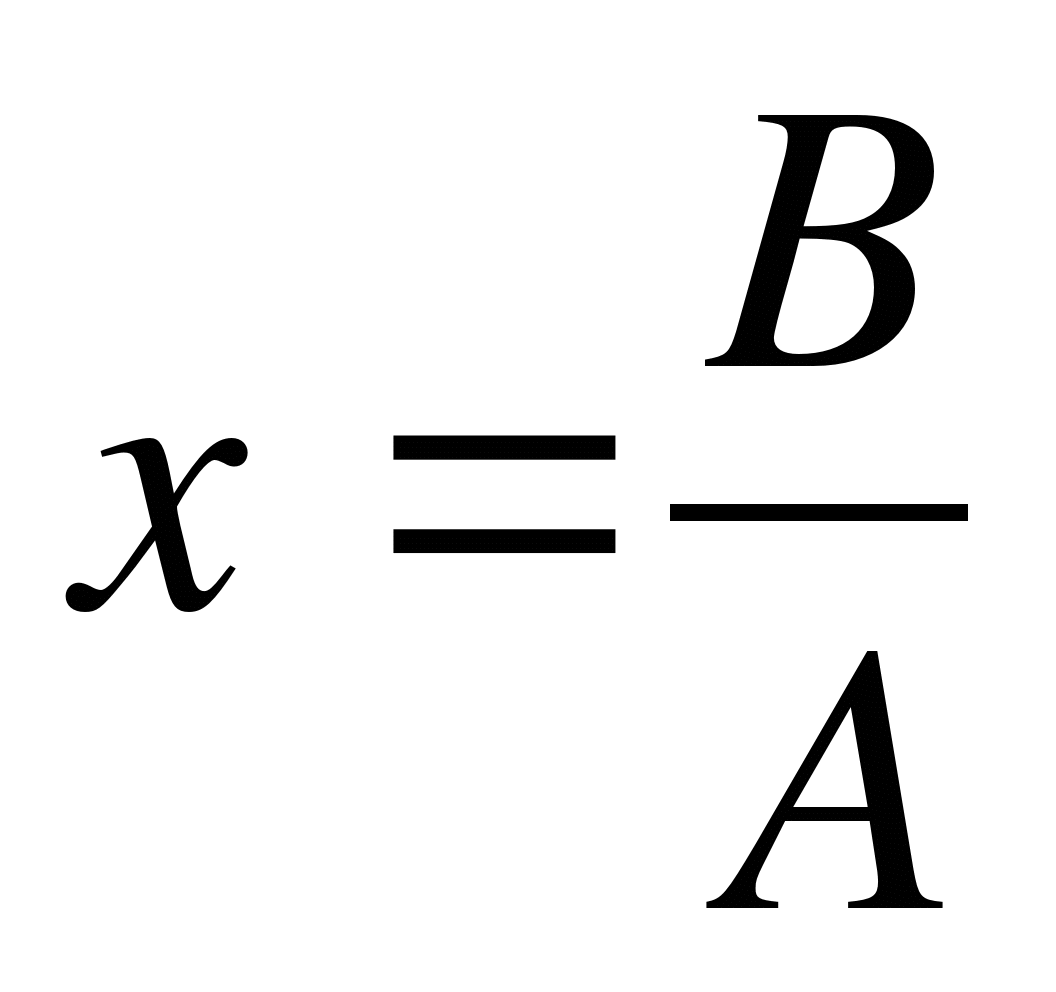 (один корень)
(один корень)
-
Если А=0 и В=0, то
 (корни все действительные числа)
(корни все действительные числа)
-
Если А=0 и В≠ 0, то
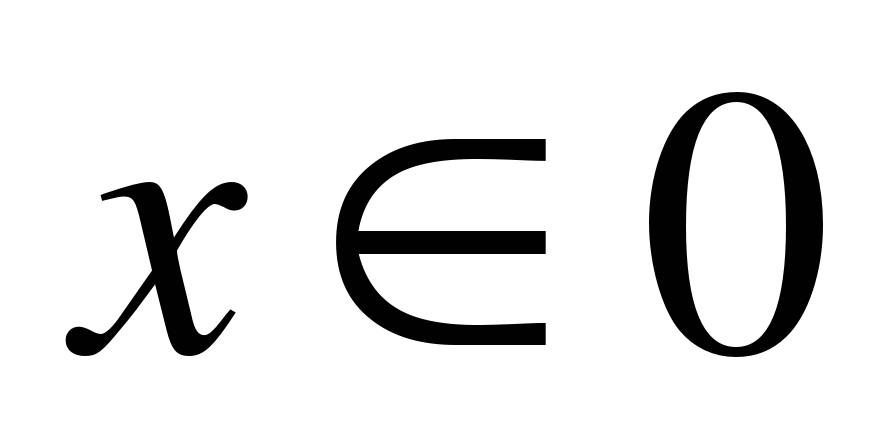 (корней нет)
(корней нет)
II. Этап самоконтроля
Учитель: С помощью заданий самоконтроля знаний (к каждому заданию даны ответы) вы проверьте свои умения решать линейные уравнения с параметром. После полученных ответов указаны команды, с помощью которых вы будете исправлять ошибки либо переходить к решению следующего задания, если ответ предыдущего верный.
Задания для самоконтроля
Выполните задания и команды, указанные после полученных ответов
-
При каждом значении а решите уравнение а(х-2)=4(х+2).
-
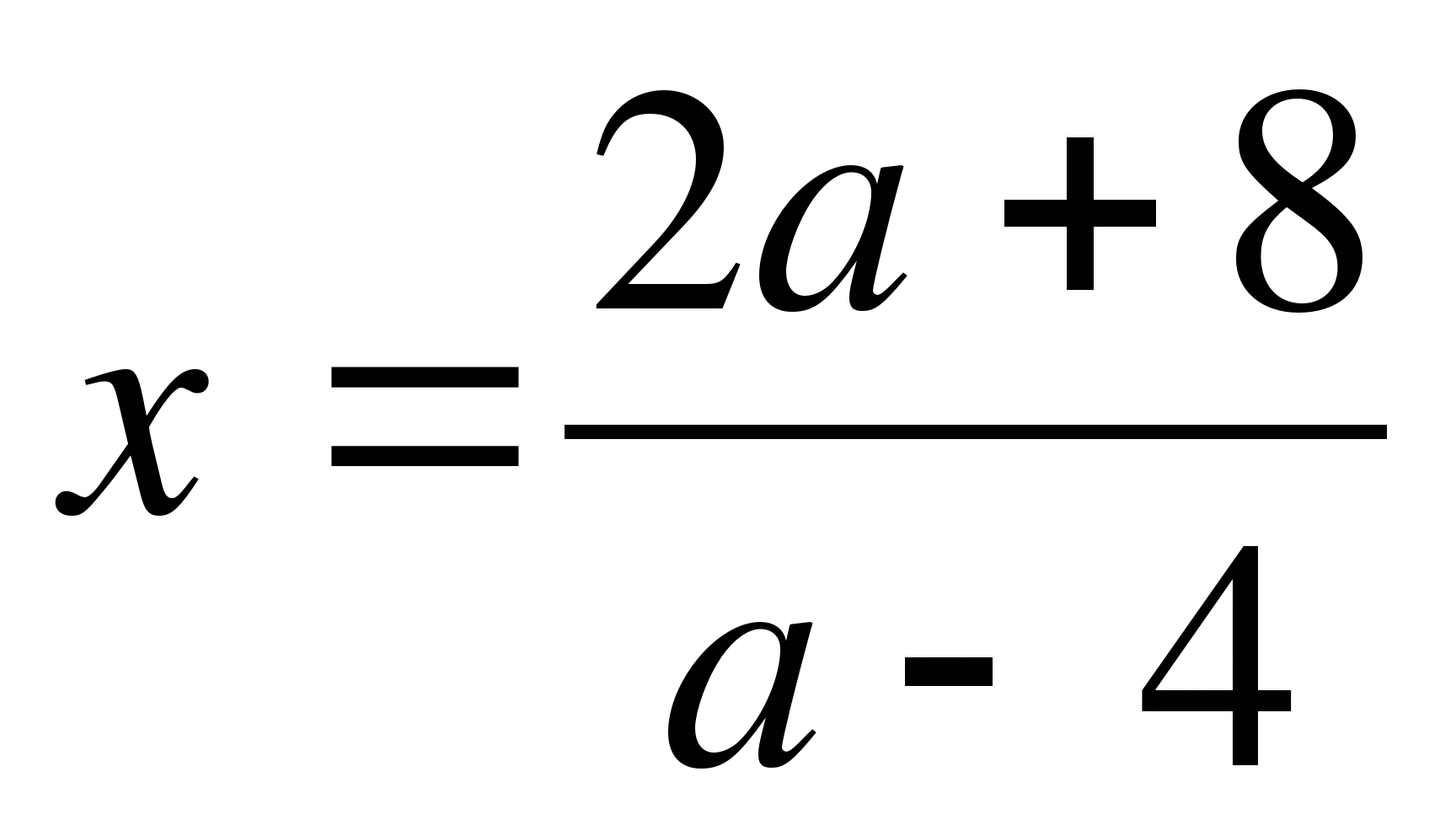 (а;б);
(а;б);
-
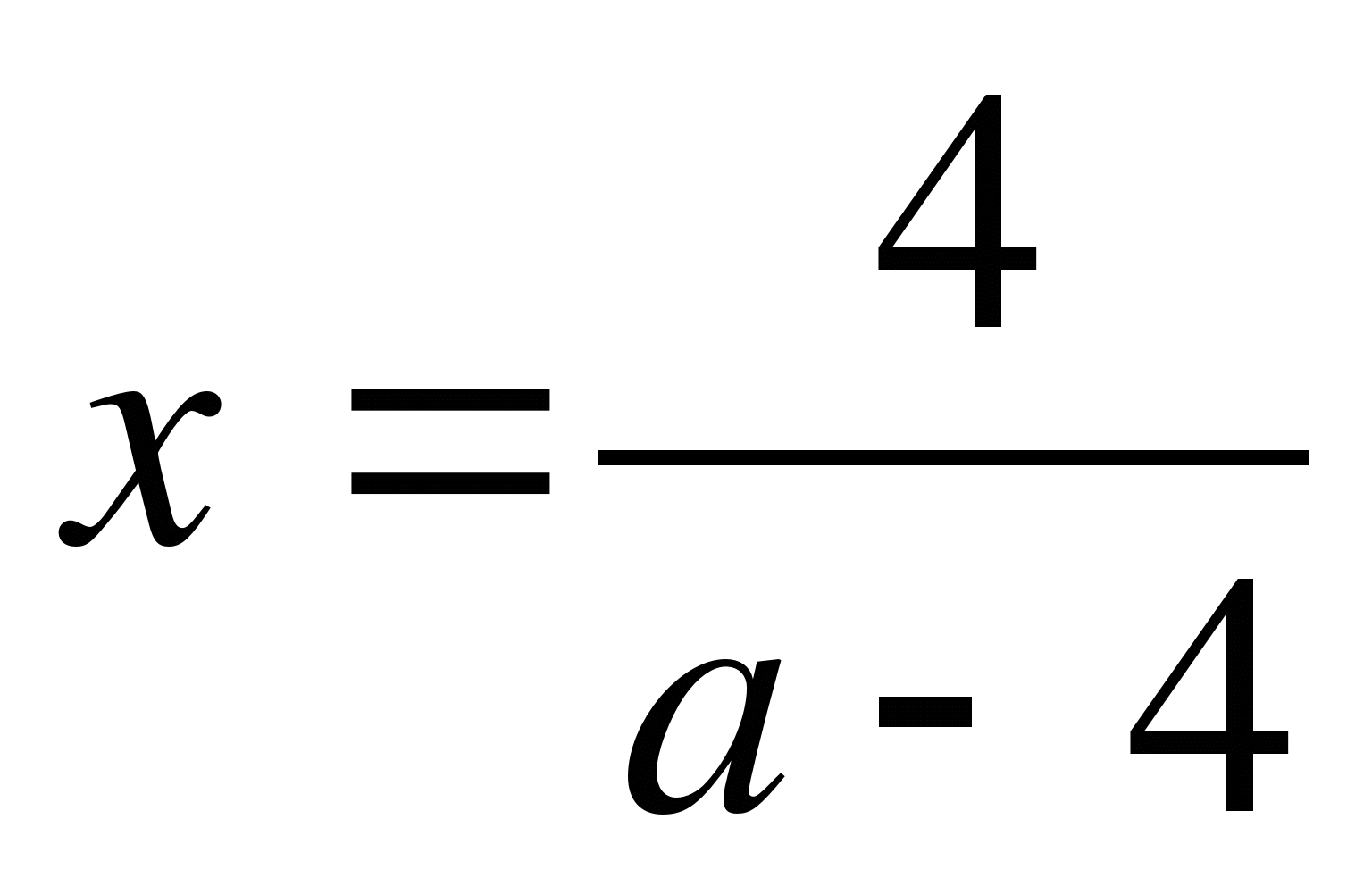 (а;г);
(а;г);
-
Нет корней при а=-4;
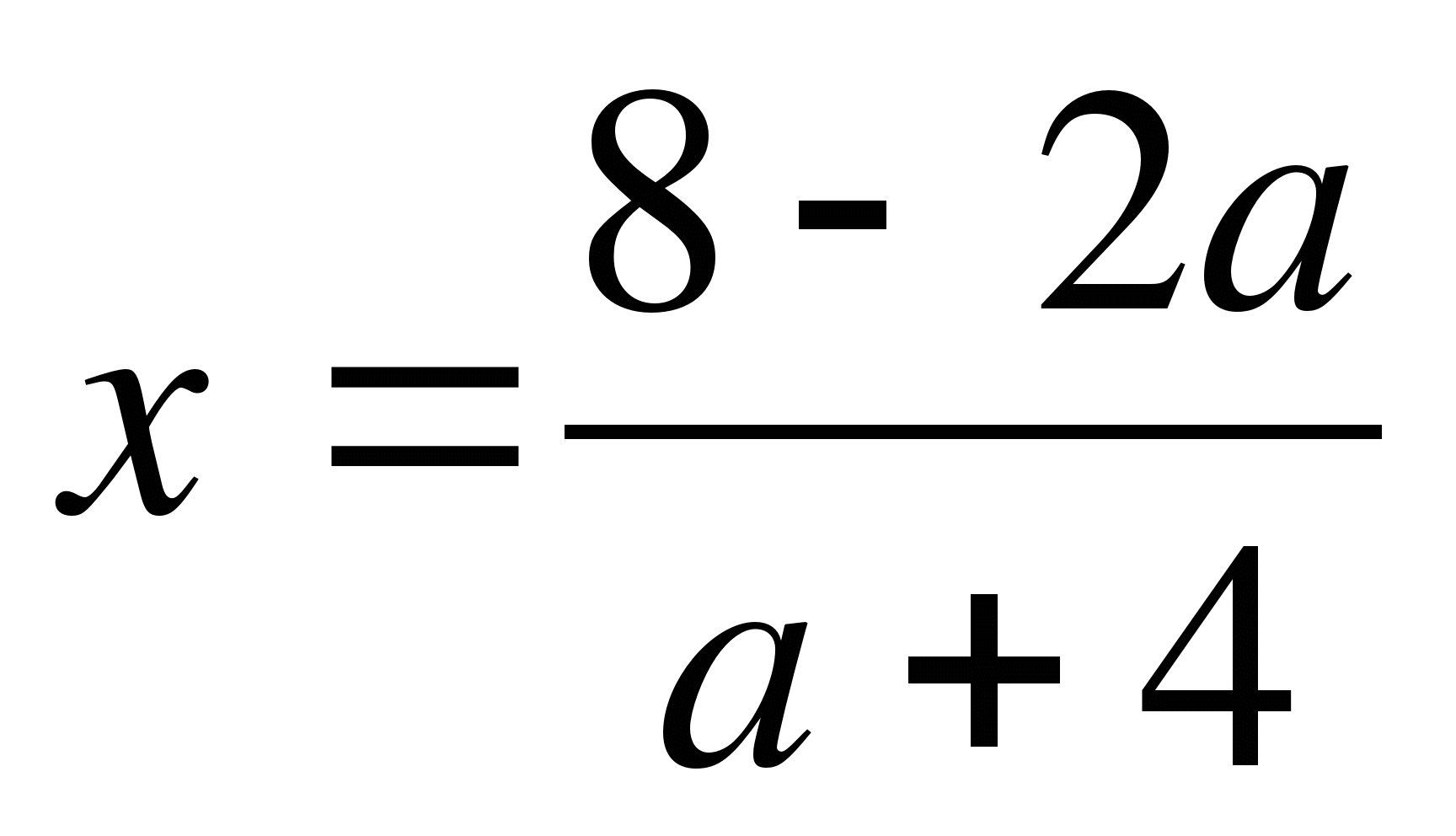 при а≠ - 4 (в).
при а≠ - 4 (в).
-
Нет корней при а=4;
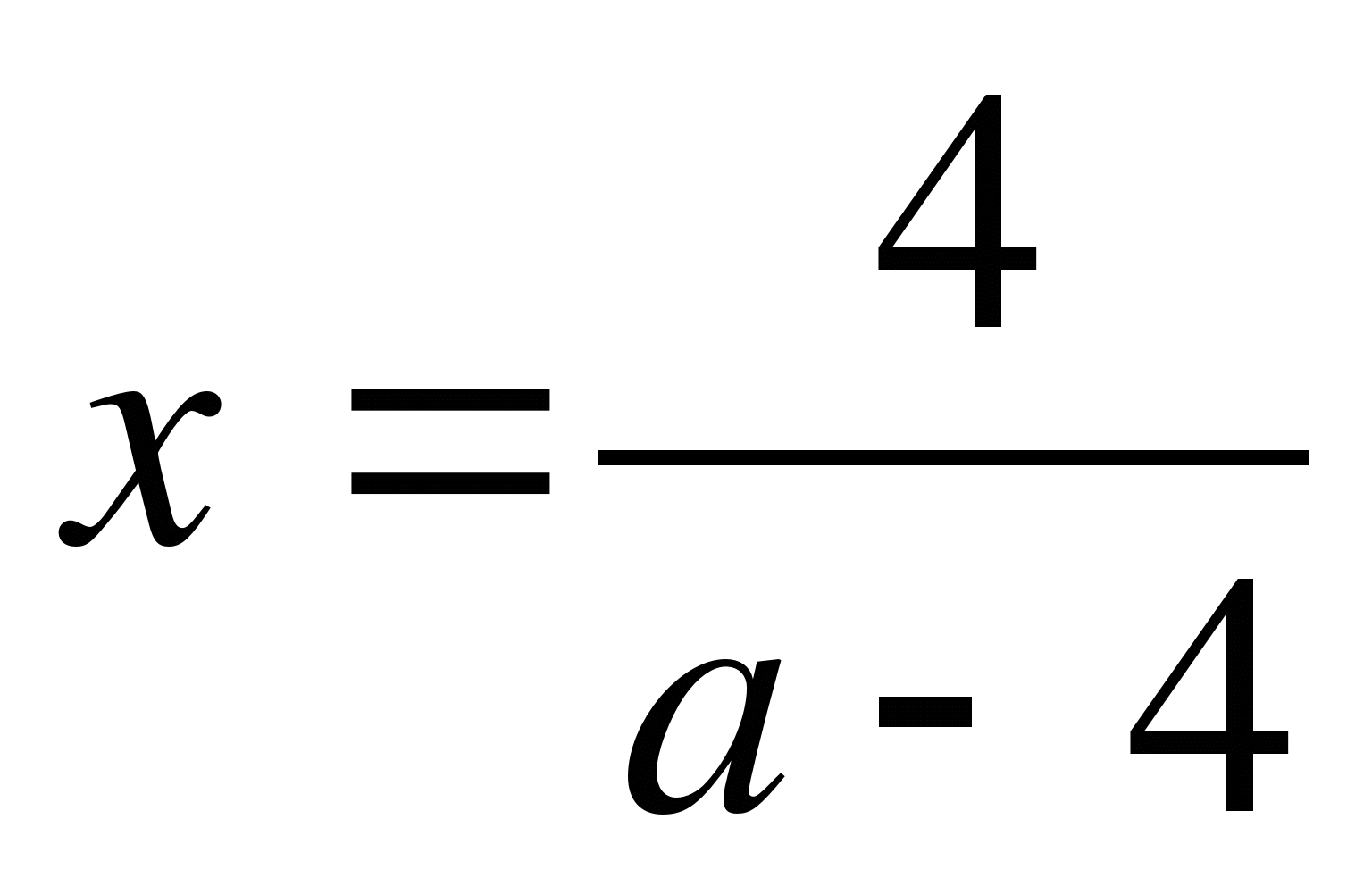 при а≠ 4 (в).
при а≠ 4 (в).
-
Нет корней при а=4.
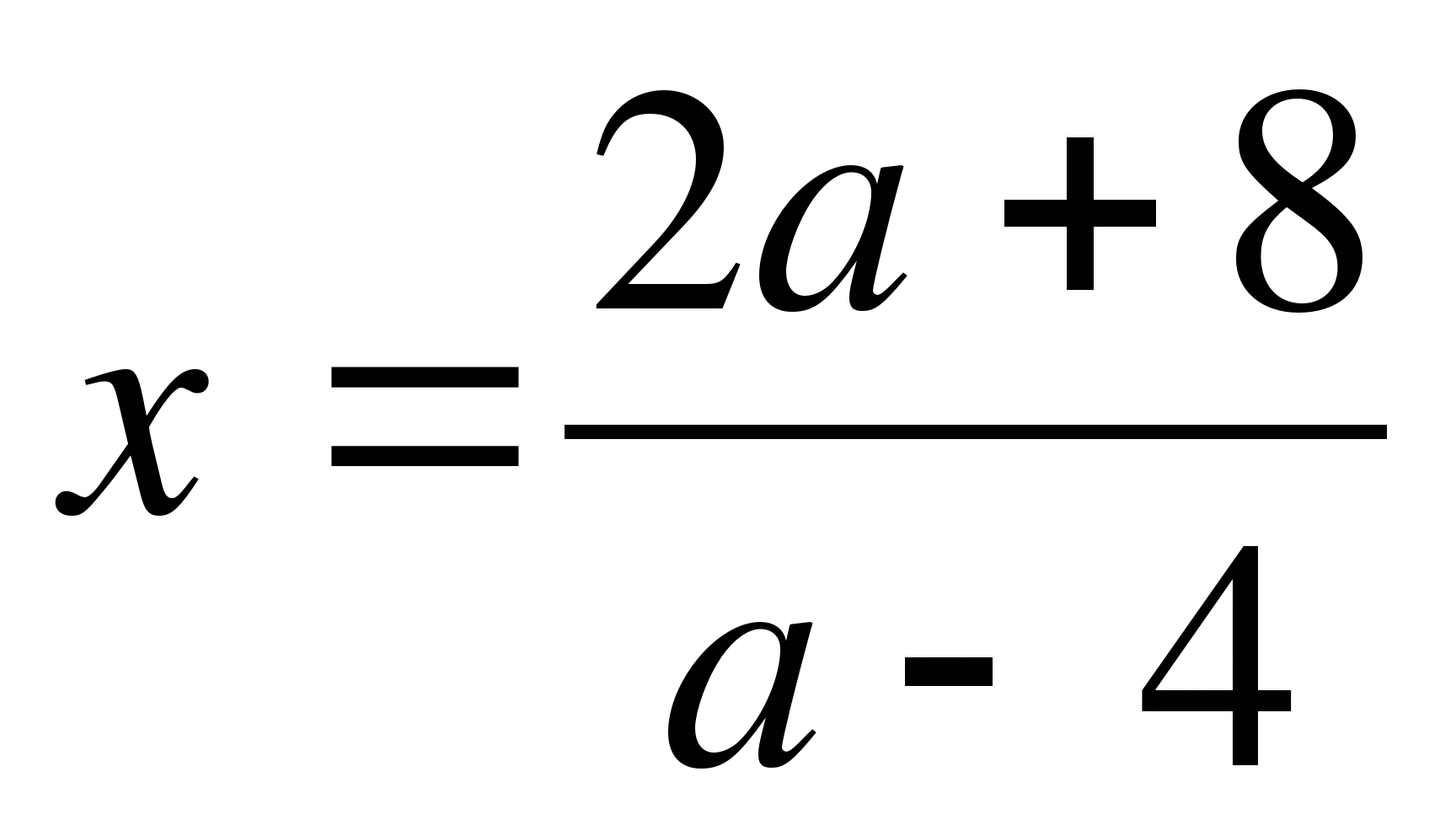 при а≠ 4 (е).
при а≠ 4 (е).
-
При каждом значении параметра а решите уравнение а2х-7=7а+х.
-
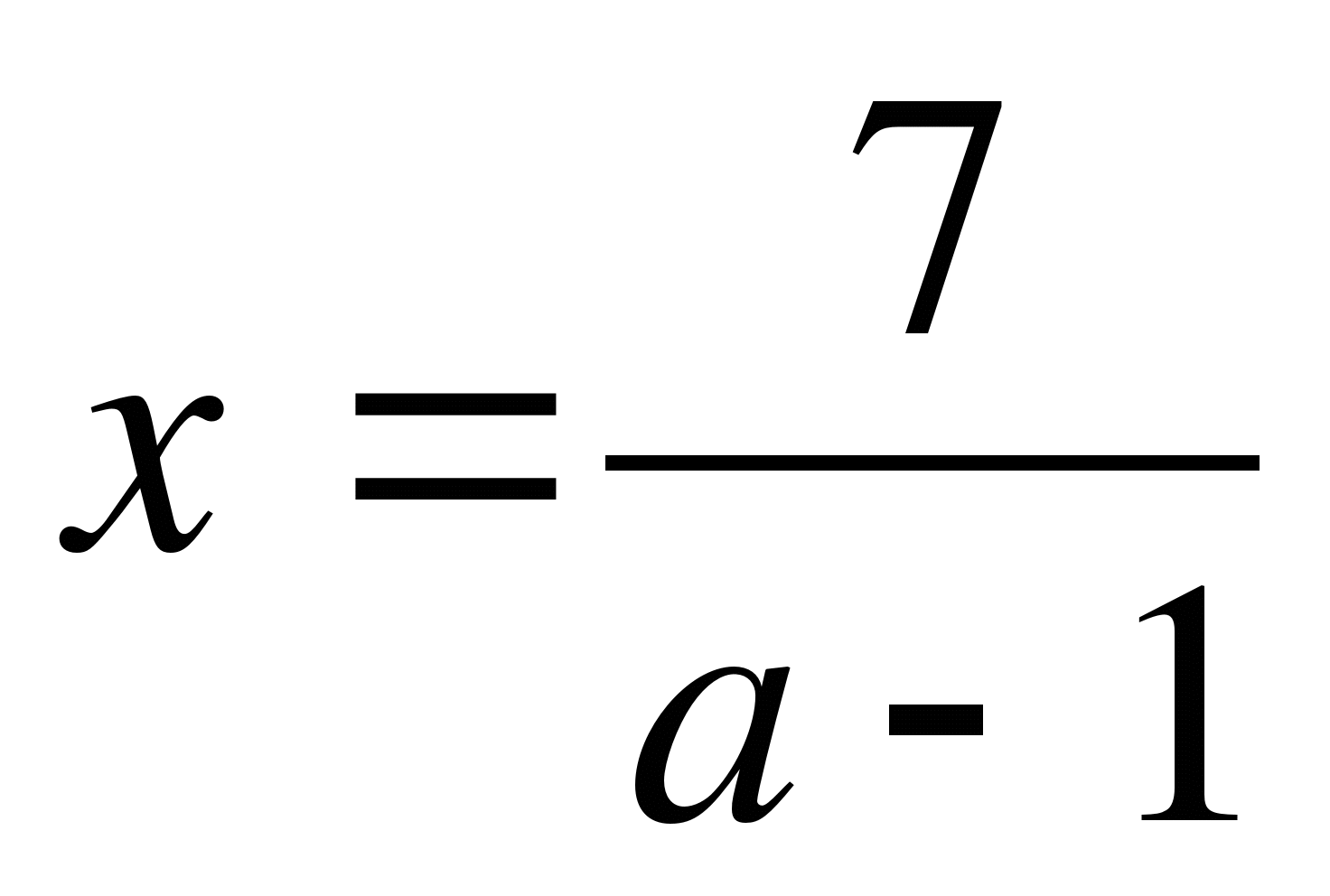 (а,б).
(а,б).
-
Нет корней при а=-1;
 при а=1;
при а=1; 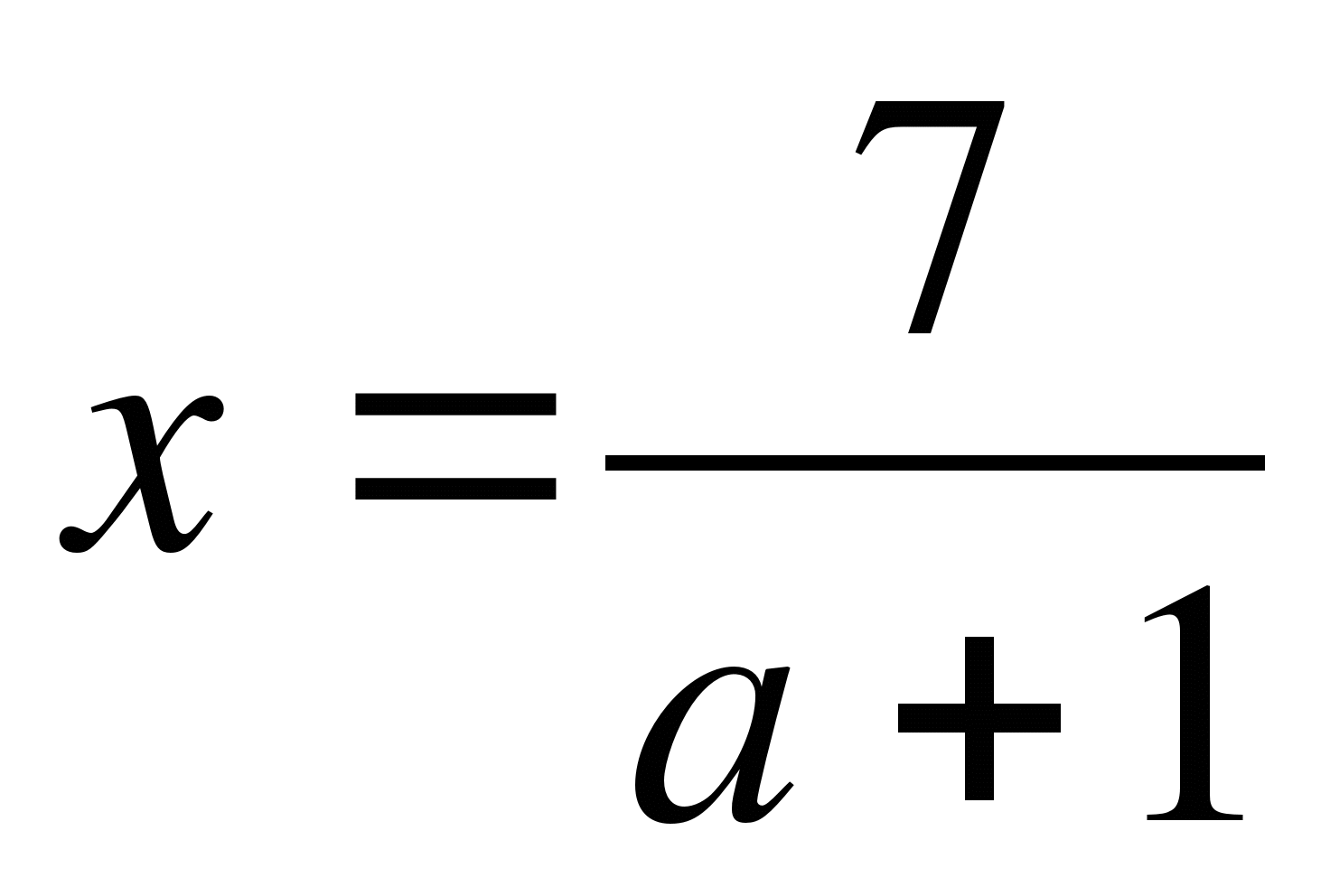 при а≠ ±1 (в).
при а≠ ±1 (в).
-
Нет корней при а=1;
 при а= -1;
при а= -1; 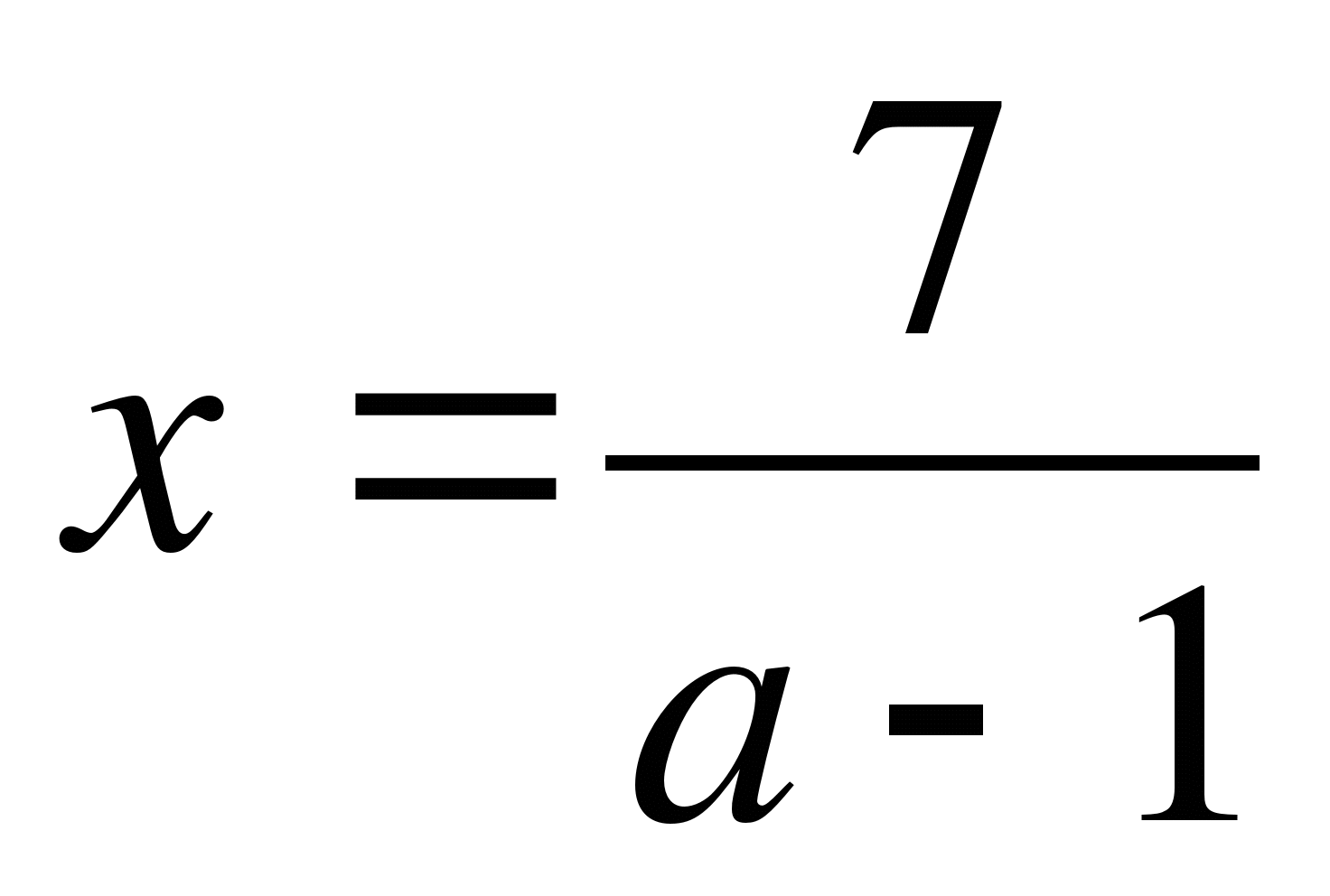 при а≠ 1 (б).
при а≠ 1 (б).
-
Нет корней при а=1;
 при а= -1;
при а= -1; 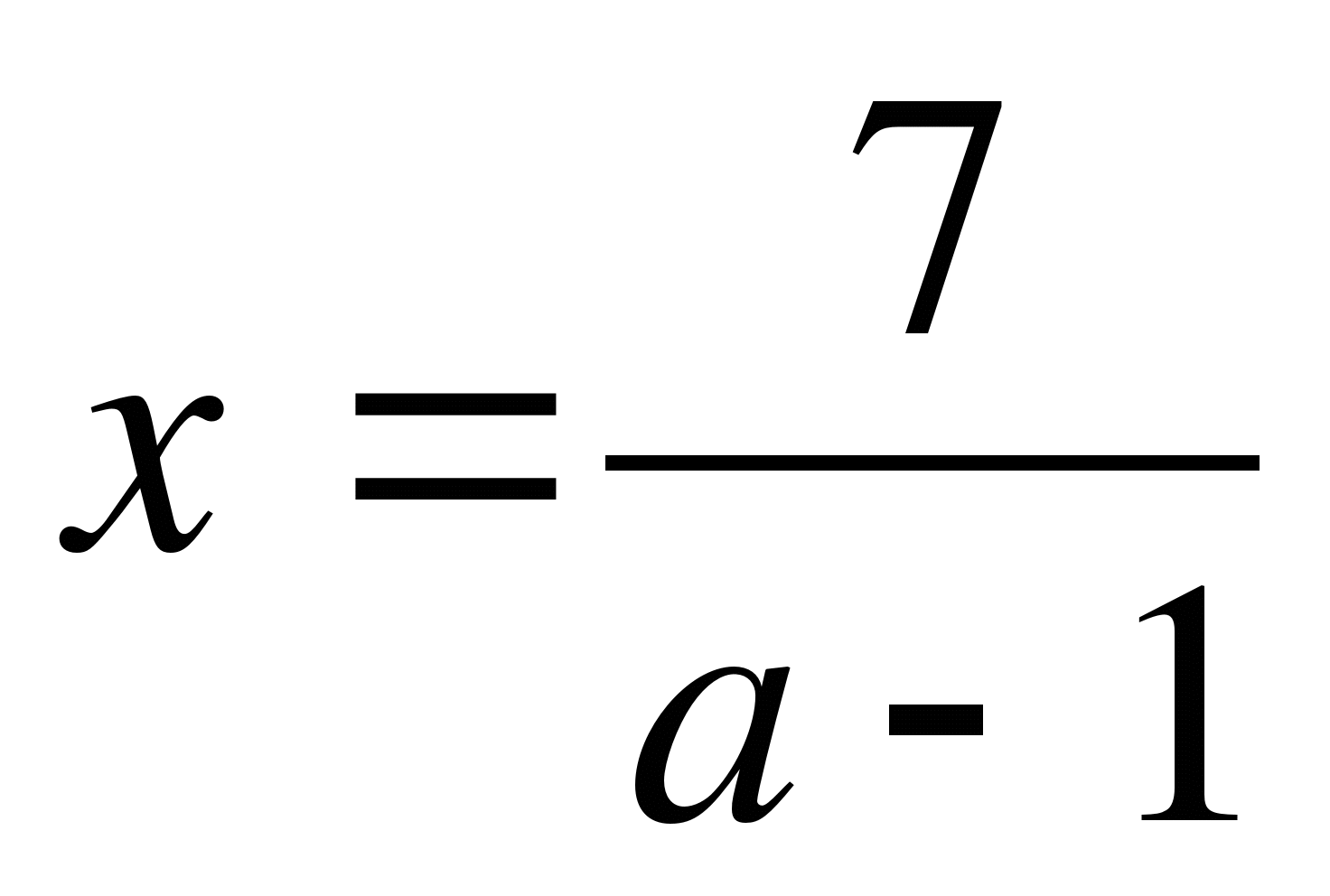 при а≠ ±1 (е).
при а≠ ±1 (е).
-
Найдите все значения параметра а, при каждом из которых число (-3) является единственным корнем уравнения а2х+6а=4х-12
-
а=-6 (в);
-
а=0; а=2 (в);
-
а=-2; а=4 (д);
-
а=4 (е)
-
-
Найдите все значения параметра а, при каждом из которых уравнения ах+1=2х+а и а2х-1=4х+а2 имеют общий корень.
-
-
-
-
-
а=1;
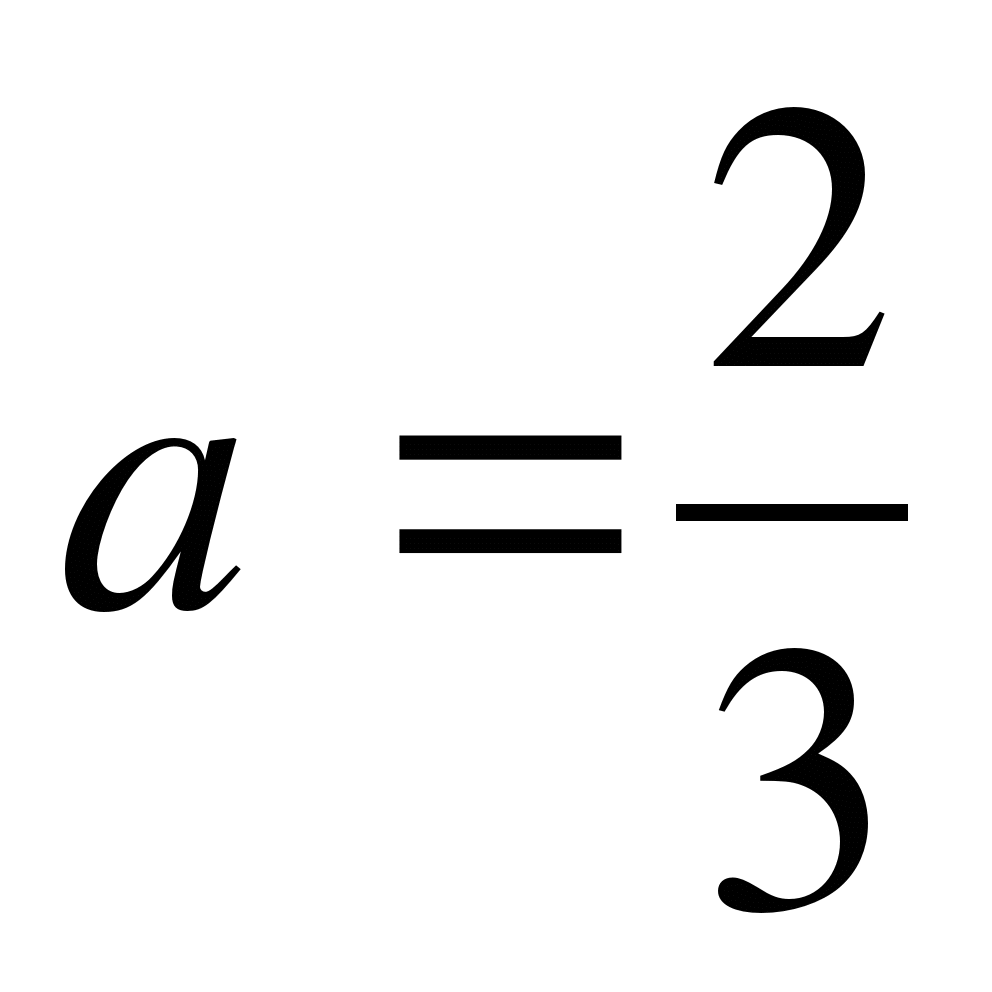 (в)
(в)
-
а=-1;
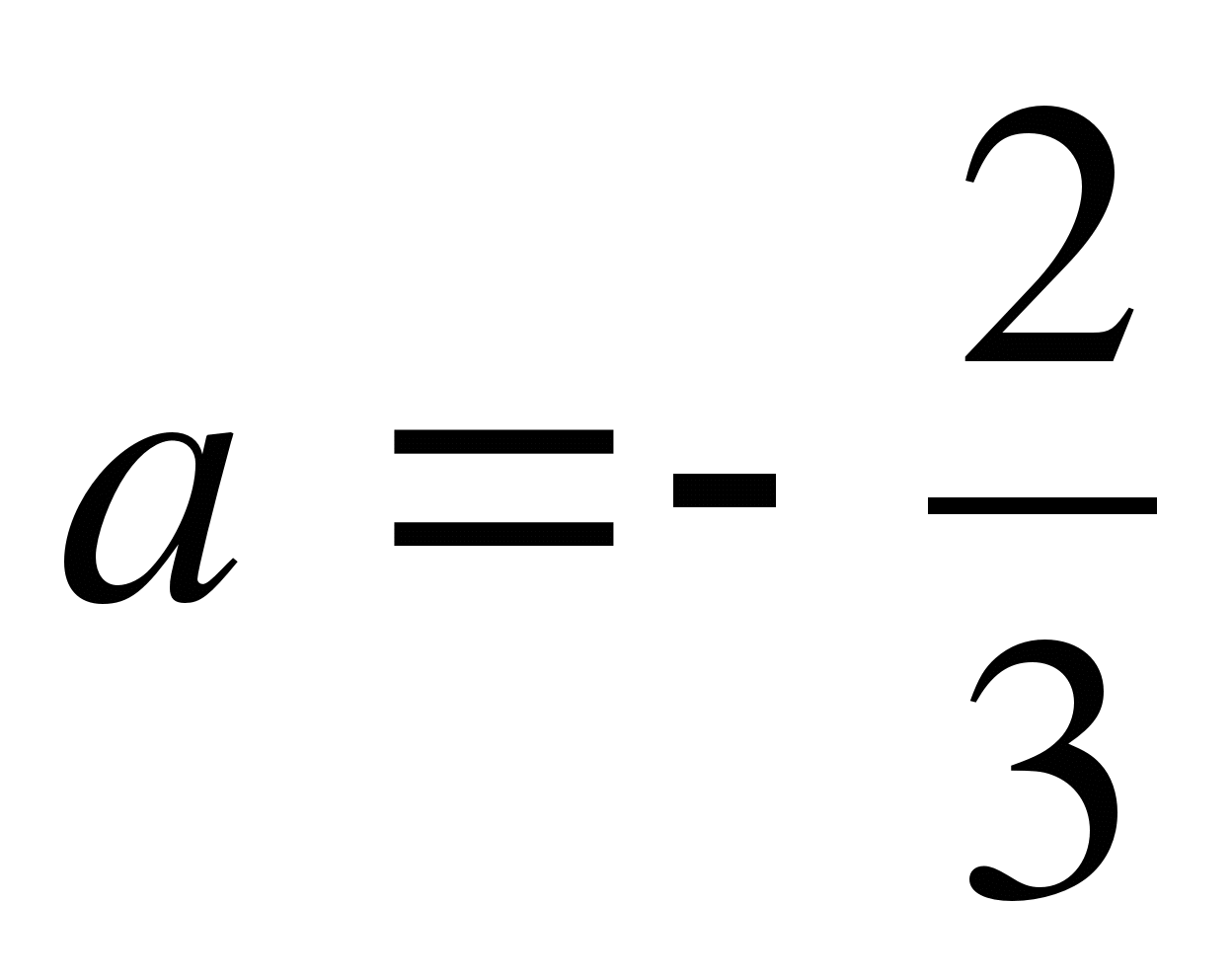 (в)
(в)
-
а=-1; а=6 (в)
-
а=3 (ж)
Команды:
а) Рассмотрите случай, когда коэффициент А в уравнении вида Ах=В равен нулю.
б) Укажите все случаи, когда коэффициент А в уравнении вида Ах=В не равен нулю;
в) Проверьте правильность переноса слагаемых из одной части уравнения в другую;
г) Проверьте правильность применения распределительного закона;
д) Проверьте, является ли данное число единственным корнем уравнения при каждом найденном значении параметра а.
е) верно, переходите к следующему заданию;
ж) верно, подготовка к самостоятельной работе закончена.
III. Этап рефлексии.
-
Какие трудности вы испытали при решении заданий
-
Как вы их преодолевали?
-
Оцените свою работу.
IV. По усмотрению учителя может быть проведена домашняя самостоятельная работа, два варианта которой прилагаются. Номера ответов, которые считаются правильным, ученики вписывают в специальную таблицу в правом верхнем углу тетради, например, так:
Такая же таблица имеется у учителя - см. «Вкладыш для учителя». (Это дает возможность сразу же оценить ученику свою работу). Таблицу с номерами верных ответов учитель записывает на доске. К следующему занятию.
Самостоятельная работа по теме «Линейные уравнения с параметрами» (тест)
Вариант I
-
При каждом значении параметра а решите уравнение ах-6=4а-7х
-
-
Нет корней при а=-7;
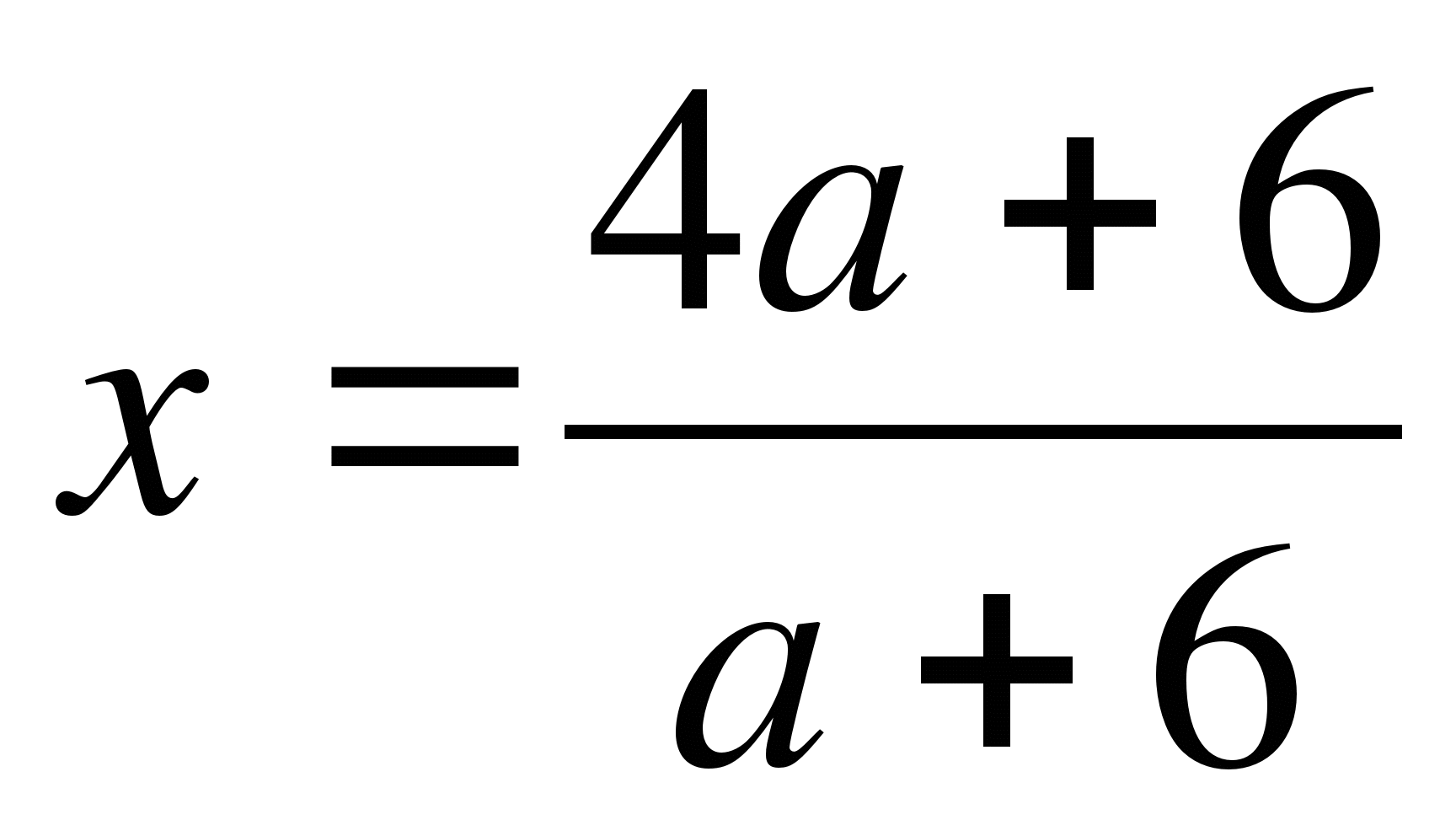 при а≠-7.
при а≠-7.
-
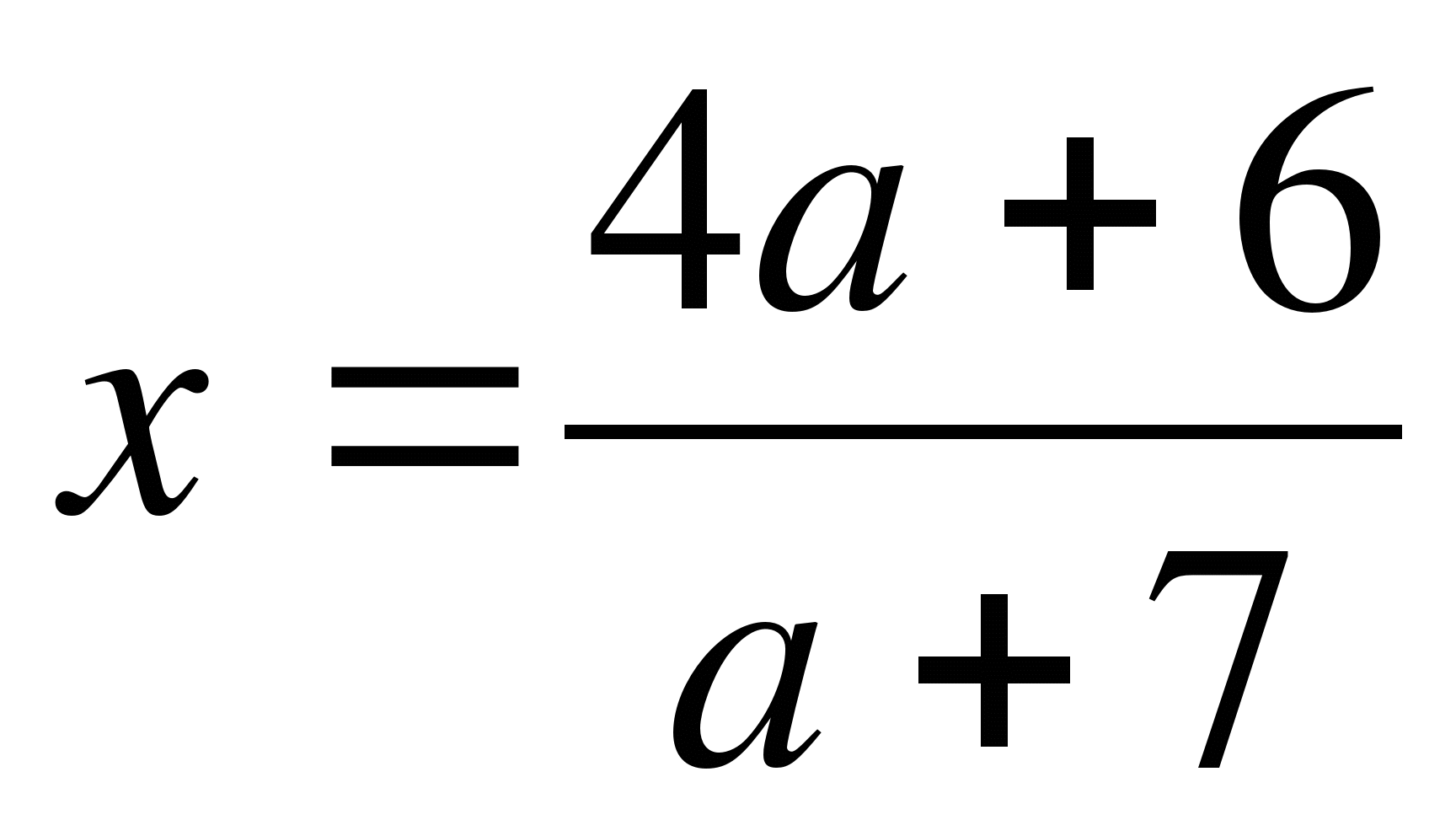 ;
;
-
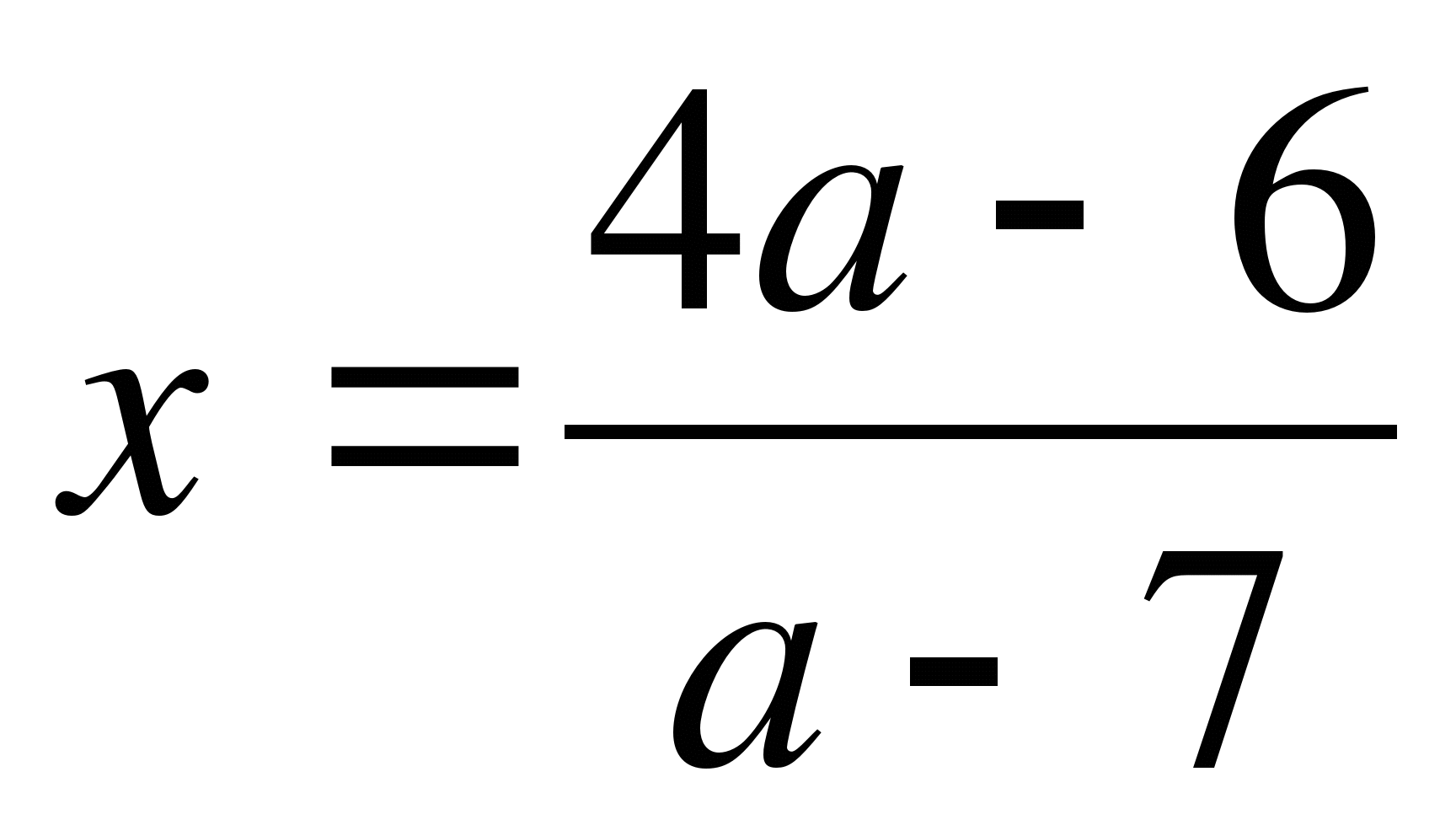 ;
;
-
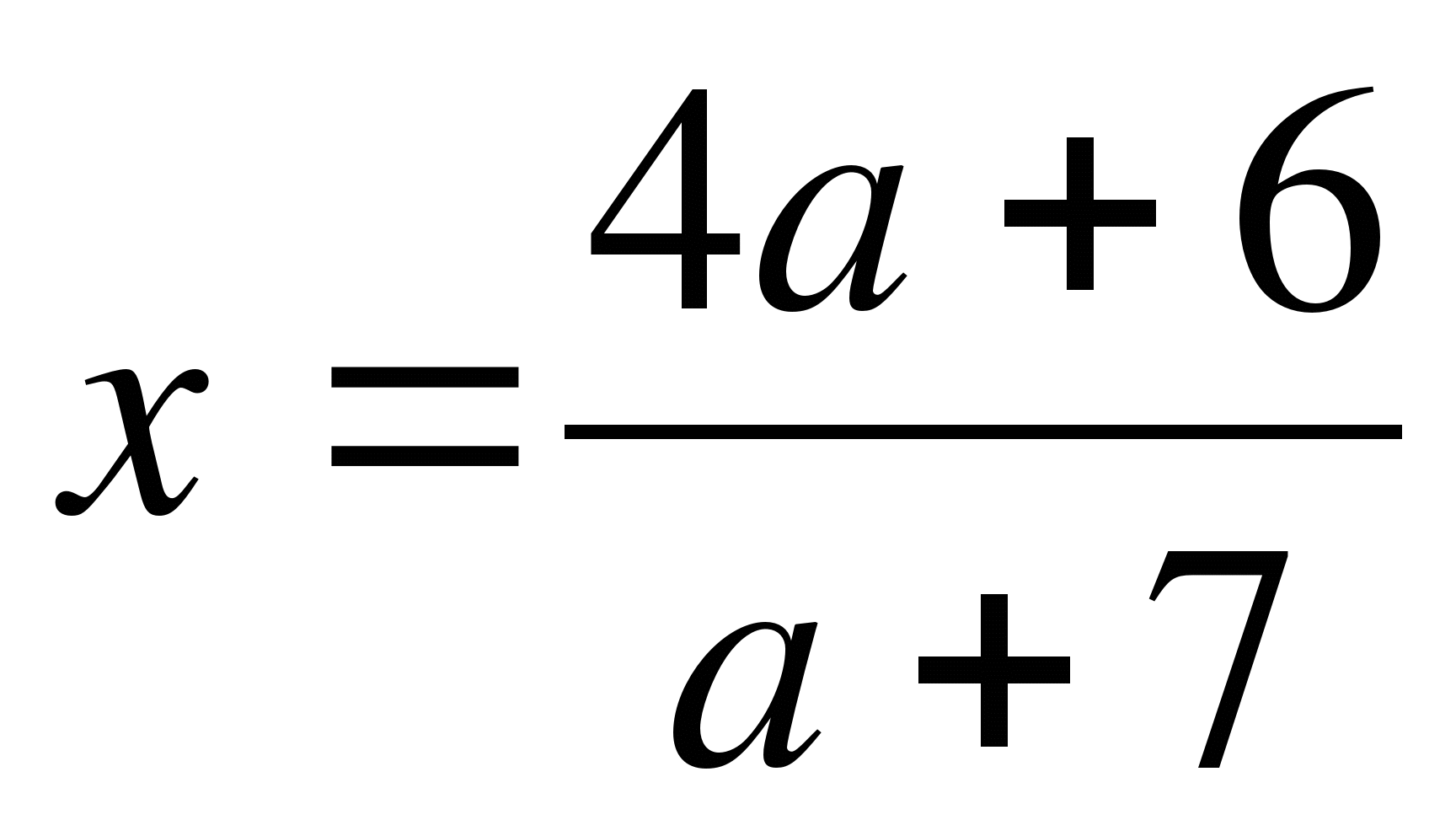 при а≠-7;
при а≠-7;
-
Нет корней при а=7.
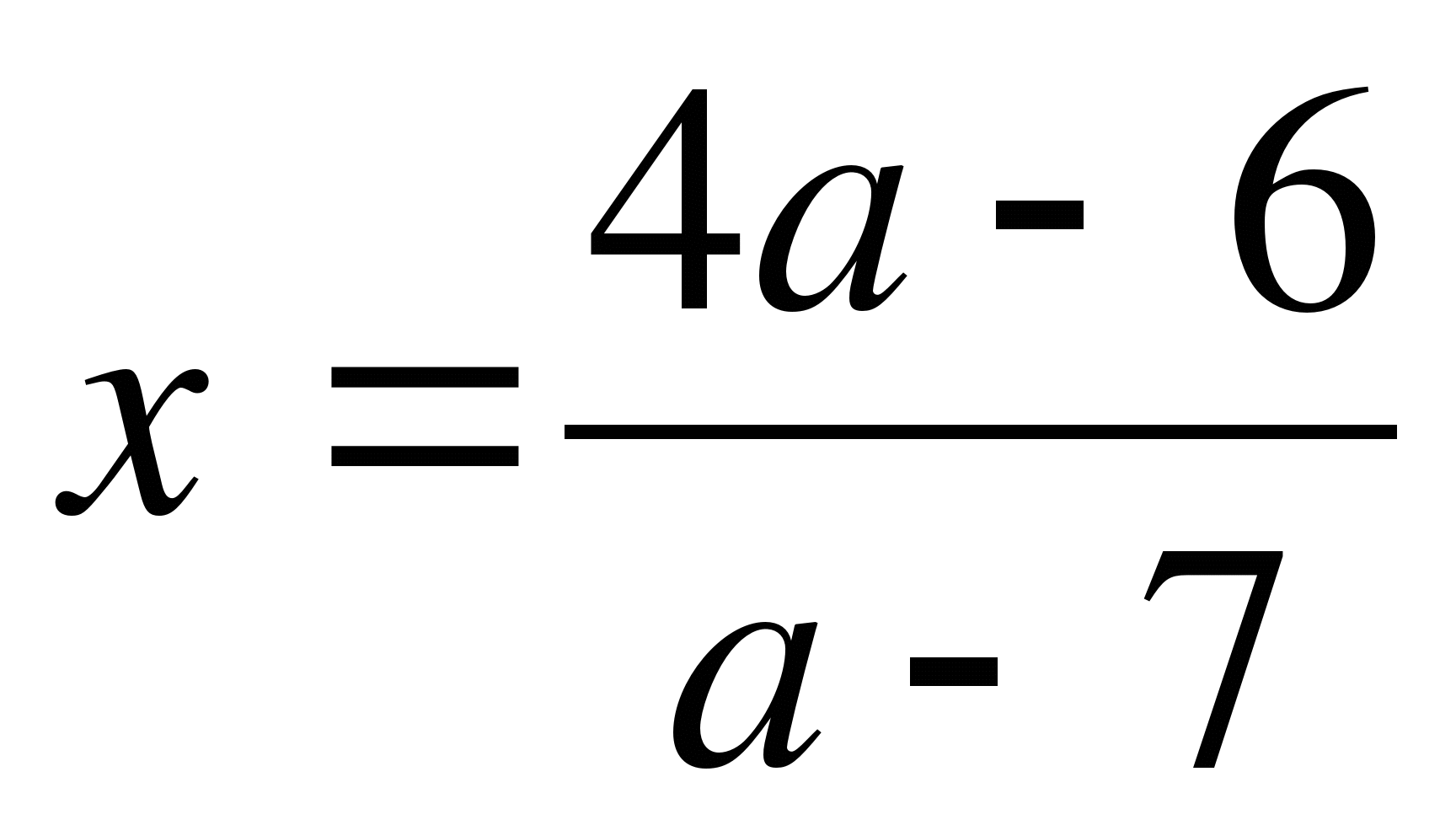 при
а≠-7.
при
а≠-7.
-
-
При каждом значении параметра а решите уравнение ах2-6=3а+4х
-
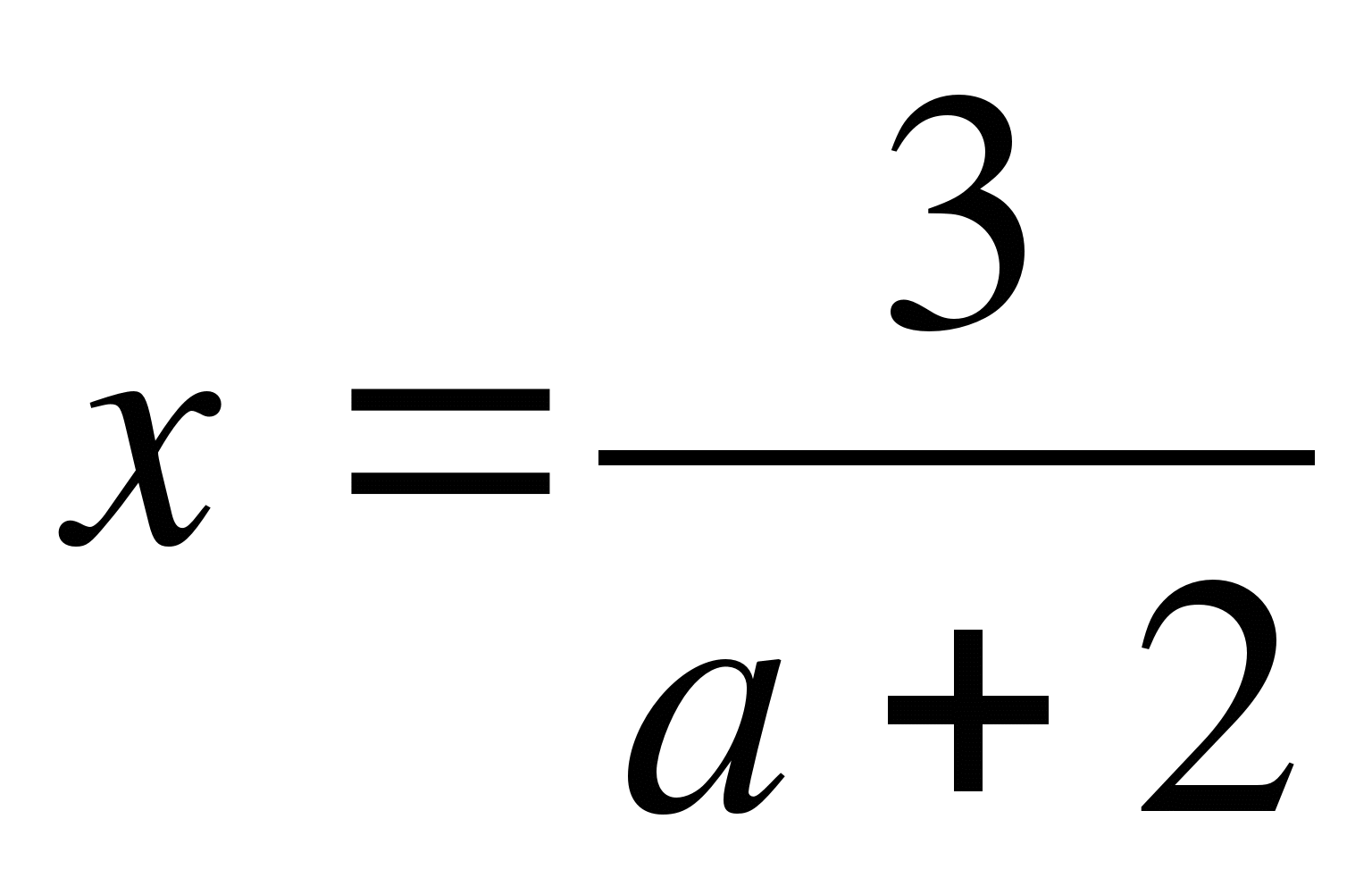 ;
;
-
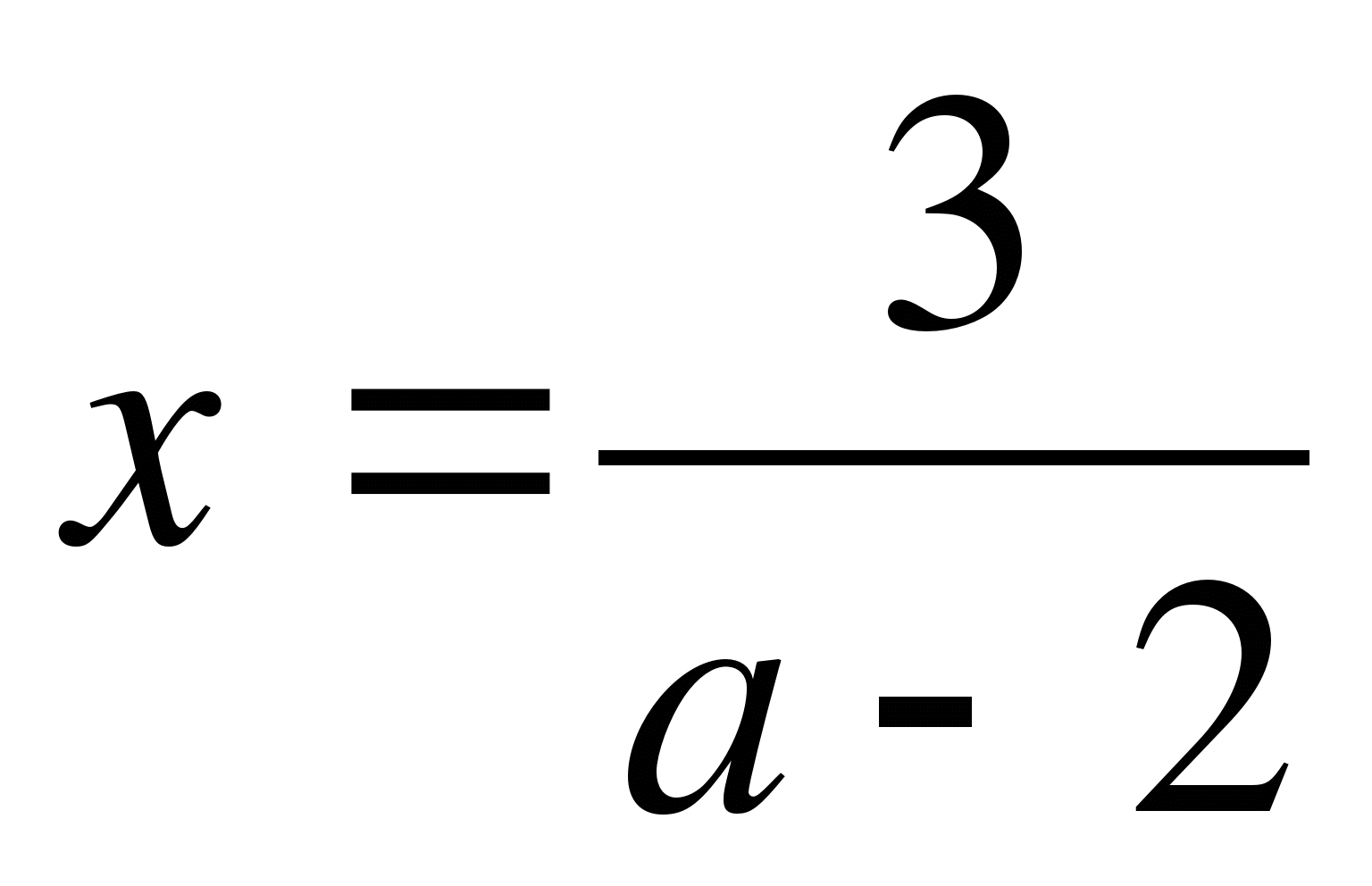 ;
;
-
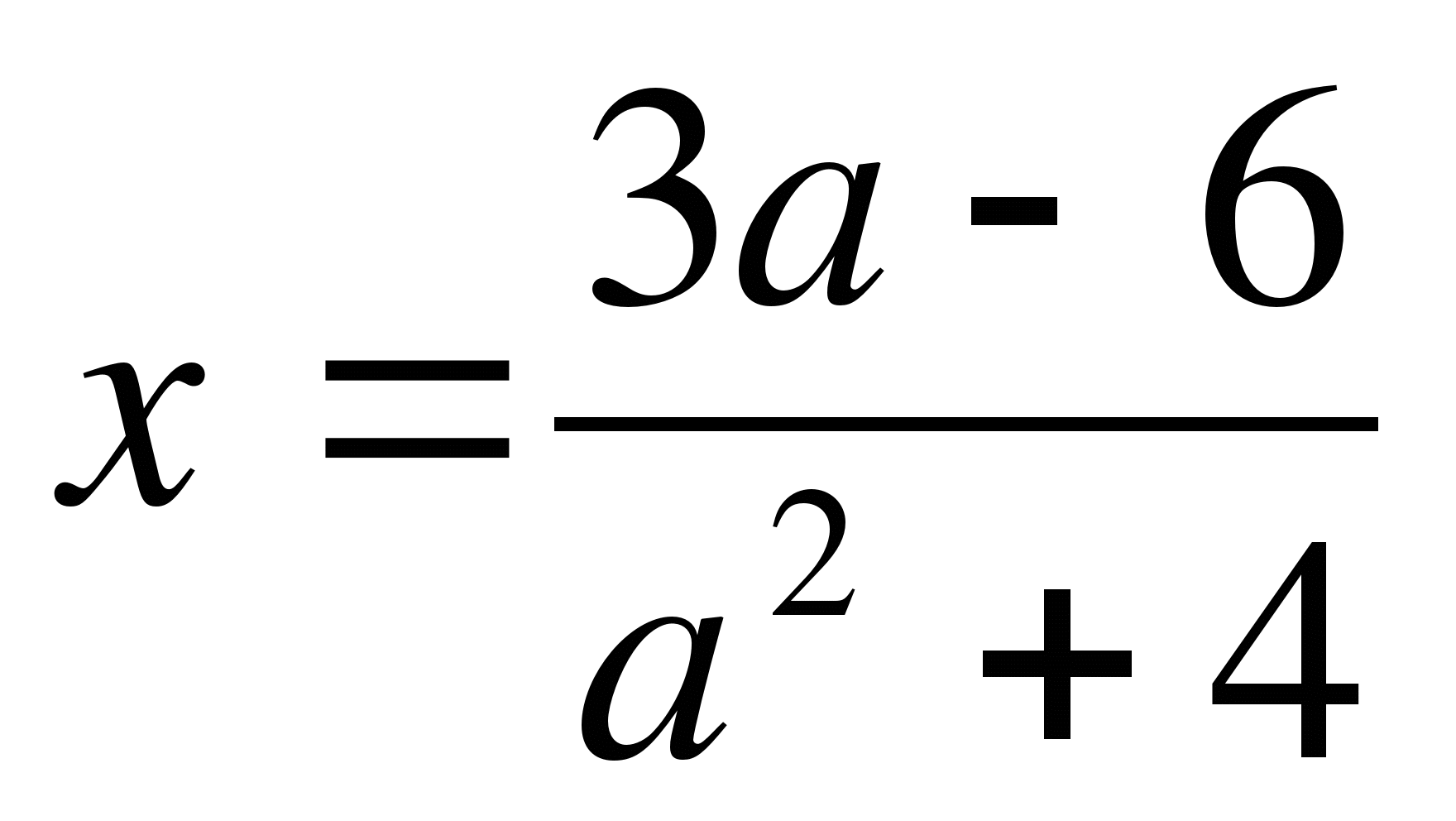 ;
;
-
Нет корней при а=2;
 при а=-2;
при а=-2; 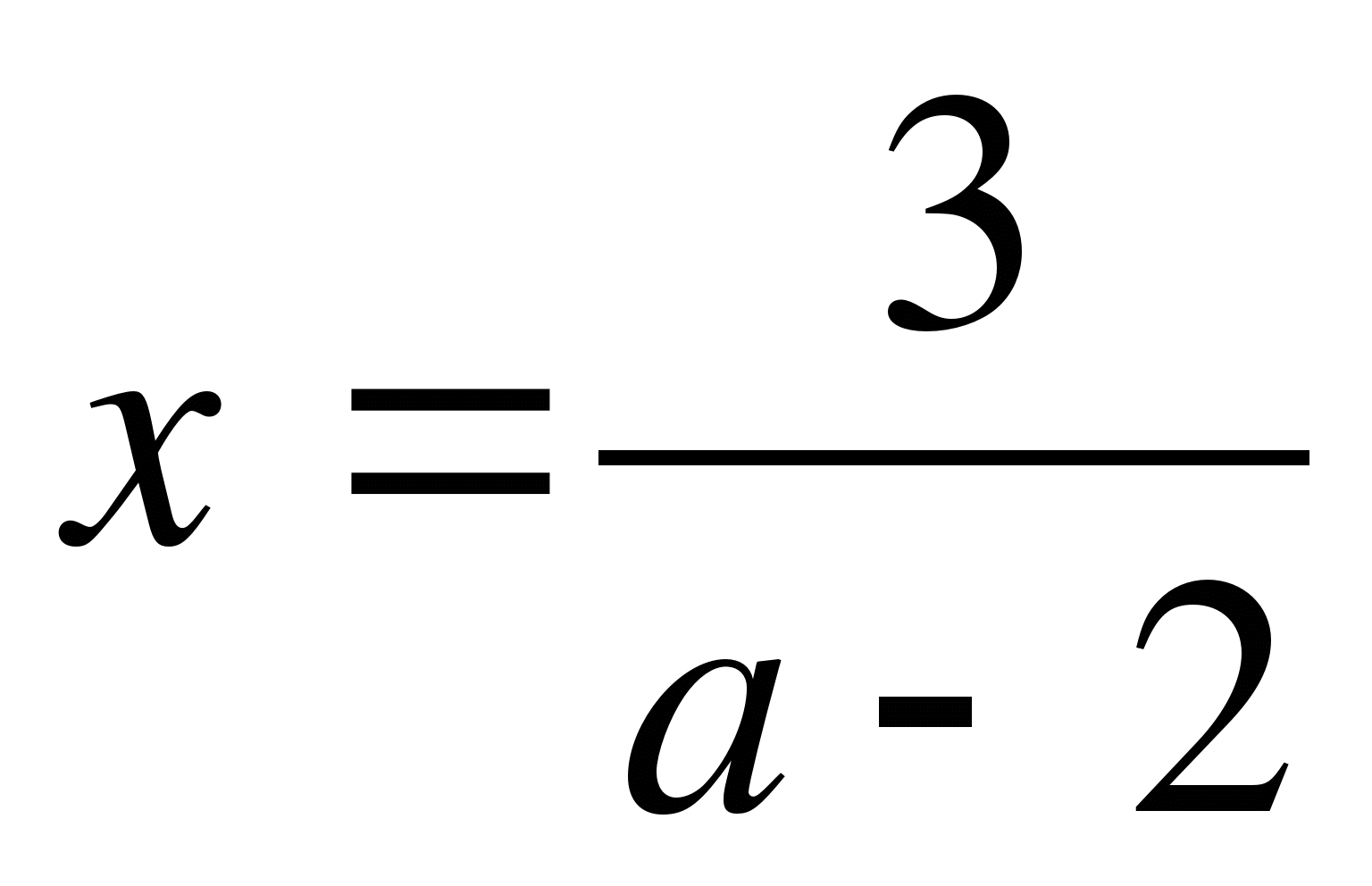 при а ≠±2;
при а ≠±2;
-
Нет корней при а=-2;
 при а=2;
при а=2; 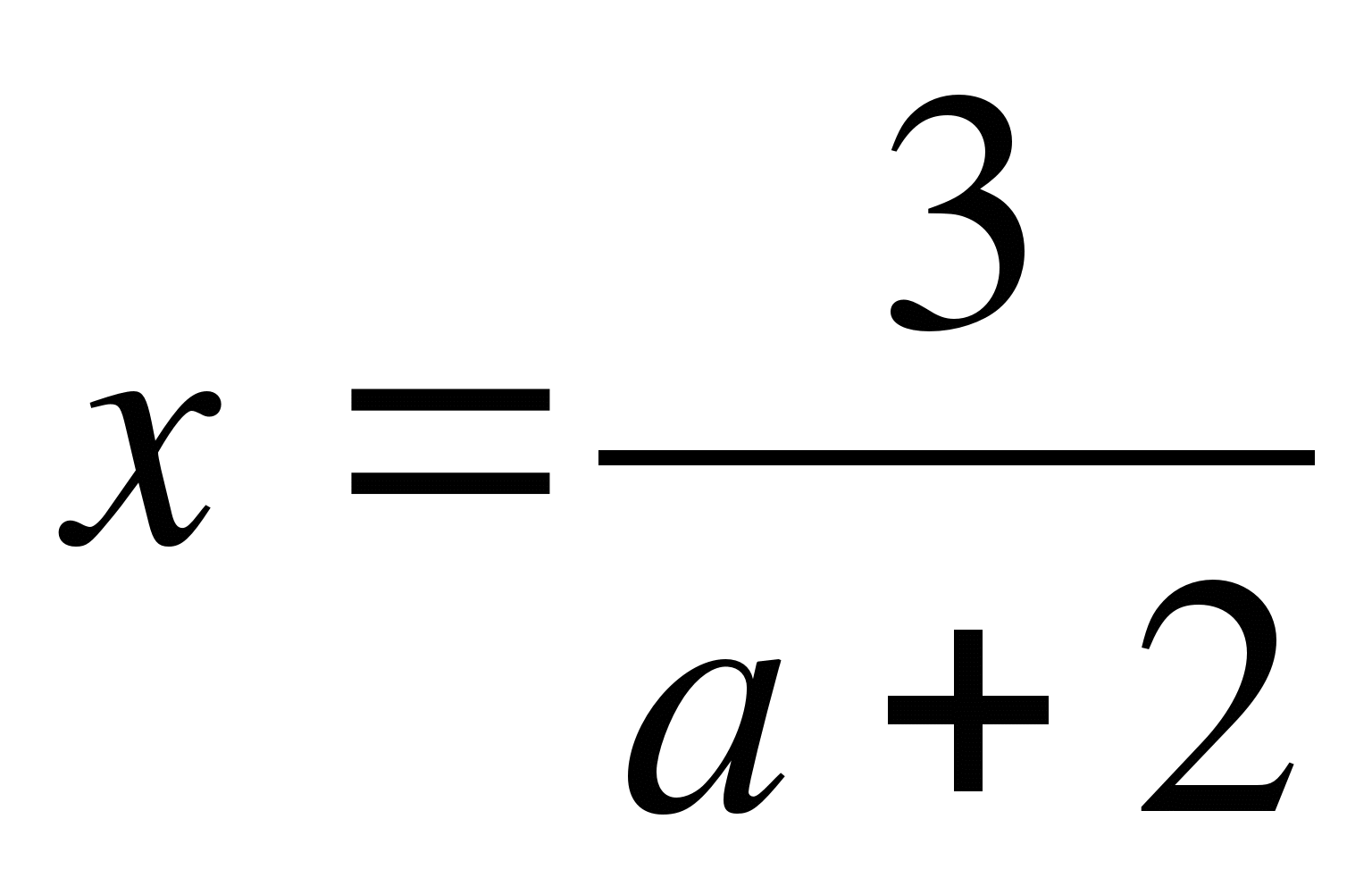 при
а ≠±2;
при
а ≠±2;
-
-
Найдите все значения параметра а при каждом из которых число 5 является единственным корнем уравнения ах-5а=10-2х;
-
-
 ,
а≠-2;
,
а≠-2;
-
а=-2
-
а=4;
-

-
а=1.
-
-
Найдите все значения параметра а при каждом из которых уравнения ах=х-2 и х+а=2-ах имеют общий корень.
-
а=0;
-
а=4;
-
а=5;
-
а=1; а=-4;
-
а=0; а=5.
-
Вариант II
-
При каждом значении параметра а решите уравнение 2ах-3=5а-4х.
-
-
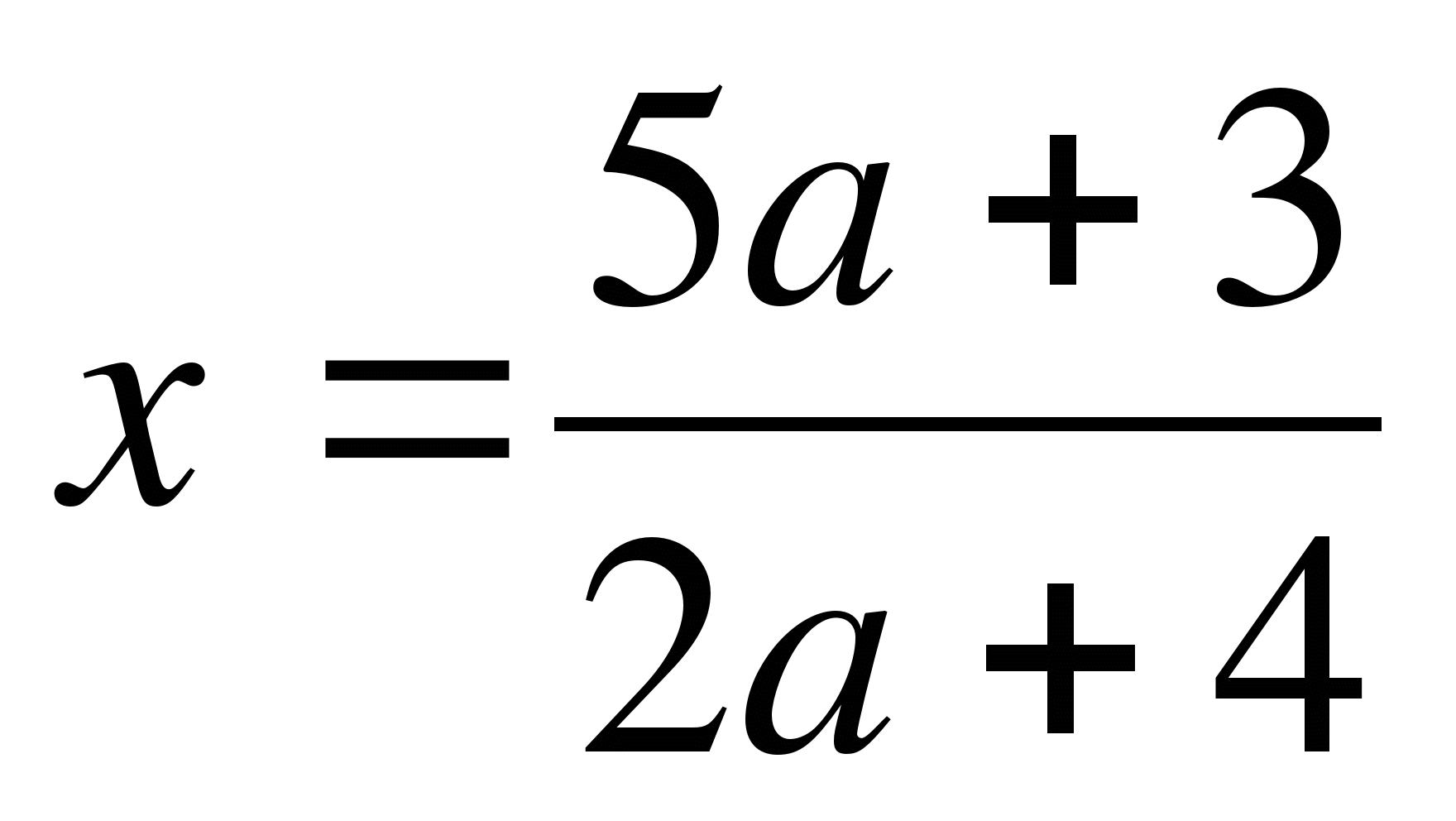 ;
;
-
Нет корней при а=-2;
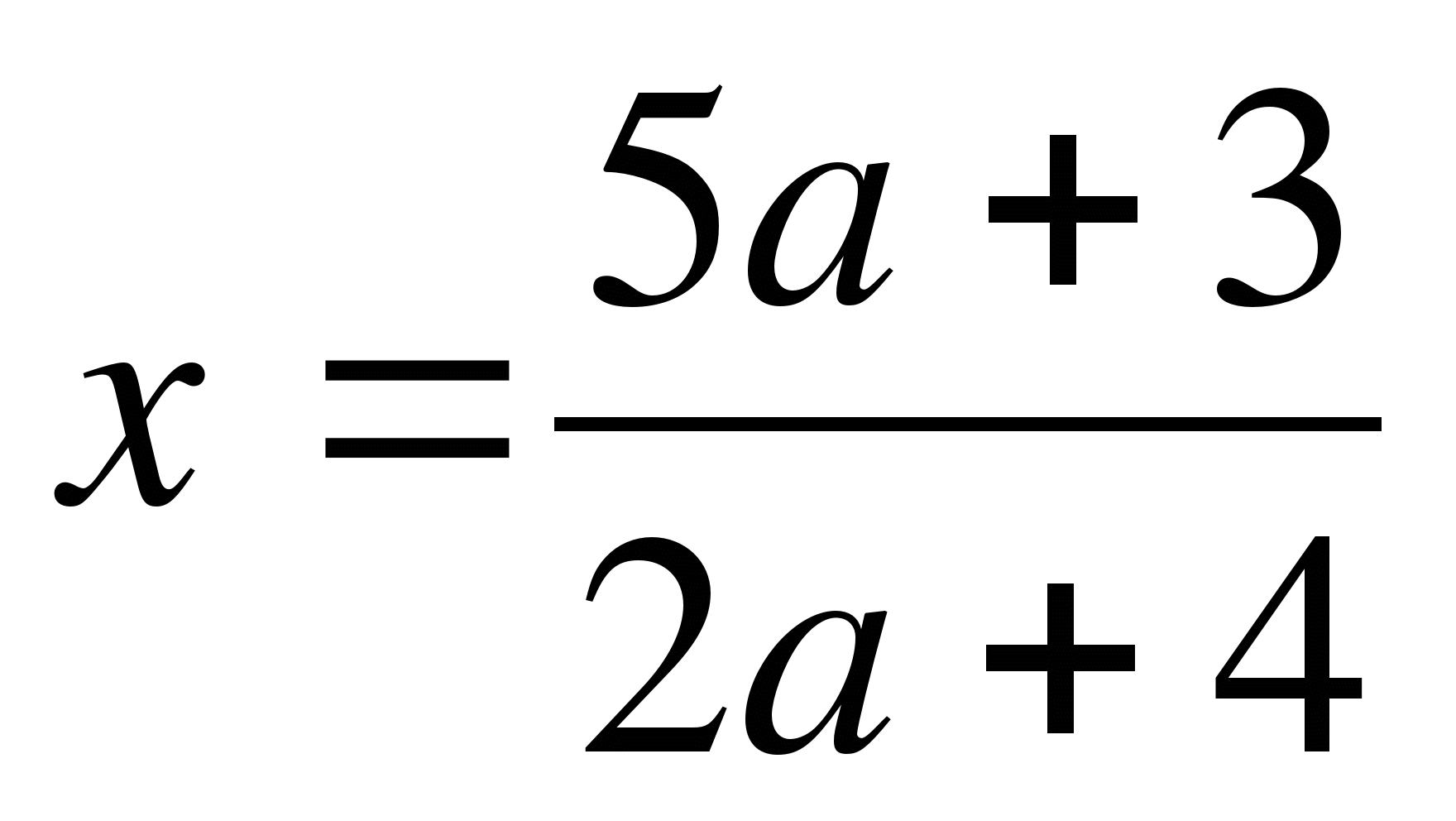 при
а≠-2;
при
а≠-2;
-
Нет корней при а=2;
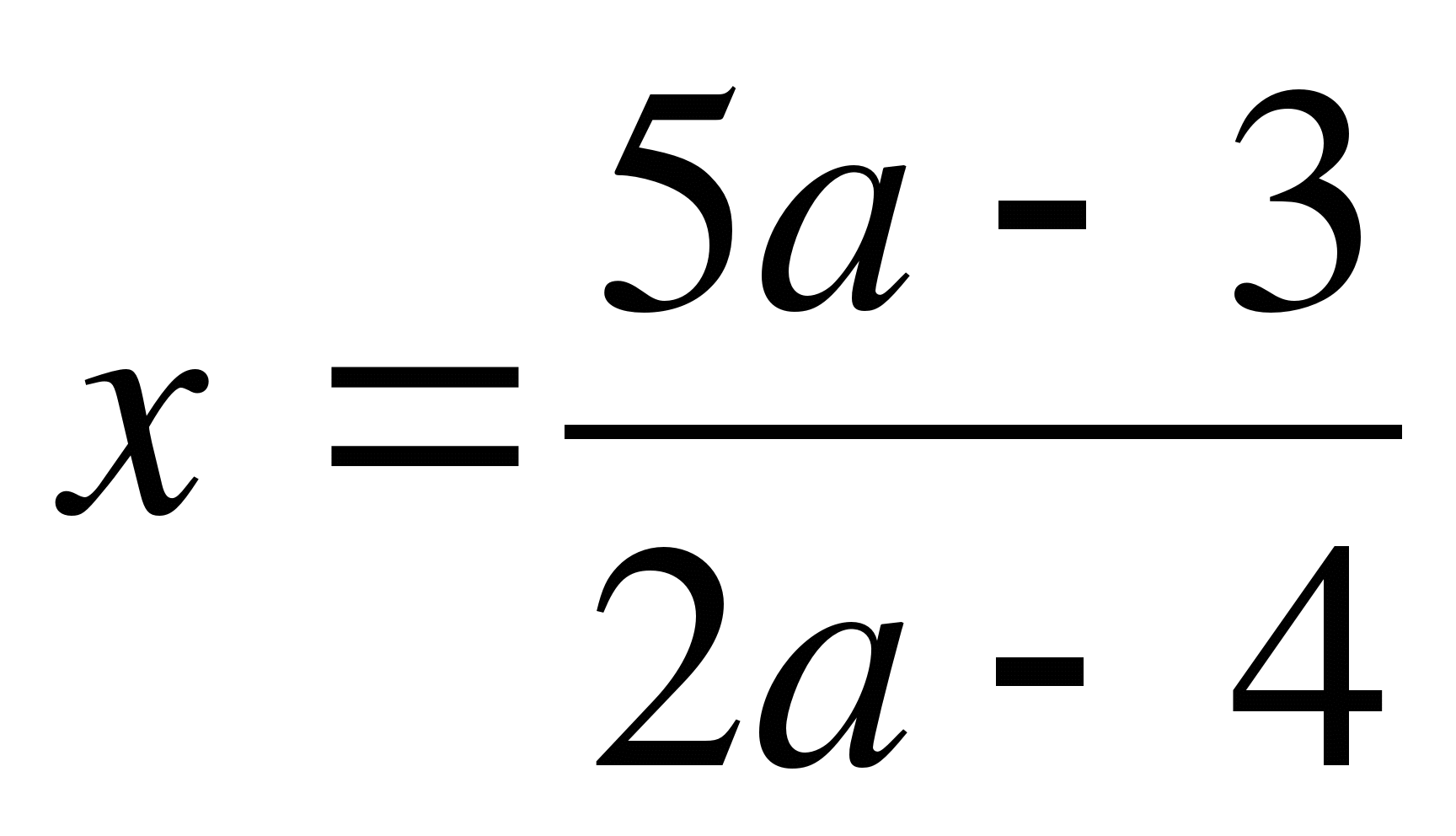 при а≠2;
при а≠2;
-
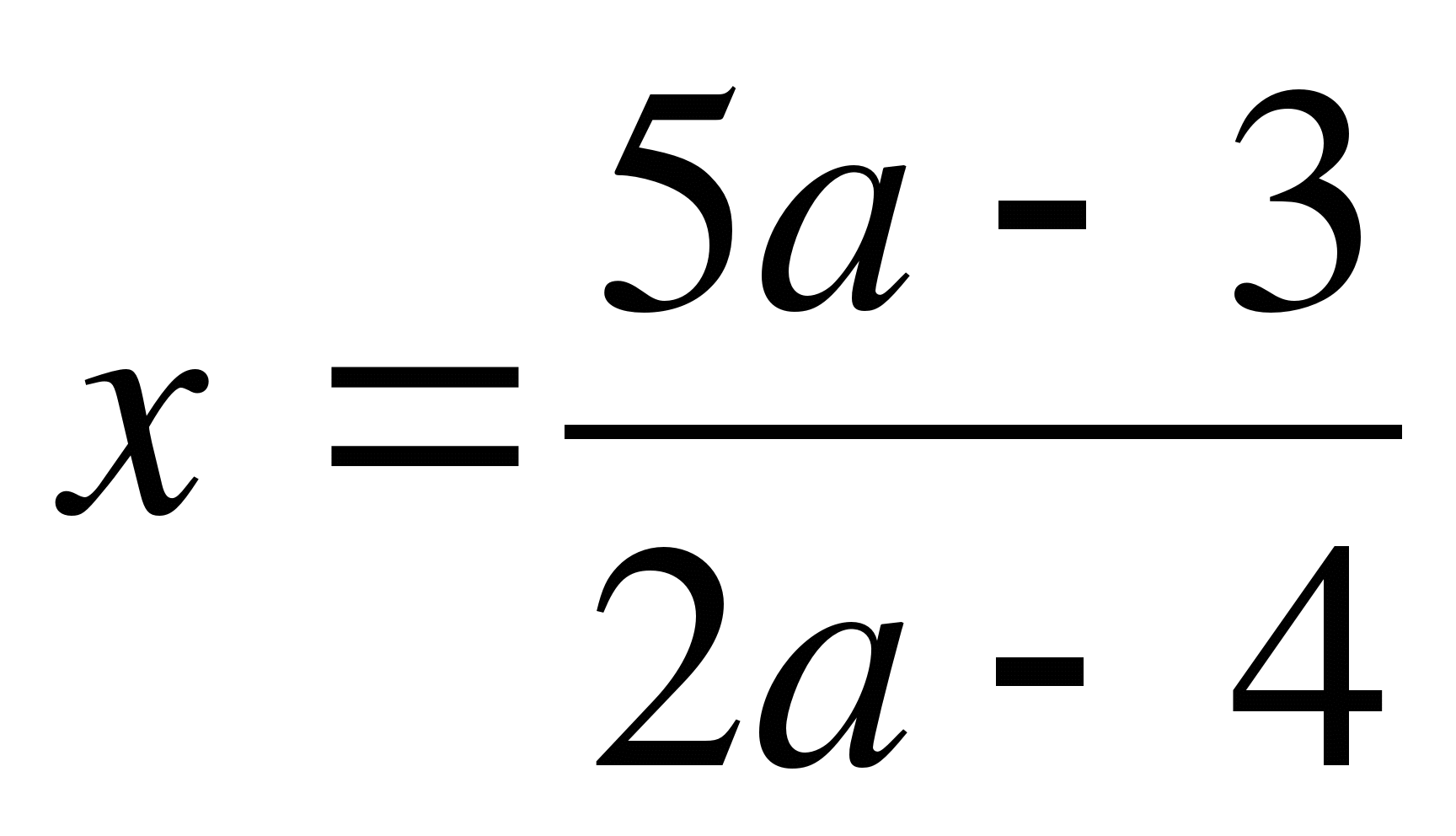 ;
;
-
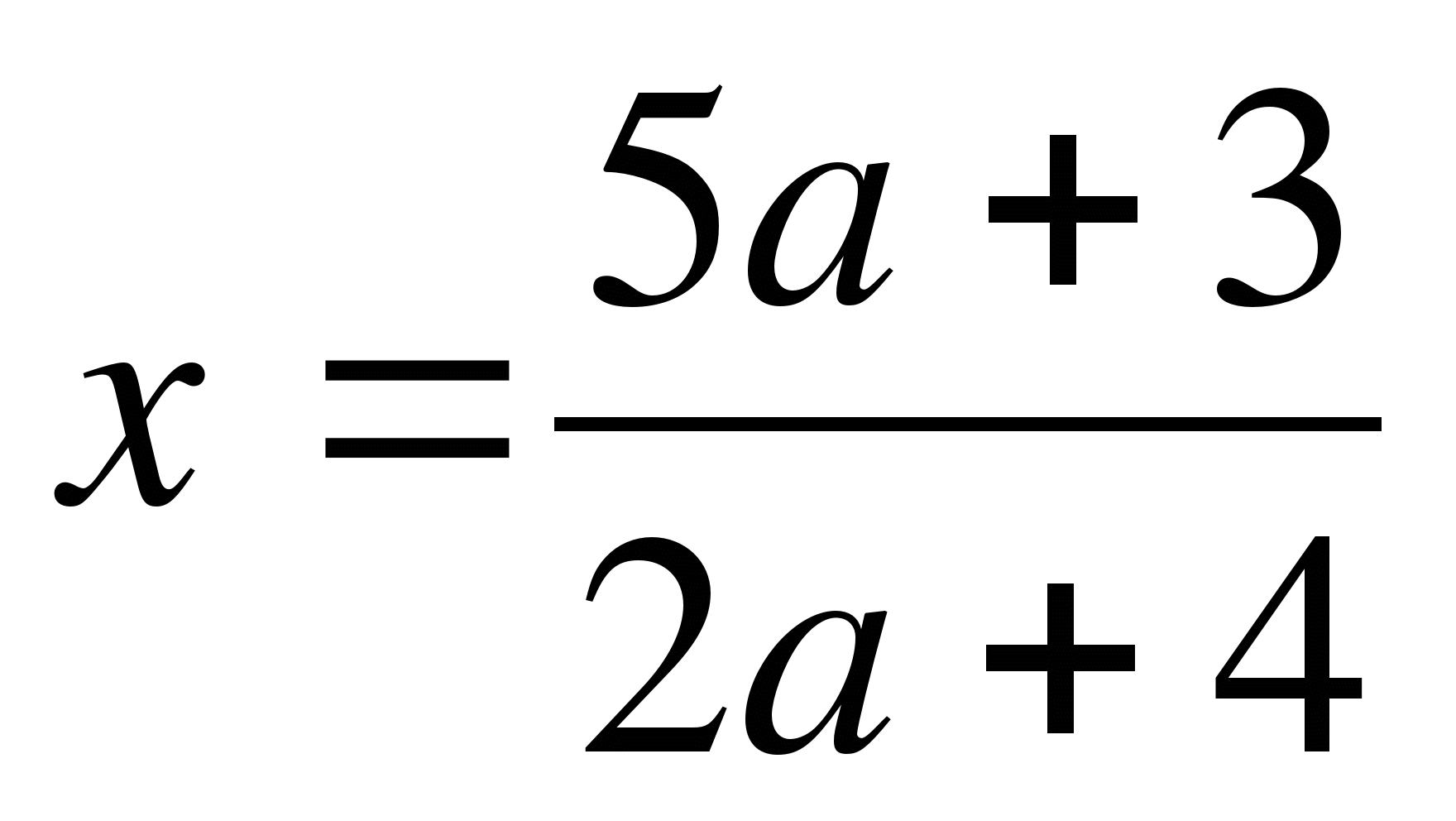 при а≠-2.
при а≠-2.
-
-
При каждом значении параметра а решите уравнение а2х-2а=4(х-1)
-
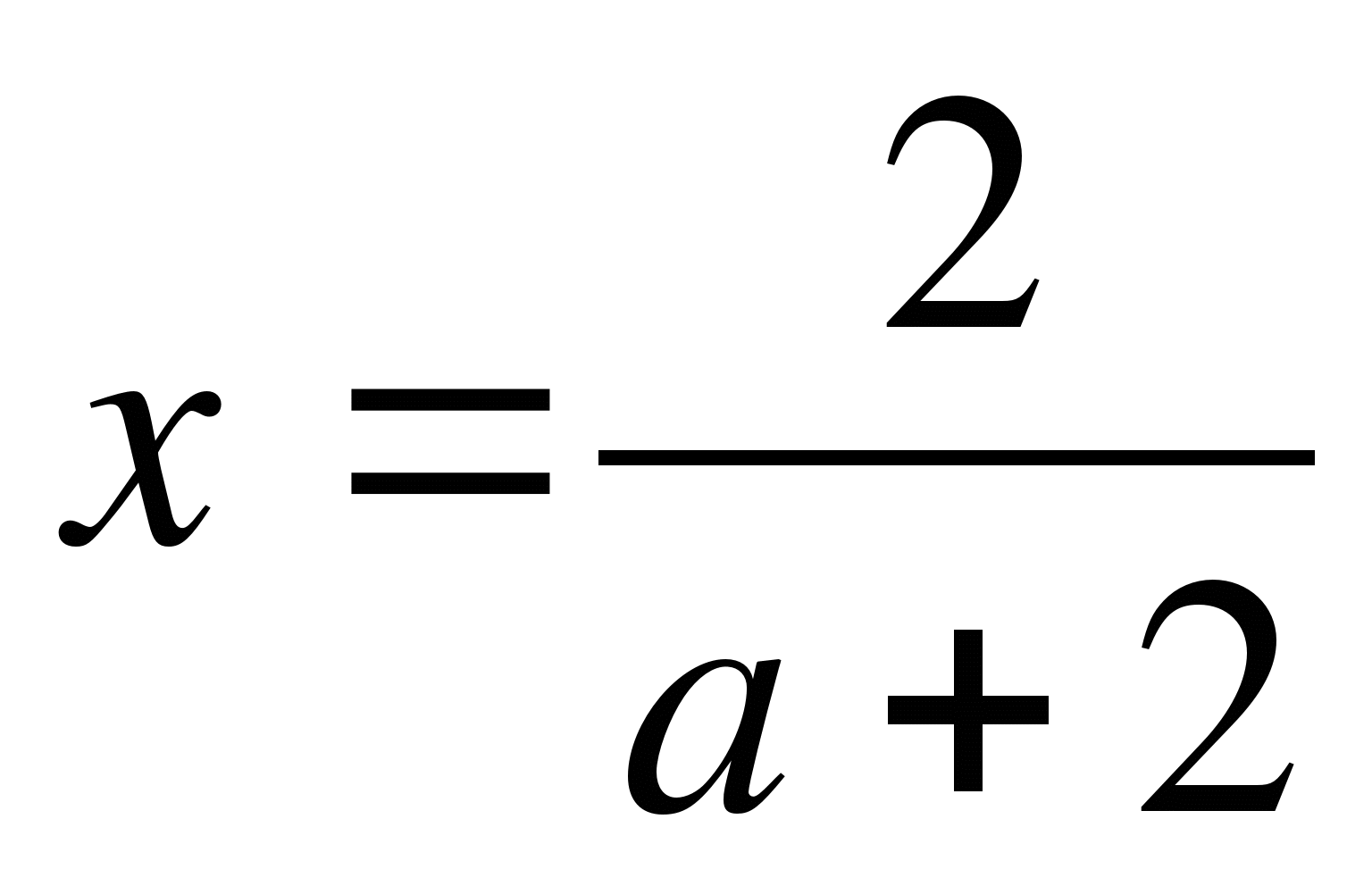 ;
;
-
Нет корней при а=-2;
 при
а=2.
при
а=2. 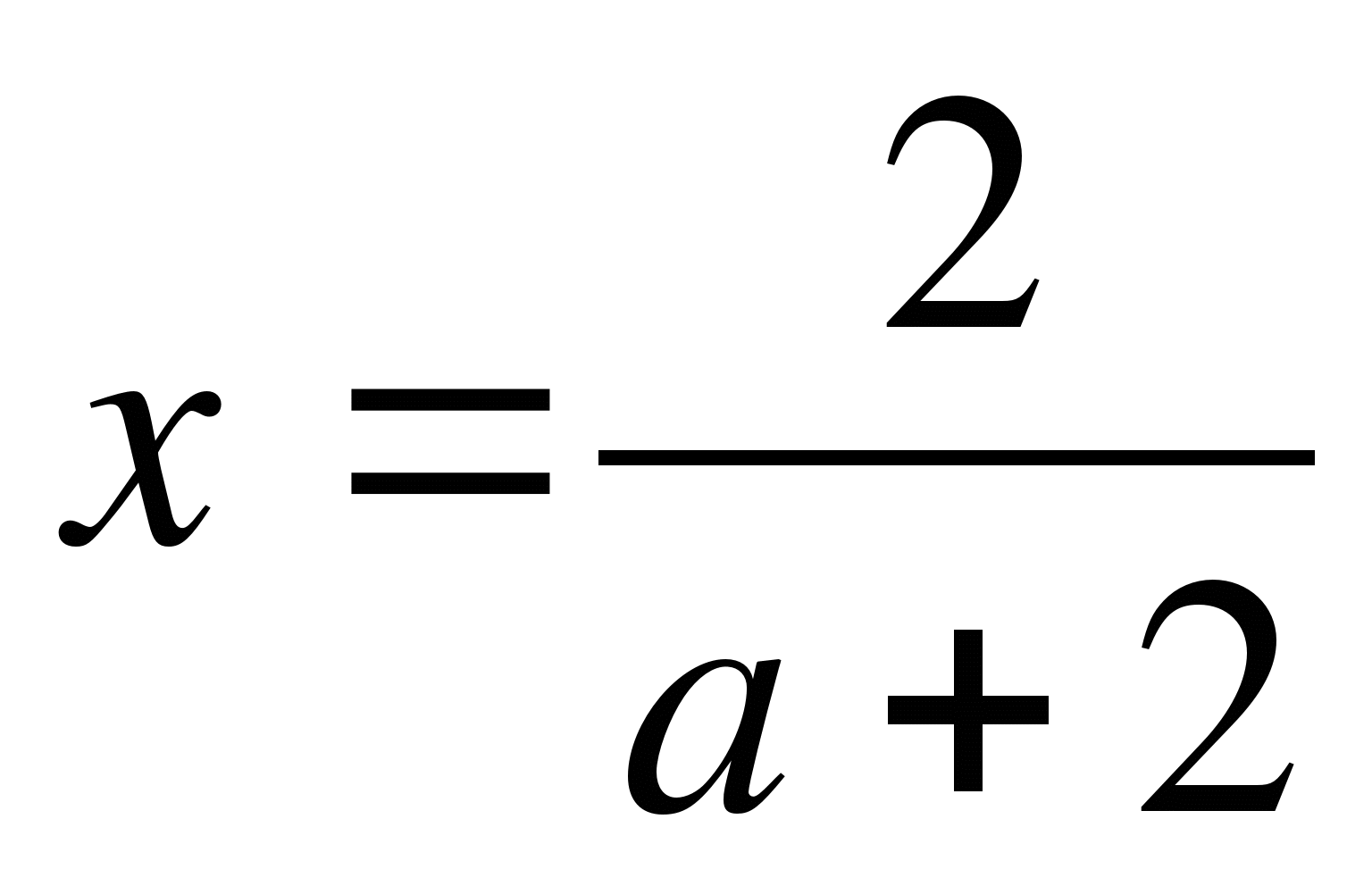 при
а≠-2
при
а≠-2
-
Нет корней при а=2;
 при
а=-2,
при
а=-2, 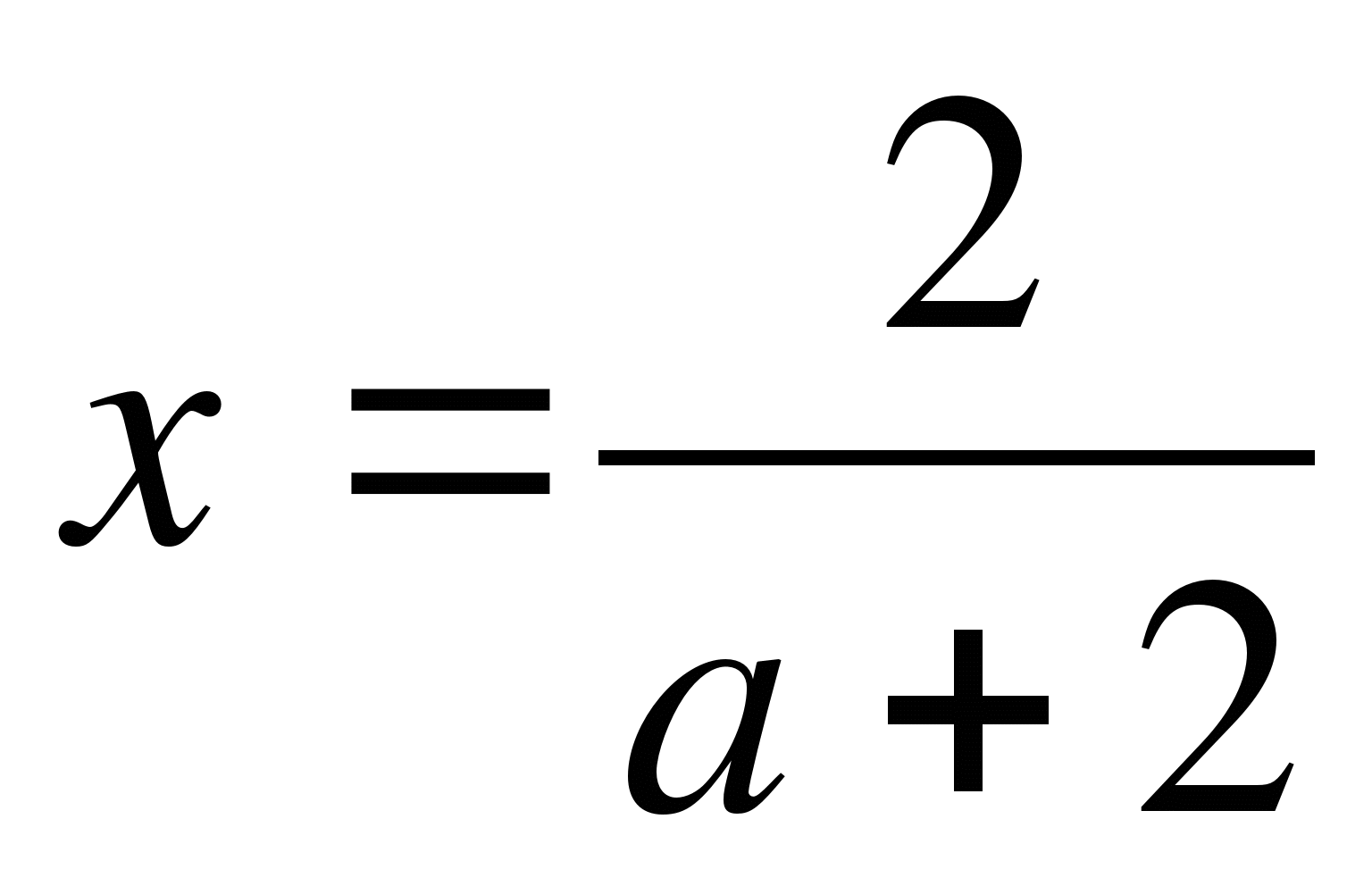 при а≠±2.
при а≠±2.
-
Нет корней при а≠±2;
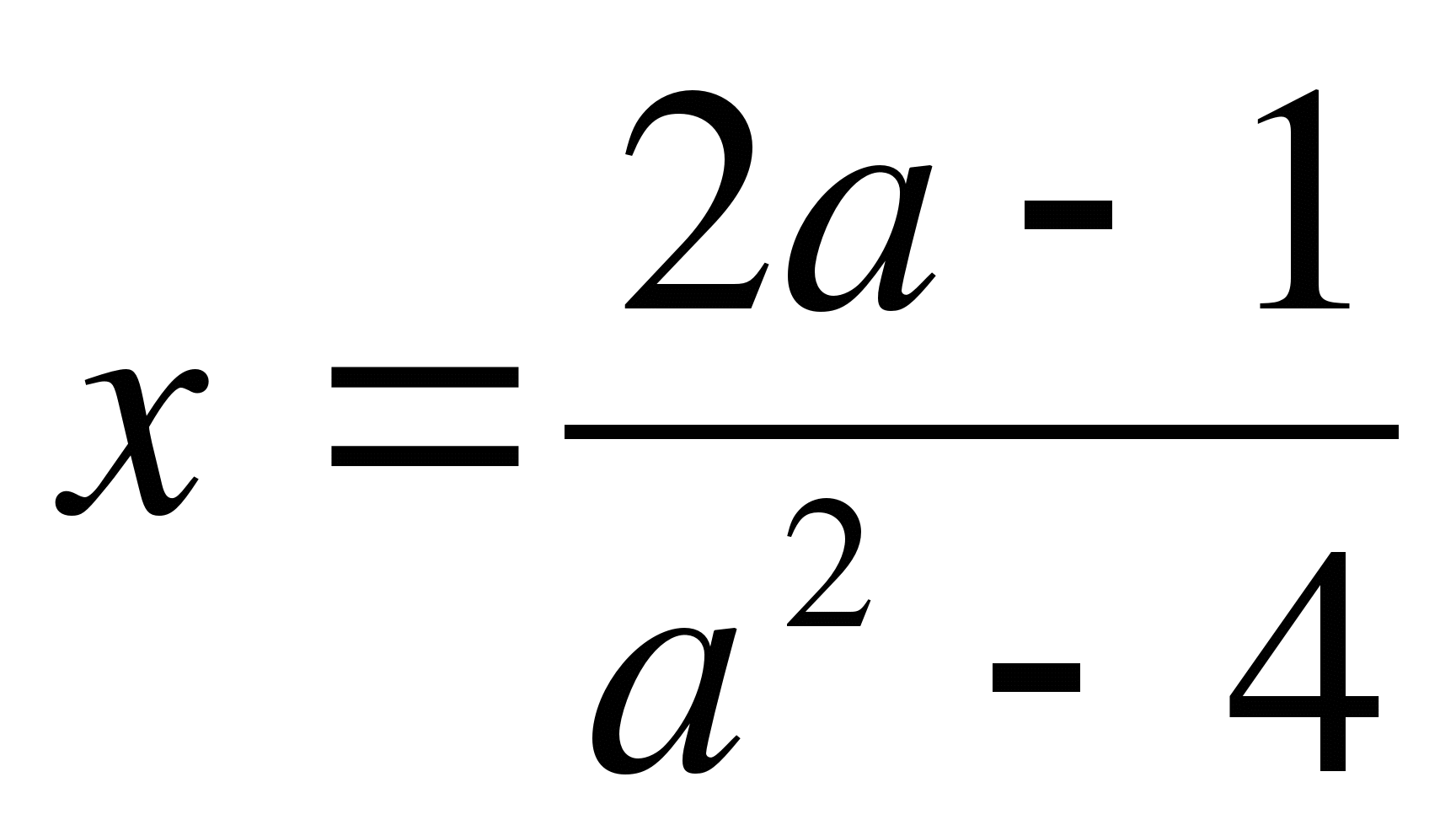 при
а≠±2.
при
а≠±2.
-
Нет корней при а=-2;
 при
а=2;
при
а=2; 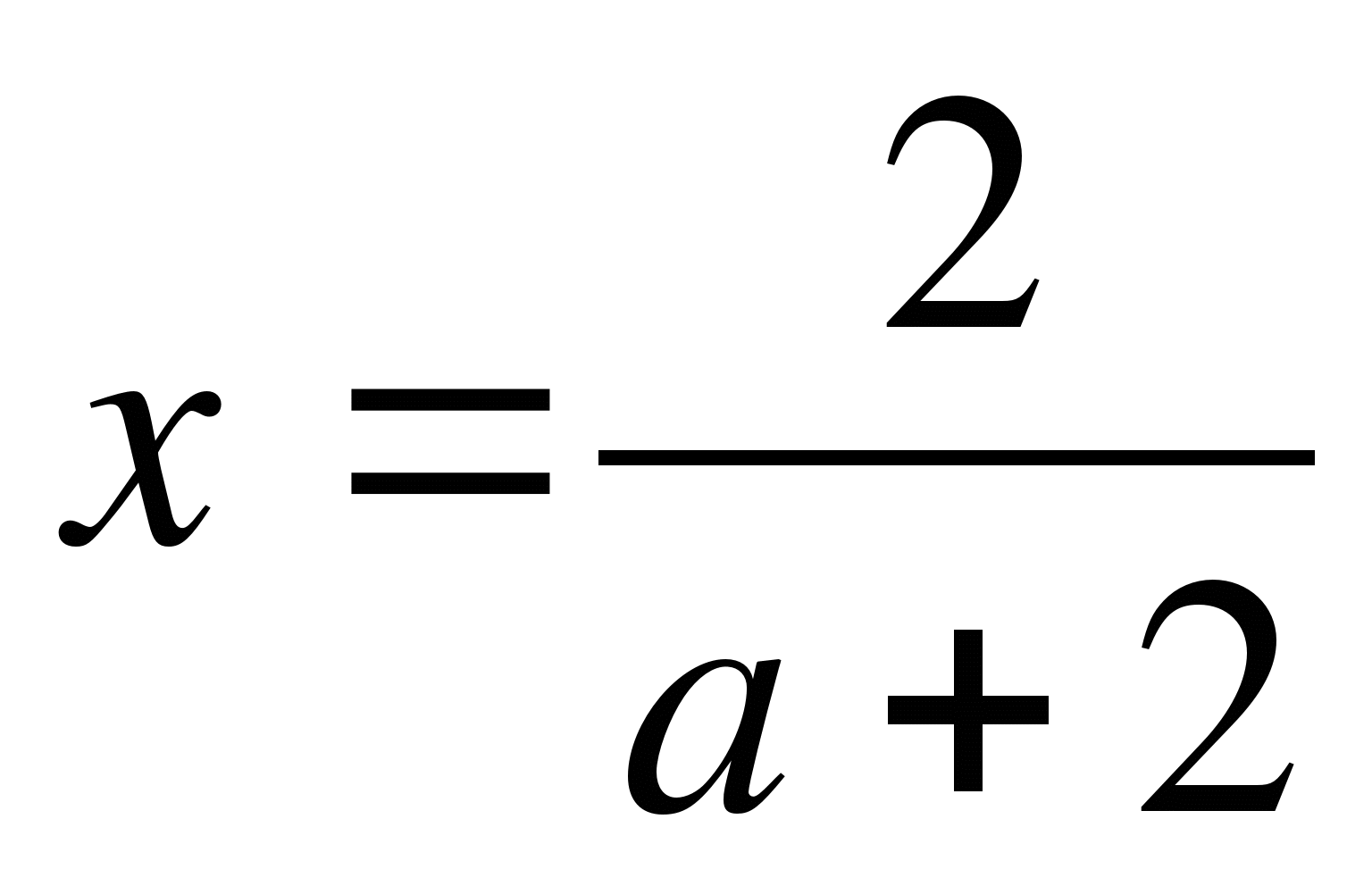 при
а≠±2.
при
а≠±2.
-
Найдите все значения параметра а, при при каждом из которых число -3 является единственным корнем уравнения ах+3а=-3-х;
-
-
а - любое число, а≠-1;
-
а - любое число.
-
а=3.
-
а=2.
-
а=1.
-
-
Найдите все значения параметра а при каждом из которых уравнения ах=2-х и ах+2=х-а имеют общий корень.
-
а=0; а=3;
-
а=1; а=-4;
-
а=0;
-
а=-5;
-
а=0; а=-5.
-
-
Вкладыш для учителя
Ответы к самостоятельной работе.
Блок II. Тема 4. Системы линейных уравнений с параметром.
Занятия 1-2.
Цели занятия:
- знать условия, когда система линейных уравнений с параметрами имеет единственное решение, бесконечное множество решений, не имеет решений;
- формировать умения определять число решений систем линейных уравнений с параметрами;
- формировать умения при всех значениях параметра решать систему линейных уравнений.
Ход занятия:
I. Этап подготовки учащихся к усвоению знаний.
Пусть дана система линейных уравнений 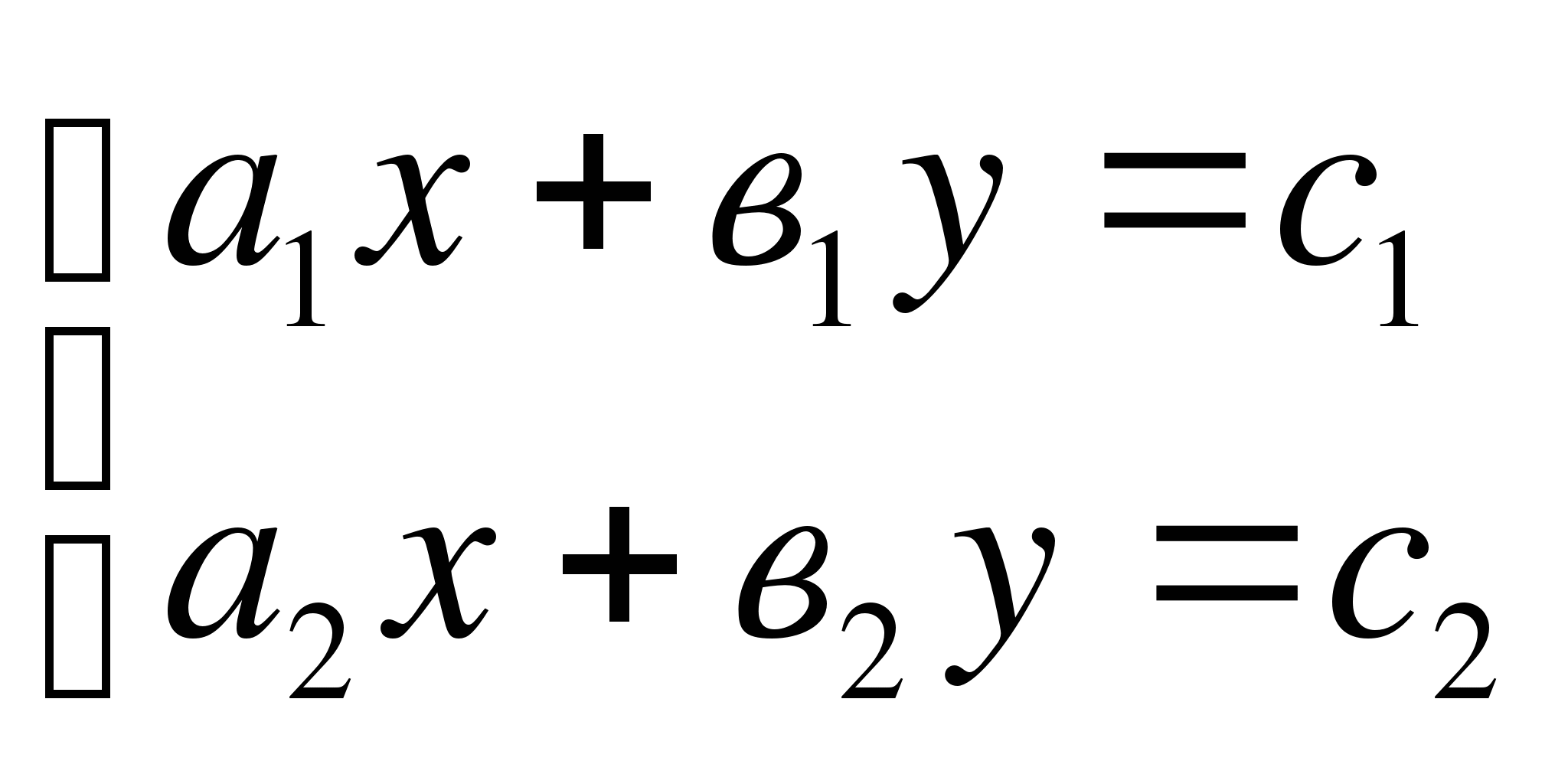 (1).
(1).
В этой системе хотя бы один из коэффициентов ![]() и
и
![]() при х
отличен от нуля, пусть для определенности
при х
отличен от нуля, пусть для определенности ![]() ≠0.
Тогда из второго уравнения системы получим, что х =
≠0.
Тогда из второго уравнения системы получим, что х = ![]() .
Подставив полученное выражение вместо х в первое уравнение системы
и умножив уравнение на
.
Подставив полученное выражение вместо х в первое уравнение системы
и умножив уравнение на ![]() ≠0,
получим
≠0,
получим ![]() (2).
(2).
Возможны три случая:
1) Если ![]() ≠0
(3), то уравнение (2) имеет единственный корень, поэтому и система
(1) имеет единственный корень.
≠0
(3), то уравнение (2) имеет единственный корень, поэтому и система
(1) имеет единственный корень.
Если не только ![]() ≠0, но и
≠0, но и
![]() ≠0, то
условие (3) можно записать в виде
≠0, то
условие (3) можно записать в виде ![]() ≠
≠![]() (коэффициенты при
(коэффициенты при ![]() и
и
![]() не
пропорциональны).
не
пропорциональны).
2) Если ![]() =0 и
=0 и
![]() =0 (4),
то уравнение (2) имеет бесконечное множество корней, поэтому
система (1) имеет бесконечное множество решений.
=0 (4),
то уравнение (2) имеет бесконечное множество корней, поэтому
система (1) имеет бесконечное множество решений.
Если не только ![]() ≠0, но и
≠0, но и
![]() ≠0, и
≠0, и
![]() ≠0, то
условия (4) можно записать в виде
≠0, то
условия (4) можно записать в виде ![]() =
=![]() =
=![]() (коэффициенты первого уровня пропорциональны коэффициентам второго
уровня).
(коэффициенты первого уровня пропорциональны коэффициентам второго
уровня).
3) Если ![]() =0 и
=0 и
![]() ≠0 (5),
то уравнение (2) не имеет корней, поэтому система (1) не имеет
решений.
≠0 (5),
то уравнение (2) не имеет корней, поэтому система (1) не имеет
решений.
Если не только ![]() ≠0, но и
≠0, но и
![]() ≠0, и
≠0, и
![]() ≠0, то
условия (5) можно записать в виде
≠0, то
условия (5) можно записать в виде ![]() =
=![]() ≠
≠![]() (коэффициенты при
(коэффициенты при ![]() пропорциональны коэффициентам при
пропорциональны коэффициентам при ![]() , но не
пропорциональны свободным членам).
, но не
пропорциональны свободным членам).
Если в уравнении (1) не ![]() ≠0,
≠0,
![]() ≠0, то,
проведя аналогичные рассуждения, мы получим тот же результат -
уравнение (2).
≠0, то,
проведя аналогичные рассуждения, мы получим тот же результат -
уравнение (2).
Это означает, что сделанные выводы не зависят от того, какой из
коэффициентов ![]() или
или
![]() (или
оба) отличны от нуля.
(или
оба) отличны от нуля.
II. Этап усвоения новых знаний.
Пример 1: Определить число решений системы
а) ![]() , б)
, б)
![]() , в)
, в)
![]() .
.
Решение: а) коэффициенты при ![]() и
и
![]() второго
уровня системы не равны нулю и
второго
уровня системы не равны нулю и ![]() ≠
≠
![]() ,
поэтому система имеет единственное решение.
,
поэтому система имеет единственное решение.
б) Все коэффициенты второго уравнения системы не равны нулю и
![]() =
=
![]() =
=
![]() ,
поэтому система имеет бесконечное множество решений.
,
поэтому система имеет бесконечное множество решений.
в) Все коэффициенты второго уравнения системы не равны нулю и
![]() =
=
![]() ≠
≠
![]() ,
поэтому система не имеет решений.
,
поэтому система не имеет решений.
Ответ: а) система имеет единственное решение;
б) система имеет бесконечное множество решений;
в) система не имеет решений.
Пример 2: Определите все значение параметра ![]() при
которых система уравнений
при
которых система уравнений ![]() (1)
имеет единственное решение.
(1)
имеет единственное решение.
Решение: Если ![]() ≠0, то
система имеет единственное решение при выполнении условия
≠0, то
система имеет единственное решение при выполнении условия ![]() ≠
≠![]() , а для
любых
, а для
любых ![]() система
имеет единственное решение, если выполняется условие
система
имеет единственное решение, если выполняется условие ![]() (2).
(2).
Так как уравнение ![]() имеет
два корня
имеет
два корня ![]() =1 и
=1 и
![]() = -
= -
![]() , то при
всех
, то при
всех ![]() ≠1,
≠1,
![]() ≠-
≠-
![]() выполняется условие (2) т.е. система (1) имеет единственное
решение.
выполняется условие (2) т.е. система (1) имеет единственное
решение.
Ответ: при ![]() ≠1,
≠1,
![]() ≠-
≠-
![]() .
.
Пример 3: Определите все значения параметра ![]() , при
которых система уравнений
, при
которых система уравнений 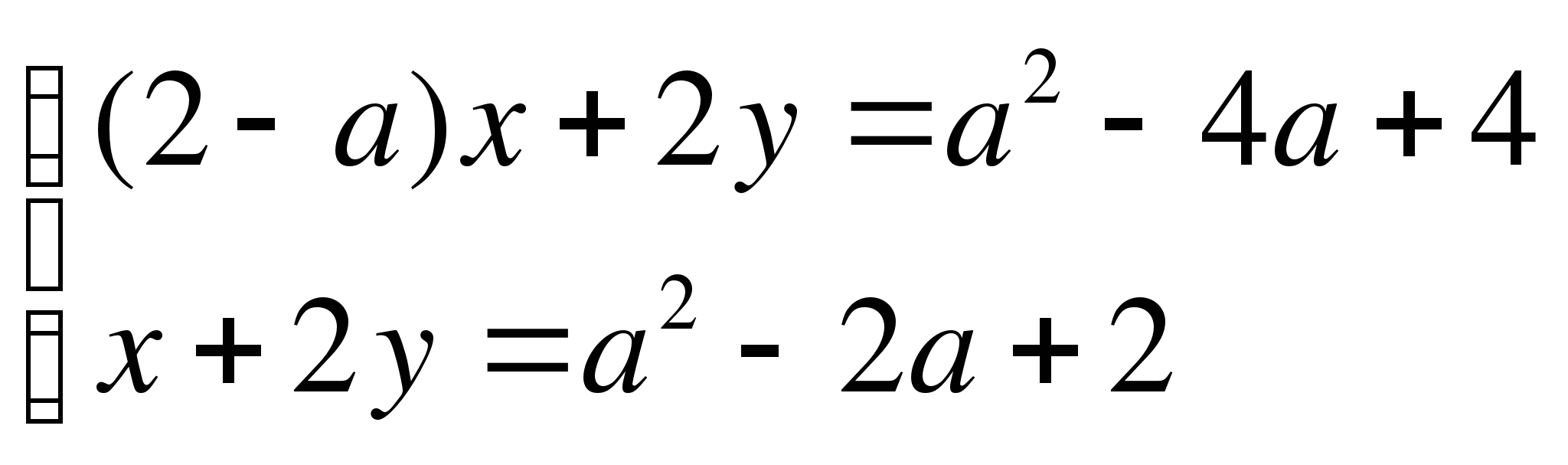 имеет
бесконечно много решений.
имеет
бесконечно много решений.
Решение: ![]() =
=
![]() , то
есть все коэффициенты второго уровня системы отличны от нуля.
, то
есть все коэффициенты второго уровня системы отличны от нуля.
Тогда система имеет бесконечно много решений при условии
![]() =
=![]() =
=![]() .
.
Так как уравнение ![]() =
=![]() имеет
единственный корень
имеет
единственный корень ![]() =1 и при
=1 и при
![]() =1
справедливо равенство
=1
справедливо равенство ![]() =
=![]() , то
система имеет бесконечно много решений только при
, то
система имеет бесконечно много решений только при ![]() =1.
=1.
Ответ: при ![]() =1.
=1.
Пример 4: При каком значении параметра ![]() система
уравнений
система
уравнений
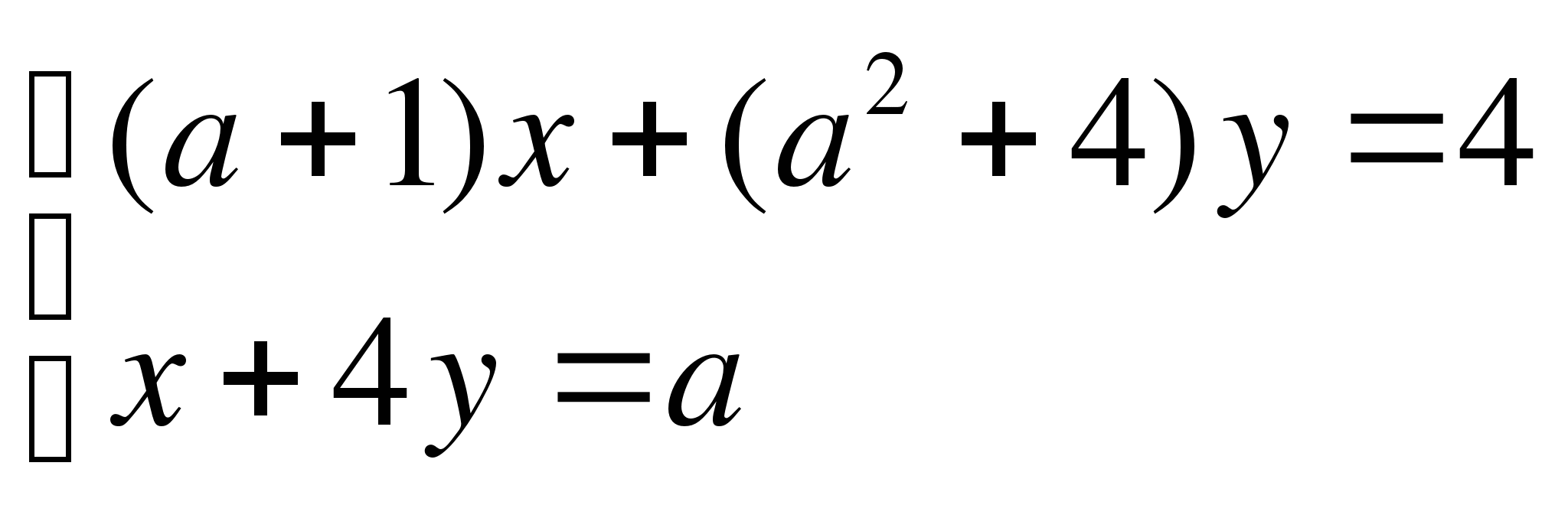 не
имеет решений?
не
имеет решений?
Решение: Система не имеет решен6ий при выполнении условий
![]() =
=![]() ≠
≠![]() (если
(если
![]() ≠0) или
условий
≠0) или
условий ![]() и
и
![]() (для
любых значений
(для
любых значений ![]() ).
Уравнение
).
Уравнение ![]() имеет корни
имеет корни ![]() =0 и
=0 и
![]() = 4, при
каждом из этих двух значений
= 4, при
каждом из этих двух значений ![]() выполняется условие
выполняется условие ![]() ,
поэтому система не имеет решений при
,
поэтому система не имеет решений при ![]() = 0 и
= 0 и
![]() = 4.
= 4.
Ответ: при ![]() = 0
и
= 0
и ![]() = 4.
= 4.
III. Этап закрепления знаний (самостоятельная работа в группах).
Пример 5. При всех значениях параметра ![]() решить
систему уравнений
решить
систему уравнений
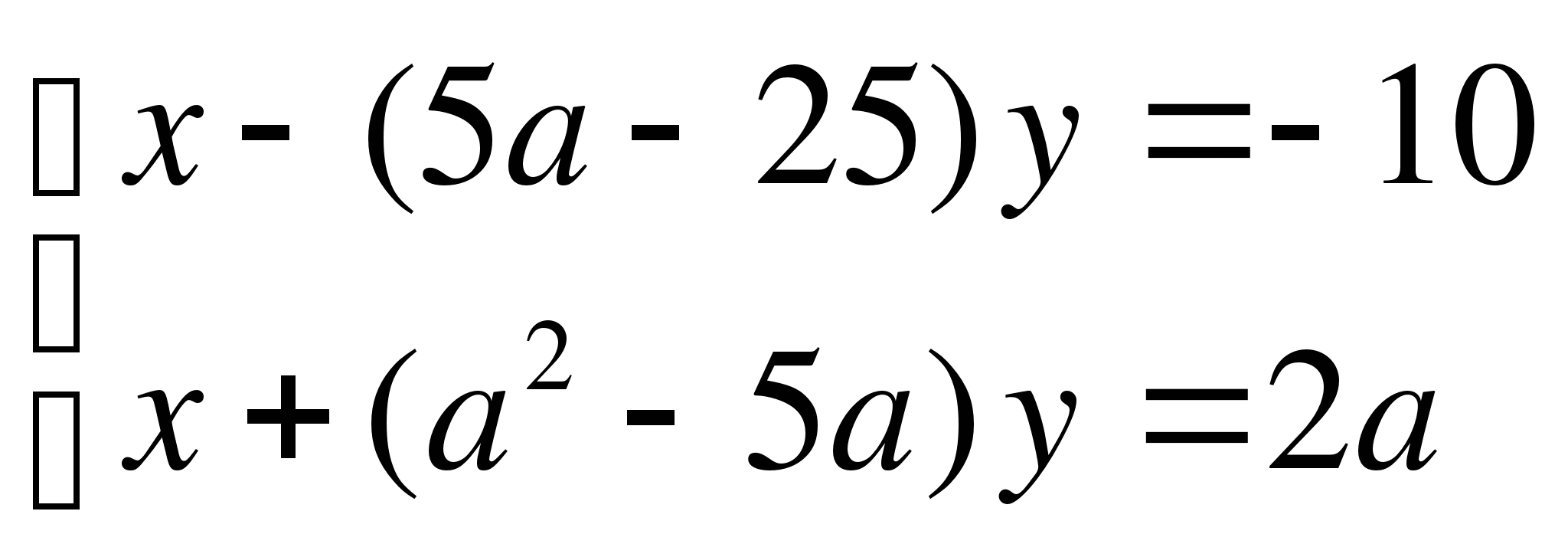 (1).
(1).
Решение: Система равносильна системе
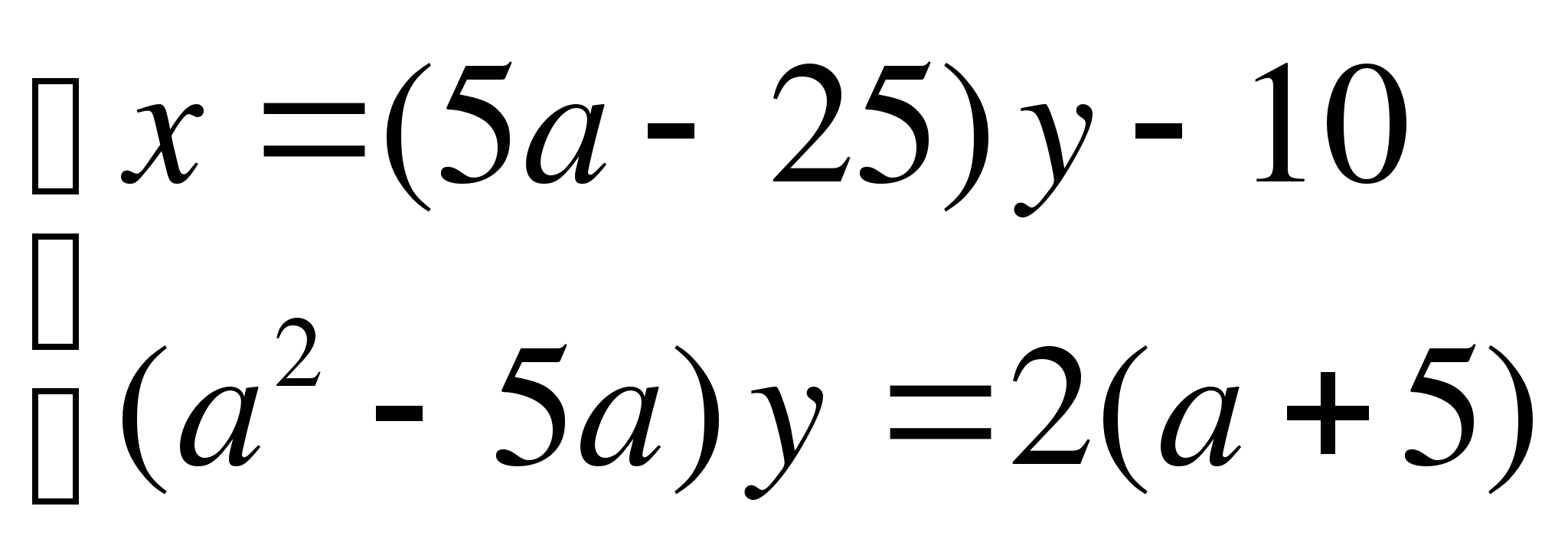 (2).
(2).
1) Если ![]() =5,
то второе уравнение системы (2) не имеет корней. В этом случае
система (2) не имеет решений.
=5,
то второе уравнение системы (2) не имеет корней. В этом случае
система (2) не имеет решений.
2) Если ![]() =-5,
то решением второго уравнения системы (2) является любое
действительное число
=-5,
то решением второго уравнения системы (2) является любое
действительное число ![]() . Тогда,
. Тогда,
![]() , т.е.
решением системы (1) является любая пара чисел (
, т.е.
решением системы (1) является любая пара чисел (![]() ;
;![]() ), где
), где
![]()
![]() R.
R.
3) Если ![]() ≠
±5, то второе уравнение системы (2) имеет единственный корень
≠
±5, то второе уравнение системы (2) имеет единственный корень
![]() =
=![]() . Из
первого уравнения системы (2) вычитаем значение
. Из
первого уравнения системы (2) вычитаем значение ![]()
![]() =
=![]() =
=![]() =0.
=0.
В этом случае система (1) имеет решение (0; ![]() ).
).
Ответ: если ![]() =5, то
система не имеет решений;
=5, то
система не имеет решений;
если ![]() =-5, то
решением является (
=-5, то
решением является (![]() ;
;![]() ),
),![]()
![]() R.;
R.;
если ![]() ≠ ±5, то
(0;
≠ ±5, то
(0; ![]() ) -
решение системы.
) -
решение системы.
IV. Этап рефлексии, итоги занятия.
Занятие 3.
Цель: самоконтроль знаний.
-
Этап подготовки учащихся к самоконтролю знаний.
Учитель: Как в общем виде записывается система двух уравнений с двумя неизвестными?
Ученик: 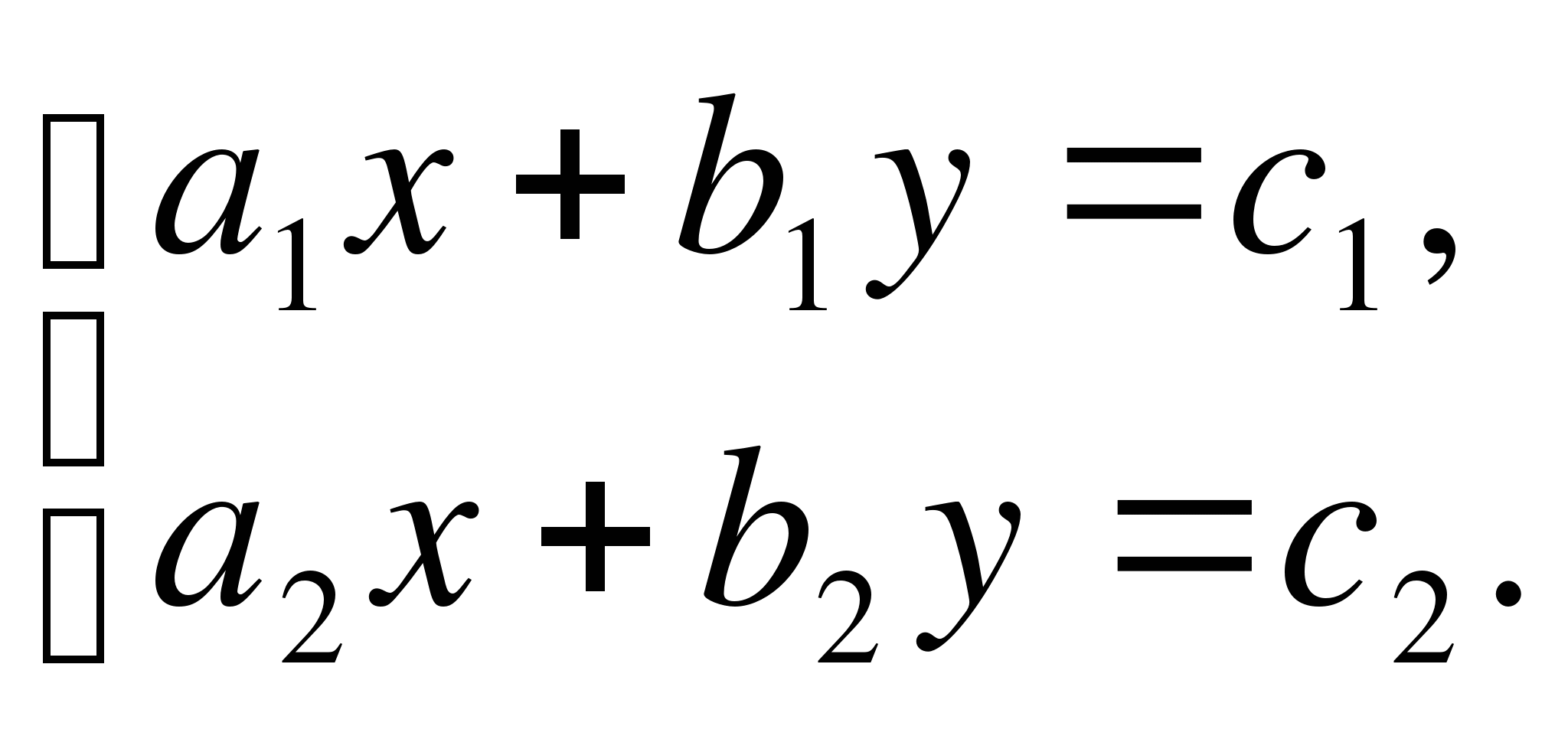 (*)
(*)
Учитель: Как решается система (*) двух уравнений с двумя неизвестными?
Ученик: При решении системы (*) следует рассмотреть 3 случая:
-
Если
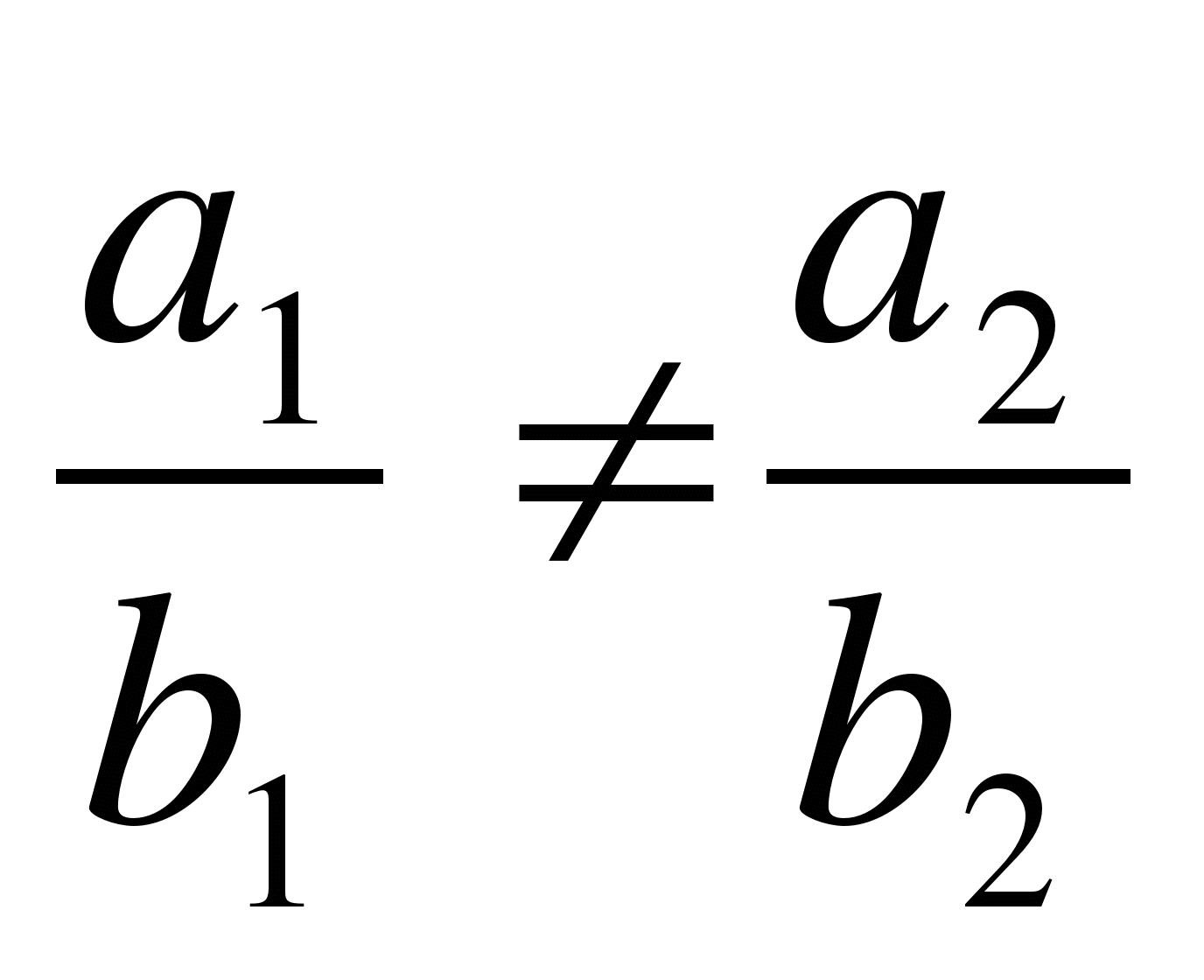 , то
система (*) имеет одно решение.
, то
система (*) имеет одно решение.
-
Если
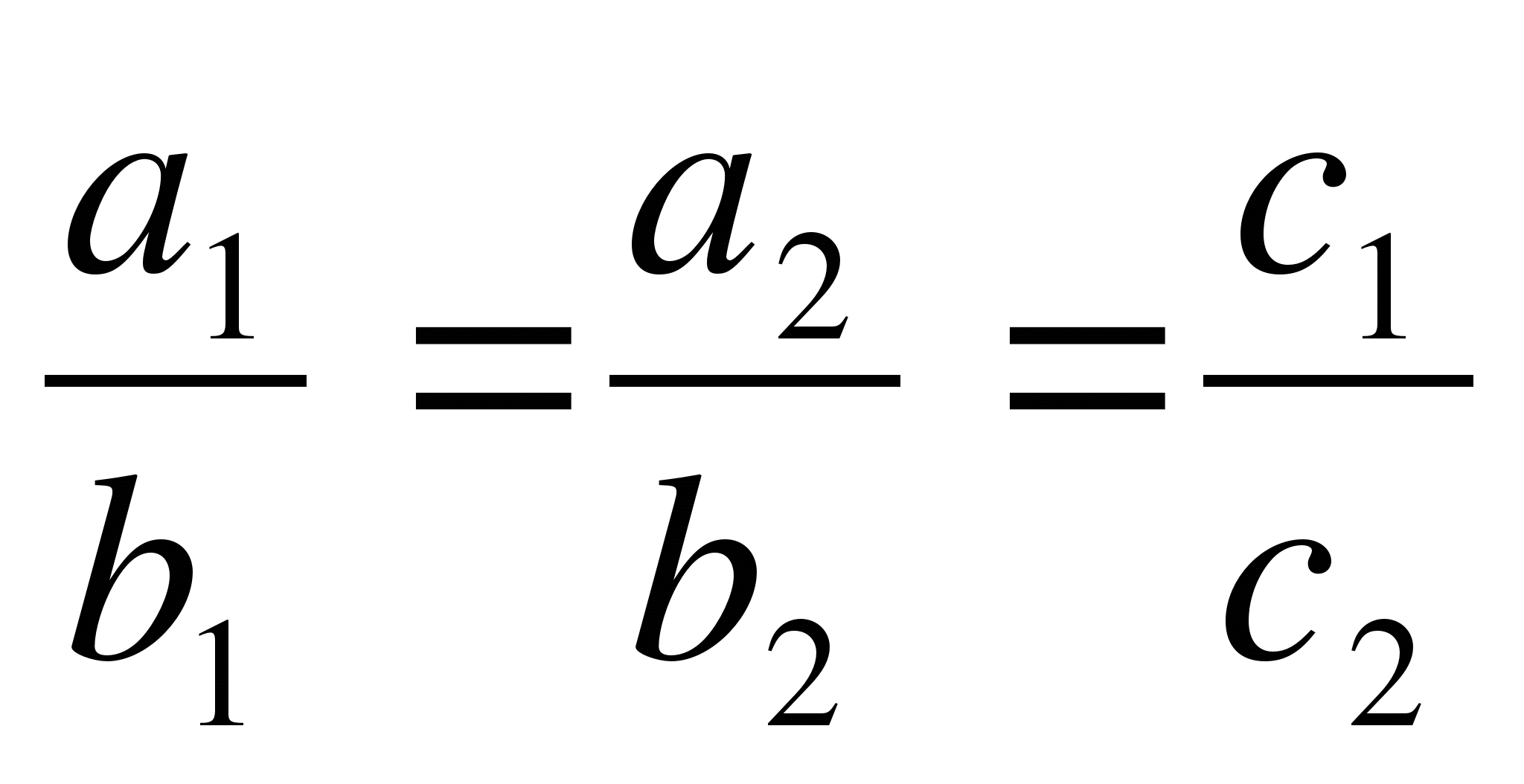 , то
система (*) имеет бесконечное множество решений
, то
система (*) имеет бесконечное множество решений
-
Если
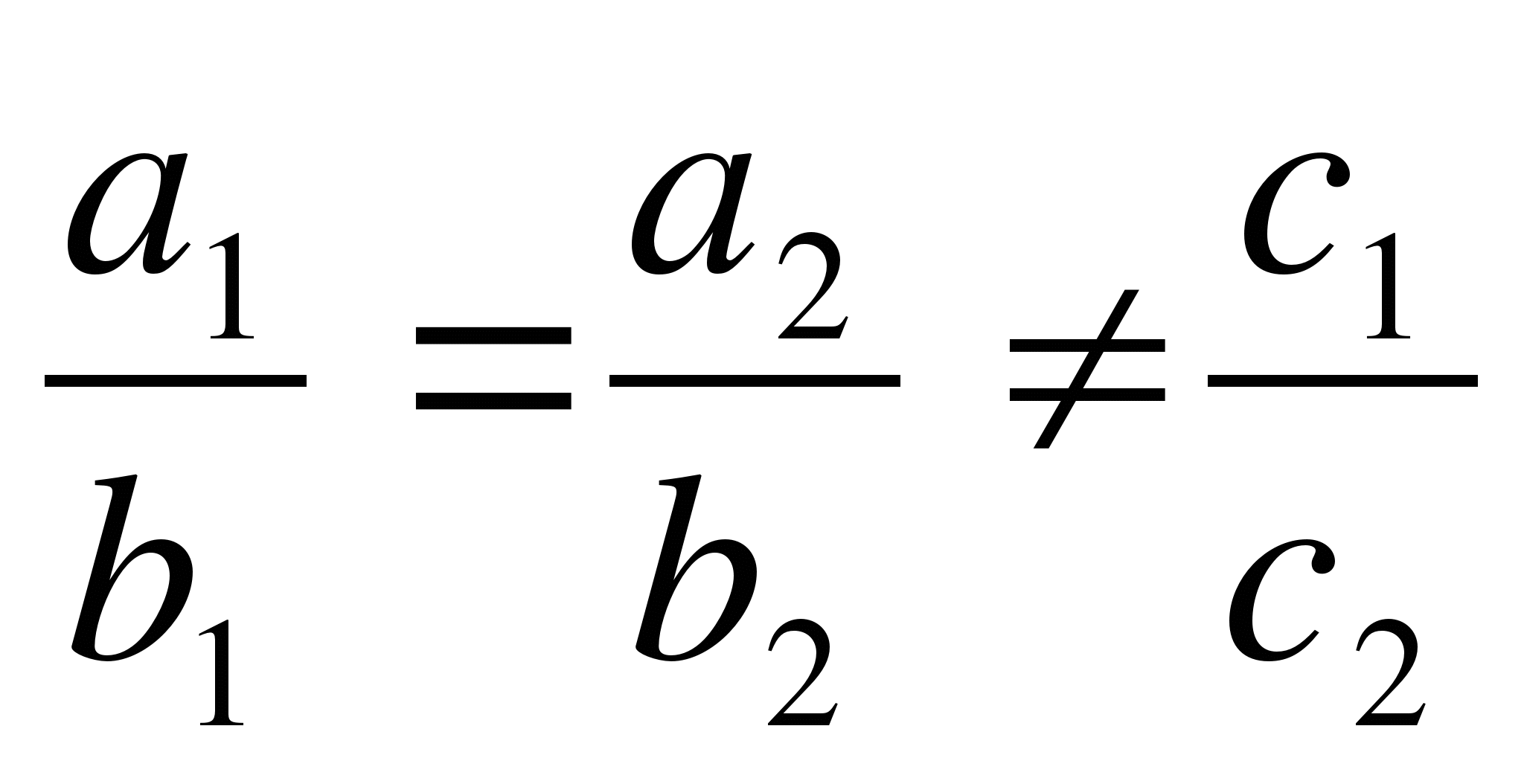 , то
система (*) не имеет решений
, то
система (*) не имеет решений
-
Этап самоконтроля знаний.
Учитель: С помощью предложенных заданий (к каждому заданию даны ответы) вы проверите свои умения решать системы линейных уравнений с параметром. После полученных ответов указаны команды, с помощью которых вы будете исправлять ошибки либо будете переходить к решению следующего задания, если ответ предыдущего верный.
Выполните задания и команды, указанные после полученных ответов.
-
Укажите все значения параметра а, при котором система уравнений
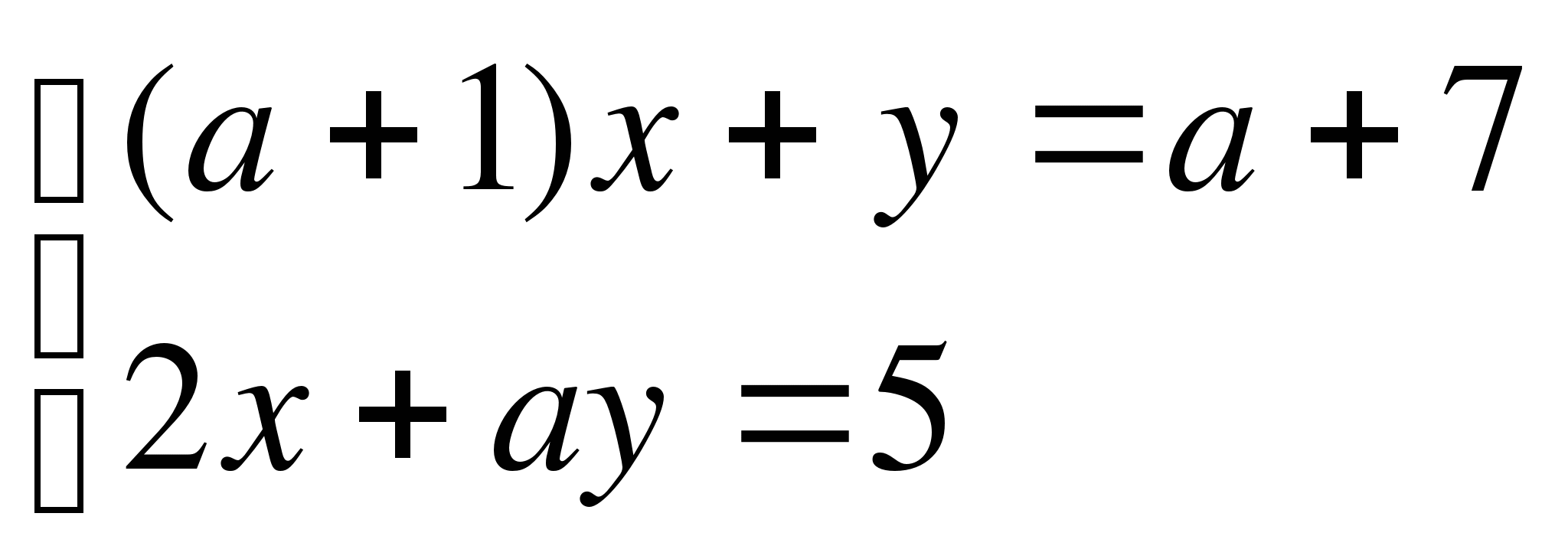 имеет единственное решение.
имеет единственное решение.
-
-
Укажите все значения параметра а, при котором система уравнений
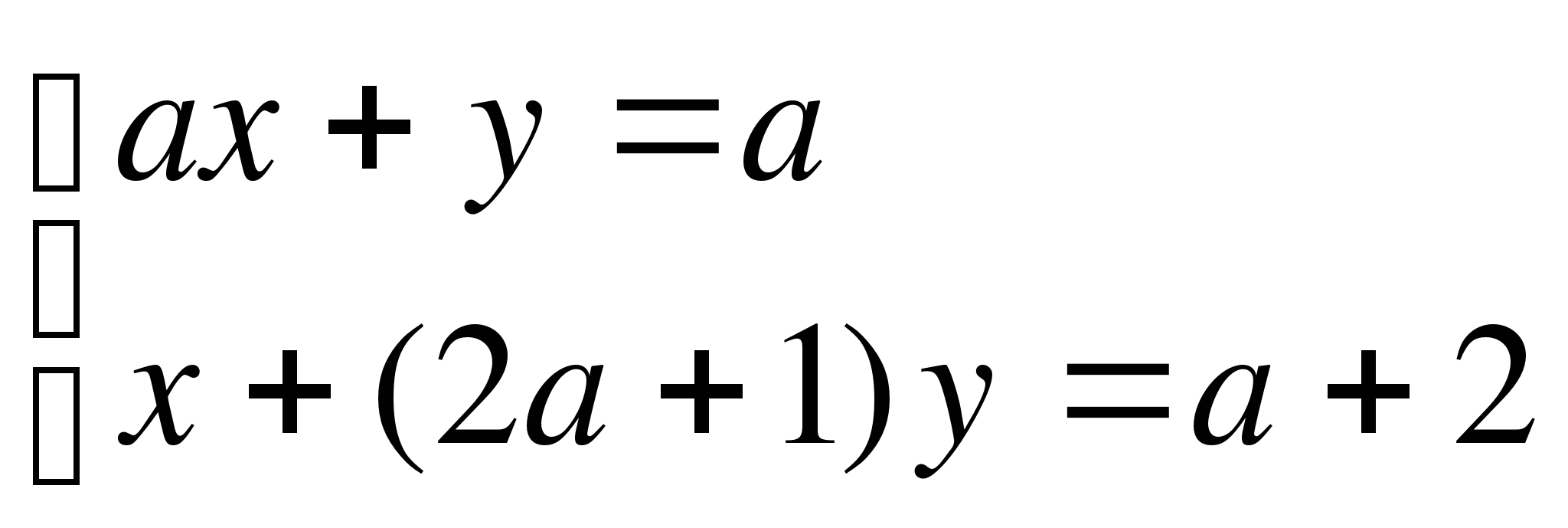 имеет бесконечно много решений.
имеет бесконечно много решений.
-
Укажите все значения параметра а, при котором система уравнений
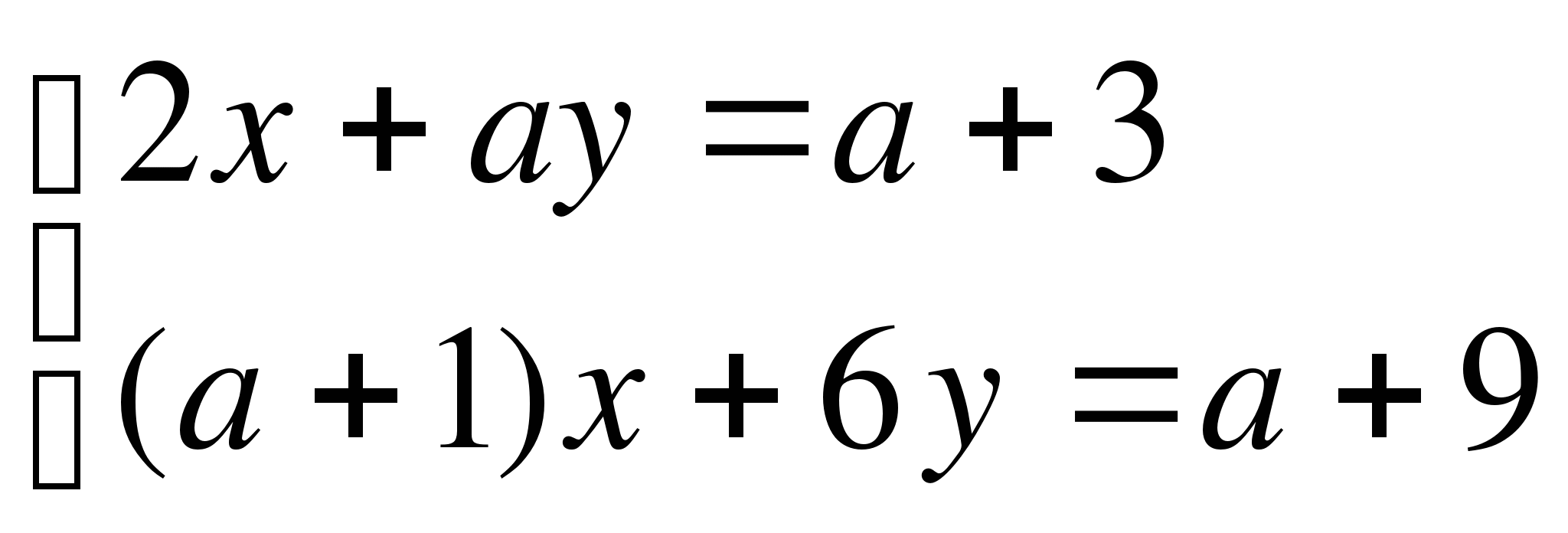 не имеет решений.а=-4 (ж)
не имеет решений.а=-4 (ж)
-
При всех значениях параметра а решите систему уравнений
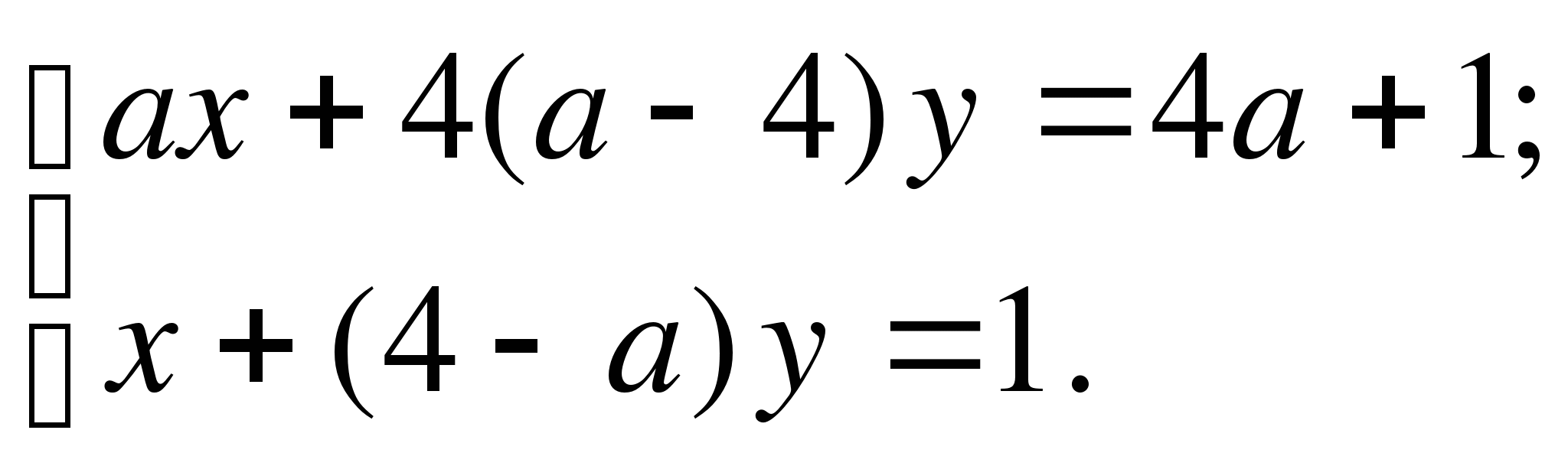
При а=4;
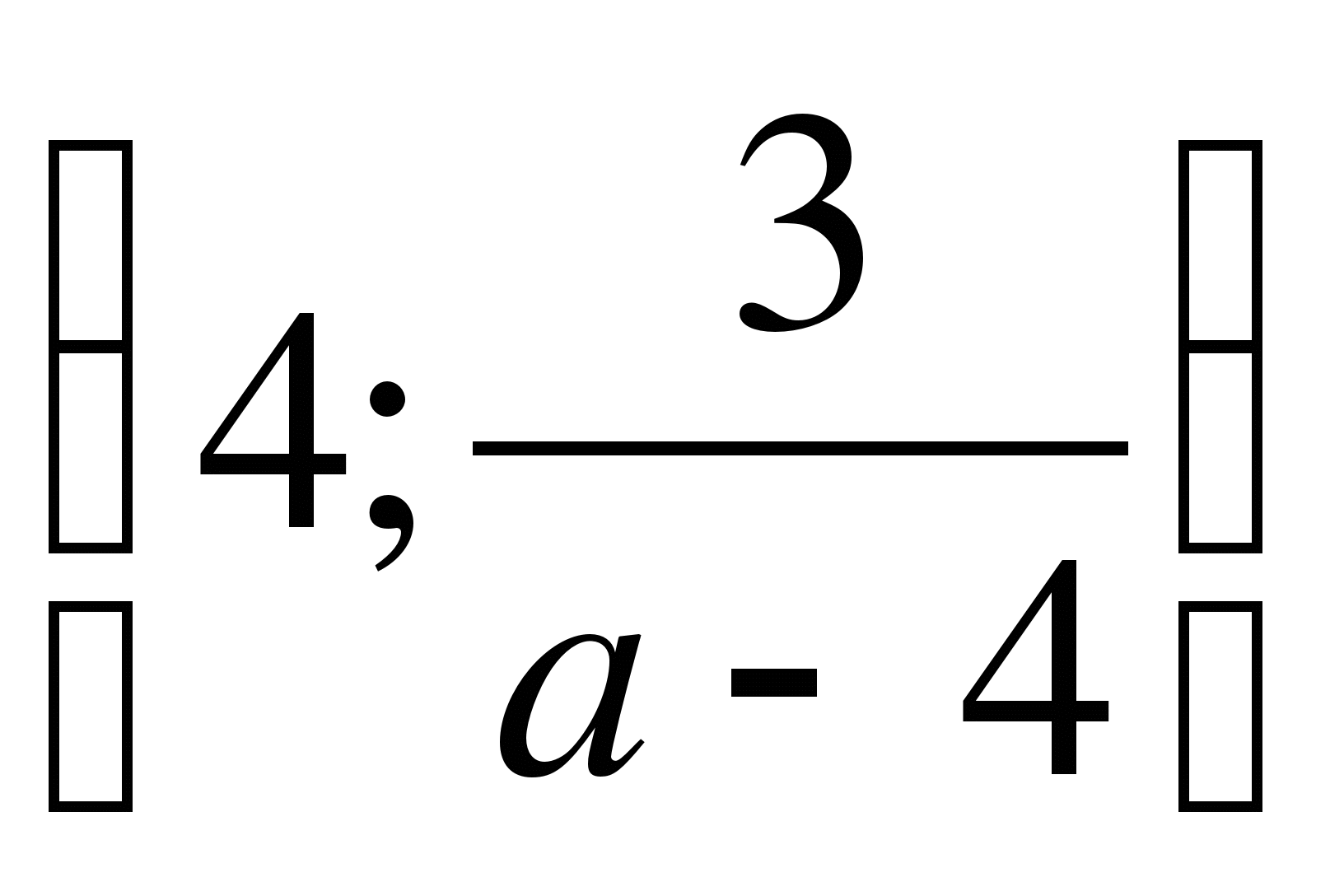 при
а=-4 (е,г)
при
а=-4 (е,г)
При а=4;
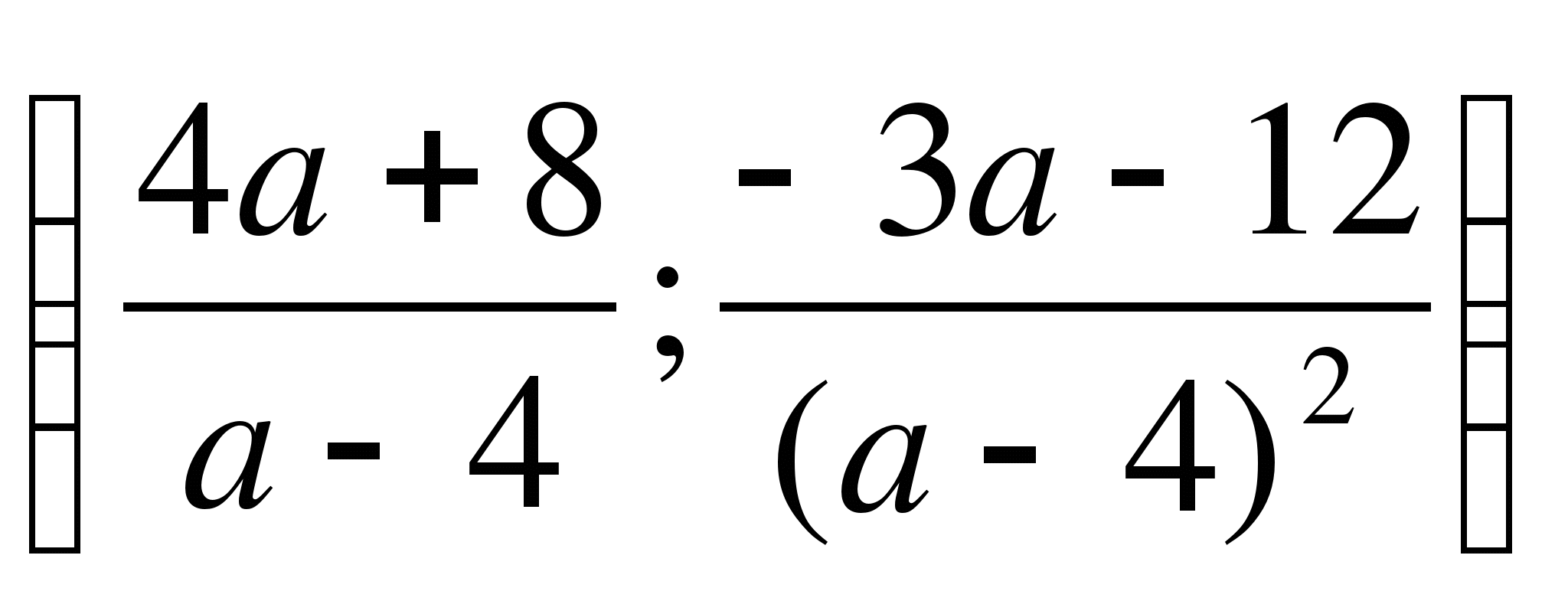 при
а=4 (е)
при
а=4 (е)
При а=-4; (1;у),
 при
а=4;
при
а=4; 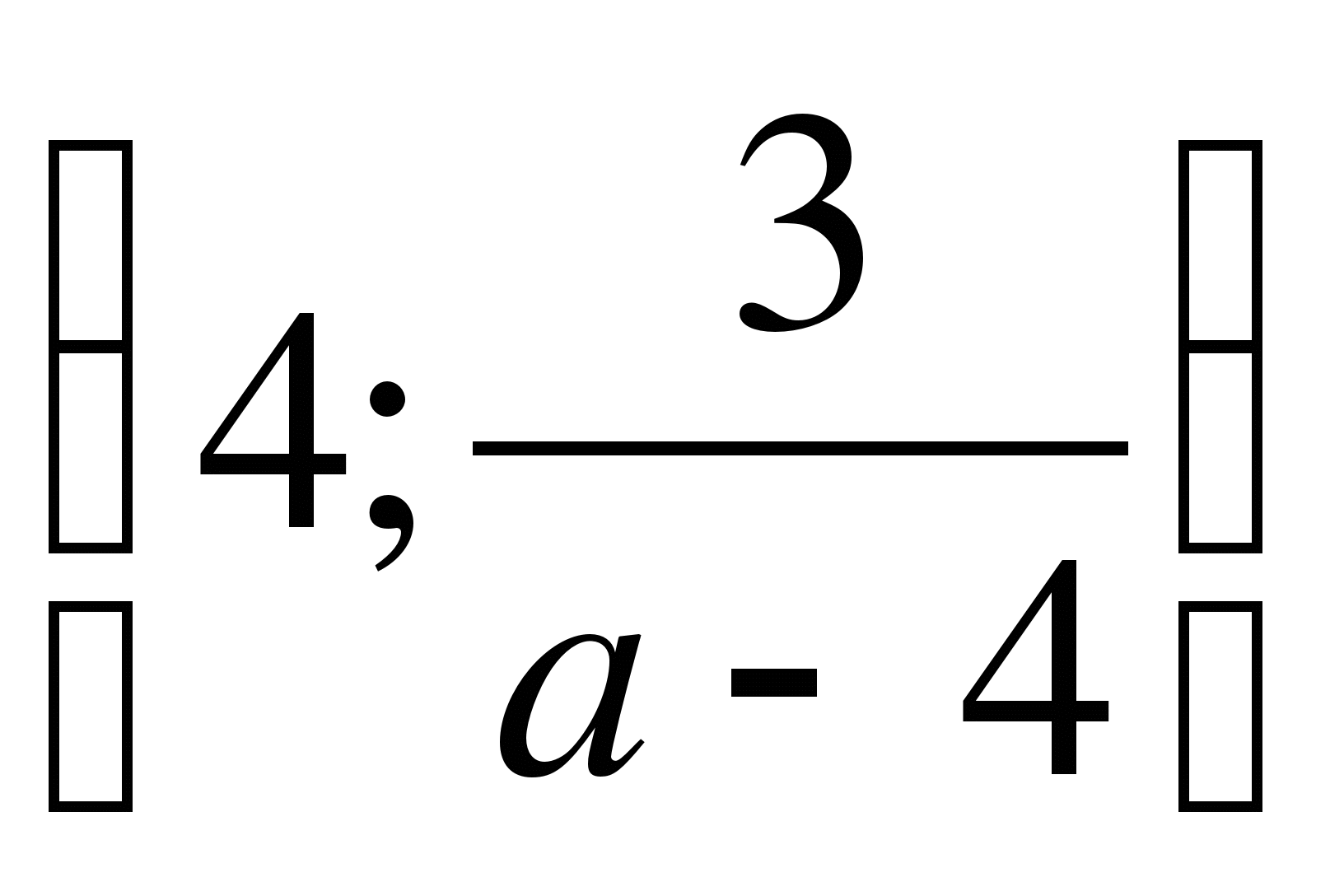 при
а ≠ ± 4 (г)
при
а ≠ ± 4 (г)
При а=4; (1-8у;у),
 при
а=-4;
при
а=-4; 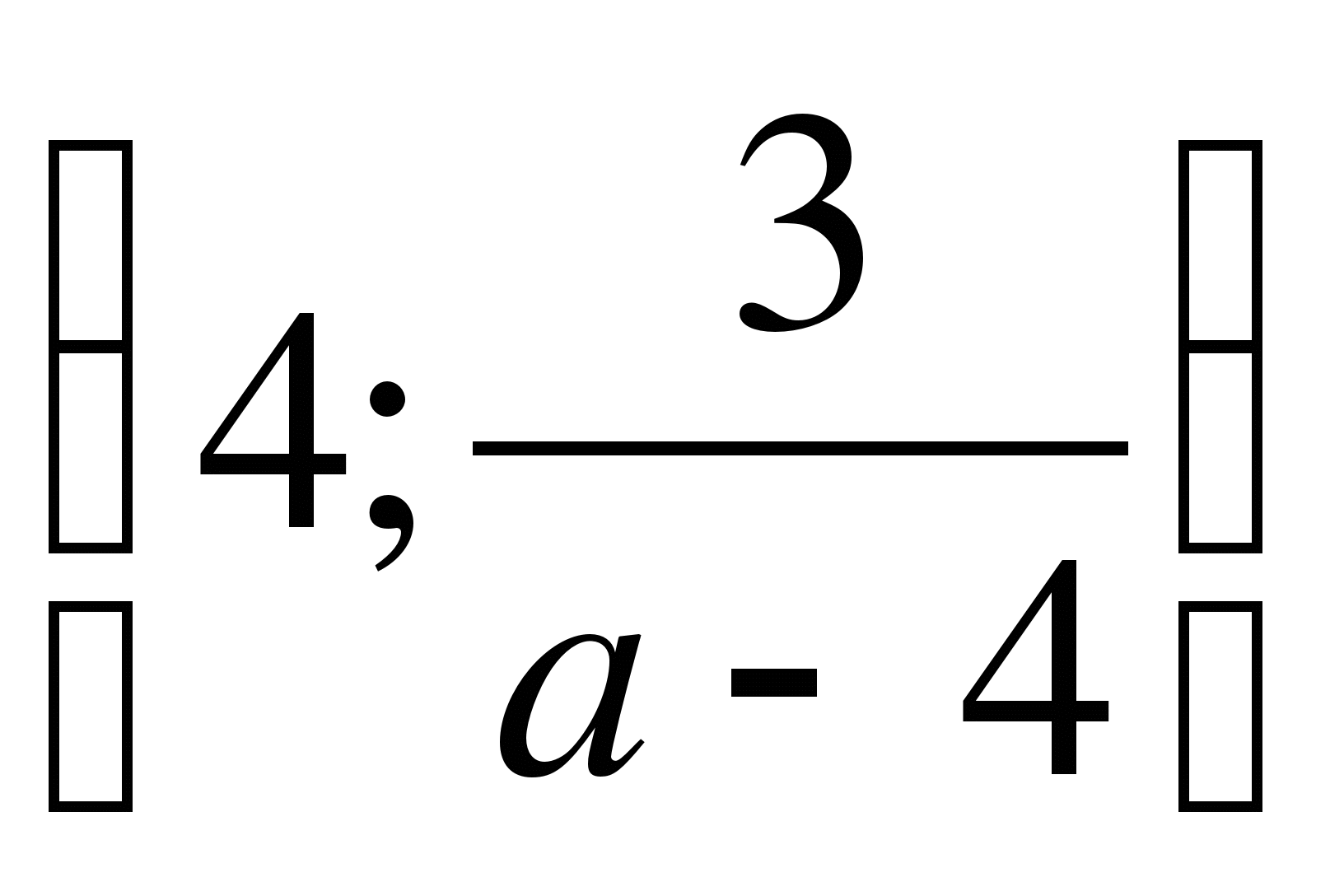 при
а ≠ ± 4 ( з)
при
а ≠ ± 4 ( з)
Команды
а) Прочитайте п.1 объяснения и разберите пример 2,
б) прочитайте п.2 объяснения и разберите пример 3,
в) прочитайте п.3 объяснения и разберите пример 4,
г) разберите пример 5,
д) найдите все значения параметра а, удовлетворяющие условию задачи,
е) неверно решено линейное уравнение с одним неизвестным,
ж) верно, переходите к следующему заданию,
з) верно, подготовка к самостоятельной работе окончена.
-
Этап рефлексии.
-
Какие трудности вы испытали при решении заданий?
-
Как вы справились с ними?
-
Оцените свою работу.
-
Блок II. Тема 5. Линейные неравенства с параметром.
Занятие 1. Решение линейных неравенств, содержащих параметр.
Цели занятия:
- научиться решать линейные неравенства, содержащие параметр и неравенства с
параметром, приводимые к линейным, обеспечить благоприятные условия для
дифференцированного обучения;
- научиться выписывать ответ;
- познакомиться с алгоритмами решения неравенств, содержащих параметр;
- обеспечить устойчивую мотивационную среду, интерес к изучаемой теме;
- создать условия для самостоятельной и творческой работы.
Ход занятия:
I. Подготовительный этап.
На доске записаны следующие неравенства:
Задание. Решите неравенства и запишите ответ.
Решение
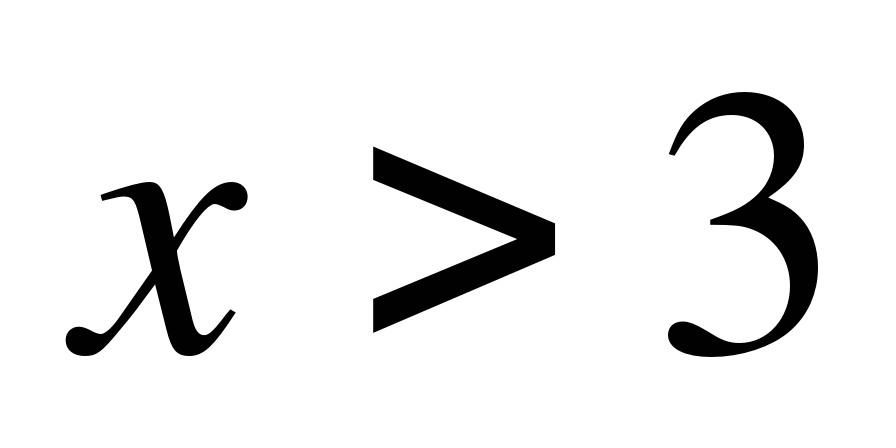
Ответ:
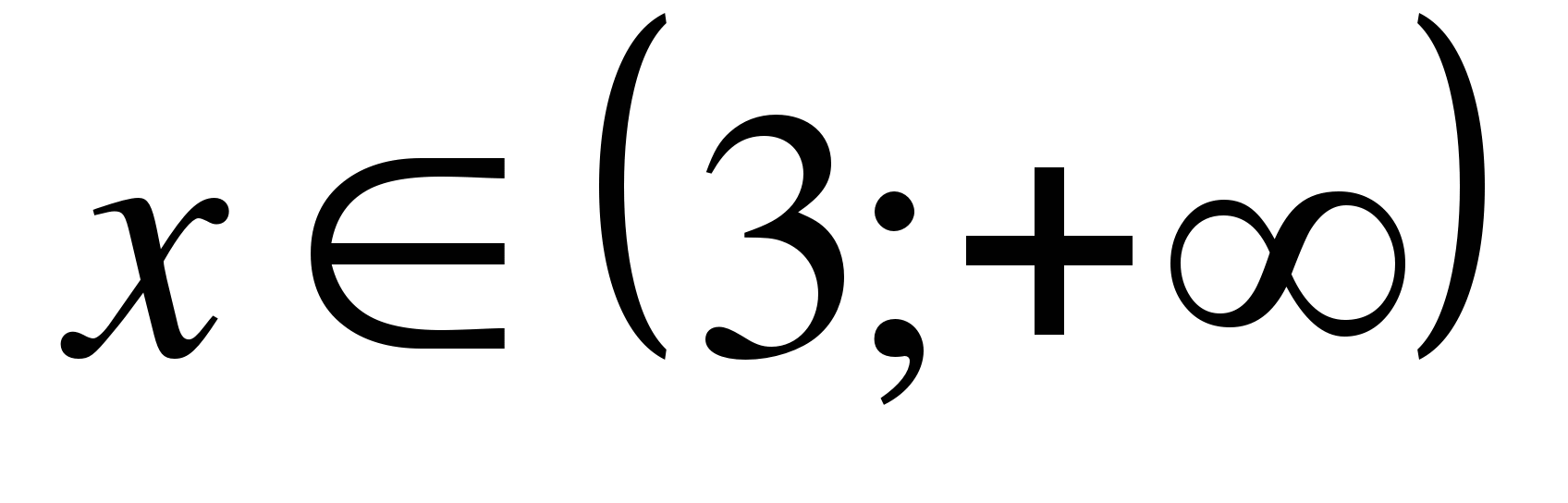
б)
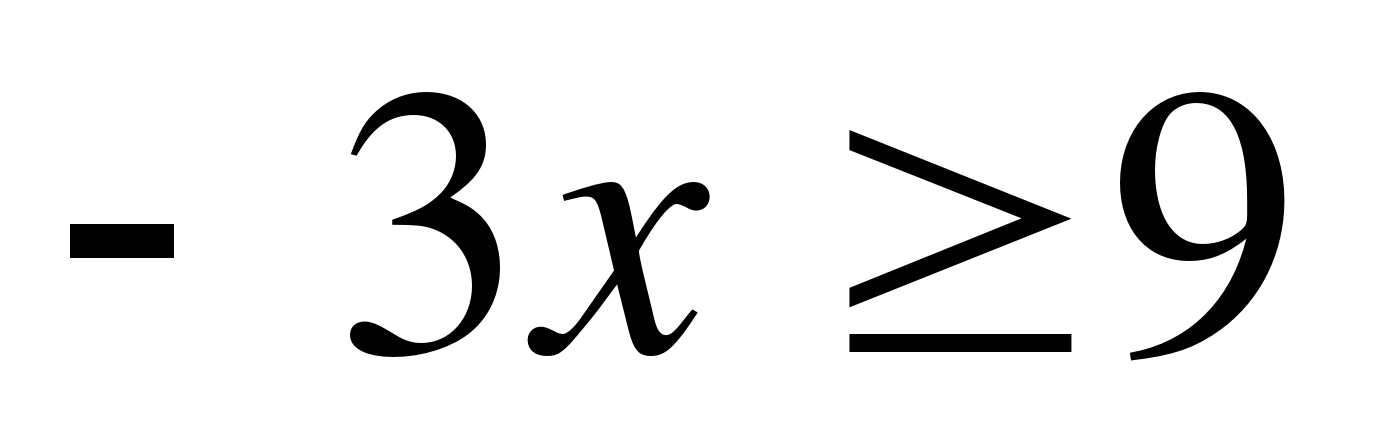
Решение
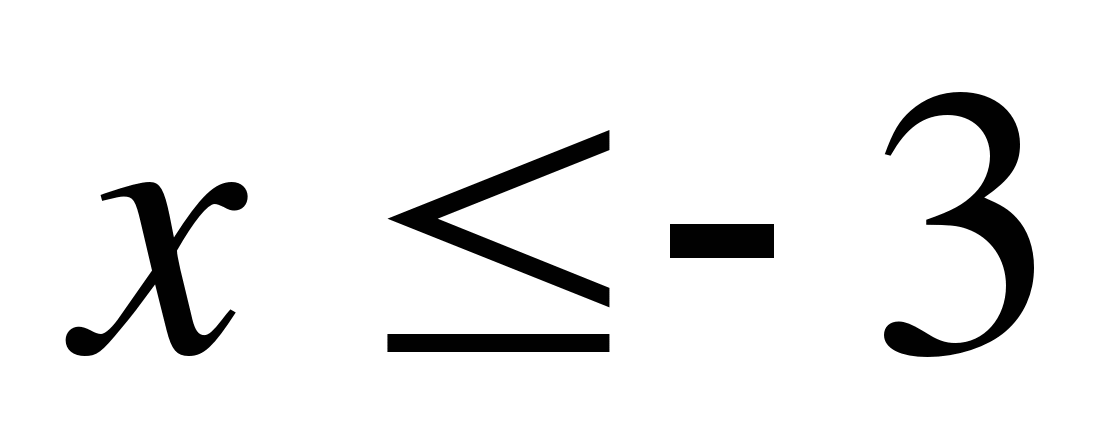
Ответ:
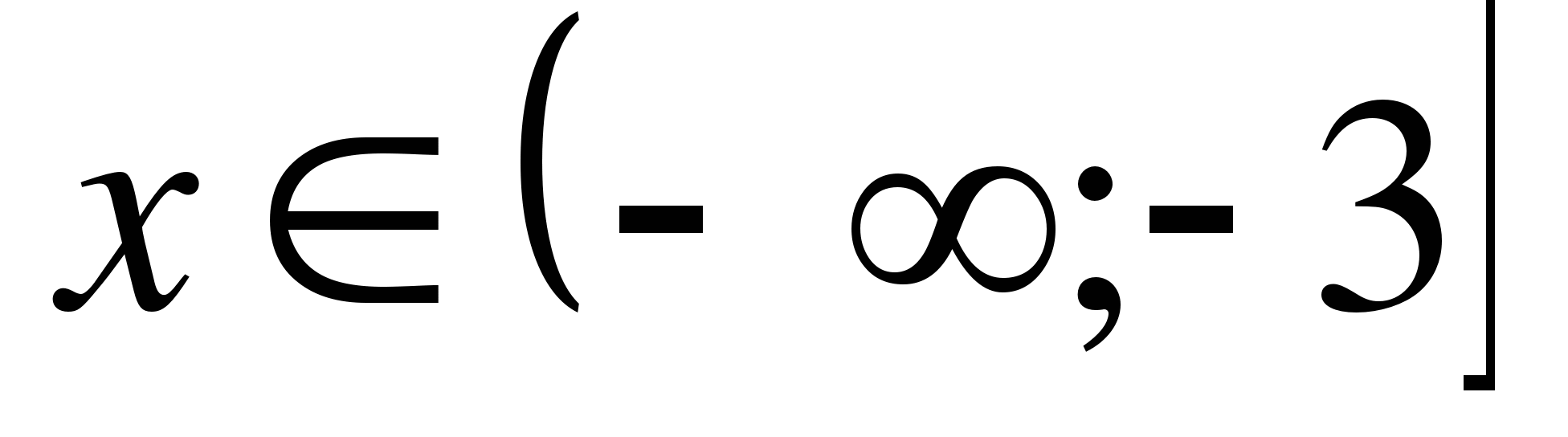
в)
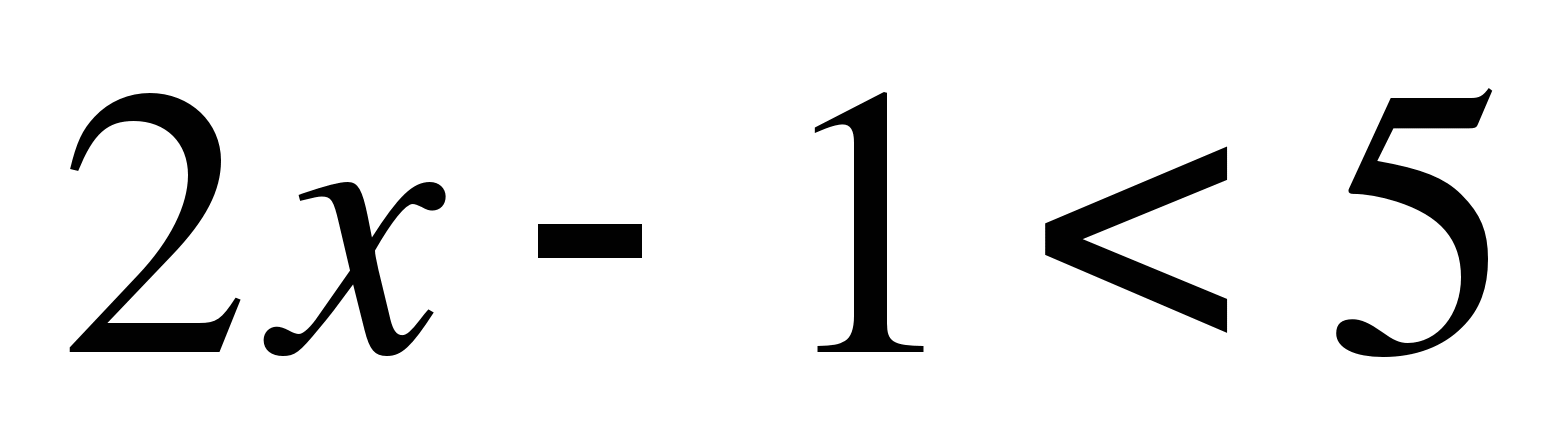
Решение
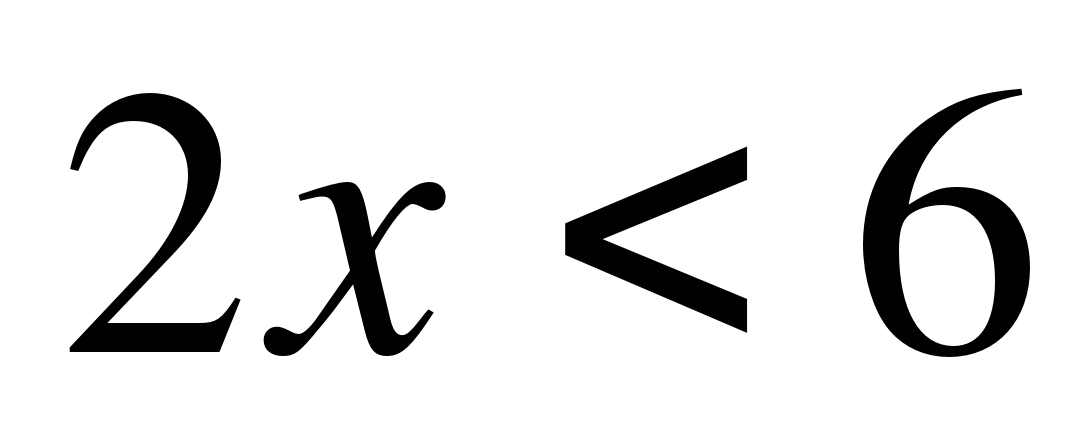 ,
,
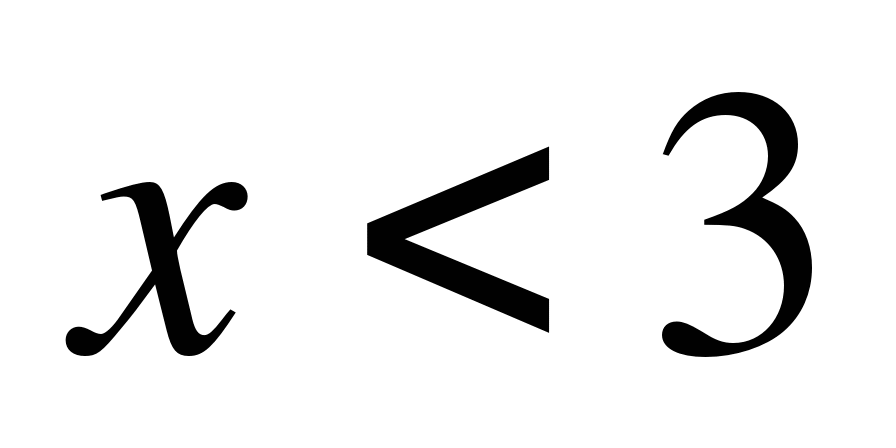
Ответ:
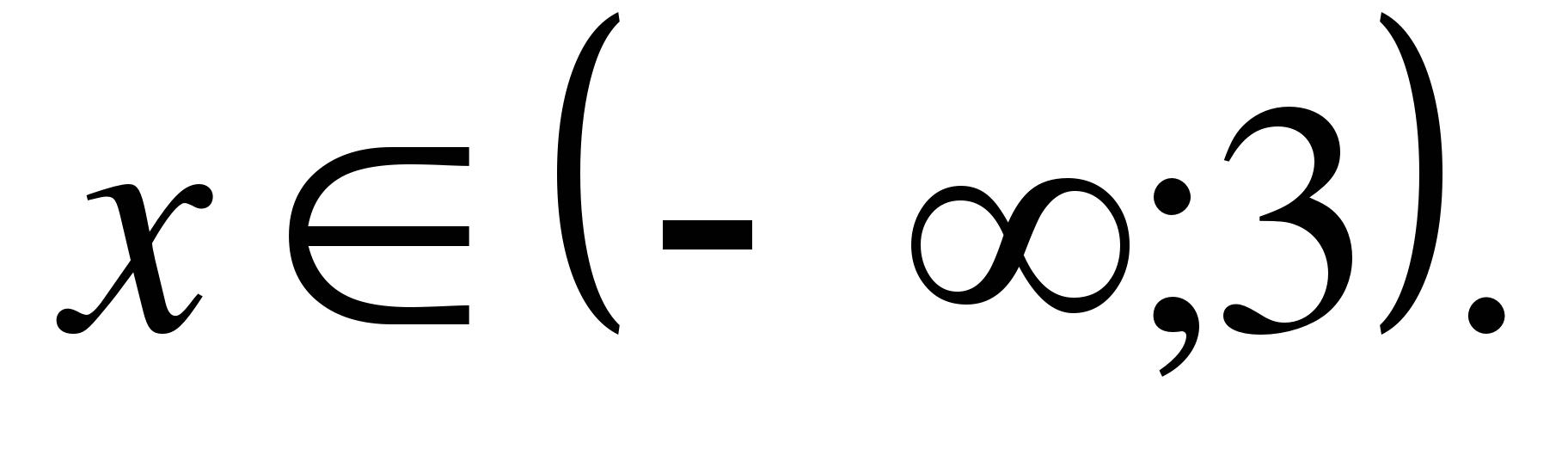
Сформулируйте свойства неравенств, которые использованы при решении.
-
Если из одной части неравенства, перенести в другую часть слагаемое с противоположным знаком, то получится равносильное неравенство.
-
Если обе части неравенства умножить или разделить на одно и тоже положительное число, то получится равносильное неравенство.
-
Если обе части неравенства умножить или разделить на одно и тоже отрицательное число, изменив при этом знак неравенства на противоположный, то получится равносильное неравенство.
Приведите примеры неравенств.2x>6
3x>4
2x<6
3x<4
2x
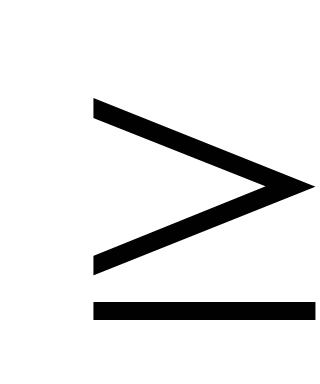 6
6
3x
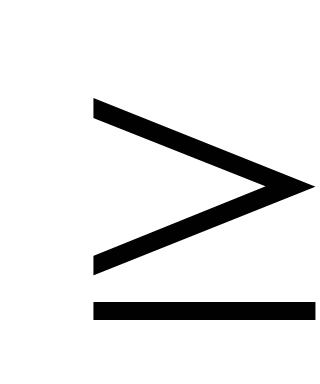 4
4
2x
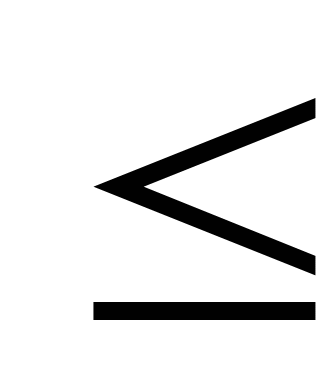 6
6
3x
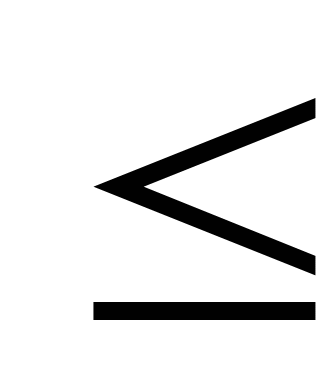 4
4
Неравенства вида ax
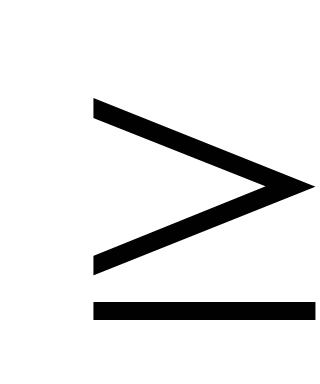 b
ax
b
ax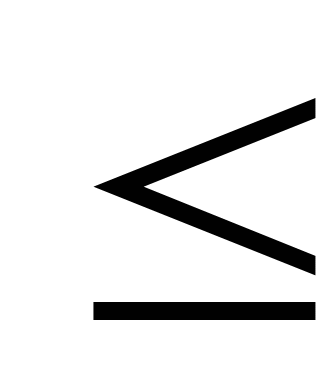 b,
где a и b действительные числа или выражения,
зависящие от параметров, а x - неизвестное, называются
линейными неравенствами.
b,
где a и b действительные числа или выражения,
зависящие от параметров, а x - неизвестное, называются
линейными неравенствами.
В зависимости от коэффициентов a и b решением линейного неравенства может быть либо неограниченный промежуток, либо числовая прямая, либо пустое множество.
I. Решение линейных неравенств вида aх>b.
-
если a>0, то
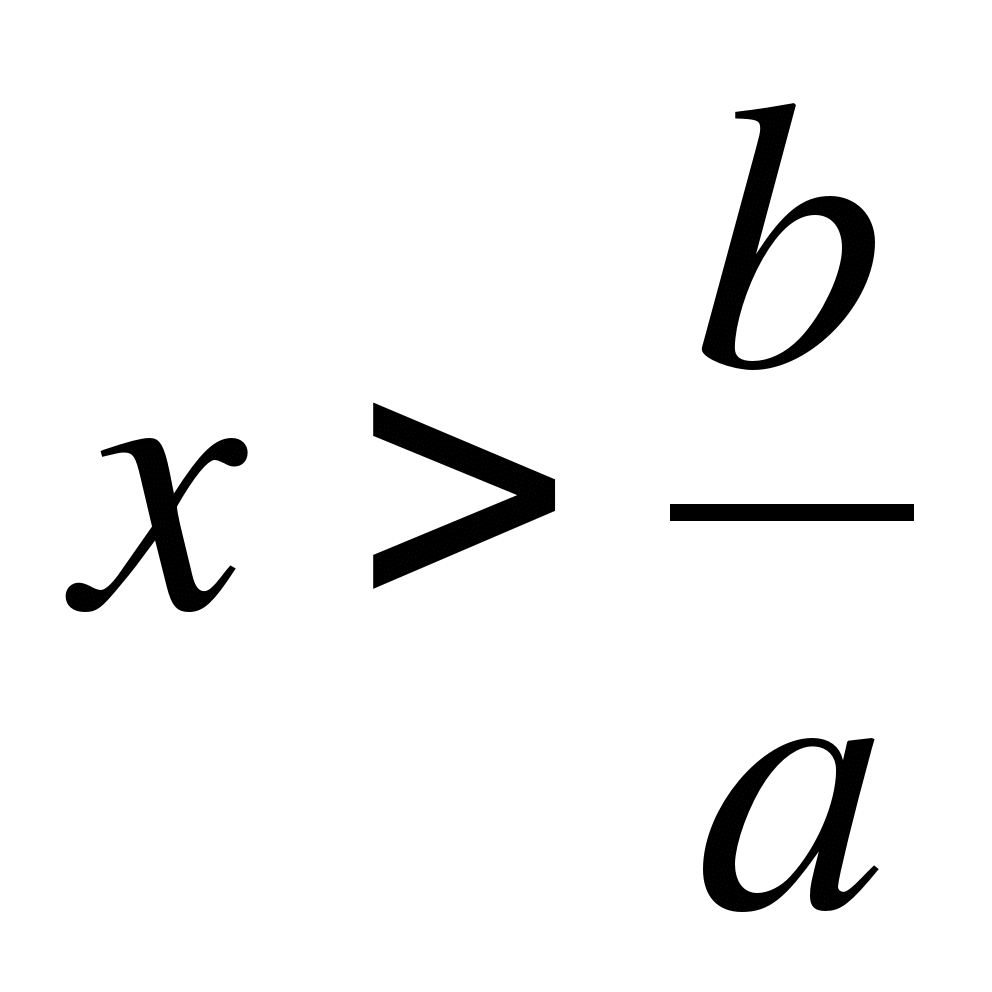 .
.
-
если a<0, то
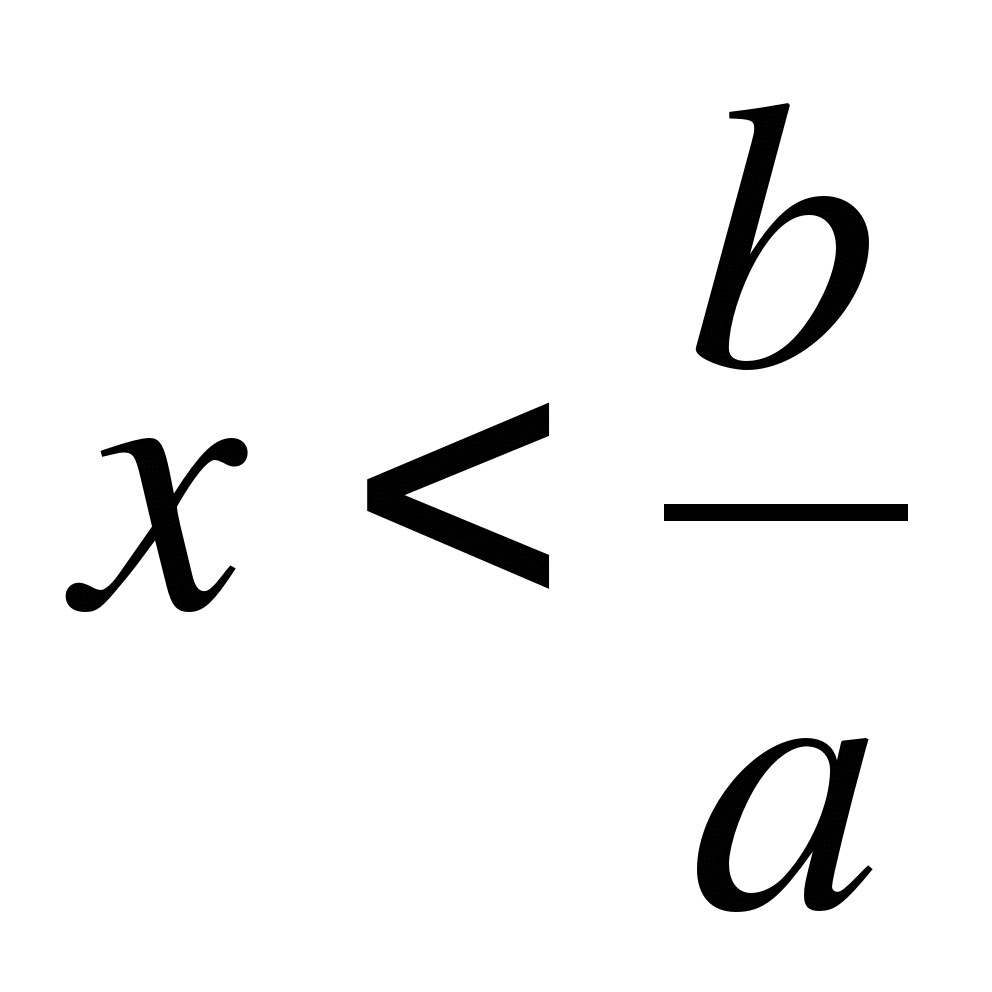 .
.
-
если a=0 и b<0, то
 .
.
Если a=0 и b
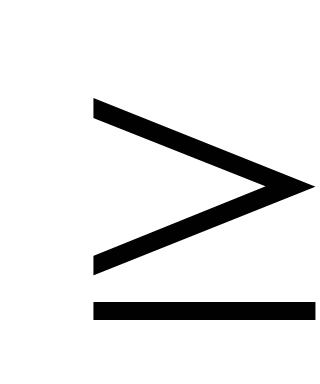 0,
то решений нет.
0,
то решений нет.
Пример 1. Решите неравенство ах>1.
1) если a>0, то
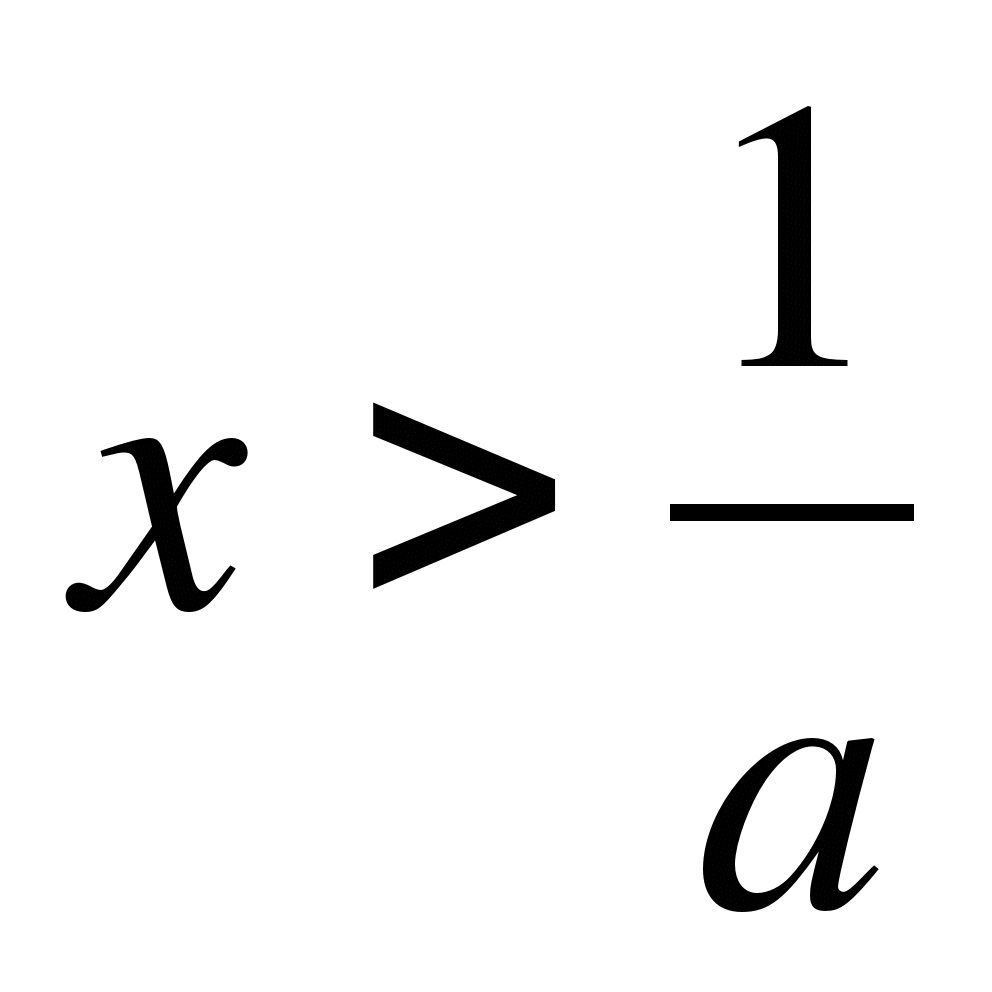
2) если a<0, то
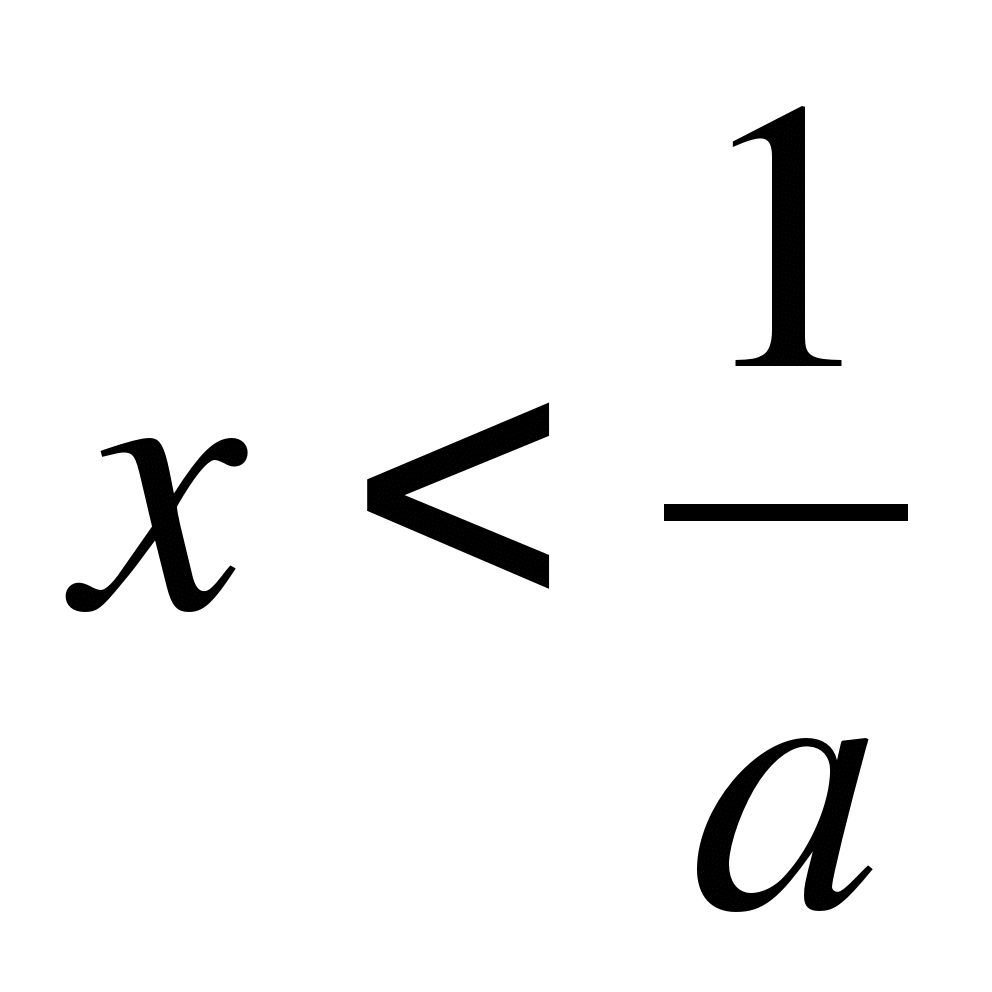
3) если a=0, то решений нет.
II. Решение линейных неравенств вида aх<b.
-
если a>0, то
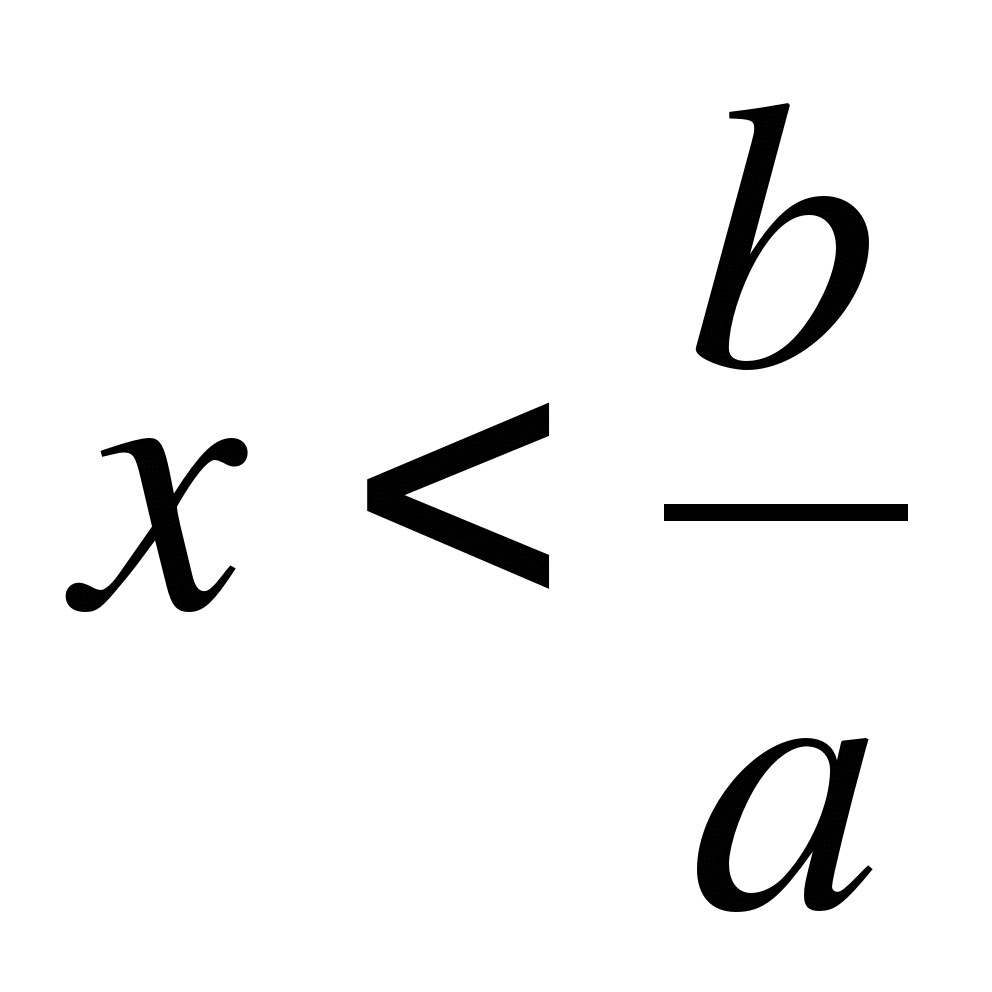 .
.
-
если a<0, то
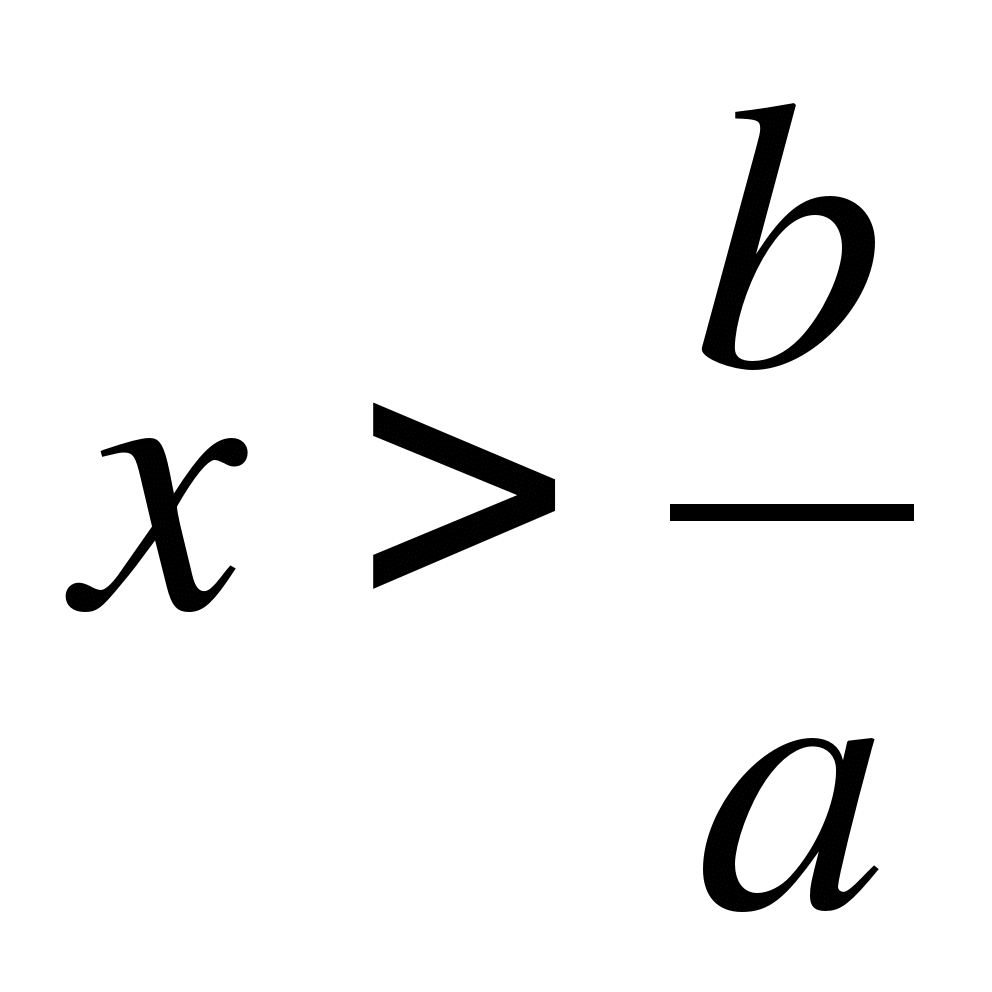 .
.
-
если a=0 и b>0, то
 .
.
-
если a=0 и b
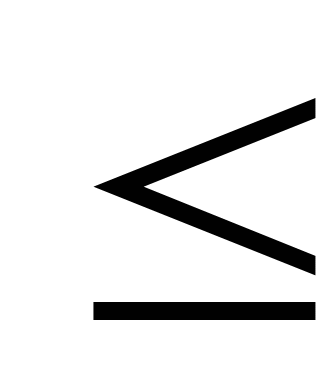 0,
то решений нет.
0,
то решений нет.
Пример 2. Решите неравенство ах<5.
1) если a>0, то
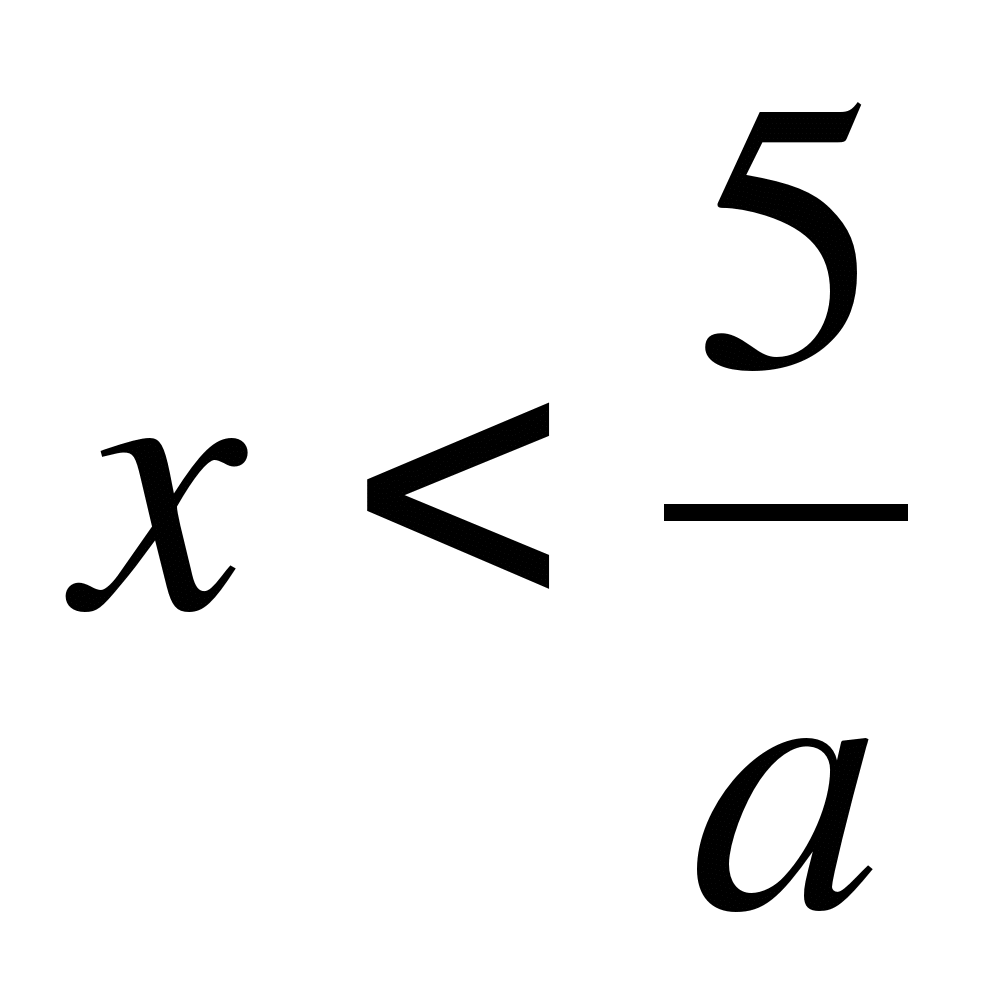
2) если a<0, то
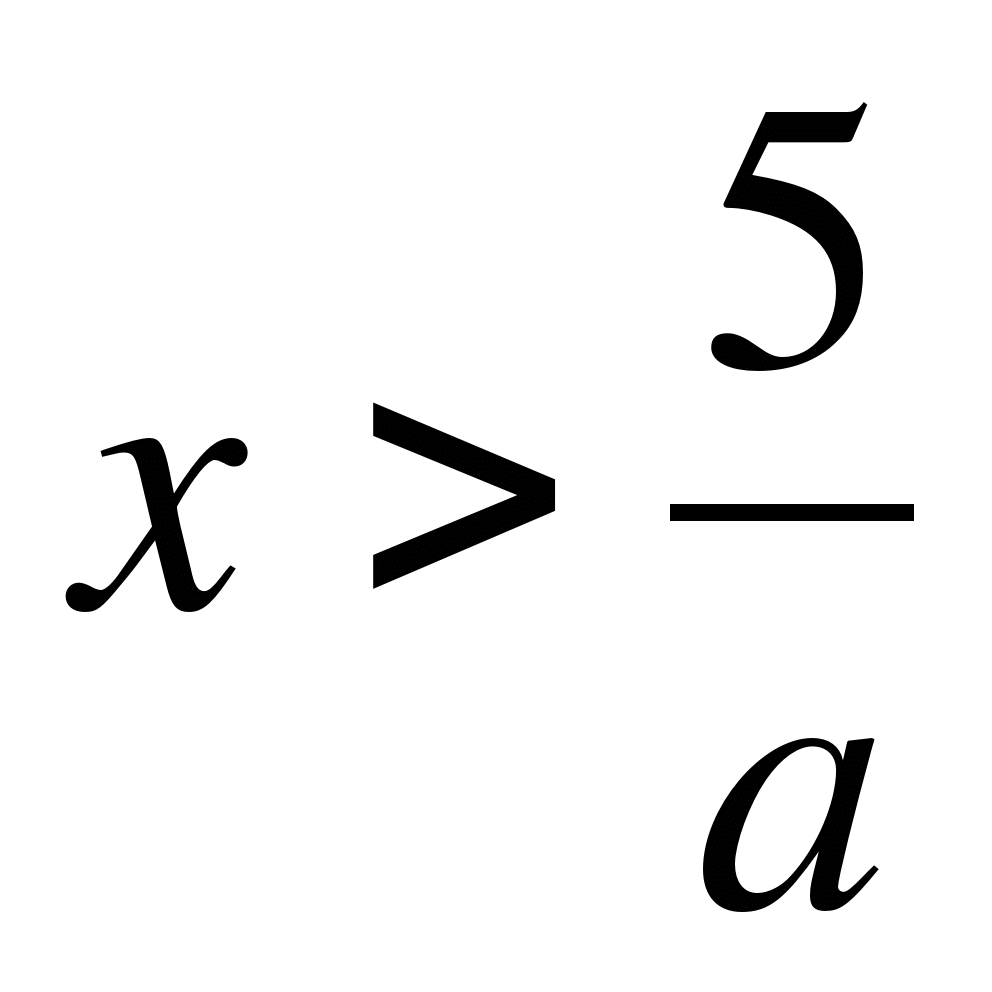
3) если a=0, то
 .
.
III. Решение линейных неравенств вида ax
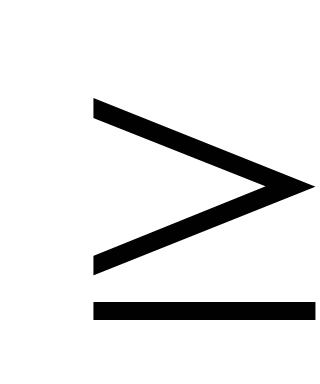 b.
b.
-
если a>0, то
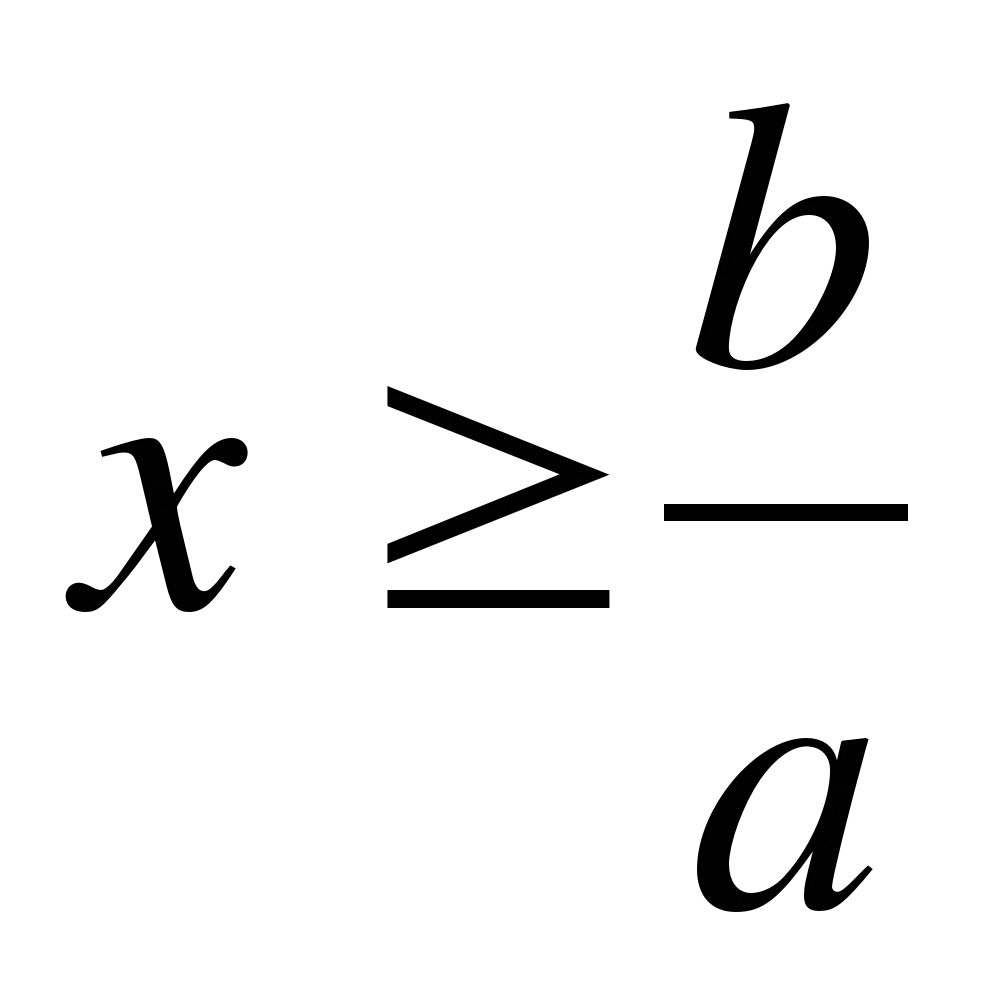 .
.
-
если a<0, то
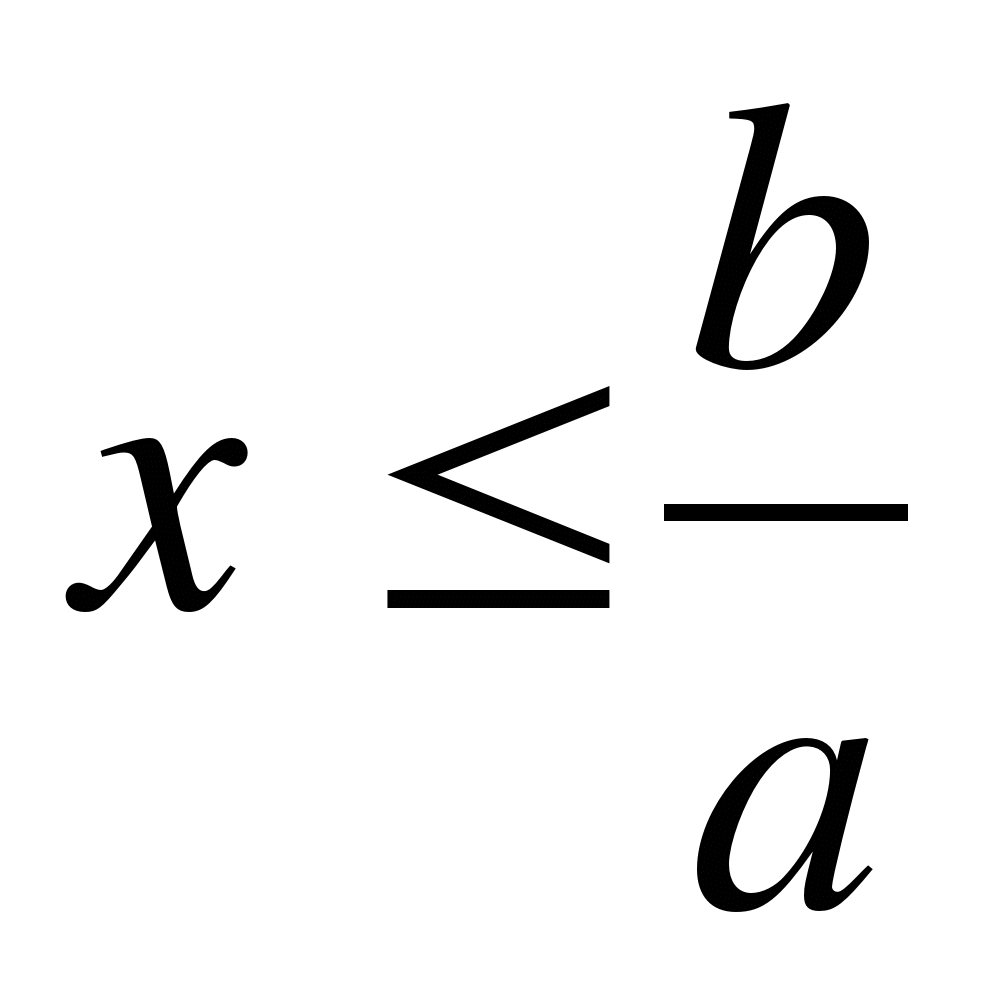 .
.
-
если a=0 и b
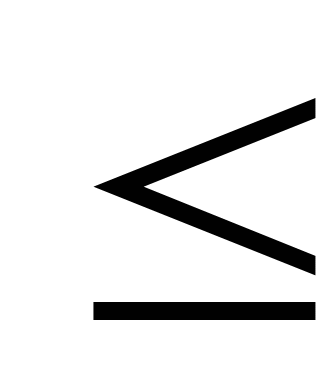 0,
то
0,
то  .
.
-
если a=0 и b>0, то решений нет.
Пример 3. Решите неравенство ax
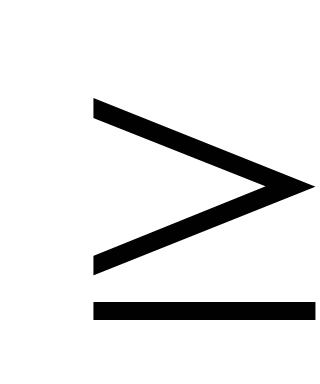 4.
4.
1) если a>0, то
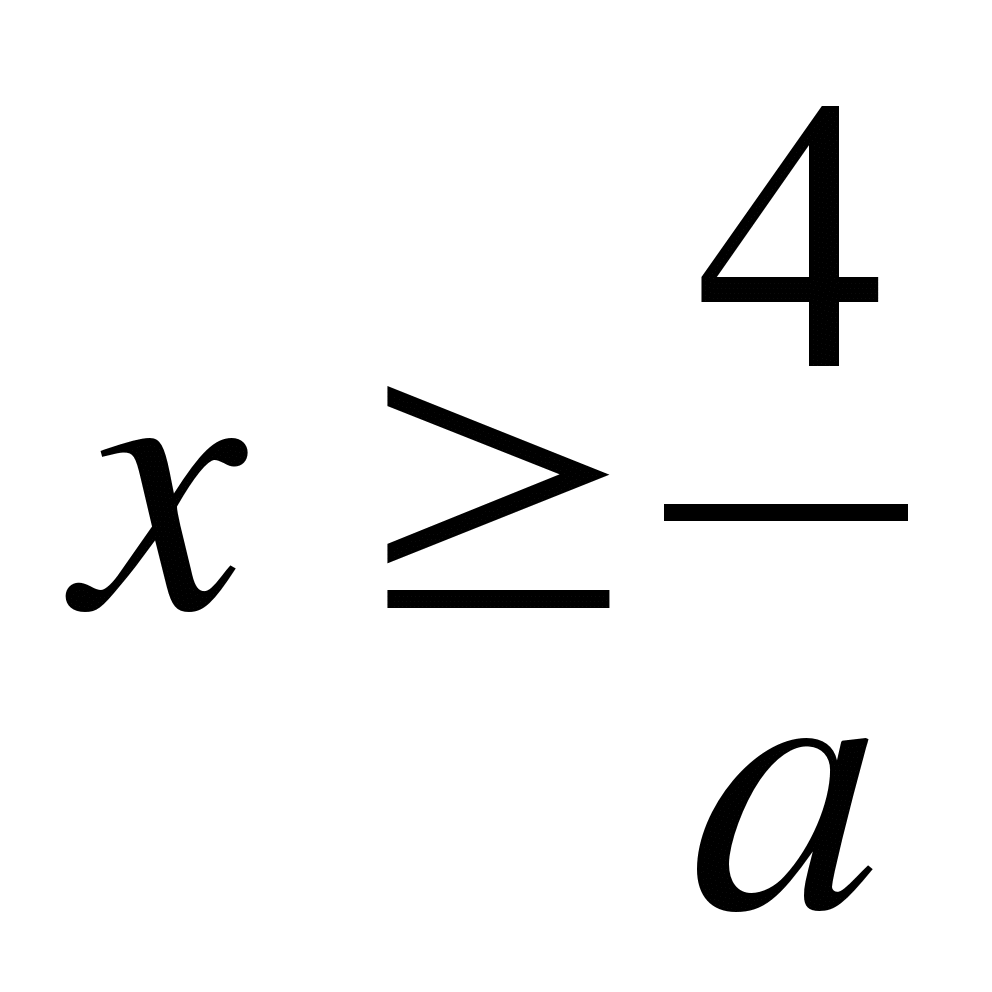
2) если a<0, то
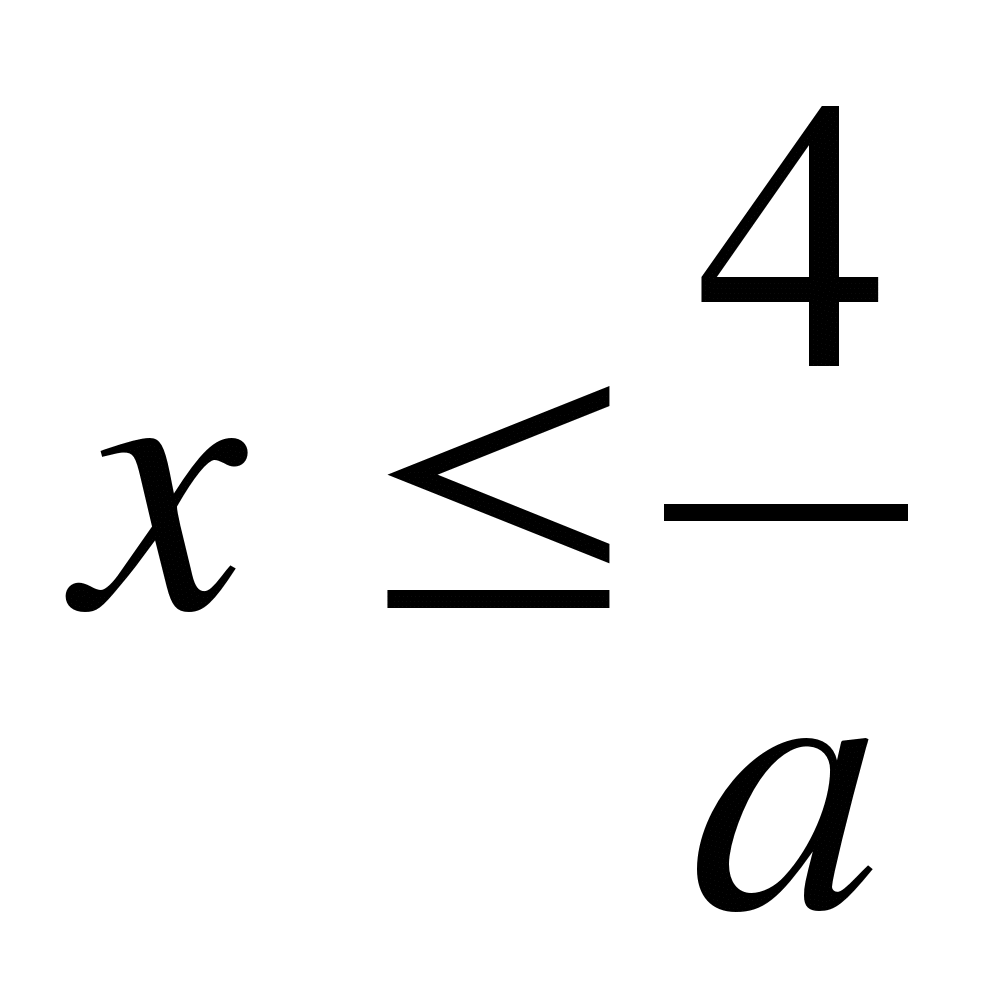
3) если a=0, то решений нет.
IV. Решение линейных неравенств вида ax
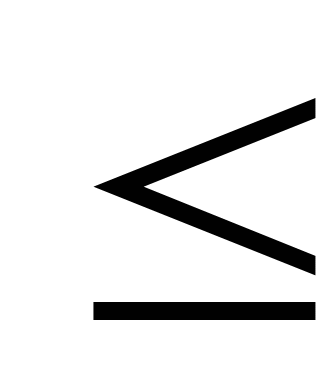 b
b
-
если a>0, то
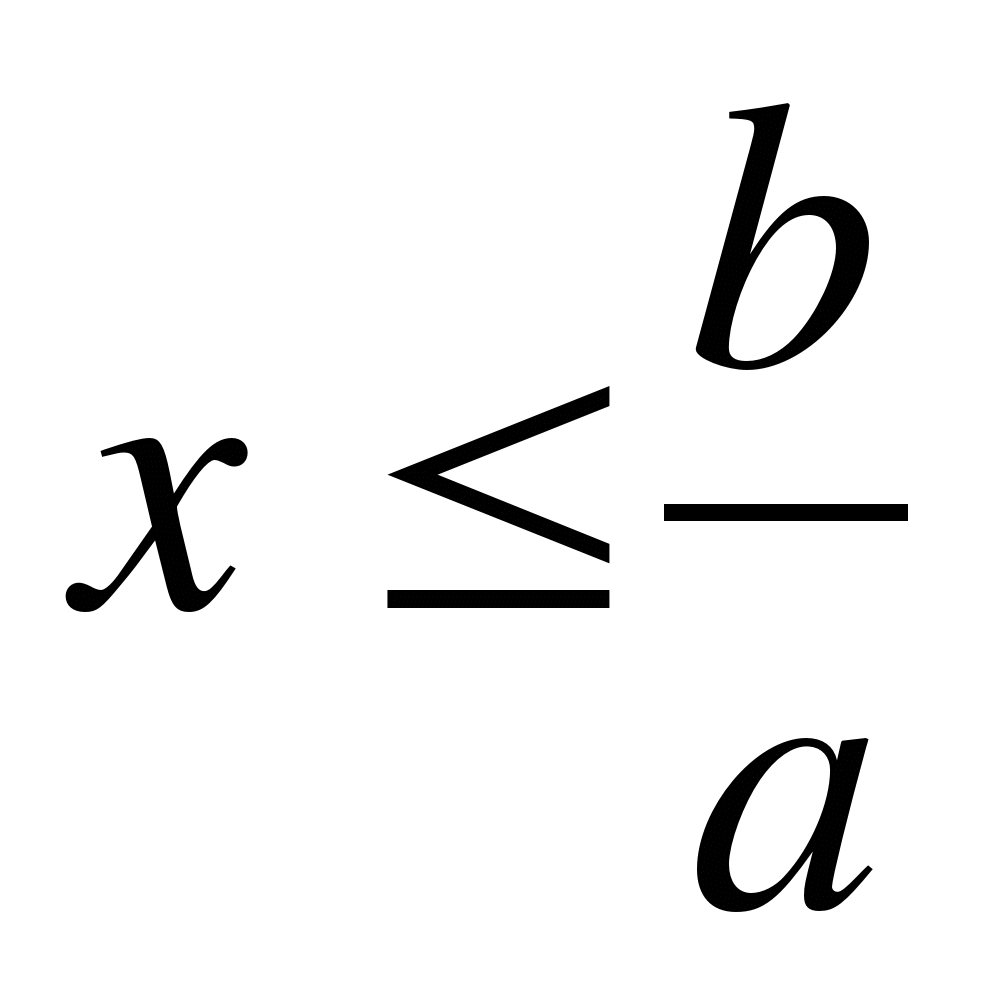 .
.
-
если a<0, то
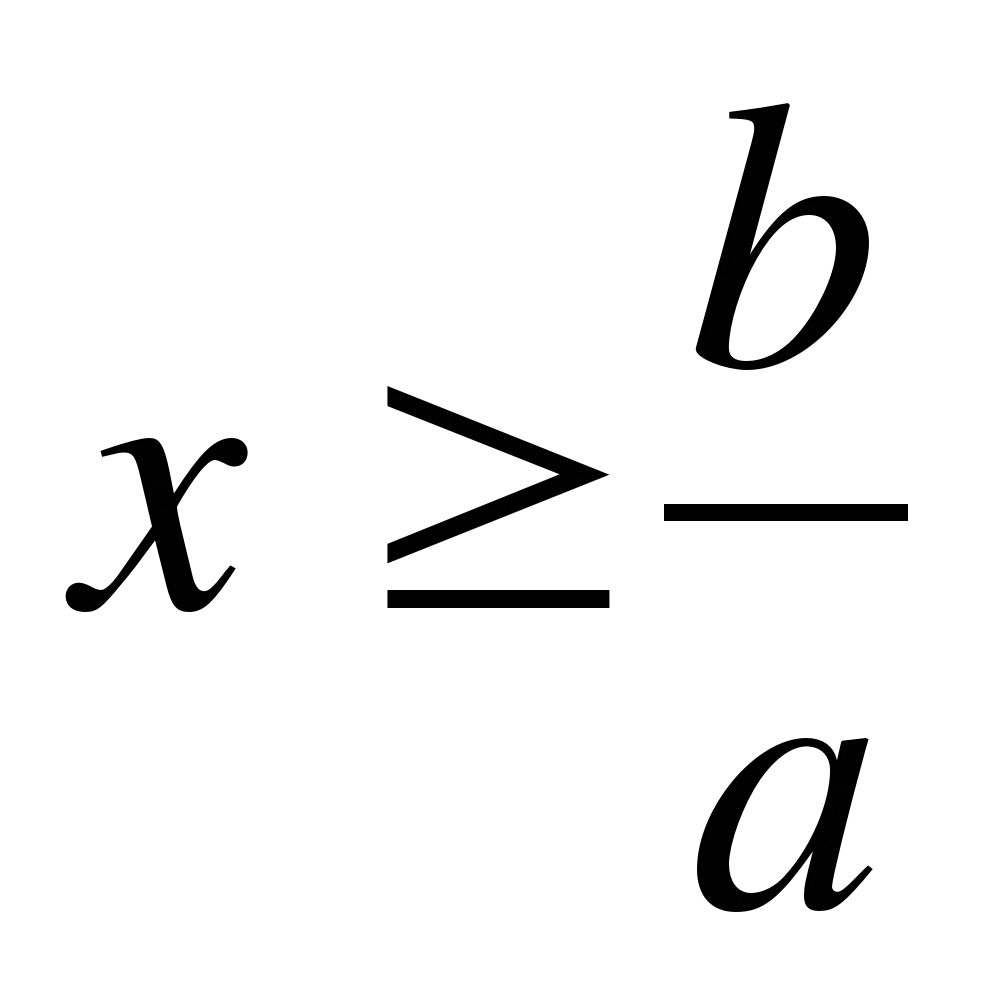 .
.
-
если a=0 и b
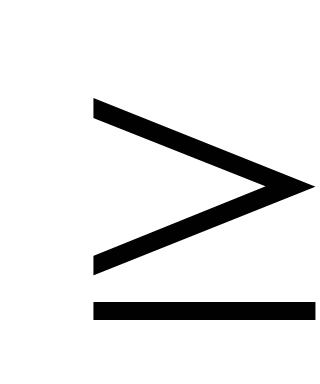 0,
то
0,
то  .
.
-
если a=0 и b<0, то решений нет.
Пример 4. Решите неравенство ах
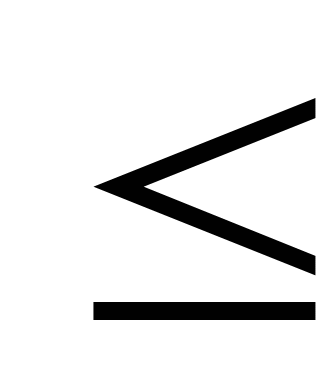 6.
6.
1) если a>0, то
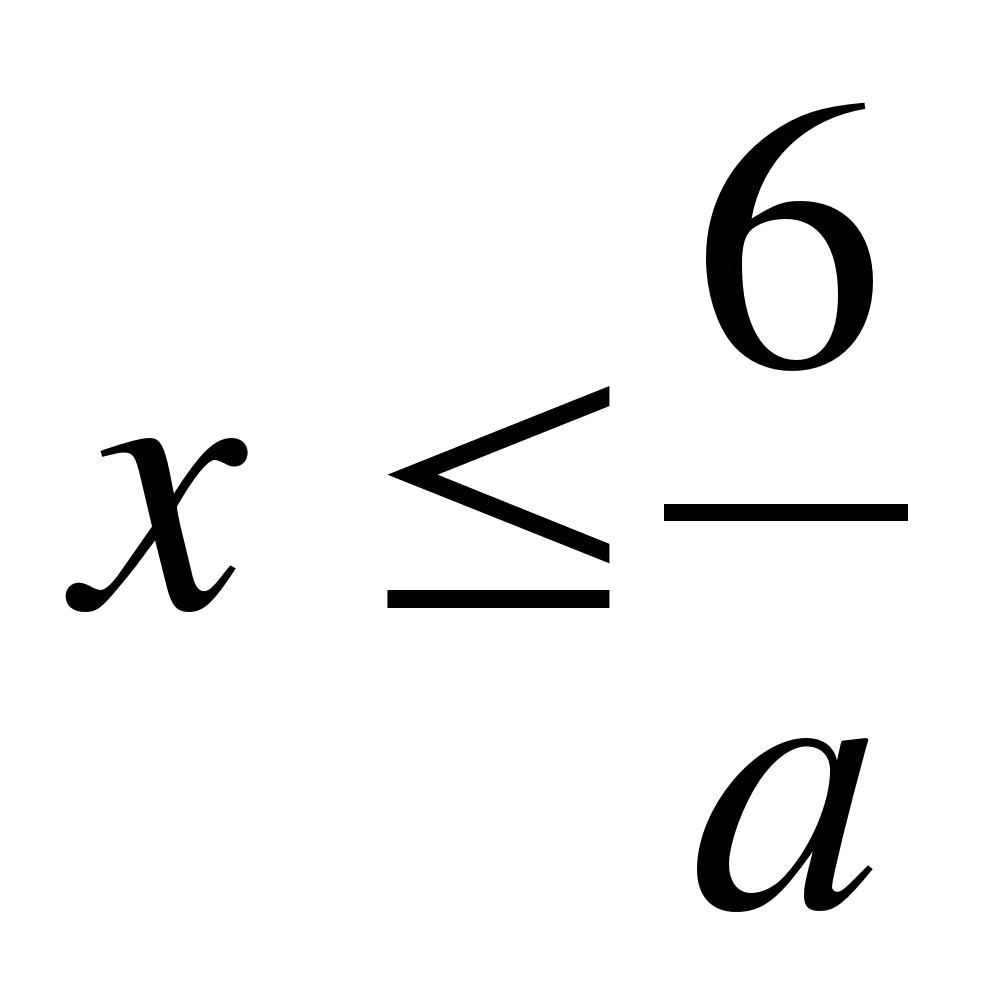 ;
;
2) если a<0, то
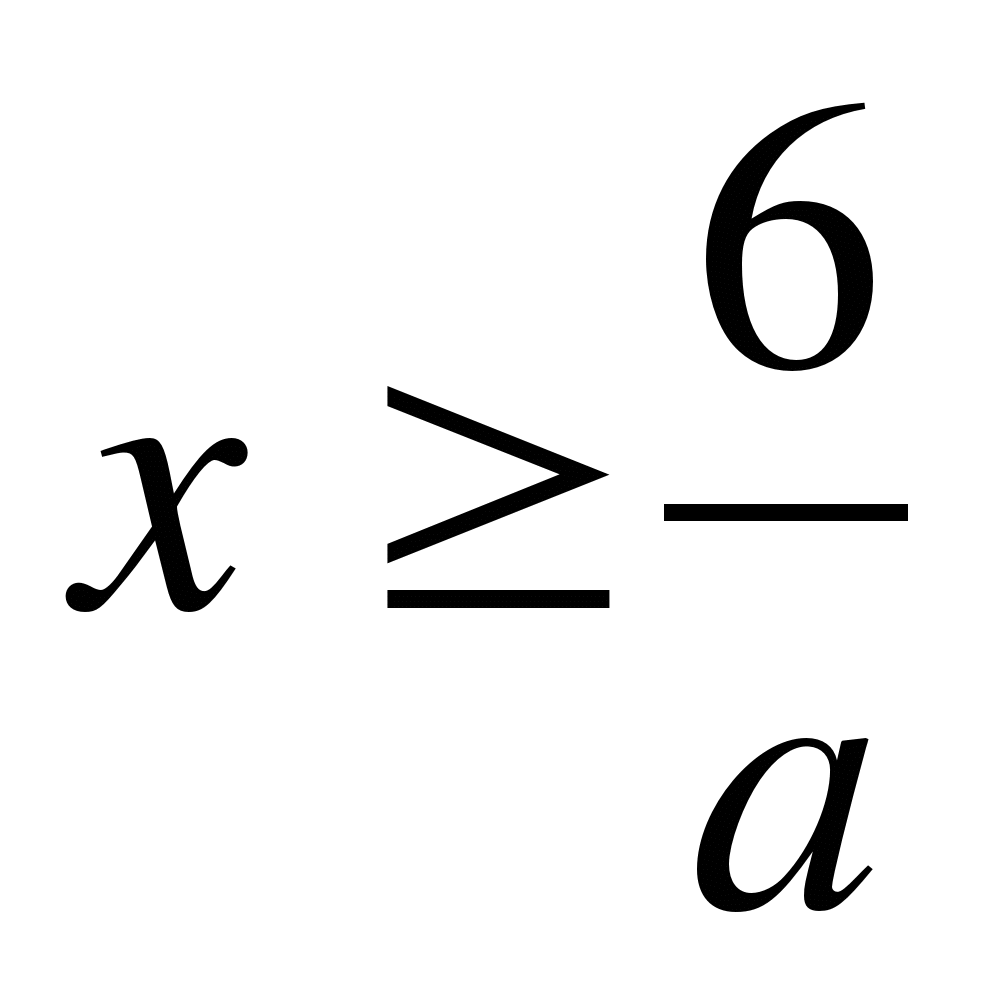 ;
;
3) если a=0, то
 .
.
II. Тренировочные упражнения.
Решить неравенства.
-
(m-1)x<5m
-
если m-1>0, т.е. m>1, то
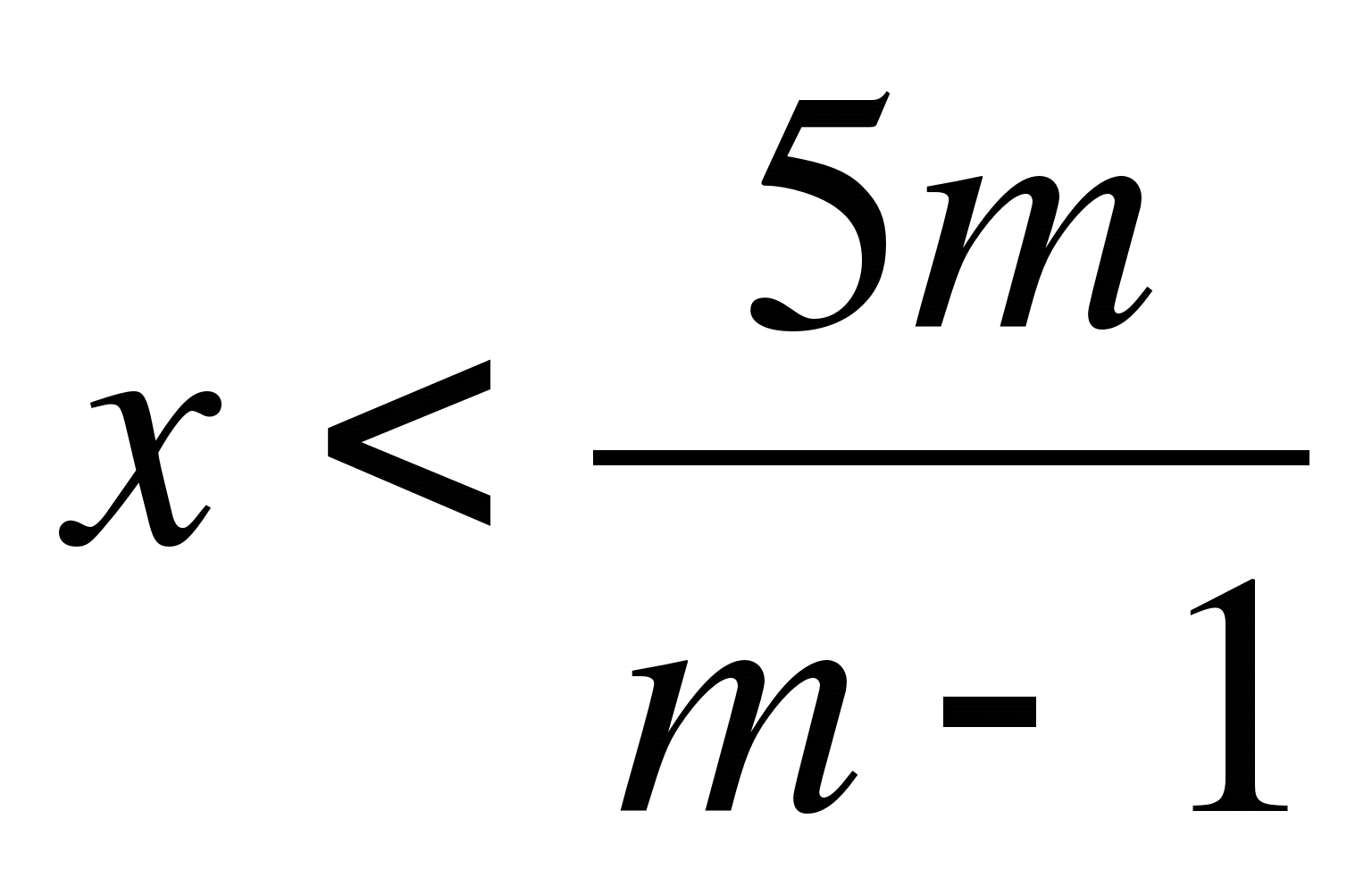 ,
,
2. если m-1<0, т.е. m<1, то
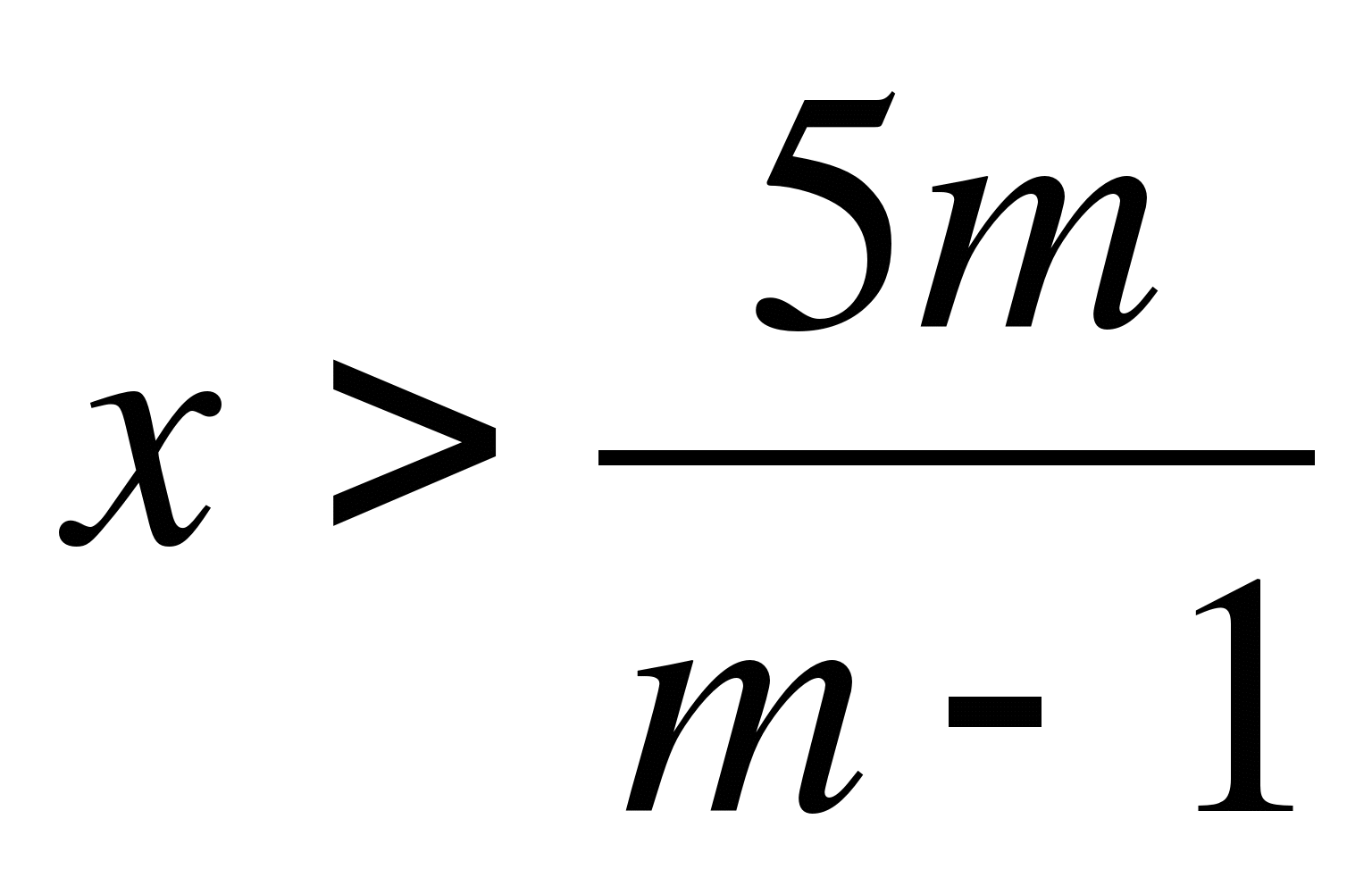 ,
,
3. если m-1=0, т.е. m=1, то
 .
.
-
(a-1)x>6
-
если a-1>0, т.е. a>1, то
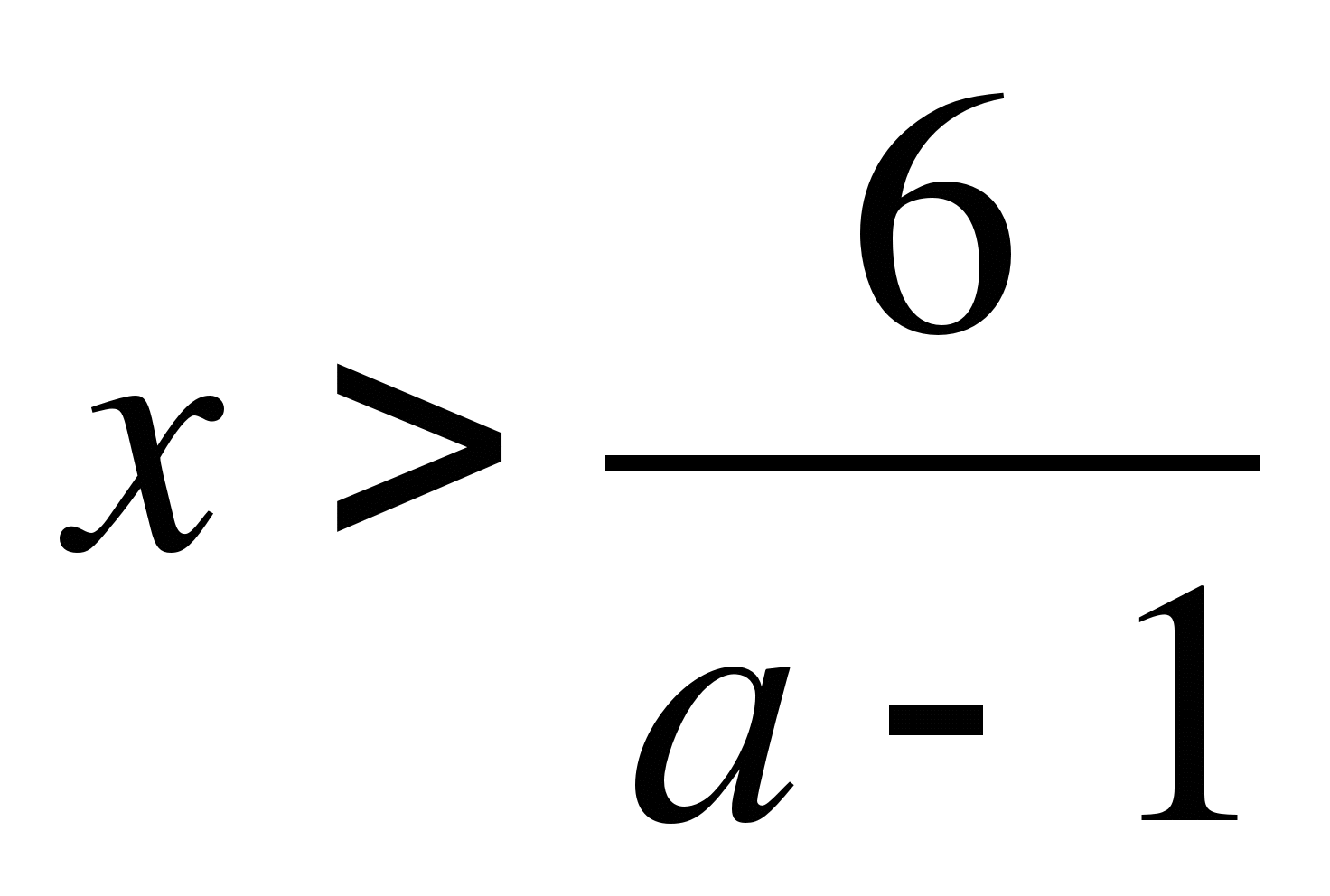 ,
,
2. если a-1<0, т.е. a<1, то
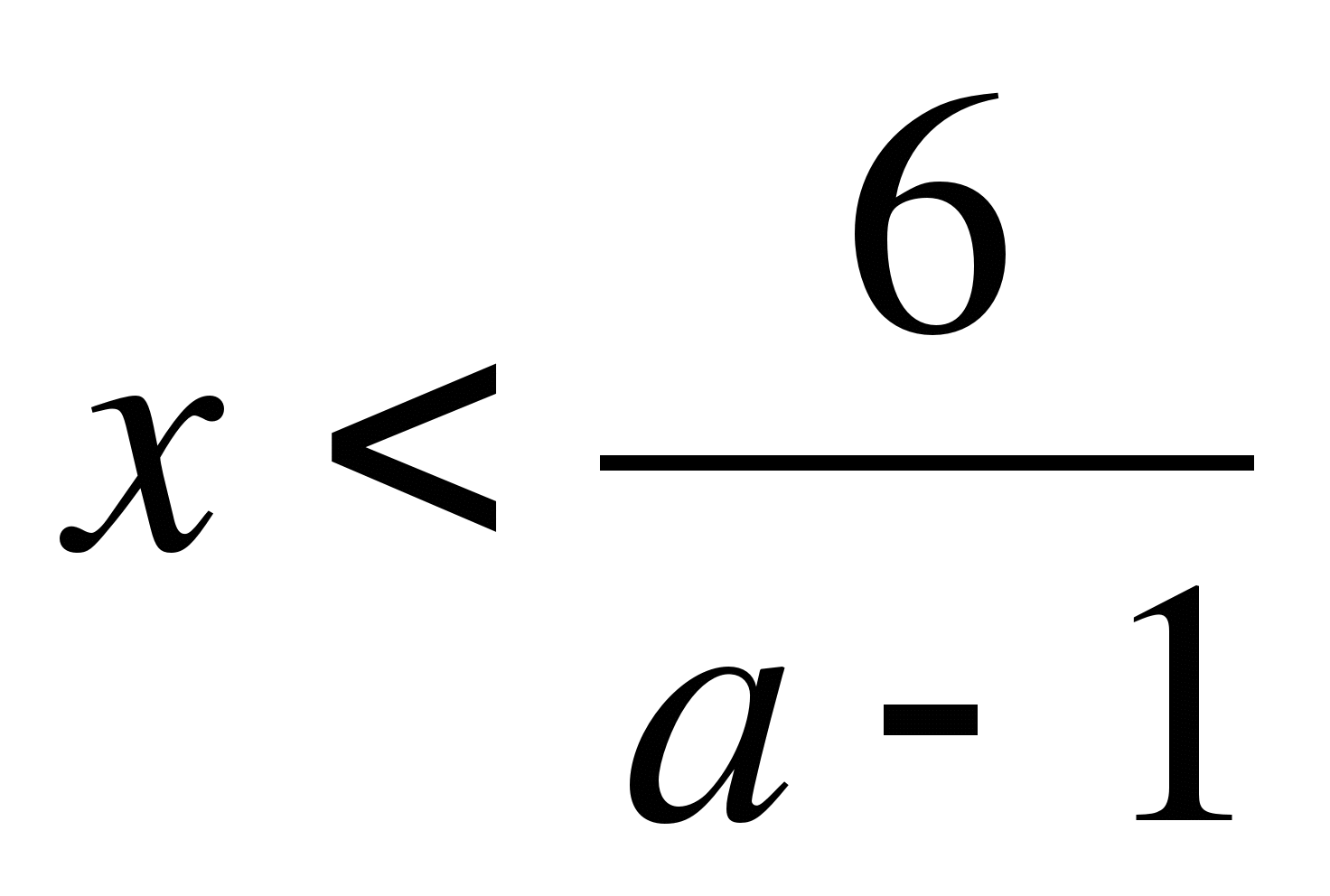 ,
,
3. если a-1=0, т.е. а=1, то решений нет.
-
При каких значениях параметра b уравнение
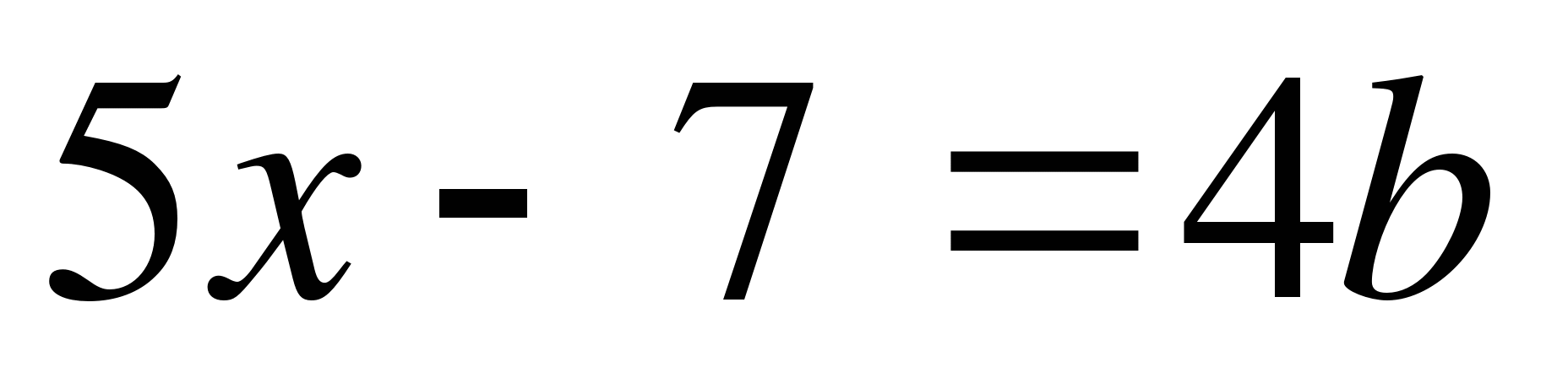 имеет положительный корень?
имеет положительный корень?
Решение.
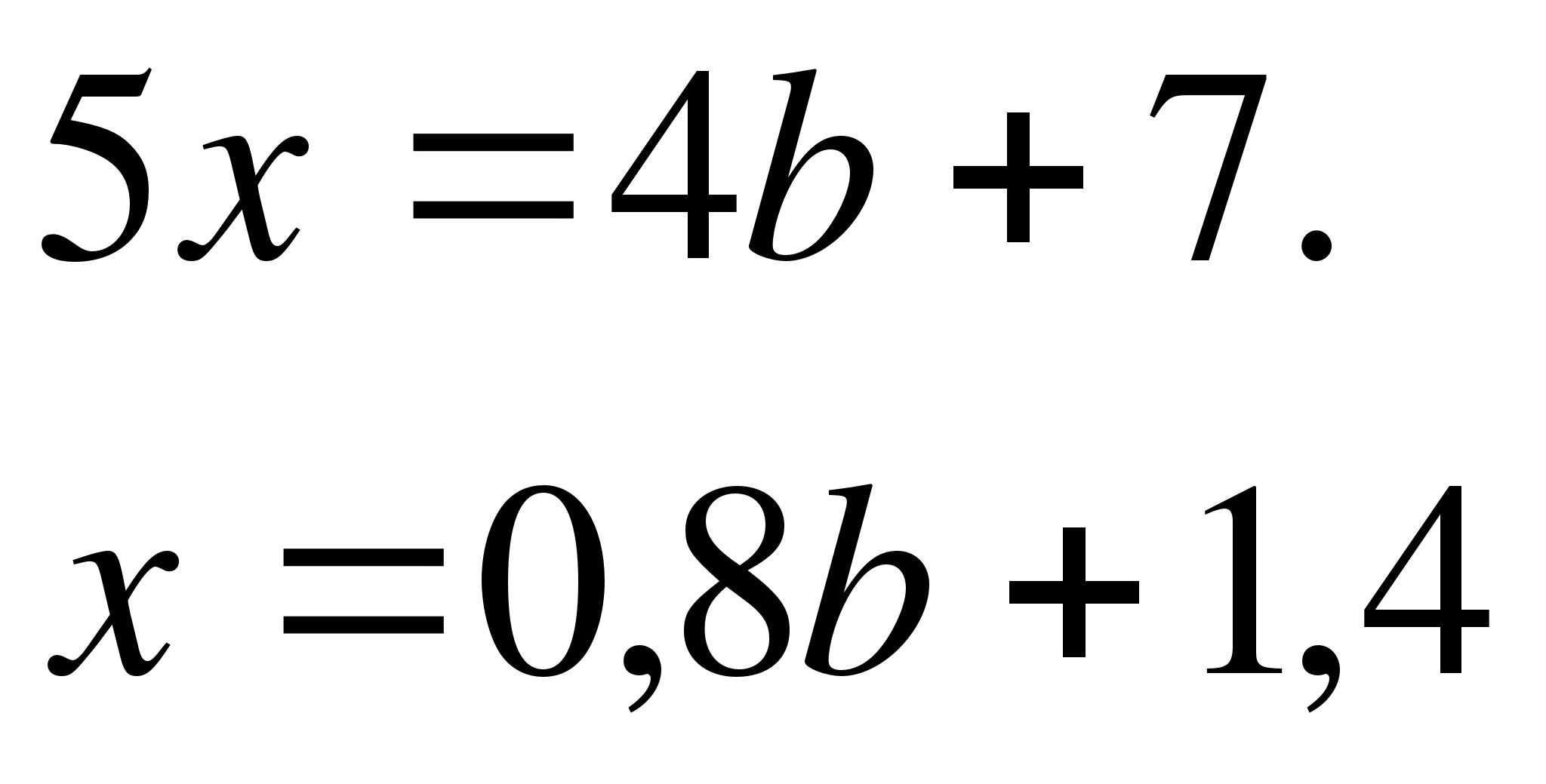 Так
как корень х>0, то 0,8 b+14>0; 0,8
b>-14; b>-1,75.
Так
как корень х>0, то 0,8 b+14>0; 0,8
b>-14; b>-1,75.
Ответ: при b>-1,75
III. Итоги занятия.
Занятие 2. Решение неравенств с параметром, сводящихся к линейным.
-
Упражнения по совершенствованию и закреплению знаний и умений.
Решить неравенство
-
2ах
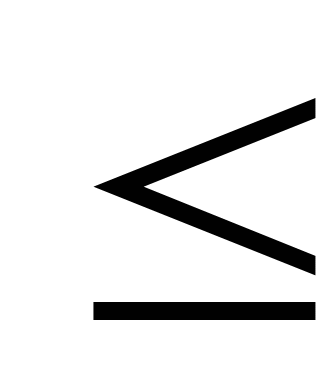 1-х.
1-х.
Решение:
2ах+х
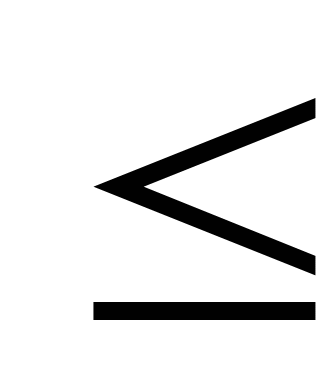 1,
1,
(2а+1)х
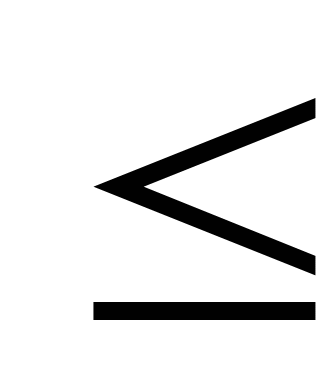 1;
1;
-
-
если 2a+1>0, т.е. а>-0,5, то
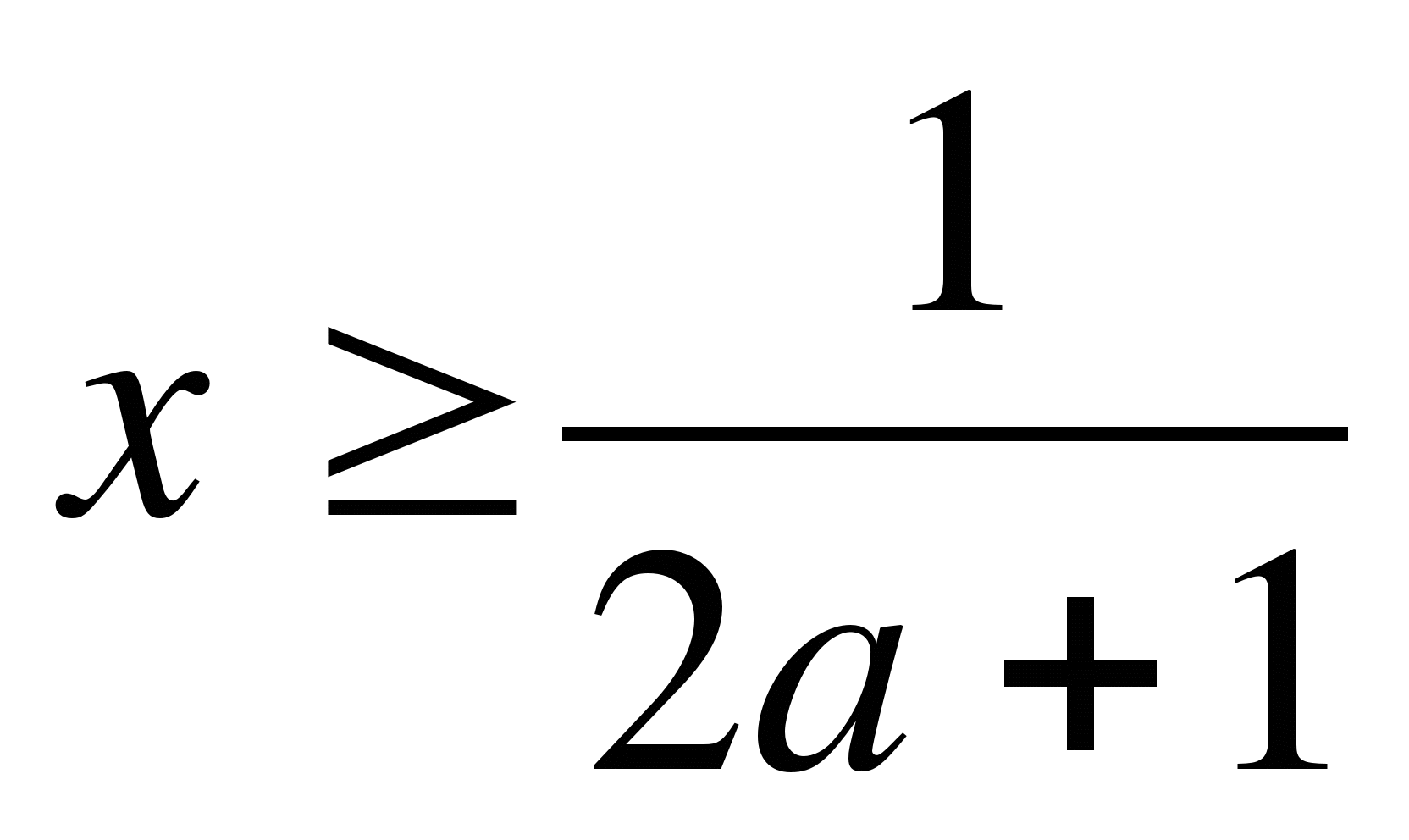 ;
;
-
если 2a+1<0, т.е. а<-0,5, то
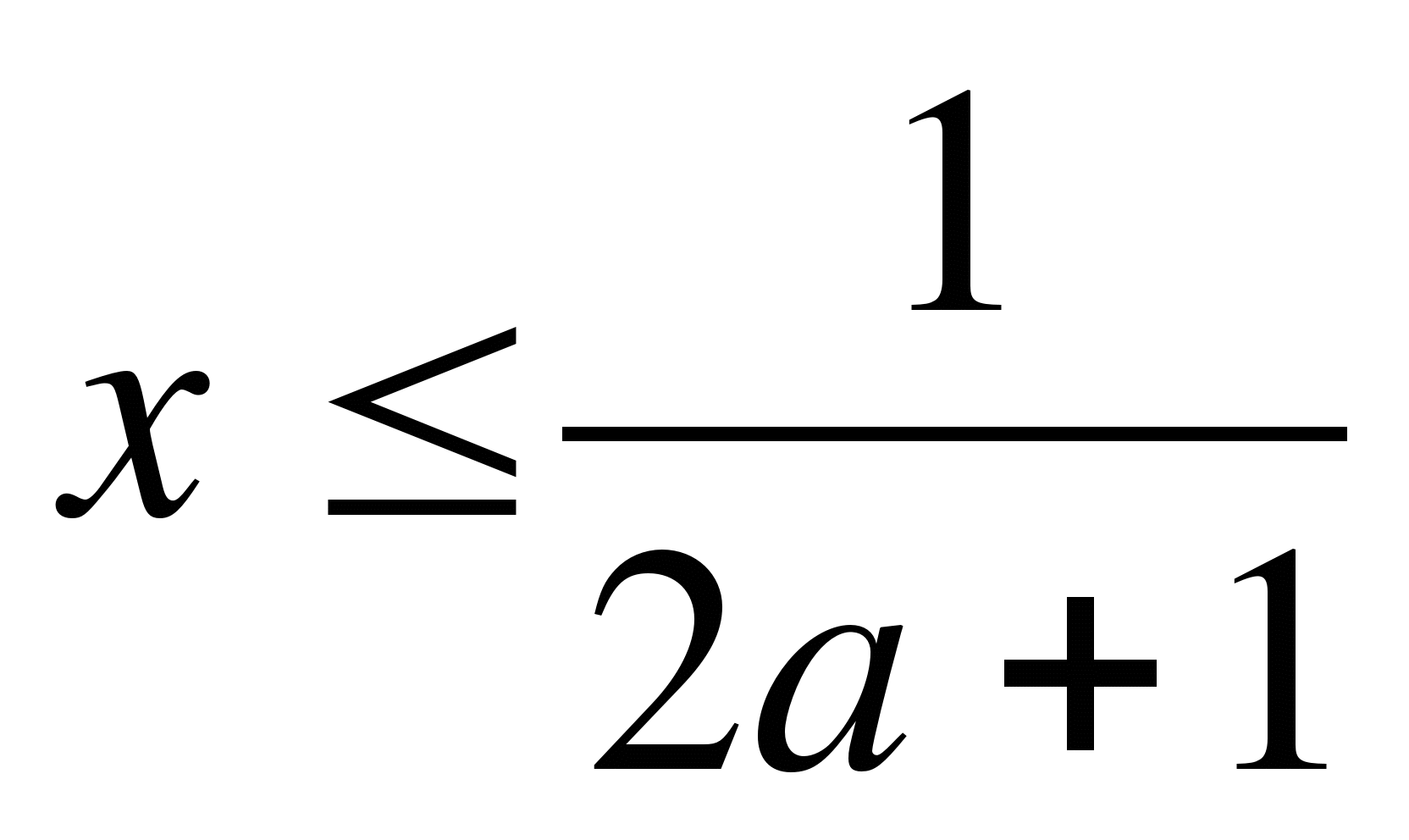 ;
;
-
если 2a+1=0, т.е. а=-0,5, то
 .
.
-
Ответ: если а>-0,5 , то
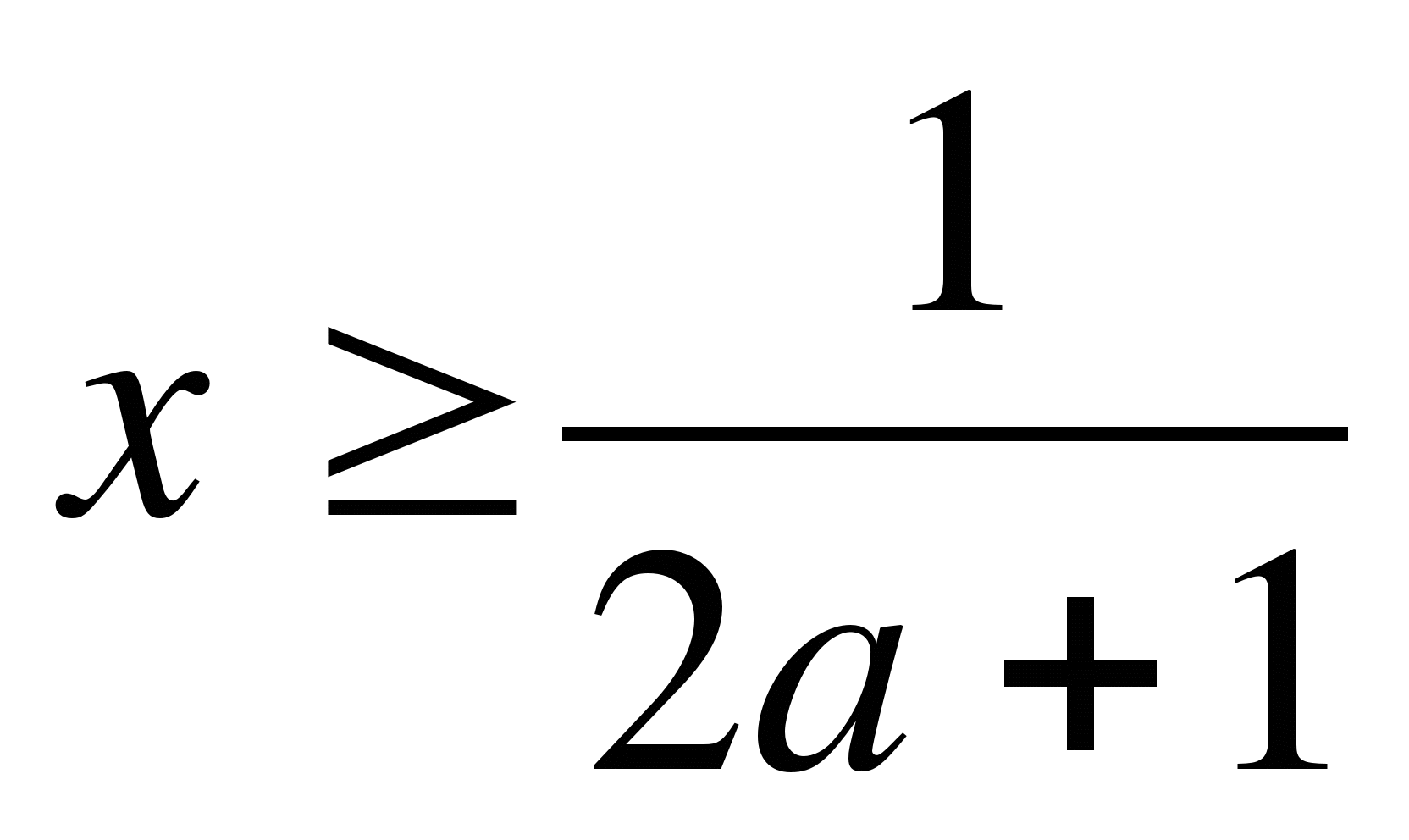 ;
если а<-0,5, то
;
если а<-0,5, то 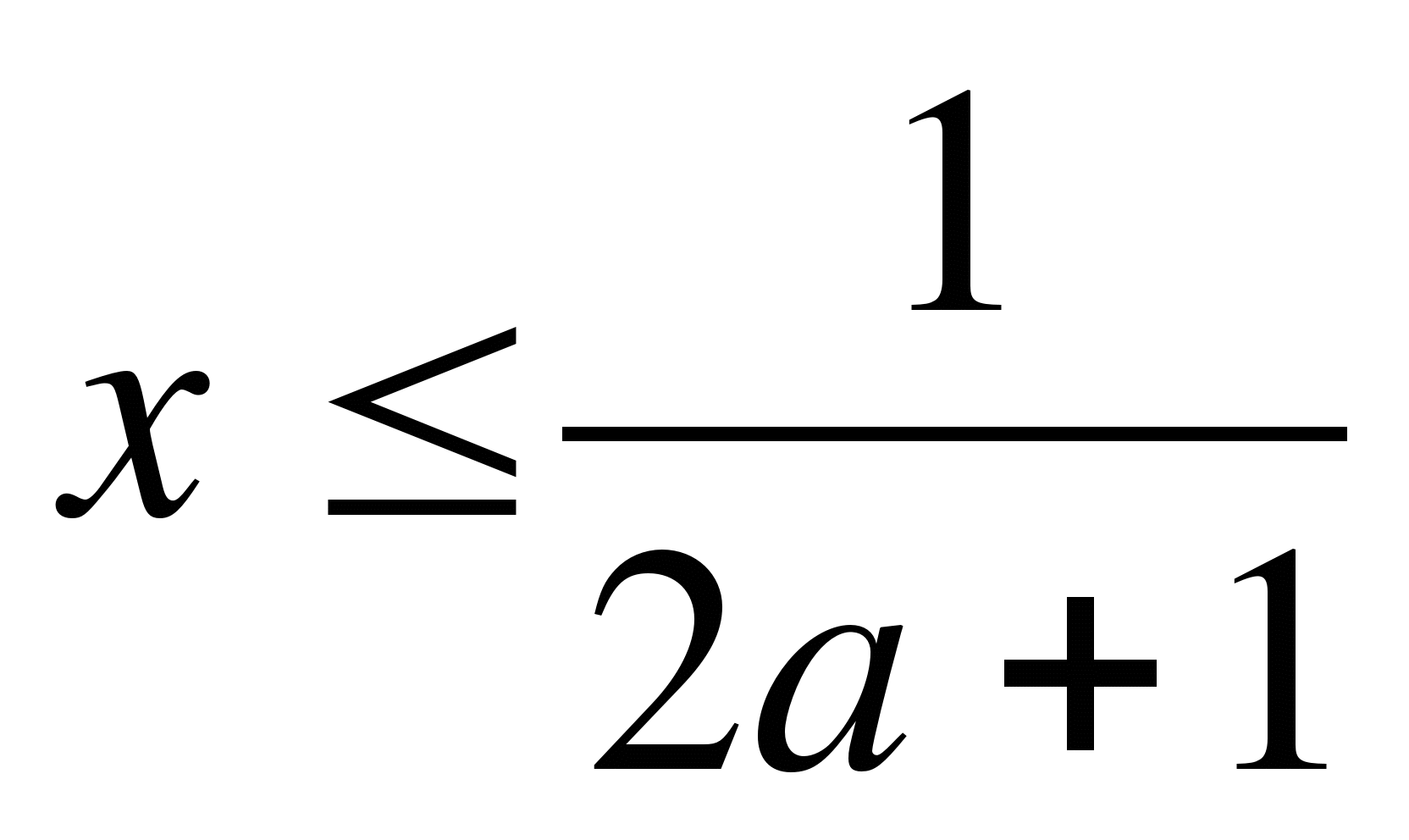 ;
;
если а=-0,5, то
 .
.
-
3-ах>x.
Решение:
х+ах<3,
(1+а)х<3;
-
-
если а+1>0, т.е. a>-1, то
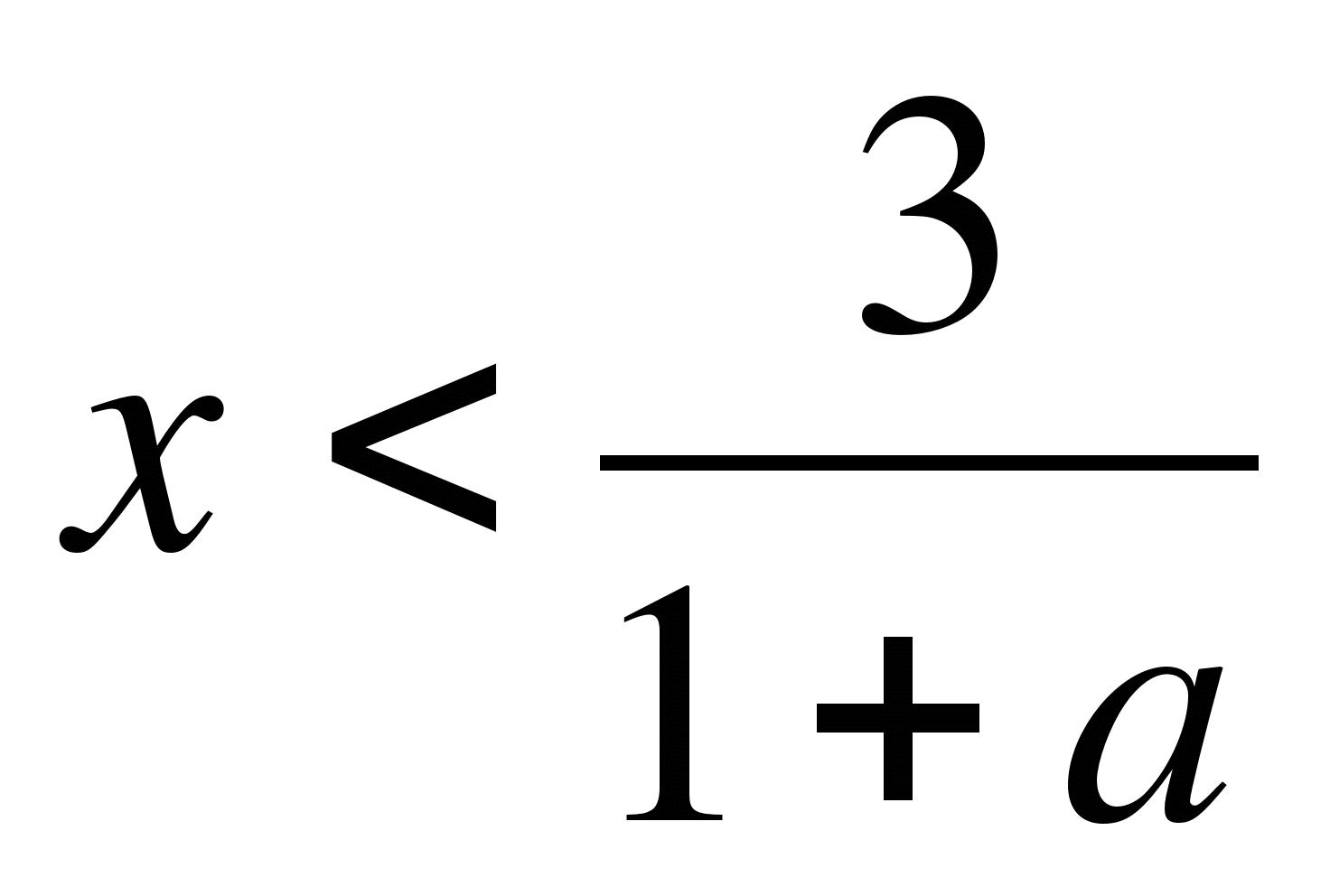 ;
;
-
если a<-1, то
 ;
;
-
если a=-1, то
 .
.
-
Ответ: если a>-1, то
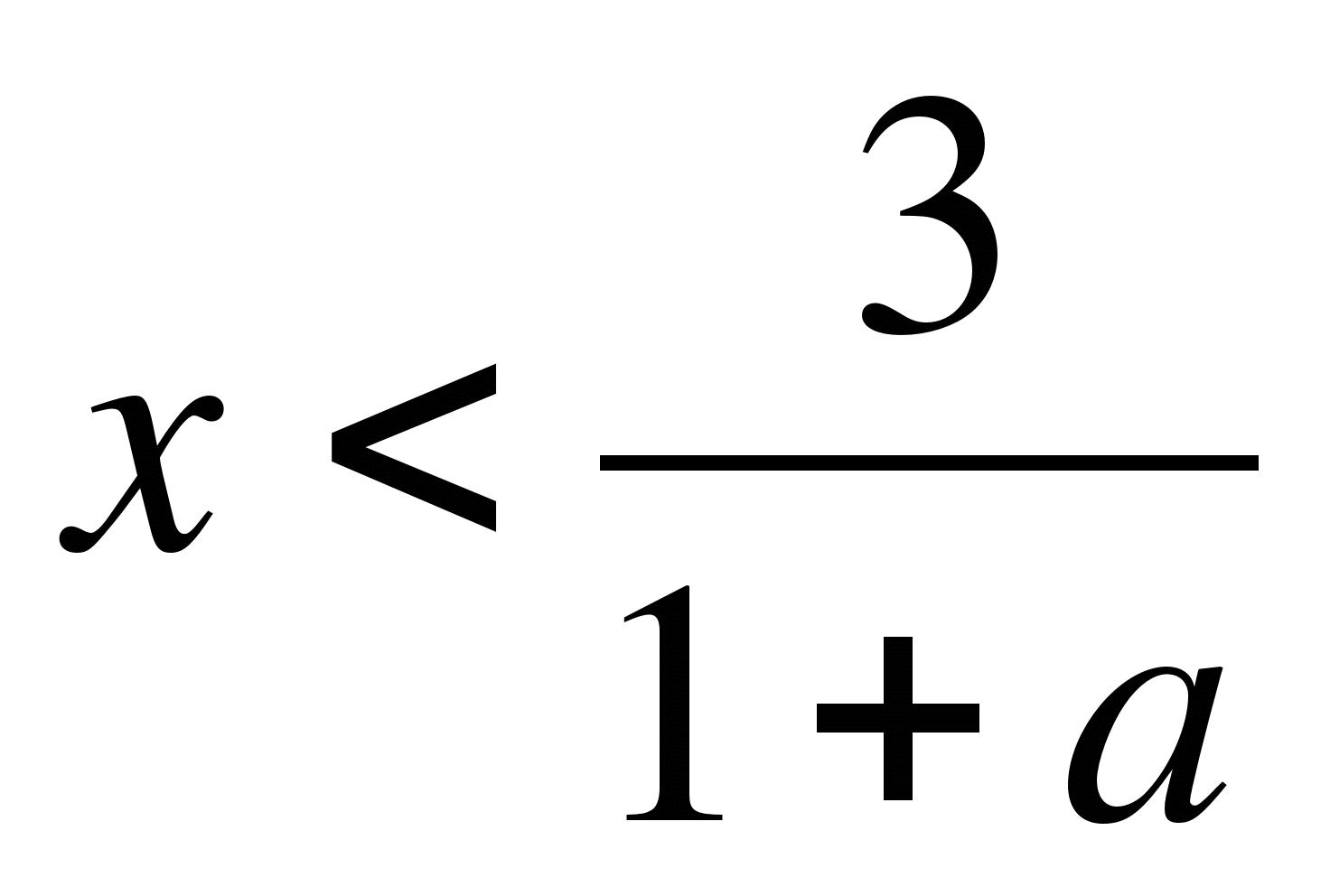 ;
если a<-1, то
;
если a<-1, то  ;
если a=1, то
;
если a=1, то  .
.
-
5x-а<ax+3.
Решение:
5x-аx<3+a
(5-а)x<3+a
-
-
если 5-a>0, т.е. a<5, то
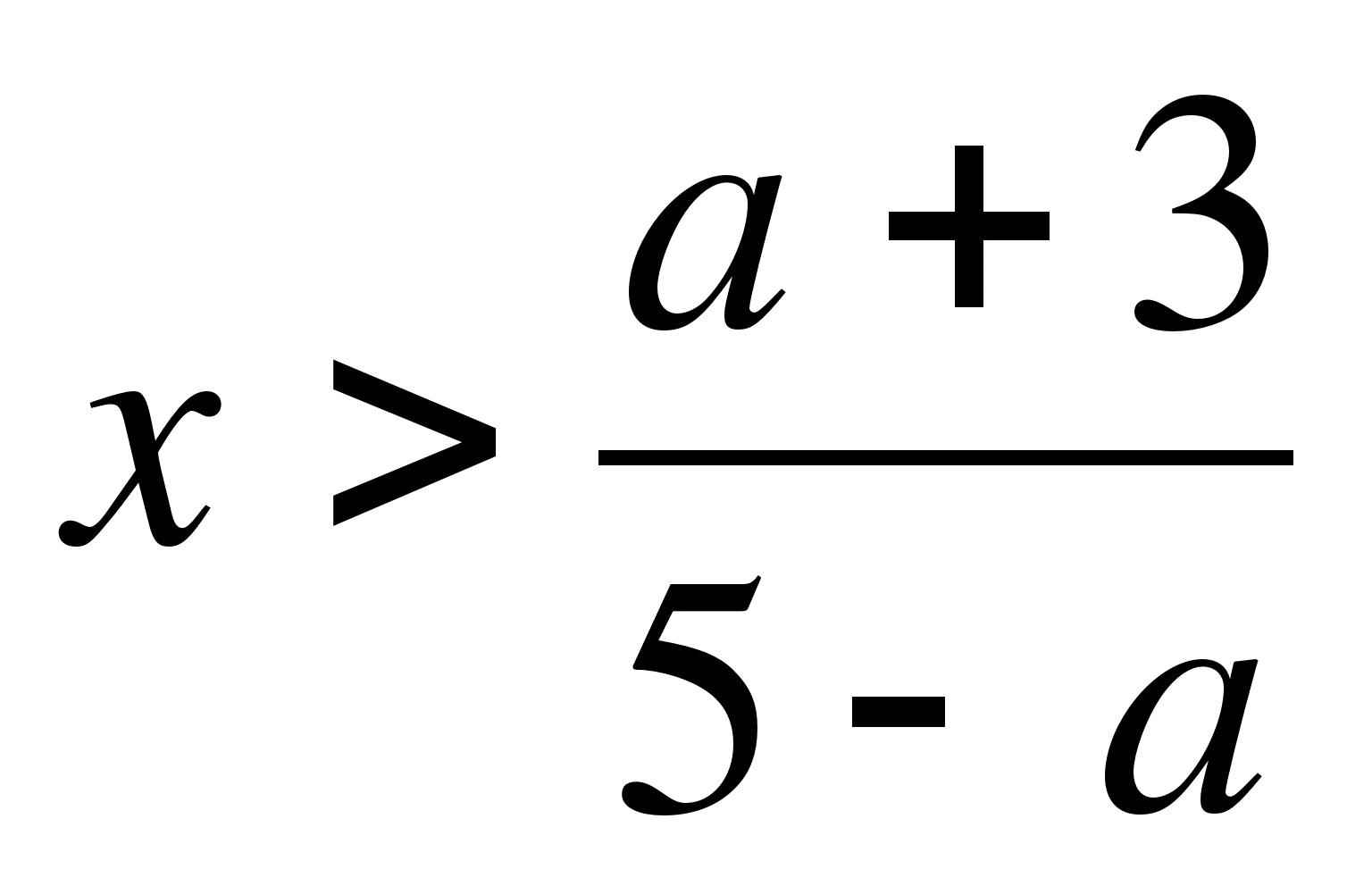 ;
;
-
если 5-a<0, т.е. a>5, то
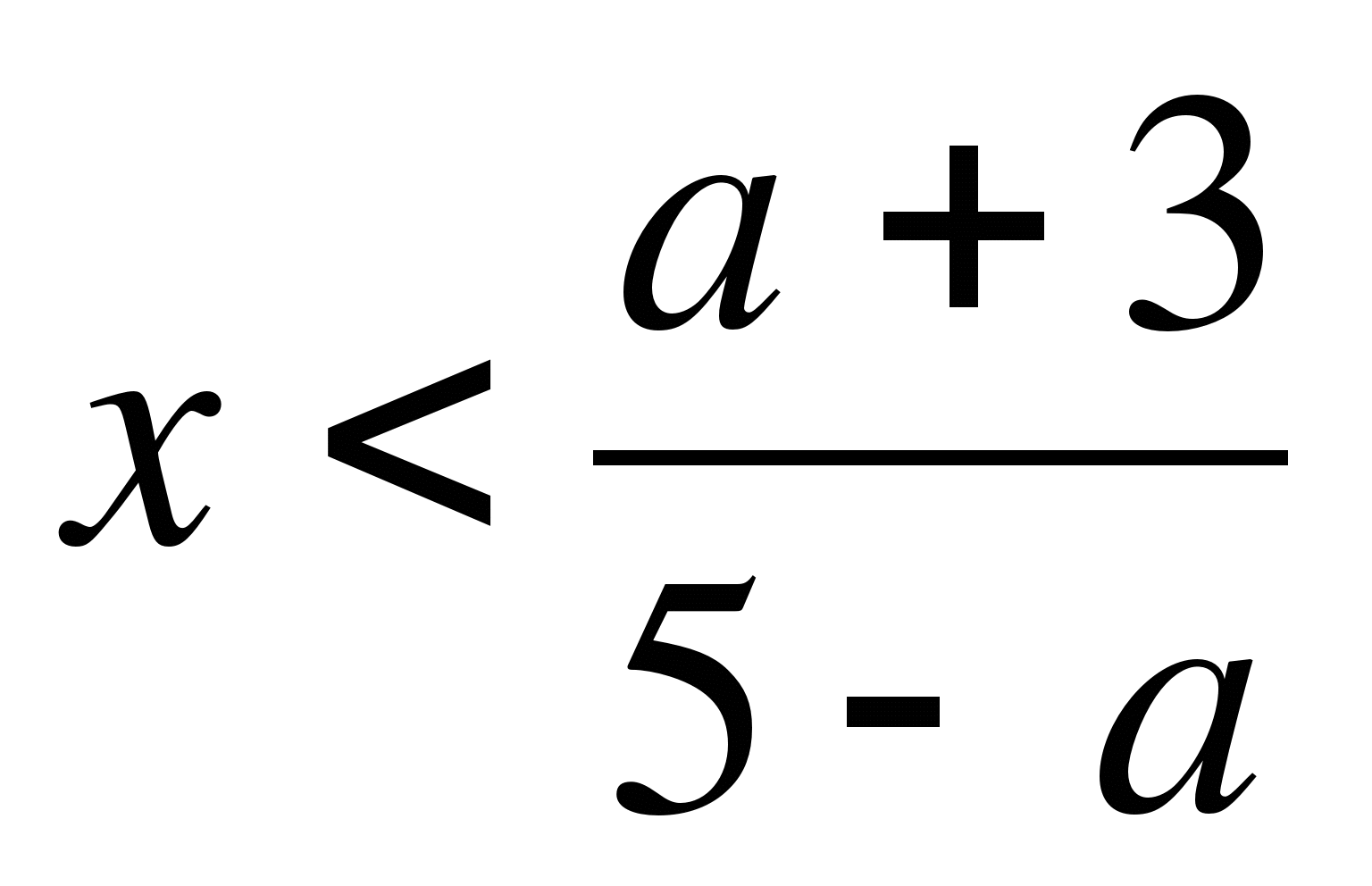 ;
;
-
если a=5, то
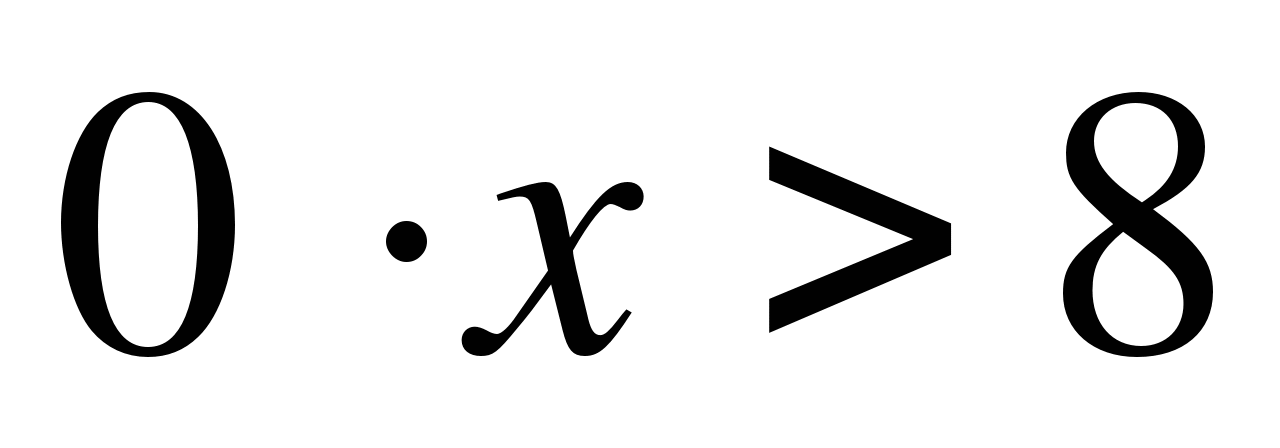 , решений нет.
, решений нет.
-
Ответ: если
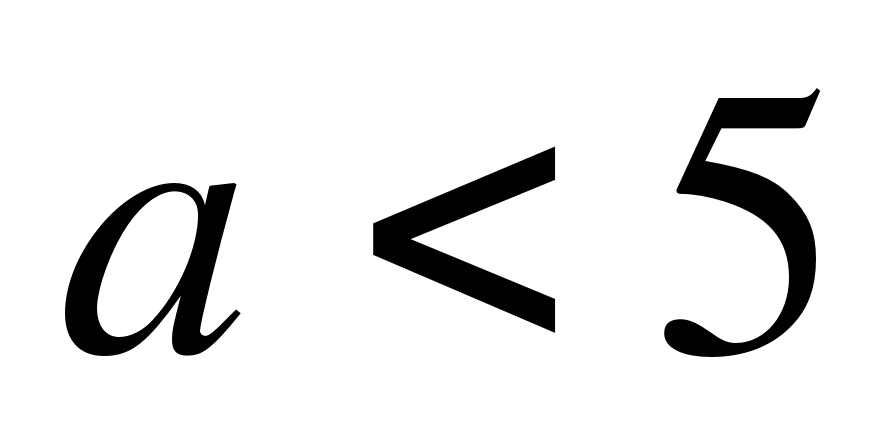 , то
, то
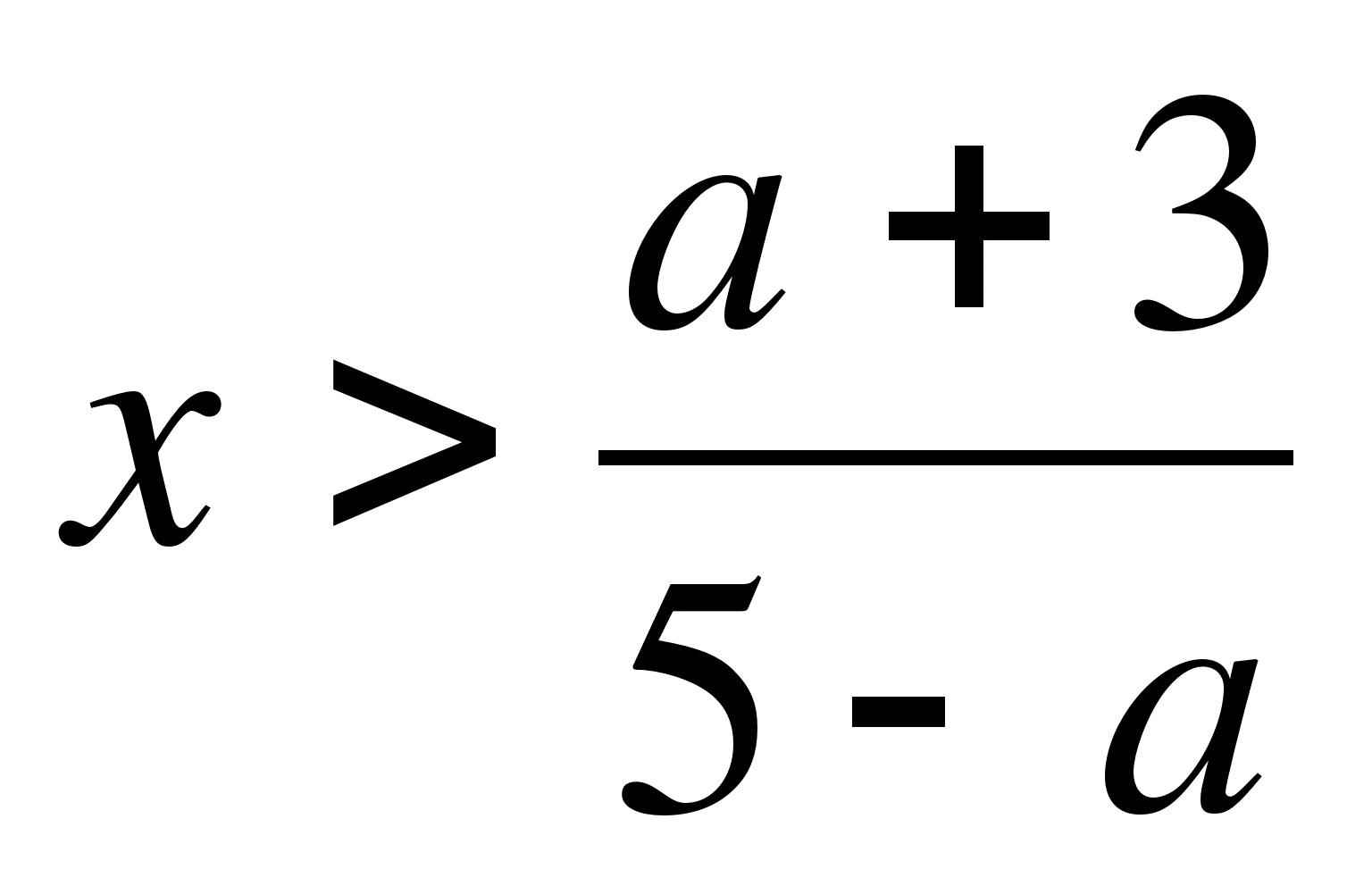 ;
если
;
если 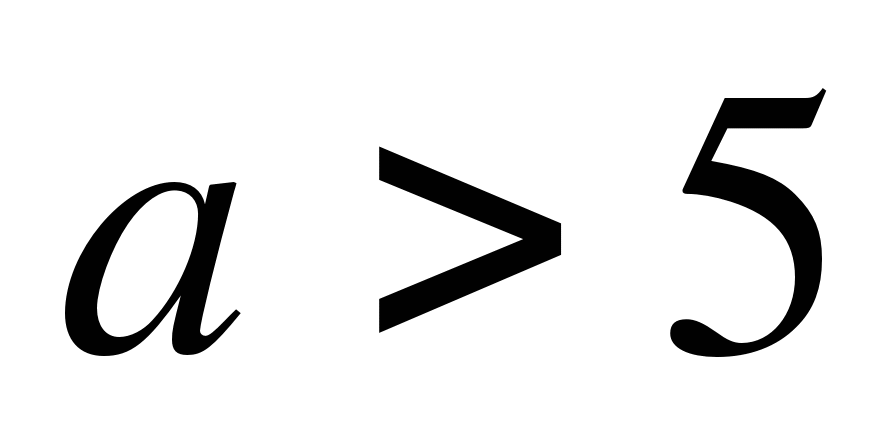 , то
, то
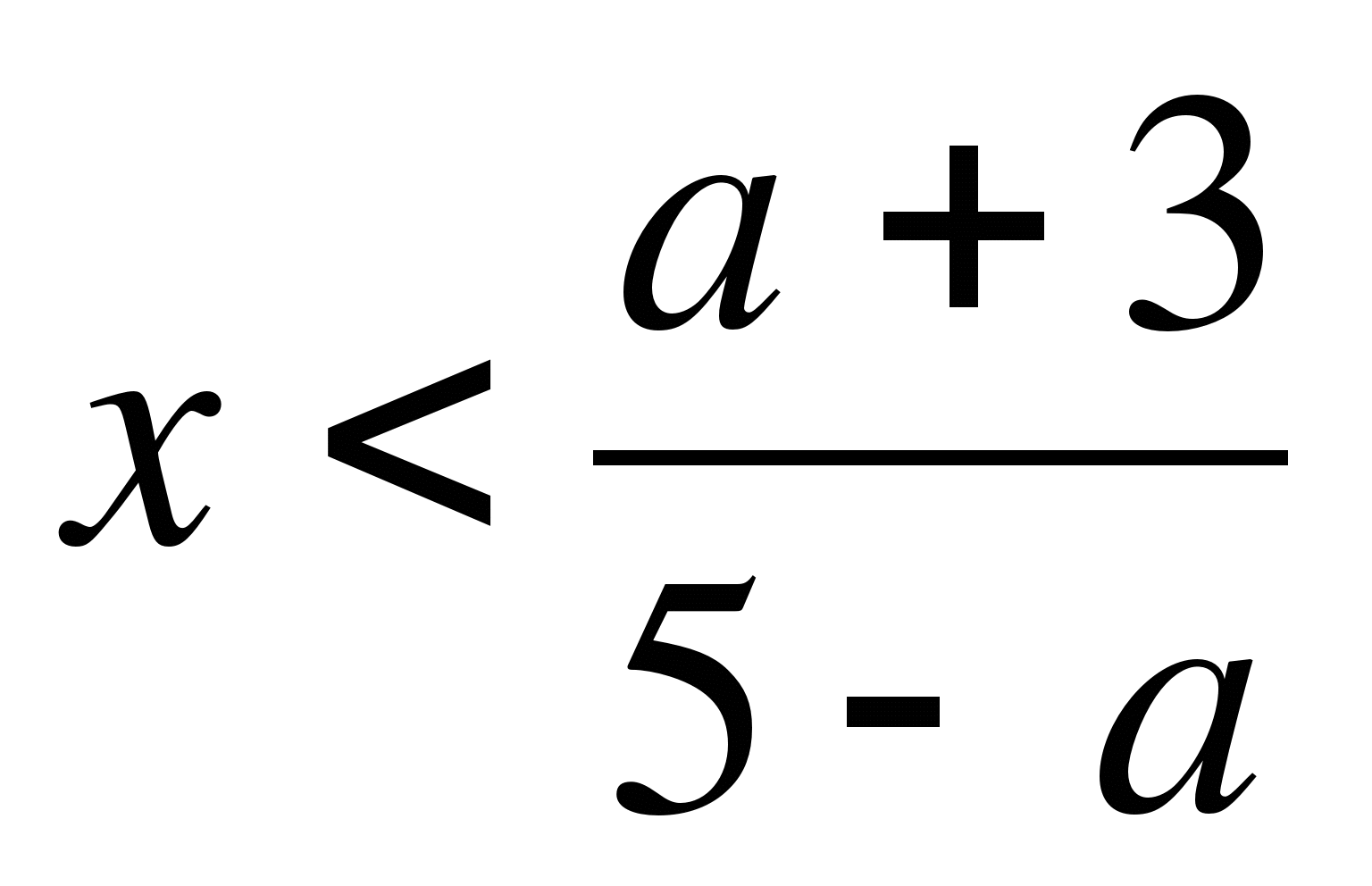 ;
если
;
если 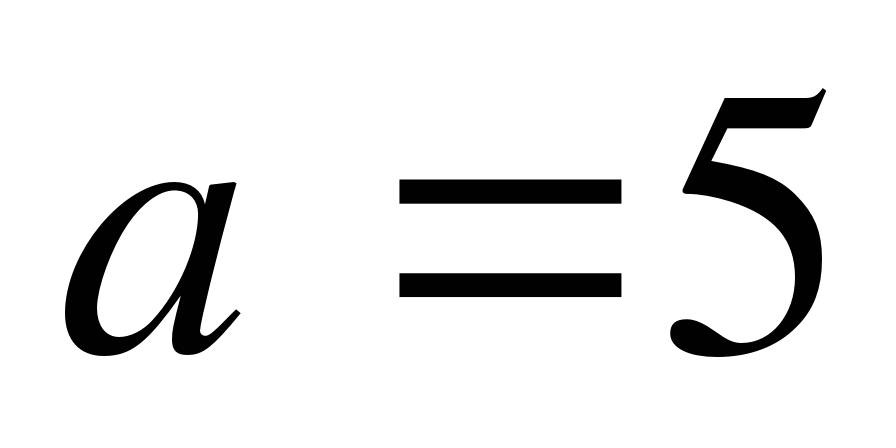 , то
решений
, то
решений
нет.
-
Решить неравенство 3(2а-х)<ax+1.
3(2а-х)<ax+1;
6a-3x<ax+1;
ax+3x>6a-1;
(a+3)x>6a-1.
-
-
если a+3>0, т.е. a>-3, то
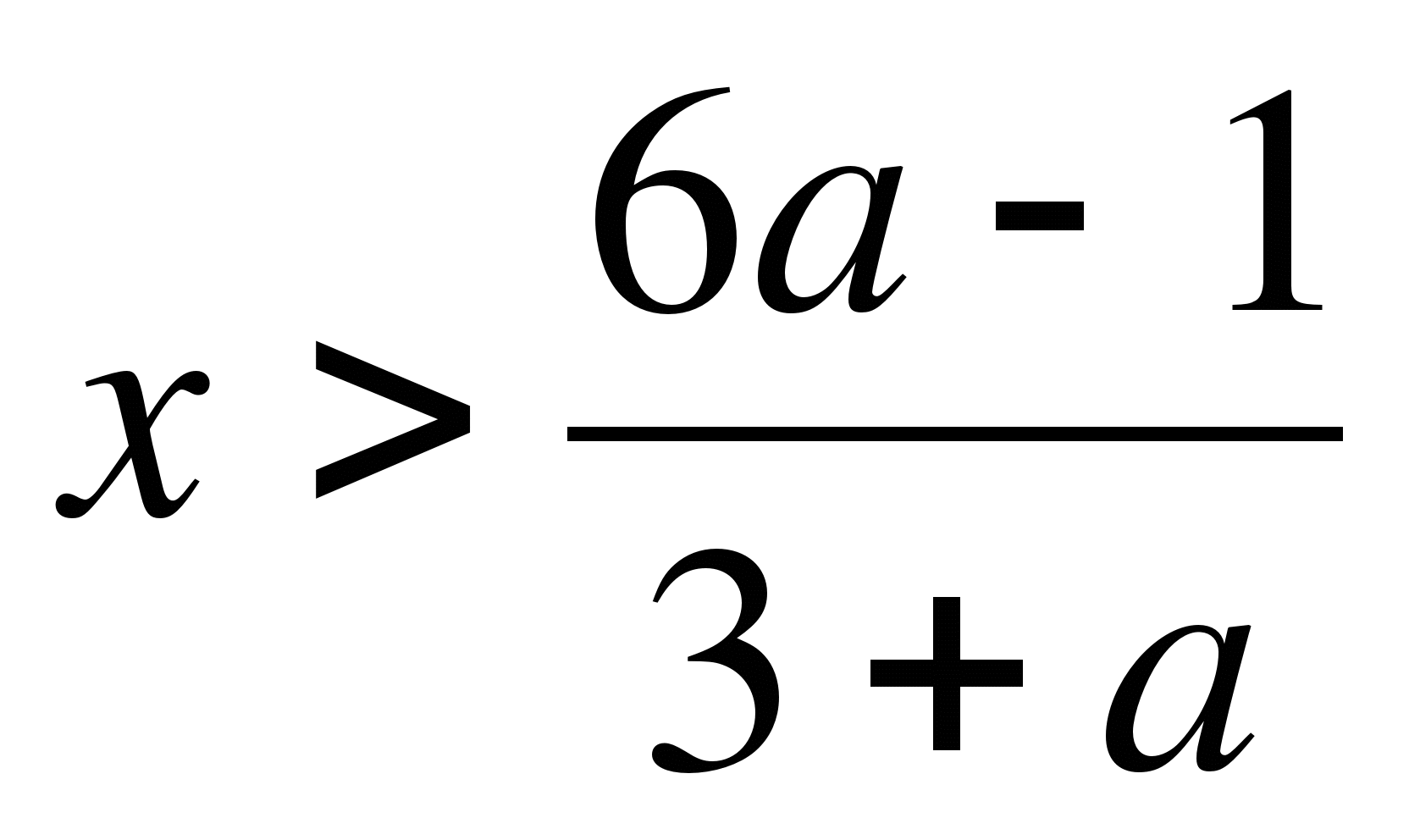 ;
;
-
если a+3<0, т.е. a<-3, то
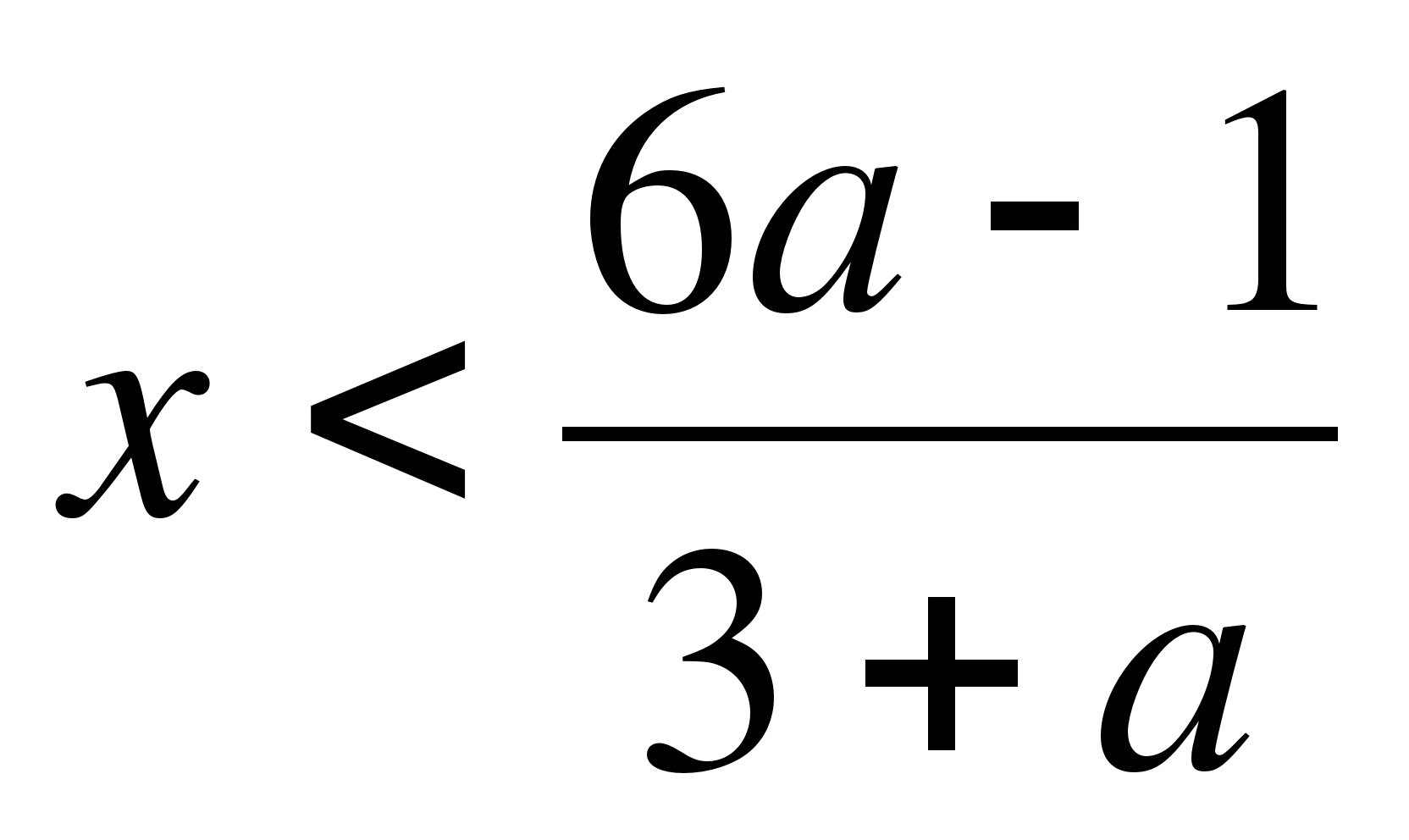 ;
;
-
если a+3=0, т.е. a=-3, то
 .
.
-
Ответ: если а>-3, то
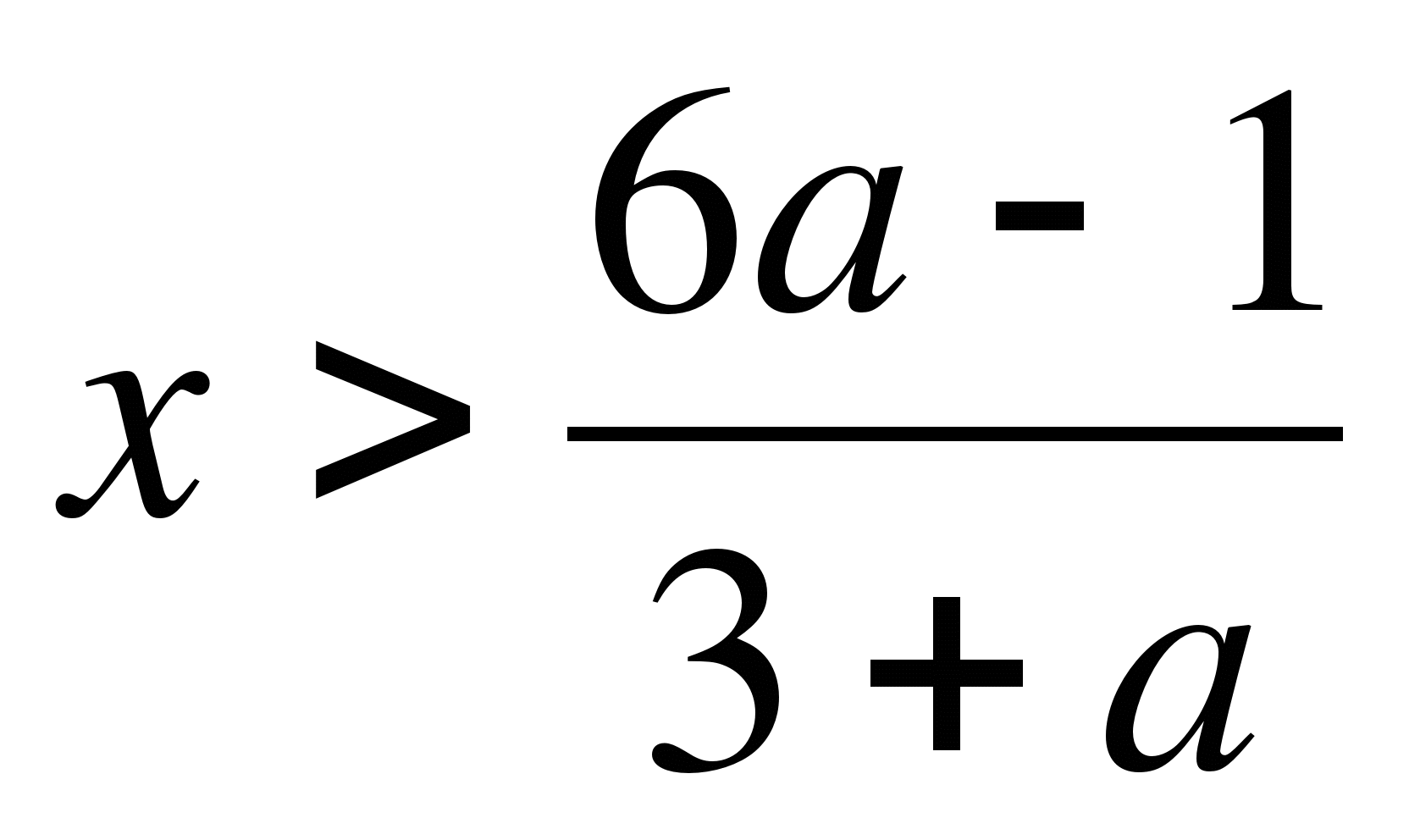 ;
если а<-3, то
;
если а<-3, то 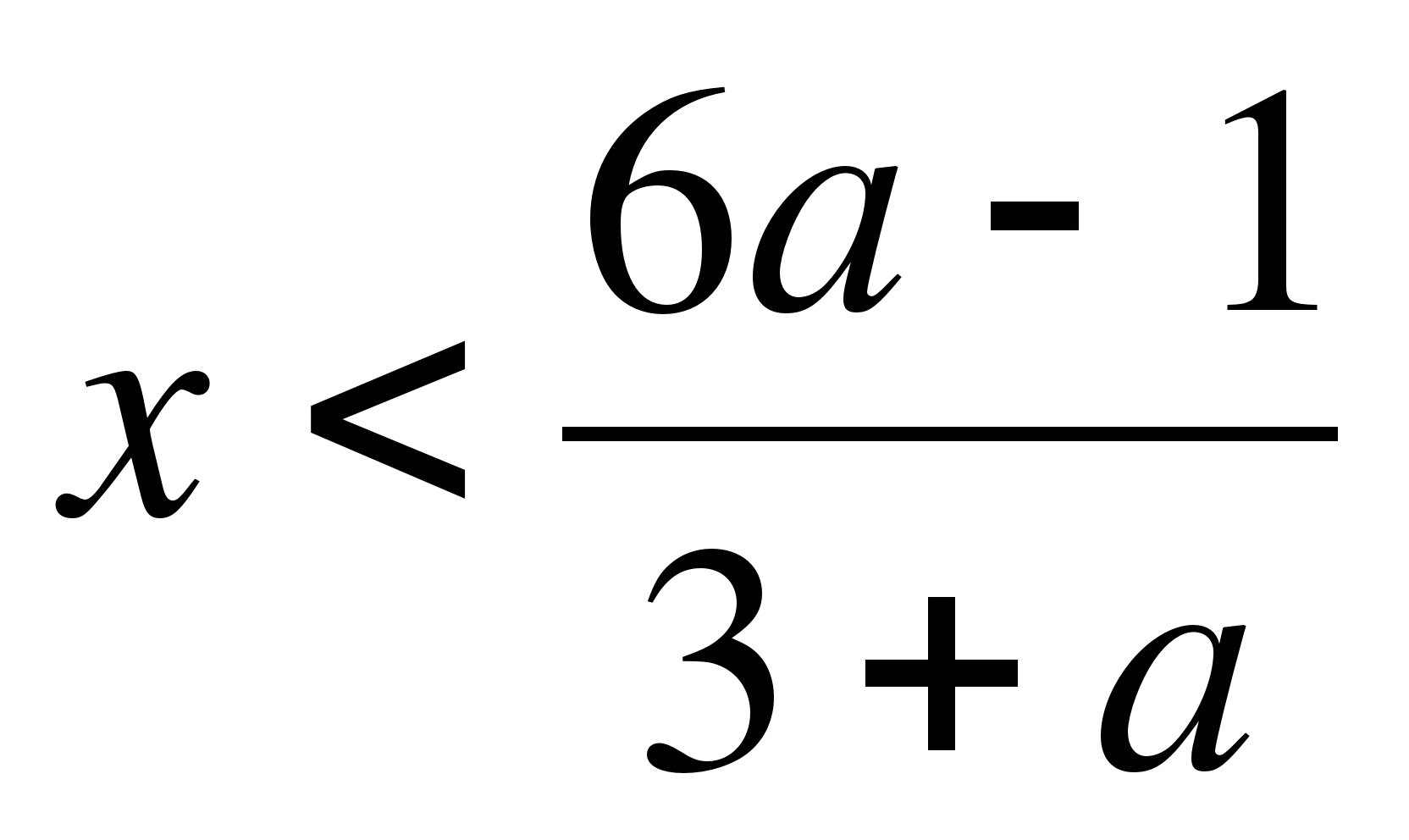 ;
если а=-3, то
;
если а=-3, то  .
.
II. Этап проверки знаний
Самостоятельная работа3mx-5>2m+1
б) 2x(a+1)<3(x+1)
a) 2bx-5<7+3b
б) (a+2)x-2<4x-1
Вариант 1
а) 3mx-5>2m+1
Решение:
3mx-5>2m+1
3mx>2m+6
-
если 3m>0, т.е. m>0, то
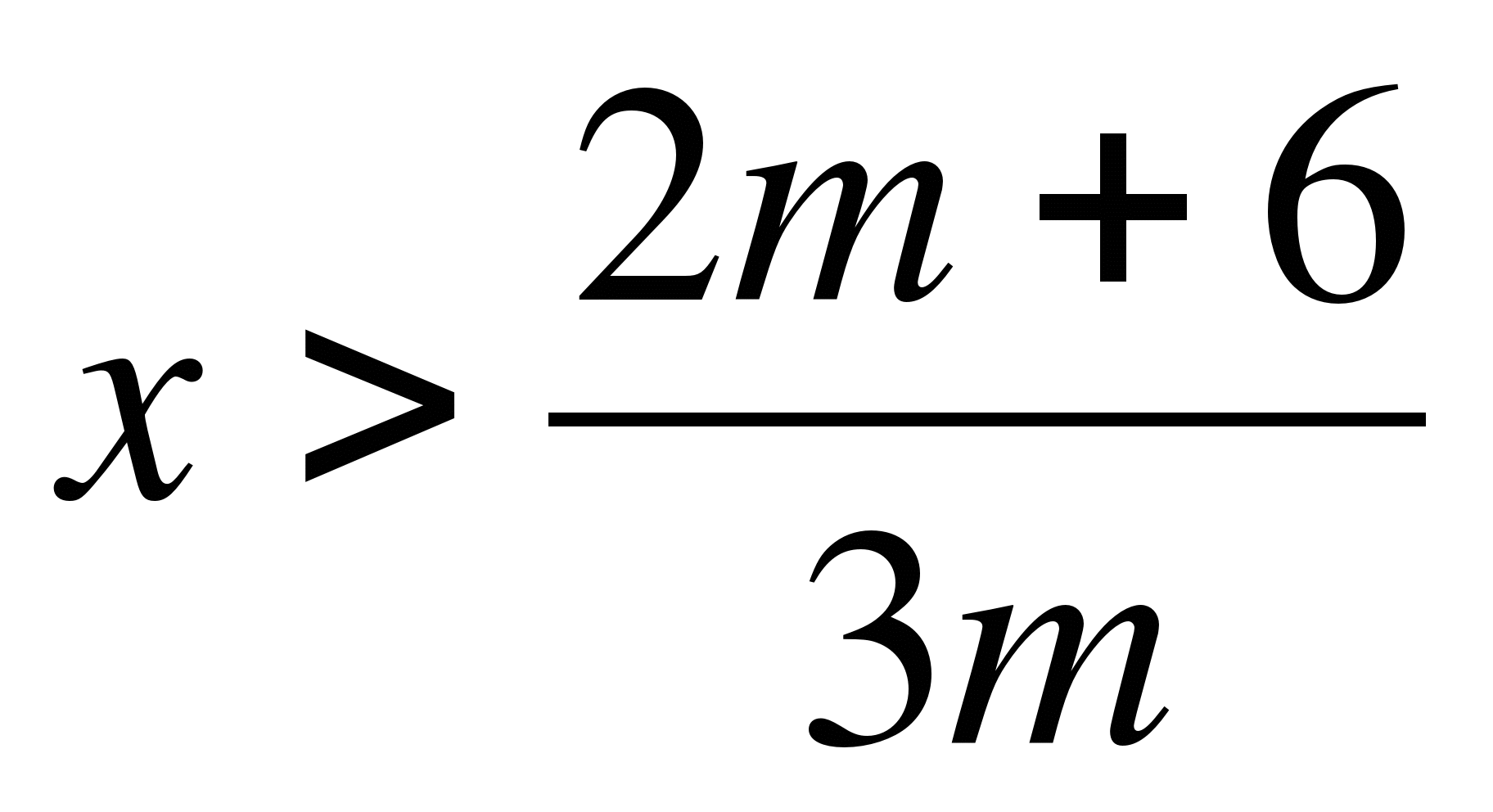 ;
;
-
если 3m<0, т.е. m<0, то
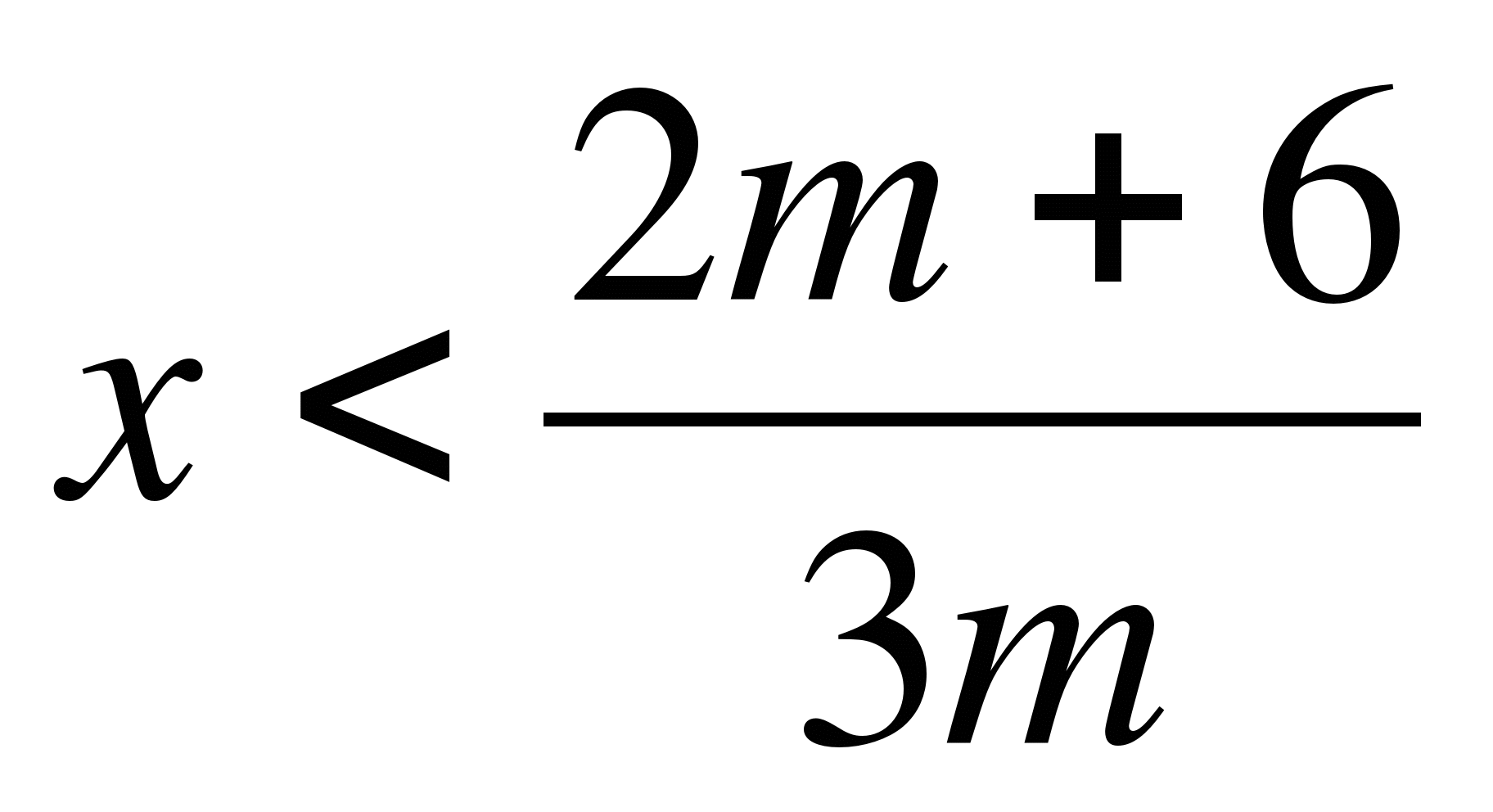 ;
;
-
если 3m=0, т.е. m=0, то
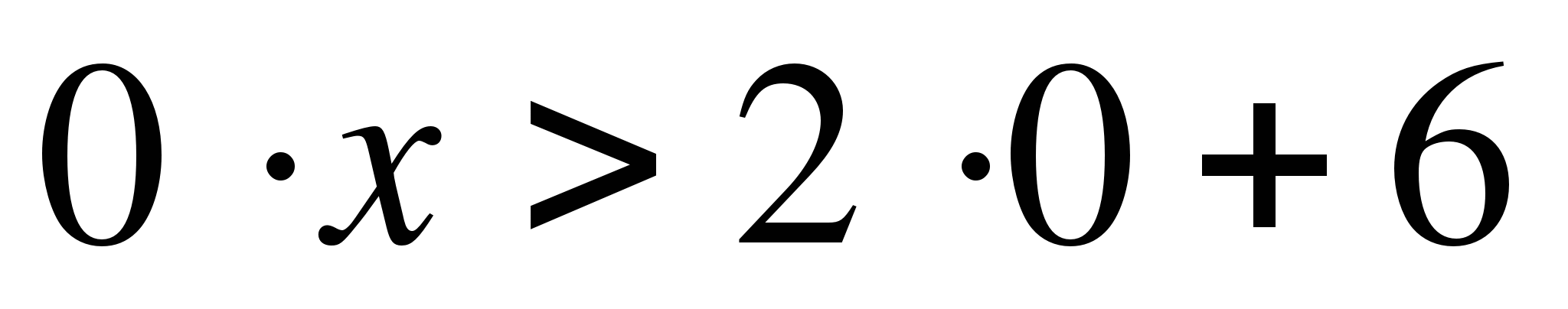
 решений нет;
решений нет;
Ответ: если m<0 , то
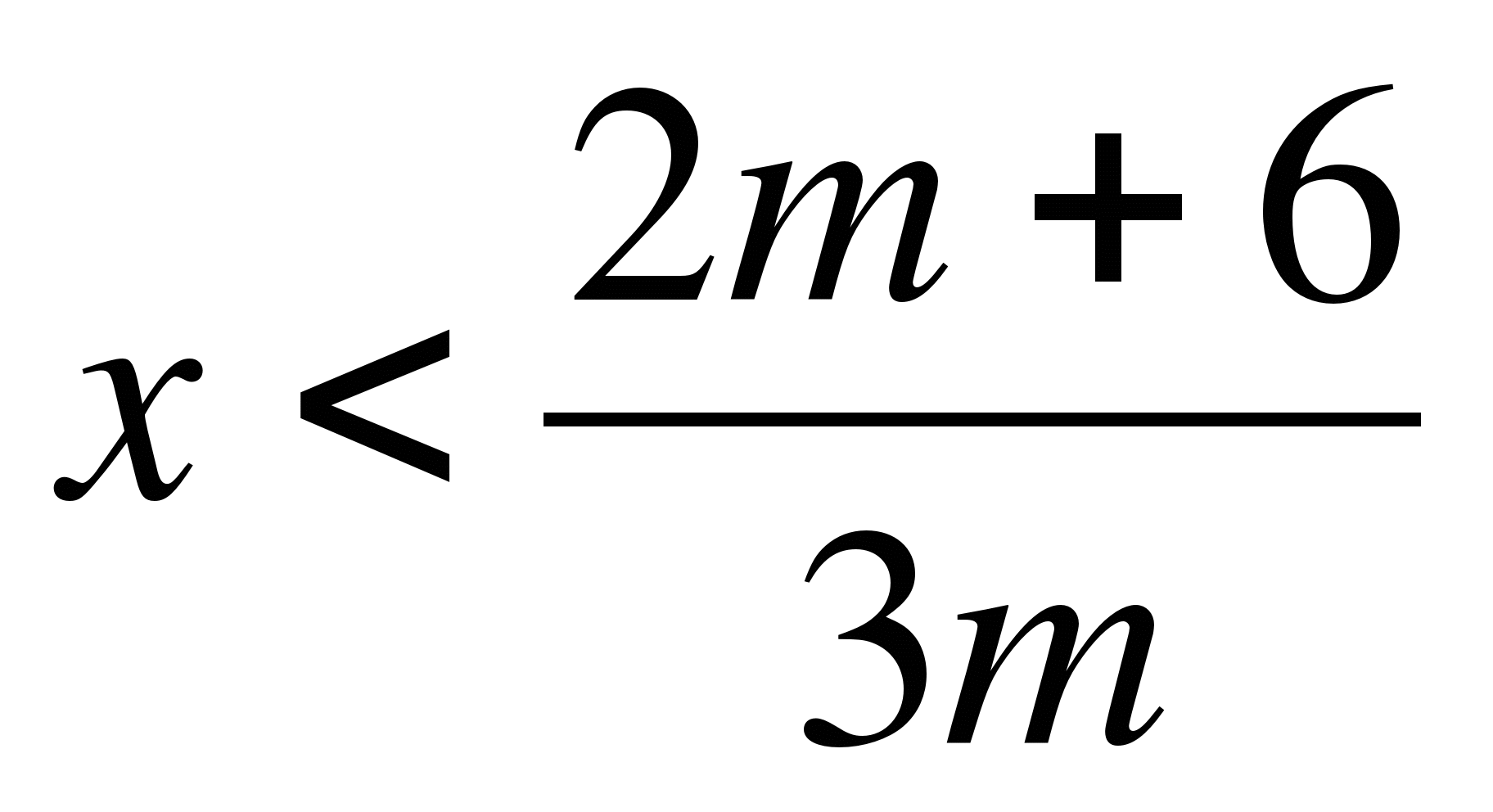 ;
если m>0, то
;
если m>0, то 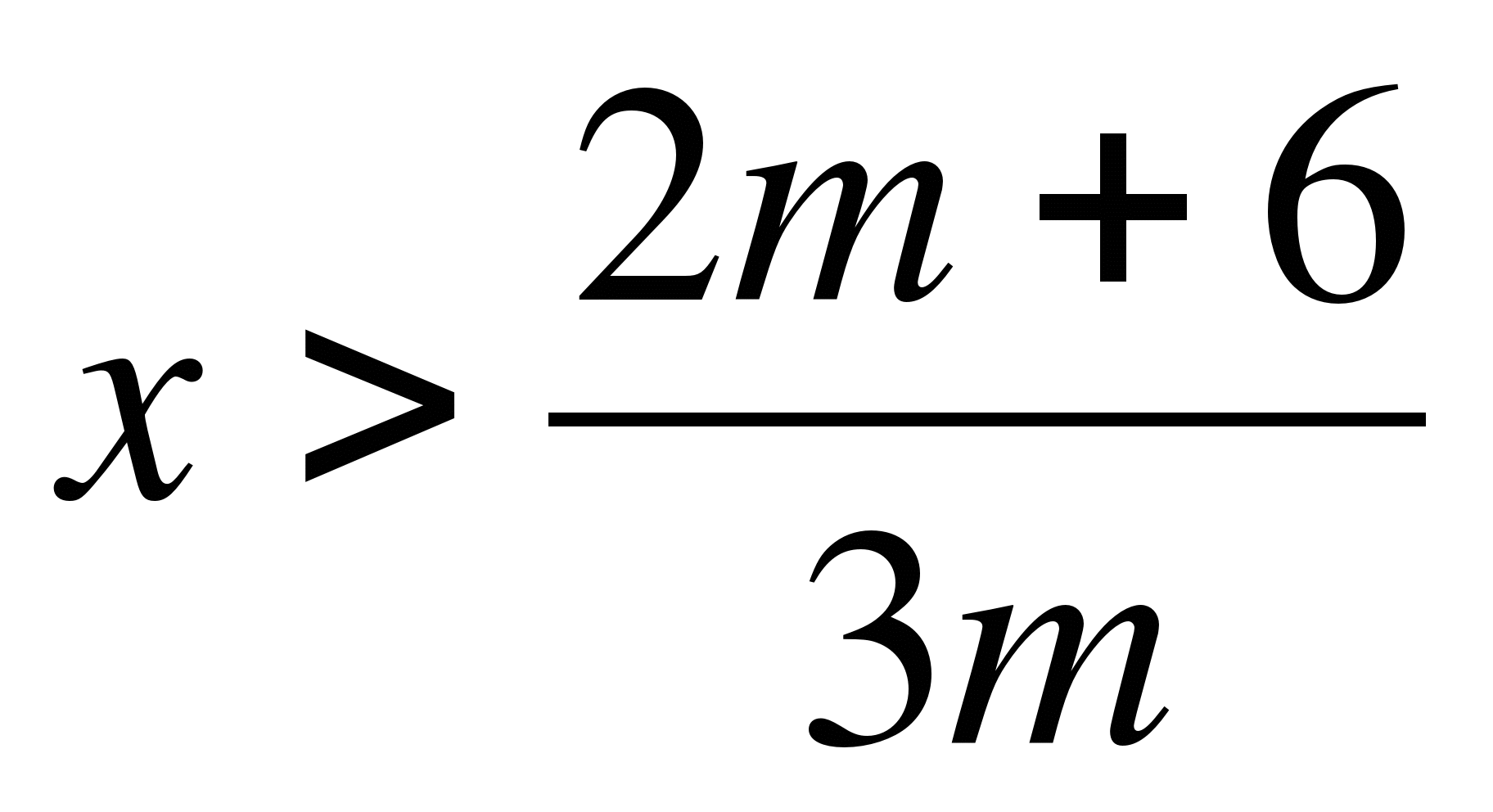 ;
если m=0, то решений
;
если m=0, то решений
нет.
б) 2x(a+1)<3(x+1)
Решение:
2ах+2x<3x+3;
2ax+2x-3x<3;
(2a-1)x<3
-
если 2a-1>0, т.е. a>
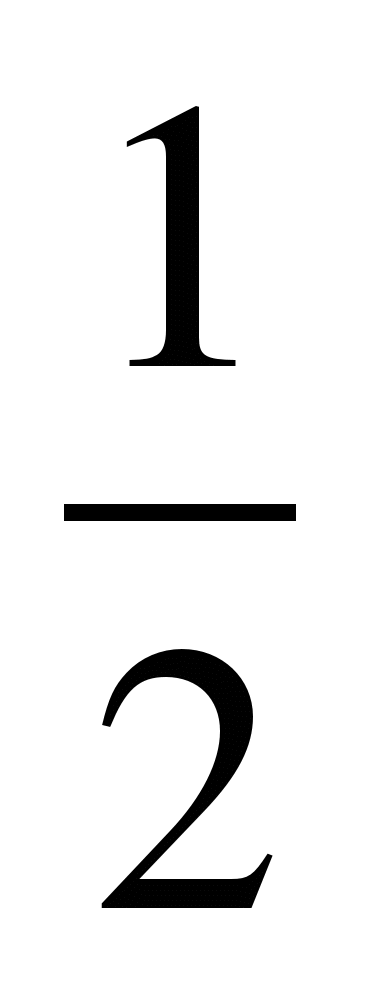 , то
, то 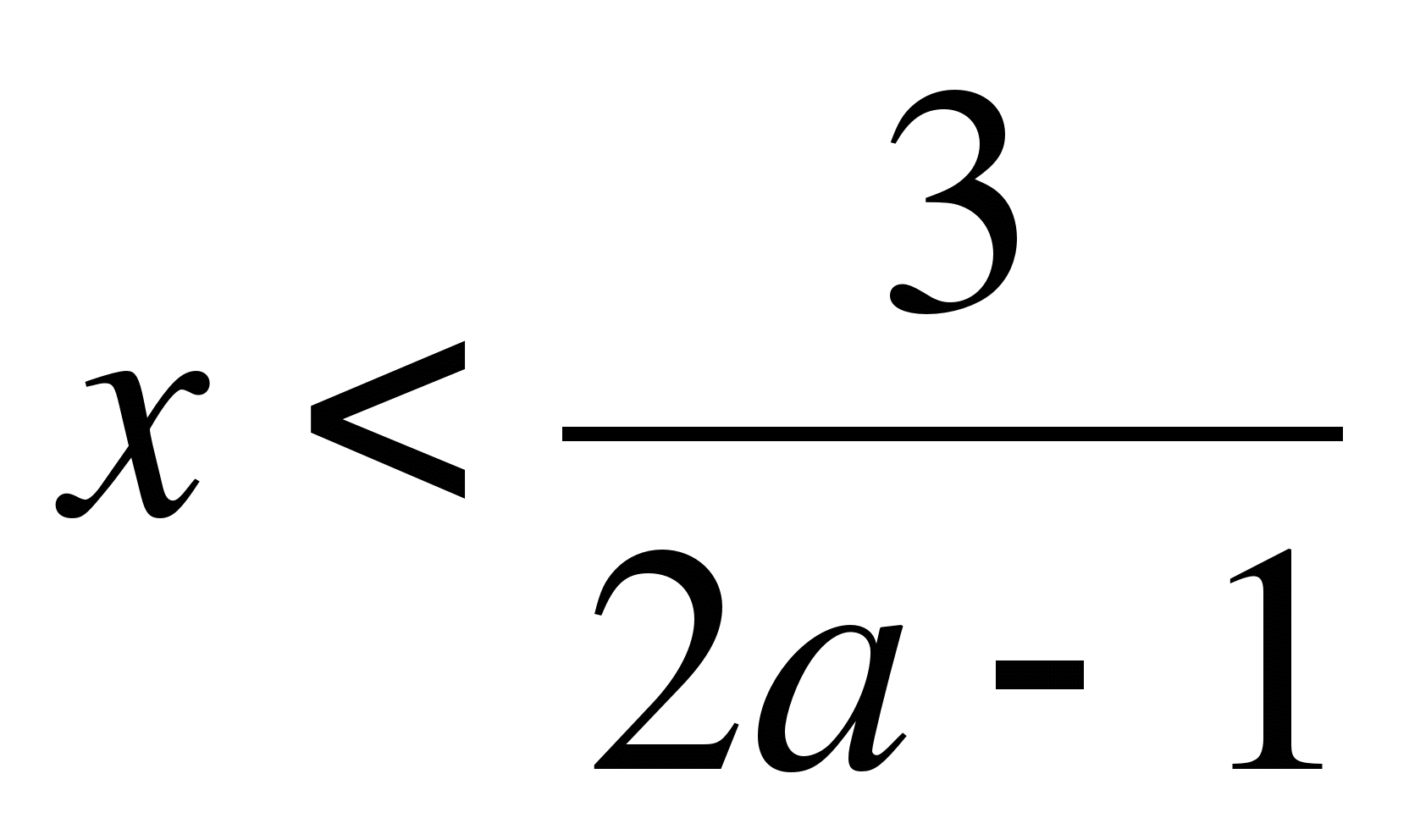 ;
;
-
если 2a-1<0, т.е. a<
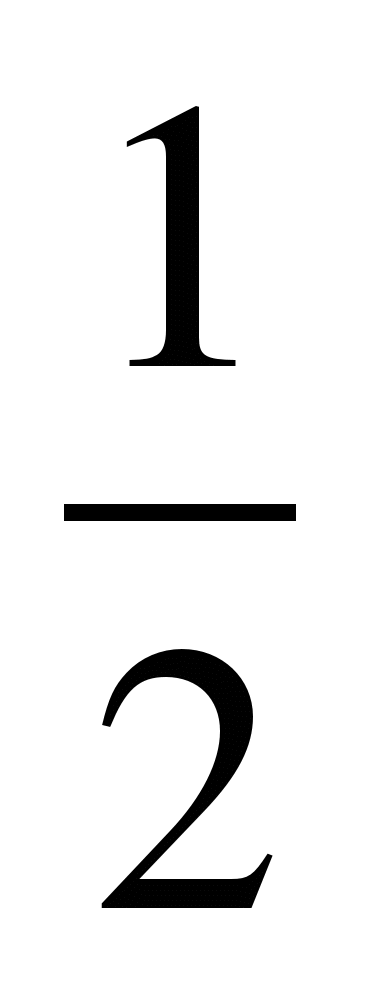 ,
то
,
то 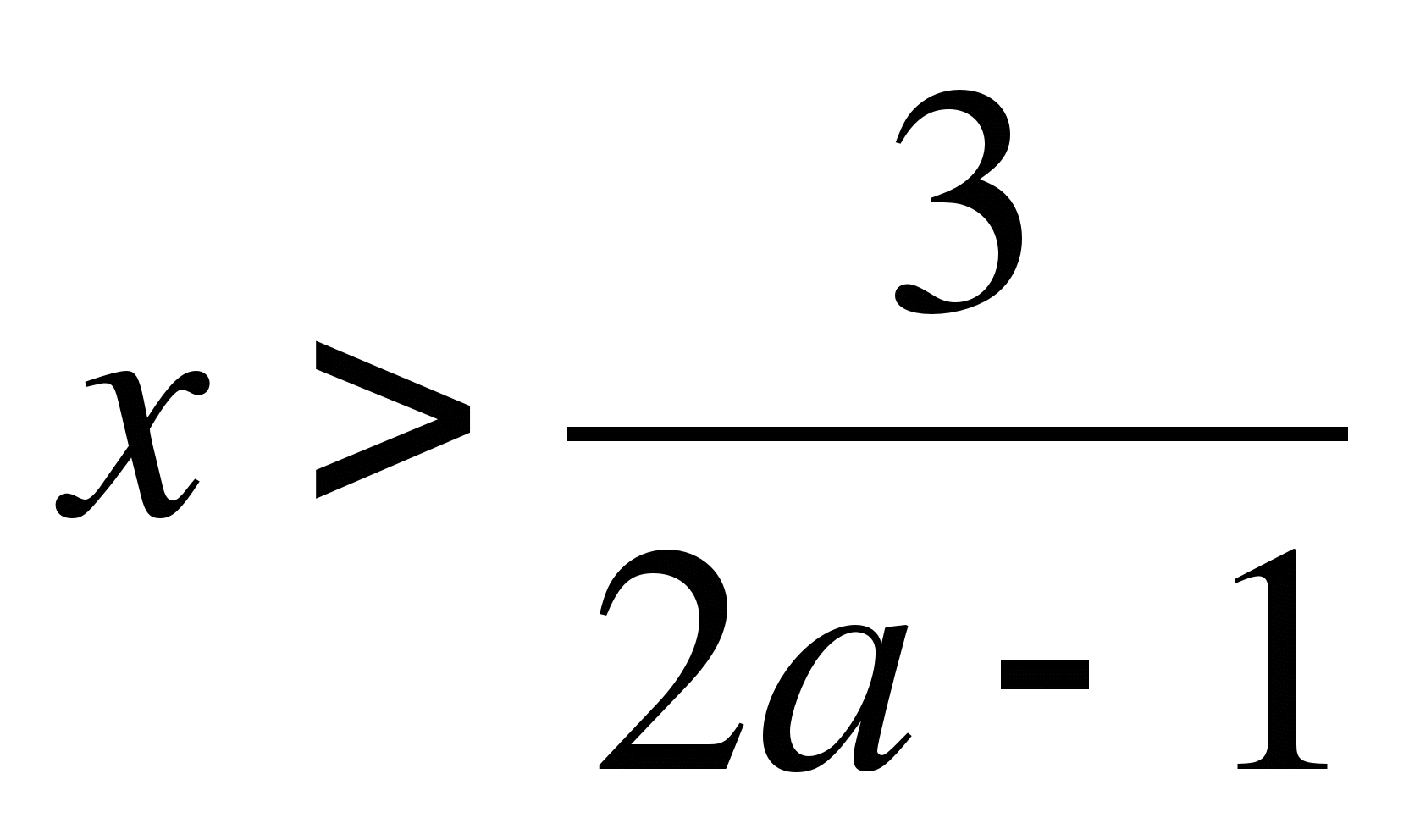 ;
;
-
если
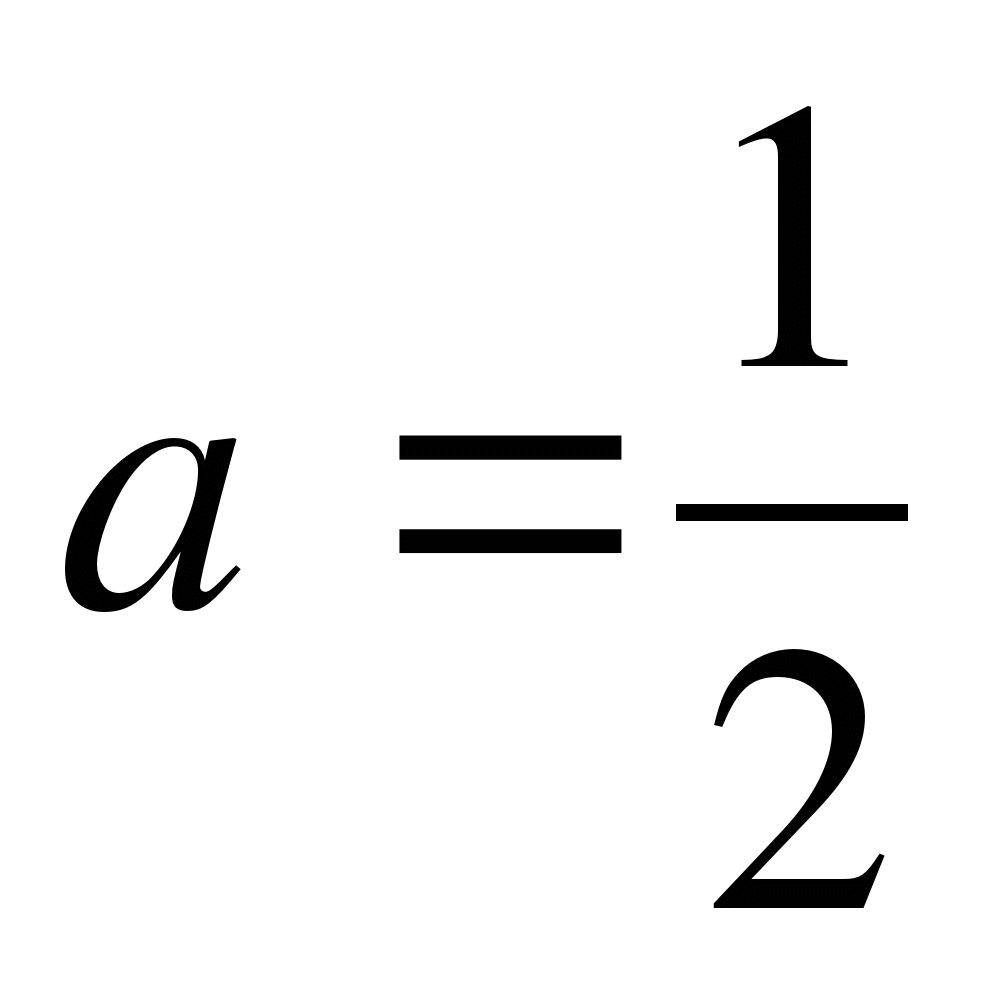 ,
то
,
то  .
.
Ответ: если
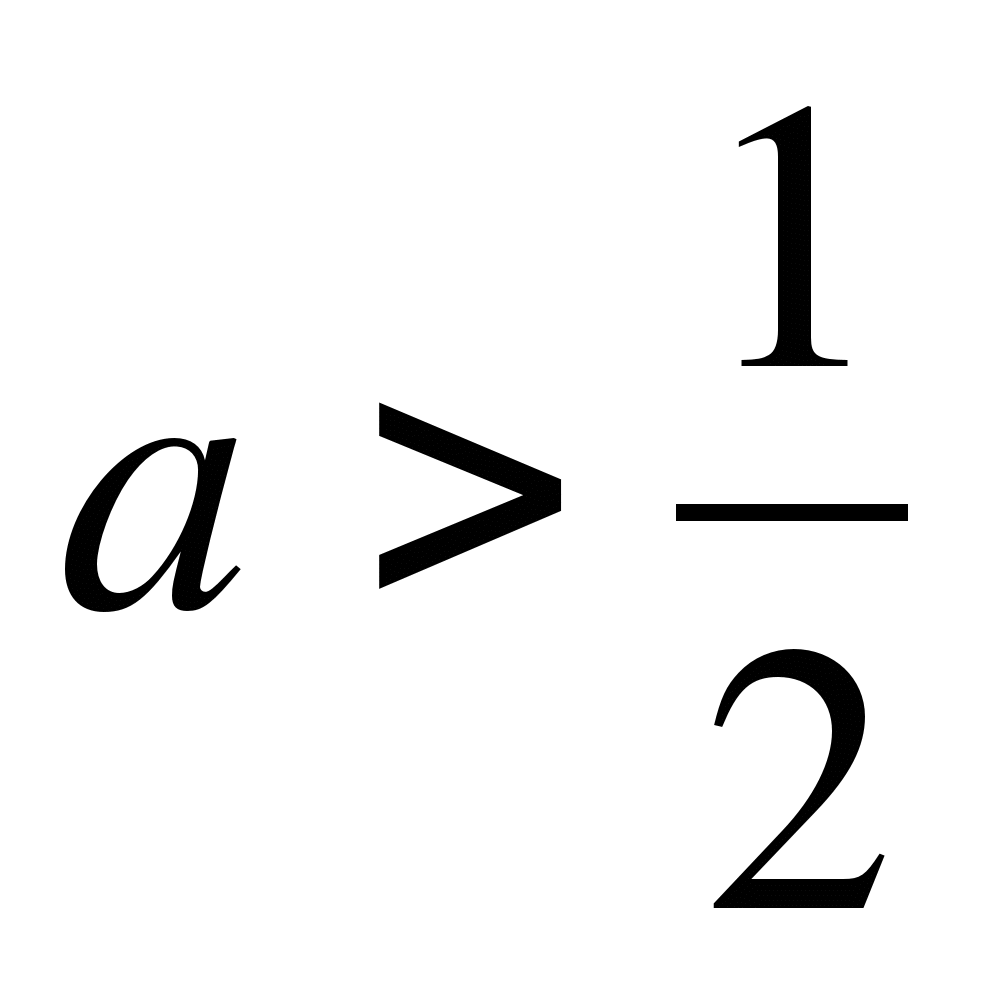 , то
, то
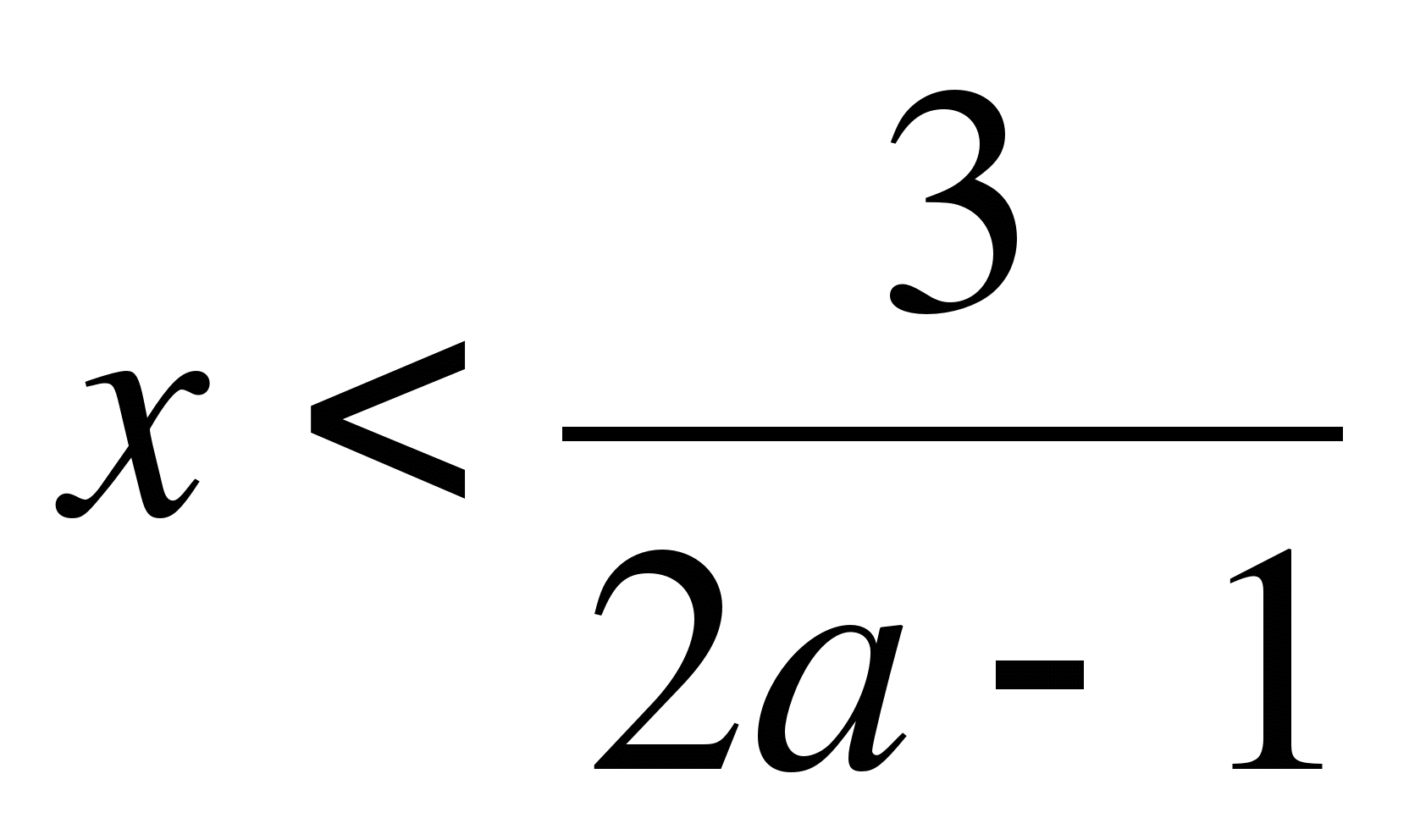 ;
если
;
если 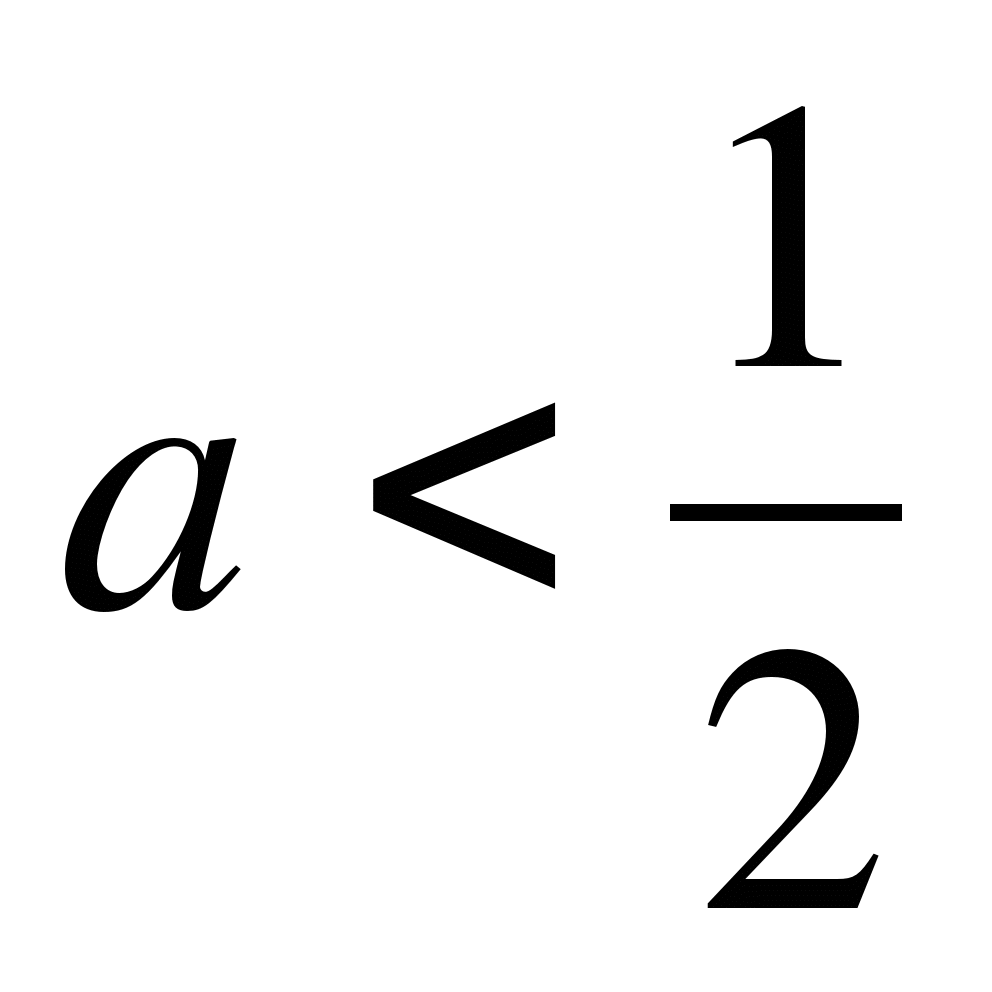 ,
то
,
то 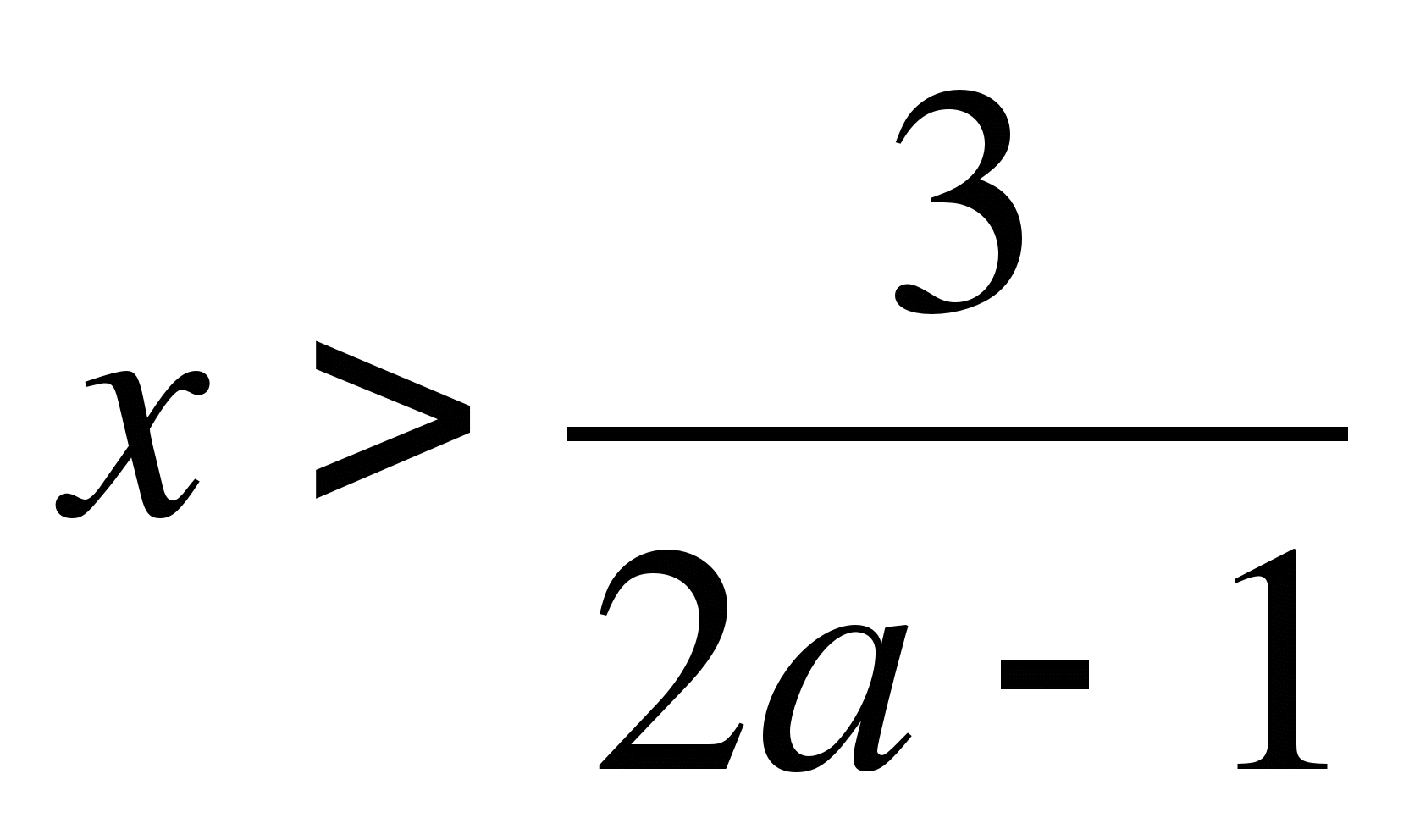 ;
если
;
если 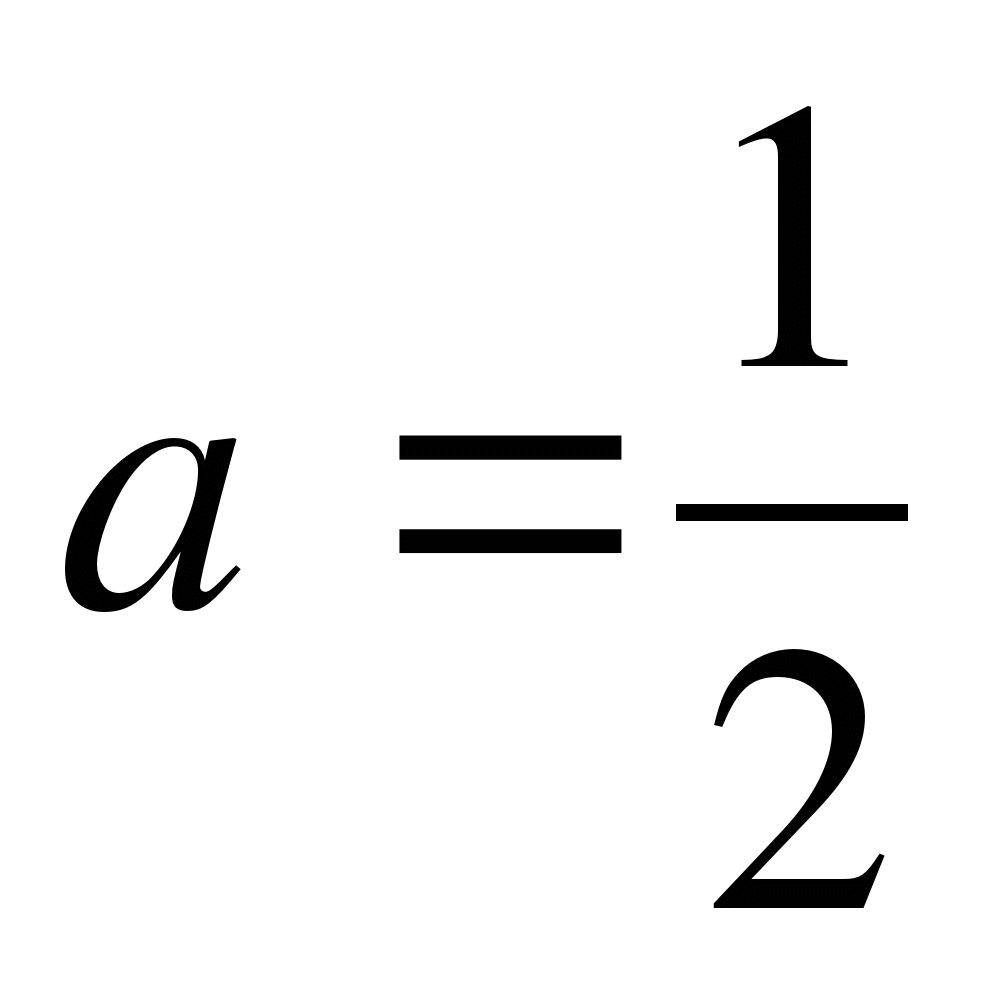 , то
, то
 .
.
Вариант 2.
a) 2bx-5<7+3b
Решение:
2bx-5<7+3b
2bx<12+3b
-
если b>0, то
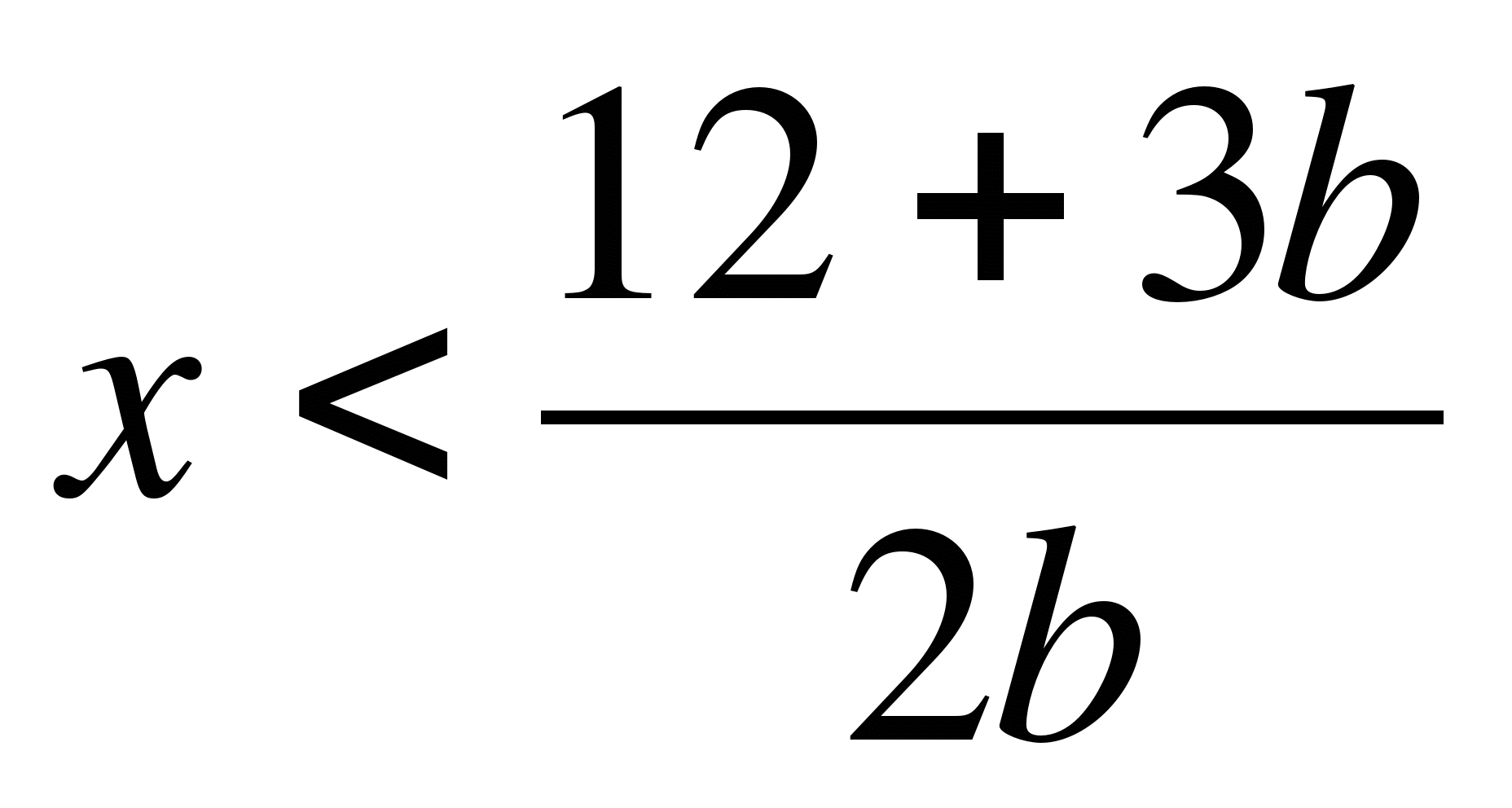 ;
;
-
если b<0, то
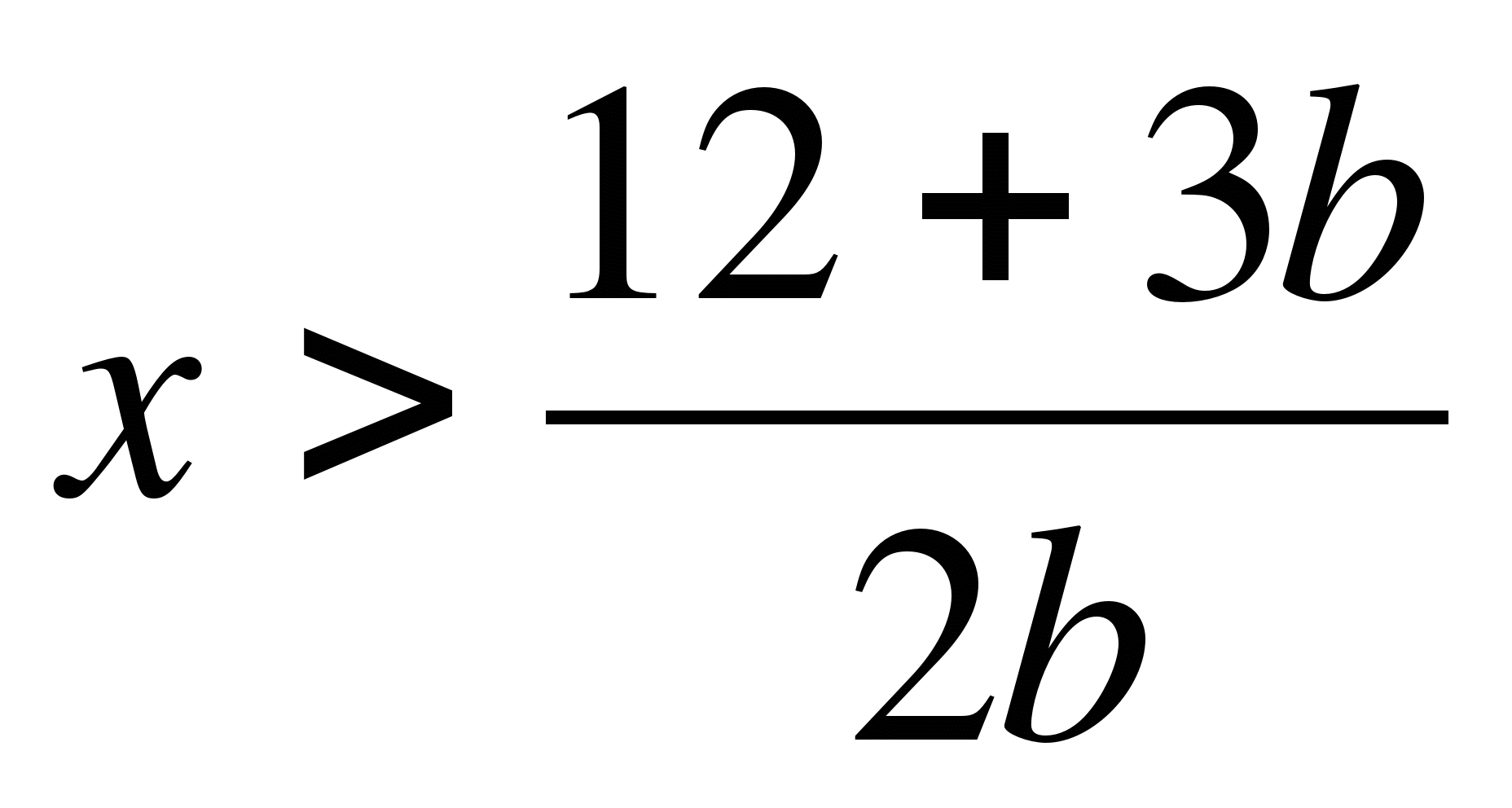 ;
;
-
если b=0, то
 .
.
Ответ: если b>0, то
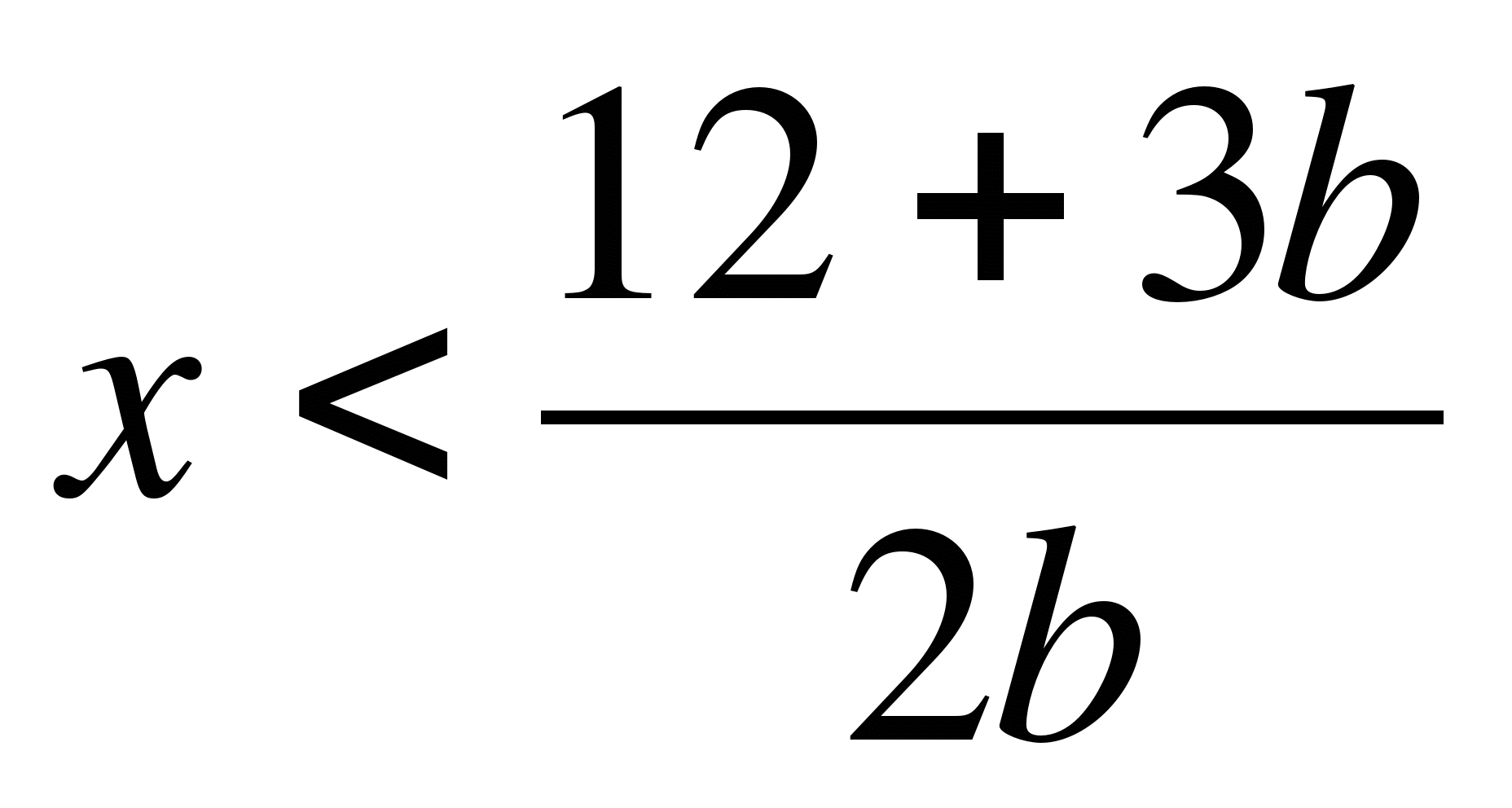 ;
если b<0, то
;
если b<0, то 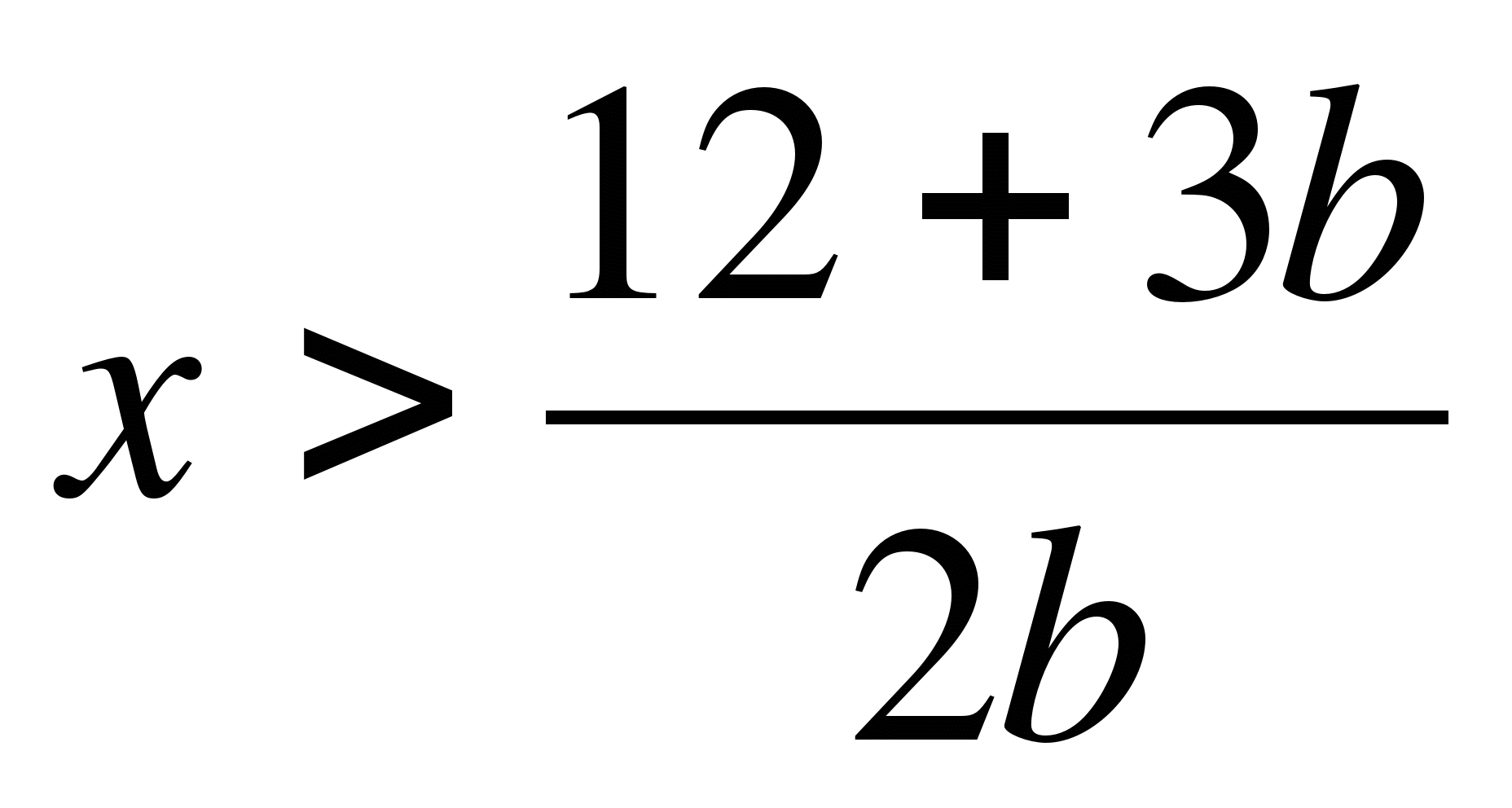 ;
если b=0, то
;
если b=0, то  .
.
б) (a+2)x-2<4x-1
Решение:
(a+2)х-4x<1;
(a-2)x<1;
(2a-1)x<3
-
если a-2>0, т.е. a>2, то
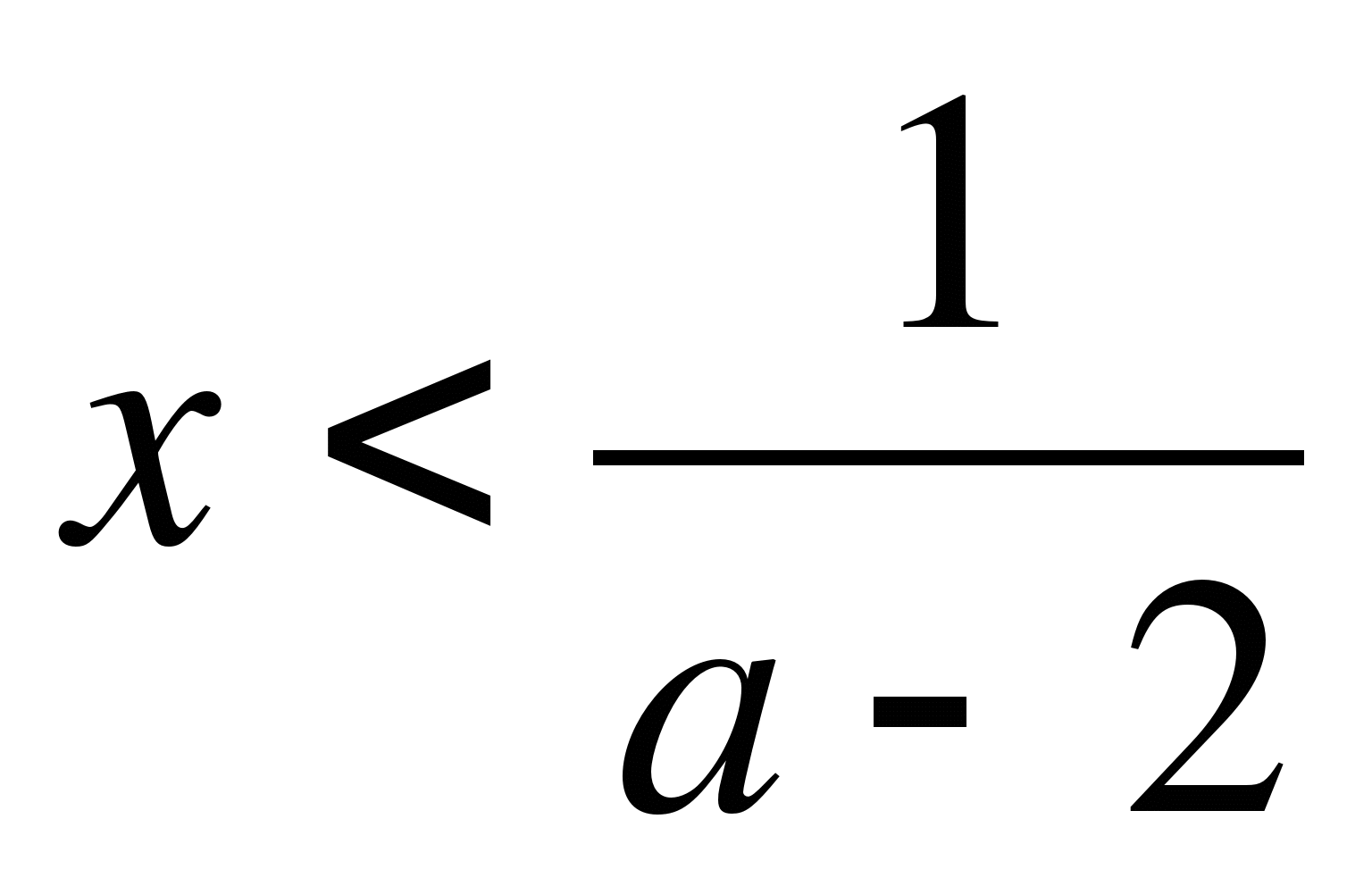 ;
;
-
если
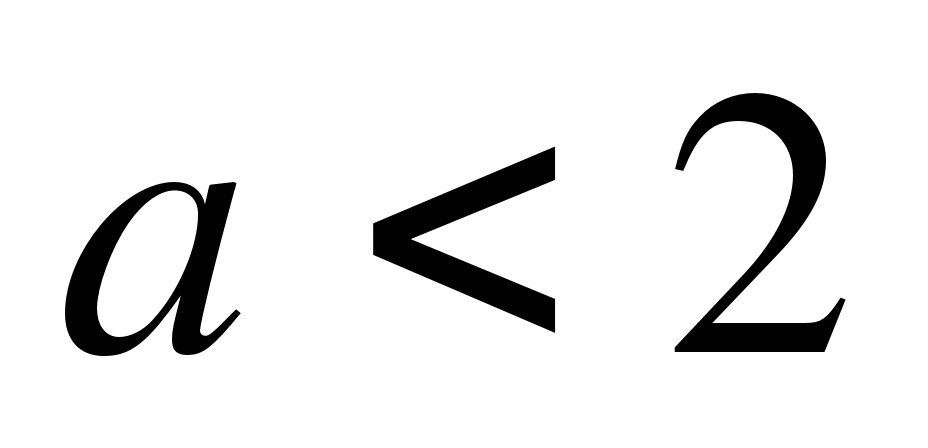 ,
то
,
то 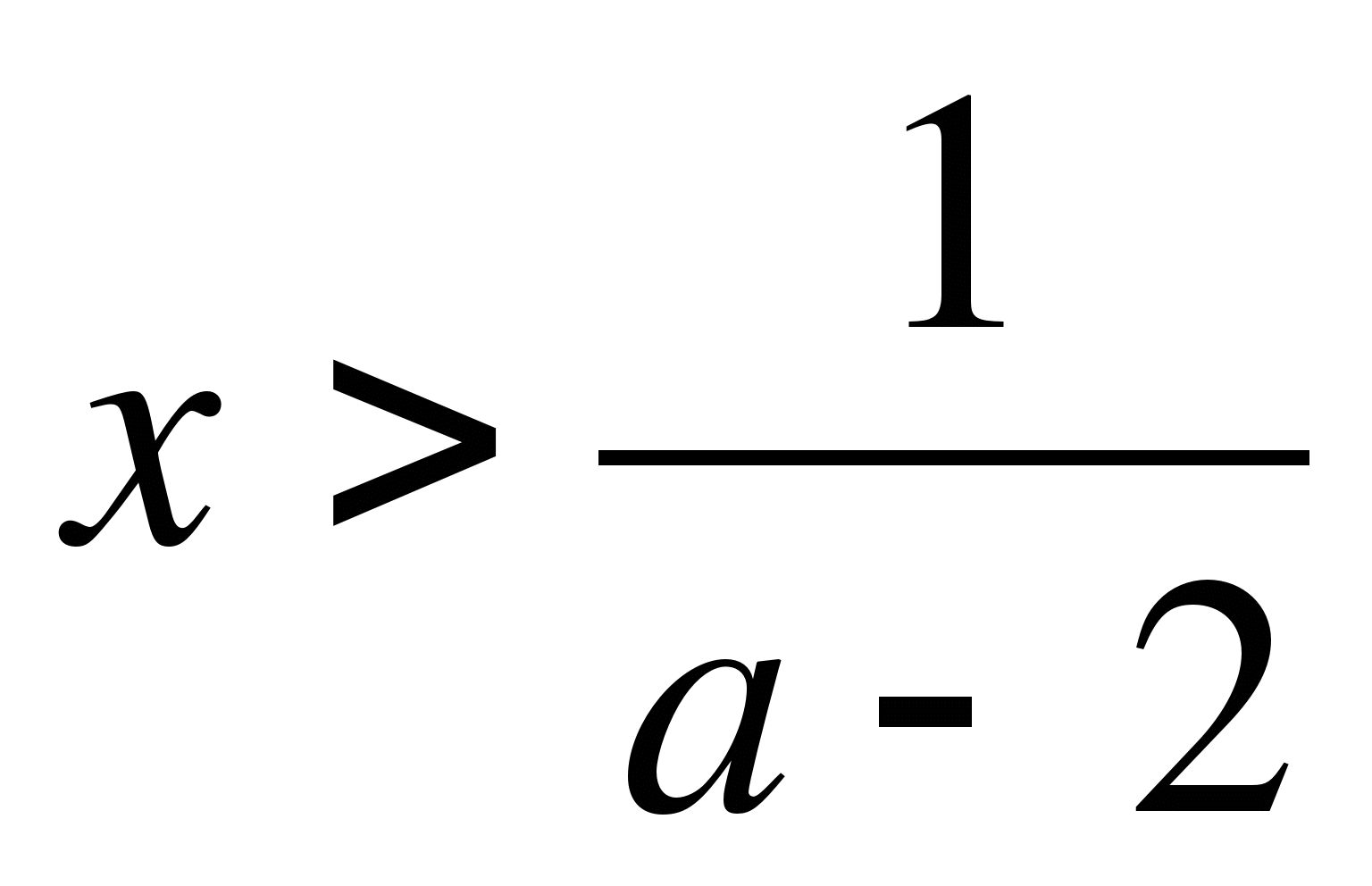 ;
;
-
если
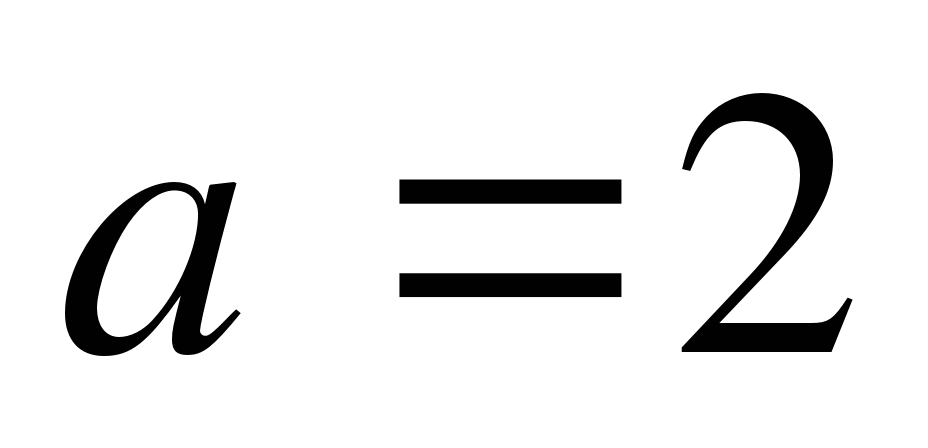 ,
то
,
то  .
.
Ответ: если
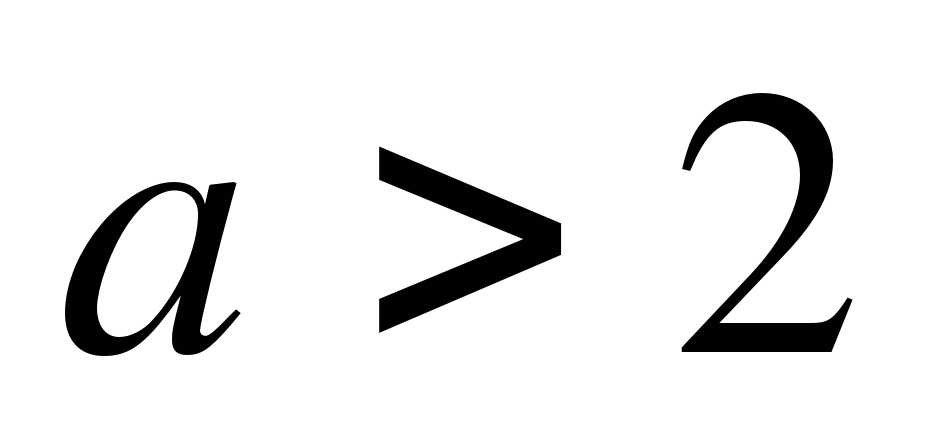 , то
, то
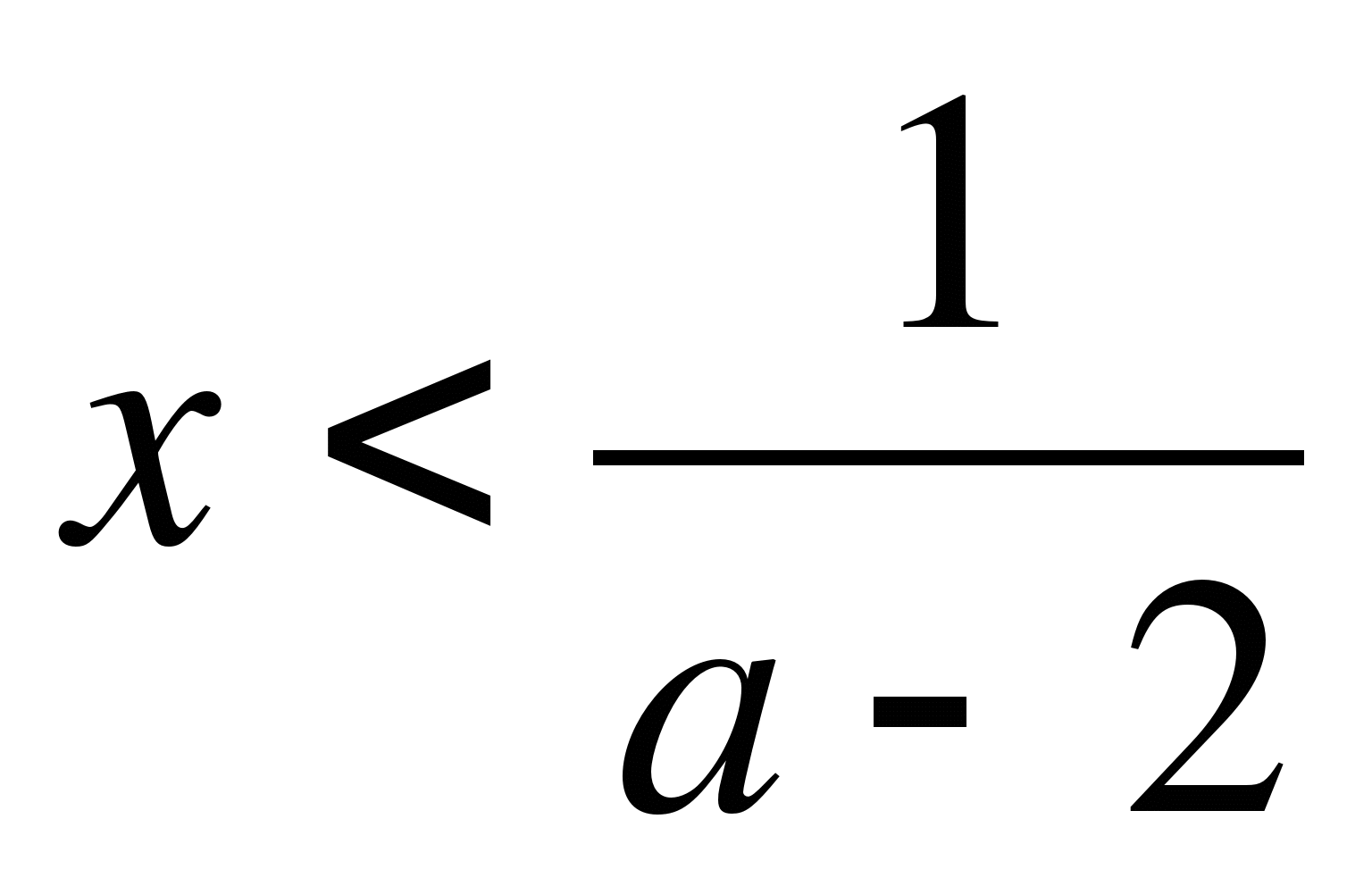 ;
если
;
если 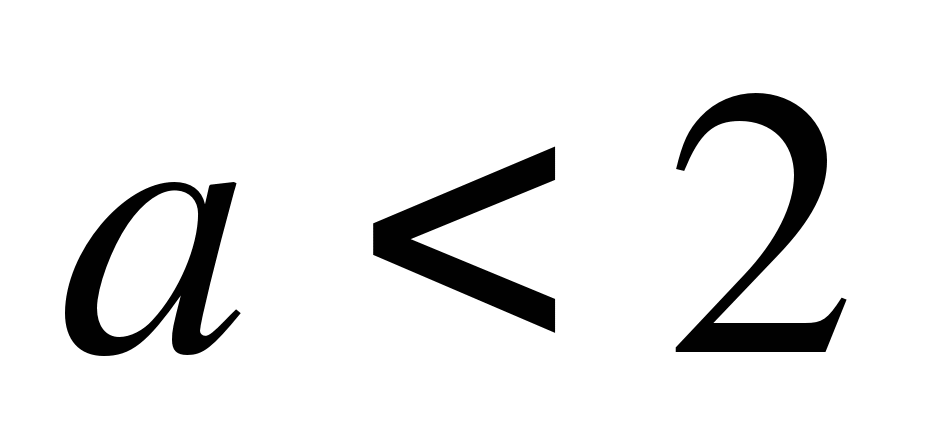 , то
, то
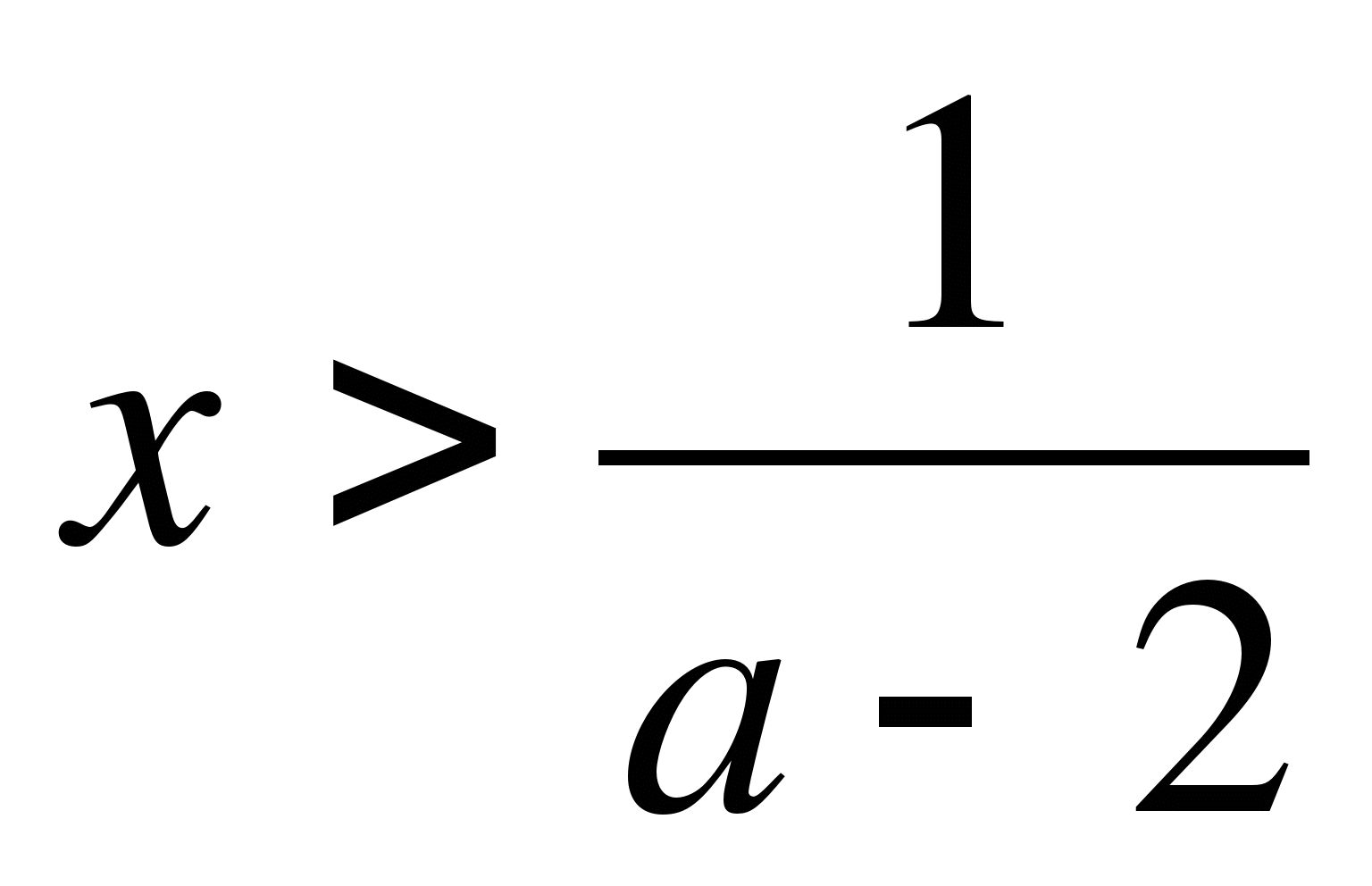 ;
если
;
если 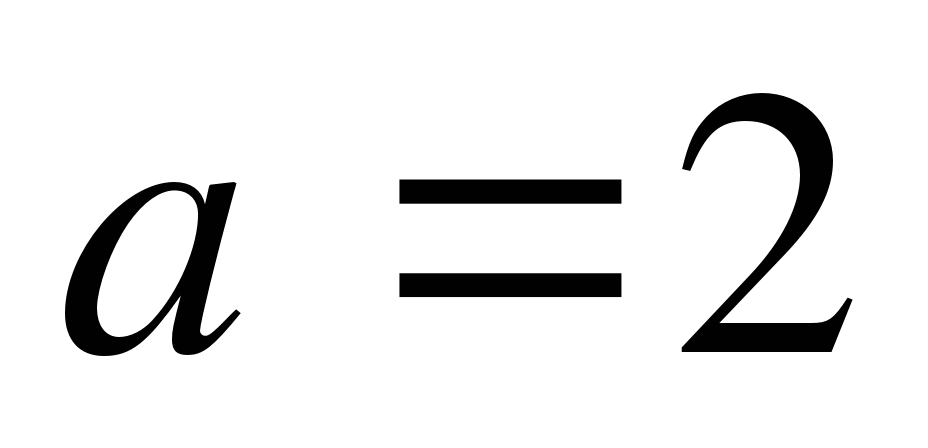 , то
, то
 .
.
III. Этап рефлексии.
Занятие 3.
Цели занятия:
- научиться решать линейные неравенства, содержащие параметр и
неравенства с параметром, приводимые к линейным, обеспечить
благоприятные условия для дифференцированного обучения;
- научиться выписывать ответ;
- познакомиться с алгоритмами решения неравенств, содержащих параметр;
- обеспечить устойчивую мотивационную среду, интерес к изучаемой теме;
- создать условия для самостоятельной и творческой работы.
Ход занятия.
-
Актуализация уже полученных знаний.
ах>b.
Если a>0, то
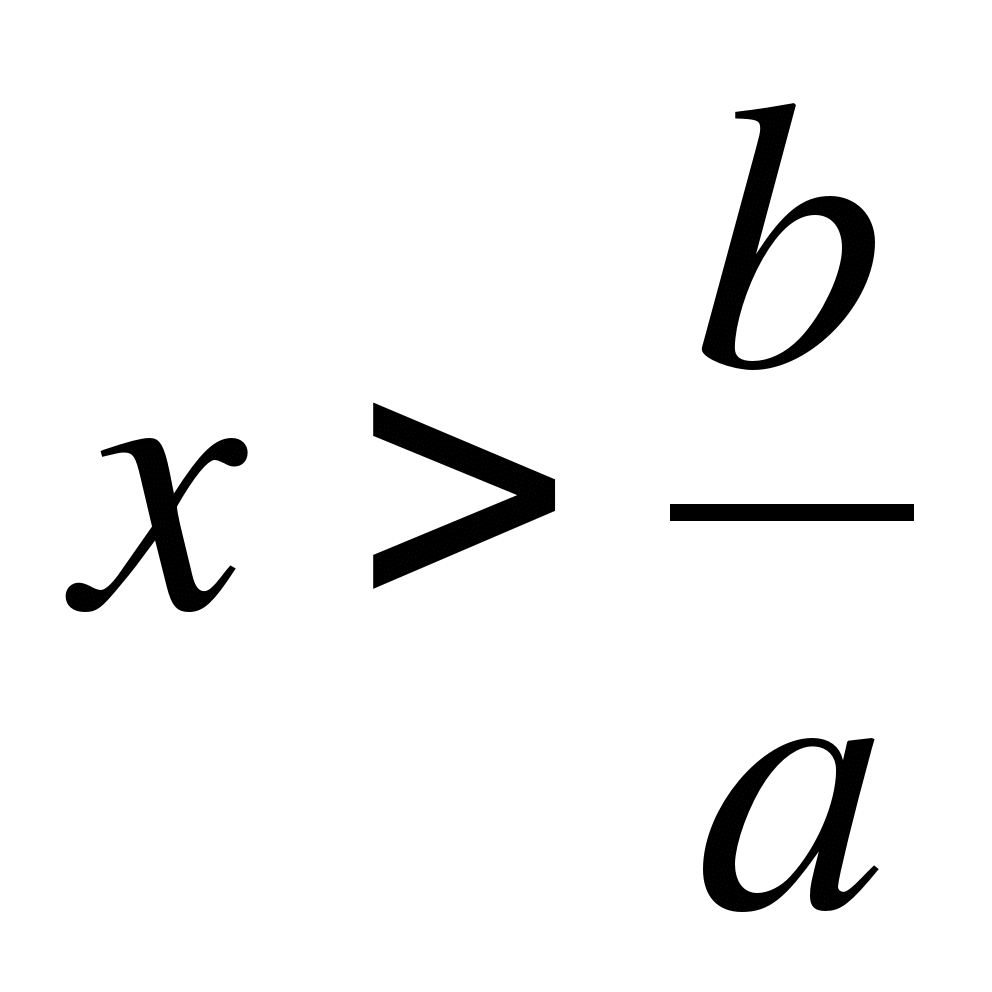 .
.
Если a<0, то
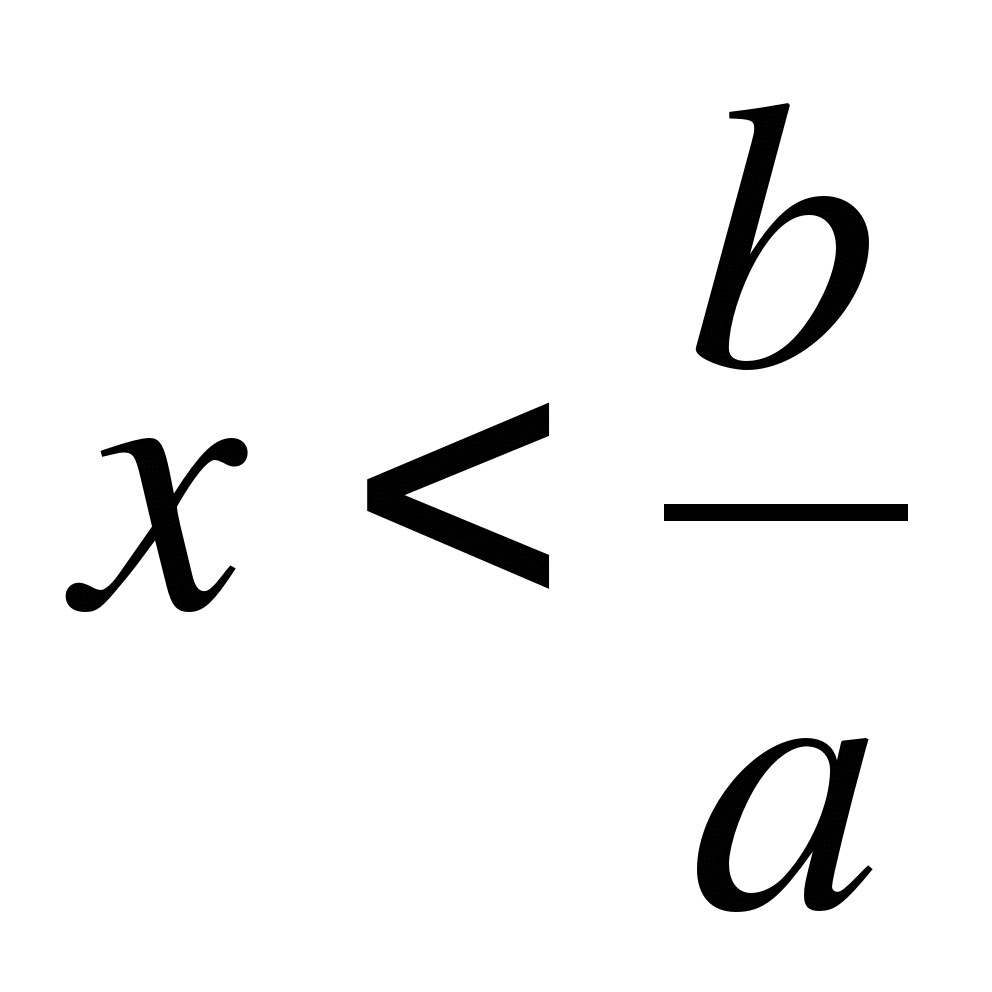 .
.
Если a=0 и b<0, то
 .
.
Если a=0 и b
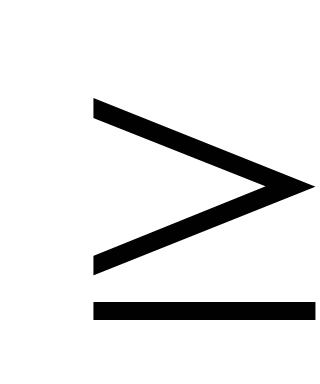 0,
то решений нет.
0,
то решений нет.
-
-
a<b
-
ax.
Если a>0, то
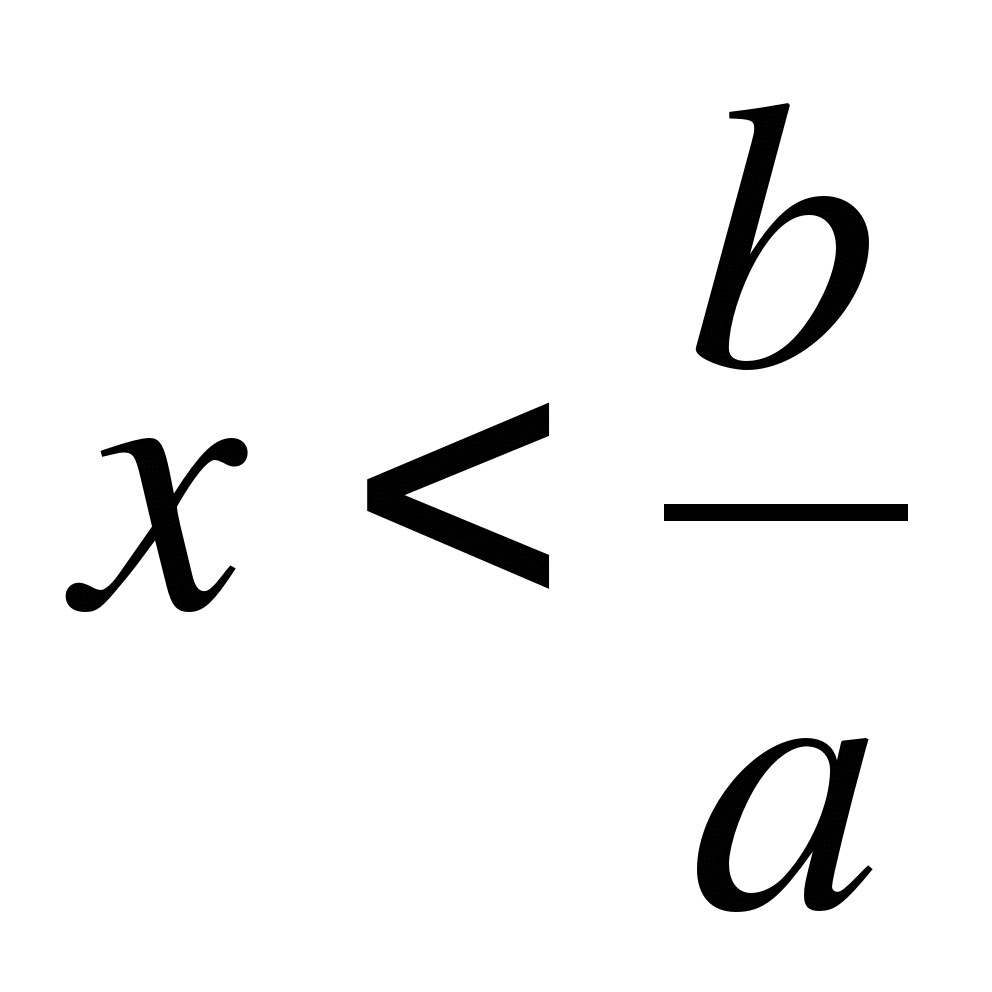 .
.
Если a<0, то
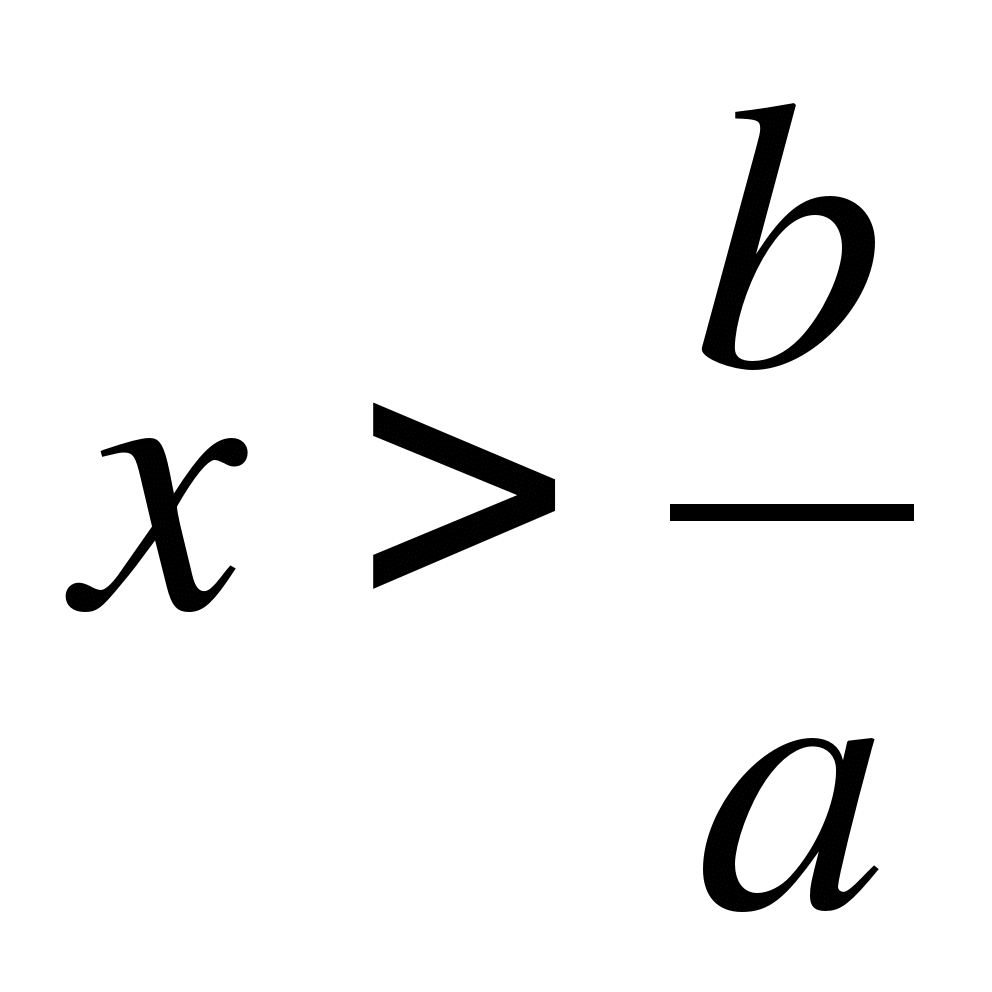 .
.
Если a=0 и b>0, то
 .
.
Если a=0 и b
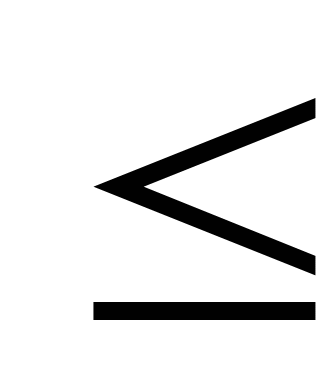 0,
то решений нет.
0,
то решений нет.
-
-
ax
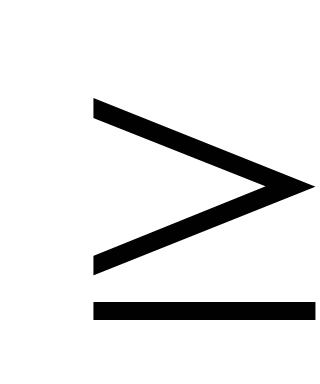 b
b
-
Если a>0, то
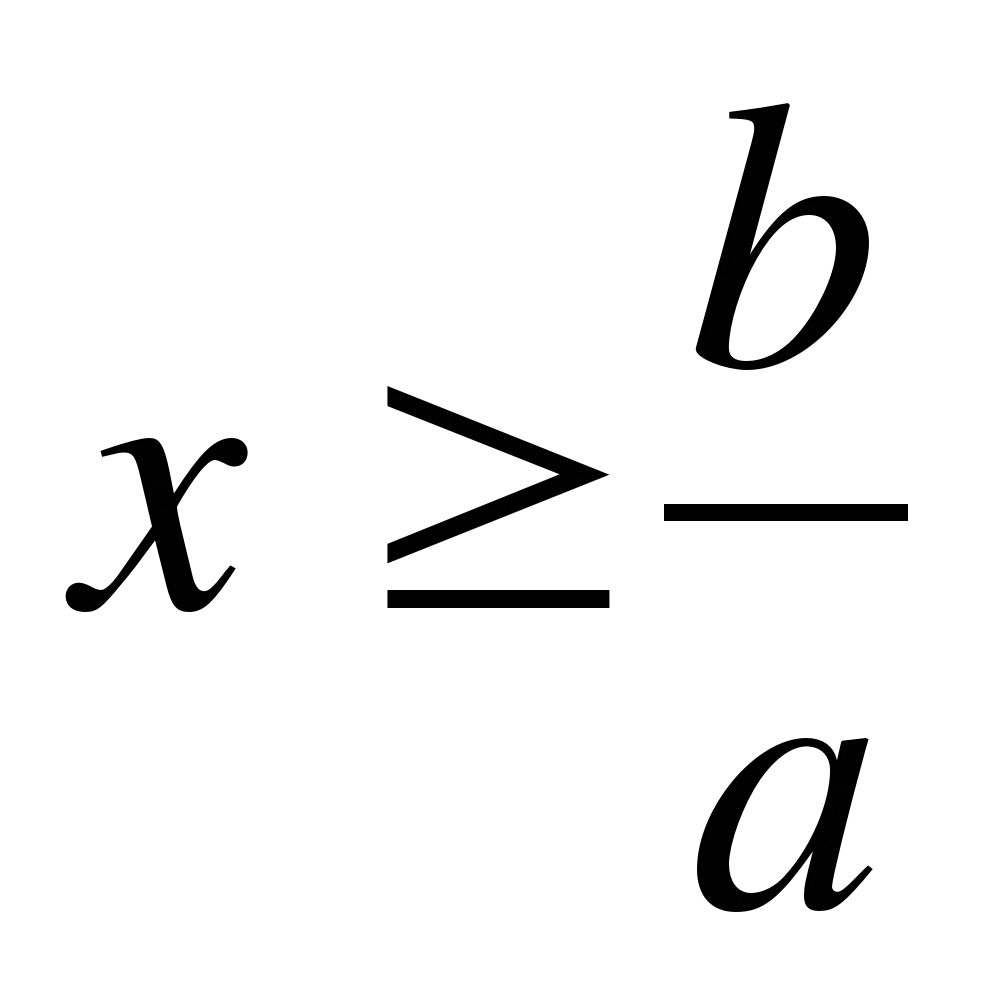 .
.
Если a<0, то
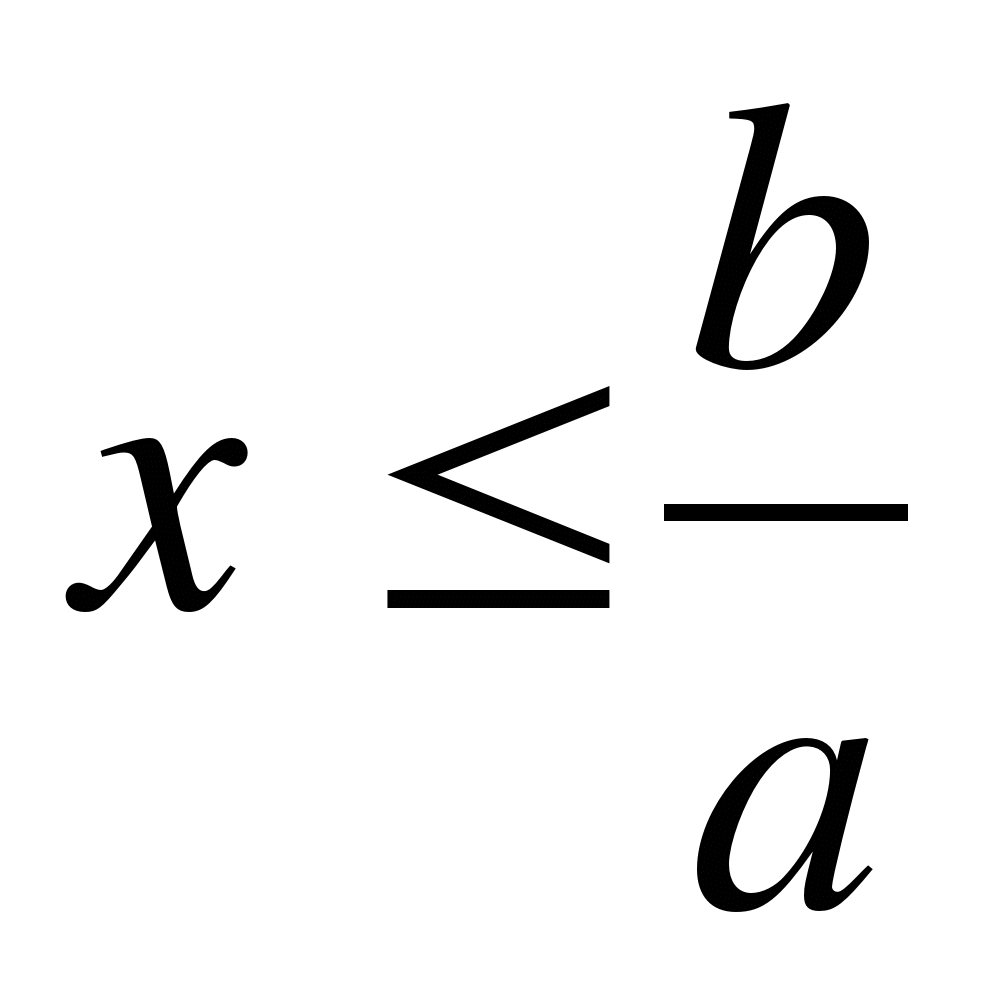 .
.
Если a=0 и b
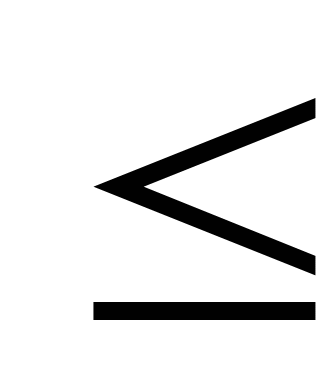 0,
то
0,
то  .
.
Если a=0 и b>0, то решений нет.
4. ax
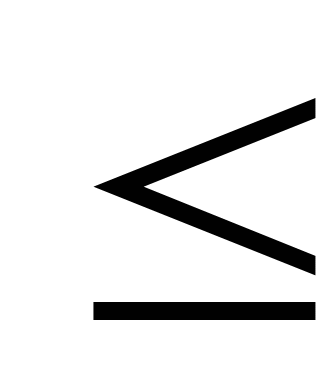 b
b
Если a>0, то
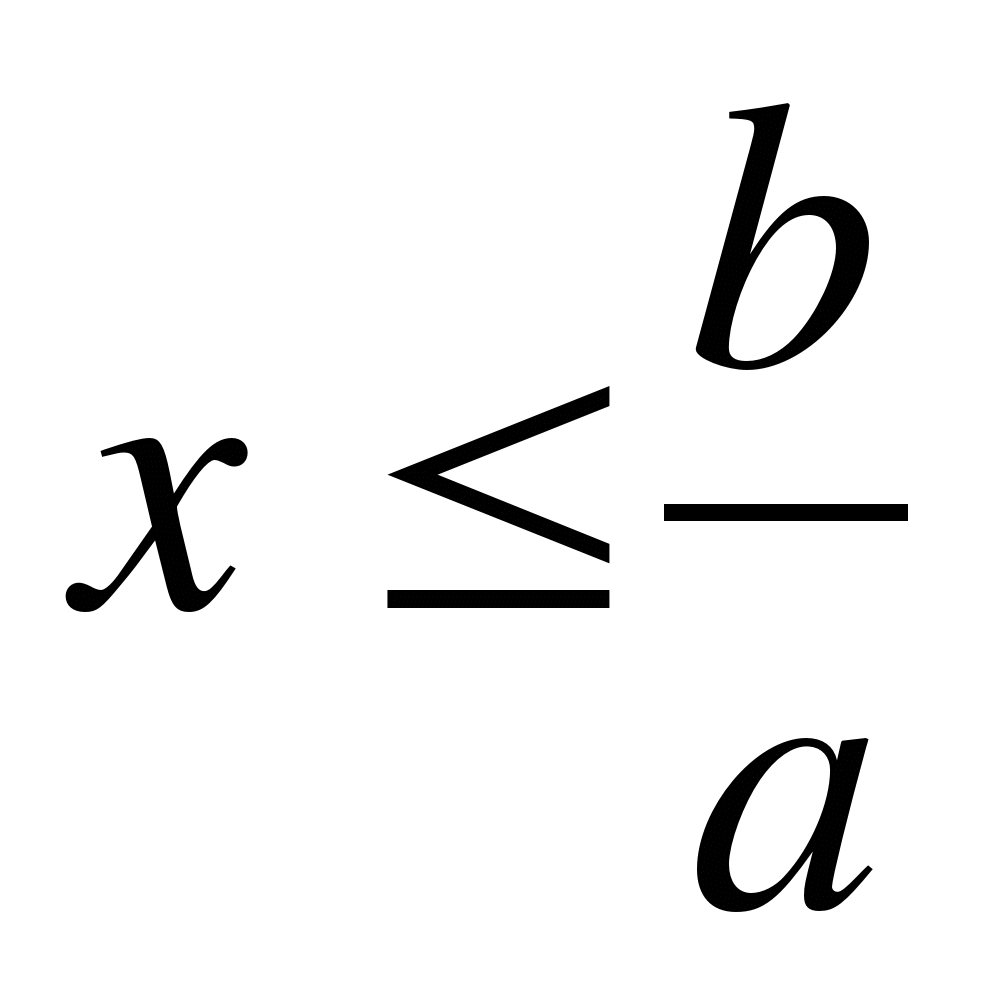 .
.
Если a<0, то
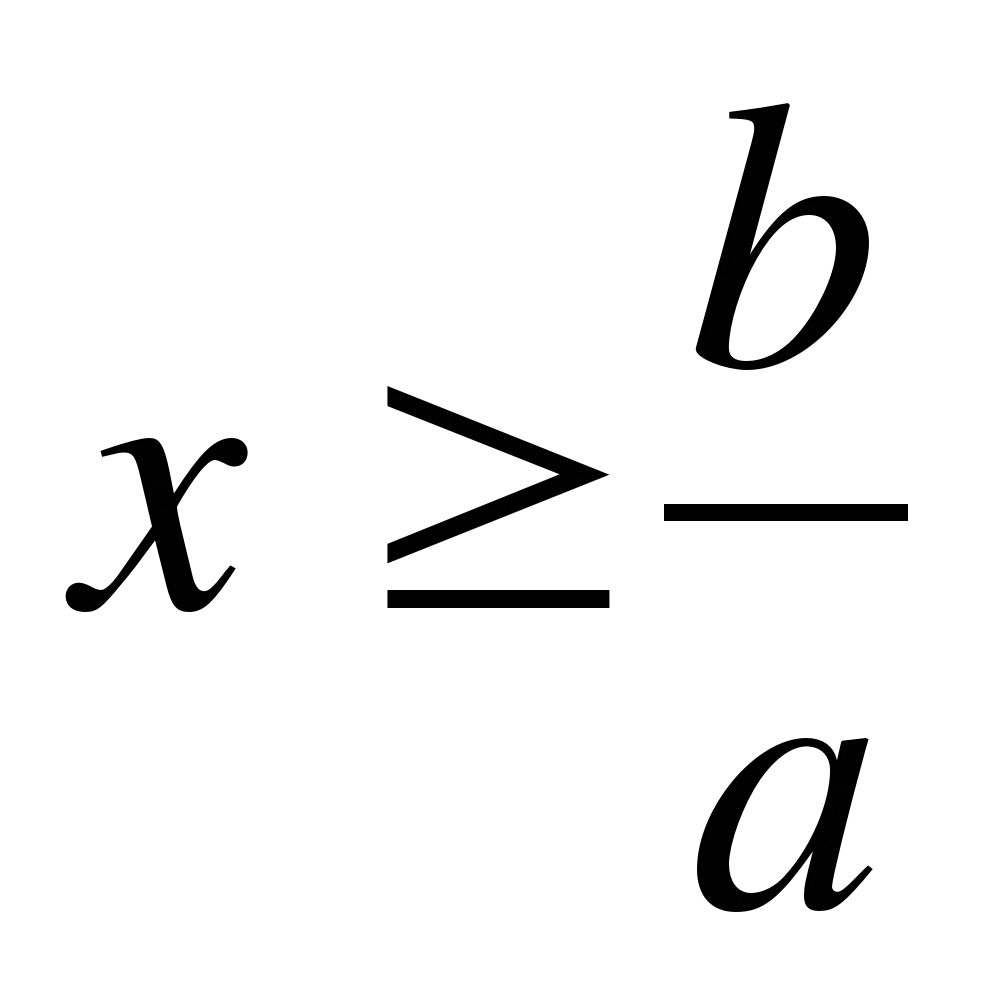 .
.
Если a=0 и b
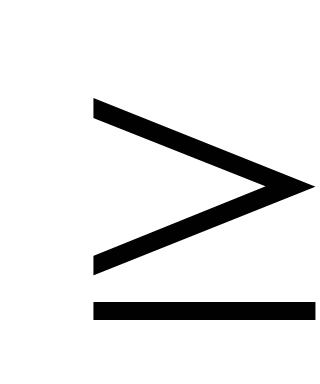 0,
то
0,
то  .
.
Если a=b и b<0, то решений нет.
-
Алгоритмические неравенства
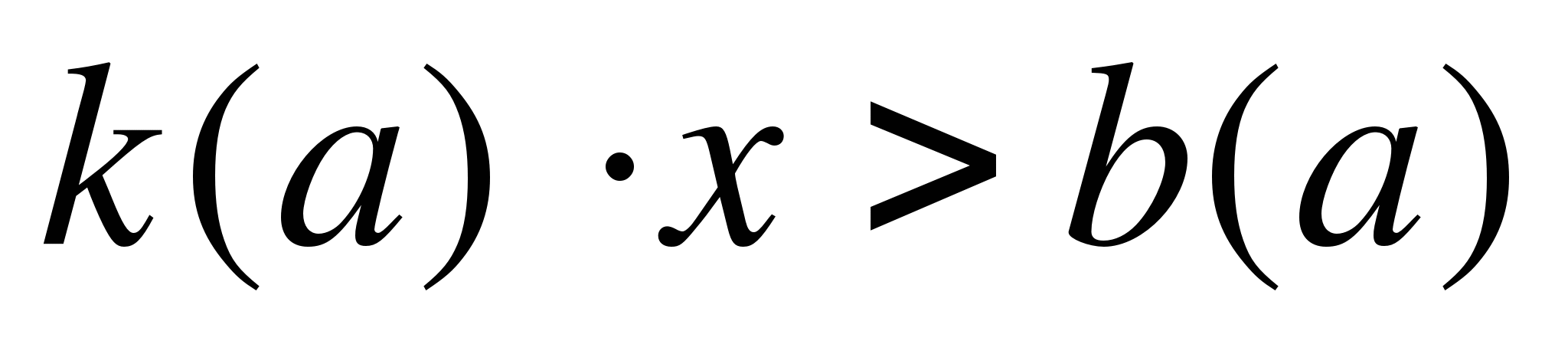
b(a) не имеет смысла
k(a)=0 b(a)>0
k(a)>0, b(a) имеет смысл
-
-
-
k(a)<0, b(a) имеет смысл
-
-
-
-
-
k(a)=0, b(a)<0
-
-
решений нет
решений нет
решений нет
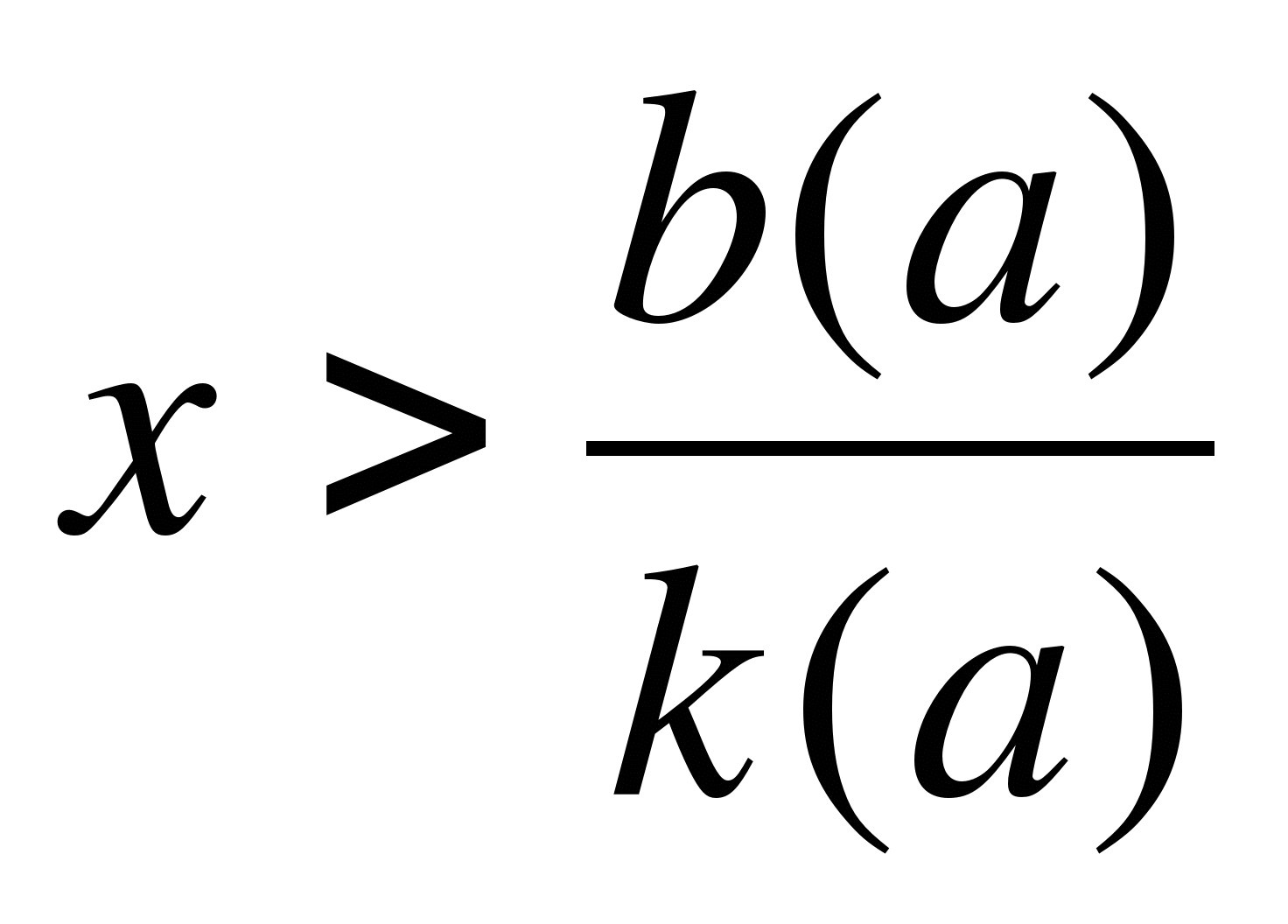
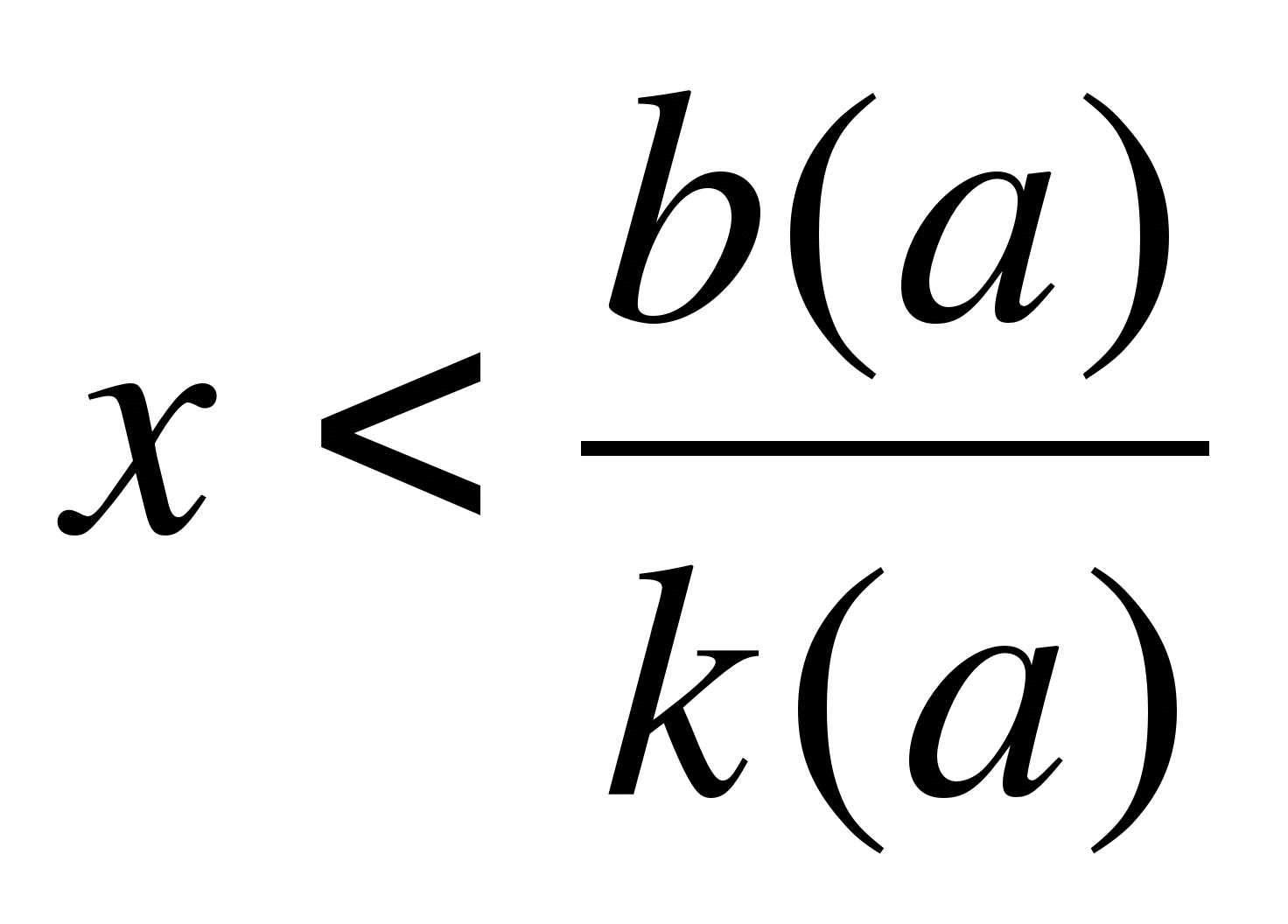
 .
.
-
Упражнения по совершенствованию и закреплению знаний и умений.
1. Решить неравенство
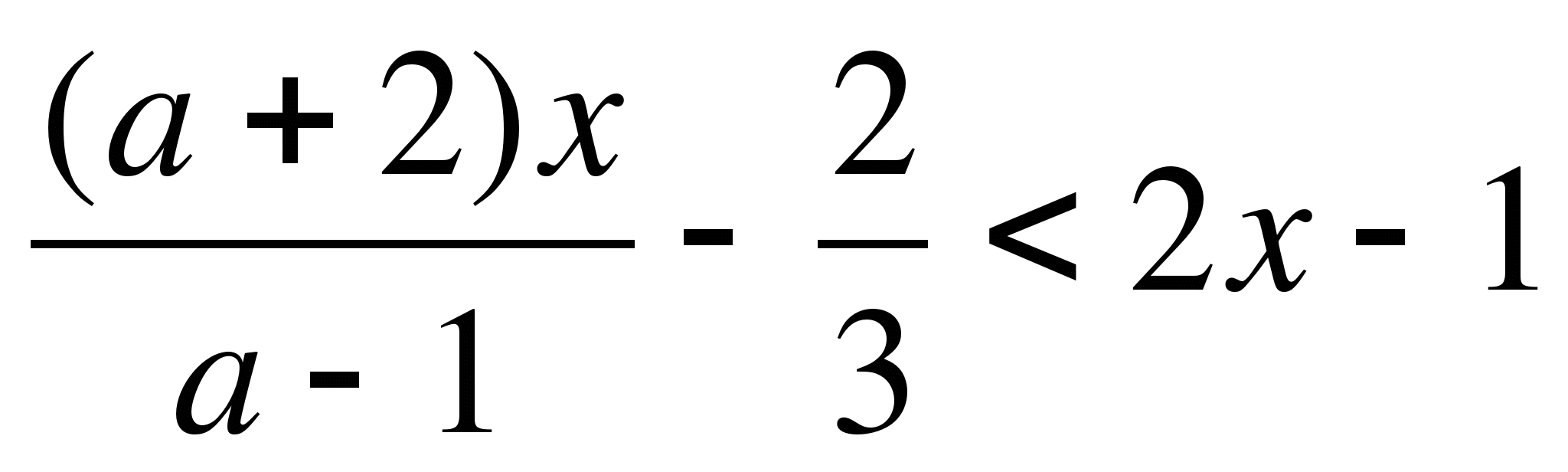 ;
;
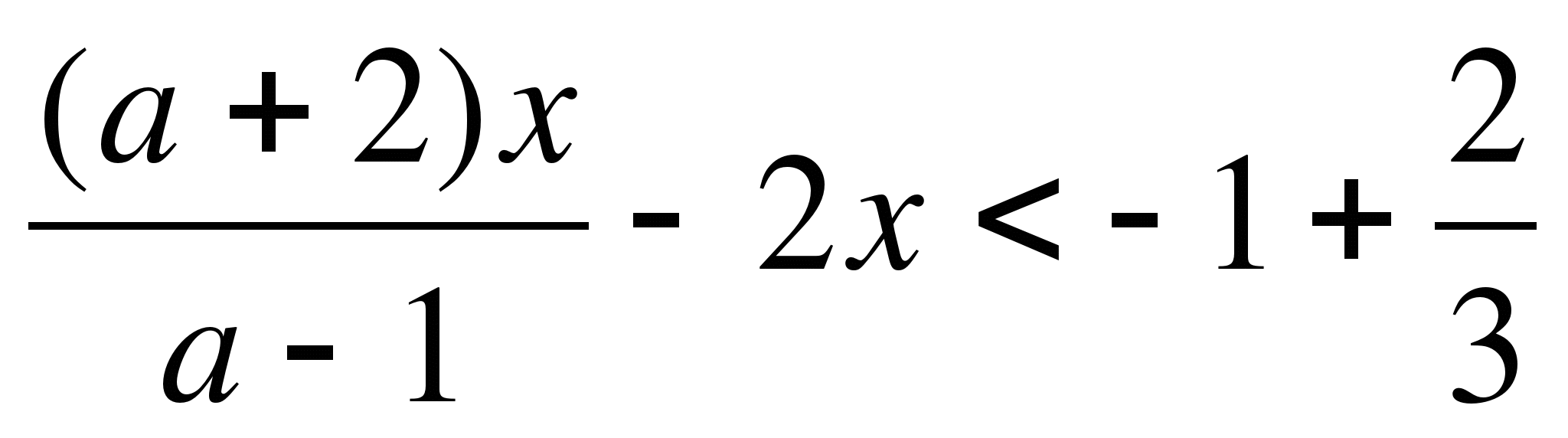 ;
;
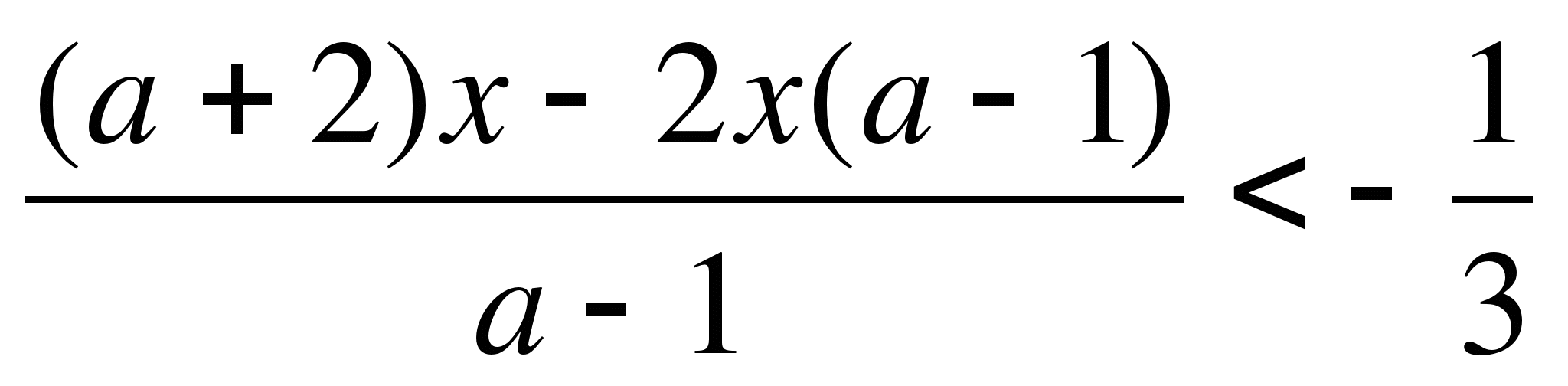 ;
;
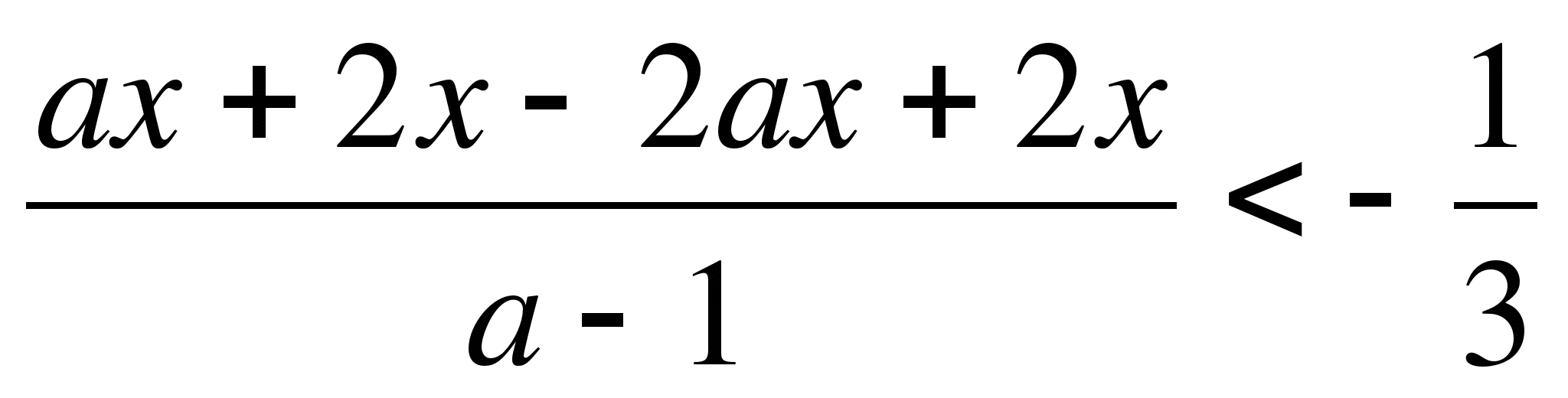 ;
;
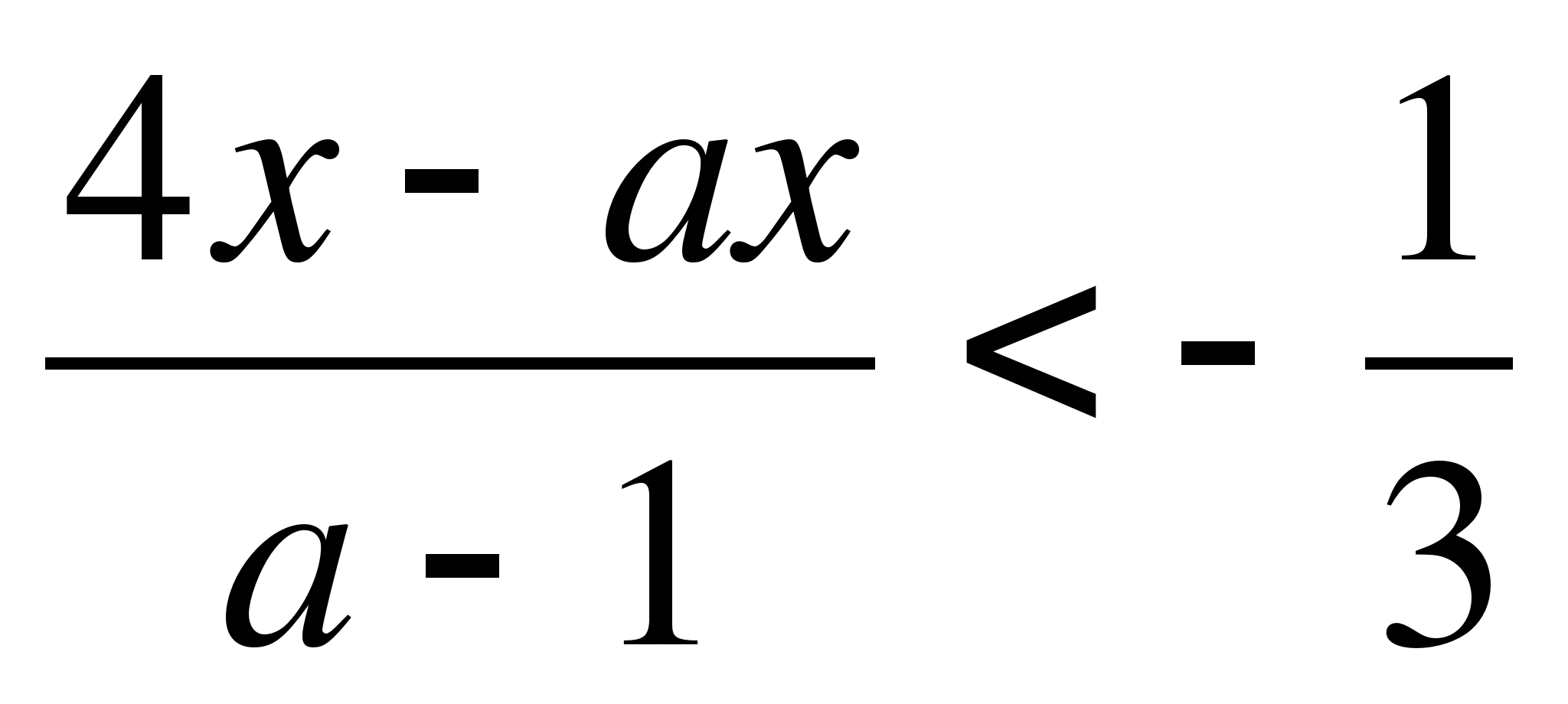 ;
;
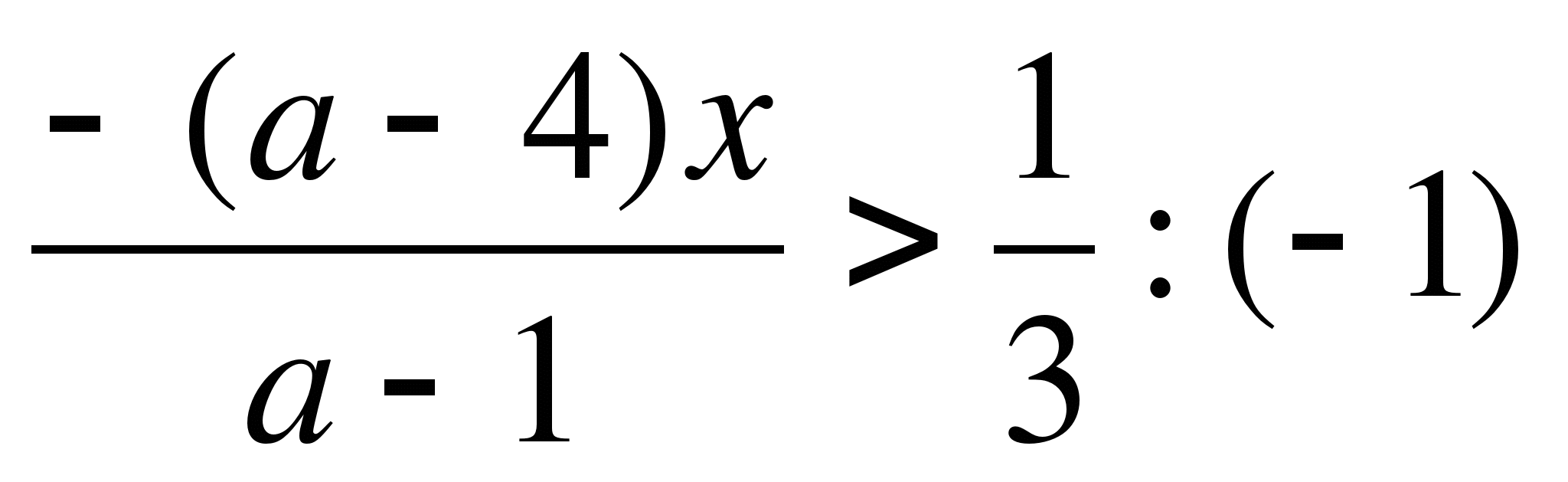
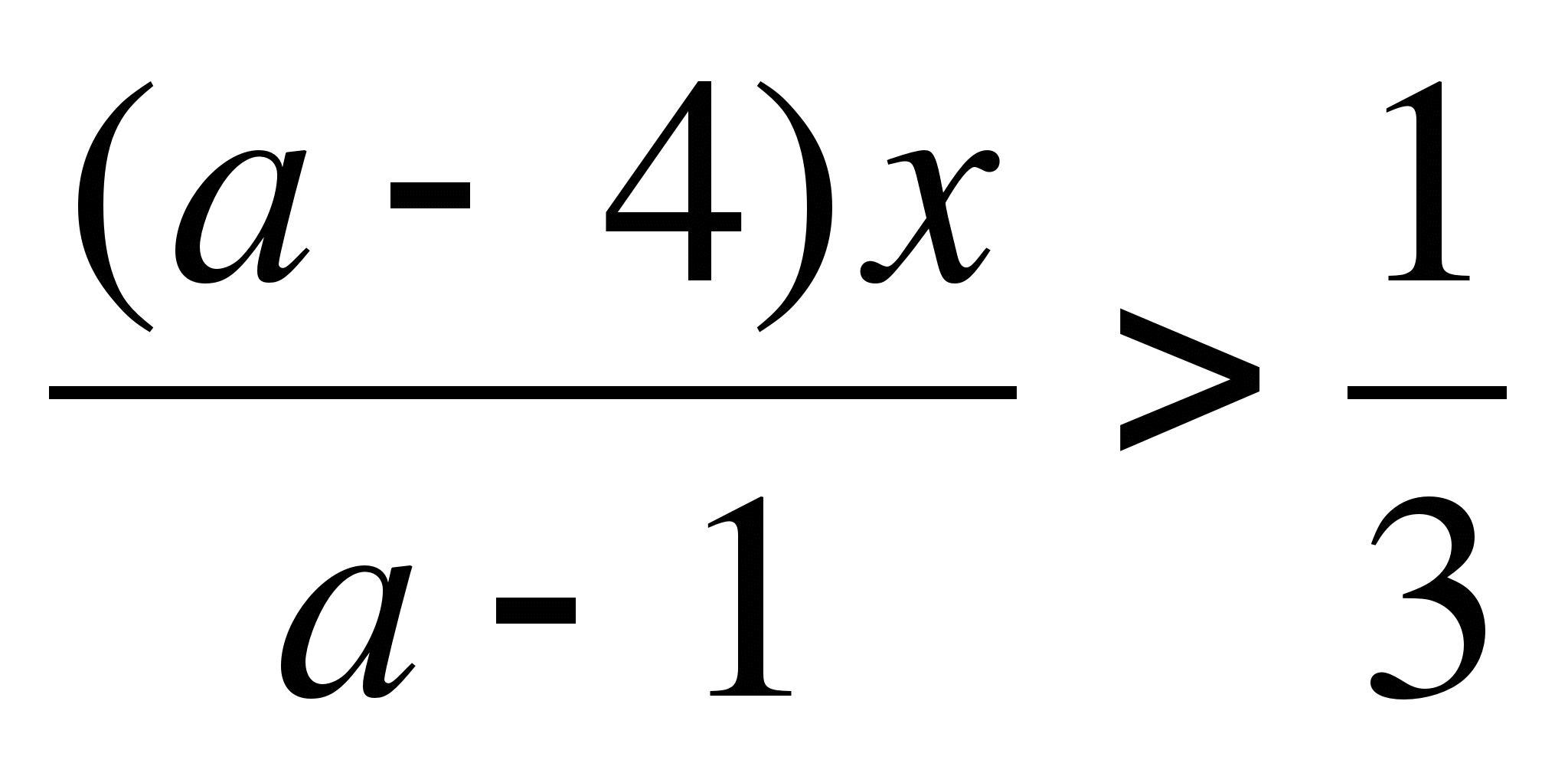
-
-
-
Если a=1, то решений нет
-
Если а=4, то решений нет
-
-
Исследуем знак выражения



1 4 а
-
если 1</</i>, то
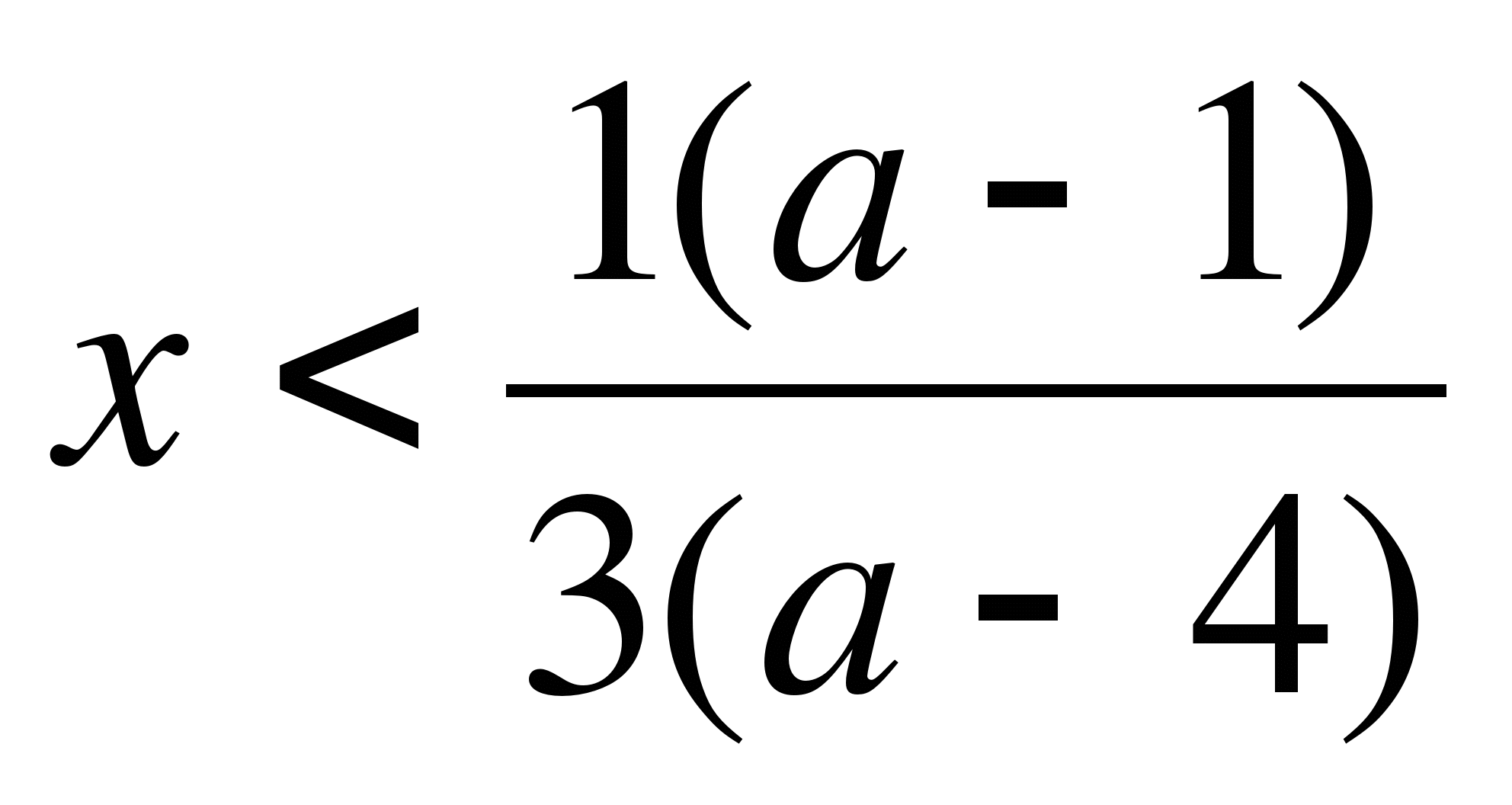
-
если a<1, то
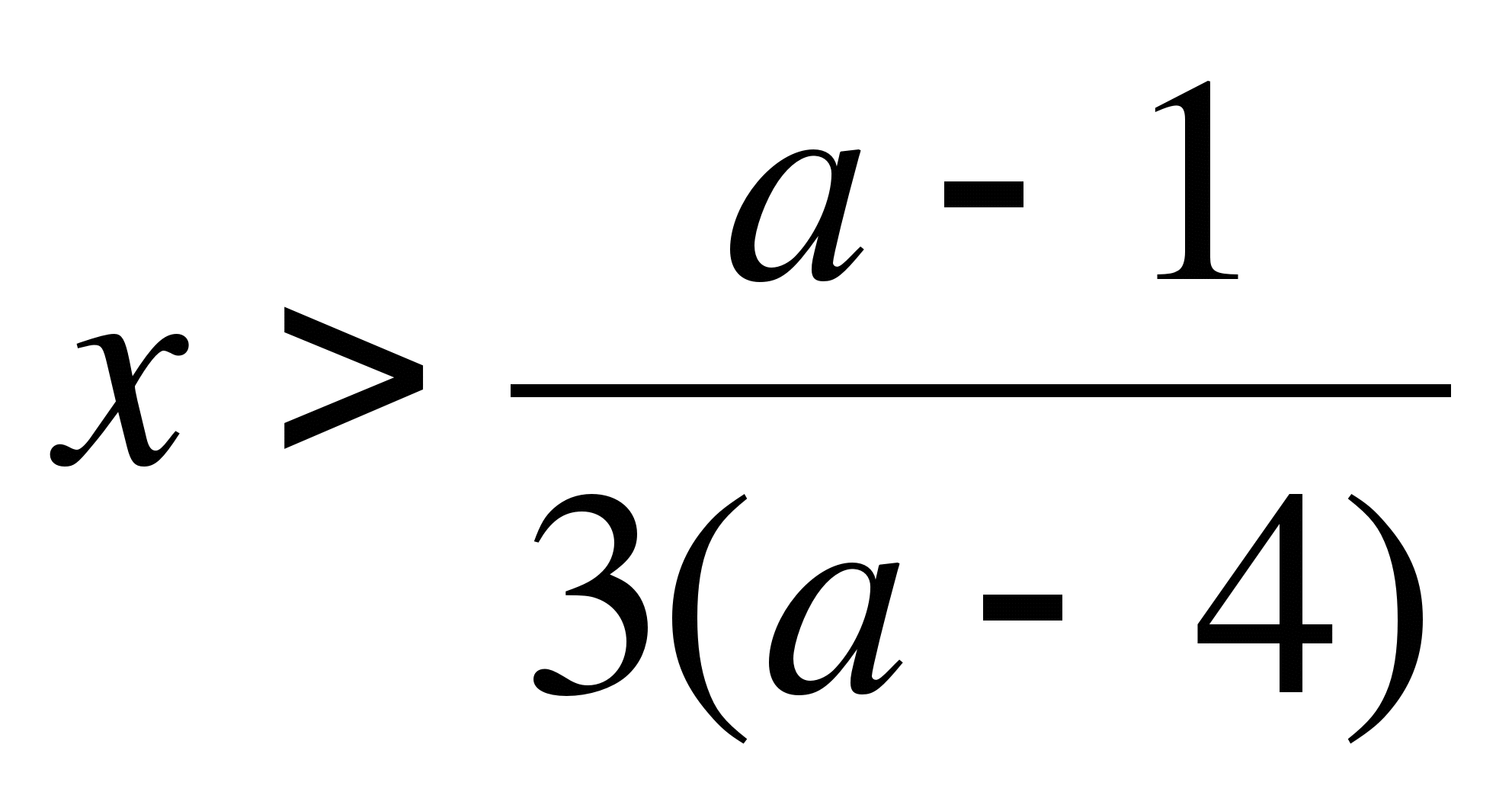
-
если a>4, то
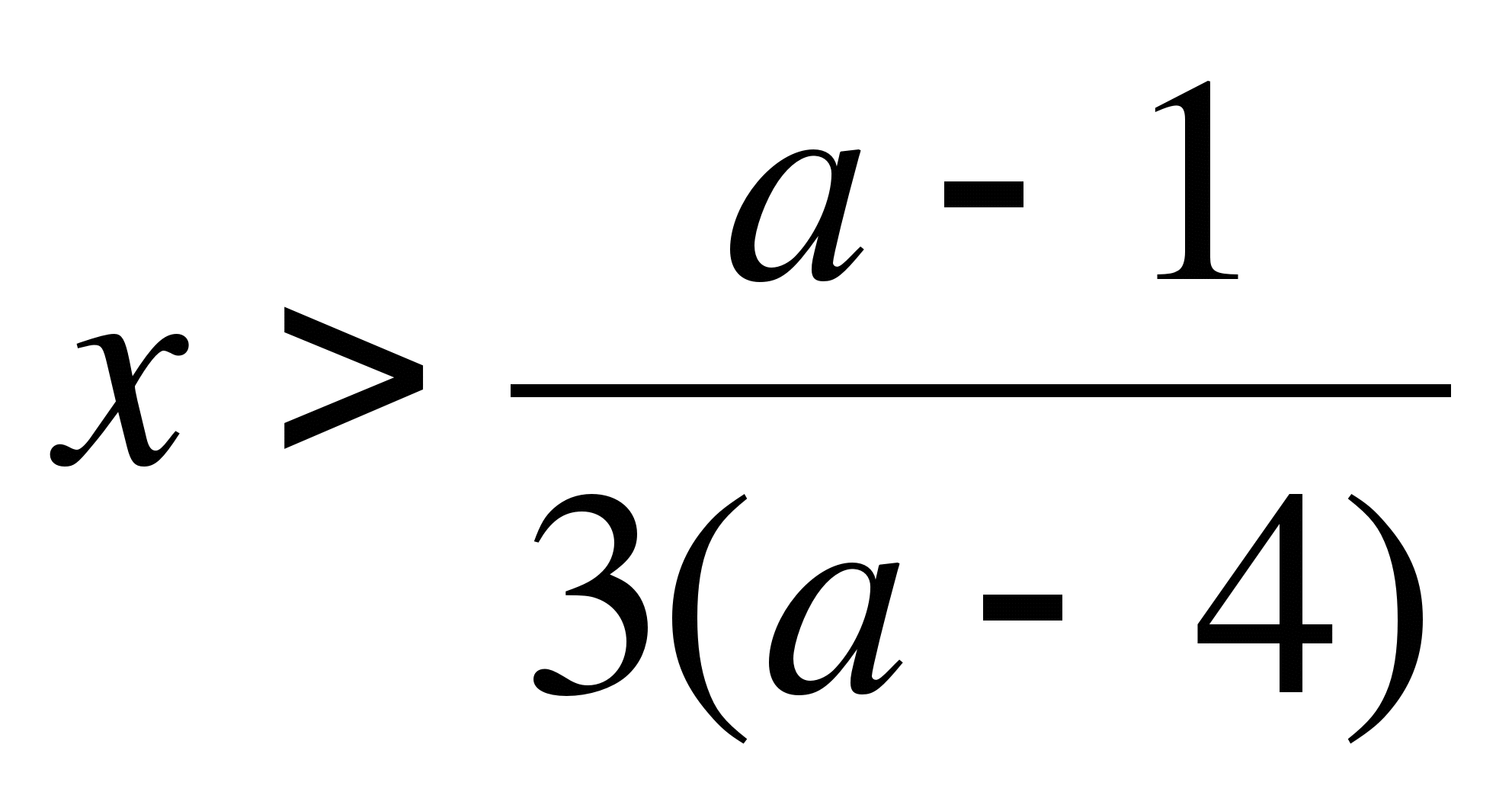
Ответ: если a=1, a=4, то решений нет; если a<1 и a>4, то
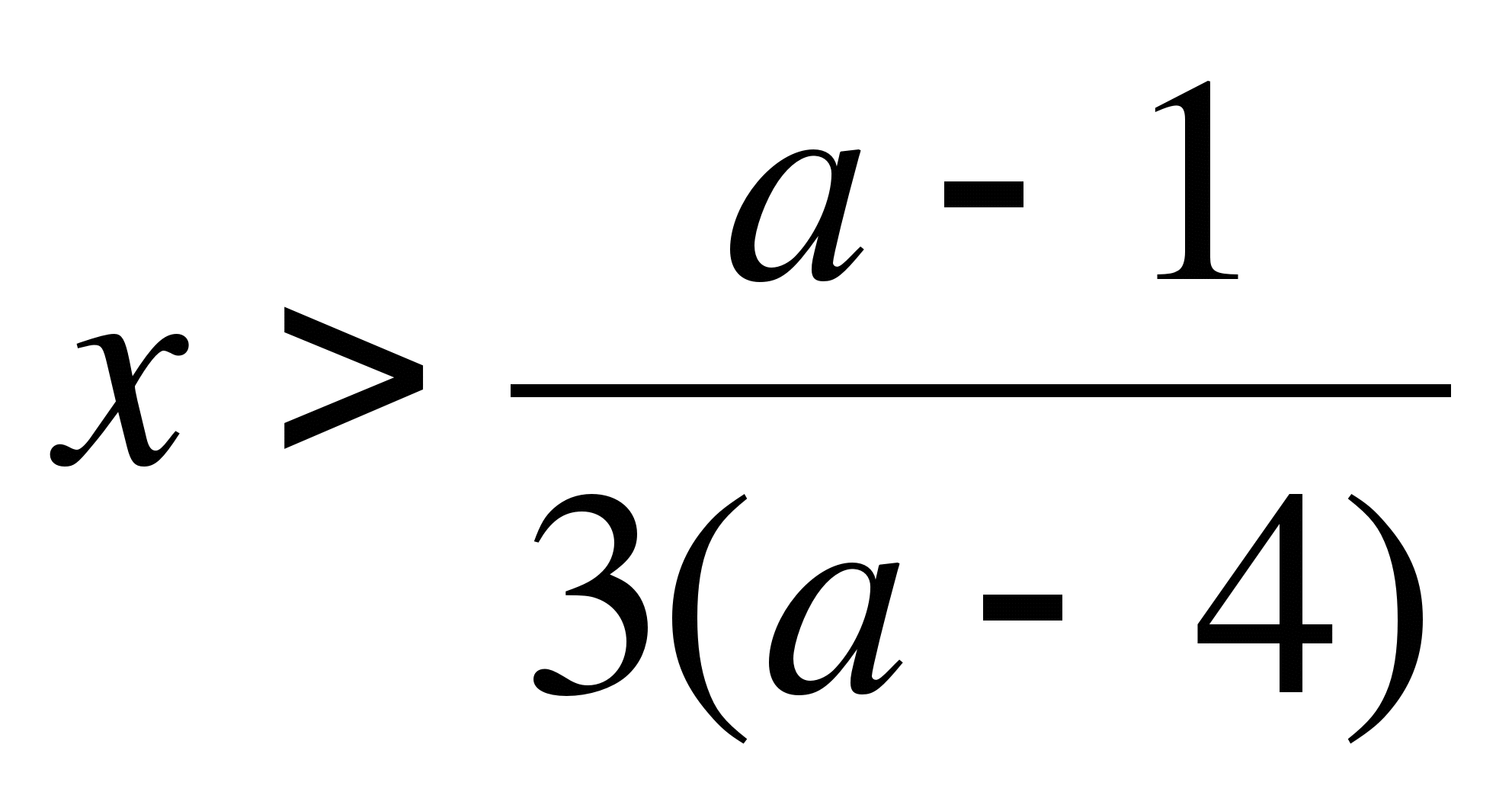 ;
;
если 1<a<4, то
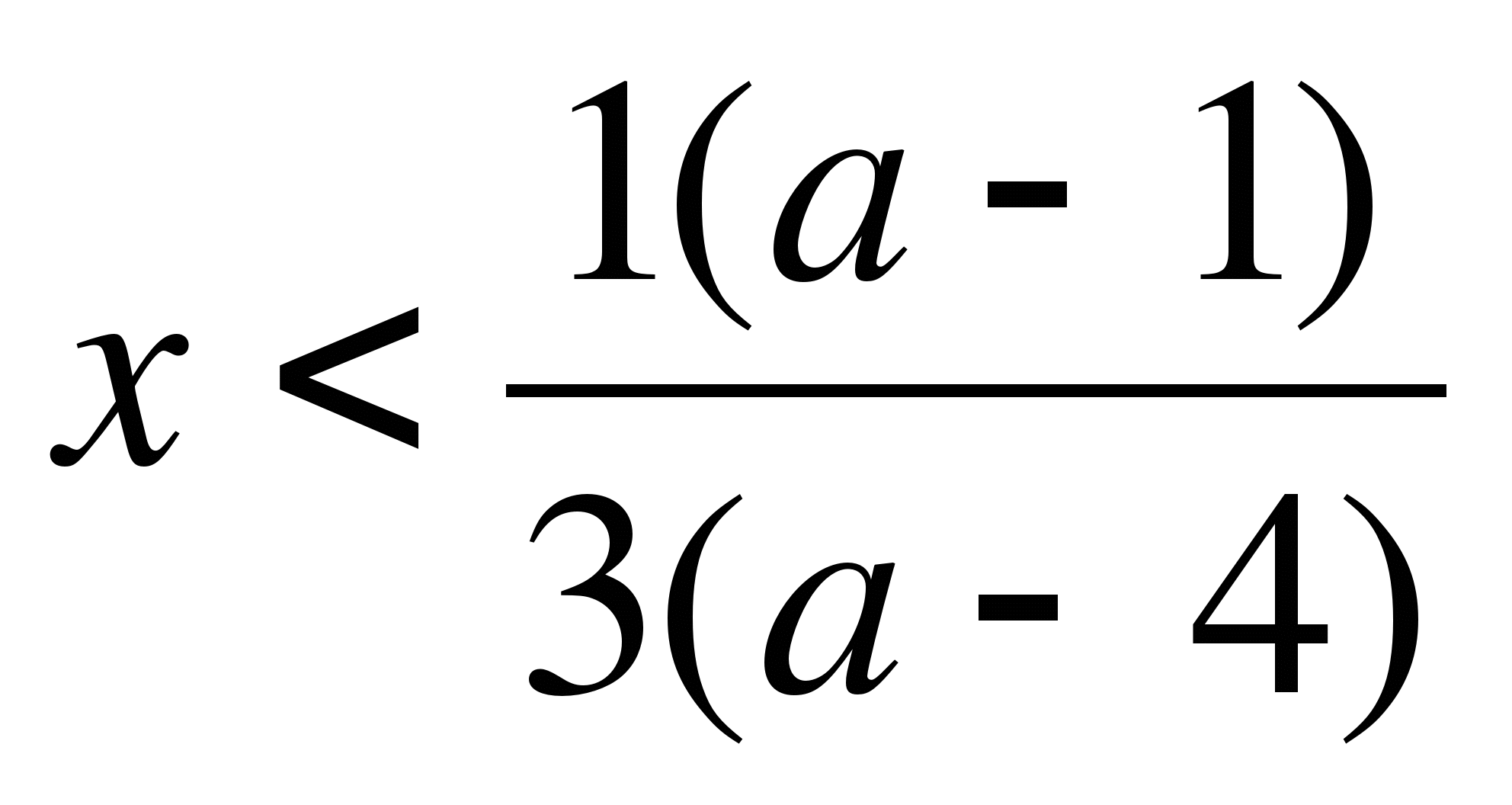 .
.
-
-
Решить неравенство
-
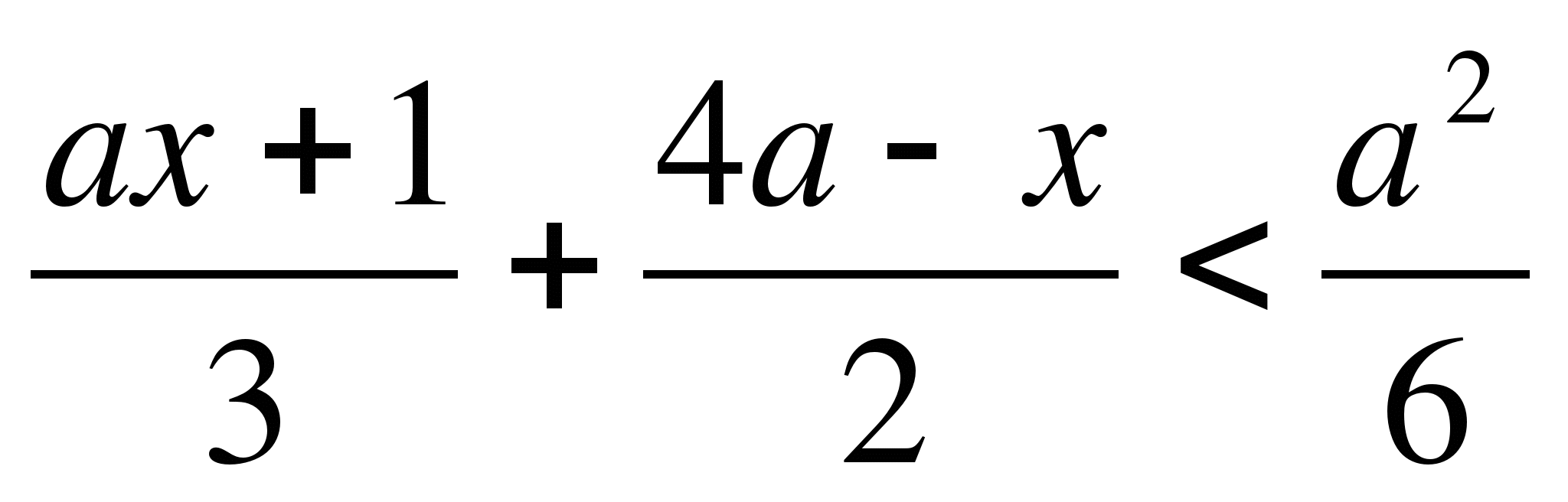
Ответ:
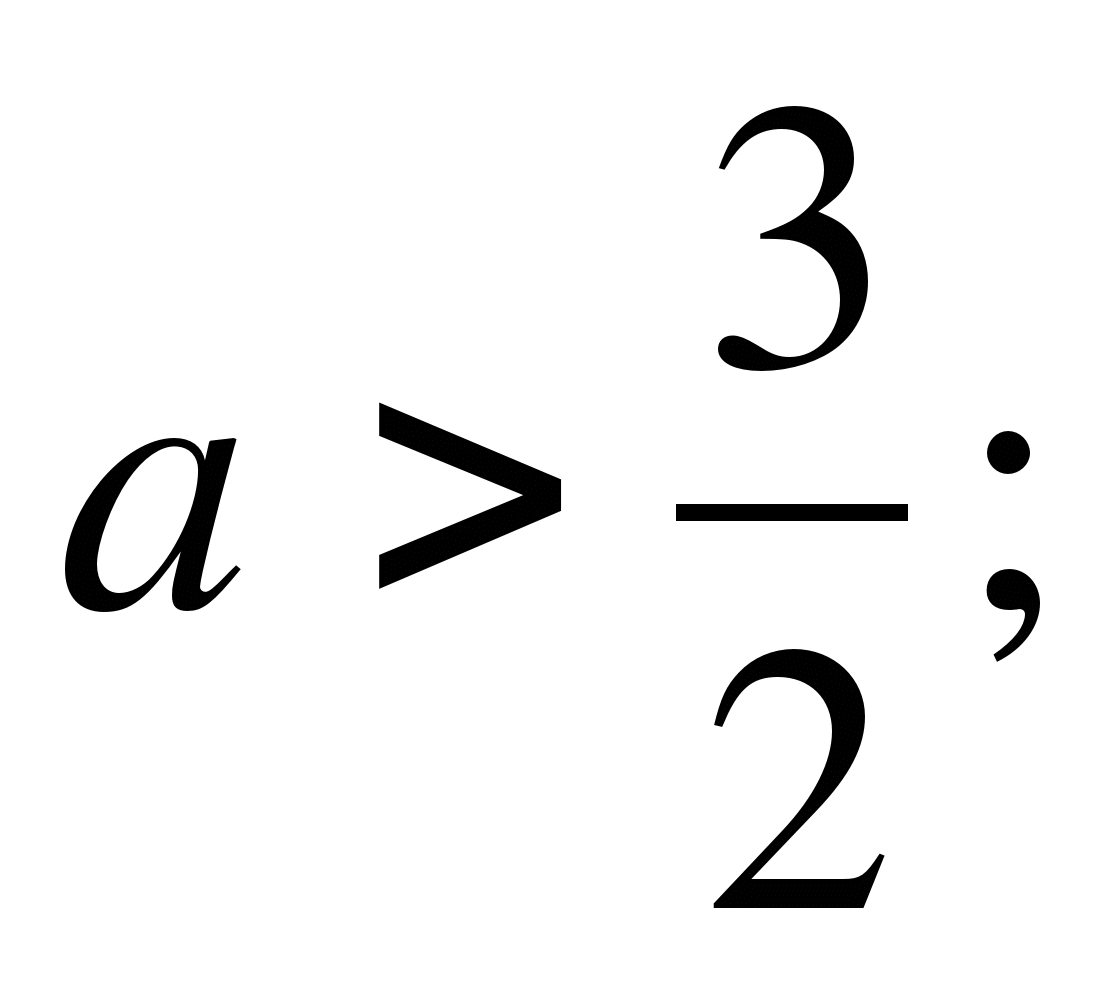
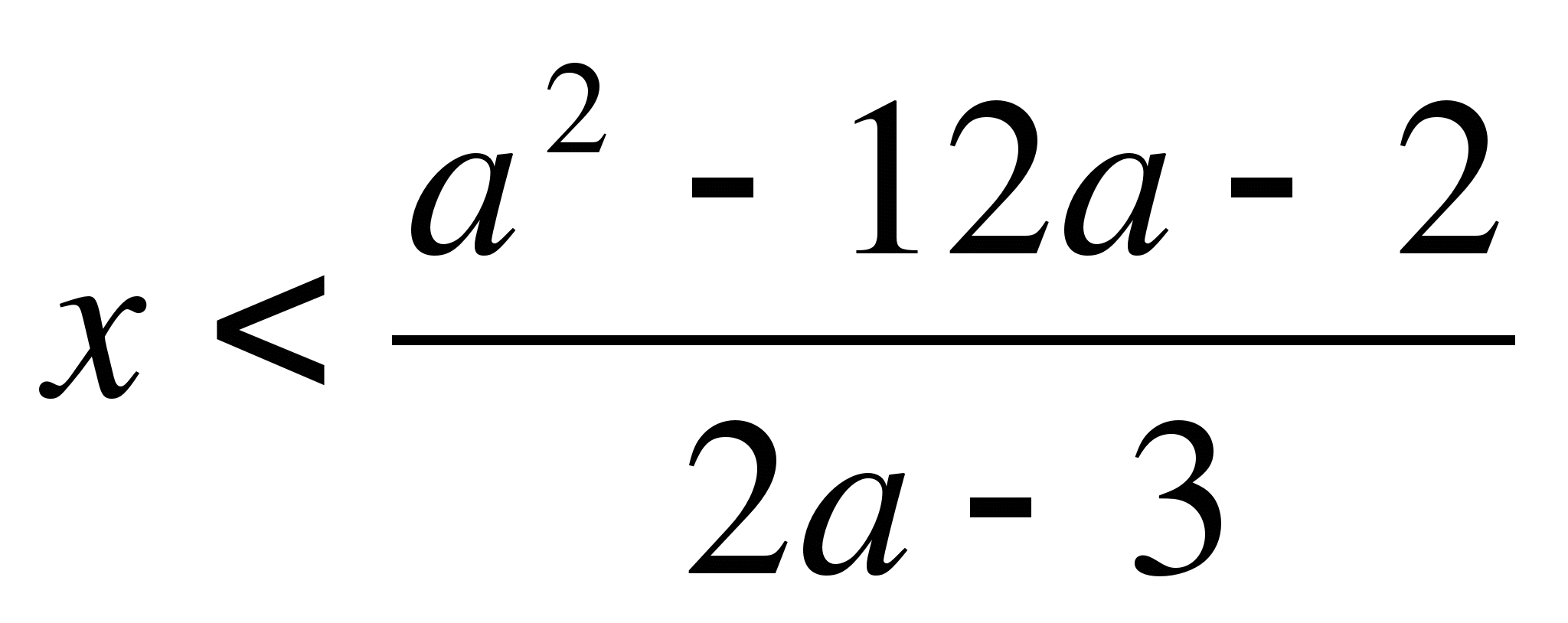
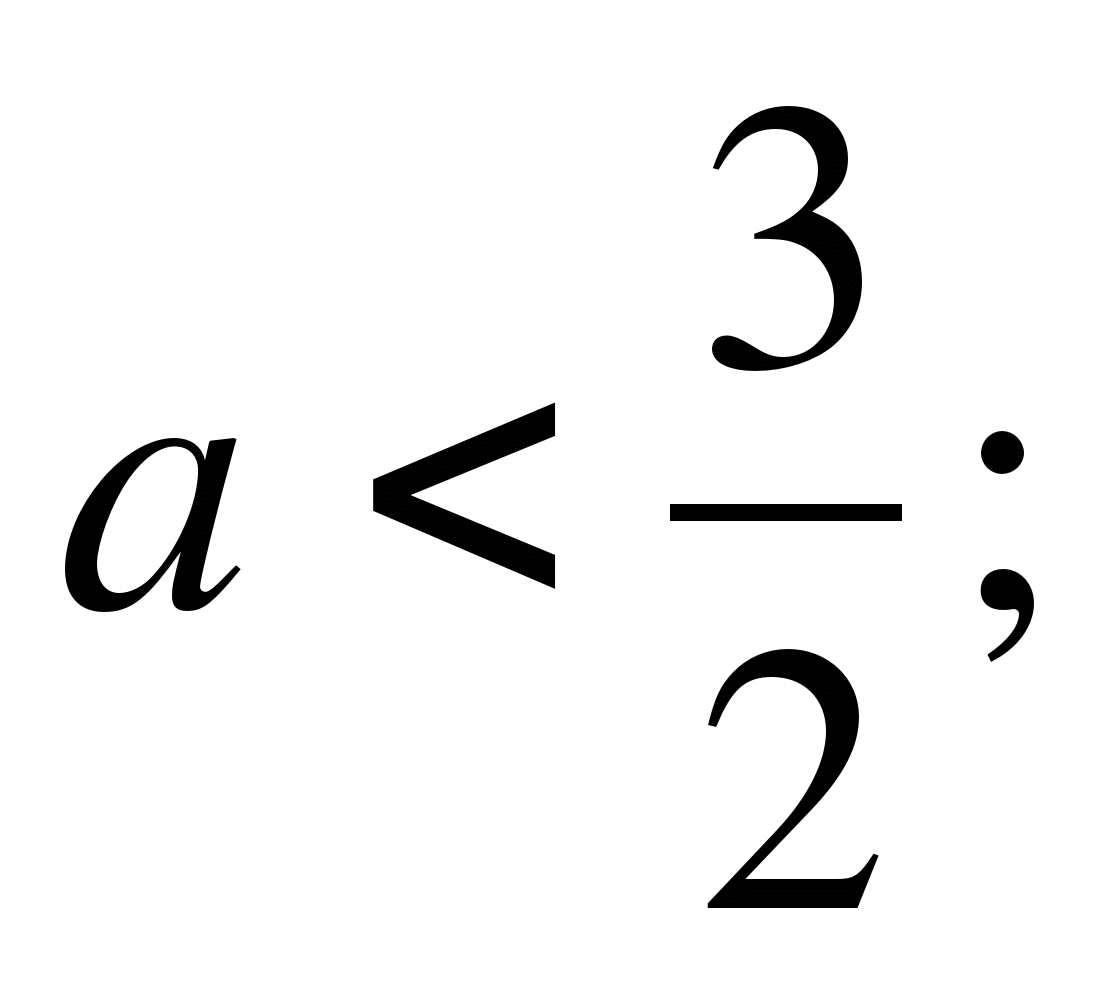
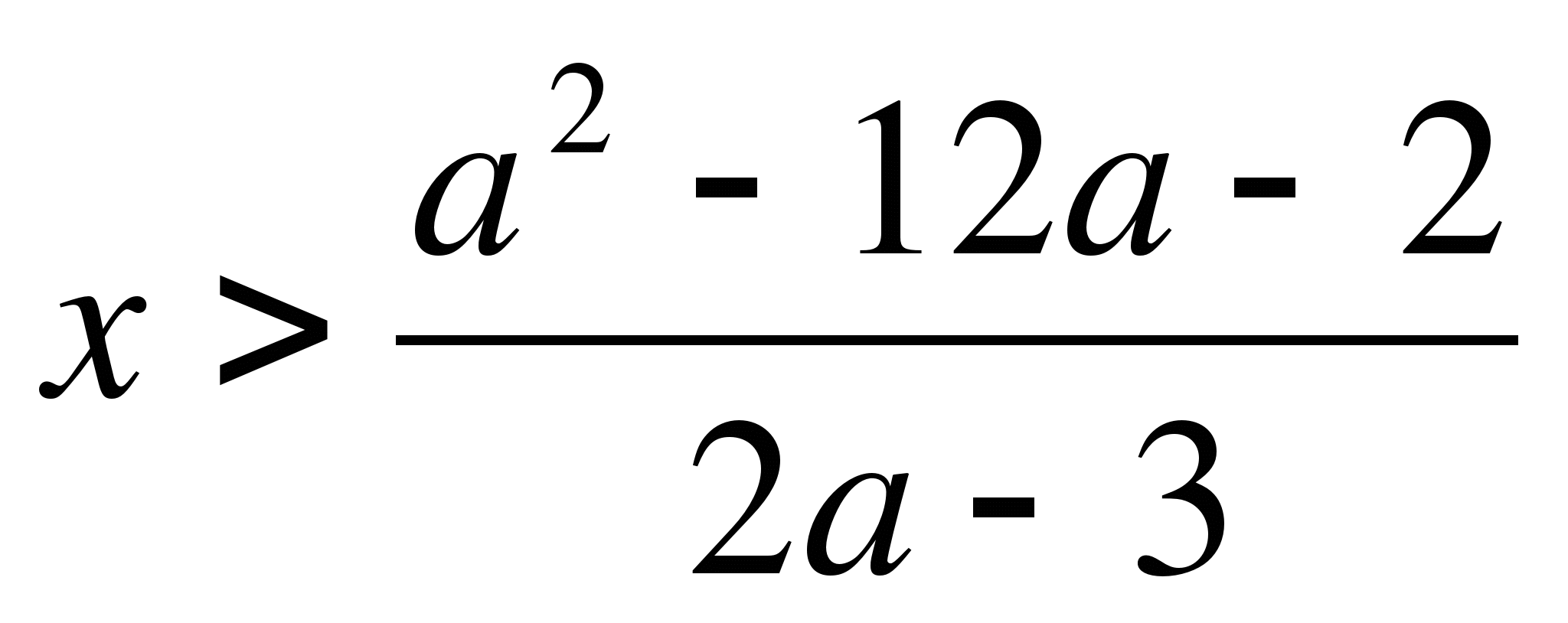
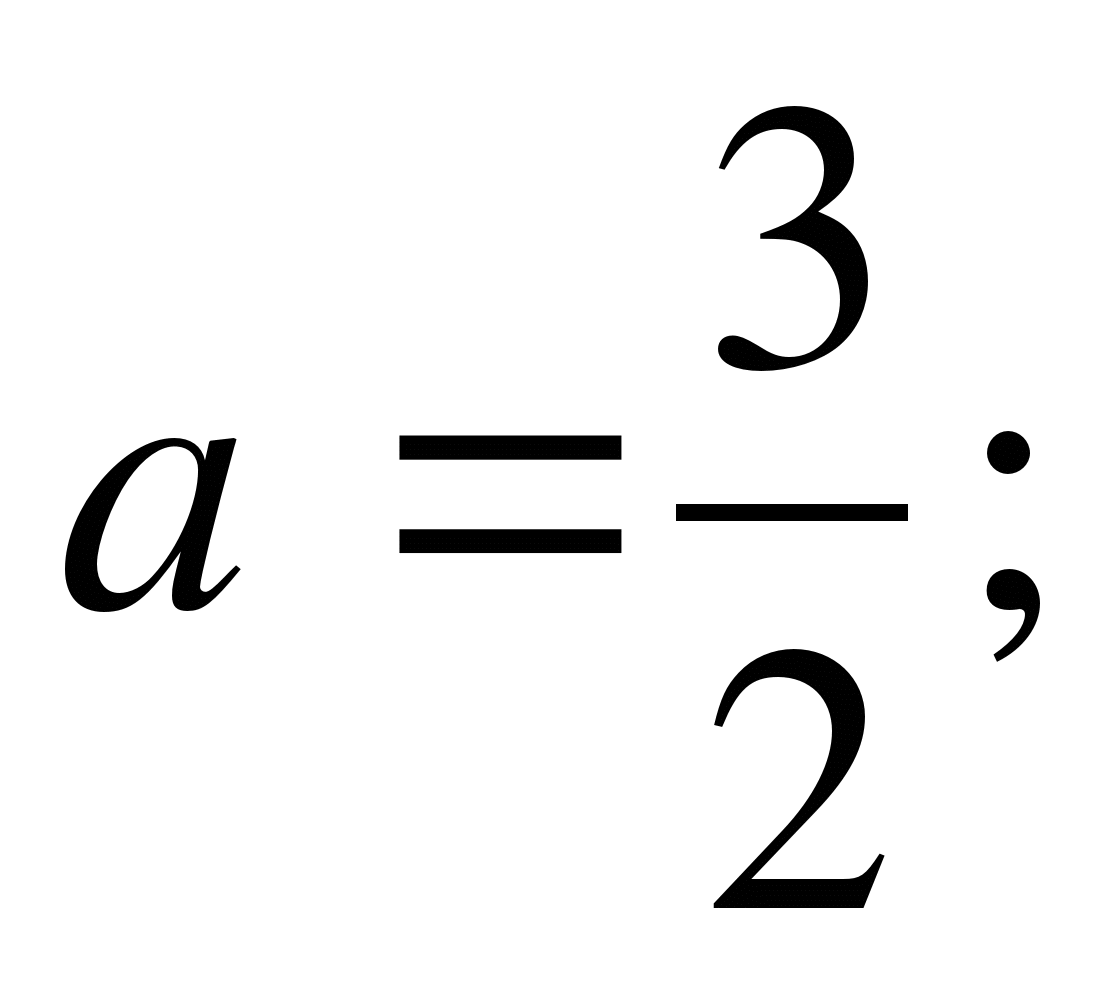 решений нет.
решений нет.
-
-
Решите неравенство
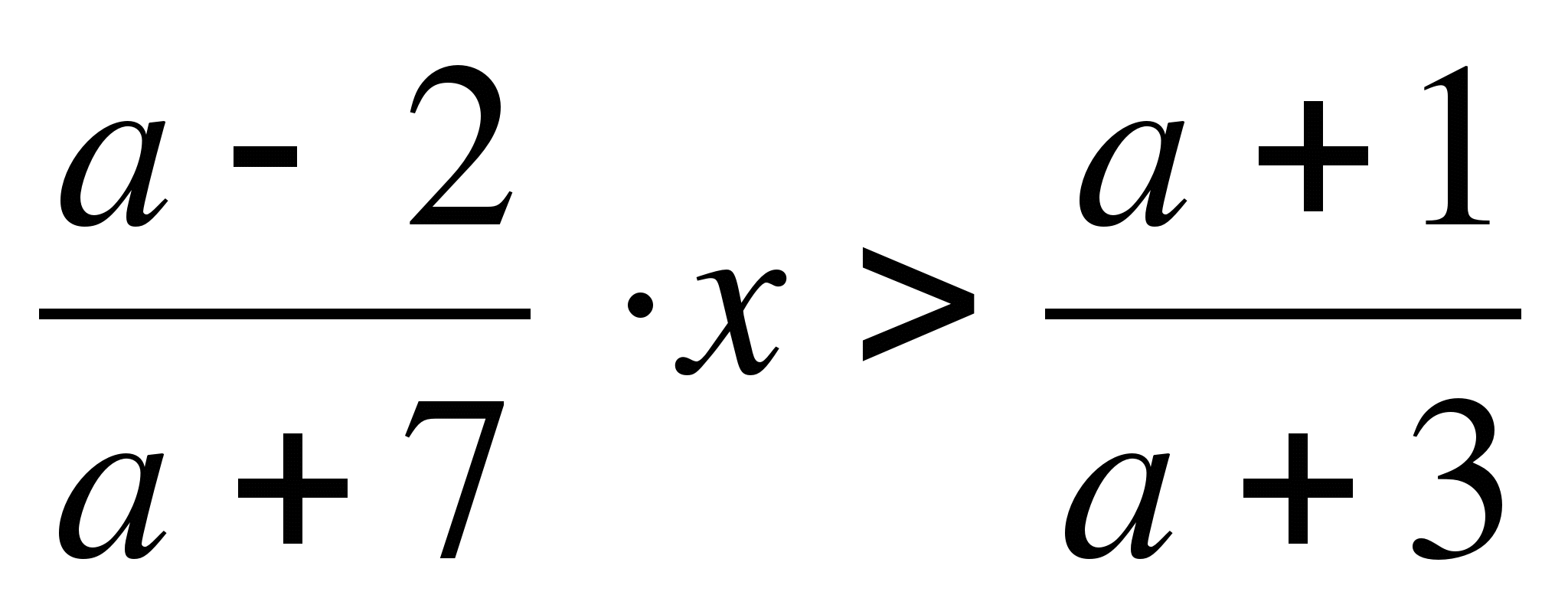 .
.
-
-
если а= -7 и а= -3, то решений нет.
-
если а=2, то решений нет.
Исследуем знак выражения на промежутках


-7 -3 2 а
1) если a>-7 и a>2, то
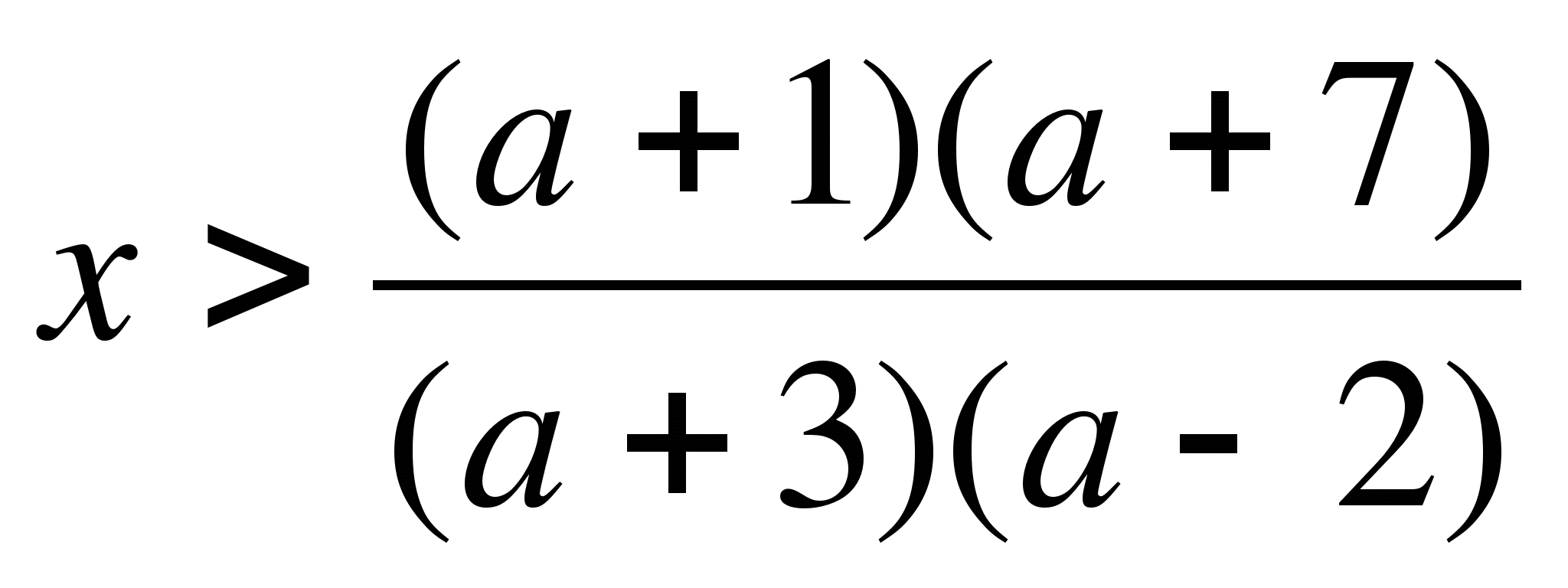 ,
,
2) если -7<a<-3, -3<a<2, то
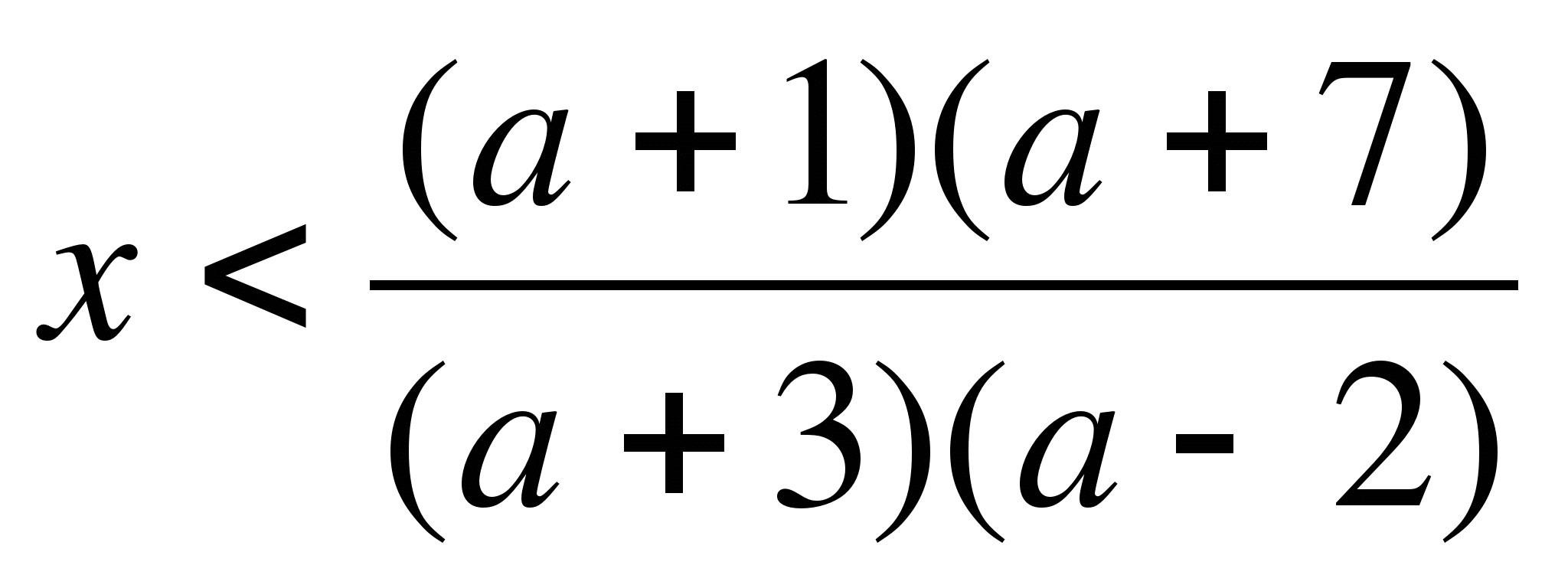 .
.
Ответ: 1) если a>-7 и a>2, то
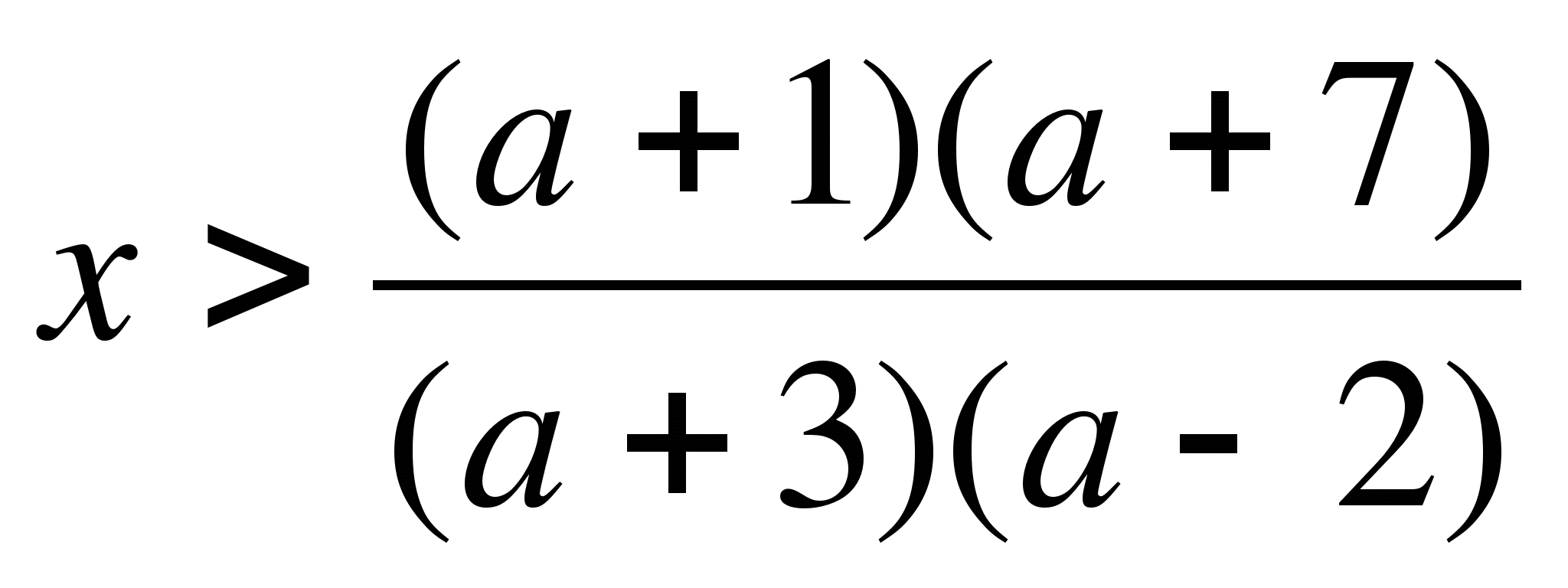 ,
,
2) если -7<a<-3, -3<a<2, то
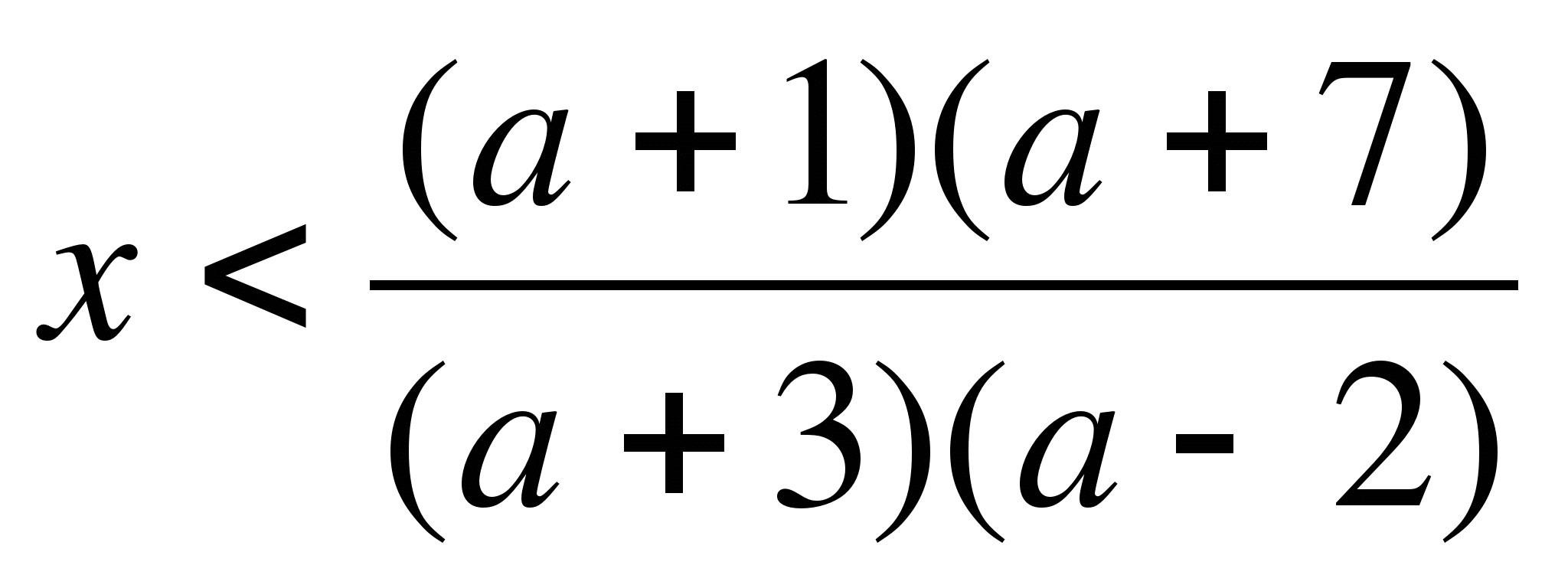 .
.
IV. Самостоятельная работа (либо самопроверка)
Уровень А
Решите неравенство
а) ах<0
Ответ: 1) если а>0, то x<0.
2) если а<0, то x>0.
3) если a=0, то решений нет.
б) a+x<2-ax
Решение:
x-ах<2-a
(1-a)x<2-a
1) если 1-a>0, т.е. a<1, то
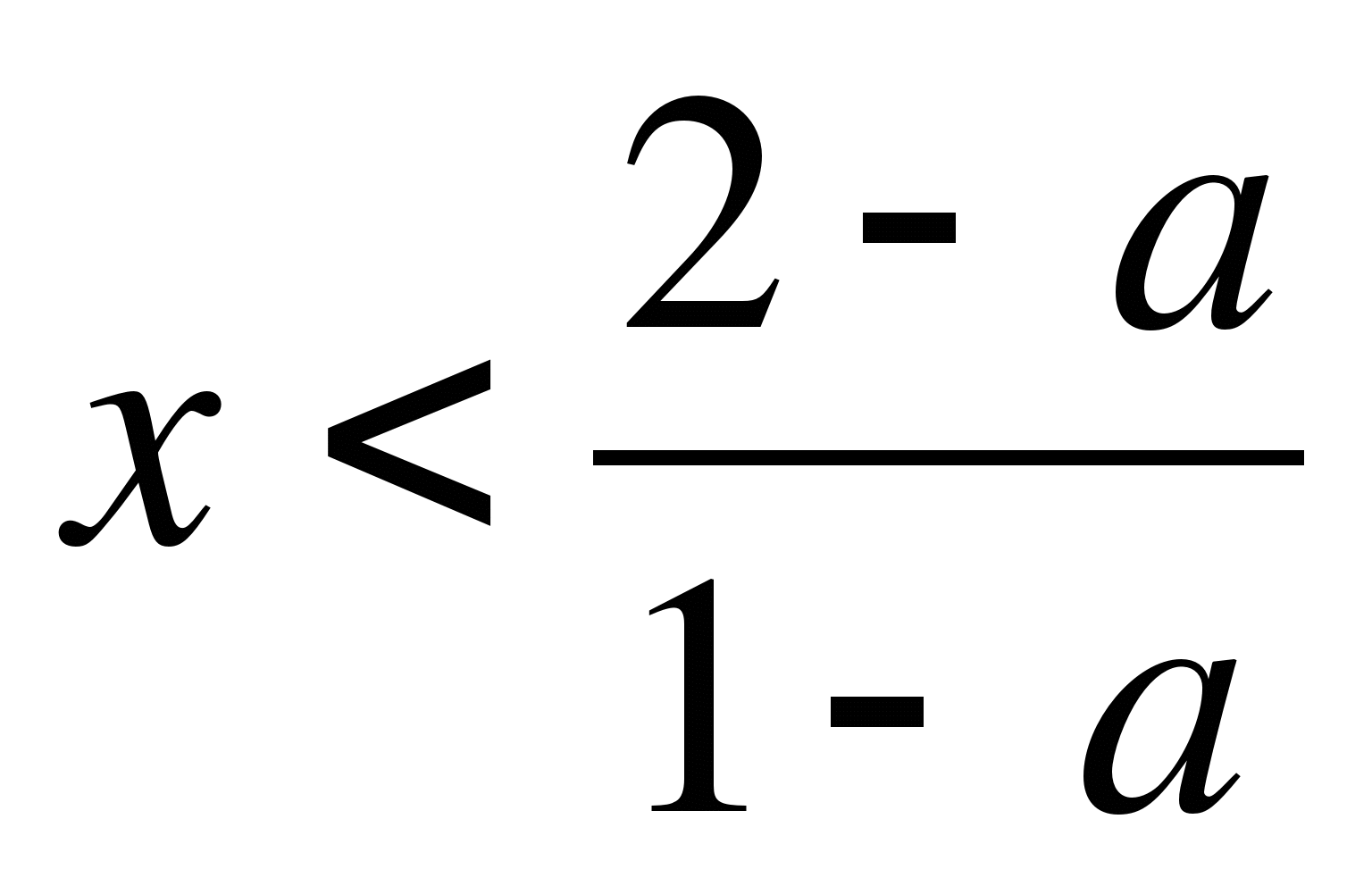 ;
;
2) если 1-a<0, т.е. a>1, то
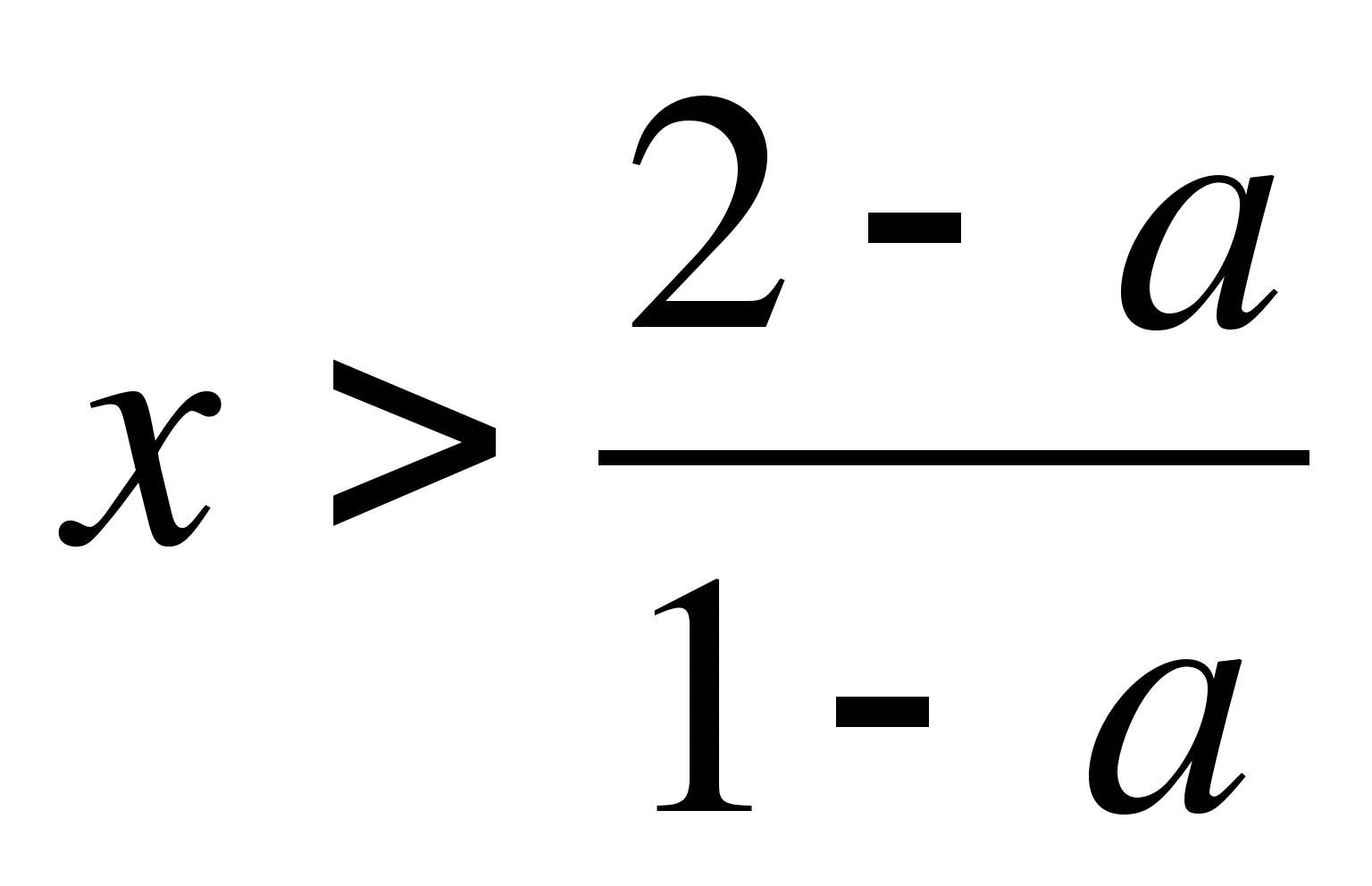 ;
;
3) если а=0, то
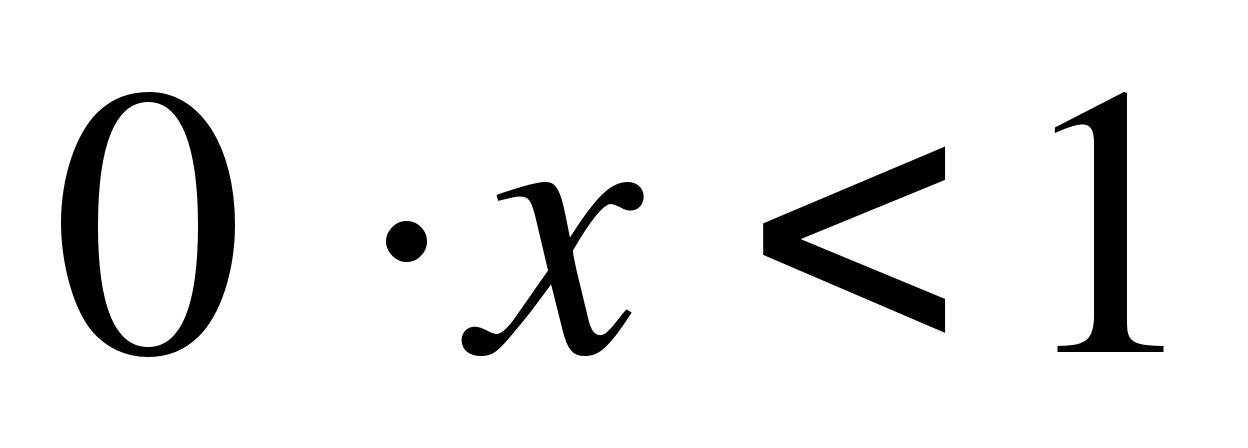 решений нет.
решений нет.
Ответ: если
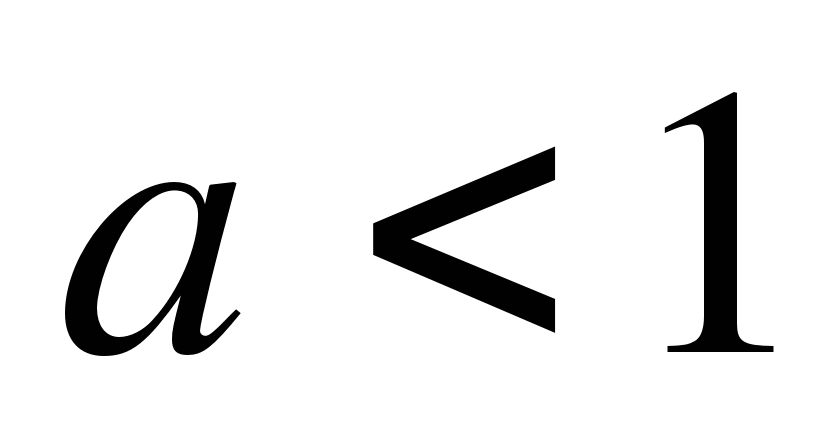 , то
, то
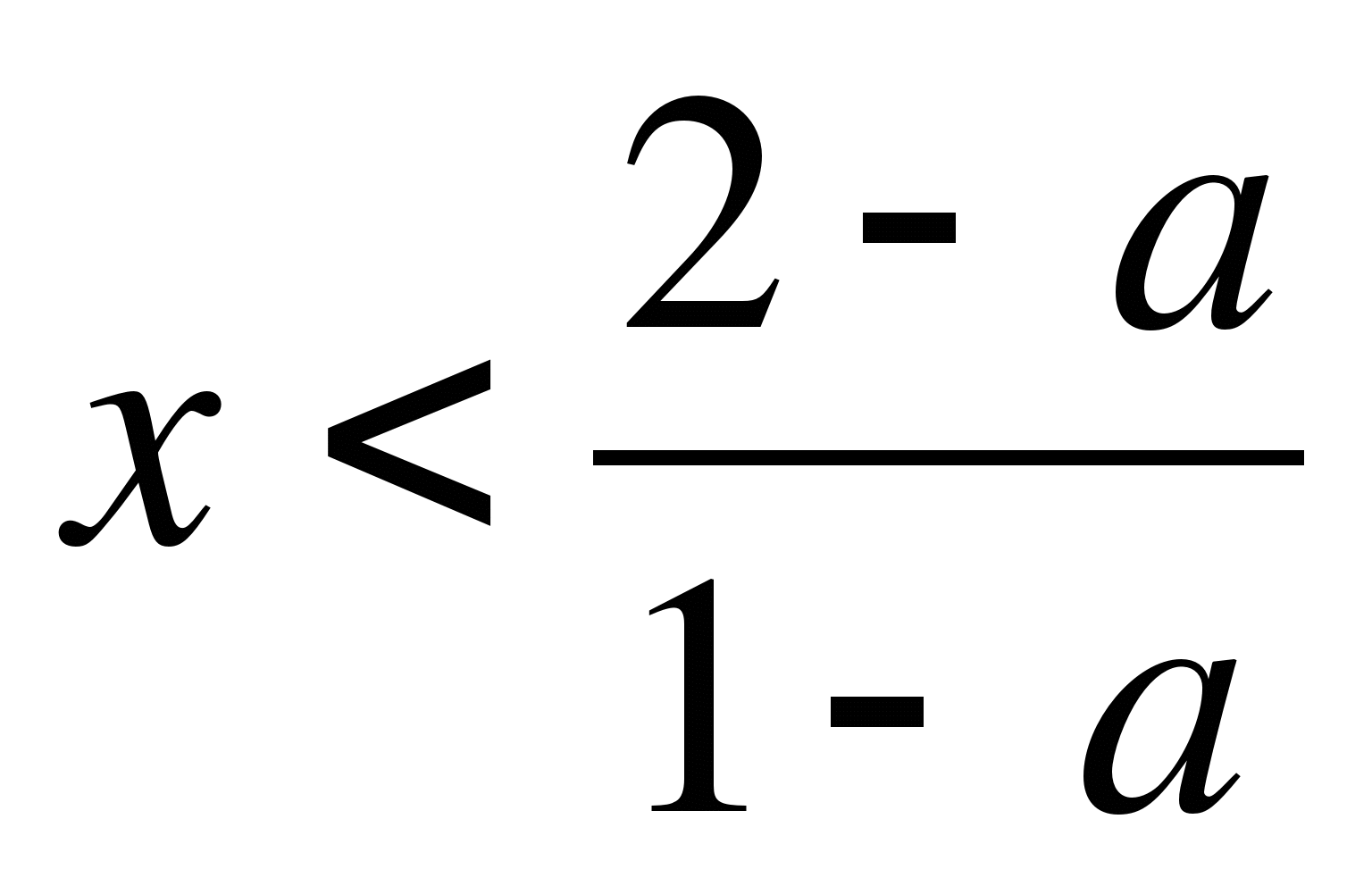 ;
если
;
если 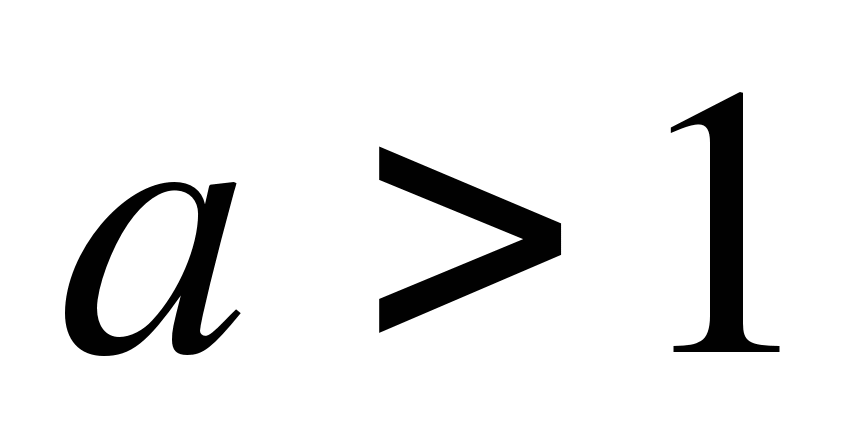 , то
, то
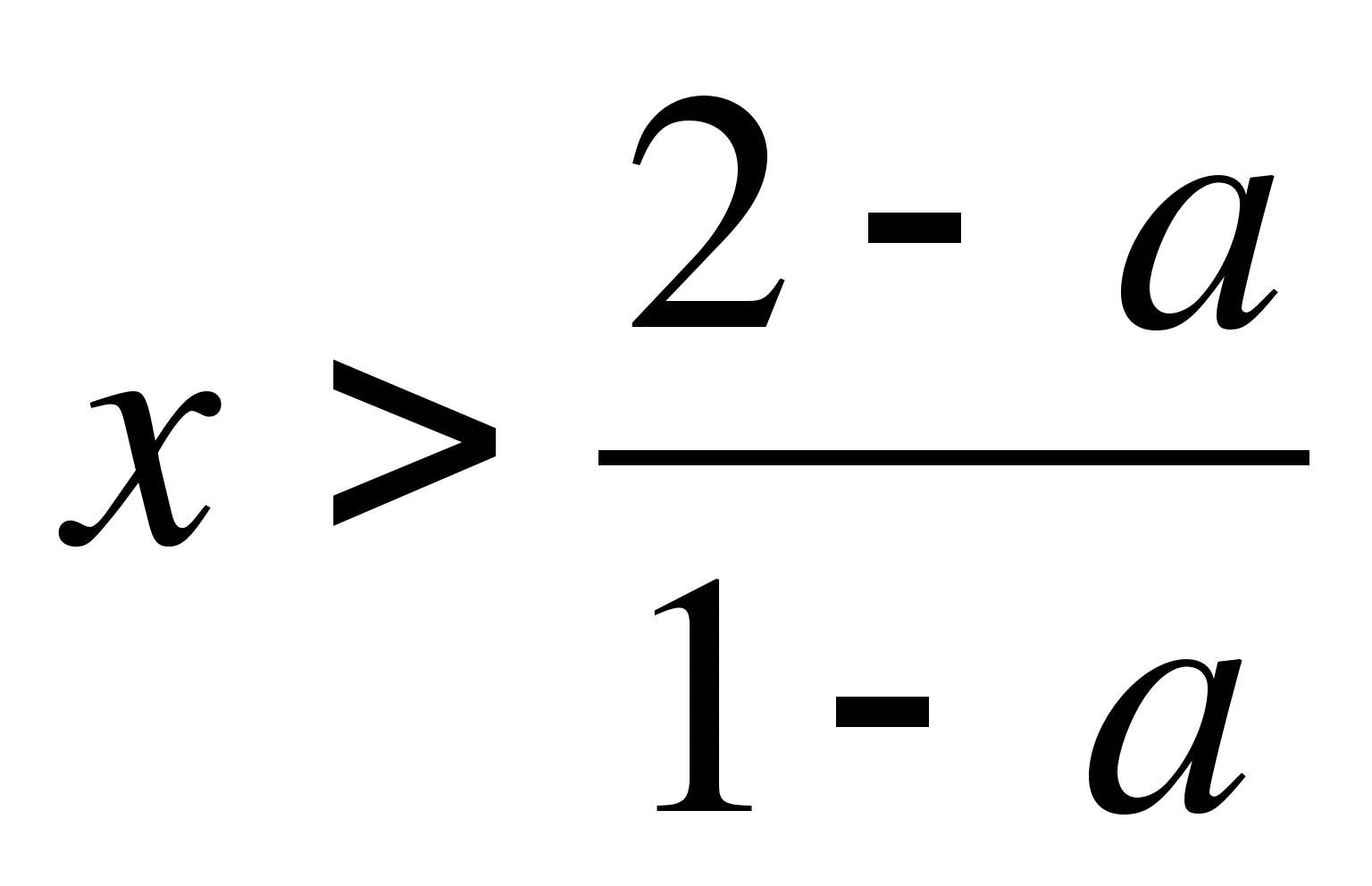 ;
если а=0, то решений нет.
;
если а=0, то решений нет.
Уровень В
а) ах>a
Ответ: 1) если а>0, то x>1;
2) если а<0, то x<1;
3) если a=0, то решений нет.
б) 2(x-a)<ax-4
Решение:
2х-2а
2x-ax<2a-4;
(2-a)x<2a-4
1) если 2-a>0, т.е. a<2, то
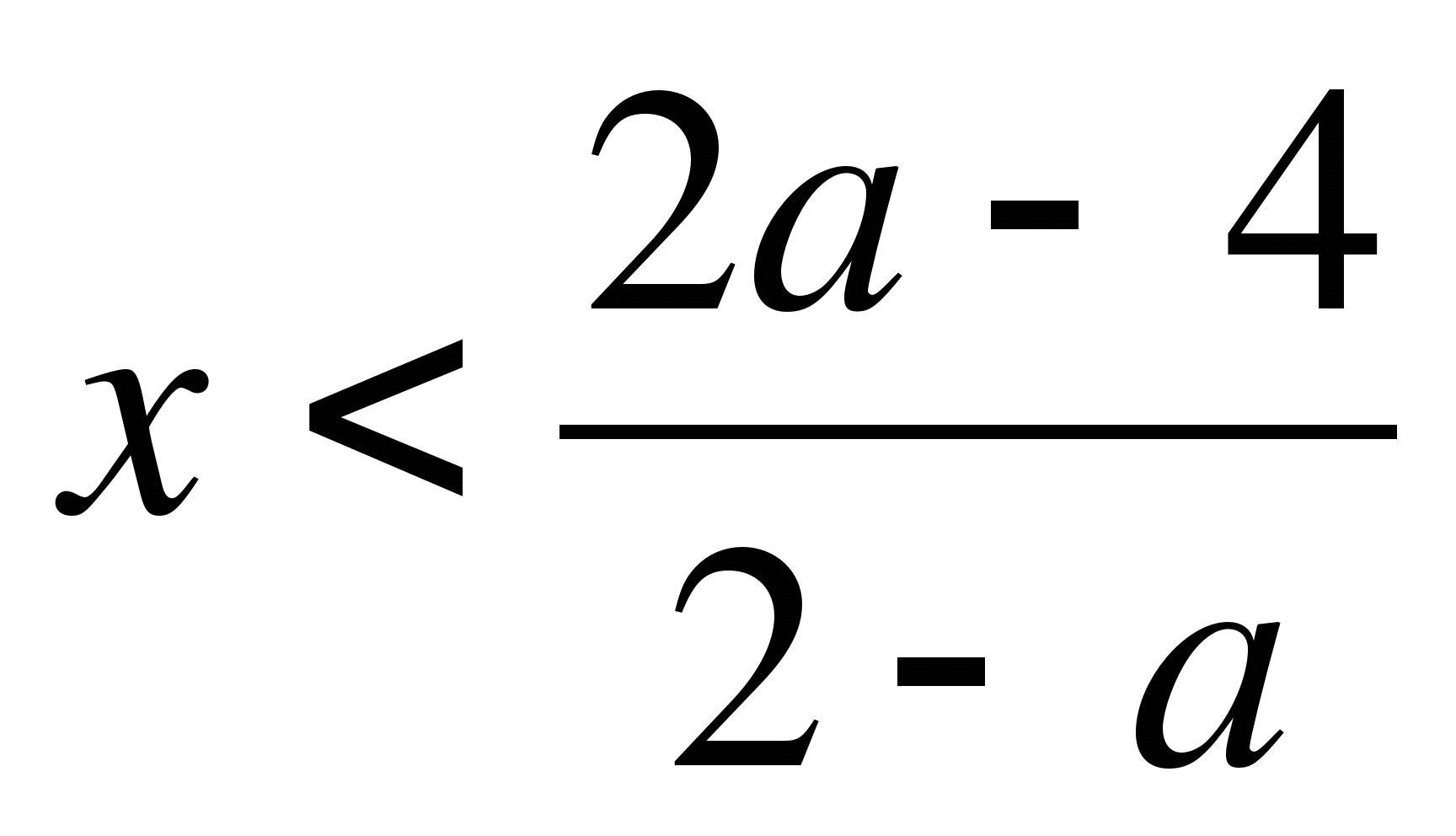 ;
;
2) если 2-a<0, т.е. a>2, то
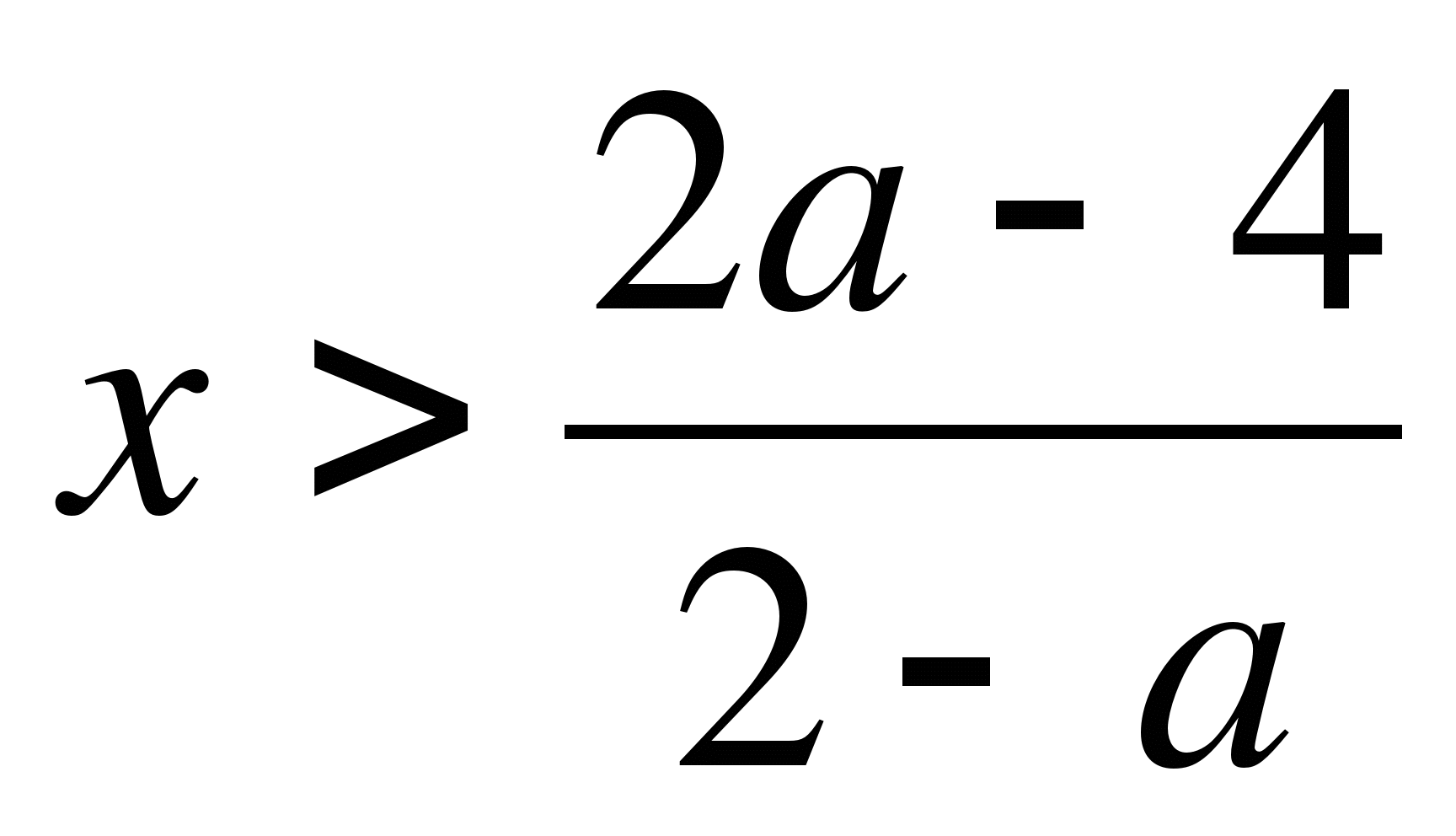 ;
;
3) если 2-a=0, т.е. a=2, то
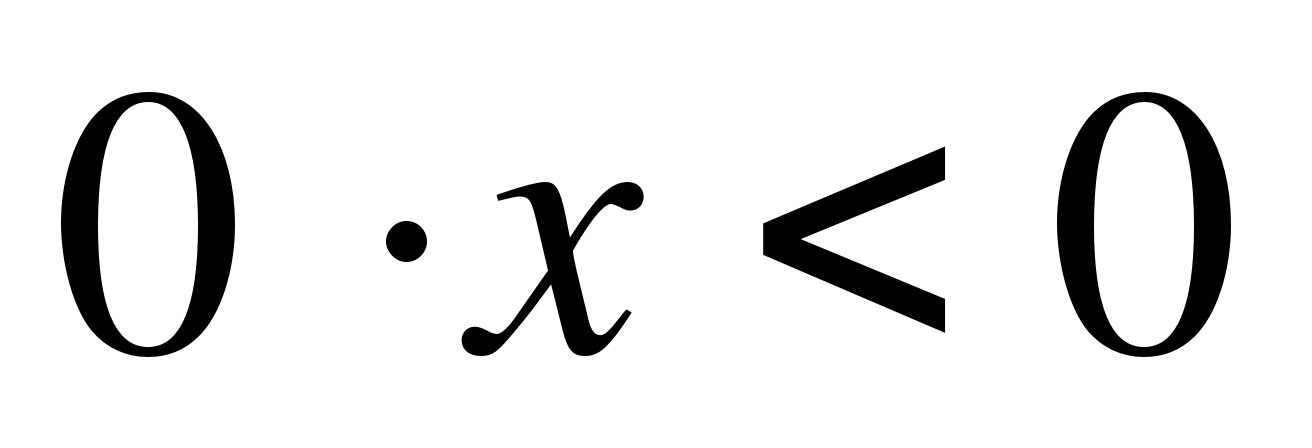 решений нет.
решений нет.
Ответ: если
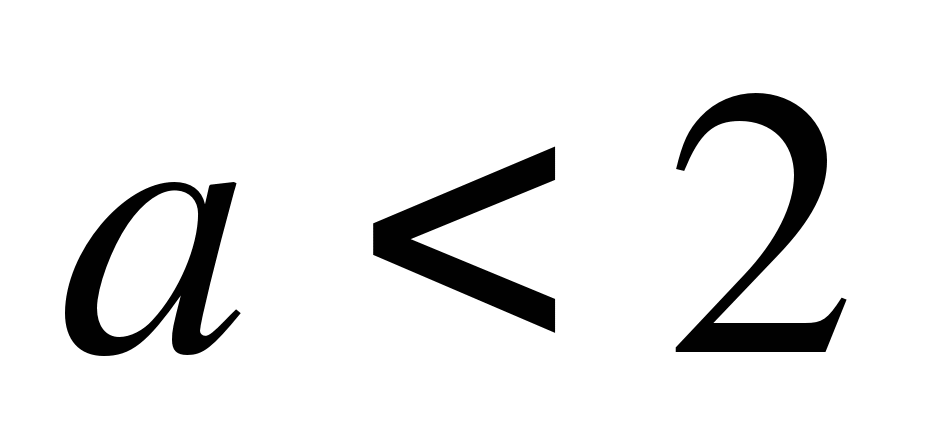 , то
, то
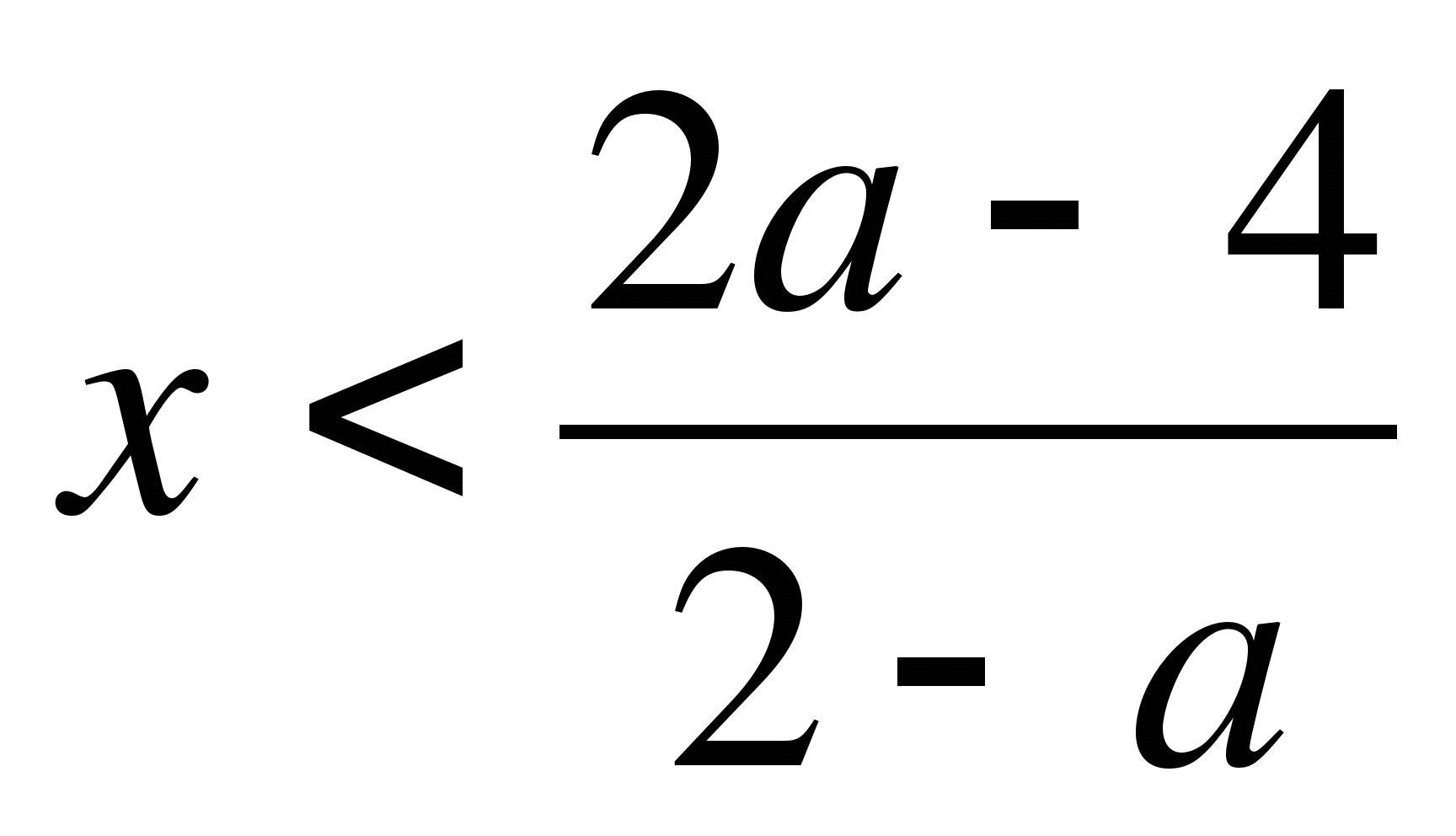 ;
если
;
если 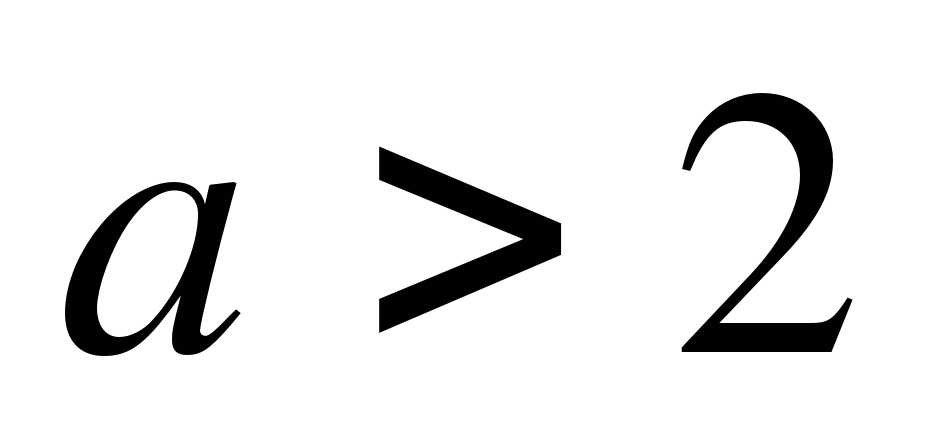 , то
, то
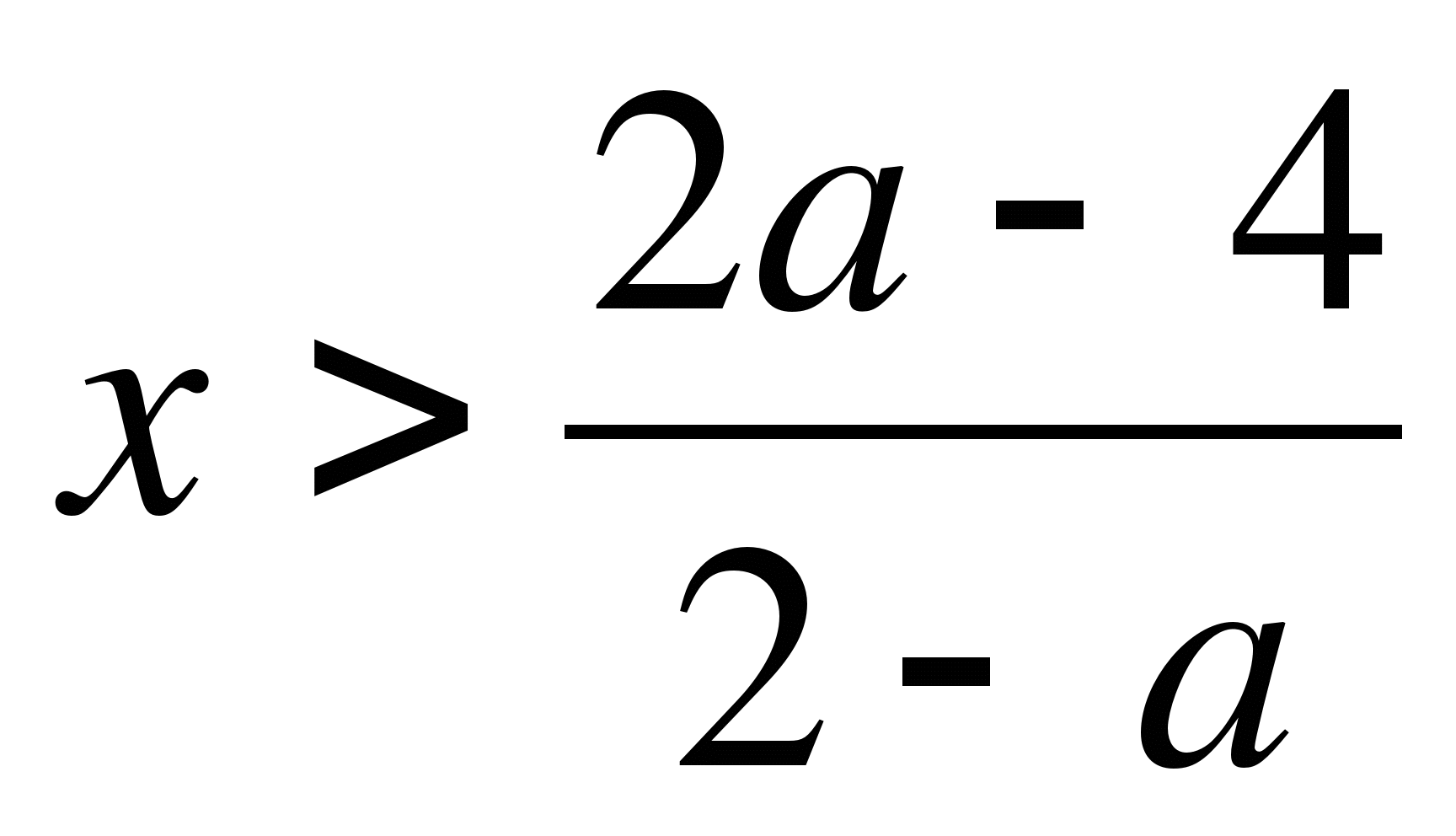 ;
если
;
если 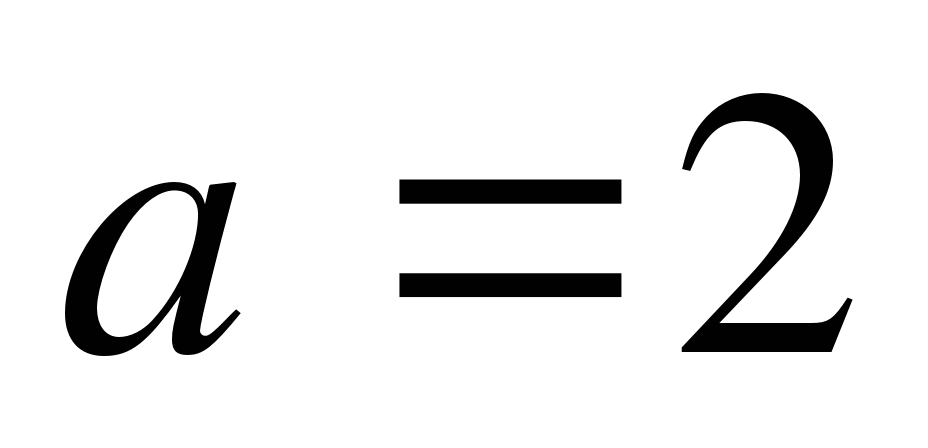 , то
решений нет.
, то
решений нет.
Уровень С
а) 3(а-х)<9-ax
Решение:
3a-3x<9-ax;
ax-3x<9-3a;
(a-3)x<9-3a.
1) если a-3>0, т.е. a>3, то
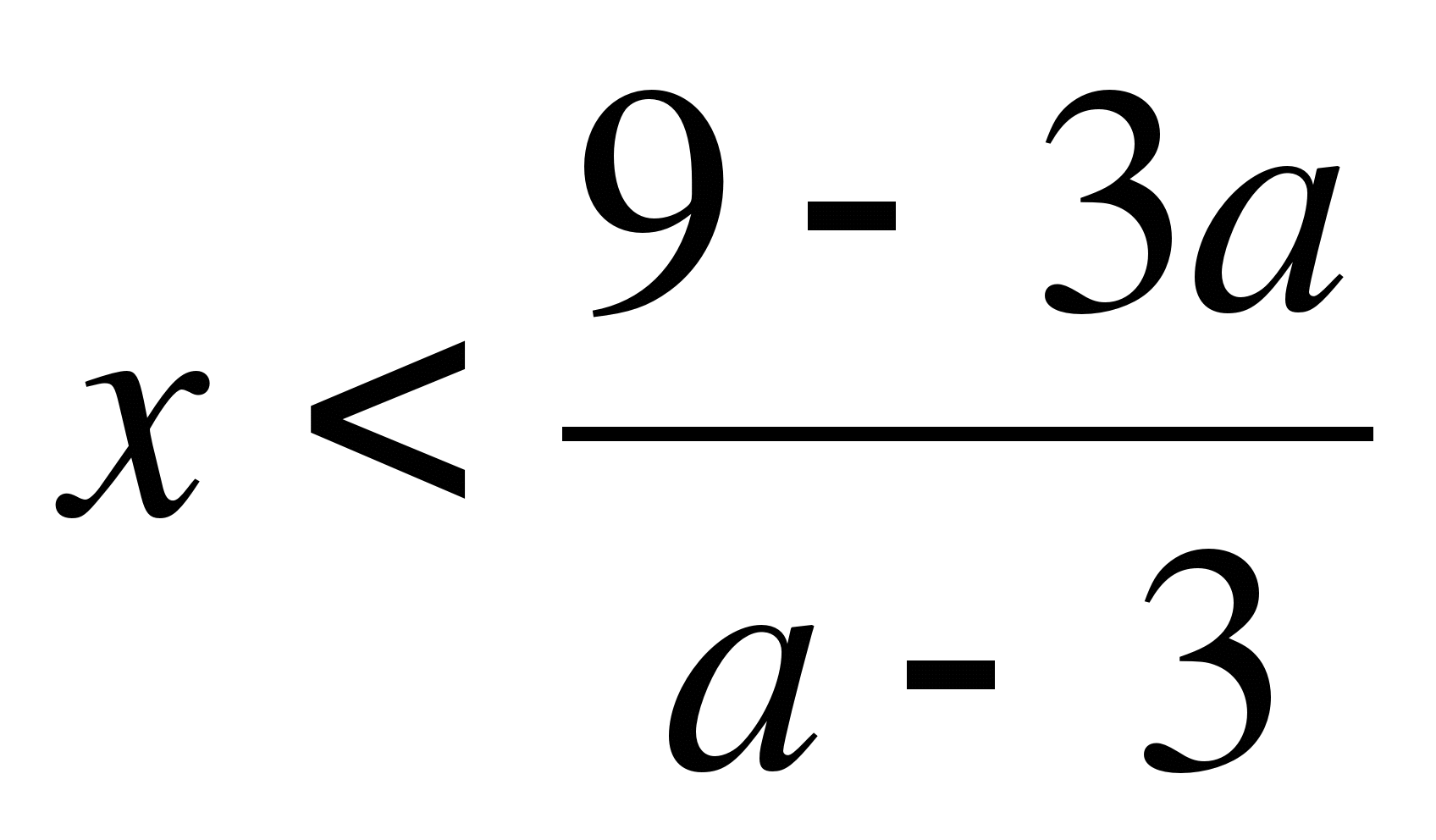 ;
;
2) если a-3<0, т.е. a<3, то
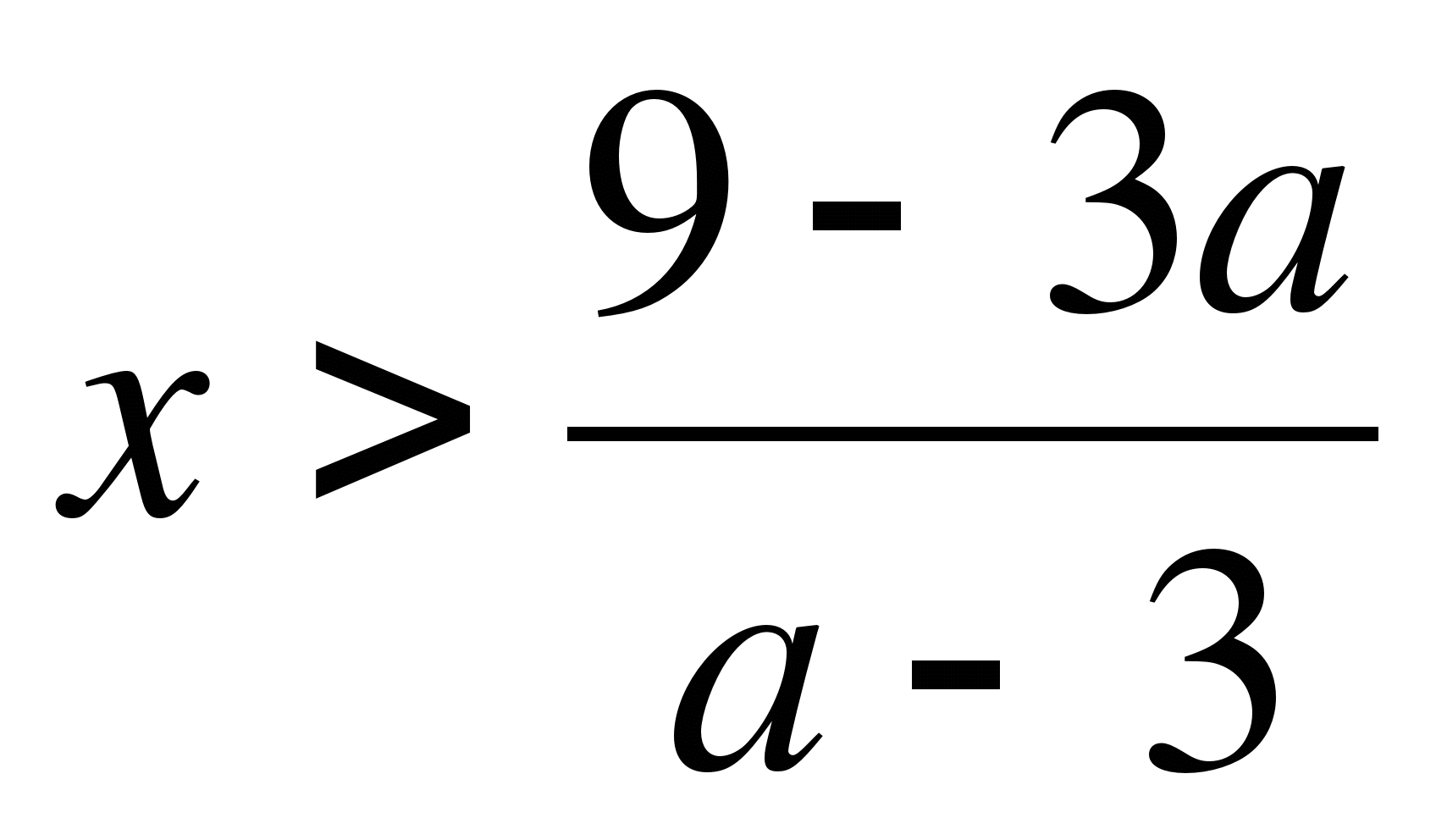 ;
;
3) если а=3, то
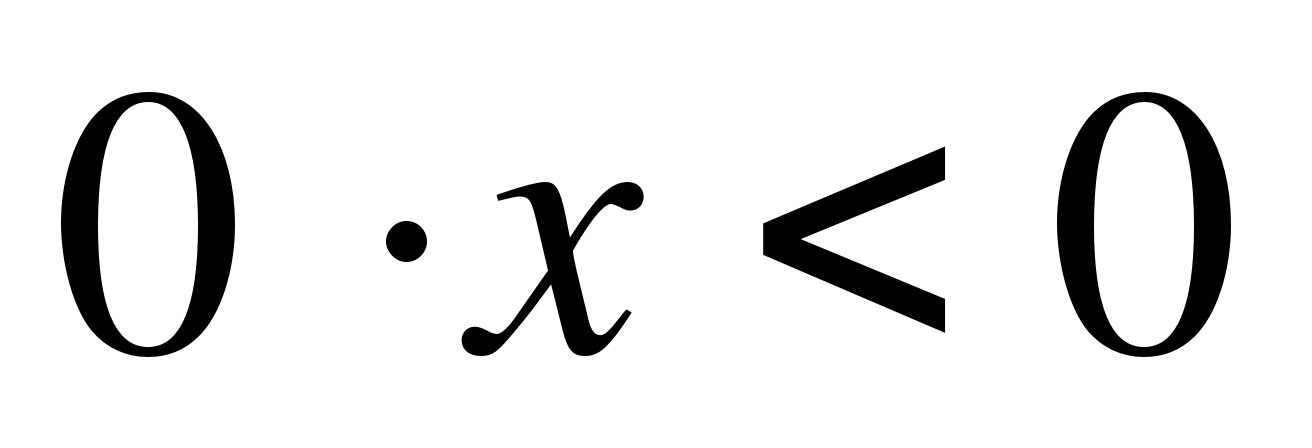 решений нет.
решений нет.
Ответ: если a>3 , то
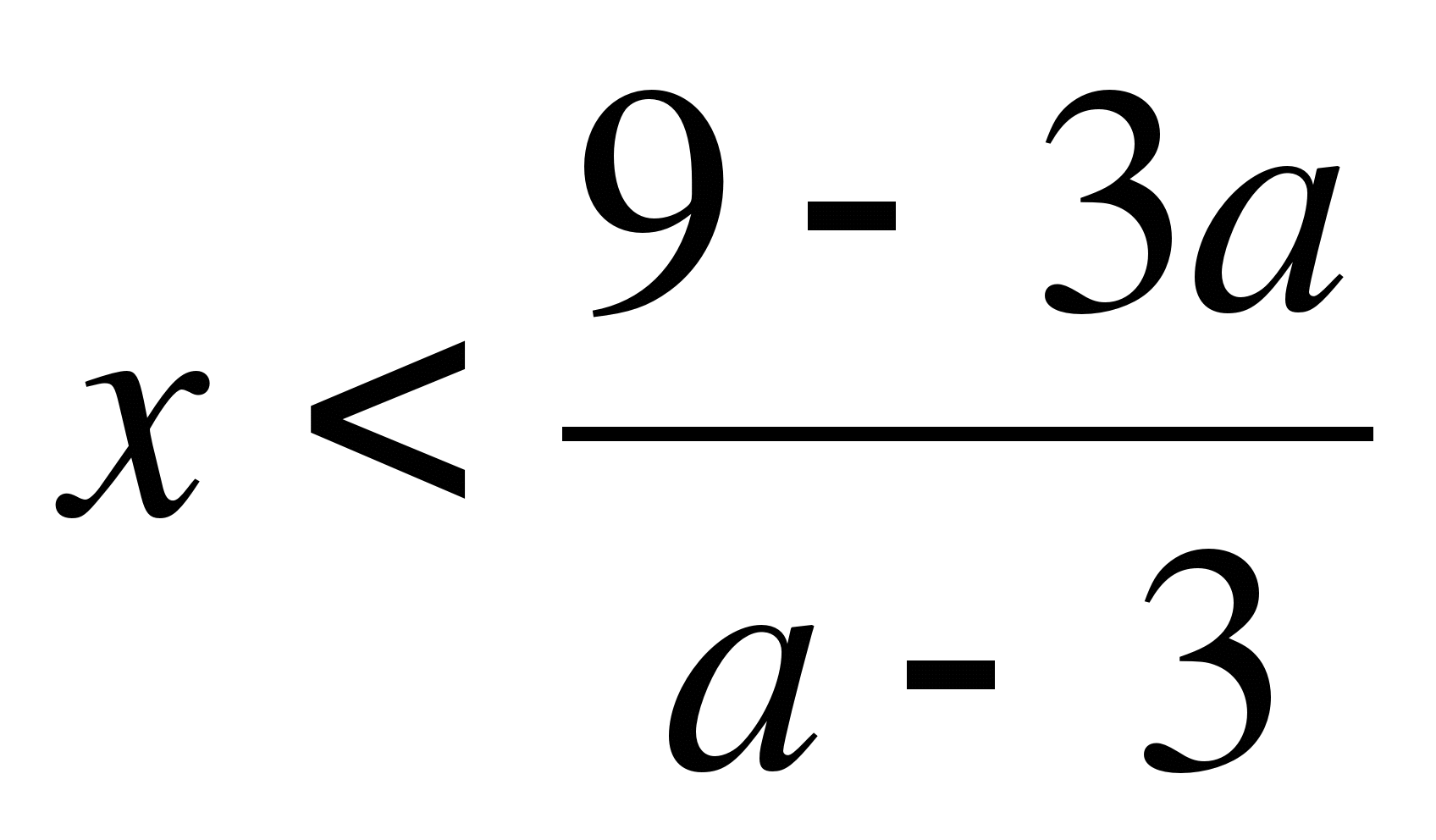 ;
если
;
если 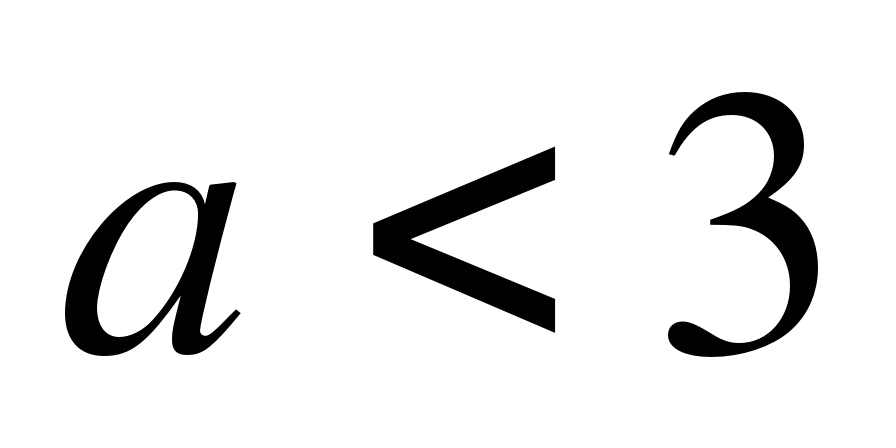 ,
то;
,
то; 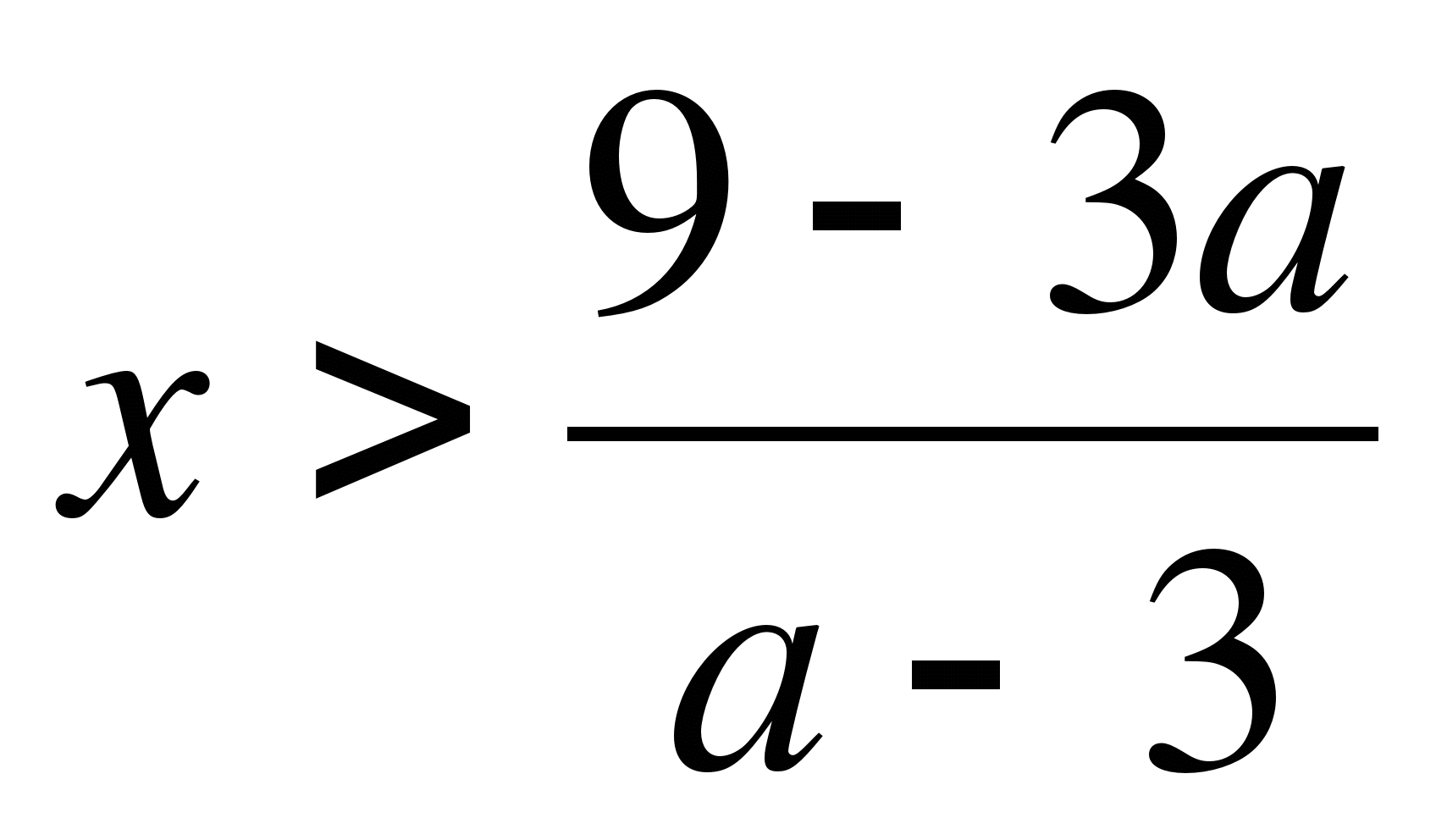 ;
если а=3, то решений нет.
;
если а=3, то решений нет.
б) (a-3)x>a2-9
Решение:
-
если a-3>0, т.е. a>3, то
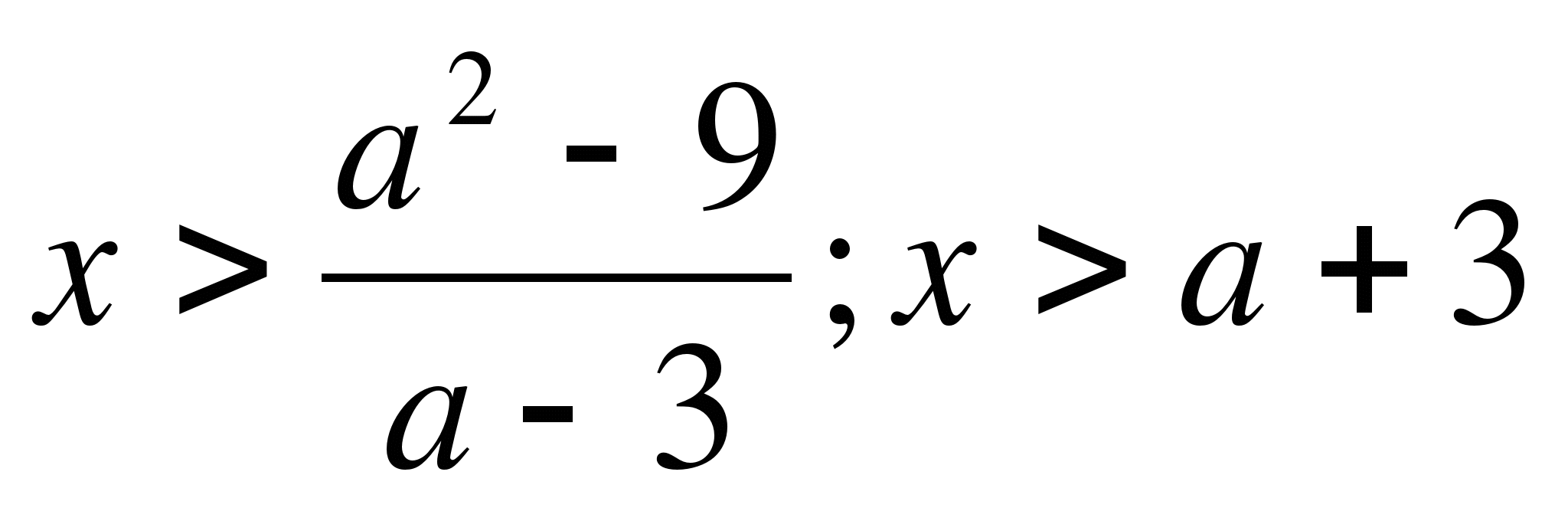 ;
;
-
если a-3<0, т.е. a<3, то
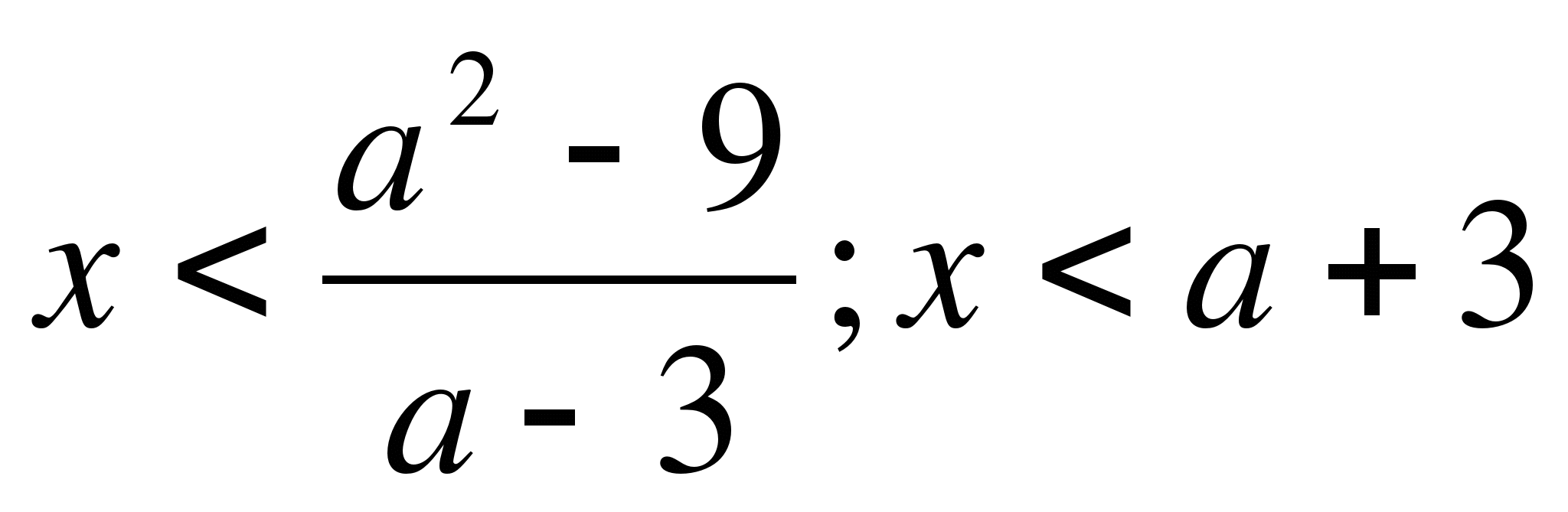 ;
;
-
если а=3, то
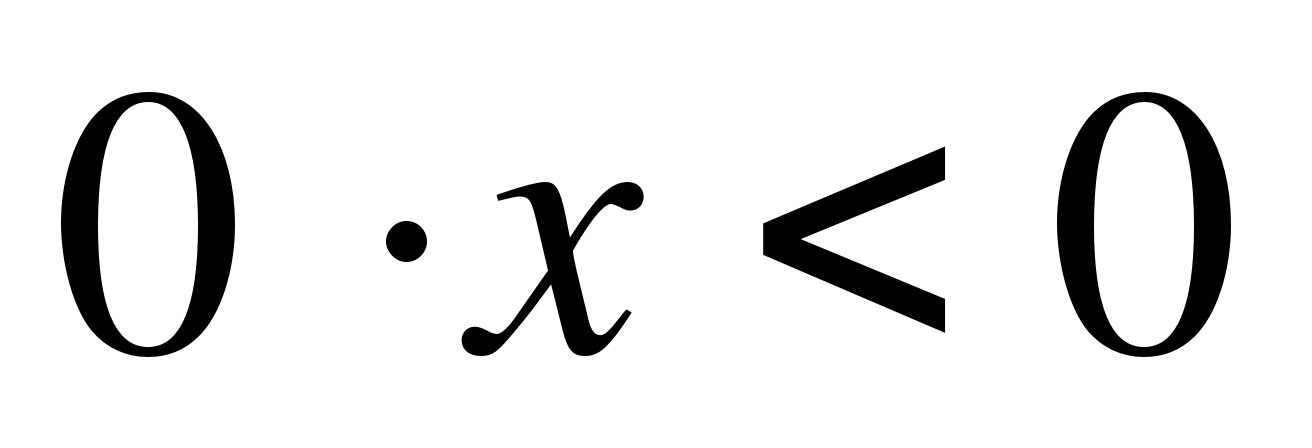 решений нет.
решений нет.
Ответ: если а>3, то
 ;
если а<3, то
;
если а<3, то 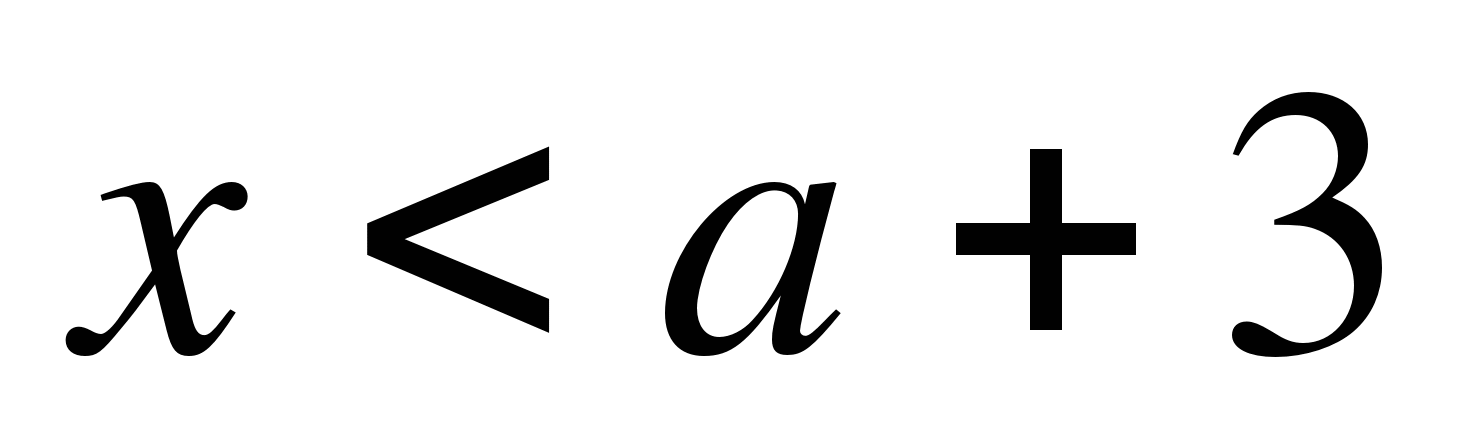 ;
если а=3, то решений нет.
;
если а=3, то решений нет.
V. Задания для домашней самостоятельной работы (по желанию).
а) (а+2)х>0
б) x(a+2)2
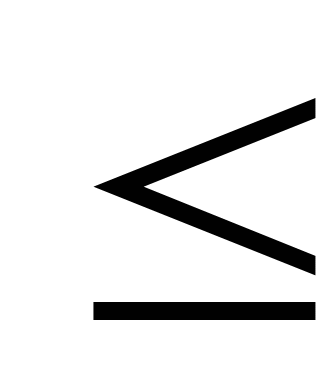 0
0
в) (a+2)x<a2-4
г) 2(a-2x)<8-ax
д) a-2x<1+ax
Ответы.
а) (а+2)х>0,
если а<-2, то х<0; если а>-2, то х>0; если а=-2, то решений нет.
б) x(a+2)2
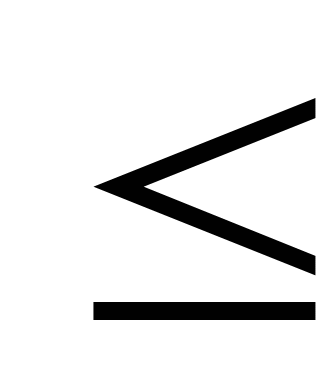 0,
0,
если a<-2 и a>-2, то х≤0; если a=-2, то

в) (a+2)x<a2-4,
если а<-2, то х>a+2; если а>-2, то х<a+2; если а=-2, то решений нет.
г) 2(a-2x)<8-ax,
если а<4, то х>-2, если а>4, то х<-2; если а=4, то решений нет.
д) a-2x<1+ax,
если а<-2, то
 ;
если а>-2, то
;
если а>-2, то 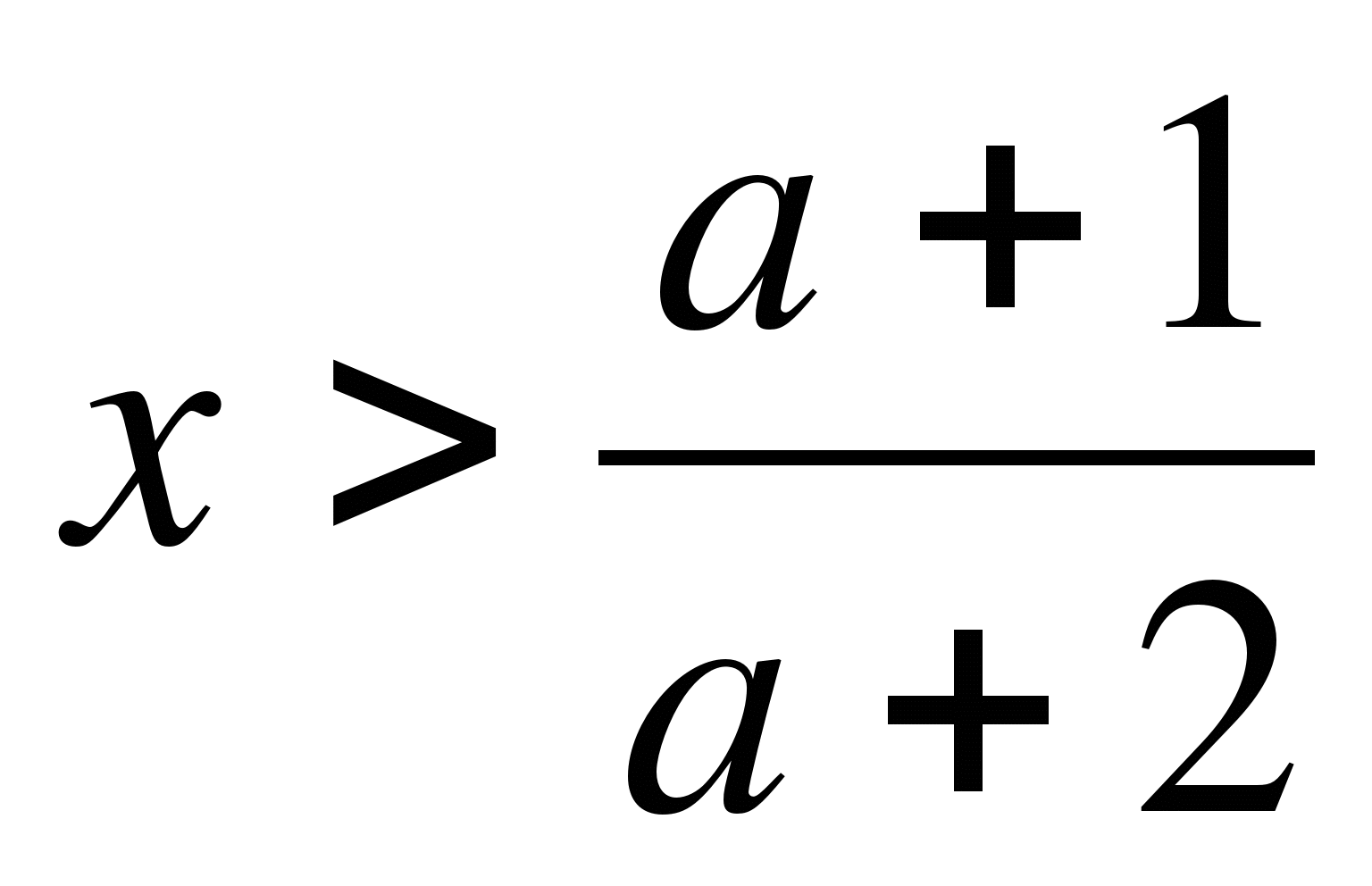 ;
если а=-2, то решений нет.
;
если а=-2, то решений нет.
Блок III. Квадратные уравнения
Цели занятий:
- способствовать формированию умений применять приемы сравнения, обобщения, выделения главного, переноса знаний в новой ситуации; развитию творческих способностей учеников путем решения заданий, содержащих параметр;
- обобщить, углубить знания школьников по изучаемой теме, установить связь между коэффициентами квадратного уравнения, его корнями через графическую интерпретацию.
Занятие 1.
Ход занятия.
I . Теоретический материал.
Учитель предлагает двум учащимся собрать на доске из заранее подготовленных карточек схему, которая отражает связь числа корней квадратного уравнения
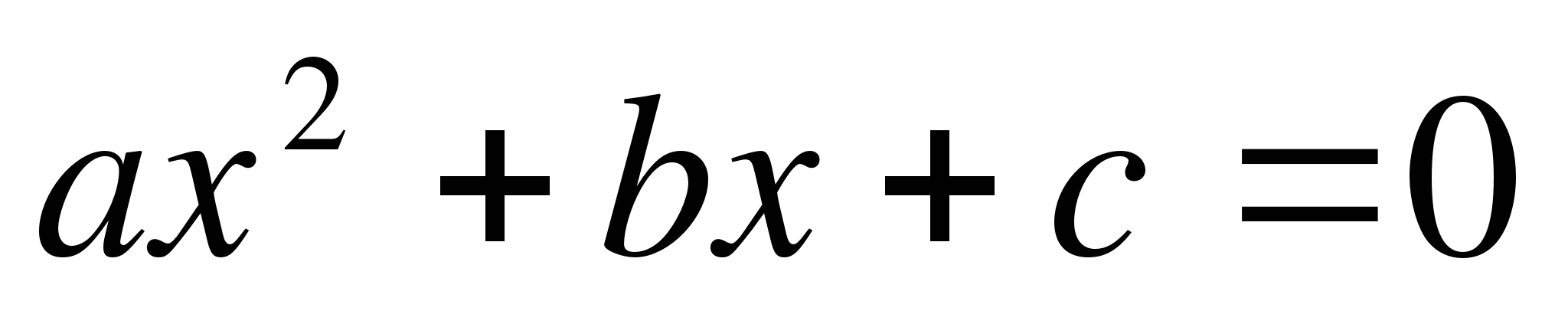 (a≠0)
с его дискриминантом, и для каждого случая аналитического
решения указать геометрическую модель.
(a≠0)
с его дискриминантом, и для каждого случая аналитического
решения указать геометрическую модель.
Остальным учащимся демонстрируется плакат (см. приложение 1 и приложение 2).
Вопрос: Что бы означало?
Ответ: (1),(3)-квадратные уравнения. В этих уравнениях параметр входит в состав коэффициента и свободного члена; (2)- это так же уравнение с параметром, но параметр а входит в состав коэффициента при x2 многочлена второй степени. Это уравнение нельзя сразу решить по формулам для отыскания корней квадратного уравнения, т. к. о заданном уравнении мы не можем сказать, квадратное оно или линейное.
Вывод: Если коэффициент при x2 многочлена второй степени содержит параметр, необходимо разбирать случай, когда он обращается в нуль.
Решим уравнение (2) ax
 -
2x + 4 = 0
-
2x + 4 = 0 .
.
Решение. Рассмотрим два случая, когда a = 0 и когда, a ≠ 0.
1. При a = 0, уравнение линейное -2х + 4 = 0. Откуда x = 2.
2. При a ≠ 0, уравнение квадратное. Его дискриминант равен D = 4 - 16a.
Если D < 0, т.е. a > 1/4, то уравнение решений не имеет.
Если D = 0, т. е. a = 1/4, то уравнение имеет единственный корень х = 4.
Если D > 0, т. е. то уравнение имеет два корня
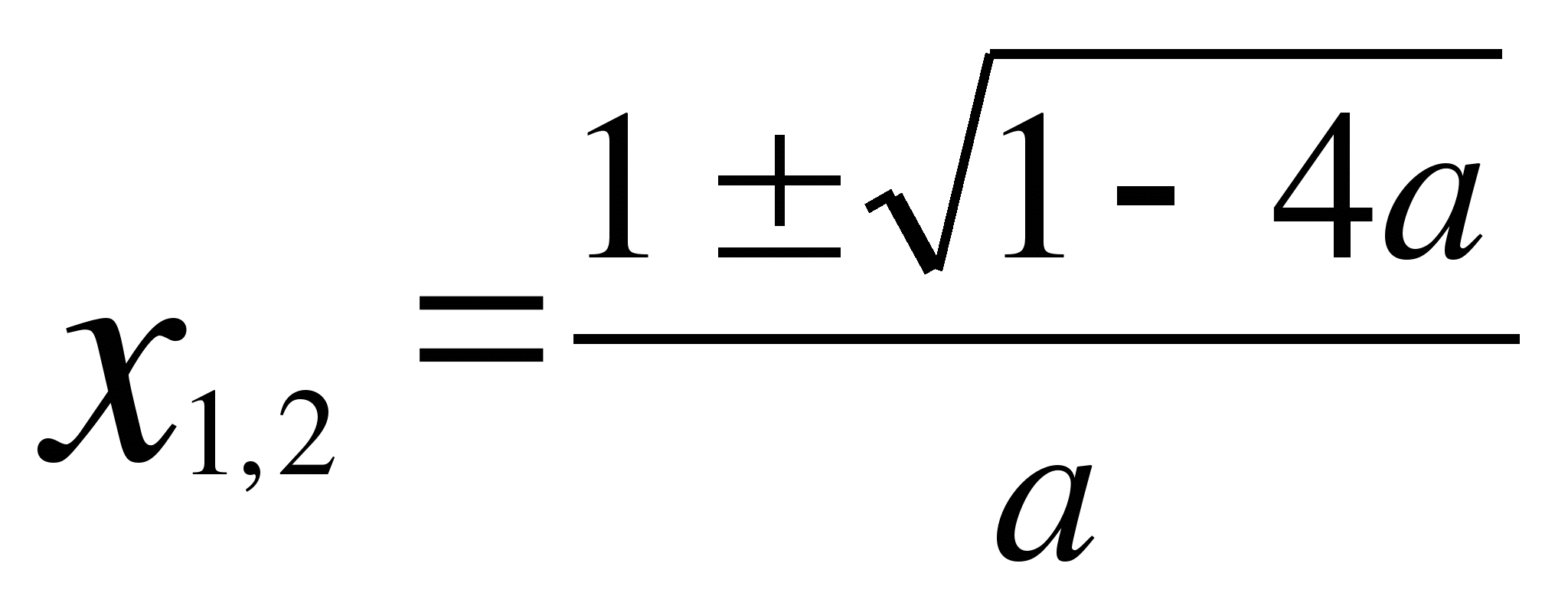
Ответ: при а > 1/4, решений нет; при а = 1/4, уравнение имеет единственное решение x = 4; при а < 1/4, а ≠ 0 , то уравнение имеет два корня
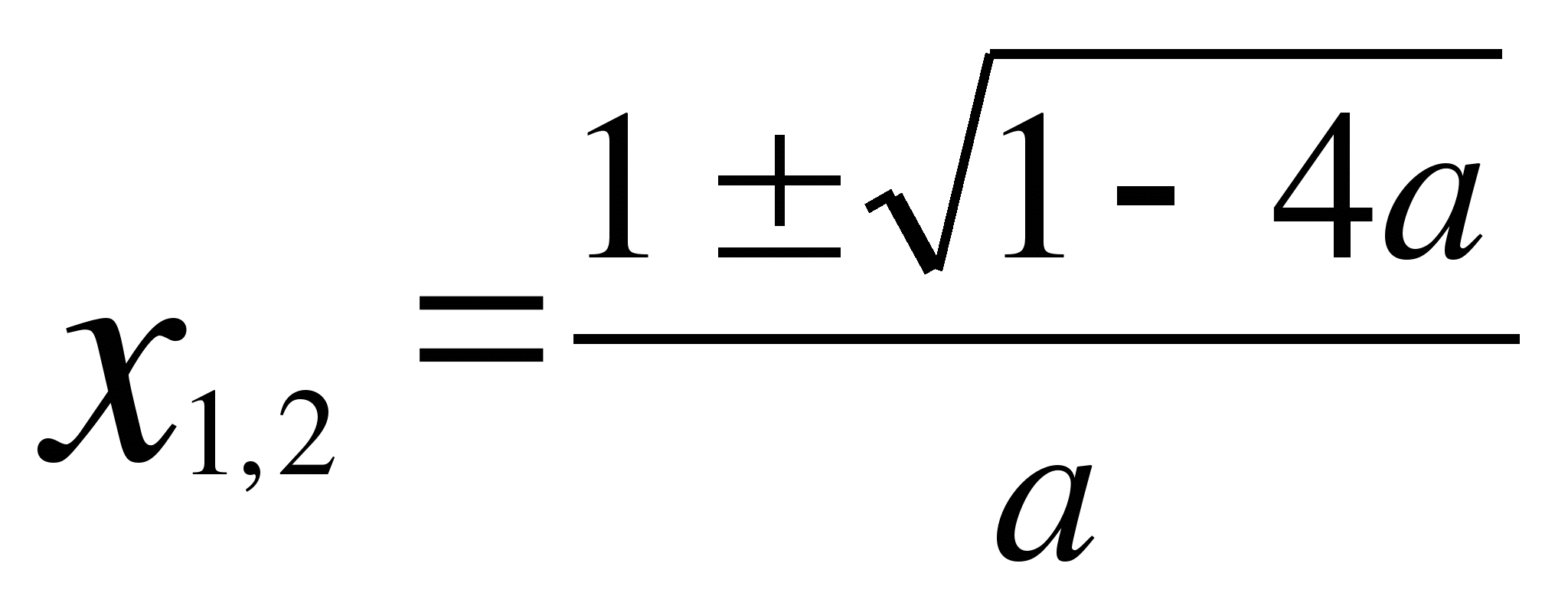 ;
при а = 0, то x = 2.
;
при а = 0, то x = 2.
II. Этап самоконтроля знаний.
Самоконтроль знаний производится при выполнении теста (два варианта). По окончанию выполнения теста открываются правильные ответы. Учащиеся меняются
схемами, проверяют, исправляют ошибки, оценивают работу по следующим критериям: оценка «5»- нет ошибок; «4»- одна ошибка; «3»- две - три ошибки, «2» - более трех ошибок.
1 вариант.
Задание. Покажите с помощью стрелок связь между коэффициентами неполного квадратного уравнения и его корнями.
Покажите с помощью стрелок связь между коэффициентами полного квадратного уравнения
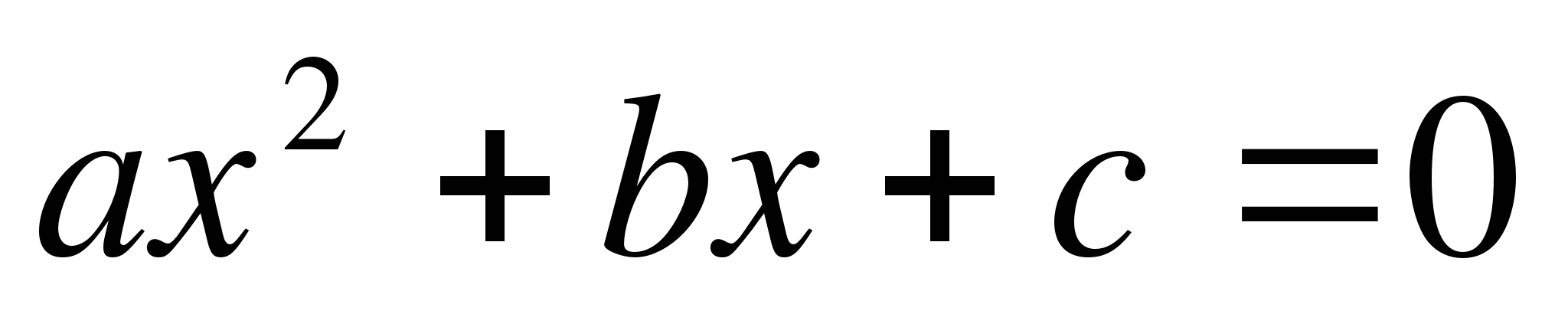 (a ≠ 0) и его корнями.
(a ≠ 0) и его корнями.
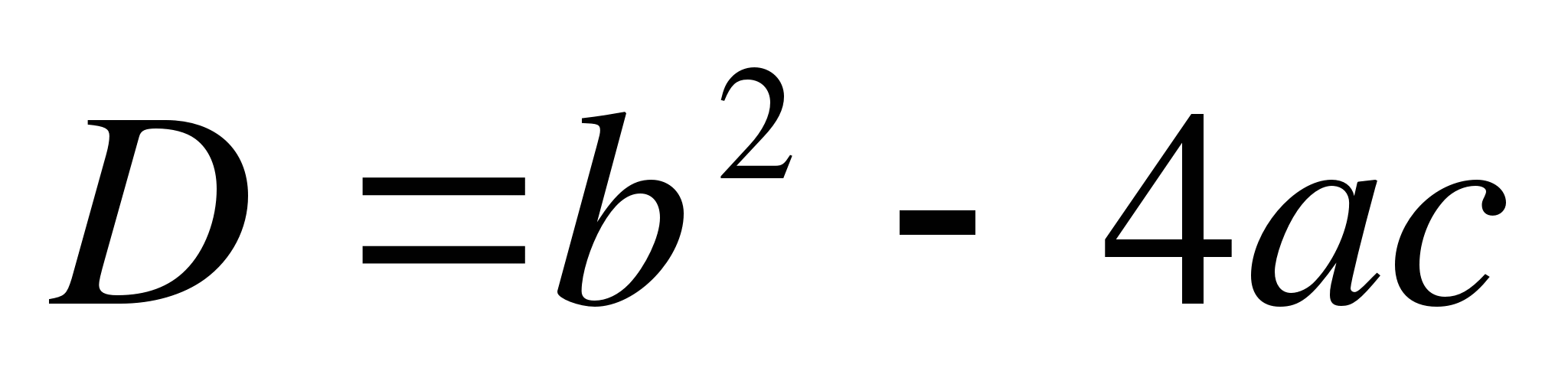
разных знаков, если
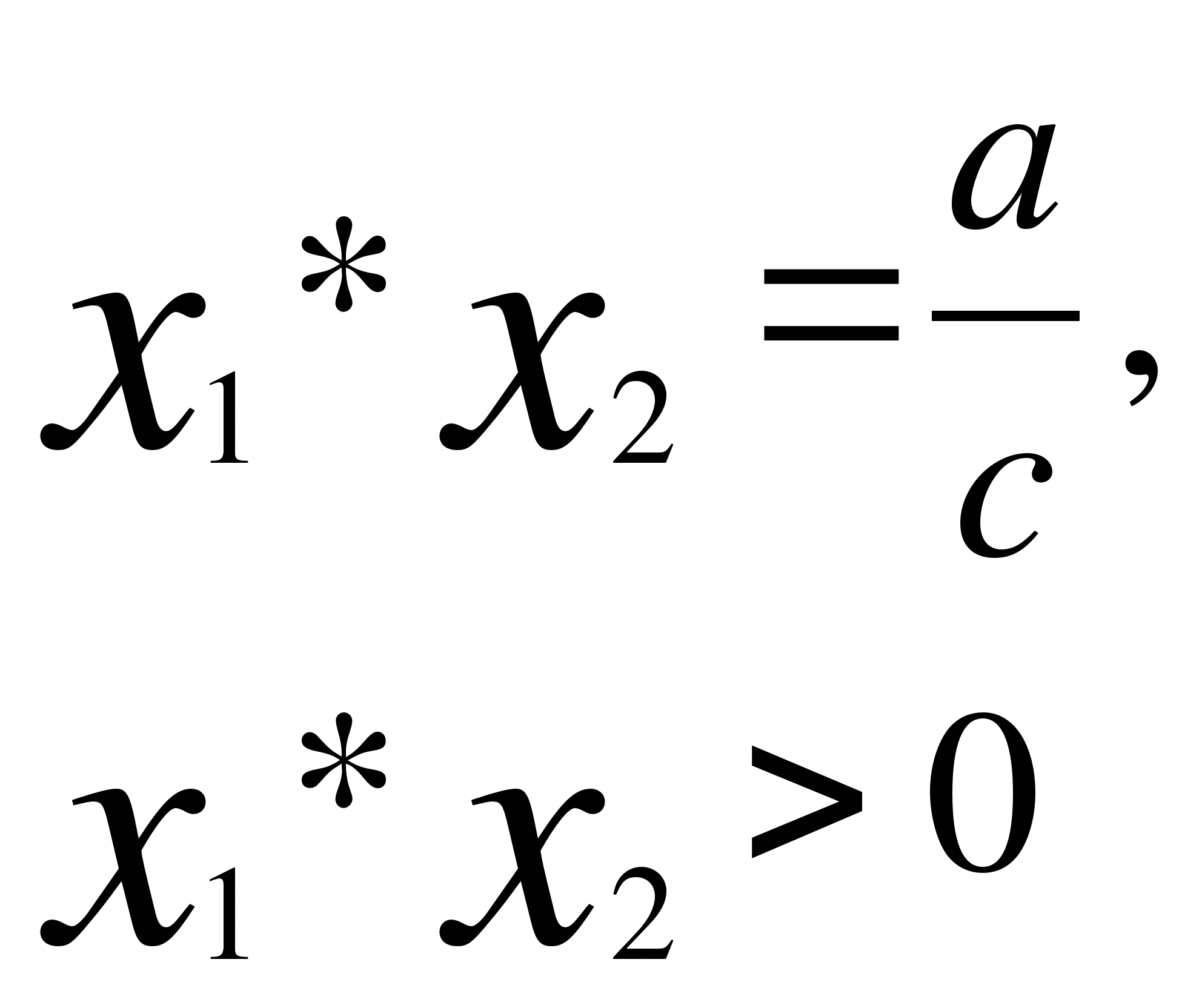
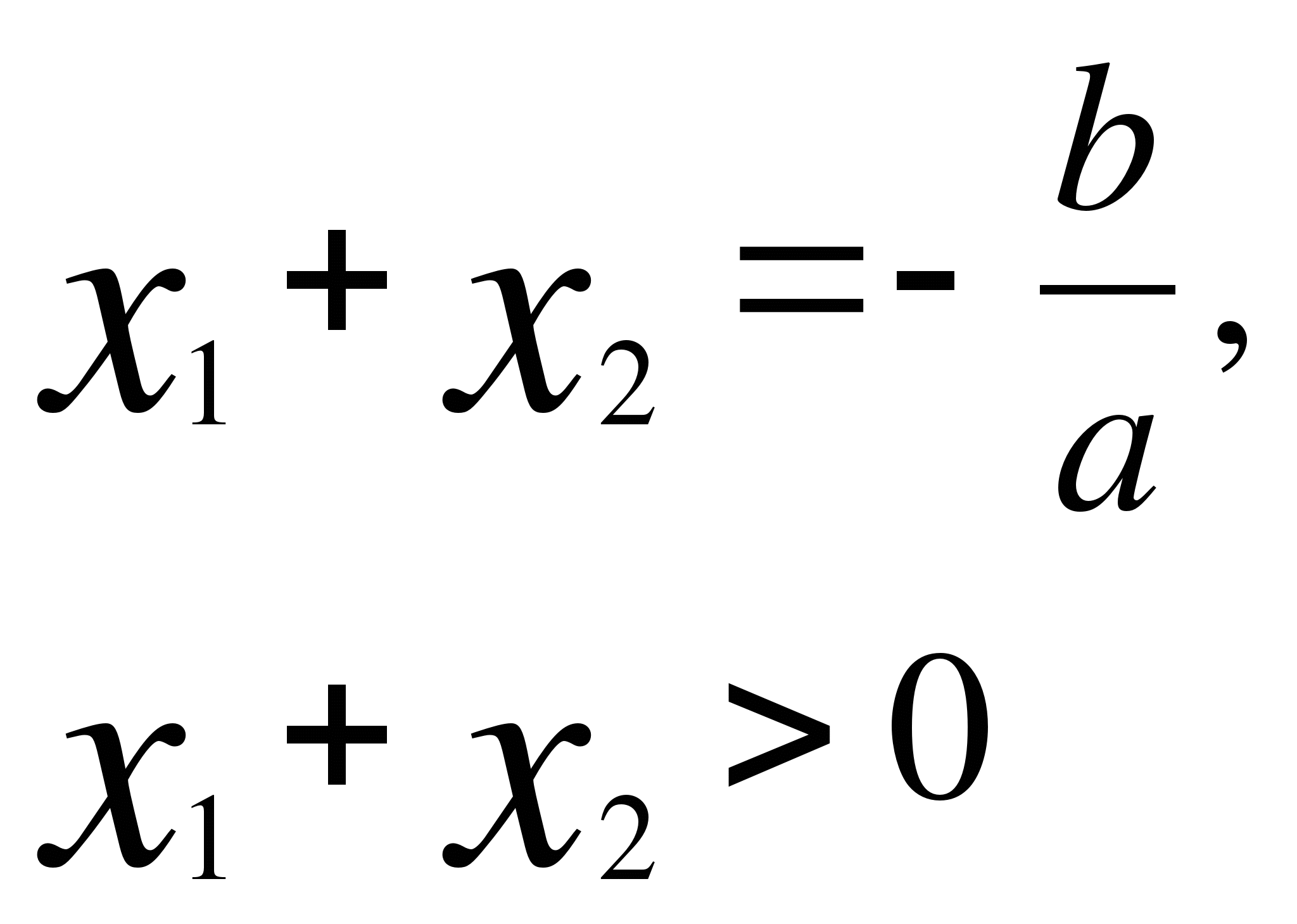
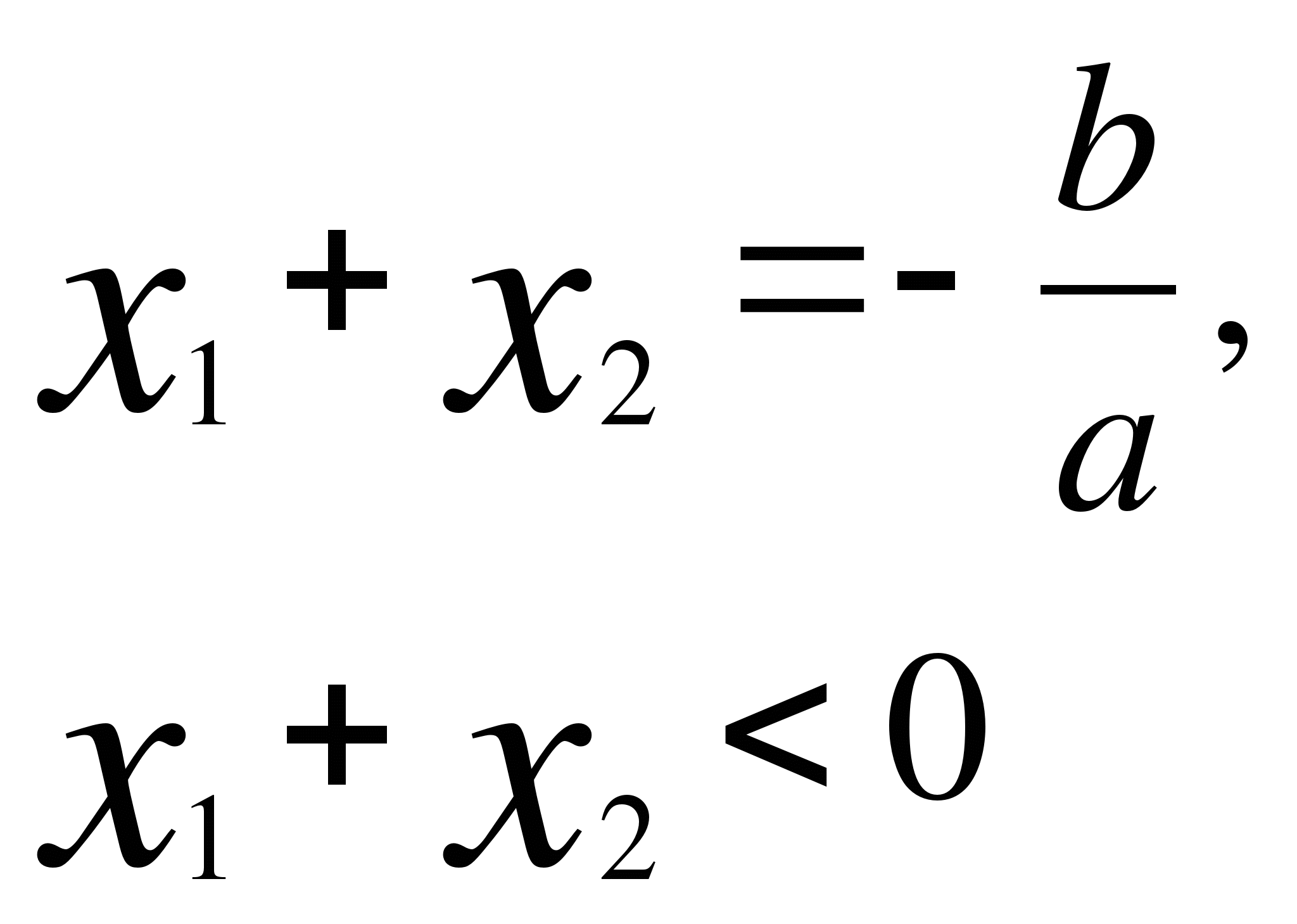
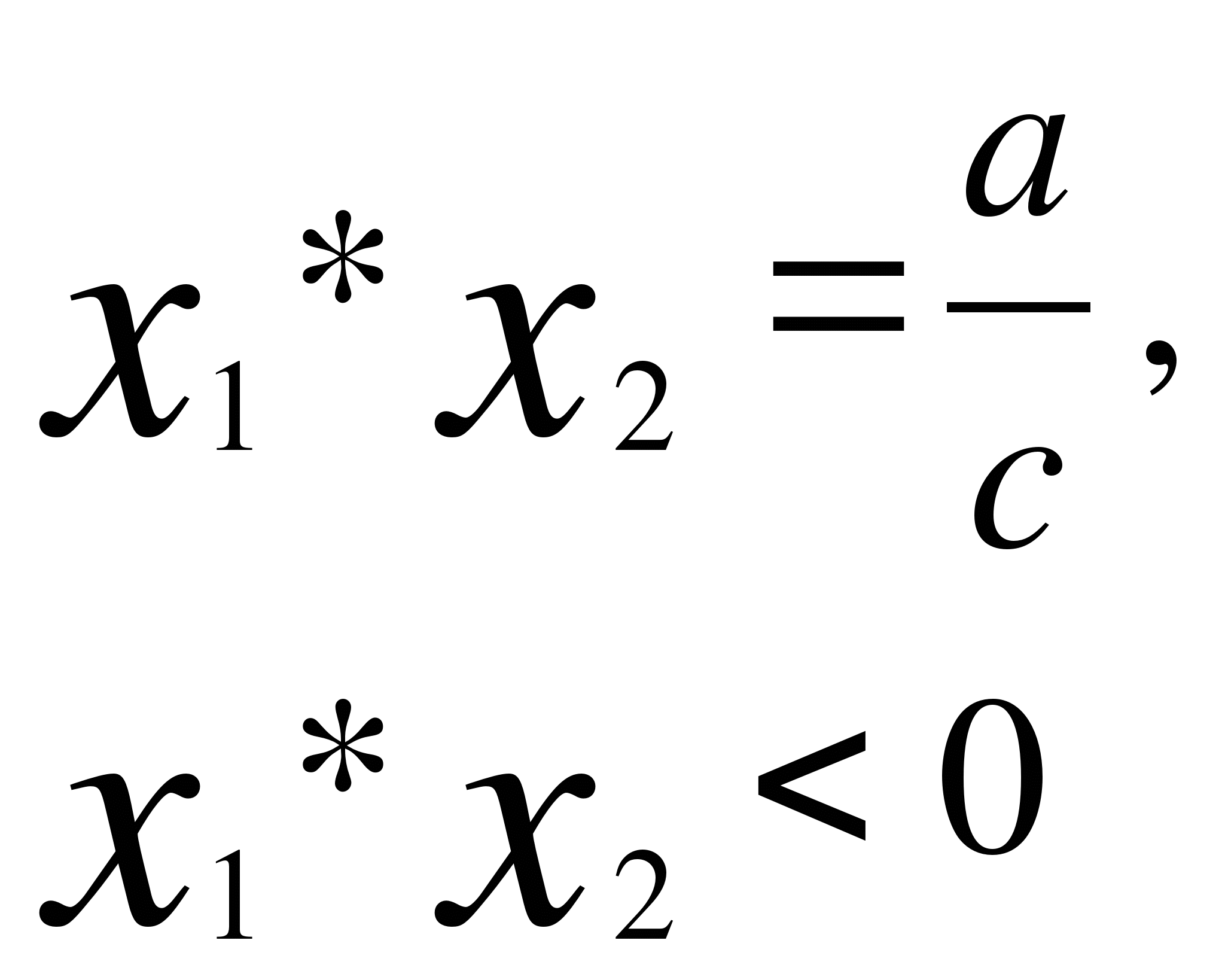
Занятие 2. Решение основных типов уравнений с параметрами.
I этап. Рассмотрение решение параметрических квадратных уравнений, с их геометрической иллюстрацией.
Задание. Найти все значения параметра p, при которых уравнение
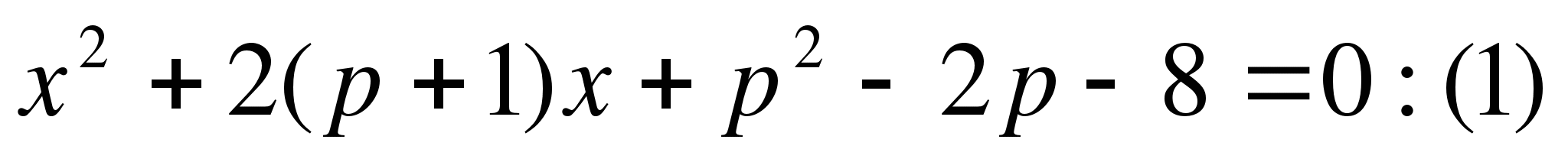 а)
имеет одно решение; б) имеет два решения; в) имеет решение; г)
не имеет решение. Проанализировать знаки корней уравнения.
а)
имеет одно решение; б) имеет два решения; в) имеет решение; г)
не имеет решение. Проанализировать знаки корней уравнения.
Решение: Для нахождения корней уравнения проанализируем возможные случаи, в зависимости от параметра p.
Найдем
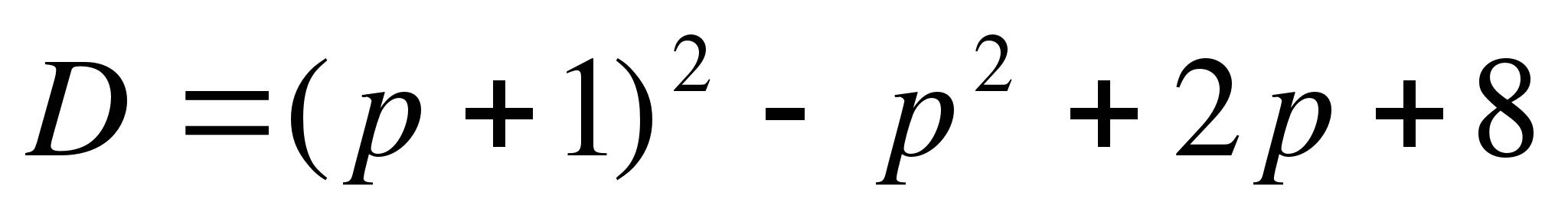 ;
D=
;
D=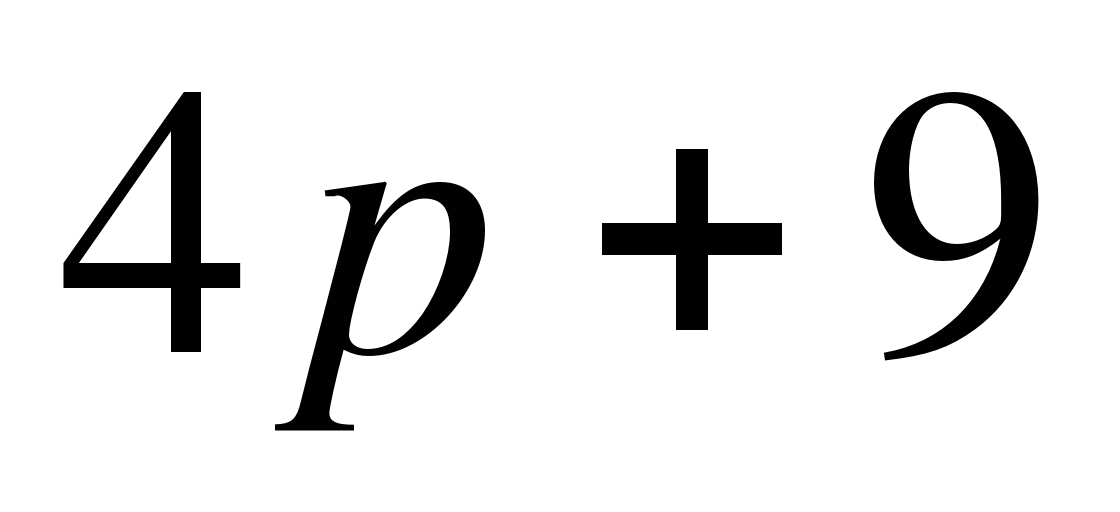 .
.
1






 .
Уравнение имеет два совпадающих корня, т. е. одно решение. Это
возможно, если D = 0,
.
Уравнение имеет два совпадающих корня, т. е. одно решение. Это
возможно, если D = 0, 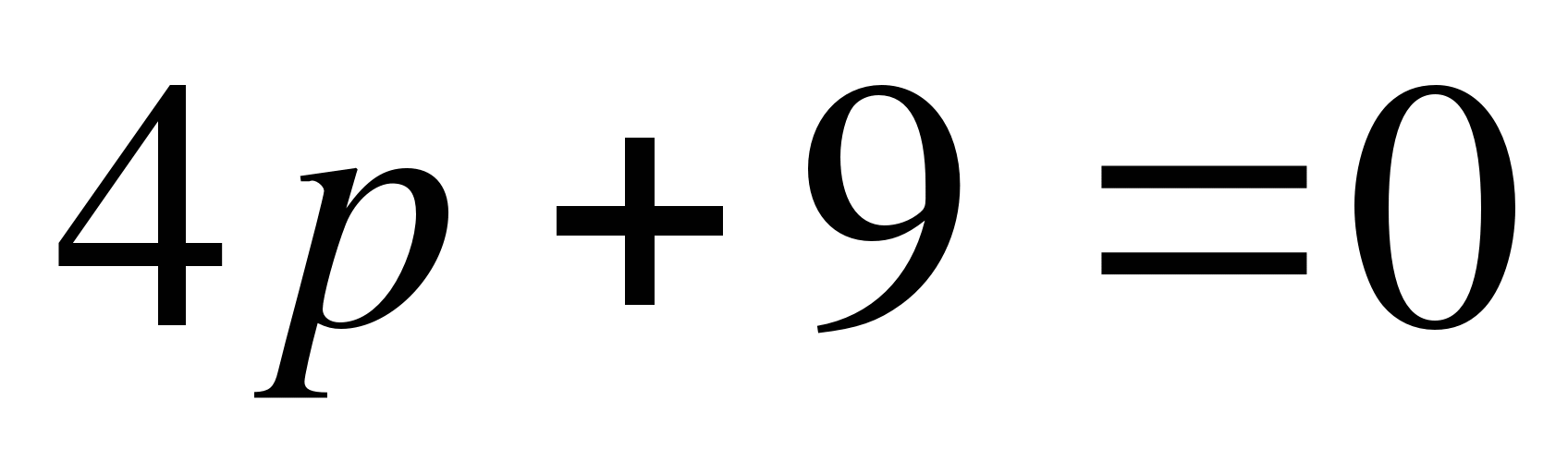 ;
;
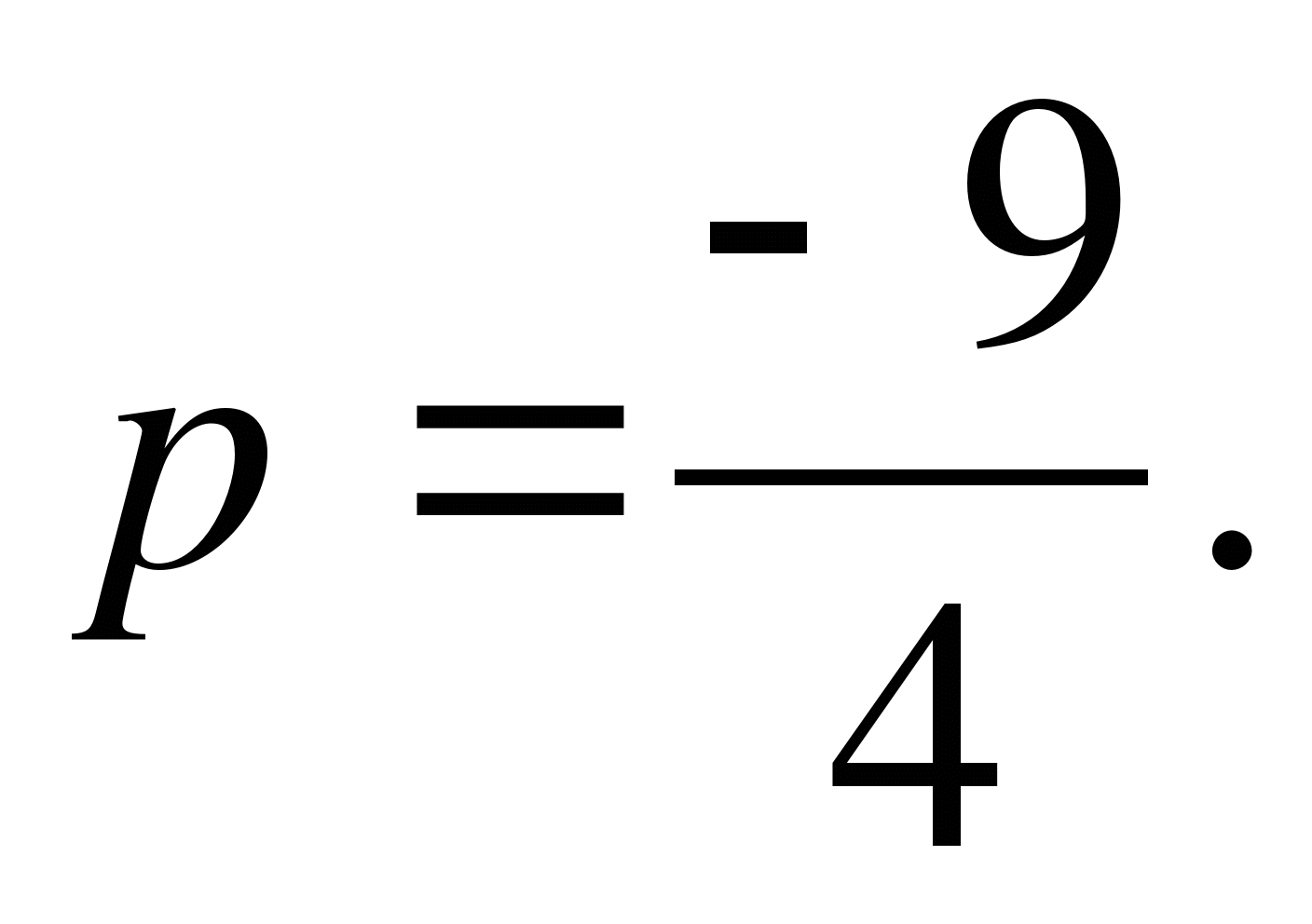 Проверим знаки корней:
Проверим знаки корней: 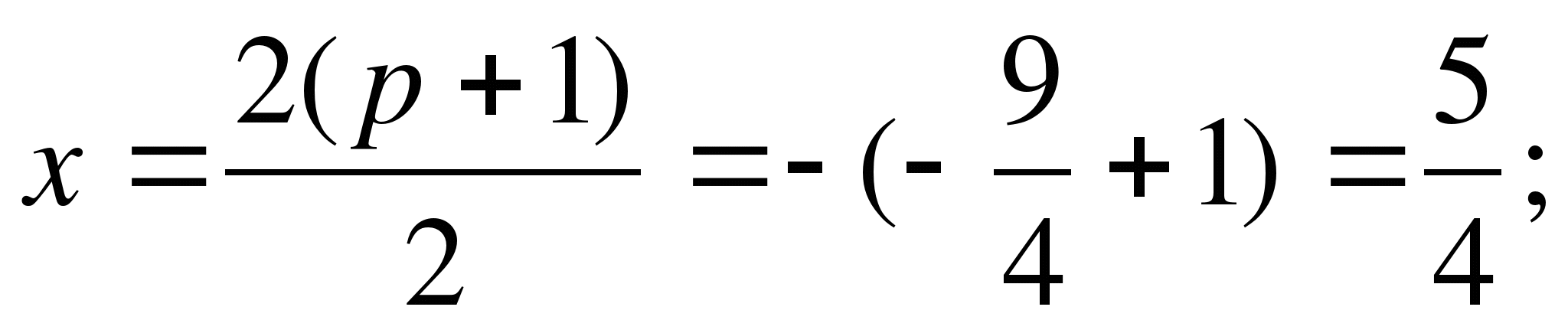
y y
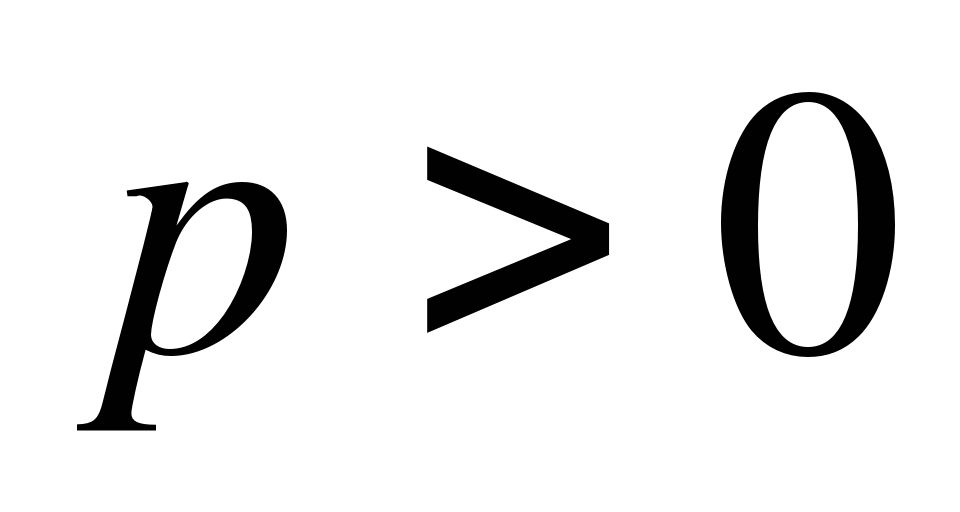 ;
;
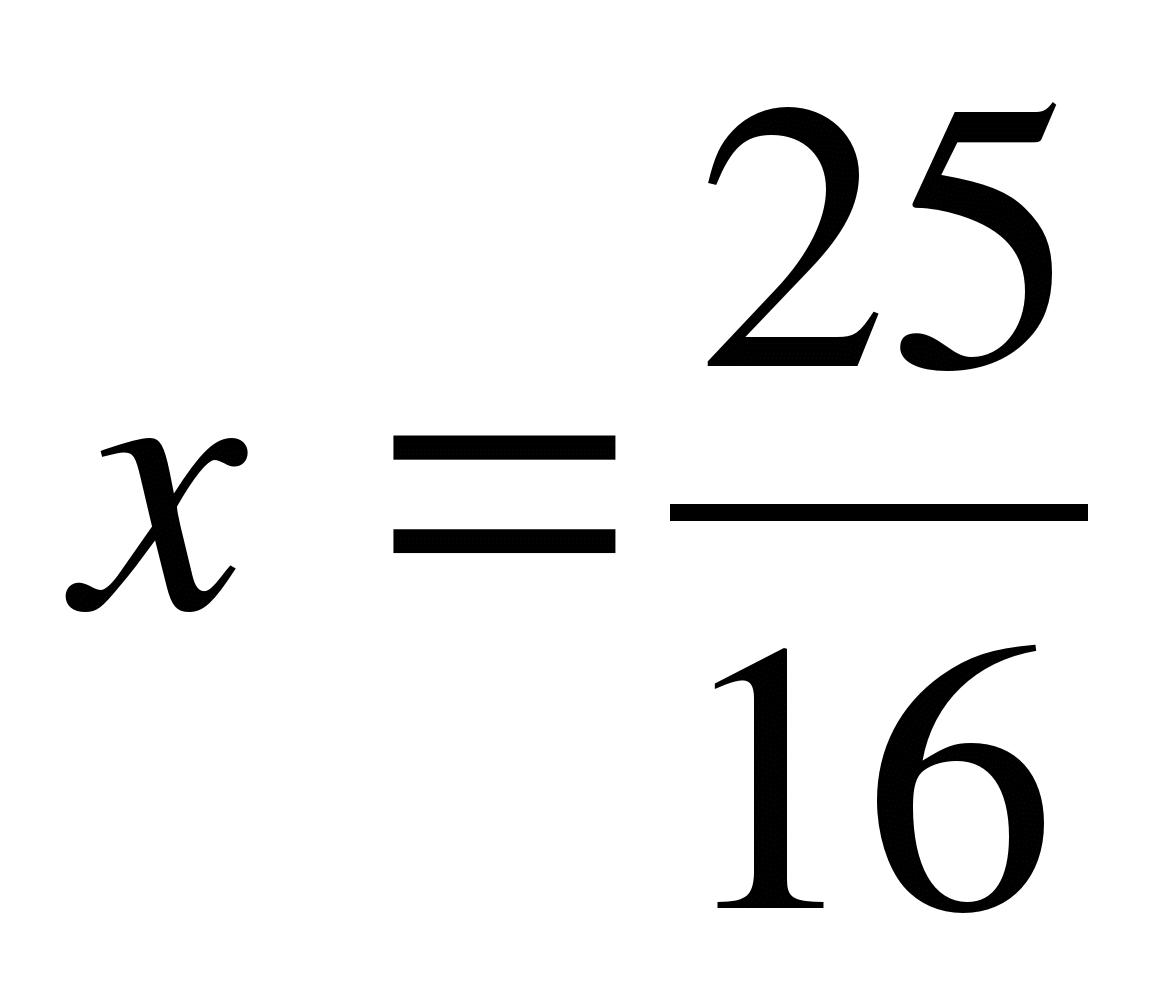 (рис
1)
(рис
1)
x x
Рис.1 Рис.2
2. Уравнение имеет корни разного знака, если
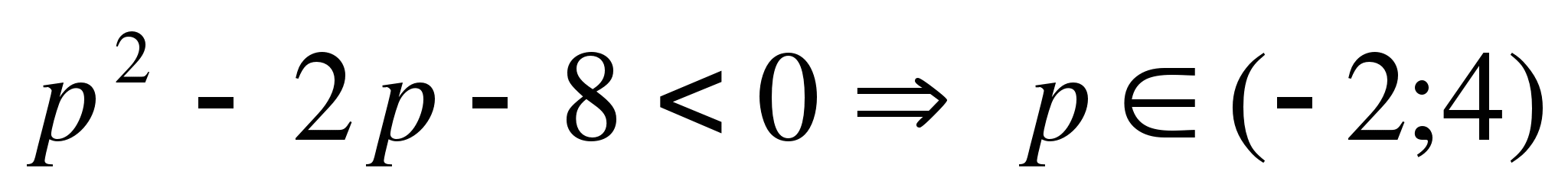 (Рис.2)
(Рис.2)
а). Оба корня уравнения положительные. Это возможно тогда и только тогда, когда выполняется условие:
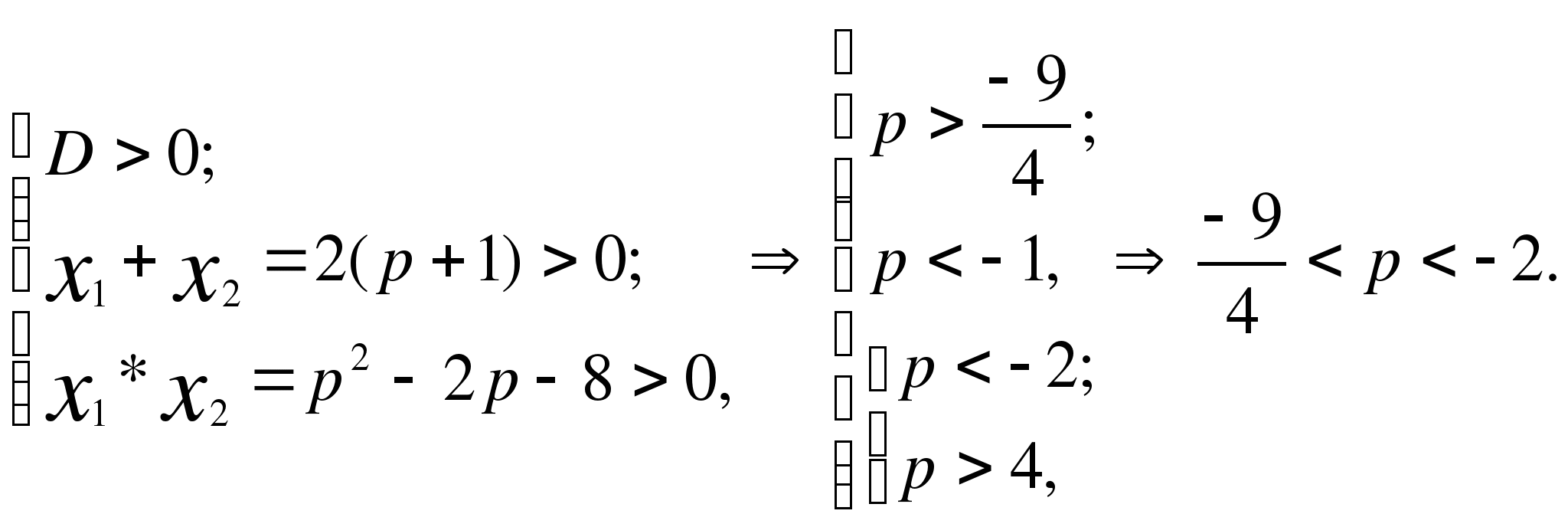 (рис.3)
(рис.3)



 y y
y y

 x
Рис.3 x Рис.4
x
Рис.3 x Рис.4
б). Оба корня уравнения отрицательны, если выполняется условие:
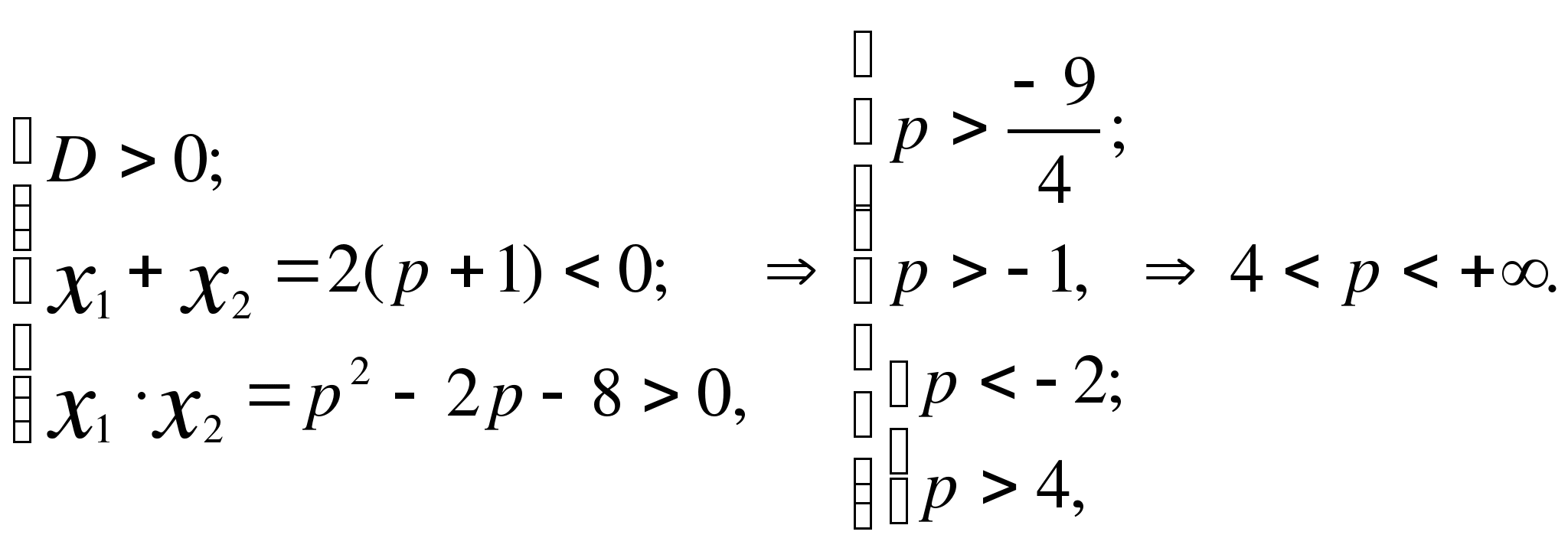 (рис.4)
(рис.4)

 y
y

Рис.5 x
3.Уравнение вообще не имеет корней. Это возможно, если D <0, т. е.
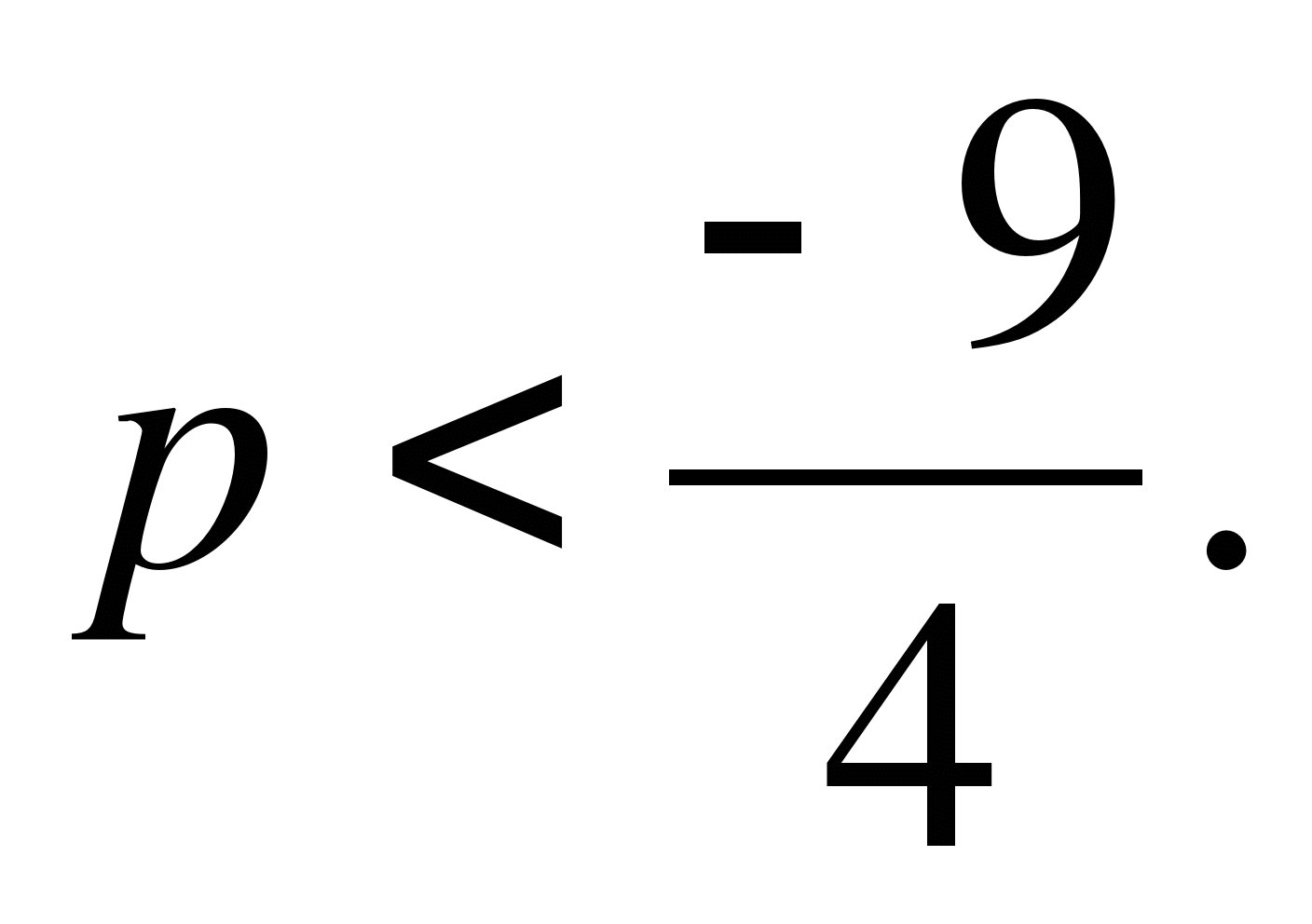 (рис.5)
(рис.5)
Ответ: а) имеет единственное решение, если
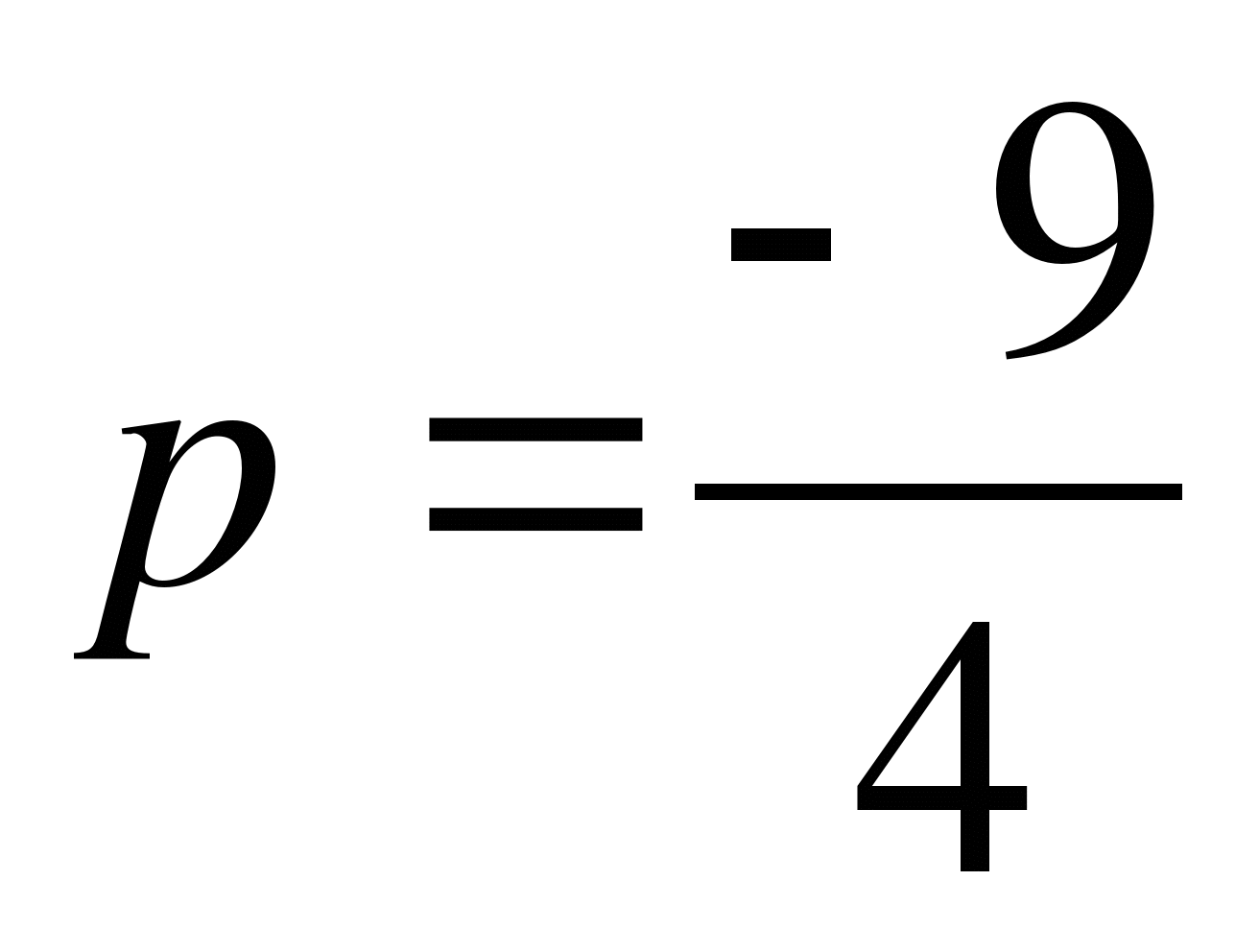 ; б)
имеет два решения,
; б)
имеет два решения,
если
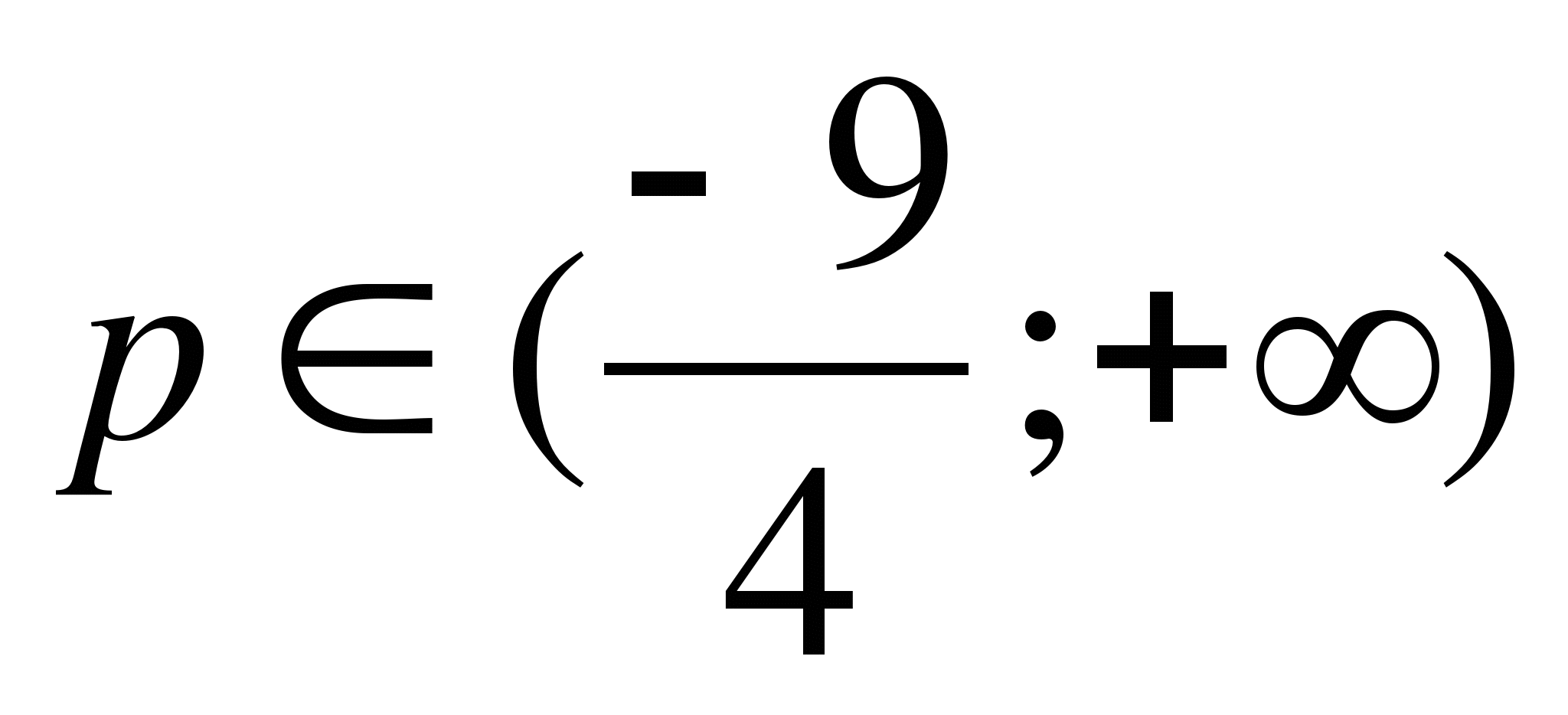 ; в)
не имеет решение, если
; в)
не имеет решение, если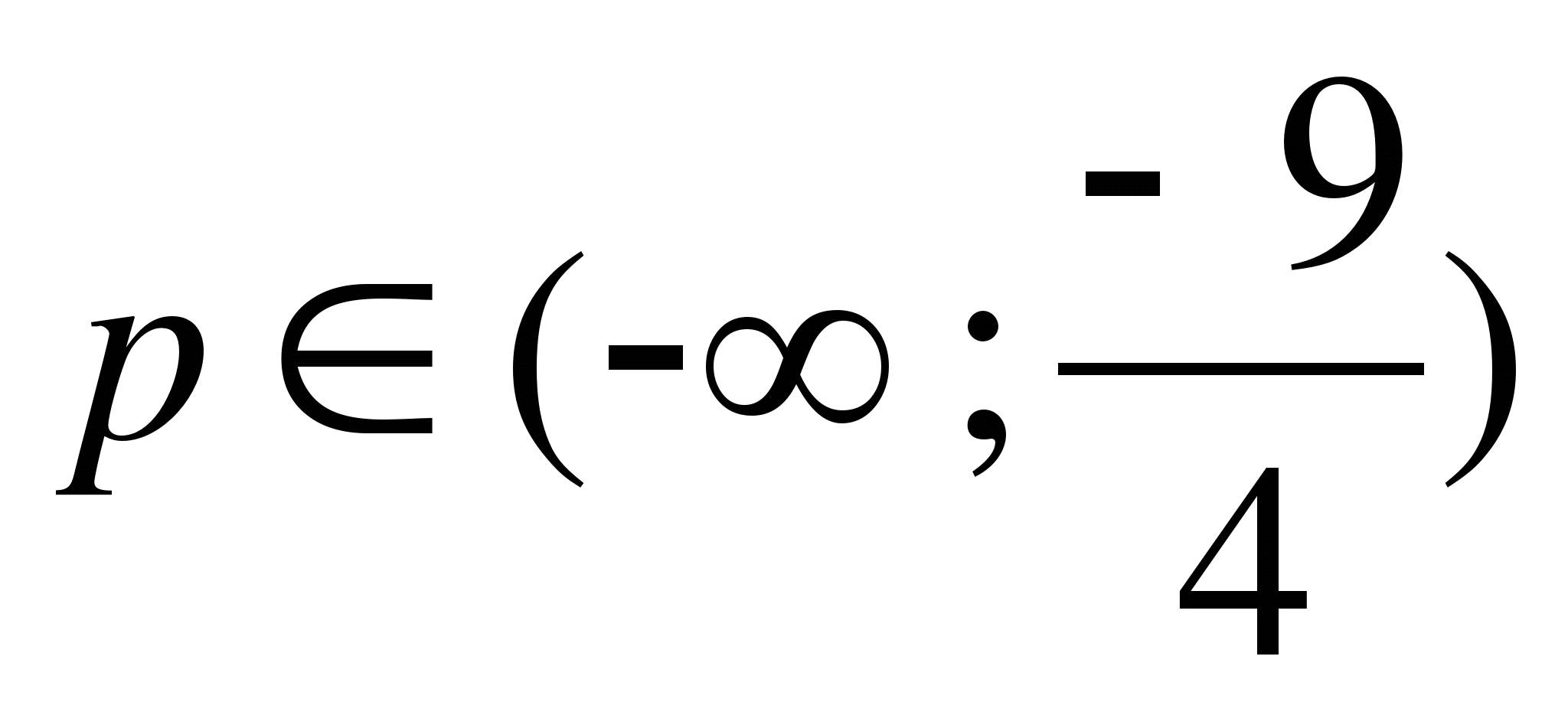 .
.
II . Фронтальная работа.
Решить уравнения:
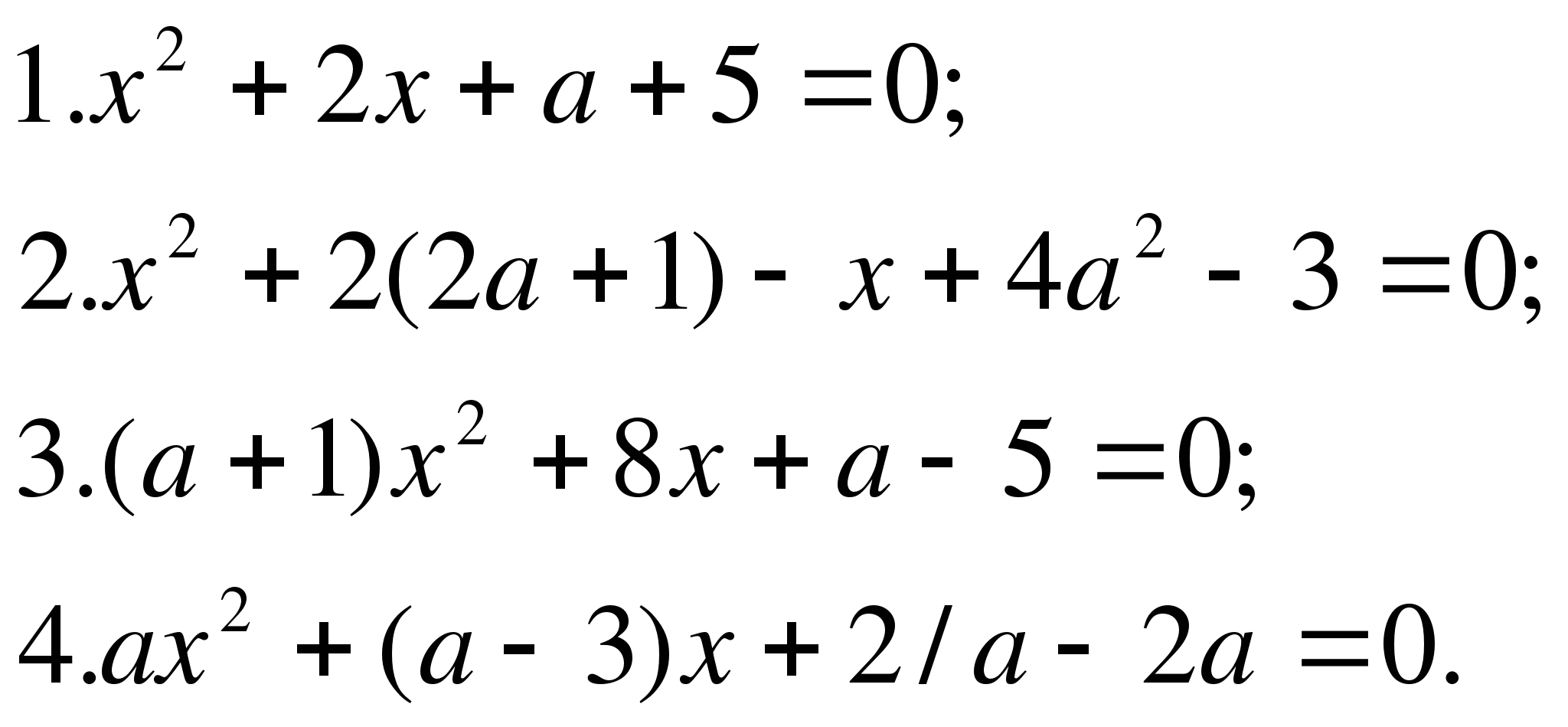 Ответы:
Ответы: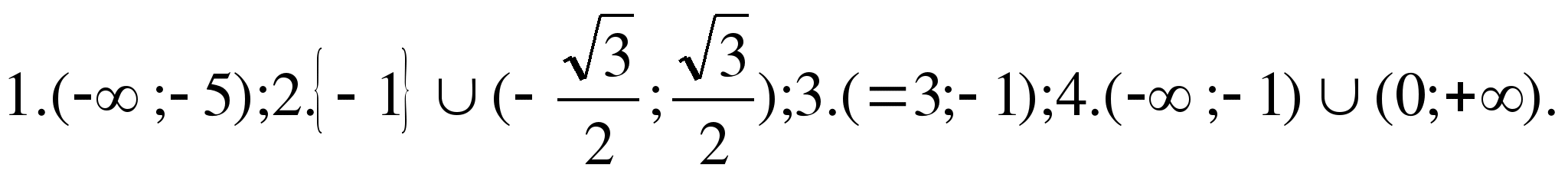
Занятие 3.
Цель: обобщить и углубить знания школьников по изучаемой теме.
Ход занятия.
I. Упражнения по совершенствованию и закреплению знаний и умений.
Совместно с учителем решаются оставшиеся уравнения с
 предыдущего
урока.
предыдущего
урока.
II. Самостоятельная работа учащихся (выполняется в парах).
Решите уравнения.
1вариант. 2 вариант.
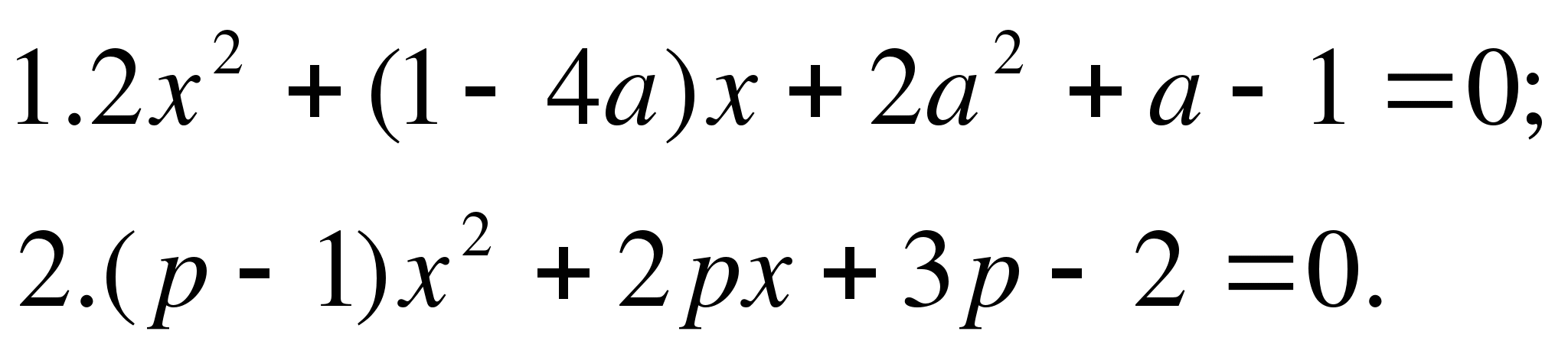
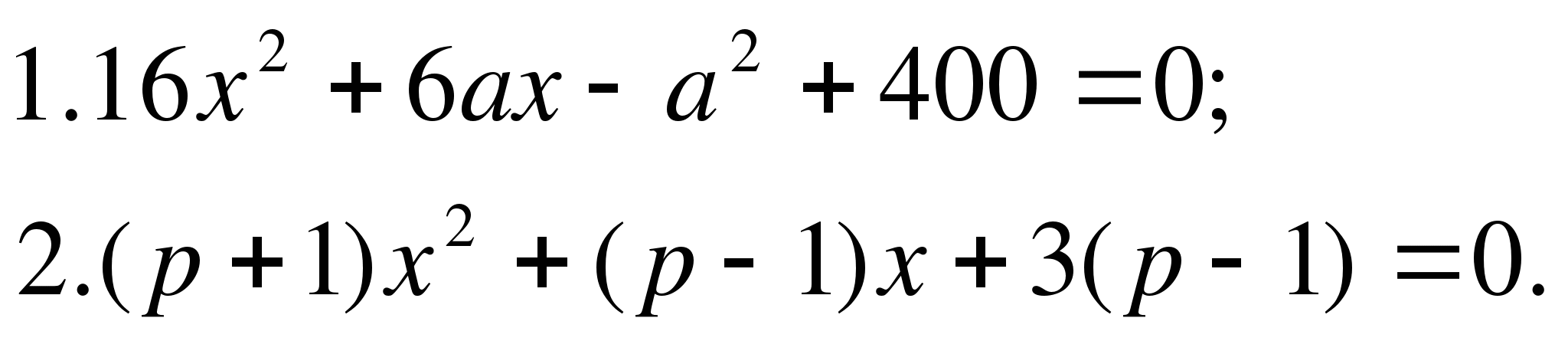
Ответы: 1вариант.
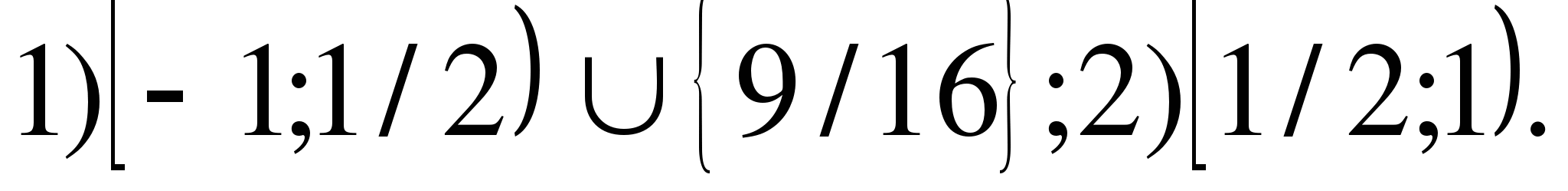 2
вариант.
2
вариант.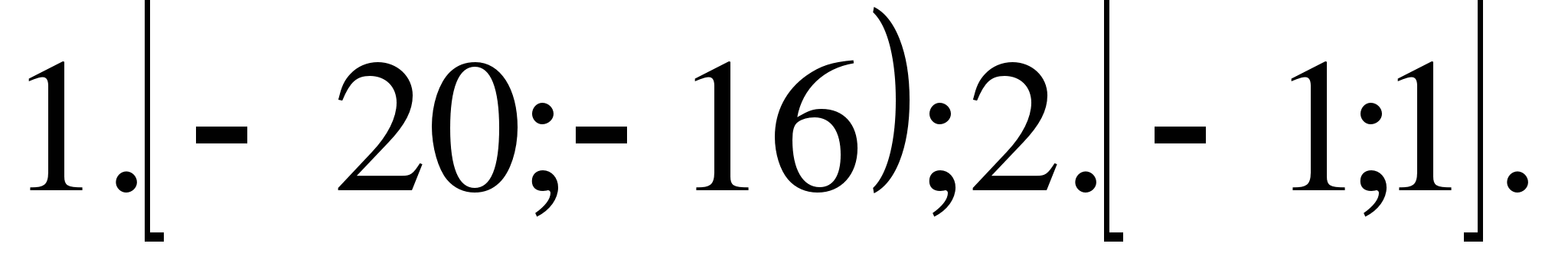
По окончанию урока учитель отмечает, в какой мере достигнута цель урока, оценивает работу каждой пары, дает пояснение по работе.
III. Итог занятия.
Занятие 4.
Ход занятия.
I. Фронтальная работа.
Задание 1. При каких значениях параметра а, число 2 находится между корнями квадратного уравнения
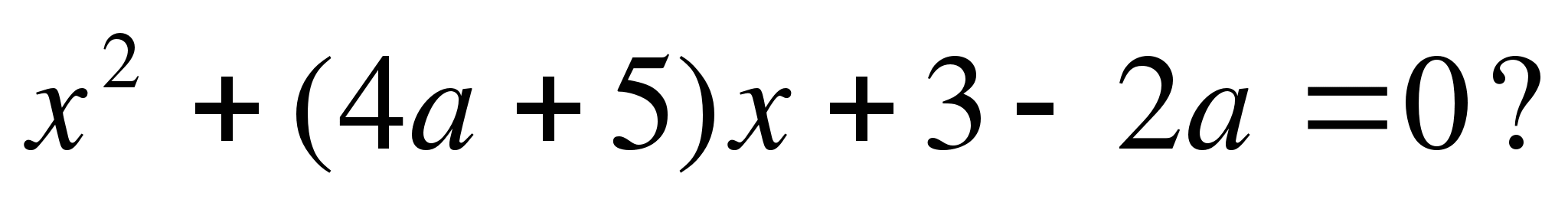
Решение: Пусть x
 и
x
и
x корни
квадратного уравнения, причем
корни
квадратного уравнения, причем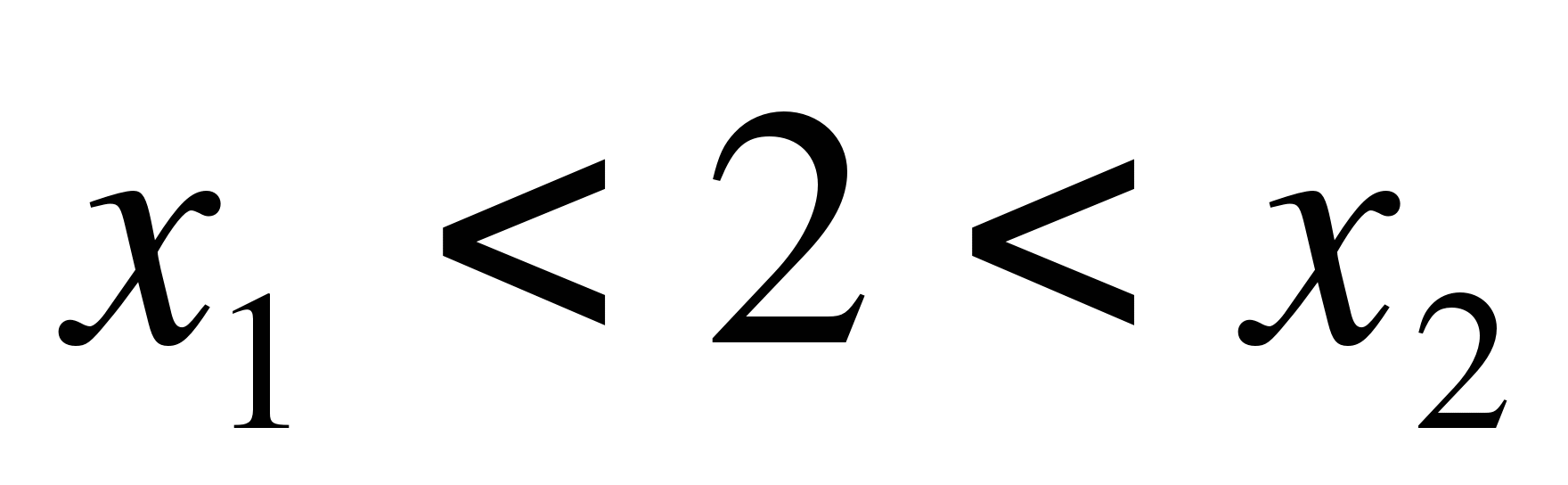 .
.
Воспользуемся теоремой о расположении корней квадратного трехчлена и придем к следующей системе:
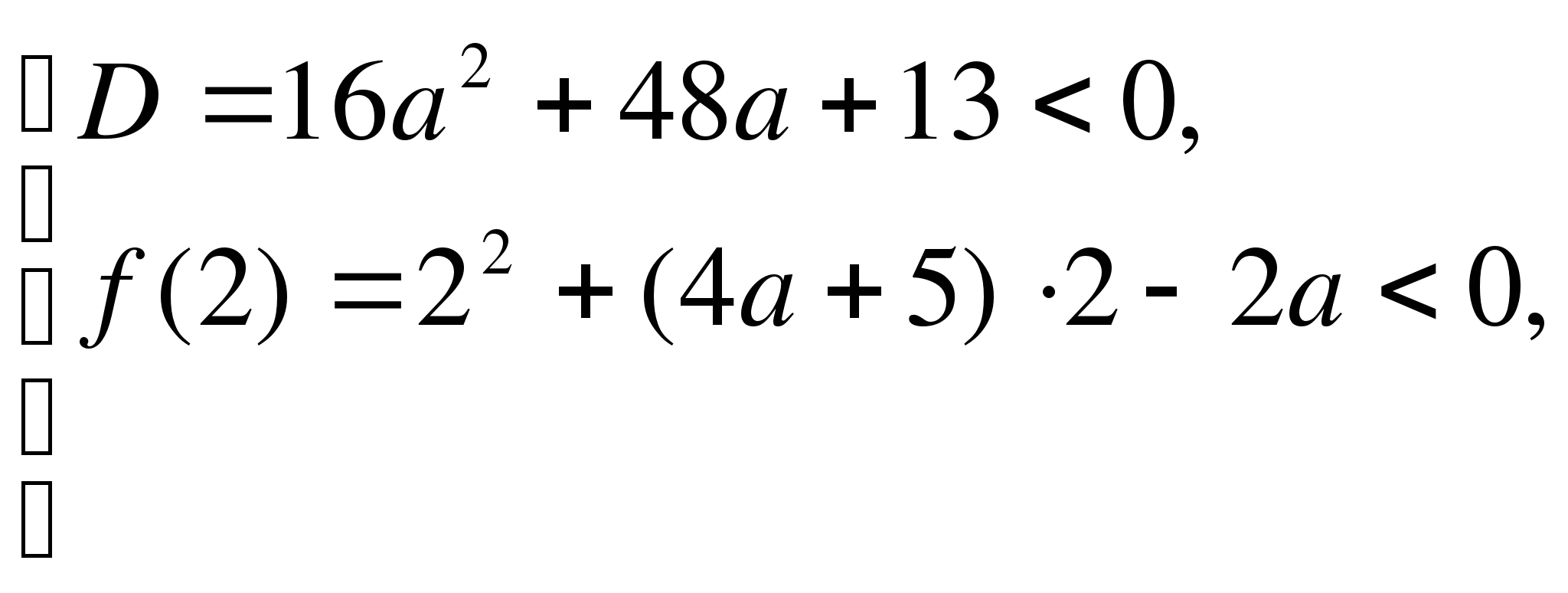 или
17+6a<0, откуда a<-
или
17+6a<0, откуда a<-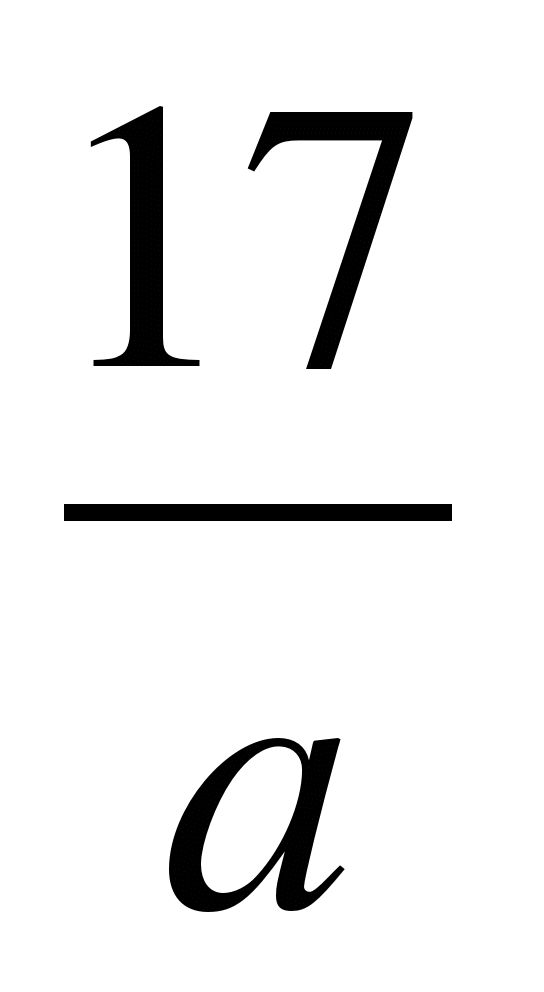 .
Ответ: a<-
.
Ответ: a<-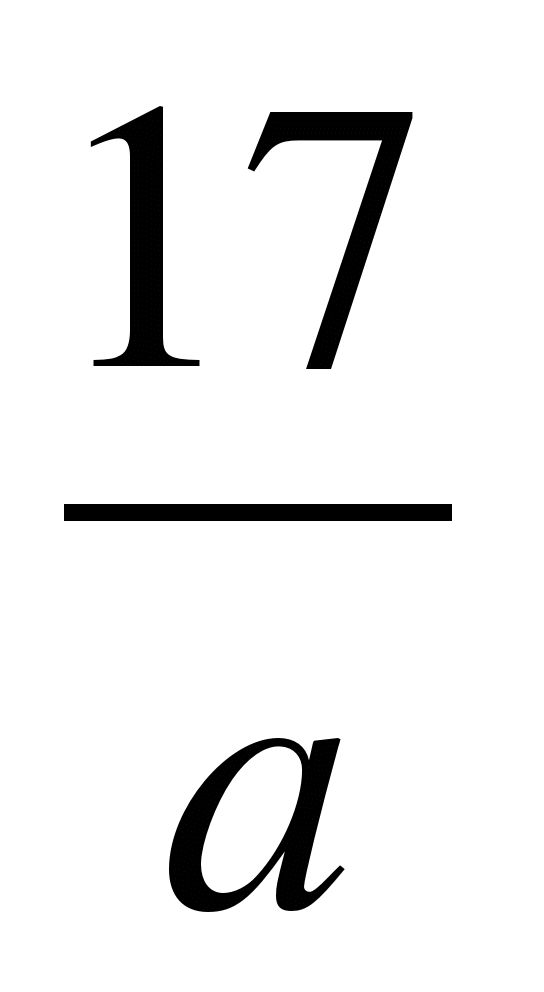 .
.
Задание 2. Найти все значения параметра a, при каждом из которых корни квадратного уравнения
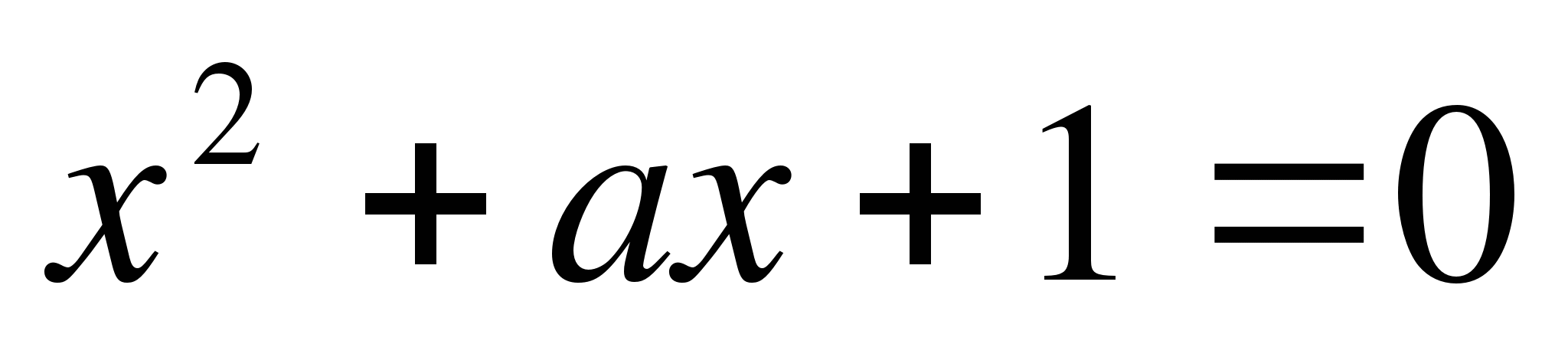 различны и лежат на отрезке
различны и лежат на отрезке 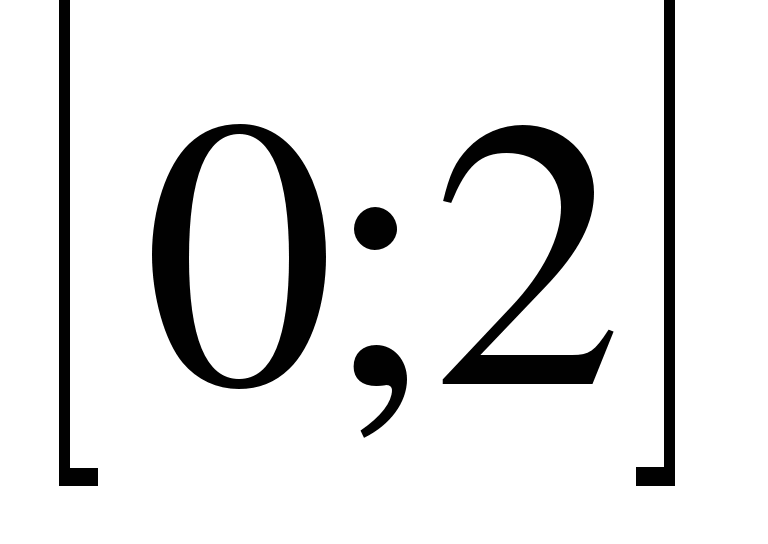 .
.
Решение:
Изобразим схематично условие задачи:
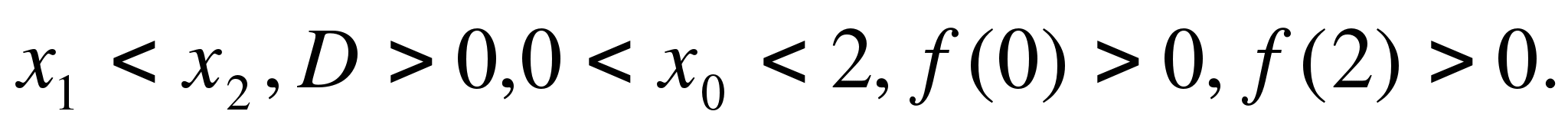








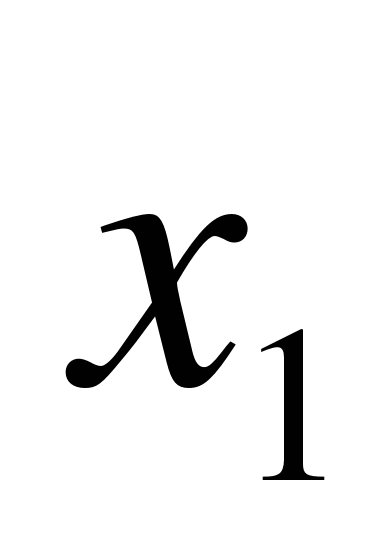
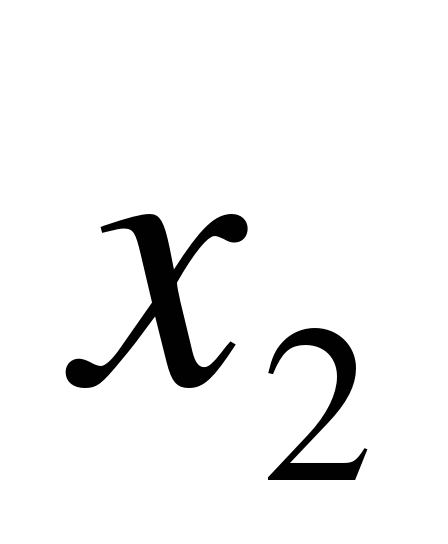 0
0
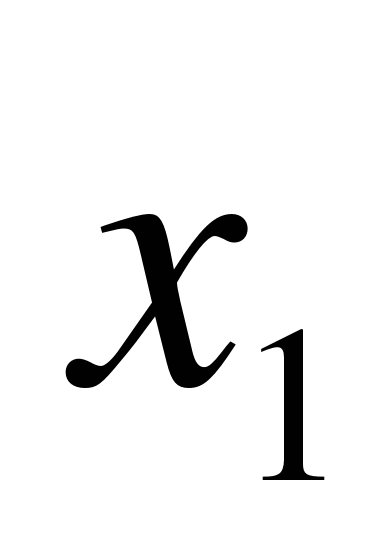
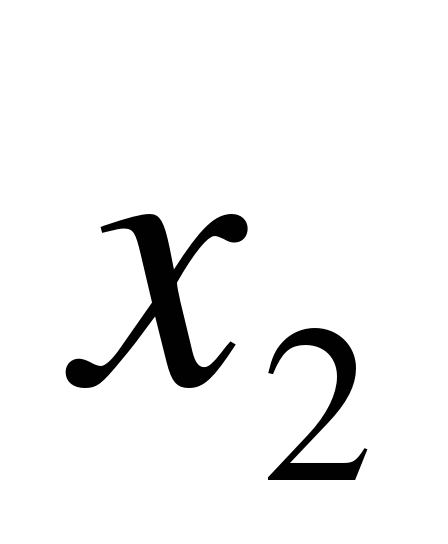 2 х
0 2 х
2 х
0 2 х
D=
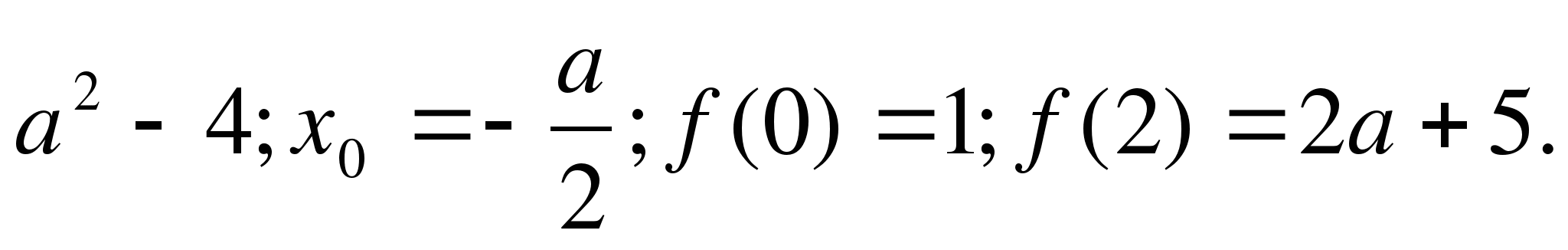
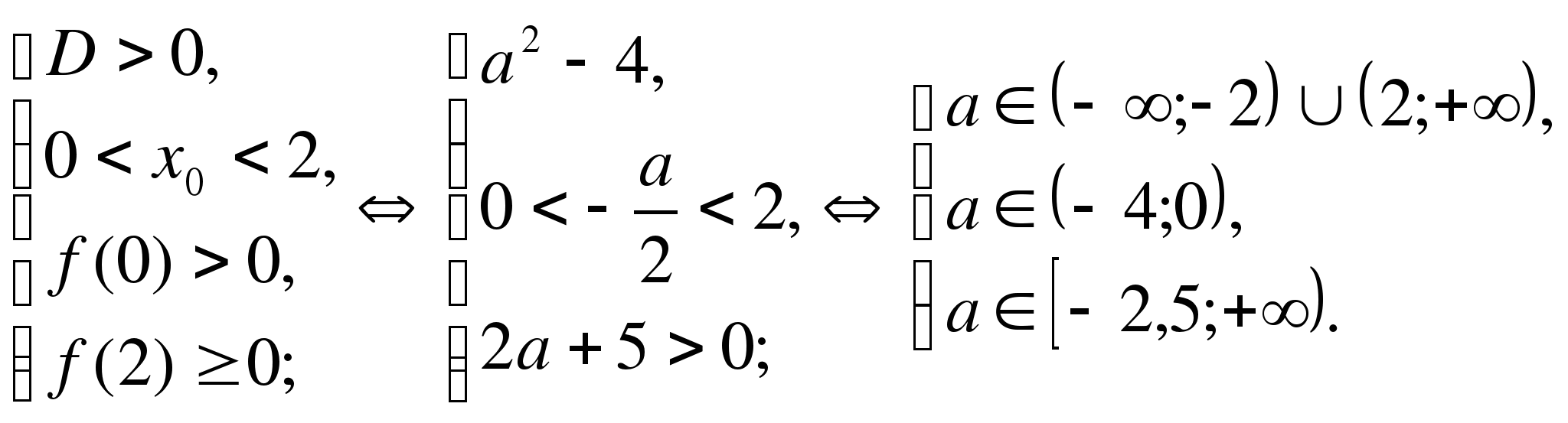 Если
Если 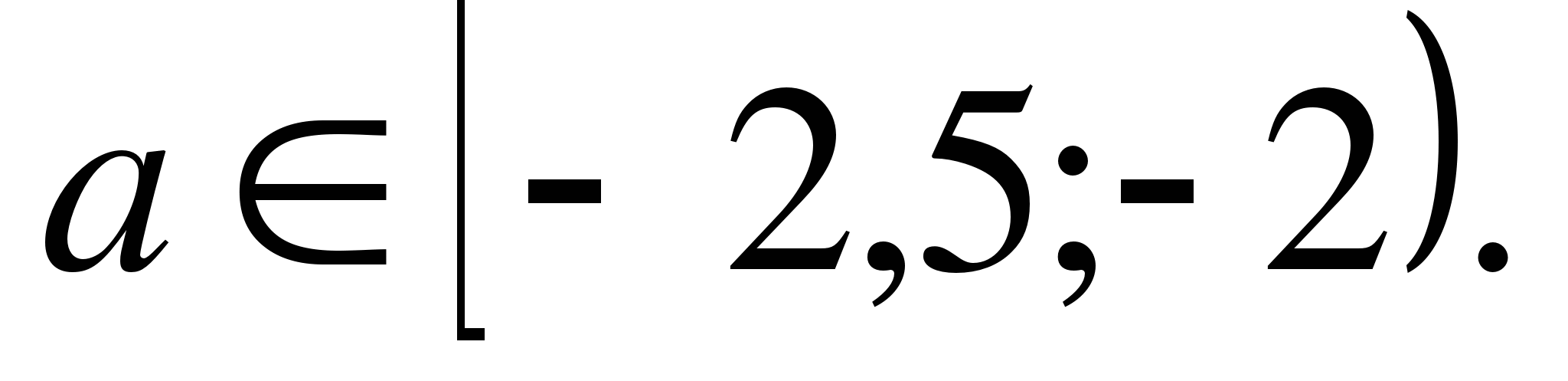
Ответ:
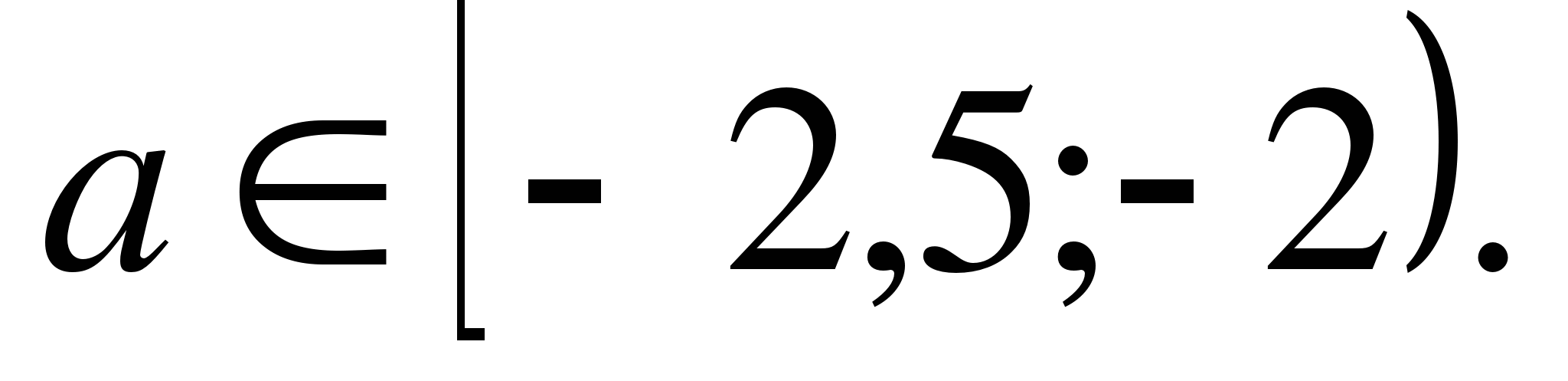
II. Самостоятельное решение задач.
-
Найдите все значения параметра a, оба корня уравнения
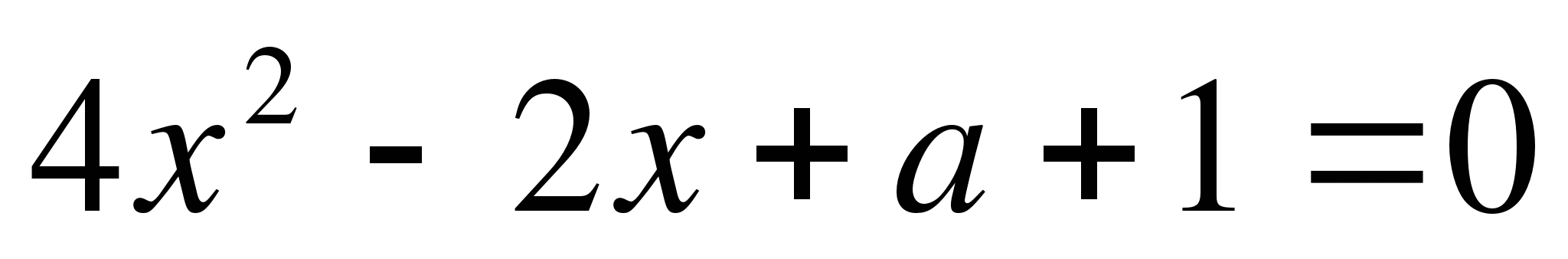 меньше 1, но больше -1.
меньше 1, но больше -1.
Ответ:
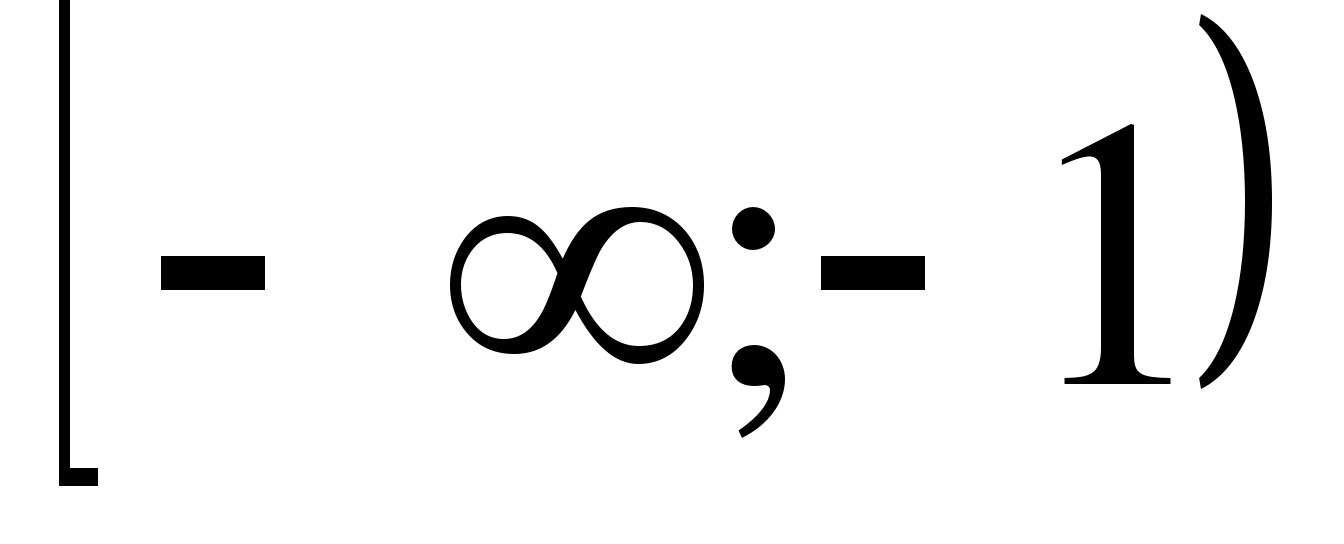 .
.
2.Уравнение
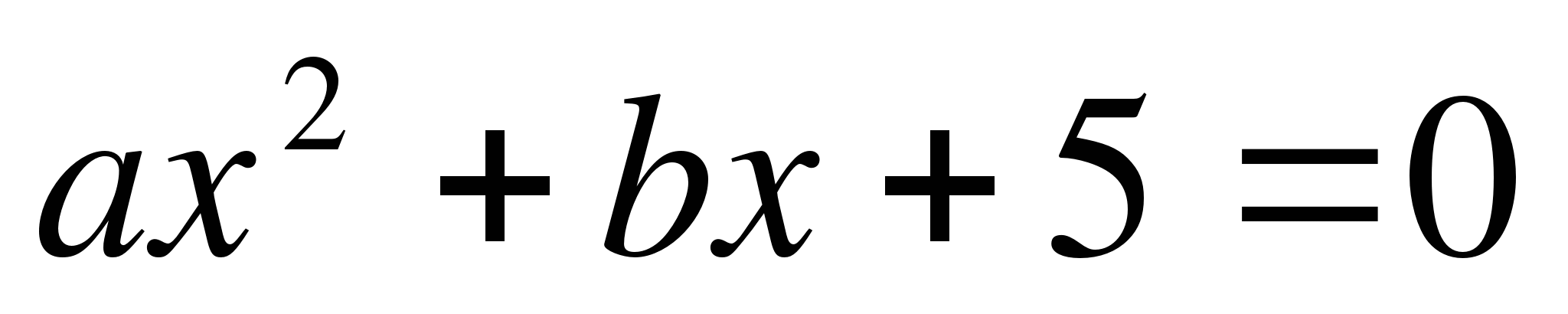 имеет корень равный 1. Чему равны a и b?
имеет корень равный 1. Чему равны a и b?
Ответ: 0; -5; 5; -10.
III. Итоги занятия.
Занятие 5. Решение уравнений с параметром, приводимых к квадратным уравнениям.
Цель: систематизировать, обобщить знания и умения учащихся по применению предыдущего материала при решении уравнений, приводимых к квадратным.
-
-
Повторение.
-
Учитель предлагает учащимся вспомнить решение дробно - рациональных уравнений.
Решить уравнение:
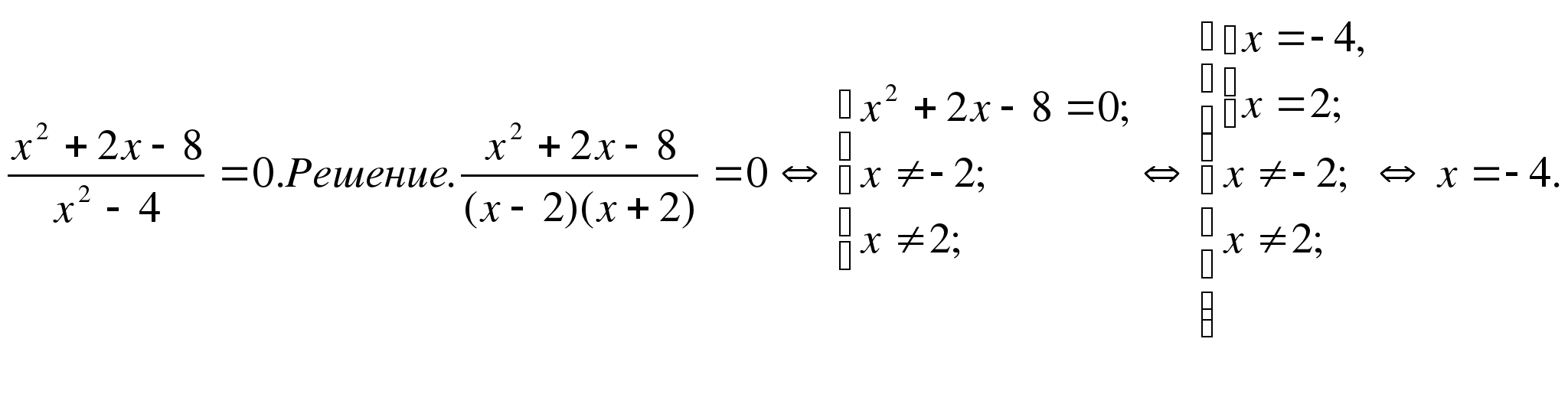
Вывод (условие равенства дроби нулю): дробь равна нулю, если числитель дроби равен нулю, а знаменатель не равен нулю.
-
-
Объяснение нового материала.
-
Рассматривается метод решения дробно - рациональных уравнений с параметром.
Задание 1. При каких a уравнение
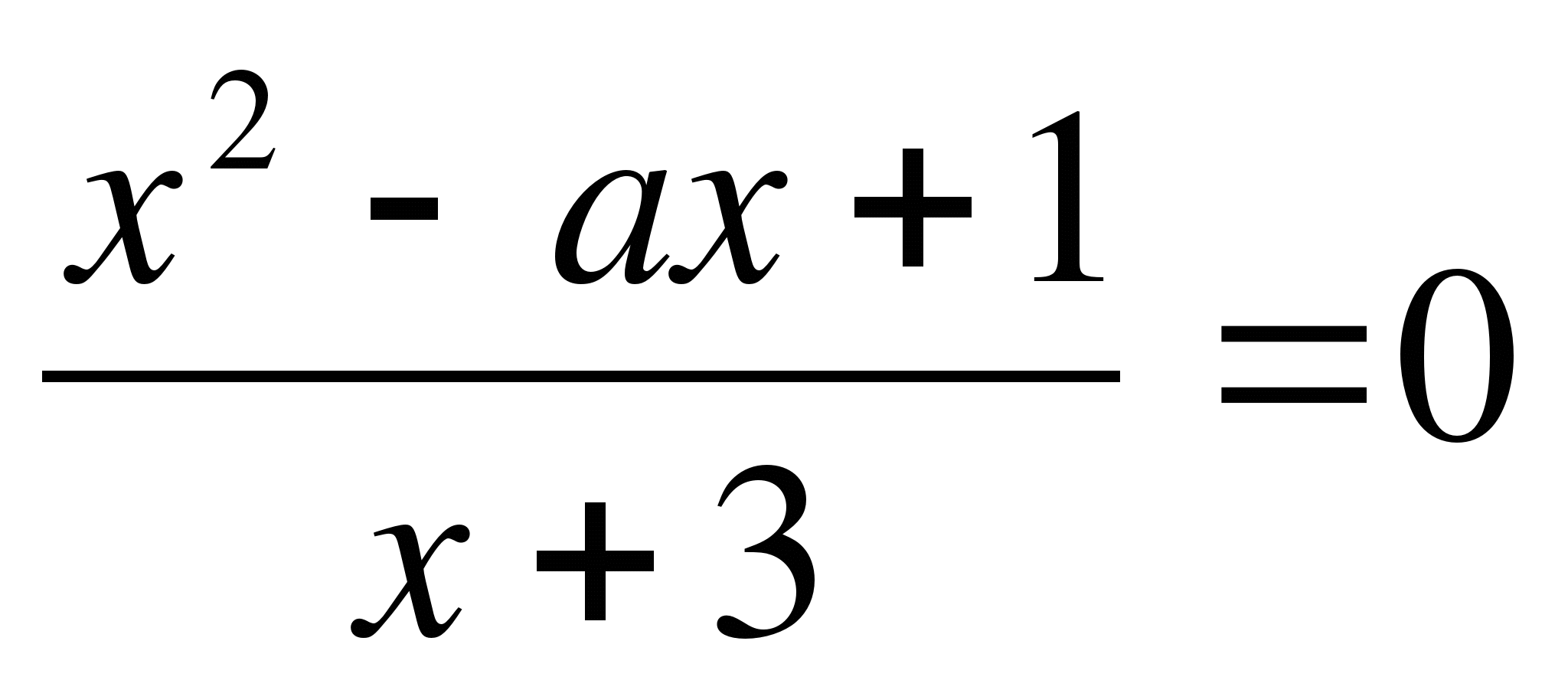 имеет единственное решение?
имеет единственное решение?
Решение: Данное уравнение равносильно системе
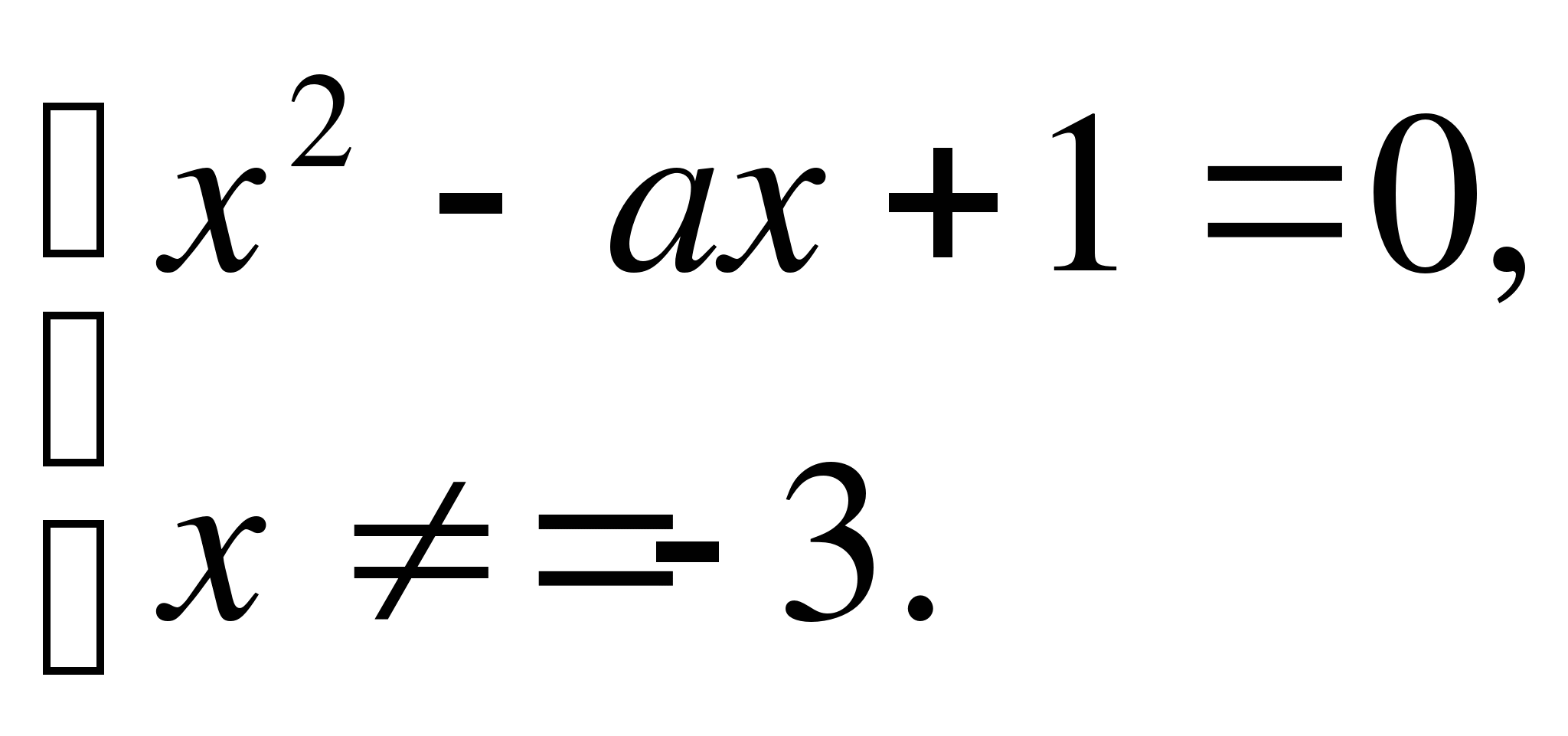
Наличие квадратного уравнения и условие единственности приводит к поиску корней дискриминанта. Вместе с тем условие
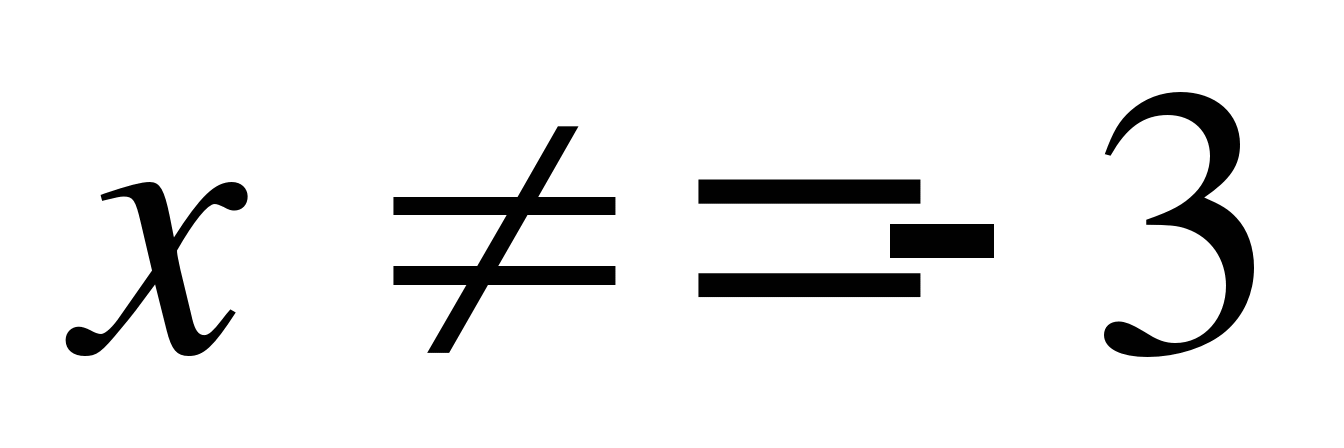 должно привлечь внимание. Квадратное уравнение системы может
иметь два корня, но обязательно только один из них должен
равняться -3. Имеем
должно привлечь внимание. Квадратное уравнение системы может
иметь два корня, но обязательно только один из них должен
равняться -3. Имеем 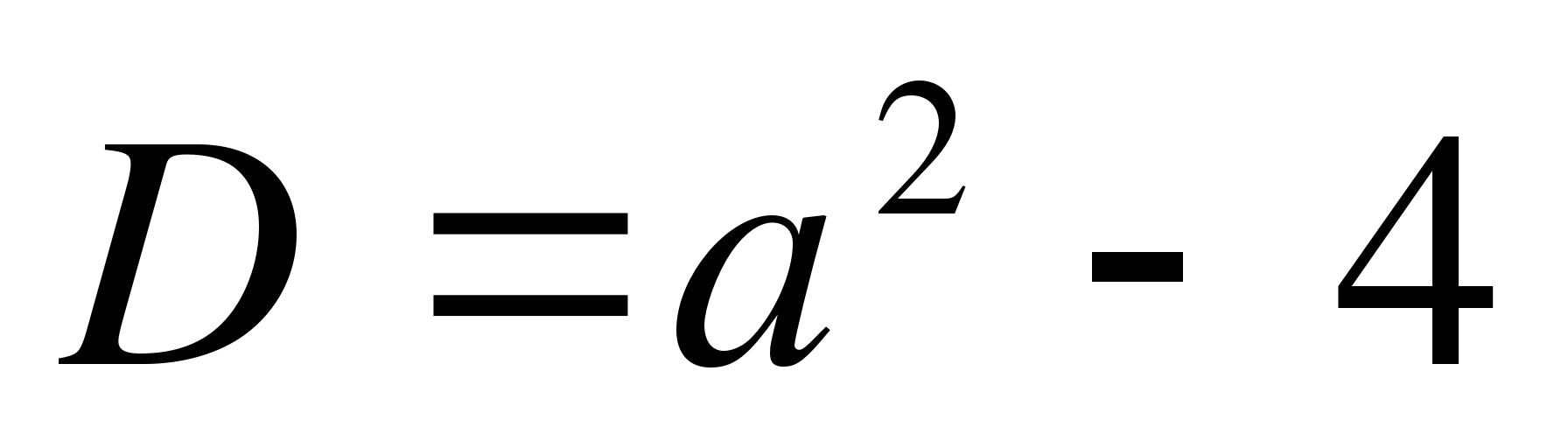 ,
отсюда
,
отсюда 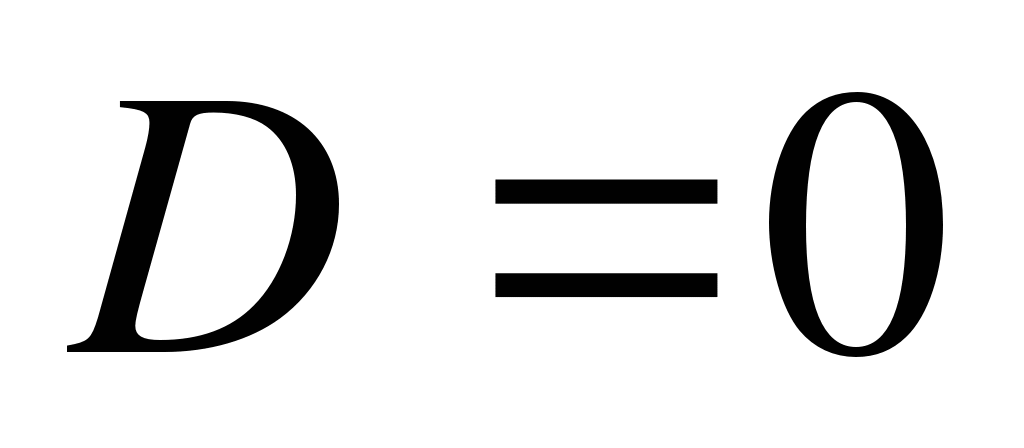 ,
если
,
если 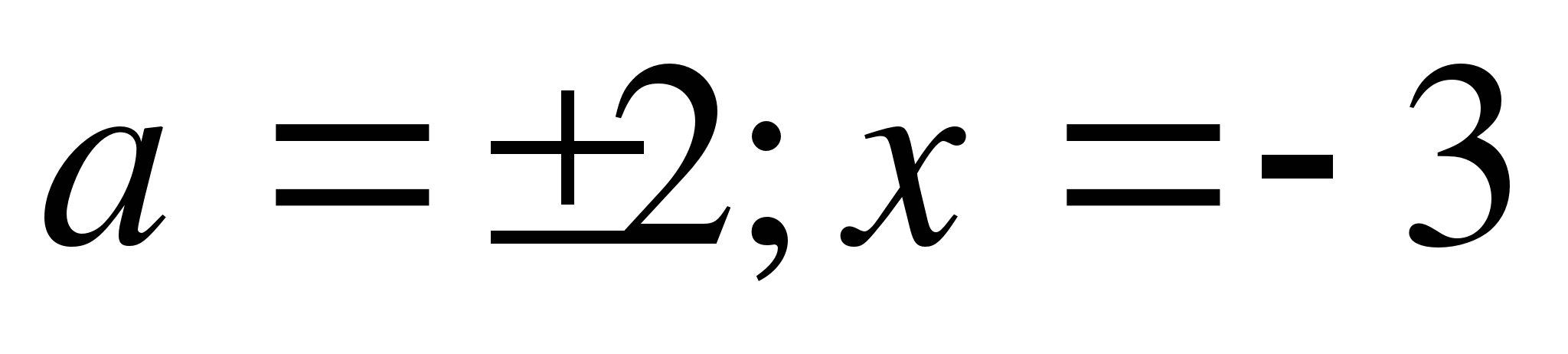 -
корень уравнения
-
корень уравнения 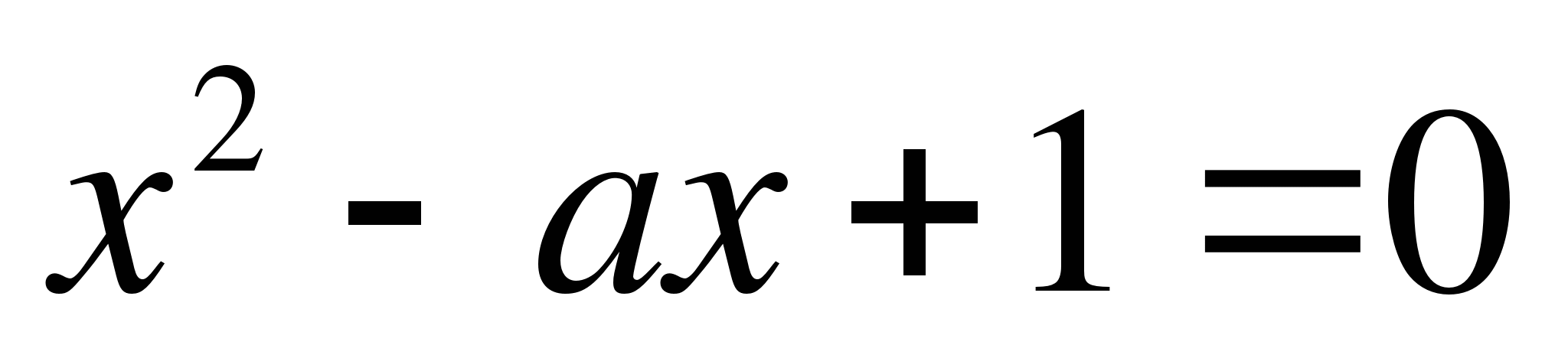 при
при
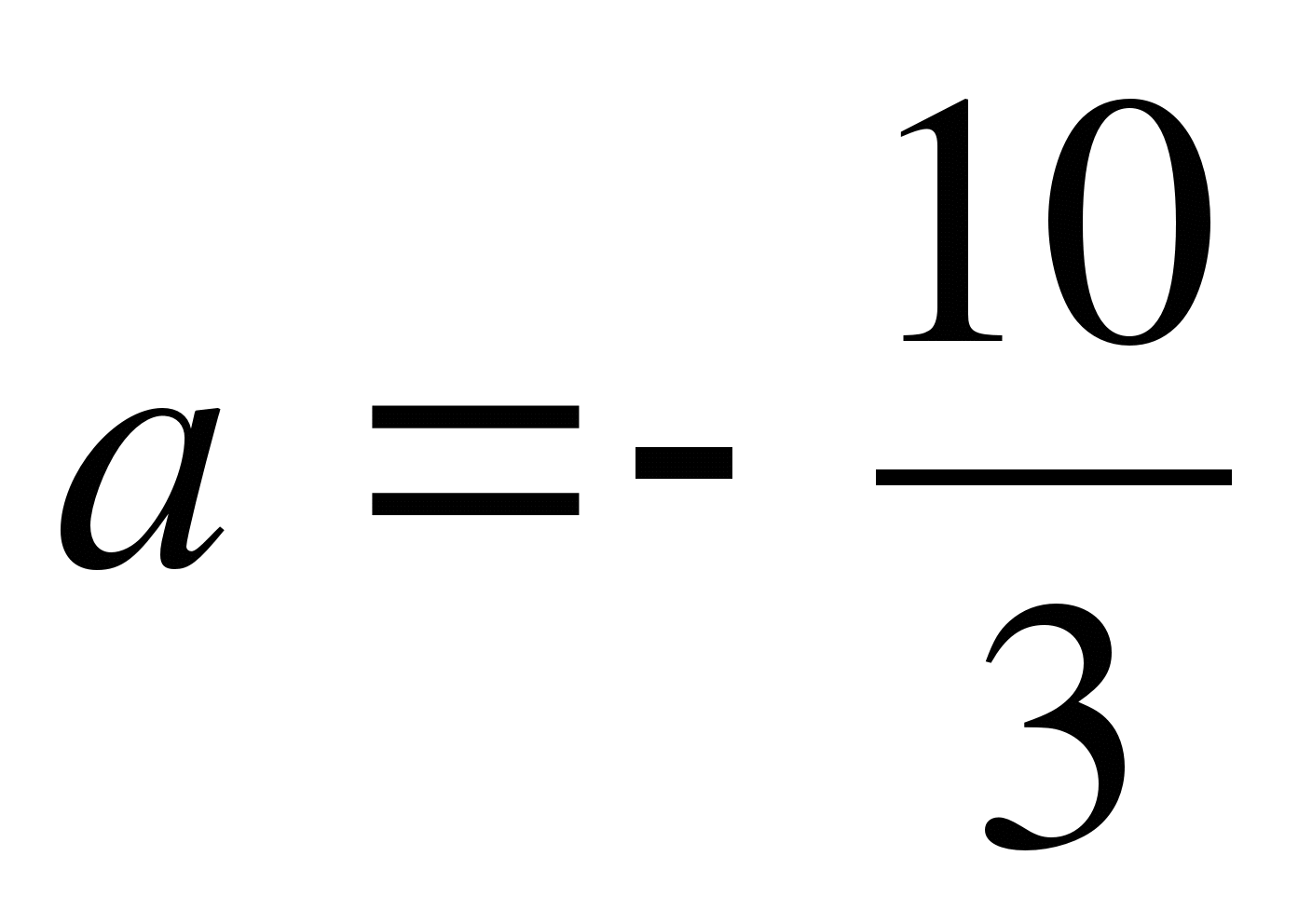 ,
,
Причем при таком значение а, второй корень квадратного уравнения отличен от -3. Ответ: a=±2 или а =-10/3.
Задание 2.Решить уравнение
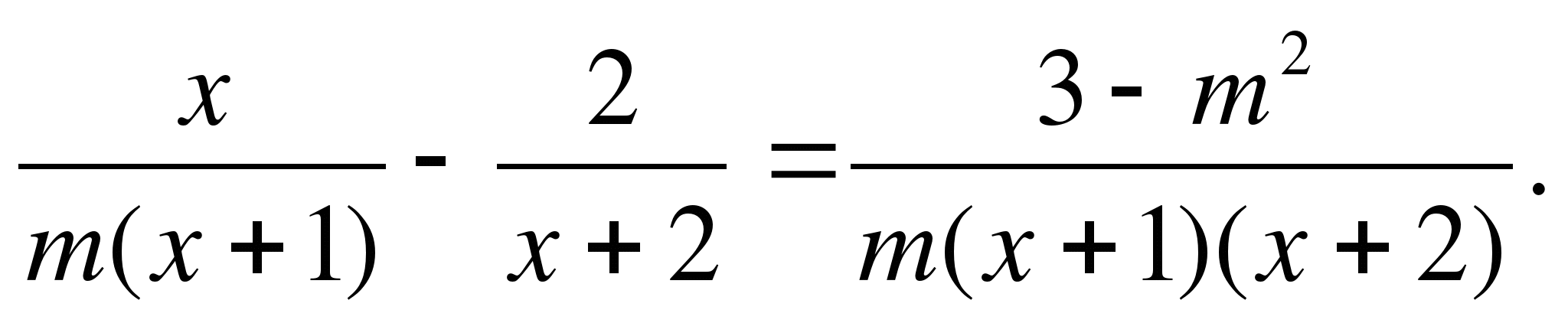
Решение: при m = 0 уравнение не имеет смысла, значение x должно удовлетворять условию x ≠ -1, x ≠ -2. Умножив все члены уравнения на m(x+1)(x+2)≠0, получим уравнение
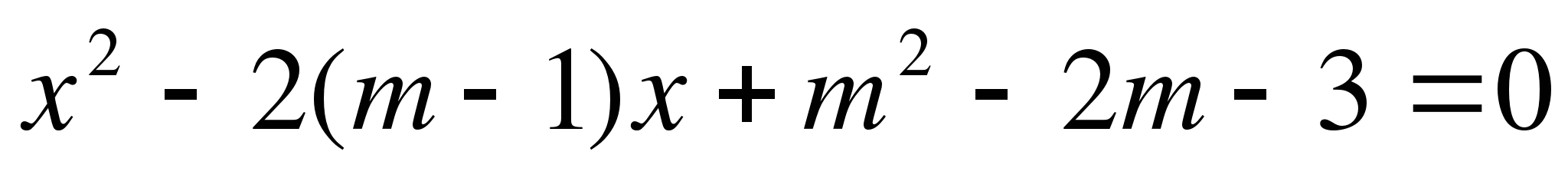 ,
равносильное данному. Его корни
,
равносильное данному. Его корни 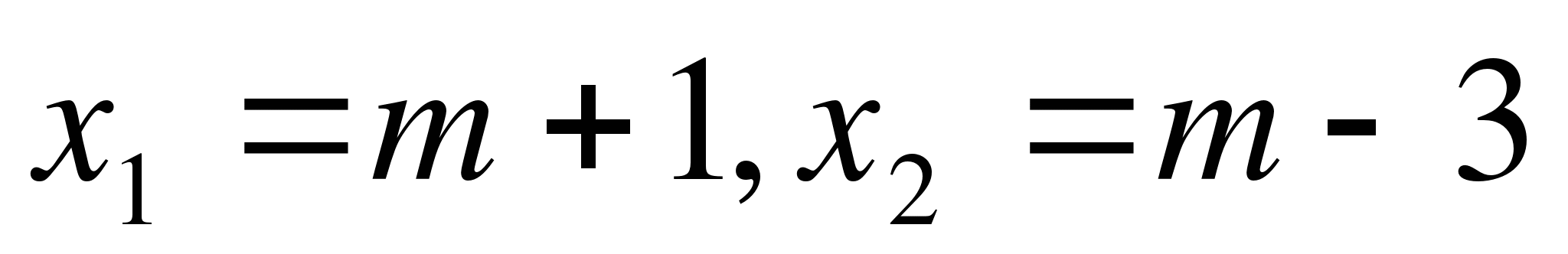 .
Выделим из этих корней посторонние, т. е. те корни которые
равны -1 и -2:
.
Выделим из этих корней посторонние, т. е. те корни которые
равны -1 и -2:
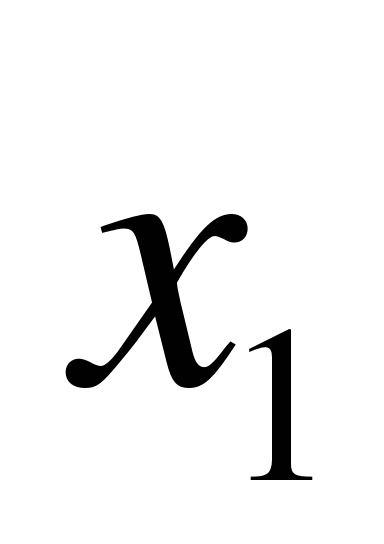 =
m + 1=-1, m = - 2, но при m = -2,
=
m + 1=-1, m = - 2, но при m = -2,
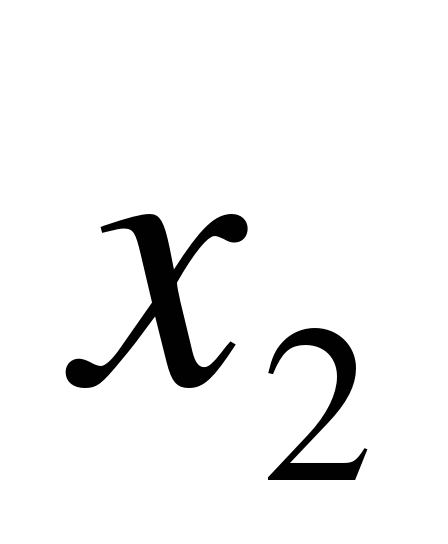 =
-5;
=
-5; 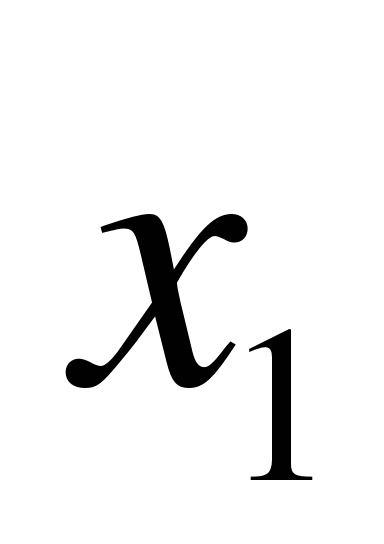 =
m+ 1, m = - 3, но при m = -3
=
m+ 1, m = - 3, но при m = -3 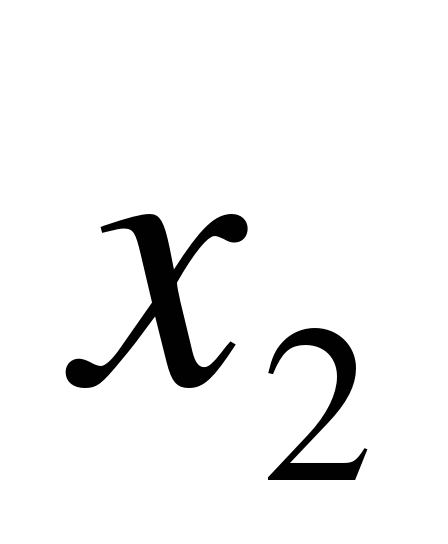 = -
6;
= -
6; 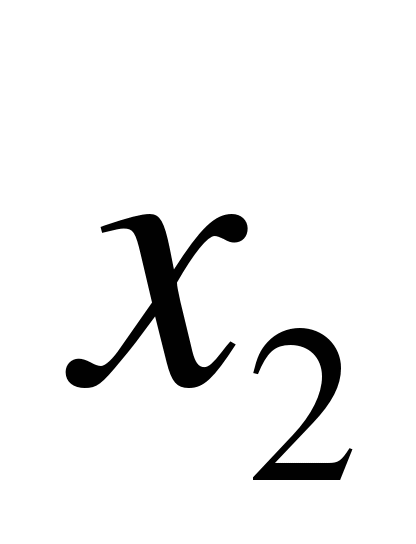 =
m - 3 = -1, m = 2, но при m = 2
=
m - 3 = -1, m = 2, но при m = 2 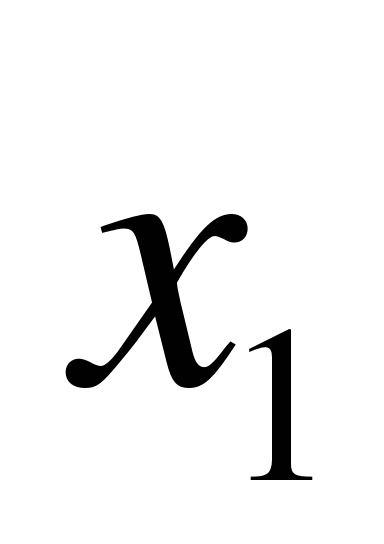 = 3;
= 3;
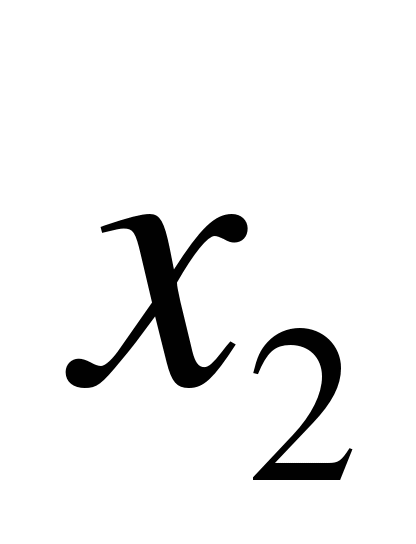 =
m- 3 = -2, m = 1, но при m = 1
=
m- 3 = -2, m = 1, но при m = 1
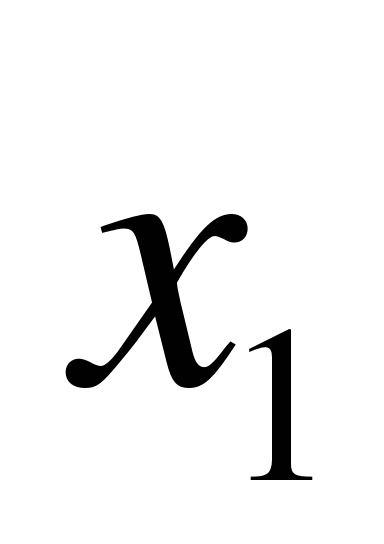 = 2.
= 2.
Ответ: при m ≠ 0, m ≠ ±2, m ≠ 1
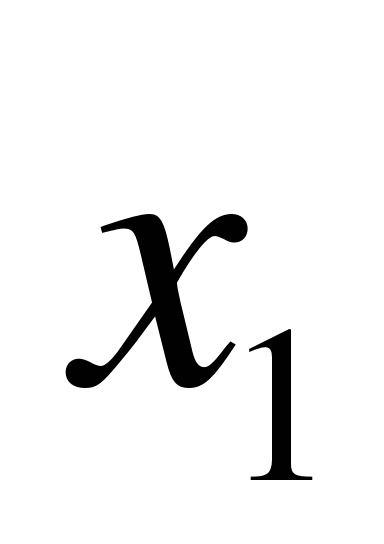 =
m + 1,
=
m + 1, 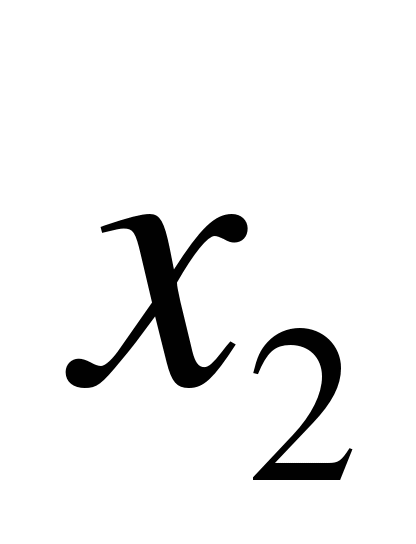 =
m - 3; при m = -2
=
m - 3; при m = -2 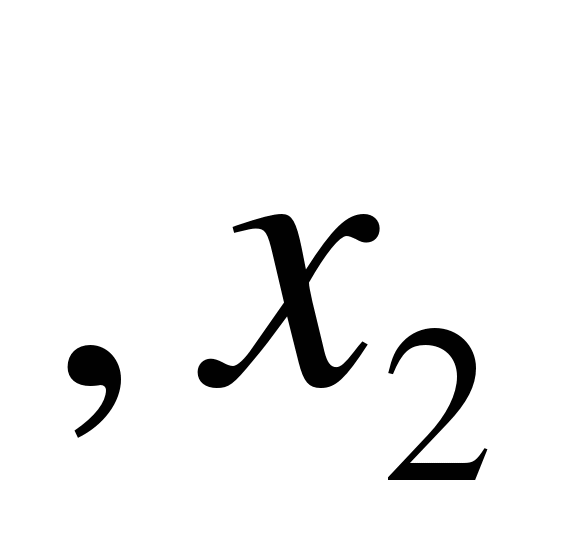 =
-5; при m = -3,
=
-5; при m = -3, 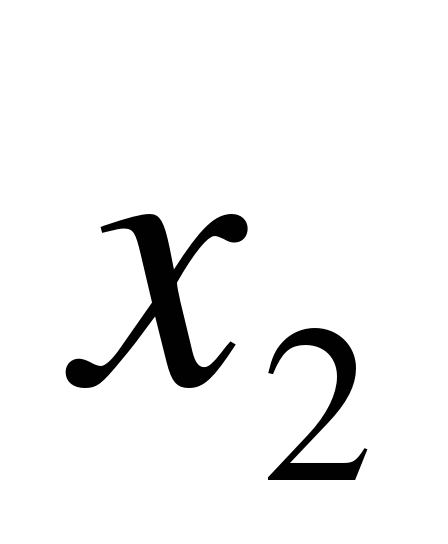 =
-6; при m = 2
=
-6; при m = 2 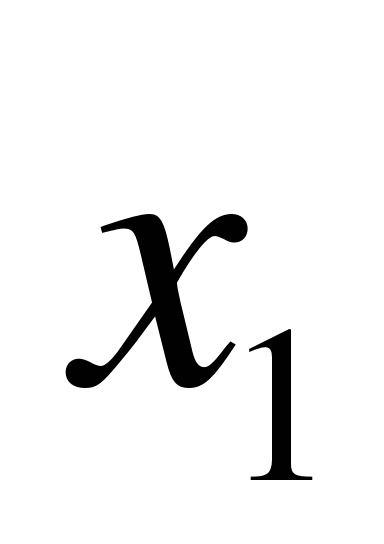 = 3;
при m = 1
= 3;
при m = 1 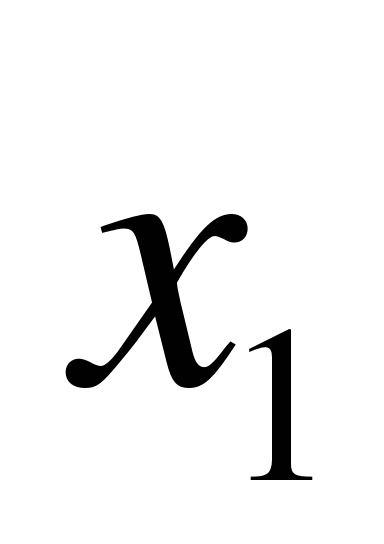 = 2;
при m = 0 решений нет.
= 2;
при m = 0 решений нет.
Задание 3. Решите уравнение
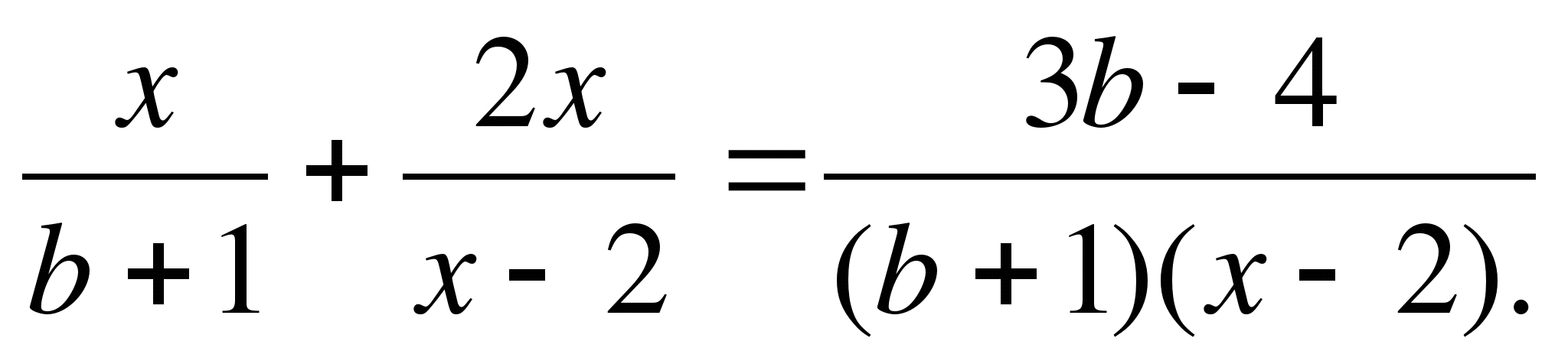 .
.
Решение: при b ≠ -1, x ≠ 2 получаем
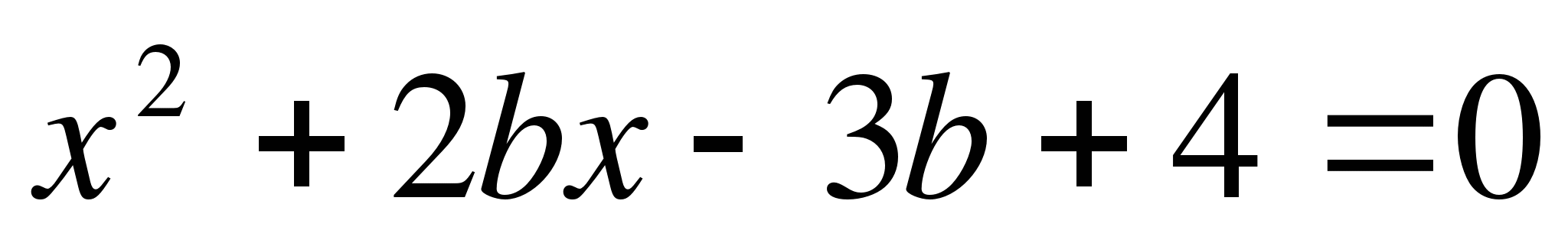 (1)
и корни
(1)
и корни 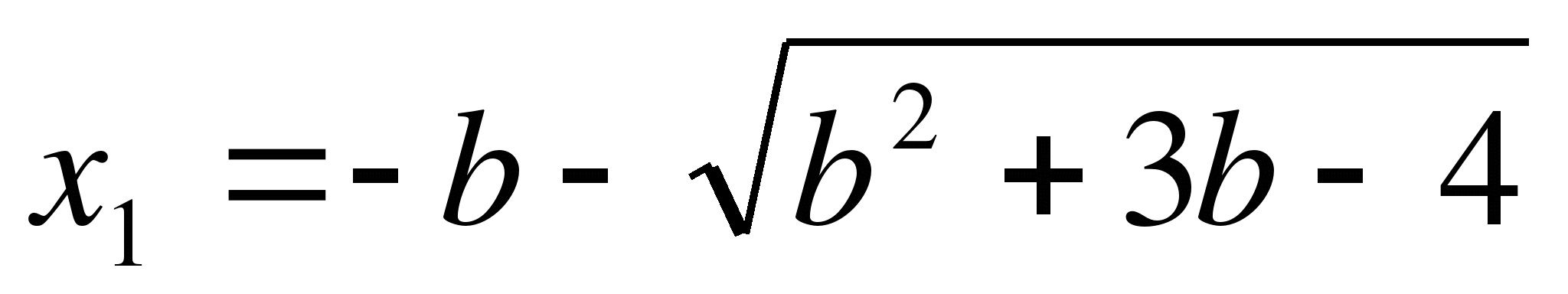 ,
,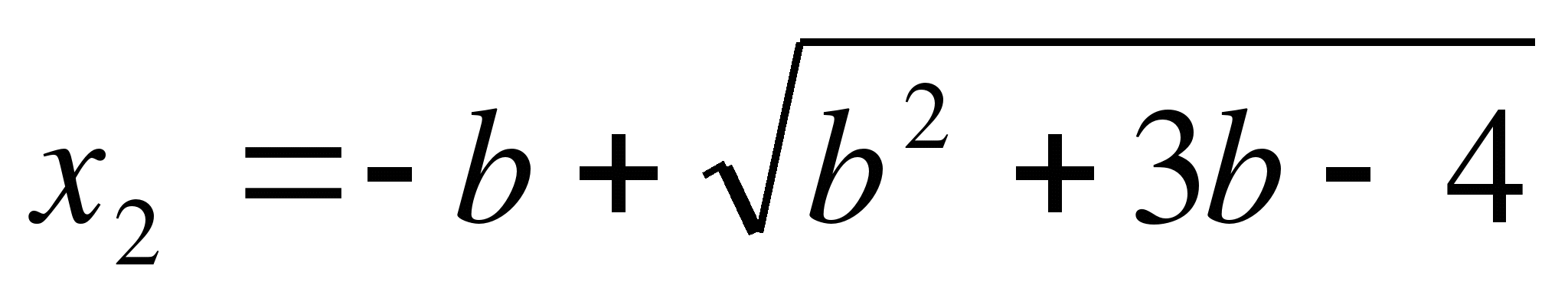 ,
существующие при
,
существующие при 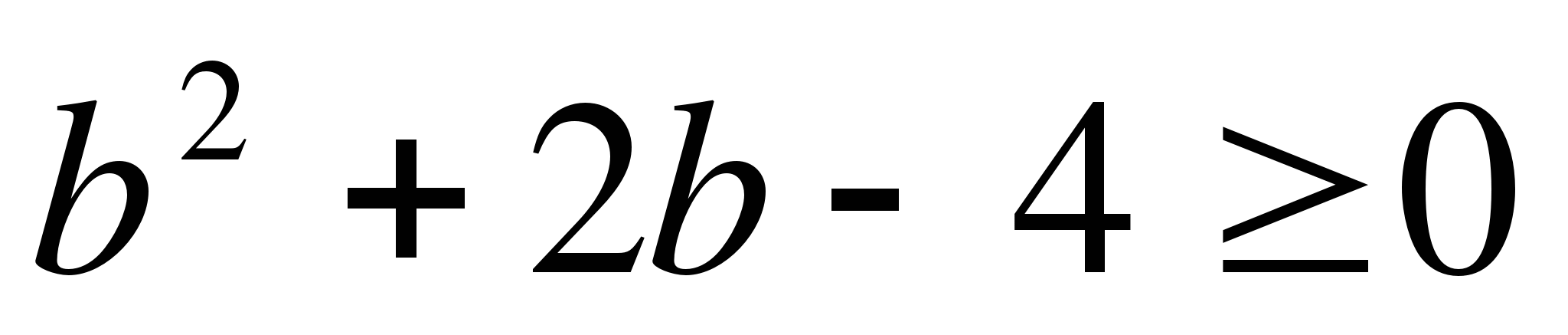 , т.
е. при
, т.
е. при 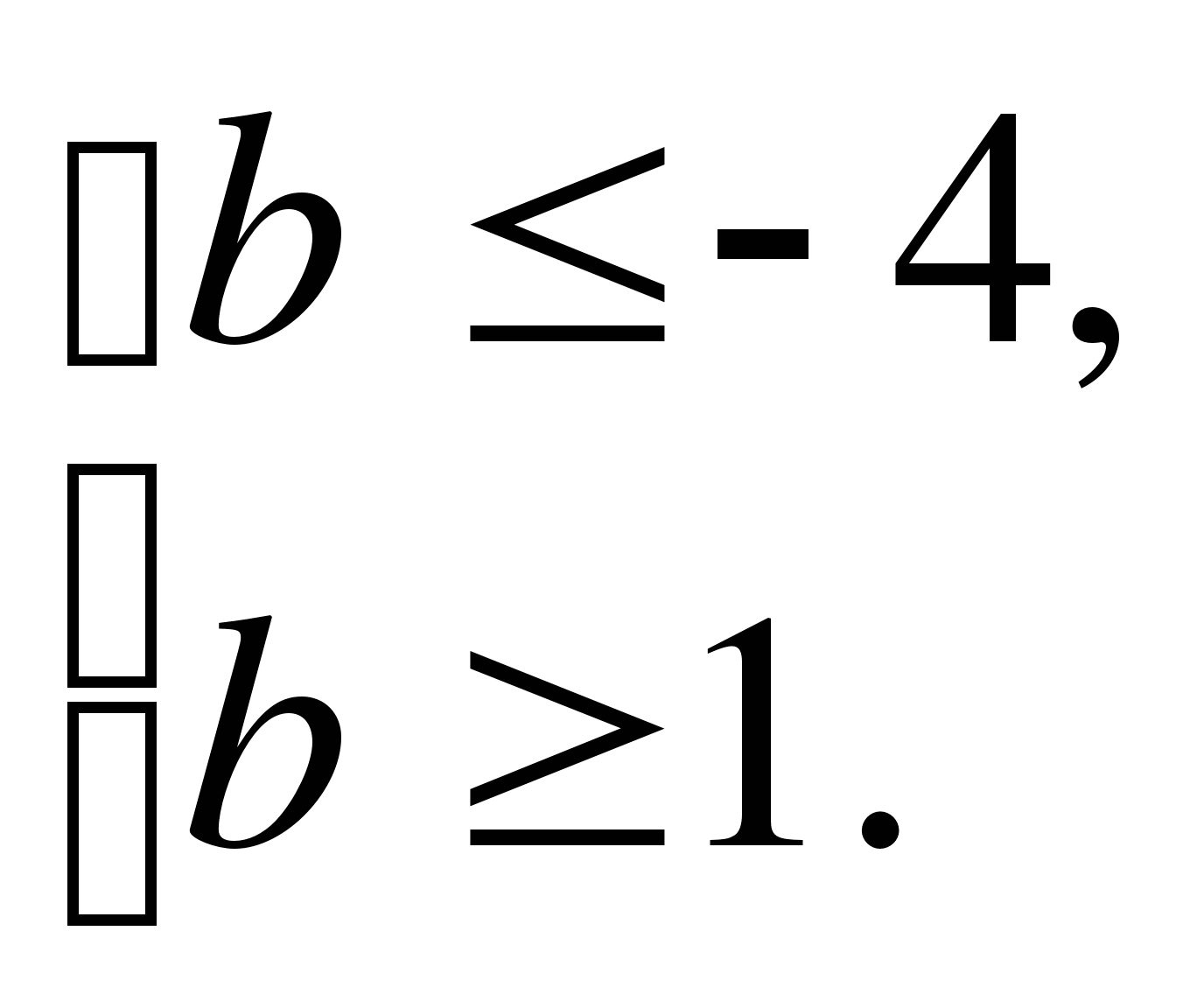 Теперь проверим, нет ли таких b при которых
либо
Теперь проверим, нет ли таких b при которых
либо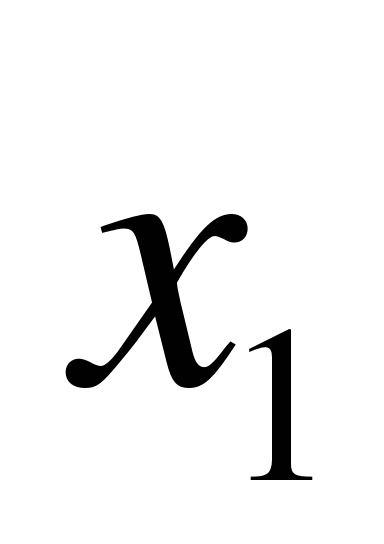 ,
либо
,
либо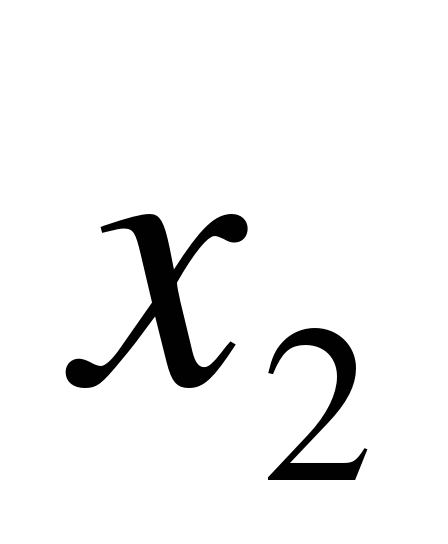 равен 2. Это легче определить по уравнению (1), подставив x =
2, при этом получим b = -8.
равен 2. Это легче определить по уравнению (1), подставив x =
2, при этом получим b = -8.
Второй корень в таком случае равен
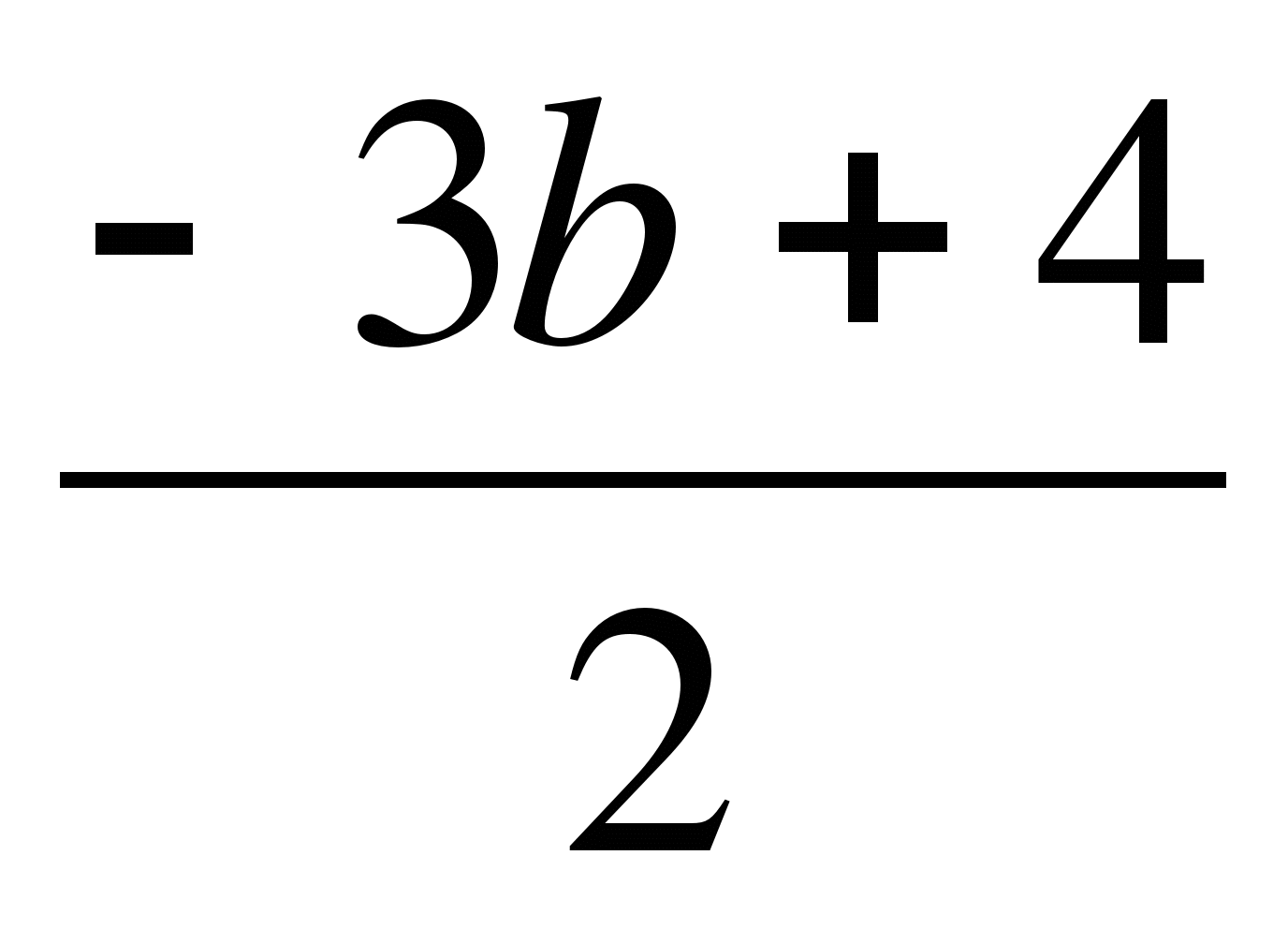 (по
теореме Виета) и при b = -8 равен 14.
(по
теореме Виета) и при b = -8 равен 14.
Ответ: при b = -8 единственный корень x = 14; при b
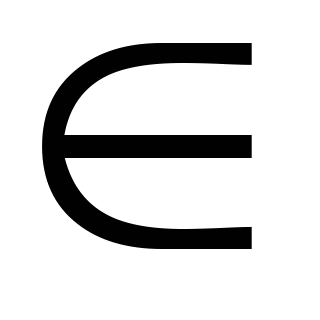 (-∞;-8)
(-∞;-8) (-8;-4)
(-8;-4)  (1;+∞)-
два корня
(1;+∞)-
два корня 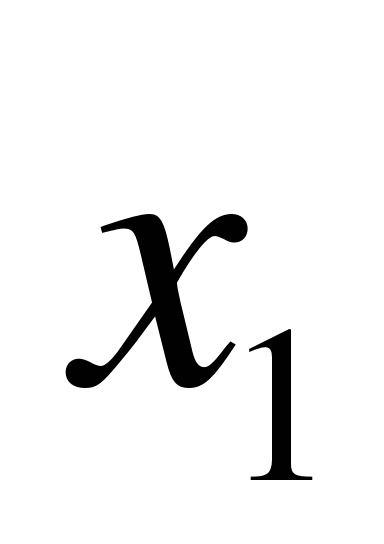 ,
,
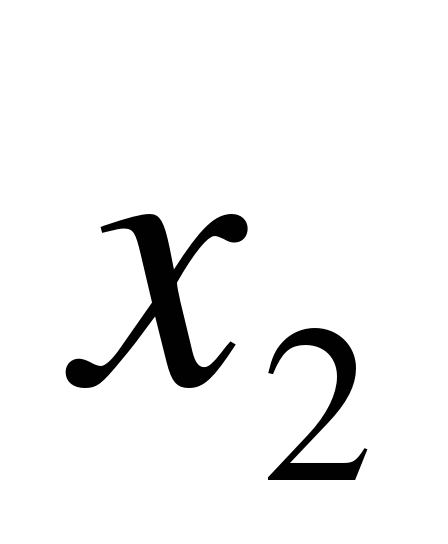 ;
при b=
;
при b=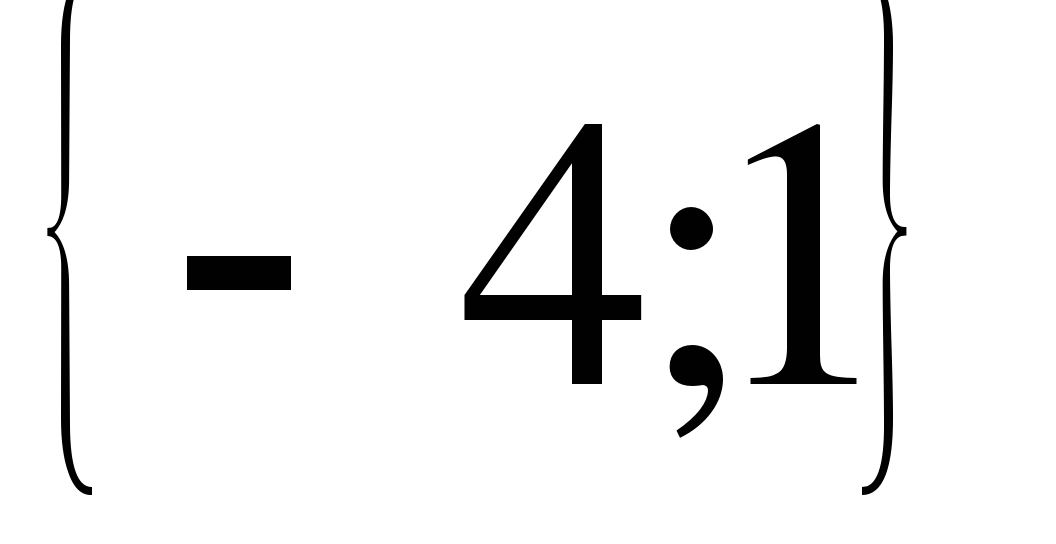 единственное решение x=
единственное решение x=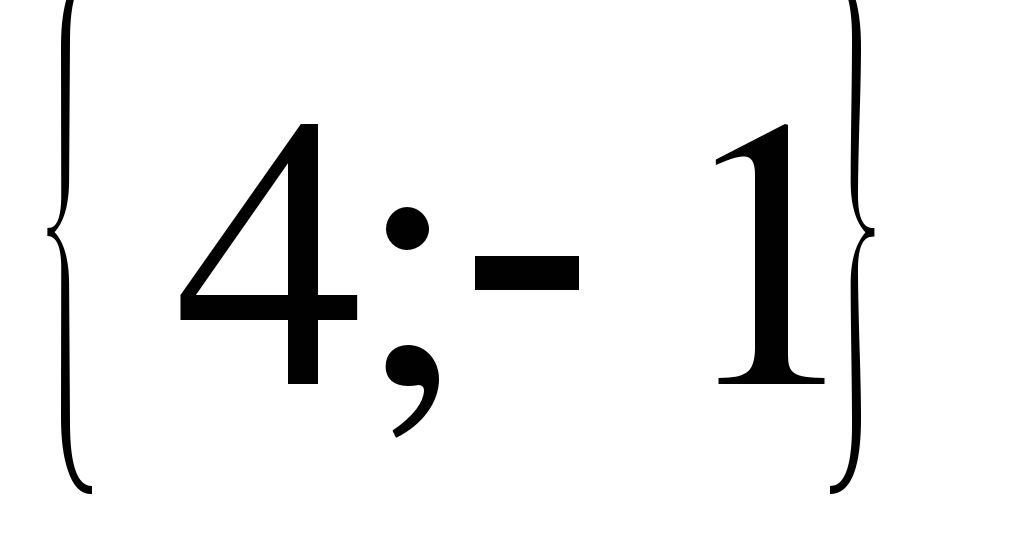 ;
при b
;
при b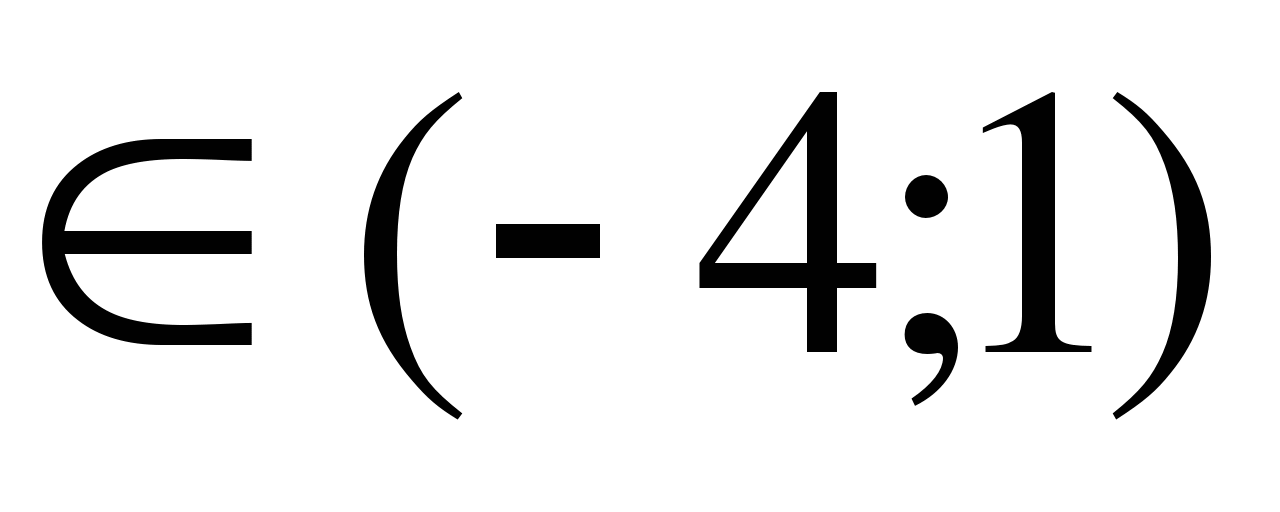 корней нет.
корней нет.
III. Итоги занятия.
Занятие 6.
Цель: способствовать выработке навыков решения заданий с параметрами.
Ход занятия.
I. Самостоятельное решение примеров в группах по выбору учащихся.
Решите уравнения.
1.
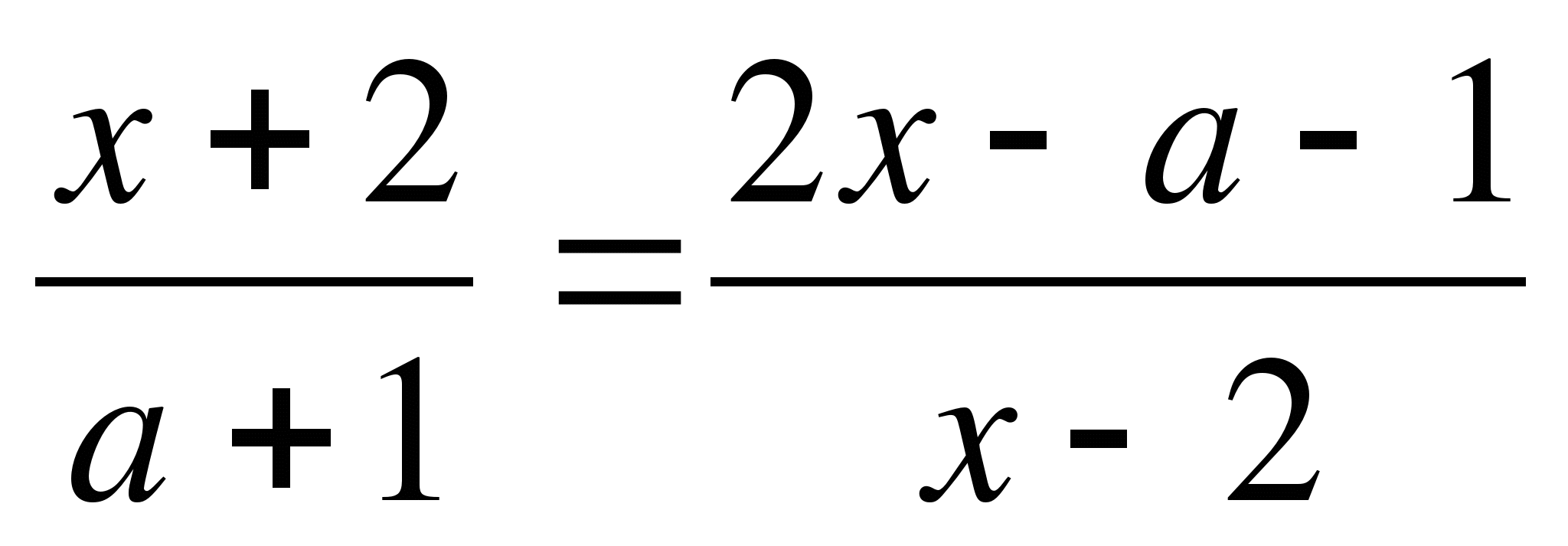 .
Ответ: при a≠3,a≠-1
.
Ответ: при a≠3,a≠-1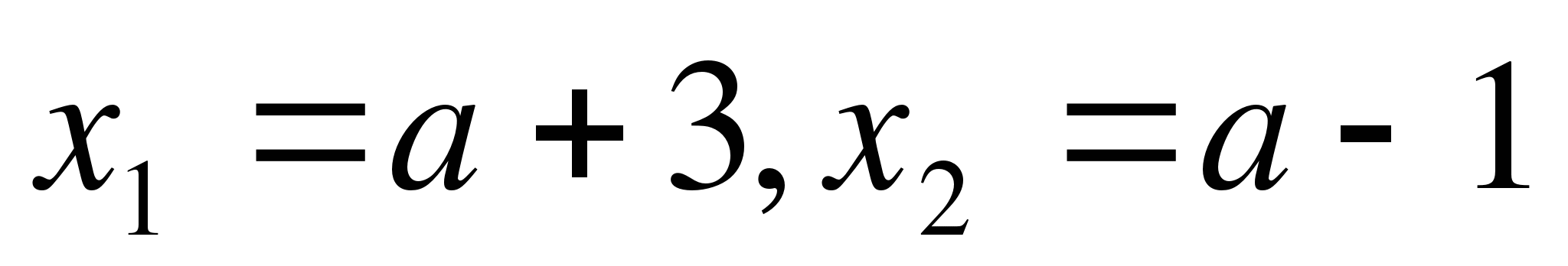 ;
при a=3 x=6; при a=-1
;
при a=3 x=6; при a=-1
корней нет.
2.
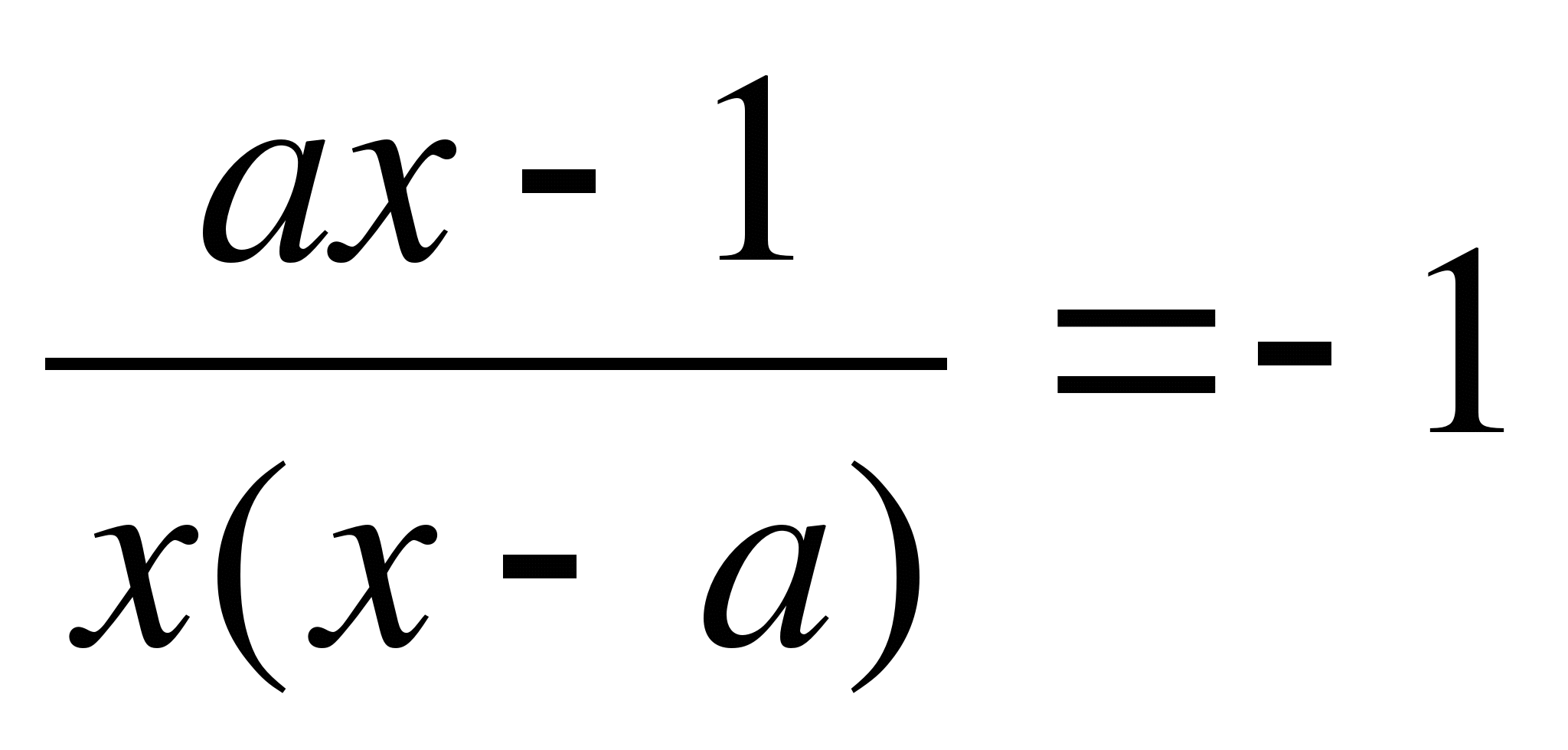 .
Ответ: при
.
Ответ: при 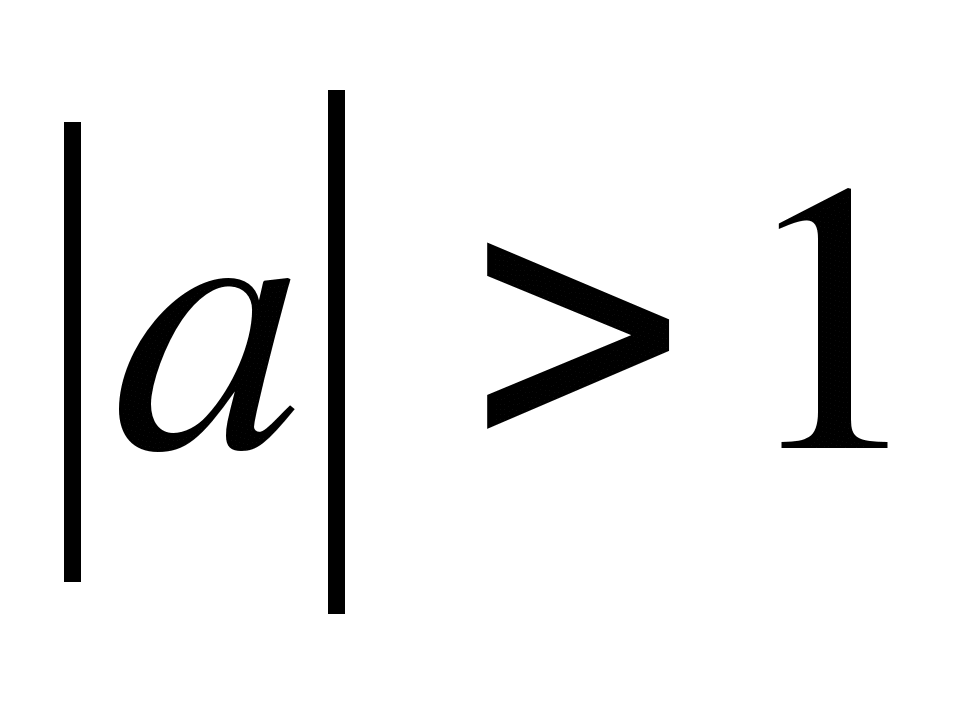
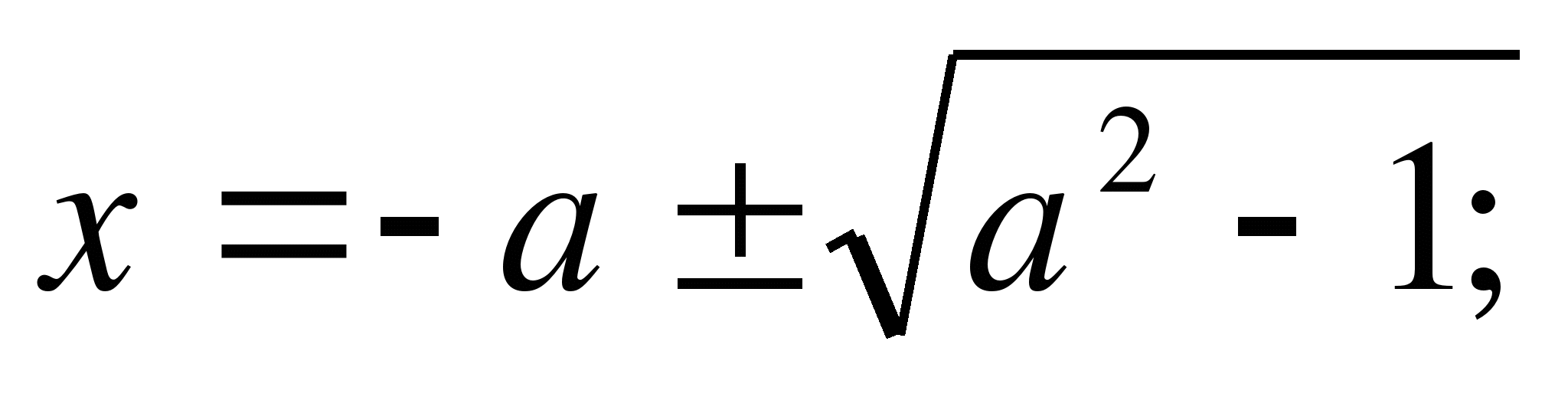 при
при
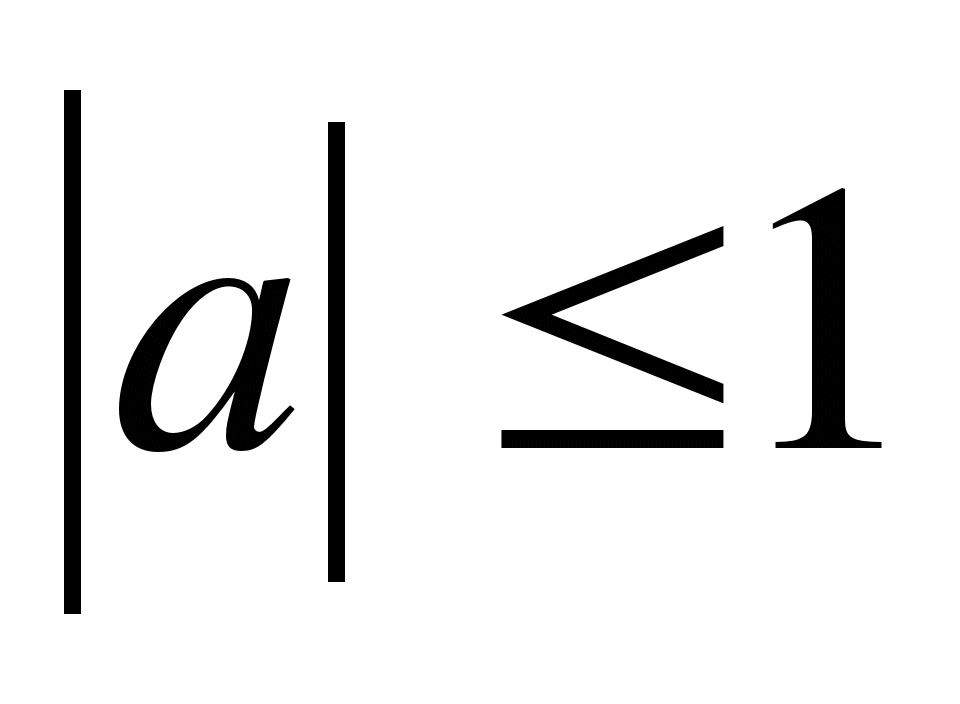 корней нет.
корней нет.
3.
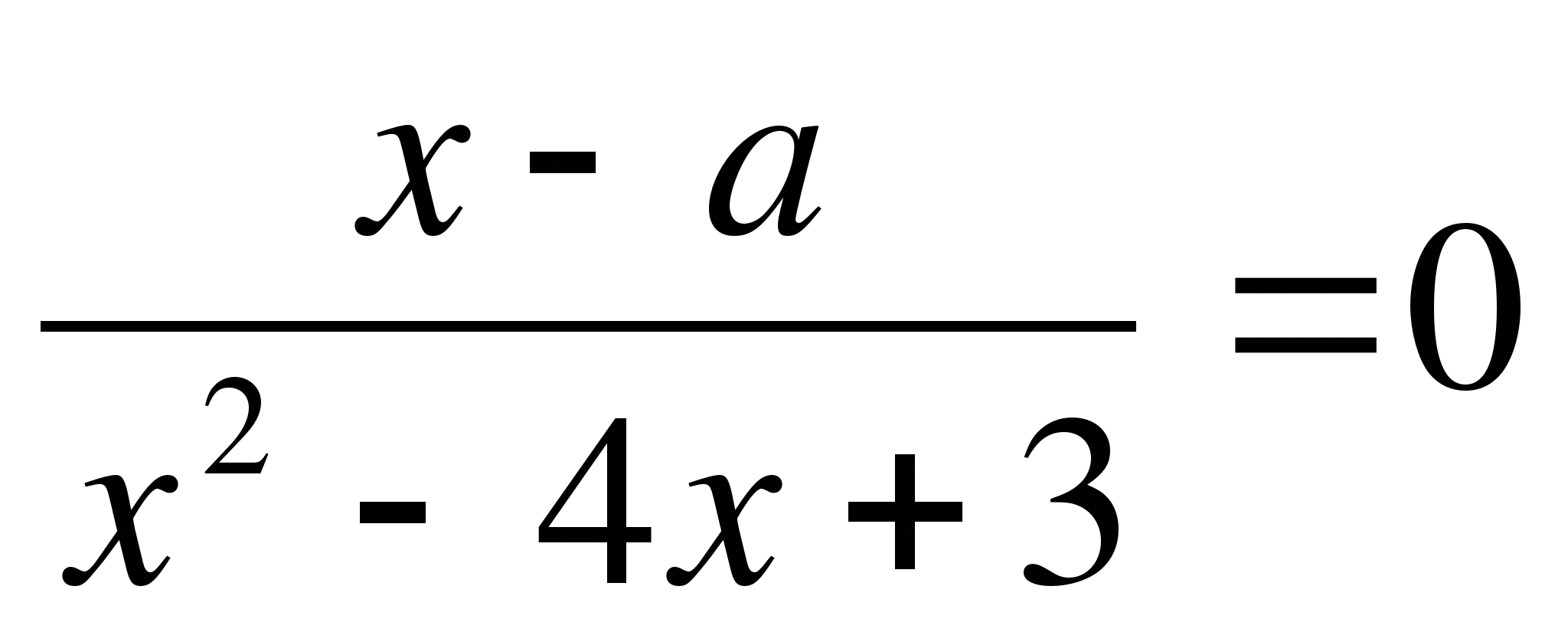 .
Ответ: если а=1 или а=3, то решений нет; если
а ≠1и а ≠3, то х =а.
.
Ответ: если а=1 или а=3, то решений нет; если
а ≠1и а ≠3, то х =а.
4.
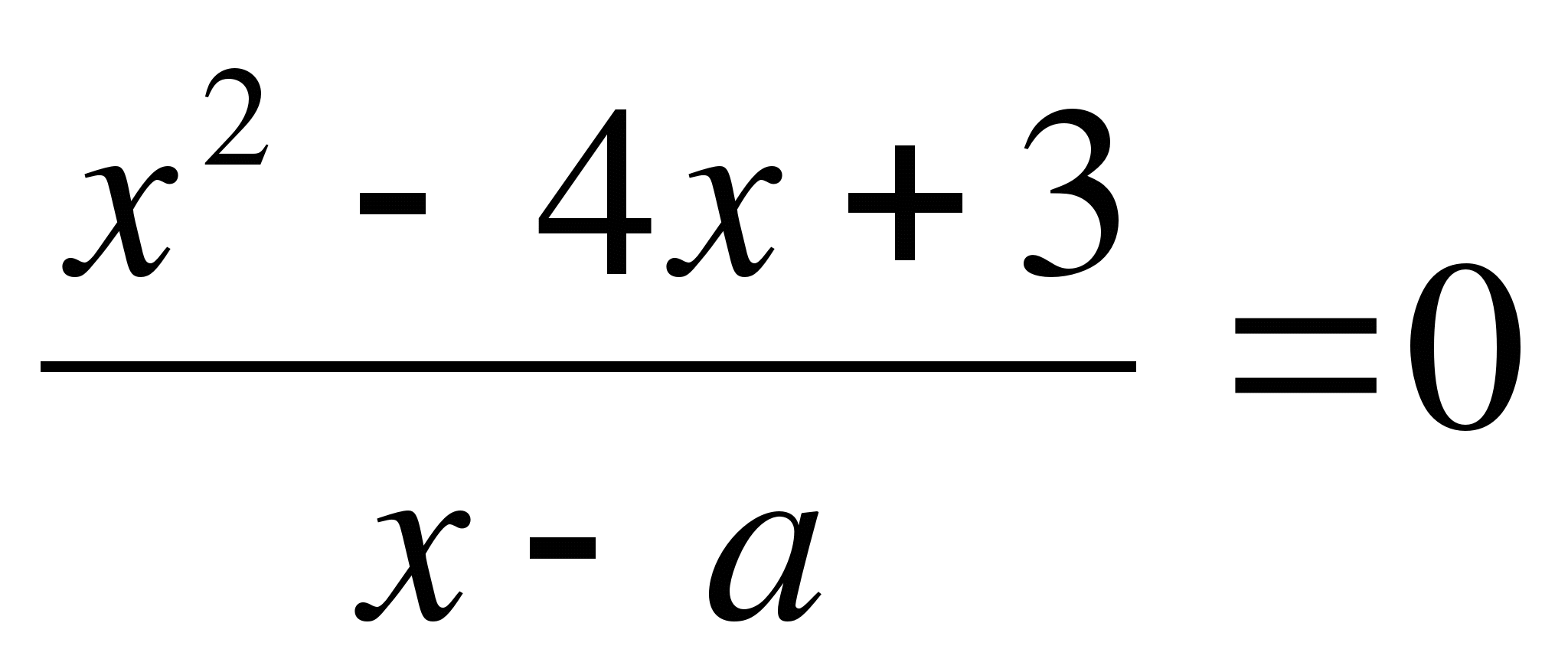 .
Ответ: если а = 1, то х = 3; если а =3, то х=1;
если а≠1 и а≠3, то
.
Ответ: если а = 1, то х = 3; если а =3, то х=1;
если а≠1 и а≠3, то
х=1или х=3.
5.
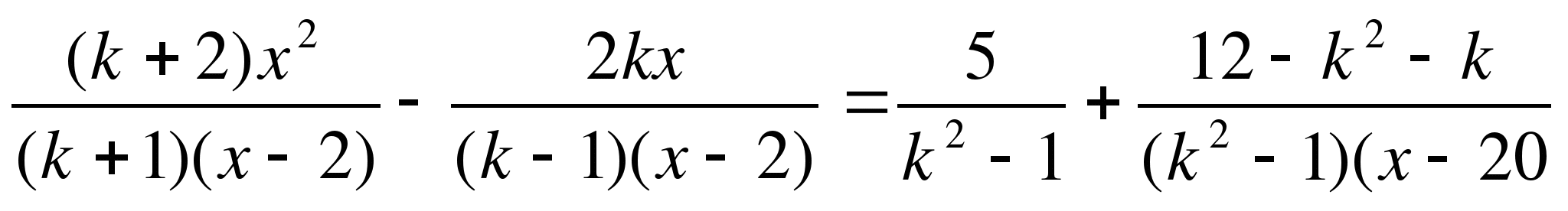 .
.
Ответ: при k≠±1, k=4, k≠-5
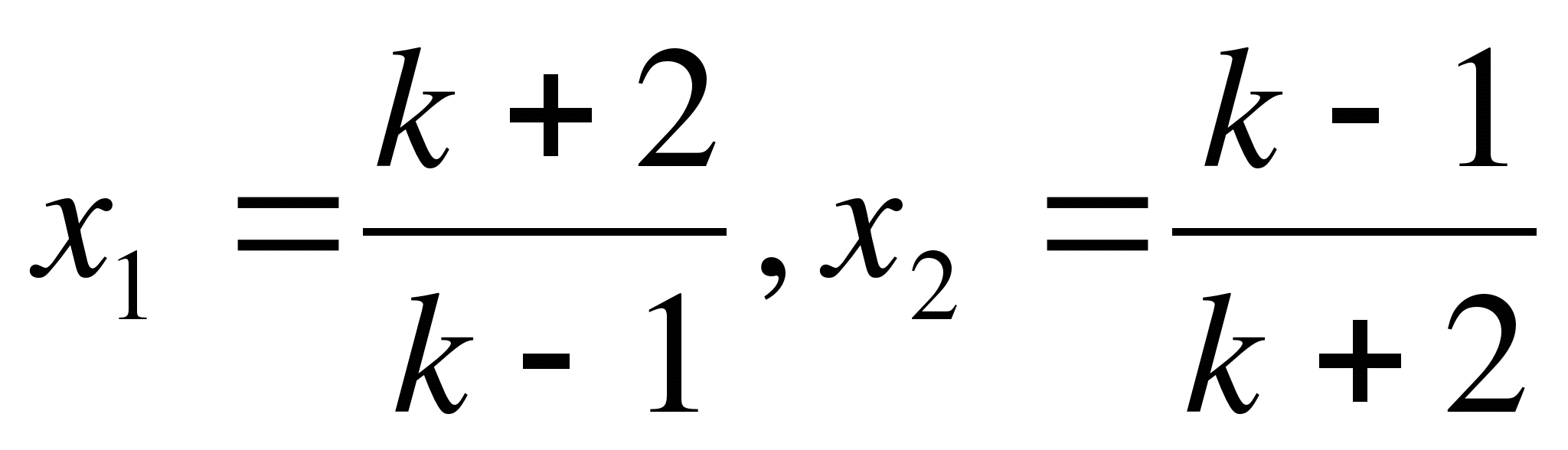 ;
при k=-2 x=0; при
;
при k=-2 x=0; при
k=4 и k=-5 x=0,5; при k=±1 корней нет.
Учитель оценивает работу каждой группы, дает пояснение по выполненным заданиям.
II. Итоги занятия.
Занятие 7.
Ход занятия.
I. Устная работа:
1. Дано изображение графика функции у = ах² +bх +с
Определите знаки коэффициентов а, в, с


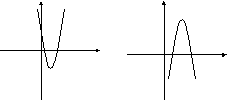
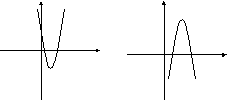
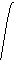
 1) y
2) y 3) y
1) y
2) y 3) y
x x x
4
 )
5) 6)
)
5) 6)


 y y
y
y y
y

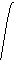
 x
x
 x
x
x
x
Ответы: 1) a>0, b>0, c>0; 2) a<0, b>0, c<0; 3)a<0, b>0, c>0; 4)a>0, b<0, c>0;
5) a>0, b>0, c=0; 6) a<0, b<0, c<0.
2. Найдите все значения а, при которых квадратное уравнение:
а) 3х² - 2х + а =0,
б) (2а - 1)х² + 2х -1=0,
в) ах² - 3х -1=0,
г) ах² - (2а -1)х + а + 2 =0
имеет два различных действительных корня.
Ответы:
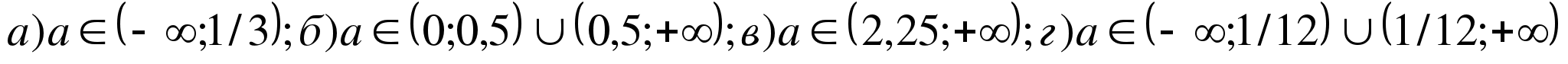 .
.
3. Найдите все значения а, при которых квадратное уравнение не имеет действительных корней:
а) х² - 4х + а =0, б) 5х² - 6ах + 1 =0,
в) (1- а)х² + 4х-3=0, г) (3а -5)х²- (6а -2)х+3а-2=0.
Ответы:
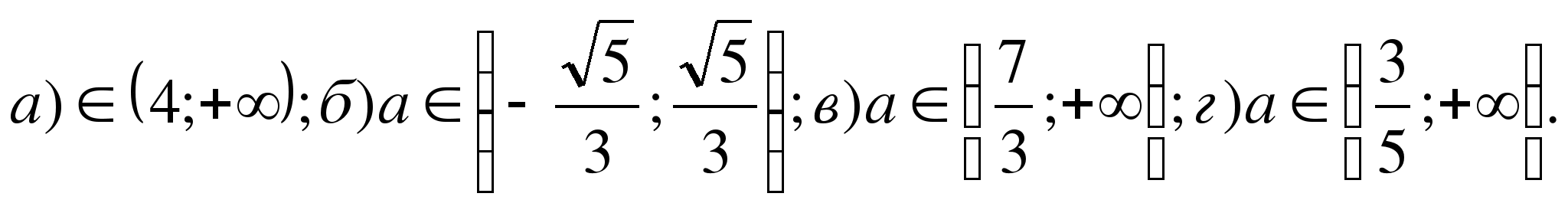
4. Найдите все значения а, при которых квадратное уравнение имеет действительные корни:
а) х² - 4х + а =0, б) ах²- 9х -2 =0,
в) (1- а)х² + 4х - 3=0, г)(а -1)х²-(2а +3)х+а+5=0.
Ответы:
ΙΙ. Фронтальная работа.
Задание 1.
-
При каких значениях а уравнение (а- 2)х² + (4 - 2а)х + 3 = 0 имеет единственный корень ?
Решение: (а - 2)х² + (4 - 2а)х + 3 = 0;
1) а - 2 = 0, а = 2, (2 - 2)х² + (4 - 2 · 2)х + 3 = 0,
0х = -3, корней нет.
2)D=0, а ≠ 2.
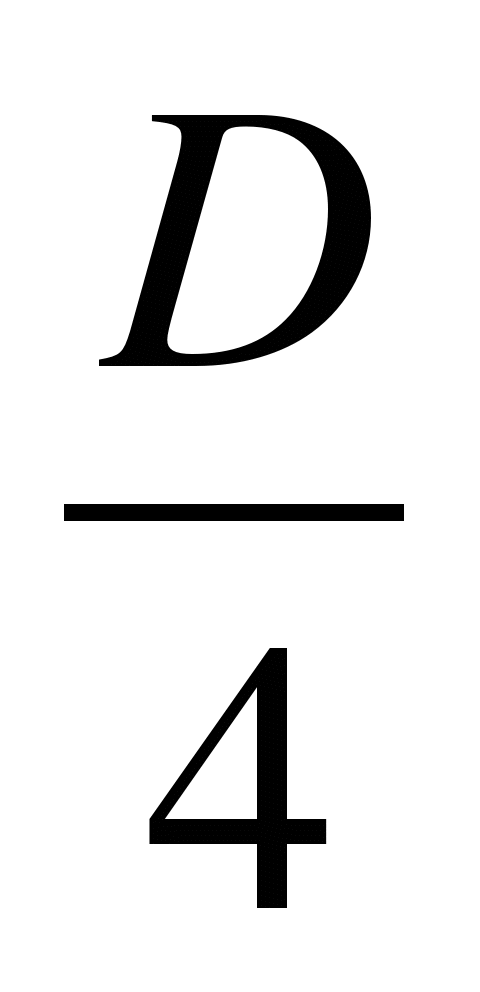 =
(2 - а)² - 3(а -2)= 4-4а + а² -
3а -6 = а²-7а +10,
=
(2 - а)² - 3(а -2)= 4-4а + а² -
3а -6 = а²-7а +10,
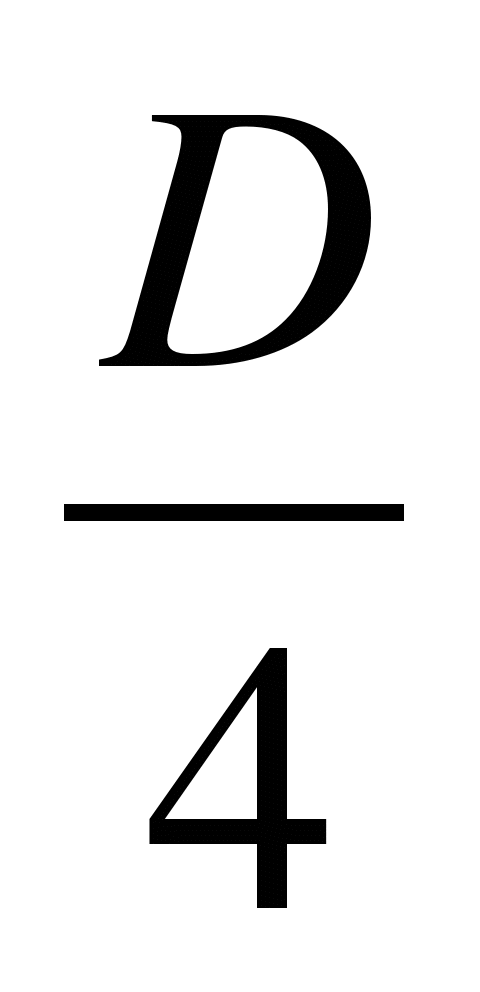 =
0- а²- 7а + 10 =0;
=
0- а²- 7а + 10 =0; 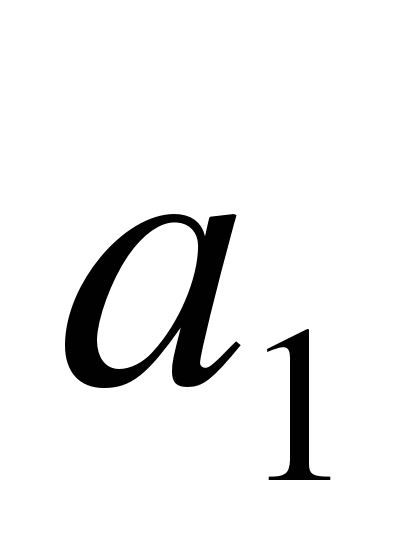 =
5,
=
5,  =
2.
=
2.
Ответ: при а=5 уравнение имеет единственный корень.
Задание 2. При каких значениях а уравнение х² + 2(а+1)х + 9а -5=0
имеет 2 различных отрицательных корня.
Решение:
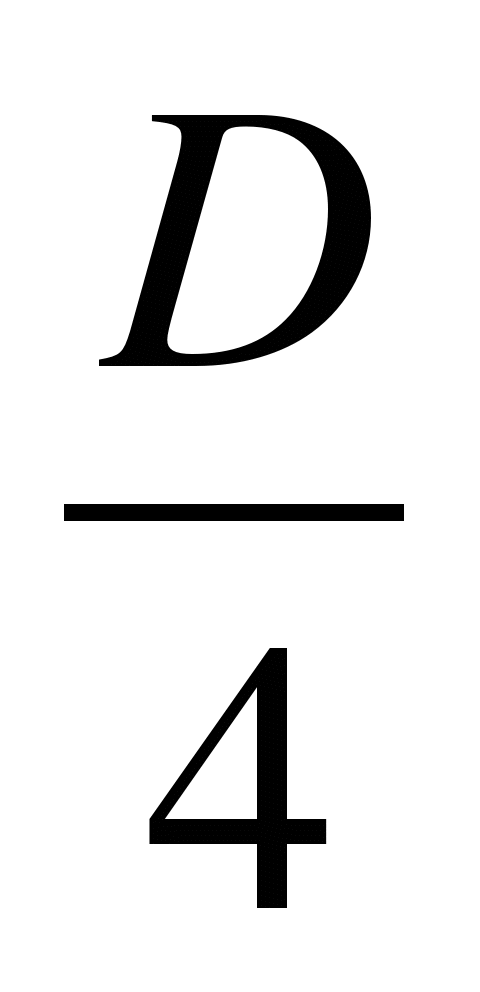 =
(а + 1)² - 9а + 5 = а² -7а +6,
=
(а + 1)² - 9а + 5 = а² -7а +6,
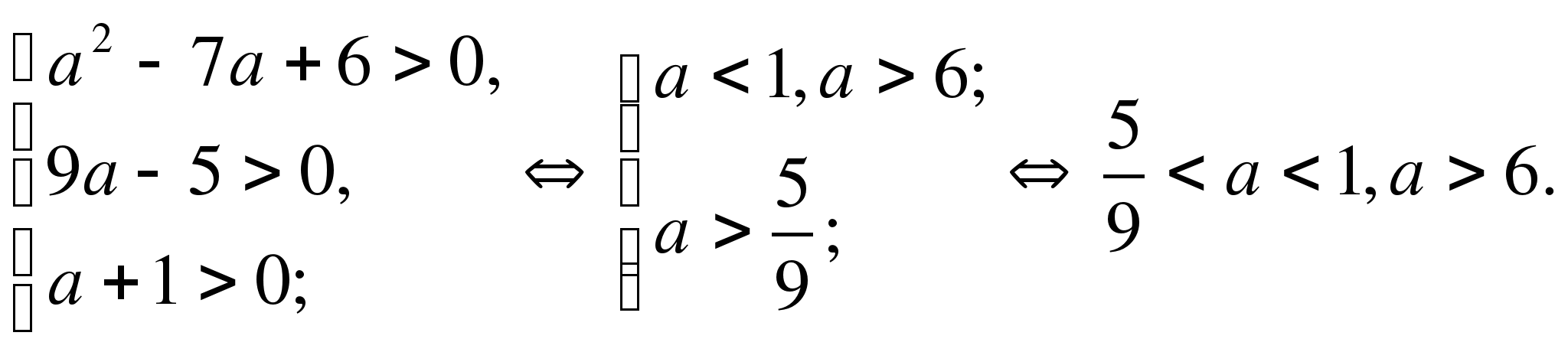
Ответ: при
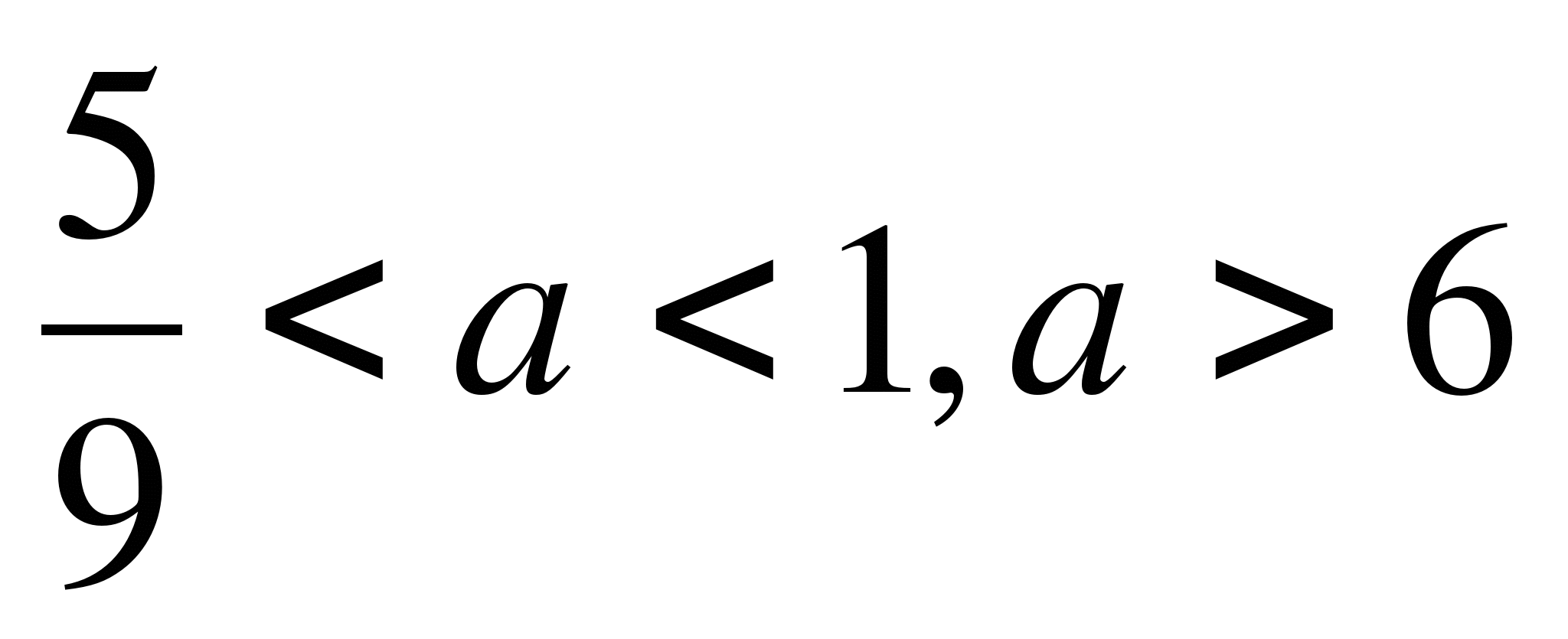 уравнение
имеет два отрицательных корня.
уравнение
имеет два отрицательных корня.
1
График квадратного трехчлена у = ах² +(а-3)х + а лежит выше оси абсцисс, если а принадлежит промежутку
1) (1; ∞)
2) (-3;10);
3) (-∞;-3) U (1; ∞)
4) (0; ∞)
5) (-3; 0)
2
Уравнение ах²+3х+а-4=0 имеет два различных корня, если а удовлетворяют условию:
1) а є (4,5; ∞)
2) а є (-0,5; ∞)
3) а є (-∞; 4,5)
4) а є (-0,5; 4,5)
5) а є (-∞; ∞)
3
Корни квадратного уравнения (а-1)х²+ах+1=0 отрицательны, если а принадлежит промежутку:
1) (1; 2) U (2; ∞)
2) (1; ∞)
3) [1; 2]
4) [2; ∞]
5) [1; 2) U (2; ∞)
4
Квадратное уравнение ах² +(а-3)х+а=0 имеет один корень, если а принадлежит промежутку :
1) (-3; 3]
2) (-∞; 3]
3) (0;1]
4) (-3;0)
5) (1;3)
5
Меньший корень квадратного уравнения х²+4ах+4а²-4=0 удовлетворяет условию х < 3 при значениях а:
1) а>-0,5
2) а>-0,4
3) а>-2,5
4) а<2,5
5) а<0,5
6
Сумма целых значений а, при которых уравнение (а - 6)х²-2 =2ах +1 не имеет решение, равна
1)-12; 2)-18; 3)-9; 4)-15; 5)-20.
Ключ ответов:
-
Занятие8. Итоговое занятие.
Тест самопроверки по теме «Исследование квадратного трехчлена и решение квадратных уравнений».
Дополнительные задания.
1. Решите уравнение a² + 4ax - 5x
 =
0.
=
0.
Ответ. Если a<0, x=a, x =-
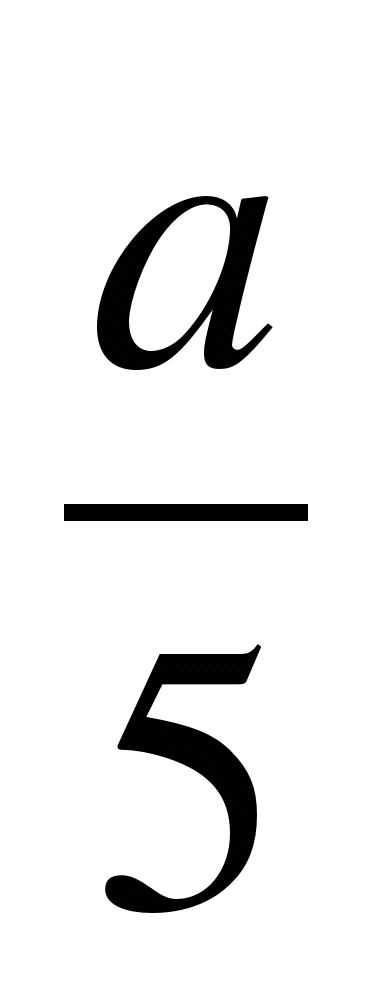 ;
если a=0, то x=0; если а>0, то x= -
;
если a=0, то x=0; если а>0, то x= -
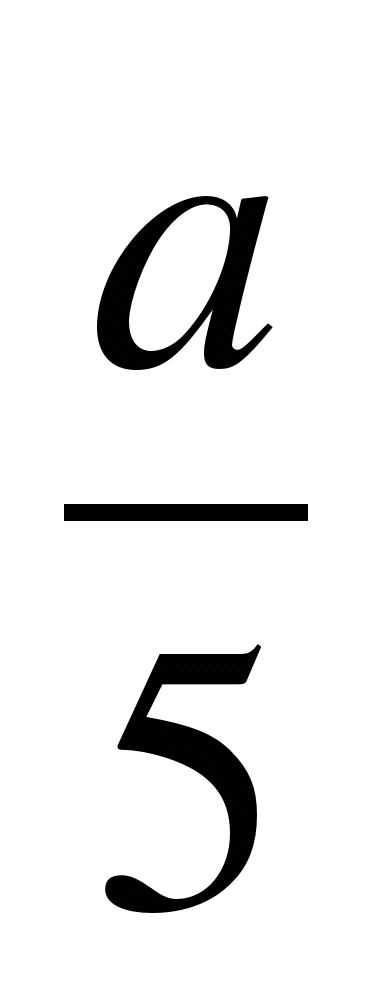 ,
x=a.
,
x=a.
Указание.
Разложить левую часть уравнения на множители и заменить уравнение равносильным: (x +
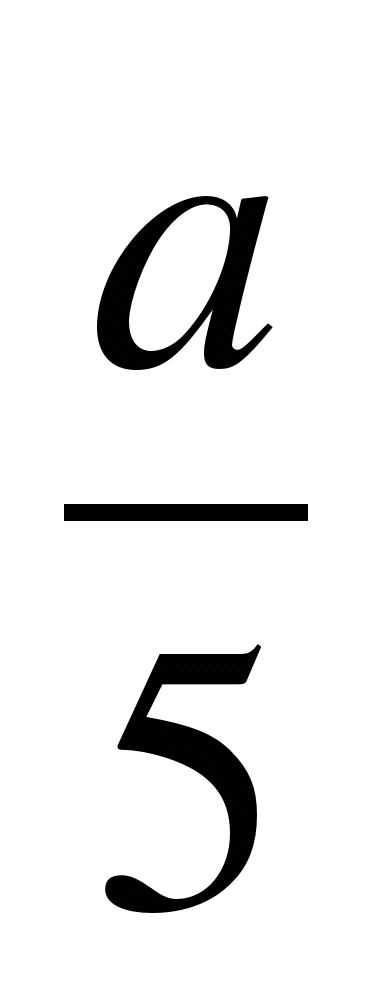 )
(x - a) = 0.
)
(x - a) = 0.
2. Найти все значения параметра а, при которых корни уравнения
x² - 6x + a = 0 удовлетворяют условию x² = x.
Ответ: a = -27, а = 8.
3. При каких значениях а все корни уравнения
3аx² + (3а³ - 12a
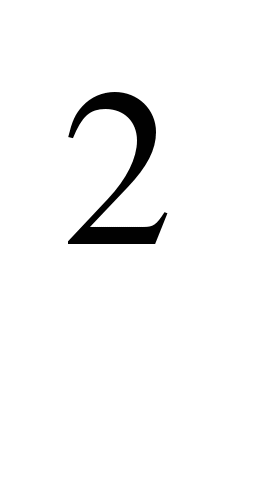 -1)
x - a (а - 4) = 0
-1)
x - a (а - 4) = 0
удовлетворяют условию |x| < 1?
Ответ: 0,2 +
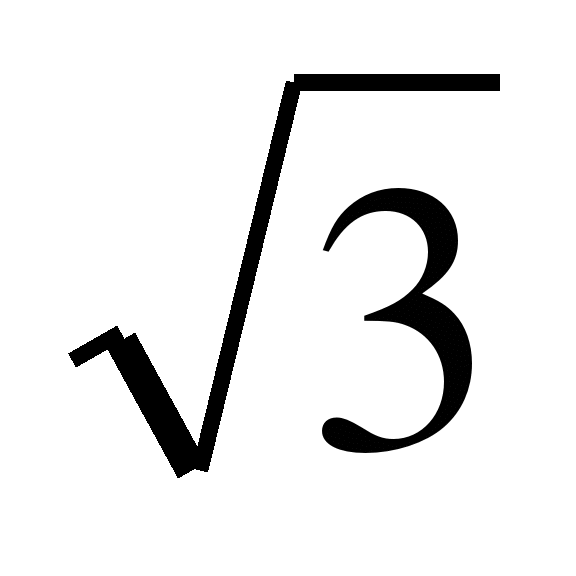 < а < 2 +
< а < 2 +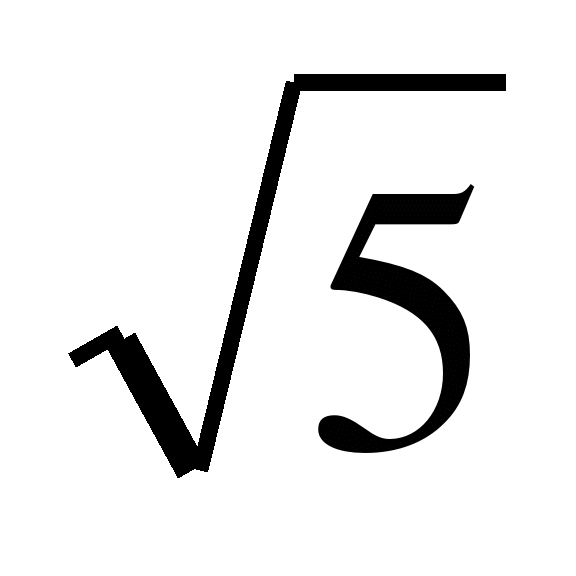 .
.
Указание:
Рассмотреть два случая: а = 0 и а ≠ 0. Во втором случае - уравнение квадратное и имеет корни x =
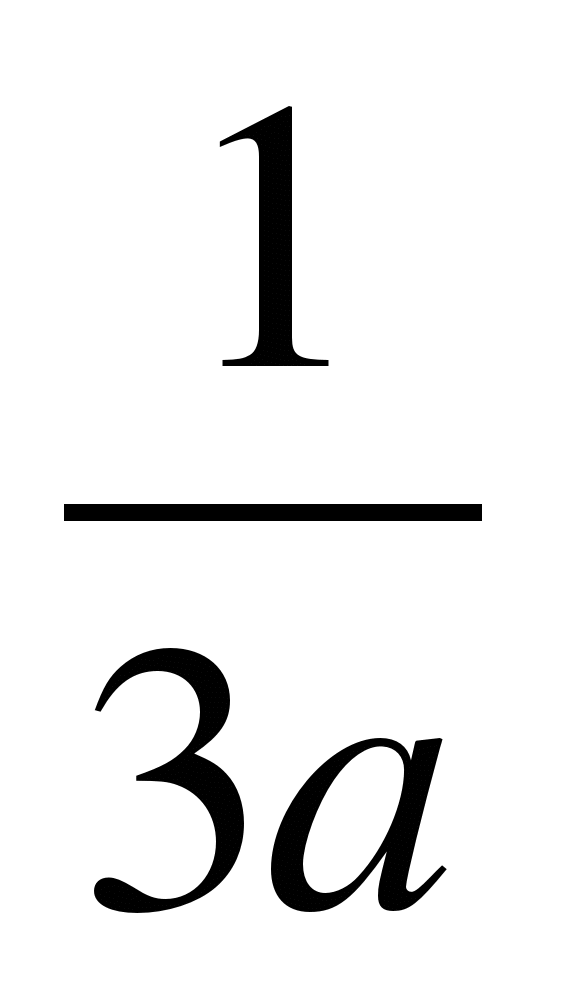 и x = - а² +4.
и x = - а² +4.
Приложение2.
СХЕМА.

Квадратные уравнения, приводимые к виду
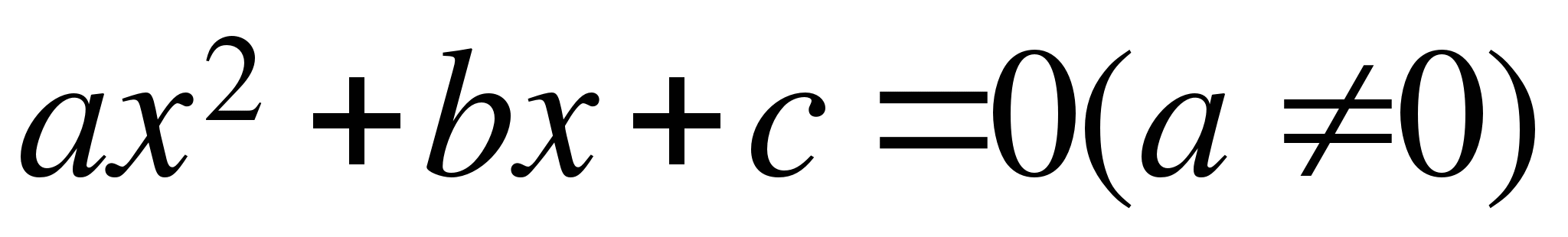



D < 0
D = 0
D > 0

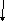
Корней нет
(рис.1,2).
Два одинаковых корня
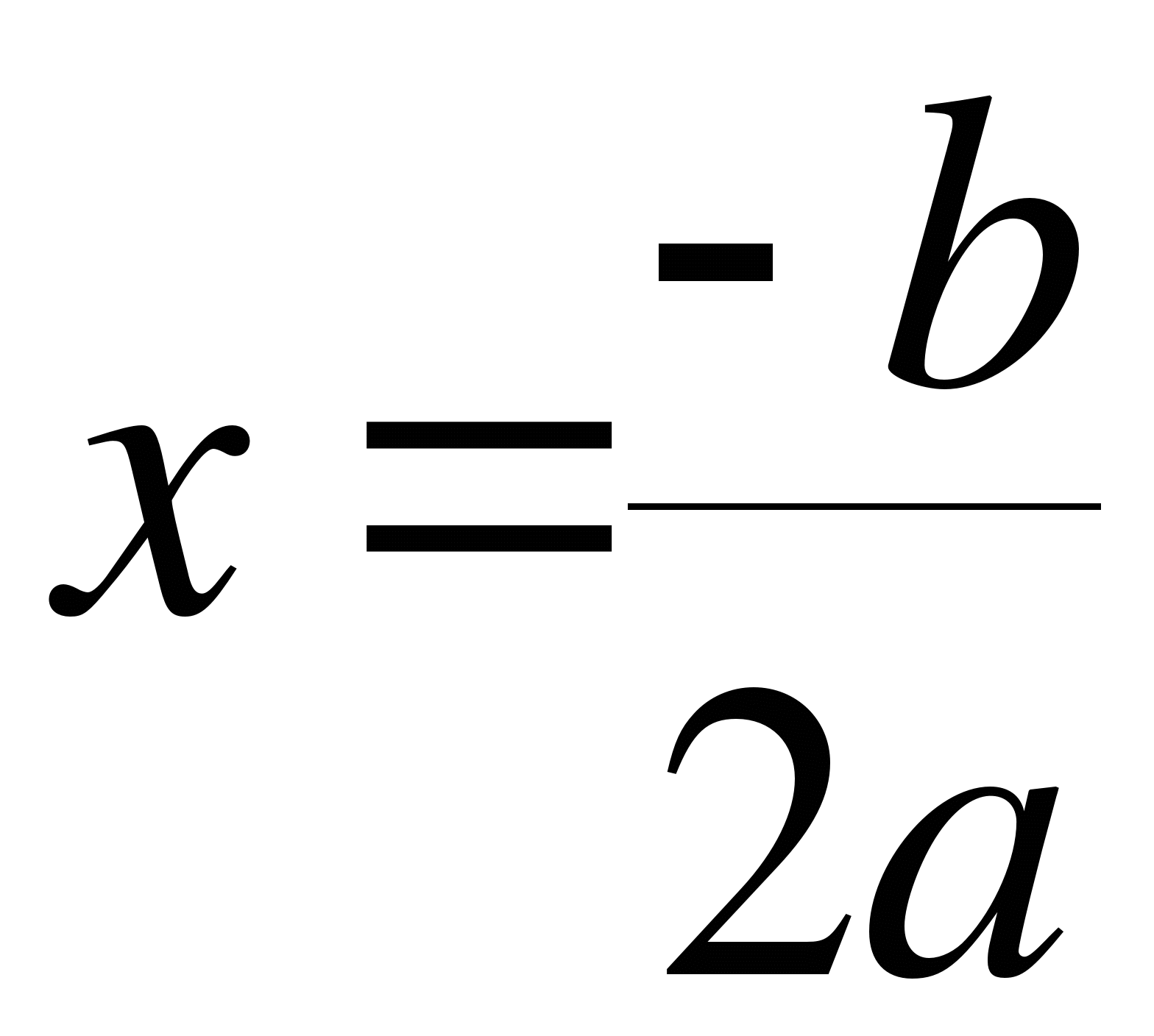
(рис.3,4).
Два различных корня
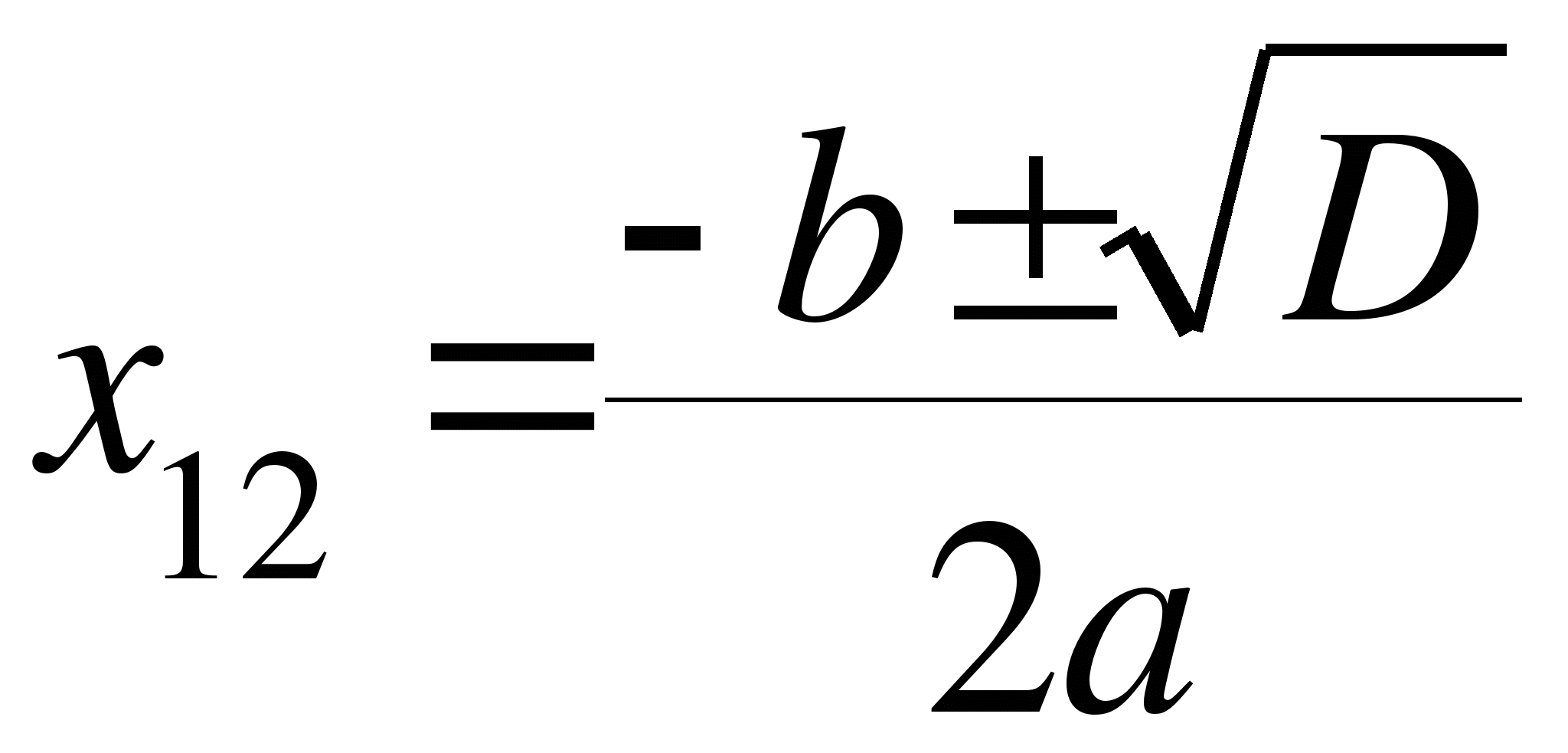
(рис.5,6).
Рис. 1 Рис. 3 Рис. 5
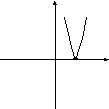
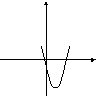 y
y y
y
y y

x x x
Рис. 2 Рис. 4 Рис. 6

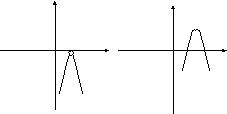

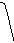 y
y y
y
y y

x x x
Блок IV. Тема 8. Квадратные неравенства с параметром.
Цели занятия:
- научиться решать квадратные неравенства с параметром;
- развивать познавательный интерес в процессе решений и исследований
параметрических квадратных неравенств.
Занятия 1 - 3.
Ход занятия.
I. Этап изучения нового материала.
Неравенства вида ах2 + bх + с>0, ах2 + bх + с < 0,
ax2+bx + c≥0, ax2 + bx + c≤0 (a≠0),
где а, b, с - действительные числа или выражения, зависящие от
параметров, называются квадратными.
Решение квадратных неравенств основано на применении свойств квадратного
трехчлена ах2+bх+с, которые допускают наглядную геометрическую
интерпретацию.
Рассмотрим, например, неравенство ах2 + bх + с>0, (a≠0).
Возможны следующие случаи.
-
Если а > 0 и дискриминант D < 0 (рис.1), то решением
неравенства являются все xЄR.
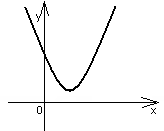
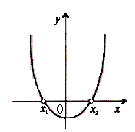
рис.1 рис.2 рис.3
2.Если а > 0 и D = 0 (рис.2), то хЄ(-∞;-b/2а)U(-b/2а;+∞).
З.Если а>0 и D>0 (рис.3), то хЄ(-∞;х1)U(x2;+∞) где х1,х2 - соответственно меньший и больший корни квадратного трехчлена.
4.Если а<0 и D < 0 (рис.4), то хЄØ.
5.Если а < 0 и D = 0 (рис.5), то хЄØ.
6.Если а<0 и D>0 (рис.6), то хЄ(х1;х2), где х1,х2 - соответственно меньший и больший корни квадратного трехчлена.
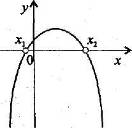
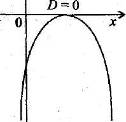
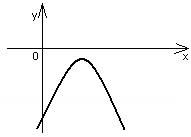
рис.4 рис.5 рис.6
II. Этап усвоения новых знаний, тренировочные упражнения.
Пример 1. Для каждого действительного значения a решить неравенство
a х2 +х+1>0.
Решение.
1) При a=0 неравенство является линейным и имеет решение х>-1.
2) При a≠0 неравенство является квадратным, D=b2-4ac=1-4a.
a) Если D=0, то есть а=1/4, то неравенство принимает вид х2+4х+4 >0, решая которое получим х<-2, x>-2.
б) Если D<0, то есть а>1/4, то неравенство справедливо при х Є R.
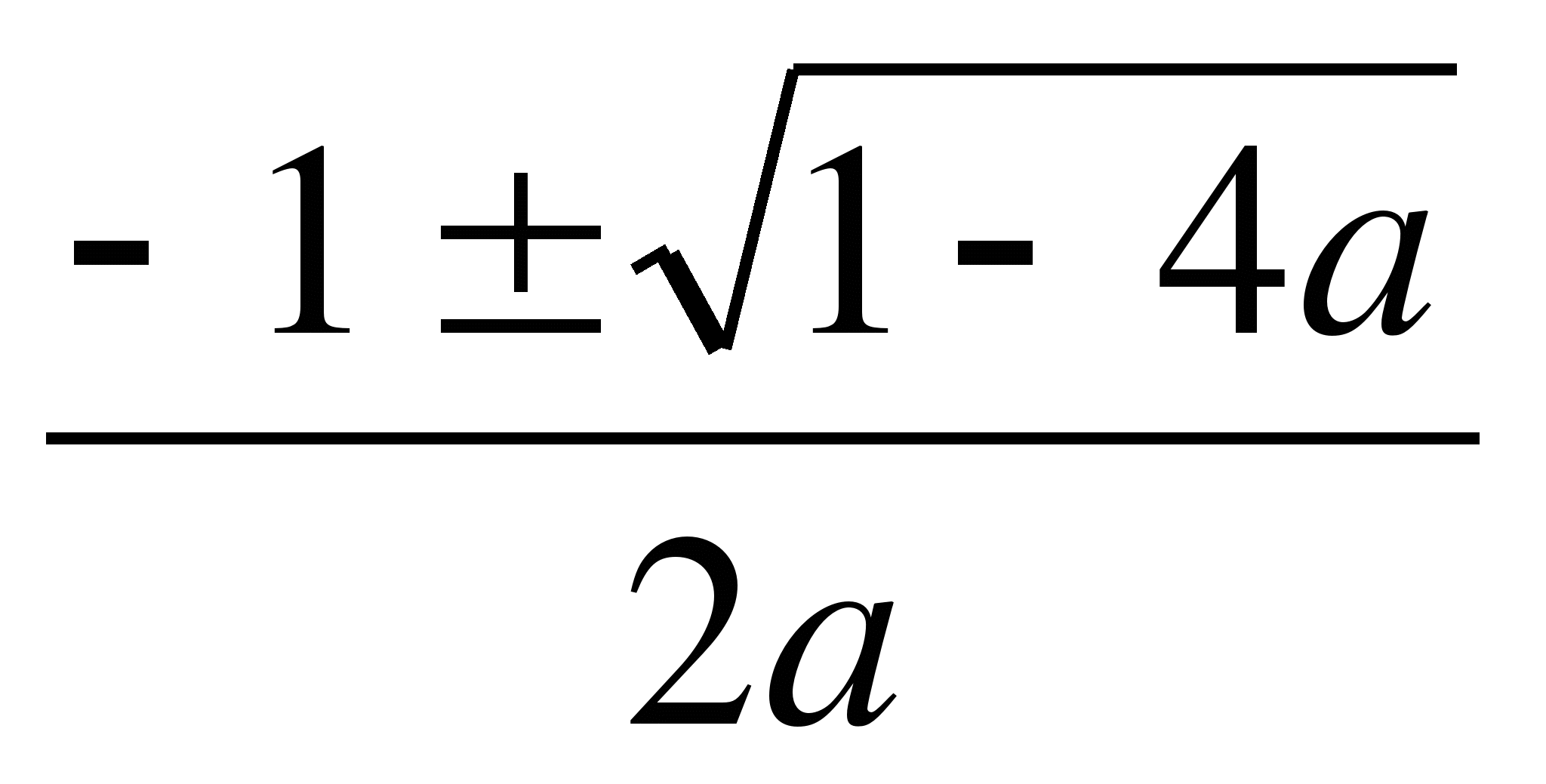
в) Если D>0 и 0<a<1/4, то х1,2=
 .
.
Разложим левую часть исходного неравенства на линейные
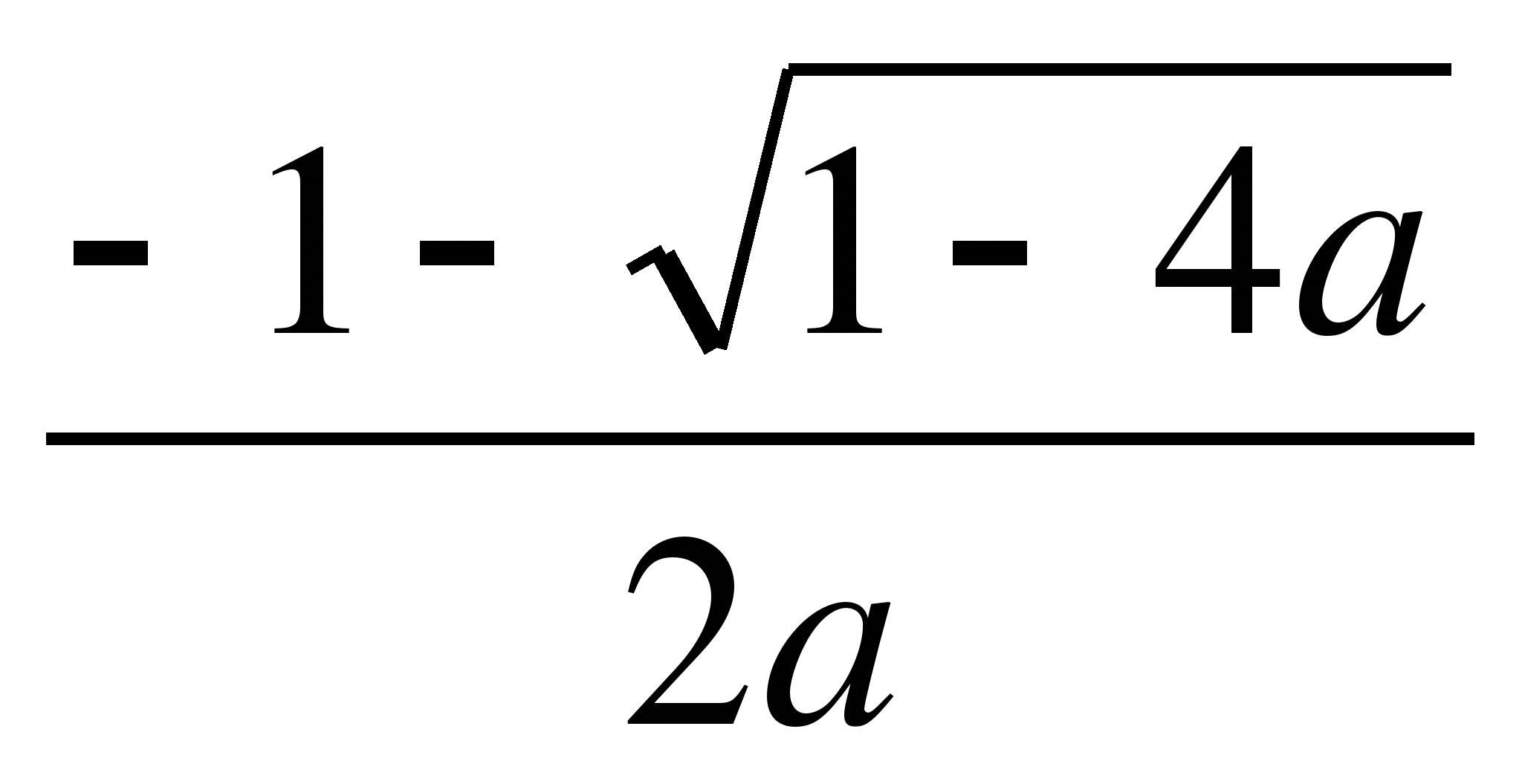
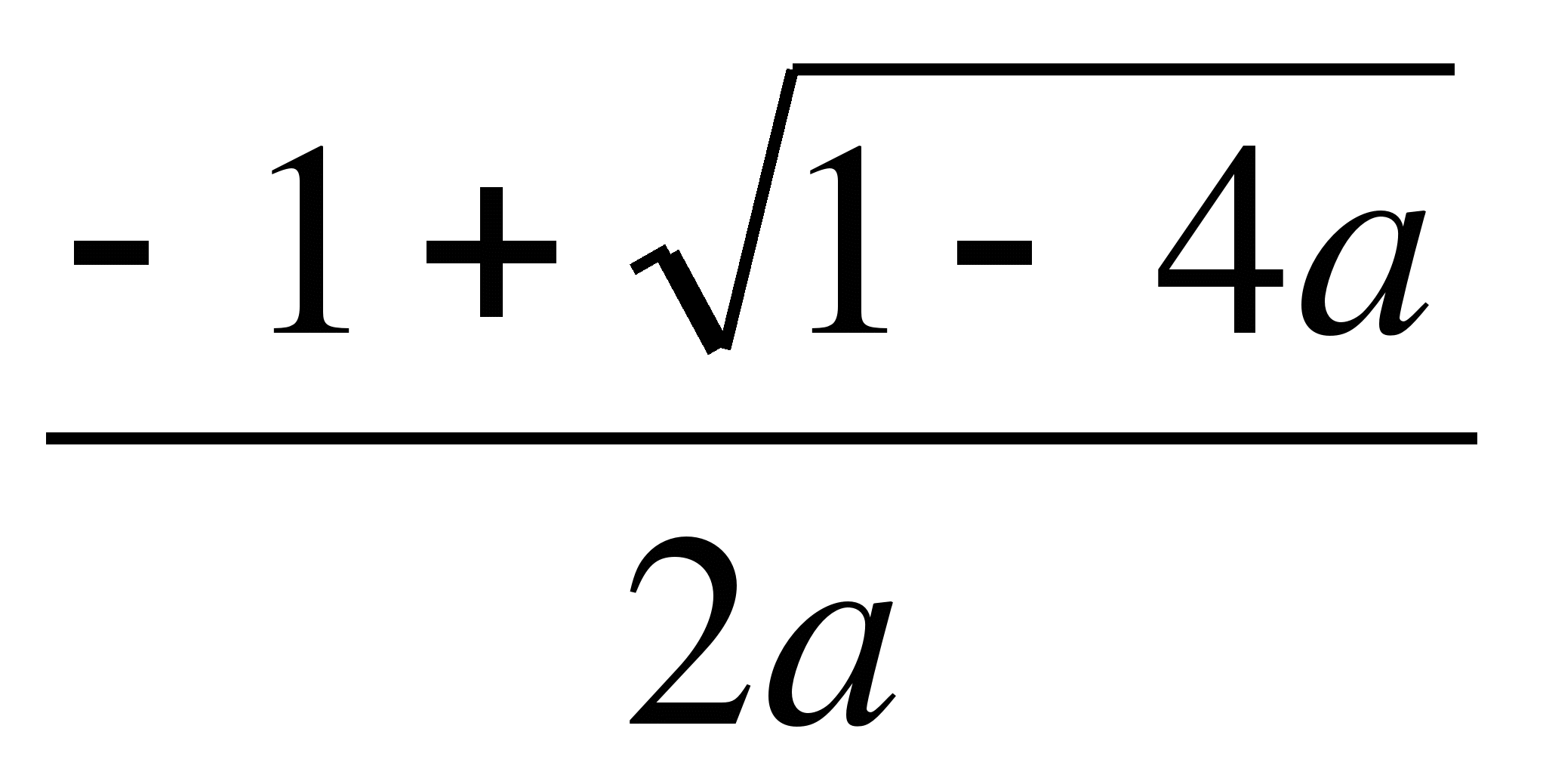
множители а(х- )(х- ) >0. Решив методом интервалов,
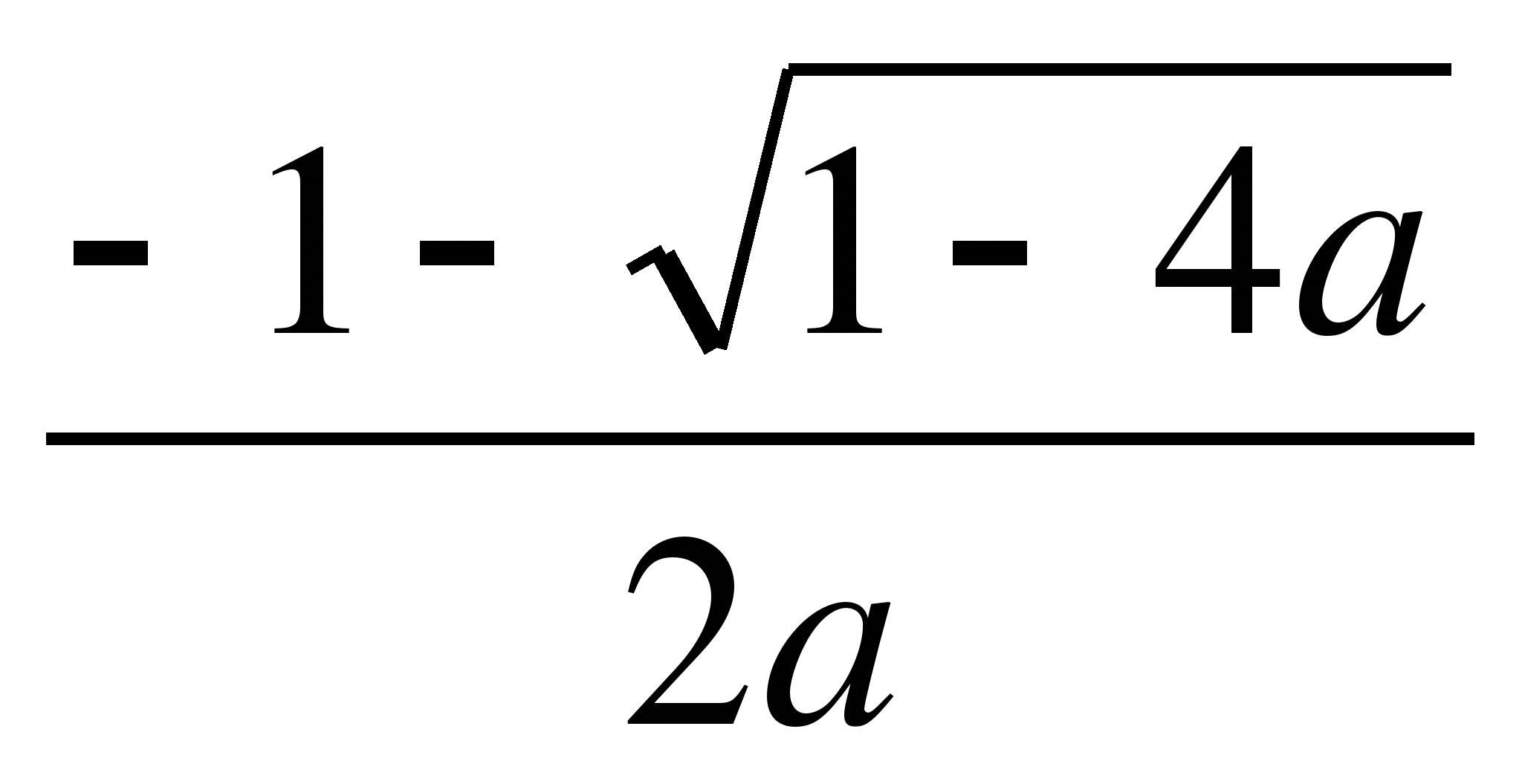
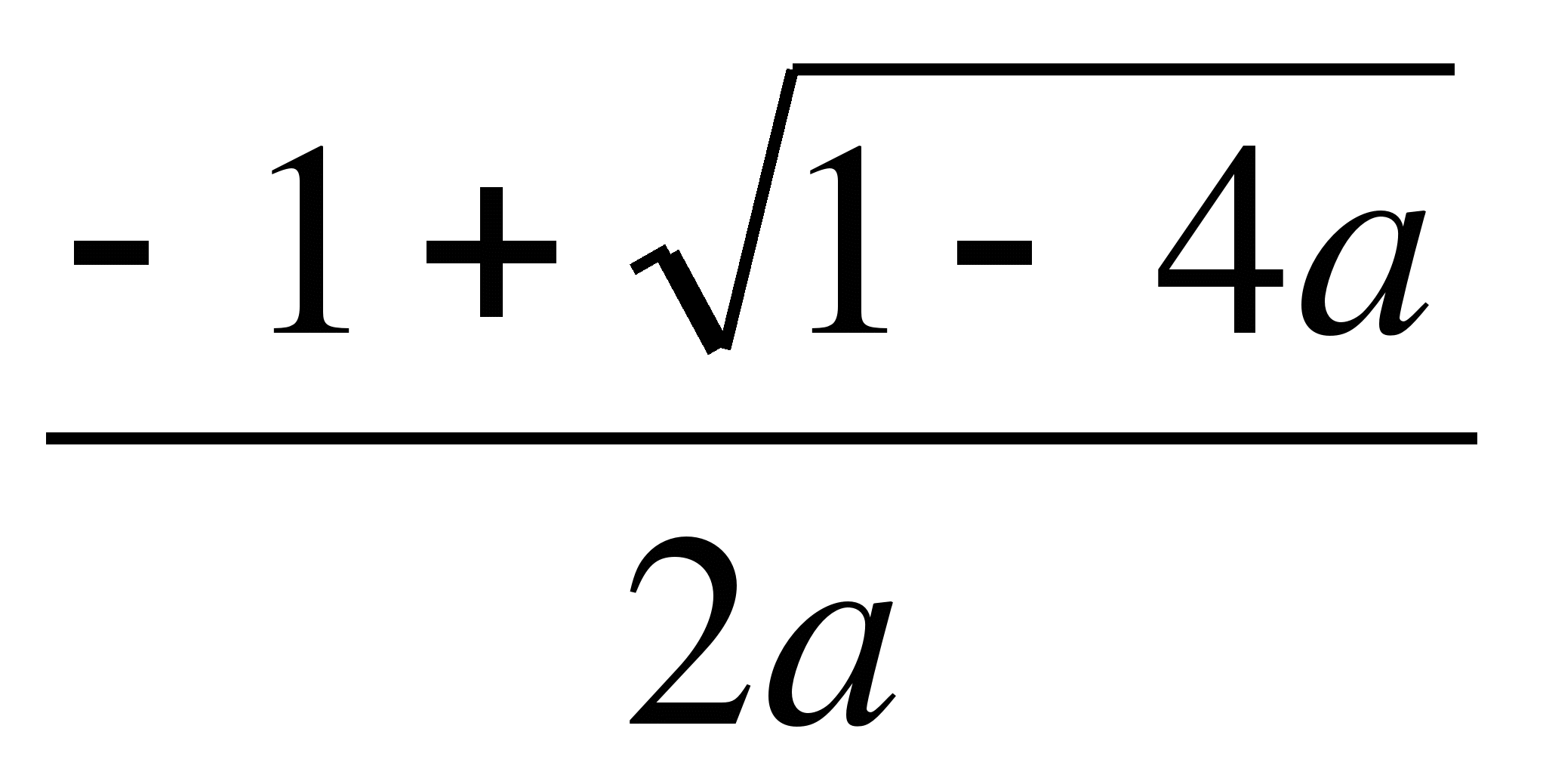
получим х< и х> .

г) Если D>0 и а<0, то с учётом предыдущего рисунка получим
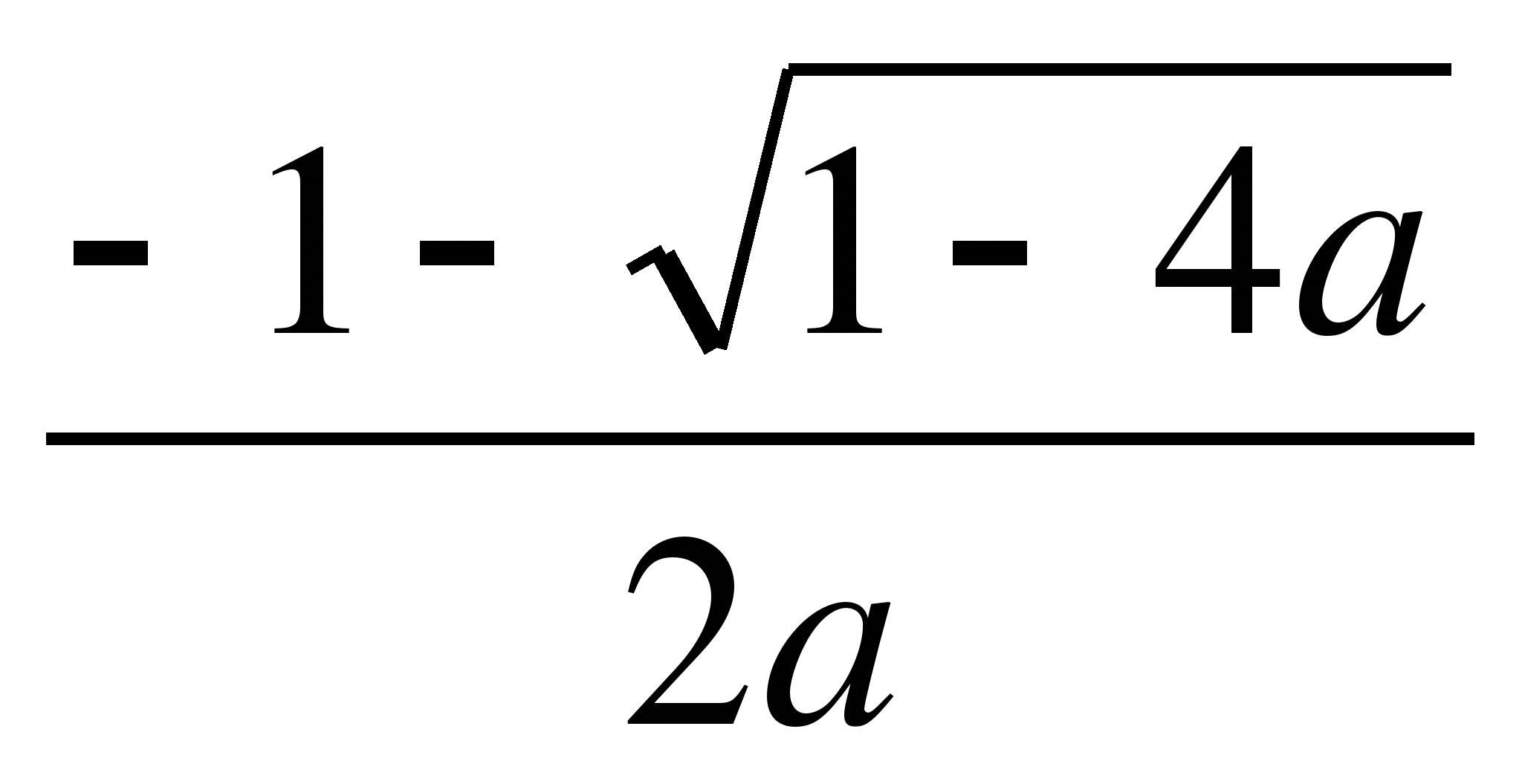
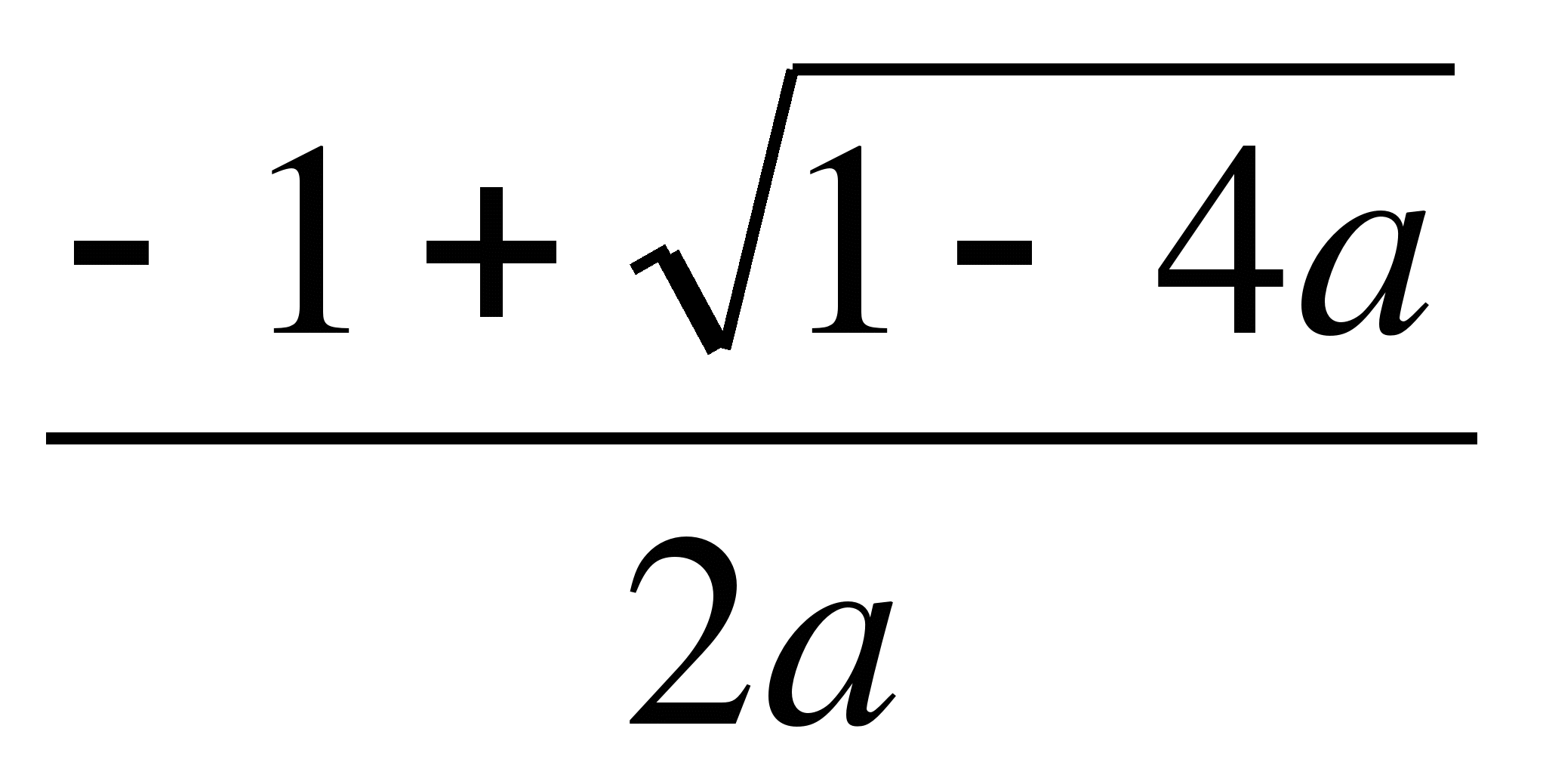
решение <x< .
Ответ: 1) при а=0 х> -1; 2) при а=1/4 х<-2, х>-2;
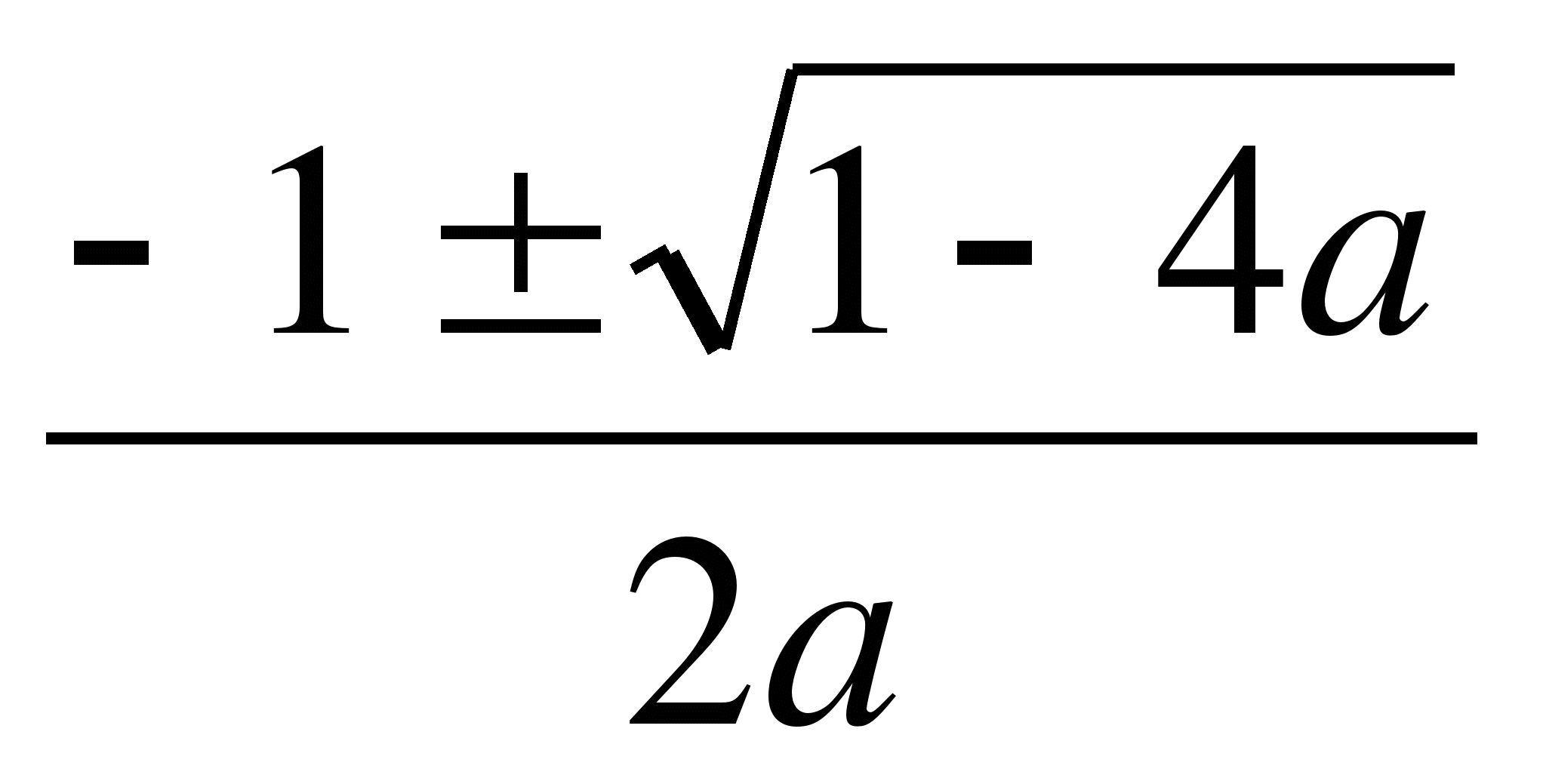
3) при 0<a<1/4 х1,2=
Пример 2. Решить для любых вещественных значений а неравенство
х2-4ах+9≤0.
Решение.
Данное неравенство является квадратным, D=16a2-36.
1) Если D=0, то получим 16a2-36=0, a2=9/4, a=±1,5.
а) при а=1,5 неравенство примет вид х2-6х+9≤0, решением
которого является х=3;
б) при а=-1,5 неравенство примет вид х2+6х+9≤0, решением
которого является х=-3.
2) Если D<0 при -1,5<x<1,5 , то действительных решений исходное
неравенство не имеет (см. рис.7).
3) Если D>0 при а<-1,5 и a>1,5 , то хЄ[2a-
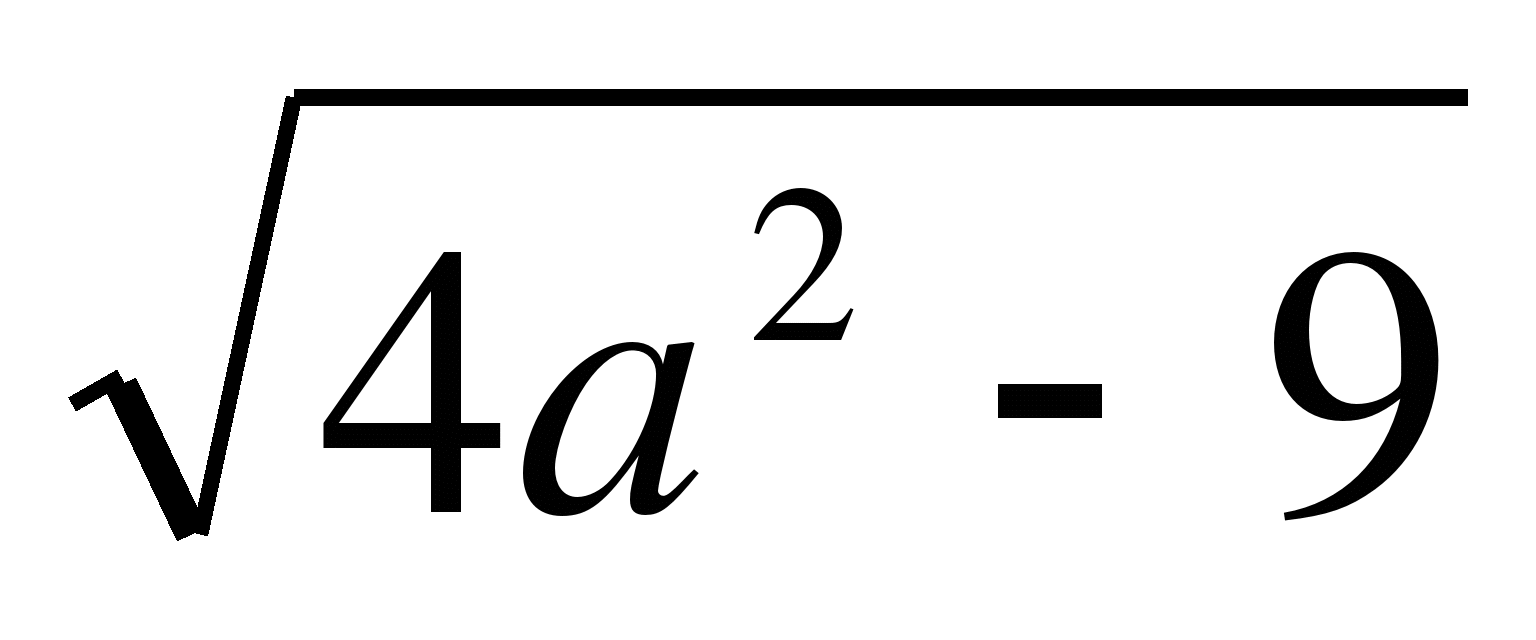 ;
2а+
;
2а+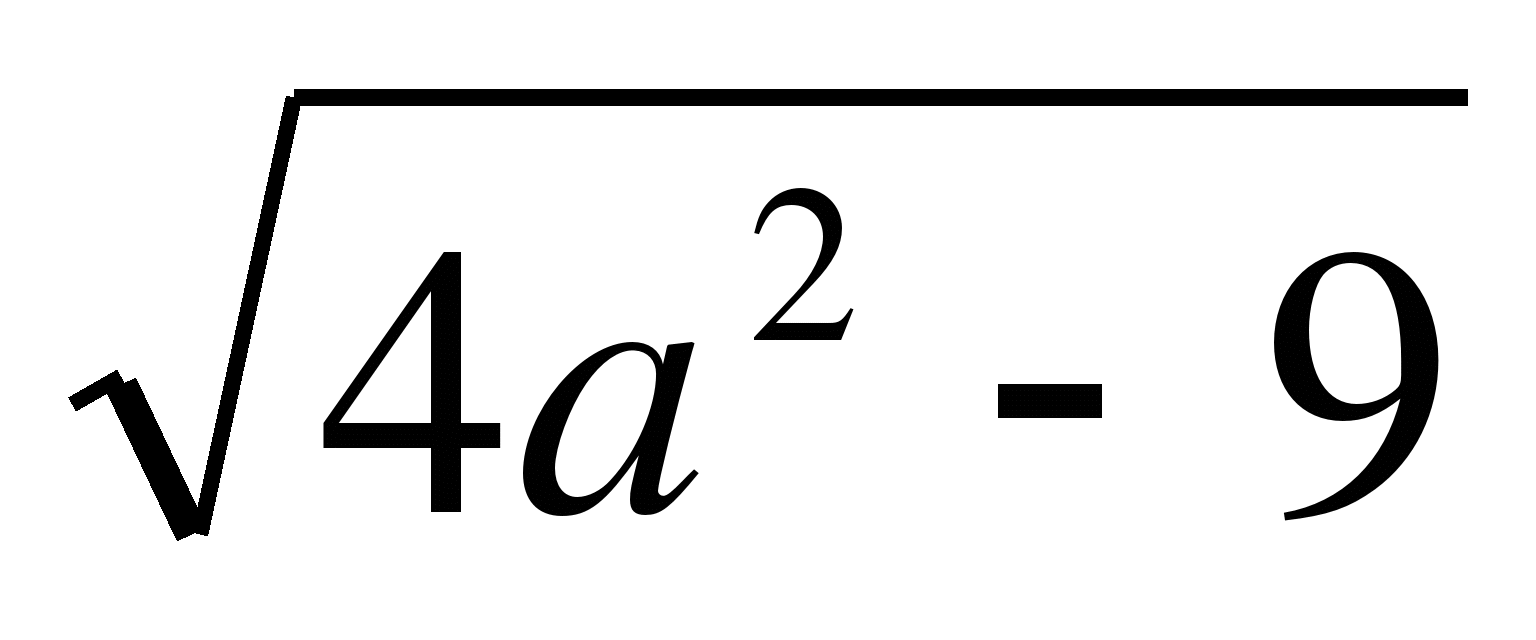 ]
]
(см. рис. 8).
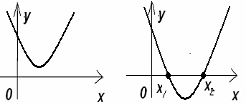
рис.7 рис.8
Пример3. При каких значениях параметра а неравенство х2 - ах+а >0 выполняется при всех х, таких, что -1<х<0?
Решение.
Данное неравенство является квадратным при любых действительных
значениях параметра а. Рассмотрим поведение соответствующего квадратного трехчлена в зависимости от знака его дискриминанта.
«Ветви» параболы направлены вверх, поэтому неравенство выполняется при указанных значениях х в трех случаях:
-
парабола расположена выше оси абсцисс при всех значениях х ( рис .9);
-
парабола пересекает ось абсцисс (или касается ее) в точках, расположенных не правее точки -1 (рис. 10);
-
парабола пересекает ось абсцисс (или касается ее) в точках, расположенных не левее точки 0 (рис. 11).
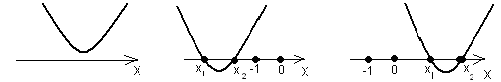
рис. 9 рис. 10 рис. 11
Рассмотрим эти случаи.
Сначала найдем дискриминант и корни соответствующего уравнения:
А=1, В=-а, С=а, D=a2-4a, х1=
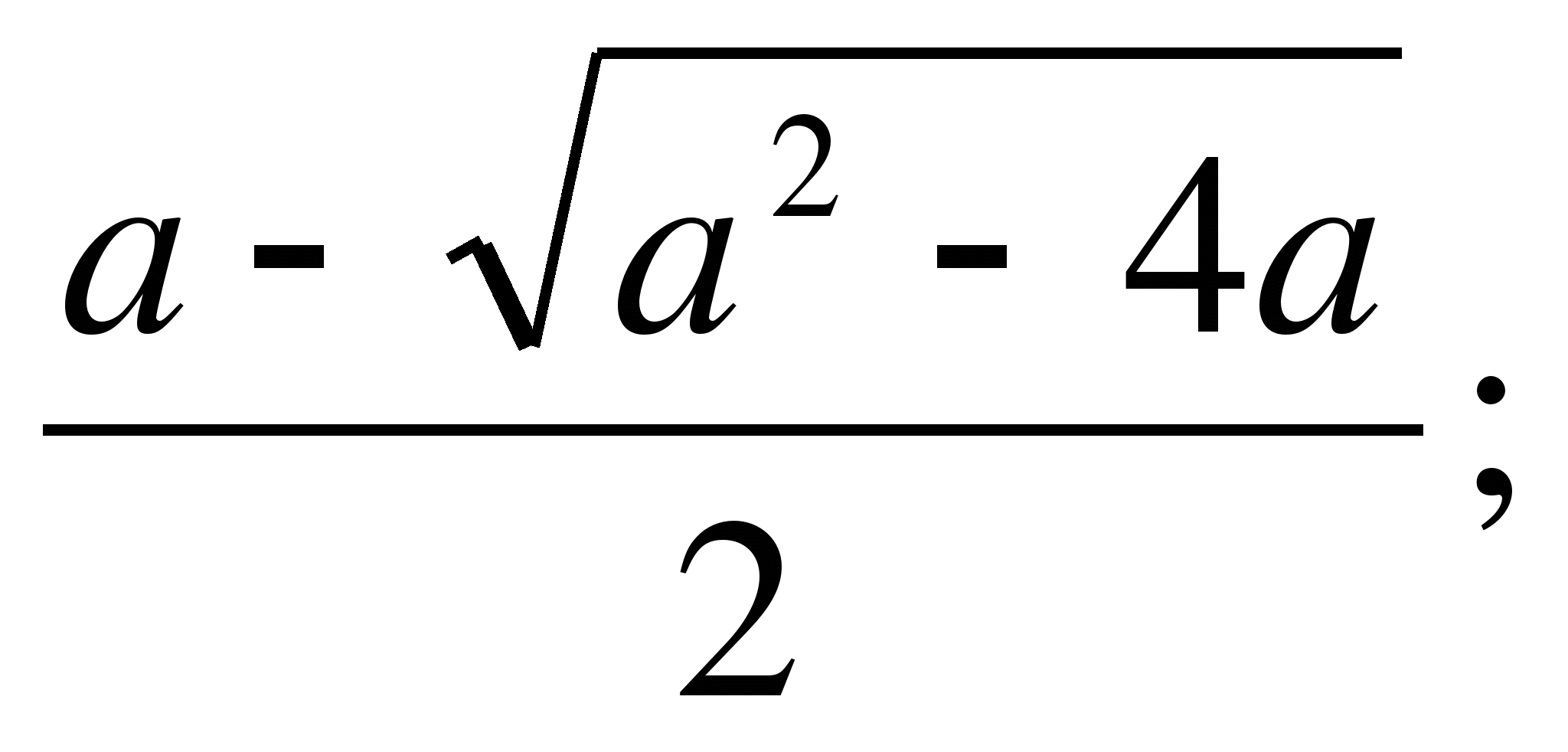 x2=
x2= x1≤x2.
x1≤x2.
1 случай (см. рис. 9). Этот случай определяется условием D<0, тогда получаем: а2-4а<0, из чего следует решение 0<a<4.
2 случай (см. рис.10).Данная ситуация задается системой неравенств:
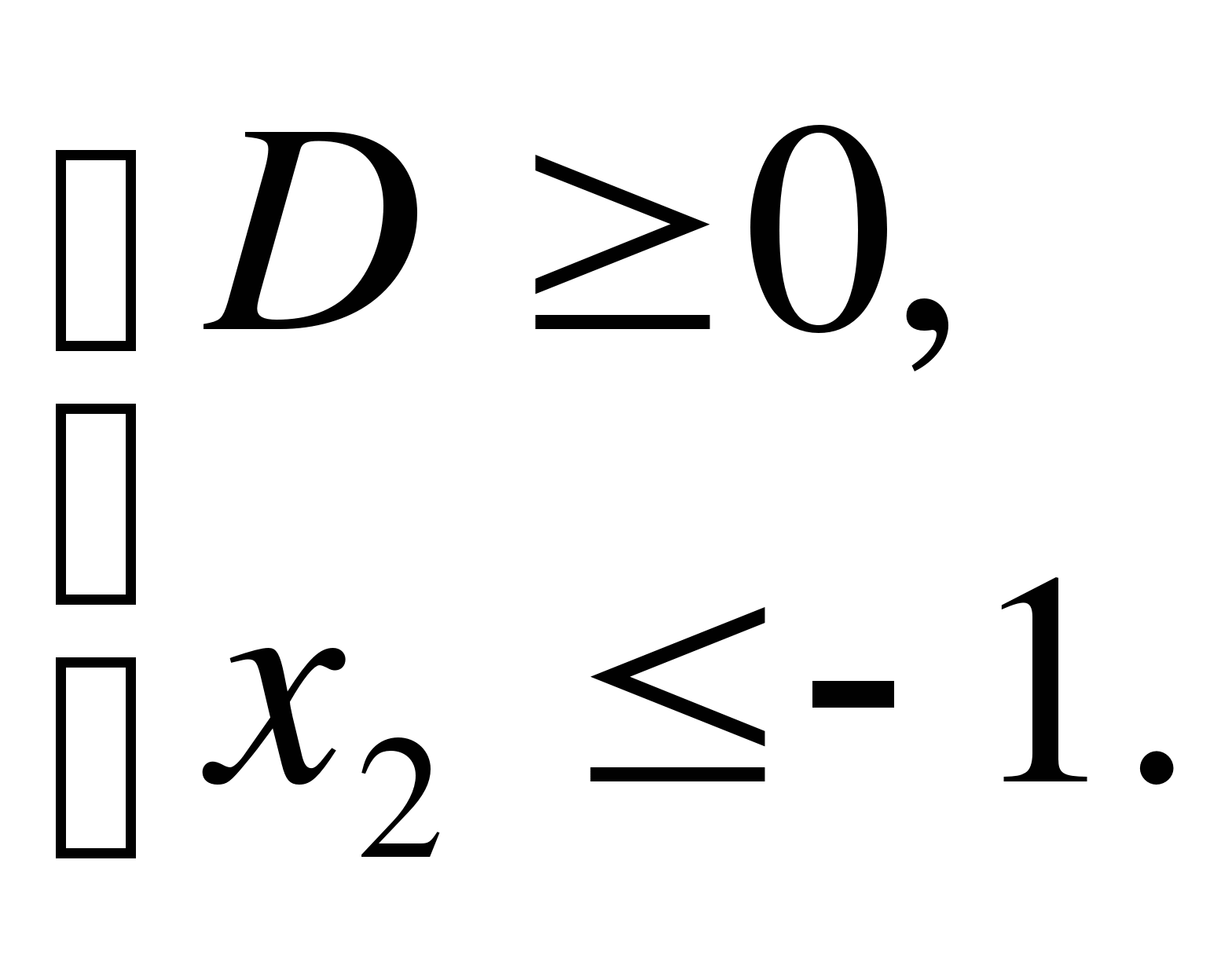
Находим её решение:
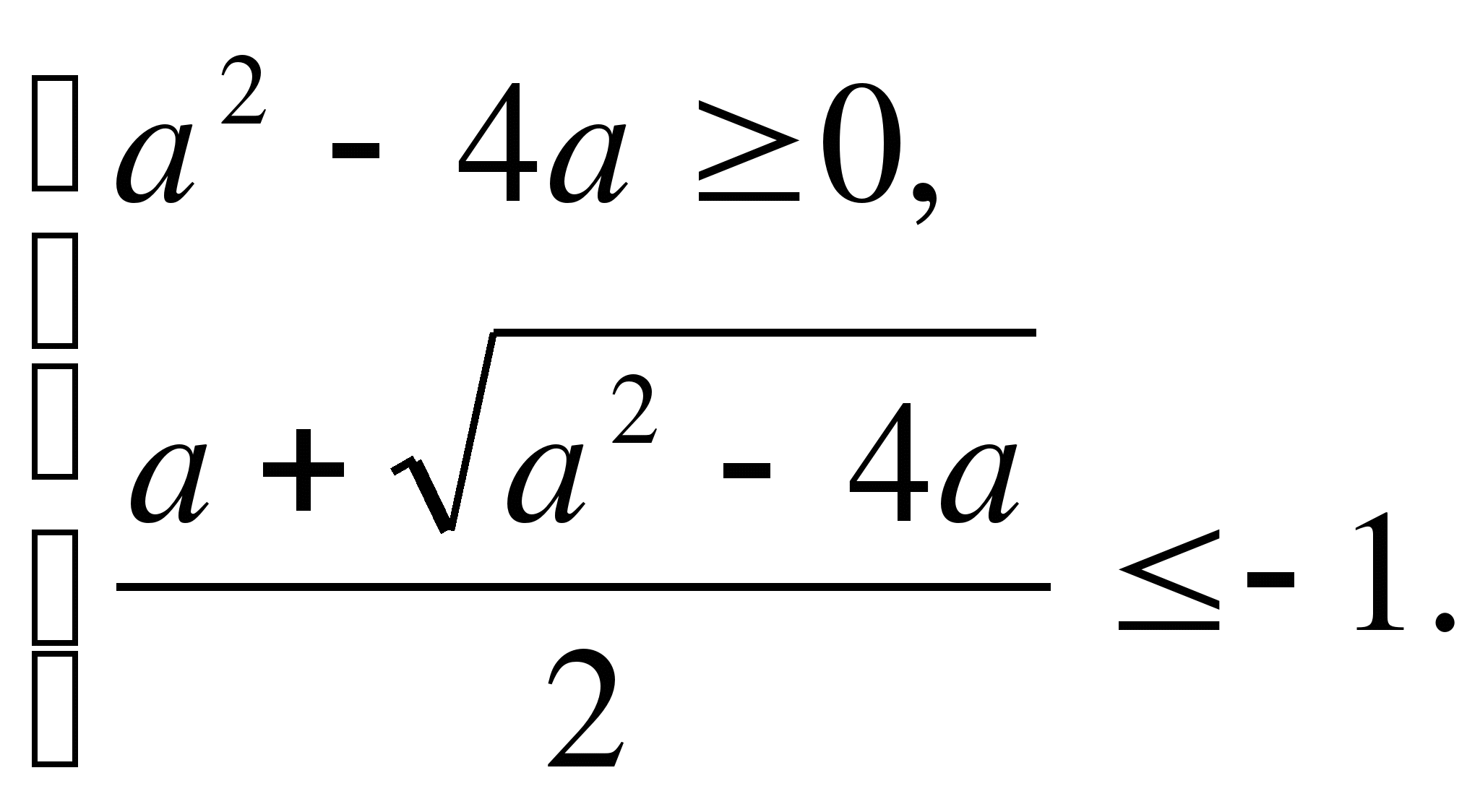 Решив второе неравенство системы, получим
Решив второе неравенство системы, получим 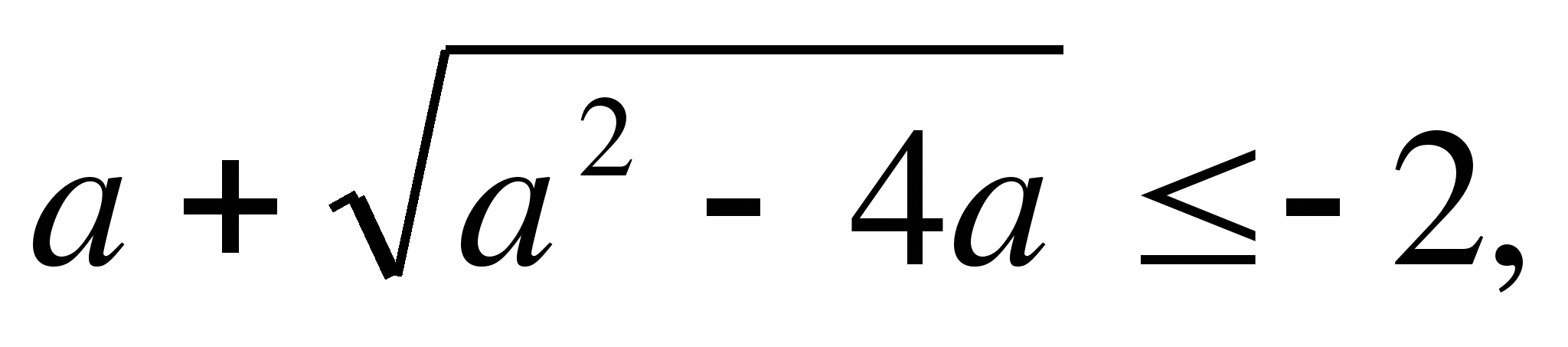 =>
=>
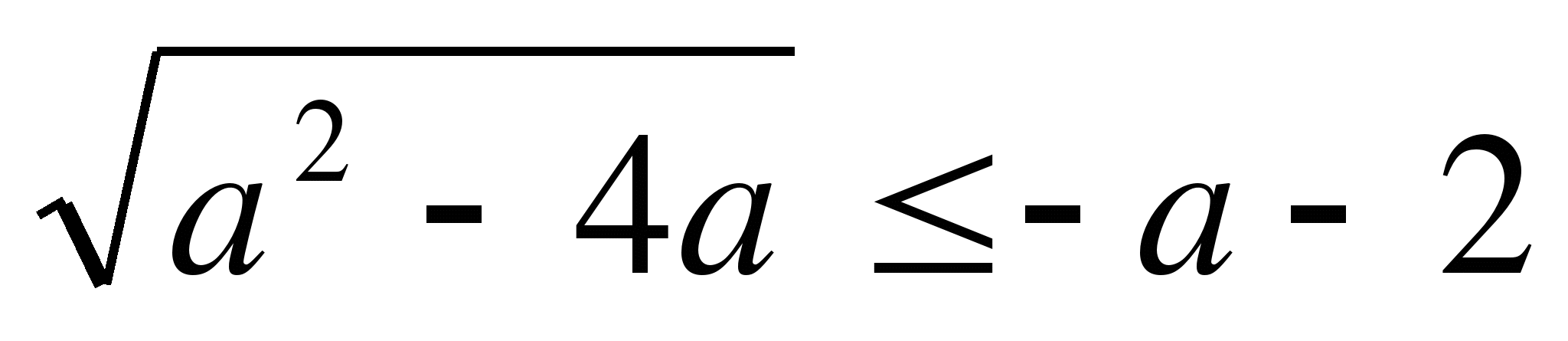 =>
=> 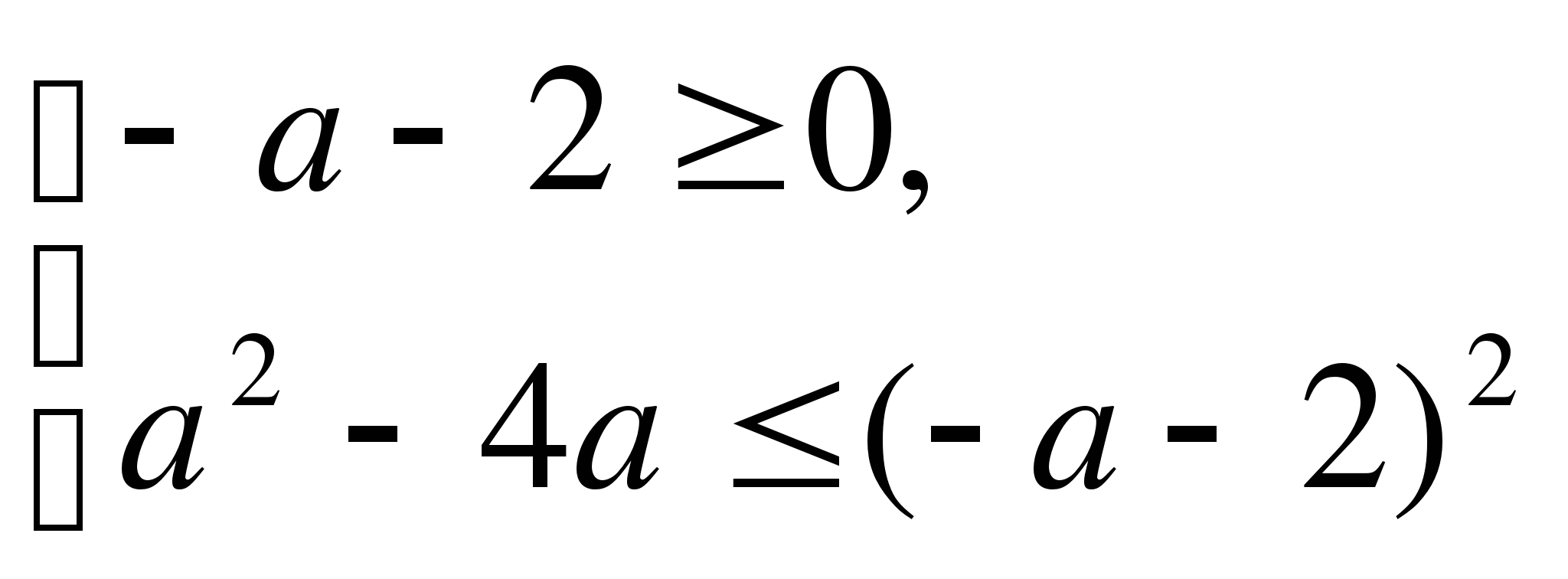 =>
=> 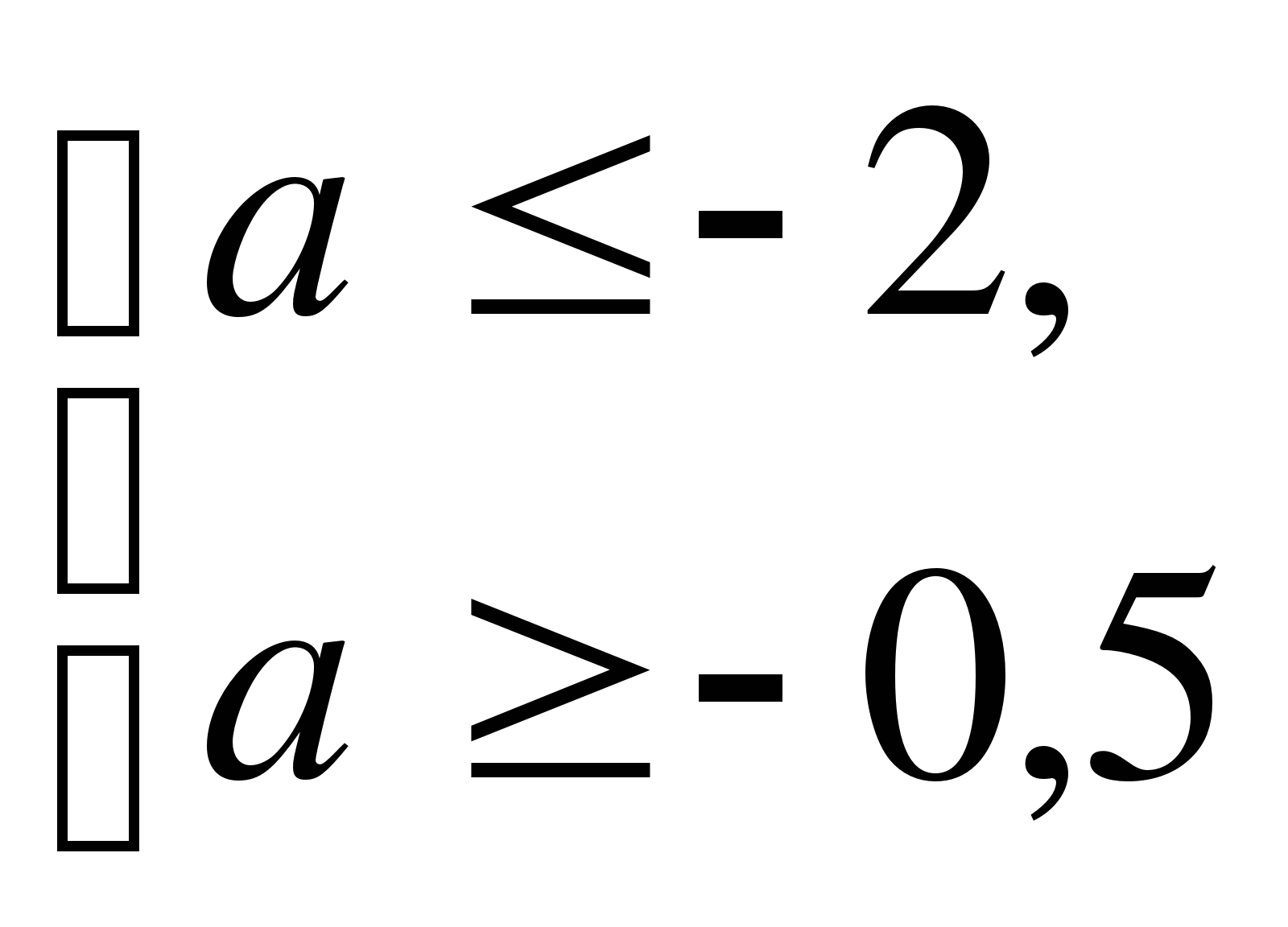 => Ø.
=> Ø.
3 случай (см. рис.11).Этот случай определяется следующей системой неравенств:
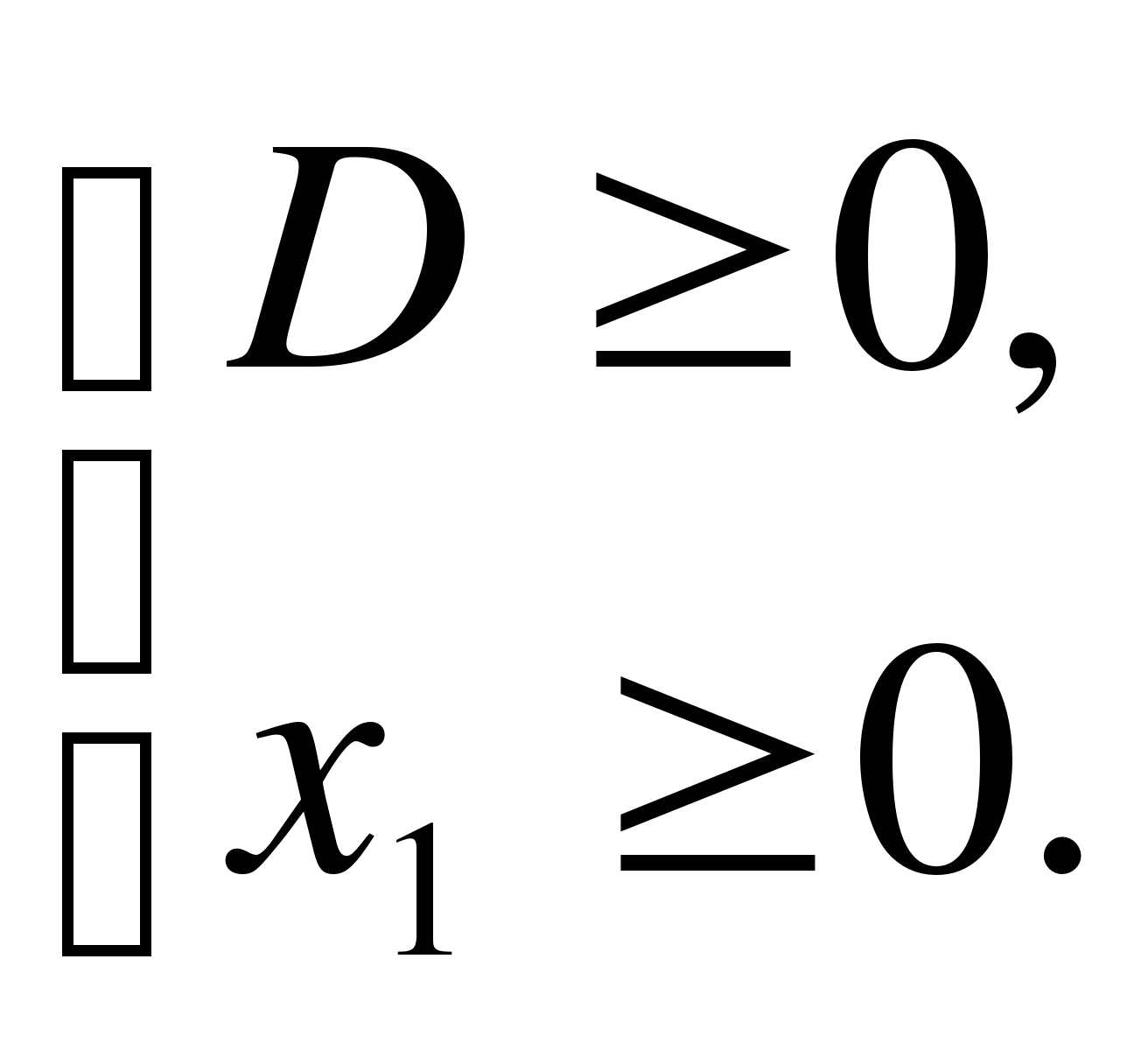 Находим решение данной системы:
Находим решение данной системы: 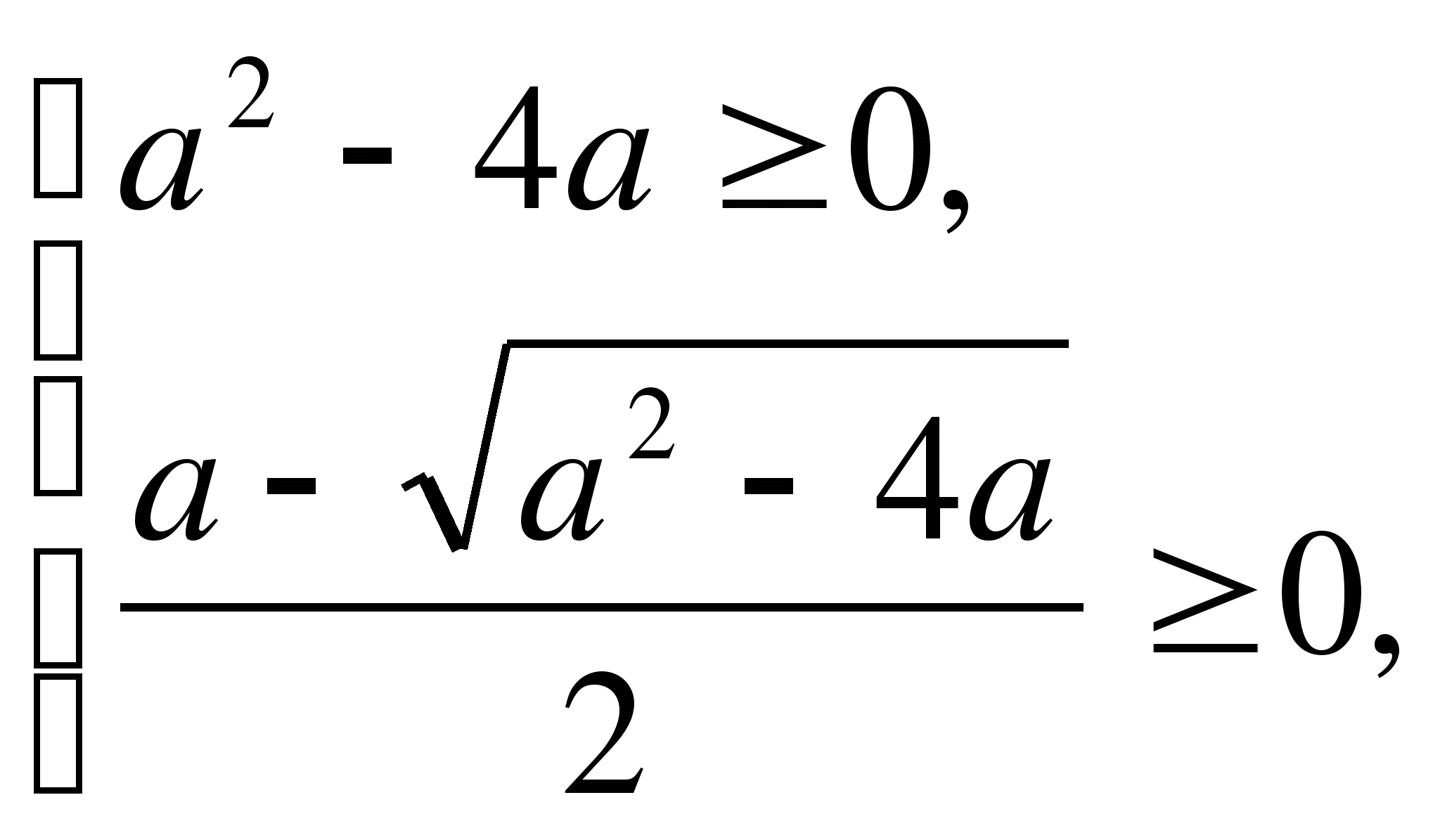 =>
=>
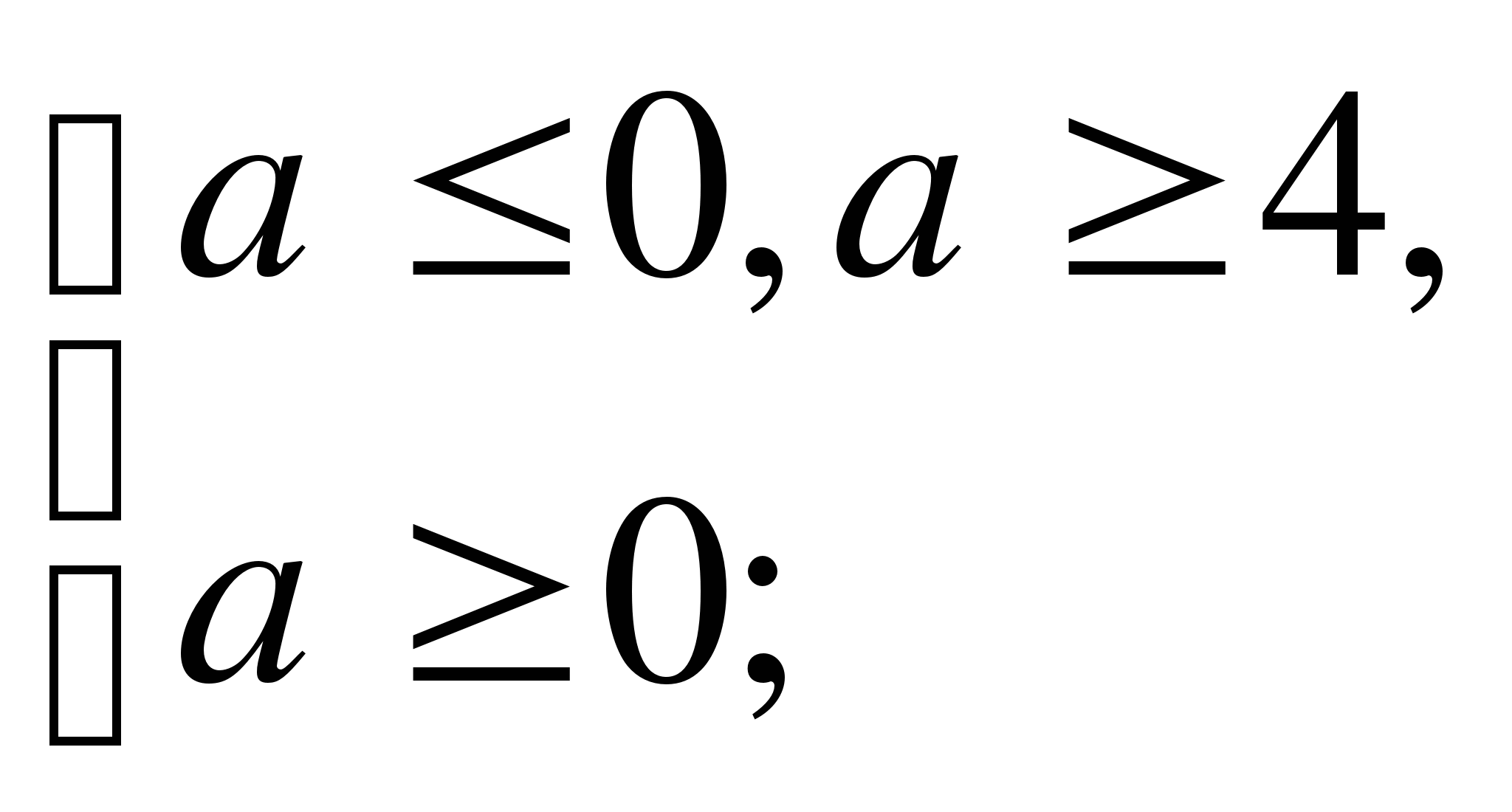 => a=0, a≥4. (Действительно, решая второе
неравенство системы, получаем: а-
=> a=0, a≥4. (Действительно, решая второе
неравенство системы, получаем: а-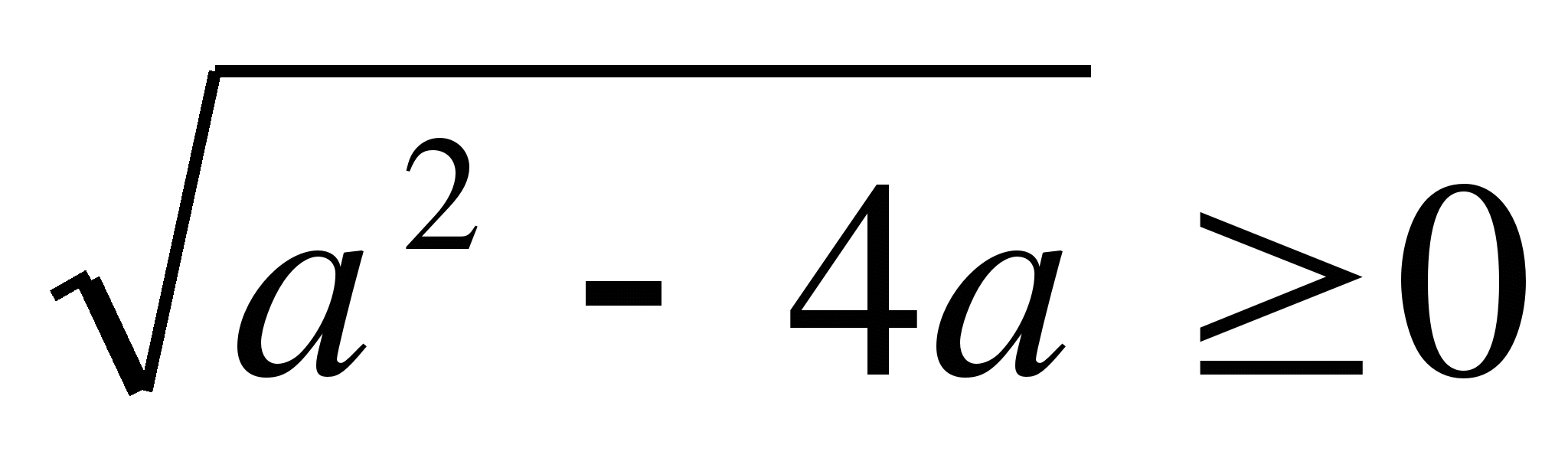 =>
=> 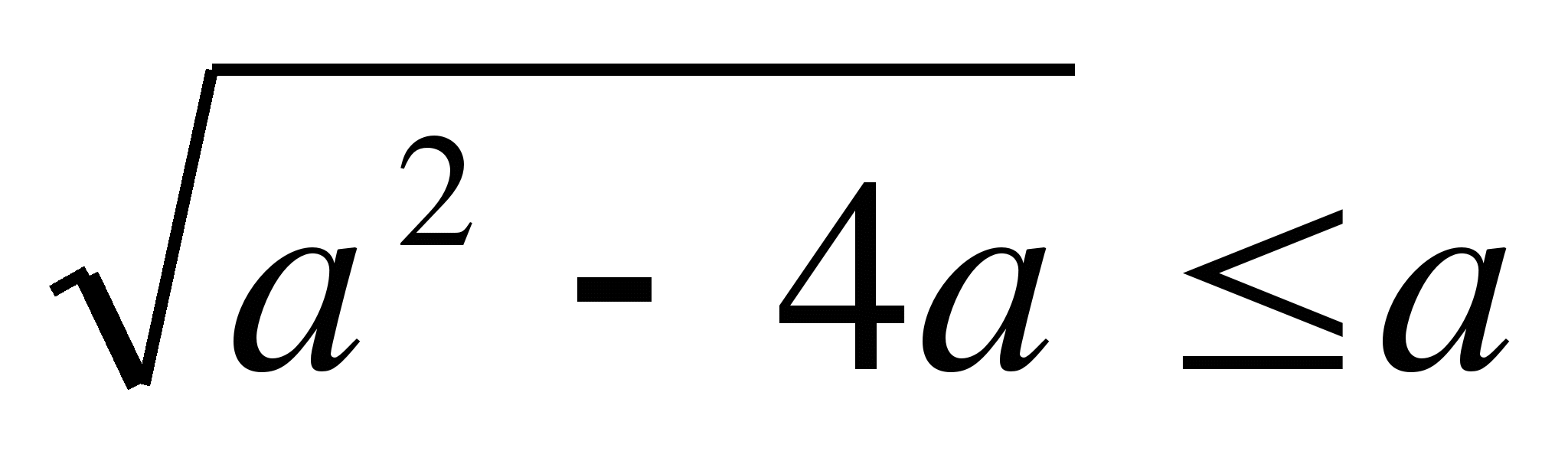 =>
=> 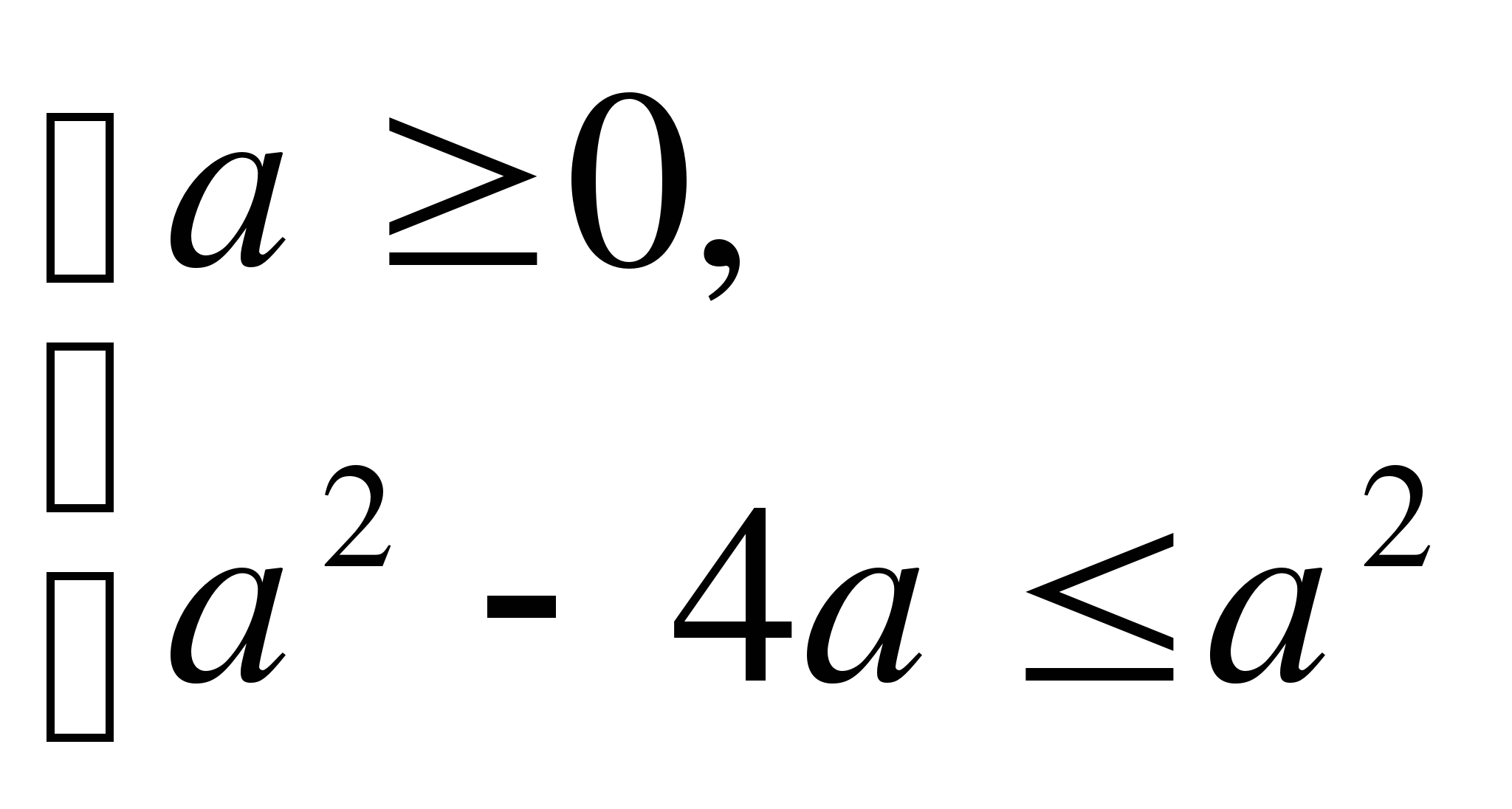 =>
=> 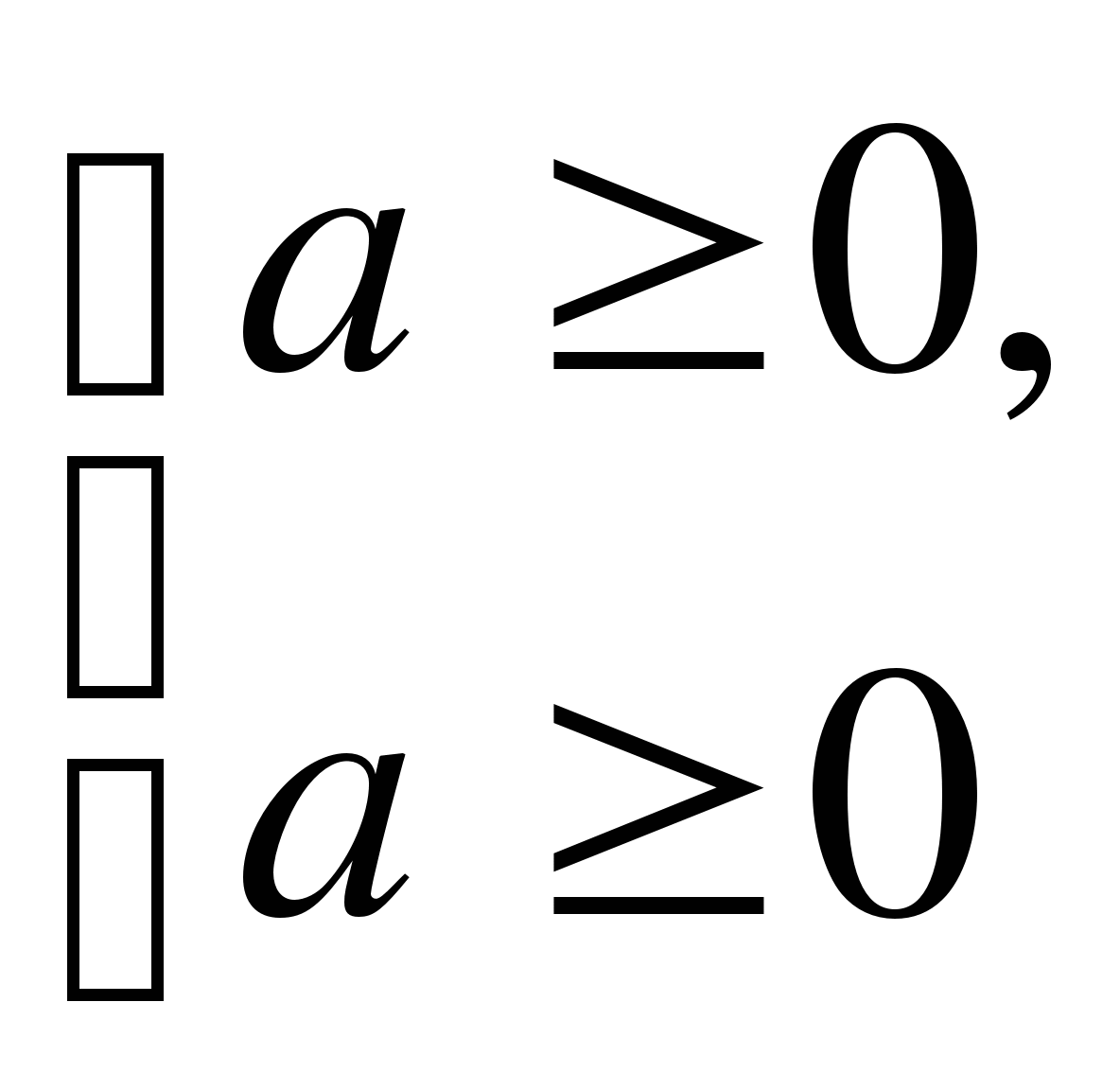 => a≥0).
=> a≥0).
Учитывая решение первого неравенства (а≤0, а≥4), находим ответ: а=0, а≥4.
Объединяя все найденные решения, получаем окончательный ответ.
Ответ: а≥0.
Пример 4. Определить все значения параметра m, при которых неравенство
(m-1)х2 +(m+1)х+m+1>0 справедливо для любых действительных значений х.
Решение.
Пусть m=1. Исходное неравенство примет вид 2х+2>0 и не может выполняться при всех х Є R.
Пусть m≠1, тогда квадратный трехчлен f(х)=(m-1)х2+(m+1)х+m+1 принимает положительные значения при х Є R (график лежит выше оси абсцисс) тогда и только тогда, когда выполняются условия:
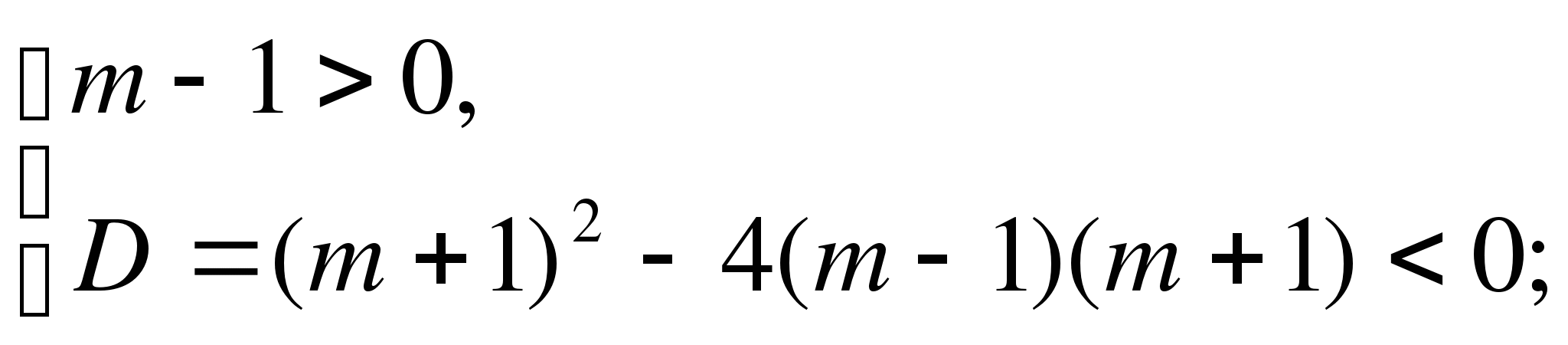 <=>
<=> 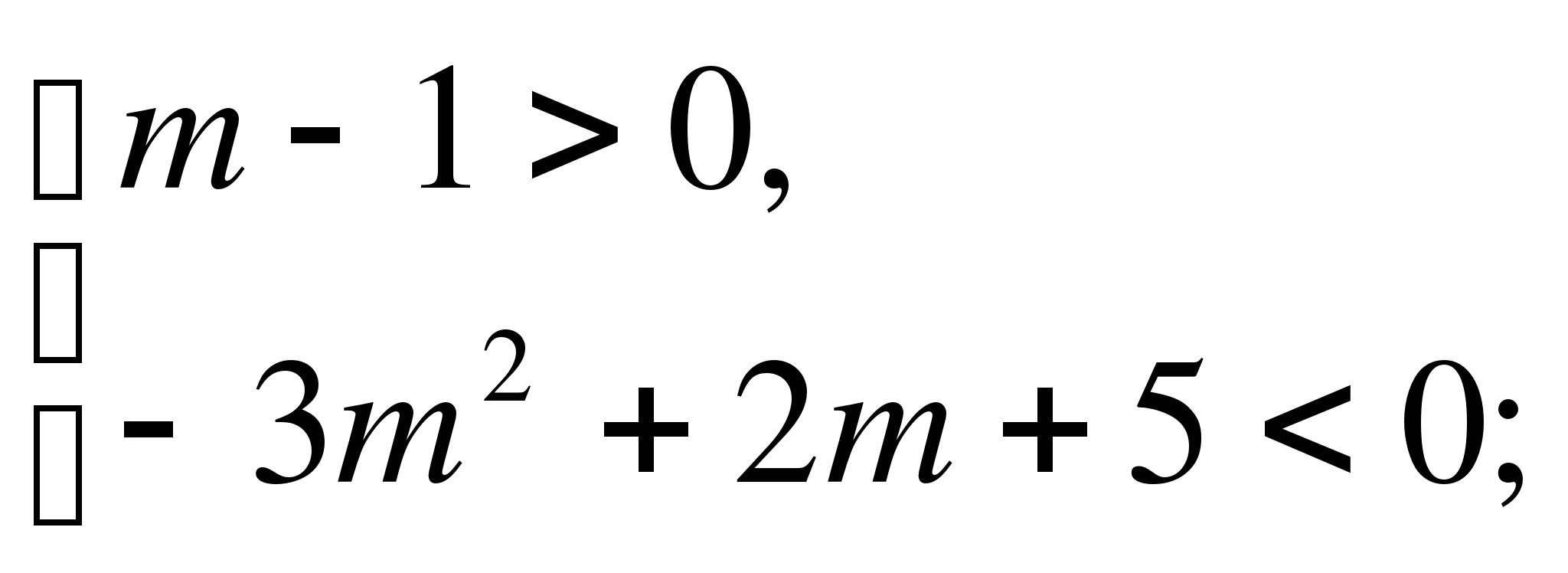 <=>
<=> 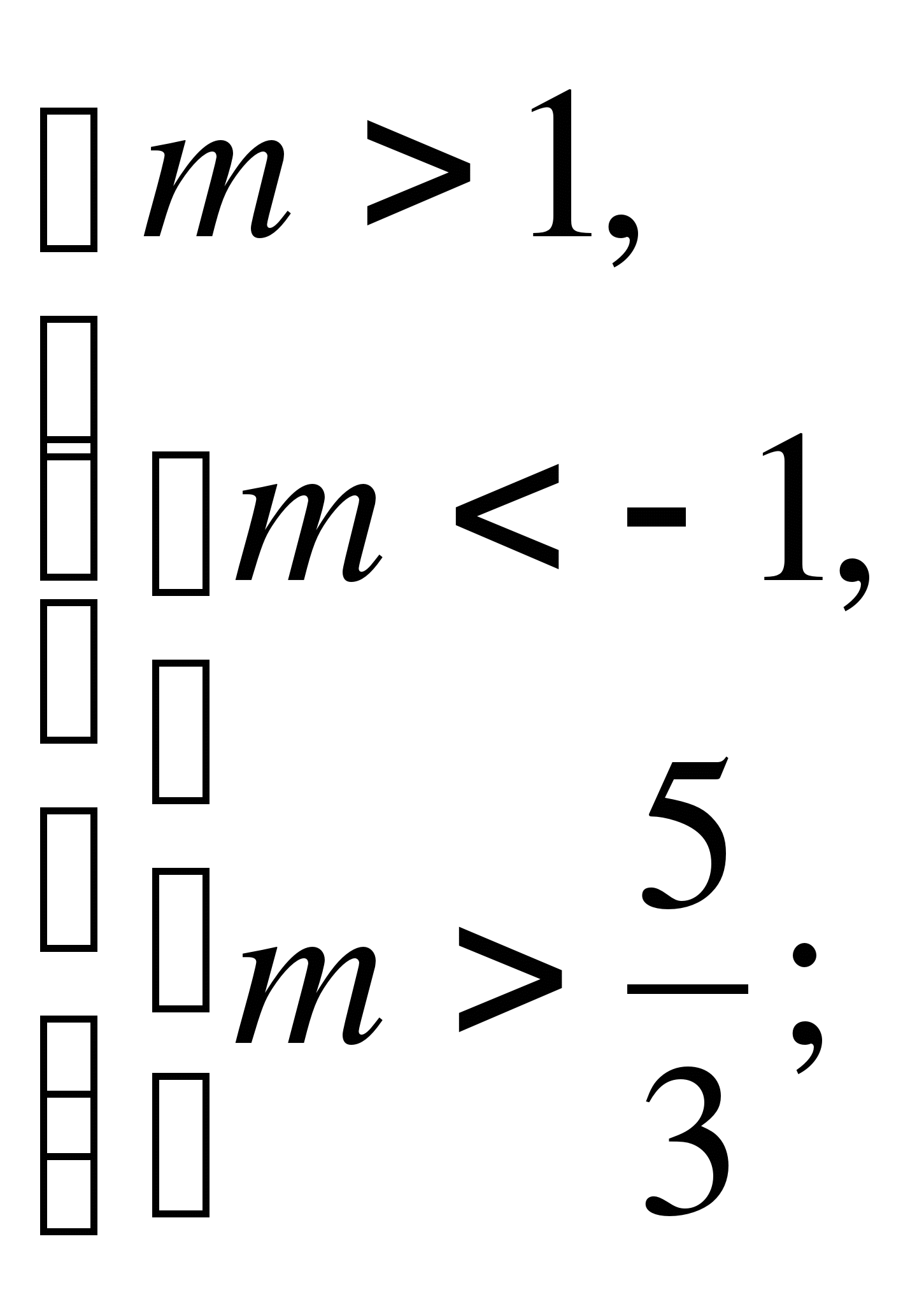 <=>
<=> 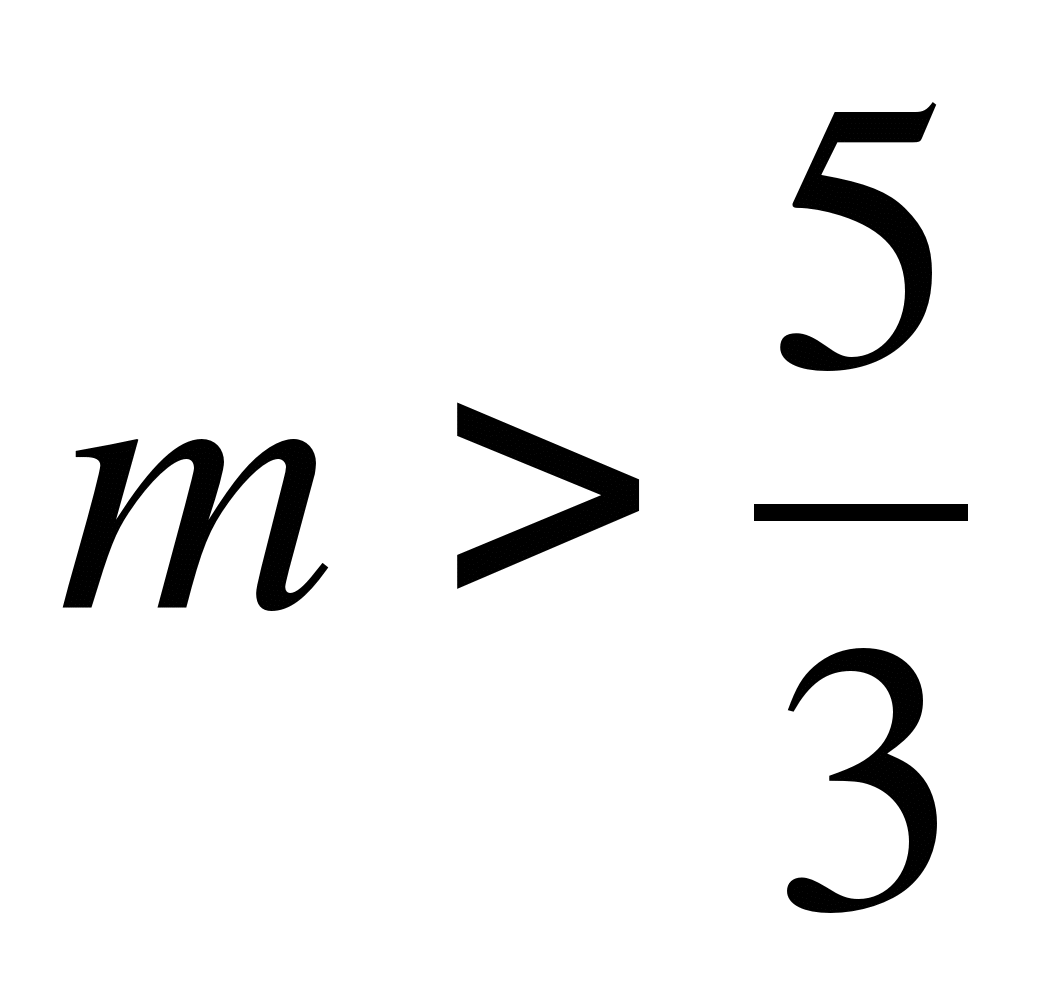 .
.
Ответ: mЄ(5/3;+∞).
Пример 5. При каких а неравенство (х-а)(х-2)≤0 имеет единственное решение?
Решение.
1). Если а=2, то требование задачи удовлетворяется, т.к. при а=2 получаем
неравенство (х-2)2≤0, имеющее единственное решение х=2.
2). Если а≠2, то решением исходного неравенства будет отрезок.
Ответ: а=2.
Пример 6. При каких а решением неравенства (х-а)2(х-2)(х+3)≤0 будет отрезок?
Решение.
1). Так как (х-а)2≥0, то исходное неравенство равносильно системе
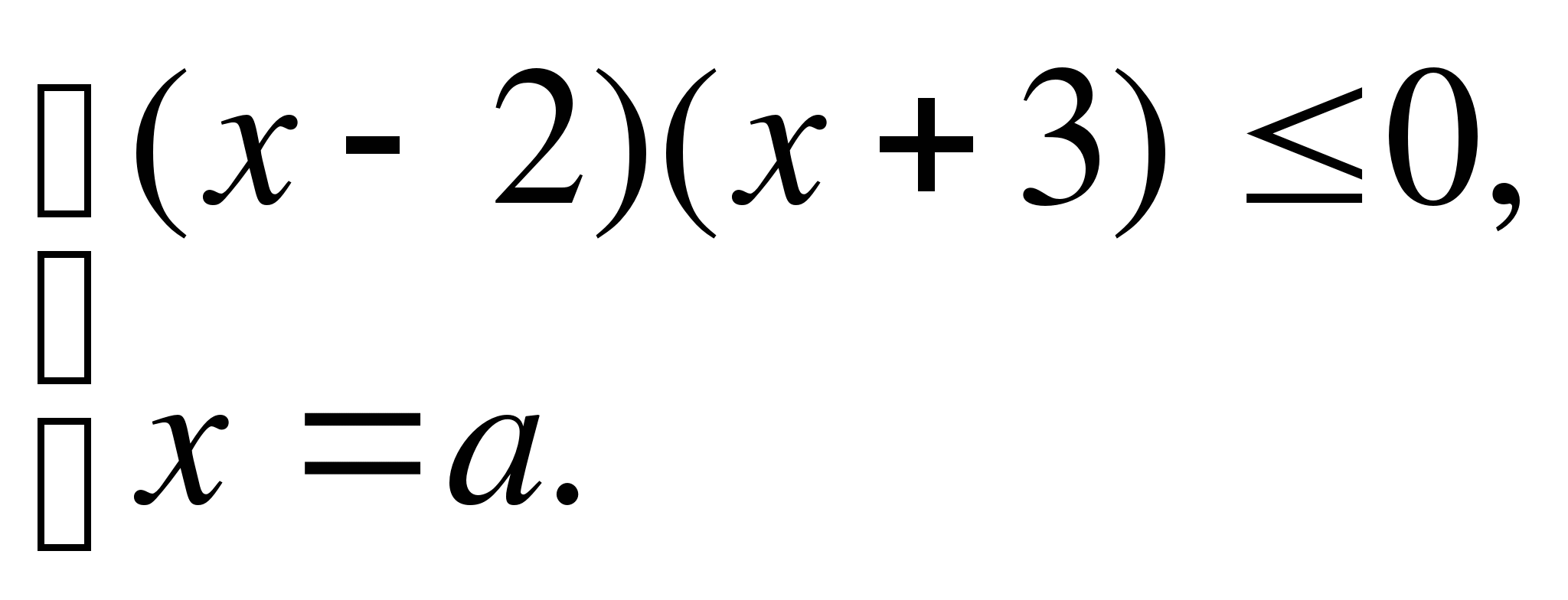 (*)
(*)
2). Решением системы неравенства будет отрезок -3≤х≤2. Следовательно,
при аЄ[-3;2] решением системы (*) также будет отрезок.
Ответ: -3≤a≤2.
Пример 7. Найти все значения а, при которых неравенство (х-3а)(х-а-3)<0
Выполняется при всех х, таких, что 1≤х≤3.
Решение.
Решением неравенства является один из промежутков: (3а; а+3) или (а+3; 3а).
Причем по условию задачи каждый из этих промежутков должен содержать отрезок [1;3], и возможны два варианта:
а) б)
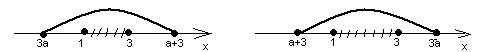
Итак, искомые значения параметра - это решение двух систем:
а)
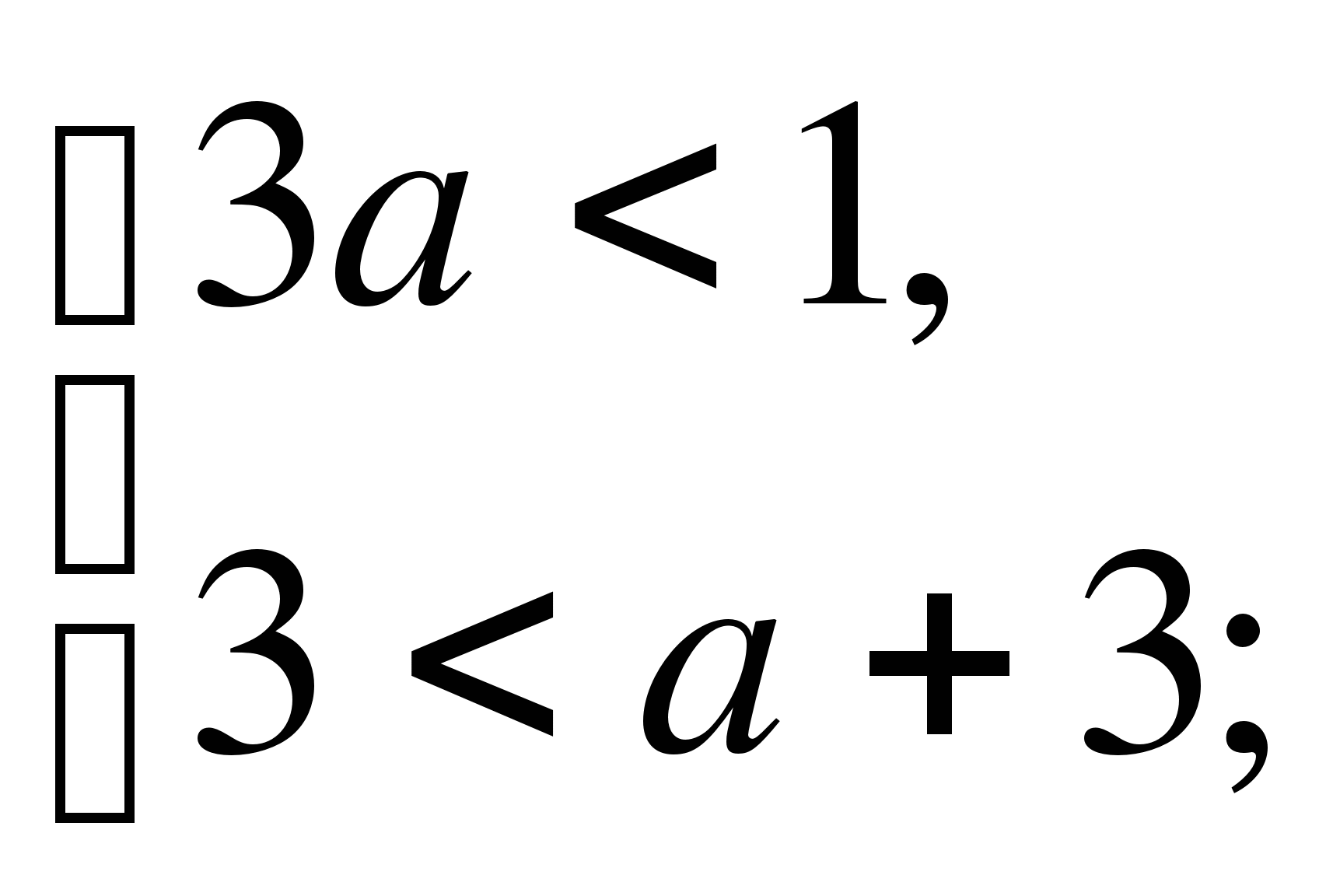 б)
б) 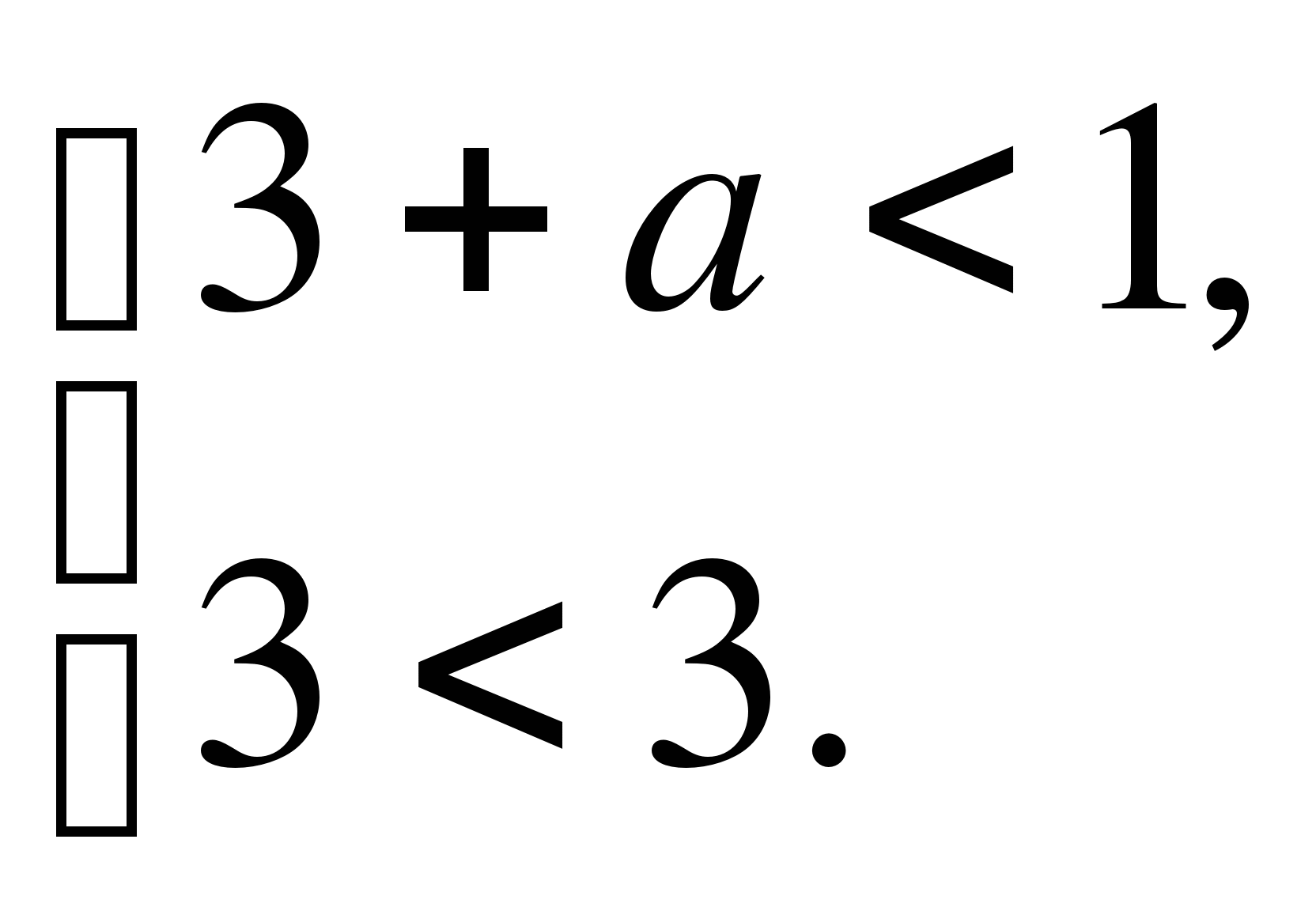
Решая эти системы, получим 0<а<1/3.
Ответ: 0<а<1/3.
Пример 8. Найти все значения параметра m, при которых всякое решение неравенства 1≤х≤2 является решением неравенства х2-mх+1≤0.
Решение.
Исходная задача может быть переформулирована следующим образом:
при каких значениях m множество решений неравенства х2-mх+1≤0 содержит отрезок [1;2]? График квадратного трехчлена должен располагаться так, как показано на рис.12:
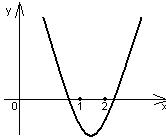
рис.12
Положение параболы определяется условиями:
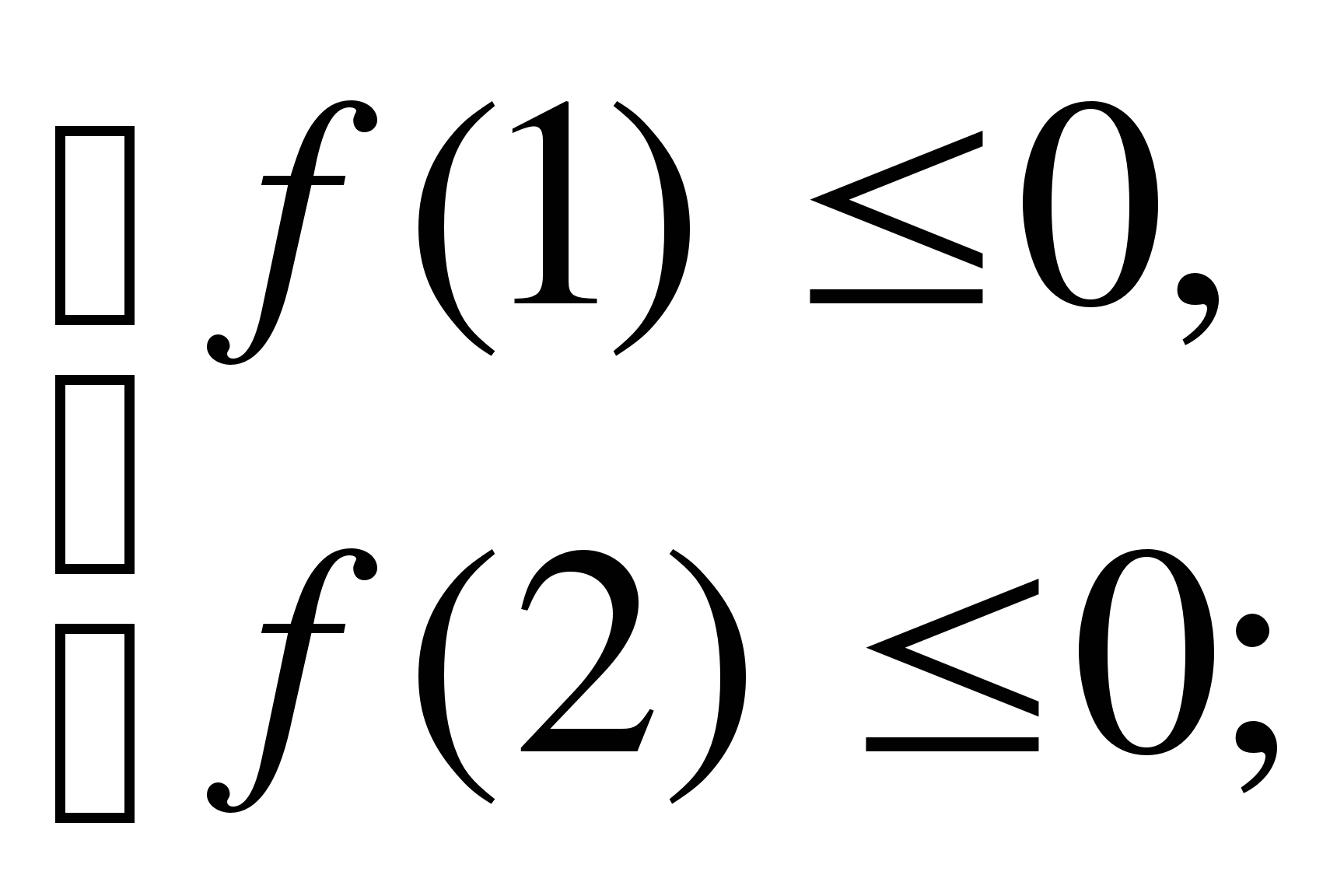 <=>
<=> 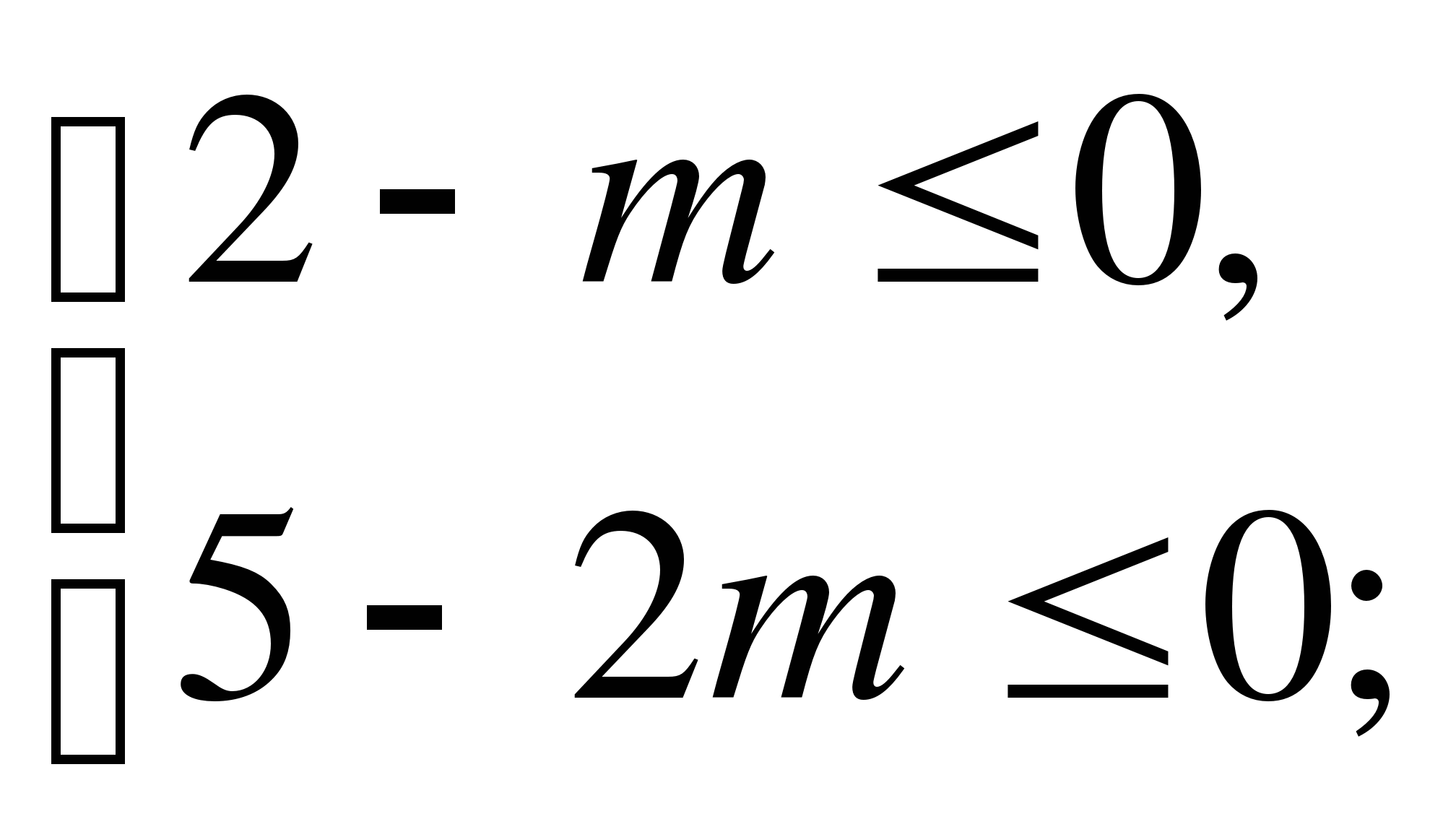 <=> m≥2,5.
<=> m≥2,5.
Ответ: mЄ[2,5;+∞).
Пример 9. Найти все значения параметра а, при которых любое значение х, удовлетворяющее неравенству ах2+(1-а2)х-а>0, удовлетворяет также неравенству │х│≤2.
Решение.
Исходную задачу можно переформулировать следующим образом: при каких значениях а все решения исходного неравенства принадлежат отрезку -2≤х≤2?
Если а=0,то исходное неравенство принимает вид х>0.Видно, что значение а=0 не удовлетворяет условию задачи.
Пусть а≠0. Вычислим дискриминант квадратного трехчлена, находящегося в левой части неравенства: D=(1-а2)2+4а2=(а2+1)2. Очевидно, что D>0 при любых значениях а. Поэтому при любых значениях а≠0 рассматриваемый квадратный трехчлен имеет два действительных различных корня х1=а, х2=-1/а, причем х1<х2. Тогда решением исходного квадратного неравенства является либо промежуток (х1; х2), что соответствует случаю а<0 ( рис. 13), либо множество, состоящее из двух неограниченных промежутков (-∞;х2) и (х1;+∞), что
соответствует случаю а>0 (рис.14).
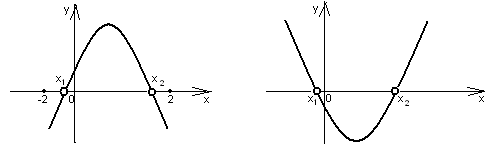
рис. 13 рис. 14
Видно, что все а>0 не удовлетворяют условию задачи. Рассмотрим случай
а<0. Тогда искомые значения а определяются системой -2≤а<-1/2≤2, откуда учитывая, что а<0, получим -2≤а≤-1/2.
Ответ: аЄ[-2;-1/2].
Пример 10. При каких а неравенство ах2+(2а+3)х+а-1≥0 не имеет решений?
Решение.
-
Если а=0, то неравенство примет вид 3х-1≥0, которое имеет решение при х≥1/3, то есть условие задания не выполняется.
-
Если а≠0, то исходное неравенство является квадратным.
а) а<0, ветви параболы направлены вниз. В этом случае исходное неравенство не будет иметь решение, если D<0 (см. рис.15).
D=(2а+3)2-4а(а-1)=16а+9; 16а+9<0, если а<-9/16.
б) а>0, ветви параболы направлены вверх, в этом случае исходное
неравенство обязательно будет иметь решение, то есть условие задания
не выполняется ( см. рис. 16).
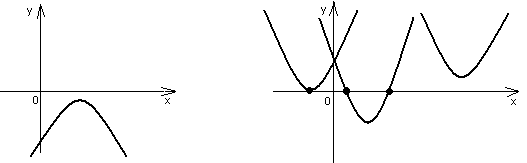
рис. 15 рис. 16
Ответ: а< -9/16.
III. Итоги занятий.
Блок IV. Тема 8. Системы квадратных уравнений и неравенств с параметром.
Цели занятия:
- повторить понятия «система уравнений», «решение системы уравнений»,
«система неравенств», «решение системы неравенств», основные способы
решения систем уравнений и неравенств;
- научиться решать системы квадратных уравнений с параметром;
- научиться решать системы квадратных неравенств с параметром;
- развивать логическое мышление и познавательный интерес через решение систем
квадратных уравнений и неравенств.
Занятия 1 - 2.
Ход занятия.
-
Этап изучения нового материала.
СИСТЕМЫ УРАВНЕНИЙ.
Процесс решения системы уравнений состоит, как правило, в последовательном переходе с помощью некоторых преобразований от данной системы к более простой, затем ещё к более простой и т.д. Если в результате преобразований мы получим равносильную систему, то, решив её, мы найдём решение исходной системы; если же мы придём к следствию, то подстановкой решений в исходную систему необходимо исключить лишние корни.
Основными методами решения систем уравнений являются:
- метод подстановки,
- замена переменных,
- разложение уравнений на множители,
- алгебраические преобразования уравнений,
- функциональный и графический метод.
СИСТЕМЫ НЕРАВЕНСТВ
Решить систему неравенств с одним неизвестным, содержащую параметры, это значит определить, при каких значениях параметров каждое неравенство имеет решение и для всех таких значений параметров найти все решения каждого неравенства, а затем найти решения, удовлетворяющие всем неравенствам.
Решить систему неравенств с несколькими неизвестными, содержащую параметры, это значит определить, при каких значениях параметров система имеет решение и для всех таких значений найти все решения системы.
При решении неравенств будем использовать методы, которые мы применяли при решении рациональных и иррациональных неравенств и систем уравнений.
Решение систем квадратных неравенств с параметром проводится по стандартной схеме: сначала исследуется каждое неравенство по отдельности, затем находится их общее решение.
В ходе решения следует рассмотреть все возможные случаи взаимного расположения точек (концов интервалов) на числовой оси.
II. Этап усвоения новых знаний, тренировочные упражнения.
Пример 1. Найти решения системы
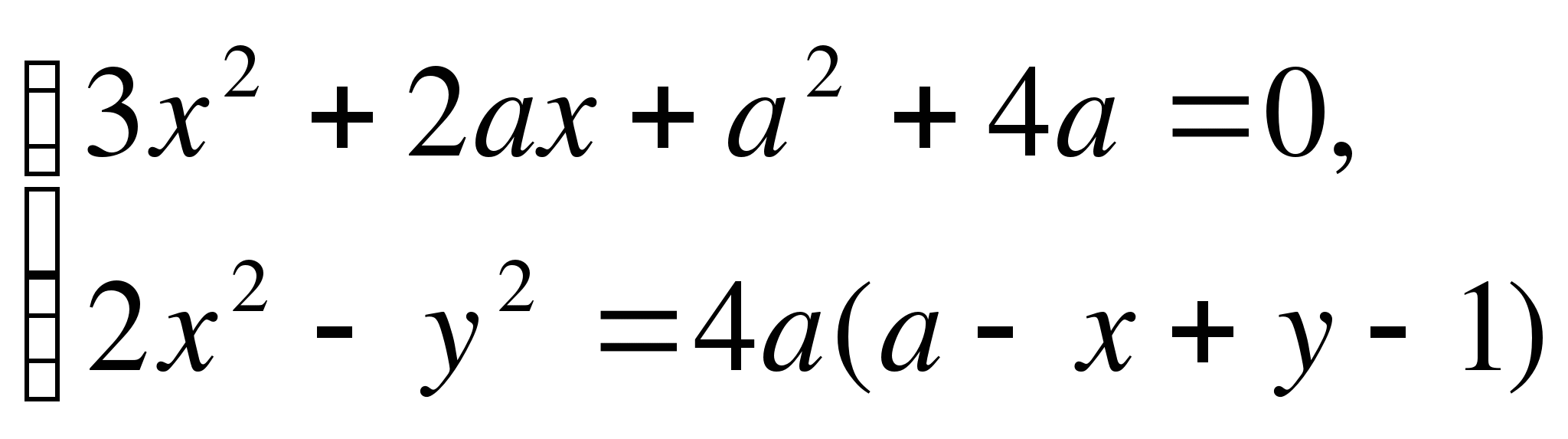 при
различных значениях параметра а.
при
различных значениях параметра а.
Решение.
Вычтем второе уравнение системы из первого и сгруппируем, тогда получим ( х-а)2 + (у+2а)2 =0. Учитывая, что (х-а)2≥0 и (у+2а)2≥0 мы имеем
х-а=0 и у+2а=0, откуда х=а, у=2а.
После подстановки х=а в первое уравнение, получим а=0 или а=-2/3. При этих значениях а и соответствующих значениях х и у, найденных выше, как первое уравнение системы, так и второе уравнение являются верными, то есть мы получили решения исходной системы .
Таким образом, при а=0 имеем решение (0;0); при а=-2/3 имеем решение ( -2/3; 4/3); при остальных значениях параметра а решений нет.
Ответ: (0;0) при а=0, (-2/3; 4/3) при а=-2/3, решений нет при а≠0 и а≠-2/3.
Пример 2. При каком значении параметра а данная система
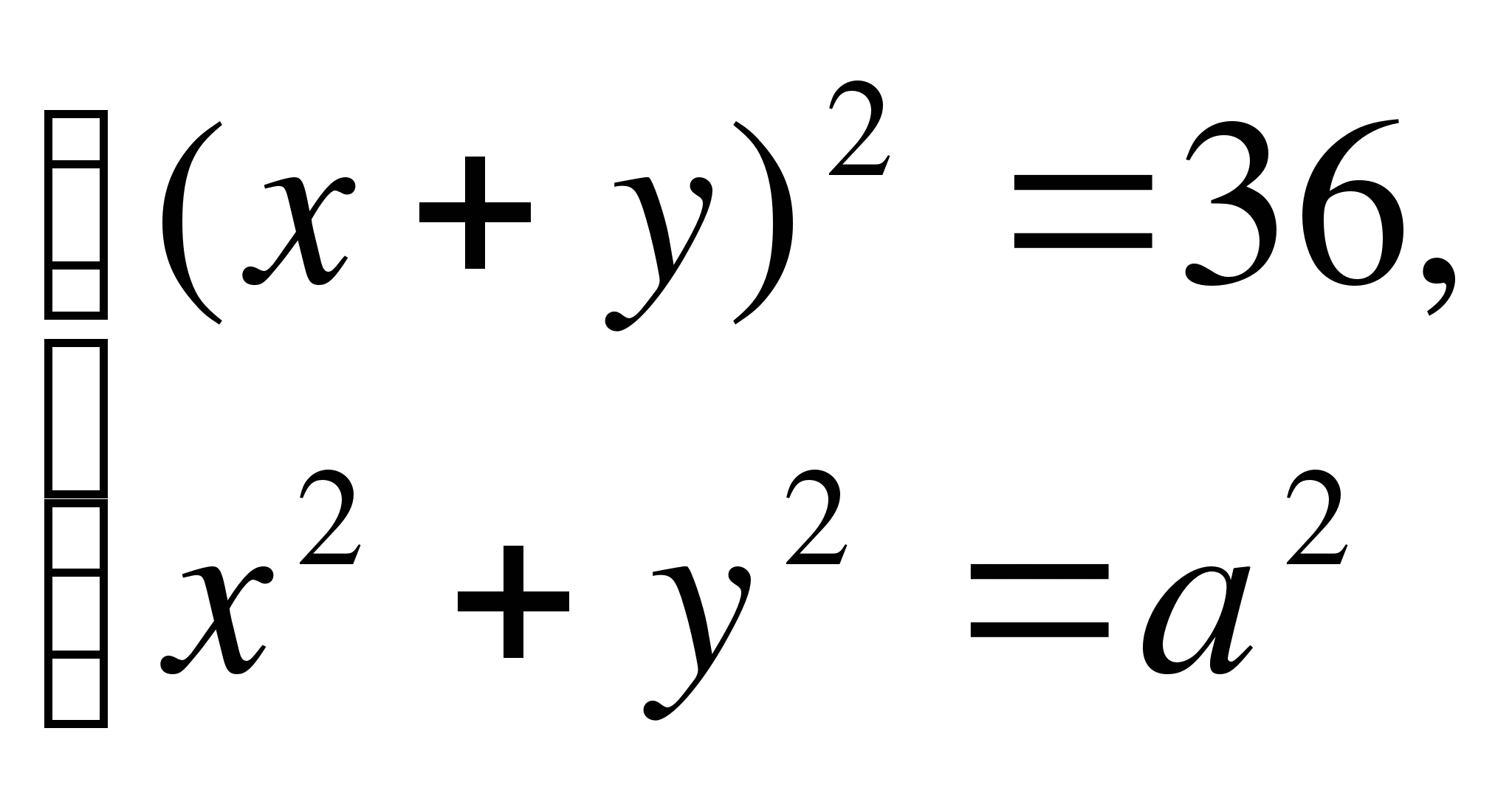
имеет ровно два решения?
Решение.
Рассмотрим второе уравнение системы х2 + у2=а2. Его графиком является семейство концентрических окружностей с центром в начале координат (0;0) и радиусом R=а.
Рассмотрев второе уравнение системы ( х+у )2 =36, получим, что х+у=6 или х+у=-6. Графиками этих функций являются две прямые.
Изобразив графики уравнений исходной системы на одной координатной плоскости, получим, что система имеет ровно два решения только в том случае, если графики изображены так, как показано на рис. 18.
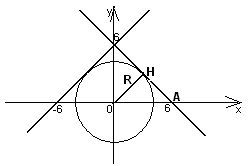
рис.18
Из прямоугольного равнобедренного треугольника ОАН получим, что R=3
 .
Тогда а=±3
.
Тогда а=±3 .
.
Ответ: а=±3
 .
.
Пример 3. При каком а система
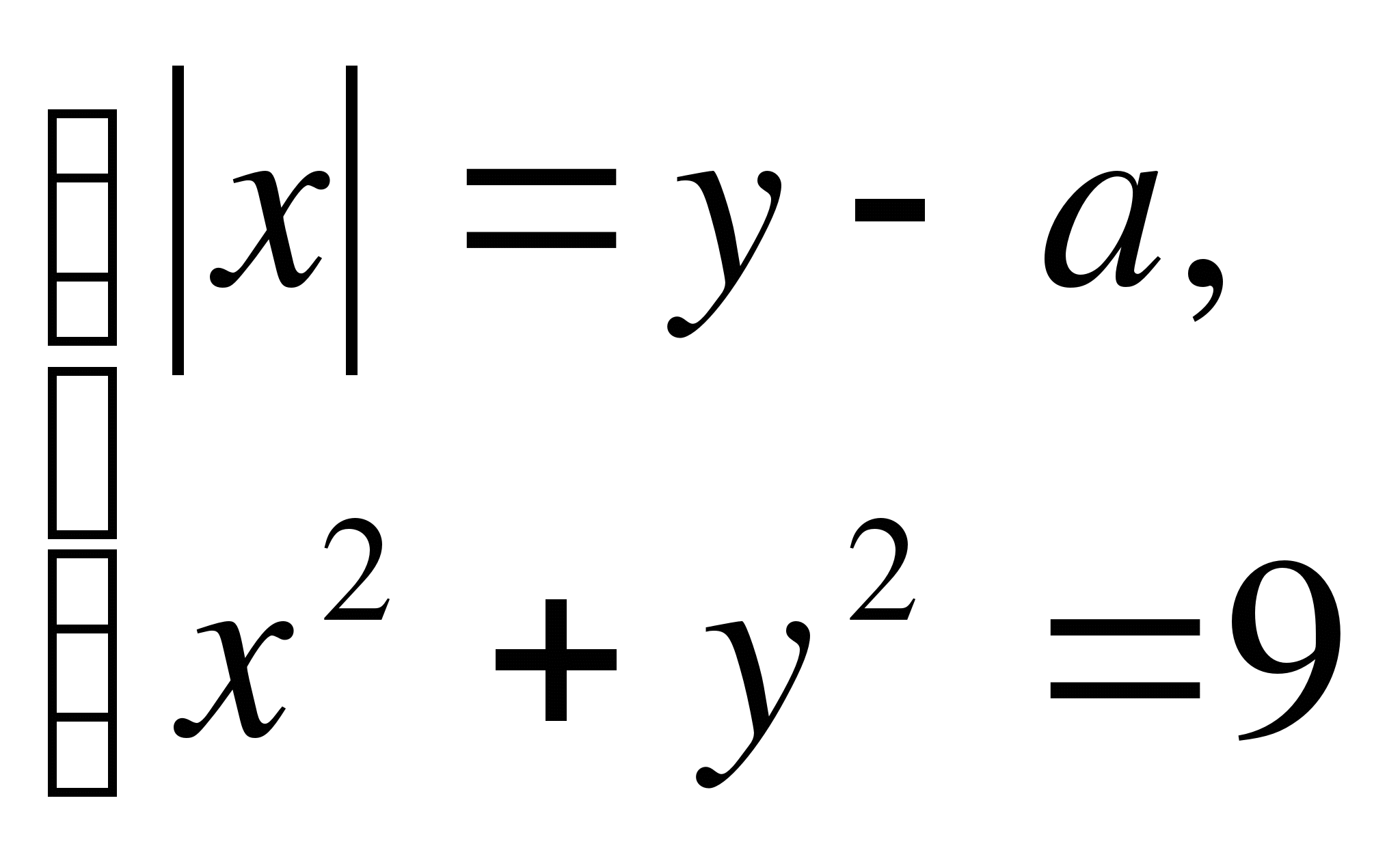 имеет ровно три решения?
имеет ровно три решения?
Решение.
Решим систему графически.
1). х2 + у2=9. Графиком является окружность с центром в точке (0;0) и R=3.
2). |х|=у-а , у=|х|+а, график данной функции получен при помощи параллельного переноса графика функции у=|х| на а единиц вдоль оси Оу.
Таким образом, исходная система имеет ровно три решения только в том случае, если графики указанных функций имеют равно три точки пересечения (см. рис.19):
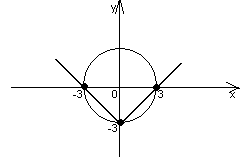 рис.19
рис.19
Пример 4. При каких значениях параметра а система
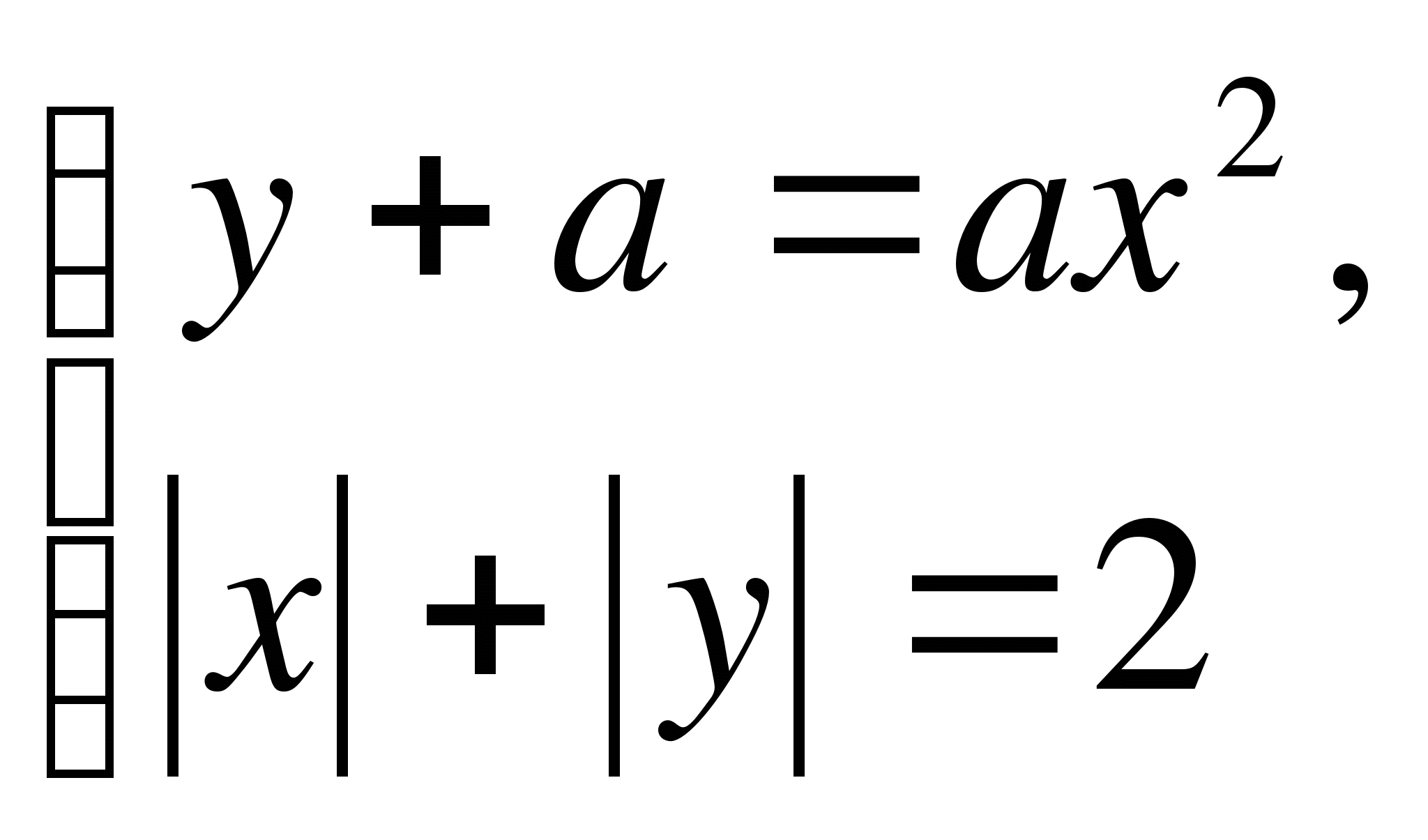 имеет наибольшее число решений?
имеет наибольшее число решений?
Решение.
Изобразим графики уравнений в одной системе координат. Из геометрических соображений видно, что система будет иметь наибольшее число решений только в том случае, если в первом уравнении системы а≠0. Тогда графиком уравнения является парабола, и наибольшее число решений (пять точек) будет иметь система, если вершина параболы находится в точке В, а ее ветви направлены вниз (см. рис. 20), или, если вершина параболы находится в точке D, а ее ветви направлены вверх (см. рис.21).
Такое возможно при а=-2 или а=2.
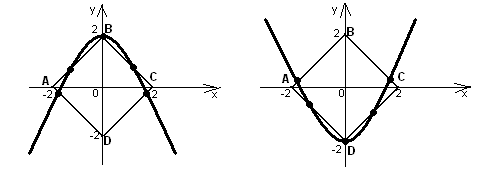
рис.20 рис.21
Ответ: а=-2 или а=2.
Пример 5. При каких значениях р двойное неравенство
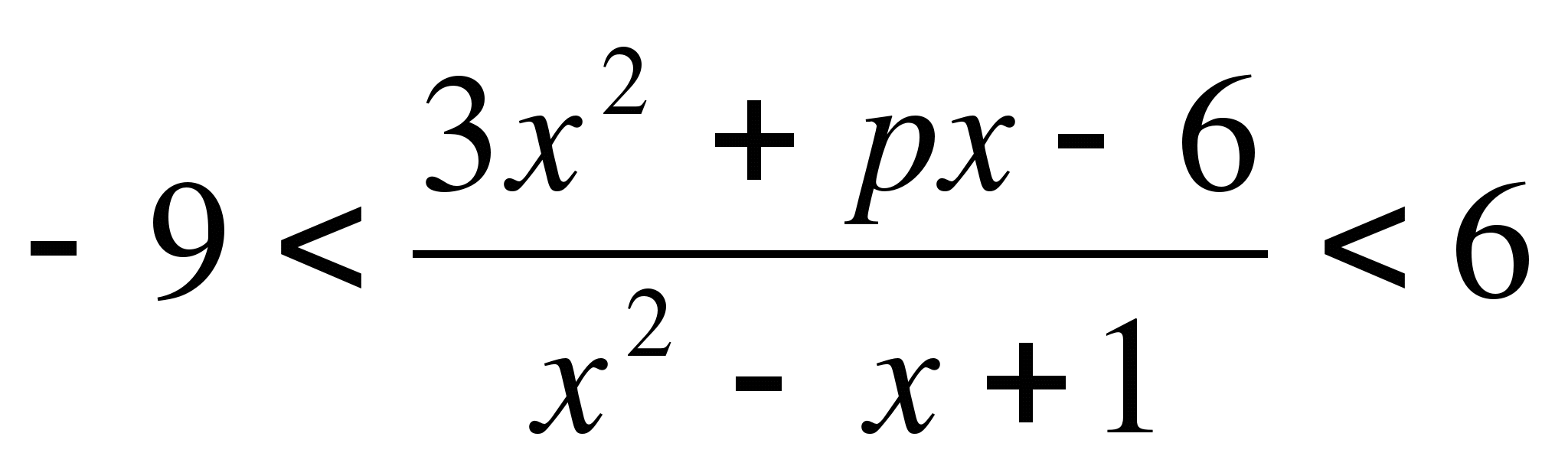
 выполняется
при всех действительных значениях х?
выполняется
при всех действительных значениях х?
Решение.
Представим данное неравенство в виде системы неравенств:
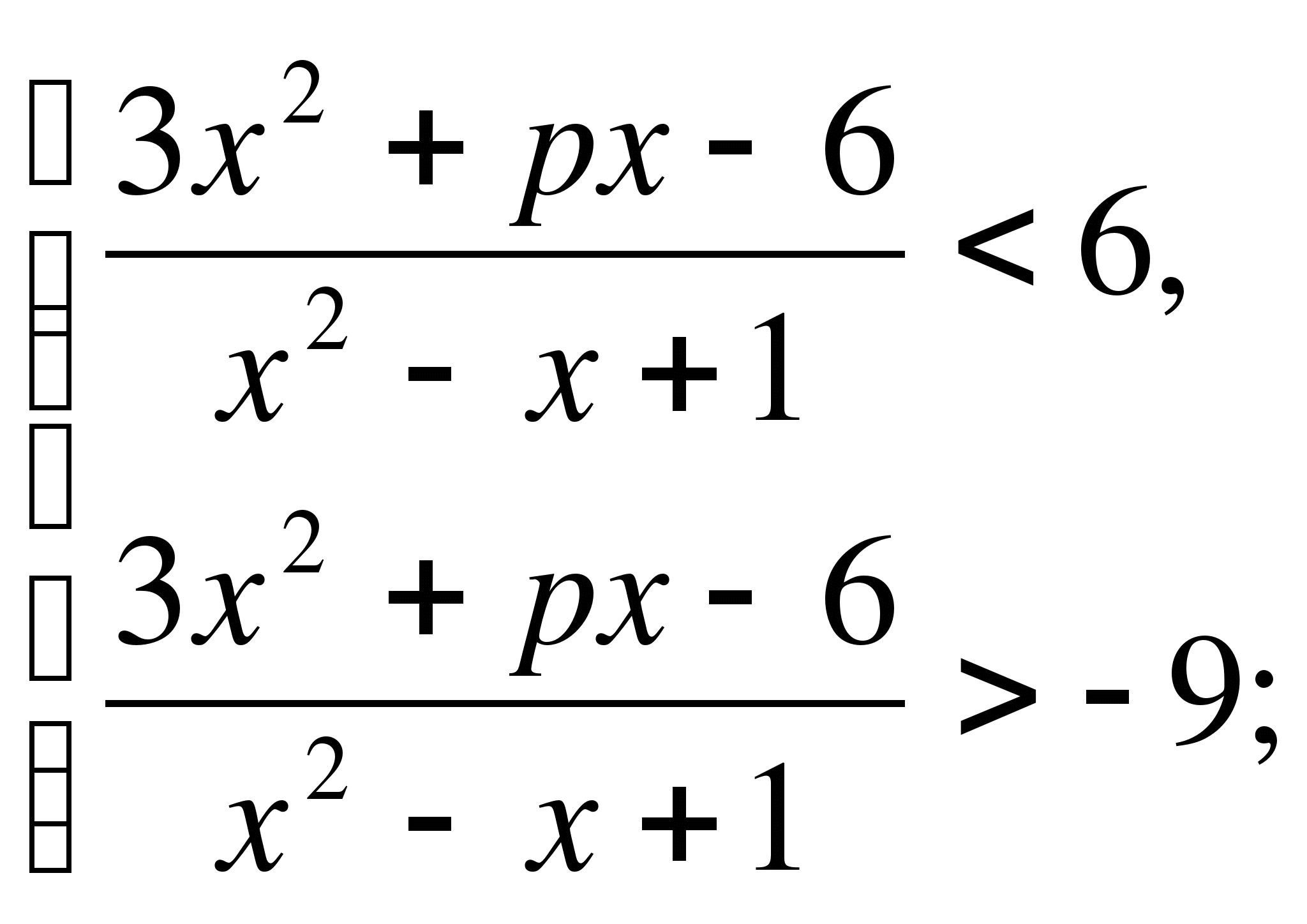 =>
=> 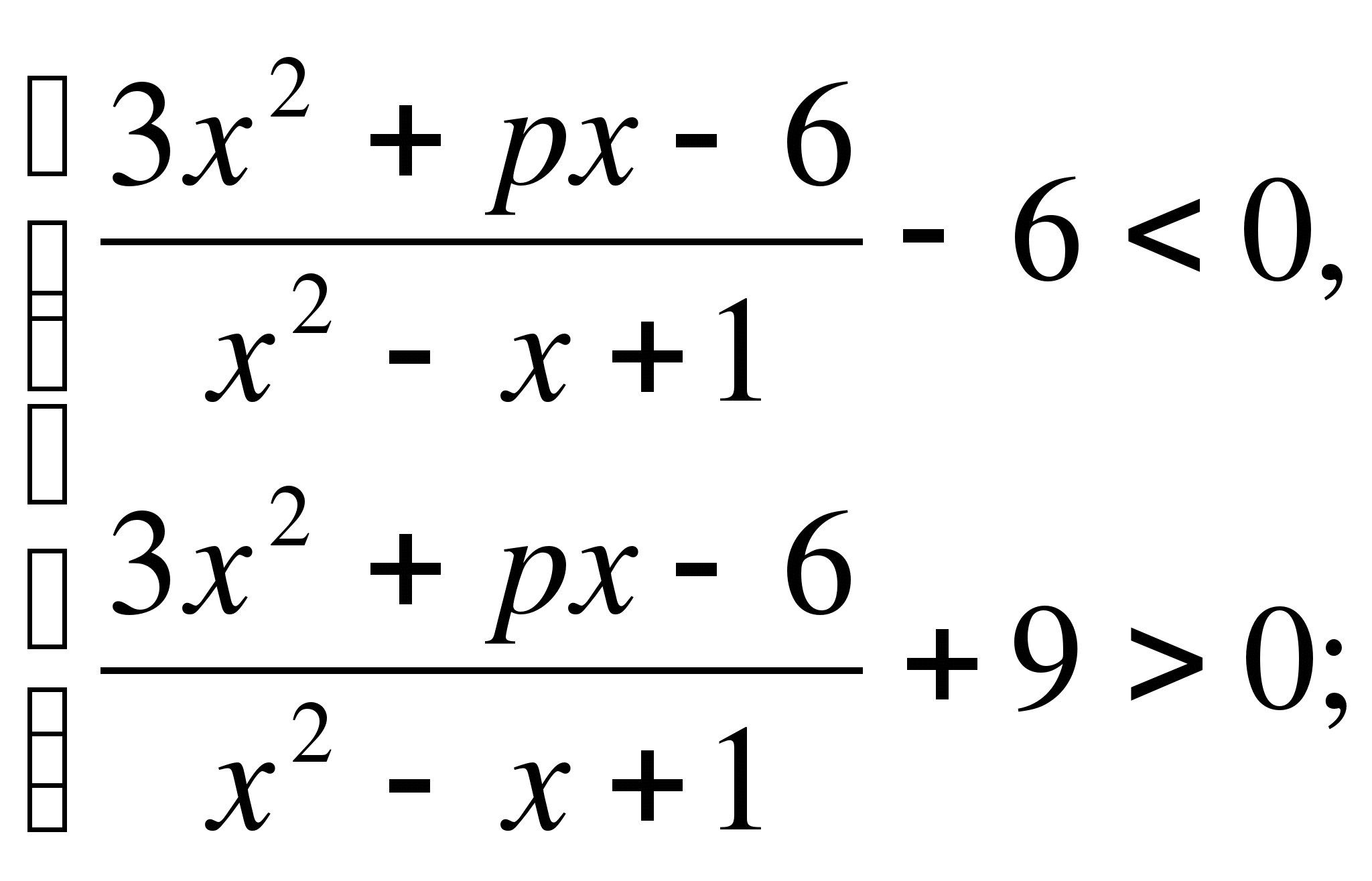 =>
=> 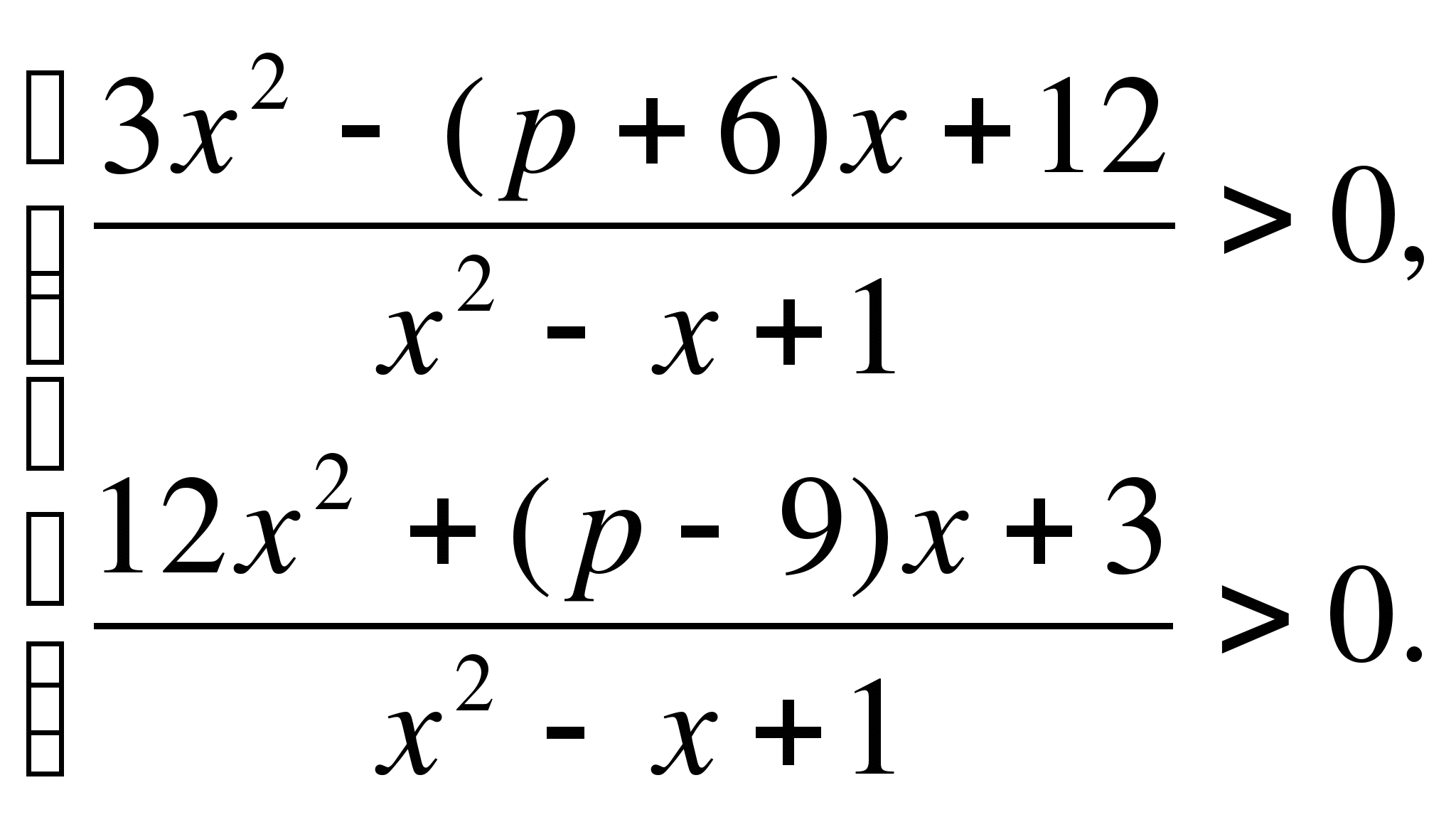
Так как х2 -х +1>0 при х Є R, то эта система неравенств равносильна системе:
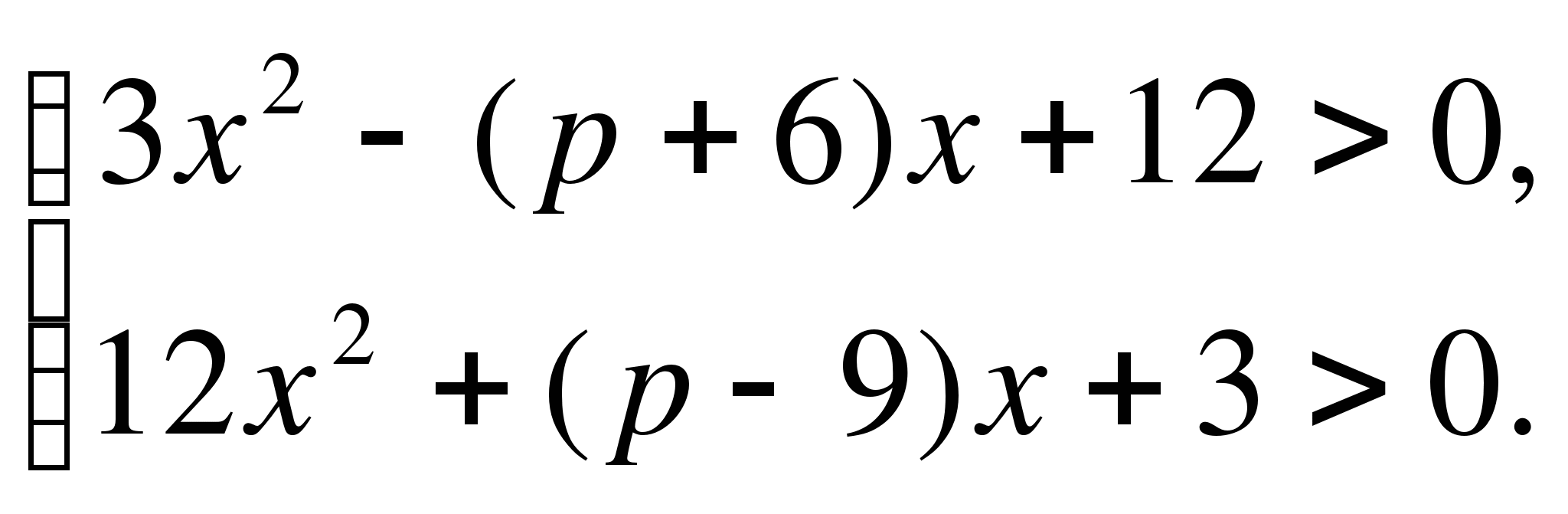
Квадратные трехчлены будут положительны для х Є R при условии отрицательности дискриминанта, т.е. D < 0. Следовательно,
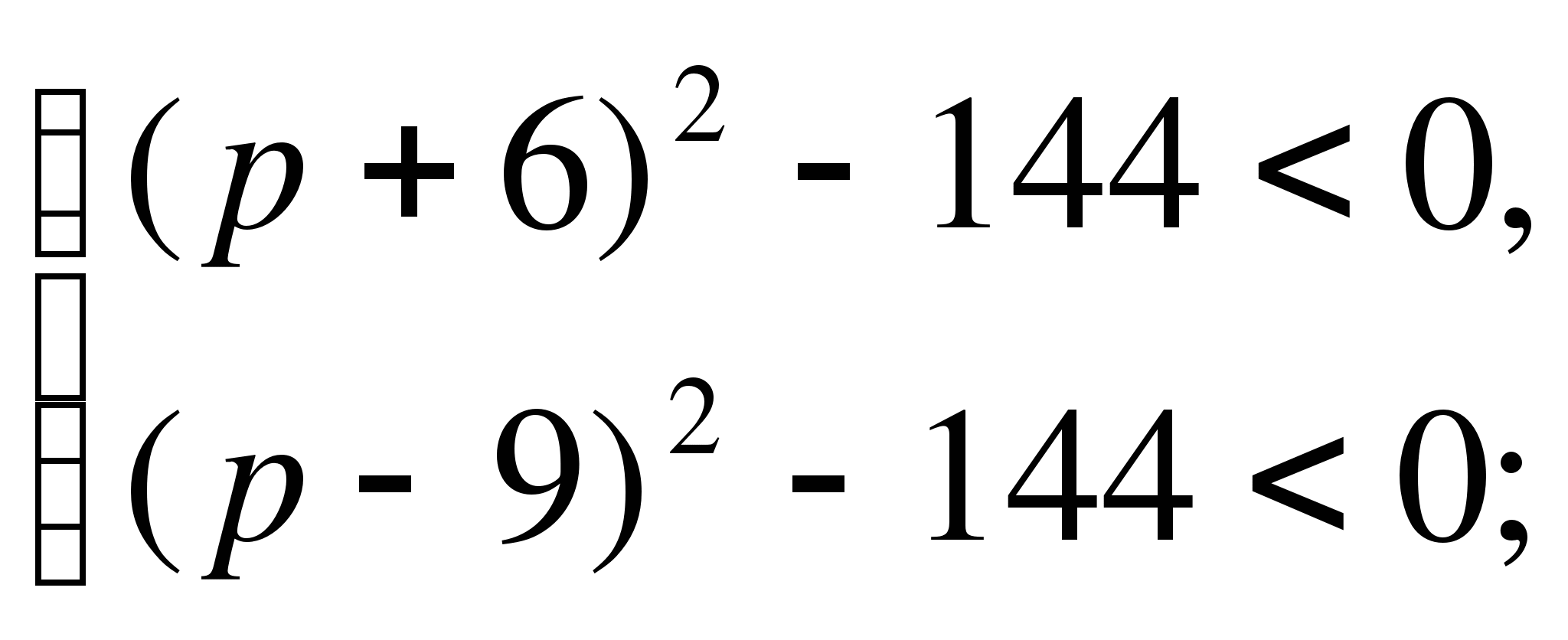 =>
=>
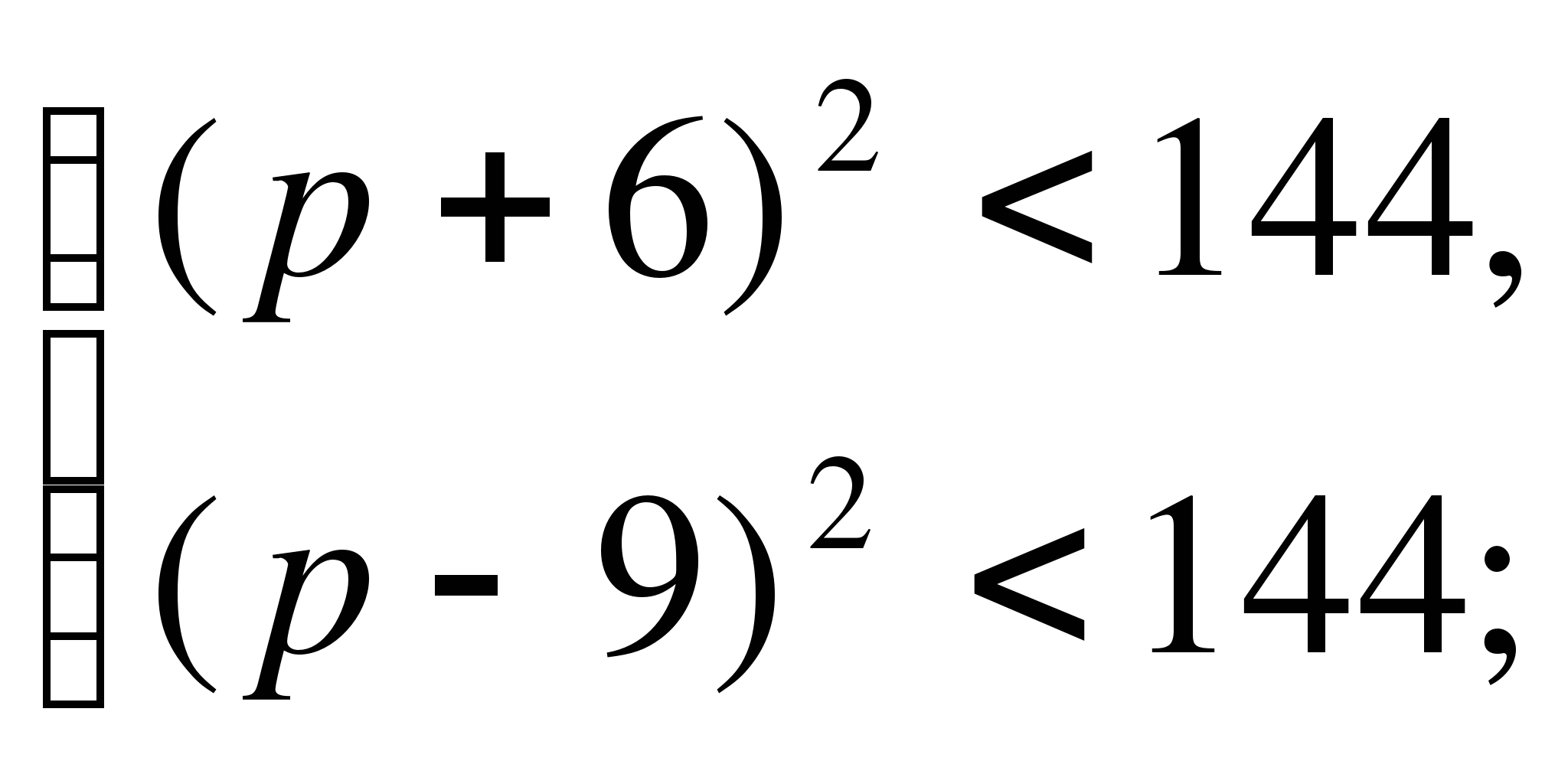 =>
=> 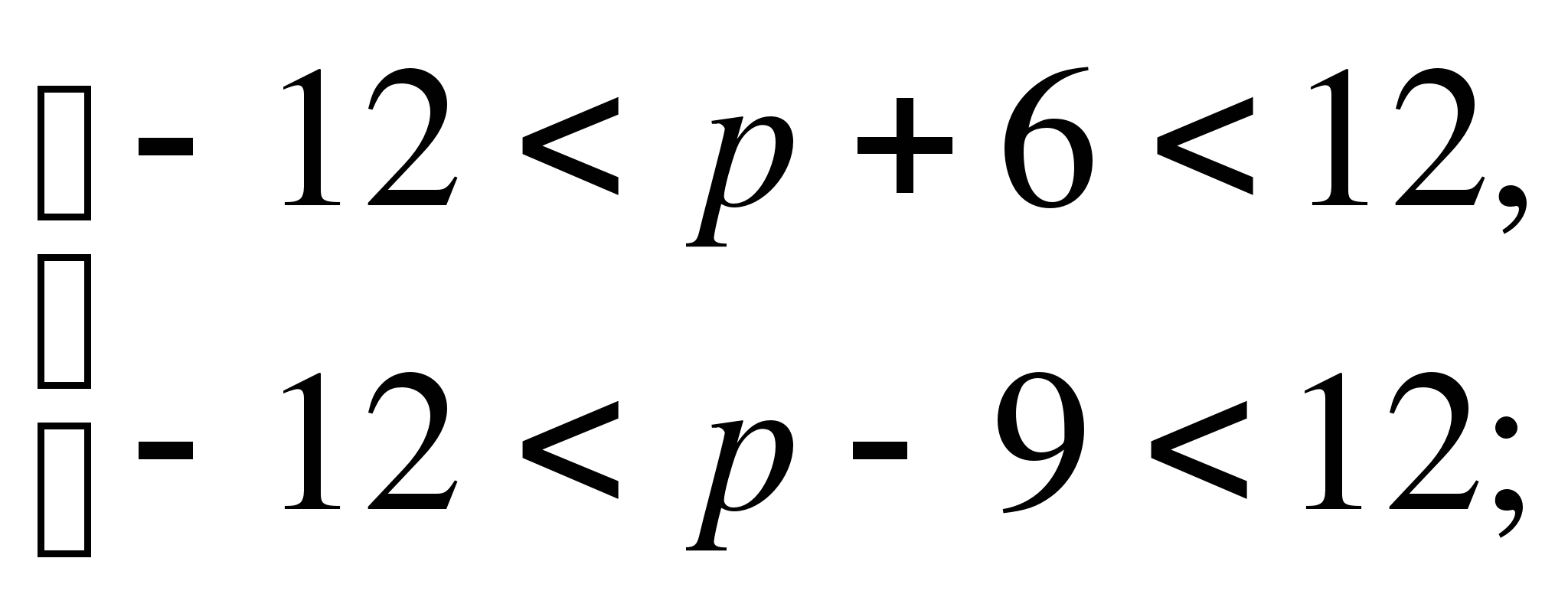 =>
=> 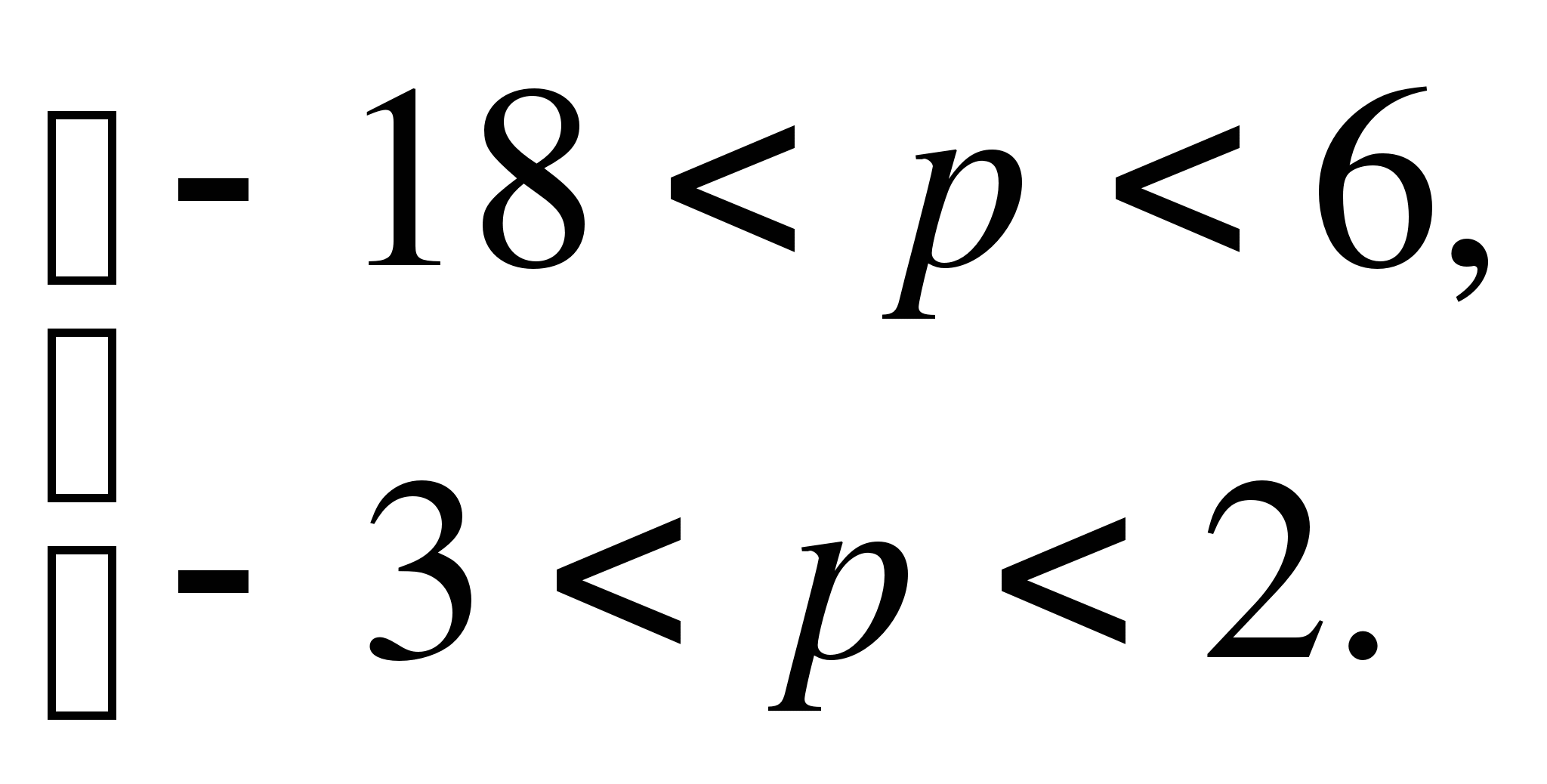
Отметив решение каждого двойного неравенства на числовой прямой, получим р Є (-3; 6).
Ответ: р Є (-3; 6).
Пример 6. Найти все значения параметра k, при каждом из которых существует хотя бы одно общее решение у неравенств x2 + 4kx + 3k2 > 1 + 2k и x2 + 2kx ≤ 3k2 - 8k + 4.
Решение. Исходная задача может быть переформулирована следующим образом: найти все значения параметра k, при каждом из которых система неравенств
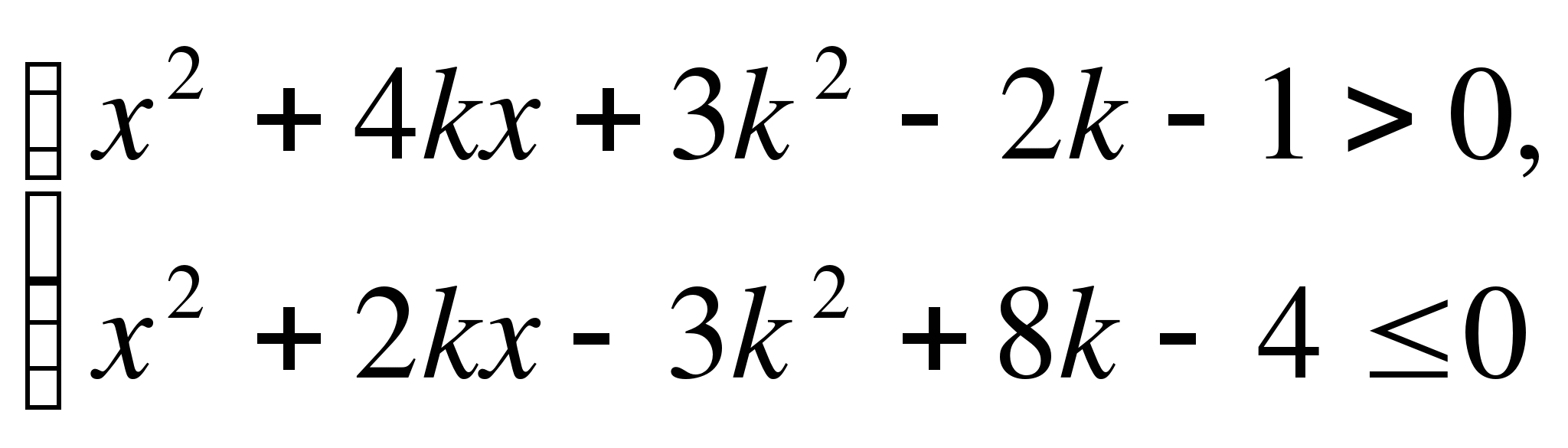 имеет хотя бы одно решение. При любом фиксированном
k корнями квадратного уравнения x2 +
2kx - 3k2 + 8k - 4 = 0
являются числа х1=k-2,
x2=-3k+2. Поэтому множество решений
второго неравенства системы есть интервал, образуемый
точками, лежащими между данными корнями.
имеет хотя бы одно решение. При любом фиксированном
k корнями квадратного уравнения x2 +
2kx - 3k2 + 8k - 4 = 0
являются числа х1=k-2,
x2=-3k+2. Поэтому множество решений
второго неравенства системы есть интервал, образуемый
точками, лежащими между данными корнями.
Найдём все значения k, при которых рассматриваемая система неравенств не имеет решений. Система не имеет решений (см. рис.17) тогда и только тогда, когда выполняются условия:
где f(x)= x2 + 4kx + 3k2 - 2k -1.
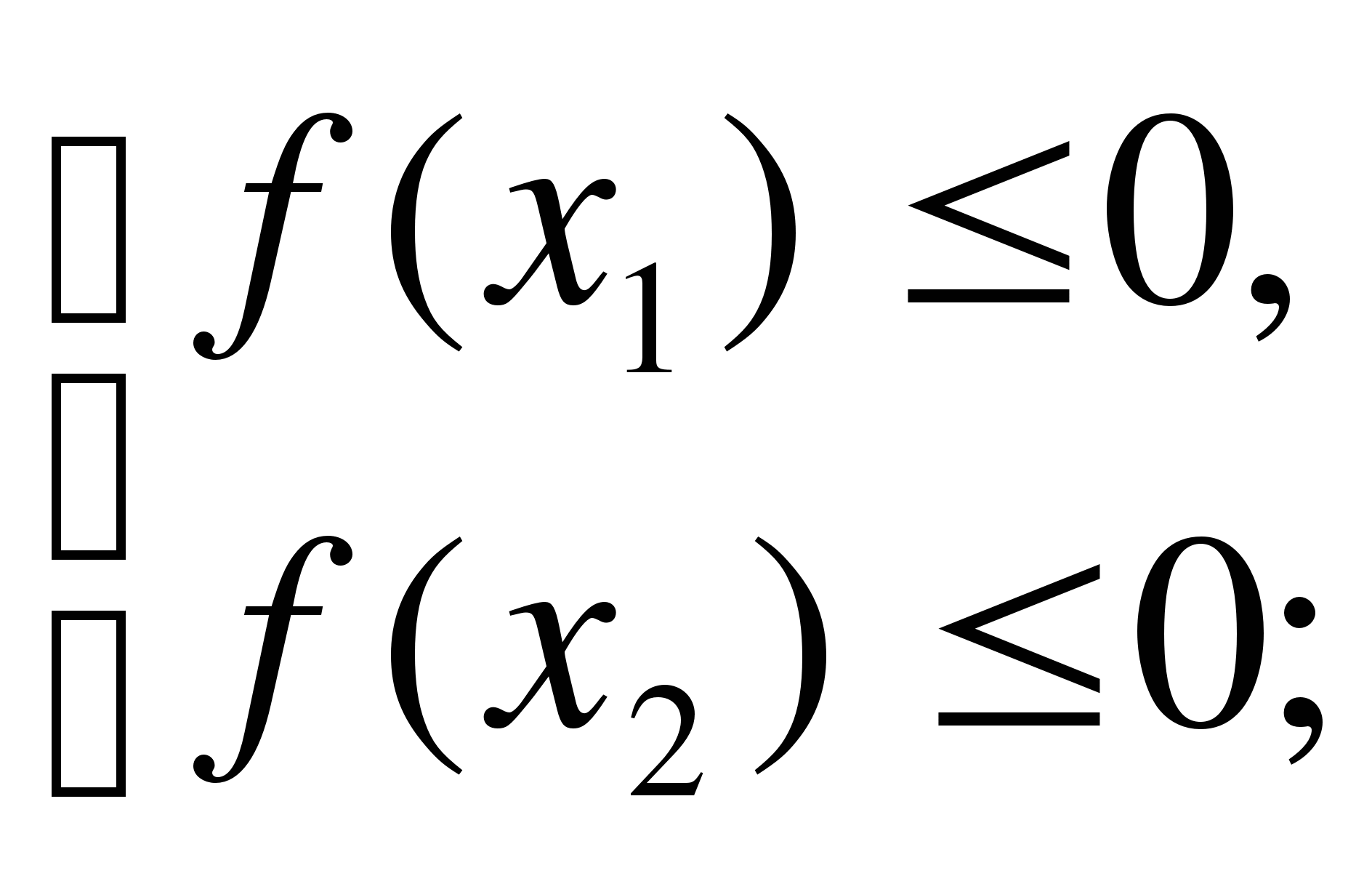
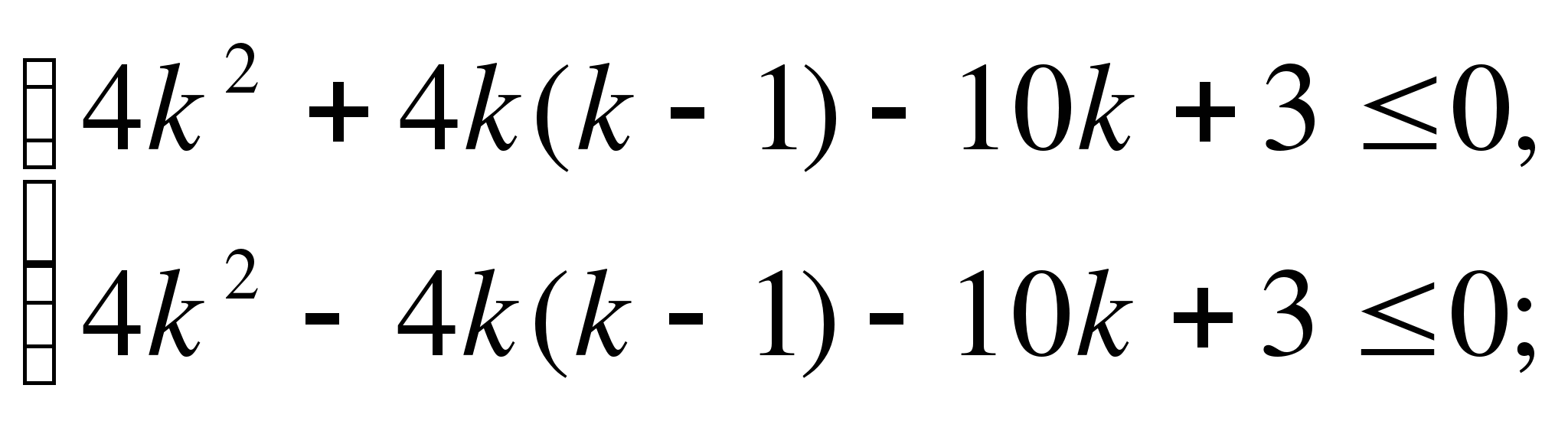
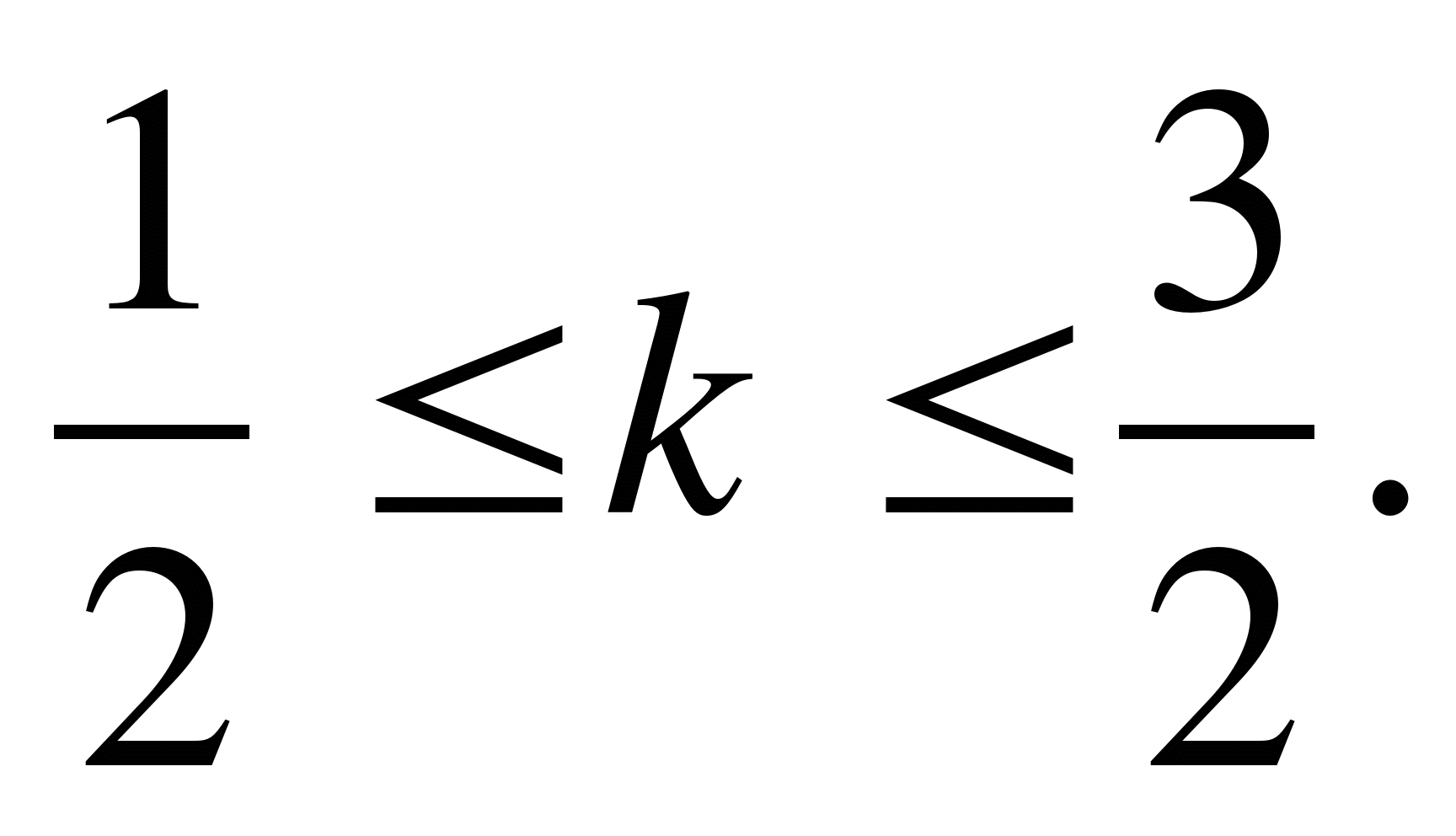
Рис.17
Таким образом, система неравенств не имеет решений при kє
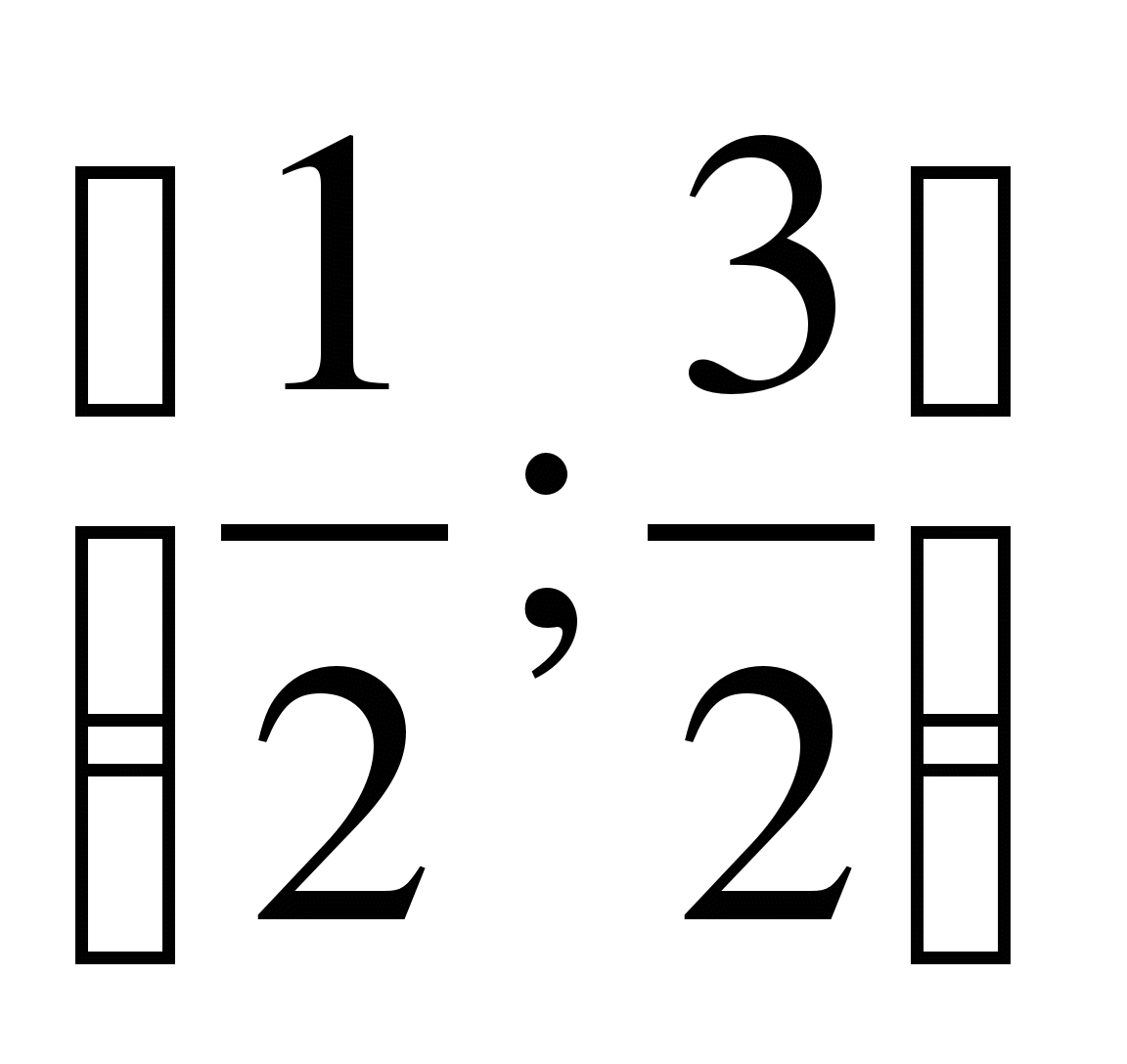 .
.
Значит, при kє(-∞;
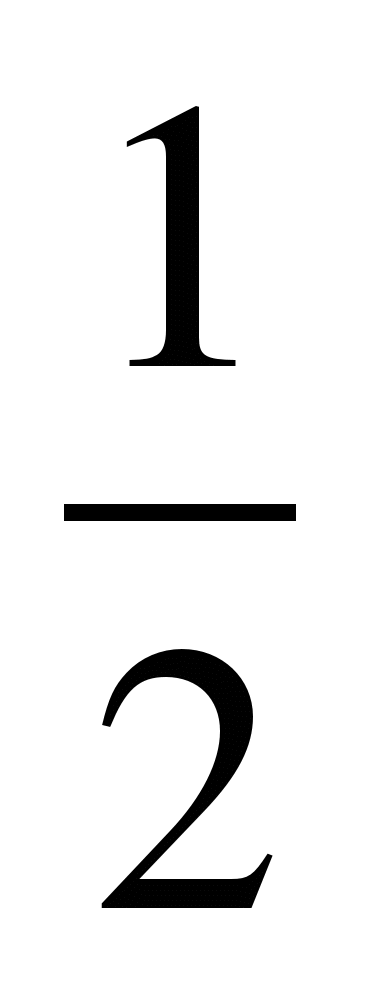 )U(
)U(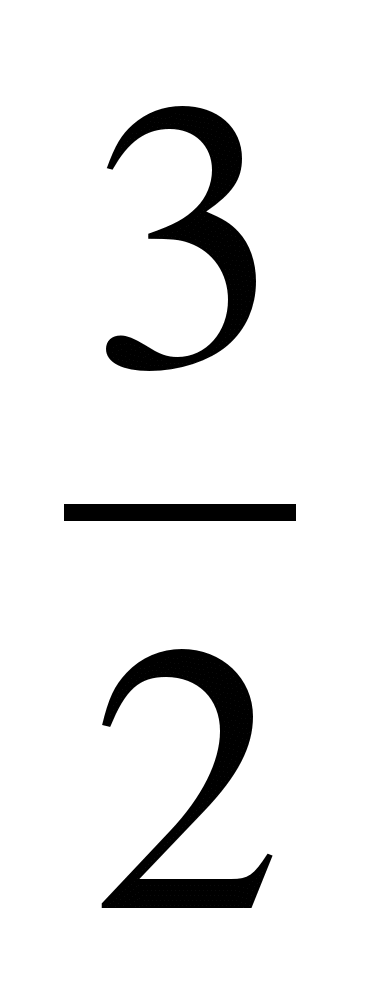 ;+∞)
данная система имеет хотя бы одно решение.
;+∞)
данная система имеет хотя бы одно решение.
Ответ: kє(- ∞;
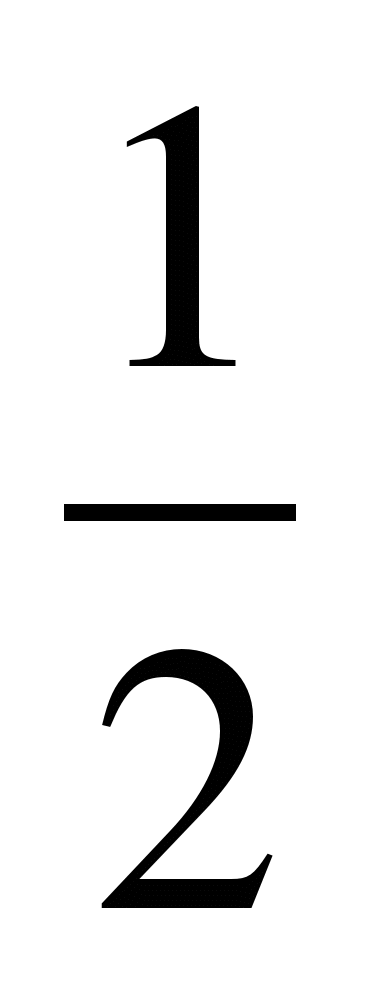 )U(
)U(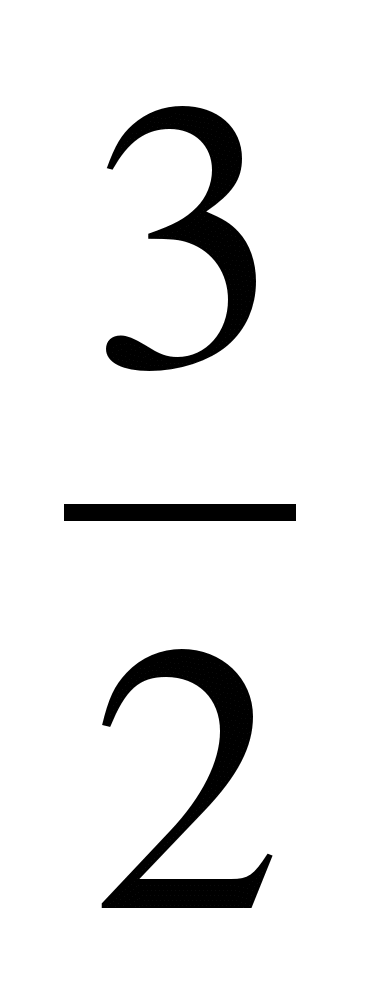 ;+
∞).
;+
∞).
Пример 7. Для каждого значения параметра а решить систему неравенств
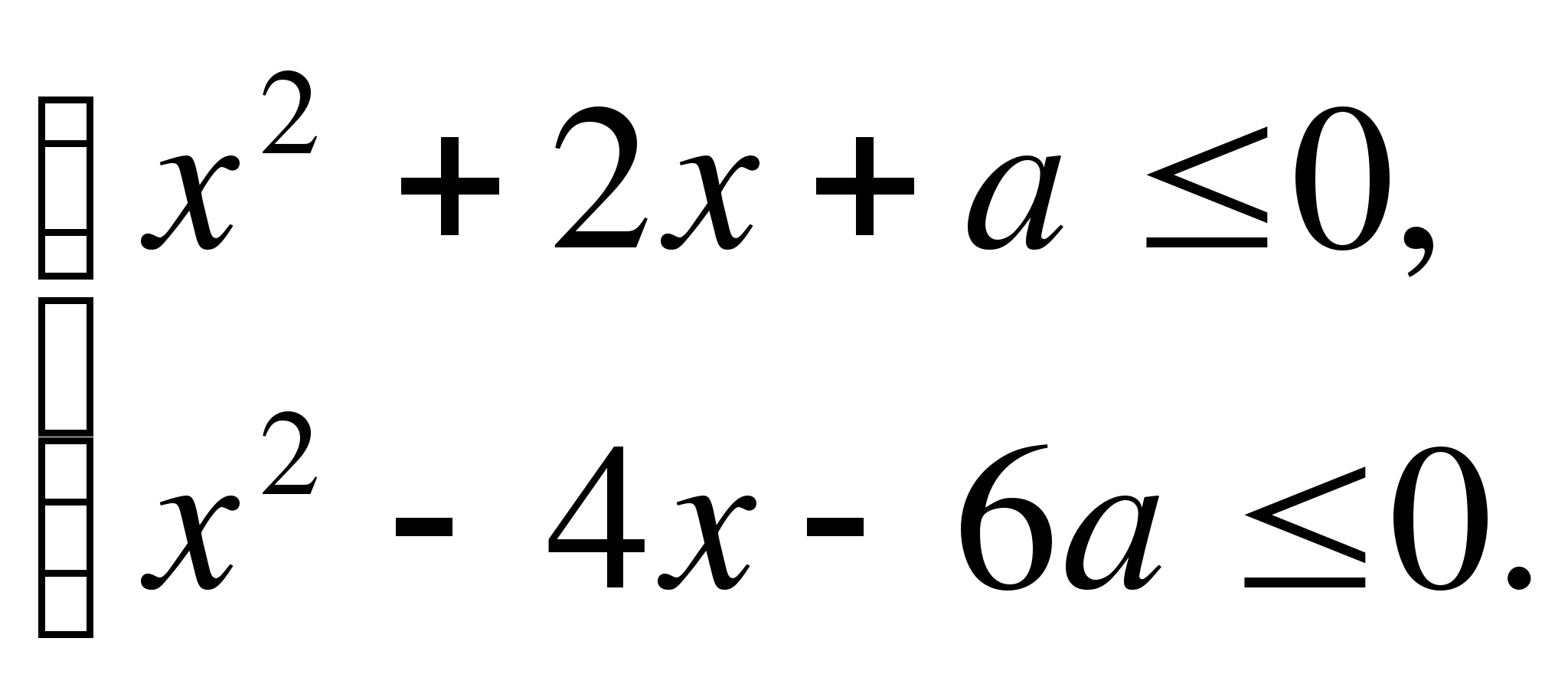
Решение. Вычислим дискриминанты первого и второго квадратных трёхчленов: D1= 4-4а, D2= 16+24a. Чтобы система неравенств имела решения, необходимо, чтобы D1,2≥0, т.е. aє [-
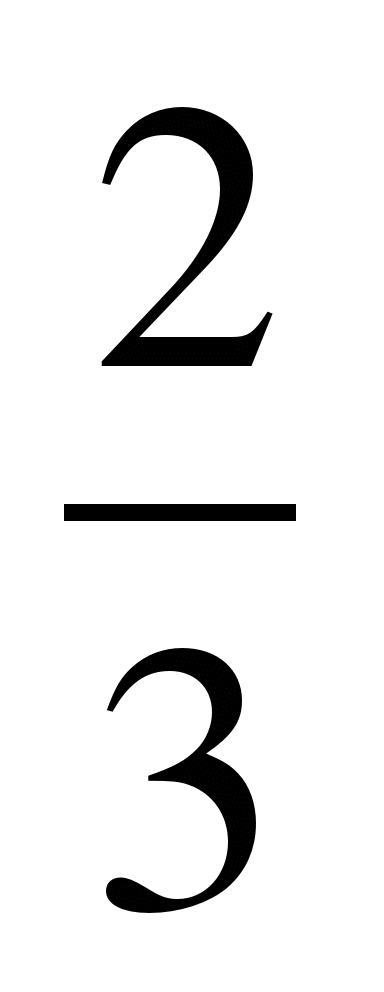 ;1].
С учётом того, что абсцисса вершины графика квадратного
трёхчлена
f2(x)=x2-4x-6a равна 2,
возможны следующие четыре случая расположения графиков
квадратных трёхчленов у=
f1(x)=x2 +2x+a и у=
f2(x)=x2-4x-6a, имеющих
пересечения с осью абсцисс (см. рис.22-25).
;1].
С учётом того, что абсцисса вершины графика квадратного
трёхчлена
f2(x)=x2-4x-6a равна 2,
возможны следующие четыре случая расположения графиков
квадратных трёхчленов у=
f1(x)=x2 +2x+a и у=
f2(x)=x2-4x-6a, имеющих
пересечения с осью абсцисс (см. рис.22-25).
Рис.22 Рис.23
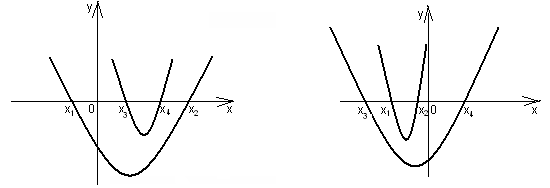
Рис.24 Рис.25
Далее в решении х1,2 - корни уравнения f1(x)=0, а х3,4 - корни уравнения f2(x)=0 (см. рис.26).
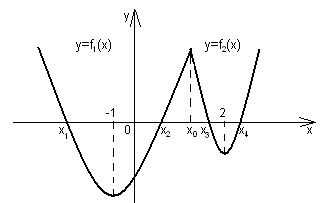
рис. 26
Найдём абсциссу точки пересечения двух графиков: f1(x)=x2 +2x+a=x2-4x-6a= f2(x) => x0=
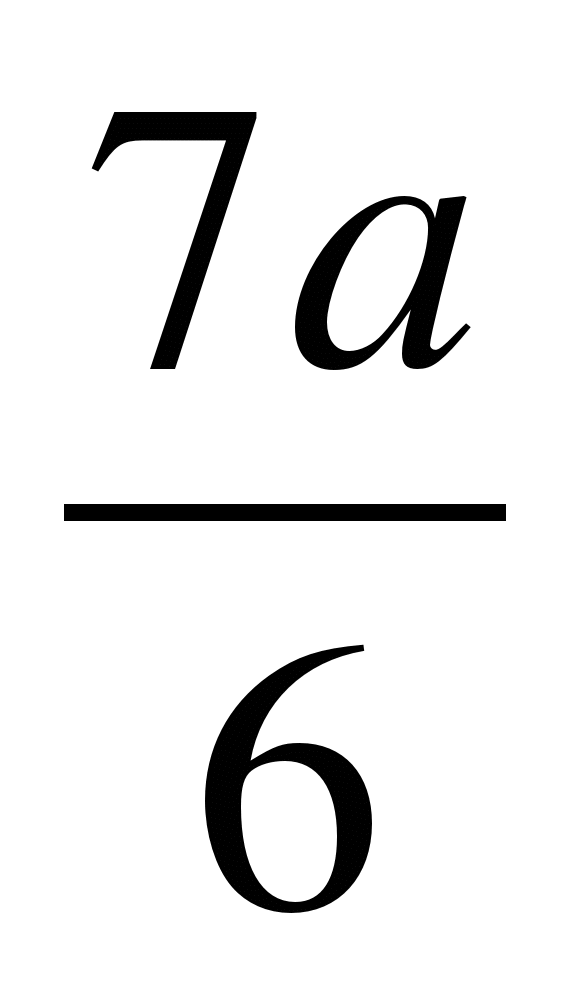 .
.
Система неравенств имеет единственное решение x0=
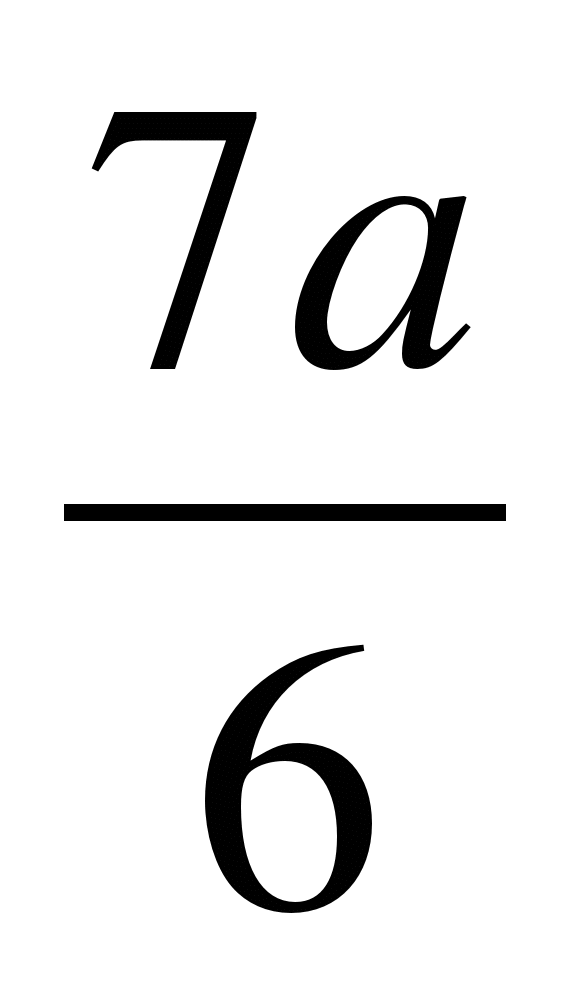 ,
если
,
если 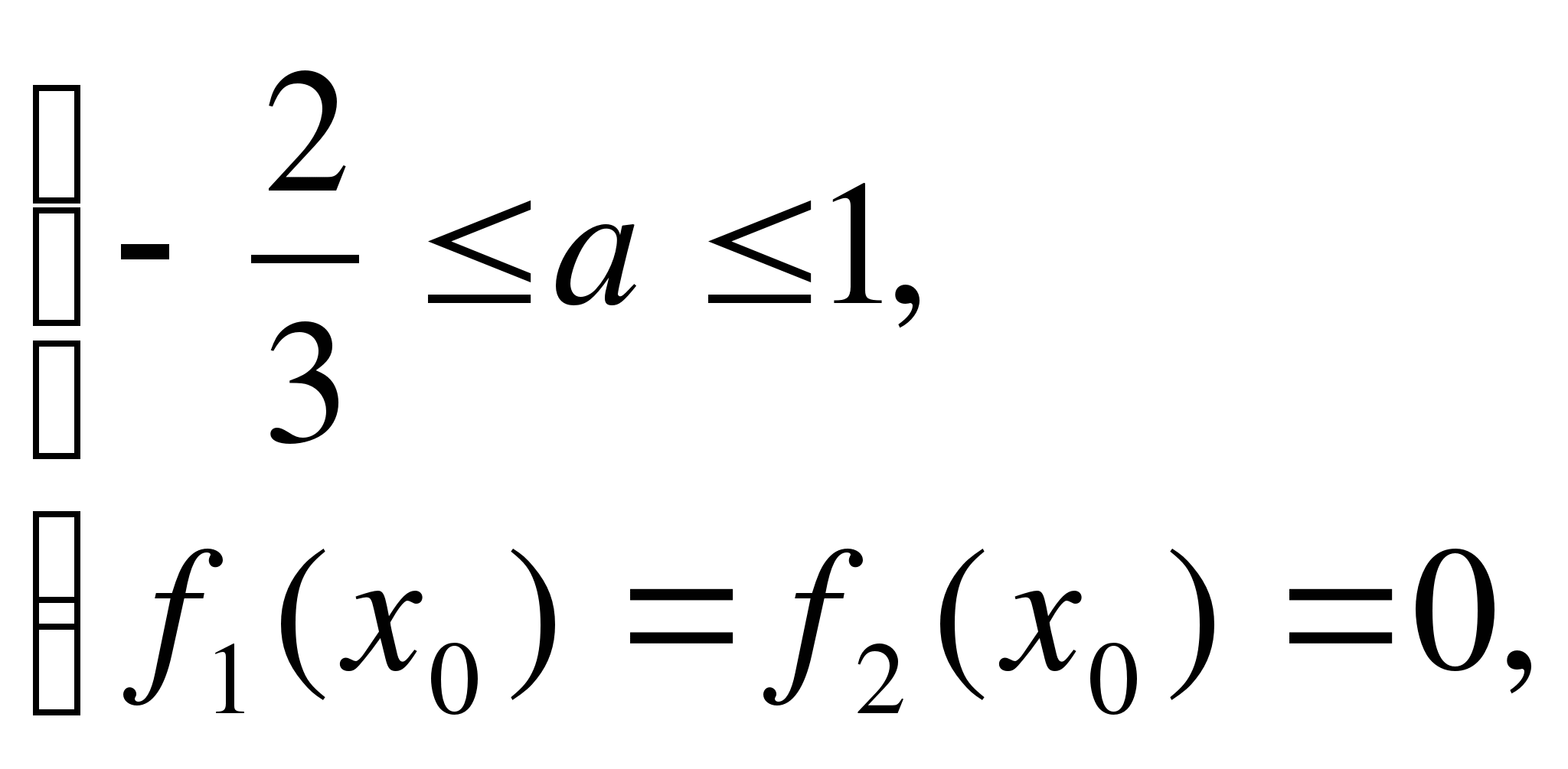
т. е. если а=0, х=0 (см. рис. 22).
Система имеет решение хє[x3;x2] (см. рис.23), если
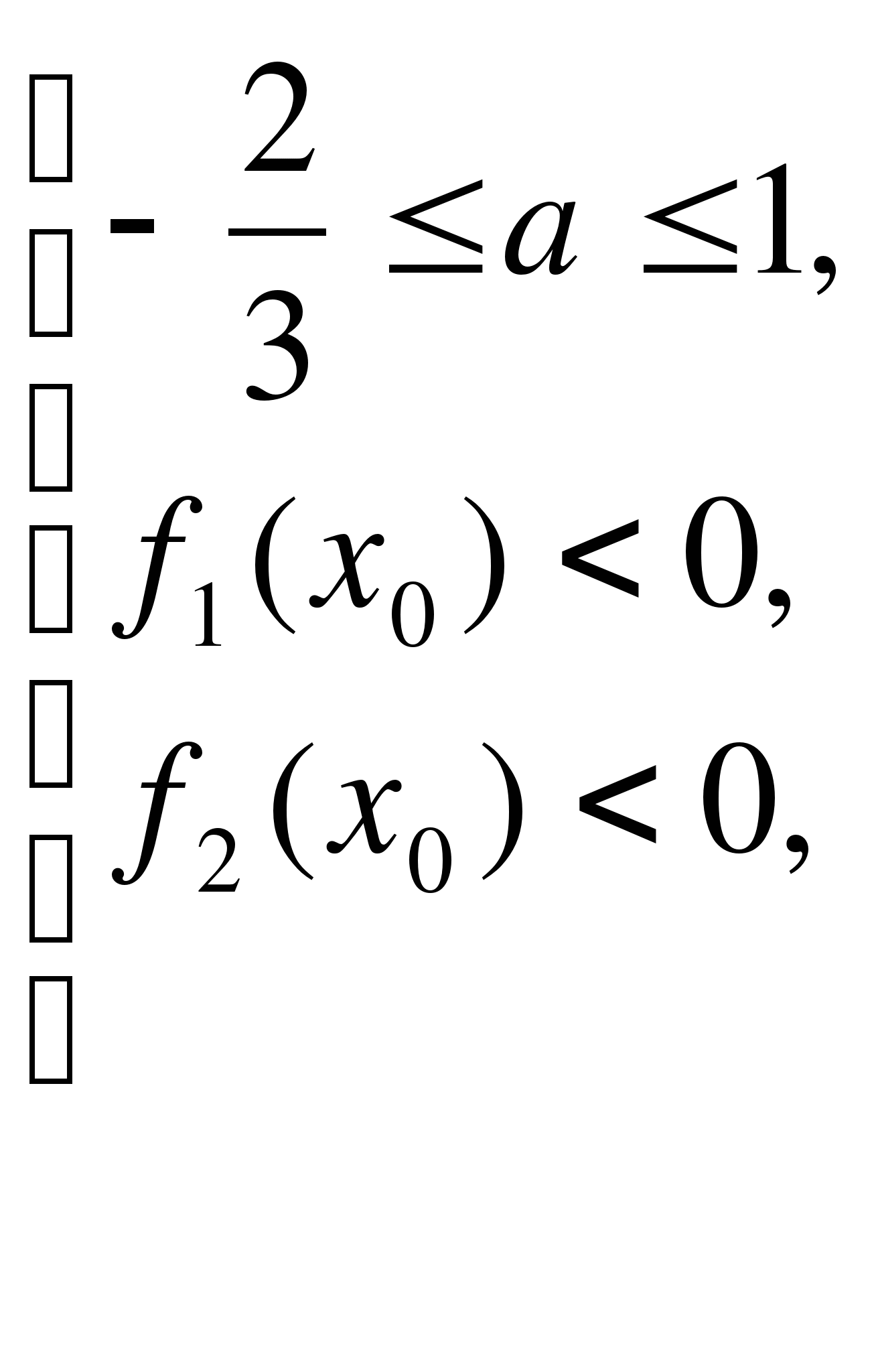 т.е. при ає Ø.
т.е. при ає Ø.
Система имеет решение хє[x3;x4] (см. рис.24), если
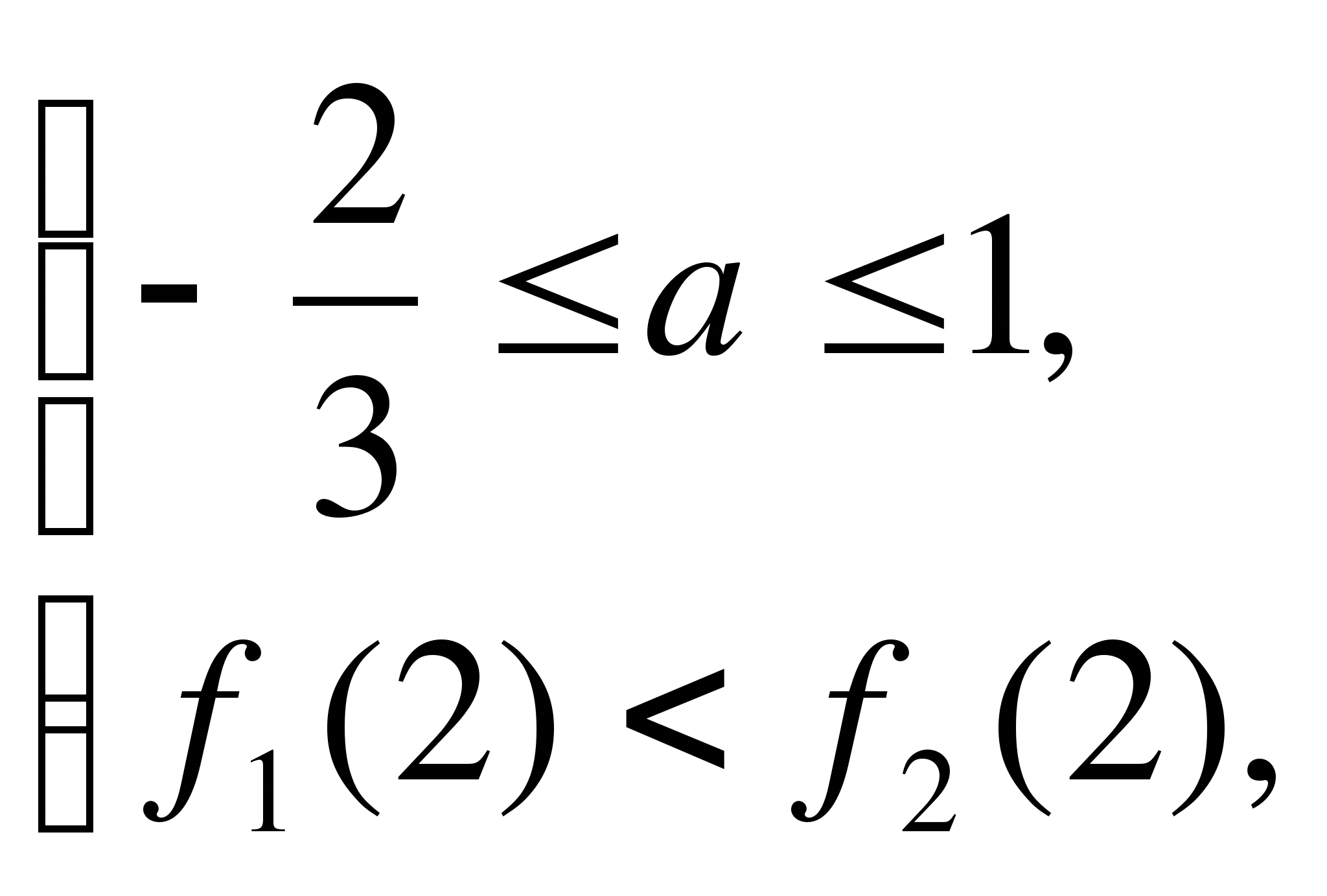 т.е. при аєØ.
т.е. при аєØ.
Система имеет решение хє[x1;x2] (см. рис.25), если
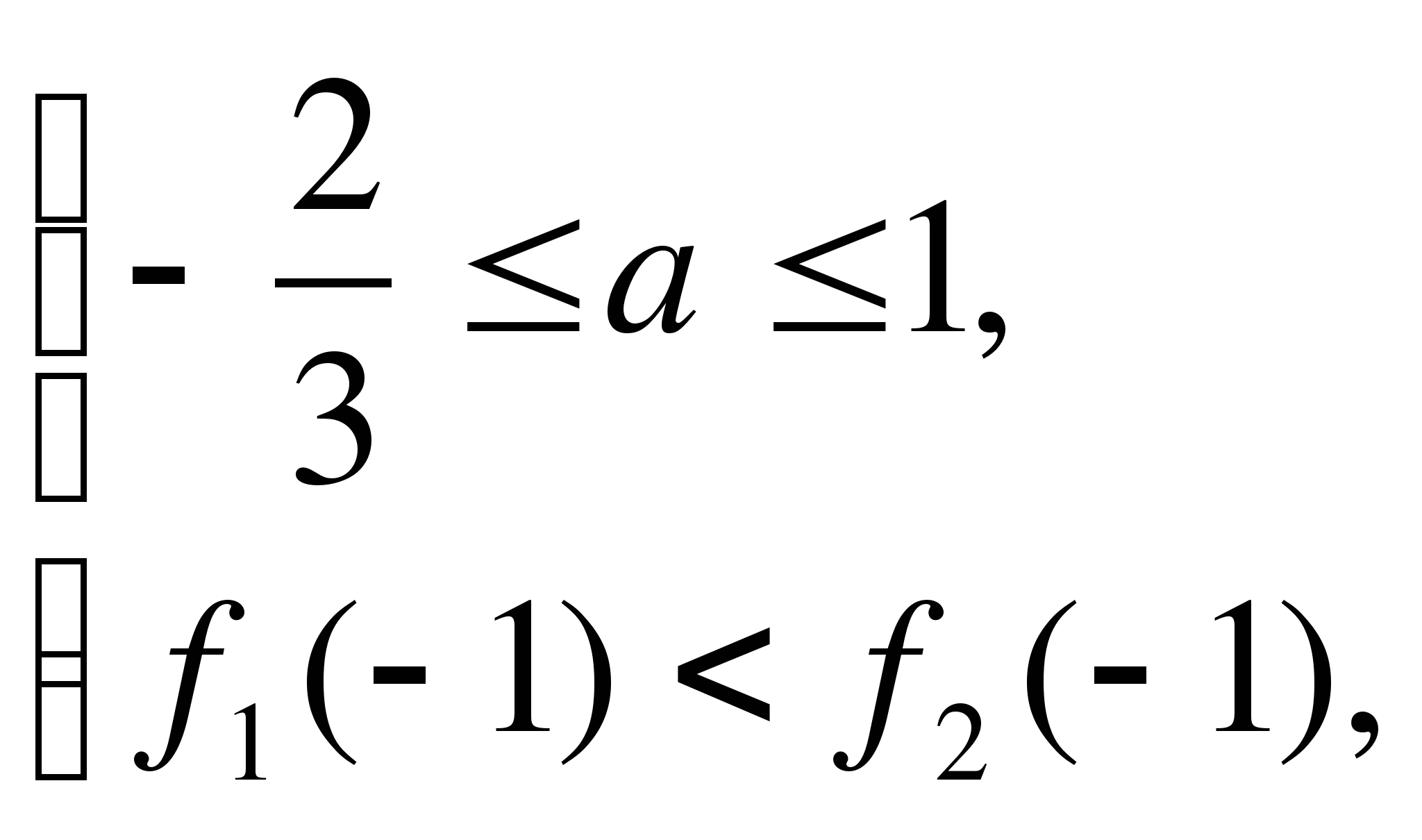 т.е.
при аєØ.
т.е.
при аєØ.
Во всех остальных случаях исходная система неравенств не имеет решений.
Ответ: если а=0, то х=0; если ає (-∞;0)U(0;+∞), то нет решений.
Пример 8. Найти все значения параметра а, при которых система неравенств
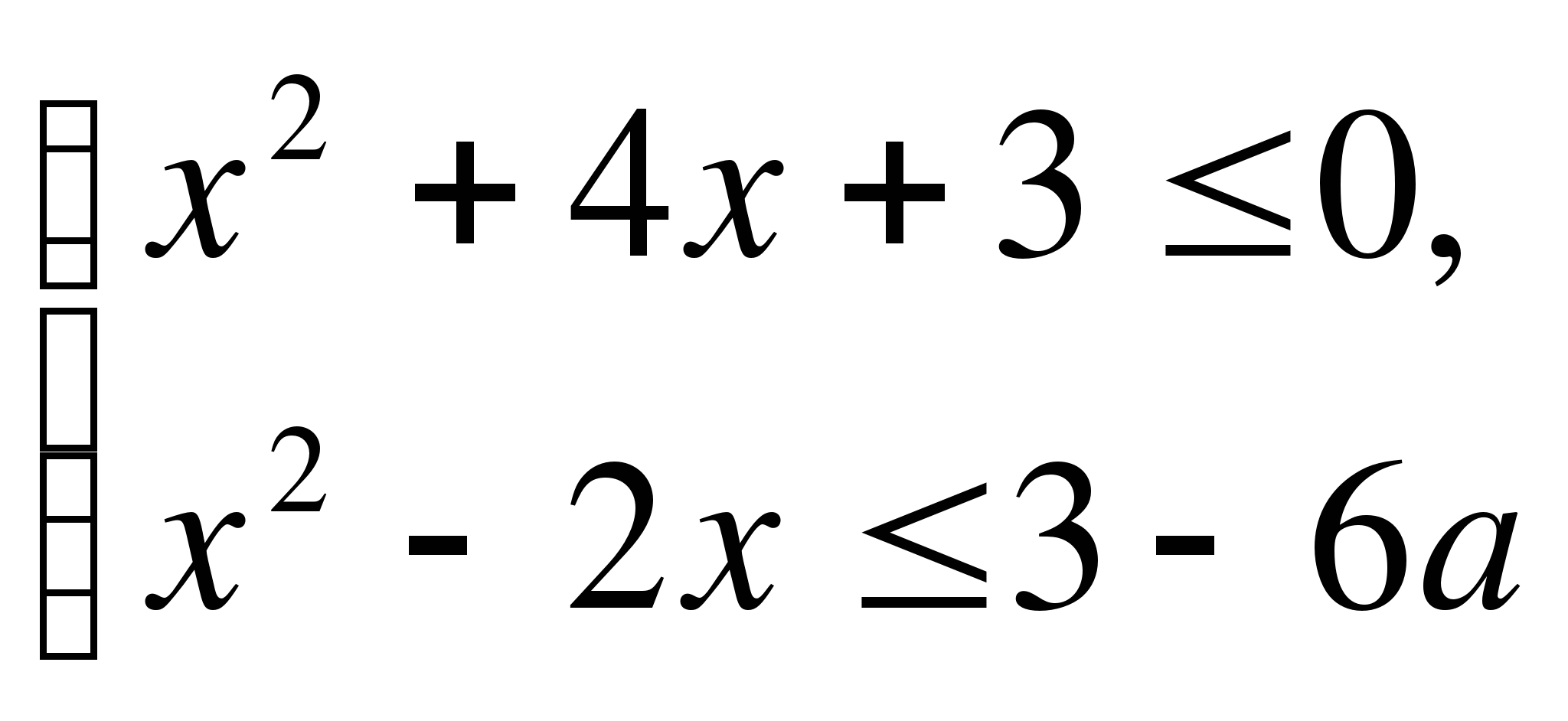 имеет единственное решение?
имеет единственное решение?
Решение. Данная система равносильна системе
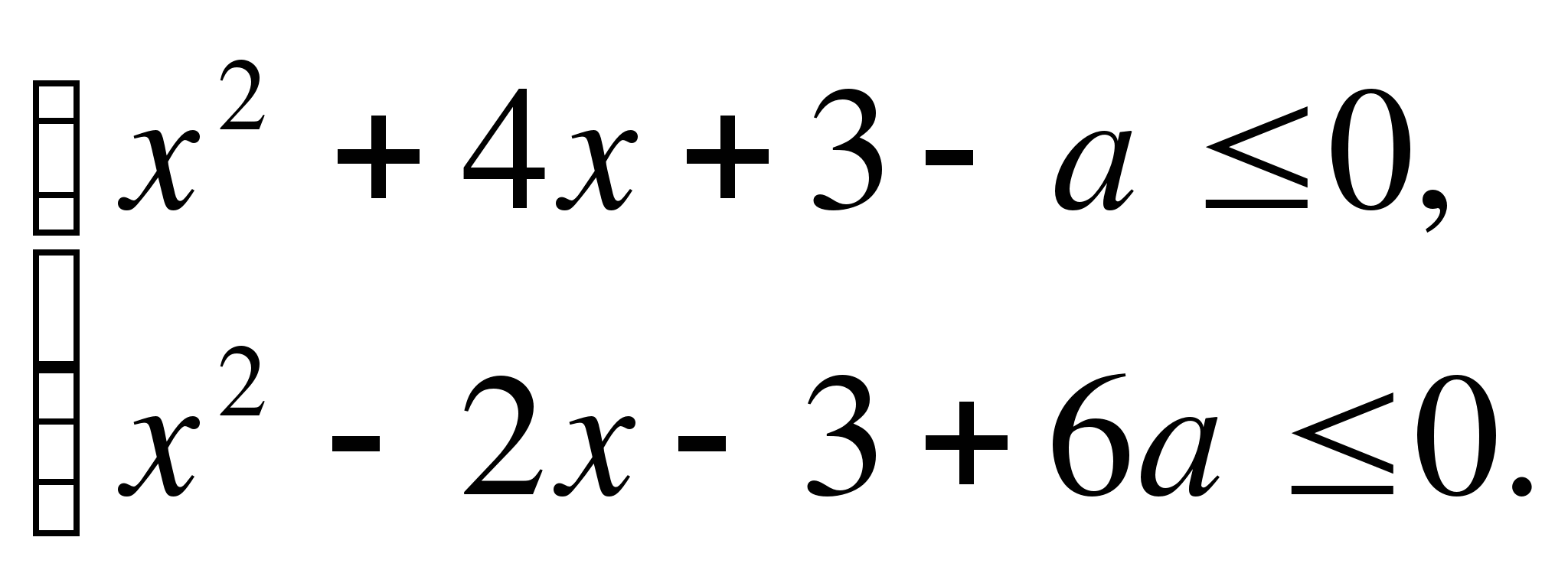

Дискриминанты трёхчленов, стоящих в левых частях, соответственно равны D1=1+a, D2 = 4-6a. Система неравенств может иметь решения только при таких значениях а, для которых одновременно выполнены неравенства D1,2≥0, то есть лишь при ає
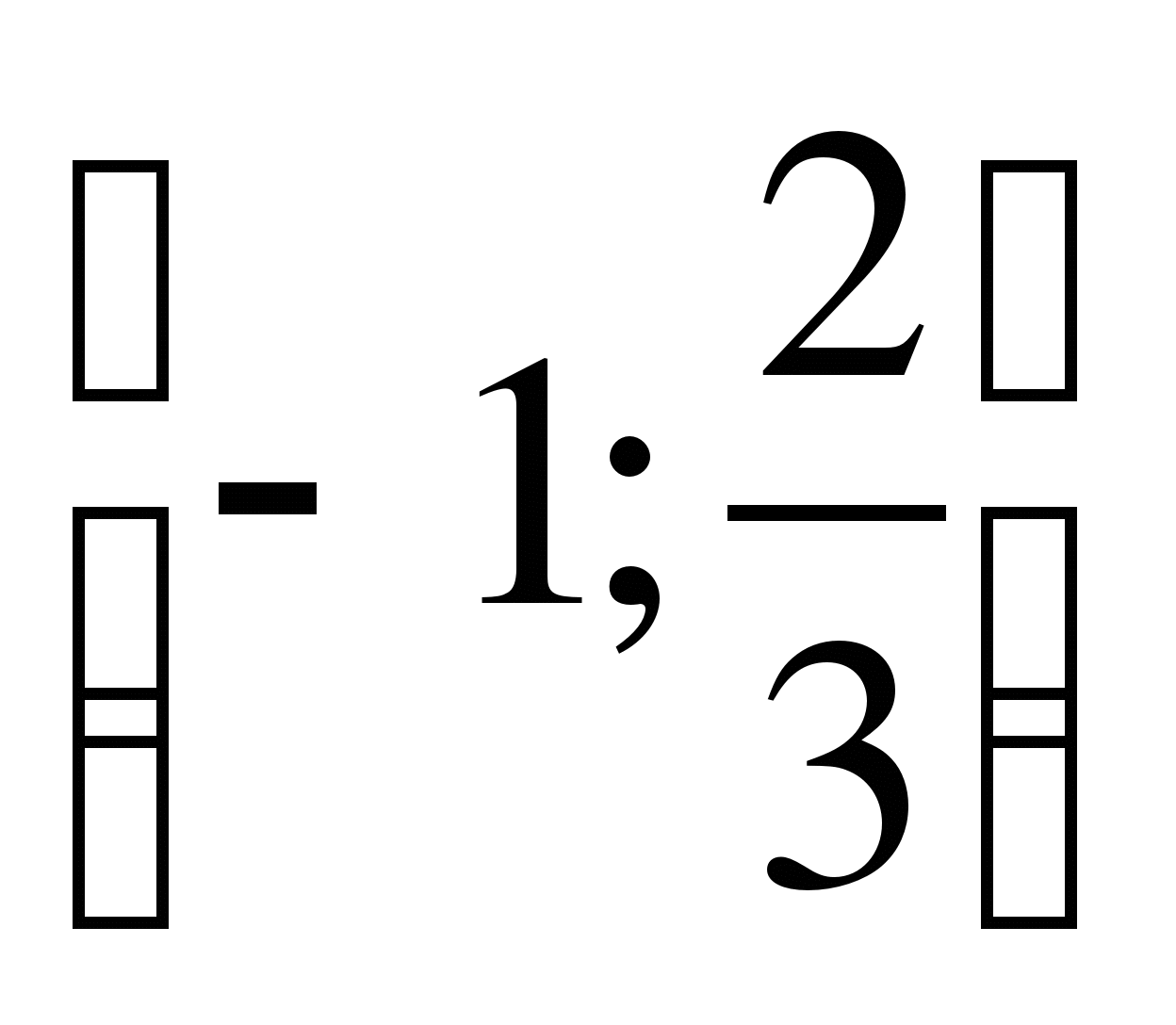 .
.
Пусть а = -1. Тогда первое неравенство системы справедливо только при х = -2. Непосредственно проверяется, что это значение удовлетворяет и второму неравенству. Таким образом, при а = -1 система неравенств имеет единственное решение.
Пусть а =
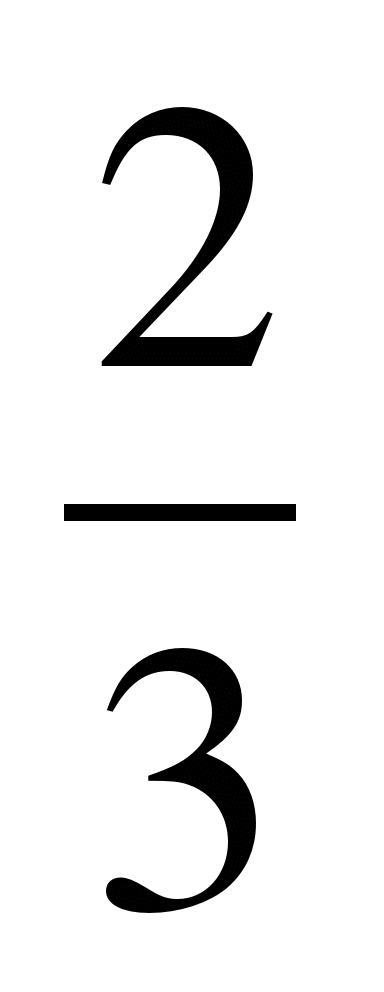 .
Тогда второе неравенство выполняется только при х=1, а
первое - при х=1 несправедливо.
.
Тогда второе неравенство выполняется только при х=1, а
первое - при х=1 несправедливо.
Следовательно, при а =
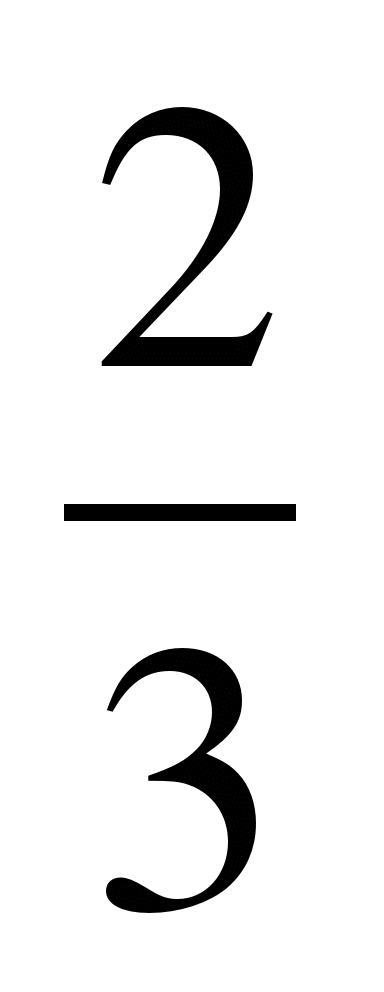 система неравенств не имеет решений.
система неравенств не имеет решений.
Пусть теперь а- некоторое число из промежутка (-1;
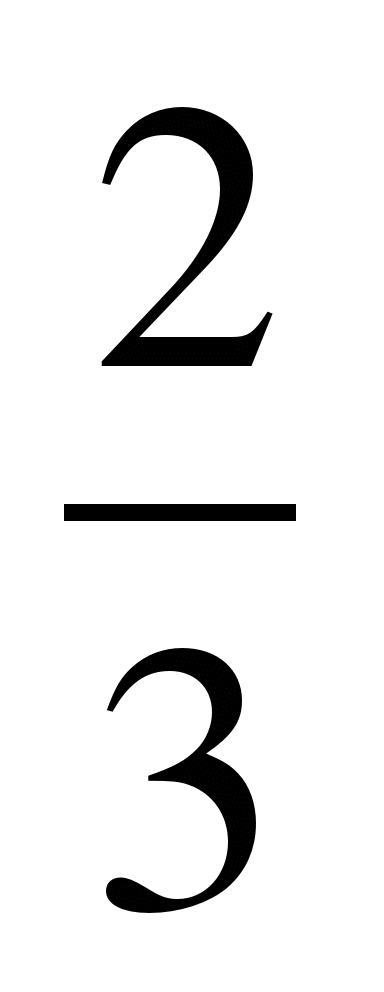 ).
В этом случае решением первого неравенства является отрезок
).
В этом случае решением первого неравенства является отрезок
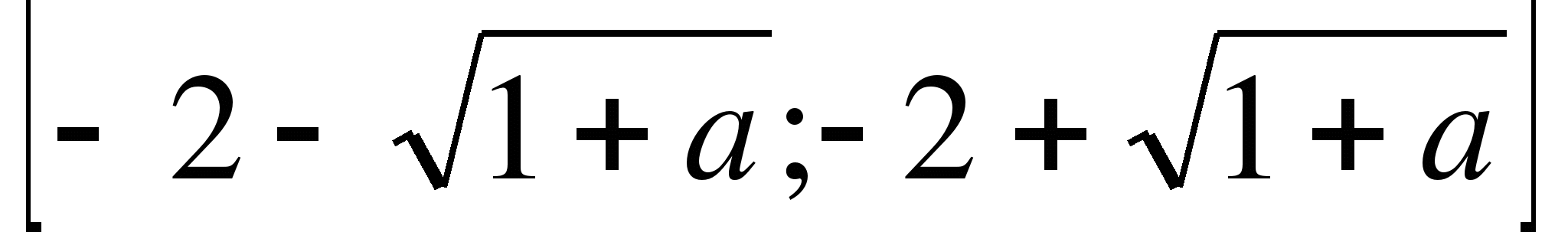 ,
а решением второго - отрезок
,
а решением второго - отрезок 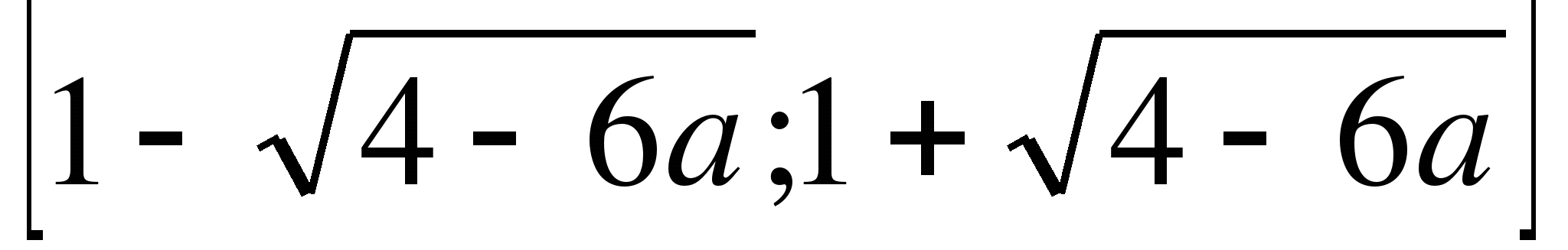 .
Система неравенств имеет единственное решение, если эти
множества имеют лишь одну общую точку.
.
Система неравенств имеет единственное решение, если эти
множества имеют лишь одну общую точку.
Так как -2-
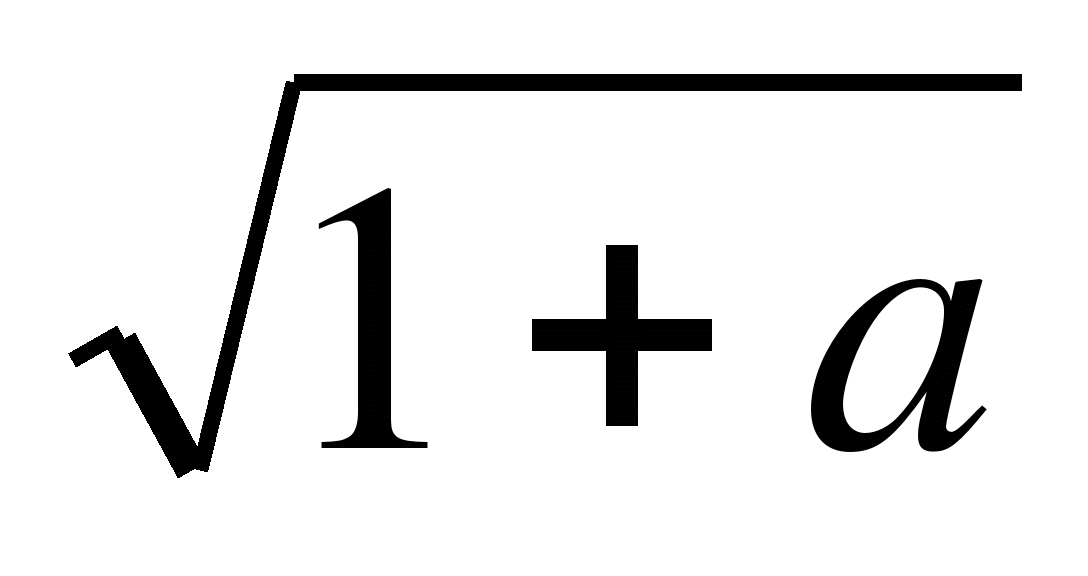 <1+
<1+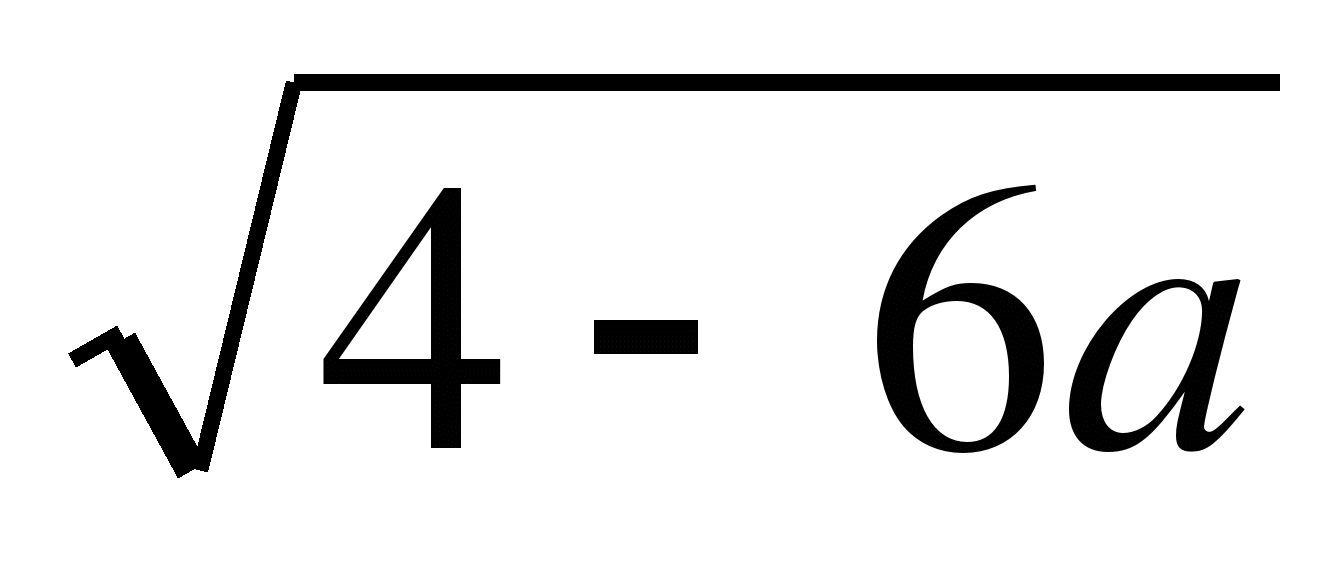 ,
то отрезки имеют одну общую точку, если -2+
,
то отрезки имеют одну общую точку, если -2+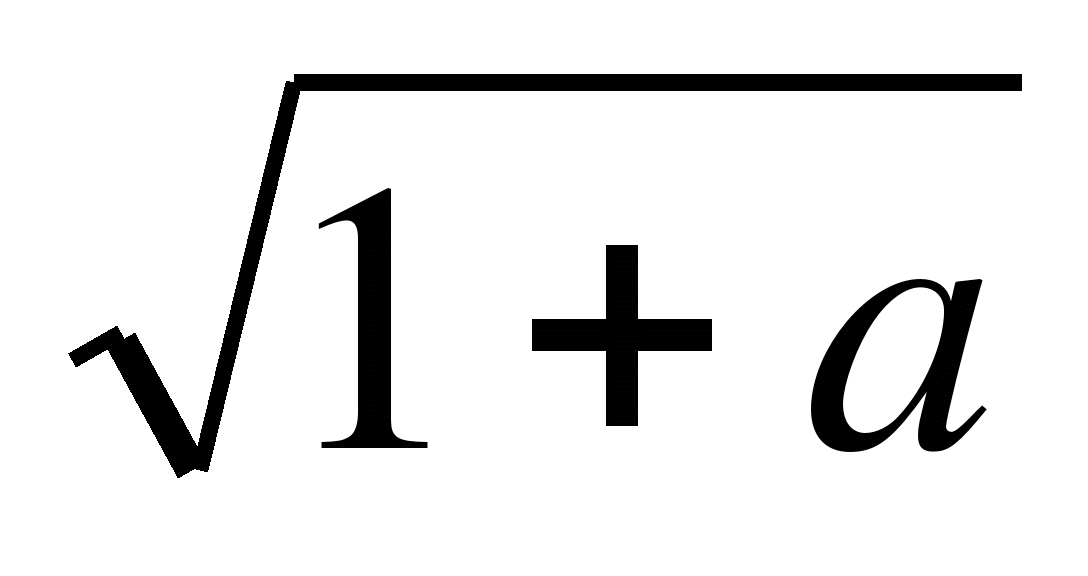 =1-
=1-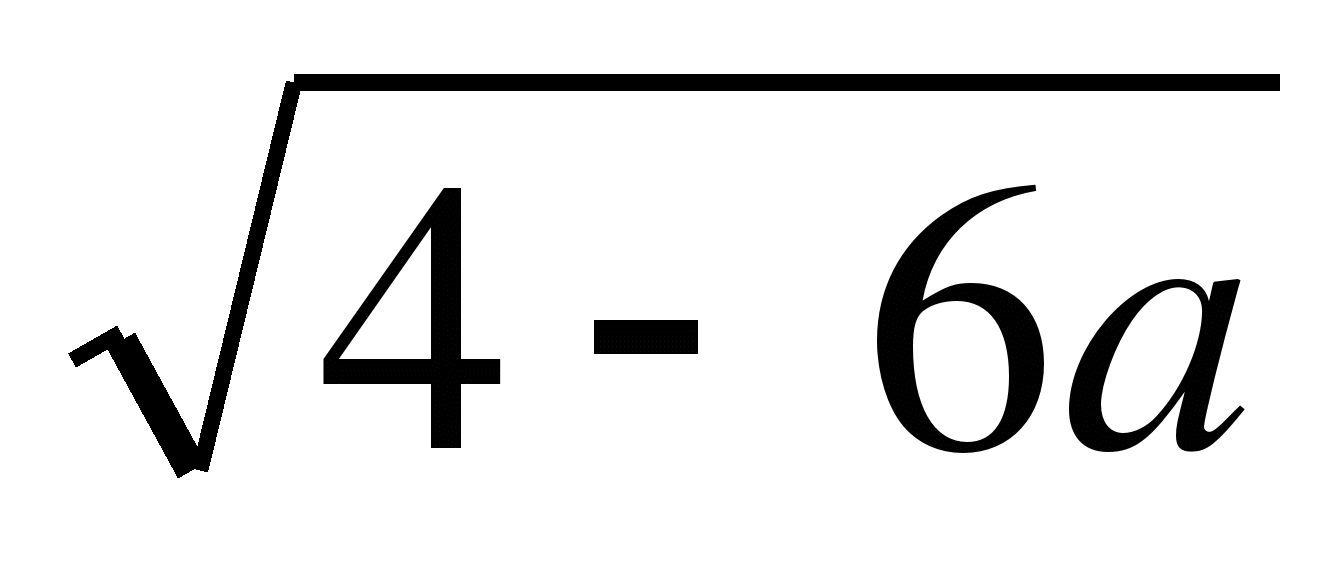 ,
т.е. а=0.
,
т.е. а=0.
Ответ: ає{0;1}.
Пример 9. Найти все значения параметра а, при каждом из которых система неравенств
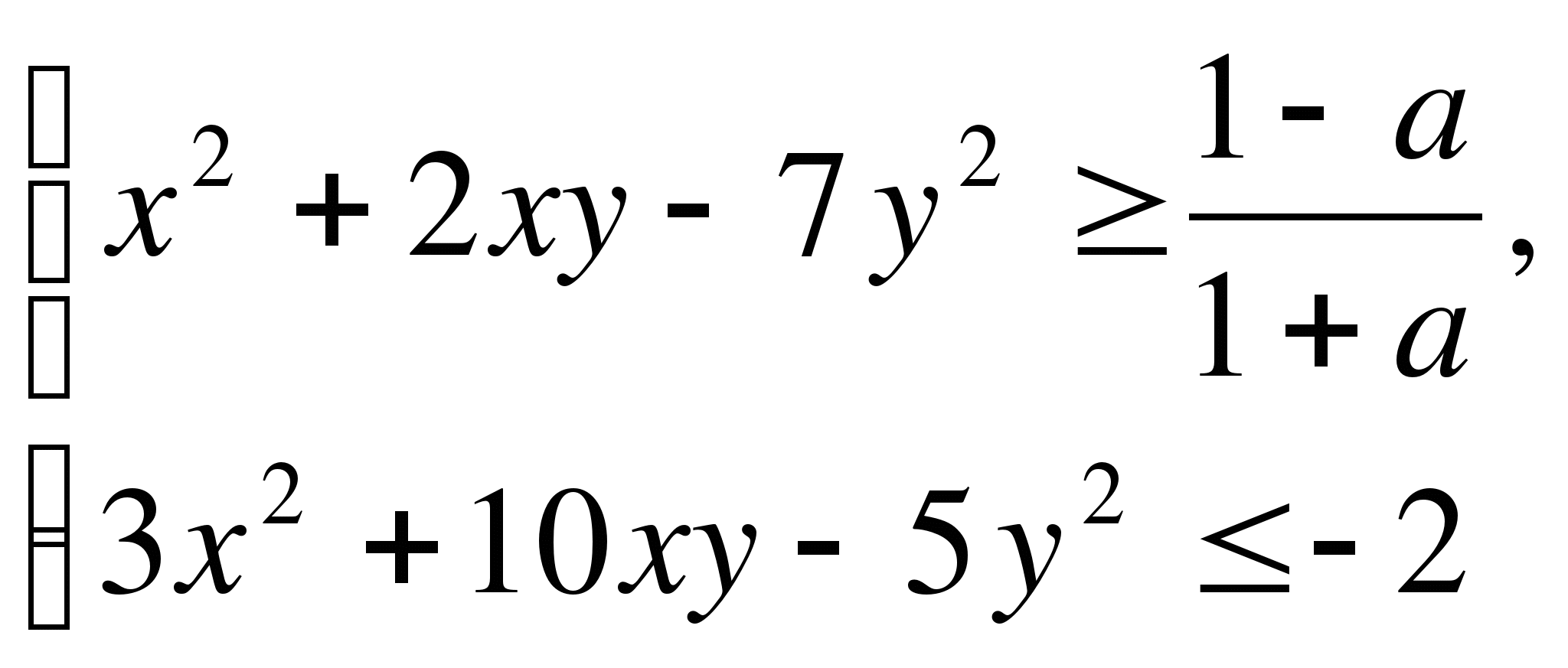 имеет решение.
имеет решение.
Решение. Пусть а0 - то значение параметра а, при котором данная система имеет решение, и пусть(х0; у0) - её решение. Тогда справедливы неравенства
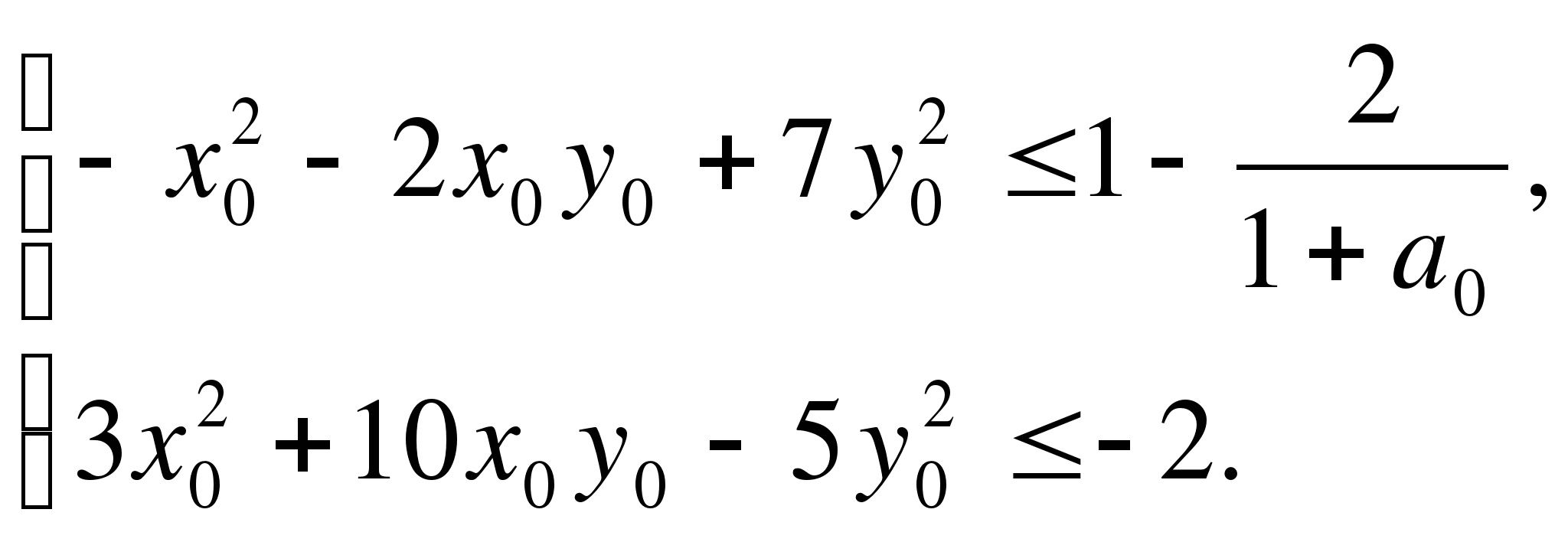
Умножив первое неравенство на 3 и прибавив его ко второму, получим
(х0 + 3у0)2≤ -
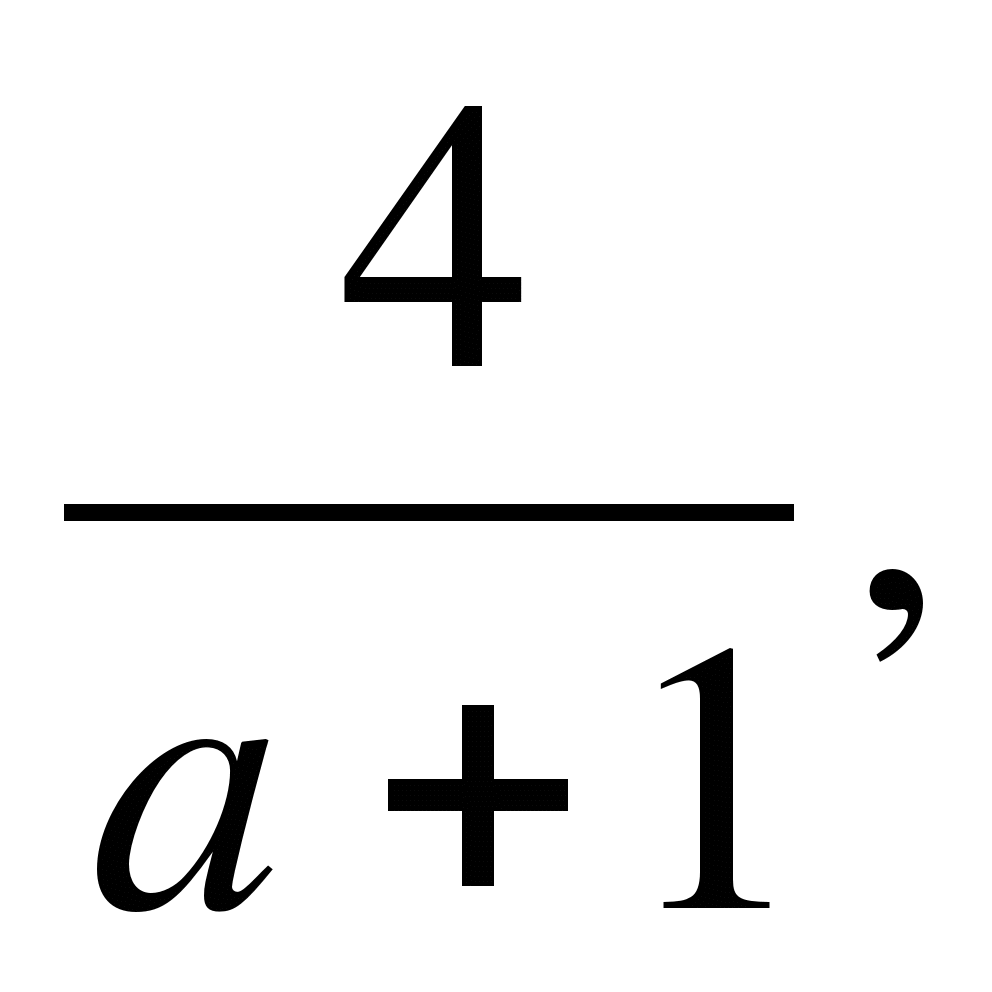
откуда следует, что 0≤ -
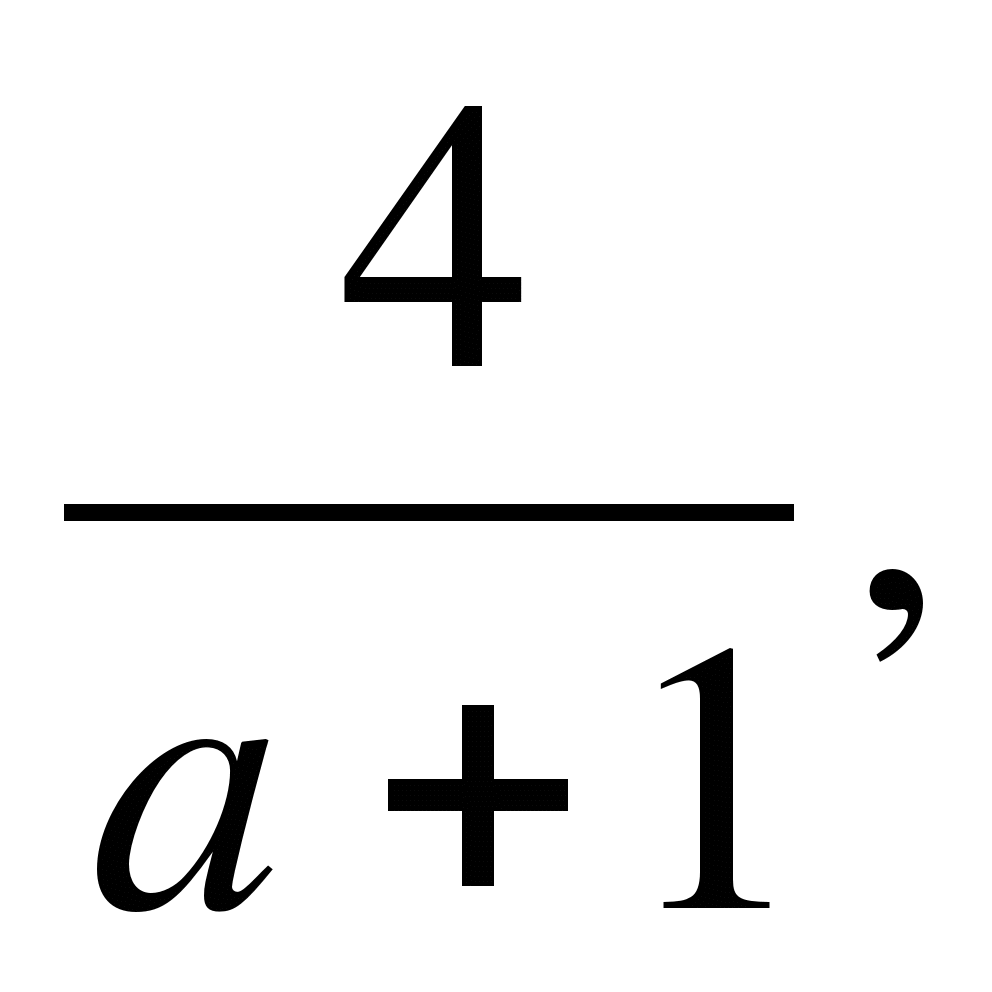 т.е.
а < -1. Следовательно, все искомые значения
параметра лежат в области ає (-∞;-1).
т.е.
а < -1. Следовательно, все искомые значения
параметра лежат в области ає (-∞;-1).
Докажем теперь, что для каждого ає (-∞;-1) исходная система имеет решение. Так как при а < -1 выполнено неравенство
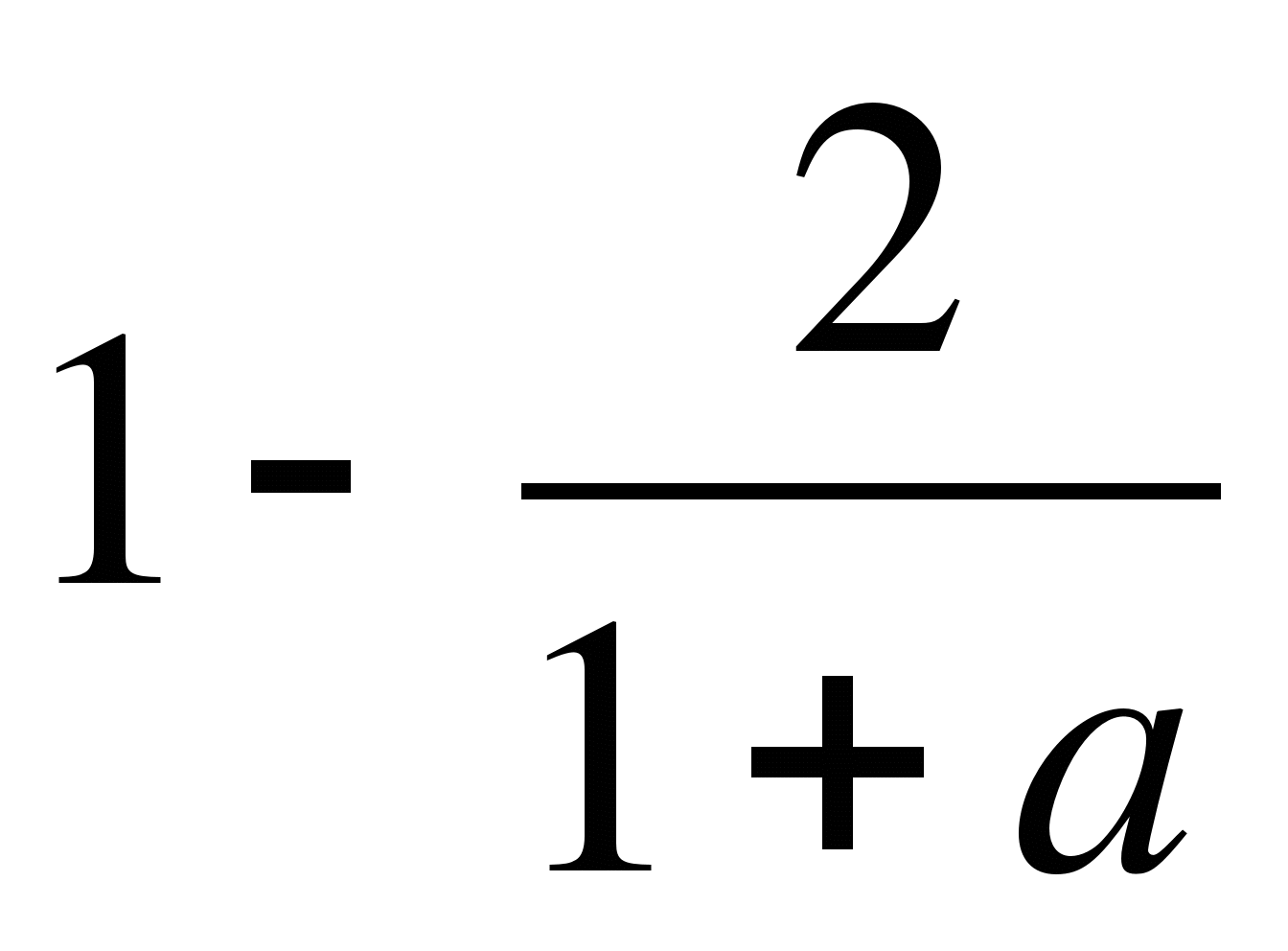 >1,
то достаточно показать, что система уравнений
>1,
то достаточно показать, что система уравнений 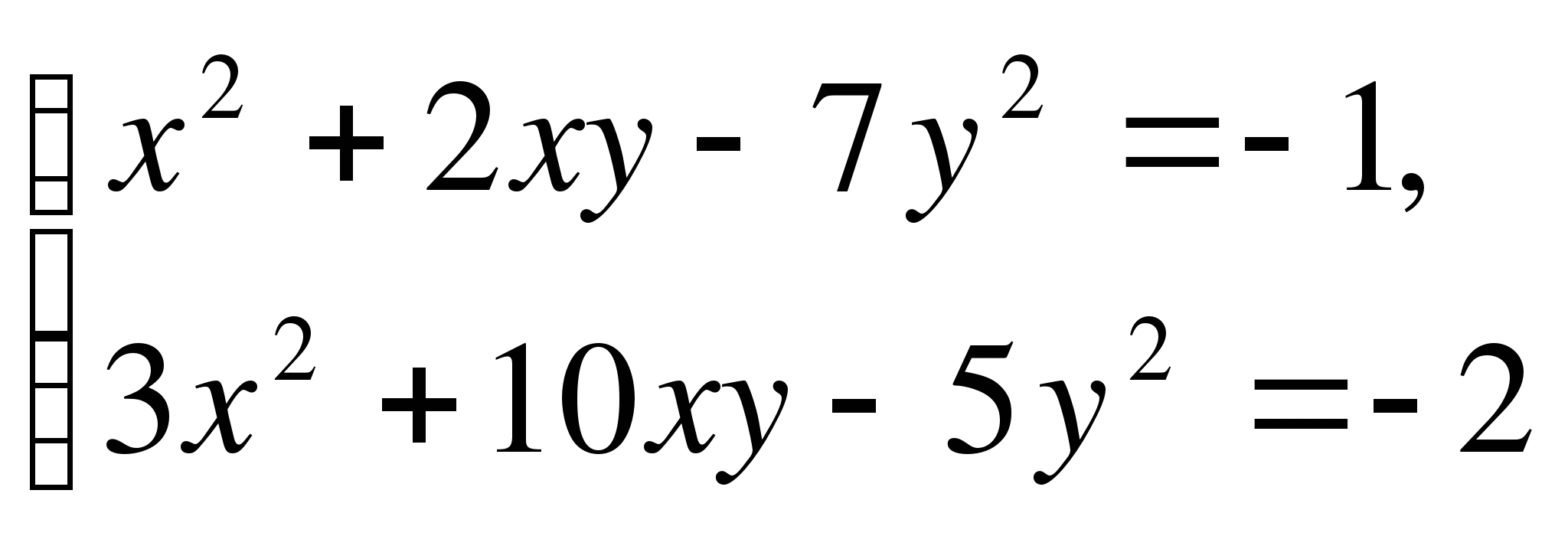 имеет решение. Каждое решение этой системы уравнений будет
решением исходной системы неравенств. Решим систему
уравнений. Умножив первое уравнение на -2 и прибавив ко
второму, получим (х+3у)2=0, откуда х = -3у.
Подставляя это значение в первое уравнение, получим
4у2=1. Отсюда у1=
имеет решение. Каждое решение этой системы уравнений будет
решением исходной системы неравенств. Решим систему
уравнений. Умножив первое уравнение на -2 и прибавив ко
второму, получим (х+3у)2=0, откуда х = -3у.
Подставляя это значение в первое уравнение, получим
4у2=1. Отсюда у1=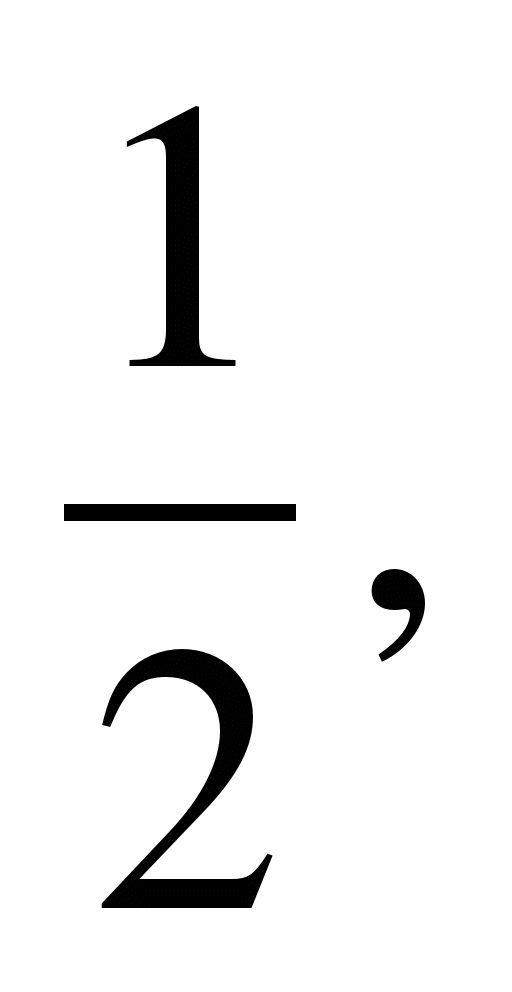 у2= -
у2= -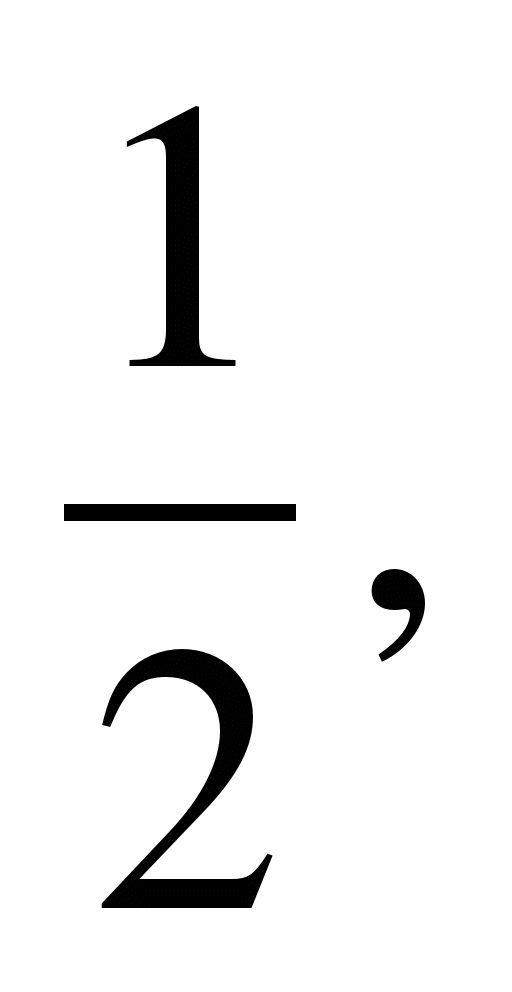 х1= -
х1= - 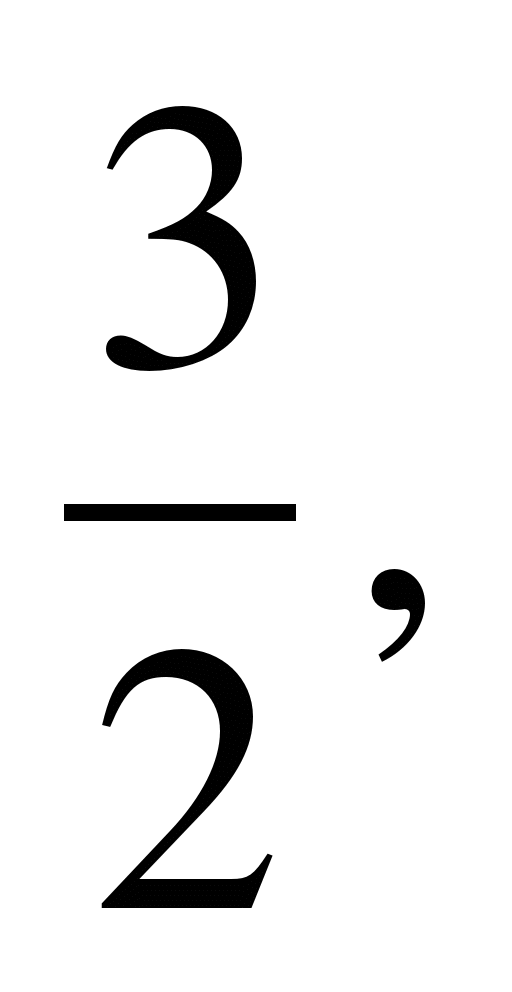 х2 =
х2 = 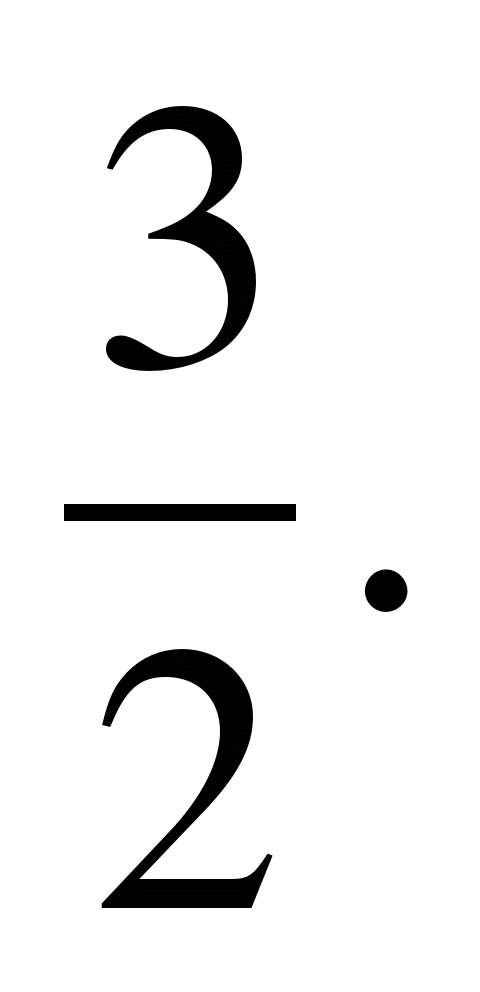
Проверкой устанавливаем, что обе пары чисел ( -
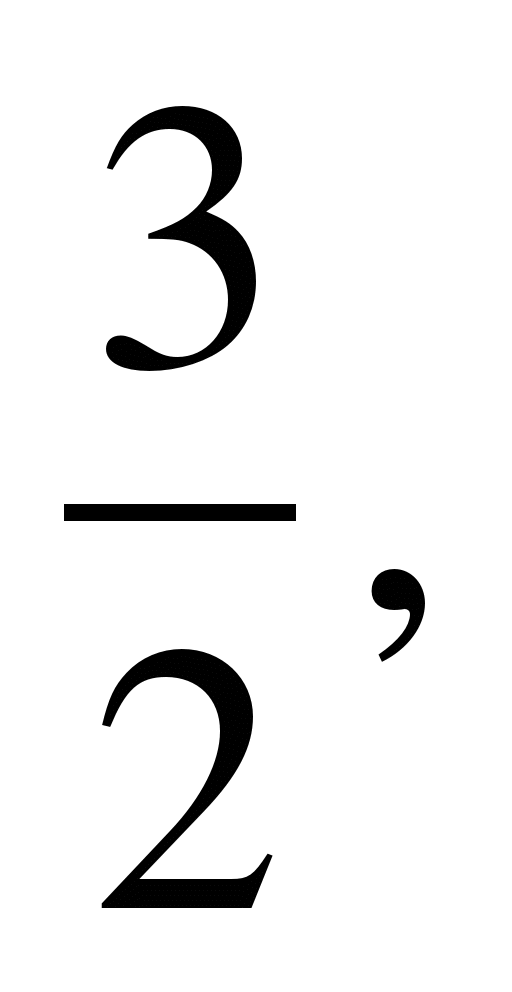
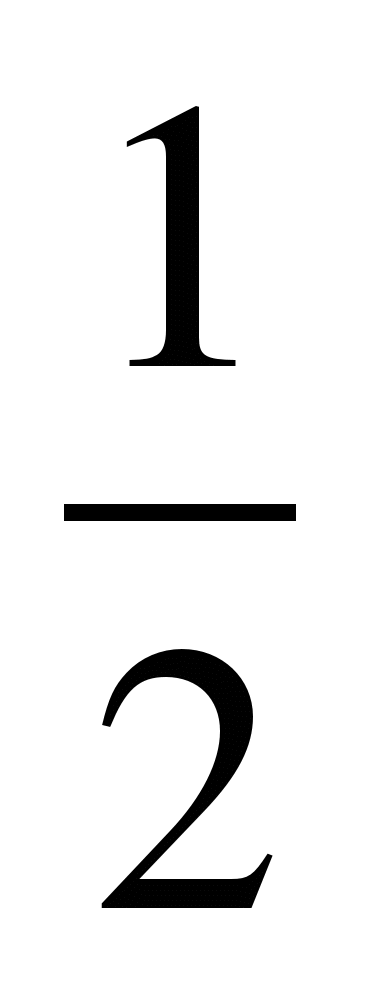 )
и (
)
и (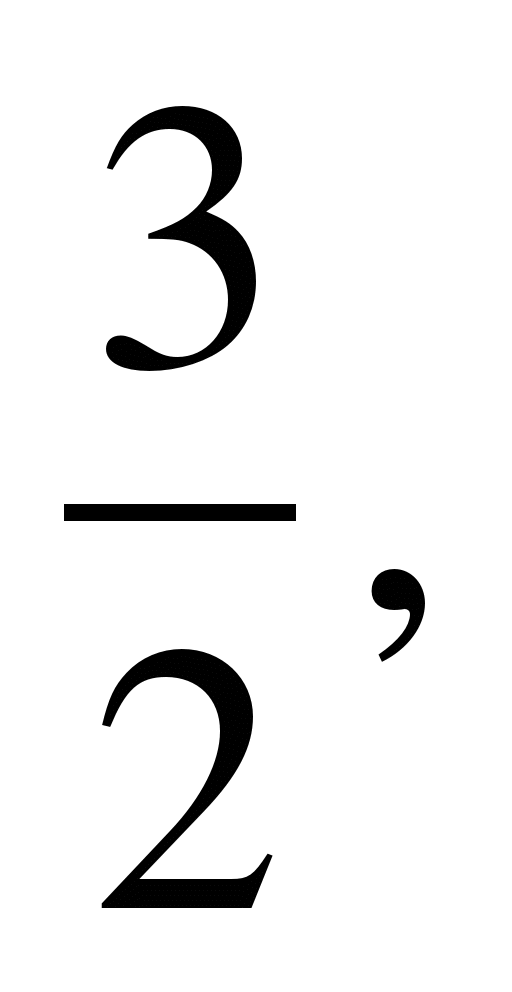 -
-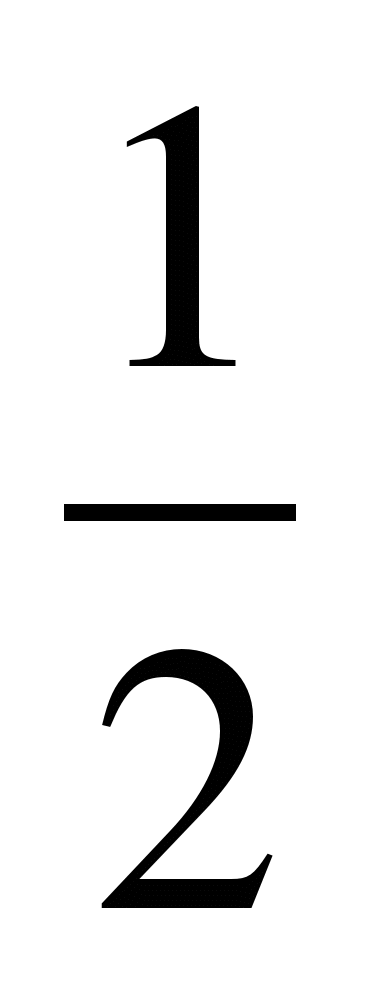 )
будут решениями системы неравенств.
)
будут решениями системы неравенств.
Ответ: ає (-∞;-1).
III. Итоги занятий.
Тема 9. Практикум (4 часа).
Цели занятия:
- обобщение и систематизация знаний и умений по темам курса;
- отработка навыков решения уравнений, неравенств и их систем, содержащих
параметр;
- самоконтроль.
Задания по теме «Линейные уравнения и неравенства с параметром».
№ 1. Решить уравнение (а - 1)х = 6.
Ответ: при а=1 корней нет, при а≠ 1 х=
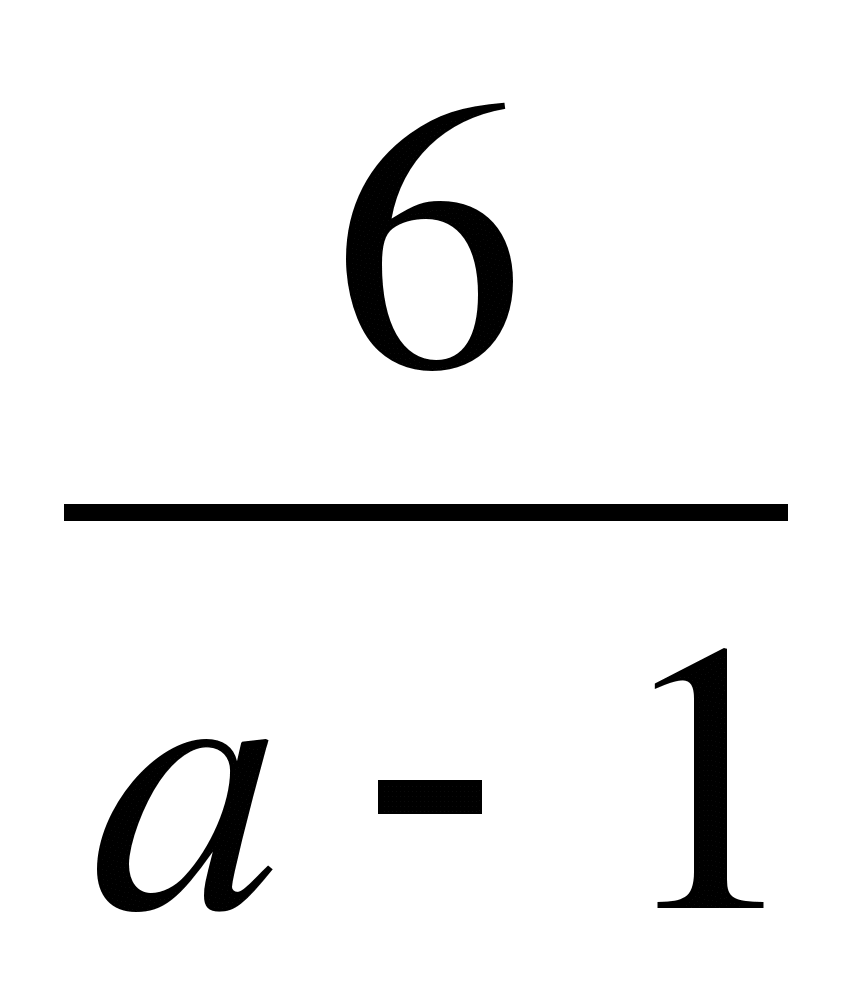 .
.
№ 2. Решить уравнение 2 ах = 1-х.
Ответ: при а=-0,5 корней нет, при а≠ -0,5 х=
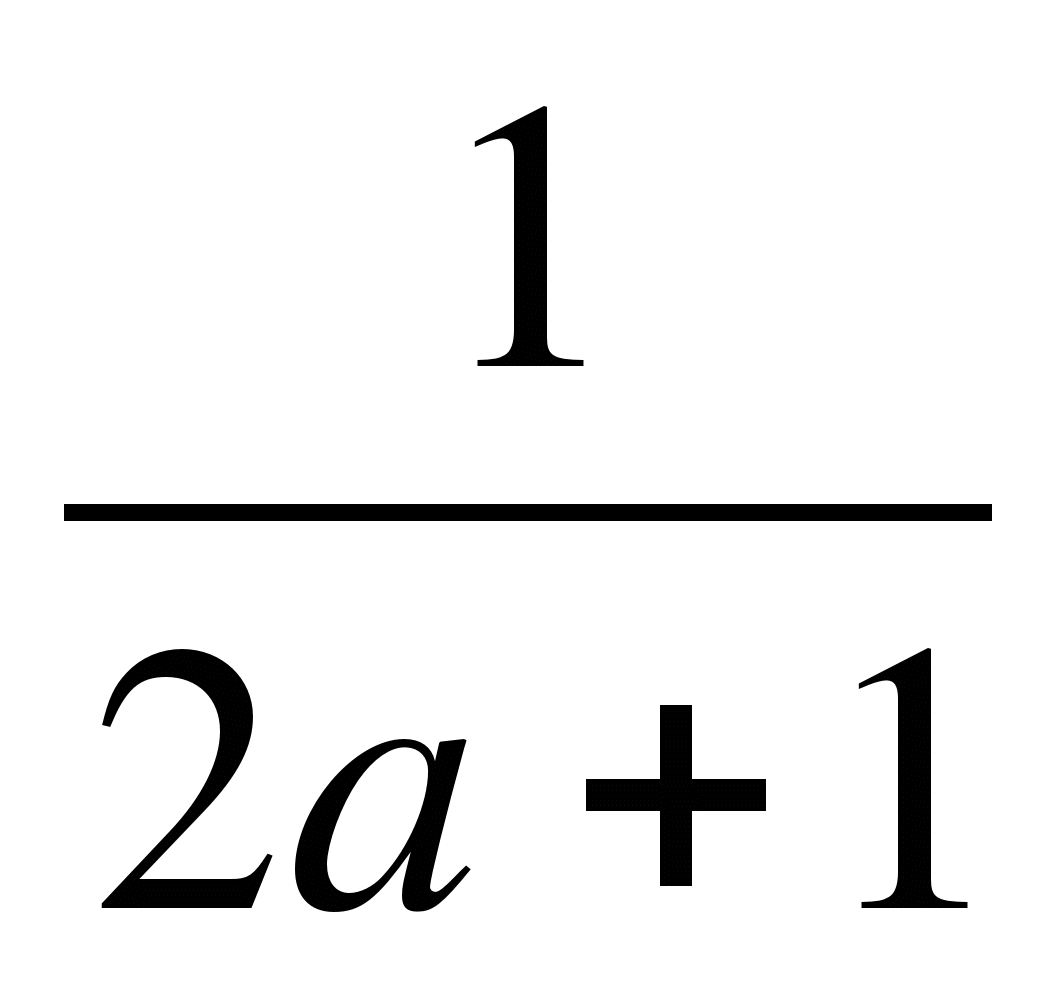 .
.
№ 3. Решить уравнение (а2-4)х = а2 + а-6.
Ответ: при а=2 хєR, при а=-2 корней нет, при других а х=
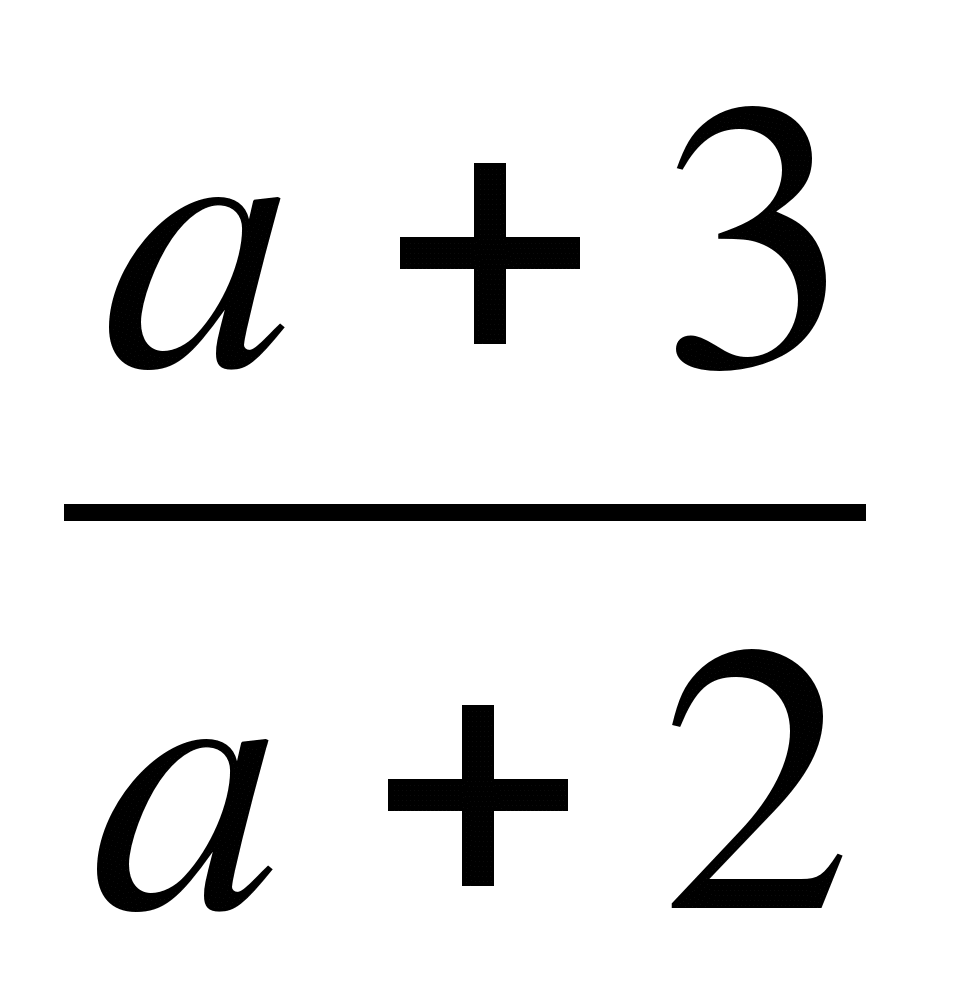 .
.
№ 4. Решить уравнение (а2-9)х =9а2 -10а-51.
Ответ: при а=3 хєR, при а=-3 корней нет, при других а х=
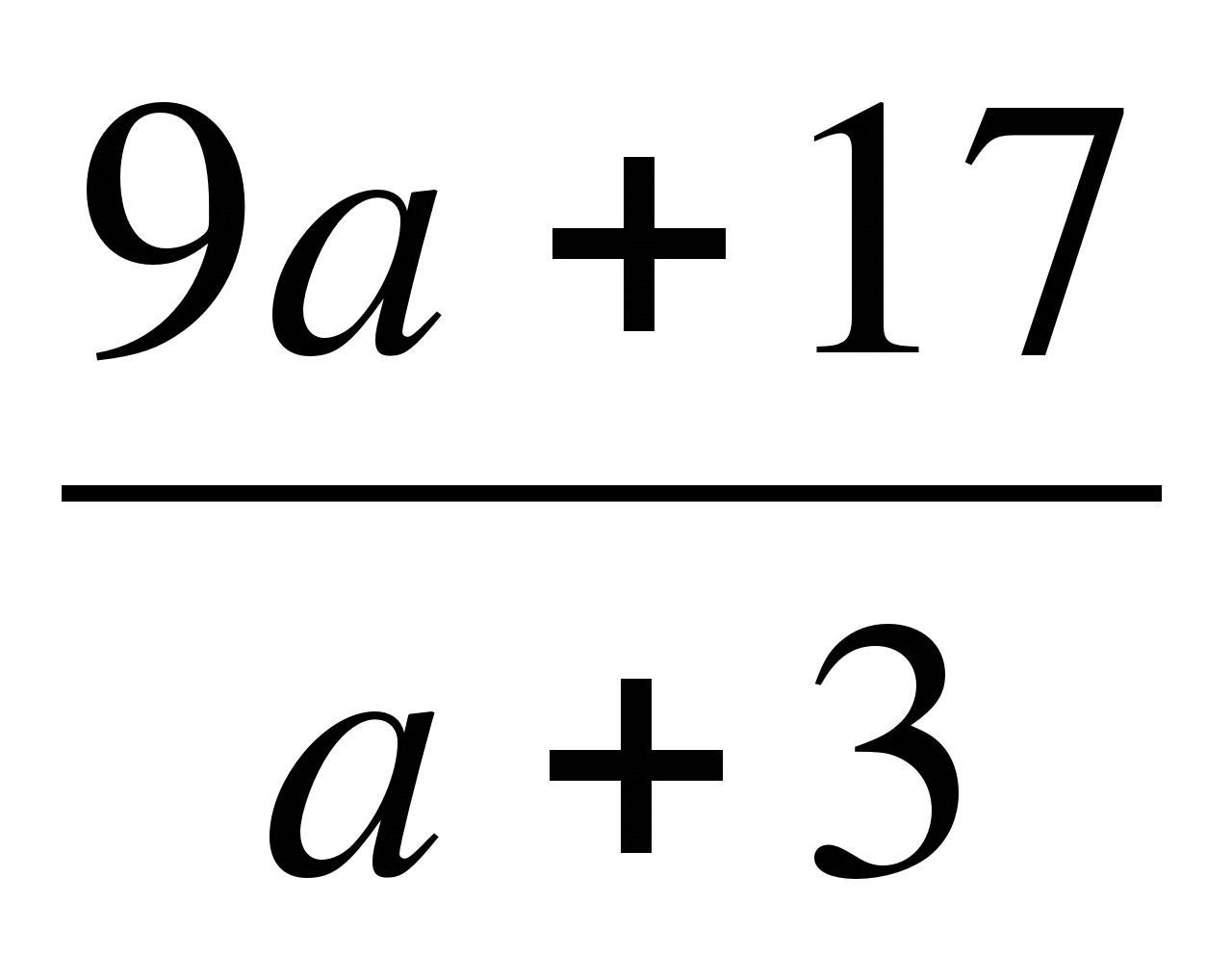 .
.
№ 5. Решить уравнение
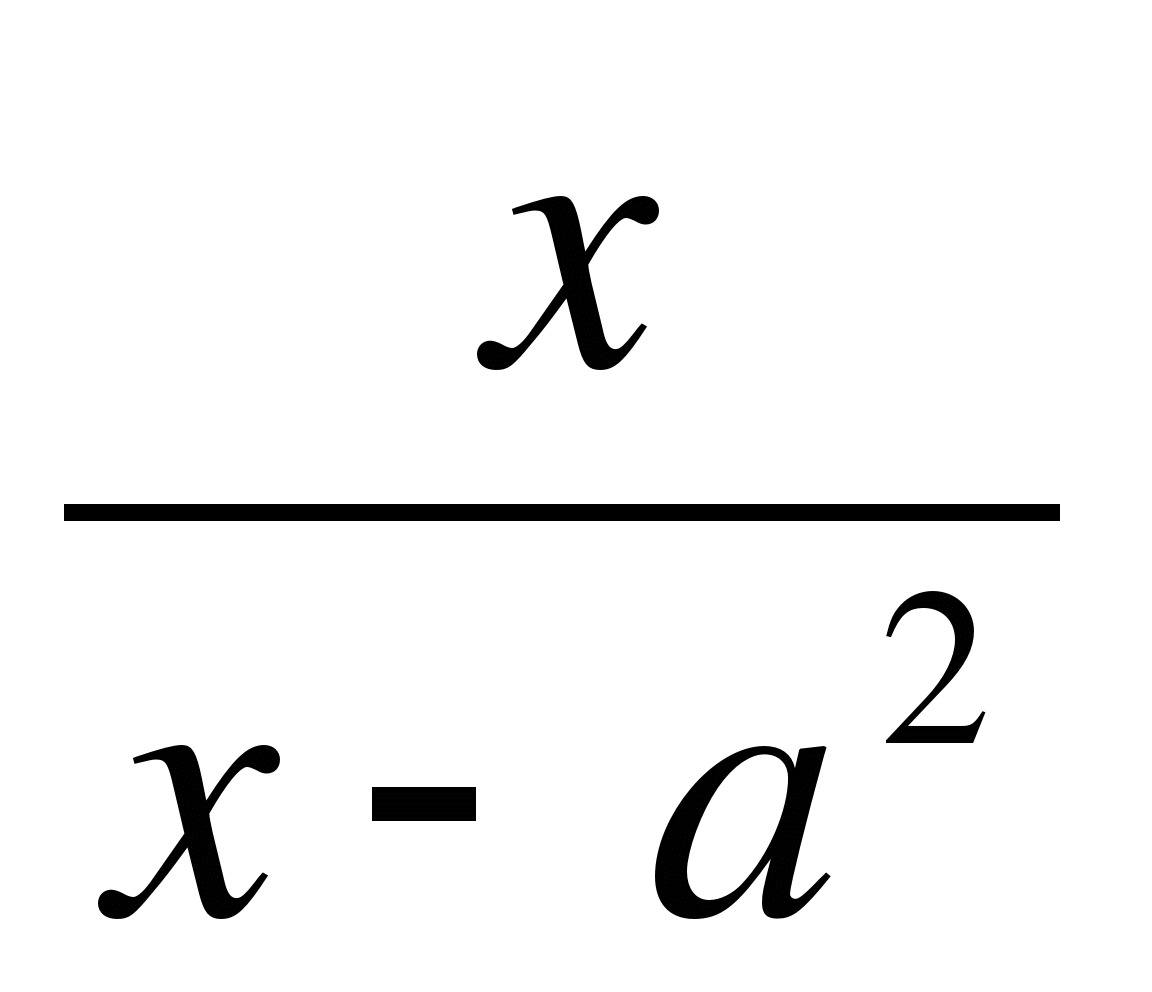 =0.
=0.
Ответ: при а=0 корней нет, при а≠0 х=0.
№ 6. Решить уравнение
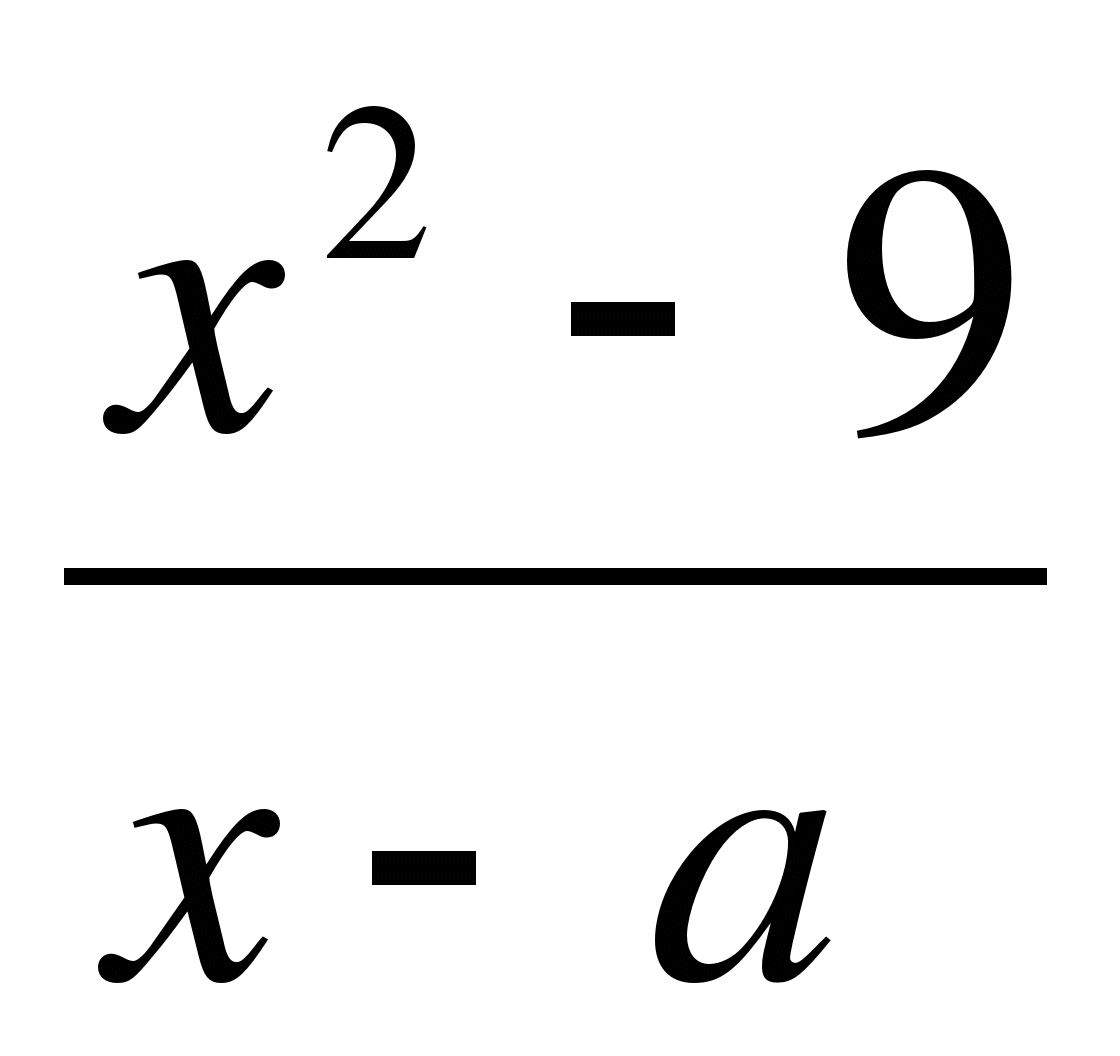 =0.
=0.
Ответ: при а=3 х=-3, при а=-3 х=-3, при других а х=±3.
№ 7. Решить неравенство (а-1)х>6.
Ответ: при а=1 решений нет, при а>1 x>
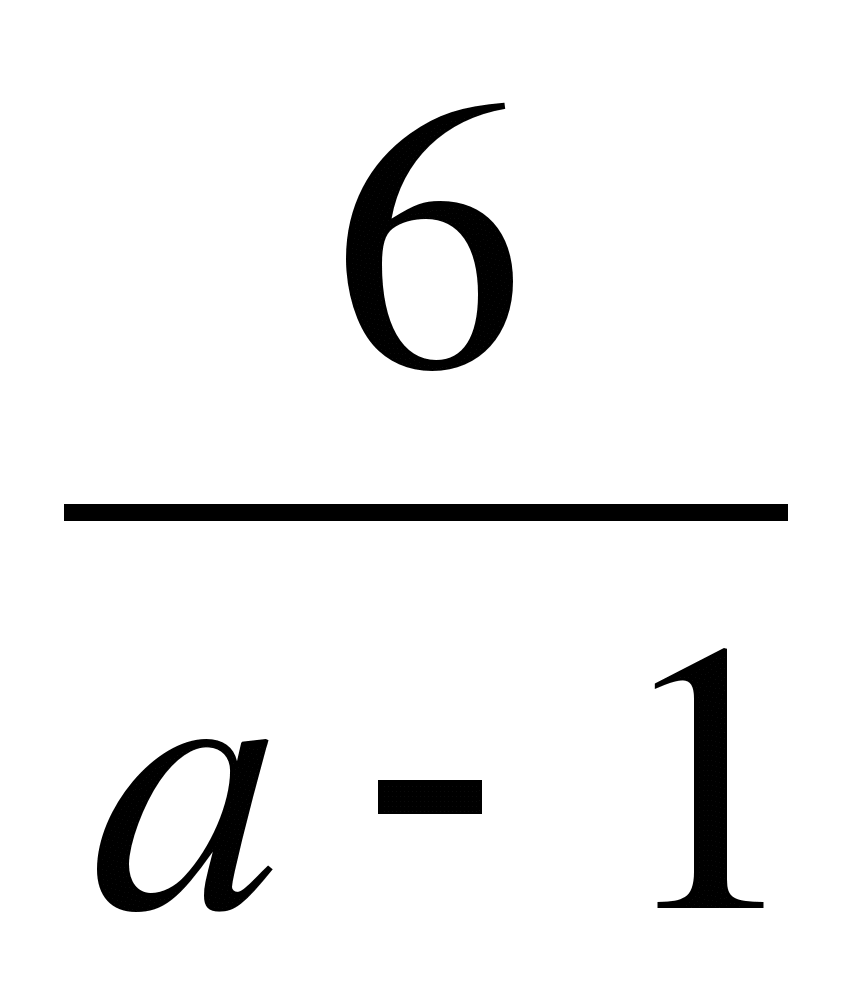 ,
при а<1 x<
,
при а<1 x<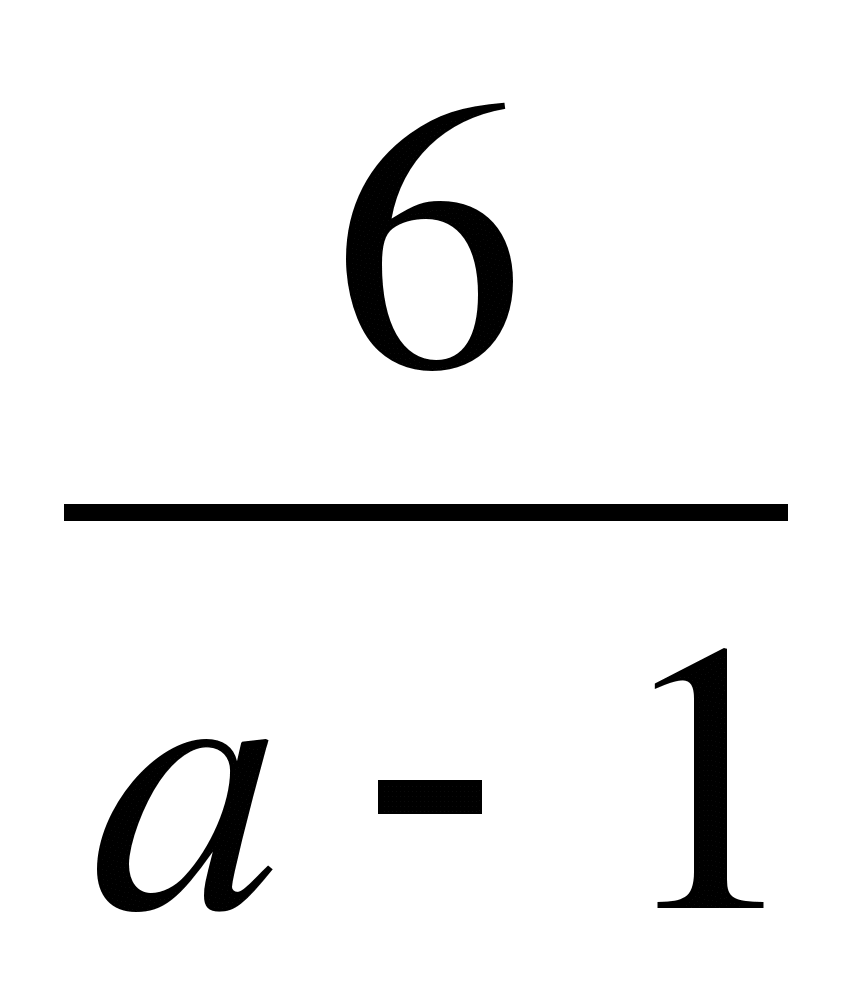 .
.
№ 8. Решить неравенство 2ах≤1-х.
Ответ: при а=-0,5 х є R, при а>-0,5 х≤
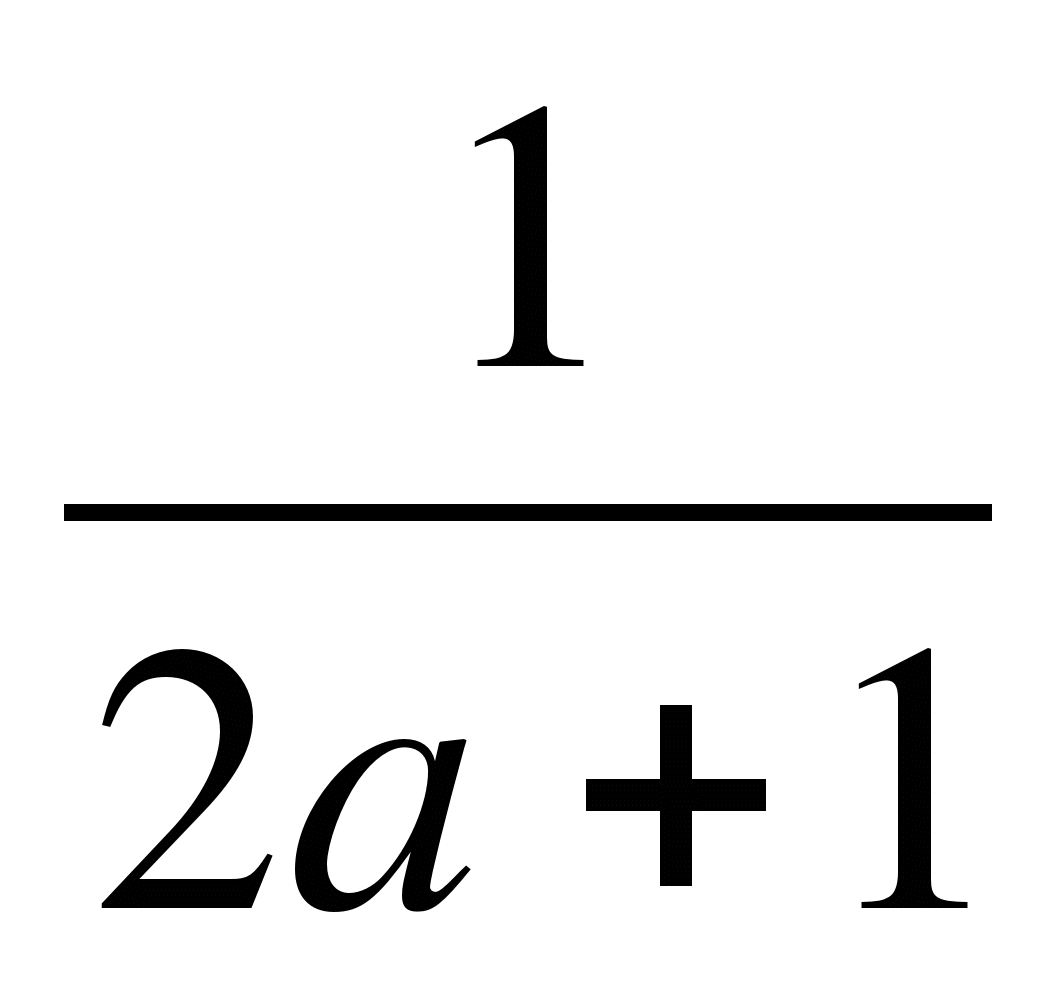 ,
при а<-0,5 х≥
,
при а<-0,5 х≥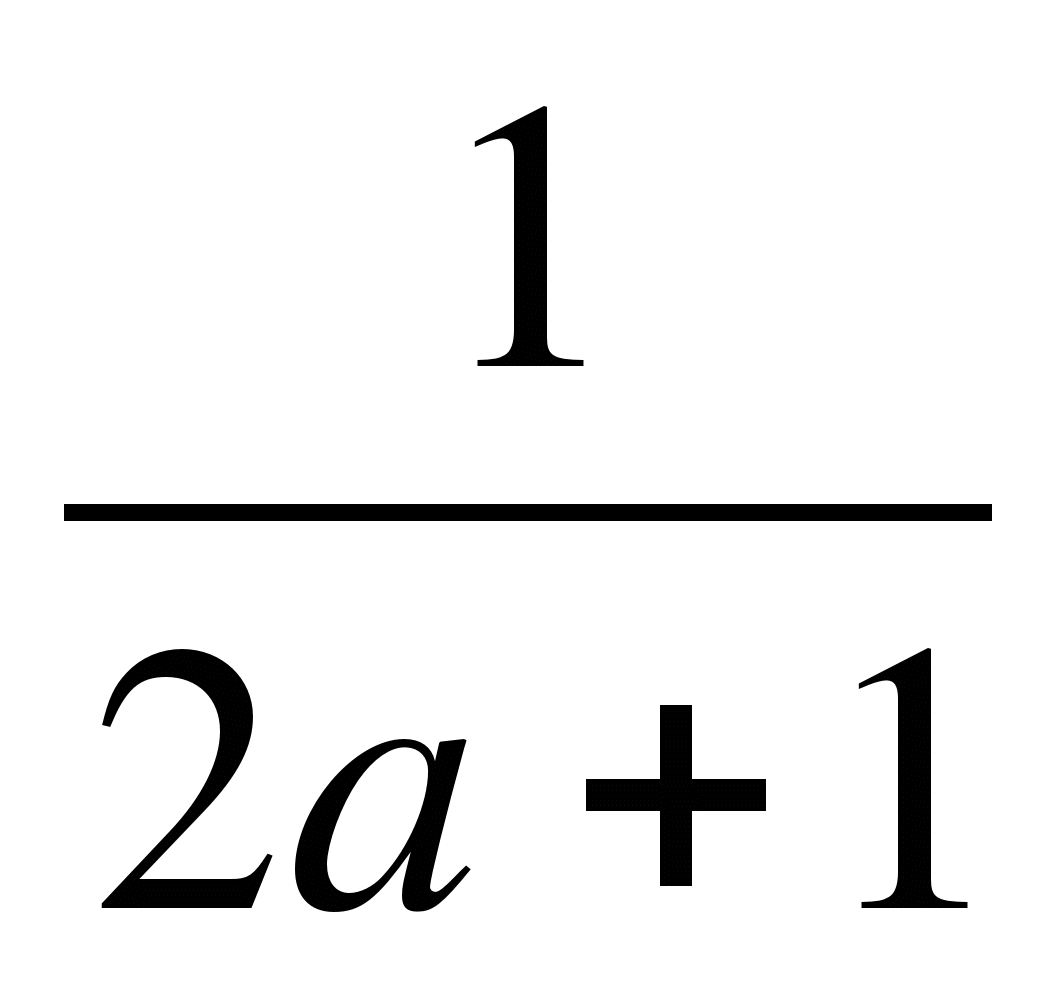 .
.
№ 9. Решить неравенство (а2-9)х ≤а+3.
Ответ: при а=±3 хєR, при│а│>3 х≤
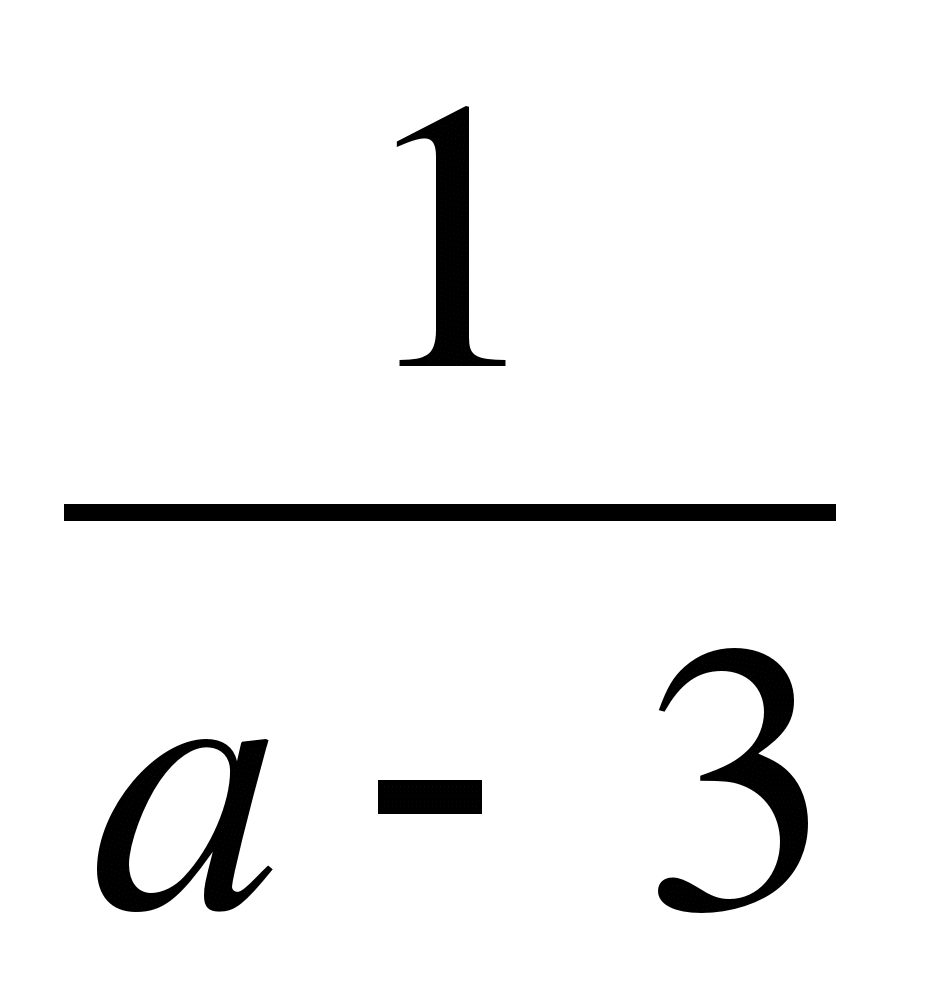 ,
при других а х≥
,
при других а х≥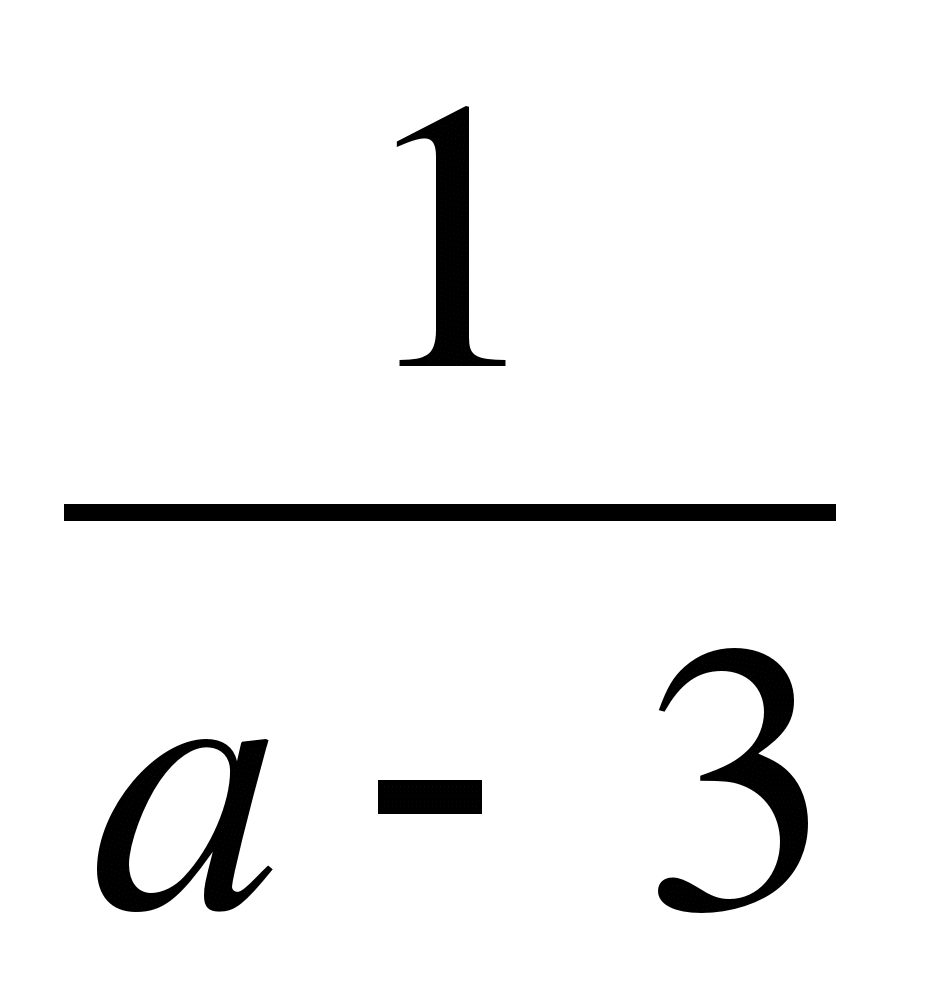 .
.
№ 10. Решить неравенство (а2-9)х >а+3.
Ответ: при а=±3 решений нет, при│а│>3 х>
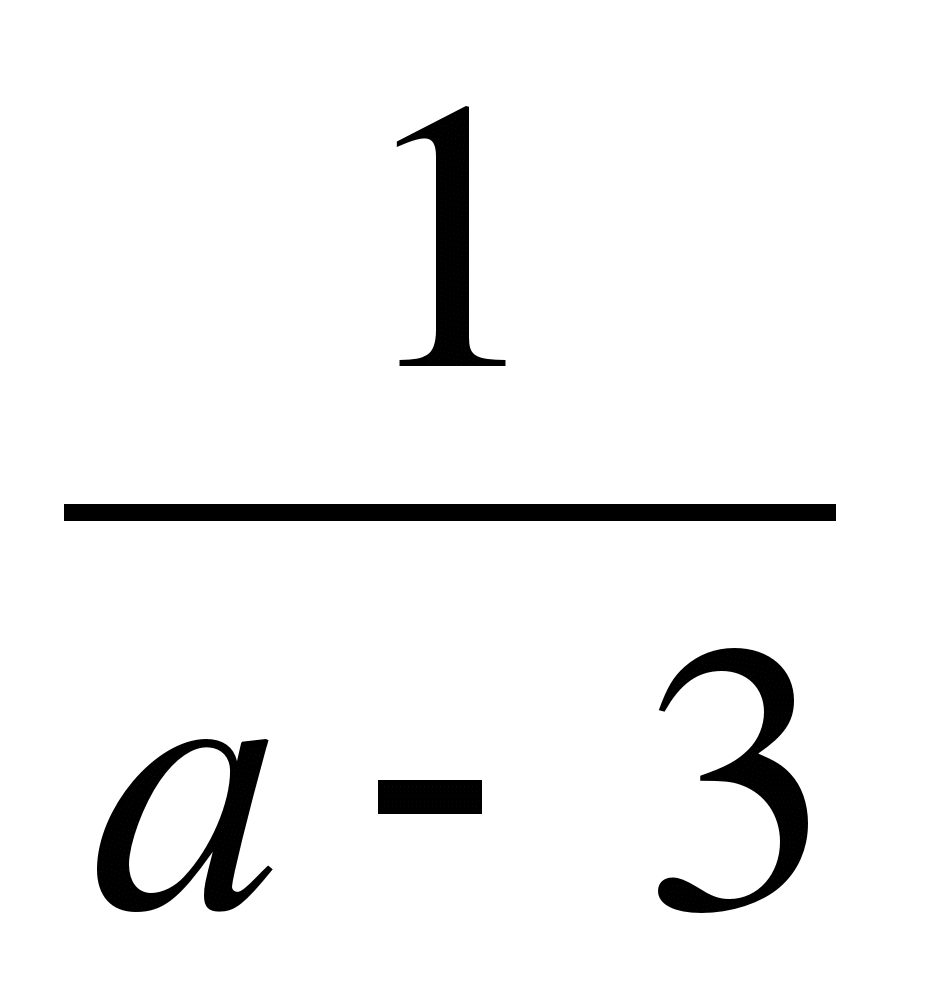 ,
при других а х<
,
при других а х<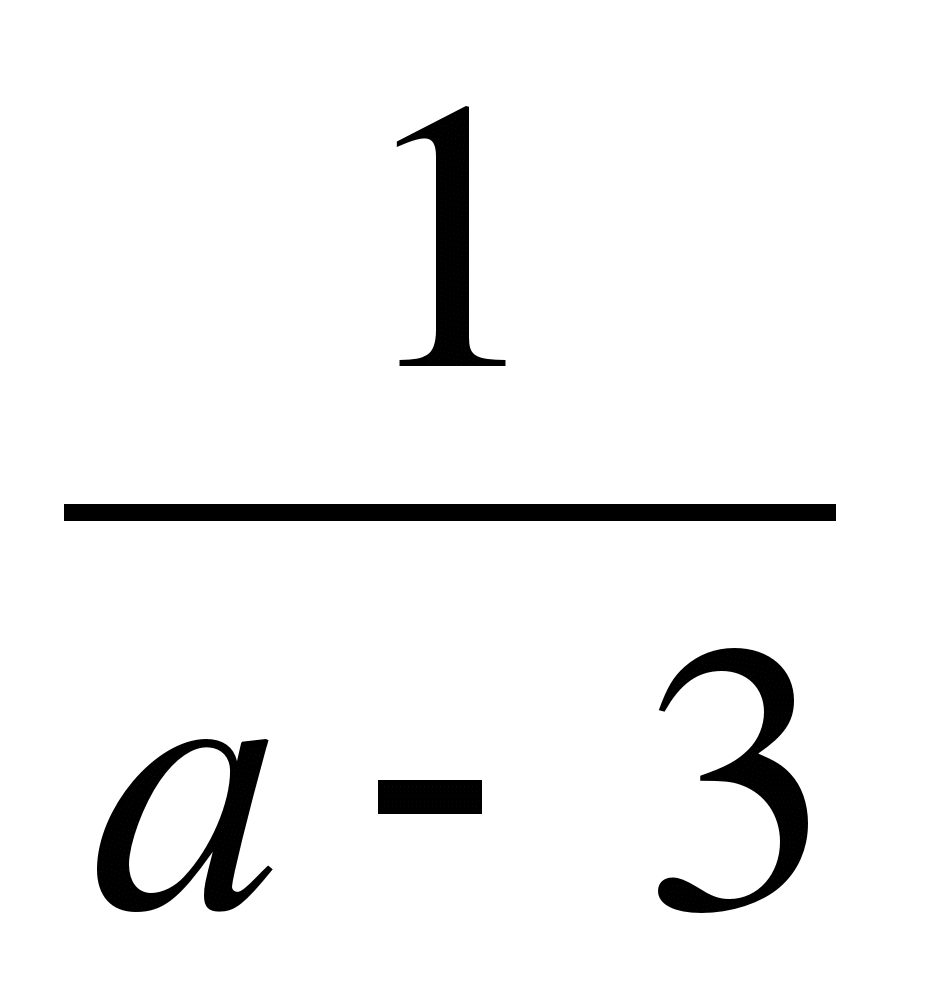 .
.
Задания по теме «Квадратные уравнения и неравенства с
параметром и их системы».
№ 1. Решить уравнение х2+а2 - 1 =0.
Ответ: при │а│>1 корней нет, при других а х=±
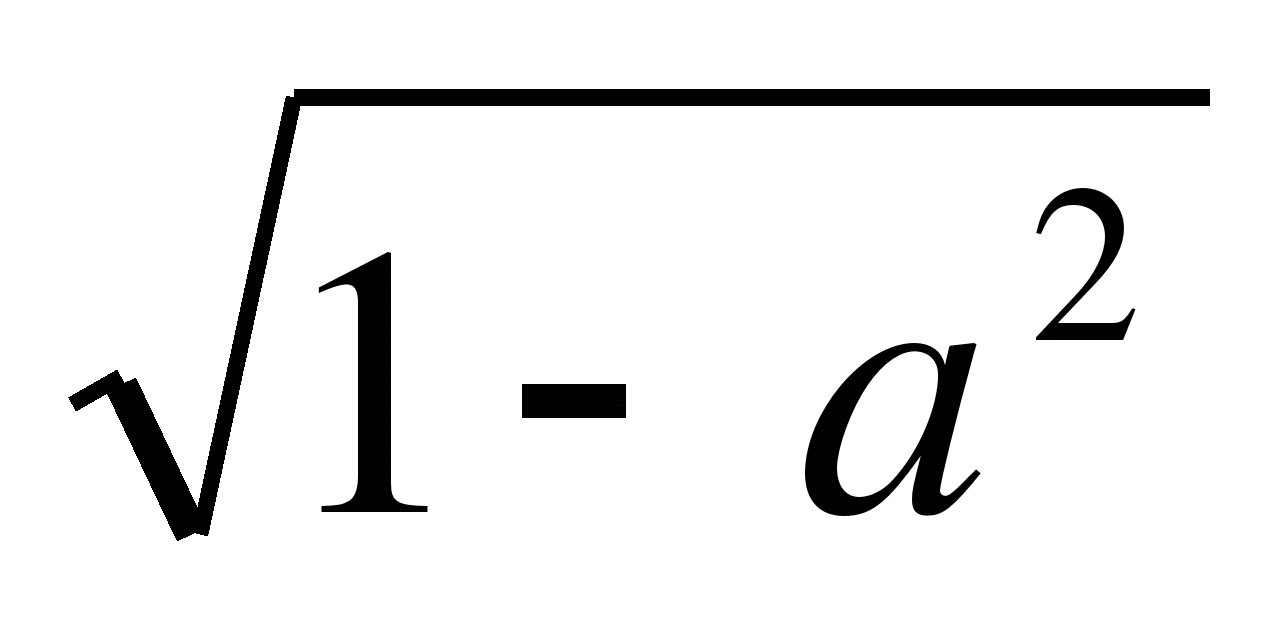 .
.
№ 2. Решить уравнение ах2-х+3 =0.
Ответ: при а=0 х=3, при а=
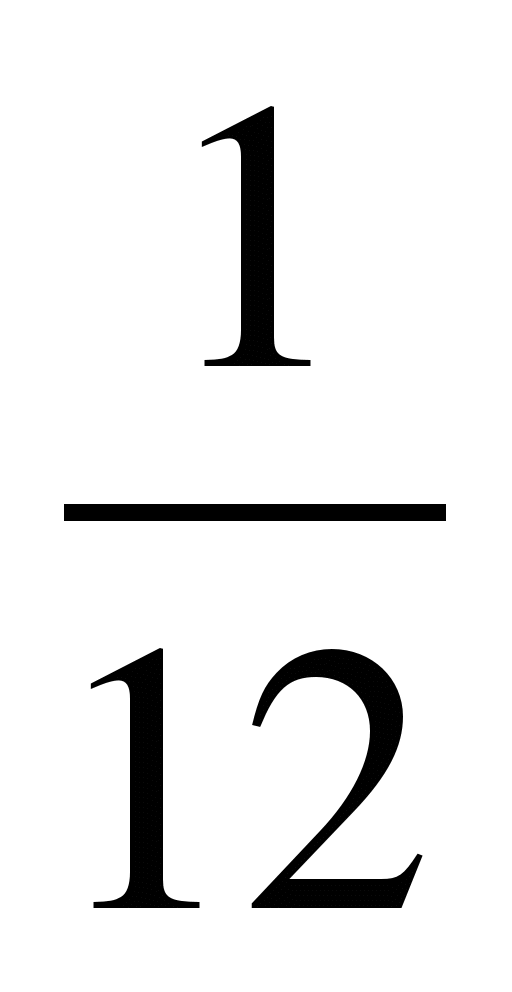 х=6, при а>
х=6, при а>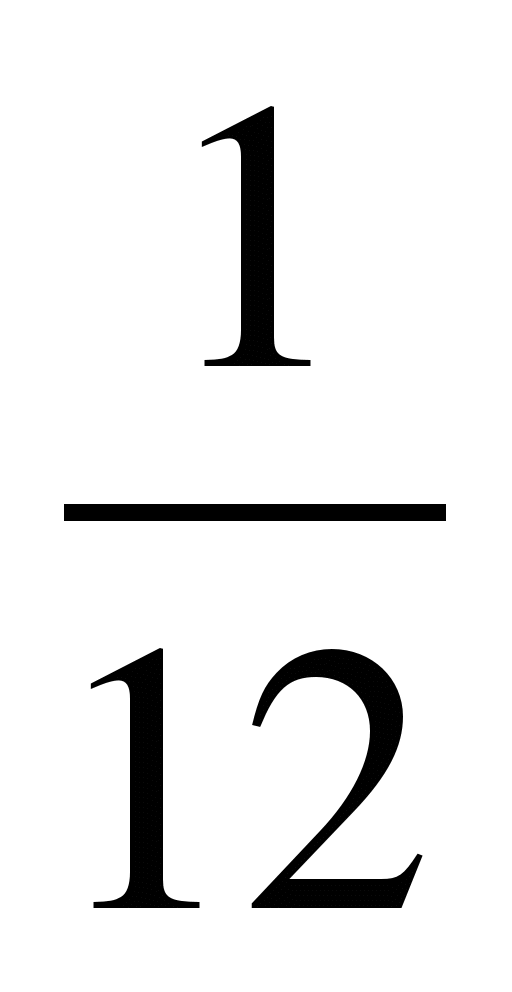 корней нет, при других а
корней нет, при других а
х=
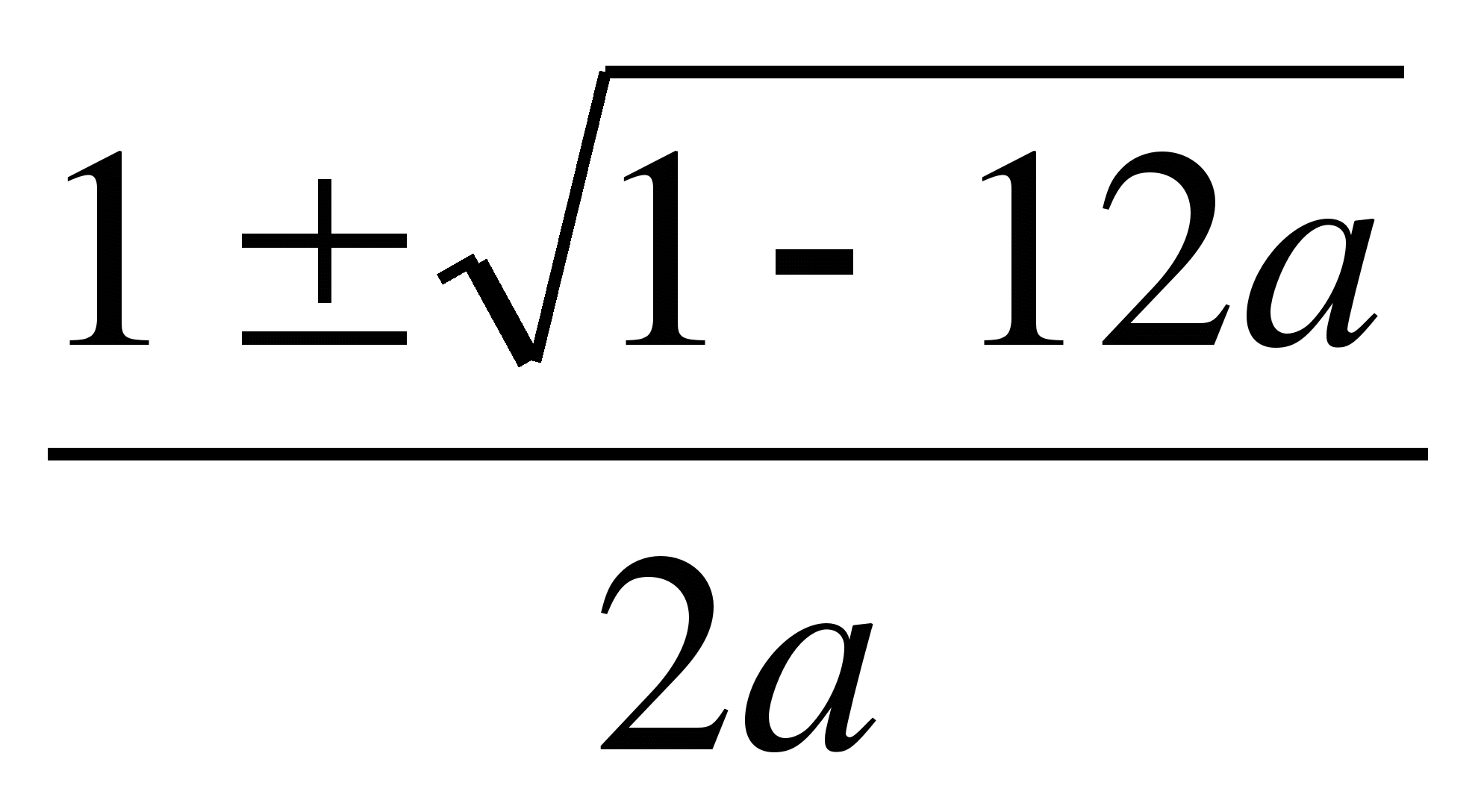 .
.
№ 3. Решить неравенство ах2 +( а+1)х+1>0 при различных значениях а.
Ответ: при а=0 х>-1,
при а=1 х Є (-∞; -1)U(-1; +∞),
при а>1 х Є (-∞; -1)U( -1/а; +∞),
при а<0 х Є (-1; -1/а),
при а Є (0;1) х Є (-∞; -1/а)U(-1; +∞).
№ 4. При каких значениях параметра а неравенство х2+ах+1<0 не имеет решений?
Ответ: аЄ[-1;1].
№ 5. Решить неравенство х2-4ах+9 ≤0.
Ответ: при │а│>1,5 решений нет, при а=1,5 х=3, при а=-1,5 х=-3, при других а хє[2а-
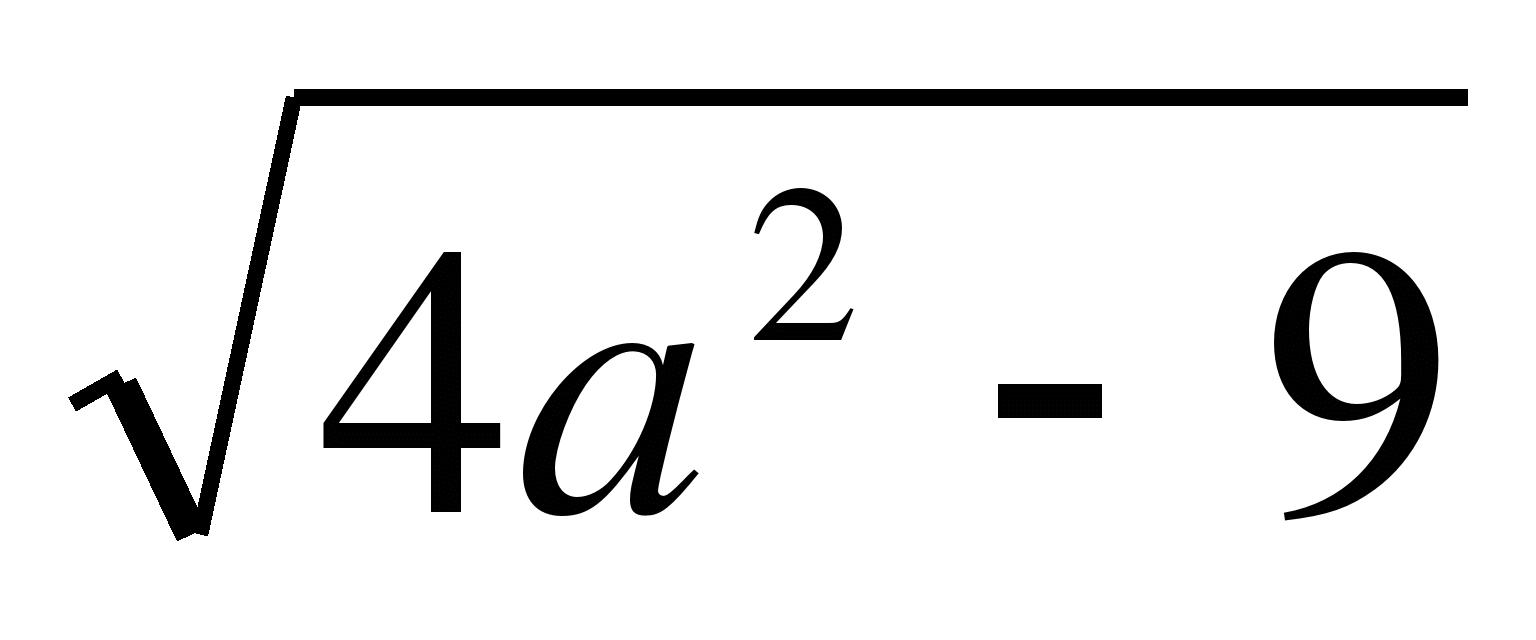 ;
2а+
;
2а+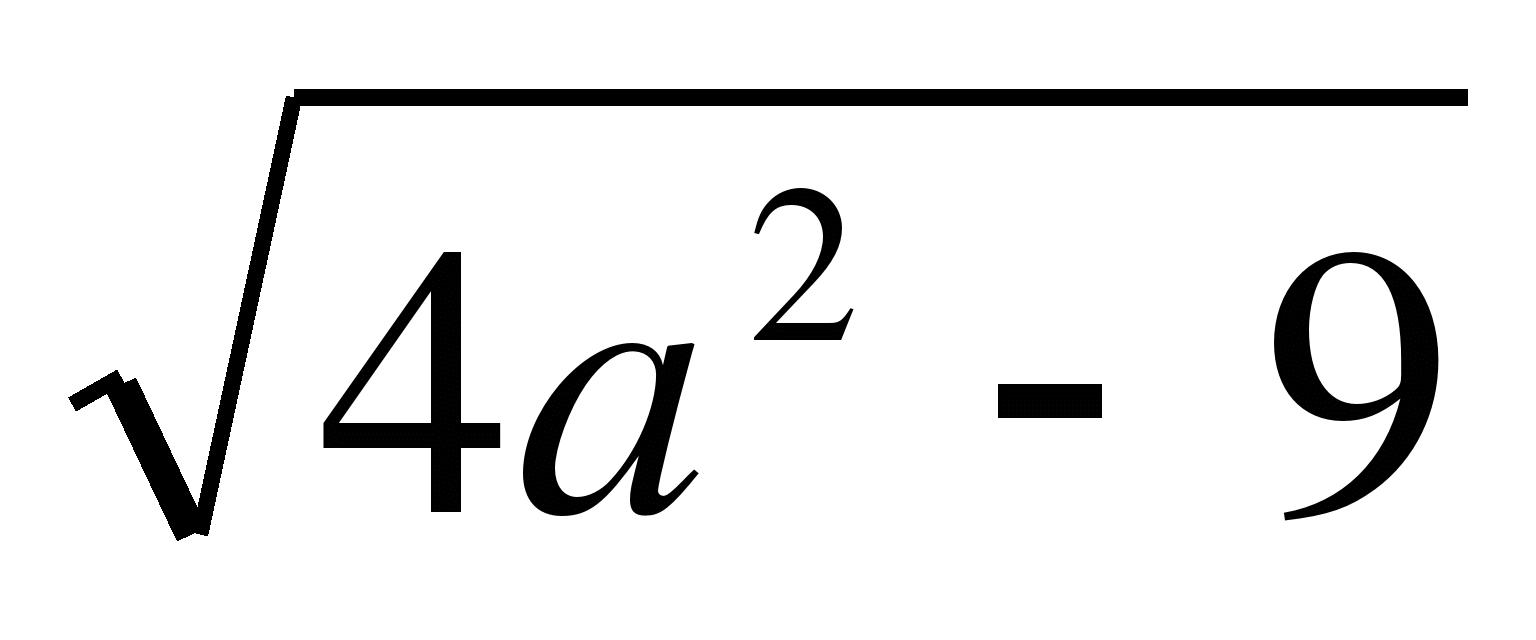 ].
].
№ 6. При каком значении параметра а система
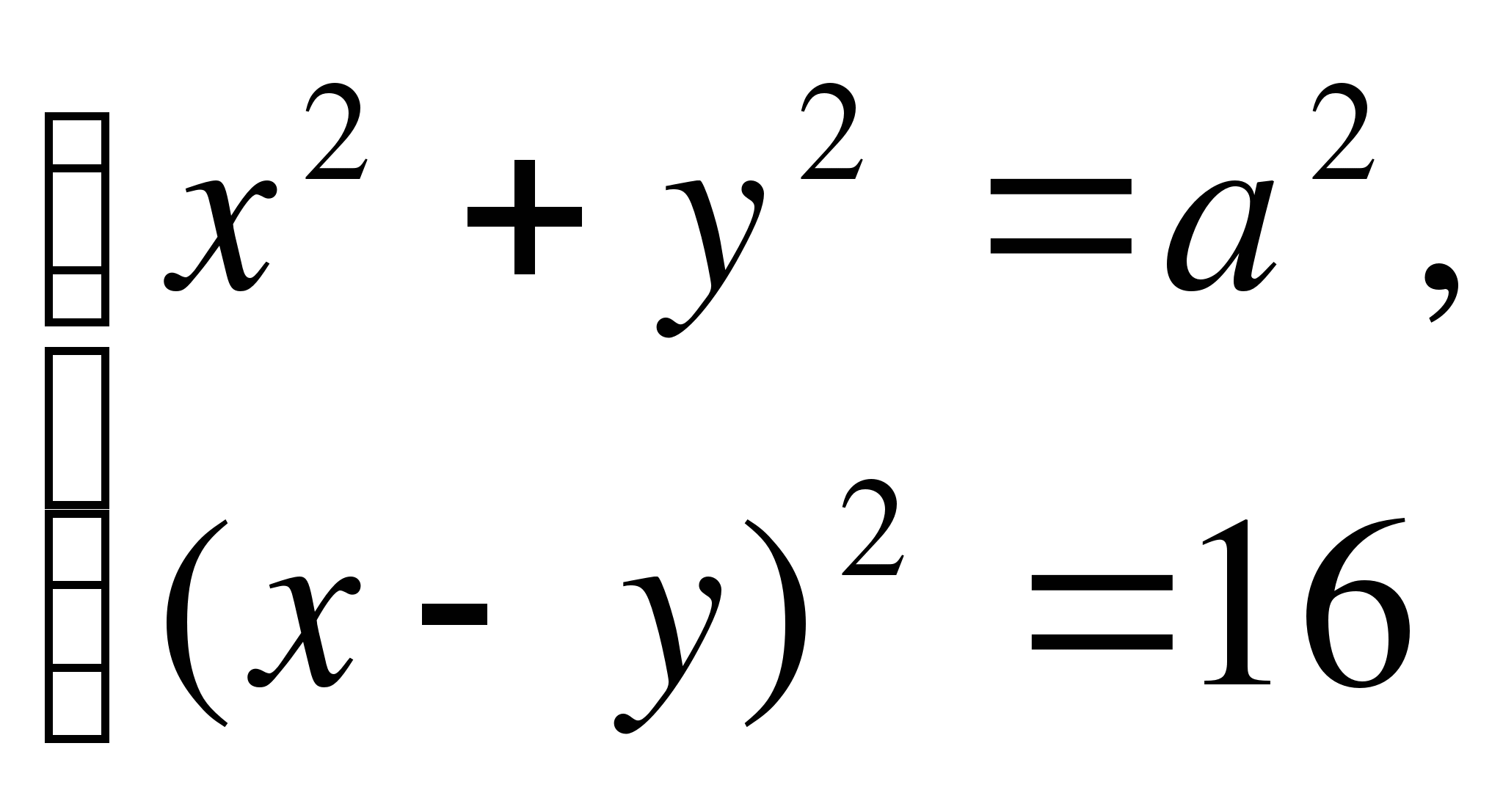 имеет ровно два решения?
имеет ровно два решения?
Ответ: а=2
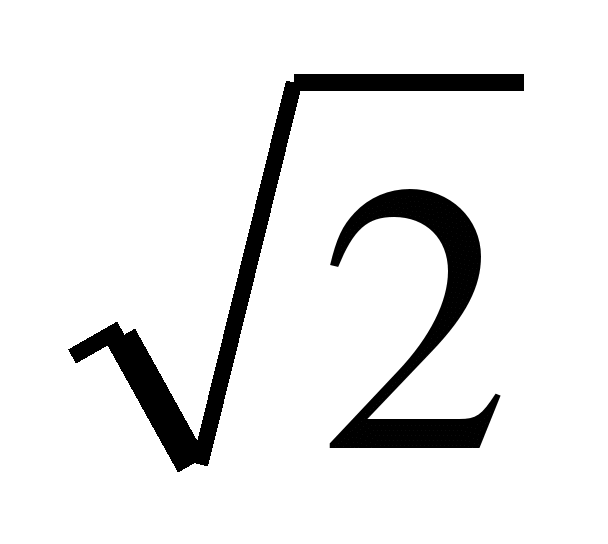 .
.
№ 7 . Решить неравенство х2 - 2ах + 1>0 для всех значений параметра а.
Ответ: при |а|>1 х Є R,
при а=1 х Є R, где х ≠ 1,
при а=-1 х Є R, где х ≠ -1,
при -1<a<1 х Є (-∞;-
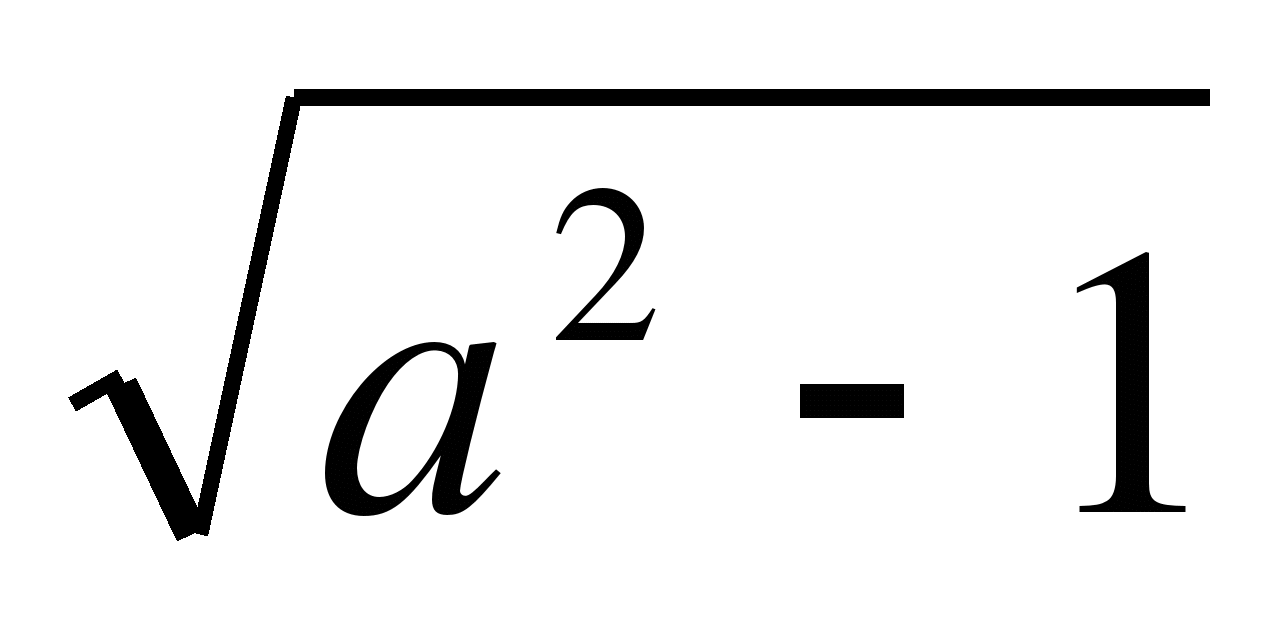 )U(а+
)U(а+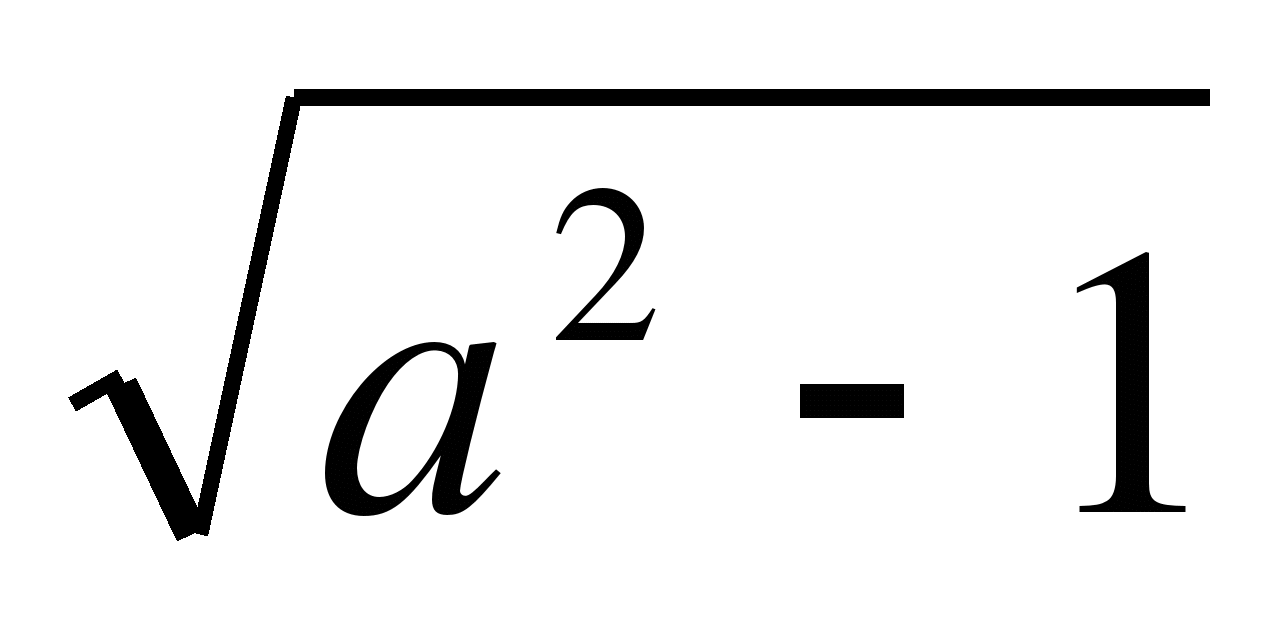 ;
+∞).
;
+∞).
№ 8. При каких значениях а неравенство ах2 +4ах +а+3<0 выполняется для всех действительных значений х?
Ответ: а Є (-∞; -4).
№ 9. При каких значениях параметра m двойное неравенство
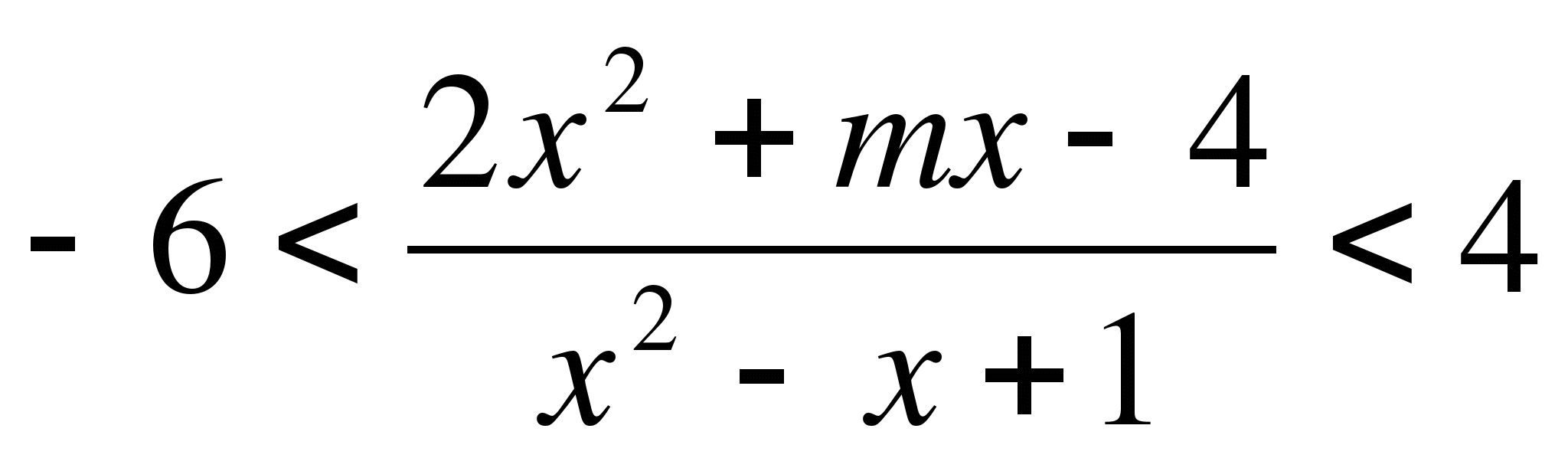 выполняется при всех действительных значениях х?
выполняется при всех действительных значениях х?
Ответ: m Є (-2; 4).
№ 10. Найти все значения параметра а, при каждом из которых система неравенств
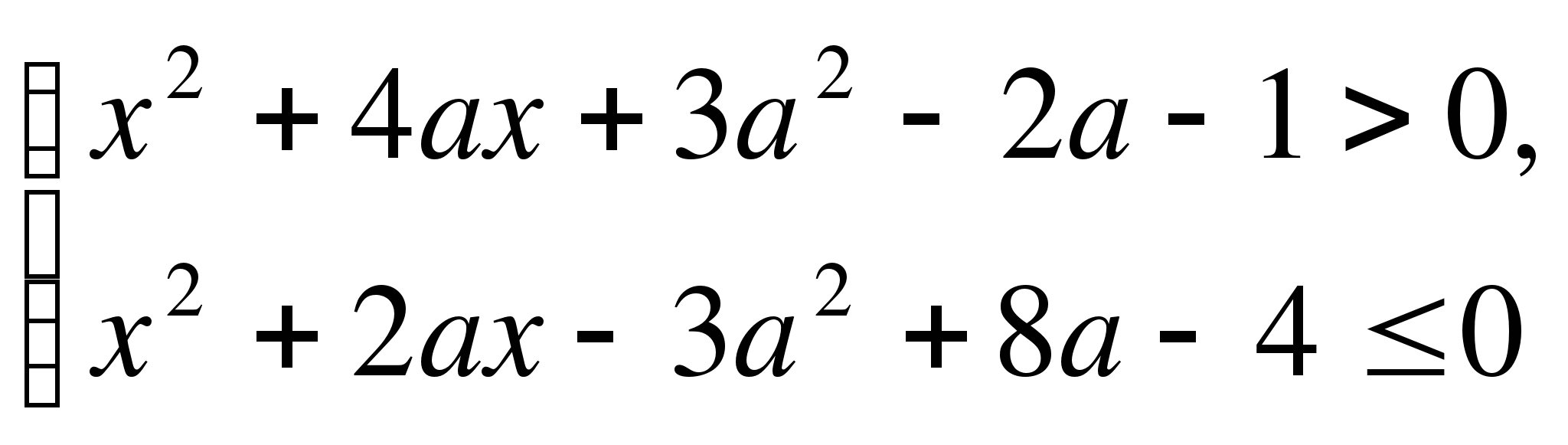 имеет хотя бы одно решение.
имеет хотя бы одно решение.
Решение. Так как дискриминант второго квадратного трёхчлена в системе равен D=4(a2-2a+1), а ветви параболы f(x)=x2 +2ax-3a2+8a-4 направлены вверх, то множество решений второго неравенства системы есть множество хє[x1;x2], где х1=-а-|2а-1|, х2=-а+|2а-1|. Найдём все значения а, при которых система не имеет решений. Если система неравенств не имеет решений, то одновременно выполнены неравенства f(x1)≤0, f(x2)≤0, где f(x)=x2 +4ax+3a2-2a-1; в противном случае хоть одно из чисел было бы решением данной системы. С другой стороны, если выполнены неравенства f(x1)≤0, f(x2)≤0, то числа х1,2 лежат между корнями (включая сами корни) квадратного трёхчлена f(x). Это значит, что для каждого решения х0 второго неравенства исходной системы выполнено условие f(x0)≤0, т. е. система не имеет решений. Итак, система не имеет решений тогда и только тогда, когда выполнены неравенства
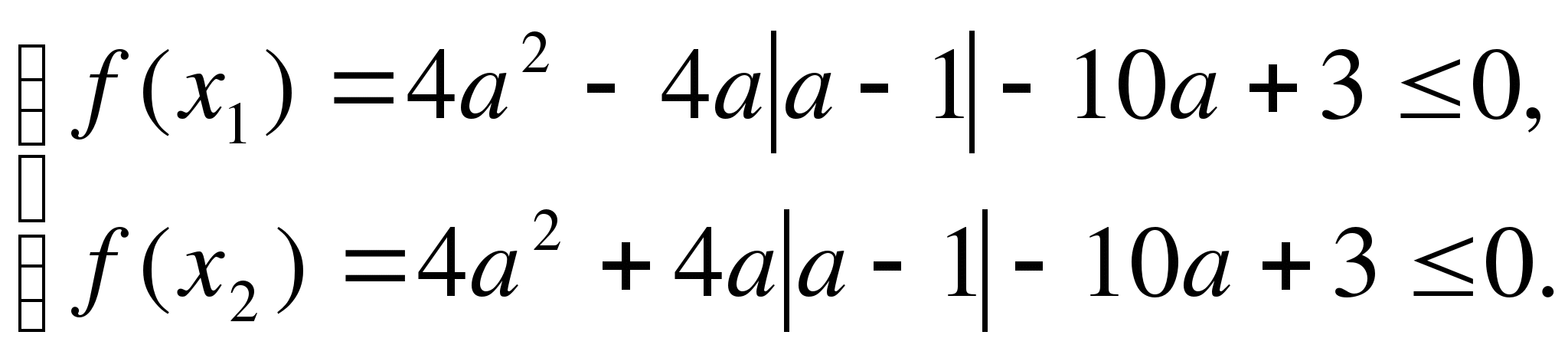 Рассматривая
два случая а≥1 и а<1, получим, что
последняя система неравенств равносильна системе
Рассматривая
два случая а≥1 и а<1, получим, что
последняя система неравенств равносильна системе 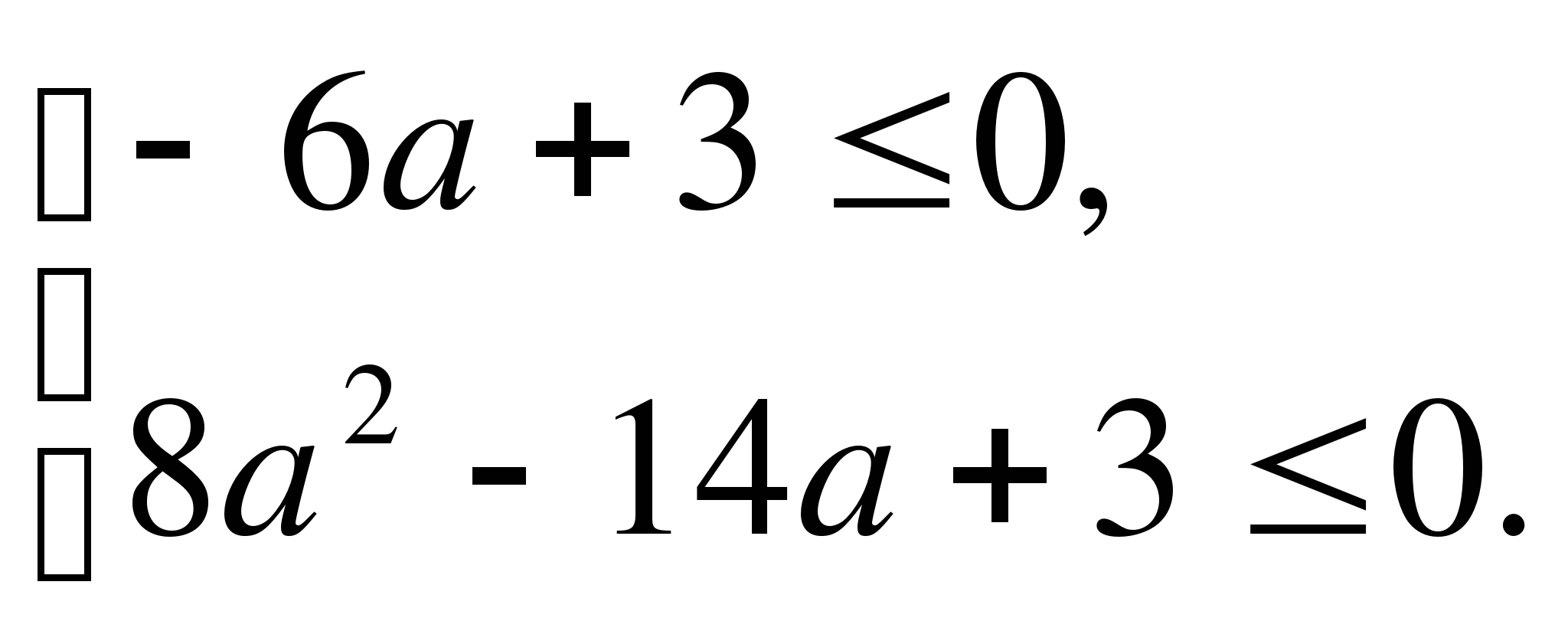 В
этой системе множеством решений первого неравенства
является
В
этой системе множеством решений первого неравенства
является 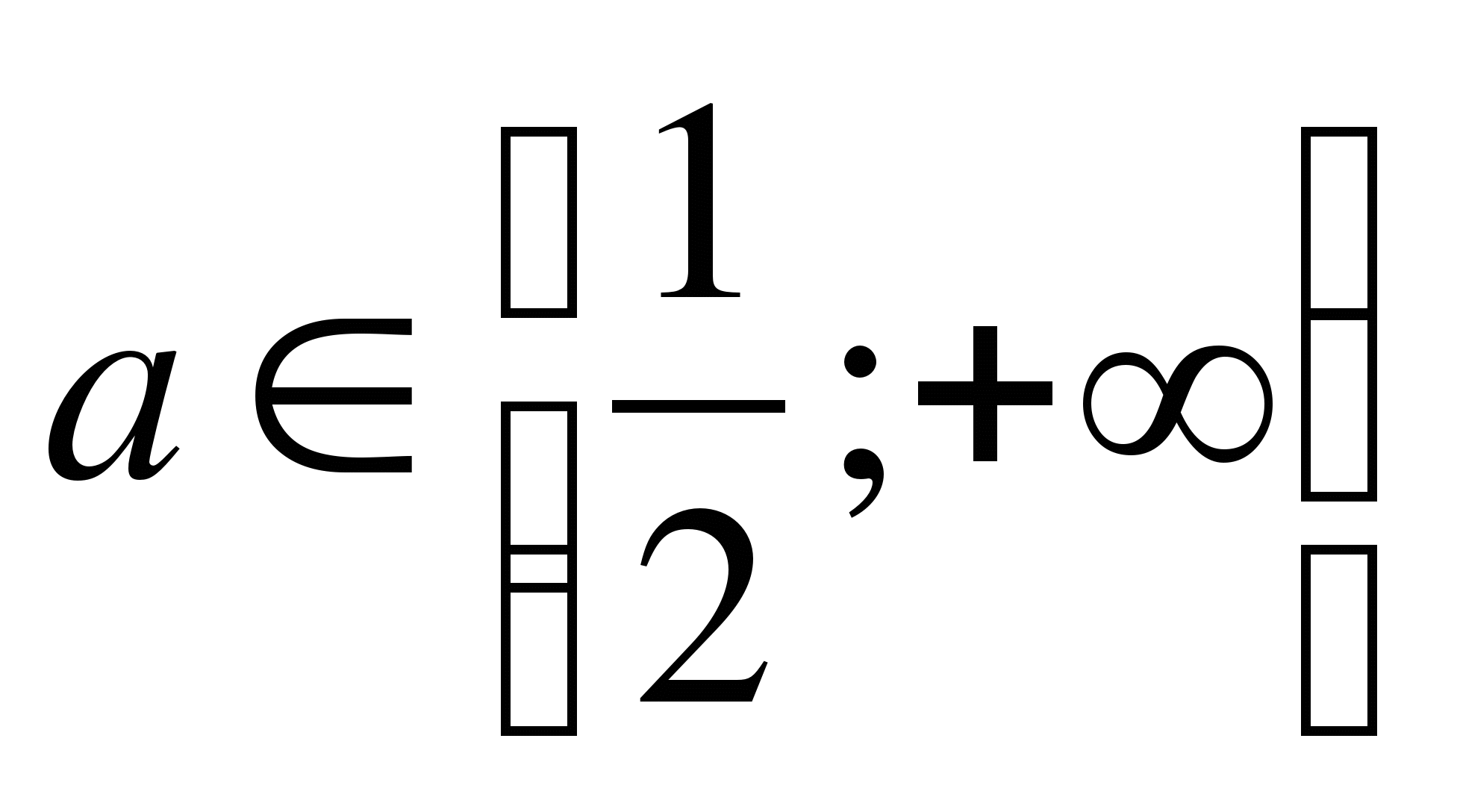 ,
а второго неравенства- множество
,
а второго неравенства- множество 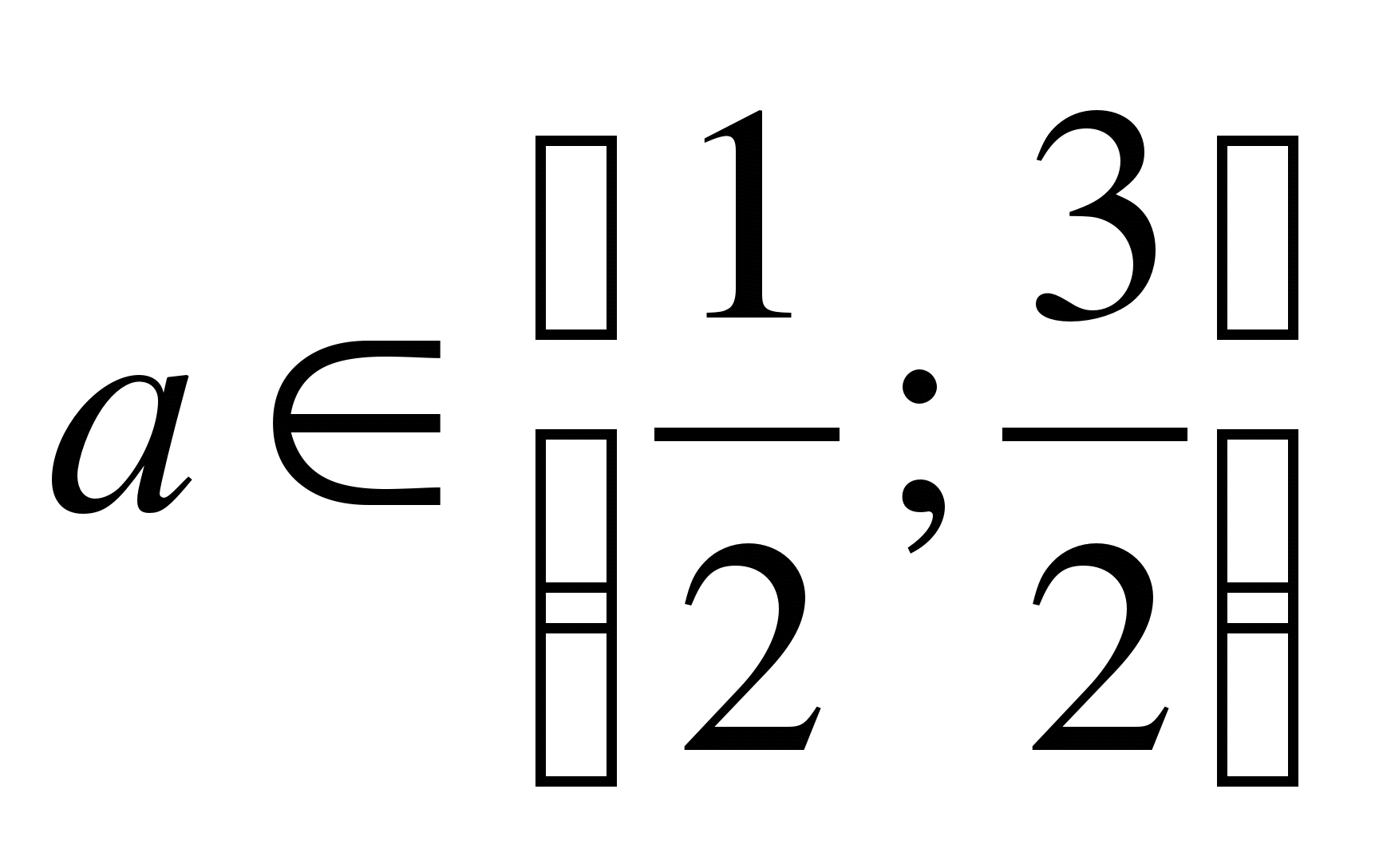 .
Поэтому множеством решений этой системы является промежуток
.
Поэтому множеством решений этой системы является промежуток
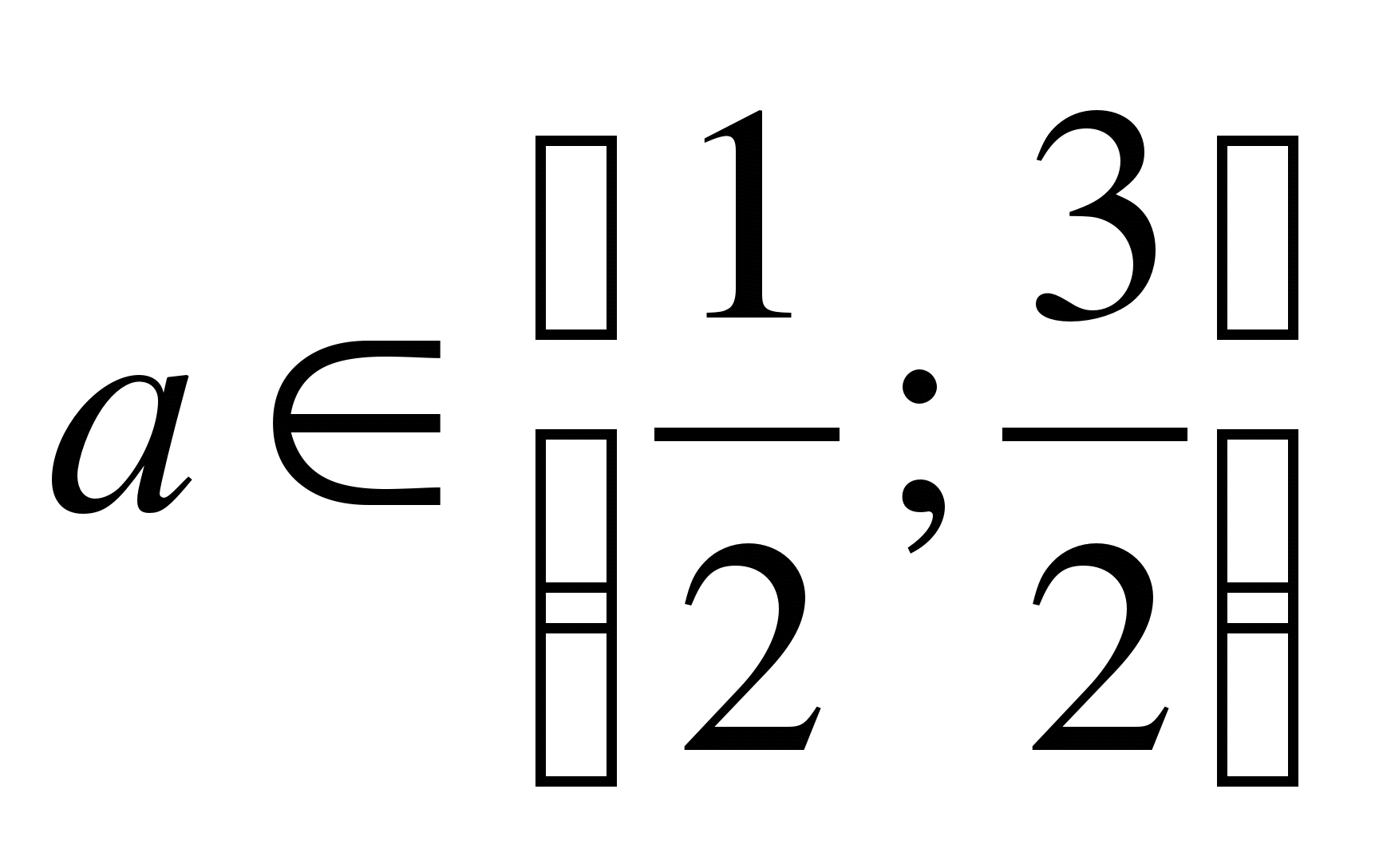 .
Таким образом, первоначальная система неравенств не имеет
решений тогда и только тогда, когда
.
Таким образом, первоначальная система неравенств не имеет
решений тогда и только тогда, когда 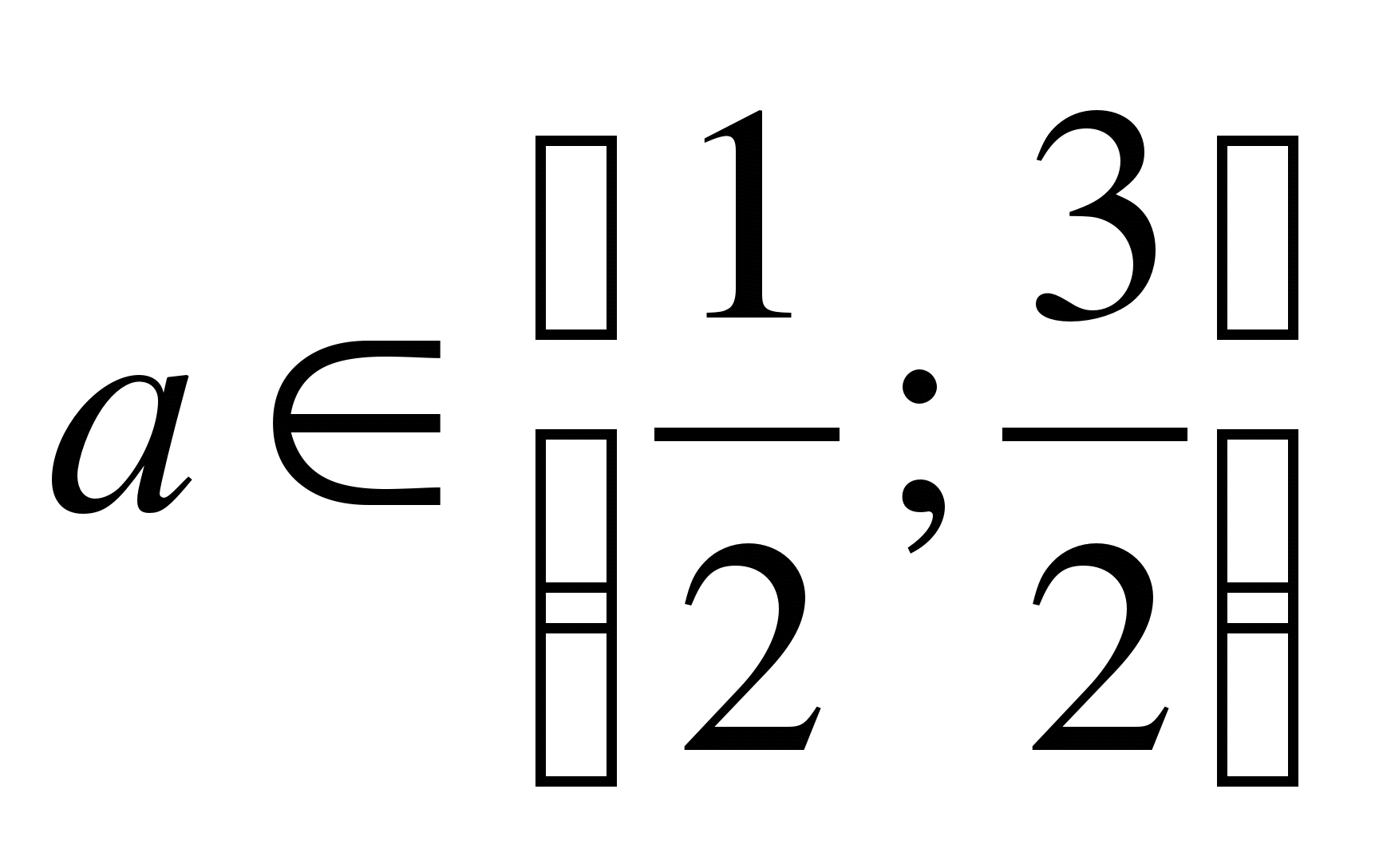 .
Следовательно, если
.
Следовательно, если 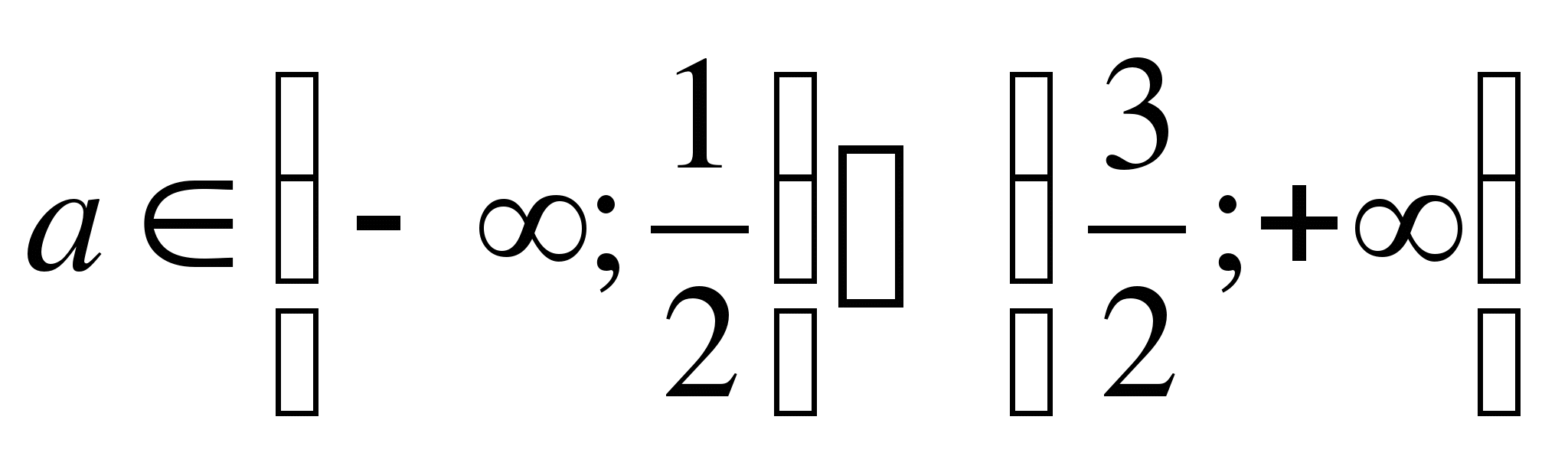 ,
то система имеет хотя бы одно решение.
,
то система имеет хотя бы одно решение.
Ответ.
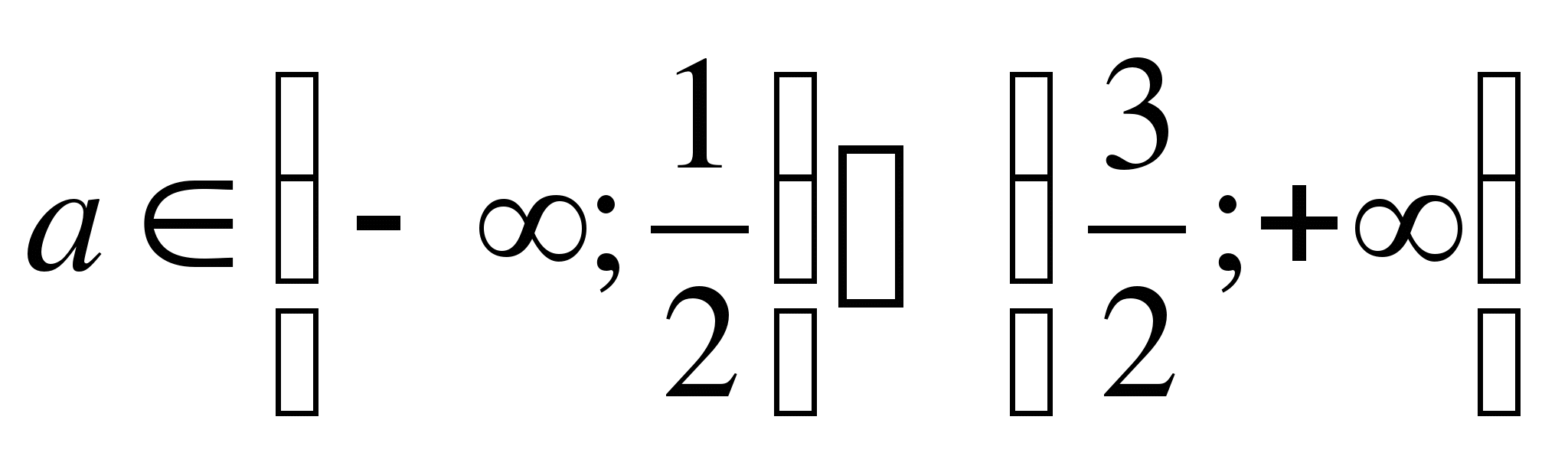 .
.
Дополнительный набор задания для практикума по теме
«Решение линейных уравнений и неравенств».
-
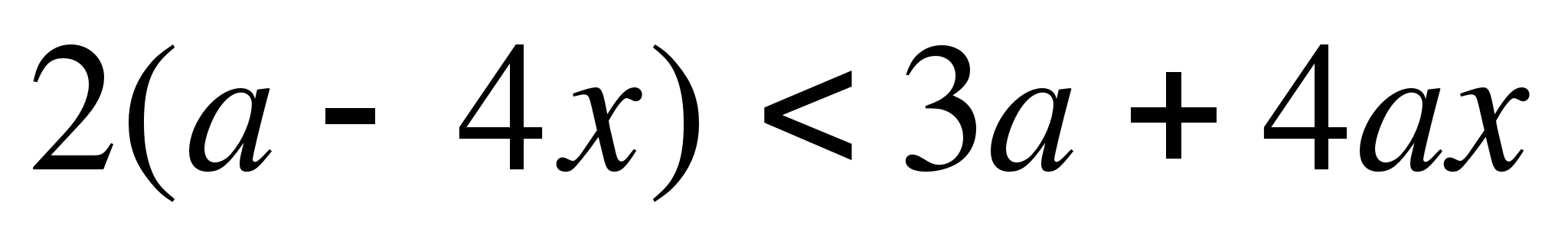 .
.
Ответ: если а=-2, то решений нет; если а<-2, то
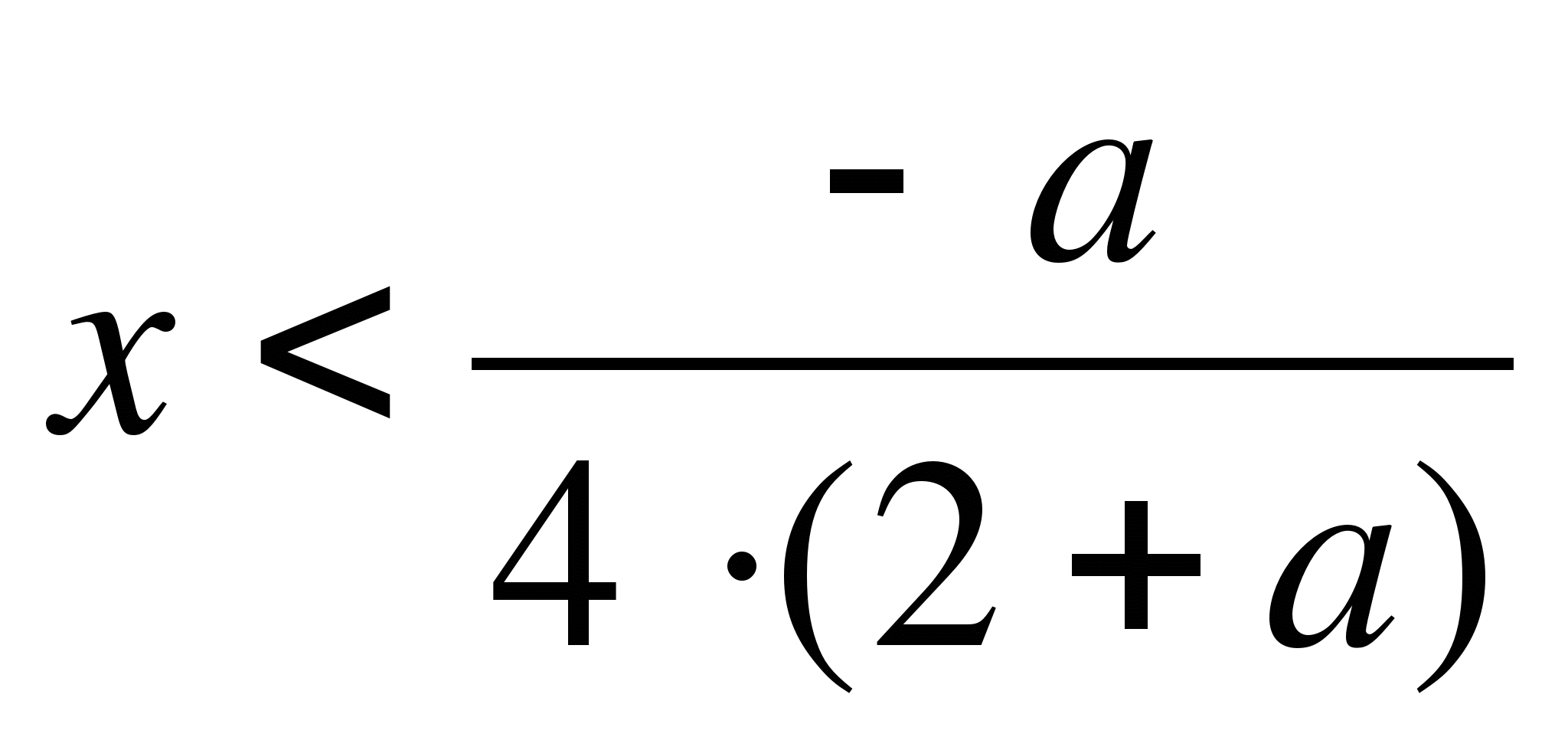 ;
;
если a>-2, то
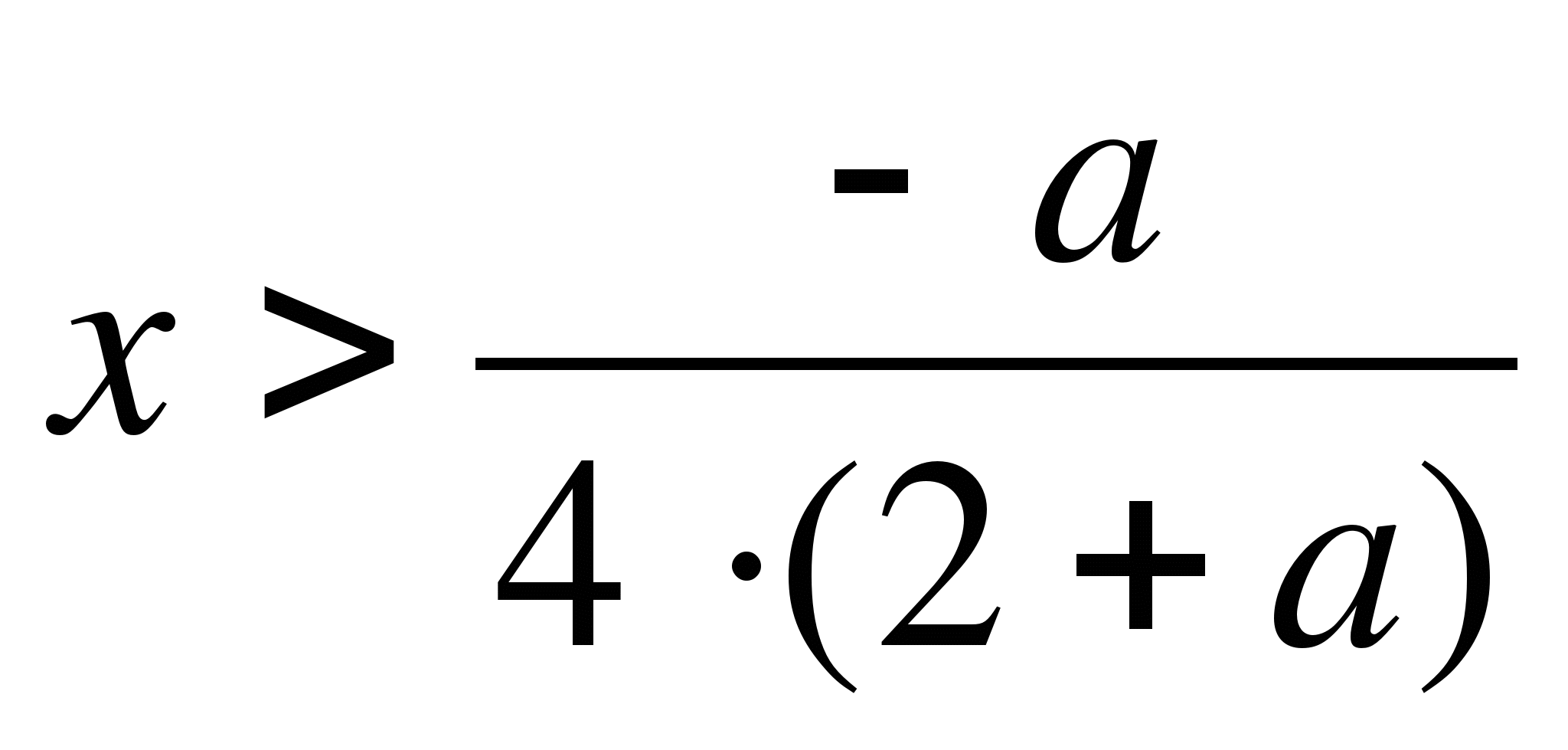 .
.
-
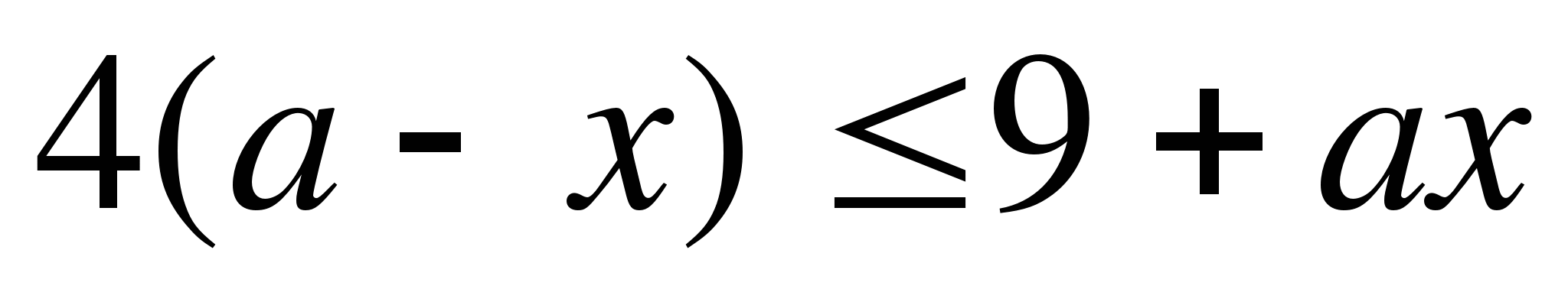 .
.
Ответ: если а=-4, то решений нет; если a>-4, то
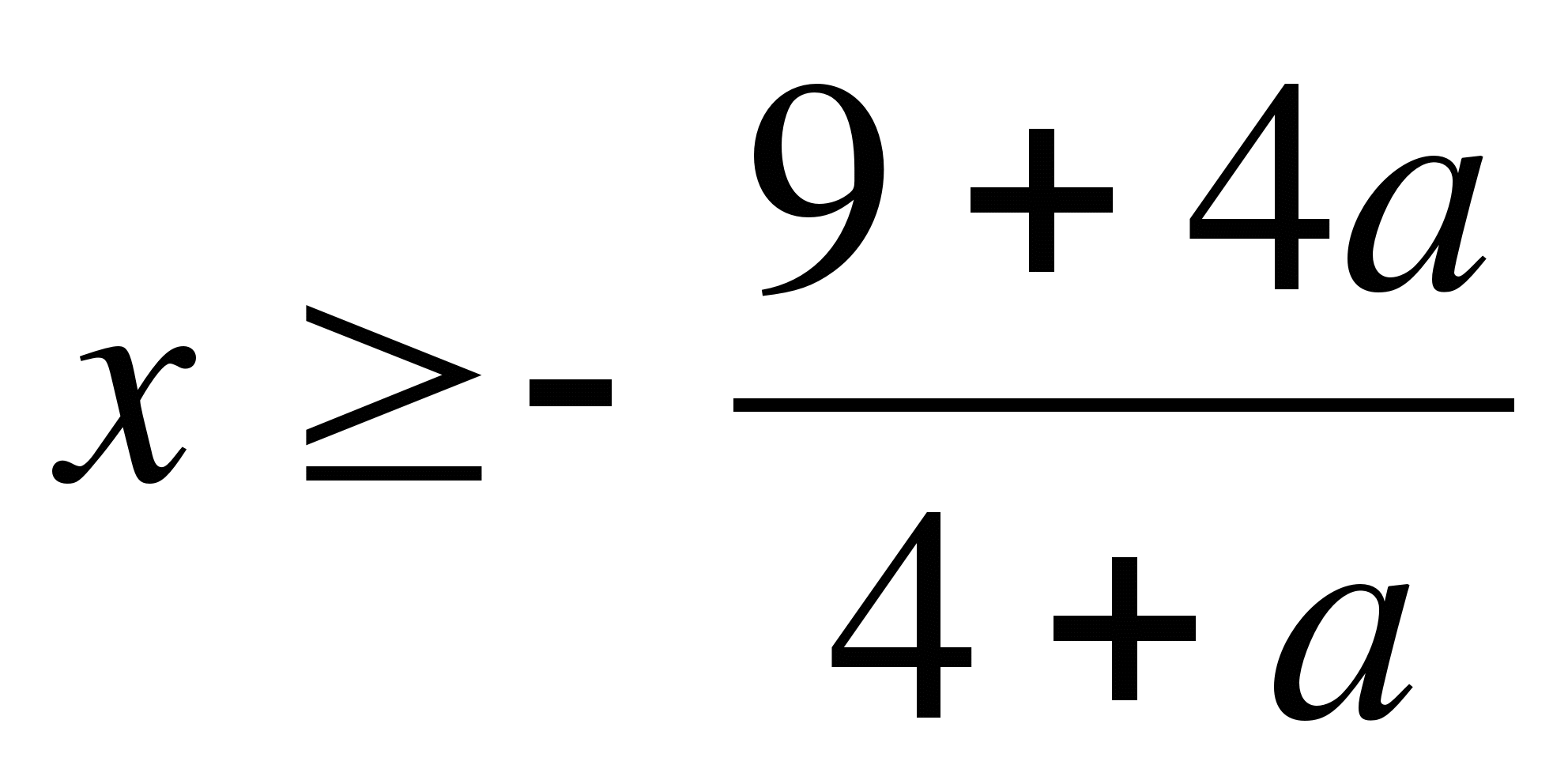 ;
;
если a<-4, то
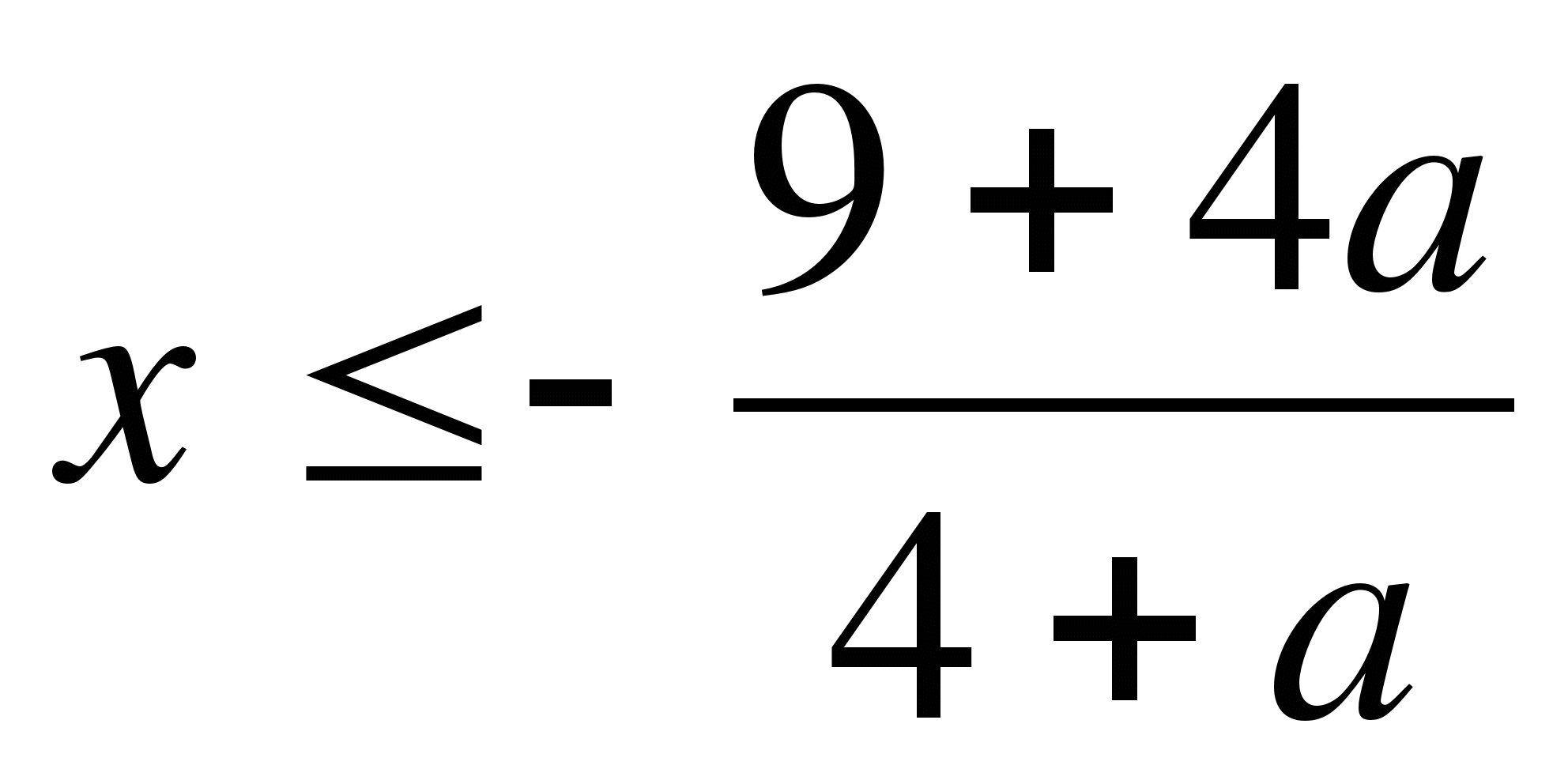 .
.
-
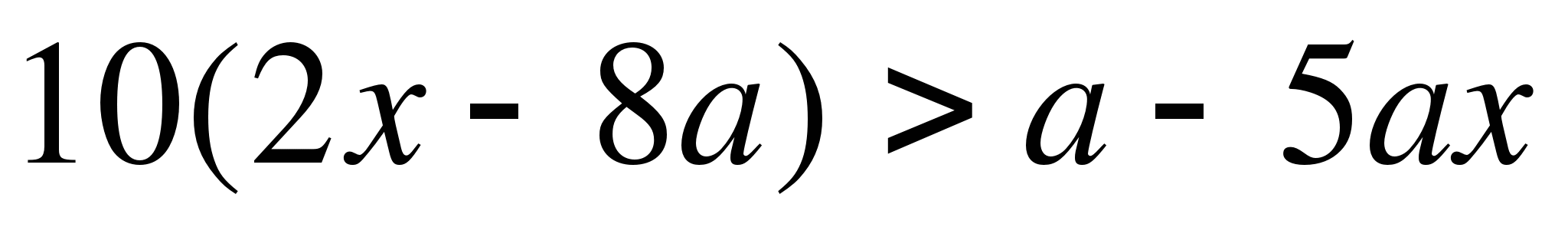 .
.
Ответ: если а=-4, то
 ;
если a>-4, то
;
если a>-4, то 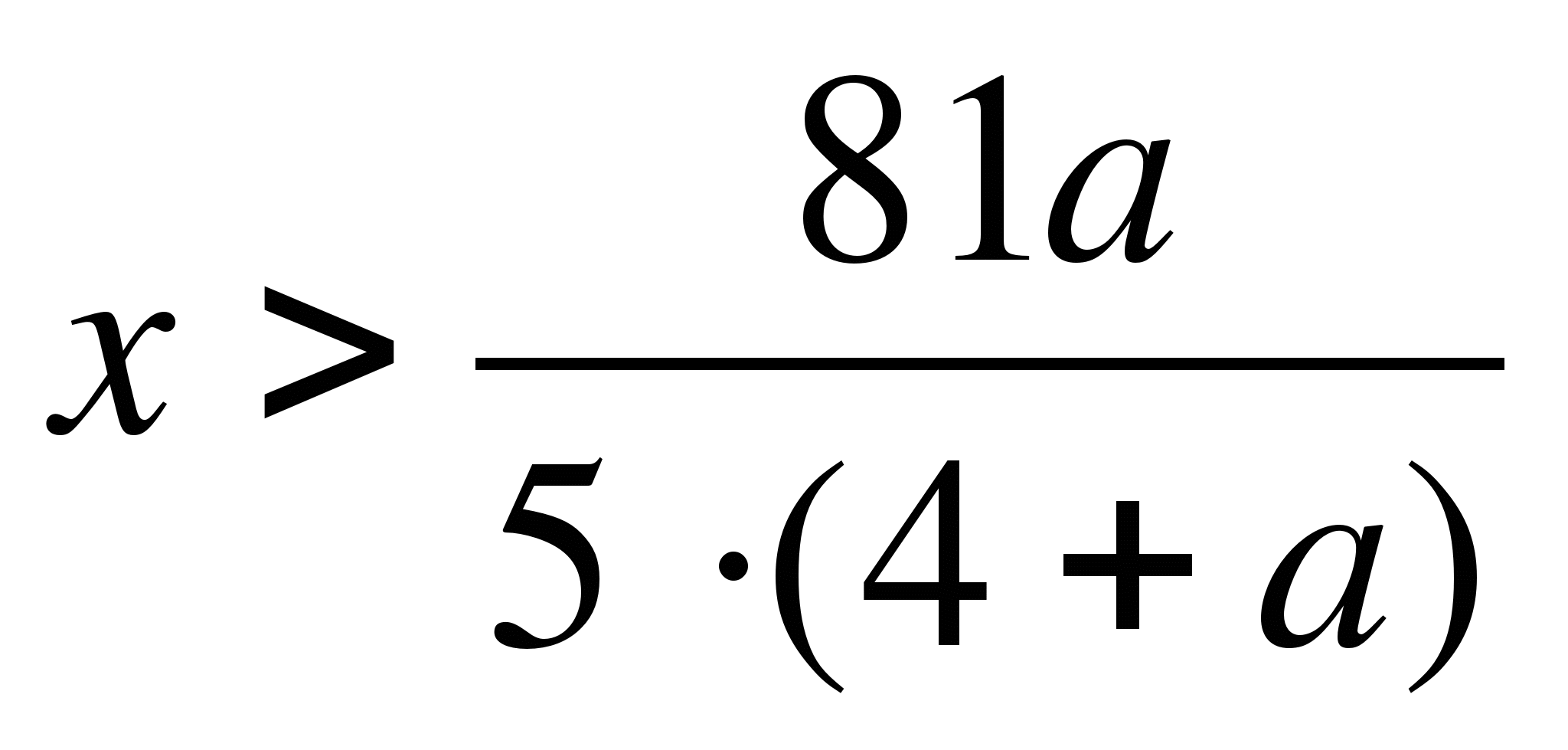 ;
;
если a<-4, то
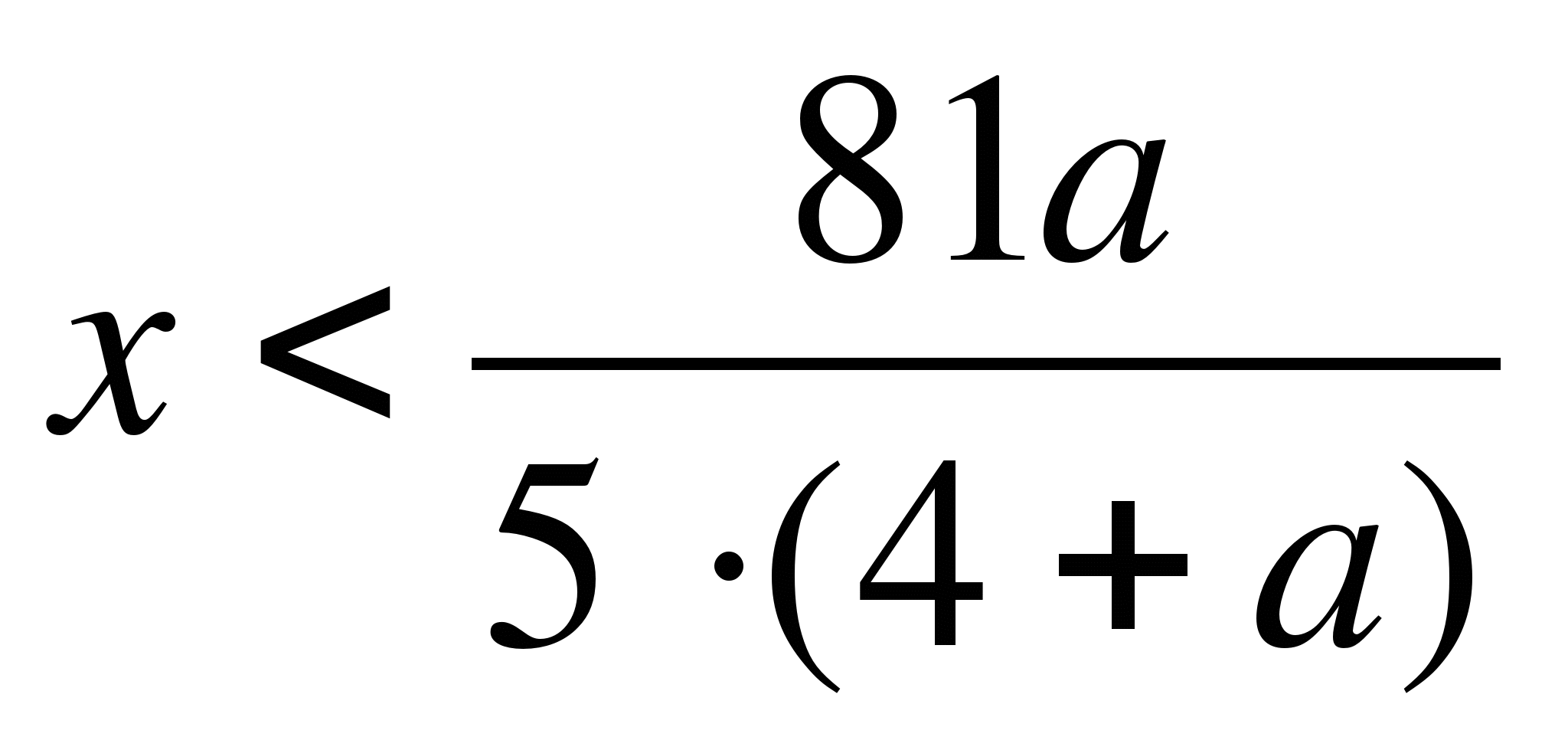 .
.
-
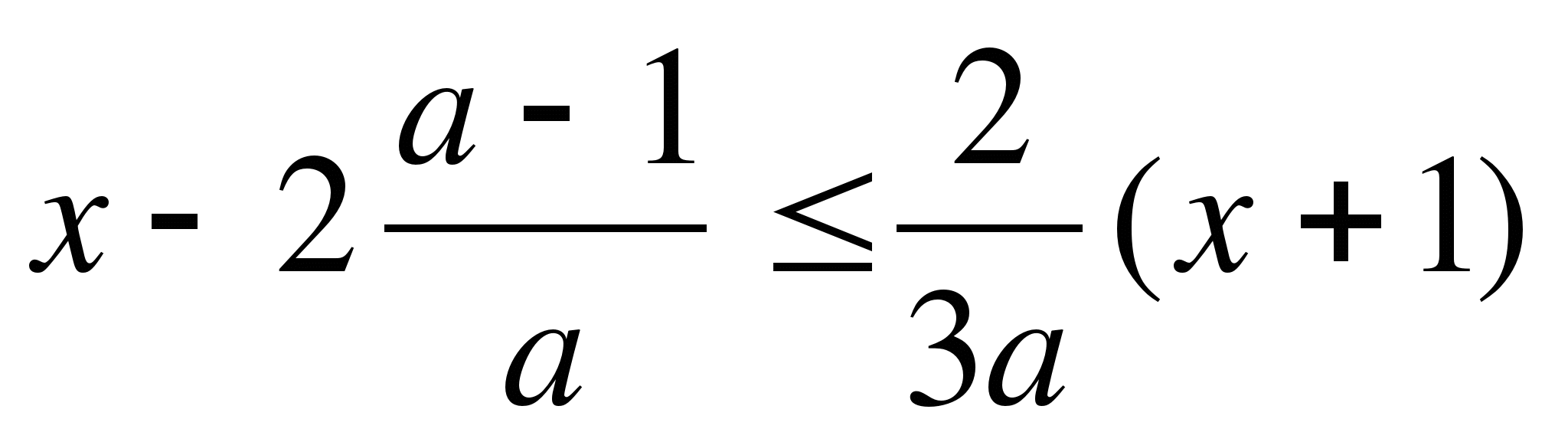 .
.
Ответ: если а=0, то решений нет; если а=
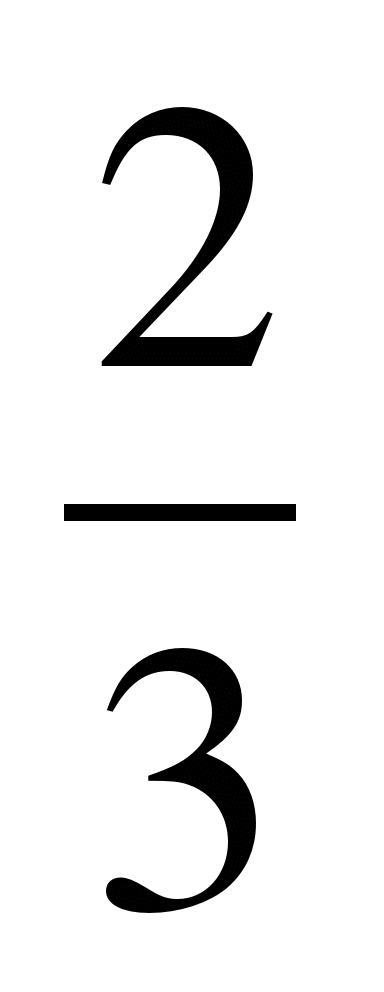 ,
то
,
то  ;
;
если а<0 и a>
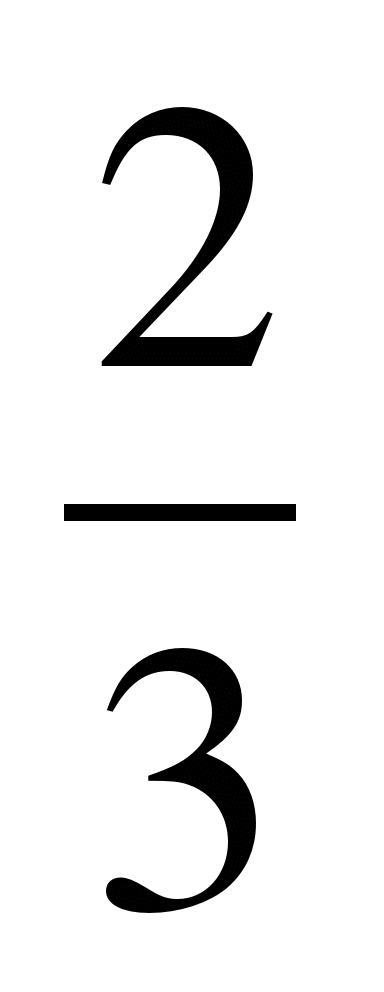 ,
то x≤2; если
,
то x≤2; если 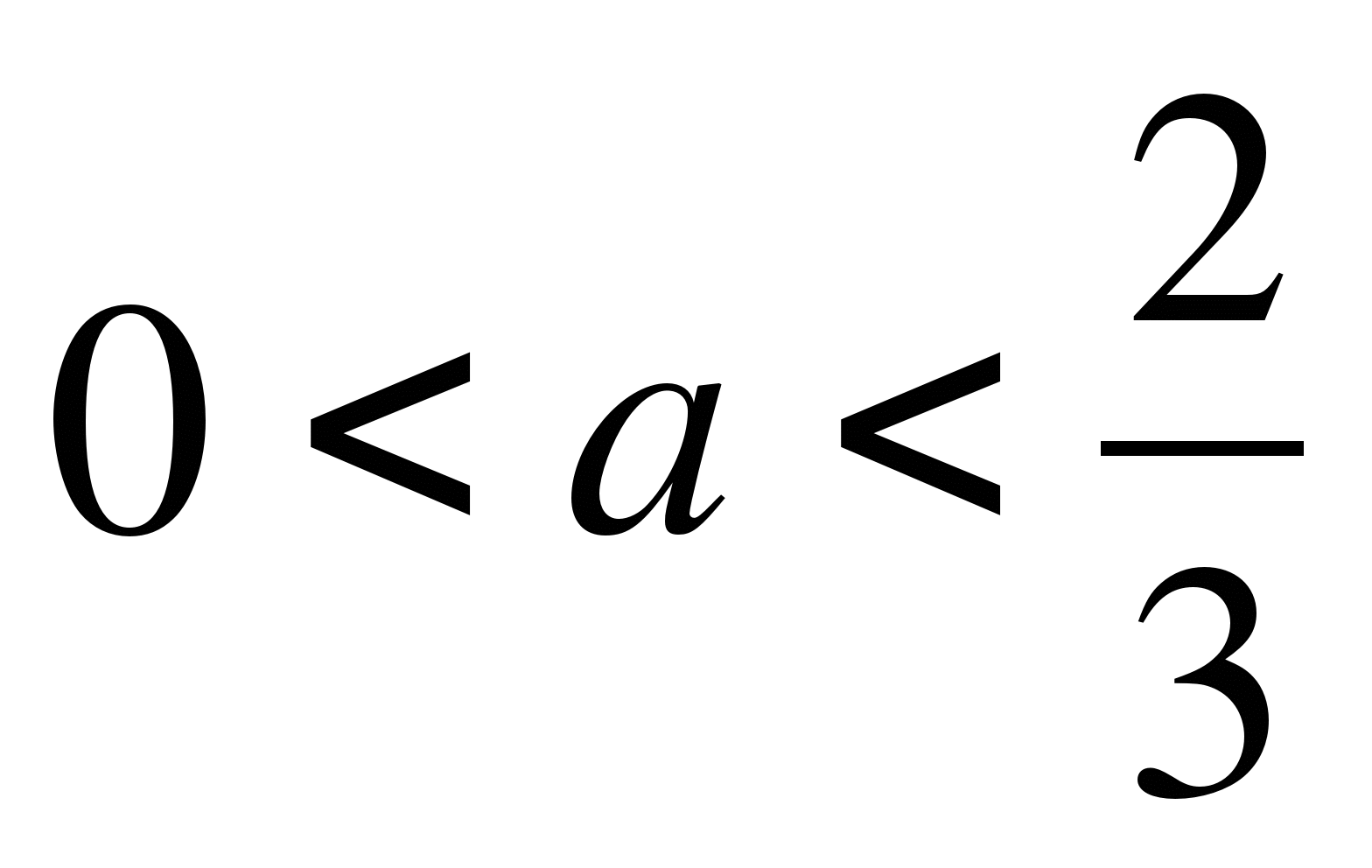 ,
то x≥2.
,
то x≥2.
5.
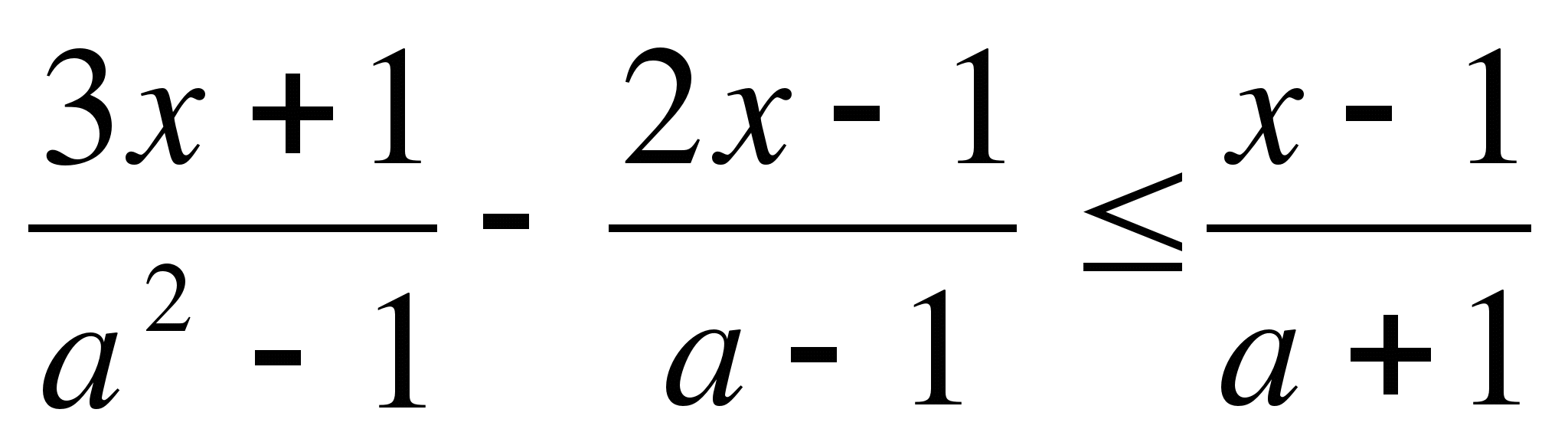 .
.
Ответ: если а=
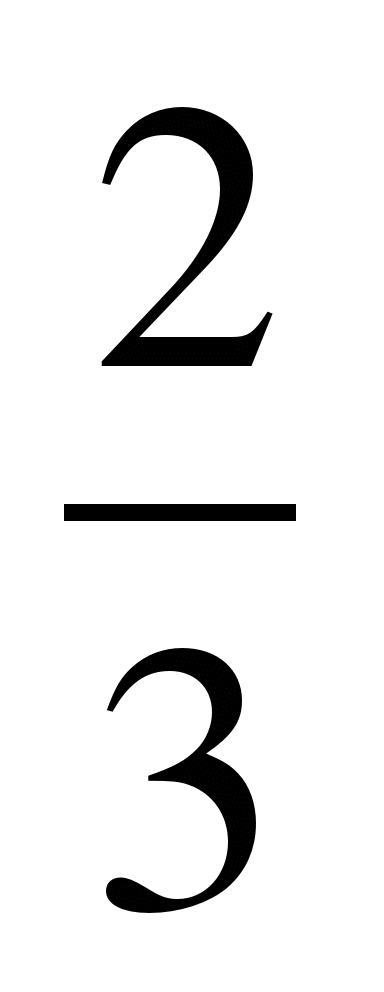 ,
то
,
то  ;
если а=±1, то решений нет;
;
если а=±1, то решений нет;
если
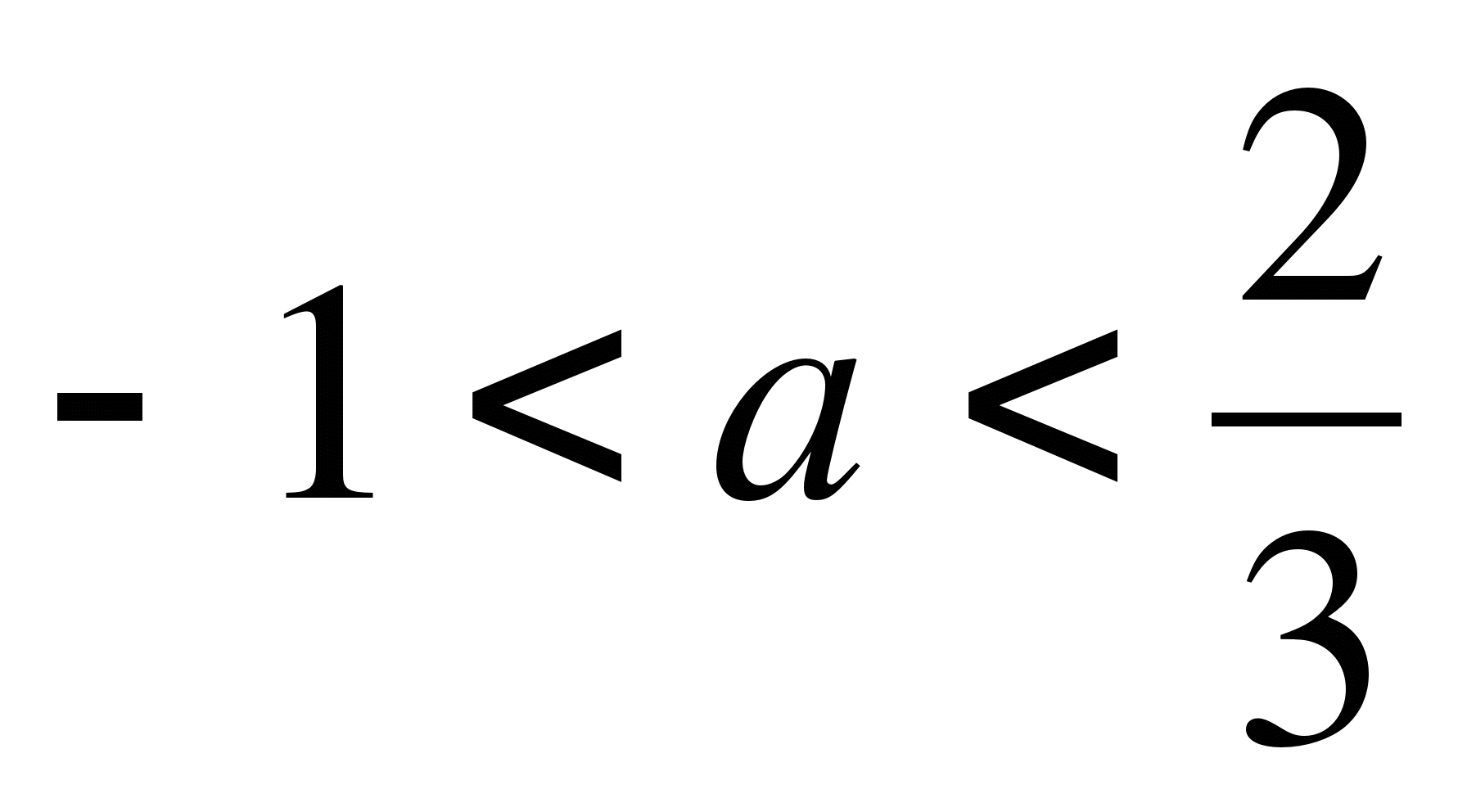 и а>1, то
и а>1, то 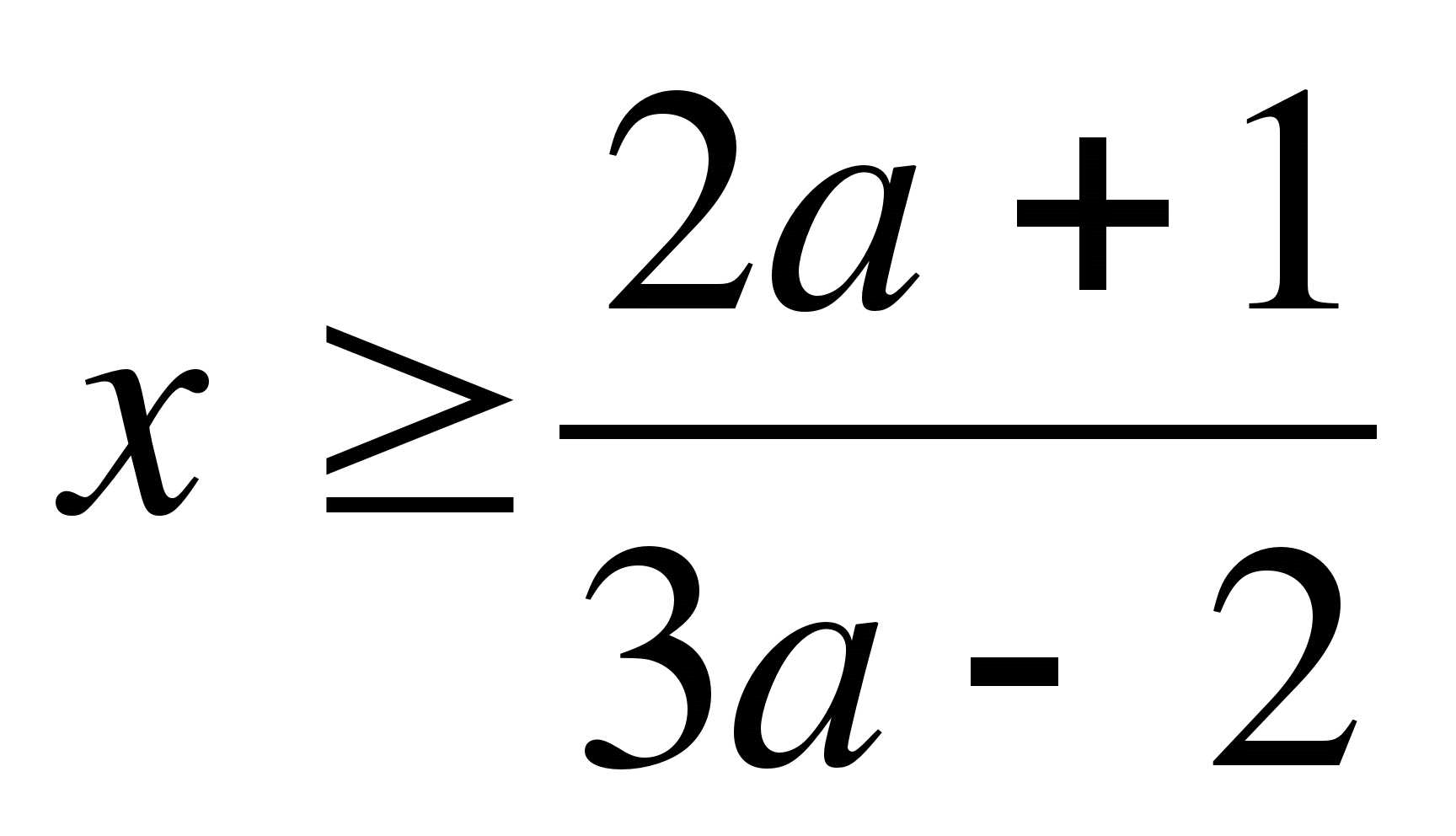 ;
если а <-1 и
;
если а <-1 и 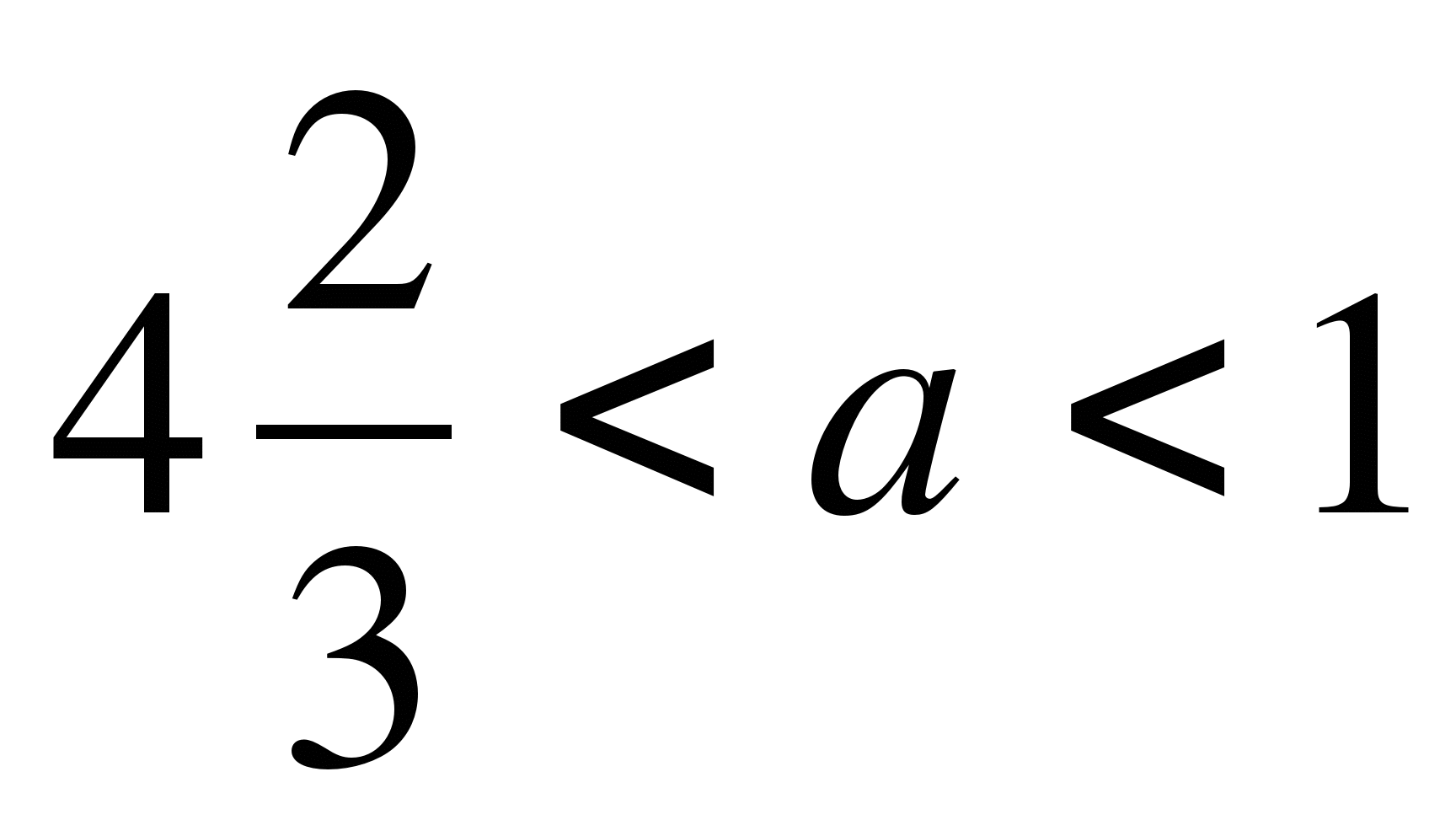 ,
то
,
то 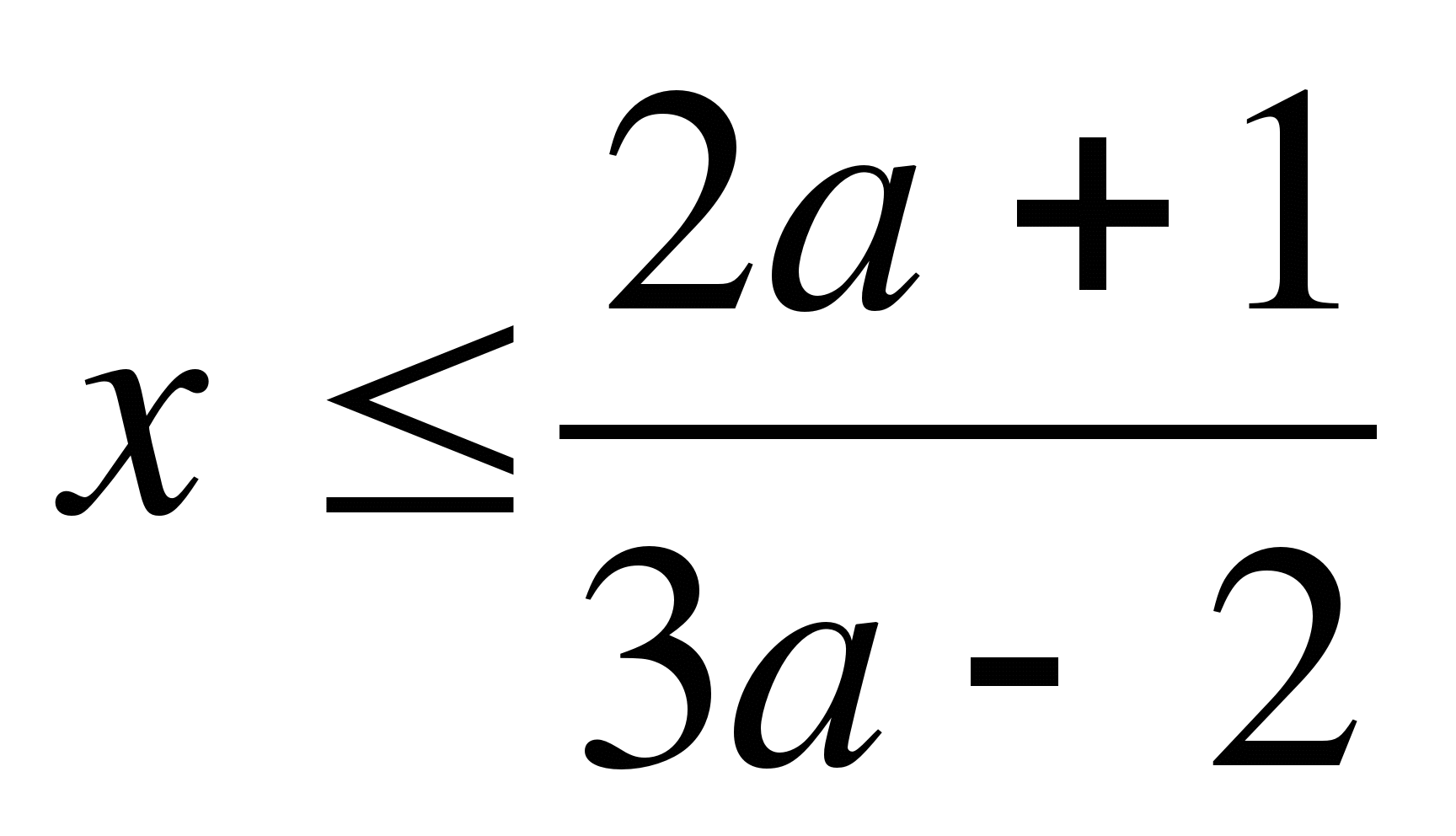 .
6.
.
6. 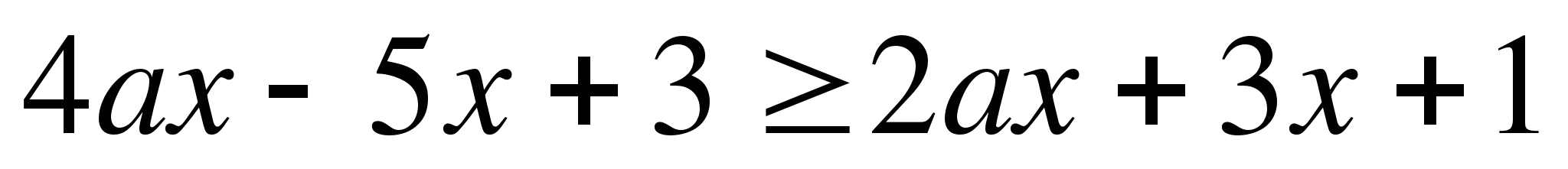
Ответ: если а=4, то решений нет; если а<4, то
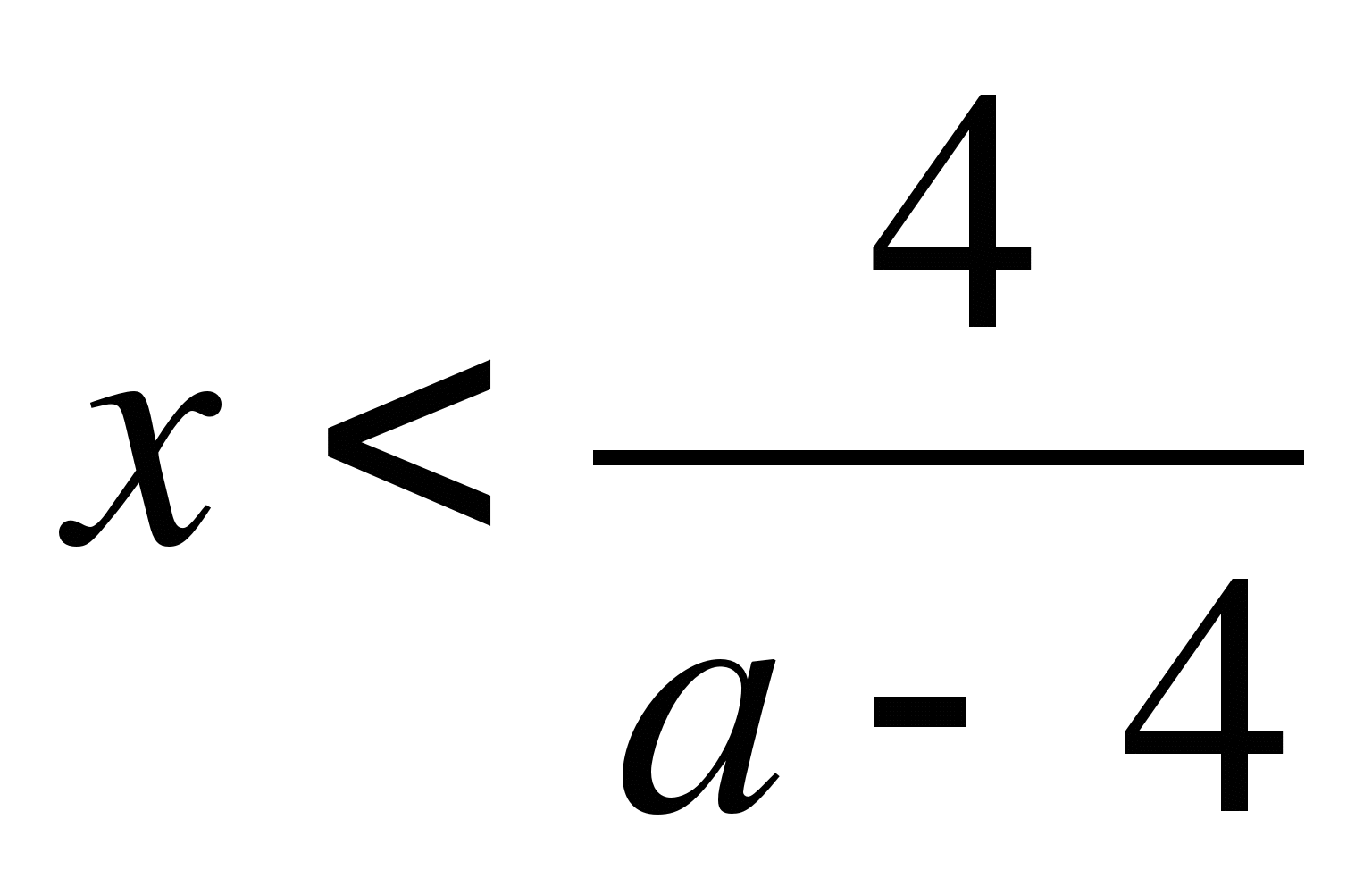 ;
;
если а>4, то
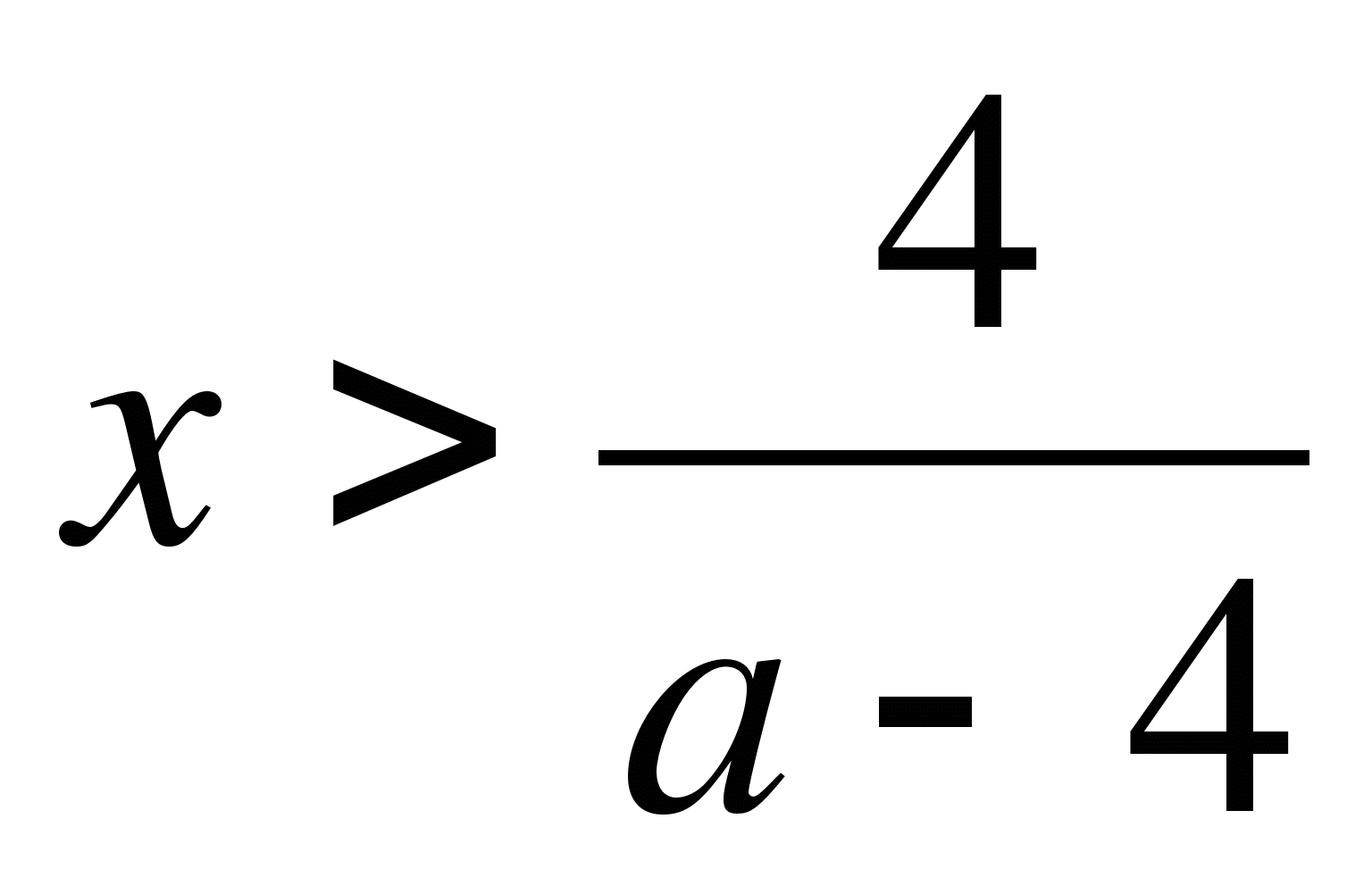 .
.
-
-
При каких k неравенство
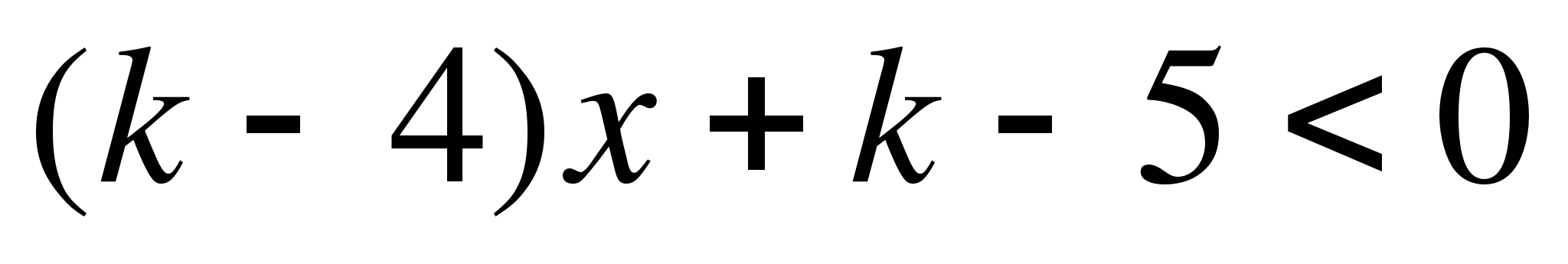 справедливо для всех х, удовлетворяющих
условию
справедливо для всех х, удовлетворяющих
условию 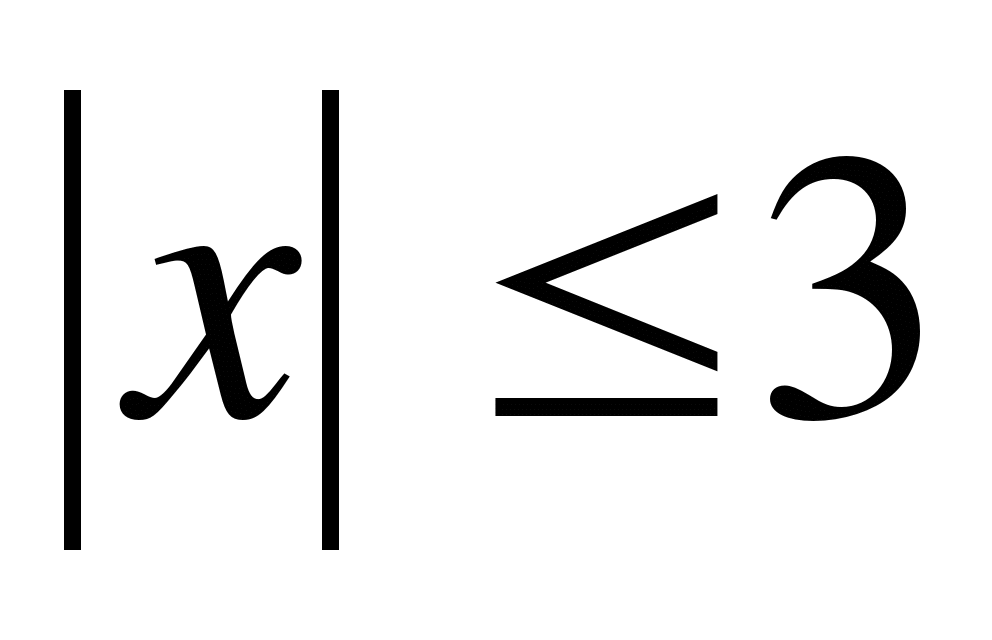 ?
?
-
Ответ: 3,5<k<4,25
9. При каких значениях m неравенство (m-2)x+2m-16<0 верно при всех х, удовлетворяющих условию
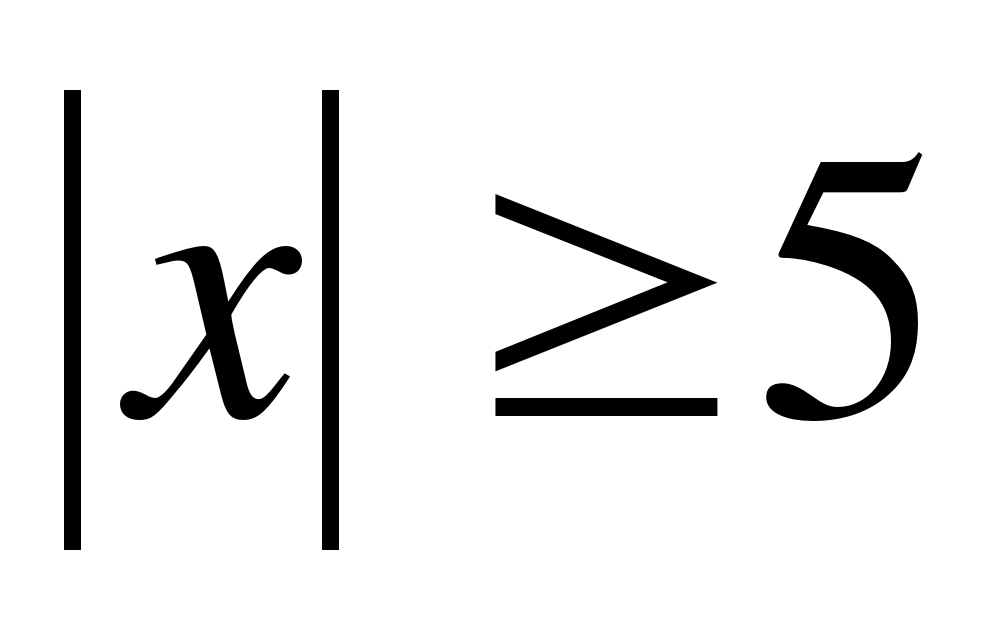 .
.
Ответ: m=2.
10. При каких значениях параметра а среди корней уравнения
2ах-4х-а2+4а-4=0 есть корни больше 1?
Ответ: при а=2, а>4.
11. Найти значения а, при каждом из которых уравнение а(3х-а)=6х-4 имеет положительный корень.
Ответ: при а>-2.
Итоговые занятия.
Занятие 1.
I. Тест.
№ 1. Решить уравнение ах-7=2х+10.
Ответ: а) при а≠2 х=
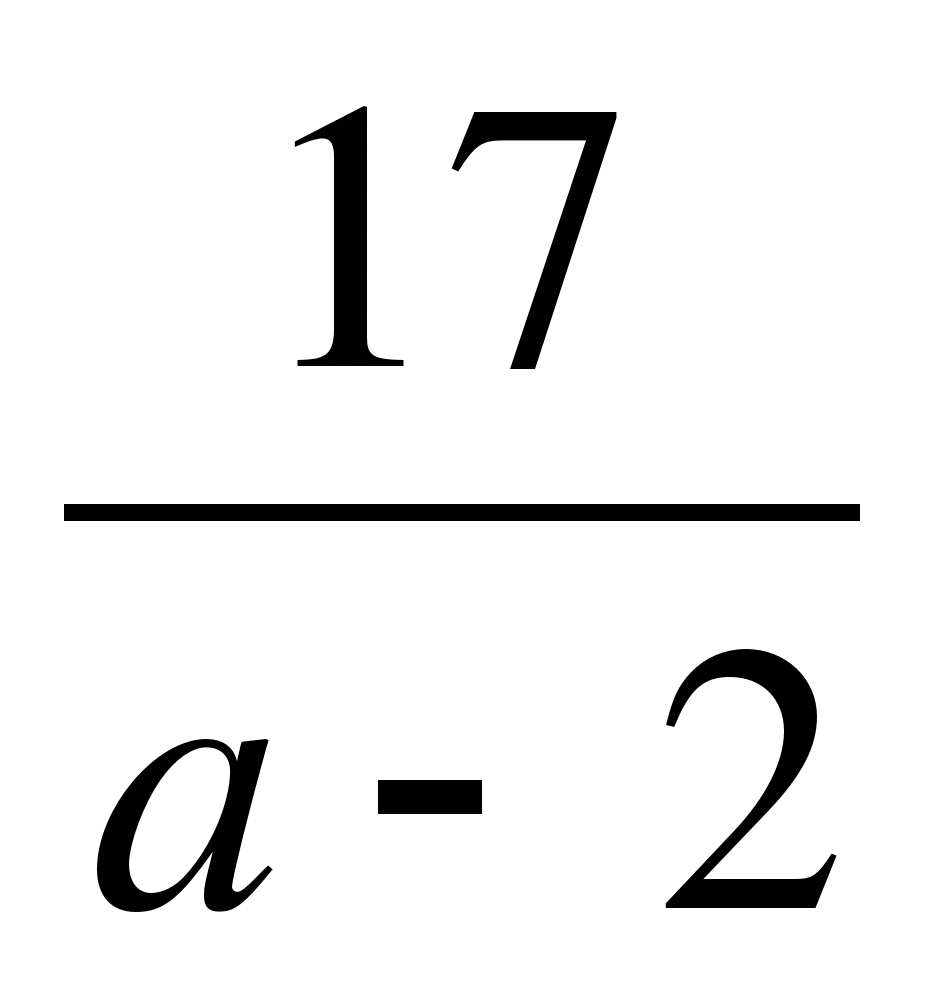 ,
при а=2 корней нет;
,
при а=2 корней нет;
б) х=
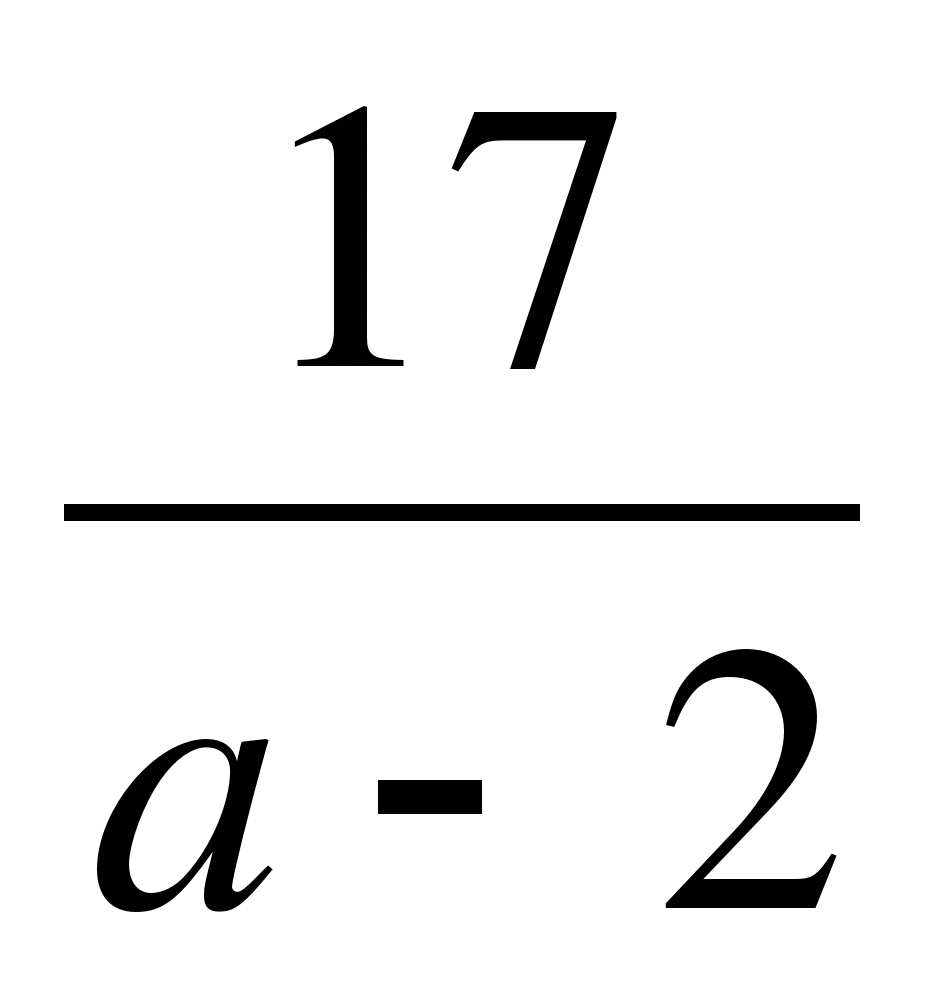 ;
;
в) при а≠±2 х=
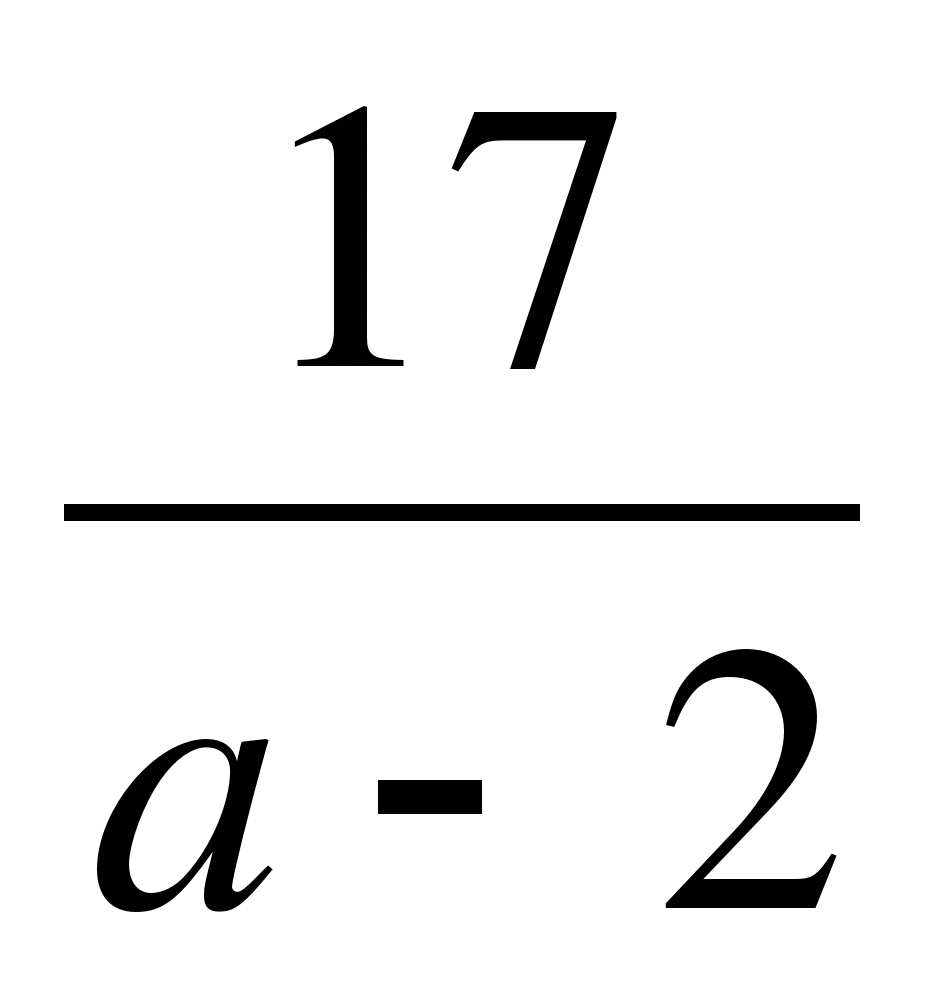 .
.
№ 2. Решить уравнение (а2-1)х - (2а2+а-3) = 0.
Ответ: а) х=
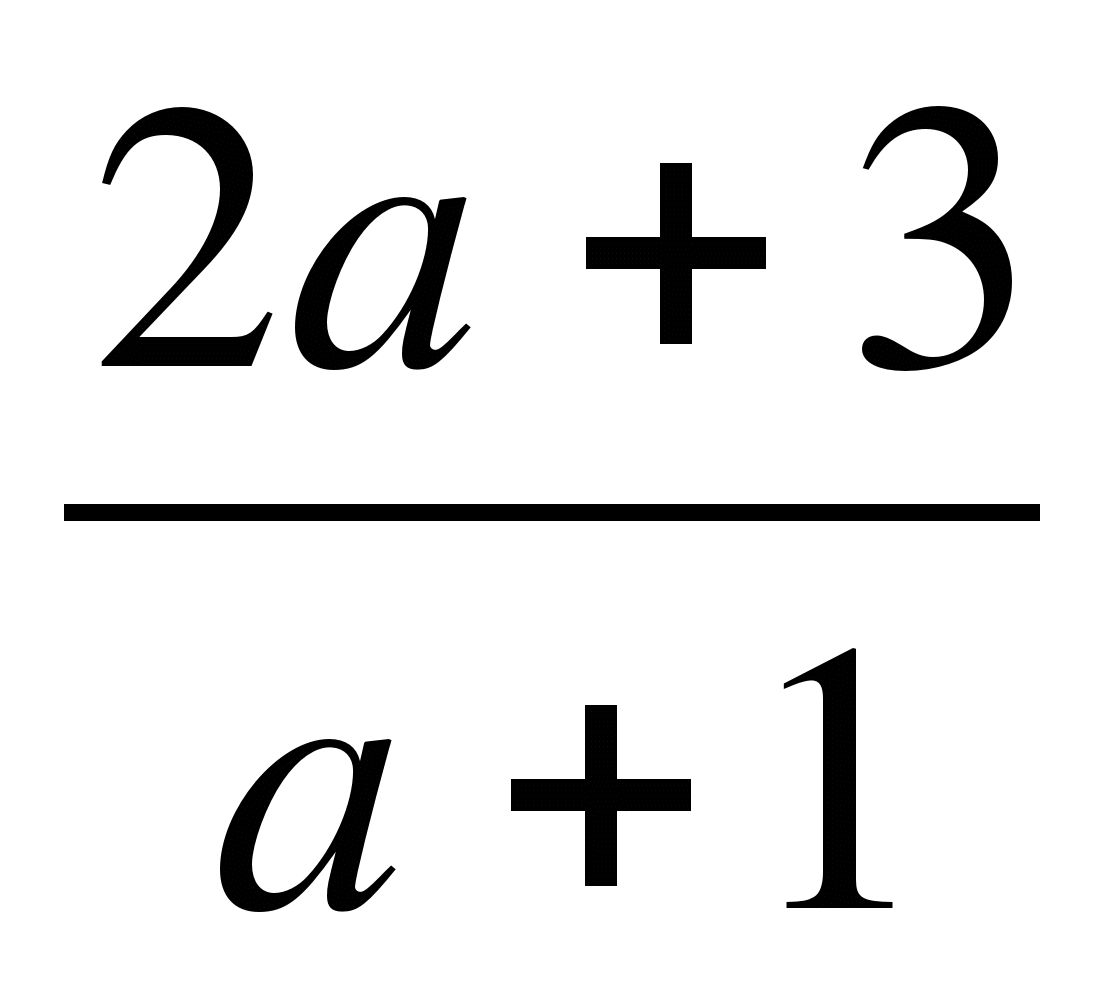 ;
;
б) при а≠±1 х=
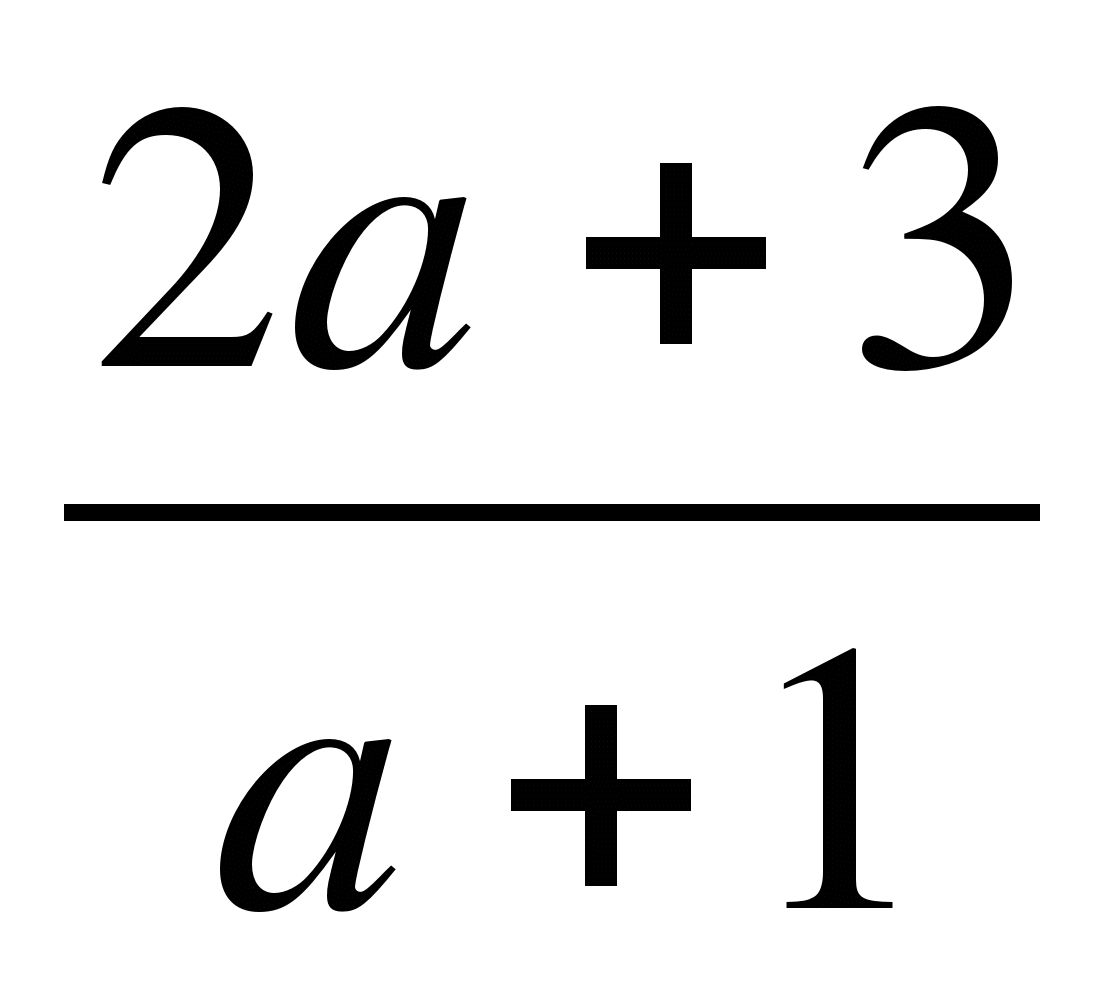 ,
при а=1 хєR, при а=-1 корней нет;
,
при а=1 хєR, при а=-1 корней нет;
в) при а≠±1 х=
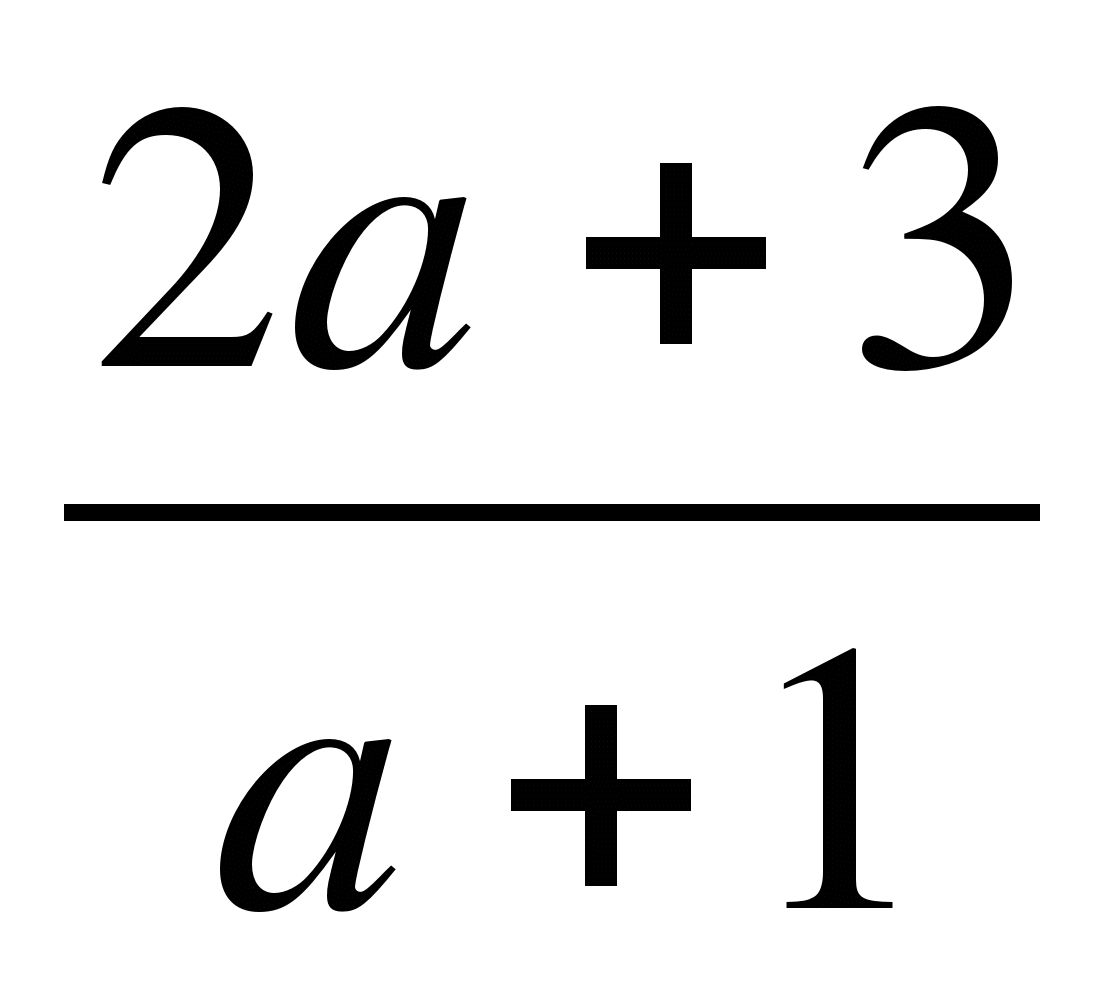 ,
при а=±1 корней нет.
,
при а=±1 корней нет.
№ 3. При каких значениях а среди корней уравнения х-ах+а2-1=0 есть корни больше 1?
Ответ: а) а<0;
б) а=0;
в) а>0.
№ 4. Решите неравенство
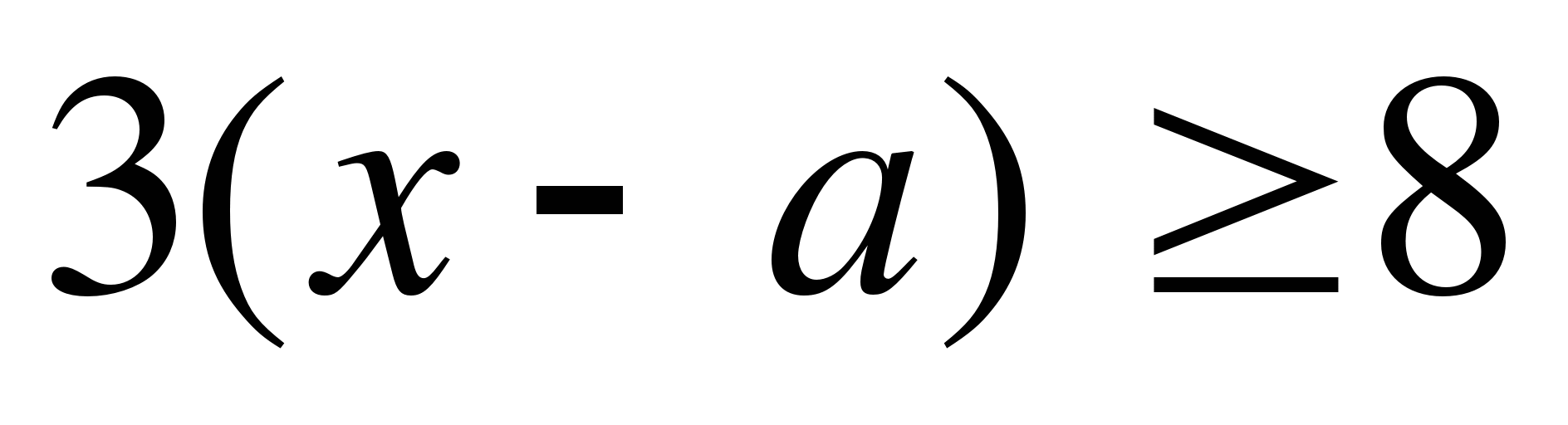 .
.
Ответ: а) если а=-3, то решений нет; если а<-3, то
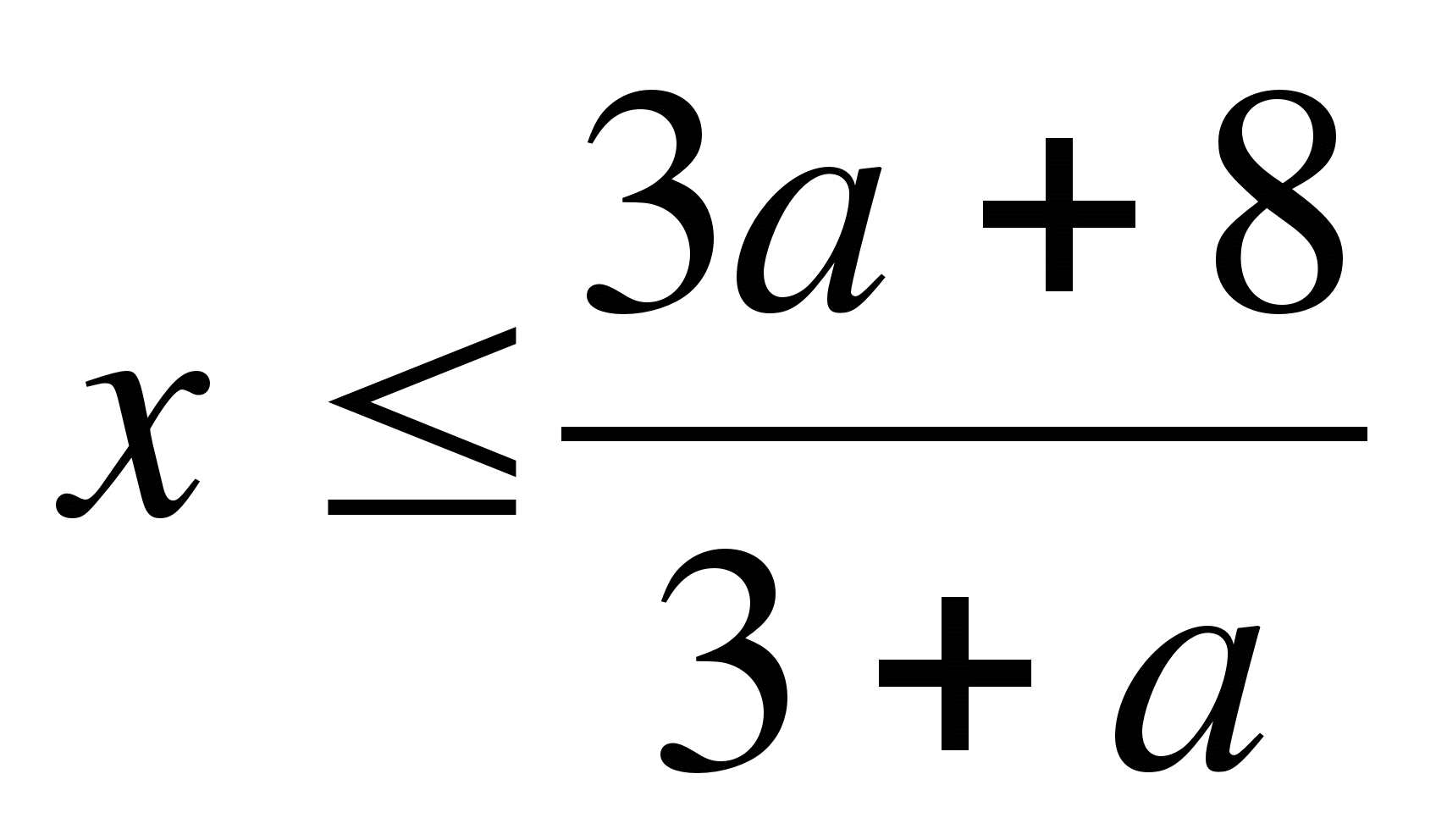 ;
;
если a>-3, то
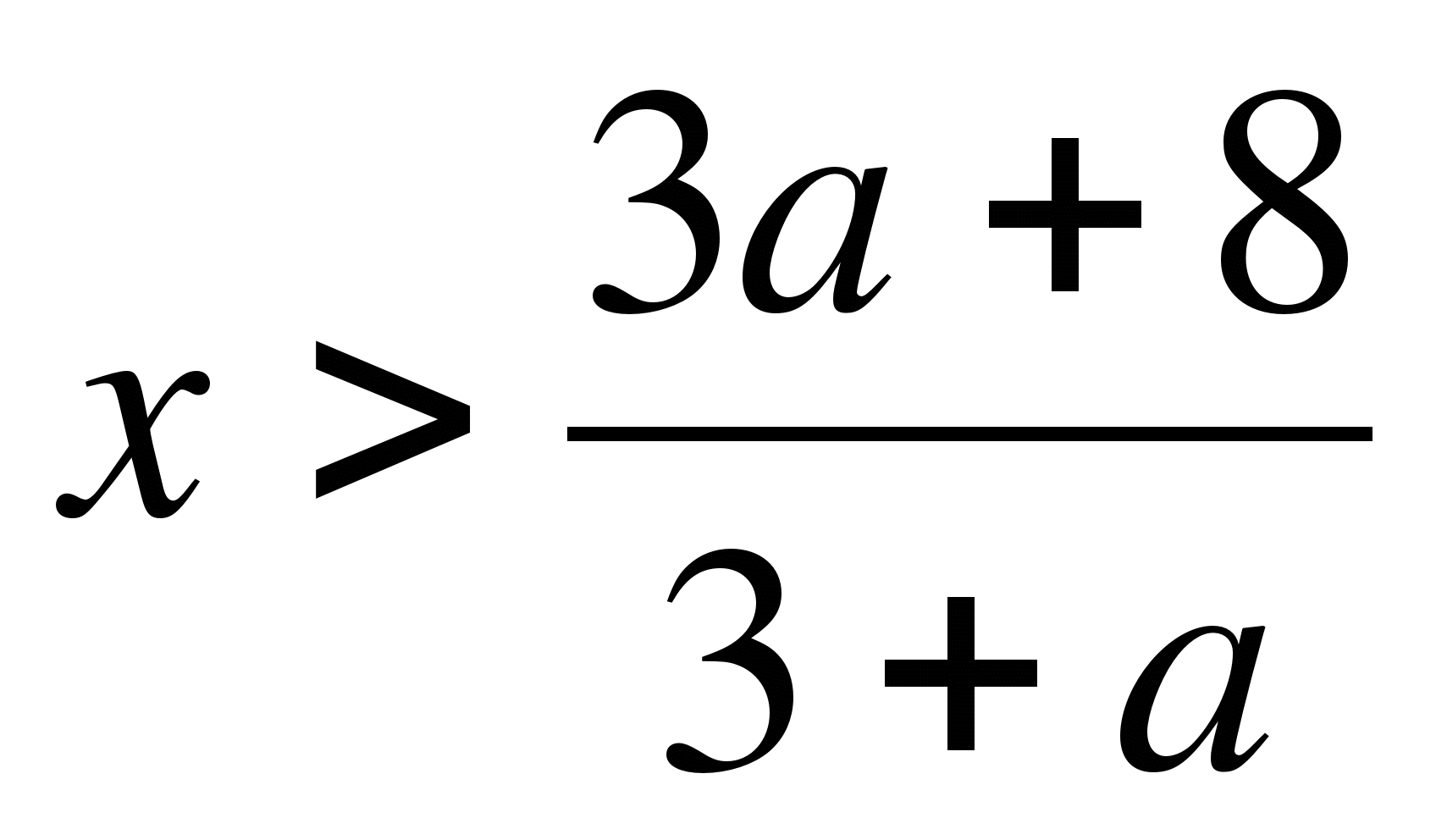 ;
;
б) если а≠ ±3, то решений нет; если а=-3, то
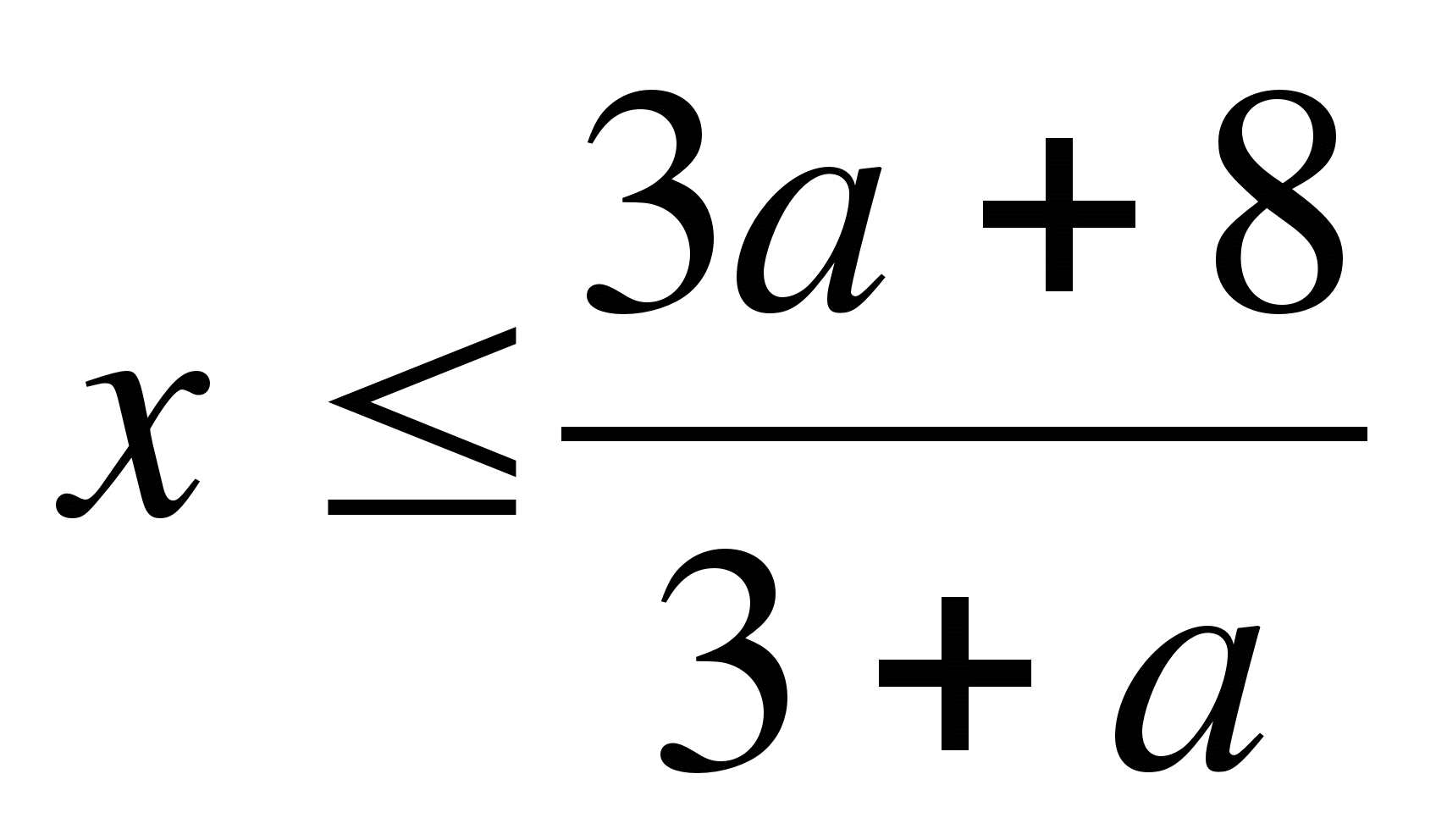 ;
;
в) если а<-3, то
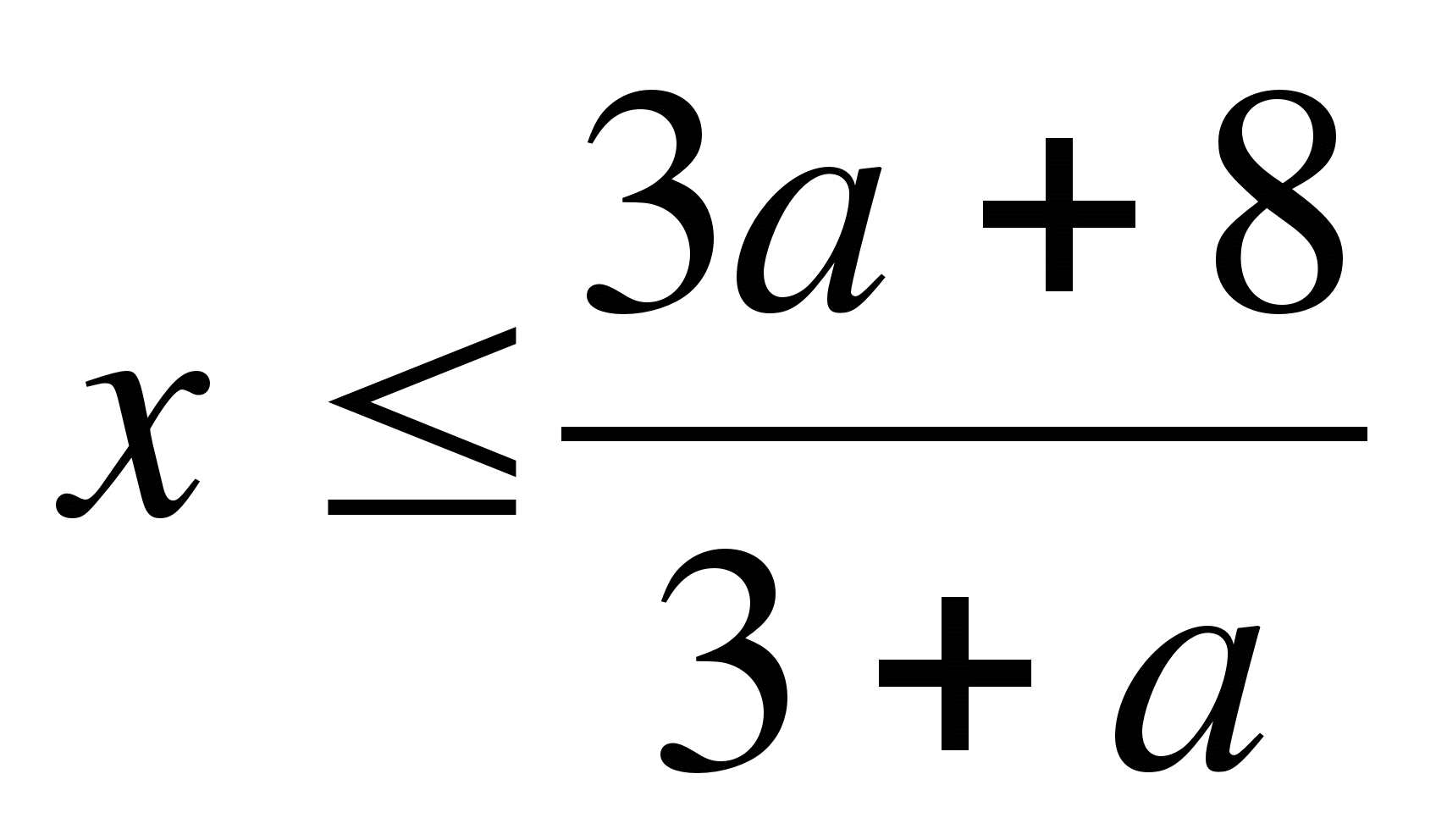 ,
если a>-3, то
,
если a>-3, то 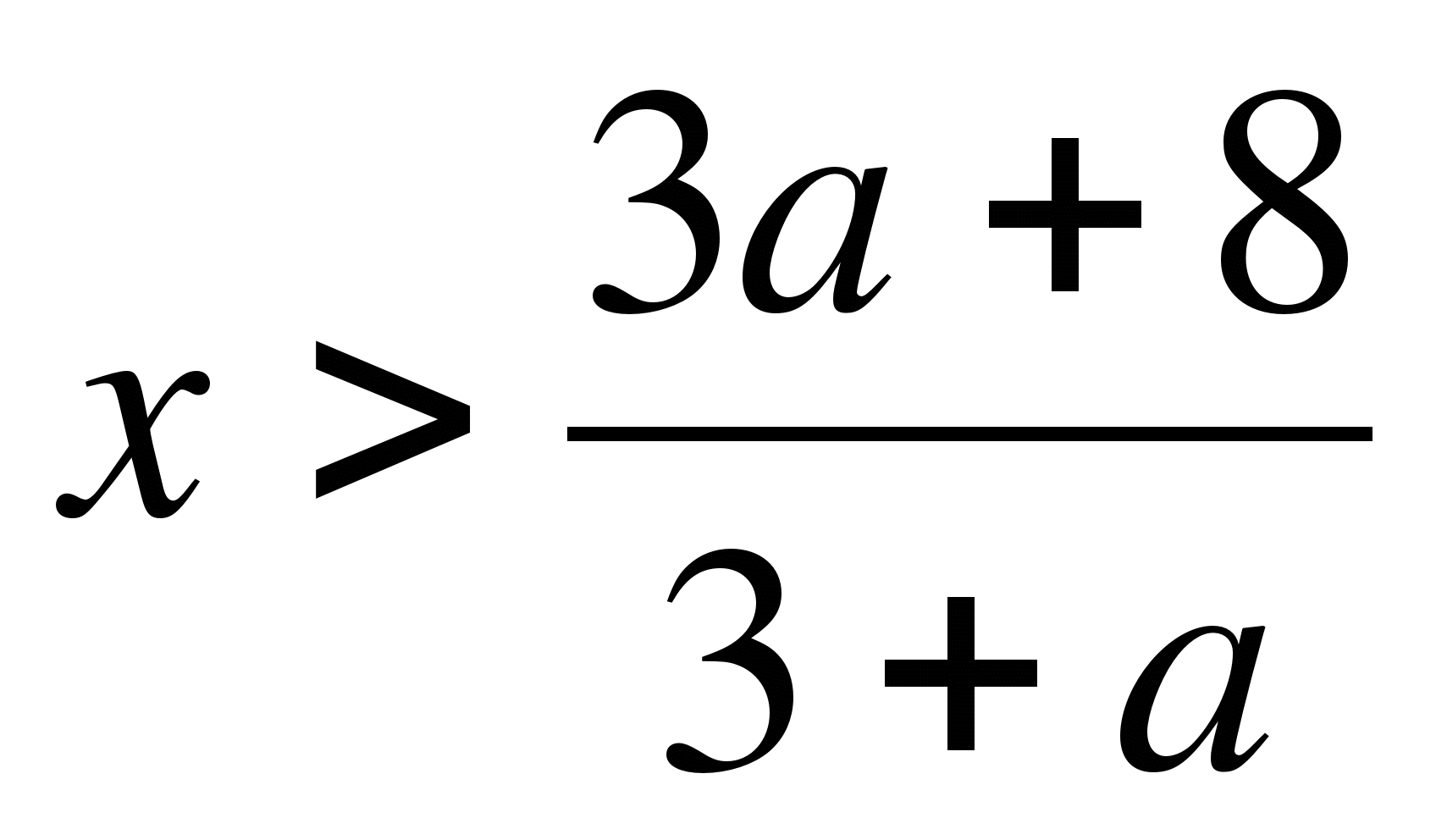 .
.
№ 5. При каких значениях а неравенство 2х-а2+5<0 верно при всех х, удовлетворяющих условию
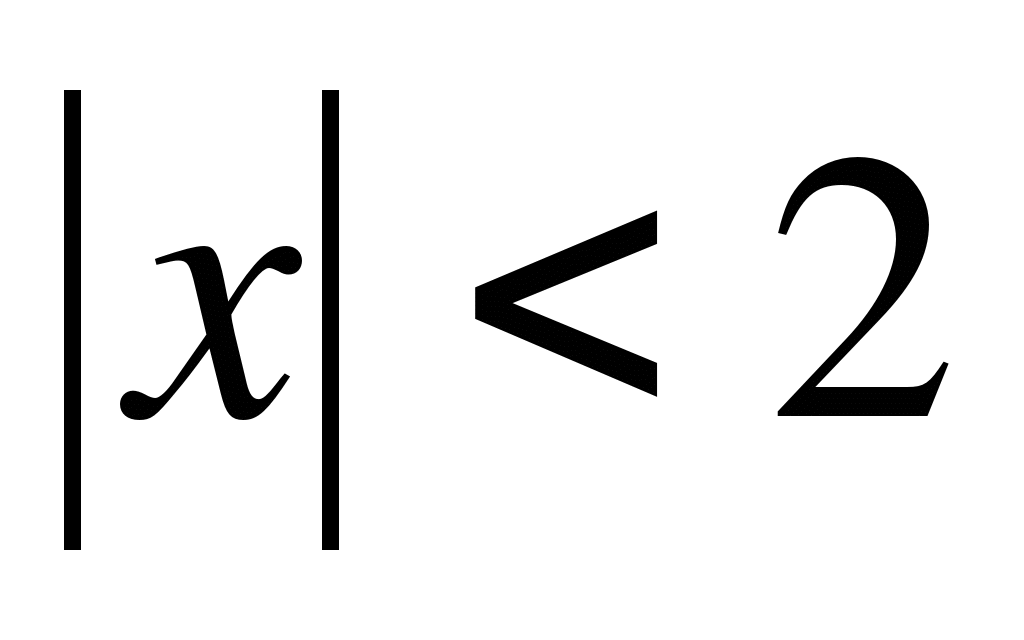 .
.
Ответ: а) -3<а<3;
б) а ≠ ± 3;
в) а<-3; a>3.
Ключ ответов к тесту
-
-
Итоги занятия. Этап рефлексии.
1. Какие из предложенных заданий вы считаете наиболее легкими, наиболее трудными?
2. Как высчитаете, в чем причина ваших затруднений?
3. Оцените свой уровень усвоения темы «Решение линейных уравнений и неравенств с параметром».
Занятие 2.
I. Тест.
№ 1. Решить уравнение ах2 +6=0.
Ответ: а) при а≥0 корней нет, при а<0 х=±
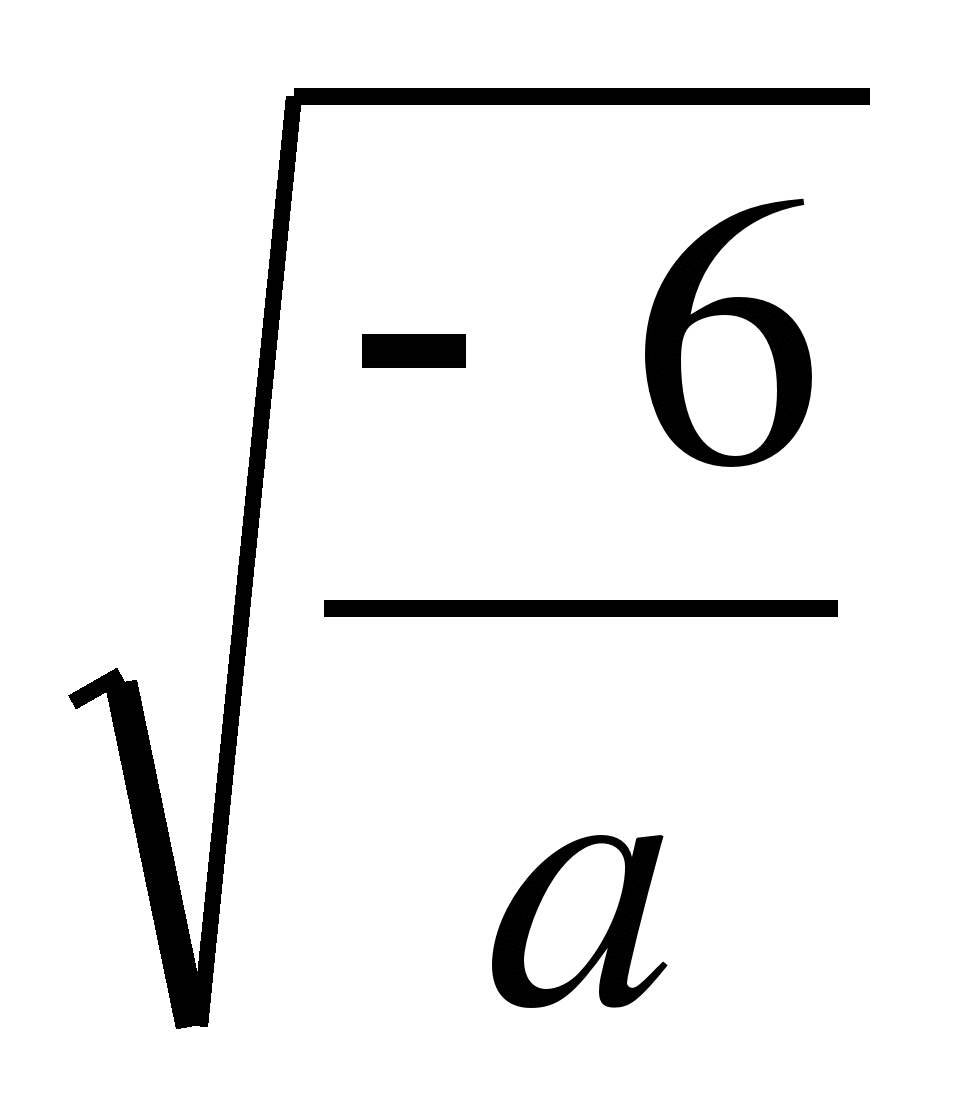 ;
;
б) при а<0 корней нет, при а>0 х=±
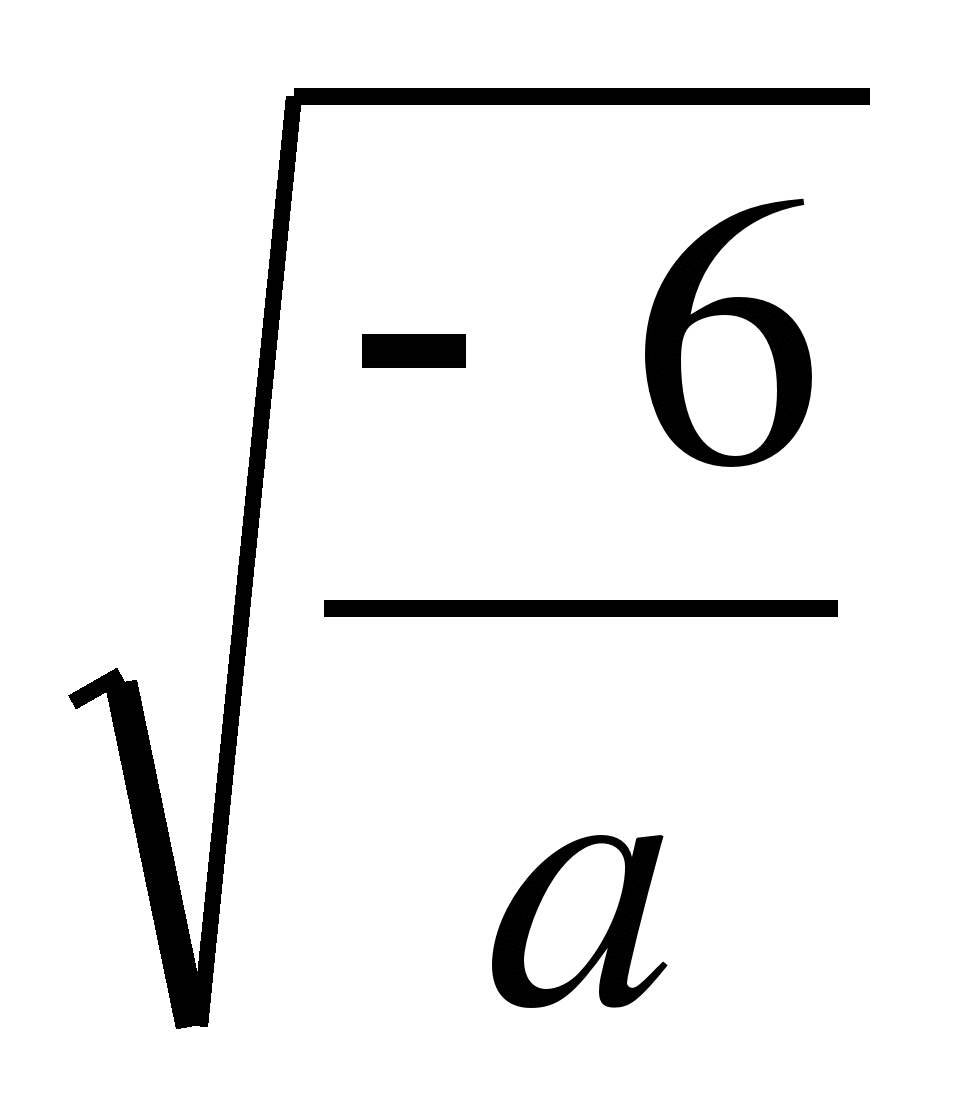 ;
;
в) при а=0 корней нет, при a>0 хєR, при а<0 х=±
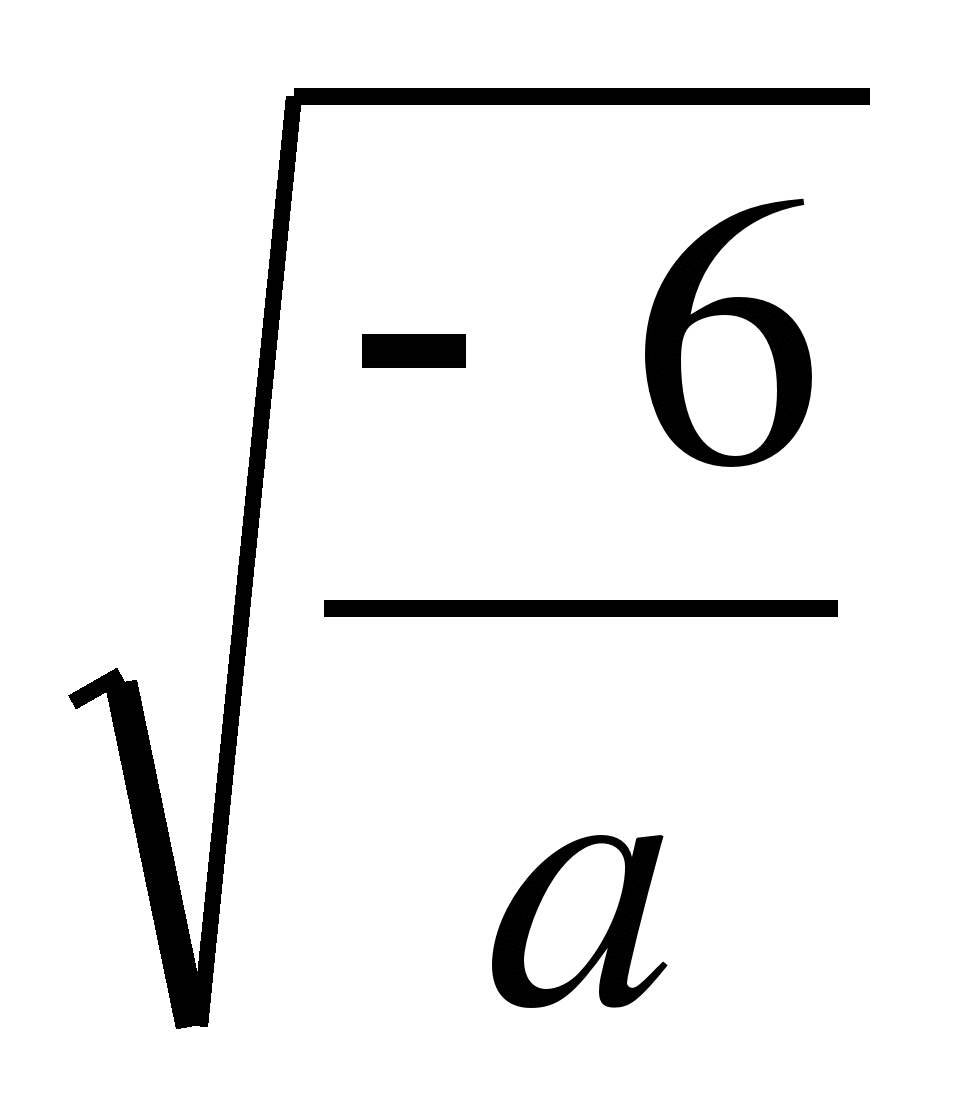 .
.
№ 2. Решить уравнение ах2-2х+4 =0.
Ответ: а) при а=0 х=2, при а≠0 х=
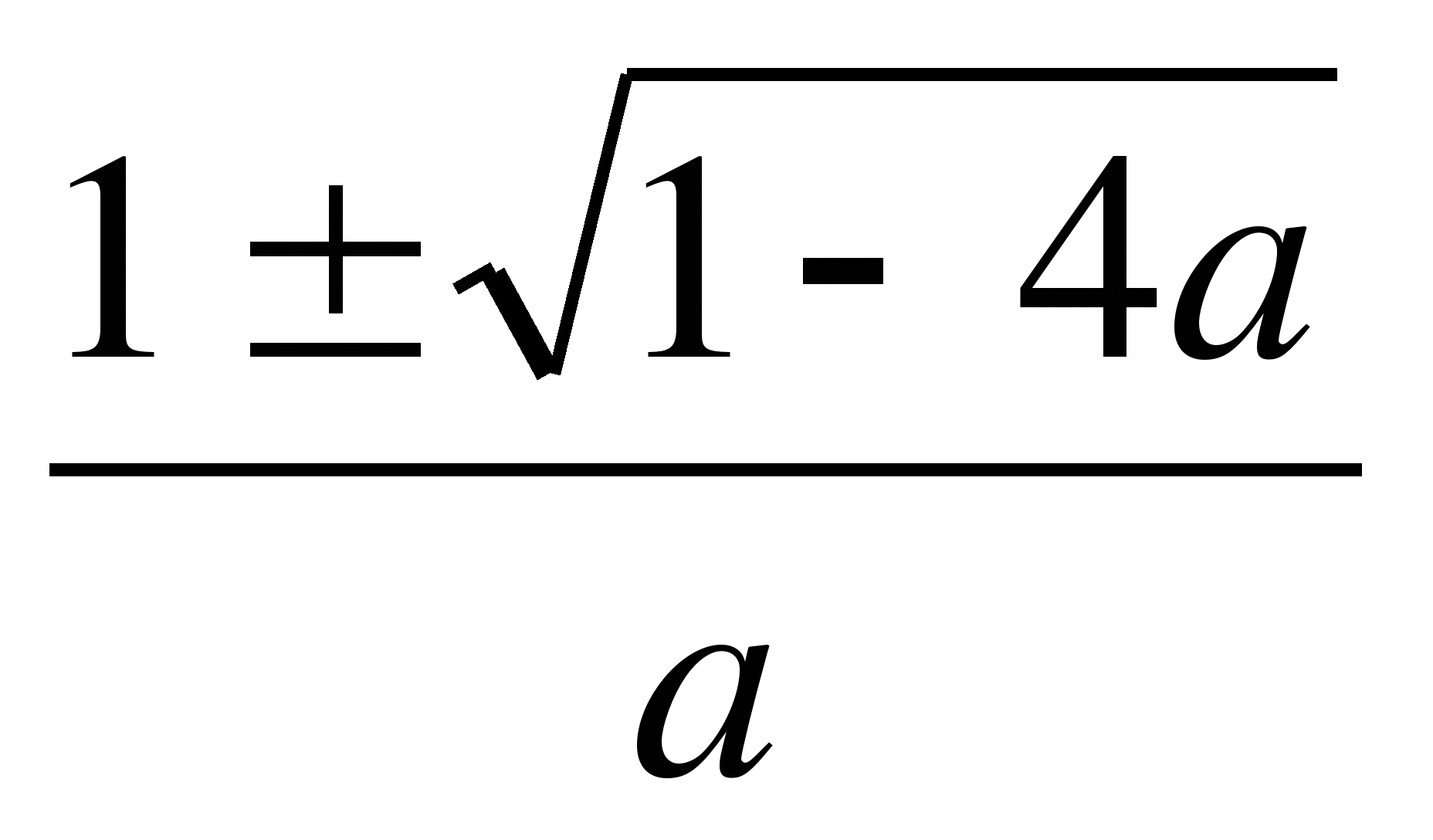 :
:
б) при а=0,25 х=4, при а=0 х=2, при а>0,25 корней нет, при
других а х=
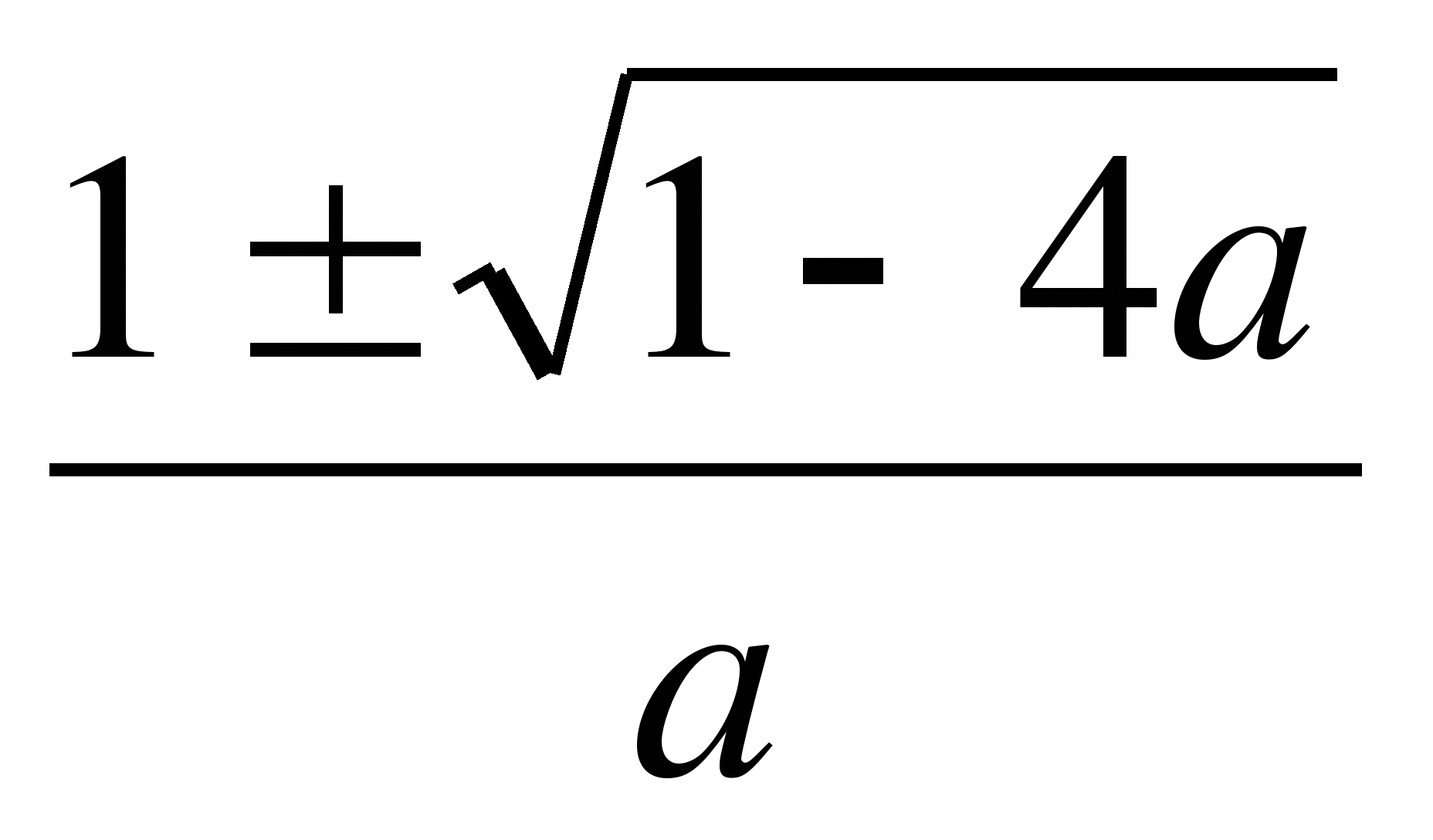 ;
;
в) при а=0,25 х=4, при а>0,25 корней нет, при других а х=
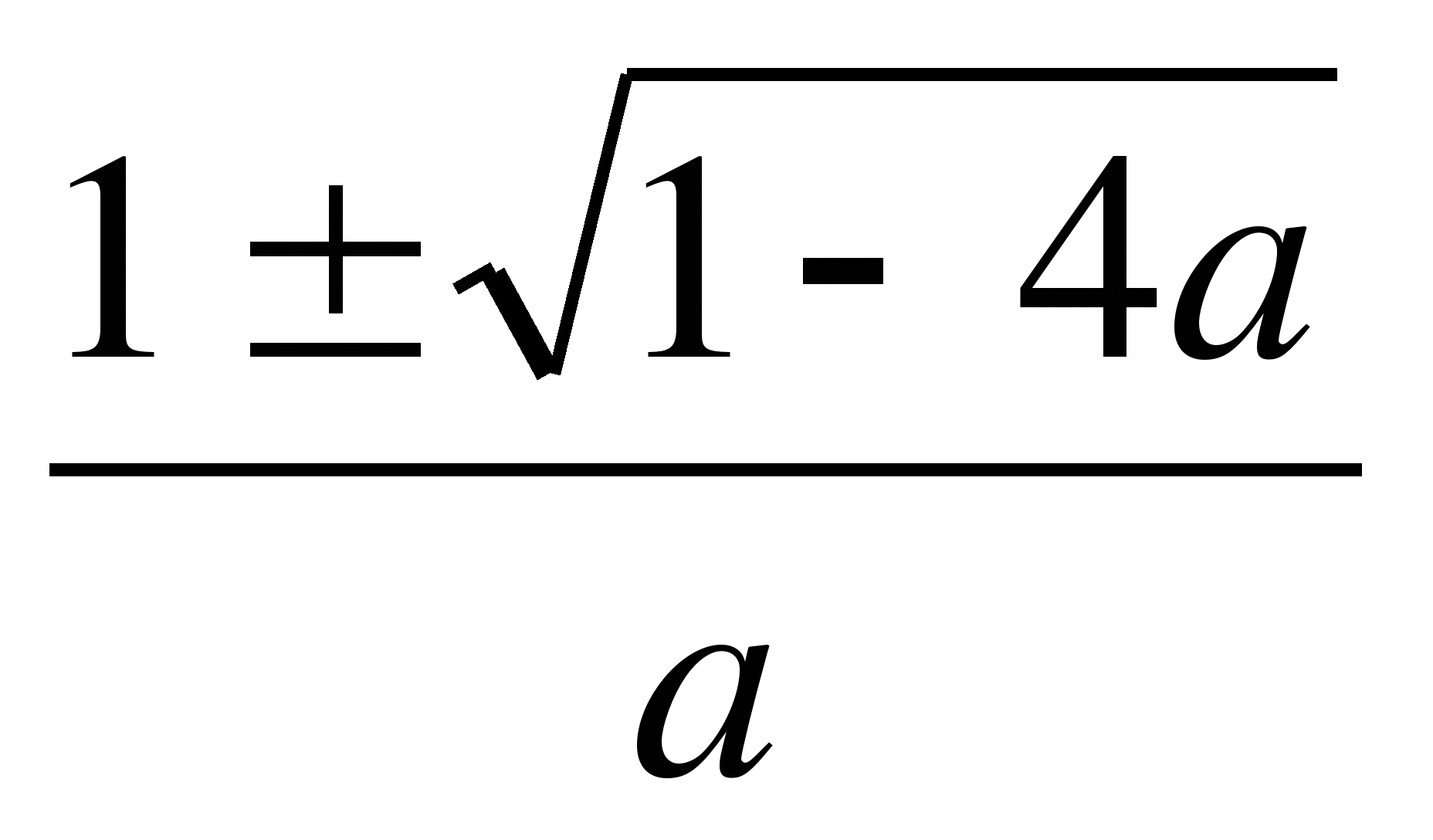 .
.
№ 3. Решить неравенство х2+х+а≥0.
Ответ: а) решений нет;
б) при а≥0,25 решений нет, при а<0.25 хє(-∞;
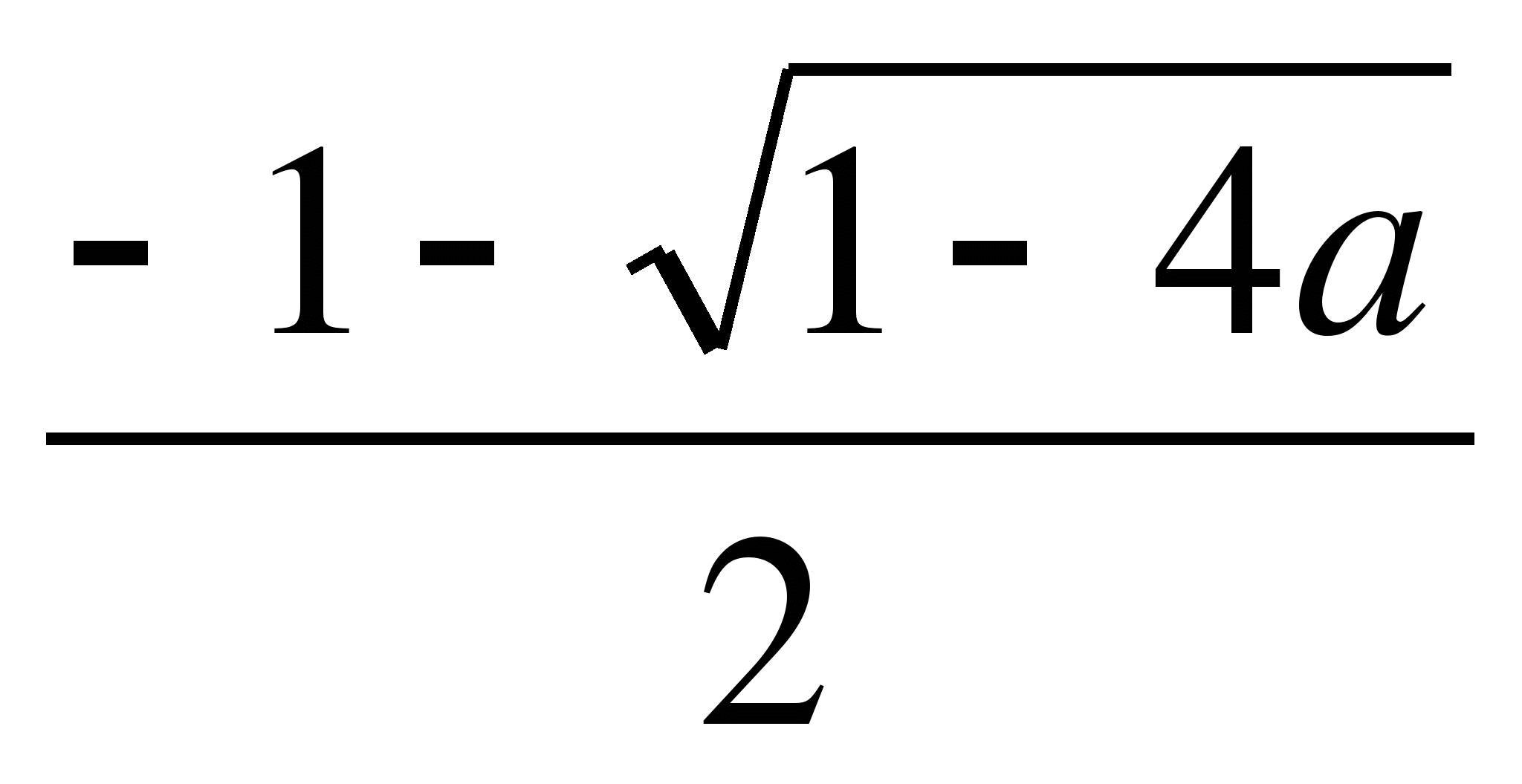 ]
U [
]
U [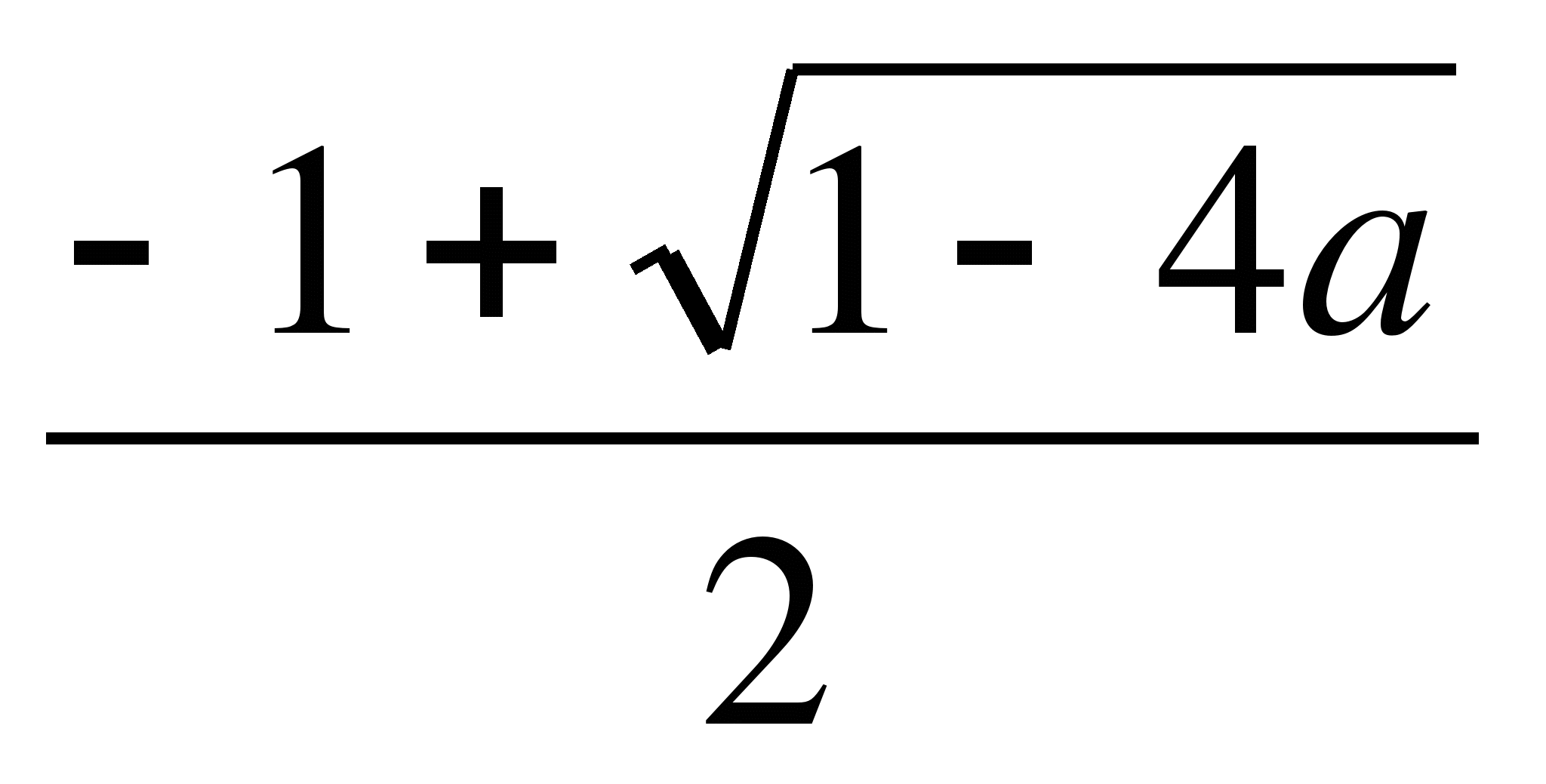 ;
+∞);
;
+∞);
в) при а≥0,25 хєR, при а<0.25 хє(-∞;
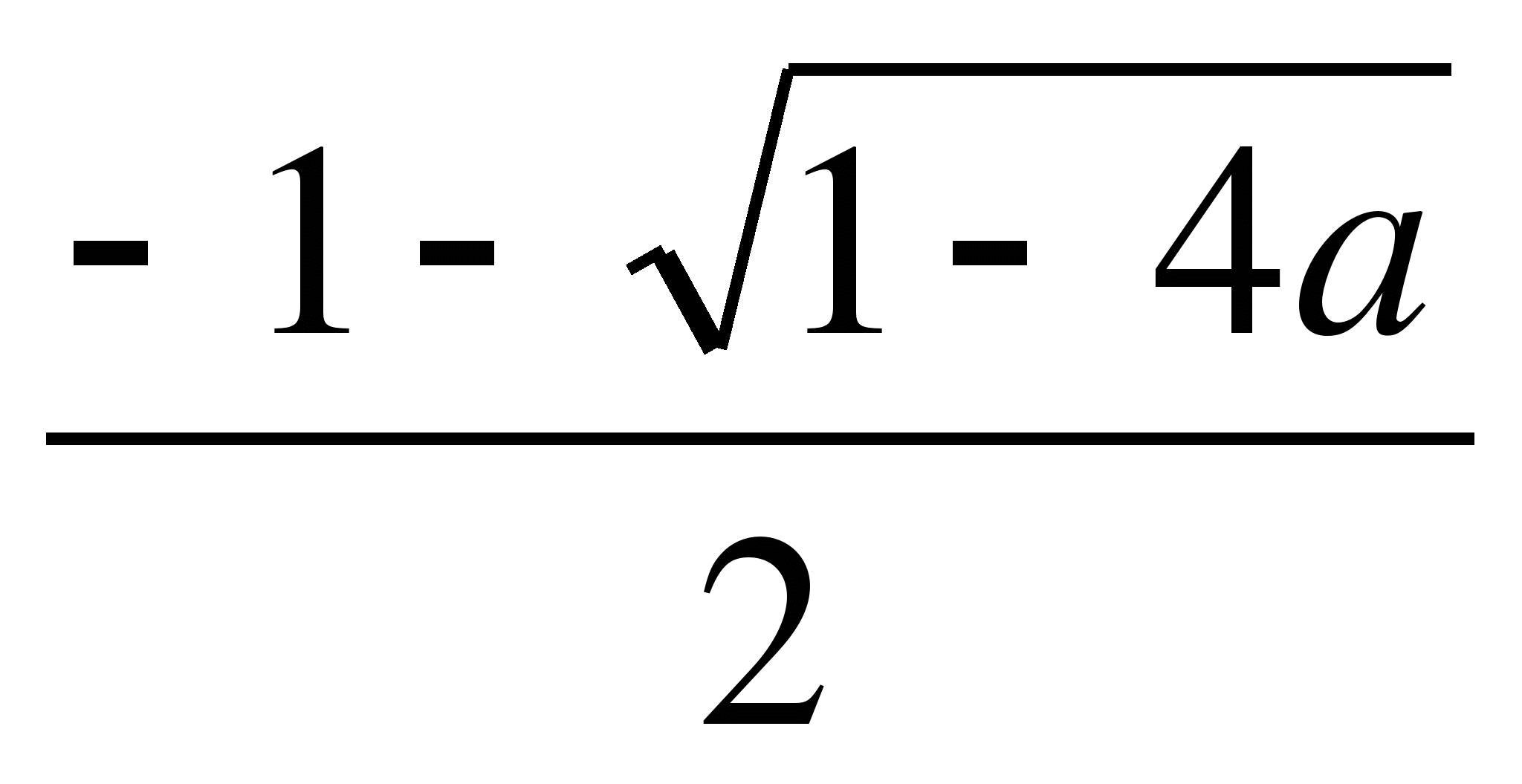 ]
U [
]
U [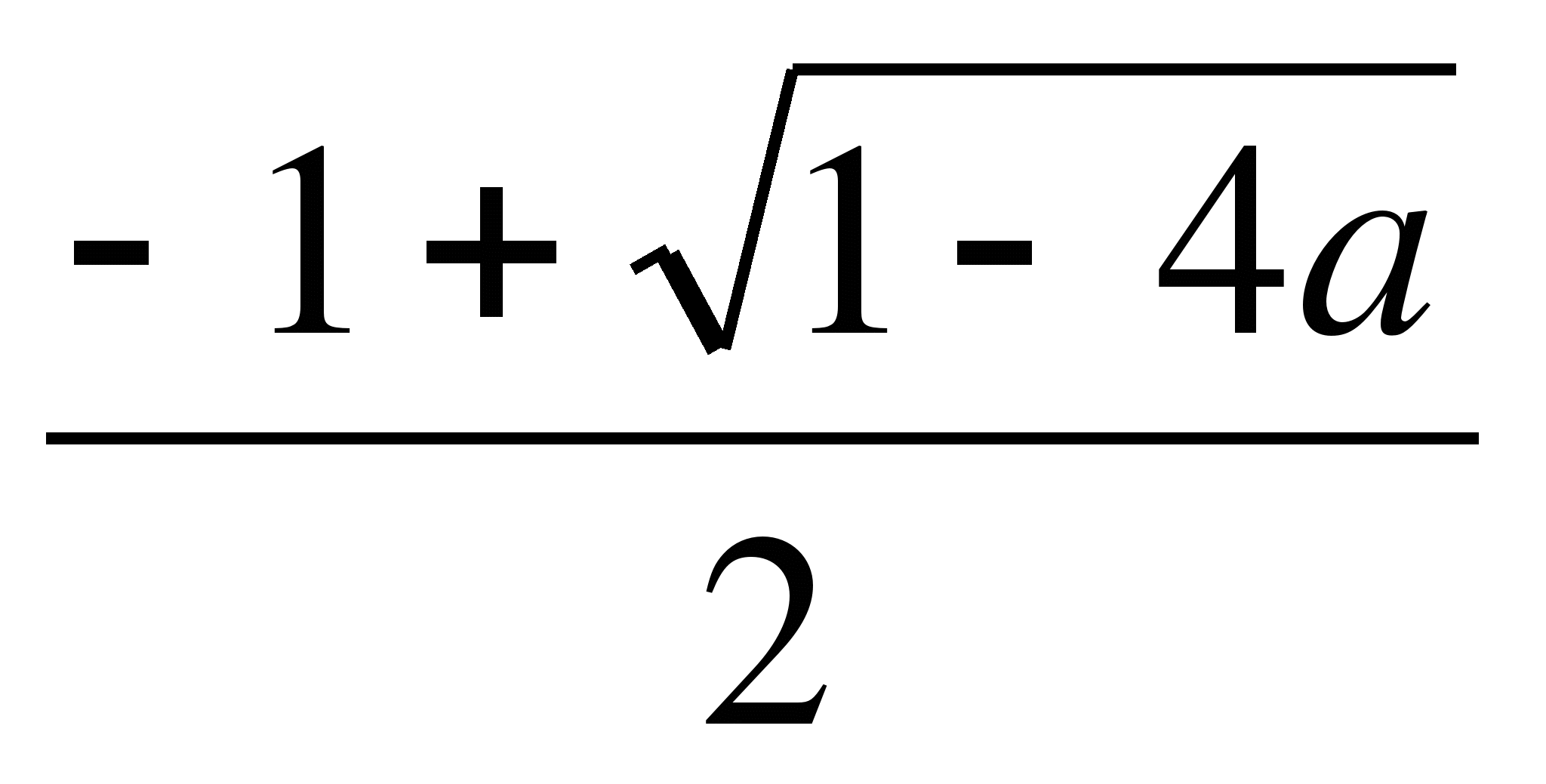 ;
+∞).
;
+∞).
№4. При каком значении параметра а система
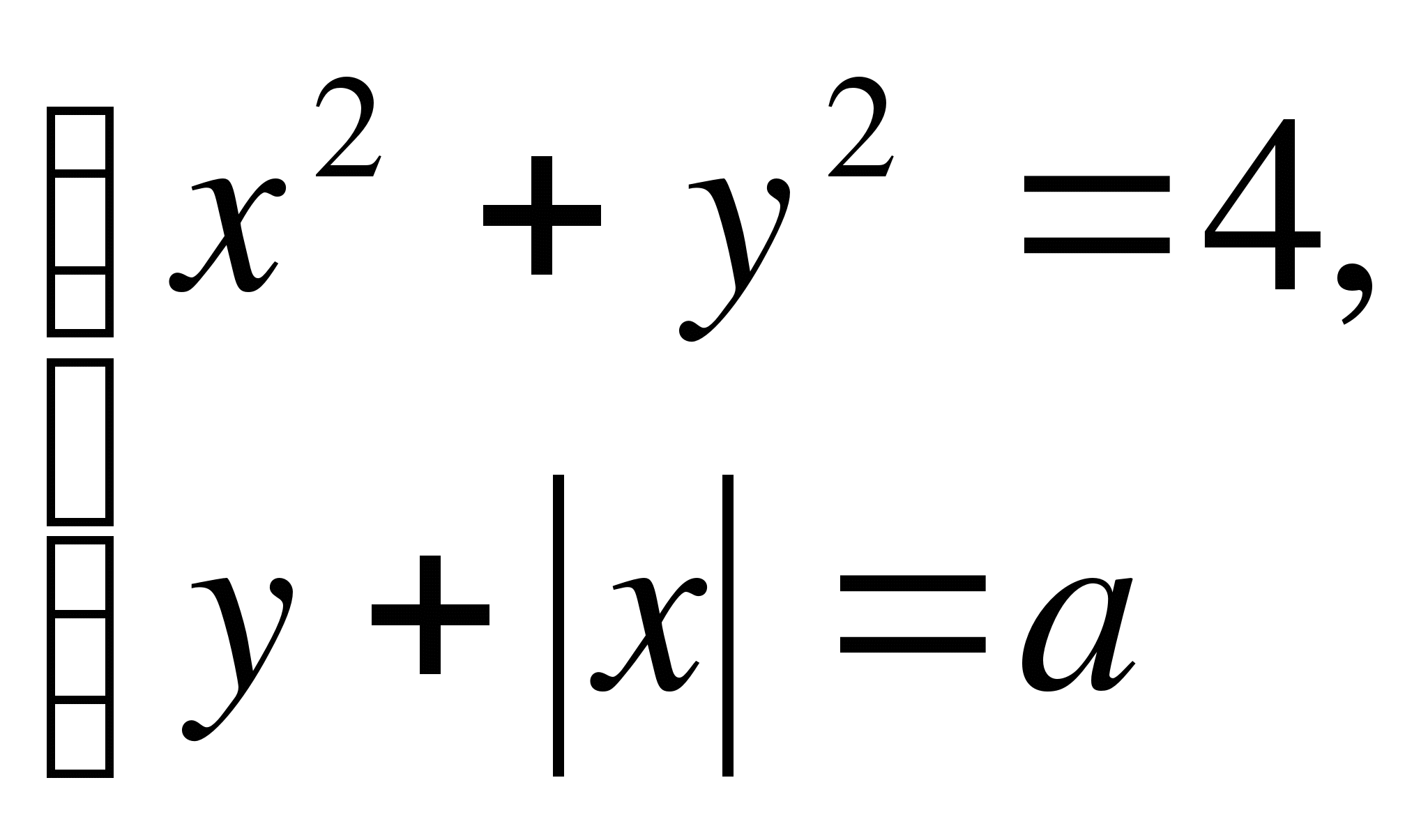 имеет ровно три решения?
имеет ровно три решения?
Ответ: а) а= ±2; б) а=2; в) а=0.
№ 5. При каких значениях параметра а неравенство (4 - а2)х2+2(а+2)х - 1>0
не имеет решений?
Ответ: а) а Є (-∞; -2); б) а Є (2; +∞); в) а Є (- 2; 2).
Ключ ответов к тесту
-
-
Итоги занятия. Этап рефлексии.
1. Какие из предложенных заданий вы считаете наиболее легкими, наиболее трудными?
2. Как высчитаете, в чем причина ваших затруднений?
3. Оцените свой уровень усвоения темы «Решение квадратных уравнений и неравенств с параметром».
-
-
-
-