Производная функции. Обобщающий урок в 10 классе.

Производная функции.

Обобщающий урок в 10 классе.

Девиз урока: Решай, ищи, твори и мысли. (Ритм) И в задачах тех ищи удачу, где получить рискуешь сдачу!

Цели урока:

1. Обобщить знания учащихся по теме «Производная функции».

2. Способствовать развитию навыков применения теоретических знаний в практической деятельности.

3. Способствовать воспитанию ответственности за качество и результат выполняемой работы на уроке.

Задачи:

1. Повторить алгоритм нахождения производной.

2. Используя правила нахождения производной, применить их для решения конкретных задач.

3. Сформировать глубину и оперативность мышления.

Планируемый результат урока:

1. Учащиеся знают правила нахождения производных.

2. Учащиеся отработали навыки применения теоретических знаний расчета производной функции на учебных примерах.

3. Учащиеся почуствовали ответственность за качество и результат выполняемой работы на уроке.

Тип урока: урок повторения и обобщения знаний

Оборудование: раздаточный материал (разноуровневые карточки с практическими заданиями, листы учета знаний), карточки с основными формулами.

Ход урока:

1. Организационный момент

   1. Постановка целей и задач урока

2) Повторение теоретического материала

«Вы уже накопили некоторый опыт нахождения производной. И сегодня мы посмотрим, чему же вы научились. Повторим теоретический материал».

2 ученика идут к доске выписывать известные им правила нахождения производной. В это время класс отвечает на вопросы учителя:

а) что такое производная?

б) какие смыслы производной существуют?

в) что такое производная с геометрической точки зрения?

г) какой угол образует прямая с осью абсцисс:

• если k>0

• если k<0

• если k=0

• если прямые a || в?

д) что такое производная с механической точки зрения?

е) что значит продифференцировать?

ж) какая функция называется дифференцируемой в точке?

и) какую формулу имеет уравнение касательной?

3) Применение теоретического материала к решению задач

«Рассмотрев теоретический материал вычисления производной, применим его при решении задач».

В это время на интерактивной доске высвечиваются примеры для устного нахождения производной (отвечают все учащиеся класса по цепочке).

Найдите производную функции

y=3x

y=-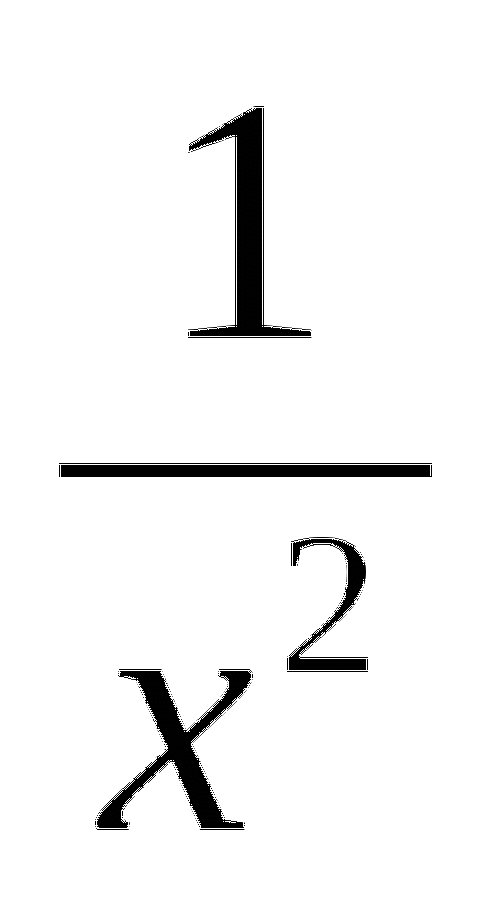+5

y=sin²x

y=cos3x

y=4x²

y=

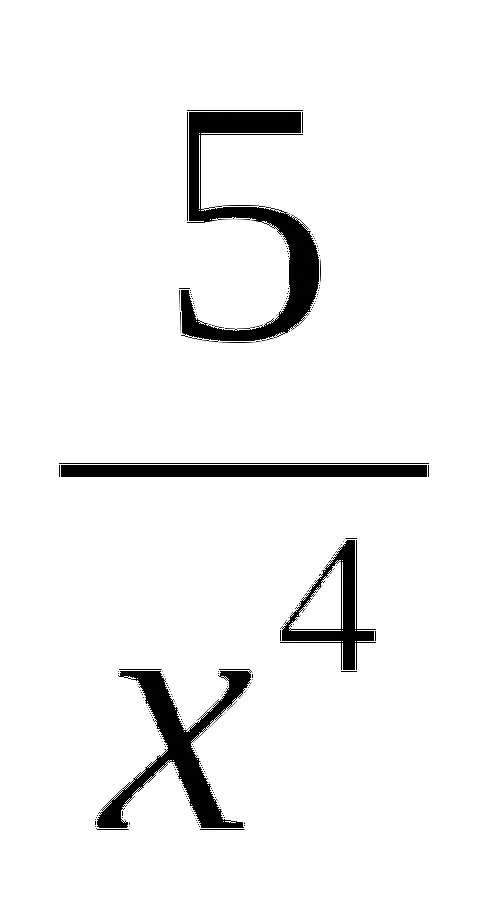
y=cos²2x

y=cos(4x-1)

y=x^-5

y=

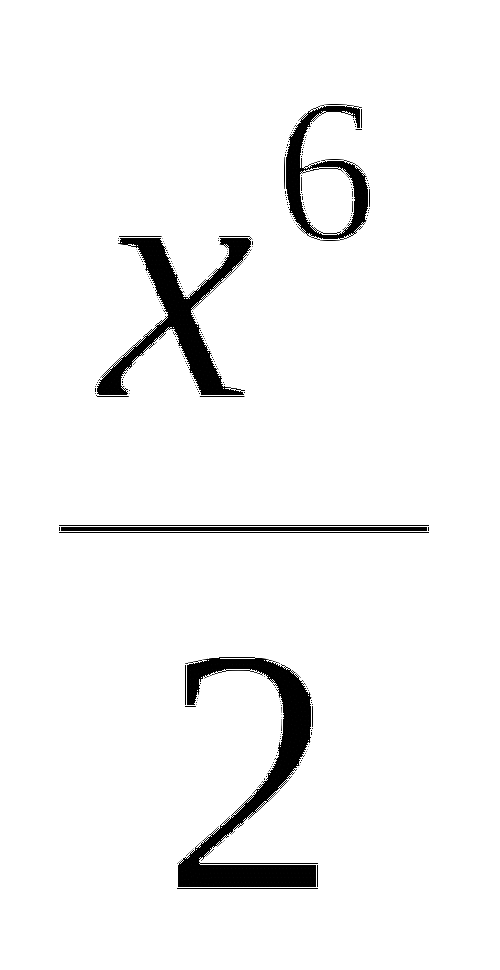
y=

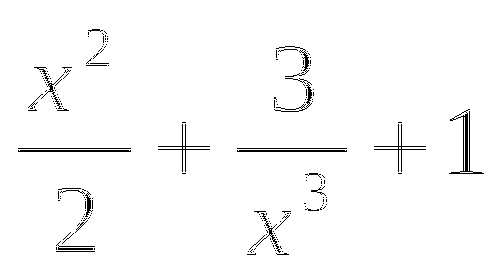
y=ctg(x-)

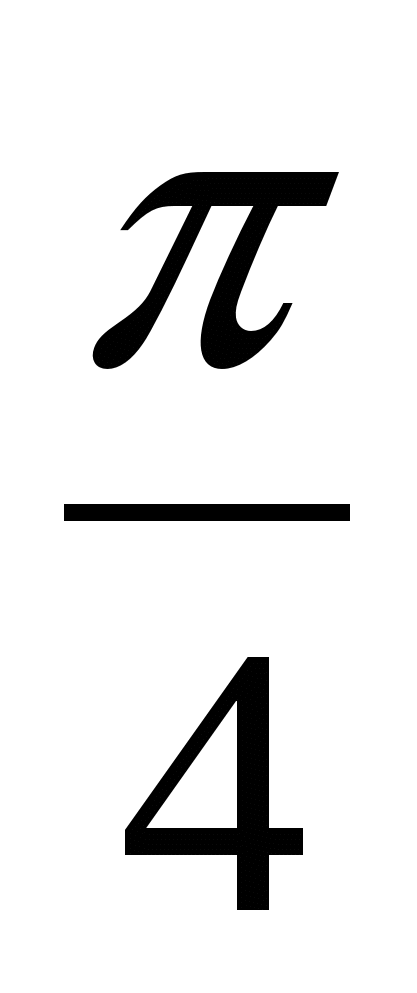y=

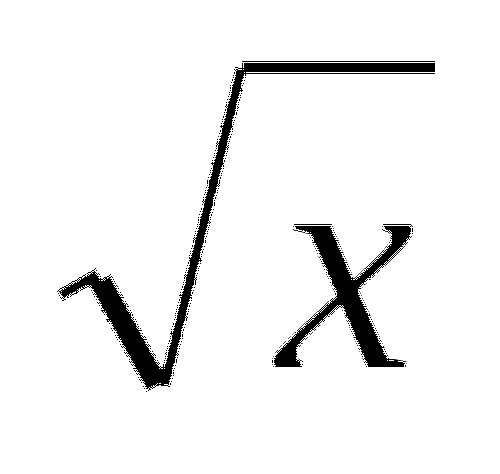
y=

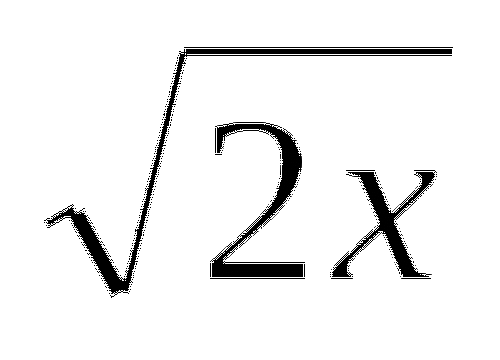
y=4x²+

y=tg(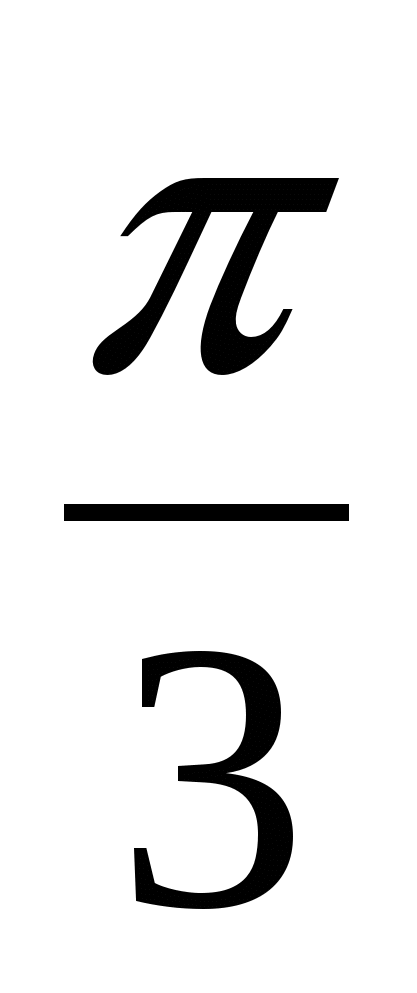-2x)

y=

y=4-x⁴

y=

y=

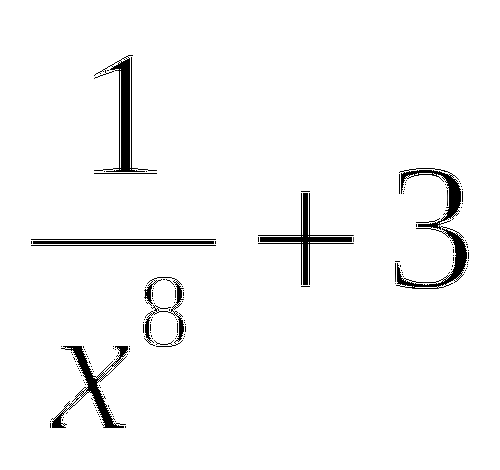
y=x²+3sinx

y=

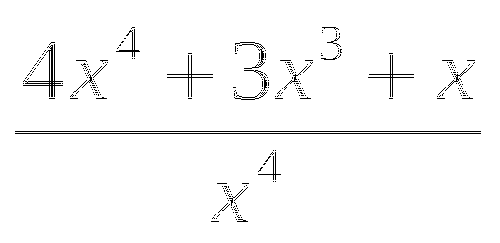
y=cos2x

y=3x²+2x+5

y=

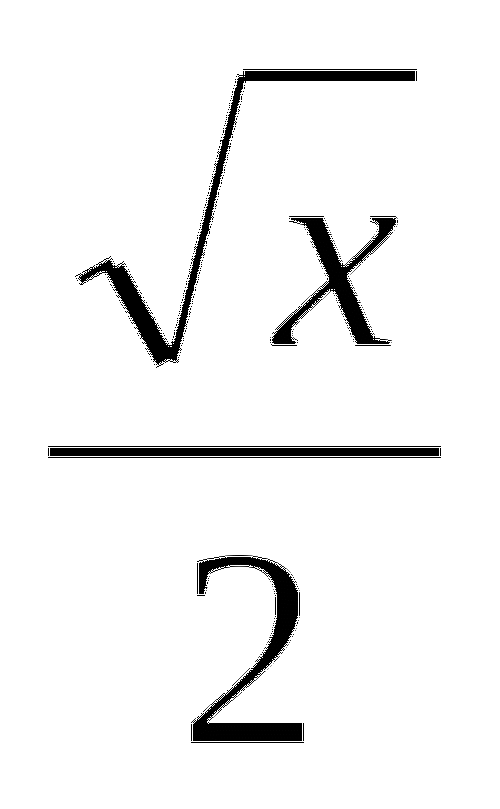
y=

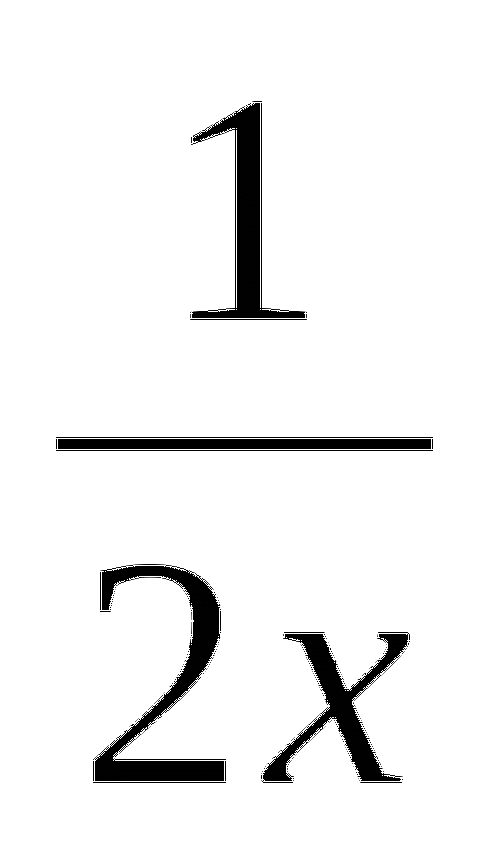
После решения этих примеров на интерактивной доске высвечивается следующее задание для устного счета. Учащиеся выходят по одному к доске и стрелками устанавливают соответствие между левым и правым столбцами таблицы.

Установите соответствие

Далее на интерактивной доске высвечиваются следующие задания для устного счета. Учащиеся выходят по одному к доске для их выполнения.

Производная какой функции равна:

Задайте формулой функцию h, если f(x)=3-2x, g(x)=x²,p(x)=sinx

1. 2x+4

2. 6x+1

3. 16x³-4

4. 8x-2

5. 9x²-

a) h (x)=g(f(x))

b) h (x)=g(p(x))

c) h (x)=p(f(x))

4.Работа по карточкам (разноуровневая работа, выполняется учащимися на местах):

Карточка №1 (уровень А).

Найдите производную функции:

1. у = 5 - 7х

2. у = (х - 5)(2х - 5)

3. y = 4x⁵ + tg 3x - cos²x

4.у =

Карточка №2 (уровень В).

Найдите производную функции:

1. у = (х³ - 2х² + 5)⁶;

2. у = cos(х³-3)

3. у =

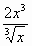
4. у =

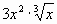
Карточка №3 (уровень С).

Найдите производную функции:

1. у = sin² 5x

2. y =

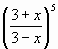
3. y =

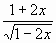
5. Геометрический смысл производной.

1) в какой точке параболы у = +3x -1 касательная наклонена к оси абсцисс под углом ?

2) найти тангенс угла наклона касательной у = 2 cos 3x в точке = .

3) найти тангенс угла наклона касательной к графику функции f(x)=2x³-5x в точке М(2;6).

4) какой угол с осью ОХ образует касательная к графику функции у = ctg 2x в точке с абсциссой x = -

5) при каком значении а прямая у = - 10x +a является касательной к графику функции

у = 3- 4x -2?

6) при каком значении b прямая у=3x+b, является касательной к графику у = 2 - 5x +1?

7) какой угол образует с направлением оси ОХ касательная к графику функции f(x)= (1-3)?, проведенная в точке х=3

6. Повторим механический смысл производной.

Что является производной от расстояния? От скорости?

1. Материальная точка движется по закону S(t)=3t²+4cos(0,5t). Найдите скорость материальной точки в момент времени t=2с.

2.Найти скорость точки, движущейся прямолинейно по закону x(t)=2t³+t²-4 в момент времени t=4с.

3.Тело движется по координатной прямой по закону S(t)= t³ +6 t² +5 t. Найдите скорость и ускорение при t=2.
Решение: V(t)= 3t²+12t, V(2)=12+24=48
a(t)=6t+12, a(2)=12+12=24

7. Химический смысл производной.
Пусть дана функция m=m(t),где m-количество некоторого вещества, вступившего в химическую реакцию в момент времени t. Приращению времени Δt будет соответствовать приращение Δm величины m. Отношение Δm/Δt- есть средняя скорость химической реакции за промежуток времени Δt. Предел этого отношения при стремлении tΔ к нулю- есть скорость химической реакции в данный момент времени .

Задача по химии: Пусть количество вещества, вступившего в химическую реакцию задается зависимостью:
р(t) = t²/2 + 3t -3 (моль)
Найти скорость химической реакции через 3 секунды.
Решение. V(t)=t+3
V(3)=6

8. Самостоятельная работа ( Задания по карточкам)

5 ЭТАП. Итог урока

1. Самооценка труда учащихся.

• Выполнил ли программу урока полностью;

• Какие виды работ вызвали затруднения и требуют повторения;

• В каких знаниях уверен.

2. Оценка труда товарищей:

• Кто, по-вашему мнению, внес наибольший вклад;

• Кому, над чем следовало бы еще поработать.

3. Оценка работы класса учителем.

6 ЭТАП. Домашнее задание: составить проверочную карточку из трех заданий по данной теме (разноуровневую)

Используемая литература.

1. В.С. Крамор. "Повторяем и систематизируем школьный курс алгебры и начал анализа" Просвещение, 1990

2. Л.И. Звавич, Л.Я. Шляпочник, М.В. Чинкина. "Алгебра и начала анализа: 3600 задач для школьников и поступающих в вузы"

3. Газета "Математика" (приложение к газете "Первое сентября")