- Учителю
- Рабочая программа элективного курса: Решение текстовых задач.
Рабочая программа элективного курса: Решение текстовых задач.
Министерство образования Российской Федерации
Муниципальное бюджетное общеобразовательное учреждение
средняя общеобразовательная школа
с углубленным изучением отдельных предметов №38
имени Е.А. Болховитинова г. Воронежа
Заседании МС
Протокол № __
от « » 2013 г.
Руководитель МС
______Куракова Е.В.
СОГЛАСОВАНО
Зам. директора по УВР
_____Барсукова А.И.
УТВЕРЖДАЮ
Директор школы
______ Сунцова Т.Л.
Рабочая программа
по элективному курсу
«Решение текстовых задач»
9 класс
Учитель математики: Лыков Виктор Иванович
2014 г.
Пояснительная записка
Структура документа
Рабочая программа включает шесть разделов: пояснительную записку, требования к уровню подготовки учащихся, календарно-тематическое планирование (учебно-тематический план), содержание программы учебного предмета, формы и средства контроля, перечень учебно-методических средств обучения.
Общая характеристика учебного предмета
Программы элективных курсов включают расширение отдельных тем базовых общеобразовательных программ по математике.
Элективный курс «Решение текстовых задач» дополняет базовую программу, не нарушая её целостность.
Основная задача обучения математике в школе заключается в обеспечении прочного и сознательного овладения учащимися системой математических знаний и умений, необходимых в повседневной жизни и трудовой деятельности каждому члену современного общества, достаточных для изучения смежных дисциплин и продолжения образования, а также в профессиональной деятельности, требующей достаточно высокой математической культуры.
Для жизни в современном обществе важным является формирование математического стиля мышления, проявляющего в определённых умственных навыках. В процессе решения задач в арсенал приёмов и методов человеческого мышления естественным образом включаются индукция и дедукция, обобщение и конкретизация, анализ, классификация и систематизация, аналогия.
Именно задачи обладают диагностической и прогностической ценностью, которые позволяют проверить знания основных разделов школьного курса математики, уровень логического мышления, первоначальные навыки исследовательской деятельности.
Задачи, предлагаемые в данном курсе, интересны и часто не просты в решении, что позволяет повысить учебную мотивацию учащихся и проверить свои способности к математике. Вместе с тем, содержание курса позволяет ученику любого уровня активно включаться в учебно-познавательный процесс и максимально проявить себя: занятия могут проводиться на высоком уровне сложности, но включать в себя вопросы, доступные и интересные всем учащимся.
Изучение курса способствует процессу самоопределения учащихся, помогает им адекватно оценить свои математические способности, обеспечивая системное включение ребёнка в процесс самостоятельного построения знаний.
Цели и задачи
Целью курса является:
- определение уровня способностей учащихся и уровня их готовности к профильному обучению в школе и вузе;
- систематизация ранее полученных знаний по решению текстовых задач;
- ознакомление учащихся с разными типами задач, особенностями методик и различными способами их решения;
- реализация межпредметных связей.
- предоставление возможности учащимся реализовать свои интеллектуальные и творческие способности, применить имеющиеся знания и умения из других областей деятельности (работа с учебной литературой, прессой, ПК, TV);
- умение планировать работу; вести спор, дискуссию, беседу.
Образовательная цель курса состоит в том, что учащиеся знакомятся с основными алгоритмами решения задач, учатся логически мыслить, правильно и четко определять цель решения задачи, строить логическую цепочку, при этом используя разные средства: краткую запись, схему, таблицу и др.
Решение текстовых задач уже подразумевает усвоение решения уравнений, неравенств, их систем, составление и решение пропорций, и другие навыки. То есть уже некоторый багаж знаний является усвоенным.
Воспитательное назначение курса
Обучение задачам потребует от учащихся умственных и волевых усилий, развитого внимания, воспитания таких качеств, как активность, творческая инициатива, умений коллективно-познавательного труда.
Основные задачи данного курса:
-
углубить знания по математике, предусматривающие формирование у учащихся устойчивого интереса к предмету;
-
выявить и развить их математические способности;
-
расширить математические представления учащихся о приёмах и методах решения задач;
-
повышение уровня математического и логического мышления учащихся;
-
развитие навыков исследовательской деятельности,
-
обеспечить подготовку к профессиональной деятельности, требующей высокой математической культуры.
Работа элективного курса строится на принципах:
- научности;
- доступности;
- опережающей сложности;
- вариативности;
- самоконтроля.
Количество учебных часов:
Учебный план предусматривает на изучение элективного курса «Решение текстовых задач» в 9-ом классе 1 час в неделю, 34 часа в год.
Уровень обучения - базовый.
Срок реализации рабочей учебной программы - один учебный год.
Общеучебные умения, навыки и способы деятельности
Среди общеучебных навыков важными являются: умение пользоваться техническими средствами обучения, учебно-интеллектуальные умения (умение анализировать и синтезировать информацию, заключенную в тексте задачи), учебно-информационные навыки (умение отбирать нужную информацию из различных источников), ориентироваться в различных видах текста, пользоваться справочниками, понимать невербальные средства, схемы, диаграммы, чертежи, графики; учебно-коммуникативные умения (умения составлять планы, тезисы, понимать лексику, связанную с предметом). Именно на формирование этих навыков направлена программа данного курса.
Результаты обучения
Результаты обучения представлены в Требованиях к уровню подготовки и задают систему итоговых результатов обучения, которых должны достигать все учащиеся и достижение которых является обязательным условием положительной аттестации ученика. Эти требования структурированы по трем компонентам:
«знать/понимать», «уметь», «использовать приобретенные знания и умения в практической деятельности и повседневной жизни».
Планируемые результаты: курс будет способствовать развитию познавательного интереса, поможет учащимся при сдаче ГИА.
Фиксирование результата: тестирование.
Тематический план
Содержание учебного материала
Кол-во часов
Текстовые задачи и алгоритм их решения.
1
Задачи на движение.
5
Задачи на совместную работу.
4
Задачи на части и числа.
3
Задачи, решаемые с помощью неравенств.
2
Творческая работа учащихся.
1
Задачи на прогрессии.
3
Задачи на сплавы, смеси и растворы.
5
Задачи на составление систем уравнений с несколькими переменными.
5
Задачи повышенной сложности.
3
Творческая работа учащихся.
1
Контрольная работа по итогам прослушанного курса.
1
Требования к уровню подготовки учащихся:
В результате усвоения курса учащиеся:
-
должны иметь элементарные умения решать задачи повышенного по сравнению с обязательным уровнем сложности;
-
точно и грамотно формулировать изученные теоретические положения и излагать собственные рассуждения при решении задач;
-
правильно пользоваться математической символикой и терминологией;
-
применять рациональные приемы тождественных преобразований;
-
использовать наиболее употребляемые эвристические приемы.
должны знать:
-
алгоритмы решений текстовых задач;
-
свойства решений уравнений, неравенств и их систем;
-
свойства функций.
должны уметь:
-
уметь решать линейные, квадратные уравнения;
-
уметь решать линейные, квадратные неравенства;
-
строить графики уравнений;
-
уметь решать линейные, квадратные, рациональные уравнения;
-
уметь решать неравенства;
-
находить корни квадратичной функции;
-
строить графики квадратичных функций;
-
исследовать квадратный трехчлен;
-
знать и уметь применять нестандартные приемы и методы решения уравнений, неравенств и систем.
Календарно-тематическое планирование
п/п
Наименование раздела и тем
Часы учебного времени
Сроки прохождения
Примечание
план
факт
Текстовые задачи и алгоритм их решения.
1
Задачи на движение
5
Задачи на движение тел по течению и против
1
Задачи на равномерное и равноускоренное движение тел по прямой линии в одном направлении и навстречу друг другу.
1
Задачи на движение тел по окружности в одном направлении и навстречу друг другу.
1
Задачи на движение: графики движения в прямоугольной системе координат
1
Задачи на движение: таблицы данных задачи и ее значение для составления математической модели.
1
Задачи на совместную работу.
4
Задачи на совместную работу.
1
Формула зависимости объема выполненной работы от производительности и времени ее выполнения
1
Особенности выбора переменных и методика решения задач на работу.
1
Тестирование
1
Задачи на части и числа.
3
Представление многозначного числа в виде суммы разрядных слагаемых.
1
Особенности выбора переменных
1
Методика решения задач на части
1
Задачи, решаемые с помощью неравенств.
2
Задачи, решаемые с помощью неравенств.
1
Задачи, решаемые с помощью систем неравенств.
1
Творческая работа учащихся.
1
Задачи на прогрессии.
3
Задачи на арифметическую прогрессии.
1
Задачи на геометрическую прогрессии.
1
Задачи на прогрессии. Самостоятельная работа
1
Задачи на сплавы, смеси и растворы.
5
Зависимость массы вещества от концентрации.
1
Зависимость массы вещества от объема.
1
Зависимость объема вещества от концентрации
1
Зависимость объема вещества от массы
1
Выбор переменных и методика решения задач на сплавы
1
Задачи на составление систем уравнений с несколькими переменными.
5
Типы задач на составление систем уравнений с несколькими переменными.
1
Способы решения задач на составление систем уравнений с несколькими переменными.
1
Табличный способ решения задач на составление систем уравнений с несколькими переменными.
1
Графический способ решения задач на составление систем уравнений с несколькими переменными.
1
Тестирование
1
Задачи повышенной сложности.
3
Задачи, решаемые составлением неравенств.
1
Приемы решения задач повышенной сложности. Составление таблицы данных задачи.
1
Построение математической модели задач повышенной сложности
1
Творческая работа учащихся.
1
Контрольная работа по итогам прослушанного курса.
1
Содержание программы курса
с внесенными изменениями и их обоснованием
Содержание программы
-
На вводной лекции следует отметить значимость умения решать текстовые задачи. Рассмотреть виды текстовых задач и их примеры, как правильно анализировать текст задачи и составлять её краткую запись. Научить строить алгоритм решения. Рассмотреть решение текстовых задач арифметическими приемами (по действиям), методами составления уравнения, неравенства. Показать значение правильного письменного оформления текстовой задачи. Решение текстовой задачи с помощью графика. Чертеж к текстовой задаче и его значение для построения математической модели.
-
При решении задач на движение стоит рассмотреть следующие темы: движение тел по течению и против, равномерное и равноускоренное движение тел по прямой линии в одном направлении и навстречу друг другу, движение тел по окружности в одном направлении и навстречу друг другу. Определить зависимость между скоростью, временем, расстоянием. Рассмотреть графики движения в прямоугольной системе координат, таблицы данных задачи и ее значение для составления математической модели.
-
В задачах на совместную работу стоит обратить внимание на формулу зависимости объема выполненной работы от производительности и времени ее выполнения. Рассмотреть особенности выбора переменных и методику решения задач на работу.
-
Прежде чем приступить к решению задач на части и числа необходимо дать пояснение к представлению многозначного числа в виде суммы разрядных слагаемых. Рассмотреть особенности выбора переменных и методику решения задач на части.
-
По условиям задач на составление неравенств можно рассмотреть разные типы задач. Также можно рассмотреть задачи, в которых решением будет система неравенств.
-
Уметь по условию задачи определить, какая из прогрессий имеет место в данной задаче. Применять основные формулы арифметической и геометрической прогрессий: нахождение n-го члена прогрессии, суммы n первых членов прогрессии. Уметь выражать переменные из данных формул.
-
В задачах на сплавы, смеси и растворы важно правильно определить формулу зависимости массы или объема вещества от концентрации и массы или объема. Рассмотреть особенности выбора переменных и методику решения задач на сплавы, смеси, растворы. Составлять таблицы данных задачи и математическую модель.
-
По условиям задач на составление систем уравнений с двумя переменными или с несколькими можно рассмотреть разные типы задач. Также можно рассмотреть задачи, в которых решением будет система уравнений.
Программа выполняется полностью и не содержит изменений
Форма и средства контроля
-
Рейтинг - таблица.
-
Уроки самооценки и оценки товарищей.
Работы могут быть как индивидуальные, так и парные, групповые.
Административной проверки усвоения материала курса не предполагается, соответствующие задачи не будут включаться в административные контрольные работы.
В технологии проведения занятий присутствует этап самопроверки, который представляет учащимся возможность самим проверить, как ими усвоен изучаемый материал.
Предусматривается проведение обучающих самостоятельных работ, которые позволят оценить уровень усвоения вопросов курса. Тексты решаемых во время занятий задач в приложении 1.
Форма итогового контроля - контрольная работа.
Содержание данного курса предлагает следующие возможности самоопределения для учеников:
-
выбор вопросов для самостоятельного обучения;
-
темы и формы представления итоговой работы;
-
возможность самостоятельно составлять задачи;
-
возможность выбора информационных данных в средствах массовой информации.
Оценка учебных достижений учащихся осуществляется:
-
на занятиях во время обсуждений;
-
при выполнении практических заданий;
-
при выполнении итоговой работы.
Перечень учебно-методических средств обучения
Учебно-методический комплект обеспечивает возможность преподавания элективного курса «Решение текстовых задач» в соответствии с требованиями нового образовательного стандарта основного общего среднего образования. В состав учебно-методического комплекта входят:
1. «Сборник для подготовки к итоговой аттестации по алгебре в 9 классе» авторы: Л.В.Кузнецова и др., изд. Просвещение, 2009-2010г.
2. Государственная итоговая аттестация выпускников 9 классов в новой форме. Алгебра. 2009 / ФИПИ авторы-составители: Е.А. Бунимович, Т.В. Колесникова, Л.В. Кузнецова, Л.О. Рослова, С.Б. Суворова - М.: Интеллект-Центр, 2009.
3. ГИА-2010. Экзамен в новой форме. Алгебра. 9 класс / ФИПИ авторы- составители: Л.В. Кузнецова, С.Б. Суворова, Е.А. Бунимович и др.- М.: Астрель, 2009.
4. Государственная итоговая аттестация выпускников 9 классов в новой форме. Алгебра. 2010 / ФИПИ авторы - составители: Е.А. Бунимович, Т.В. Колесникова, Л.В. Кузнецова, Л.О. Рослова, С.Б. Суворова - М.: Интеллект-Центр, 2009.
-
Государственная итоговая аттестация (по новой форме): 9 класс. Тематические тренировочные задания. Алгебра/ ФИПИ автор - составитель: В.Л. Кузнецова - М.: Эксмо, 2010.
-
В.Н.Литвиненко, А.Г.Мордкович «Практикум по элементарной математике. Алгебра. Тригонометрия» Москва, «Просвещение», 1991 г.
-
Л.М.Фридман, Е.Н.Турецкий «Как научить решать задачи» Москва, «Просвещение», 1984 г.
Приложение 1
Дидактический материал для занятий.
Тема 1. Составные части задач. Структура и сущность решения задач.
Типы задач:
-
Изменение величины и сравнение её значений.
-
Задачи на работу.
-
Задачи на движение двух тел. 4.Задачи на смеси и сплавы.
Алгоритм решения текстовых задач.
-
Ввод переменных, т.е. обозначение буквами x, y, z,... величины, которые требуется найти по условию задачи.
-
Перевод условий задачи на язык математических соотношений, т.е. составление уравнений, неравенств, введение ограничения.
-
Решение уравнений или неравенств.
-
Проверка полученных решений на выполнение условий задачи.
Указания к решению текстовых задач
-
Набор неизвестных должен быть достаточным для перевода условий задачи на язык математических соотношений. Как правило, за неизвестные следует принимать искомые величины.
-
Выбрав неизвестные, в процессе перевода условий задачи в уравнения или неравенства необходимо использовать все данные и условия задачи.
-
При составлении уравнений или неравенств необходимо исходить из требования о решении задачи в общем виде.
-
В составленных уравнениях надо проверить размерность членов уравнений
-
В процессе решения задачи, надо избегать результатов, противоречащих физическому смыслу.
Тема 2. Задачи на движение двух тел.
Задача 1. (Средняя скорость движения)
Средней скоростью движения на некотором участке пути называют постоянную скорость, с которой можно тот же участок пути пройти за то же время.
Турист шёл со скоростью А км/ч , а точно такое же время со скоростью В км/ч. Какова средняя скорость движения туриста на всём участке пути?
Решение:
Пусть турист шёл Х ч. со скоростью А км/ч и столько же Х ч. - со скоростью В км/ч. Тогда за 2Х ч он прошёл АХ+ВХ=Х(А+В) км. Средняя скорость туриста равна:
![]()
Задача 2.
Автомобиль ехал из А в В порожняком со скоростью 60 км/ч, а возвращался с грузом со скоростью 40 км/ч. Найдите среднюю скорость движения на всём участке движения.
Задача 3.
В гору велосипедист ехал со скоростью 10 км/ч, а с горы с некоторой другой скоростью. Как он подсчитал, средняя скорость движения была12 км/ч. С какой скоростью он ехал с горы?
Решение в общем виде: х=
Задачи на «Движение по реке»
Сформулируем задачу в общем виде:
Лодка от А до В плывёт по течению t часов, а от В до А(против течения) k часов. Сколько часов будет плыть бревно от А до В?
Задача 4.
Я грёб вверх по течению и, проплывая под мостом, потерял шляпу. Через 10 мин. Я это заметил и, повернув и гребя с той же силой, нагнал шляпу в 1 км ниже моста. Какова скорость течения?
Тема 3. Задачи на работу.
При решении задач на работу нередко в условии задачи говорится о выполнении некоторого задания без указания конкретных единиц, в которых измеряется работа. В этом случае обычно принимают всю работу за единицу: А=1. Как правило, для составления уравнения или системы уравнений, буквами обозначаются в первую очередь производительности участников работы, а остальные величины вводятся по мере необходимости.
Некоторые указания к задачам на совместную работу.
Основными компонентами этого типа задач являются:
а) работа;
б) время;
в) производительность труда (работа, выполненная в единицу времени).
План решения задачи обычно сводится к следующему:
а) Принимаем всю работу, которую необходимо выполнить, за 1, если речь идет о выполнении некоторой работы, не охарактеризованной в количественном плане.
б) Находим производительность труда каждого рабочего в отдельности, т. е. 1/t, где t - время, за которое указанный рабочий может выполнить всю работу, работая отдельно.
в) Находим ту часть всей работы, которую выполняет каждый рабочий отдельно, за то время, которое он работал.
г) Составляем уравнение, приравнивая объем всей работы (т. е. 1) к сумме слагаемых, каждое из которых есть часть всей работы, выполненная отдельно каждым из рабочих (если в условии сказано, что при совместной работе всех рабочих выполнен весь объем работы).
Следует заметить, что в указанных задачах не всегда сравнивается выполненная работа. Основанием для составления уравнения может служить также указанное в условии соотношение затраченного времени или производительности труда.
Задача 5.
Два экскаватора разной мощности, работая совместно, выполняют работу за 6 часов. Если первый проработает 4 часа, а затем второй 6 часов, то они выполнят 80% всей работы. За какое время каждый экскаватор отдельно может выполнить всю работу?
Решение:
Пусть Х-производительность первого экскаватора, а У- производительность второго экскаватора. Вся работа-1.
Так как экскаваторы работают совместно 6ч с производительностью Х+У и выполняют всю работу, то составим уравнение: (Х+У)6=1.
Первый экскаватор работает 4ч с производительностью Х., а затем 6ч второй экскаватор с производительностью У, и выполняют 0,8 всей работы, то 4Х+6У=0,8. Решим систему уравнений:
![]()
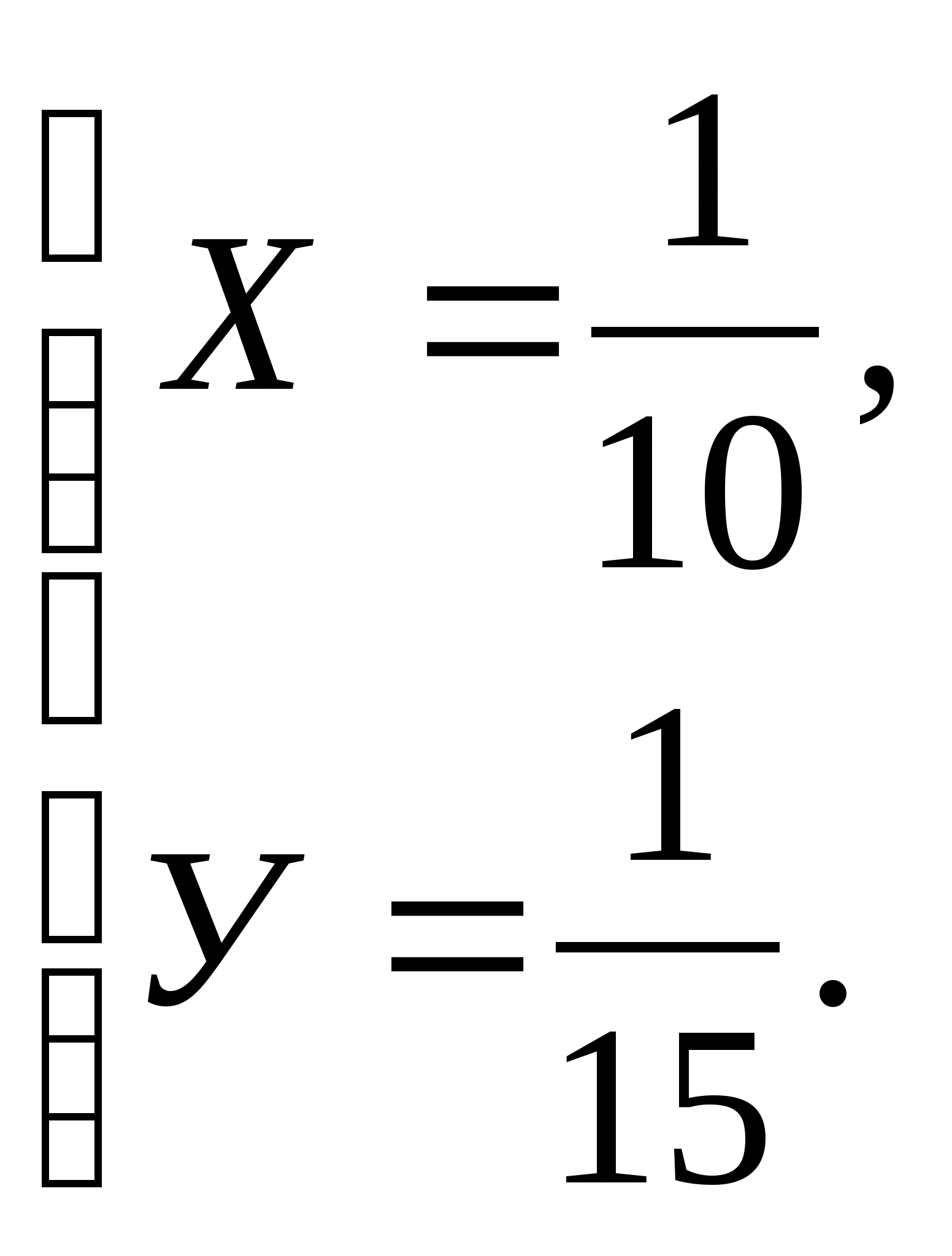
Поскольку время, необходимое для выполнения всей работы, и
производительность связаны соотношением t![]() =
=![]() t
t![]() =
=![]() ,
то t
,
то t![]() =10ч,
t
=10ч,
t![]() =15ч.
=15ч.
Ответ: 10ч, 15ч.
Задача 6.
Два каменщика, второй из которых начинает работать позже первого на 3 дня, могут выстроить стену за 14 дней. Первому каменщику потребовалось бы на выполнение этой работы на 6 дней больше, чем второму. За сколько дней может выстроить эту стену каждый каменщик в отдельности?
Задача 7.
Для разгрузки баржи имеется три крана. Первому крану для разгрузки всей баржи требуется времени в четыре раза меньше, чем второму, и на 9 часов больше, чем третьему. Три крана, работая вместе, разгрузили бы баржу за 18 часов, но по условиям эксплуатации одновременно могут работать только два крана. Определите наименьшее время (в часах) необходимое для разгрузки баржи.(Производительность каждого крана постоянна в течении всей работы)
Ответ: 20ч.
Задачи для самостоятельного решения
-
Два печника, работая вместе, могут сложить печь за 12 ч. Если первый печник будет работать 2 ч, а второй 3 ч, то они выполнят только 20 % всей работы. За сколько часов может сложить печь каждый печник, работая отдельно?
-
Две бригады, работая вместе, могут закончить уборку урожая за 8 дней. Если первая бригада будет работать 3 дня, а вторая 12 дней, то они выполнят 75% всей работы. За сколько дней может закончить уборку урожая каждая бригада, работая отдельно?
-
Два мастера, работая вместе, могут выполнить заказ за 6 ч. Если первый мастер будет работать 9 ч, а потом его сменит второй, то он закончит работу через 4 ч. За сколько времени может выполнить заказ каждый из мастеров, работая отдельно?
-
Две машины, работая вместе, могут расчистить каток за 20 мин. Если первая машина будет работать 25 мин, а затем ее сменит вторая, то она закончит расчистку катка через 16 мин. За сколько времени может расчистить каток каждая машина, работая отдельно?
-
Две трубы при совместном действии могут наполнить бассейн за 4 ч. Если бы сначала первая труба наполнила половину бассейна, а затем ее перекрыли и открыли вторую, то наполнение бассейна было бы закончено за 9 ч. За сколько времени может наполнить этот бассейн каждая труба в отдельности?
-
Первый рабочий может выполнить задание за 8 ч, а второй за 6 ч. Они работали вместе 2 ч, а заканчивал задание один второй рабочий. Сколько времени потребовалось для выполнения второго задания?
-
Двое рабочих, работая одновременно, выполнили задание за 5 дней. Если бы первый рабочий работал в 2 раза быстрее, а второй в 2 раза медленнее, то они выполнили бы задание за 4 дня. За сколько дней выполнил бы задание один первый рабочий?
-
Бассейн наполняется водой из двух кранов. Сначала открыли первый кран на 1/3 часть того времени, за которое наполняет бассейн один второй кран. Затем был открыт один второй кран на 1/2 часть того времени, за которое наполняет бассейн первый кран. После этого оказалось, что уже заполнено 5/6 объема бассейна. За какое время наполняет бассейн каждый кран в отдельности, если открытые вместе они наполняют бассейн за 2,4 ч?
Тема 4.Задачи на проценты.
1. Процент - сотая часть числа.
2. Чтобы найти р% от всего числа, надо всё число умножить на 0.01р.
3. Чтобы найти всё число по его р% процентам, надо известное число разделить на 0.01р.
4. Чтобы найти сколько процентов одно число составляет от другого, надо одно число разделить на другое и умножить на 100%.
Задача 8.
Сколько процентов соли содержится в растворе, если в 200г. раствора содержится 150г. воды?
Решение:
200-150=50(г.) - соли
50*100%=25% - соли
Ответ: 25%
Задача 9.
Кофе при жарке теряет 12% своей массы. Сколько свежего кофе надо взять, чтобы получить 14.08 кг. жареного кофе?
Задача 10.
На сколько процентов увеличится произведение двух чисел, если одно из них увеличить на 30%, а другое - на 20 %?
Задача 11.
Свежие грибы содержали по массе 90% воды, а сухие 12%. Сколько получится сухих грибов из 22 кг свежих?
Решение:
1) 22 . 0,1 = 2,2 (кг) - грибов по массе в свежих грибах;
2) 2,2 : 0,88 = 2,5 (кг) - сухих грибов, получаемых из свежих.
Ответ: 2,5 кг.
Задача 12.(из ЕГЭ).
Цену товара повышали: первый раз на р%, затем новую цену повысили на 2р%. После этого цену товара снизили на 15%. В итоге окончательная цена оказалась выше первоначальной на 12.2%. На сколько процентов была повышена цена товара в первый раз?
Простые проценты.
Обозначим через А![]() сумму первоначального вклада. Банк обязуется выплачивать вкладчику
в конце каждого p% (годовая процентная ставка) от первоначальной
суммы А
сумму первоначального вклада. Банк обязуется выплачивать вкладчику
в конце каждого p% (годовая процентная ставка) от первоначальной
суммы А![]() .
По истечении одного года величина вклада станет равной А=
А
.
По истечении одного года величина вклада станет равной А=
А![]() (1+
(1+![]() )
рублей. Если по прошествии каждого года вкладчик снимает со счёта
начисленные проценты, то через n лет на вкладе по формуле
простого процента будет:
)
рублей. Если по прошествии каждого года вкладчик снимает со счёта
начисленные проценты, то через n лет на вкладе по формуле
простого процента будет:
А![]() =
А
=
А![]() (1+
(1+![]() ) .
) .
Задача 13.
Банк выплачивает вкладчикам каждый год 8% от внесённой суммы. Клиент сделал вклад в размере 200000р.Какая сумма будет на его счёте через 5 лет, 10 лет?
Решение:
Используя формулу : А![]() =
А
=
А![]() (1+
(1+![]() )
)
А![]() =200000(1+
=200000(1+![]() )=280000
(р)
)=280000
(р)
А![]() =200000(1+
=200000(1+![]() )=360000
(р)
)=360000
(р)
Ответ: 280000 р., 360000 р.
Задача 14.
При какой процентной ставке вклад на сумму 500р. Возрастёт за 6 месяцев до 650р.
Ответ: 5%.
Задача 15.
Каким должен быть начальный вклад, чтобы при ставке 4% в месяц он увеличился за 8 месяцев до 33000р.
Ответ: 25000р.
Сложные проценты
Если обозначить через А![]() сумму первоначального вклада, А
сумму первоначального вклада, А![]() -
сумма, которая будет на вкладе к концу n-го года, то при
начислении p% годовых, не снимая со счёта сумму начисленных
процентов, можно пользоваться формулой сложных процентов:
-
сумма, которая будет на вкладе к концу n-го года, то при
начислении p% годовых, не снимая со счёта сумму начисленных
процентов, можно пользоваться формулой сложных процентов:
А![]() =
А
=
А![]()
![]() .
.
Задача 16.
Банк предлагает вклад «студенческий». По этому вкладу сумма, имеющаяся на 1 января, ежегодно увеличивается на одно и то же число процентов. Вкладчик вложил 1 января 1000 рублей и в течение 2 лет не производил со своим вкладом никаких операций. В результате вложенная им сумма увеличилась до 1210 рублей. На сколько процентов ежегодно увеличивается сумма денег, положенная на этот вклад?
Решение:
Пусть на a% ежегодно увеличивается сумма денег,
положенная на «студенческий» вклад. Так как было положено 1000
рублей, а к концу второго года получилось 1210 рублей, то
А![]() =1000;
А
=1000;
А![]() =1210;
n=2.
=1210;
n=2.
Решим уравнение :
1210=1000![]() .
.
а= 10.
Ответ : 10%.
Задача 17.
Рассчитайте, что выгоднее для вкладчика: получить 20 000 рублей сегодня или получить 35 000 рублей через 3 года, если процентная ставка равна 17%.
Рассчитаем будущую стоимость 20000 рублей через 3 года, под 17% годовых.
А![]() =
20000 * (1 + 0,17)3 = 32032 рубля.
=
20000 * (1 + 0,17)3 = 32032 рубля.
Ответ. Получить 35000 рублей через 3 года является более выгодным решением, при данном значении процентной ставки.
Задача 18.
Какой должна быть ставка ссудного процента, чтобы 10000 рублей дошли до30000 рублей, за срок вклада 5 лет?
Ответ. 10 000 рублей дойдут до 30 000 рублей за 5 лет при ставке ссудного процента 24,573%
Тема 5. Задачи на смеси, сплавы и растворы.
Смесь состоит из «чистого вещества» и «примеси». Долей а чистого вещества в смеси называется отношение количества чистого вещества m в смеси к общему количеству М смеси при условии, что они измерены одной и той же единицей массы или объёма: а=m/М.
Процентным содержанием чистого вещества в смеси с называют его долю, выраженную процентным отношением: с=а 100%.
Задача 19.
В 2 литра 10% раствора уксусной кислоты добавили 8 литров чистой воды. Определить процентное содержание уксусной кислоты в полученном растворе.
Решение:
2л - 100%
Воды - 1,8л.
Кислота - 0,2л.
После добавления воды стало 9,8л. Воды, поэтому процентное содержание
(0,2\(0,2+9,8))*100%=2%
Ответ: 2%.
Задача 20.
Сплав содержит 10 кг олова и 15 кг цинка. Каково процентное содержание олова и цинка в сплаве?
Решение:
Процентное содержание вещества в сплаве - это часть, которую составляет вес данного вещества от веса всего сплава.
1) 10 + 15 = 25 (кг) - сплав;
2) 10/25 . 100% = 40% - процентное содержание олова в сплаве;
3) 15/25 . 100% = 60% - процентное содержание цинка в сплаве;
Ответ: 40%, 60%.
Задача 21.
Сплав олова с медью весом 12кг. Содержит 45% меди. Сколько чистого олова нужно добавить, чтобы получить сплав, содержащий 40% меди.
Задача 22.
Имеется 2 сплава, в одном из которых содержится 40%, а в другом 20% серебра. Сколько кг второго сплава нужно добавить к 20 кг первого, чтобы после сплавления вместе получить сплав, содержащий 32% серебра?
Задача 23.
К 15 л 10%-ного раствора соли добавили 5%-ный раствор соли и получили 8%-ный раствор. Какое количество литров 5%-ного раствора добавили?
Задача 24. (вариант 13 , стр.53. для подготовки к ГИА- 9, 2011)
При смешивании первого раствора сахара, концентрация которого 25%, и второго раствора сахара, концентрация которого 35% , получили раствор, содержащий 32,5 % сахара. В каком отношении были взяты первый и второй растворы?
Решение:
Пусть масса первого раствора - х литров, второго - у литров, то первый раствор содержит 0,25 х л сахара, а второй- 0,35у л сахара, то общая масса сахара равна их сумме. С другой стороны, масса полученного раствора равна (х+у) л, в нем содержится 0,325 (х+у) л сахара, то получим уравнение 0,25х+0,35у= 0,325(х+у). Раскрывая скобки и перенеся слагаемые с х в левую, с у- в правую, получим:
0,075 х = 0,025у / : 0,075 х
х/у= 1/3
Ответ: 1/3.
Задачи на концентрацию.
Формула концентрации смеси (сплава) :
n=![]() ,где n - концентрация, m
,где n - концентрация, m![]() -
масса вещества в растворе (сплаве), m
-
масса вещества в растворе (сплаве), m![]() -
масса всего раствора.
-
масса всего раствора.
Если концентрация вещества в соединении по массе составляет р%, то это означает, что масса этого вещества составляет р% от массы всего соединения.
Отношения объема чистой компоненты в растворе ко всему объему смеси называется объемной концентрацией этой компоненты.
Сумма концентраций всех компонент, составляющих смесь, равна 1. В этом случае концентрация - безразмерная величина.
Если известно процентное содержание вещества, то его
концентрация находится по формуле: n=![]() ,
где n - концентрация вещества; р - процентное содержание
вещества (в процентах).
,
где n - концентрация вещества; р - процентное содержание
вещества (в процентах).
Задача 25.
К 20кг. 12%-раствора соли добавили 3кг. соли. Сколько надо долить воды, чтобы концентрация соли в растворе не изменилась.
1) 0.12*20=2.4(кг.) - масса соли в первоначальном растворе
2) 2.4+3=5.4(кг.) - масса соли в полученном растворе
Пусть Х(л.) воды требуется долить.
Запишем пропорцию:
20+Х=5.4
20 2.4
2.4(20+Х)=5.4*20
48+2.4х=108
2.4х=60
х=25(кг.)
Ответ: 25(кг.)
Задача 26.
Если смешать 8 кг и 2кг растворов серной кислоты разное концентрации, то получим 12% раствор кислоты. При смешивании двух одинаковых масс тех же растворов получим 15% раствор. Определите первоначальную концентрацию каждого раствора.
Ответ: 10%-й и 20%-й растворы.
Задача 27.
Сколько граммов надо добавить к 100г. 30-% соляной кислоты, чтобы получить 10%-кислоту?
Задача 28.
К раствору, содержащему 39г. соли, добавили 1л. воды, после чего концентрация соли уменьшилась на 10%. Найти первоначальную концентрацию соли в растворе
Задача 29.
В колбе было 800г 80% спирта. Провизор отлил из колбы 200г этого спирта и добавил в неё 200г воды. Определите концентрацию ( в %) полученного спирта.
Задача 30. (вариант 13 , стр.53. для подготовки к ГИА- 9, 2011)
При смешивании первого раствора сахара, концентрация которого 25%, и второго раствора сахара, концентрация которого 35% , получили раствор, содержащий 32,5 % сахара. В каком отношении были взяты первый и второй растворы?
Решение:
Пусть масса первого раствора - х литров, второго - у литров, то первый раствор содержит 0,25 х л сахара, а второй- 0,35у л сахара, то общая масса сахара равна их сумме. С другой стороны, масса полученного раствора равна (х+у) л, в нем содержится 0,325 (х+у) л сахара, то получим уравнение 0,25х+0,35у= 0,325(х+у). Раскрывая скобки и перенеся слагаемые с х в левую, с у- в правую, получим:
0,075 х = 0,025у / : 0,075 х
х/у= 1/3
Ответ: 1/3.
Тема 6. Комбинированные задачи.
Задачи, решаемые с помощью уравнений.
Задача 31.
Магазин в первый день продал половину привезённых гусей да ещё
![]() гуся; во второй день
гуся; во второй день ![]() часть остатка да ещё
часть остатка да ещё ![]() гуся, а в третий день магазин продал оставшихся 33 гусей. Сколько
всего гусей было привезено в магазин?
гуся, а в третий день магазин продал оставшихся 33 гусей. Сколько
всего гусей было привезено в магазин?
Решение:
Пусть было привезено в магазин х гусей. Тогда магазин продал:
-
в первый день
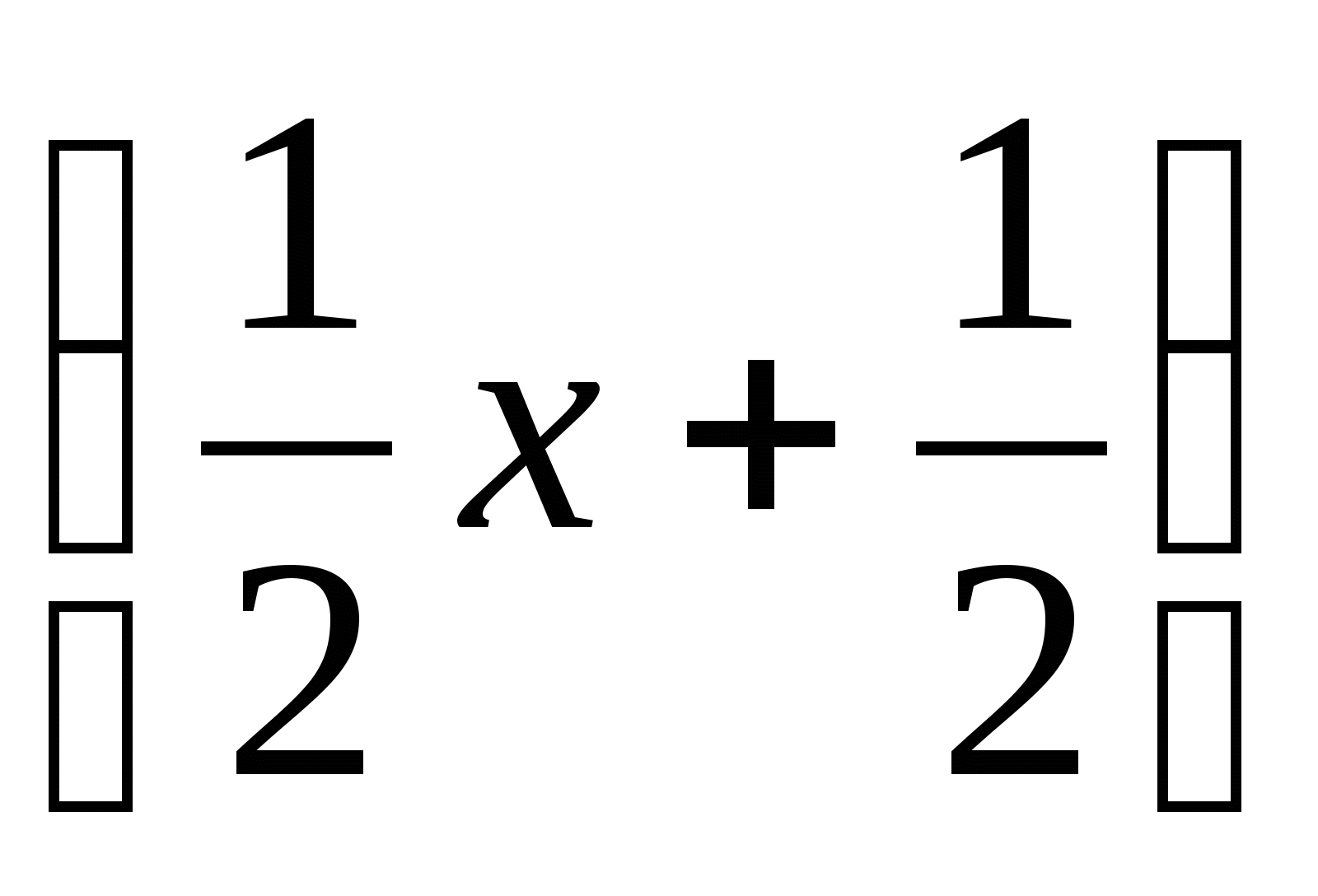 гусей;
гусей;
-
во второй день
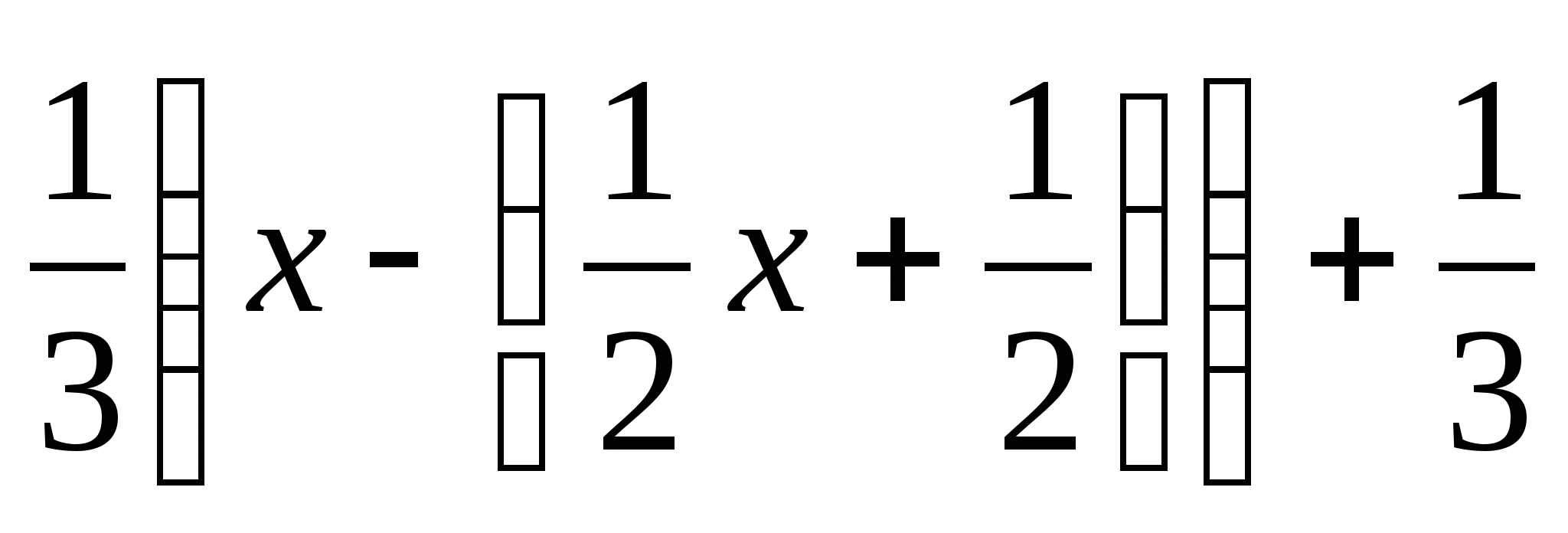 гусей;
гусей;
-
в третий день 33 гуся.
Составим уравнение и решим его.
![]() +
+![]() +33=х,
+33=х,
![]() ,
,
-![]() ,
,
х=101.
Ответ: 101 гусь.
Задача 32.
Автомобилист проехал расстояние между двумя городами за 3 дня. В
первый день он проехал![]() всего
пути и ещё 60 км, во второй он проехал
всего
пути и ещё 60 км, во второй он проехал![]() всего пути и ещё20 км, а в третий день он проехал
всего пути и ещё20 км, а в третий день он проехал ![]() всего пути и оставшиеся 25 км. Найдите расстояние между городами.
всего пути и оставшиеся 25 км. Найдите расстояние между городами.
Ответ:400 км.
Задача 33.
В течении года завод дважды увеличивал выпуск продукции на одно и то же число процентов. Найдите это число, если известно, что в начале года завод ежемесячно выпускал 600 изделий, а в конце года стал выпускать ежемесячно 726 изделий.
Ответ:10%.
Задача 34.
Моторная лодка, скорость которой в стоячей воде равна 10 км/ч, проплыла по течению 91 км и вернулась обратно. Найдите скорость течения реки, если лодка провела в пути 20 часов.
Ответ: 3 км/ч.
Задачи, решаемые с помощью систем уравнений.
Задача 35.
Имеются два раствора серной кислоты в воде: первый - 40%-й, второй- 60%-й. Эти два раствора смешали , после чего добавили 5 кг чистой воды и получили 20% раствор. Если бы вместо 5 кг чистой воды добавили 5 кг 80%-го раствора, то получился бы 70%-й раствор. Сколько было 40%-го раствора и 60%-го раствора?
Решение:
Масса серной
Кислоты, кг
Масса
раствора
Концентрация
1-й раствор
0,4х
х
40%=0.4
2-й раствор
0,6у
у
60%=0,6
Первая смесь
0,4х+0,6у
х+у+5
![]()
Вторая смесь
(0,4х+0,6у)+
+5![]()
=0,4х+0,6у+4
х+у+5
![]()
По условию доля серной кислоты в первой смеси равна 20%=0,2, а во второй смеси равна 70%=0,7.
Составим и решим систему уравнений:
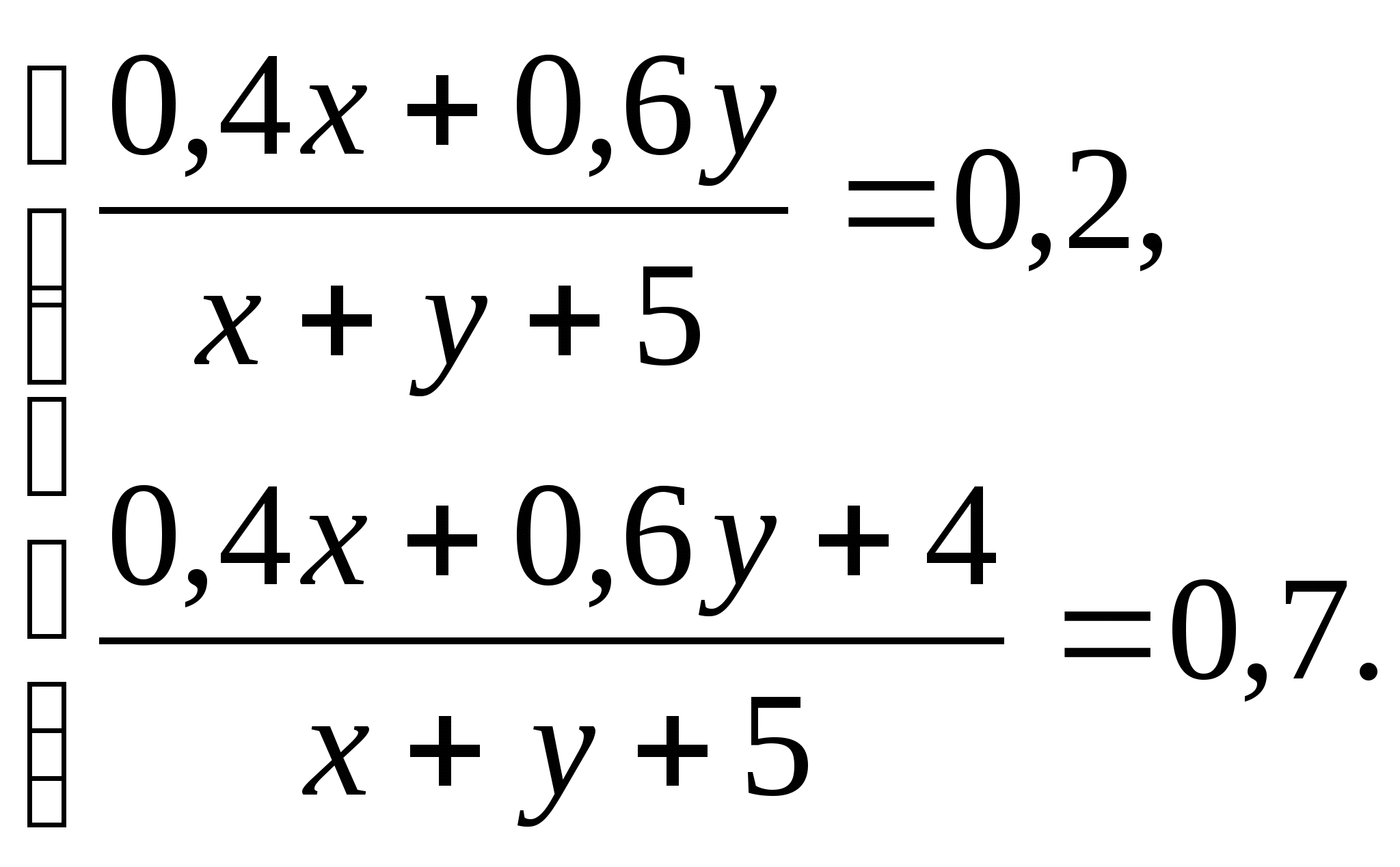
Пусть 0,4х+0,6у=а, х+у+5=b. Тогда система примет вид
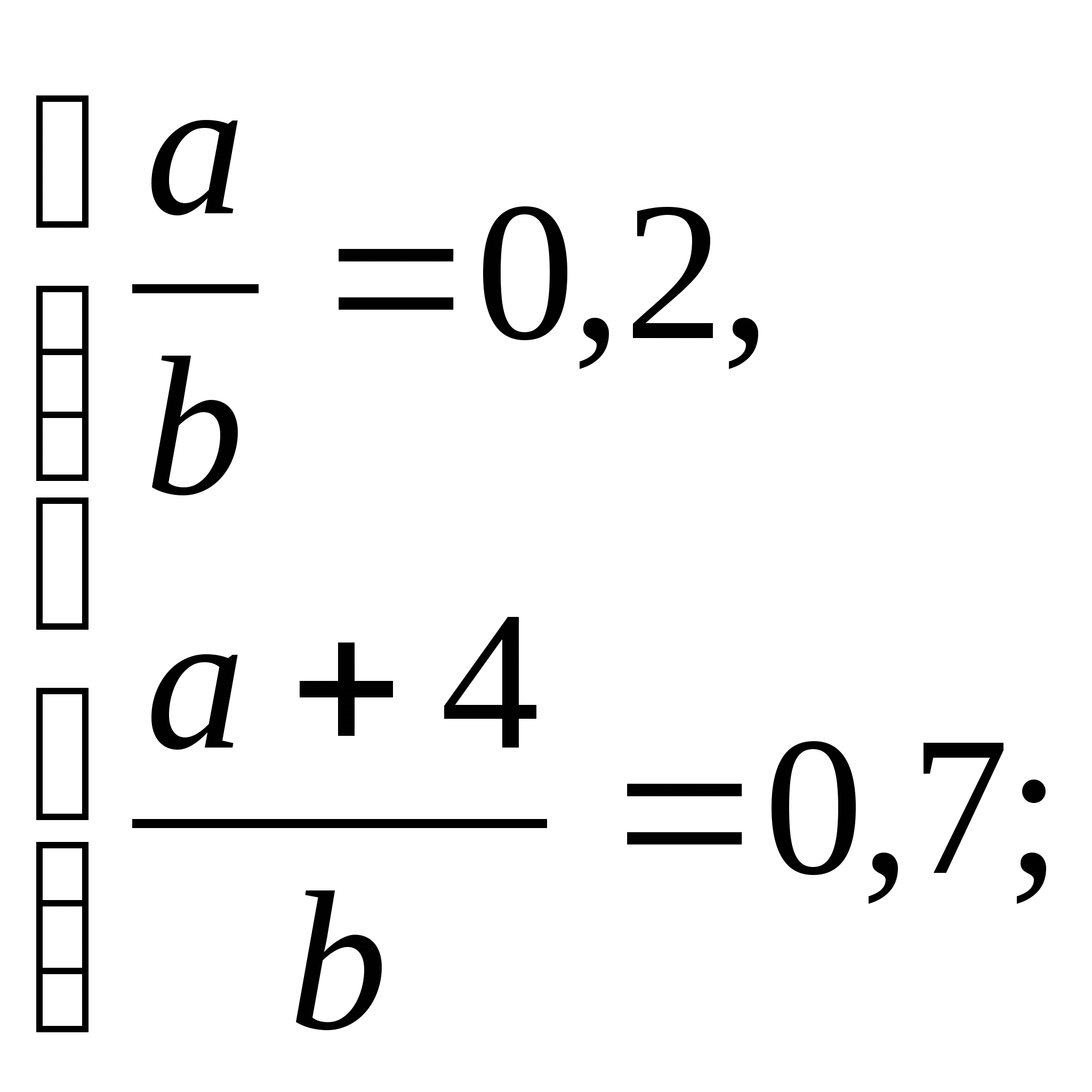
![]()
![]()
![]()
1 кг -масса 40%-го раствора серной кислоты.
2 кг- масса 60%-го раствора серной кислоты.
Ответ: 1 кг, 2 кг.
Задача 36.
Имеется кусок сплава меди с оловом общей массой 12 кг, содержащий 45% меди. Сколько чистого олова надо прибавить к этому куску сплава, чтобы получившийся новый сплав содержал 40% меди?
Ответ: 1,5 кг.
Задача 37.
В реку впадает приток. Катер отходит от пункта А, находящегося на притоке, плывёт по течению 80 км до впадения притока в реку в пункте В, а затем идёт вверх по реке до пункта С. На путь от А до С он затратил 18 часов, на обратный путь - 15 часов. Найдите расстояние от В до С, если известно, что скорость течения реки3км/ч, а собственная скорость катера 18 км/ч.
Ответ: 210 км.
Задача 38.
Фирма А может выполнить заказ на производство игрушек на 4 дня быстрее, чем фирма В. За какое время может выполнить этот заказ каждая фирма, если известно, что при совместной работе за 24 дня они выполняют заказ в 5 раз больший?
Ответ: фирма А за 8 дней, фирма В за 12 дней
Задачи, которые решают при помощи неравенств.
Задача 39.
В контейнере находятся коробки и ящики общим числом более 16. Если вдвое увеличить количество коробок и на 20 - количество ящиков, то ящиков будет больше, чем коробок.
Решение.
Пусть х- количество коробок, а у- количество ящиков в контейнере. По смыслу задачи х и у- натуральные числа. По условию задачи составим систему неравенств:
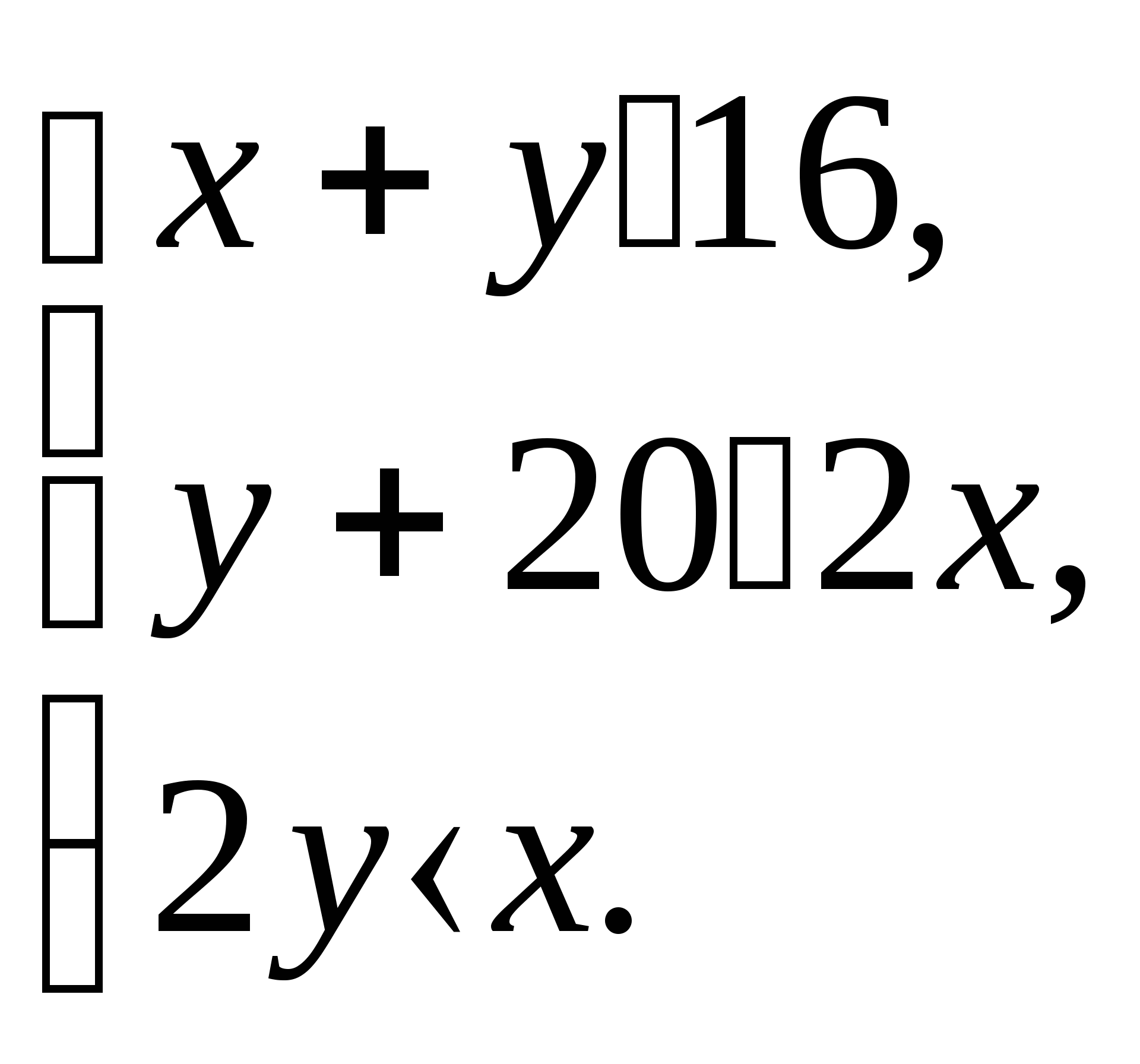
Преобразуем данную систему:
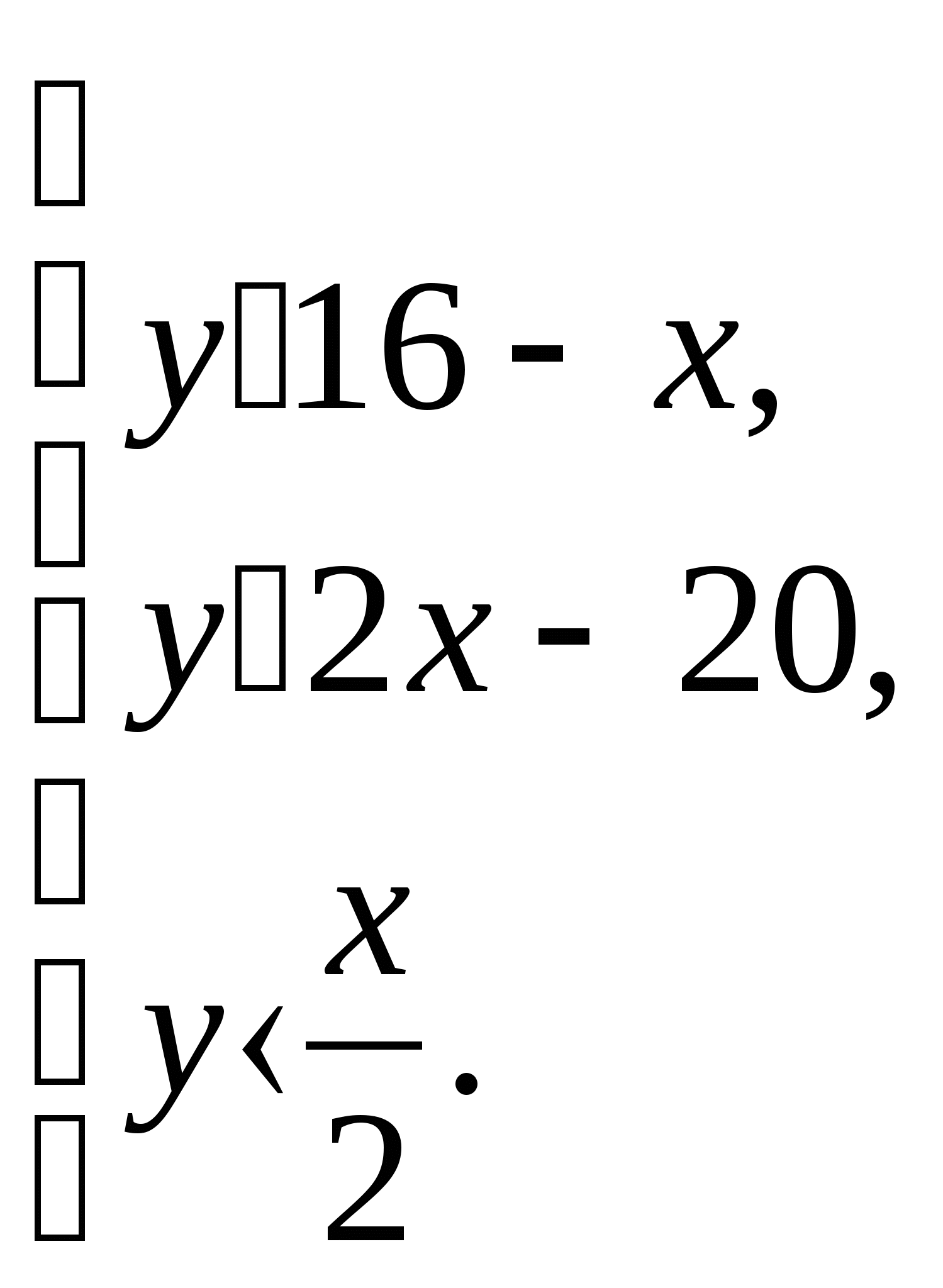
На координатной плоскости найдём множество точек (х;у), удовлетворяющих этим условиям.

Точки лежащие внутри ΔАВС, и будут удовлетворять данным условиям. Это одно точка с натуральными координатами-(12;5). Следовательно, количество коробок может быть только 12, при этом ящиков должно быть 5.
Проверка:
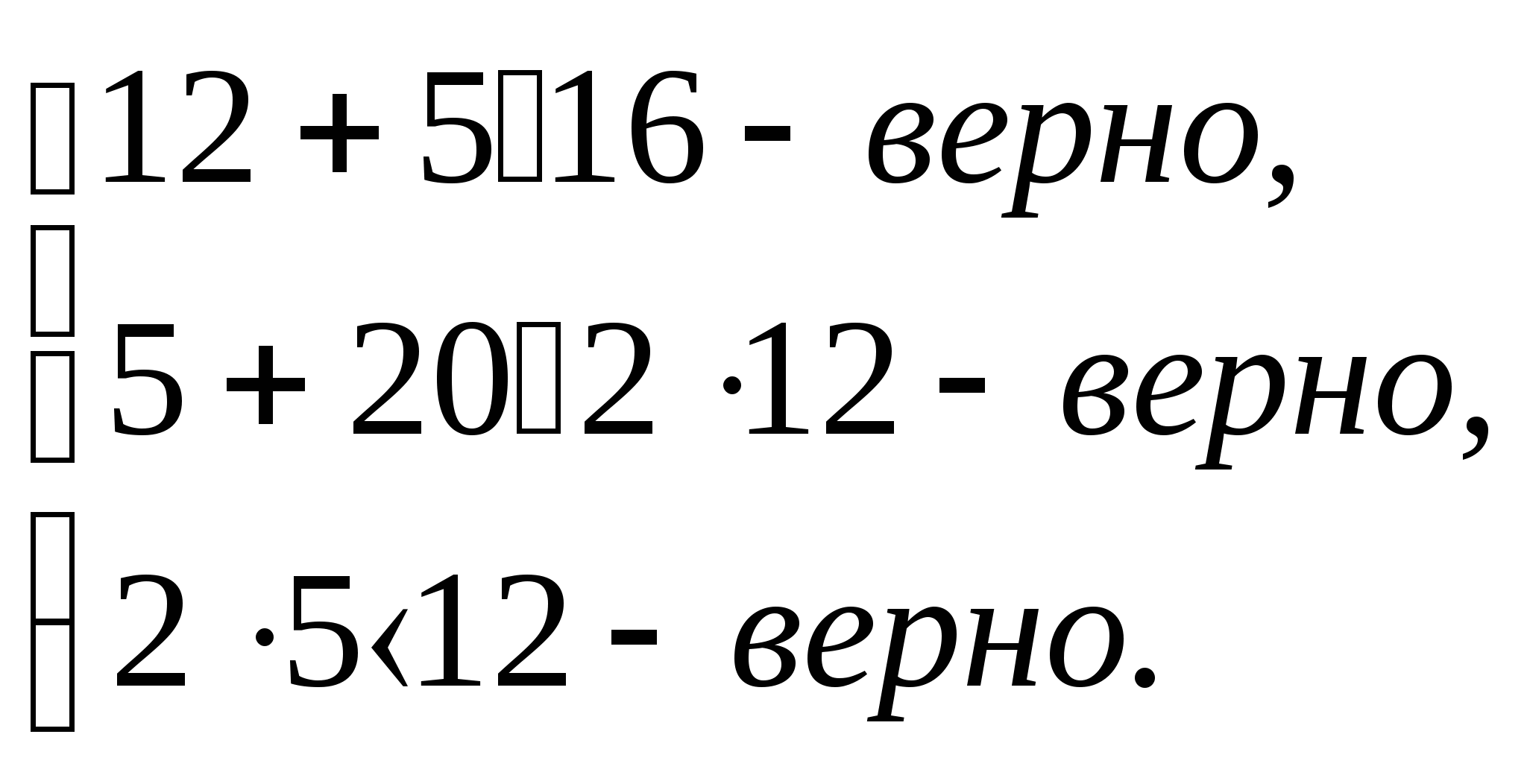
Ответ : 12 коробок.
Задача 40.
Из пункта А в пункт В, находящийся на расстоянии 105 км от пункта А, со некоторой скоростью выезжает автобус. Через 30 минут вслед за ним из А со скоростью 40 км/ч отправляется автомобиль, который догнав автобус, поворачивает обратно. Определите скорость автобуса, при которой автомобиль возвращается в А позже, чем автобус приходит в В.
Решение.
Пусть х км - расстояние от пункта А до места встречи автобуса и автомобиля. Обозначим v км/ч скорость автобуса.
Время, которое затрачивает автобус на путь из А в В, равно
![]() ч.
Время, которое затрачивает автомобиль, чтобы догнать автобус и
вернуться в А, с учётом его более позднего, на 0,5 ч, отправления,
составляет
ч.
Время, которое затрачивает автомобиль, чтобы догнать автобус и
вернуться в А, с учётом его более позднего, на 0,5 ч, отправления,
составляет ![]() ч.
По условию задачи время движения автомобиля больше времени
автобуса, т.е.
ч.
По условию задачи время движения автомобиля больше времени
автобуса, т.е. ![]()
![]()
![]() .
По условию задачи время, затраченное автобусом на путь от А до
места встречи, на 0,5 ч больше времени, которое потребовалось
автомобилю, чтобы догнать автобус, т.е.
.
По условию задачи время, затраченное автобусом на путь от А до
места встречи, на 0,5 ч больше времени, которое потребовалось
автомобилю, чтобы догнать автобус, т.е. ![]() ,
х=
,
х=![]() В
результате неравенство примет вид:
В
результате неравенство примет вид:
![]()
![]()
![]() ,
,
![]()
![]() .
.
как 0![]() ,
0
,
0![]() ,
то умножая обе части неравенства на 2v(40-v)
,
то умножая обе части неравенства на 2v(40-v)![]() 0,
имеем:
0,
имеем:
2v![]() +(40-v)
v
+(40-v)
v![]() 210(40-v),
210(40-v),
v![]() +250v-840
+250v-840![]() 0,
0,
Учитывая условие задачи, решение неравенства имеет вид:
v![]() 30.
30.
По условию задачи встреча произошла до пункта В, т.е. 0![]() .В
результате имеем ещё одно неравенство:
.В
результате имеем ещё одно неравенство:
0![]() ,
так как 0
,
так как 0![]() ,то
,то
0![]() ,
,
0![]() .
.
Учитывая, что : v![]() 30
, окончательный результат:
30
, окончательный результат:
30![]() ,
при таких скоростях, автомобиль возвращается в А позже, чем автобус
приходит в В.
,
при таких скоростях, автомобиль возвращается в А позже, чем автобус
приходит в В.
Ответ: 30![]() .
.
Задача 41.
На реке, скорость течения которой 5 км/ч, в направлении её течения расположены пристани А,В и С, причём В находится посередине между А и С. От пристани В одновременно отходят плот , который движется по течению к пристани С, и катер, который идёт к пристани А, причём скорость катера в стоячей воде равна v км/ч. Дойдя до пристани А, катер разворачивается и движется по направлению к пристани С. Найдите все те значения v, при которых катер приходит в С позже, чем плот.
Ответ: 5![]() 15
км/ч.
15
км/ч.
Тема 7. Решение задач по всему курсу.
Задача 42.( производительность)
В бассейн проведена труба. Вследствие её засорения приток воды уменьшился на 60%. На сколько процентов вследствие увеличится время, необходимое для заполнения бассейна?
Ответ: 150%
Задача 43.
Имеются 2 слитка, содержащие медь. Масса 2 слитка на 3кг. Больше, чем масса 1 слитка. Процентное содержание меди в первом слитке - 10%; во втором - 40%. После сплавления этих двух слитков получился слиток, процентное содержание меди в котором - 30%. Определить массу полученного слитка.
Ответ: 9кг.
Задача 44.
Из турбазы в одном направлении выходят три туриста с интервалом в 30 мин. Первый идёт со скоростью 5 км/ч, второй - 4 км/ч. Третий турист догоняет первого. Найдите скорость третьего туриста.
Ответ: 6 км/ч.
Задача 45.
За определённое время на автозаводе должны были собрать 160 автомобилей. Первые 2 ч выполнялась установленная почасовая норма, а затем стали забирать на 3 автомобиля больше. В результате за 1 ч до срока было собрано 155 автомобилей. Сколько автомобилей в час планировали собирать первоначально?
Ответ: 20автомобилей.
Житейские истории.
Задача 46.
Бочонок кваса.
Один человек выпивает бочонок кваса за 14 дней, а вместе с женой выпивает такой же бочонок кваса за 10 дней. Нужно узнать, за сколько дней жена одна выпивает такой же бочонок кваса.
Решение: За 140 дней человек выпьет 10 бочонок кваса, а вдвоем с женой за 140 дней они выпьют 4 бочонка кваса. Значит, за 140 дней жена выпьет 14-10= 4 бочонка кваса, а тогда один бочонок она выпьет за 140: 4= 35 дней.
Задача 47.
Голова рыбы весит столько, сколько хвост и половина туловища, туловище столько, сколько голова и хвост вместе. Хвост весит 1 кг. Сколько весит рыба? ( решить с помощью уравнения).
Задача 48. (из книги «Математический кружок» А.В.Спивак, стр.46.).
Четверо товарищей покупают лодку. Первый вносит половину суммы, вносимой остальными; второй- треть суммы, вносимой остальными; третий- четверть суммы, вносимой остальными; четвертый- 130 рублей. Сколько стоит лодка?
При составлении программы использовались материалы следующих авторов:
-
Программа учителя муниципального общеобразовательного учреждения «Хотмыжская средняя общеобразовательная школа» Гридуновой О.А. «Решение текстовых задач»
-
«Сборник для подготовки к итоговой аттестации по алгебре в 9 классе» авторы: Л.В.Кузнецова и др., изд. Просвещение, 2009-2010г.
-
Государственная итоговая аттестация выпускников 9 классов в новой форме. Алгебра. 2009 / ФИПИ авторы-составители: Е.А. Бунимович, Т.В. Колесникова, Л.В. Кузнецова, Л.О. Рослова, С.Б. Суворова - М.: Интеллект-Центр, 2009.
-
ГИА-2010. Экзамен в новой форме. Алгебра. 9 класс / ФИПИ авторы- составители: Л.В. Кузнецова, С.Б. Суворова, Е.А. Бунимович и др.- М.: Астрель, 2009.
-
Государственная итоговая аттестация выпускников 9 классов в новой форме. Алгебра. 2010 / ФИПИ авторы - составители: Е.А. Бунимович, Т.В. Колесникова, Л.В. Кузнецова, Л.О. Рослова, С.Б. Суворова - М.: Интеллект-Центр, 2009.
-
Государственная итоговая аттестация (по новой форме): 9 класс. Тематические тренировочные задания. Алгебра/ ФИПИ автор - составитель: В.Л. Кузнецова - М.: Эксмо, 2010.
-
В.Н.Литвиненко, А.Г.Мордкович «Практикум по элементарной математике. Алгебра. Тригонометрия» Москва, «Просвещение», 1991 г.
-
Л.М.Фридман, Е.Н.Турецкий «Как научить решать задачи» Москва, «Просвещение», 1984 г.