- Учителю
- Конспект урока по математике на тему 'Решение однородных тригонометрических уравнений' (10 класс)
Конспект урока по математике на тему 'Решение однородных тригонометрических уравнений' (10 класс)
Урок
«Решение однородных тригонометрических уравнений»
Цели:
-
Сформировать у учащихся умение решать однородные тригонометрические уравнения, отработать навыки решения всех видов тригонометрических уравнений.
-
Развивать и совершенствовать умения, применять имеющиеся у учащихся знания в измененной ситуации; развивать логическое мышление, умение делать выводы и обобщения.
-
Воспитывать у учащихся актуальность, культуру поведения, чувство ответственности.
План урока.
-
Организационный момент.
-
Этап проверки домашнего задания.
-
Этап подготовки учащихся к активному и сознательному усвоению нового материала.
-
Этап усвоения новых знаний.
-
Этап проверки понимания учащимися нового материала.
-
Этап закрепления нового материала.
-
Этап информирования учащихся о домашнем задании.
-
Этап всесторонней проверки знаний.
Ход урока.
Задача 1 - подготовить учащихся к работе на уроке.
Французский писатель Анатоль Франс однажды заметил: «Учиться можно только весело…. Чтобы переваривать знания, надо поглощать их с аппетитом».
Так вот, давайте сегодня на уроке будем следовать этому совету писателя, будем активны, внимательны, будем поглощать знания с большим желанием, ведь они пригодятся вам в вашей дальнейшей жизни.
Наша задача на уроке - показать свои знания и умения по решению уже известных видов тригонометрических уравнений и овладеть умением решать новый тип уравнений - однородные уравнения.
Задача 2 - установить осознанность и правильность выполнения заданий всеми учащимися; установить пробелы в знаниях; совершенствовать знания, умения и навыки учащихся в области решения простейших тригонометрических уравнений.
а) Математический диктант.
Диктант проводится в двух вариантах. Вопросы распечатываются каждому учащемуся. По окончании диктанта, учащиеся обмениваются работами и проверяют правильность ответов, которые высвечены на экране.
1 вариант.
-
Каково будет решение уравнения
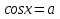 при ׀
при ׀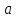 ׀>1?
׀>1? -
При каком значении
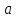 уравнение
уравнение 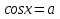 имеет решение?
имеет решение? -
Какой формулой выражается это решение?
-
На какой оси откладывается значение
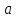 при решении уравнения
при решении уравнения 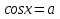 ?
? -
В каком промежутке находится значение
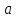 ?
? -
В каком промежутке находится значение
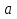 ?
? -
Каким будет решение уравнения
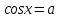 ?
? -
Каким будет решение уравнения
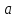 ?
? -
Каким будет решение уравнения
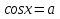 ?
? -
Чему равняется
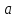 ?
? -
В каком промежутке находится
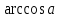 ?
? -
Какой формулой выражается решение уравнения
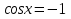 ?
? -
Чему равняется
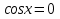 ?
?
2 вариант.
-
Каково будет решение уравнения
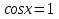 при ׀
при ׀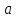 ׀>1?
׀>1? -
При каком значении
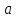 уравнение
уравнение 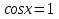 имеет решение?
имеет решение? -
Какой формулой выражается это решение?
-
На какой оси откладывается значение
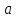 при решении уравнения
при решении уравнения 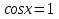 ?
? -
В каком промежутке находится значение
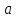 ?
? -
В каком промежутке находится значение
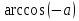 ?
? -
Каким будет решение уравнения
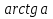 ?
? -
Каким будет решение уравнения
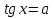 ?
? -
Каким будет решение уравнения
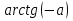 ?
? -
Чему равняется
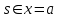 ?
? -
В каком промежутке находится
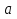 ?
? -
Какой формулой выражается решение уравнения
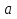 ?
? -
Чему равняется
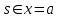 ?
?
б) Сообщения учащихся.
Выступают заранее подготовленные учащиеся.
-
Доклад об истории развития тригонометрии.
-
О прикладной направленности изучаемой темы.
в) Самостоятельная работа №1.
Самостоятельная работа проводится на 3 варианта. Вариант 3 предлагается учащимся по выбору. Тетради с работой собираются учителем для проверки.
Вариант 1.
Решите уравнения: 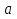 ;
;
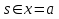
Вариант 2.
Решите уравнения: 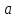 ;
;
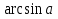
Вариант 3.
Решите уравнения: 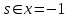 ;
;
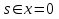
Задача 3 - с помощью создания проблемной ситуации подвести учащихся к новому виду тригонометрических уравнений.
Уравнения на магнитной доске: 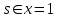

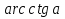
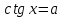
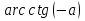
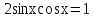
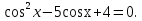
Задание: назовите те уравнения, название и метод решения которых знаете.
В результате на доске остаются уравнения: 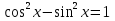
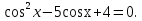
Задача 4 - дать учащимся понятие однородных тригонометрических уравнений, способ их решения, добиться умения определять вид однородных тригонометрических уравнений, отработать навыки их решения.
Уравнения данного вида называются однородными.
Учащиеся записывают тему урока в тетрадях.
Вообще, уравнения вида
 , где
, где
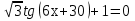 - числа, n
- числа, n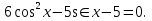 называются однородными относительно
называются однородными относительно 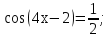 и
и 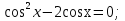 .
.
Сумма показателей степеней 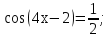 и
и 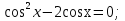 во всех членах одинакова. Она называется степенью однородности уравнения.
во всех членах одинакова. Она называется степенью однородности уравнения.
Метод решения - деление на 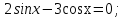 .
.
Задание: Почему возможно это деление?
Если предположить, что 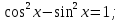 , то и
, то и 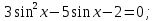 , что противоречит основному тригонометрическому тождеству, поэтому деление возможно.
, что противоречит основному тригонометрическому тождеству, поэтому деление возможно.
Задание: Решить уравнение 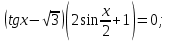 [Отв.:
[Отв.: 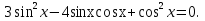 ]
]
На доске решается уравнение с подробным разбором хода решения.
Задача 5 - установить усвоение учащимися способа решения нового вида уравнений.
Задание: Укажите вид уравнения и способ его решения.
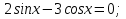
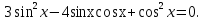
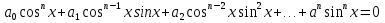
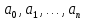
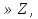
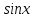
Задача 6 - закрепить у учащихся знания и умения, которые они получили на уроке для выполнения письменной работы.
Задание: Решить уравнения:
а) 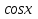
[Отв.: 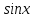 ]
]
б) 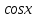 [Отв.:
[Отв.: 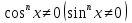 ].
].
Уравнения решаются на доске с подробным разбором хода решения.
Задача 7 - сообщить учащимся домашнее задание, дать краткий инструктаж по его выполнению.
Задача 8 - проверить знания учащихся при решении всех видов тригонометрических уравнений, стимулировать учащихся к самоанализу, самоконтролю.
а) Самостоятельная работа №2.
Работа на 3 варианта, носит обучающий характер. Учащиеся самостоятельны в выборе варианта. Желающие сдают работу для оценивания.
Вариант 1 - 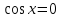
Вариант 2 - 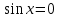
Вариант 3 - 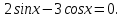
б) Устный фронтальный опрос:
-
С каким видом уравнений мы познакомились?
-
Каков метод решения уравнений этого вида?
-
Почему возможно деление на
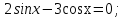 ?
? -
Каков метод решения уравнения после указанного деления?
Учащимся дается оценка их работе на уроке. Выставляются отметки.