- Учителю
- План конспект урока по алгебре и началам анализа Тригонометрические уравнения (10 класс)
План конспект урока по алгебре и началам анализа Тригонометрические уравнения (10 класс)
Открытый урок по алгебре и началам анализа учителя математики
Доевой Евы Кимовны учителя МКОУ СОШ № 3 им. Героя Советского Союза К.Д. Карсанова с. Эльхотово МО Кировский район РСО-Алания
Технологическая карта урока
Тема: «Решение тригонометрических уравнений. Уравнения, сводящиеся к простейшим заменой неизвестного».
Тип урока: Урок обобщения и систематизации знаний.
Формируемые результаты:
-
Предметные: обеспечить повторение и систематизацию учебного материала.
Научить при решении уравнений ориентироваться на координатной плоскости и правильно записывать решение уравнений, имея ввиду неоднозначность ответа,
Проконтролировать степень владения УУД.
-
Личностные: Формировать: независимость суждений, содействовать воспитанию интереса к математике и ее приложениям, умению объективно оценивать себя, активности, мобильности, умению общаться, общую культуру учащихся.
-
Метапредметные: способствовать формированию умений применять приемы: сравнения, обобщения, выявления главного, переноса знаний в новую ситуацию, развитию математического кругозора и зоркости, мышления и речи, внимания и памяти.
Планируемые результаты: Учащийся научится: решать уравнения по обобщающей схеме: 1)сводить тригонометрическое уравнение к алгебраическому,
2)решать тригонометрические уравнения разложением на множители,
3)вводить новую переменную,
4)вводить вспомогательный аргумент,
5)решать тригонометрические уравнения переводом суммы в произведение
6)применять формулы понижения степени;
делать системные обобщения, выполнять самопроверку, выполнять взаимопроверку.
Основные понятия: синус угла, косинус угла, период, чётность функции, корень уравнения, тригонометрическая окружность.
Организационная структура урока.Устно:
слайд №1-10
5.Самостоятельная работа
И
Слайд:
№11,12,13
6.Взаимопроверка и оценка
П
Слайд:
№14, 15
7.Систематизация знаний (профильный уровень)
И
Слайд:
№16-21
7.Информация о домашнем задании
п.11.2-11.4,11.8
№207 (а,б,в,д)
Ф - фронтальная работа И - индивидуальная работа П - парная работа
1. Организационный момент. (Презентация. Слайды 1 - 2)
Альберт Эйнштейн (1879 - 1955) однажды заметил:
«Мне приходится делить время между политикой и уравнениями. Однако, уравнения гораздо важнее. Политика существует только для данного момента, а уравнения будут существовать вечно».
Сегодня у нас заключительный урок по теме «Решение тригонометрических уравнений». Повторяем, обобщаем, приводим в систему изученные виды, типы уравнений, методы и приемы решений тригонометрических уравнений.
2.Актуализация знаний.
-
(Презентация. Слайды 3,4.)
-
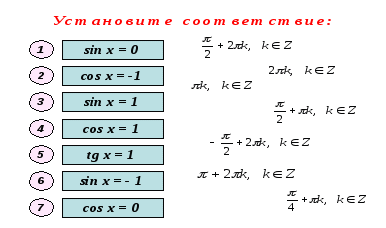
(Презентация. Слайды 5-8.)
5)
Решение какого уравнения показано на тригонометрической окружности?
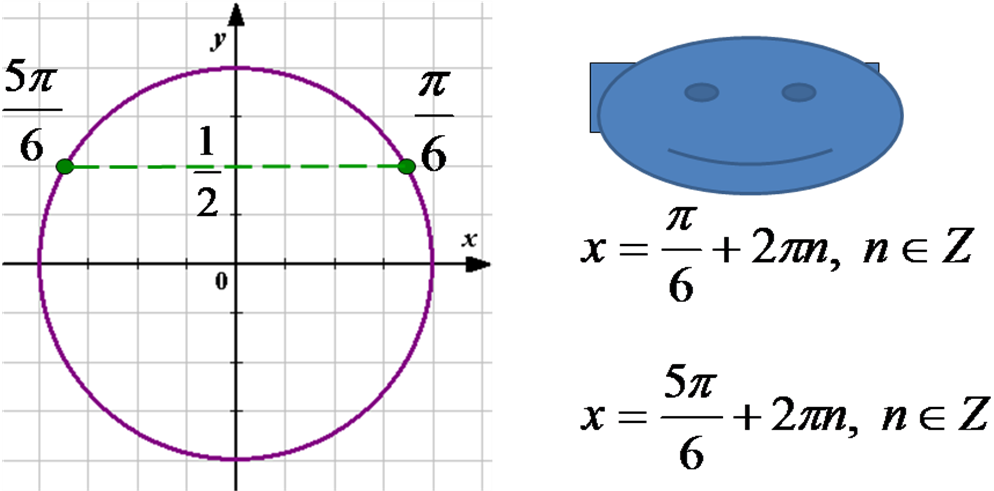
6)
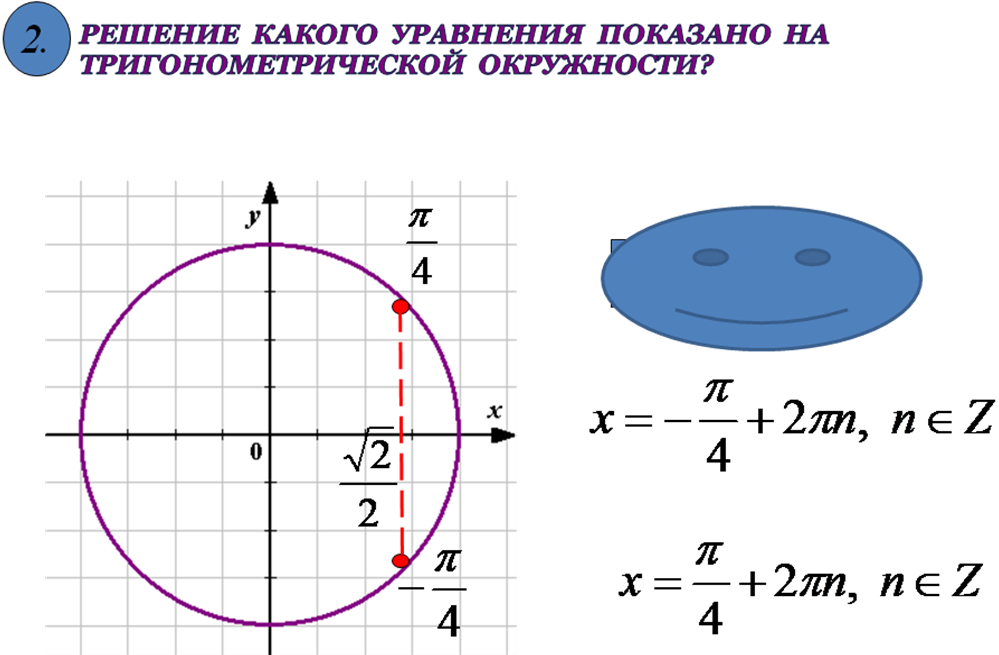
7)
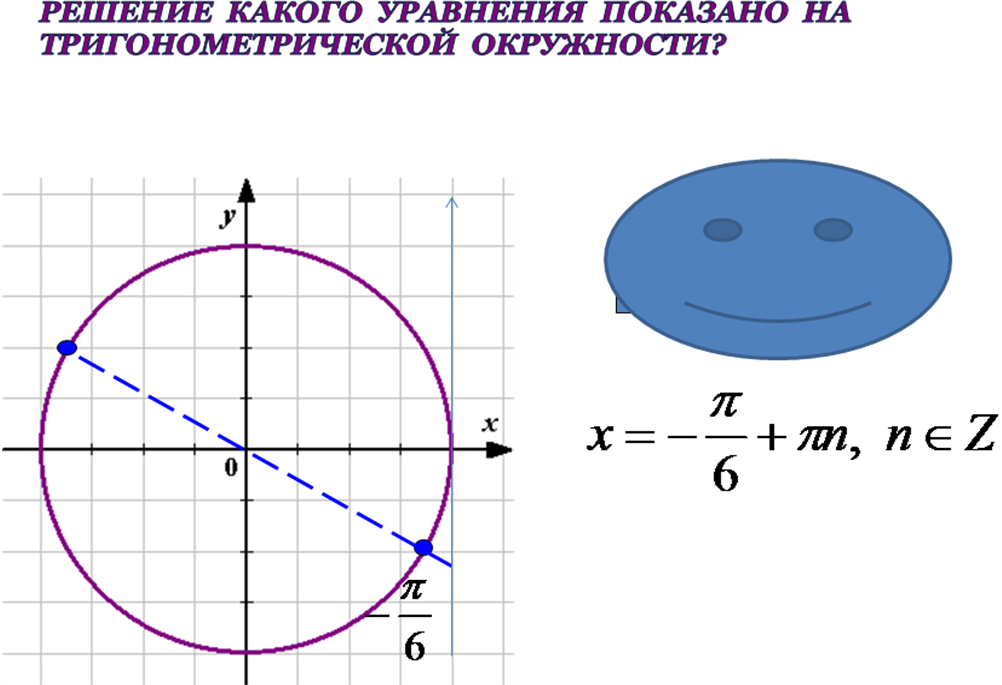
8)
9) Какая из схем лишняя?
Слайд 8. 5 - я схема лишняя, так как эта схема
изображает решение уравнения вида 
; 1, 2, 3, 4, 6 - изображают решение уравнений вида 
.
Слайд 9. 1 - я схема лишняя, так как она
изображает решение уравнения вида
;
5 - я схема лишняя, так как эта схема изображает решение
уравнения вида 
;
2, 3, 4, 6 - изображают решение уравнений вида 
.
3.Самостоятельная работа по теме: «Решение тригонометрических уравнений» 10 класс
УМК С.М.Никольский (профильное преподавание предмета 4 ч/нед)
-
Каково будет решение уравнения
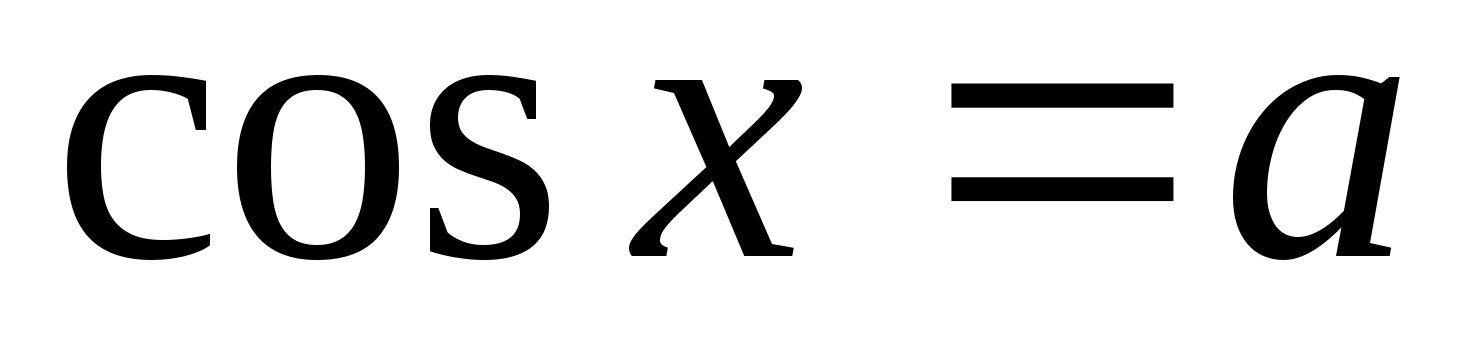при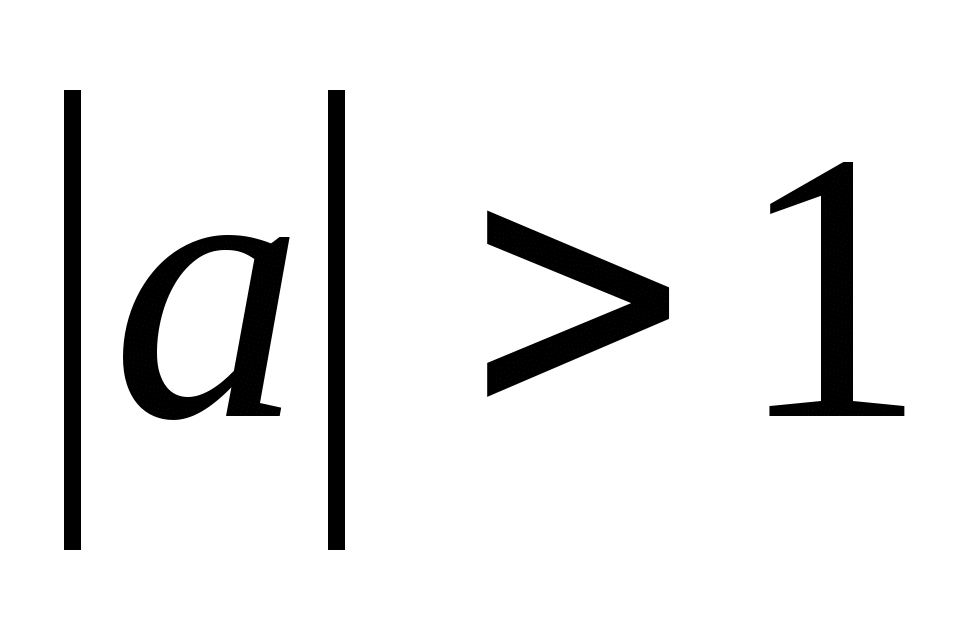 
?
-
При каком значении а уравнение
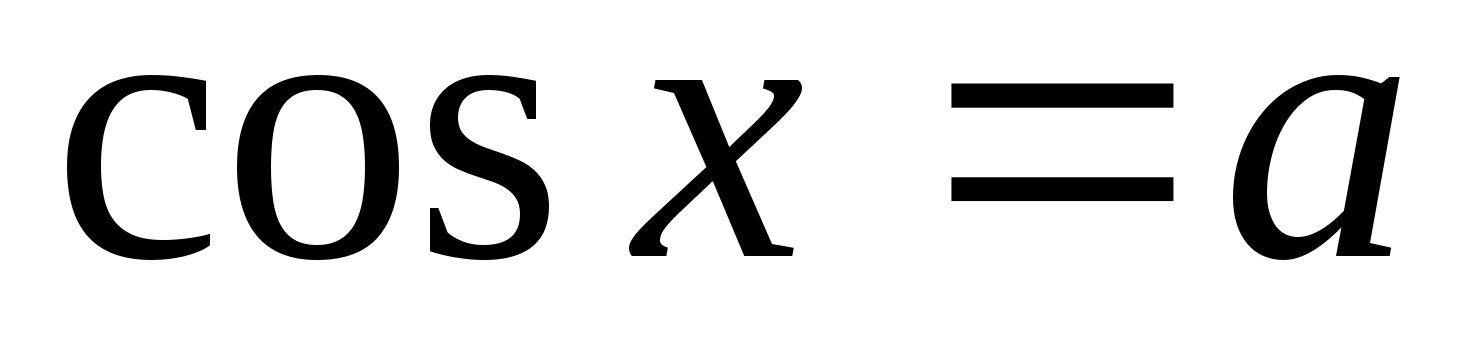имеет решение?
-
Какой формулой выражается это решение?
-
На какой оси откладывается значение а при решении уравнения
?
-
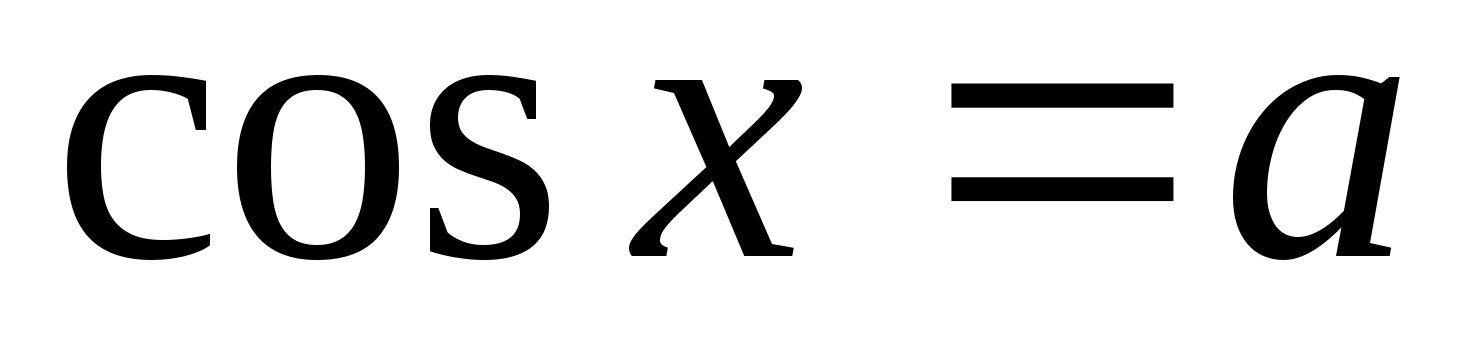В каком промежутке находится
?
-
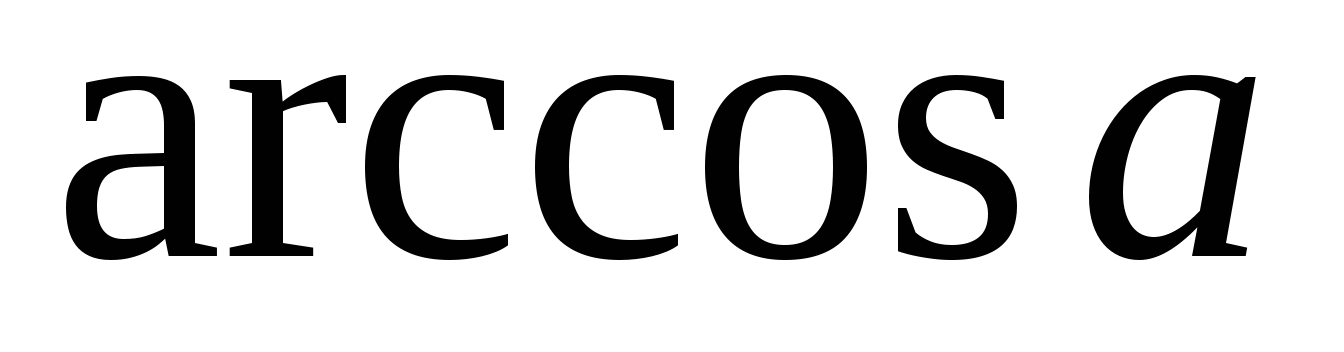В каком промежутке находится значение а?
-
Каким будет решение уравнения
?
-
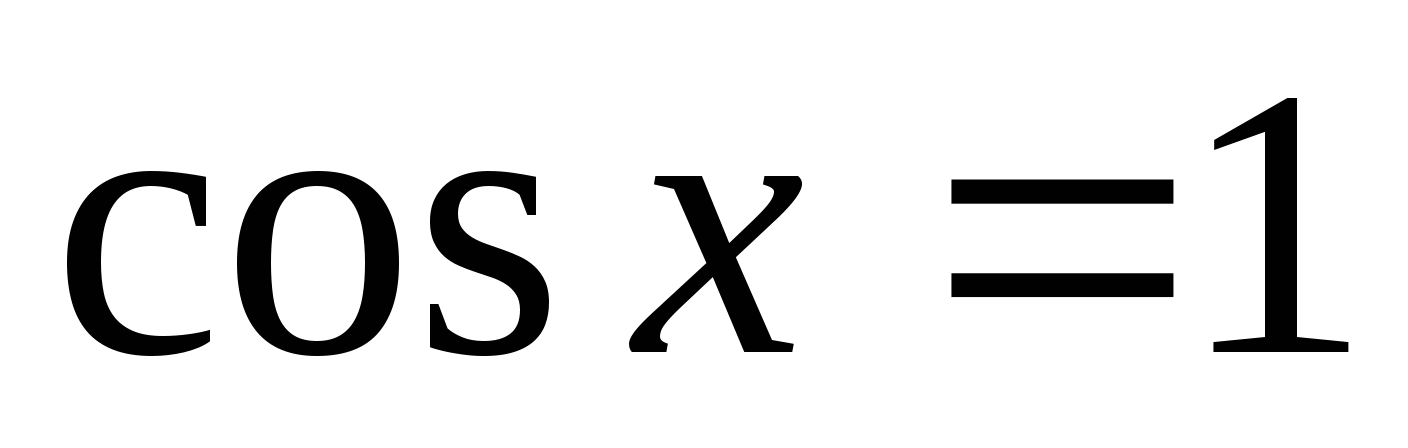Каким будет решение уравнения
?
-
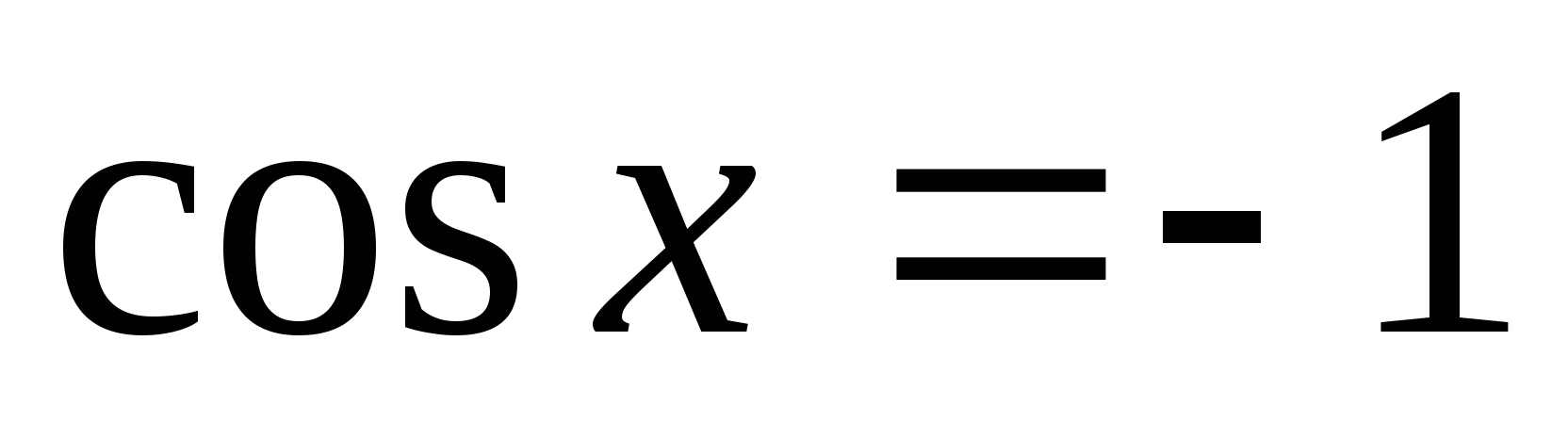Каким будет решение уравнения
?
-
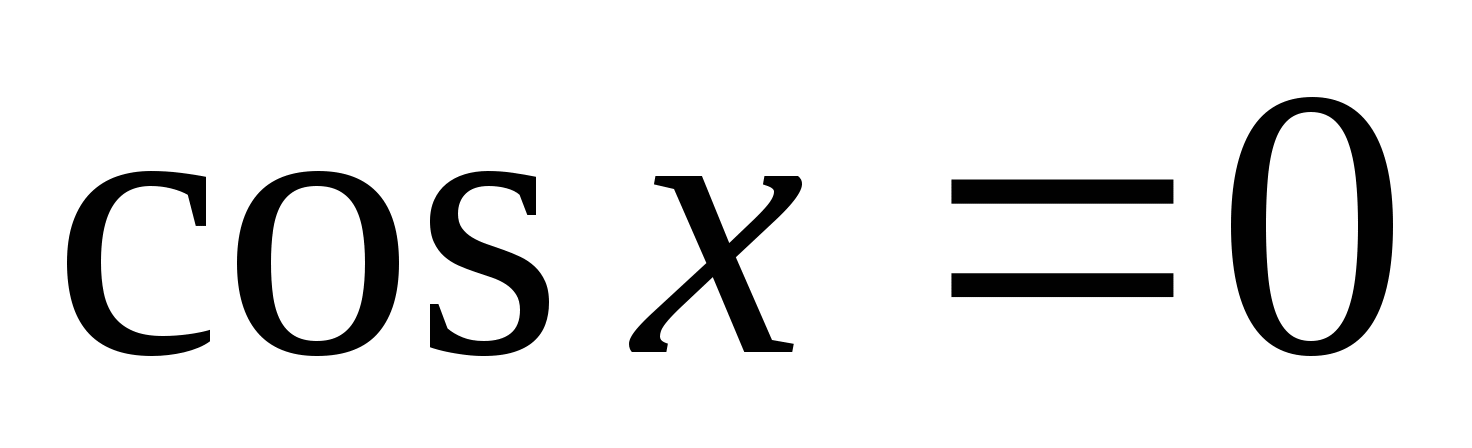Чему равняется
?
-
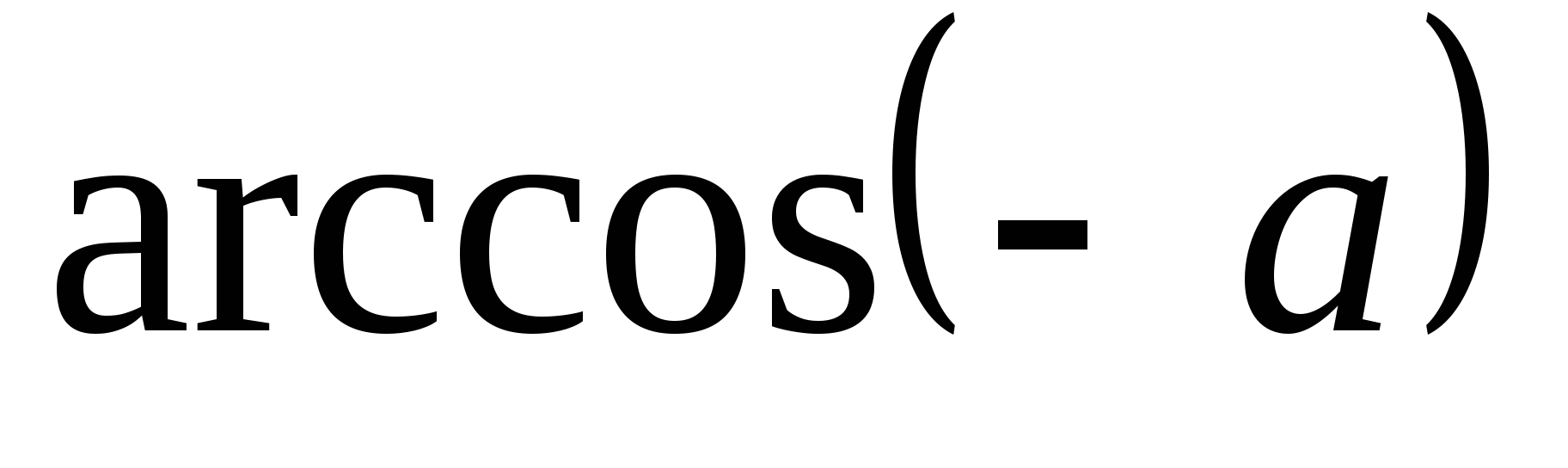В каком промежутке находится
?
-
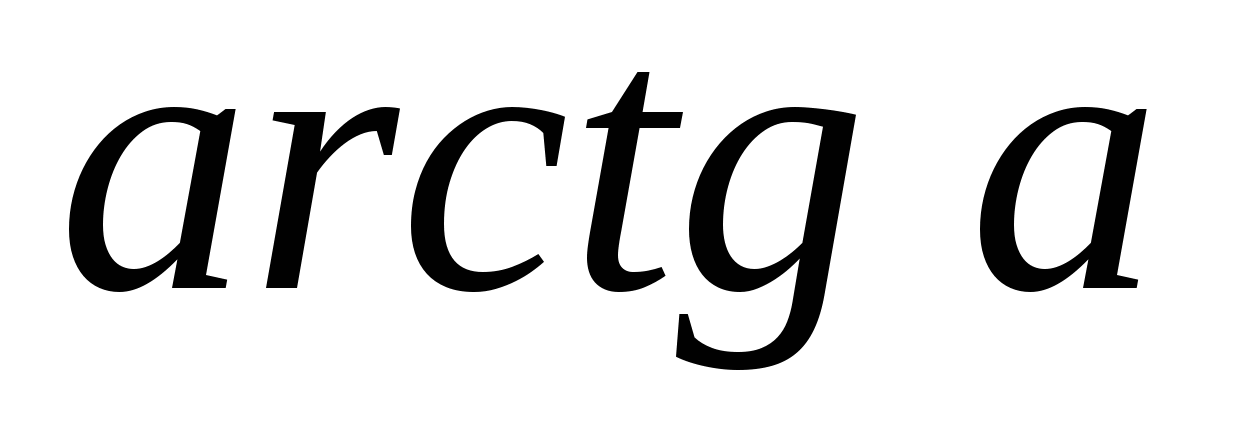Какой формулой выражается решение уравнения
?
-
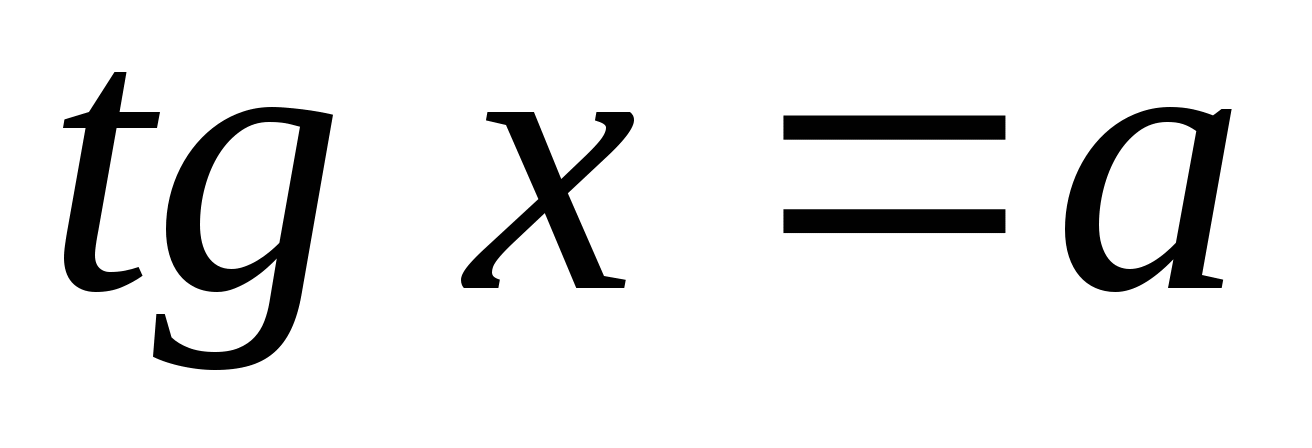Каково будет решение уравнения
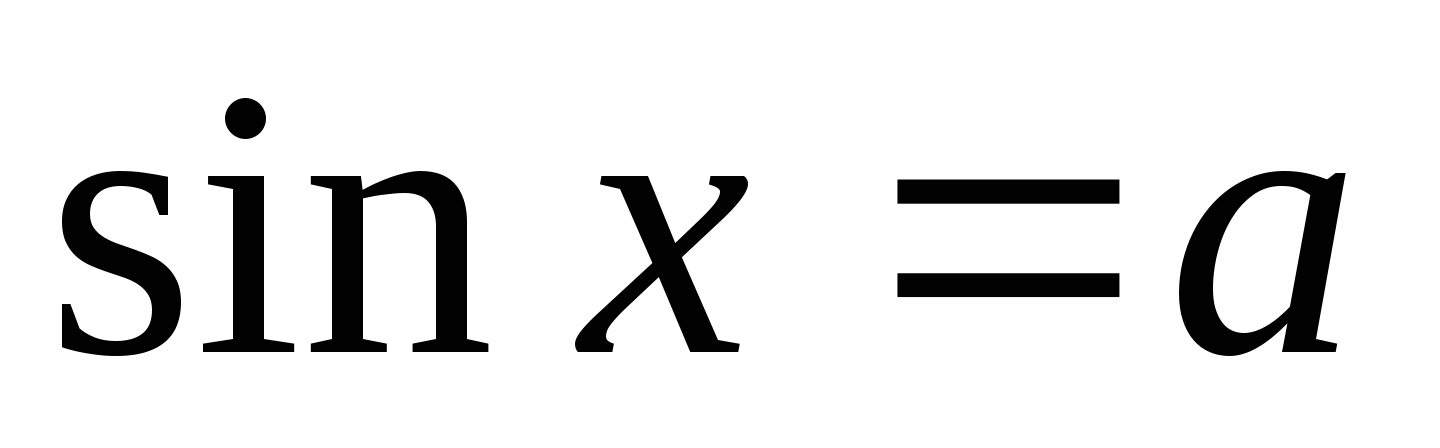при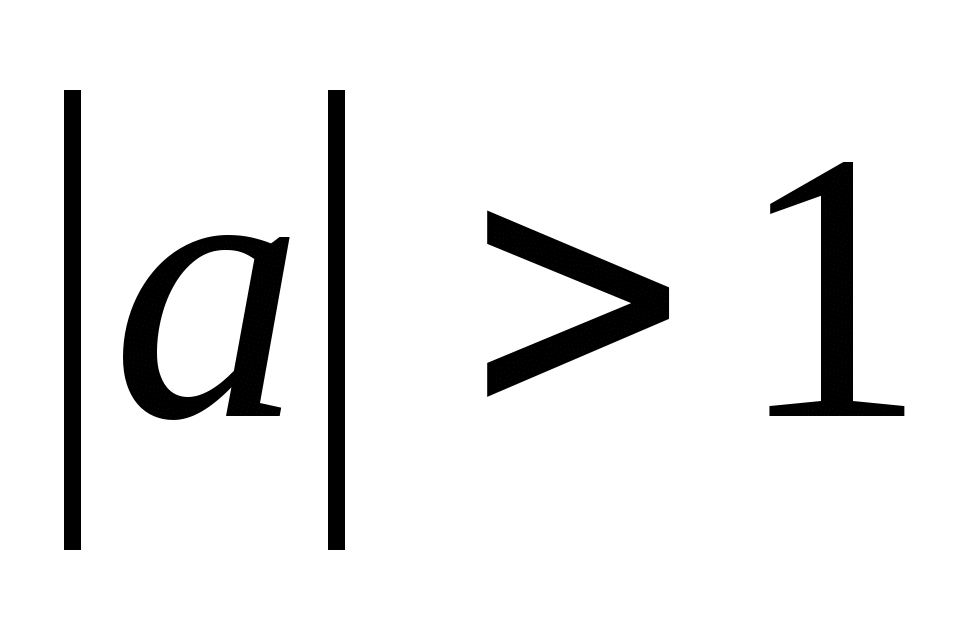
?
-
При каком значении а уравнение
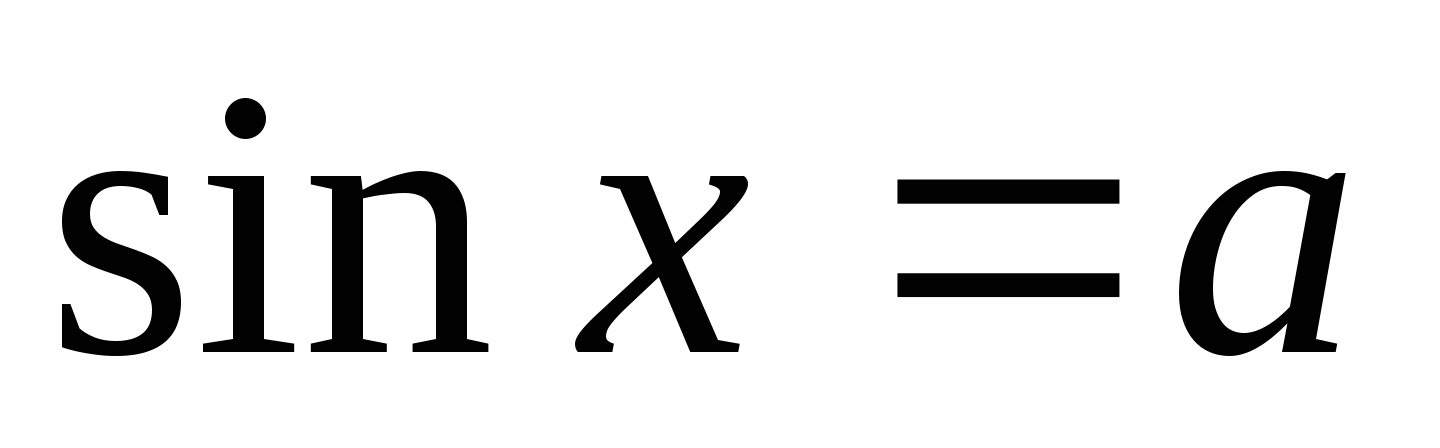имеет решение?
-
Какой формулой выражается это решение?
-
На какой оси откладывается значение а при решении уравнения
?
-
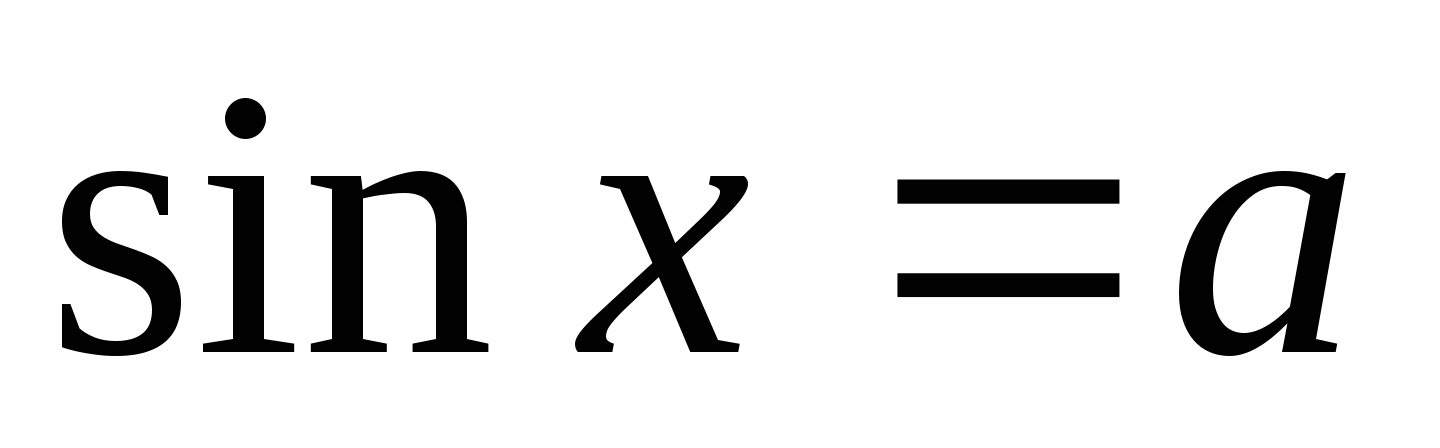В каком промежутке находится
?
-
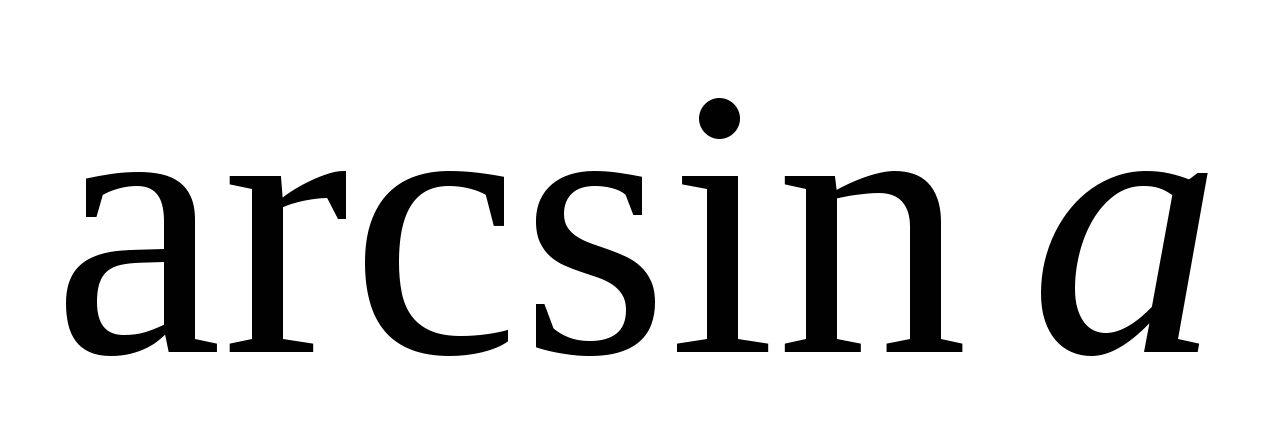В каком промежутке находится значение а?
-
Каким будет решение уравнения
?
-
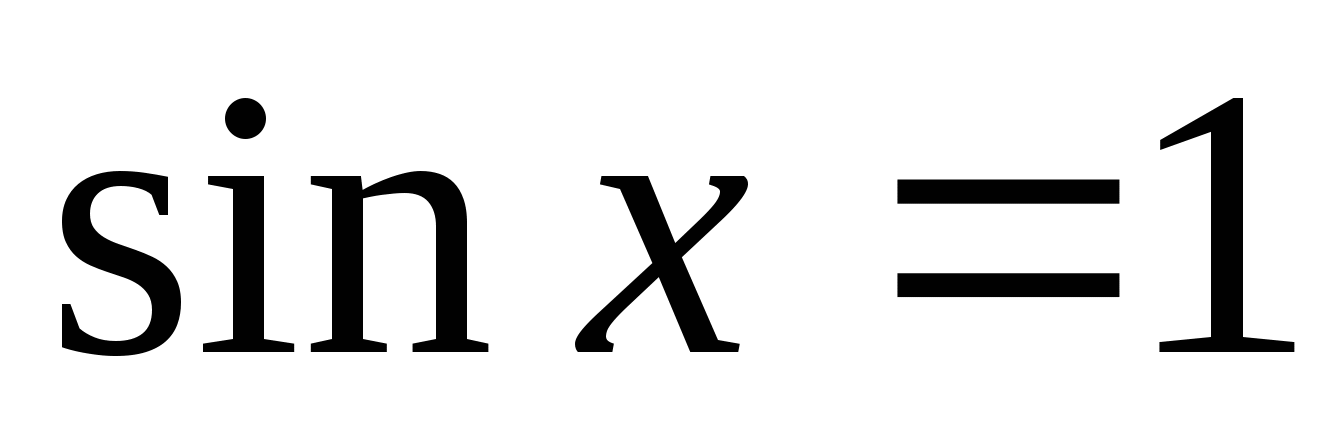Каким будет решение уравнения
?
-
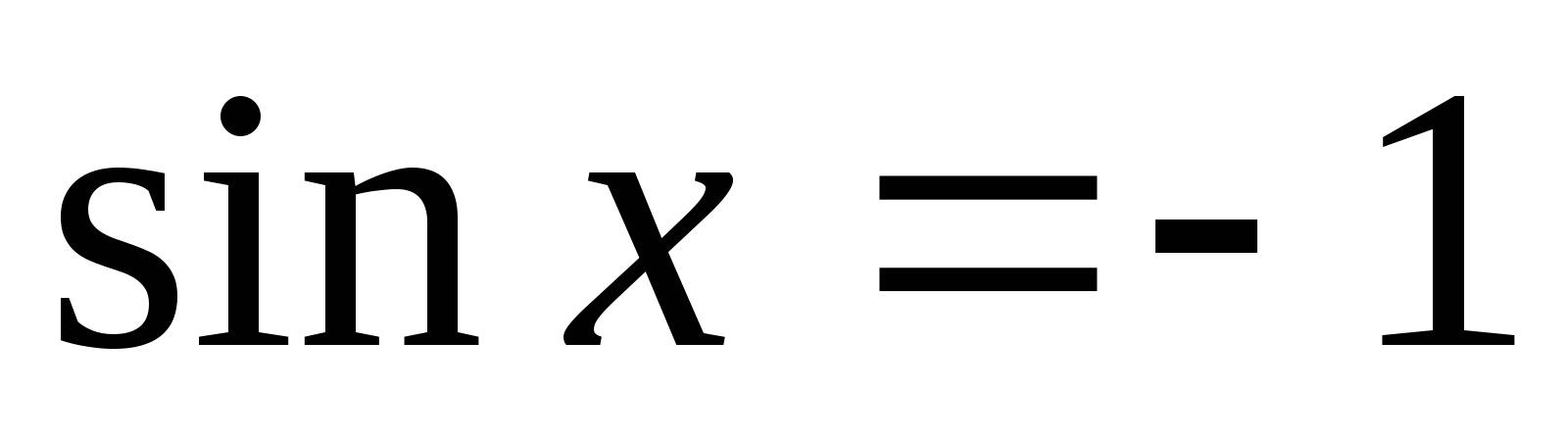Каким будет решение уравнения
?
-
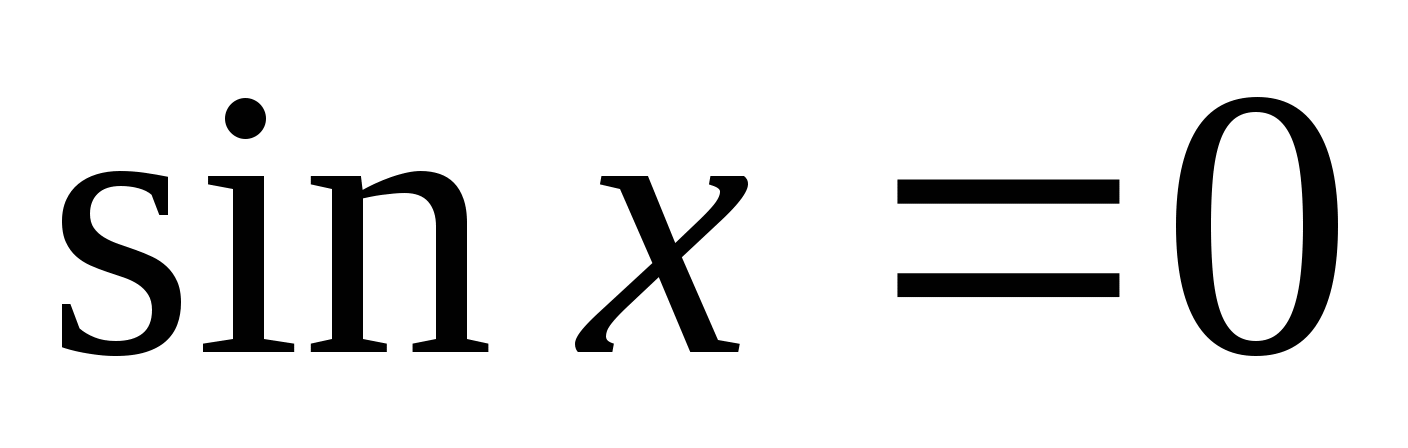Чему равняется
?
-
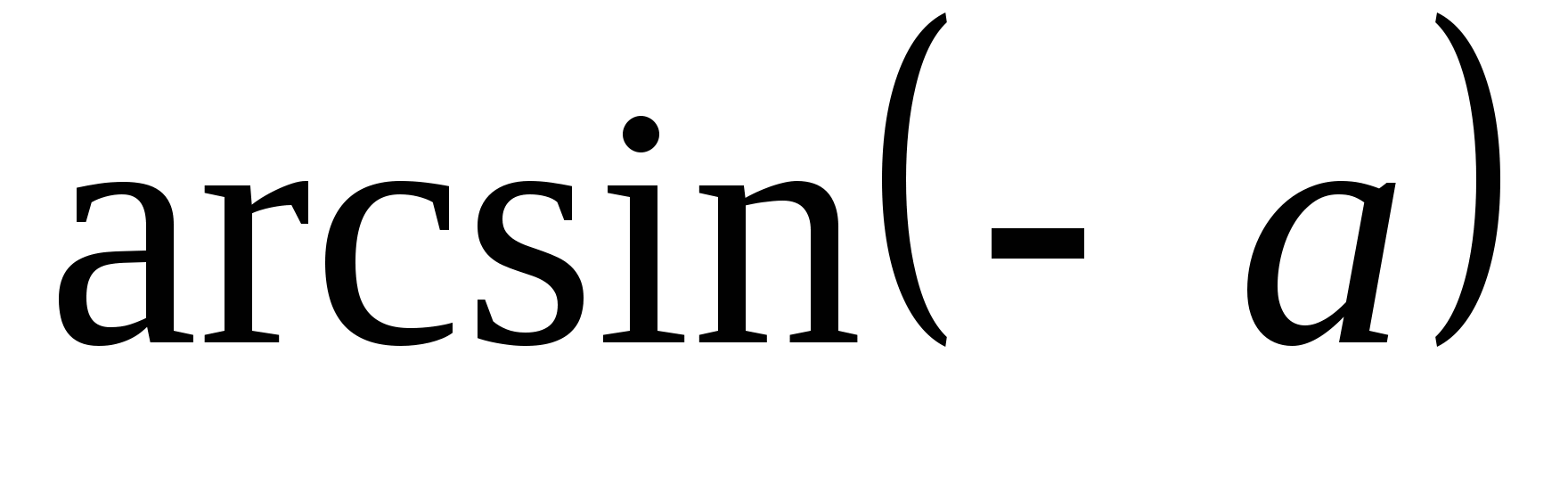В каком промежутке находится
?
-
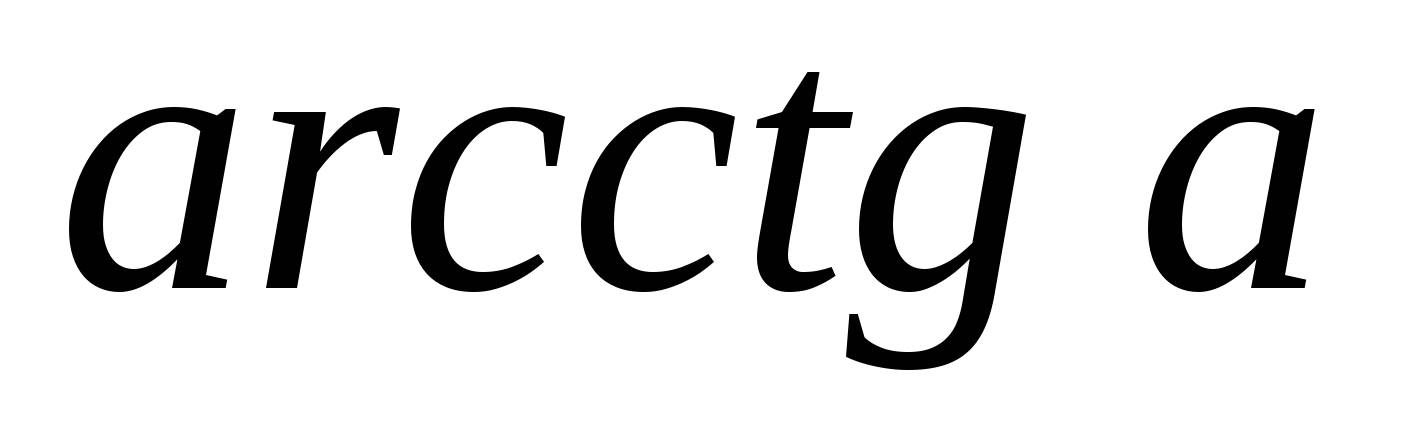Какой формулой выражается решение уравнения
?
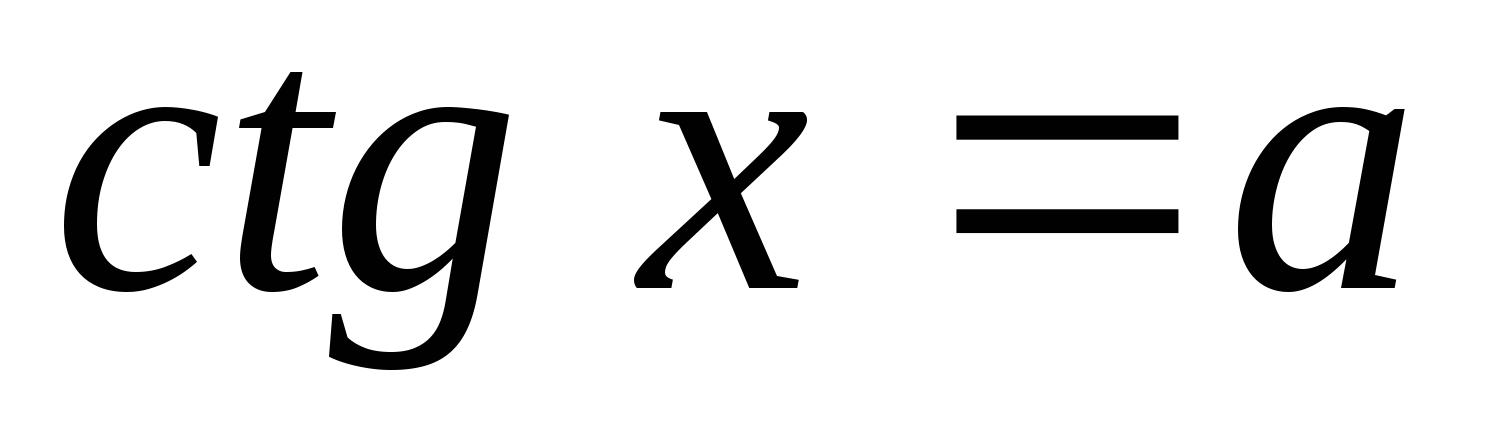На экране - 14слайд (Ответы)
Слайд 15 - оценивание сам работы.
3. Классификация тригонометрических уравнений. Систематизация знаний.
Цель: привести в систему знания по типам и методам решения тригонометрических уравнений.
Слайды 16 - 21 . Составление таблицы по методам решения тригонометрических уравнений.
Учащимся предлагается решить уравнения ( по вариантам) предварительно определив, что это за уравнение и каким методом оно решается. У доски данную работу выполняет один ученик - решение уравнения одного варианта. Учащиеся, выполняющие работу другого варианта, решают уравнение на листочках.
В а р и а н т 1.
В а р и а н т 2.
1) Уравнения сводимые к алгебраическим. Слайд 16
2) Разложение на множители. Слайд 17
3) Введение новой переменной. Слайд 18
4) Введение вспомогательного аргумента. Слайд 19*
5) Уравнения решаемые с помощью формул сложения.Слайд 20
6)Применение формул понижения степени.
Решение
c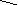
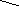os2x
- sin2x+ sin2x+ sinx- ¼ = 0
1- sin2x+ sinx- ¼ =0
sin2x- sinx- ¾ =0
[sinx=t]
t 2- t-¾ =0
4 t 2-4 t- 3=0
D=64
t 1 = 3/2 t2= - ½
s
inx=
3/2 sinx= - ½
решений нет x= -π/6 +2πn n€Z
x= 7π/6 + 2πk k€Z
Ответ: x= -π/6 +2πn n€Z
x= 7π/6 + 2πk k€Z
1)
3 cos2x- 3 sin2x - 5 cosx - 1=0
3 cos2x- 3(1 - cos2x)- 5 cosx - 1=0
6 cos2x-5 cosx - 4=0
[cosx= t]
6 t2-5 t-4=0
D=121
t 1= 4/3 t= - ½
cosx=4/3 cosx= - ½
решений нет x1= 2π/3 + 2πk k€Z
x2= 4π/3 +2πn n€Z
Ответ: x1= 2π/3 + 2πk k€Z
x2= 4π/3 +2πn n€Z
2)
sinx(3sinx - √3 cosx)=0
sinx=0 или 3sinx - √3 cosx=0
x=πk ctgx= - √3/3
k€Z x=5π/6 + πn n€Z
Ответ: x=πk ctgx= √3/3
k€Z
x=5π/6 + πn n€Z
2)
√3сosx(√3cosx - sinx)=0
√3cosx + 1 =0 или ctgx= - √3/3
x=π/2 +πn x=2π/3 + πk k€Z
n€Z
Ответ: x=π/2 +πn x=2π/3 + πk
k€Z
n€Z
3)
3 cos2x-5 sin2x-2 sinx cosx=0
3-5tg2x- 2 tgx =0
5 tg2x+2 tgx - 3=0
[tgx = t]
5t2+2t - 3=0
D=64
t1=0,6 t2=-1
tgx=0,6 tgx=-1
x=arctg 0,6 +πn n€Z x=3π/4 + πk k€Z
Ответ: x=arctg 0,6 +πn n€Z
x=3π/4 + πk k€Z
3)
2
cos2x- sin2x+cosxsinx=0 : sin2x
2сtg2x + сtgx -1=0
[сtgx=t]
2t2+t -1= 0
D=9
t1=
t2= -1
сtgx=
сtgx= -1
x=arcctg
+ πk x=
+ πn
k€Z n€Z
Ответ: x=arcctg
+ πk x=
+ πn
k€Z n€Z
4
)
- 
=1
-x)=1
-x=
+ 2πn
-x= 
-
+2πn
x= - 
+ 2πn n€Z
Ответ:
x= -
+ 2πn n€Z
4)
+
=
+ 
=
+x)
=
+x =
+2πn или
+x = 
+2πk
x= -
+2πn n€Z x=
+2πk k€Z
Ответ: x= -
+2πn n€Z x=
+2πk k€Z
5)
2
= 4cos3x
2
= 4cos3x I :соs x
2
= 4 cos2x
4
cos2x
I :4сosx
=
tgx - 1 =0
x=
+πn n€Z
Ответ: x=
+πn n€Z
5)
-2
=
2
=
2-
=0
(2-1)=
0
или 2-1=
0
x1=πn
=
n€Z x2=
+2πk x3=
+2πm
k€Z m€Z
Ответ: x1=πn n€Z
x2=
+2πk k€Z
x3=
+2πm m€Z
6)
+
+
=0
cos4x (2 cos2x +1)=0
cos4x=0 или 2cos2x = -1
4x =
+πn cos2x = -
x= 
+ 
2x=
+ 2πk или 2x = -
+2πm
n€Z x=
+
k€Z x= -
+ πm m€Z
Ответ: x=
+
n€Z
x=
+
k€Z
x= -
+ πm m€Z
6) 
2сos2x + 2 сos22x +2 сos23x = 3
cos2x + сos4x + сos6x 0
2 cos3x cos4x + cos4x =0
cos4x (2 cos2x +1)=0
cos4x=0 или 2 cos2x = -1
4x =
+πn cos2x = -
x1=
+
n€Z 2x=
+ 2πk или 2x=-+2πk
x2=
+
x3= -
+πm
k€Z m€Z
Ответ: x1=
+
n€Z
x2=
+
k€Z
x3= -
+πm m€Z
введение вспомогательного аргумента
Аsinx +Bcosx=C
cosxcosα+sinxsinα=C
cos(x-α)=C
-
Подведение итогов урока.
-
Домашнее задание:
№ 207 (а,б,в,д) стр. 389 - «Алгебра и начала анализа - 10» Никольский С.М.
8