Система повторения по теме «Отбор корней в тригонометрических уравнениях» для 11 класса

Система повторения по теме «Отбор корней в тригонометрических уравнениях»

учителя МОУ Октябрьская СОШ Радищевского района Ульяновской области

Волик Татьяны Геннадьевны

1. Примерное планирование учебного времени при организации повторения темы «Отбор корней в тригонометрических уравнениях» (проведено на занятиях кружка «Готовимся к ЕГЭ по математике» в 11 классе)

Содержание занятий

Цели занятий

Количество часов

Простейшие тригонометрические уравнения

Повторить общие и частные случаи решения простейших тригонометрических уравнений, опираясь на единичную окружность. Деление множеств корней уравнений sinx=a и cosx=a на две группы с целью упрощения дальнейшего отбора.

1

Виды тригонометрических уравнений и методы их решения

Повторение основных методов решения тригонометрических уравнений: однородных 1 и 2 степеней - делением на степень косинуса; вынесением общего множителя за скобки; применением формул приведения, двойного угла, понижения степени и т.д.

2

Отбор корней при решении тригонометрических уравнений

Повторение алгоритмов отбора корней в тригонометрических уравнениях: по единичной окружности; непосредственным перебором; аналитически с помощью решения неравенств; графически.

2

Проверочная работа по теме «Отбор корней при решении тригонометрических уравнений

Проверка умений решать задания ЕГЭ типа С1.

1

2. План-конспект урока-обобщения по теме

"Отбор корней при решении тригонометрических уравнений"

Цели:

- повторить основные тригонометрические формулы и закрепить их знания в ходе выполнения упражнений;

-развивать вычислительные навыки, логическое мышление, навыки контроля и самоконтроля, умение работать с компьютерной презентацией;

-воспитание ответственного отношения к учебному труду, воли и настойчивости для достижения конечных результатов;

-рассмотреть основные способы отбора корней при решении тригонометрических уравнений:
аналитический, графический, по единичной окружности, перебором целых значений.

Девиз урока: «Не бойтесь формул!

Учитесь владеть этим инструментом

Человеческого гения!

В формулах заключено величие и могущество

разума…»

Марков А.А.

Тип урока: обобщающий

Оборудование: дидактические карточки, мультимедийная аппаратура.

Ход урока

1. Актуализация. Оргмомент.

2. Проверка знаний учащимися тригонометрических формул.

У доски 3 уч-ся записывают тригонометрические формулы:

1 уч.: Формулы, которые устанавливают соотношения между тригонометрическими функциями одного и того же угла.

2 уч.: Формулы сложения.

3 уч.: Формулы суммы и разности и разности тригонометрических функций.

В это время с остальными уч-ся провести устную разминку.

Устная разминка (задания на экране):

1.Какому выражению соответствует значение ?

а) sin30; б) cos; в) tg

2.Выбрать возможный вариант.

а) sin =; б) cos = -2; в) sin = -3,7.

3. Какой из углов является углом II четверти?

а) ; б) -145 ; в)

4.В каких четвертях sin и cos имеют разные знаки?

а) II, III и IV; б) I и III; в) I и IV.

5. Каким выражением можно заменить ?

а) cos ; б) sin ; в) - sin.

3. Работа в парах.

Задание: заполнить 3 столбец таблицы: формулы решения простейших тригонометрических уравнений .

Значения

а

Уравнение

Формулы решения уравнений

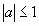
sinx=a

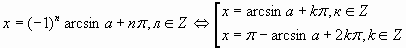
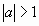
sinx=a

уравнение решений не имеет

а=0

sinx=0

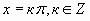
а=1

sinx= 1

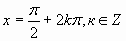
а= -1

sinx= -1

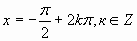
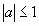
cosx=a

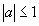
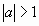
cosx=a

уравнение решений не имеет

а=0

cosx=0

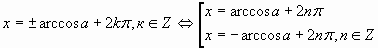
а=1

cosx= 1

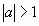
а= -1

cosx= -1

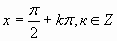
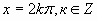
tgx=a

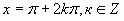
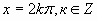
ctgx=a

Учащиеся заполняют 3 столбец таблицы, проверка осуществляется сразу же по слайду на экране.

4. Учащимся предлагается выполнить задание С1:

а) Решите уравнение .

б) Найдите все корни этого уравнения, принадлежащие промежутку .

Решение.

а) (один ученик у доски):
Так как (формула косинуса двойного угла), (формула приведения), то , , (вынесение за скобки общего множителя).

Корни уравнения: , .

б) Работа по группам:

1 группа. Отбор корней по единичной окружности.

Корни уравнения изображаются точками А и В, а корни уравнения - точками C и D, промежуток изображен жирной дугой (см. рис.). В указанном промежутке содержатся три корня уравнения: и .



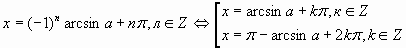
б)Ответ: .

2 группа. Отбор корней по графику.

б) Корни, принадлежащие промежутку, отберем по графику. Прямая (ось ) пересекает график в единственной точке, абсцисса которой принадлежит промежутку.

Прямая пересекает график ровно в двух точках, абсциссы которых принадлежат(см. рис.). Так как период функции равен , то эти абсциссы равны, соответственно, и .



В промежуткесодержатся три корня: .

3 группа. Отбор корней перебором значений.

б) Пусть . Подставляя , получаем . Промежутку принадлежит только .

Пусть . Подставляя , получаем:

.

Промежутку принадлежат только .

Промежутку принадлежат корни: .

4 группа. Отбор корней аналитически с помощью неравенств.

б) Отберем корни, принадлежащие промежутку.

Пусть .. Тогда .

Корень, принадлежащий промежутку: .

Пусть Z.

Тогда .

Корень, принадлежащий промежутку: .

Пусть Z.

Тогда .

Корень, принадлежащий промежутку: .

Промежутку принадлежат корни: .


Отчет групп.

Каждая группа подробно рассказывает о процедуре отбора корней уравнения.

5. Рефлексия.

В каких случаях необходимо производить отбор корней в тригонометрических уравнениях?

Какими способами можно произвести отбор корней?

Какой способ вам показался легче и понятнее? Почему?

6. Домашнее задание.

1. 6 sin²x + cos x 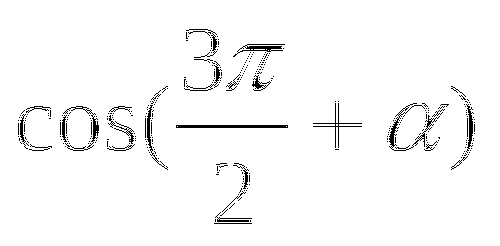если x∊.

2. 4 cos²x + 4cos (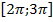если x∊.

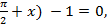3. cos 2x + 3 sin²x = 1,25, если x∊.

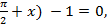4. sin 2x = cos x|cosx|, удовлетворяющие условию x 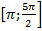[0; 2].

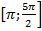3. Проверочная работа по теме «Отбор корней при решении тригонометрических уравнений»

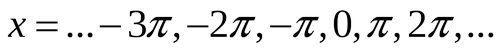
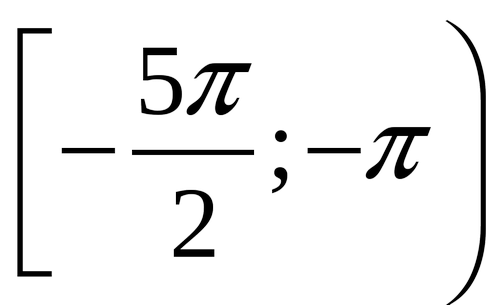
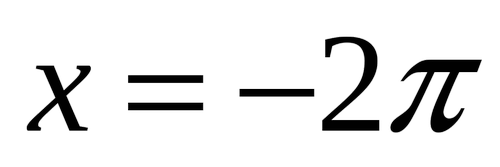
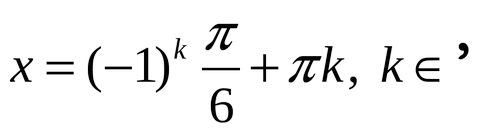
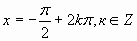
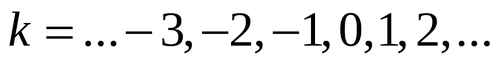
4. Краткий анализ результатов

Количество выполнявших работу

Процент учащихся, допустивших ошибки в №1-№2

Процент учащихся, допустивших ошибки в применении формул приведения

Процент учащихся, допустивших ошибки при решении простейшего тригонометрического уравнения

Процент учащихся, допустивших ошибки при отборе корней

21

20

30

10

40

Результаты показывают, что тема «Отбор корней в тригонометрических уравнениях» представляет большую сложность для многих учащихся, чем весьма оправдано включение задания на эту тему во вторую часть ЕГЭ. Несмотря на это 60% выполнявших работу верно отобрали корни. Из этих учащихся 40 % выбрали способ отбора корней с помощью решения неравенств, 20 % - способ отбора по единичной окружности, графический способ и способ перебора целых значений не выбрал никто.

Выводы: продолжить работу по закреплению навыков отбора корней в тригонометрических уравнениях, применяя при этом различные способы.