Тема урока: Площади.Подготовка к ЕГЭ.

I. Организационный момент

- Приветствие учащихся.

- Психологический настрой для вовлечения в работу по теме.

- Объяснение учащимся правил работы на уроке.

- Мотивация учебной деятельности через осознание учащимися значимости изучаемого материала.

- Сообщение темы, цели и задачи урока, этапов урока.

II. Обобщение и коррекция опорных знаний по теме «Площади плоских фигур»

Учащимся предлагается составить кластер по теме «Площади». На столах у каждого находится лист (формат А4).

На листе делается посередине надпись «Площади». Затем учащимся предлагается слева записать виды плоских фигур и их площадей.

Одному обучающемуся можно предложить это задание выполнить на доске. Затем групповое обсуждение полученного кластера. Корректировка кластера.

III. Деятельность учащихся по самостоятельному применению знаний и умений при решении простейших геометрических задач. Работа устно.

Учащимся предлагается устно решить несколько задач из сборника «Банк открытых заданий ЕГЭ по математике». Работать предлагается в парах или индивидуально. Обязательно необходимо подчеркнуть, что при решении задач необходимо применять формулы площадей, можно пользоваться составленным кластером.

После небольшого обсуждения в парах, ответы вслух. Обсуждение.

Учитель показывает чертеж из сборника, дети говорят ответ.

Вопросы, задаваемые при обсуждении задач:

• Площадь какой фигуры находили?

• Какую формулу применяли?

• Можно ли решить данную задачу другим способом?

Предлагаемые задачи для устной работы:

(количество заданий можно увеличить или уменьшить в зависимости от времени урока)

На клетчатой бумаге с клетками размером 1 см х 1 см изображена фигура. Найдите его площадь.

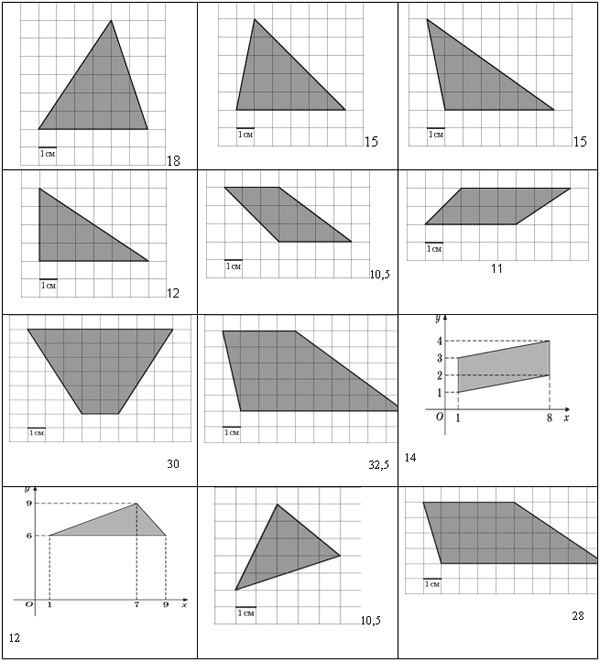
IV. Обобщение и коррекция опорных знаний по теме «Площади многогранников и тел вращения»

Учащимся предлагается составить вторую часть кластера по теме «Площади».

Необходимо записать справа виды многогранников и тел вращения и их площадей.

Предлагается групповое обсуждение, при котором учитель записывает все варианты, которые предлагают учащиеся, учащиеся заполняют свой кластер. Одновременно идет корректировка знаний по теме.

(Приложение 1</<font color="#333333"> - примерный кластер по теме «Площади» и основные формулы площадей. В зависимости от времени урока, учащимся можно предложить заготовку с рисунками или чистый лист, на котором они будут составлять кластер. При этом все чертежи разрешается строить без линейки и карандаша).

V. Деятельность учащихся по самостоятельному применению знаний и умений при решении геометрических задач

Учащимся предлагается решить несколько задач из сборника «Банк открытых заданий ЕГЭ по математике». Работа у доски с записями решений. Учащиеся делают записи в тетради.

Обсуждение.

Вопросы, задаваемые при обсуждении задач:

• Площадь какой фигуры находили?

• Какие формулы применяли?

Задачи из сборника для решения у доски

(количество задач может быть от 3 до 10 в зависимости от времени урока и уровня данного класса)

1. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины.

2. Площадь поверхности куба равна 18. Найдите его диагональ.

3. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота 10.

4. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 10.

5. Правильная четырехугольная призма описана около цилиндра, радиус основания и высота которого равны 1. Найдите площадь боковой поверхности призмы.

6. Через среднюю линию основания треугольной призмы, площадь боковой поверхности которой равна 24, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.

7. Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.

8. Найдите площадь боковой поверхности правильной треугольной призмы, описанной около цилиндра, радиус основания которого равен v3, а высота равна 2.

9. Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды.

VI. Деятельность учащихся по самостоятельному применению знаний и умений при решении геометрических задач практического содержания.

Учащимся предлагается решить практическую задачу.

Задача: Определить площадь поверхности тетрапакета для молока (или сока)

• Закрепить практические навыки вычисления площади поверхности многогранников, формирование умений у учащихся вести исследовательскую работу;

• Определить количество картона, необходимое для изготовления тетрапакетов различной формы.

• Выяснить экономическую выгоду.

Ход работы:

• Определить основные формулы для работы

• Измерить размеры тетрапакетов

• Сделать необходимые вычисления и заполнить таблицу

Таблица 1. Определение площади поверхности тетрапакета, имеющего форму прямоугольного параллелепипеда (вместимость 0,2 литра)