ОКРУЖНОЙ ЭТАП РЕГИОНАЛЬНОЙ

НАУЧНОЙ КОНФЕРЕНЦИИОБУЧАЮЩИХСЯ

Государственное бюджетное образовательное учреждение

Самарской области

средняя общеобразовательная школа

п.г.т. Мирный муниципального района Красноярский

Самарской области

СЕКЦИЯ «Математика»

Справедливая чаша

Автор:

Клементьев Тимофей, учащийся 5 класса

ГБОУ СОШ п.г.т. Мирный

Научный руководитель:

Алексашина И.В.,

учитель математики

ГБОУ СОШ п.г.т. Мирный

Красный Яр, 2016 г.

Структура научно-исследовательской работы

Лучший способ изучить что-либо -

это открыть самому.

Д. Пойа

Введение

Однажды я увидел, как учитель математики Ирина Викторовна показывает своему классу привезённый с греческого острова Крит сувенир, который называется «Справедливая чаша». Этим предметом нельзя было не заинтересоваться. Чаша с виду напоминает керамическую кружку или бокал для питья. Учитель попросил ученика налить немного воды в чашу и выпить её - ничего необычного. Потом второй ученик налил воды побольше, и тут произошла удивительная вещь - вода стала выливаться прямо из дна чаши. Оказывается, это была не простая кружка, а хитрая чаша Пифагора. У меня возникло много вопросов, в том числе: почему вода не вытекла из чаши в первый раз, а во второй раз стала вытекать. Как такое может быть?

Найти ответ на возникшие вопросы и узнать: это только остроумный сувенир или нечто большее, помогла мне исследовательская работа.

Тема моей исследовательской работы - «Справедливая чаша» - выбрана не случайно.

Актуальность. В природе и в быту мы часто сталкиваемся с явлениями и современными предметами, основанными на уникальном изобретении Пифагора Самосского - Справедливая чаша.

Проблема исследования: отсутствие знаний по данной теме.

Цель работы: научиться производить расчеты, позволяющие выяснить особенности функционирования Справедливой чаши.

Объект исследования - Справедливая чаша, предметом исследования является современная область применения устройства Справедливой чаши.

Гипотеза. Если налить полную чашу, то вытечет тот объём жидкости, который превышает определённую отметку. Чаша Справедливости уберёт только лишнее.

Задачи исследования:

1. Изучить научную литературу по теме исследования.

2. Выяснить, кто изобрёл Справедливую чашу?

3. Почему она так называется?

4. Рассмотреть особенности устройства чаши.

5. Изучить приёмы вычисления объёмов двух разных по размеру чаш.

6. Выявить зависимость объёма жидкости от размера чаши.

7. Рассчитать объём жидкости в чашах по контрольную линию.

8. Изготовить чашу в домашних условиях.

9. Определить области современного применения устройства.

В процессе работы были использованы следующие методы:

• наблюдение;

• прогнозирование;

• сравнение;

• анализ;

• эксперимент;

• сбор и обобщение информации.

Теоретическая значимость исследовательской работы состоит в сборе информации об открытии Пифагора и современной области применения данного изобретения.

Практическая значимость. Знакомство окружающих людей с легендами о Справедливой чаше и принципом её работы. Полученные знания об изобретениях, устроенных по принципу Пифагоровой чаши, позволяют широко применять их в современной жизни.

Глава I. Подготовительный этап. Из истории

1.1. Поэтапный план работы

1.1.1. Наметить план работы

1. Сформулировать проблему.

2. Выдвинуть гипотезу.

3. Определить цель, задачи, объект исследования.

4. Предположить результат.

5. Наметить этапы работы.

1.1.2. Информационный этап

Цель: сбор информации.

Задачи:

1. Узнать, что собой представляет Справедливая чаша.

2. Изучить научную литературу по теме исследования.

3. Определить области современного применения устройства.

1.1.3. Практический этап

Цель: произвести все измерения и выполнить расчёты.

Задачи:

1. Рассмотреть особенности устройства чаши.

2. Изучить приёмы вычисления объёмов двух разных по размеру чаш.

3. Выявить зависимость объёма жидкости от размера чаши.

4. Рассчитать объём жидкости в чашах по контрольную линию.

5. Изготовить чашу в домашних условиях.

1.1.4. Оформительский этап

Цель: оформление собранной информации.

Задачи:

1. Оформить портфолио исследовательской работы.

2. Подготовить презентацию.

1.2. Из истории

1.2.1. Кто изобрёл Справедливую чашу?

Справедливая чаша является одним из уникальных изобретений философа, математика, мистика и политика Пифагора Самосского.

Справедливая чаша известна также как Кружка жадности, Чаша умеренности или Стакан Пифагора, кружка Пифагора, Чаша Пифагора, Кубок Пифагора. Чаша Пифагора - это кубок, сосуд для напитков и в то же время игрушка, тренирующая вашу внимательность и чувство меры. По-гречески чашу Пифагора называют Πυθαγόρειο κούπα (ПифагОриокУпа), что переводится как кружка, чашка или кубок Пифагора.

Изучение специальной литературы позволило выяснить, что учёным, придумавшим такую оригинальную чашу, был Пифагор Самосский - древнегреческий математик, философ и политик, основатель пифагореизма, известный нам по учебникам геометрии. Пифагор появился на свет в 570 году до н. э. на острове Самос (Греция). Отец, Мнесарх, был по разным версиям или камнерезом, или богатым купцом. Имя Пифагор означает «тот, кого предсказала Пифия»: рождение ребенка, согласно легенде, было предсказано Пифией в Дельфах. Историю жизни Пифагора трудно отделить от легенд, представляющих его в качестве совершенного мудреца и великого посвящённого во все таинства греков и варваров. Ещё Геродот называл его «величайшим эллинским мудрецом».

Умер в 495 году до нашей эры в г. Метапонт (древнегреческий город-колония в Италии).

Интересные факты из жизни Пифагора

• Пифагор - это на самом деле прозвище, а не имя.

• Первая прочитанная лекция привлекла к Пифагору сразу 2 000 учеников. Вскоре они объединились вокруг учителя вместе с семьями.

• Увлекался спортом, побеждал в кулачном бою на Олимпийских играх.

• Придумал специальную кружку, которая вынуждала пить только в ограниченных количествах. Сегодня она продается на Родосе, Самосе и Крите как сувенир.

• Письменных работ Пифагора не осталось. О его достижениях можно судить только по устным преданиям.

• Имел хорошее образование, играл на лире, интересовался поэзией, читал Гомера.

Основные достижения Пифагора

• Как религиозный новатор, Пифагор создал тайное общество, целью которого было очищение души и тела. Пифагор считал, что душа человека после смерти переселяется в других живых существ до тех пор, пока не искупит грехов и не вернется на небо.

• Учение Пифагора поспособствовало развитию физики, математики, географии, астрономии.

• Современные исследователи считают Пифагора выдающимся античным космологом и математиком, хотя авторы древности этого не подтверждают. Пожалуй, самое известное достижение Пифагора - теорема, согласно которой квадрат гипотенузы прямоугольного треугольника равняется сумме квадратов катетов.

• Согласно некоторым античным авторам, Пифагор написал целый ряд книг. Тем не менее, цитат из них не встречено.

1.2.2. Почему Справедливая чаша получила такое название?

Википедия. Кружка Пифагора (или кружка жадности) - специальный сосуд, придуманный Пифагором. Заставляет человека пить в умеренных количествах. Позволяет человеку заполнить чашу вином только до определенного уровня. Если человек заполняет кружку только до определенного уровня, он может пить.

Если он заполняет выше, то содержимое выливается.

Разные версии происхождения Справедливой чаши

Первая версия. Сосуд, придуманный Пифагором, отличается своим внешним видом и конструкцией и, что важно, назначением. В исторических документах нашли упоминание о том, что Пифагор решил придумать чашу, которая бы отмеряла определенное количество жидкости для того, чтобы уровнять всех рабов в количестве употребляемой воды.

В то время на Самосе были проблемы с питьевой водой, и людям приходилось экономить. Философ считал, что таким образом людям будет проще себя ограничить. Суть чаши Пифагора заключается в том, что важно соблюсти меру при ее наполнении. Человек может без труда наполнить чашу до определенного уровня, если же он превышен, то содержимое сосуда начинает выливаться наружу, тем самым контролируя количество жидкости внутри.

По второй версии чашу Пифагора активно использовали для того, чтобы ограничить рабов в потреблении вина. В Древнем мире знать пила изысканное разбавленное вино, а низшие слои населения крепкие виды напитка. Чтобы рабы сильно не пьянели, им было предписано пить из чаши Пифагора.

Пифагор сделал такую необычную кружку не столько для того, чтобы его ученики не перебрали вина, сколько для того, чтобы научить их чувству меры во всех областях жизни.

Пифагор называл свой кубок чашкой закона, поскольку принцип действия чаши отражал основные принципы права - когда мера была превышена, все достигнутое ранее пропадало, терялось, как и вино из этого сосуда Пифагора.

Пифагор противопоставлял чувство меры гордыне и хотел, чтобы люди освобождались от этого плохого качества, которое мешает им жить в гармонии и равновесии. А чашка Пифагора служила тренажером, игрушкой для приобретения чувства меры.

1.2.3. Как пользоваться Справедливой чашей?

Внутренняя часть чаши Пифагора - золотистый ободок - это контрольная линия. За неё переливать нельзя, иначе - все вытечет!

Выводы по первой главе:

В первой главе я изучил материал:

1. о Пифагоре Самосском,

2. об истории хитрой чаши великого ученого,

3. об идее ее изобретения.

Глава II. Практический этап

2.1. Особенности устройства чаши

Справедливая чаша в разрезе

Почему жидкость не остаётся в чаше, если её налить выше уровня? Из энциклопедий «Научные эксперименты дома. Энциклопедия для детей» и «Простая наука» я узнал, что в этом столбике, есть еще один, внутренний столбик (он нам не виден) с дырочкой на вершине. Он чуть поменьше и пониже основного - внешнего столбика. Пространство между внешним и внутренним столбиком заполняется жидкостью. То есть вода омывает внутренний столбик со всех сторон и движется к его вершине.

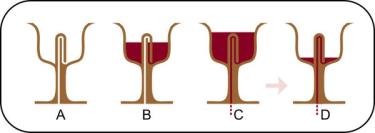
Как только уровень воды поднялся до верха внутреннего столбика, вода начинает выливаться, утекая в отверстие, которое находится в ножке чаши. Верх внутреннего столбика находится на том же уровне, что и контрольная линия. Это устройство работает по принципу сообщающихся сосудов, основанному на законах физики. Сообщающиеся сосуды - это сосуды, соединенные ниже

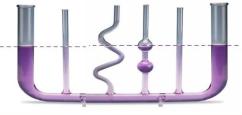
поверхности жидкости, так что жидкость может перетекать из одного сосуда в

другой. А чаша разделена центральным столбиком на два таких сосуда. Это

эффект сифона.

2.2. Расчёты

2.2.1. Расчёт объёма полной чаши

Я решил сравнить чаши. Одинаковые ли у них объёмы, одинаковое ли количество воды вытечет? Как это зависит от объёма воды в чаше? Вытечет вода полностью или только до контрольной линии?

Я знал, как найти объём куба и параллелепипеда. А как высчитать объём чаши, я не знал. Оказывается, можно воспользоваться мерным стаканчиком, но не всегда он есть под рукой. Пришлось найти кроме этого способа и другой: с помощью формулы, которую мы ещё не изучали. Объём можно найти, используя такие величины, как радиус и высота. А вот что такое π - я не знал.

π 3,14 или π

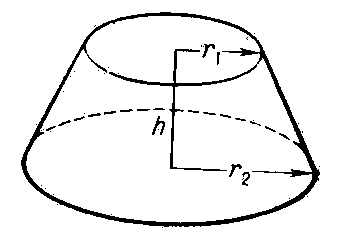
• Высота двух чаш разная. Точно высоту и объём чаш высчитать сложно, так как они неправильной формы и находятся на ножках. Я воспользовался пластмассовым стаканом. Налил воду в первую чашу, предварительно закрыв отверстие в ножке чаши, чтобы вода не вытекала. Затем перелил воду в стакан, который имел геометрическую форму усечённого конуса. Задача состояла в том, чтобы высчитать объём двух разных чаш. Учитель мне подсказал, что формулу можно найти в учебнике геометрии за 10 - 11 классы. Я нашел её.

• Измерил высоту стакана и высчитал радиусы. Чтобы найти высоту стакана, я поставил его на картон и сверху на стакан положил такой же. Расстояние между ними и будет высота стакана. Высоту жидкости в стакане можно измерить и более простым способом: поставив линейку от начала измерения (от нуля) в стакан. Посмотреть уровень воды по линейке, это и будет высота жидкости в стакане. Высота самого стакана h = 6см = 60 мм.

• Чтобы найти радиусы, я поставил стакан на бумагу и обвёл дно. Затем, перевернув стакан вверх дном, также обвёл верх стакана. Не всегда так можно определить нужные длину окружности и радиус. Можно измерить длину окружности, используя нитку. Для этого надо «опоясать» стакан ниткой, а потом измерить этот «поясок», распрямив его. Длина нитки будет приближенно равна длине окружности на нужной высоте стакана. (Приложение 1)

Я нашел длину окружности и из формулы C = 2πr вычислил радиус

r = С : 2π. Получилось, что d₁ = 5 см 6 мм = 56 мм, а d₂ = 7 см 6 мм = 76 мм. Значит,

r ₁ = d : 2, т.е. r₁ = 28мм, r₂ = 38 мм.

Подставим в формулу:

V₁ = () = 62,8 (784 + 1444 + 1064) =

62,83292 = 206738 мм³207см³ 200 см³

1 л = 1 дм³ = 1000 см³

1 л = 1000 мл

1см³ = 1 мл

V₁200 см³ 200 мл

h = 5 см 3 мм = 53 мм

d₁ = 5 см 6 мм = 56 мм, а d₂ = 7 см 2 мм = 72 мм.

Значит, r₁ = d : 2, т.е. r₁ = 28мм, r₂ = 36 мм.

Подставим в формулу:

V₂ = ()55,47 (784 + 1296 + 1008)

55,47171291 мм³ 171 см³ 170 см³

V₂170 см³ 170 мл

Вывод: таким образом, выяснилось, что объём чаш разный.

V₁ = 200 мл; V₂ = 170 мл.

Объём первой чаши на 30 мл больше второй.

2.2.2. Расчёт объёма жидкости в чаше по контрольную линию

По аналогии найдём объём в чашах по контрольную линию.

Высота жидкости в стакане h = 3 см 4 мм = 34 мм

d₁ = 5 см 6 мм = 36 мм, а d₂ = 6 см 8 мм = 68 мм.

Значит, r₁ = d : 2, т.е. r₁ = 28мм, r₂ = 34 мм.

Подставим в формулу:

V₁ = () 35,6 (784 + 1156 + 952)

35,6102955 мм³ 103см³ 100 см³

V₁ 100 см³ 100 мл

h = 3 см 3 мм = 33 мм

d₁ = 5 см 6 мм = 36 мм, а d₂ = 6 см 6 мм = 66 мм.

Значит, r₁ = d : 2, т.е. r₁ = 28мм, r₂ = 33 мм.

Подставим в формулу:

V₂ = ()34,54 (784 + 1089 + 924)

34,5496608 мм³ 97 см³ 97 см³

V₂ 97 см³ 97 мл

Таким образом, объём воды до контрольной линии так же разный.

V₁ = 100 мл; V₂ = 97 мл. Объём первой чаши на 33 мл больше второй.

Вывод. Если в первую чашу налить по контрольную линию 100 мл и более, то жидкость вытечет. Несмотря на то, что полная чаша имеет объём 200 мл, столько жидкости в неё налить невозможно: она, превысив контрольную линию, начнёт вытекать. Со второй чашей произойдёт тоже, если в чашу налить по контрольную линию 97 мл и более, то жидкость вытечет, несмотря на то, что полная чаша имеет объём 170 мл. Справедливая чаша хитра! Действительно, она учит быть внимательным, воспитывает чувство меры.

2.3. Изготовление чаши (сифона) в домашних условиях

Можно ли в домашних условиях сделать чашу?

Для работы нужны:

• маленький пластиковый стакан;

• сосуд с водой;

• изогнутая трубочка для коктейля;

• ножницы;

• кусочек пластилина;

• вспомогательные емкости для воды.

Время работы 10 минут.

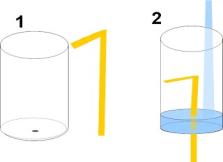
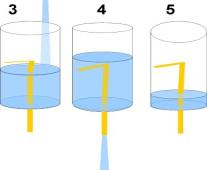
(Приложение 1)

1. В дне стаканчика ножницами я сделал маленькое отверстие, в которое с усилием вставляем соломинку. Загерметизируем пластилином. Изогнутый конец соломинки должен почти касаться дна (на рисунке это неточно отражено), но не должен упираться в дно или стенку.

2. Начинаю наливать в стакан воду из сосуда с водой. Делаю это над вспомогательной ёмкостью.

3. Довольно долго ничего не происходит.

4. Но как только вода покрывает изогнутое колено соломинки полностью, из нее начинает активно вытекать жидкость… и вытекает практически полностью.

Именно такая конструкция называется сифоном.

В практической части показали, как просто собрать такое устройство.

2.4. Определить области современного применения устройства

Знаменитый греческий философ и математик Пифагор изобрёл особую чашу. Пифагор называл свой кубок чашей закона, мы называем её Справедливой чашей. Главная мысль учения Пифагора - научись владеть собой и чувствуй меру.

Принцип действия чаши заключается в работе сифона, который спрятан во внешнем столбике. Оказывается, эффект сифона мы можем наблюдать в быту.

Владельцы аквариумов при сливе воды пользуются шлангом как сифоном. Виноделы, собираясь отведать вина в погребе, тоже наливают его из бочки через сифон. С помощью шланга можно опустошить любой сосуд, главное - чтобы свободный конец свисал ниже уровня жидкости в сосуде.

Сифон (от древнегреческого слова «трубка») - изогнутая трубка с коленами разной длины, по которой жидкость поступает из сосуда с более высоким уровнем в сосуд с более низким уровнем жидкости. Для обеспечения работоспособности сифон необходимо предварительно заполнить жидкостью.

Оглянемся вокруг. В природе тоже встречаются «природные сифоны». Это гейзеры и термальные источники.

Гейзеры парка Йелоустоун

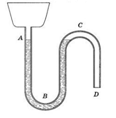
Кроме того, сифоном называют прибор, представляющий собой сосуд для газированных напитков, имеющий трубку с краном, расположенным наверху ее, доходящую практически до самого дна.

Этот сифон представляет собой сосуд с герметически закрывающейся крышкой. Сначала сифон наполняют водой. Затем в крышку сосуда вставляют баллончик с углекислым газом, специальное устройство прокалывает пробку газового баллончика, и газ из баллончика начинает поступать в сосуд. Частично газ растворяется в жидкости, а не растворившийся газ создает в сосуде избыточное давление (больше атмосферного), что заставляет жидкость при открытом кране вытекать из сосуда.

В своем доме мы видим сифоны каждый день, а иногда и используем их, но уже в другом качестве. Сифоны или водяные (гидравлические) затворы используются, например, в наших квартирах как обязательная часть сантехнического оборудования. Они препятствуют проникновению в квартиру запахов из канализационной системы. Сифоны подключаются на выходе ванны или раковины, как дополнительное оборудование, а в унитазе роль сифона выполняет изгиб корпуса, т.е. изгиб канализационного слива в основании унитаза.

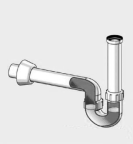
Гидравлический затвор сифона всегда должен быть заполнен водой, и именно этот слой воды не дает проникать посторонним запахам в жилое помещение. Когда еще используется сифон?

Бывают случаи, когда у владельца машины заканчивается бензин на середине пути. Что делает водитель? Он просит у проезжающего мимо автомобилиста немного бензина. А у того бензин только в бензобаке. Как поделиться? Для этого нужна резиновая трубка. Трубка погружается в бензобак, где она заполняется бензином. Верхний конец трубки плотно закрывается пальцем, быстро вынимается и опускается в ведро, стоящее ниже уровня бензина в бензобаке.

Сифон "в чести" и у виноделов, где применяется для разлива вина из огромных бочек в бутылки. Большие бочки не поднять и не опрокинуть для переливания вина, а если внизу бочки сделать кран, то в бутылки попадет осадок со дна. Здесь удобнее использовать сифон.

Сифоны используют и в технике, например, в нефтяных трубопроводах, по которым самотеком движется жидкость, при пересечении ими холмов и других возвышенностей, это позволяет избежать сильного углубления труб или рытья тоннелей. Такой сифон - это большая изогнутая металлическая или бетонная труба, опущенная концами в основную трубу с нефтью по обеим сторонам холма и имеющая вверху вентиль для выкачивания скапливающегося воздуха.

Также принцип сифона издавна использовали в водяных часах. С помощью такого автоматического устройства запросто можно было отмерять равные промежутки времени.

Выводы по второй главе:

1. В своей исследовательской работе я изучил принцип работы Справедливой чаши.

2. Выполнил вычисления объёмов двух разных по размеру чаш и выявил зависимость объёма жидкости от размера чаши.

3. Рассчитал объём жидкости в чашах по контрольную линию.

4. Основываясь на принципе работы сифона, я смог изготовить чашу.

5. Узнал, что такое сифон и как он работает, где в современном, окружающем меня мире, можно пронаблюдать принцип работы сифонов.

Заключение

Исследовательской работой заниматься мне было интересно, потому что она связана с практической деятельностью. Хочется многое в жизни узнать, рассказать одноклассникам, родителям, знакомым. Ведь многие люди даже не слышали о такой чаше Пифагора (Справедливой чаше). Работая над объектом исследования, я узнал, что математика очень тесно связана и с другой наукой -физикой. Я с большим интересом знакомился с новой информацией, ставил различные опыты и производил расчёты. В итоге получил огромное удовлетворение от результатов выполненной мною работы.

Я справился с намеченными задачами и достиг поставленной цели. Проведя эксперименты и проанализировав результаты, я пришёл к следующему выводу: если в чашу налить жидкость по контрольную линию и более, то вода вытечет полностью. Таким образом, гипотеза моя не подтвердилась. В этой чаше справедливости больше, чем я ожидал. Жадность, как всегда, будет наказана. Справедливая чаша хитра! Действительно, она учит быть внимательным, воспитывает чувство меры.

Работая над проблемой моего исследования, я научился

• самостоятельно добывать знания по математики, геометрии и физике, разбирая темы, которые мы ещё не изучали;

• производить сложные вычисления;

• пользоваться новыми математическими сложными формулами;

• находить объём усеченного конуса;

• проводить опыты;

• делать своими руками сифон;

• использовать Интернет-ресурсы и специализированную литературу для поиска материала.

Выполняя работу, я приобрел теоретические знания и практические навыки. Убедился, что математика и физика в жизни пригодятся, их надо изучать!

Список источников

1. Геккер Й. «Увлекательные опыты. Простая наука для детей» (книга четвёртая - измерения) - Москва, Эксмо, 2014. - 60 с.

2. Геометрия, 10-11: учеб. для общеобразоват. учреждений : базовый и профил. уровни / Л.С Атанасян, В.Ф. Бутузов, С.Б. Кадомцев и др. -16-е изд. - М. : Просвещение, 2010. - 256 с.

3. Кустова Т.Н. «Научные эксперименты дома. Энциклопедия для детей» - Москва: Эксмо, 2011. - 192с.

4. Математика.5 класс: учеб. для общеобразоват. учреждений / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. - 26-е изд., стер. - М. : Мнемозина, 2012. - 288с. : ил.

5. Математика.6 класс: учеб. для общеобразоват. учреждений / Н. Я. Виленкин, В. И. Жохов, А. С. Чесноков, С. И. Шварцбурд. - 24-е изд., стер. - М. : Мнемозина, 2012. - 288с. : ил.Физика. 7 кл. : для общеобразоват. учреждений / А.В. Перышкин, Е.М. Гутник.- 12-е изд., стереотип. - М.: Дрофа, 2011.

6. Электронный ресурс. Кружка Пифагора. Википедия. Режим доступа: https://ru.wikipedia.org/wiki/Кружка_Пифагора

7. Электронный ресурс. Режим доступа: FunFacts.ru: энциклопедия фактов. Интересные факты обо всем на свете.

   funfacts.ru/interesnye-fakty-biografii/293-interesnye-fakty-o-pifagore.html

8. Электронный ресурс. Чаша Пифагора - Наука детям. Режим доступа:

virtuallab.by/news/chasha_pifagora/2014-04-20-51</</p>

Приложение 1

1. Измерение длины окружности с помощью нитки и линейки

2. Изготовление сифона по принципу Справедливой чаши