Олимпиадные задания по математике

Олимпиадные задания по математике 10-11 класс.

1. При каких значениях параметра m уравнение

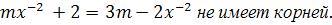
2. Из вершины острого угла прямоугольного треугольника проведена биссектриса, которая разделила противоположный катет на отрезки а = 4 см, b = 5 см. Вычислите площадь треугольника.

3. Путь из села в город таков: сначала 15 км в гору, потом 6 км с горы. Велосипедист едет без остановок в гору с одной постоянной скоростью, с горы - с другой. В один конец он ехал 3,1 ч, обратно 2,5 ч. Какова скорость велосипедиста в гору и с горы?

4. Постройте эскиз графика функции:.

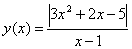5. Найдите все значения числового параметра а, при которых корни уравнения 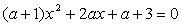положительны.

6. М. В. Ломоносов тратил одну денежку на хлеб и квас. Когда цены выросли на 20%, на ту же денежку он приобретал полхлеба и квас. Хватит ли той же денежки ему хотя бы на квас, если цены вырастут еще на 20%?

7. В равнобедренном треугольнике основание равно 8, боковая сторона 5. Вычислите радиусы вписанной и описанной окружностей и расстояние между их центрами.

Критерии оценивания.

10 баллов - Получен правильный ответ. Приведено полное, правильное решение. Все шаги обоснованы и верны.

8 баллов - Получен правильный ответ. Приведено полное, правильное решение. Один из шагов решение пропущен или не обоснован.

6 баллов - Получен правильный ответ. Приведено правильное решение, но не полное. Пропущено несколько шагов решения, или обоснование приведенного решение не точно (с описками, недочетами).

4 балла - Приведено правильное решение, но допущена одна вычислительная ошибка, которая привела к не правильному ответу. Шаги решения приведены.

2 балла - Приведен правильный ответ, без обоснования, или рассмотрен частный случай.

0 баллов - Решение не соответствует ни одному из критериев, перечисленных выше.

Решение.

Задача №1

При каких значениях параметра m уравнение

ешение.

ОДЗ: х

1-й случай. Если 3m-2=0, то m = имеем m + 2 = +2 В этом случае в левой части преобразованного уравнения будет выражение, отличное от нуля при любом х из ОДЗ уравнения, а в правой части - нуль. Следовательно, при m = данное уравнение решений не имеет, то есть m =

2-й случай. 3m-2 . Тогда х² = Так как х≠0, то полученное уравнение не имеет решений тогда и только тогда, когда Решая это неравенство, получим -2m.

Так как в первом случае показано, что m = , также удовлетворяет условию задачи, то получим

Ответ: m∈ [-2; ].

Задача №2.

И

AFз вершины острого угла прямоугольного треугольника проведена биссектриса, которая разделила противоположный катет на отрезки а = 4см, b = 5см. Вычислите площадь треугольника.

Решение. прямой

см, DB = 5см.

Катет СB = 4 + 5 = 9. Используя свойство

биссектрисы угла треугольника:

теореме Пифагора AC ² + CB² = AB^{2 ;}

A

C

D

BC² + 81 = AC² ; 16AC² + 16 81 = 25AC² ;

16 ∙ 81= 9 AC² ; AC = = 12.

S_ABC = AC CB = .

Ответ: 54см²

Задача №3

Путь из села в город таков: сначала 15км в гору, потом 6км с горы. Велосипедист едет без остановок в гору с одной постоянной скоростью, с горы - с другой. В один конец он ехал 3,1ч, обратно 2,5ч. Какова скорость велосипедиста в гору и с горы?

Решение.

Пусть в гору велосипедист ехал со скоростью х км/ч, а с горы - у км/ч. Больше времени заняла дорога с большим подъемом, поэтому + и b = и решим систему уравнений: Она имеет единственное решение

a = , b = . Откуда х = 6, у= 10. Это означает, что скорость велосипедиста в гору 6 км/ч, а с горы 10 км/ч.

Ответ: 6 км/ч, 10 км/ч.

Задача 4. Постройте эскиз графика функции:.





Решение.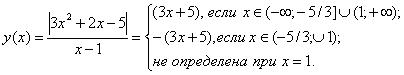

Отсюда график:

Задача 5. Найдите все значения числового параметра а, при которых корни уравнения положительны.





Решение. Если (а+1)=0, то уравнение будет линейным, и его корнем приа=-1 является х=1. Подходит.

Если а?-1, то уравнение будет квадратным. По теореме Виета его корни положительны тогда и только тогда, когда выполняется

.

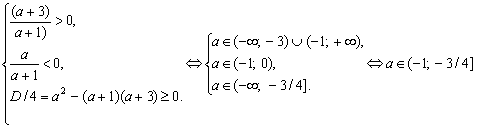С учетом первого случая получаем ответ .



Ответ

Задача 6. М. В. Ломоносов тратил одну денежку на хлеб и квас. Когда цены выросли на 20%, на ту же денежку он приобретал полхлеба и квас. Хватит ли той же денежки ему хотя бы на квас, если цены вырастут еще на 20%?





Решение. Пусть первоначально квас стоил х% от денежки, а хлеб - (100-х)%. После подорожания цен на 20%, получим следующий баланс . Отсюда . При двукратном подорожании цен эта величина увеличится в 1,44 раза и достигнет величины 96%, что меньше стоимости денежки.

Ответ. Хватит.

Задача №7

В равнобедренном треугольнике основание равно 8, боковая сторона 5. Вычислите радиусы вписанной и описанной окружностей и расстояние между их центрами.

Р

Cешение.

О

B- центр описанной окружности,

М

M - центр вписанной окружности,

А

D

DВ = ВС = 5, АС = 8, МD = r, ВО = R.

Найдем площадь и периметр данного

Oтреугольника. S_ABC = ACBD;

ABD = = 3 , S_ABC = = 12

p = 1.

R = =;

OM = OB + DM = R BD + r =

Ответ: ; R = 4 OM = 2,5.