- Учителю
- Рабочая программа по математике для 8 класса
Рабочая программа по математике для 8 класса
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА №4 ГОРОДСКОГО ОКРУГА ГОРОД ВОРОНЕЖ
Рассмотрено Согласовано Утверждаю
на заседании ШМО учителей Зам директора по УВР Директор МБОУ СОШ №4
естественно-математического цикла -------------- Смагина С.М. -------------Черняева В.А.
«--------»-------------- 2014 г. «-----------»---------------2014 г. «--------»-------------- 2014 г.
РАБОЧАЯ ПРОГРАММА
по математике для 8 класса
Смагиной Светланы Михайловны,
учителя математики 1 квалификационной категории
Воронеж 2014
ПОЯСНИТЕЛЬНАЯ ЗАПИСКА
-
Перечень нормативно-правовых документов;
Рабочая программа учителя разрабатывается на основе:
-
федерального компонента государственного образовательного стандарта основного общего образования, утвержденного приказом МО РФ «Об утверждении федерального компонента государственных стандартов начального общего, основного общего и среднего (полного) общего образования от 05. 03. 2004г. № 1089»;
-
санитарно-эпидемиологических требований к условиям и организации обучения в ОУ (утверждены постановлением Главного государственного санитарного врача РФ от 29.12.2010г. № 189)
-
учебного плана МБОУ школа № 4 (федерального и регионального компонента, компонента ОУ);
-
годового учебного календарного графика на текущий учебный год;
-
основной образовательной программы МБОУ СОШ № 4
-
программы общеобразовательных учреждений «Алгебра» (7-9 классы), «Геометрия» (7-9 классы) - М.: Просвещение, 2009 г., составитель: Т.А. Бурмистрова;
-
учебно-методического комплекса.
Описание места учебного предмета, курса в учебном плане
Программа рассчитана на 210 часов в год (6 часов в неделю). Согласно действующему учебному плану для 8 класса предусматривается обучение в объёме 6 часов в неделю (всего за год 210 часов). В данной программе количество часов в неделю по алгебре увеличено по сравнению с федеральным компонентом с 3 часов до 4 часов за счет часов школьного компонента. Рабочая программа соответствует 2 варианту планирования программы общеобразовательных учреждений « Алгебра» 7-9 классы авторов Макарычева Ю.Н. и др. и « Геометрия» 7-9 классы авторов Атанасян Л.С. и другие.
Общие цели образования, с учётом специфики учебного предмета, курса.
Рабочая программа учебного курса по математике для 8 класса составлена на основе Примерной программы основного общего образования по математике, с учетом требований федерального компонента государственного стандарта основного общего образования и в соответствии с базисным учебным планом школы с использованием примерной программы курса алгебры авторов Ю. Н. Макарычев, и др., курса геометрии авторов Л. С. Атанасян и др.(М.: Просвещение,2009 ).
Изучение математики на ступени основного общего образования направлено на достижение следующих целей:
-
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
-
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;
-
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
-
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии.
В ходе освоения содержания курса учащиеся получают возможность:
-
развить представления о числе и роли вычислений в человеческой практике;
-
сформировать практические навыки выполнения устных, письменных, инструментальных вычислений, развить вычислительную культуру;
-
овладеть символическим языком алгебры, выработать формально-оперативные алгебраические умения и научиться применять их к решению математических и нематематических задач;
-
изучить свойства и графики функций, научиться использовать функционально-графические представления для описания и анализа реальных зависимостей;
-
получить представления о статистических закономерностях в реальном мире и о различных способах их изучения, об особенностях выводов и прогнозов, носящих вероятностный характер;
-
развить логическое мышление и речь - умения логически обосновывать суждения, проводить несложные систематизации, приводить примеры и контрпримеры, использовать различные языки математики (словесный, символический, графический) для иллюстрации, интерпретации, аргументации и доказательства.
Геометрия - один из важнейших компонентов математического образования, необходимая для приобретения конкретных знаний о пространстве и практически значимых умений, формирования языка описания объектов окружающего мира, для развития пространственного воображения и интуиции, математической культуры, для эстетического воспитания учащихся. Изучение геометрии вносит вклад в развитие логического мышления, в формирование понятия доказательства.
Изучение математики на ступени основного общего образования направлено на достижение следующих целей:
-
овладение системой математических знаний и умений, необходимых для применения в практической деятельности, изучения смежных дисциплин, продолжения образования;
-
интеллектуальное развитие, формирование качеств личности, необходимых человеку для полноценной жизни в современном обществе, свойственных математической деятельности: ясности и точности мысли, критичности мышления, интуиции, логического мышления, элементов алгоритмической культуры, пространственных представлений, способности к преодолению трудностей;
-
формирование представлений об идеях и методах математики как универсального языка науки и техники, средства моделирования явлений и процессов;
-
воспитание культуры личности, отношения к математике как к части общечеловеческой культуры, играющей особую роль в общественном развитии.
Цели изучения курса 8 класса:
-развивать пространственное мышление и математическую культуру;
-учить ясно и точно излагать свои мысли ;
-формировать качества личности необходимые человеку в повседневной жизни: умение преодолевать трудности ,доводить начатое дело до конца;
-помочь приобрести опыт исследовательской работы.
Задачи курса:
-научить пользоваться геометрическим языком для описания предметов;
-начать изучение многоугольников и их свойств, научить находить их площади;
-ввести теорему Пифагора и научить применять её при решении прямоугольных треугольников;
-ввести тригонометрические понятия синус, косинус и тангенс угла в прямоугольном треугольнике научить применять эти понятия при решении прямоугольных треугольников;
-ввести понятие подобия и признаки подобия треугольников, научить решать задачи на применение признаков подобия;
-ввести понятие вектора , суммы векторов, разности и произведения вектора на число;
-ознакомить с понятием касательной к окружности.
Программой отводится на изучение алгебры 140 часов, геометрии 70 часов в учебный год. Предусмотрено 14 контрольных работ 3 административные контрольные работы.
Учебный материал алгебры и геометрии изучаются блоками.
Данное планирование определяет достаточный объем учебного времени для повышения математических знаний учащихся в среднем звене школы, улучшения усвоения других учебных предметов.
Статистическая линия в 8 классе реализуется в количестве 4 часов
Промежуточная аттестация проводится в форме тестов, самостоятельных, проверочных работ (по 10 - 15 минут) в конце логически законченных блоков учебного материала. Итоговая аттестация предусмотрена в виде административной контрольной работы.
Для реализации рабочей программы используется учебно-методический комплект, включающий:
-
Программы общеобразовательных учреждений. Алгебра 7-9 классы, геометрия 7-9 классы. Составитель Бурмистрова Т.А. - М,.: «Просвещение», 2009.
-
Макарычев Ю. Н., Миндюк Н. Г., Нешков К. И., Суворова С. Б. Алгебра 8: Учебник для общеобразов ательных учреждений. - М.: Просвещение, 2011.
-
Атанасян, В.Ф. Бутузов и др. Геометрия 7 -9: Учебник для общеобразовательных учреждений. - М.: Просвещение, 2011..
Выбор УМК обусловлен особенностями психо-эмоционального состояния обучающихся и уровнем их подготовки. Поэтому УМК является наиболее доступным для обучающихся. Кроме того, данный УМК продолжает линию учебно-методических пособий, соответствующих примерной программе основного общего образования по математике.
Отличительные особенности рабочей программы:
Раздел
Количество часов в примерной программе
Количество часов в рабочей программе
Изменения (с указанием перераспределения тем и часов)
Повторение изученного в 7 классе (алгебра)
0
6
6 ч за счёт школьного компонента
Повторение изученного в 7 классе (геометрия)
0
2
2ч за счет итогового повторения по геометрии
Рациональные дроби
26
30
4 ч за счёт школьного компонента
Квадратные корни
24
26
2 ч за счёт школьного компонента
Квадратные уравнения
24
26
2 ч за счёт школьного компонента
Неравенства
20
21
1 ч за счёт школьного компонента
Степень с целым показателем. Элементы статистики.
13
15
2 ч за счёт школьного компонента
Повторение курса алгебры
12
12
Четырёхугольники
14
14
Площади фигур
14
14
Подобные треугольники
19
19
Окружность
17
17
Повторение курса геометрии. Решение задач
4
2
Резерв
5
6 (4 ч алгебра и 2 часа геометрия)
1 ч за счёт школьного компонента
Итого
192
210
18
ФОРМЫ КОНТРОЛЯ
-
Контрольная работа после изучения отдельного раздела;
-
Самостоятельная работа;
-
Тест;
-
Административная контрольная работа (входная, полугодовая, годовая).
Система проведения уроков условна, однако выделим следующие основные виды уроков:
Урок-лекция. Предполагаются совместные усилия учителя и учеников для решения общей проблемной познавательной задачи. На таком уроке используется демонстрационный материал на компьютере, разработанный учителем или учениками, мультимедийные продукты.
Урок-практикум. На уроке учащиеся работают над различными заданиями в зависимости от своей подготовленности. Виды работ могут быть самыми разными: письменные исследования, решение различных задач, практическое применение различных методов решения задач. Компьютер на таких уроках используется как электронный калькулятор, тренажер устного счета, виртуальная лаборатория, источник справочной информации.
Комбинированный урок предполагает выполнение работ и заданий разного вида.
Урок-игра. На основе игровой деятельности учащиеся познают новое, закрепляют изученное, отрабатывают различные учебные навыки.
Урок решения задач. Вырабатываются у учащихся умения и навыки решения задач на уровне обязательной и возможной подготовке. Любой учащийся может использовать компьютерную информационную базу по методам решения различных задач, по свойствам элементарных функций и т.д.
Урок-тест. Тестирование проводится с целью диагностики пробелов знаний, контроля уровня обученности учащихся, тренировки технике тестирования. Тесты предлагаются как в печатном так и в компьютерном варианте, причем в компьютерном варианте всегда с ограничением времени.
Урок - самостоятельная работа. Предлагаются разные виды самостоятельных работ.
Урок - контрольная работа. Контроль знаний по пройденной теме
Основные виды контроля:
Срезовые работы: входной контроль, промежуточный контроль, итоговый контроль;
Текущий контроль (письменные опросы): контрольные работы, тесты, математические диктанты, самостоятельные работы;
Текущий контроль (устные опросы): собеседование.
Устный опрос - устная форма контроля знаний и умений, используется взаимопроверка, самопроверка по образцу, заслушивание ответа и его оценивание учителем.
Самостоятельная работа - письменная форма контроля, рассчитанная на 5 - 20 мин, применяется для оценивания уровня сформированности знаний и умений по изучаемому вопросу в теме. Самостоятельные работы проводятся в форме тестов по пройденному материалу.
Математический диктант - письменная форма контроля, применяемая для проверки умения правильно понимать и записывать числа, математические термины и понятия.
Контрольная работа - письменная форма контроля знаний, умений и навыков по изучаемой теме, рассчитана на выполнение в течение урока.
Критерии оценки устных индивидуальных и фронтальных ответов.
-
Активность участия.
-
Умение собеседника прочувствовать суть вопроса.
-
Искренность ответов, их развернутость, образность, аргументированность.
-
Самостоятельность.
-
Оригинальность суждений.
В основу критериев оценки учебной деятельности учащихся положены объективность и единый подход. При 5-балльной оценке для всех установлены общедидактические критерии.
Оценка «5» ставится в случае:
-
Знания, понимания, глубины усвоения обучающимся всего объёма программного материала.
-
Умения выделять главные положения в изученном материале, на основании фактов и примеров обобщать, делать выводы, устанавливать межпредметные и внутрипредметные связи, творчески применяет полученные знания в незнакомой ситуации.
-
Отсутствие ошибок и недочётов при воспроизведении изученного материала, при устных ответах устранение отдельных неточностей с помощью дополнительных вопросов учителя, соблюдение культуры письменной и устной речи, правил оформления письменных работ.
Оценка «4»:
-
Знание всего изученного программного материала.
-
Умений выделять главные положения в изученном материале, на основании фактов и примеров обобщать, делать выводы, устанавливать внутрипредметные связи, применять полученные знания на практике.
-
Незначительные (негрубые) ошибки и недочёты при воспроизведении изученного материала, соблюдение основных правил культуры письменной и устной речи, правил оформления письменных работ.
Оценка «3» (уровень представлений, сочетающихся с элементами научных понятий):
-
Знание и усвоение материала на уровне минимальных требований программы, затруднение при самостоятельном воспроизведении, необходимость незначительной помощи преподавателя.
-
Умение работать на уровне воспроизведения, затруднения при ответах на видоизменённые вопросы.
-
Наличие грубой ошибки, нескольких негрубых при воспроизведении изученного материала, незначительное несоблюдение основных правил культуры письменной и устной речи, правил оформления письменных работ.
Оценка «2»:
-
Знание и усвоение материала на уровне ниже минимальных требований программы, отдельные представления об изученном материале.
-
Отсутствие умений работать на уровне воспроизведения, затруднения при ответах на стандартные вопросы.
-
Наличие нескольких грубых ошибок, большого числа негрубых при воспроизведении изученного материала, значительное несоблюдение основных правил культуры письменной и устной речи, правил оформления письменных работ.
-
Ставится за полное незнание изученного материала, отсутствие элементарных умений и навыков.
Учитель может повысить отметку за оригинальный ответ на вопрос или оригинальное решение задачи, которые свидетельствуют о высоком математическом развитии обучающегося; за решение более сложной задачи или ответ на более сложный вопрос, предложенные обучающемуся дополнительно после выполнения им каких-либо других заданий.
Оценка устных ответов обучающихся по математике
Оценка «5» ставится, если ученик:
-
показывает глубокое и полное знание и понимание всего объёма программного материала; полное понимание сущности рассматриваемых понятий, явлений и закономерностей, теорий, взаимосвязей;
-
умеет составить полный и правильный ответ на основе изученного материала; выделять главные положения, самостоятельно подтверждать ответ конкретными примерами, фактами; самостоятельно и аргументировано делать анализ, обобщения, выводы. Устанавливать межпредметные (на основе ранее приобретенных знаний) и внутрипредметные связи, творчески применять полученные знания в незнакомой ситуации. Последовательно, чётко, связно, обоснованно и безошибочно излагать учебный материал; давать ответ в логической последовательности с использованием принятой терминологии; делать собственные выводы; формулировать точное определение и истолкование основных понятий, законов, теорий; при ответе не повторять дословно текст учебника; излагать материал литературным языком; правильно и обстоятельно отвечать на дополнительные вопросы учителя. Самостоятельно и рационально использовать наглядные пособия, справочные материалы, учебник, дополнительную литературу, первоисточники; применять систему условных обозначений при ведении записей, сопровождающих ответ; использование для доказательства выводов из наблюдений и опытов;
-
самостоятельно, уверенно и безошибочно применяет полученные знания в решении проблем на творческом уровне; допускает не более одного недочёта, который легко исправляет по требованию учителя; имеет необходимые навыки работы с приборами, чертежами, схемами и графиками, сопутствующими ответу; записи, сопровождающие ответ, соответствуют требованиям.
Оценка «4» ставится, если ученик:
-
показывает знания всего изученного программного материала. Даёт полный и правильный ответ на основе изученных теорий; незначительные ошибки и недочёты при воспроизведении изученного материала, определения понятий дал неполные, небольшие неточности при использовании научных терминов или в выводах и обобщениях из наблюдений и опытов; материал излагает в определенной логической последовательности, при этом допускает одну негрубую ошибку или не более двух недочетов и может их исправить самостоятельно при требовании или при небольшой помощи преподавателя; в основном усвоил учебный материал; подтверждает ответ конкретными примерами; правильно отвечает на дополнительные вопросы учителя.
-
умеет самостоятельно выделять главные положения в изученном материале; на основании фактов и примеров обобщать, делать выводы, устанавливать внутрипредметные связи. Применять полученные знания на практике в видоизменённой ситуации, соблюдать основные правила культуры устной речи и сопровождающей письменной, использовать научные термины;
-
не обладает достаточным навыком работы со справочной литературой, учебником, первоисточниками (правильно ориентируется, но работает медленно). Допускает негрубые нарушения правил оформления письменных работ.
Оценка «3» ставится, если ученик:
-
усвоил основное содержание учебного материала, имеет пробелы в усвоении материала, не препятствующие дальнейшему усвоению программного материала;
-
материал излагает несистематизированно, фрагментарно, не всегда последовательно;
-
показывает недостаточную сформированность отдельных знаний и умений; выводы и обобщения аргументирует слабо, допускает в них ошибки.
-
допустил ошибки и неточности в использовании научной терминологии, определения понятий дал недостаточно четкие;
-
не использовал в качестве доказательства выводы и обобщения из наблюдений, фактов, опытов или допустил ошибки при их изложении;
-
испытывает затруднения в применении знаний, необходимых для решения задач различных типов, при объяснении конкретных явлений на основе теорий и законов, или в подтверждении конкретных примеров практического применения теорий;
-
отвечает неполно на вопросы учителя (упуская и основное), или воспроизводит содержание текста учебника, но недостаточно понимает отдельные положения, имеющие важное значение в этом тексте;
-
обнаруживает недостаточное понимание отдельных положений при воспроизведении текста учебника (записей, первоисточников) или отвечает неполно на вопросы учителя, допуская одну-две грубые ошибки.
Оценка «2» ставится, если ученик:
-
не усвоил и не раскрыл основное содержание материала;
-
не делает выводов и обобщений.
-
не знает и не понимает значительную или основную часть программного материала в пределах поставленных вопросов;
-
или имеет слабо сформированные и неполные знания и не умеет применять их к решению конкретных вопросов и задач по образцу;
-
или при ответе (на один вопрос) допускает более двух грубых ошибок, которые не может исправить даже при помощи учителя.
-
не может ответить ни на один из поставленных вопросов;
-
полностью не усвоил материал.
Примечание. По окончанию устного ответа учащегося педагогом даётся краткий анализ ответа, объявляется мотивированная оценка. Возможно привлечение других учащихся для анализа ответа, самоанализ, предложение оценки.
Оценка самостоятельных письменных и контрольных работ.
Оценка «5» ставится, если ученик:
-
выполнил работу без ошибок и недочетов;
-
допустил не более одного недочета.
Оценка «4» ставится, если ученик выполнил работу полностью, но допустил в ней:
-
не более одной негрубой ошибки и одного недочета;
-
или не более двух недочетов.
Оценка «3» ставится, если ученик правильно выполнил не менее половины работы или допустил:
-
не более двух грубых ошибок;
-
или не более одной грубой и одной негрубой ошибки и одного недочета;
-
или не более двух-трех негрубых ошибок;
-
или одной негрубой ошибки и трех недочетов;
-
или при отсутствии ошибок, но при наличии четырех-пяти недочетов.
Оценка «2» ставится, если ученик:
-
допустил число ошибок и недочетов превосходящее норму, при которой может быть выставлена оценка «3»;
-
или если правильно выполнил менее половины работы;
-
не приступал к выполнению работы;
-
или правильно выполнил не более 10 % всех заданий.
Примечание.
1) Учитель имеет право поставить ученику оценку выше той, которая предусмотрена нормами, если учеником оригинально выполнена работа.
2) Оценки с анализом доводятся до сведения учащихся, как правило, на последующем уроке, предусматривается работа над ошибками, устранение пробелов.
Общая классификация ошибок.
При оценке знаний, умений и навыков обучающихся следует учитывать все ошибки (грубые и негрубые) и недочёты.
Грубыми считаются ошибки:
-
незнание определения основных понятий, законов, правил, основных положений теории, незнание формул, общепринятых символов обозначений величин, единиц их измерения;
-
незнание наименований единиц измерения;
-
неумение выделить в ответе главное;
-
неумение применять знания, алгоритмы для решения задач;
-
неумение делать выводы и обобщения;
-
неумение читать и строить графики;
-
неумение пользоваться первоисточниками, учебником и справочниками;
-
потеря корня или сохранение постороннего корня;
-
отбрасывание без объяснений одного из них;
-
равнозначные им ошибки;
-
вычислительные ошибки, если они не являются опиской;
-
логические ошибки.
К негрубым ошибкам следует отнести:
-
неточность формулировок, определений, понятий, теорий, вызванная неполнотой охвата основных признаков определяемого понятия или заменой одного - двух из этих признаков второстепенными;
-
неточность графика;
-
нерациональный метод решения задачи или недостаточно продуманный план ответа (нарушение логики, подмена отдельных основных вопросов второстепенными);
-
нерациональные методы работы со справочной и другой литературой;
-
неумение решать задачи, выполнять задания в общем виде.
Недочетами являются:
-
нерациональные приемы вычислений и преобразований;
-
небрежное выполнение записей, чертежей, схем, графиков.
Требования к уровню подготовки учащихся по предмету.
В результате изучения алгебры в 8 классе ученик должен
знать/понимать
-
существо понятия математического доказательства; примеры доказательств;
-
существо понятия алгоритма; примеры алгоритмов;
-
как используются математические формулы, уравнения и неравенства; примеры их применения для решения математических и практических задач;
-
как математически определенные функции могут описывать реальные зависимости; приводить примеры такого описания;
-
как потребности практики привели математическую науку к необходимости расширения понятия числа;
-
вероятностный характер многих закономерностей окружающего мира; примеры статистических закономерностей и выводов;
-
смысл идеализации, позволяющей решать задачи реальной действительности математическими методами, примеры ошибок, возникающих при идеализации.
-
уметь
-
выполнять основные действия со степенями с целыми показателями, с многочленами и с алгебраическими дробями; выполнять разложение многочленов на множители; выполнять тождественные преобразования рациональных выражений;
-
применять свойства арифметических квадратных корней для вычисления значений и преобразований числовых выражений, содержащих квадратные корни;
-
решать линейные, квадратные уравнения и рациональные уравнения, сводящиеся к ним;
-
решать линейные неравенства с одной переменной и их системы;
-
находить значения функции, заданной формулой, таблицей, графиком по ее аргументу; находить значение аргумента по значению функции, заданной графиком или таблицей;
-
определять свойства функции по ее графику; применять графические представления при решении уравнений, систем, неравенств;
-
описывать свойства изученных функций, строить их графики; использовать приобретенные знания и умения в практической деятельности и повседневной жизни для:
-
выполнения расчетов по формулам, составления формул, выражающих зависимости между реальными величинами;
-
нахождения нужной формулы в справочных материалах;
-
моделирования практических ситуаций и исследования построенных моделей с использованием аппарата алгебры;
-
описания зависимостей между физическими величинами соответствующими
В результате изучения геометрии в 8 классе ученик должен
Уметь объяснить, какая фигура называется многоугольником, назвать его элементы; знать, что такое периметр многоугольника, какой многоугольник называется выпуклым; уметь вывести формулу формулами при исследовании несложных практических ситуаций; суммы углов выпуклого многоугольника .
Уметь находить углы многоугольников, их периметры.
Знать определения параллелограмма и трапеции, виды трапеций, формулировки свойств и признаки параллелограмма и равнобедренной трапеции, уметь их
доказывать и применять при решении задач
Уметь выполнять деление отрезка на n равных частей с помощью циркуля и линейки; используя свойства параллелограмма и равнобедренной трапеции уметь доказывать некоторые утверждения.
Уметь выполнять задачи на построение четырехугольников.
Знать определения частных видов параллелограмма: прямоугольника, ромба и квадрата, формулировки их свойств и признаков.
Уметь доказывать изученные теоремы и применять их при решении задач типа 401 - 415.
Знать определения симметричных точек и фигур относительно прямой и точки.
Уметь строить симметричные точки и распознавать фигуры, обладающие осевой симметрией и центральной симметрией.
Знать основные свойства площадей и формулу для вычисления площади прямоугольника. Уметь вывести формулу для вычисления площади прямоугольника
Знать формулы для вычисления площадей параллелограмма, треугольника и трапеции; уметь их доказывать, а также знать теорему об отношении площадей треугольников, имеющих по равному углу, и уметь применять все изученные формулы при решении задач
Уметь применять все изученные формулы при решении задач, в устной форме доказывать теоремы и излагать необходимый теоретический материал.
Знать теорему Пифагора и обратную ей теорему, область применения, пифагоровы тройки. Уметь доказывать теоремы и применять их при решении задач
Знать определения пропорциональных отрезков и подобных треугольников, теорему об отношении подобных треугольников и свойство биссектрисы треугольника.
Уметь определять подобные треугольники, находить неизвестные величины из пропорциональных отношений, применять теорию при решении задач
Знать признаки подобия треугольников, определение пропорциональных отрезков. Уметь доказывать признаки подобия и применять их при решении задач
Знать теоремы о средней линии треугольника, точке пересечения медиан треугольника и пропорциональных отрезках в прямоугольном треугольнике.
Уметь доказывать эти теоремы и применять при решении задач, а также уметь с помощью циркуля и линейки делить отрезок в данном отношении и решать задачи на построение
Знать определения синуса, косинуса и тангенса острого угла прямоугольного треугольника, значения синуса, косинуса и тангенса для углов 30°, 45° и 60°, метрические соотношения. Уметь доказывать основное тригонометрическое тождество, решать задачи
Уметь применять все изученные формулы, значения синуса, косинуса, тангенса, метрические отношения при решении задач
Знать возможные случаи взаимного расположения прямой и окружности, определение касательной, свойство и признак касательной.
Уметь их доказывать и применять при решении задач, выполнять задачи на построение окружностей и касательных, определять отрезки хорд окружностей.
Знать определение центрального и вписанного углов, как определяется градусная мера дуги окружности, теорему о вписанном угле, следствия из нее и теорему о произведении отрезков пересекающихся хорд.
Уметь доказывать эти теоремы и применять при решении задач
Знать теоремы о биссектрисе угла и о серединном перпендикуляре к отрезку, их следствия, а также теорему о пересечении высот треугольника.
Уметь доказывать эти теоремы и применять их при решении задач.
Уметь выполнять построение замечательных точек треугольника.
Знать, какая окружность называется вписанной в многоугольник и какая описанной около многоугольника, теоремы об окружности, вписанной в треугольник, и об окружности, описанной около треугольника, свойства вписанного и описанного четырехугольников.
Уметь доказывать эти теоремы и применять при решении задач, выполнять задачи на построение окружностей и касательных, определять отрезки хорд окружностей.
Знать, какой угол называется центральным и какой вписанным, как определяется градусная мера дуги окружности, теорему о вписанном угле, следствия из нее и теорему о произведении отрезков пересекающихся хорд.
Уметь доказывать эти теоремы и применять при решении задач
Знать теоремы о биссектрисе угла и о серединном перпендикуляре к отрезку, их следствия, а также теорему о пересечении высот треугольника.
Уметь доказывать эти теоремы и применять их при решении задач.
Уметь выполнять построение замечательных точек треугольника.
Знать определения вектора и равных векторов.
Уметь изображать и обозначать векторы, откладывать от данной точки вектор, равный данному, решать задачи
Знать законы сложения векторов, определение разности двух векторов; знать, какой вектор называется противоположным данному; уметь объяснить, как определяется сумма двух и более векторов; уметь строить сумму двух и более данных векторов, пользуясь правилами треугольника, параллелограмма, многоугольника, строить разность двух данных векторов двумя способами.
Знать, какой вектор называется произведением вектора на число, какой отрезок называется средней линией трапеции.
Уметь формулировать свойства умножения вектора на число, формулировать и доказывать теорему о средней линии трапеции.
Содержание учебного предмета, курса.
Содержание обучения по алгебре
-
Рациональные дроби.(30 ч)
Рациональная дробь. Основное свойство дроби, сокращение дробей.
Тождественные преобразования рациональных выражений. Функция 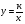 и её график.
и её график.
О с н о в н а я ц е л ь - выработать умение выполнять тождественные преобразования рациональных выражений.
Так как действия с рациональными дробями существенным образом опираются на действия с многочленами, то в начале темы необходимо повторить с учащимися преобразования целых выражений.
Главное место в данной теме занимают алгоритмы действий с дробями. Учащиеся должны понимать, что сумму, разность, произведение и частное дробей всегда можно представить в виде дроби. Приобретаемые в данной теме умения выполнять сложение, вычитание, умножение и деление дробей являются опорными в преобразованиях дробных выражений. Поэтому им следует уделять особое внимание. Нецелесообразно переходить к комбинированным заданиям на все действия с дробями прежде, чем будут усвоены основные алгоритмы. Задания на все действия с дробями не должны быть излишне громоздкими и трудоёмкими.
При нахождении значений дробей предлагаются упражнения на вычисление с помощью калькулятора. В данной теме расширяются сведения о статистических характеристиках. Вводится понятие среднего гармонического ряда положительных чисел.
Изучение темы завершается рассмотрением свойств графика функции 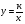 .
.
Контрольная работа по теме «Рациональные дроби и их свойства. Сумма и разность дробей». Контрольная работа по теме «Произведение и частное дробей».
2. Квадратные корни.(26 ч)
Понятие об иррациональных числах. Общие сведения о действительных числах. Квадратный корень. Понятие о нахождении приближённого значения квадратного корня. Свойства квадратных корней. Преобразования выражений, содержащих квадратные корни. Функция 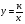 , её свойства и график.
, её свойства и график.
О с н о в н а я ц е л ь - систематизировать сведения о рациональных числах и дать представление об иррациональных числах, расширив тем самым понятие о числе; выработать умение выполнять преобразования выражений, содержащих квадратные корни.
В данной теме учащиеся получают начальное представление о понятии действительного числа. С этой целью обобщаются известные учащимся сведения о рациональных числах. Для введения понятия иррационального числа используется интуитивное представление о том, что каждый отрезок имеет длину и потому каждой точке координатной прямой соответствует некоторое число. Показывается, что существуют точки, не имеющие рациональных абсцисс.
При введении понятия корня полезно ознакомить учащихся с нахождением корней с помощью калькулятора.
Основное внимание уделяется понятию арифметического квадратного корня и свойствам арифметических квадратных корней. Доказываются теоремы о корне из произведения и дроби, а также тождество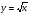 , которые получают применение в преобразованиях выражений, содержащих квадратные корни. Специальное внимание уделяется освобождению от иррациональности в знаменателе в выражениях вида
, которые получают применение в преобразованиях выражений, содержащих квадратные корни. Специальное внимание уделяется освобождению от иррациональности в знаменателе в выражениях вида 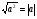 ,
, 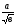 . Умение преобразовывать выражения, содержащие корни, часто используется как в самом курсе алгебры, так и в курсах геометрии, алгебры и начал анализа.
. Умение преобразовывать выражения, содержащие корни, часто используется как в самом курсе алгебры, так и в курсах геометрии, алгебры и начал анализа.
Продолжается работа по развитию функциональных представлений учащихся. Рассматриваются функция y = √x, ее свойства и график. При изучении функции 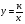 показывается ее взаимосвязь с функцией
показывается ее взаимосвязь с функцией 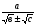 , где
, где 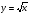 .
.
Контрольная работа по теме «Свойства арифметического квадратного корня». Контрольная работа по теме «Применение свойств арифметического квадратного корня».
-
Квадратные уравнения.(25 ч)
Квадратное уравнение. Формула корней квадратного уравнения. Решение рациональных уравнений. Решение задач, приводящих к квадратным уравнениям и простейшим рациональным уравнениям.
О с н о в н а я ц е л ь - выработать умения решать квадратные уравнения и простейшие рациональные уравнения и применять их к решению задач.
В начале темы приводятся примеры решения неполных квадратных уравнений. Этот материал систематизируется. Рассматриваются алгоритмы решения неполных квадратных уравнений различного вида.
Основное внимание следует уделить решению уравнений вида 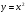 , где
, где 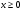 , с использованием формулы корней. В данной теме учащиеся знакомятся с формулами Виета, выражающими связь между корнями квадратного уравнения и его коэффициентами. Они используются в дальнейшем при доказательстве теоремы о разложении квадратного трехчлена на линейные множители.
, с использованием формулы корней. В данной теме учащиеся знакомятся с формулами Виета, выражающими связь между корнями квадратного уравнения и его коэффициентами. Они используются в дальнейшем при доказательстве теоремы о разложении квадратного трехчлена на линейные множители.
Учащиеся овладевают способом решения дробных рациональных уравнений, который состоит в том, что решение таких уравнений сводится к решению соответствующих целых уравнений с последующим исключением посторонних корней.
Изучение данной темы позволяет существенно расширить аппарат уравнений, используемых при решении текстовых задач.
Контрольная работа по теме «Квадратное уравнение и его корни». Контрольная работа по теме «Дробные рациональные уравнения».
-
Неравенства.(21 ч)
Числовые неравенства и их свойства. Почленное сложение и умножение числовых неравенств. Погрешность и точность приближения. Линейные неравенства с одной переменной и их системы.
О с н о в н а я ц е л ь - ознакомить учащихся с применением неравенств для оценки значений выражений, выработать умение решать линейные неравенства с одной переменной и их системы.
Свойства числовых неравенств составляют ту базу, на которой основано решение линейных неравенств с одной переменной. Теоремы о почленном сложении и умножении неравенств находят применение при выполнении простейших упражнений на оценку выражений по методу границ. Вводятся понятия абсолютной погрешности и точности приближения, относительной погрешности.
Умения проводить дедуктивные рассуждения получают развитие как при доказательствах указанных теорем, так и при выполнении упражнений на доказательства неравенств.
В связи с решением неравенств с одной переменной даётся понятие о числовых промежутках и вводятся соответствующие названия и обозначения. Рассмотрению систем неравенств с одной переменной предшествует ознакомление учащихся с понятиями пересечения и объединения множеств.
При решении неравенств используются свойства равносильных неравенств, которые разъясняются на конкретных примерах. Особое внимание следует уделить отработке умения решать простейшие неравенства вида ах>в, ах<������������������������������������������������������
�����������������������������������������������������������������������������������������������������
������������������������������������������������������������������������������������������
-
�������������������������������������
����ь с целым показателем и её свойства. Стандартный вид числа. Начальные сведения об организации статистических исследований.
О с н о в н а я ц е л ь - выработать умение применять свойства степени с целым показателем в вычислениях и преобразованиях, сформировать начальные представления о сборе и группировке статистических данных, их наглядной интерпретации.
В этой теме формулируются свойства степени с целыми показателем. Метод доказательства этих свойств показывается на примере умножения степеней с одинаковыми основаниями. Дается понятие о записи числа в стандартном виде. Приводятся примеры использования такой записи в физике, технике и других областях знаний.
Учащиеся получают начальные представления об организации статистических исследований. Они знакомятся с понятиями генеральной и выборочной совокупности. Приводятся примеры представления статистических данных в виде таблиц частот и относительных частот. Учащимся предлагаются задания на нахождение по таблице частот таких статистических характеристик, как среднее арифметическое, мода, размах. Рассматривается вопрос о наглядной интерпретации статистической информации. Известные учащимся способы наглядного представления статистических данных с помощью столбчатых и круговых диаграмм расширяются за счет введения таких понятий, как полигон и гистограмма.
Контрольная работа по теме «Степень с целым показателем и её свойства».
-
Повторение.(19 ч)
Административные контрольные работы (входная, полугодовая, итоговая).
Содержание обучения по геометрии
-
Четырёхугольники.(14 ч)
Многоугольник, выпуклый многоугольник, четырехугольник. Параллелограмм, его свойства и признаки. Трапеция. Прямоугольник, ромб, квадрат, их свойства. Осевая и центральная симметрии.
О с н о в н а я ц е л ь - изучить наиболее важные виды четырёхугольников - параллелограмм, прямоугольник, ромб, квадрат, трапецию; дать представление о фигурах, обладающих осевой или центральной симметрией.
Доказательства большинства теорем данной темы и решения многих задач проводятся с помощью признаков равенства треугольников, поэтому полезно их повторить в начале изучения темы.
Осевая и центральная симметрии вводятся не как преобразование плоскости, а как свойства геометрических фигур, в частности четырехугольников. Рассмотрение этих понятий как движений плоскости состоится в 9 классе.
Контрольная работа по теме «Четырёхугольники».
2. Площадь.(14 ч)
Понятие площади многоугольника. Площади прямоугольника, параллелограмма, треугольника, трапеции. Теорема Пифагора.
О с н о в н а я ц е л ь - расширить и углубить полученные в 5-6 классах представления учащихся об измерении и вычислении площадей; вывести формулы площадей прямоугольника, параллелограмма, треугольника, трапеции; доказать одну из главных теорем геометрии - теорему Пифагора.
Вывод формул для вычисления площадей прямоугольника, параллелограмма, треугольника, трапеции основывается на двух основных свойствах площадей, которые принимаются исходя из наглядных представлений, а также на формуле площади квадрата, обоснование которой не является обязательным для учащихся.
Нетрадиционной для школьного курса является теорема об отношении площадей треугольников, имеющих по равному углу. Она позволяет в дальнейшем дать простое доказательство признаков подобия треугольников. В этом состоит одно из преимуществ, обусловленных ранним введением понятия площади.
Доказательство теоремы Пифагора основывается на свойствах площадей и формулах для площадей квадрата и прямоугольника. Доказывается также теорема, обратная теореме Пифагора.
Контрольная работа по теме «Площадь».
-
Подобные треугольники.(19 ч)
Подобные треугольники. Признаки подобия треугольников. Применение подобия к доказательствам теорем и решению задач. Синус, косинус и тангенс острого угла прямоугольного треугольника.
О с н о в н а я ц е л ь - ввести понятие подобных треугольников; рассмотреть признаки подобия треугольников и их применения; сделать первый шаг в освоении учащимися тригонометрического аппарата геометрии.
Определение подобных треугольников дается не на основе преобразования подобия, а через равенство углов и пропорциональность сходственных сторон.
Признаки подобия треугольников доказываются с помощью теоремы об отношении площадей треугольников, имеющих по равному углу.
На основе признаков подобия доказывается теорема о средней линии треугольника, утверждение о точке пересечения медиан треугольника, а также два утверждения о пропорциональных отрезках в прямоугольном треугольнике. Дается представление о методе подобия в задачах на построение.
В заключение темы вводятся элементы тригонометрии - синус, косинус и тангенс острого угла прямоугольного треугольника.
Контрольная работа по теме «Признаки подобия треугольников». Контрольная работа по теме «Соотношения между сторонами и углами прямоугольного треугольника».
-
Окружность.(17 ч)
Взаимное расположение прямой и окружности. Касательная к окружности, её свойство и признак. Центральные и вписанные углы. Четыре замечательные точки треугольника. Вписанная и описанная окружности.
О с н о в н а я ц е л ь - расширить сведения об окружности, полученные учащимися в 7 классе; изучить новые факты, связанные с окружностью; познакомить учащихся с четырьмя замечательными точками треугольника.
В данной теме вводится много новых понятий и рассматривается много утверждений, связанных с окружностью. Для их усвоения следует уделить большое внимание решению задач.
Утверждение о точке пересечения биссектрис треугольника и точке пересечения серединных перпендикуляров к сторонам треугольника выводятся как следствия из теорем о свойствах биссектрисы угла и серединного перпендикуляра к отрезку. Теорема о точке пересечения высот треугольника (или их продолжений) доказывается с помощью утверждения о точке пересечения серединных перпендикуляров.
Наряду с теоремами об окружностях, вписанной в треугольник и описанной около него, рассматриваются свойство сторон описанного четырехугольника и свойство углов вписанного четырехугольника.
Контрольная работа по теме «Окружность».
-
Повторение. Решение задач.(4 ч)
Тематическое планирование
(с указанием количества часов на изучение темы и контрольных работ)
Тема
Кол-во часов
Кол-во контрольных работ
Повторение
6
1 административная контрольная работа
Рациональные дроби
30
2
Квадратные корни
26
2
Квадратные уравнения
25
2
Неравенства
21
2
Степень с целым показателем. Элементы статистики.
15
1
Повторение курса геометрии 7 класса
2
Четырёхугольники
14
1
Площади фигур
14
1
1 Административная контрольная работа
Подобные треугольники
19
2
Окружность
17
1
Повторение курса алгебры
13
1Административная контрольная работа (итоговая)
Повторение курса геометрии. Решение задач
2
Резерв
6
Итого
210
17
Рассмотрено Согласовано Утверждаю
на заседании ШМО учителей Зам директора по УВР Директор МБОУ СОШ №4
естественно-математического цикла -------------- Смагина С.М. -------------Черняева В.А.
«--------»-------------- 2014 г. «-----------»---------------2014 г. «--------»-------------- 2014 г.
Календарно - тематическое планирование
по ____математике_______
Класс: : ____8 «А»_______
Учитель____Смагина Светлана Михайловна____
Количество часов: всего _210 часов; в неделю 6 часов
Плановых контрольных работ 14 ,
Административных контрольных работ -3:
Планирование составлено на основе : программы общеобразовательных учреждений. Алгебра 7-9 классы, геометрия 7-9 классы. Составитель Бурмистрова Т.А. - М,.: «Просвещение», 2009.
Учебники: Макарычев Ю. Н., Миндюк Н. Г., Нешков К. И., Суворова С. Б. Алгебра 7: Учебник для общеобразов ательных учреждений. - М.: Просвещение.
Атанасян, В.Ф. Бутузов и др. Геометрия 7 -9: Учебник для общеобразовательных учреждений. - М.: Просвещение.
Календарно-тематическое планирование:
№ п/п
Тема урока
Тип урока
Вид контроля
Домашнее задание (параграф учебника)
Дата прове-
дения (план)
Дата прове-
дения (факт)
1.
А: Вводный инструктаж по охране труда и технике безопасности. Повторение курса алгебры. Функции.
УПЗУ
Групповой, индивидуальный контроль
2.
А: Повторение курса алгебры. Многочлены.
УПЗУ
Групповой, индивидуальный контроль
3.
А: Повторение курса алгебры. Формулы сокращённого умножения.
УПЗУ
Групповой, индивидуальный контроль
4.
А: Повторение курса алгебры. Системы линейных уравнений.
УПЗУ
Групповой, индивидуальный контроль
5.
А: Повторение курса алгебры. Преобразования выражений.
УПКЗУ
Групповой, индивидуальный контроль
6.
Г: Повторение курса геометрии. Решение задач.
УПЗУ
Групповой, индивидуальный контроль
7.
Г: Повторение курса геометрии. Решение задач.
УПЗУ
Групповой, индивидуальный контроль
8.
А :Административная контрольная работа.
УКЗ
Индивидуальный контроль
9.
А: Рациональные выражения.
УОНМ
Групповой, индивидуальный контроль
П.1
10.
А: Рациональные выражения.
УЗИ
Групповой, индивидуальный контроль
П.1
11.
А: Рациональные выражения.
УПЗУ
Групповой, индивидуальный контроль
П.1
12.
А: Основное свойство дроби. Сокращение дробей.
УОНМ
Групповой, индивидуальный контроль
П.2
13.
А: Основное свойство дроби. Сокращение дробей.
УЗИ
Групповой, индивидуальный контроль
П.2
14.
А: Основное свойство дроби. Сокращение дробей.
УПЗУ
Групповой, индивидуальный контроль
П.2
15.
А: Сложение и вычитание дробей с одинаковыми знаменателями.
УОНМ
Групповой, индивидуальный контроль
П.3
16.
А: Сложение и вычитание дробей с одинаковыми знаменателями.
УЗИ
Групповой, индивидуальный контроль
П.3
17.
А: Сложение и вычитание дробей с одинаковыми знаменателями.
УПЗУ
Групповой, индивидуальный контроль
П.3
18.
А: Сложение и вычитание дробей с разными знаменателями.
УОНМ
Групповой, индивидуальный контроль
П.4
19.
А: Сложение и вычитание дробей с разными знаменателями.
УЗИ
Групповой, индивидуальный контроль
П.4
20.
А: Сложение и вычитание дробей с разными знаменателями.
УПЗУ
Групповой, индивидуальный контроль
П.4
21.
А: Сложение и вычитание дробей с разными знаменателями.
УПЗУ
Групповой, индивидуальный контроль
П.4
22.
А: Подготовка к контрольной работе.
УОСЗ
Групповой, индивидуальный контроль
23.
А: Контрольная работа по теме «Рациональные дроби и их свойства. Сумма и разность дробей».
УПКЗУ
Индивидуальный контроль
24.
А: Работа над ошибками в контрольной работе.
УКЗ
Индивидуальный контроль
25.
А: Умножение дробей. Возведение дроби в степень.
УОНМ
Групповой, индивидуальный контроль
П.5
26.
А: Умножение дробей. Возведение дроби в степень.
УЗИ
Групповой, индивидуальный контроль
П.5
27.
А: Умножение дробей. Возведение дроби в степень.
УПЗУ
Групповой, индивидуальный контроль
П.5
28.
А: Деление дробей.
УОНМ
Групповой, индивидуальный контроль
П.6
29.
А: Деление дробей.
УЗИ
Групповой, индивидуальный контроль
П.6
30.
А: Деление дробей.
УПЗУ
Групповой, индивидуальный контроль
П.6
31.
А: Преобразование рациональных выражений.
УОНМ
Групповой, индивидуальный контроль
П.7
32.
А: Преобразование рациональных выражений.
УЗИ
Групповой, индивидуальный контроль
П.7
33.
А: Преобразование рациональных выражений.
УПЗУ
Групповой, индивидуальный контроль
П.7
34.
А: Функция y=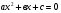 и её график.
и её график.
УОНМ
Групповой, индивидуальный контроль
П.8
35.
А: Функция y=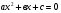 и её график.
и её график.
УЗИ
Групповой, индивидуальный контроль
П.8
36.
А: Подготовка к контрольной работе.
УОСЗ
Групповой, индивидуальный контроль
37.
А: Контрольная работа по теме «Произведение и частное дробей».
УПКЗУ
Индивидуальный контроль
38.
А: Работа над ошибками в контрольной работе.
УКЗ
Индивидуальный контроль
39.
Г: Многоугольник. Выпуклый многоугольник. Четырёхугольник.
УОНМ
Групповой, индивидуальный контроль
П.39,40,41
40.
Г: Параллелограмм.
УОНМ
Групповой, индивидуальный контроль
П.42
41.
Г: Параллелограмм.
УЗИ
Групповой, индивидуальный контроль
П.42
42.
Г: Признаки параллелограмма.
УОНМ
Групповой, индивидуальный контроль
П.43
43.
Г: Признаки параллелограмма.
УЗИ
Групповой, индивидуальный контроль
П.43
44.
Г: Трапеция.
УОНМ
Групповой, индивидуальный контроль
П.44
45.
Г: Задачи на построение циркулем и линейкой.
УПЗУ
Групповой, индивидуальный контроль
46.
Г: Задачи на построение циркулем и линейкой.
УПЗУ
Групповой, индивидуальный контроль
47.
Г: Прямоугольник.
УОНМ
Групповой, индивидуальный контроль
П.45
48.
Г: Ромб и квадрат.
УОНМ
Групповой, индивидуальный контроль
П.46
49.
Г: Осевая и центральная симметрии.
УОНМ
Групповой, индивидуальный контроль
П.47
50.
Г: Подготовка к контрольной работе.
УОСЗ
Групповой, индивидуальный контроль
51.
Г: Контрольная работа по теме «Четырёхугольники».
УПКЗУ
Индивидуальный контроль
52.
Г: Работа над ошибками в контрольной работе.
УКЗ
Индивидуальный контроль
53.
А: Рациональные числа.
УОНМ
Групповой, индивидуальный контроль
П.10
54.
А: Рациональные числа.
УЗИ
Групповой, индивидуальный контроль
П.10
55.
А: Иррациональные числа.
УОНМ
Групповой, индивидуальный контроль
П.11
56.
А: Квадратные корни. Арифметический квадратный корень.
УОНМ
Групповой, индивидуальный контроль
П.12
57.
А: Квадратные корни. Арифметический квадратный корень.
УЗИ
Групповой, индивидуальный контроль
П.12
58.
А: Уравнение х2=а.
УОНМ
Групповой, индивидуальный контроль
П.13
59.
А: Уравнение х2=а.
УЗИ
Групповой, индивидуальный контроль
П.13
60.
А: Нахождение приближённых значений квадратного корня.
УОНМ
Групповой, индивидуальный контроль
П.14
61.
А: Функция у=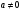 и её график.
и её график.
УОНМ
Групповой, индивидуальный контроль
П.15
62.
А: Функция у=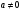 и её график.
и её график.
УЗИ
Групповой, индивидуальный контроль
П.15
63.
А: Квадратный корень из произведения и дроби.
УОНМ
Групповой, индивидуальный контроль
П.16
64.
А: Квадратный корень из произведения и дроби.
УЗИ
Групповой, индивидуальный контроль
П.16
65.
А: Квадратный корень из степени.
УОНМ
Групповой, индивидуальный контроль
П.17
66.
А: Квадратный корень из степени.
УЗИ
Групповой, индивидуальный контроль
П.17
67.
А: Подготовка к контрольной работе.
УОСЗ
Групповой, индивидуальный контроль
68.
А: Контрольная работа по теме «Свойства арифметического квадратного корня».
УПКЗУ
Индивидуальный контроль
69.
А: Работа над ошибками в контрольной работе.
УКЗ
Индивидуальный контроль
70.
А: Вынесение множителя за знак корня. Внесение множителя под знак корня.
УОНМ
Групповой, индивидуальный контроль
П.18
71.
А: Вынесение множителя за знак корня. Внесение множителя под знак корня.
УЗИ
Групповой, индивидуальный контроль
П.18
72.
А: Вынесение множителя за знак корня. Внесение множителя под знак корня.
УПЗУ
Групповой, индивидуальный контроль
П.18
73.
А: Преобразование выражений, содержащих квадратные корни.
УОНМ
Групповой, индивидуальный контроль
П.19
74.
А: Преобразование выражений, содержащих квадратные корни.
УЗИ
Групповой, индивидуальный контроль
П.19
75.
А: Преобразование выражений, содержащих квадратные корни.
УПЗУ
Групповой, индивидуальный контроль
П.19
76.
А: Подготовка к контрольной работе.
УОСЗ
Групповой, индивидуальный контроль
77.
А: Контрольная работа по теме «Применение свойств арифметического квадратного корня».
УПКЗУ
Индивидуальный контроль
78.
А: Работа над ошибками в контрольной работе.
УКЗ
Индивидуальный контроль
79.
Г: Понятие площади многоугольника. Площадь квадрата.
УОНМ
Групповой, индивидуальный контроль
П.48,49
80.
Г: Площадь прямоугольника.
УОНМ
Групповой, индивидуальный контроль
П.50
81.
Г: Площадь параллелограмма.
УОНМ
Групповой, индивидуальный контроль
П.51
82.
Г: Площадь треугольника.
УОНМ
Групповой, индивидуальный контроль
П.52
83.
Г: Площадь треугольника.
УЗИ
Групповой, индивидуальный контроль
П.52
84.
Г: Площадь трапеции.
УОНМ
Групповой, индивидуальный контроль
П.53
85.
Г: Решение задач по теме «Площадь параллелограмма, треугольника и трапеции».
УПЗУ
Групповой, индивидуальный контроль
86.
Г: Решение задач по теме «Площадь параллелограмма, треугольника и трапеции».
УПЗУ
Групповой, индивидуальный контроль
87.
Г: Теорема Пифагора.
УОНМ
Групповой, индивидуальный контроль
П.54
88.
Г: Теорема Пифагора.
УЗИ
Групповой, индивидуальный контроль
П.54
89.
Г: Теорема, обратная теореме Пифагора.
УОНМ
Групповой, индивидуальный контроль
П.55
90.
Г: Подготовка к контрольной работе.
УОСЗ
Групповой, индивидуальный контроль
91.
Г: Контрольная работа по теме «Площадь».
УПКЗУ
Индивидуальный контроль
92.
Г: Работа над ошибками в контрольной работе.
УКЗ
Индивидуальный контроль
93.
А: Административная контрольная работа.
УПКЗУ
Индивидуальный контроль
94.
А: Неполные квадратные уравнения.
УОНМ
Групповой, индивидуальный контроль
П.21
95.
А: Неполные квадратные уравнения.
УЗИ
Групповой, индивидуальный контроль
П.21
96.
А: Неполные квадратные уравнения.
УПЗУ
Групповой, индивидуальный контроль
П.21
97.
А: Повторный инструктаж по охране труда и технике безопасности. Формулы корней квадратного уравнения.
УОНМ
Групповой, индивидуальный контроль
П.22
98.
А: Формулы корней квадратного уравнения.
УЗИ
Групповой, индивидуальный контроль
П.22
99.
А: Формулы корней квадратного уравнения.
УПЗУ
Групповой, индивидуальный контроль
П.22
100.
А: Формулы корней квадратного уравнения.
УПЗУ
Групповой, индивидуальный контроль
П.22
101.
А: Решение задач с помощью квадратных уравнений.
УОНМ
Групповой, индивидуальный контроль
П.23
102.
А: Решение задач с помощью квадратных уравнений.
УЗИ
Групповой, индивидуальный контроль
П.23
103.
А: Решение задач с помощью квадратных уравнений.
УПЗУ
Групповой, индивидуальный контроль
П.23
104.
А: Теорема Виета.
УОНМ
Групповой, индивидуальный контроль
П.24
105.
А: Теорема Виета.
УЗИ
Групповой, индивидуальный контроль
П.24
106.
А: Подготовка к контрольной работе.
УОСЗ
Групповой, индивидуальный контроль
107.
А: Контрольная работа по теме «Квадратное уравнение и его корни».
УПКЗУ
Индивидуальный контроль
108.
А: Работа над ошибками в контрольной работе.
УКЗ
Индивидуальный контроль
109.
А: Решение дробных рациональных уравнений.
УОНМ
Групповой, индивидуальный контроль
П.25
110.
А: Решение дробных рациональных уравнений.
УЗИ
Групповой, индивидуальный контроль
П.25
111.
А: Решение дробных рациональных уравнений.
УПЗУ
Групповой, индивидуальный контроль
П.25
112.
А: Решение задач с помощью рациональных уравнений.
УОНМ
Групповой, индивидуальный контроль
П.26
113.
А: Решение задач с помощью рациональных уравнений.
УЗИ
Групповой, индивидуальный контроль
П.26
114.
А: Решение задач с помощью рациональных уравнений.
УПЗУ
Групповой, индивидуальный контроль
П.26
115.
А: Решение задач с помощью рациональных уравнений.
УПЗУ
Групповой, индивидуальный контроль
П.26
116.
А: Подготовка к контрольной работе.
УОСЗ
Групповой, индивидуальный контроль
117.
А: Контрольная работа по теме «Дробные рациональные уравнения».
УПКЗУ
Индивидуальный контроль
118.
А: Работа над ошибками в контрольной работе.
УКЗ
Индивидуальный контроль
119.
Г: Пропорциональные отрезки.
УОНМ
Групповой, индивидуальный контроль
П.56
120.
Г: Определение подобных треугольников. Отношение площадей подобных треугольников.
УОНМ
Групповой, индивидуальный контроль
П.57,58
121.
Г: Первый признак подобия треугольников.
УОНМ
Групповой, индивидуальный контроль
П.59
122.
Г: Первый признак подобия треугольников.
УЗИ
Групповой, индивидуальный контроль
П.59
123.
Г: Второй признак подобия треугольников.
УОНМ
Групповой, индивидуальный контроль
П.60
124.
Г: Третий признак подобия треугольников.
УОНМ
Групповой, индивидуальный контроль
П.61
125.
Г: Подготовка к контрольной работе.
УОСЗ
Групповой, индивидуальный контроль
126.
Г: Контрольная работа по теме «Признаки подобия треугольников».
УПКЗУ
Индивидуальный контроль
127.
Г: Работа над ошибками в контрольной работе.
УКЗ
Индивидуальный контроль
128.
Г: Средняя линия треугольника.
УОНМ
Групповой, индивидуальный контроль
П.62
129.
Г: Средняя линия треугольника.
УЗИ
Групповой, индивидуальный контроль
П.62
130.
Г: Пропорциональные отрезки в прямоугольном треугольнике.
УОНМ
Групповой, индивидуальный контроль
П.63
131.
Г: Пропорциональные отрезки в прямоугольном треугольнике.
УЗИ
Групповой, индивидуальный контроль
П.63
132.
Г: Практические приложения подобия треугольников. О подобии произвольных фигур.
УОНМ
Групповой, индивидуальный контроль
П.64,65
133.
Г: Синус, косинус и тангенс острого угла прямоугольного треугольника.
УОНМ
Групповой, индивидуальный контроль
П.66
134.
Г: Значения синуса, косинуса и тангенса для углов 300, 450 и 600.
УОНМ
Групповой, индивидуальный контроль
П.67
135.
Г: Значения синуса, косинуса и тангенса для углов 300, 450 и 600.
УЗИ
Групповой, индивидуальный контроль
П.67
136.
Г: Подготовка к контрольной работе.
УОСЗ
Групповой, индивидуальный контроль
137.
Г: Контрольная работа по теме «Соотношения между сторонами и углами прямоугольного треугольника».
УПКЗУ
Индивидуальный контроль
138.
А: Числовые неравенства.
УОНМ
Групповой, индивидуальный контроль
П.28
139.
А: Числовые неравенства.
УЗИ
Групповой, индивидуальный контроль
П.28
140.
А: Свойства числовых неравенств.
УОНМ
Групповой, индивидуальный контроль
П.29
141.
А: Свойства числовых неравенств.
УЗИ
Групповой, индивидуальный контроль
П.29
142.
А: Сложение и умножение числовых неравенств.
УОНМ
Групповой, индивидуальный контроль
П.30
143.
А: Сложение и умножение числовых неравенств.
УЗИ
Групповой, индивидуальный контроль
П.30
144.
А: Погрешность и точность приближения.
УОНМ
Групповой, индивидуальный контроль
П.31
145.
А: Подготовка к контрольной работе.
УОСЗ
Групповой, индивидуальный контроль
146.
А: Контрольная работа по теме «Числовые неравенства и их свойства».
УПКЗУ
Индивидуальный контроль
147.
А: Работа над ошибками в контрольной работе.
УКЗ
Индивидуальный контроль
148.
А: Пересечение и объединение множеств.
УОНМ
Групповой, индивидуальный контроль
П.32
149.
А: Пересечение и объединение множеств.
УЗИ
Групповой, индивидуальный контроль
П.32
150.
А: Числовые промежутки.
УОНМ
Групповой, индивидуальный контроль
П.33
151.
А: Числовые промежутки.
Групповой, индивидуальный контроль
П.33
152.
А: Решение неравенств с одной переменной.
УОНМ
Групповой, индивидуальный контроль
П.34
153.
А: Решение неравенств с одной переменной.
УЗИ
Групповой, индивидуальный контроль
П.34
154.
А: Решение систем неравенств с одной переменной.
УОНМ
Групповой, индивидуальный контроль
П.35
155.
А: Решение систем неравенств с одной переменной.
УЗИ
Групповой, индивидуальный контроль
П.35
156.
А: Подготовка к контрольной работе.
УОСЗ
Групповой, индивидуальный контроль
157.
А: Контрольная работа по теме «Неравенства с одной переменной и их системы».
УПКЗУ
Индивидуальный контроль
158.
А: Работа над ошибками в контрольной работе.
УКЗ
Индивидуальный контроль
159.
Г: Взаимное расположение прямой и окружности.
УОНМ
Групповой, индивидуальный контроль
П.68
160.
Г: Касательная к окружности.
УОНМ
Групповой, индивидуальный контроль
П.69
161.
Г: Касательная к окружности.
УЗИ
Групповой, индивидуальный контроль
П.69
162.
Г: Градусная мера дуги окружности.
УОНМ
Групповой, индивидуальный контроль
П.70
163.
Г: Теорема о вписанном угле.
УОНМ
Групповой, индивидуальный контроль
П.71
164.
Г: Теорема о вписанном угле.
УЗИ
Групповой, индивидуальный контроль
П.71
165.
Г: Решение задач по теме «Центральные и вписанные углы».
УПЗУ
Групповой, индивидуальный контроль
166.
Г: Свойства биссектрисы угла и серединного перпендикуляра к отрезку.
УОНМ
Групповой, индивидуальный контроль
П.72
167.
Г: Свойства биссектрисы угла и серединного перпендикуляра к отрезку.
УЗИ
Групповой, индивидуальный контроль
П.72
168.
Г: Теорема о пересечении высот треугольника.
УОНМ
Групповой, индивидуальный контроль
П.73
169.
Г: Вписанная окружность.
УОНМ
Групповой, индивидуальный контроль
П.74
170.
Г: Вписанная окружность.
УЗИ
Групповой, индивидуальный контроль
П.74
171.
Г: Описанная окружность.
УОНМ
Групповой, индивидуальный контроль
П.75
172.
Г: Описанная окружность.
УЗИ
Групповой, индивидуальный контроль
П.75
173.
Г: Подготовка к контрольной работе.
УОСЗ
Групповой, индивидуальный контроль
174.
Г: Контрольная работа по теме «Окружность».
УПКЗУ
Индивидуальный контроль
175.
Г: Работа над ошибками в контрольной работе.
УКЗ
Индивидуальный контроль
176.
А: Определение степени с целым отрицательным показателем.
УОНМ
Групповой, индивидуальный контроль
П.37
177.
А: Определение степени с целым отрицательным показателем.
УЗИ
Групповой, индивидуальный контроль
П.37
178.
А: Определение степени с целым отрицательным показателем.
УПЗУ
Групповой, индивидуальный контроль
П.37
179.
А: Свойства степени с целым показателем.
УОНМ
Групповой, индивидуальный контроль
П.38
180.
А: Свойства степени с целым показателем.
УЗИ
Групповой, индивидуальный контроль
П.38
181.
А: Свойства степени с целым показателем.
УПЗУ
Групповой, индивидуальный контроль
П.38
182.
А: Стандартный вид числа.
УОНМ
Групповой, индивидуальный контроль
П.39
183.
А: Стандартный вид числа.
УЗИ
Групповой, индивидуальный контроль
П.39
184.
А: Подготовка к контрольной работе.
УОСЗ
Групповой, индивидуальный контроль
185.
А: Контрольная работа по теме «Степень с целым показателем и её свойства».
УПКЗУ
Индивидуальный контроль
186.
А: Работа над ошибками в контрольной работе.
УКЗ
Индивидуальный контроль
187.
А: Сбор и группировка статистических данных.
УОНМ
Групповой, индивидуальный контроль
П.40
188.
А: Сбор и группировка статистических данных.
УЗИ
Групповой, индивидуальный контроль
П.40
189.
А: Наглядное представление статистической информации.
УОНМ
Групповой, индивидуальный контроль
П.41
190.
А: Наглядное представление статистической информации.
УЗИ
Групповой, индивидуальный контроль
П.41
191.
Г: Итоговое повторение.
УПЗУ
Групповой, индивидуальный контроль
192.
Г: Итоговое повторение.
УПЗУ
Групповой, индивидуальный контроль
193.
А: Итоговое повторение.
УПЗУ
Групповой, индивидуальный контроль
194.
А: Итоговое повторение.
УПЗУ
Групповой, индивидуальный контроль
195.
А: Итоговое повторение.
УПЗУ
Групповой, индивидуальный контроль
196.
А: Итоговое повторение.
УПЗУ
Групповой, индивидуальный контроль
197.
А: Итоговое повторение.
УПЗУ
Групповой, индивидуальный контроль
198.
А: Итоговое повторение.
УПЗУ
Групповой, индивидуальный контроль
199.
А: Итоговое повторение.
УПЗУ
Групповой, индивидуальный контроль
200.
А: Итоговое повторение.
УПЗУ
Групповой, индивидуальный контроль
201.
А: Итоговое повторение.
УПЗУ
Групповой, индивидуальный контроль
202.
А: Итоговое повторение.
УПЗУ
Групповой, индивидуальный контроль
203.
А: Административная контрольная работа.
УПКЗУ
Индивидуальный контроль
204.
А: Работа над ошибками в контрольной работе.
УКЗ
Индивидуальный контроль
205.
Г: Резерв.
206.
Г: Резерв.
207.
А: Резерв.
208.
А: Резерв.
209.
А: Резерв.
210
А: Резерв.
УОНМ - урок ознакомления с новым материалом УЗИ - урок закрепления изученного
УПЗУ - урок применения знаний и умений УОСЗ - урок обобщения и систематизации знаний
УПКЗУ - урок проверки и коррекции знаний и умений УКЗ - урок коррекции знаний
КР - контрольная работа
Учебно-методическая литература
Основная литература:
-
Программы общеобразовательных учреждений. Геометрия 7-9 классы. Составитель Бурмистрова Т.А. - М.: «Просвещение», 2009.
-
Программы общеобразовательных учреждений. Алгебра 7-9 классы. Составитель Бурмистрова Т.А. - М.: «Просвещение», 2009.
Алгебра: Учеб. для 8 кл. общеобразоват. учреждений/Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова; Под ред. С.А. Теляковского - М.: Просвещение, 2009.
Жохов В.И., Макарычев Ю.Н., Миндюк Н.Г. Дидактические материалы по алгебре для 8 класса. - М.: Просвещение, 2008.
Уроки алгебры в 8 классе: Метод. рекомендации для учителя/В.И. Жохов, Г.Д. Карташев - М.: Просвещение, 2008.
Геометрия: Учеб. для 7-9 кл. общеобразоват. учреждений/Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др. - М.: Просвещение, 2004-2008.
Зив Б.Г. Дидактические материалы по геометрии для 8 класса. - М.: Просвещение, 2009.
Изучение геометрии в 7-9 классах: Метод. рекомендации для учителя/Л.С.Атанасян, В.Ф.Бутузов, Ю.А.Глазков и др. - М.: Просвещение, 2008.
Дополнительная литература
-
И.Н. Данкова, С.Ф. Кузьминых, Н.Г. Пенкина, О.В. Сушкова Элементы статистики и теории вероятностей (поурочные разработки, алгебра 7-8 классы) - Воронеж, 2008.
-
Ершова А.П., Голобородько В.В., Ершова А.С. Самостоятельные и контрольные работы по алгебре и геометрии для 8 класса. - 7-е изд., испр. и доп. - М.: Илекса, - 2007, - 208 с.
Примерные контрольно-измерительные материалы
Рассмотрено Согласовано Утверждаю
на заседании ШМО учителей Зам директора по УВР Директор МБОУ СОШ №4
естественно-математического цикла -------------- Смагина С.М. -------------Черняева В.А.
«--------»-------------- 2014 г. «-----------»---------------2014 г. «--------»-------------- 2014 г.
Календарно - тематическое планирование
по ____математике_______
Класс: : ____8 «Б»_______
Учитель____Смагина Светлана Михайловна____
Количество часов: всего _210 часов; в неделю 6 часов
Плановых контрольных работ 14 ,
Административных контрольных работ -3:
Планирование составлено на основе : программы общеобразовательных учреждений. Алгебра 7-9 классы, геометрия 7-9 классы. Составитель Бурмистрова Т.А. - М,.: «Просвещение», 2009.
Учебники: Макарычев Ю. Н., Миндюк Н. Г., Нешков К. И., Суворова С. Б. Алгебра 7: Учебник для общеобразов ательных учреждений. - М.: Просвещение.
Атанасян, В.Ф. Бутузов и др. Геометрия 7 -9: Учебник для общеобразовательных учреждений. - М.: Просвещение.
Календарно-тематическое планирование:
№ п/п
Тема урока
Тип урока
Вид контроля
Домашнее задание (параграф учебника)
Дата прове-
дения (план)
Дата прове-
дения (факт)
1.
А: Вводный инструктаж по охране труда и технике безопасности. Повторение курса алгебры. Функции.
УПЗУ
Групповой, индивидуальный контроль
2.
А: Повторение курса алгебры. Многочлены.
УПЗУ
Групповой, индивидуальный контроль
3.
А: Повторение курса алгебры. Формулы сокращённого умножения.
УПЗУ
Групповой, индивидуальный контроль
4.
А: Повторение курса алгебры. Системы линейных уравнений.
УПЗУ
Групповой, индивидуальный контроль
5.
А: Повторение курса алгебры. Преобразования выражений.
УПКЗУ
Групповой, индивидуальный контроль
6.
Г: Повторение курса геометрии. Решение задач.
УПЗУ
Групповой, индивидуальный контроль
7.
Г: Повторение курса геометрии. Решение задач.
УПЗУ
Групповой, индивидуальный контроль
8.
А :Административная контрольная работа.
УКЗ
Индивидуальный контроль
9.
А: Рациональные выражения.
УОНМ
Групповой, индивидуальный контроль
П.1
10.
А: Рациональные выражения.
УЗИ
Групповой, индивидуальный контроль
П.1
11.
А: Рациональные выражения.
УПЗУ
Групповой, индивидуальный контроль
П.1
12.
А: Основное свойство дроби. Сокращение дробей.
УОНМ
Групповой, индивидуальный контроль
П.2
13.
А: Основное свойство дроби. Сокращение дробей.
УЗИ
Групповой, индивидуальный контроль
П.2
14.
А: Основное свойство дроби. Сокращение дробей.
УПЗУ
Групповой, индивидуальный контроль
П.2
15.
А: Сложение и вычитание дробей с одинаковыми знаменателями.
УОНМ
Групповой, индивидуальный контроль
П.3
16.
А: Сложение и вычитание дробей с одинаковыми знаменателями.
УЗИ
Групповой, индивидуальный контроль
П.3
17.
А: Сложение и вычитание дробей с одинаковыми знаменателями.
УПЗУ
Групповой, индивидуальный контроль
П.3
18.
А: Сложение и вычитание дробей с разными знаменателями.
УОНМ
Групповой, индивидуальный контроль
П.4
19.
А: Сложение и вычитание дробей с разными знаменателями.
УЗИ
Групповой, индивидуальный контроль
П.4
20.
А: Сложение и вычитание дробей с разными знаменателями.
УПЗУ
Групповой, индивидуальный контроль
П.4
21.
А: Сложение и вычитание дробей с разными знаменателями.
УПЗУ
Групповой, индивидуальный контроль
П.4
22.
А: Подготовка к контрольной работе.
УОСЗ
Групповой, индивидуальный контроль
23.
А: Контрольная работа по теме «Рациональные дроби и их свойства. Сумма и разность дробей».
УПКЗУ
Индивидуальный контроль
24.
А: Работа над ошибками в контрольной работе.
УКЗ
Индивидуальный контроль
25.
А: Умножение дробей. Возведение дроби в степень.
УОНМ
Групповой, индивидуальный контроль
П.5
26.
А: Умножение дробей. Возведение дроби в степень.
УЗИ
Групповой, индивидуальный контроль
П.5
27.
А: Умножение дробей. Возведение дроби в степень.
УПЗУ
Групповой, индивидуальный контроль
П.5
28.
А: Деление дробей.
УОНМ
Групповой, индивидуальный контроль
П.6
29.
А: Деление дробей.
УЗИ
Групповой, индивидуальный контроль
П.6
30.
А: Деление дробей.
УПЗУ
Групповой, индивидуальный контроль
П.6
31.
А: Преобразование рациональных выражений.
УОНМ
Групповой, индивидуальный контроль
П.7
32.
А: Преобразование рациональных выражений.
УЗИ
Групповой, индивидуальный контроль
П.7
33.
А: Преобразование рациональных выражений.
УПЗУ
Групповой, индивидуальный контроль
П.7
34.
А: Функция y=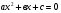 и её график.
и её график.
УОНМ
Групповой, индивидуальный контроль
П.8
35.
А: Функция y=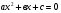 и её график.
и её график.
УЗИ
Групповой, индивидуальный контроль
П.8
36.
А: Подготовка к контрольной работе.
УОСЗ
Групповой, индивидуальный контроль
37.
А: Контрольная работа по теме «Произведение и частное дробей».
УПКЗУ
Индивидуальный контроль
38.
А: Работа над ошибками в контрольной работе.
УКЗ
Индивидуальный контроль
39.
Г: Многоугольник. Выпуклый многоугольник. Четырёхугольник.
УОНМ
Групповой, индивидуальный контроль
П.39,40,41
40.
Г: Параллелограмм.
УОНМ
Групповой, индивидуальный контроль
П.42
41.
Г: Параллелограмм.
УЗИ
Групповой, индивидуальный контроль
П.42
42.
Г: Признаки параллелограмма.
УОНМ
Групповой, индивидуальный контроль
П.43
43.
Г: Признаки параллелограмма.
УЗИ
Групповой, индивидуальный контроль
П.43
44.
Г: Трапеция.
УОНМ
Групповой, индивидуальный контроль
П.44
45.
Г: Задачи на построение циркулем и линейкой.
УПЗУ
Групповой, индивидуальный контроль
46.
Г: Задачи на построение циркулем и линейкой.
УПЗУ
Групповой, индивидуальный контроль
47.
Г: Прямоугольник.
УОНМ
Групповой, индивидуальный контроль
П.45
48.
Г: Ромб и квадрат.
УОНМ
Групповой, индивидуальный контроль
П.46
49.
Г: Осевая и центральная симметрии.
УОНМ
Групповой, индивидуальный контроль
П.47
50.
Г: Подготовка к контрольной работе.
УОСЗ
Групповой, индивидуальный контроль
51.
Г: Контрольная работа по теме «Четырёхугольники».
УПКЗУ
Индивидуальный контроль
52.
Г: Работа над ошибками в контрольной работе.
УКЗ
Индивидуальный контроль
53.
А: Рациональные числа.
УОНМ
Групповой, индивидуальный контроль
П.10
54.
А: Рациональные числа.
УЗИ
Групповой, индивидуальный контроль
П.10
55.
А: Иррациональные числа.
УОНМ
Групповой, индивидуальный контроль
П.11
56.
А: Квадратные корни. Арифметический квадратный корень.
УОНМ
Групповой, индивидуальный контроль
П.12
57.
А: Квадратные корни. Арифметический квадратный корень.
УЗИ
Групповой, индивидуальный контроль
П.12
58.
А: Уравнение х2=а.
УОНМ
Групповой, индивидуальный контроль
П.13
59.
А: Уравнение х2=а.
УЗИ
Групповой, индивидуальный контроль
П.13
60.
А: Нахождение приближённых значений квадратного корня.
УОНМ
Групповой, индивидуальный контроль
П.14
61.
А: Функция у=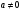 и её график.
и её график.
УОНМ
Групповой, индивидуальный контроль
П.15
62.
А: Функция у=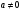 и её график.
и её график.
УЗИ
Групповой, индивидуальный контроль
П.15
63.
А: Квадратный корень из произведения и дроби.
УОНМ
Групповой, индивидуальный контроль
П.16
64.
А: Квадратный корень из произведения и дроби.
УЗИ
Групповой, индивидуальный контроль
П.16
65.
А: Квадратный корень из степени.
УОНМ
Групповой, индивидуальный контроль
П.17
66.
А: Квадратный корень из степени.
УЗИ
Групповой, индивидуальный контроль
П.17
67.
А: Подготовка к контрольной работе.
УОСЗ
Групповой, индивидуальный контроль
68.
А: Контрольная работа по теме «Свойства арифметического квадратного корня».
УПКЗУ
Индивидуальный контроль
69.
А: Работа над ошибками в контрольной работе.
УКЗ
Индивидуальный контроль
70.
А: Вынесение множителя за знак корня. Внесение множителя под знак корня.
УОНМ
Групповой, индивидуальный контроль
П.18
71.
А: Вынесение множителя за знак корня. Внесение множителя под знак корня.
УЗИ
Групповой, индивидуальный контроль
П.18
72.
А: Вынесение множителя за знак корня. Внесение множителя под знак корня.
УПЗУ
Групповой, индивидуальный контроль
П.18
73.
А: Преобразование выражений, содержащих квадратные корни.
УОНМ
Групповой, индивидуальный контроль
П.19
74.
А: Преобразование выражений, содержащих квадратные корни.
УЗИ
Групповой, индивидуальный контроль
П.19
75.
А: Преобразование выражений, содержащих квадратные корни.
УПЗУ
Групповой, индивидуальный контроль
П.19
76.
А: Подготовка к контрольной работе.
УОСЗ
Групповой, индивидуальный контроль
77.
А: Контрольная работа по теме «Применение свойств арифметического квадратного корня».
УПКЗУ
Индивидуальный контроль
78.
А: Работа над ошибками в контрольной работе.
УКЗ
Индивидуальный контроль
79.
Г: Понятие площади многоугольника. Площадь квадрата.
УОНМ
Групповой, индивидуальный контроль
П.48,49
80.
Г: Площадь прямоугольника.
УОНМ
Групповой, индивидуальный контроль
П.50
81.
Г: Площадь параллелограмма.
УОНМ
Групповой, индивидуальный контроль
П.51
82.
Г: Площадь треугольника.
УОНМ
Групповой, индивидуальный контроль
П.52
83.
Г: Площадь треугольника.
УЗИ
Групповой, индивидуальный контроль
П.52
84.
Г: Площадь трапеции.
УОНМ
Групповой, индивидуальный контроль
П.53
85.
Г: Решение задач по теме «Площадь параллелограмма, треугольника и трапеции».
УПЗУ
Групповой, индивидуальный контроль
86.
Г: Решение задач по теме «Площадь параллелограмма, треугольника и трапеции».
УПЗУ
Групповой, индивидуальный контроль
87.
Г: Теорема Пифагора.
УОНМ
Групповой, индивидуальный контроль
П.54
88.
Г: Теорема Пифагора.
УЗИ
Групповой, индивидуальный контроль
П.54
89.
Г: Теорема, обратная теореме Пифагора.
УОНМ
Групповой, индивидуальный контроль
П.55
90.
Г: Подготовка к контрольной работе.
УОСЗ
Групповой, индивидуальный контроль
91.
Г: Контрольная работа по теме «Площадь».
УПКЗУ
Индивидуальный контроль
92.
Г: Работа над ошибками в контрольной работе.
УКЗ
Индивидуальный контроль
93.
А: Административная контрольная работа.
УПКЗУ
Индивидуальный контроль
94.
А: Неполные квадратные уравнения.
УОНМ
Групповой, индивидуальный контроль
П.21
95.
А: Неполные квадратные уравнения.
УЗИ
Групповой, индивидуальный контроль
П.21
96.
А: Неполные квадратные уравнения.
УПЗУ
Групповой, индивидуальный контроль
П.21
97.
А: Повторный инструктаж по охране труда и технике безопасности. Формулы корней квадратного уравнения.
УОНМ
Групповой, индивидуальный контроль
П.22
98.
А: Формулы корней квадратного уравнения.
УЗИ
Групповой, индивидуальный контроль
П.22
99.
А: Формулы корней квадратного уравнения.
УПЗУ
Групповой, индивидуальный контроль
П.22
100.
А: Формулы корней квадратного уравнения.
УПЗУ
Групповой, индивидуальный контроль
П.22
101.
А: Решение задач с помощью квадратных уравнений.
УОНМ
Групповой, индивидуальный контроль
П.23
102.
А: Решение задач с помощью квадратных уравнений.
УЗИ
Групповой, индивидуальный контроль
П.23
103.
А: Решение задач с помощью квадратных уравнений.
УПЗУ
Групповой, индивидуальный контроль
П.23
104.
А: Теорема Виета.
УОНМ
Групповой, индивидуальный контроль
П.24
105.
А: Теорема Виета.
УЗИ
Групповой, индивидуальный контроль
П.24
106.
А: Подготовка к контрольной работе.
УОСЗ
Групповой, индивидуальный контроль
107.
А: Контрольная работа по теме «Квадратное уравнение и его корни».
УПКЗУ
Индивидуальный контроль
108.
А: Работа над ошибками в контрольной работе.
УКЗ
Индивидуальный контроль
109.
А: Решение дробных рациональных уравнений.
УОНМ
Групповой, индивидуальный контроль
П.25
110.
А: Решение дробных рациональных уравнений.
УЗИ
Групповой, индивидуальный контроль
П.25
111.
А: Решение дробных рациональных уравнений.
УПЗУ
Групповой, индивидуальный контроль
П.25
112.
А: Решение задач с помощью рациональных уравнений.
УОНМ
Групповой, индивидуальный контроль
П.26
113.
А: Решение задач с помощью рациональных уравнений.
УЗИ
Групповой, индивидуальный контроль
П.26
114.
А: Решение задач с помощью рациональных уравнений.
УПЗУ
Групповой, индивидуальный контроль
П.26
115.
А: Решение задач с помощью рациональных уравнений.
УПЗУ
Групповой, индивидуальный контроль
П.26
116.
А: Подготовка к контрольной работе.
УОСЗ
Групповой, индивидуальный контроль
117.
А: Контрольная работа по теме «Дробные рациональные уравнения».
УПКЗУ
Индивидуальный контроль
118.
А: Работа над ошибками в контрольной работе.
УКЗ
Индивидуальный контроль
119.
Г: Пропорциональные отрезки.
УОНМ
Групповой, индивидуальный контроль
П.56
120.
Г: Определение подобных треугольников. Отношение площадей подобных треугольников.
УОНМ
Групповой, индивидуальный контроль
П.57,58
121.
Г: Первый признак подобия треугольников.
УОНМ
Групповой, индивидуальный контроль
П.59
122.
Г: Первый признак подобия треугольников.
УЗИ
Групповой, индивидуальный контроль
П.59
123.
Г: Второй признак подобия треугольников.
УОНМ
Групповой, индивидуальный контроль
П.60
124.
Г: Третий признак подобия треугольников.
УОНМ
Групповой, индивидуальный контроль
П.61
125.
Г: Подготовка к контрольной работе.
УОСЗ
Групповой, индивидуальный контроль
126.
Г: Контрольная работа по теме «Признаки подобия треугольников».
УПКЗУ
Индивидуальный контроль
127.
Г: Работа над ошибками в контрольной работе.
УКЗ
Индивидуальный контроль
128.
Г: Средняя линия треугольника.
УОНМ
Групповой, индивидуальный контроль
П.62
129.
Г: Средняя линия треугольника.
УЗИ
Групповой, индивидуальный контроль
П.62
130.
Г: Пропорциональные отрезки в прямоугольном треугольнике.
УОНМ
Групповой, индивидуальный контроль
П.63
131.
Г: Пропорциональные отрезки в прямоугольном треугольнике.
УЗИ
Групповой, индивидуальный контроль
П.63
132.
Г: Практические приложения подобия треугольников. О подобии произвольных фигур.
УОНМ
Групповой, индивидуальный контроль
П.64,65
133.
Г: Синус, косинус и тангенс острого угла прямоугольного треугольника.
УОНМ
Групповой, индивидуальный контроль
П.66
134.
Г: Значения синуса, косинуса и тангенса для углов 300, 450 и 600.
УОНМ
Групповой, индивидуальный контроль
П.67
135.
Г: Значения синуса, косинуса и тангенса для углов 300, 450 и 600.
УЗИ
Групповой, индивидуальный контроль
П.67
136.
Г: Подготовка к контрольной работе.
УОСЗ
Групповой, индивидуальный контроль
137.
Г: Контрольная работа по теме «Соотношения между сторонами и углами прямоугольного треугольника».
УПКЗУ
Индивидуальный контроль
138.
А: Числовые неравенства.
УОНМ
Групповой, индивидуальный контроль
П.28
139.
А: Числовые неравенства.
УЗИ
Групповой, индивидуальный контроль
П.28
140.
А: Свойства числовых неравенств.
УОНМ
Групповой, индивидуальный контроль
П.29
141.
А: Свойства числовых неравенств.
УЗИ
Групповой, индивидуальный контроль
П.29
142.
А: Сложение и умножение числовых неравенств.
УОНМ
Групповой, индивидуальный контроль
П.30
143.
А: Сложение и умножение числовых неравенств.
УЗИ
Групповой, индивидуальный контроль
П.30
144.
А: Погрешность и точность приближения.
УОНМ
Групповой, индивидуальный контроль
П.31
145.
А: Подготовка к контрольной работе.
УОСЗ
Групповой, индивидуальный контроль
146.
А: Контрольная работа по теме «Числовые неравенства и их свойства».
УПКЗУ
Индивидуальный контроль
147.
А: Работа над ошибками в контрольной работе.
УКЗ
Индивидуальный контроль
148.
А: Пересечение и объединение множеств.
УОНМ
Групповой, индивидуальный контроль
П.32
149.
А: Пересечение и объединение множеств.
УЗИ
Групповой, индивидуальный контроль
П.32
150.
А: Числовые промежутки.
УОНМ
Групповой, индивидуальный контроль
П.33
151.
А: Числовые промежутки.
Групповой, индивидуальный контроль
П.33
152.
А: Решение неравенств с одной переменной.
УОНМ
Групповой, индивидуальный контроль
П.34
153.
А: Решение неравенств с одной переменной.
УЗИ
Групповой, индивидуальный контроль
П.34
154.
А: Решение систем неравенств с одной переменной.
УОНМ
Групповой, индивидуальный контроль
П.35
155.
А: Решение систем неравенств с одной переменной.
УЗИ
Групповой, индивидуальный контроль
П.35
156.
А: Подготовка к контрольной работе.
УОСЗ
Групповой, индивидуальный контроль
157.
А: Контрольная работа по теме «Неравенства с одной переменной и их системы».
УПКЗУ
Индивидуальный контроль
158.
А: Работа над ошибками в контрольной работе.
УКЗ
Индивидуальный контроль
159.
Г: Взаимное расположение прямой и окружности.
УОНМ
Групповой, индивидуальный контроль
П.68
160.
Г: Касательная к окружности.
УОНМ
Групповой, индивидуальный контроль
П.69
161.
Г: Касательная к окружности.
УЗИ
Групповой, индивидуальный контроль
П.69
162.
Г: Градусная мера дуги окружности.
УОНМ
Групповой, индивидуальный контроль
П.70
163.
Г: Теорема о вписанном угле.
УОНМ
Групповой, индивидуальный контроль
П.71
164.
Г: Теорема о вписанном угле.
УЗИ
Групповой, индивидуальный контроль
П.71
165.
Г: Решение задач по теме «Центральные и вписанные углы».
УПЗУ
Групповой, индивидуальный контроль
166.
Г: Свойства биссектрисы угла и серединного перпендикуляра к отрезку.
УОНМ
Групповой, индивидуальный контроль
П.72
167.
Г: Свойства биссектрисы угла и серединного перпендикуляра к отрезку.
УЗИ
Групповой, индивидуальный контроль
П.72
168.
Г: Теорема о пересечении высот треугольника.
УОНМ
Групповой, индивидуальный контроль
П.73
169.
Г: Вписанная окружность.
УОНМ
Групповой, индивидуальный контроль
П.74
170.
Г: Вписанная окружность.
УЗИ
Групповой, индивидуальный контроль
П.74
171.
Г: Описанная окружность.
УОНМ
Групповой, индивидуальный контроль
П.75
172.
Г: Описанная окружность.
УЗИ
Групповой, индивидуальный контроль
П.75
173.
Г: Подготовка к контрольной работе.
УОСЗ
Групповой, индивидуальный контроль
174.
Г: Контрольная работа по теме «Окружность».
УПКЗУ
Индивидуальный контроль
175.
Г: Работа над ошибками в контрольной работе.
УКЗ
Индивидуальный контроль
176.
А: Определение степени с целым отрицательным показателем.
УОНМ
Групповой, индивидуальный контроль
П.37
177.
А: Определение степени с целым отрицательным показателем.
УЗИ
Групповой, индивидуальный контроль
П.37
178.
А: Определение степени с целым отрицательным показателем.
УПЗУ
Групповой, индивидуальный контроль
П.37
179.
А: Свойства степени с целым показателем.
УОНМ
Групповой, индивидуальный контроль
П.38
180.
А: Свойства степени с целым показателем.
УЗИ
Групповой, индивидуальный контроль
П.38
181.
А: Свойства степени с целым показателем.
УПЗУ
Групповой, индивидуальный контроль
П.38
182.
А: Стандартный вид числа.
УОНМ
Групповой, индивидуальный контроль
П.39
183.
А: Стандартный вид числа.
УЗИ
Групповой, индивидуальный контроль
П.39
184.
А: Подготовка к контрольной работе.
УОСЗ
Групповой, индивидуальный контроль
185.
А: Контрольная работа по теме «Степень с целым показателем и её свойства».
УПКЗУ
Индивидуальный контроль
186.
А: Работа над ошибками в контрольной работе.
УКЗ
Индивидуальный контроль
187.
А: Сбор и группировка статистических данных.
УОНМ
Групповой, индивидуальный контроль
П.40
188.
А: Сбор и группировка статистических данных.
УЗИ
Групповой, индивидуальный контроль
П.40
189.
А: Наглядное представление статистической информации.
УОНМ
Групповой, индивидуальный контроль
П.41
190.
А: Наглядное представление статистической информации.
УЗИ
Групповой, индивидуальный контроль
П.41
191.
Г: Итоговое повторение.
УПЗУ
Групповой, индивидуальный контроль
192.
Г: Итоговое повторение.
УПЗУ
Групповой, индивидуальный контроль
193.
А: Итоговое повторение.
УПЗУ
Групповой, индивидуальный контроль
194.
А: Итоговое повторение.
УПЗУ
Групповой, индивидуальный контроль
195.
А: Итоговое повторение.
УПЗУ
Групповой, индивидуальный контроль
196.
А: Итоговое повторение.
УПЗУ
Групповой, индивидуальный контроль
197.
А: Итоговое повторение.
УПЗУ
Групповой, индивидуальный контроль
198.
А: Итоговое повторение.
УПЗУ
Групповой, индивидуальный контроль
199.
А: Итоговое повторение.
УПЗУ
Групповой, индивидуальный контроль
200.
А: Итоговое повторение.
УПЗУ
Групповой, индивидуальный контроль
201.
А: Итоговое повторение.
УПЗУ
Групповой, индивидуальный контроль
202.
А: Итоговое повторение.
УПЗУ
Групповой, индивидуальный контроль
203.
А: Административная контрольная работа.
УПКЗУ
Индивидуальный контроль
204.
А: Работа над ошибками в контрольной работе.
УКЗ
Индивидуальный контроль
205.
Г: Резерв.
206.
Г: Резерв.
207.
А: Резерв.
208.
А: Резерв.
209.
А: Резерв.
210
А: Резерв.
УОНМ - урок ознакомления с новым материалом УЗИ - урок закрепления изученного
УПЗУ - урок применения знаний и умений УОСЗ - урок обобщения и систематизации знаний
УПКЗУ - урок проверки и коррекции знаний и умений УКЗ - урок коррекции знаний
КР - контрольная работа
Учебно-методическая литература
Основная литература:
-
Программы общеобразовательных учреждений. Геометрия 7-9 классы. Составитель Бурмистрова Т.А. - М.: «Просвещение», 2009.
-
Программы общеобразовательных учреждений. Алгебра 7-9 классы. Составитель Бурмистрова Т.А. - М.: «Просвещение», 2009.
Алгебра: Учеб. Для 8 кл. общеобразоват. Учреждений/Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова; Под ред. С.А. Теляковского - М.: Просвещение, 2009.
Жохов В.И., Макарычев Ю.Н., Миндюк Н.Г. Дидактические материалы по алгебре для 8 класса. - М.: Просвещение, 2008.
Уроки алгебры в 8 классе: Метод. Рекомендации для учителя/В.И. Жохов, Г.Д. Карташев - М.: Просвещение, 2008.
Геометрия: Учеб. Для 7-9 кл. общеобразоват. Учреждений/Л.С.Атанасян, В.Ф.Бутузов, С.Б.Кадомцев и др. - М.: Просвещение, 2004-2008.
Зив Б.Г. Дидактические материалы по геометрии для 8 класса. - М.: Просвещение, 2009.
Изучение геометрии в 7-9 классах: Метод. Рекомендации для учителя/Л.С.Атанасян, В.Ф.Бутузов, Ю.А.Глазков и др. - М.: Просвещение, 2008.
Дополнительная литература
-
И.Н. Данкова, С.Ф. Кузьминых, Н.Г. Пенкина, О.В. Сушкова Элементы статистики и теории вероятностей (поурочные разработки, алгебра 7-8 классы) - Воронеж, 2008.
-
Ершова А.П., Голобородько В.В., Ершова А.С. Самостоятельные и контрольные работы по алгебре и геометрии для 8 класса. - 7-е изд., испр. И доп. - М.: Илекса, - 2007, - 208 с.
Примерные контрольно-измерительные материалы