- Учителю
- Урок по теме Показательные и логарифмические уравнения и неравенства в ЕГЭ
Урок по теме Показательные и логарифмические уравнения и неравенства в ЕГЭ
</ Открытый урок по теме "Показательные и логарифмические уравнения и неравенства в ЕГЭ ". 11-й класс
Класс: 11 "А"
Тип урока: обобщающе-повторительный.
Цели урока:
Дидактическая:
Повторить свойства показательной и логарифмической функций.
Отработать навыки решения показательных и логарифмических уравнений и неравенств
Проверить умение учащихся решать данные уравнения и неравенства. Подготовка к ЕГЭ.
Развивающая:
развивать способности применять теоретические знания на практике;
развивать навыки работы с тестовыми заданиями;
развивать навыки самоконтроля , логическое мышление, память, внимание.
Воспитательная:
Воспитывать аккуратность, внимательность, умение обобщать изученный материал, воспитывать умению выслушивать мнение других.
Методы обучения: исследовательский, репродуктивный.
Формы организации познавательной деятельности: фронтальная, индивидуальная, парная.
Оборудование урока: презентация, компьютер, проектор, интерактивная доска, карточки с тестовыми заданиями.
Ход урока.
1.Организационный момент.
Учитель:
Сегодня на уроке мы с вами повторим и закрепим тему: «Решение показательных и логарифмических уравнений и неравенств». Задания которые мы будем решать составлены с учетом требований при подготовке к ЕГЭ.
I этап. Устная работа:
II этап. Работа в парах ( задания уровня ЕГЭ).
Класс делится на пары, для которых предлагаются разные задания.
1 пара.
1. Найдите корень (или сумму корней, если их несколько) уравнения
2. Решите неравенство
1)
2) нет решения
3) [1;
4) (
2 пара.
-
Найдите корень (или сумму корней, если их несколько) уравнения
-
Решите неравенство
-
(2;
-
(2; 10]
-
(-]
-
[10;
-
Задания показываются на экране (доске) с комментированием в качестве проверки.
-
III Фронтальный опрос ( уравнения решаются у доски)
-
IV. Немного истории математики:
-
V.Физминутка
-

-
VI. Тестовая работа
-
Тренировочный тест по подготовке к ЕГЭ.( за 7-10 минут необходимо выполнить работу и заполнить соответствующий бланк, оценки за тест будут известны к следующему уроку)
- Самостоятельная работа
-
1 - вариант
-
Самостоятельная работа
-
- вариант
-
1.[1Б] Найдите множество значений функции
-
1) ( 2) (
-
3) 4) (25;
-
1. .[1Б] Найдите множество значений функции
-
1) ( 2) (
-
3) 4) (36;
-
2. [1Б] Найдите значение выражения
-
1) -4; 2) 4; 3) -2; 4) 2.
-
2. [1Б] Найдите значение выражения
-
1) 1+lg5; 2) 5; 3) 4; 4) 3.
-
3.[1Б] Решите неравенство:
-
1) [-1,5; 2) (
-
3) 4) [0,75;
-
3.[1Б] Решите неравенство:
-
1) [; 2) (
-
3) 4) [;
-
4) .[1Б] Укажите функцию, возрастающую на всей области определения
-
1) 2)
-
3) 4)
-
4) .[1Б] Укажите функцию, возрастающую на всей области определения
-
1) 2)
-
3) 4)
-
5.[1Б] Решите неравенство
-
(4; 2) (4; 6,5]
-
( 4) (6,5;
-
5.[1Б] Решите неравенство
-
(18; 2) (2;
-
( 4) (2; 18]
-
6 .[2Б] Найдите корень (или сумму корней, если их несколько), корней уравнения
-
6 .[2Б] Найдите корень (или сумму корней, если их несколько), корней уравнения
-
7.[2Б] Найдите корень (или сумму корней, если их несколько), корней уравнения
-
7.[2Б] Найдите корень (или сумму корней, если их несколько), корней уравнения
-
-
Критерии оценивания: «5» 8 - 9 баллов, «4» 6 - 7 баллов, «3» 4 - 5 баллов
-
VII. Дополнительное задание (разбор решения):
-
Подведение итогов и рефлексия:
-
VIII.Домашнее задание:
-
1 вариантВ1. Найдите корень уравнения
-
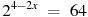
-
В2. найдите корень уравнения
-
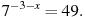
-
В3. Найдите корень уравнения
-
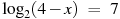
-
В4. Найдите корень уравнения
-
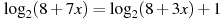
-
В5 Найдите корень уравнения
-
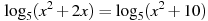
-
В6. Решите уравнение . Если уравнение имеет более одного корня, в ответе укажите меньший из них
-
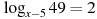
-
-
-
Ответы:
-
2 вариантВ1. Найдите корень уравнения
-
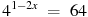
-
В2. Найдите корень уравнения
-
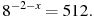 64
64
-
В3. Найдите корень уравнения
-
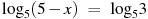
-
В4. Найдите корень уравнения
-
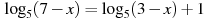
-
В5. Найдите корень уравнения
-
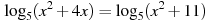
-
В6. Решите уравнение . Если уравнение имеет более одного корня, в ответе укажите меньший из них
-
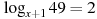
-
-
-
Ответы:
- Дополнительное задание из ЕГЭ профильного уровня (2 части):
-

-
Решите уравнение
-
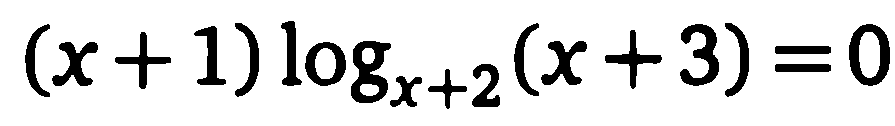
-
решите неравенство
-
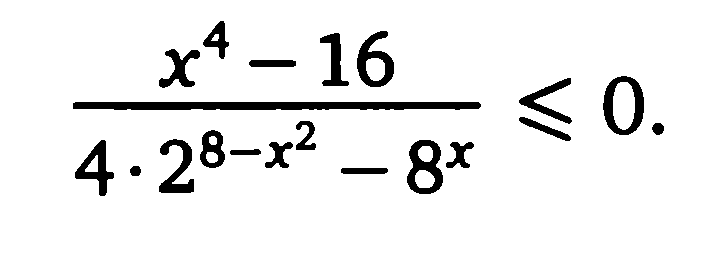
-
Приложение Памятка к уроку:
- (a>0, a≠1), f(x)=g(x)
-
af(x)=b, a>0, b>0 f(x)=logab
-
-
Свойства степенейахау=ах+у; ах:ау=ах-у;
-
(ах)у=аху; (аb)x=axbx
-
;a0=1
-
-
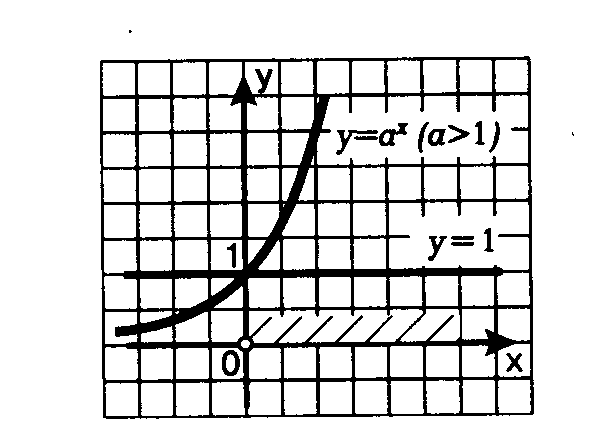
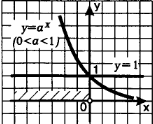
-
2. способы решения показательных уравнений
-
-приведение степеней к одному основанию в уравнении ;
-
-разложение на множители;
-
-введение новой переменной;
-
-деление на степень;
-
-графический способ;
-
-оценивание частей уравнения;
-
-подбор корня.
-
Логарифмической функцией называется функция у=logах, где а - заданное число, а>0, а≠1 Уравнения вида
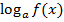 =
=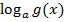 ,
где а
,
где а 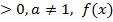 >0,
>0, 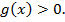
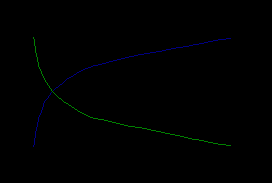
-
Простейшим примером логарифмического уравнения служит уравнение
loga х = б (а > 0, а≠ 1, б>0 ) -
Способы решения
-
Решение уравнений на основании определения логарифма, например, уравнение loga х = б (а > 0, а≠ 1, б>0 ) имеет решение х = аb.
-
Метод потенцирования. Под потенцированием понимается переход от равенства, содержащего логарифмы, к равенству, не содержащему их:
если , loga f(х) = loga g(х), то f(х) = g(х), f(х)>0, g(х)>0 , а > 0, а≠ 1. -
Метод введение новой переменной.
-
Метод логарифмирования обеих частей уравнения.
-
Метод приведения логарифмов к одному и тому же основанию.
-
Функционально - графический метод.
-