- Учителю
- Рабочая тетрадь по темеРешение тригонометрических уравнений
Рабочая тетрадь по темеРешение тригонометрических уравнений

Рабочая тетрадь рассчитана на самостоятельное (или под руководством преподавателя) изучение обучающимися темы «Тригонометрические уравнения».
Структура рабочей тетради соответствует разделам «Алгебра и начала анализа» для 10-11 классов.
Рабочая тетрадь включает следующие темы: «Понятие тригонометрического уравнения», «Частные случаи тригонометрических уравнений», «Решение тригонометрических уравнений».
В пособии коротко представлены: теория (более подробно в учебнике), разобранные примеры решений заданий, различные варианты заданий по материалам учебного пособия, позволяющие обучающимся работать самостоятельно.
Даются проверочные задания для закрепления, контроля и самоконтроля знаний обучающихся. Пособие с успехом можно использовать при подготовке к сдаче экзамена, доступная форма изложения позволит быстро восстановить знания.
Содержание
1. Решение уравнений вида cos x = a
2. Решение уравнений вида sin x = a
3. Решение уравнений вида tg x = a
4. Решение тригонометрических уравнений, приводимых к квадратному
5. Решение однородных тригонометрических уравнений
6. Проверь себя
Решение уравнений вида cos x = a
Уравнение cos x = a имеет решение, если −1 ≤ a ≤ 1.
Учитывая периодичность функции косинус, получим множества корней уравнения cos x = a:
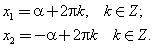
или
![]()
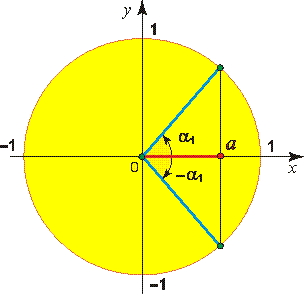
Частные случаи решения уравнения cos x = a.
Уравнение cos x = a имеет решение при а _____________
Какой формулой выражается это решение? __________________________
Имеет ли решение уравнение cos x = a при
![]()
![]()
![]() 1.
______________
1.
______________
Значение а при решении уравнения cos x = a откладывается на оси ______
В каком промежутке находится arccos a ? _______________________
Arccos (- а) = ________________________________________
Решение уравнения cos x = 1 _______________________________________
Решение уравнения cos x = - 1 ________________________________________
Решение уравнения cos x = 0 _________________________________________
Обрати внимание на решение примеров:
-
cos x =
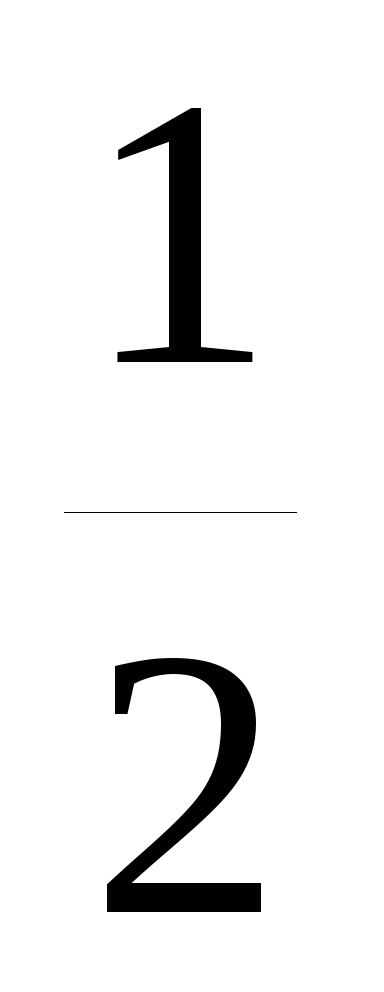 cos x = -
cos x = - 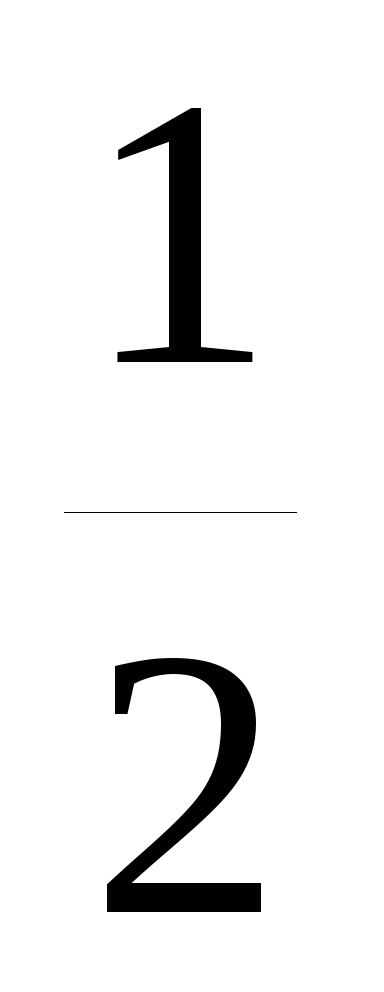
х = ![]() arccos
arccos ![]() +
2
+
2![]() n,
n
n,
n ![]() Z х
=
Z х
= ![]() arccos (-
arccos (-![]() ) +
2
) +
2![]() n,
n
n,
n ![]() Z
Z
т.к. arccos ![]() =
=
![]() ,
то т.к.. arccos (-
,
то т.к.. arccos (- ![]() ) =
) =
![]() -
-
![]() =
=
![]() ,
то
,
то
х = ![]()
![]() +
2
+
2![]() n,
n
n,
n ![]() Z х
=
Z х
= ![]()
![]() +
2
+
2![]() n,
n
n,
n ![]() Z
Z
Попробуй решить сам:
cos x = ![]() cos x = -
cos x = - ![]()
________________________ __________________________
_______________________ __________________________
______________________ _ __________________________
cos 4x = 1 cos (x +![]() )
=0
)
=0
________________________ _____________________________
__________________________ _________________________________
___________________________ _______________________________
ЗАПОМНИ!

Решение уравнений вида sin x = a
Уравнение sin x =
a имеет решение, если −1 ≤ a ≤ 1.x1
= α1; x2 = α2.
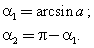
Учитывая периодичность функции синус, получим множества корней уравнения
sin x = a:
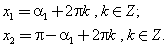
или
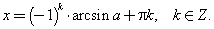
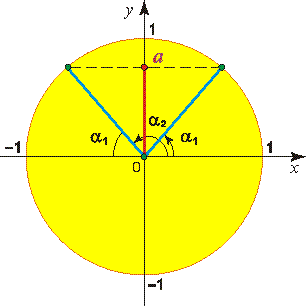
Частные случаи решения уравнения sin x = a
Какой формулой выражается это решение? __________________________
Имеет ли решение уравнение sin x = a при
![]()
![]()
![]() 1. Ответ ______________
1. Ответ ______________
Значение а при решении уравнения sin x = a откладывается на оси ______
В каком промежутке находится arcsin a ? _______________________
Arcsin (- а) = ________________________________________
Решение уравнения sin x = 1 _______________________________________
Решение уравнения sin x = - 1 ________________________________________
Решение уравнения sin x = 0 _________________________________________
Обрати внимание на решение примеров:
-
sin x =
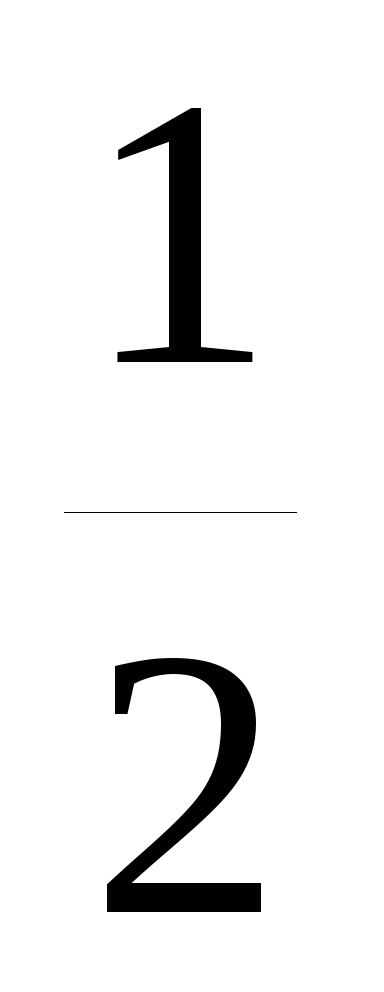 sin x = -
sin x = - 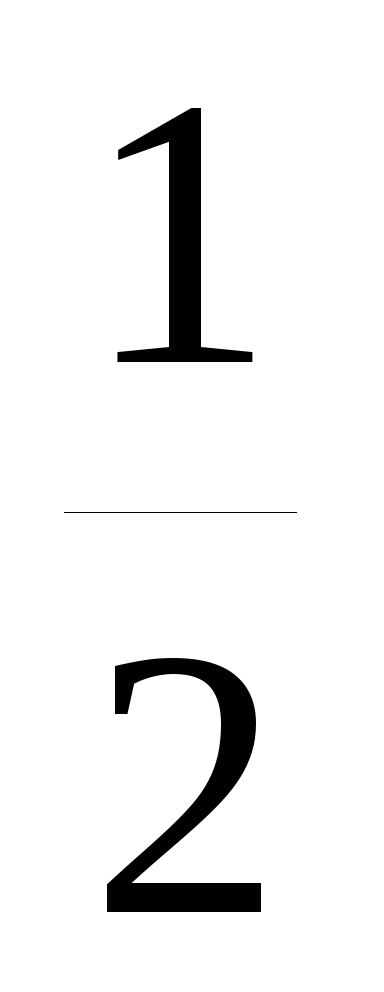
х = (- 1)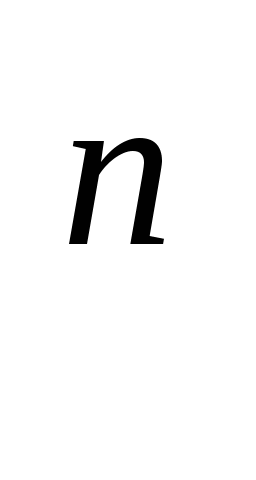 arcsin
arcsin 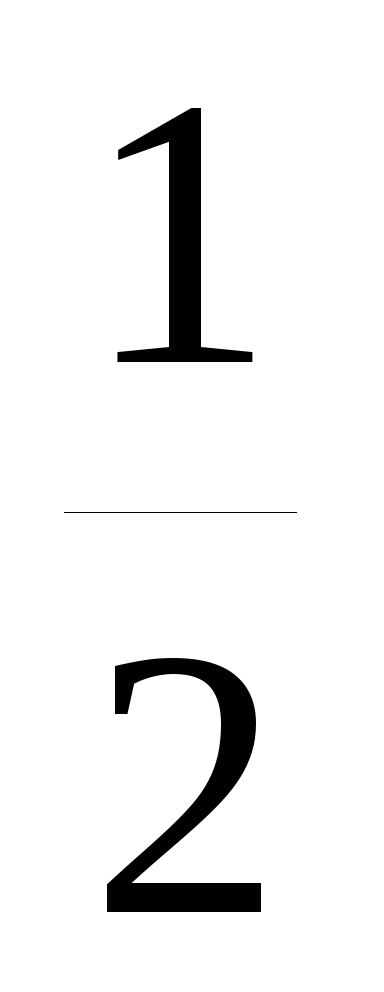 +
+  n,
n
n,
n 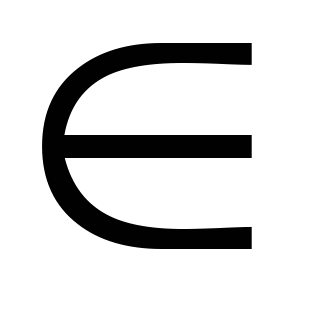 Z
х = (- 1)
Z
х = (- 1)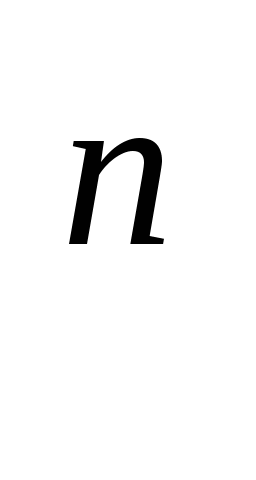 arcsin( -
arcsin( - 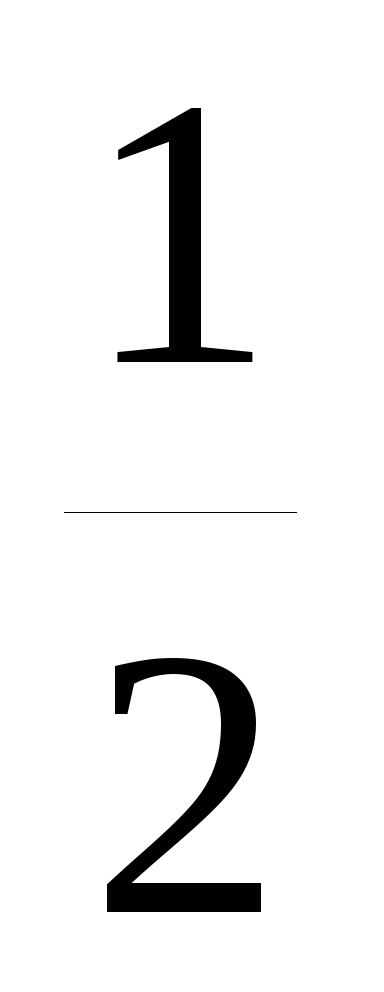 )
+
)
+  n,
n
n,
n 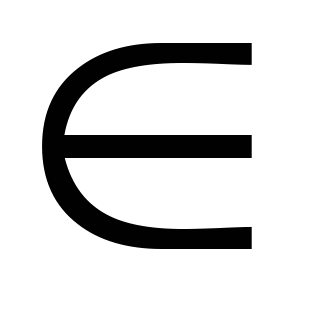 Z
Z
т.к. arcsin 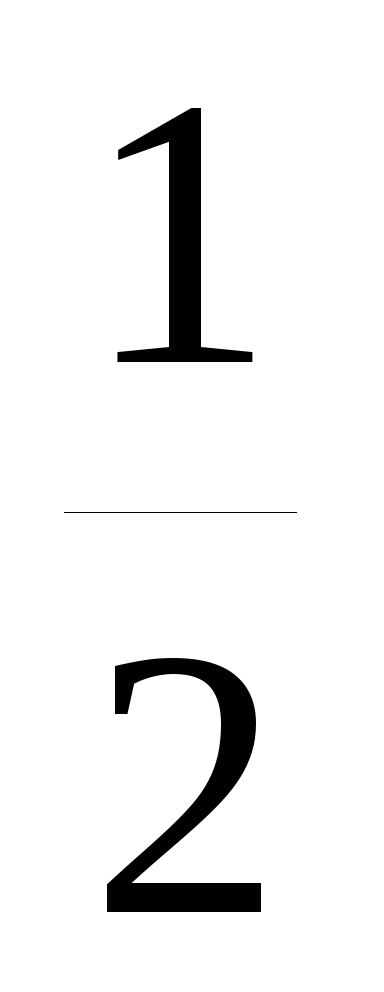 =
= 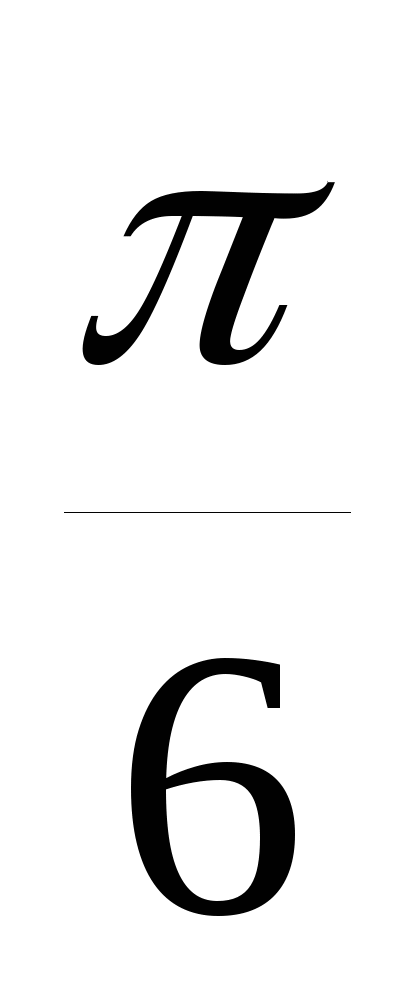 ,
то т.к. arcsin( -
,
то т.к. arcsin( - 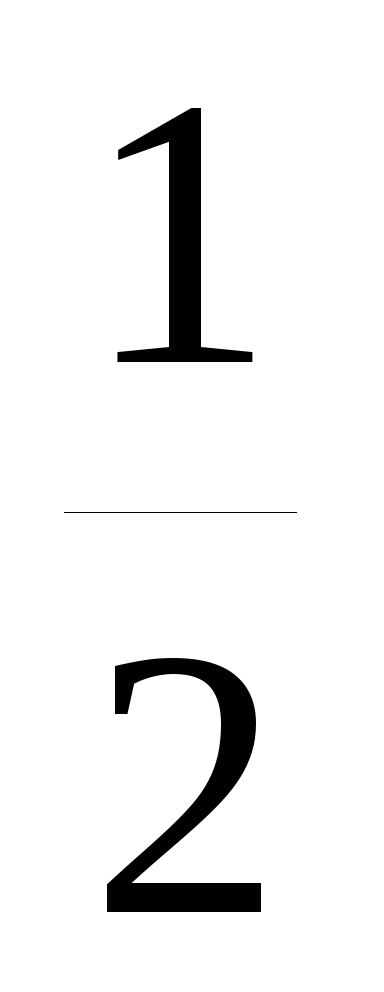 )
= -
)
= - 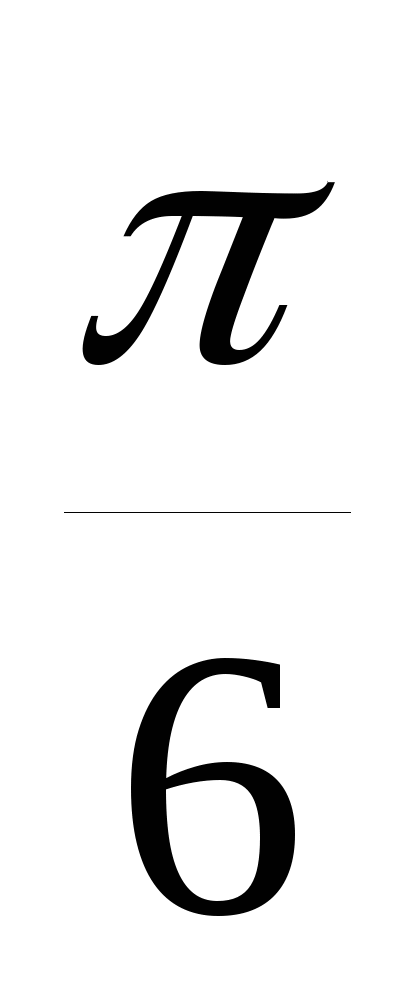 ,
то
,
то
х = (- 1)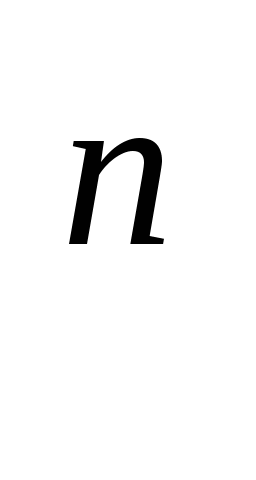
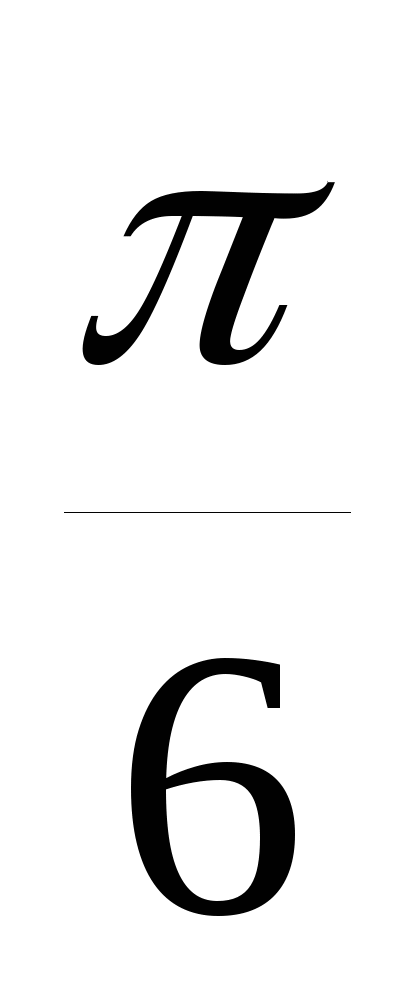 +
+
 n,
n
n,
n 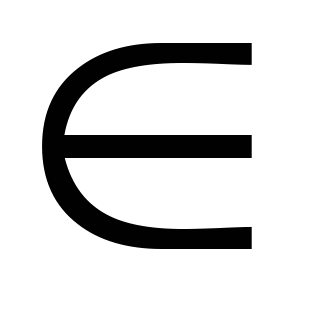 Z
х = (- 1)
Z
х = (- 1)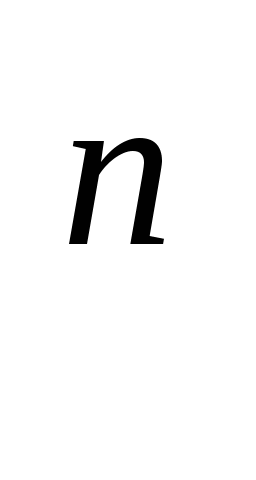 (
-
(
- 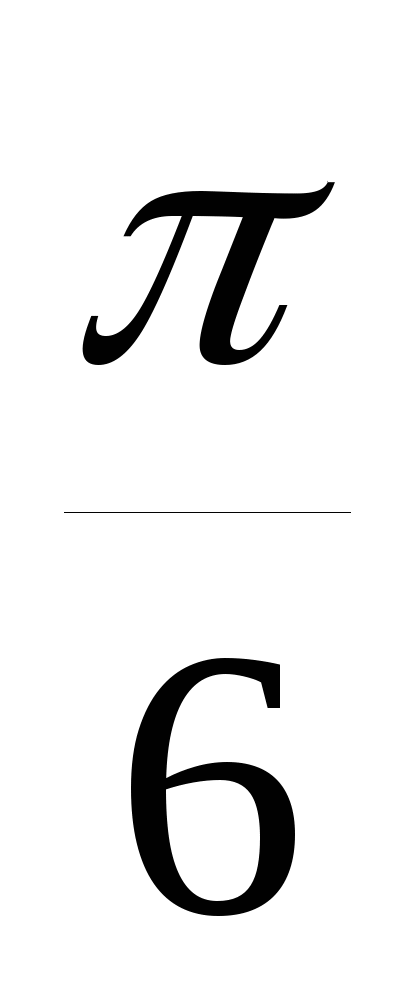 )+
)+
 n,
n
n,
n 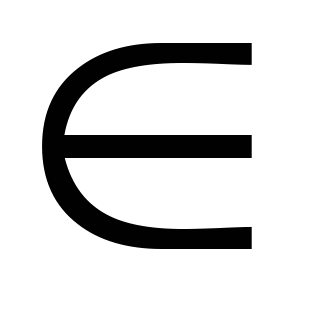 Z
Z
х = (- 1)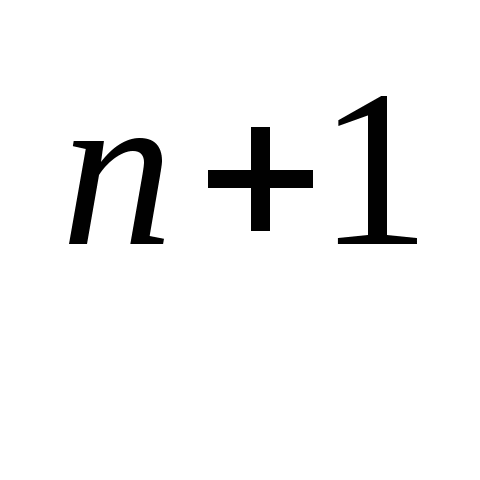
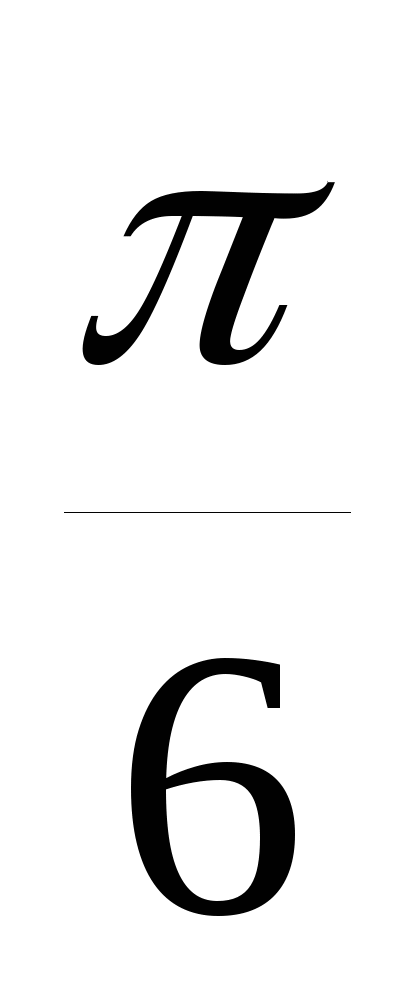 +
+
 n,
n
n,
n 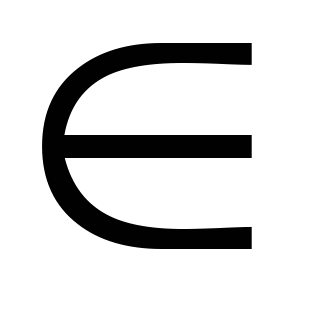 Z
Z
Попробуй решить сам:
sin x = 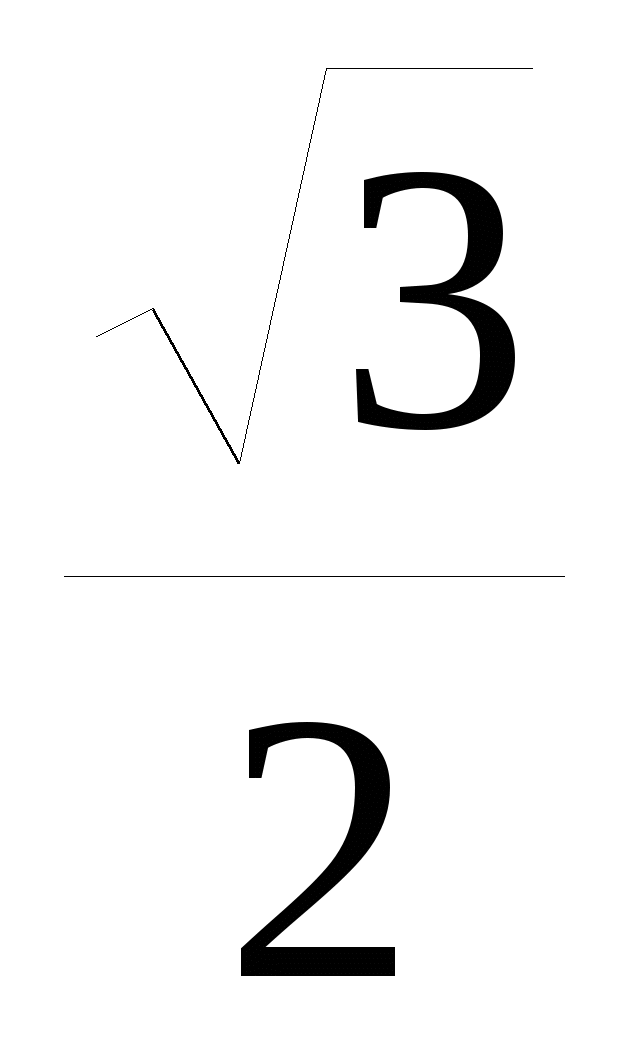 sin x = -
sin x = - 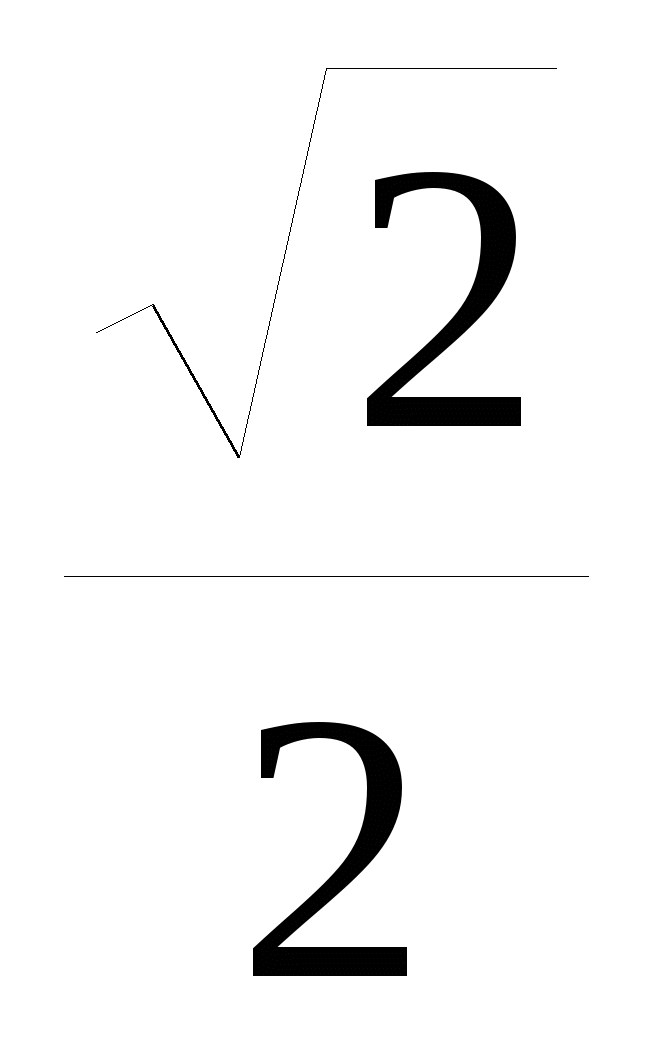 _______________________ __________________________
_______________________ __________________________
________________________ __________________________
________________________ __________________________
sin 2x = - 1 sin (x + 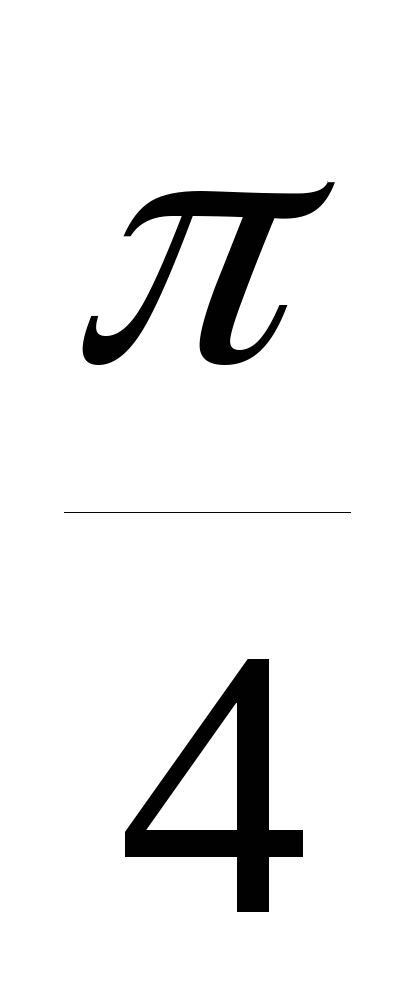 )
= 0
)
= 0
ЗАПОМНИ!
Решение уравнений вида tg x = a
Уравнение tg x = a имеет решение при любом а, так как область значений тангенса - вся числовая ось.
Значит, уравнение tg x = a на этом интервале имеет единственный корень. Учитывая, что тангенс периодическая функция, то множества решений уравнения записывают так:
![]()
tg x - это ордината точки Т, пересечения прямой ОР1 с линией тангенсов Р0Т.
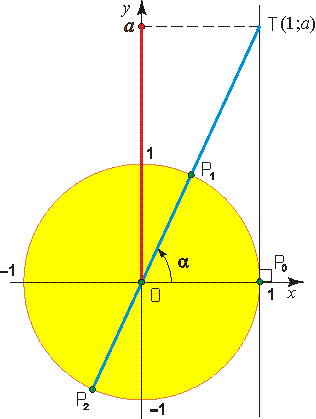
В каком промежутке находится arctg a? _________________________________
Общая формула для решения уравнения tg х = а _________________________
arctg (-а) = __________________________________________
Обрати внимание на решение примеров:
-
Tg x =
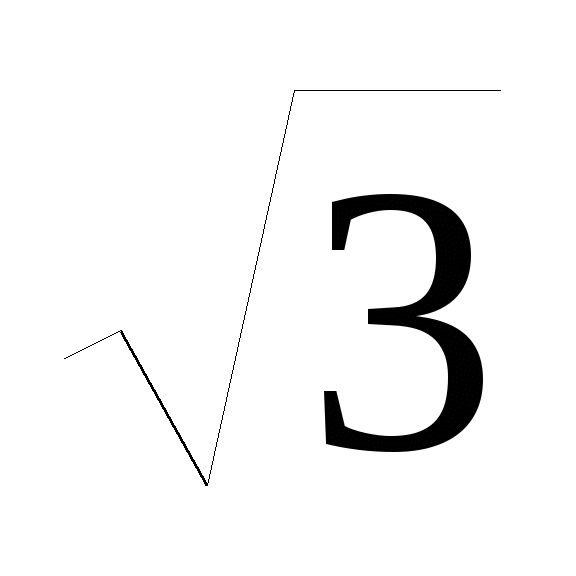 Tg x = -
Tg x = -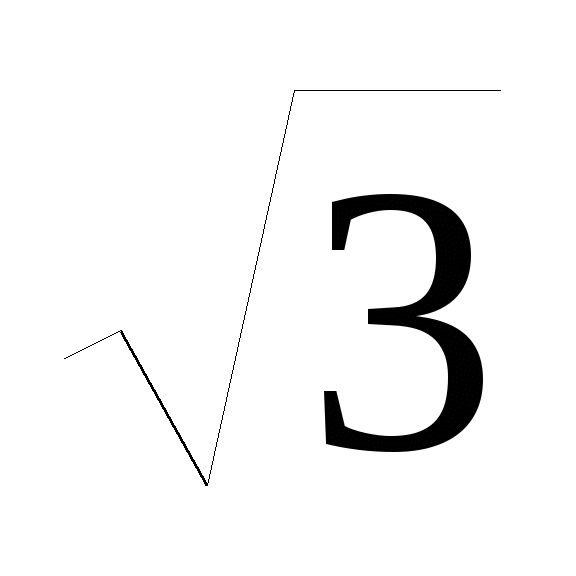
X = arctg ![]() +
+
![]() n,
n
n,
n ![]() Z.
X = arctg (-
Z.
X = arctg (-![]() )
+
)
+ ![]() n,
n
n,
n ![]() Z.
Z.
Т.к. arctg ![]() =
=
![]() ,
то т.к. arctg (-
,
то т.к. arctg (- ![]() )=
-
)=
- ![]() ,
то
,
то
x = ![]() +
+ ![]() n,
n
n,
n ![]() Z.
x = -
Z.
x = - ![]() +
+ ![]() n,
n
n,
n ![]() Z.
Z.
Попробуй решить сам:
Tg x = ![]()
_________________________________
_________________________________
_______________________________
Tg x = -1
_______________________________
______________________________
ЗАПОМНИ!
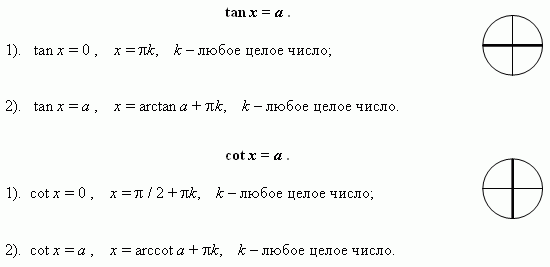
ТЕБЕ ПРИГОДИТСЯ!!!
Справедливы соотношения:
-
SIN
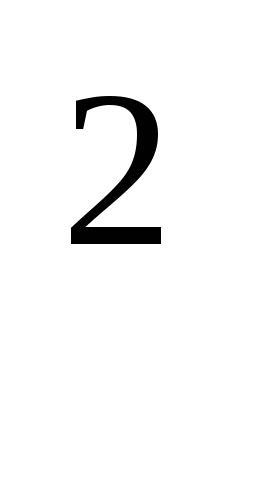
 =
1 - COS
=
1 - COS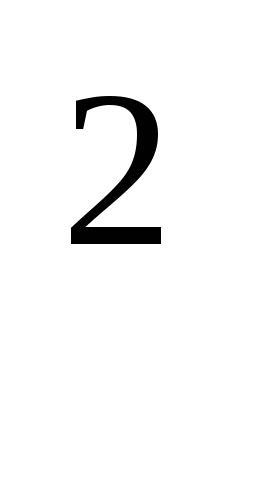
 (1);
(1);
-
COS
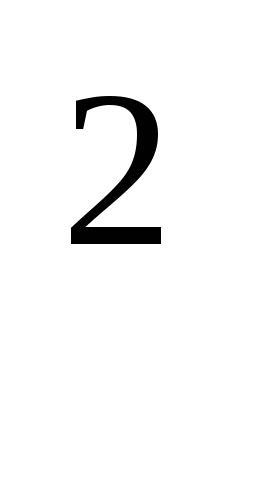
 =
1 - SIN
=
1 - SIN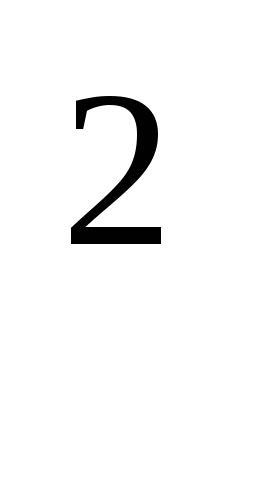
 (2).
(2).
Формулы корней уравнения:
-
Sin x = a
(3)
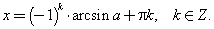
-
cos x = a
(4)
![]()
-
tg x = a
(5)
![]()
-
ах
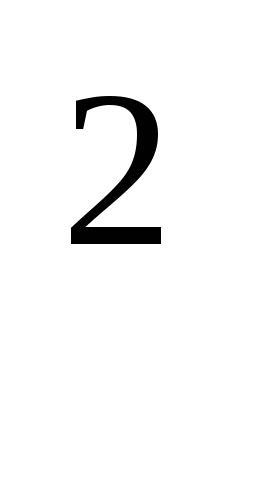 + bx + c =0
+ bx + c =0
x =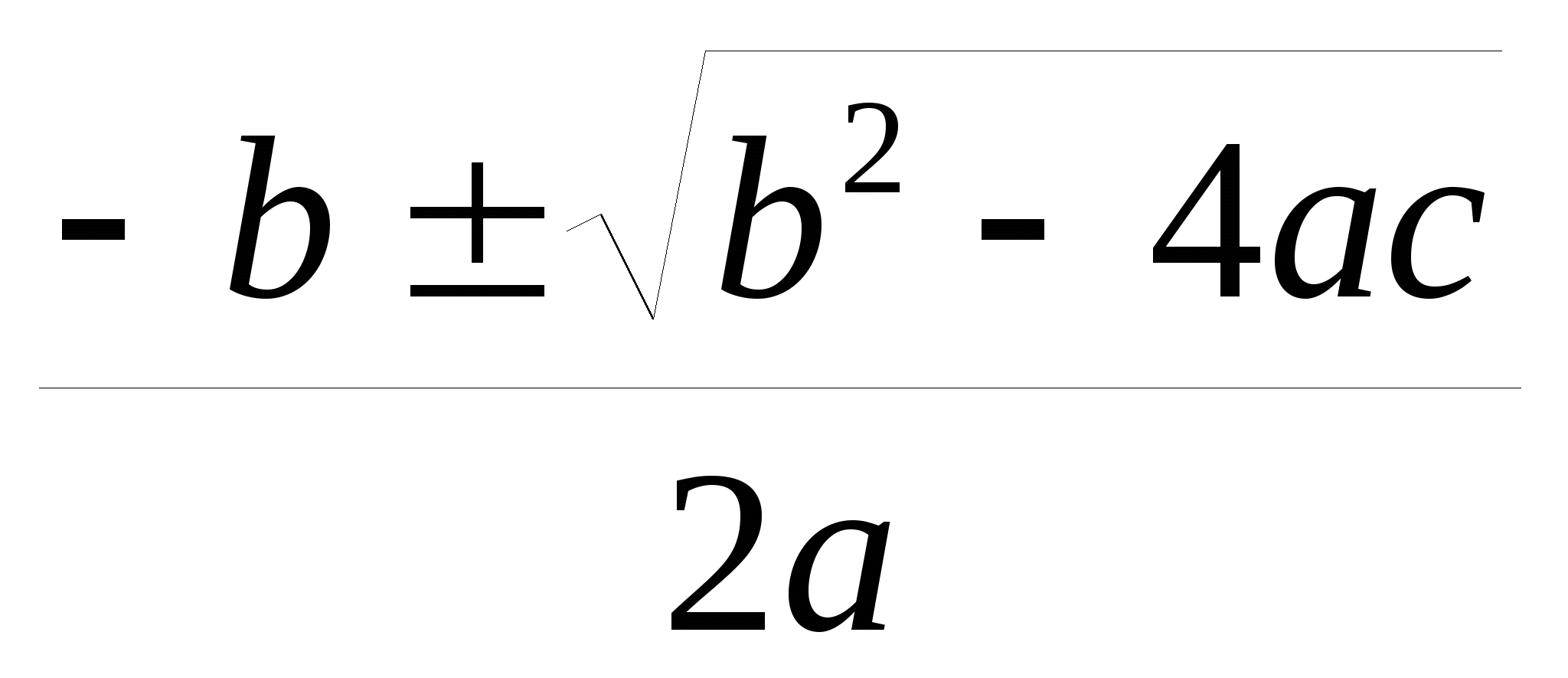 (6)
(6)
Решение тригонометрических уравнений, приводимых к квадратному.
Рассмотри решение следующих уравнений:
-
8 sin2 x - 6 sin x - 5 = 0;
Введём обозначение Sin x = a, тогда данное уравнение можно
записать в виде 8а![]() -
6а - 5 = 0.
-
6а - 5 = 0.
Решаем это квадратное уравнение относительно а.
а = ![]() ;
а
;
а![]() = -
= - ![]() ,
а
,
а![]() =
= ![]() .
.
Следовательно, Sin x = - ![]() или Sin x =
или Sin x = ![]() .
.
-
Решим уравнение Sin x = -
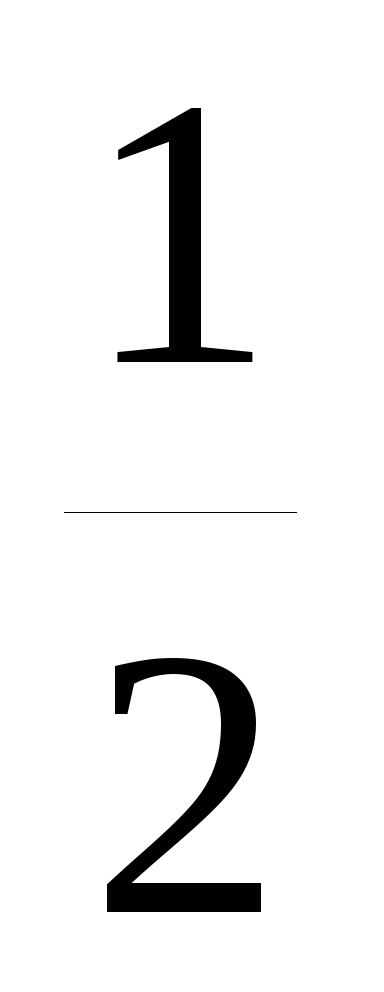
х = (- 1)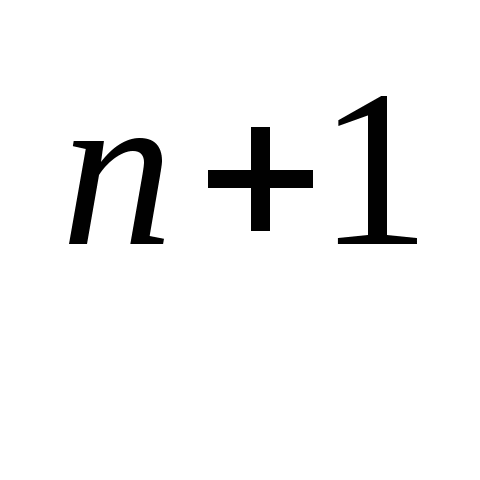
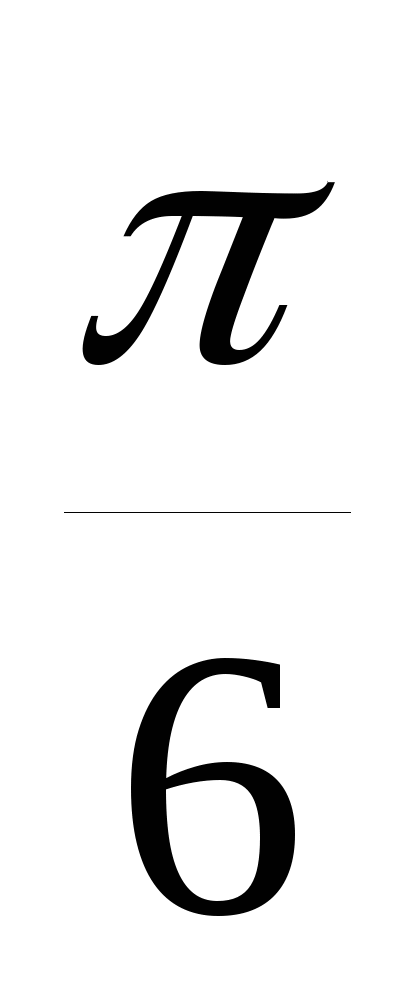 +
+
 n,
n
n,
n 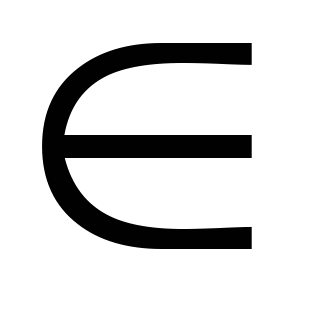 Z
.
Z
.
-
Решим уравнение Sin x =
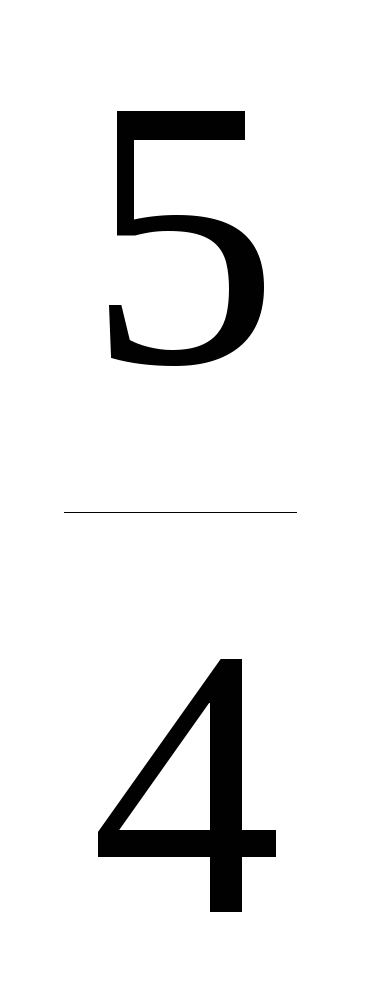 .
.
Это уравнение корней не имеет, так как Sin x не может быть больше единицы.
-
8cos2 x + 6 sin x - 3 = 0;
Заменяя cos2 x через 1 - SIN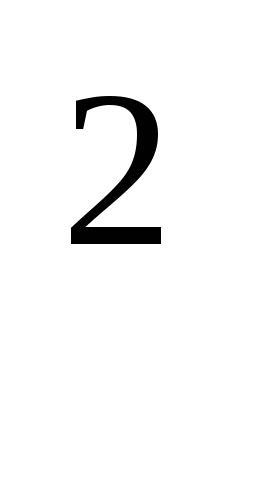 х,
получим 8(1 - SIN
х,
получим 8(1 - SIN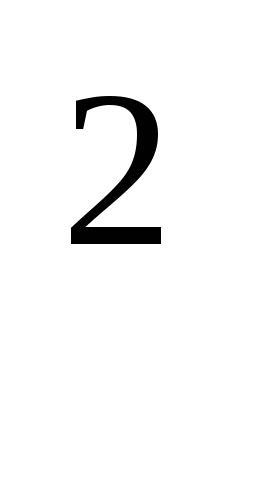 х)
+ 6 sin x - 3 = 0;
х)
+ 6 sin x - 3 = 0;
8 sin2 x - 6 sin x - 5 = 0
Пришли к уравнению, рассмотренному в первом примере.
Попробуй решить сам
3 sin2 x - 5 sin x - 2 = 0;
_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
2 sin2 x + 3 cos x = 0.
_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
6 sin2 x - 5 cos x + 5 = 0;
_____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
cos2 x + 2 sin x + 2 = 0;
__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Решение однородных тригонометрических уравнений
. Уравнение называется однородным относительно sin и cos, если все его члены одной и той же степени относительно sin и cos одного и того же угла.
-
Уравнения вида asinx + bcosx = 0 называют однородными тригонометрическими уравнениями первой степени;
-
Уравнения вида asin2х + bcosx sinx+ ccos2x = 0 называют однородными тригонометрическими уравнениями второй степени.
Ознакомься с решением примеров:
-
2sinx - 3cosx = 0
Поделив уравнение на cosx ![]() 0,
получим 2 tgх - 3 = 0, решаем это уравнение:
0,
получим 2 tgх - 3 = 0, решаем это уравнение:
Tgх =![]() ,
х = arctg
,
х = arctg![]() +
+ ![]() n,
n
n,
n ![]() Z.
Z.
-
Решить уравнение: 3sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2.
3sin 2 x + 4 sin x · cos x + 5 cos 2 x = 2sin 2 x + 2cos 2 x,
sin 2 x + 4 sin x · cos x + 3 cos 2 x = 0 ,
tg 2 x + 4 tg x + 3 = 0 , отсюда y 2 + 4y +3 = 0 ,
корни этого уравнения: y1 = 1, y2 = 3, отсюда
1) tg x = -1, 2) tg x = -3,
x = - ![]() +
+ ![]() n,
n
n,
n ![]() Z
. x = - arctg 3+
Z
. x = - arctg 3+ ![]() n,
n
n,
n ![]() Z
Z
Попробуй решить сам:
-
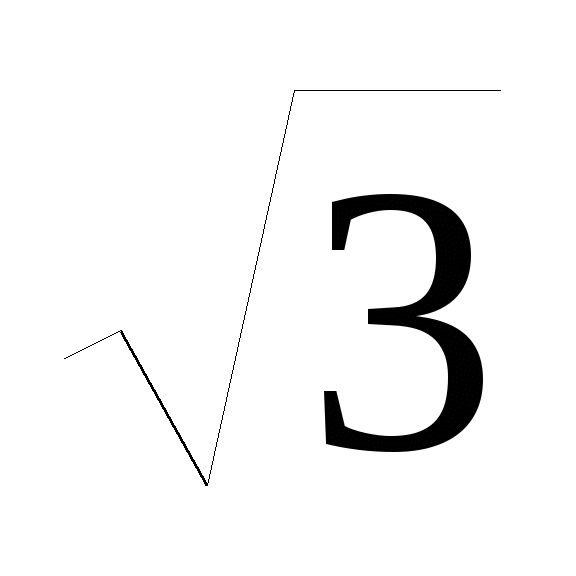 cos
x + sin x = 0
cos
x + sin x = 0
_______________________________________________________________ ______________________________________________________________ ______________________________________________________________
______________________________________________________________
-
sin x = 2 cos x
______________________________________________________________
______________________________________________________________
______________________________________________________________ ______________________________________________________________
______________________________________________________________
-
3 sin2 x - 4 sin x cos x + cos2 x = 0;
________________________________________________________________________
________________________________________________________________________
_______________________________________________________________________
_______________________________________________________________________ _______________________________________________________________________
-
6 sin2 x = 5 sin x cos x - cos2 x
_______________________________________________________________________ ______________________________________________________________________ _____________________________________________________________________ _____________________________________________________________________ __________________________________________________________________
Запомни!
Алгоритм решения уравнения a sin2+ bcosxsinx+ ccos2x =0
-
Посмотреть, есть ли в уравнении член asin2х.
-
Если этот член содержится, то уравнение решается делением обеих его частей на cos2x и последующем введением новой переменной y =tgx.
-
Если asin2х не содержится, то уравнение решается методом вынесения общего множителя за скобки.
ПРОВЕРЬ СЕБЯ
-
Решите уравнение, упростив левую часть:
а) cos![]() x - sin
x - sin![]() x
=
x
= ![]() ;
б) 2 sin
;
б) 2 sin![]() x
cos 2x = 1;
x
cos 2x = 1;
в) sin 3x cos (x + ![]() )
+ cos 3x sin (x +
)
+ cos 3x sin (x + ![]() )
= 0.
)
= 0.
-
Решите уравнение, сделав подстановку:
а) 2sin![]() x
- 5sin x + 2 = 0; б) 2 cos
x
- 5sin x + 2 = 0; б) 2 cos![]() x
+ 5 sin x - 4 = 0;
x
+ 5 sin x - 4 = 0;
в) cos 2x + 5 sin x - 3 = 0; г) 2 tg x + 2 ctg x = 5.
-
Решите уравнение методом разложения на множители:
а) 5 sin x + 3 sin 2x = 0; б) sin 7x - sin x = 0;
-
Решите уравнение, используя однородность:
а) sin x - ![]() cos x = 0;
cos x = 0;
б) sin![]() x
- 3 sin x cosx + 2 cos
x
- 3 sin x cosx + 2 cos![]() x
= 0;
x
= 0;
в) sin x cos x - ![]() cos
cos![]() x = 0;
x = 0;
16
