Статья Решение задач с параметрами

Семинар для учителей математики по теме:

«Решение задач с параметрами»

План проведения семинара:

Занятие №1. Знакомство с параметрами. Простейшие задачи с параметрами. Квадратичная функция в задачах с параметрами.

Занятие №2. Графические методы решения задач с параметрами. Метод сечений. Рассмотрение решения задачи пробного ЕГЭ 2015 года.

Занятие №3. Графические методы решения задач с параметрами. Решение задач ЕГЭ 2015года.

ГБОУ Школа №1208 ЮВАО г. Москвы.

Данный семинар посвящён решению задач с параметрами. Умение решать такие задачи

Считается признаком отличного знания математики. Некоторые при подготовке к экзаменам боятся даже браться за эти задачи, думая, что у них всё равно ничего не получится. Вместе с тем часто для решения задач с параметром нужно просто использовать свой здравый смысл, и решение окажется простым и понятным!

Цель данного семинара состоит как раз в том, чтобы помочь желающим научиться решать задачи с параметрами.

Рассмотрим несколько простейших примеров.

Пример №1.

При всех а решить неравенство

≤ 0.

Решение. При любом фиксированном значении а это обычное рациональное неравенство. Поэтому к нему можно применить метод интервалов. Для этого надо расположить на числовой оси числа а и а+1, которые обращают числитель и знаменатель в нуль. Ясно, что при всех а а+1 больше, чем а. Поэтому получается расположение точек, как показано на рисунке.

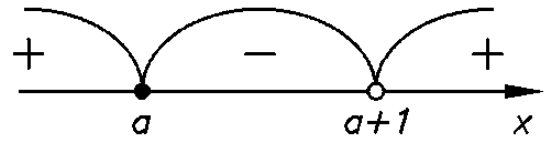
Ответ:хпри любом а.

Рассмотрим ещё один пример.

Пример №2.

При всех а решить неравенство

>0.

Решение. Как и выше, будем применять метод интервалов. Однако, здесь возникает небольшая трудность- мы не знаем как расположены числа 1 и а. Ведь а может быть больше 1, меньше 1 или равно 1. Это означает, что нам следует рассмотреть эти три случая.

1. Пусть а<1. Тогда получаем следующее расположение точек

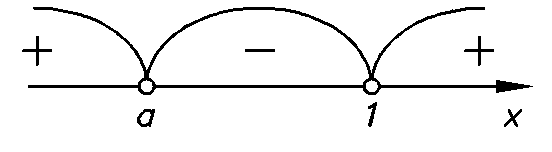
Метод интервалов даёт часть ответа: если а<1, то х(-;а)(1:+).

2. Пусть а=1. Тогда получим неравенство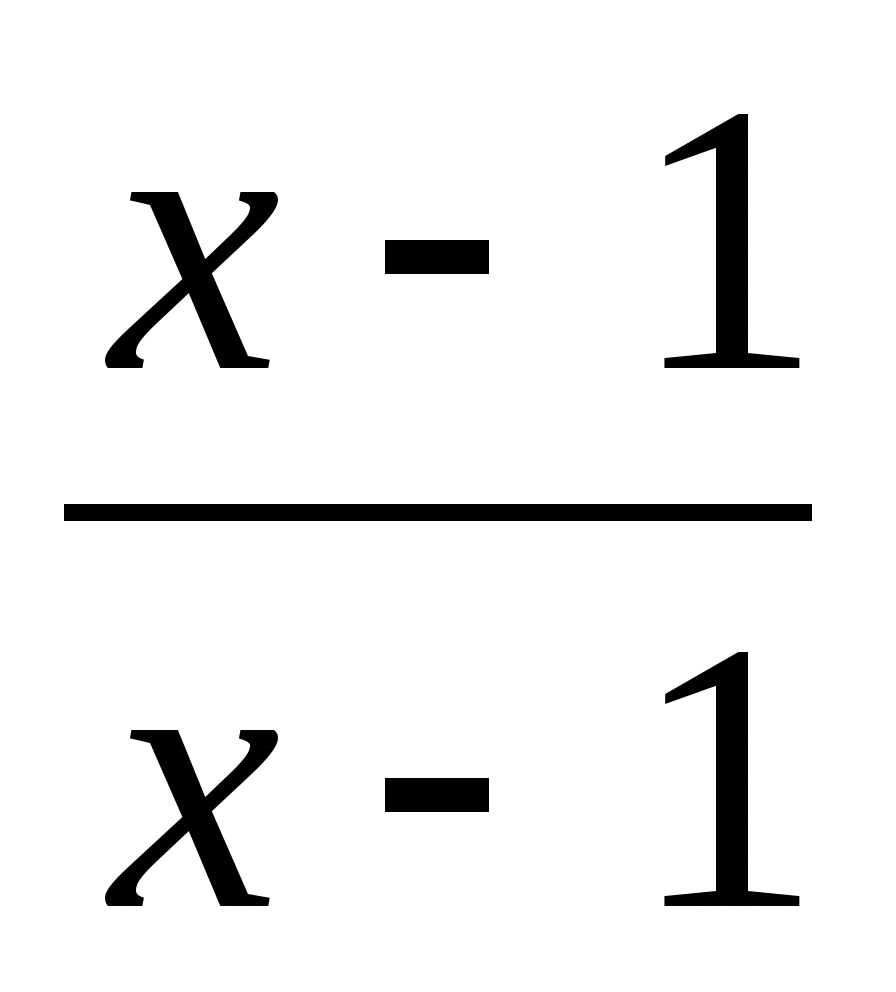>0, при х1 равносильное верному неравенству 1>0. Его решение - вся область определения неравенства, т.е. х(-:1)(1;+).

3. Пусть а>1. Тогда точки расположены, как показано на рисунке

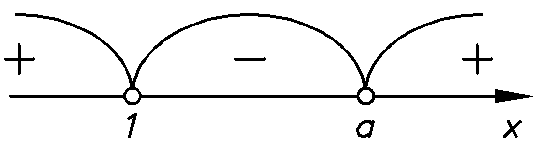
Метод интервалов даёт частичный ответ: если а>1, то х(-;1)(а;+).

Объединим части ответа и получим окончательный результат.

Ответ. Если а<1, то х(-;а)(1:+); если а=1, то х(-:1)(1;+); если а>1, то х(-;1)(а; +).

Пример№3.

При всех а решить неравенство

>1.

Решение. Преобразуем неравенство к виду <0.

При а>0 это неравенство равносильно неравенству х+а<0 и его решения х(-;-а).

При а=0 получаем неравенство <0, 0<0, у которого нет решений.

При а<0 это неравенство равносильно неравенству х+а>0, имеющему решения х(-а;+).

Ответ. Если а<0, то х(-а;+); если а=0, то решений нет; если а>0, то х(-;-а).

Рассмотренные примеры позволяют увидеть, что решение, казалось бы, одинаковых примеров имеет существенные различия.

Для успешного обучения учеников решению задач подобного типа необходимо:

решать уравнения и неравенства всех типов;

уметь строить графики всех элементарных функций;

уметь исследовать функцию и строить графики с помощью производной;

знать основные теоремы курса средней школы (теорему Виета и др.);

уметь применять различные способы решения для одной задачи.