Разработка урока по математике на тему 'Применение производной' (11 класс)

Методическая разработка урока

Обобщающий урок по теме «Применение производной»

Алгебра и начала анализа, 11 класс

БАЖЕНОВА ЛЮДМИЛА АЛЕКСАНДРОВНА, учитель математики, МКОУ «Илирская СОШ №2», Иркутская область, Братский район, п. Прибрежный.

Тип урока: урок систематизации обобщения знаний и умений

Формы работы учащихся: фронтальная, индивидуальная, групповая.

Оборудование, демонстрационный материал: компьютер, мультимедиа проектор, презентация, карточки для работы в группе, лист самооценки самостоятельной работы.

Цель урока:

Образовательная:

1. Отработка навыков исследования функции с помощью производной;

2. закрепление навыков нахождения промежутков возрастания и убывания функции, экстремумов функции с помощью производной;

3. развитие навыков чтения графиков функций; умений использовать теоретический материал при решении практических задач;

4. выявление уровня овладения знаниями и качества знаний по данной теме;

5. актуализация имеющихся знаний;

6. создание условий для объективной самооценки обучающихся.

7. расширение видов деятельности по подготовке к ЕГЭ.

Развивающие:

1. Расширение представлений об использовании применения производной в различных областях научных знаний и практической деятельности людей многих профессий;

2. развитие навыков самоорганизации, умений работать в группе; умений доводить начатое дело до конца;

3. развитие зрительного и мысленного анализа, внимания и абстрактно- логического мышления; умений анализировать и делать выводы;

4. развитие умений осуществлять поисковые действия умственного и практического плана; самоанализировать и самокорректировать свои действия;

5. привитие навыков работы с научно-популярной литературной, ресурсами Интернета; углубление знаний обучающихся, расширение их кругозора;

6. развитие умений планировать полный или частичный ход решения.

Воспитательные:

1. Повышение интереса обучающихся к предмету; воспитание сознательного отношения к обучению;

2. учить видеть практическую пользу знаний;

3. воспитание чувства любви к ближнему, доброжелательности, взаимовыручки;

4. воспитание прилежания, активности, внимания, умений переключаться с одного вида работы на другой;

5. побудить у учащихся осознание системной подготовки к ЕГЭ;

6. формирование отношения взаимной ответственности в группах;

7. продолжение формирования коммуникативных умений.

Задачи

• Контроль теоретических знаний по теме

• Контроль умений и практического опыта нахождения производной

УУД

Личностные УУД: понимать значимость понятий производная и её применение и в курсе математики и в профессиональной деятельности.

Регулятивные УУД: понимать последовательность действий на уроке; рационально использовать время на уроке; контролировать свою деятельность; давать эмоциональную оценку своей деятельности на уроке.

Коммуникативные УУД: работать в группе, оценивать качество своей деятельности.

Познавательные УУД: применять таблицу производных, геометрический, физический смысл производной и нахождение наибольшего и наименьшего значений для решения практических задач.

Планируемые результаты:

Предметные:

1. Владеть таблицей производных

2. Дифференцировать функции.

3. Находить наибольшее и наименьшее значение функций, с помощью производных, владеть знаниями геометрического и физического смысла производных.

Личностные:

1. Формирование математического кругозора.

Метапредметные:

1. Формирование общих способов интеллектуальной деятельности, характерных для математики и являющихся основой познавательной культуры, значимой для различной сферы.

ХОД УРОК

I. Организационный момент

Рефлексия настроения.

Чтобы на протяжении всего урока у вас было хорошее настроения, вам поможет вот это весеннее солнце. Улыбнитесь ему. Желаю вам творческих успехов!

II. Постановка цели и задач урока. Мотивация учебной деятельности.

Ребята, если вы правильно отгадайте ключевое слово урока, то узнаете тему нашего урока.

1) С ее появлением математика перешагнула из алгебры в математический анализ;

2) Ньютон назвал ее "флюксией" и обозначал точкой;

3) Бывает первой, второй, … ;

4) Обозначается штрихом.

Итак, тема нашего занятия "Применение производной "

Как вы думаете, ребята, какова цель нашего урока? (Дети формулируют цель.)

Цель нашего урока - повторить основные направления применения производной для решения различных (избранных) задач дифференциального исчисления. Подготовка к ЕГЭ по данной теме, применение производной в различных областях.

Постарайтесь на уроке доказать высказывание Н. И. Лобачевского о том, что:

«Дифференциальное исчисление - это описание окружающего нас мира, выполненное на математическом языке. Производная помогает нам успешно решать не только математические задачи, но и задачи практического характера в разных областях науки и техники».

Н.И. Лобачевский

Активизация знаний учащихся

Как вы думайте «Производная имеет важное значение как в математике так и в других науках? Можно ли сказать про неё, что она «Всемогущая?

Постараемся ответить на этот вопрос сегодня на уроке.

III. Актуализация знаний, умений, навыков.

1.Заполнить кроссворд (вопросы и кроссворд проецируются на экран).

1.Французкий математик XVII Ферма определял эту линию так: «Прямая, наиболее тесно примыкающая к кривой в малой окрестности заданной точки».

2.В математике это понятие возникло в результате попыток придать точный смысл таким понятиям, как «скорость движения в данный момент времени», и «касательная к кривой в заданной точке».

3.Производная какой функции имеет вид у' =.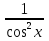

4.Точки, где производная функции не существует или равна нулю.

5.Эта точка лежит внутри области определения функции, и в ней функция принимает самое большое значение по сравнению со значением в близких точках.

6. Эта величина определяется как производная скорости по времени.

1

2

3

4

5

6

Проверка (слайд)

1

к

а

с

а

т

е

л

ь

н

а

я

2

п

р

о

и

з

в

о

д

н

а

я

3

т

а

н

г

е

н

с

4

к

р

и

т

и

ч

е

с

к

и

е

5

м

а

к

с

и

м

у

м

6

у

с

к

о

р

е

н

и

е

ІV. Обобщение и систематизация знаний

Подготовка учащихся к обобщенной деятельности

1. Графический диктант: (проверка знаний формул) 1 - верно, 0 - нет

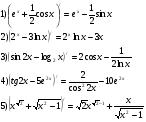
Самопроверка: 10011 (слайд)

2. Геометрический смысл производной

Подготовка к ЕГЭ ( задания № )

1 слайд

1 задание: Функция y = f(x) определена на промежутке (- 6; 6). На рисунке изображён график её производной. Найдите точки, в которых производная функции равна нулю.

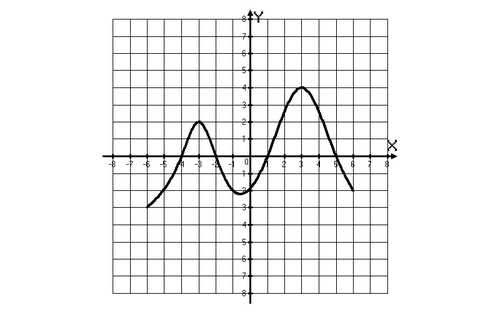
2 слайд

2 задание: Функция y = f(x) определена на промежутке (-6; 5). На рисунке изображён график её производной. Укажите количество промежутков, на которых функция возрастает.

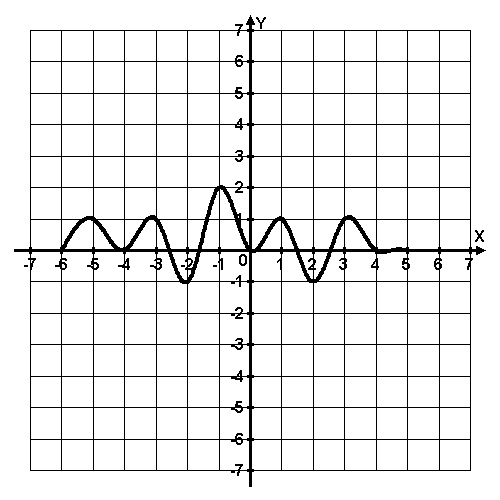
3 слайд

3 задание: Функция y = f(x) определена на промежутке (-4; 5). На рисунке изображён график её производной. Найдите точку минимума функции y = f(x).

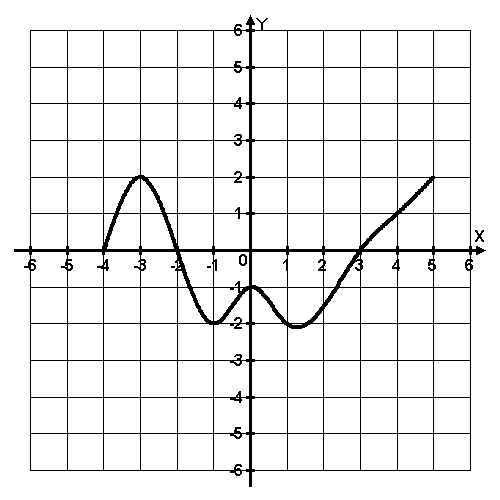
4 слайд

4 задание: Функция y = f(x) определена на промежутке (-4; 5). На рисунке изображён график её производной. Найдите точку максимума функции y = f(x).

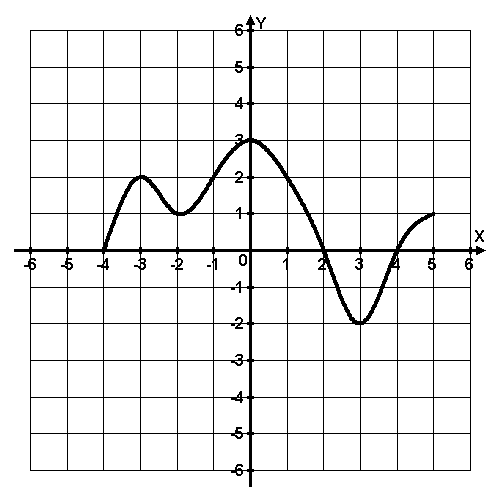
5 сайд

5 задание

На рисунке изображены графики функции у = f(x) и касательная к нему в точке с абсциссой х₀. Найдите значение производной функции в точке х _0.

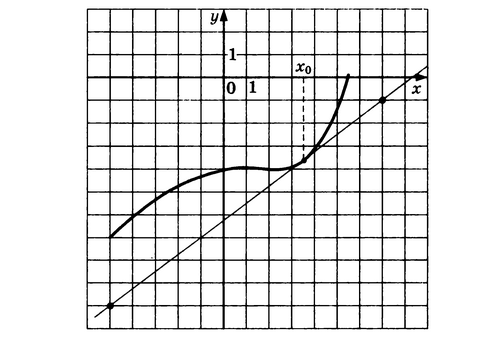
Ответы (самопроверка) слайд

Ответы: 1 задание: х = - 4; х = - 2; х = 1; х = 5

2 задание: 5

3 задание: х = 3

4 задание: х = 2

5 задание: 0,75

Физминутка

3) Применение производной. Выполните задание (ЕГЭ. В14)

Работа в группах

I группа Найдите точку максимума функции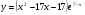

II группа Найдите наименьше значение функции у = (х - 13)е^х-12 на отрезке [11; 13]

III группа Найдите точку минимума у = х -5 lnx

Выполнение заданий проверяется у доски (взаимооценка)

Проверка домашнего задания

Применение производной в других науках (межпредметная связь)

I группа Производная в физике, химии

II группа Производная в биологии

III группа Производная в экономики, географии

Работа в группе: 1. Составление синквейна по теме «Производная»

2. Что вы можете сказать о производной функции, которую описывает поговорка "Чем дальше в лес, тем больше дров".

(Ответ: производная положительна на всей области определения, т.к. эта функция - монотонно возрастающая)

Домашнее задание: 1.Повторить теоретический материал по теме «Производная и ее применение»

2. Составить презентацию на основе банка заданий ЕГЭ по теме «Производная»

Итог урока:

1. Можно ли сказать, что производная «всемогущая»

2. Выставление оценок (самооценка) комментировано

В заключении урока я хочу вам прочитать стихотворение:

"Музыка может возвышать или умиротворять душу,
Живопись - радовать глаз,
Поэзия - пробуждать чувства,
Философия - удовлетворять потребности разума,
Инженерное дело - совершенствовать материальную сторону жизни людей,
А математика способна достичь всех этих целей".

Так сказал американский математик Морис Клайн.

Спасибо за работу

Литература:

1.Алгебра и начала математического анализа. 10 - А45 11 классы: учеб. для общеобразоват. учреждений с приложением на электронном носителе / [. М. Абрамов. Ю. П. Дудницин и др.]; под ред.А. Н. Колмогорова. - 18 -е изд. М.: Просвещение, 2009, - 384 с.

2. Ершова А. П., Голобородько В. В. Самостоятельные и контрольные работы по алгебре и началам анализа для 10 - 11 классов. - 4 - е изд., испр. - М.: Илекса. - 2008. - 208 с.

3.ЕГЭ - 2014 под редакцией А. Л. Семенова и И. В. Ященко Математика самое полное издание типовых вариантов заданий

4.

5. http://images.yandex.ru

Приложение:

Лист самооценки

Ф. И. учащегося:

Домашнее задание

Кроссворд

Графический

диктант

Подготовка

к ЕГЭ

Работа в группе

Синквейн

Дополни-

тель баллы

Всего баллов

Оценка

Кол - во баллов (о - 5)

Кол - во баллов (о - 6)

Кол - во баллов (о - 5)

Кол - во баллов (о - 5)

Кол - во баллов (о - 5)

Кол - во баллов (о - 5)

1…

1. от 0 - 10 баллов - оценка «2» от 11 - 20 баллов - оценка «3» от 21 - 29 баллов - оценка «4» от 30 - … оценка «5»