Урок в 7 классе по геометрии с элементами исследования с использованием ПО «Динамическая геометрия»

ПРИЛОЖЕНИЕ №6

Урок в 7 классе по геометрии с элементами исследования с использованием ПО «Динамическая геометрия»

Тема: « Медианы, биссектрисы

и высоты треугольника»

Цели

Образовательная: формирование умений строить медиану, биссектрису и высоту треугольника, работа с компьютером,

Воспитательная: воспитание организованности, аккуратности, дисциплинированности.

Развивающая: Формирование устойчивого познавательного интереса к изучению геометрии, развитие навыков устной речи, памяти, способности четко формулировать свои мысли.

Ход урока:

I) Организационный момент (Сообщение темы, постановка цели и задач урока)

II) Техника безопасности при работе на ПК;

III) Актуализация знаний ( презентация ):

1. Перпендикуляр к прямой

2. определение треугольника

3. определение медианы треугольника

4. свойство медиан треугольника

5. определение биссектрисы треугольника

6. свойство биссектрис треугольника

7. определение высоты треугольника

8. положение высот треугольника:

a) остроугольного

b) прямоугольного

c) тупоугольного

IV) Первичное закрепление (тест «Учитель»)

Для того, чтобы проверить как вы уяснили что такое медиана, биссектриса и высота треугольника предлагаю ответить на вопросы теста №1. Вам предложены три варианта определения для каждого понятия Вам необходимо выбрать верный и записать на листочке нужный шифр (номера верных ответов). На выполнение задания Вам отводится 3 минуты (+3мин. на обсуждение результатов теста).

Тест №1

А. Медианой треугольника называется …

1) линия, проходящая через вершину и середину противоположной стороны треугольника

2) отрезок, соединяющий вершину с противоположной стороной треугольника

3) отрезок, соединяющий угол с серединой противоположной стороны треугольника

4) отрезок, соединяющий вершину треугольника с серединой противоположной стороны

Б. Биссектрисой треугольника называется …

1) биссектриса, проведенная из вершины треугольника

2) отрезок биссектрисы угла треугольника, соединяющий вершину с точкой противоположной стороны

3) прямая, проведенная из вершины треугольника как биссектриса угла

В. Высотой треугольника называется …

1) наибольшее расстояние между вершиной и противоположной стороной данного треугольника

2) перпендикуляр из вершины к прямой, содержащей противоположную сторону

3) отрезок из вершины треугольника, перпендикулярный к противоположной стороне

Давайте проверим, что у Вас получилось. (мы получаем верный шифр: 422.) Прошу учащихся получивших верный шифр поднять руку ( тем самым я сразу могу отследить, кто из учащихся справился с заданием, а у кого оно вызвало затруднения).

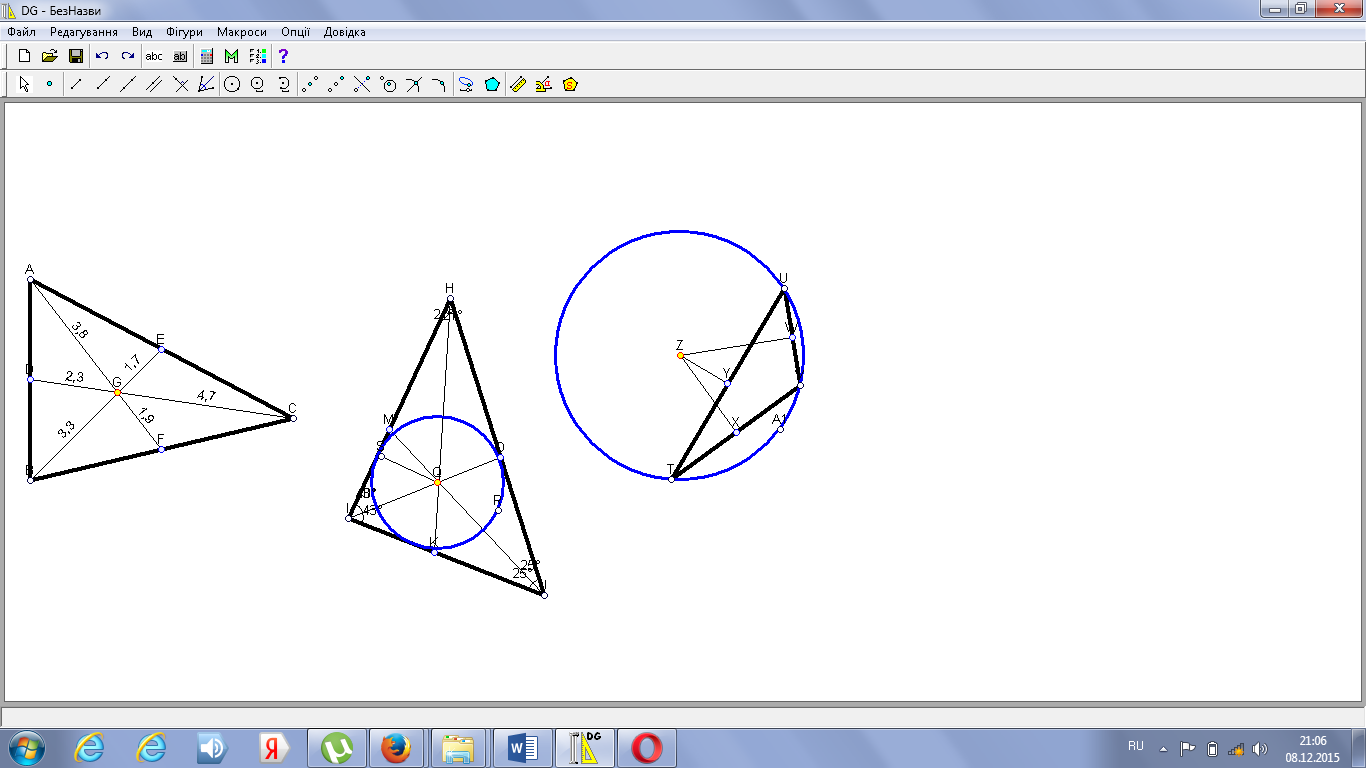
V) Самостоятельная поисковая работа ( ПО «Динамическая геометрия»):

1. Построить треугольник и проведя медианы треугольника заметить, что медианы пересекаются в одной точке (центр тяжести)

2. Проводя соответствующие измерения, выяснить, в каком отношении делятся медианы их точкой пересечения

3. Результаты поисковой работы записать в виде выводов.

4. Построить треугольник и проведя биссектрисы треугольника заметить, что биссектрисы пересекаются в одной точке (центр вписанной окружности)

5. Построить треугольник и проведя высоты треугольника заметить, что они пересекаются в одной точке (ортоцентр)

6. Построить треугольник и проведя серединные перпендикуляры треугольника заметить, что они пересекаются в одной точке (центр описанной окружности)

VI) Физминутка (рисунки + стихи)

Биссектриса - это крыса,

Которая бегает по углам

И делит угол пополам

Медиана-обезьяна,

У которой зоркий глаз,

Прыгнет точно в середину

Стороны против вершины,

Где находится сейчас

Высота похожа на кота,

Который, выгнув спину,

И под прямым углом

Соединит вершину

И сторону хвостом.

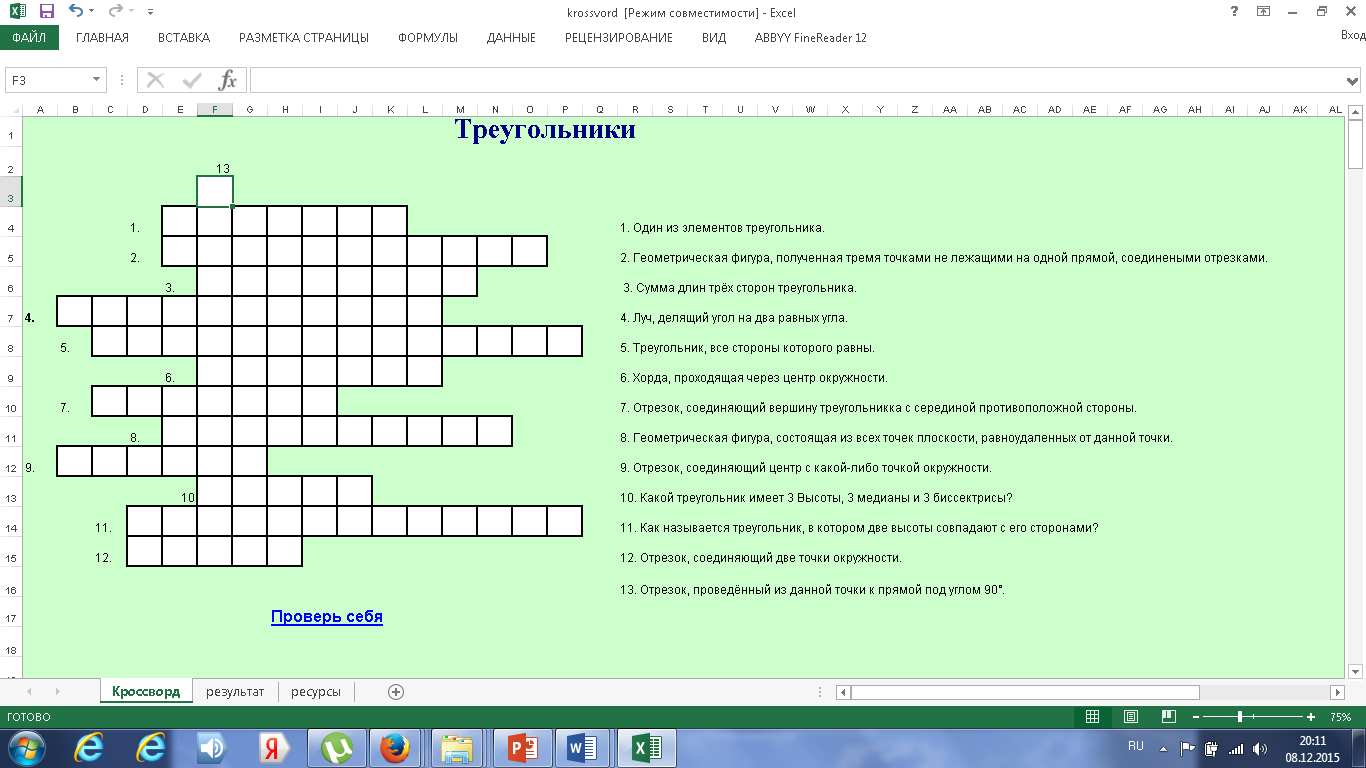
VII) Игровой момент:предложить учащимся заполнить кроссворд по теме «Треугольники» Программа Excel

VIII) Контроль усвоения учащимися материала (тест). Подсчитываются баллы и выставляются оценки.

IX) Домашнее задание (на готовых чертежах) Программа Word

X) Рефлексия (Подведение итогов урока) Программа Paint.

4