- Учителю
- Урок геометрии на тему «Свойства равнобедренного треугольника» (7 класс)
Урок геометрии на тему «Свойства равнобедренного треугольника» (7 класс)















 МАОУ СОШ № 17 г. Липецка
МАОУ СОШ № 17 г. Липецка
Учитель: Ишкова Татьяна Николаевна
Предмет: математика
Класс: 7 - общеобразовательный
Учебник: Л.С. Атанасян, «Геометрия 7 - 9 », М.: Просвещение, 2010.
Тема: «Свойства равнобедренного треугольника».
Учебный элемент
Учебный материал с указанием заданий
Руководство по усвоению материала
УЭ 0
Знать определения равнобедренного и равностороннего треугольников, теорему о свойстве углов при основании равнобедренного треугольника.
Уметь доказывать теорему о свойстве углов при основании равнобедренного треугольника, применять определения и теорему при решении задач.
УЭ 1
Цель: актуализировать знания учащихся.
Треугольник есть первая фигура, которая не может разложиться в другой вид более простой фигуры (между тем как, наоборот, четырехугольник разлагается на треугольники) и поэтому есть первый фундамент всякой вещи, имеющей границу и фигуру.
Бруно Д.
Действительно, треугольник это особая геометрическая фигура. К ней мы будем неоднократно возвращаться при изучении геометрии. Используя признаки и свойства различных треугольников, мы будем доказывать утверждения, и решать задачи.
Задание 1. Найдите пары равных треугольников и докажите их равенство.
М N B C
O
K A D
L
Рис. 1 N Рис.2
M K
Рис. 3
Задание 2. Среди данных треугольников найдите:
-
треугольники, в которых проведены высоты;
-
треугольники, в которых проведены медианы;
-
треугольники, в которых проведены биссектрисы.
При выполнении задания необходимо повторить определения и научить распознавать на рисунке медианы, биссектрисы и высоты треугольника.

Дают развернутый ответ:
1) ∆MNO = ∆LOK
(по двум сторонам и углу между ними)
-
МО = OK;
-
NO = LO;
(по условию)
(по свойству вертикальных углов)
Выполняют задание устно с подробным пояснением.
УЭ 2
Цель: сформулировать тему и цели урока.
Провести классификацию треугольников.
Вопросы:
1) Как называется треугольник, у которого все углы острые?
2) Как называется треугольник, у которого один из углов прямой?
3) Как называется треугольник, у которого тупой?
Треугольники можно классифицировать не только по углам, но и по длине их сторон. Все треугольники можно разделить на разносторонние и равнобедренные.
Сформулируйте тему и цели урока.
Отвечают на вопросы.
Формулируют тему и цели урока. Записывают тему урока в тетрадь.
УЭ 3
Цель: сформулировать определения равнобедренного и равностороннего треугольников, проверить правильность усвоения учащимися этих понятий.
-
Вслушайтесь в слово «равнобедренный».
-
Как вы понимаете смысл этого слова?
Для того чтобы дать точное определение обратимся к учебнику стр. 35.
1. Сформулируйте определение равнобедренного треугольника с помощью «если…, то…».
2. Заполните схему:
Запись в тетрадях учащихся.
Равнобедренным треугольником называется
треугольник, у которого две стороны равны.
На доске: С
∆ ABC - равнобедренный
AC=BC- боковые стороны
AB- основание
т.C вершина ∆ ABC
 C - угол при вершине А А В
C - угол при вершине А А В
 A и
A и  B - углы при основании
B - углы при основании
Задание 3. Какие из треугольников, изображенных на рисунке, являются равнобедренными? Назовите их основания и боковые стороны.
C K D
7 7 6 5 5 3
A B M N C E
5 6 4
S
5 5
P Q
5
При рассмотрении ∆PSQ ответить на вопросы:
1) Что можно сказать о треугольнике PSQ?
2) Как вы назвали бы такой треугольник?
3) Является ли равносторонний треугольник равнобедренным?
(Любую сторону в таком треугольнике можно взять за основание, тогда две другие стороны будут являться боковыми.)
5. Сформулируйте определение равностороннего треугольника с помощью «если…, то…».
6. Заполните схему:
Запись в тетрадях учащихся.
Равносторонним треугольником называется
треугольник, у которого все стороны равны.
На доске: K
 NKS- равносторонний
NKS- равносторонний
NK = KS = NS
N S
Отвечают на поставленный вопрос.
Работают с учебником.
Формулируют определение, записывают его в тетрадь.
Выполняют устно с подробным обоснованием.
Записывают.
Дают развернутый ответ:
1) ∆ ABC - равнобедренный
AC=BC- боковые стороны
AB- основание
2) ∆ MNK - равнобедренный
MK=MN- боковые стороны
NK- основание
3) ∆ CDE - разносторонний.
4) Отвечают на вопросы.
-
В ∆PSQ все стороны равны;
-
Равносторонний;
-
Да, т. к. есть две равные стороны.
Записывают.
УЭ4
Цель: сформулировать и доказать теорему об углах в равнобедренном треугольнике.
Задание 5.(исследовательская работа)
1 вариант.
-
Постройте равнобедренный треугольник BCD, в котором боковые стороны равны 5 см, а основание 3 см.
-
С помощью транспортира найдите градусную меру всех углов треугольника.
-
Что можно заметить?
-
Сформулируйте и запишите вывод.
2 вариант.
-
Постройте равнобедренный треугольник BCD, в котором боковые стороны равны 7 см, а основание 4 см.
-
С помощью транспортира найдите градусную меру всех углов треугольника.
-
Что можно заметить?
-
Сформулируйте и запишите вывод.
Сравнить полученные по вариантам выводы.
8. Сформулируйте полученное утверждение с помощью «если…, то…». Данное утверждение является свойством равнобедренного треугольника.
Можно использовать сейчас это свойство при решении задач?
Теорема (свойство равнобедренного треугольника): Если треугольник равнобедренный, то углы при основании равны.
-
Выделите условие и заключение теоремы.
-
Что дано по условию теоремы?
-
Что требуется доказать?
-
Запишите краткое условие и сделайте чертеж.
-
Докажите теорему по данному чертежу.
Дано: С
∆ ABC - равнобедренный
Доказать, что 
Доказательство:
1) Проведем биссектрису CD.
2) Рассмотрим ∆ ACD и ∆BCD
-
АС = ВС (по условию) А D В
-
 (т.к. CD - биссектриса)
(т.к. CD - биссектриса) -
CD - общая сторона
3) ∆ ACD = ∆BCD (по двум сторонам и углу между ними)
4)  (т.к. в равных треугольниках соответственные элементы равны)
(т.к. в равных треугольниках соответственные элементы равны) 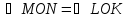
Выполняют построение, отвечают на поставленные вопросы.
Нет, так как любое полученное в результате исследования утверждение следует доказать.
Формулируют теорему.
Отвечают на поставленные вопросы
Доказывают теорему
под руководством учителя (один ученик у доски, остальные в тетрадях)
УЭ5
Цель: научить решать задачи, используя определение и свойство равнобедренного треугольника. K
Задача 1
Треугольник ∆MNK -
равнобедренный с
основанием MN. 3 1 2 4
1) Докажите, что  M N
M N
2) Найдите  .
.
3) Найдите  .
.
Ответ: 2) 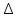
3) 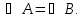
Задача 2
Треугольник ∆ABC - равносторонний.
1) Докажите, что 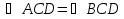 .
.
2) Найдите градусную меру этих углов.
Решают (один учащийся у доски, остальные в тетрадях).
УЭ6
Цель: подвести итоги урока, пояснить домашнее задание, оценить работу на уроке.
-
Повторить виды треугольников и изученное свойство, заполнив схему;
-
Достигнуты ли поставленные в начале урока цели?
-
Где возникли затруднения?
А: п.18,вопросы 10-12, №108, №112 .
В: Одна из сторон равнобедренного треугольника равна 8 см, а периметр равен 26см. Какими могут быть другие стороны этого треугольника?
Заполняют схему.
Отвечают.
Записывают домашнее задание.
