- Учителю
- Дидактические материалы по алгебре и началам анализа 10 класс
Дидактические материалы по алгебре и началам анализа 10 класс
Дидактические материалы по алгебре и началам анализа 10 кдасс
Контрольная работа ![]() №
1 (10 класс)
№
1 (10 класс)
Тема «Степень с рациональными показателями» 1урок - 45 мин
а) Вариант 1 б) Вариант 2
1) Вычислите:
а) 2 2-3 = б) 5 5-2 =
![]()
![]()
![]()
![]()
![]()
![]()
![]() =
=
![]() =
=
![]()
![]()
![]()
![]()
![]()
![]()
![]() =
=
![]()
2) Упростить:
а) б)
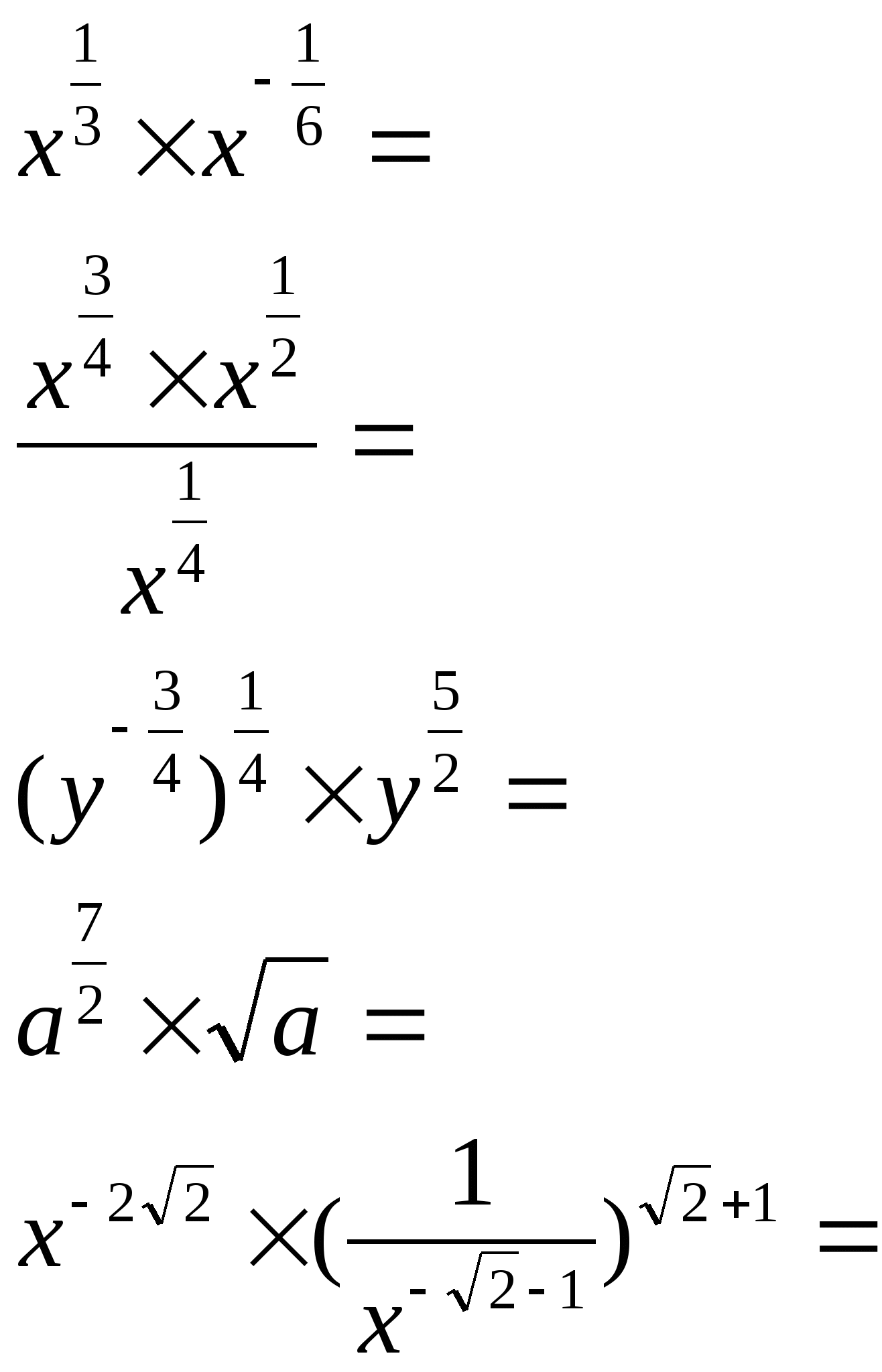
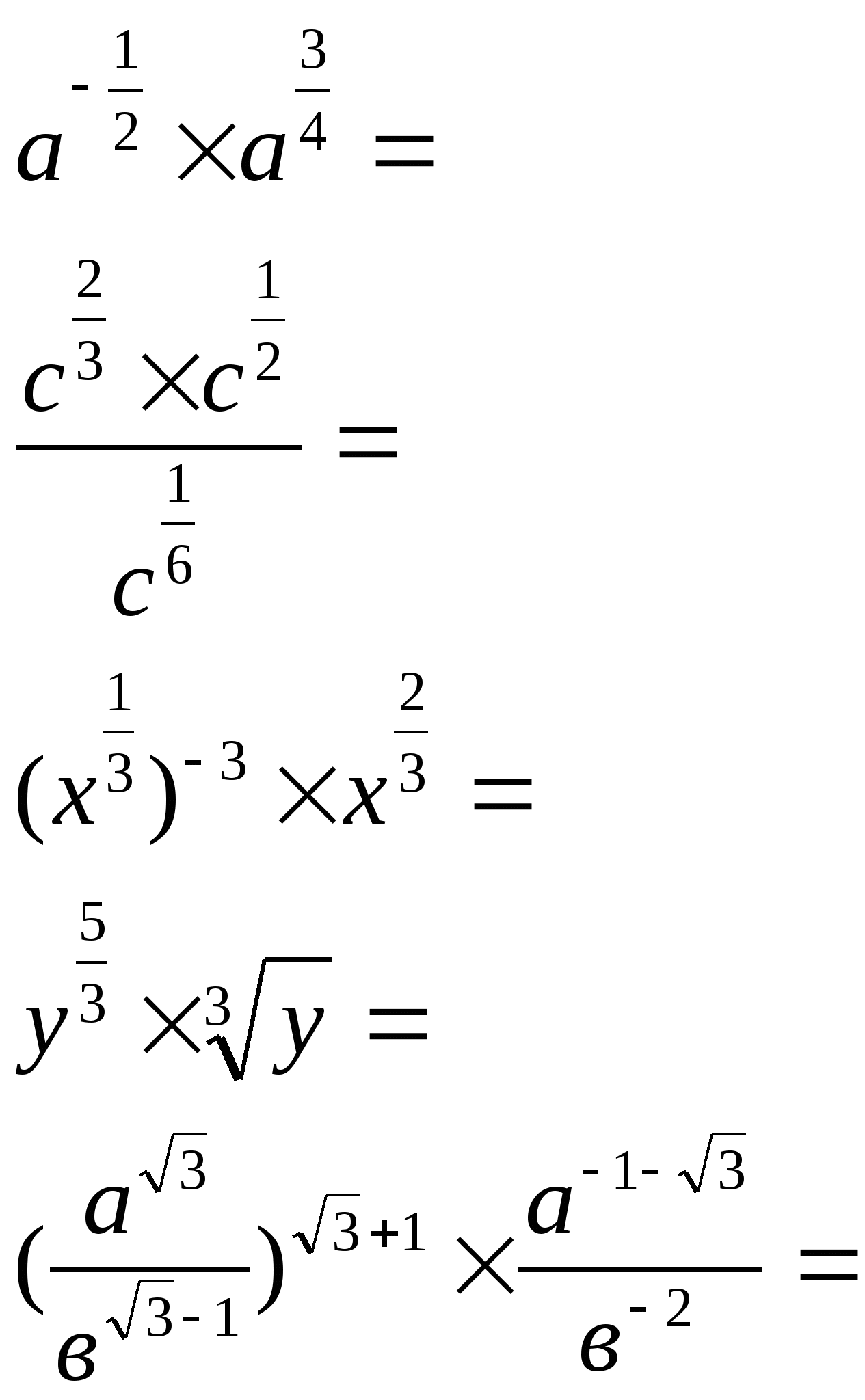
3) Сократить дробь
а) б)
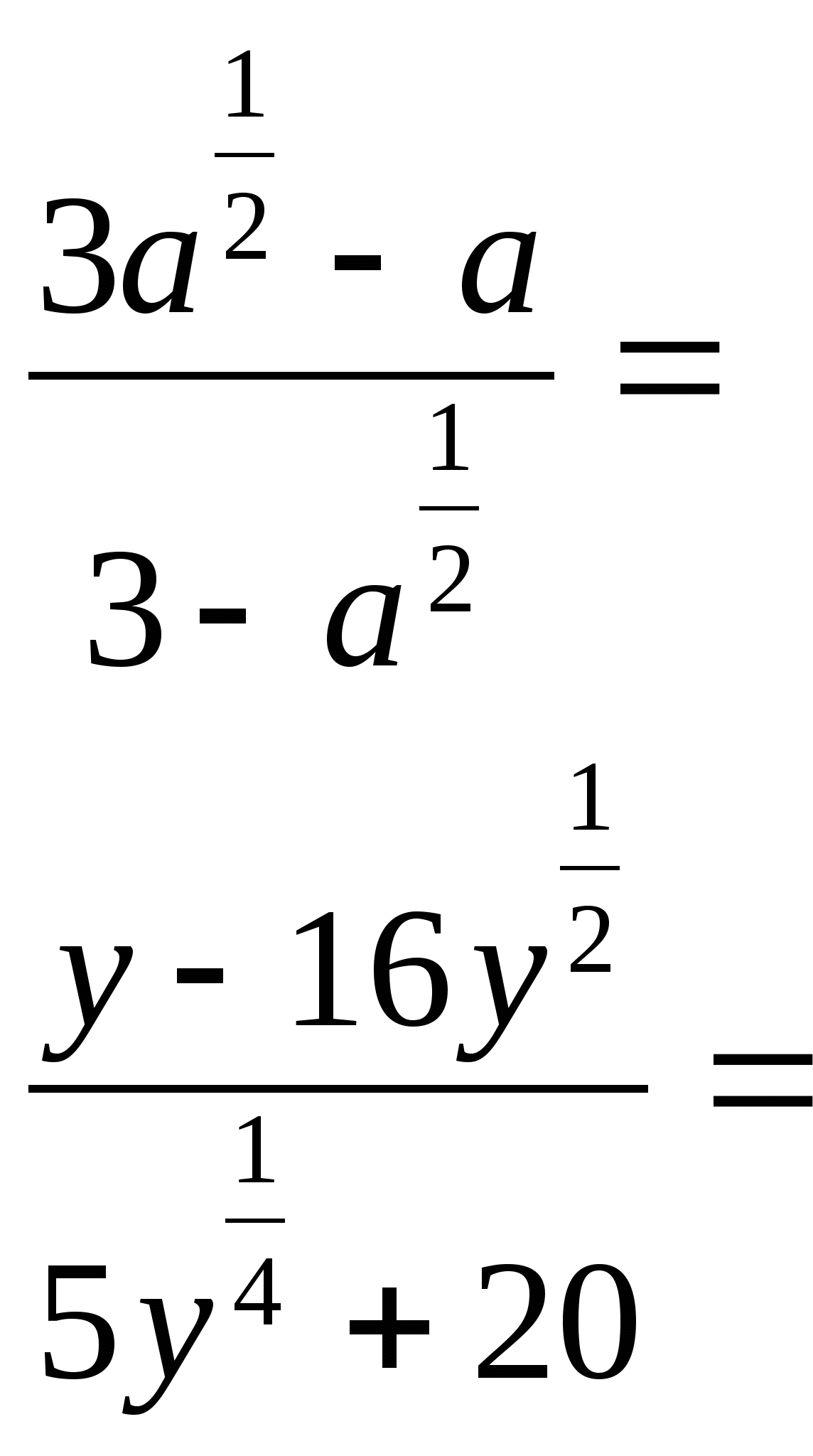
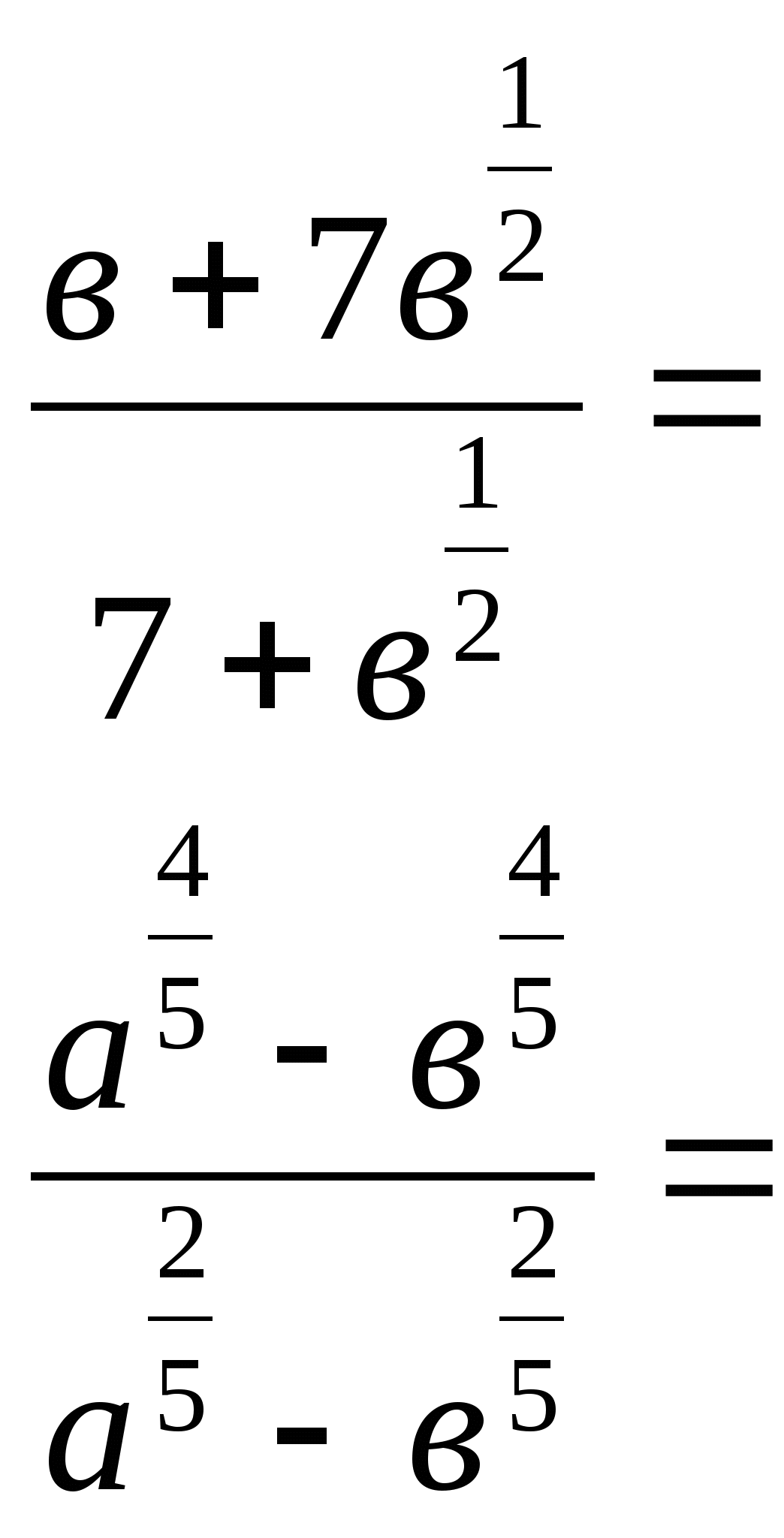
4) Упростить:
а) ![]()
б) 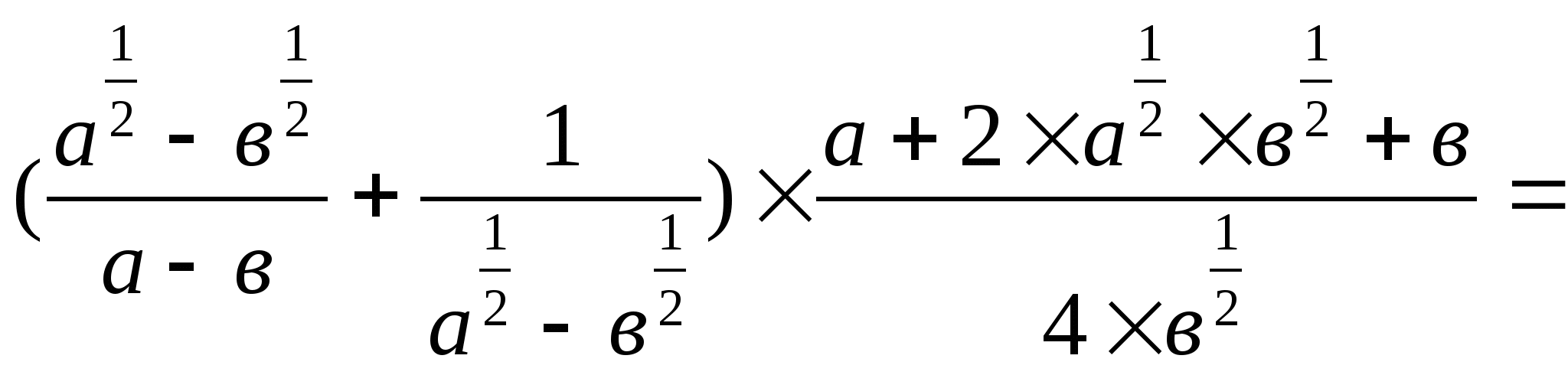
5) Упростить выражения:
а) ![]() б)
б) ![]()
6) Представить в виде обыкновенной дроби:
а) 1,10(209) б) 0,108(32)
Контрольная работа №2 (10 класс)
«Степенная функция»
1 вариант - а) 2 вариант - б)
№ 1 Найдите область определения функции:
а) б)
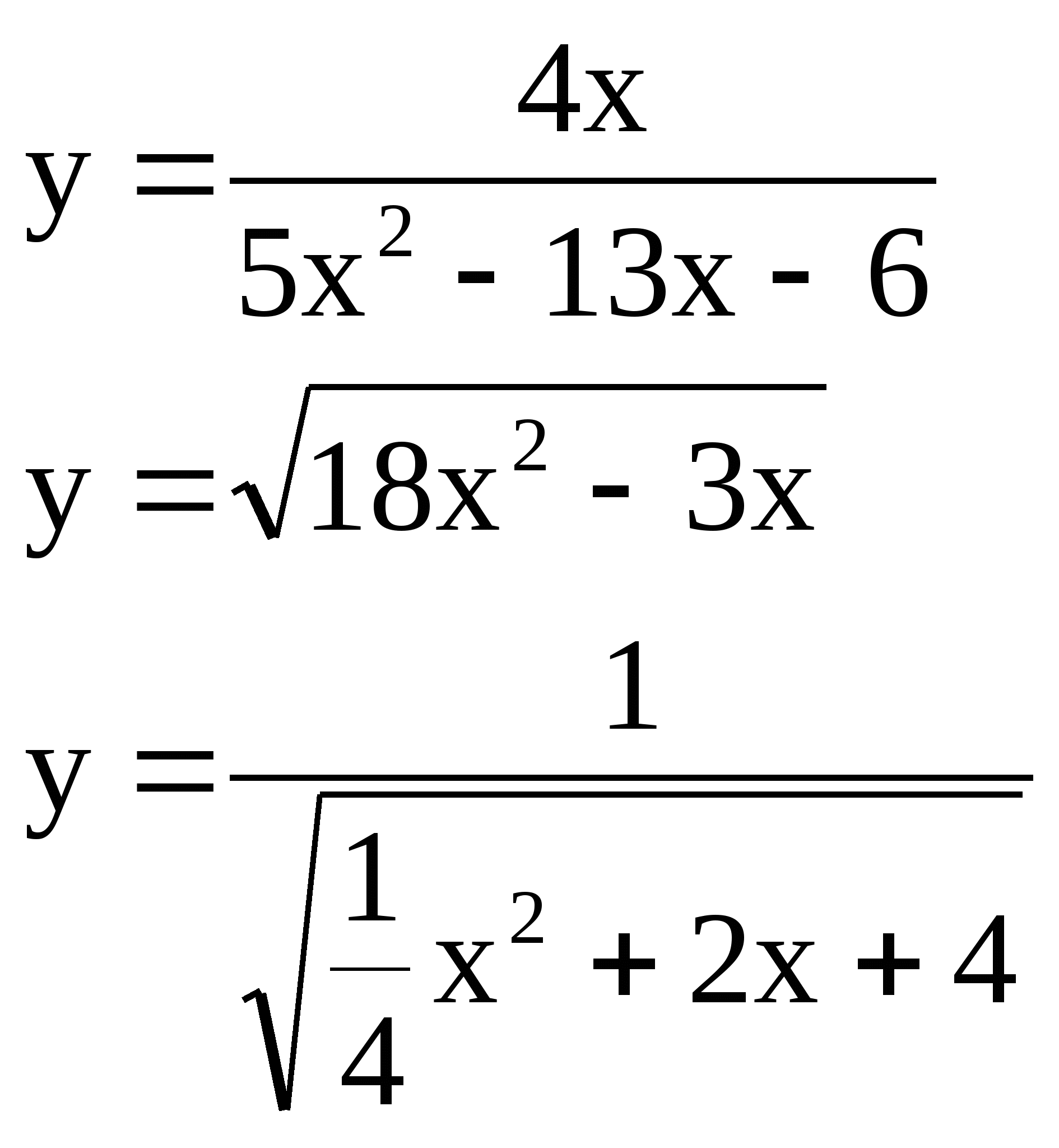
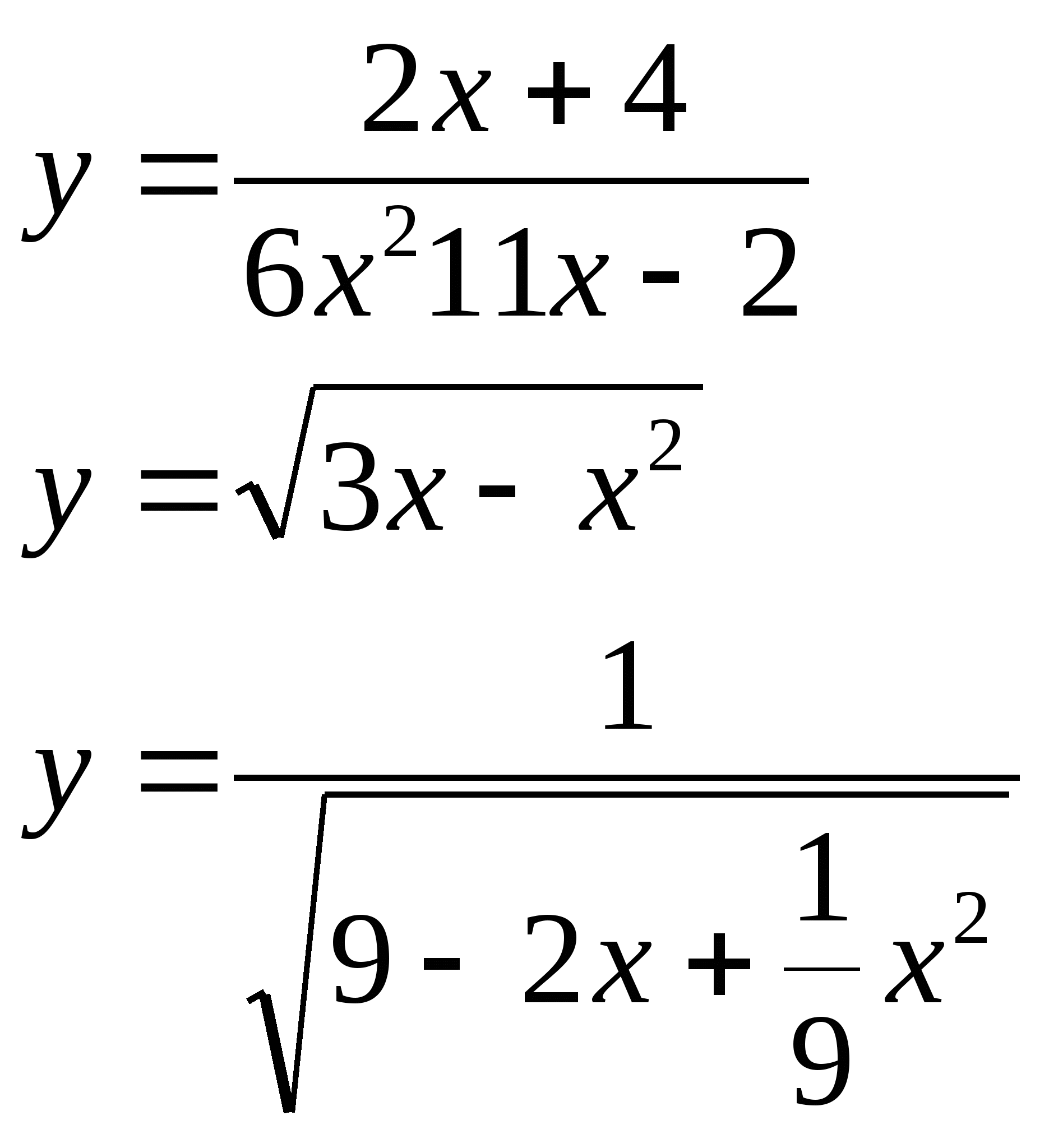
№ 2 Постройте графики и укажите точки пересечения этих графиков:
а) ![]() б)
б)
![]()
№ 3 Не выполняя построения графиков найдите координаты их точек пересечения:
а) ![]() б)
б)
![]() и
и
![]()
№ 4 Решить уравнение:
а) б)
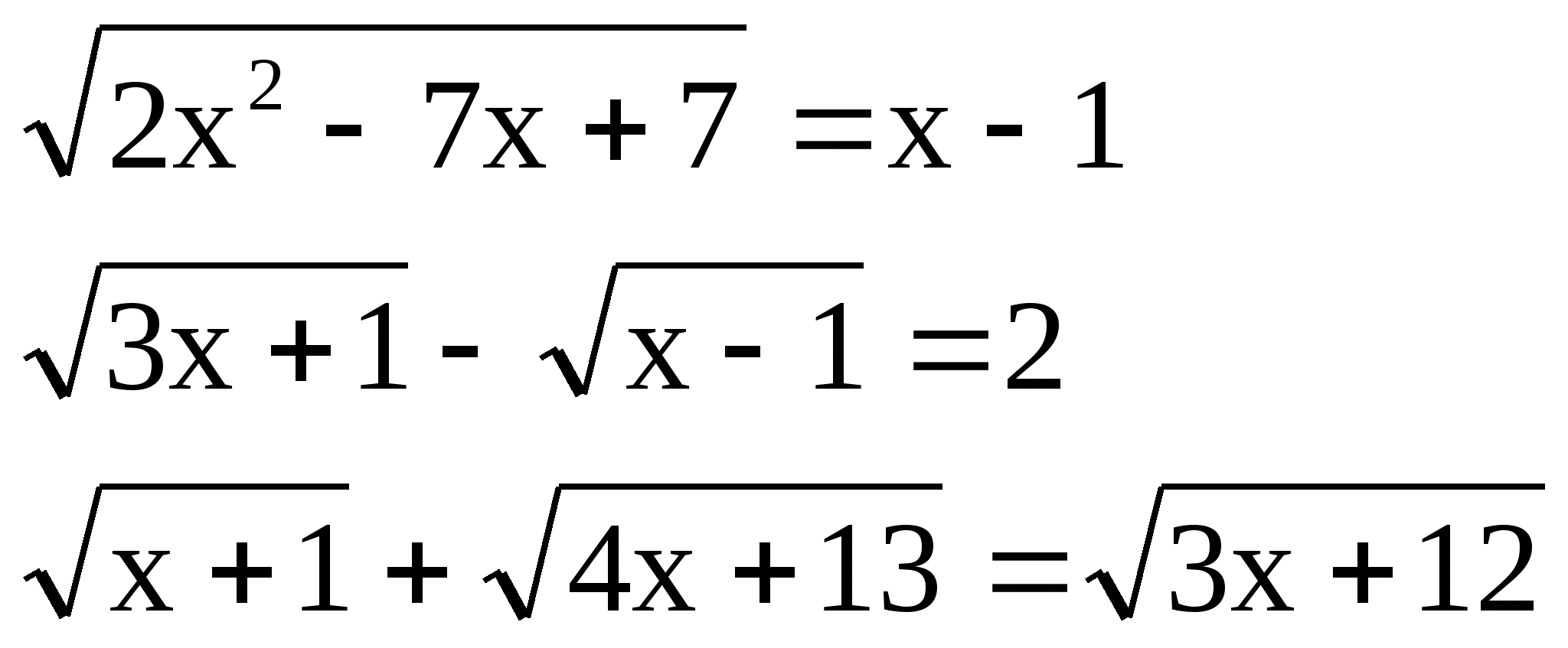
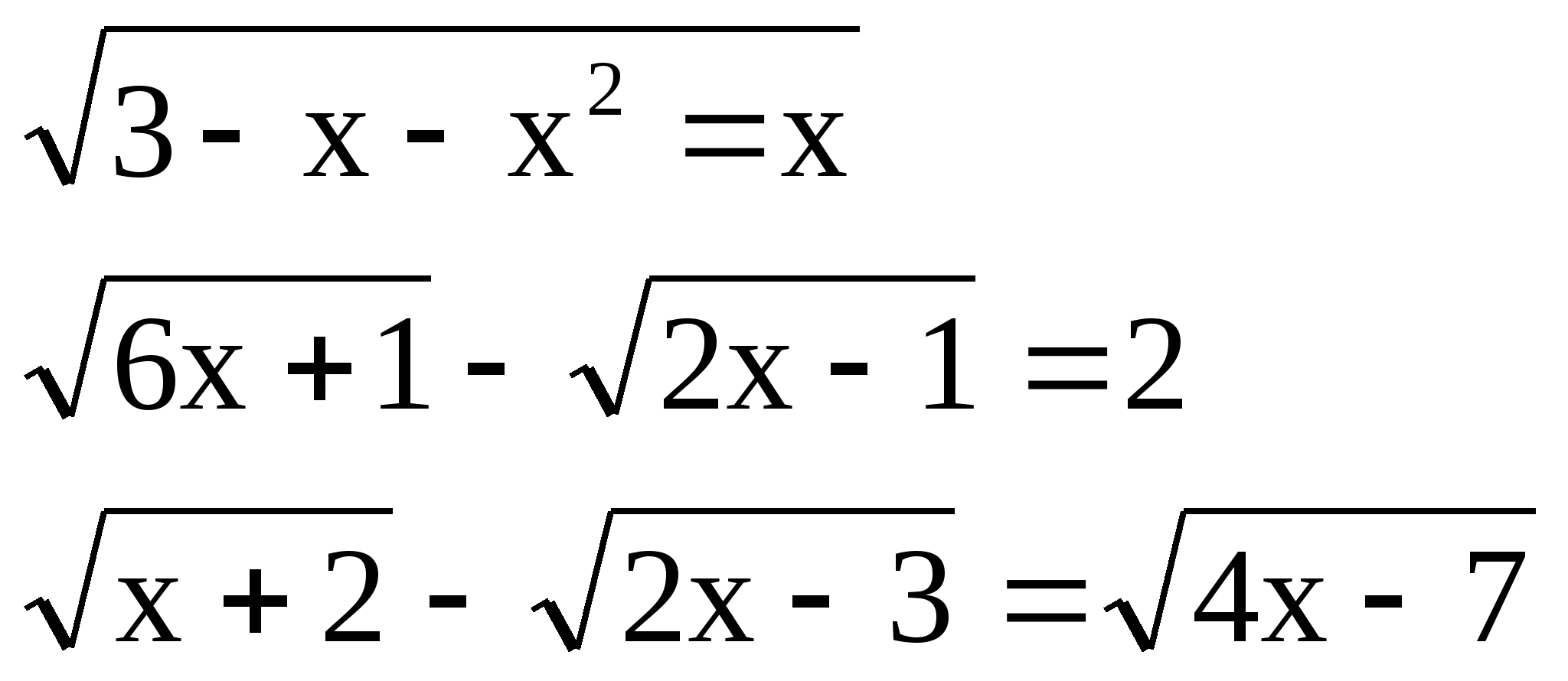
№ 5 Решить неравенство:
а) б)
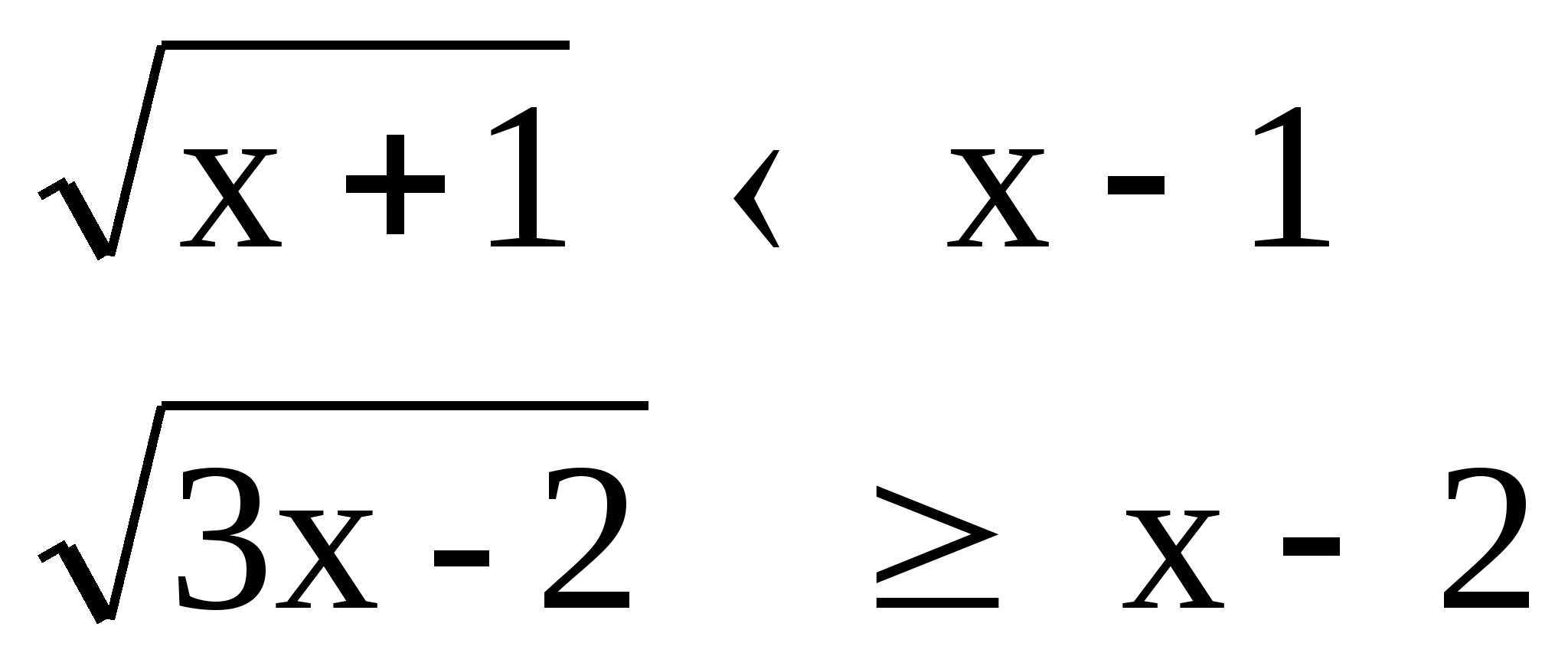
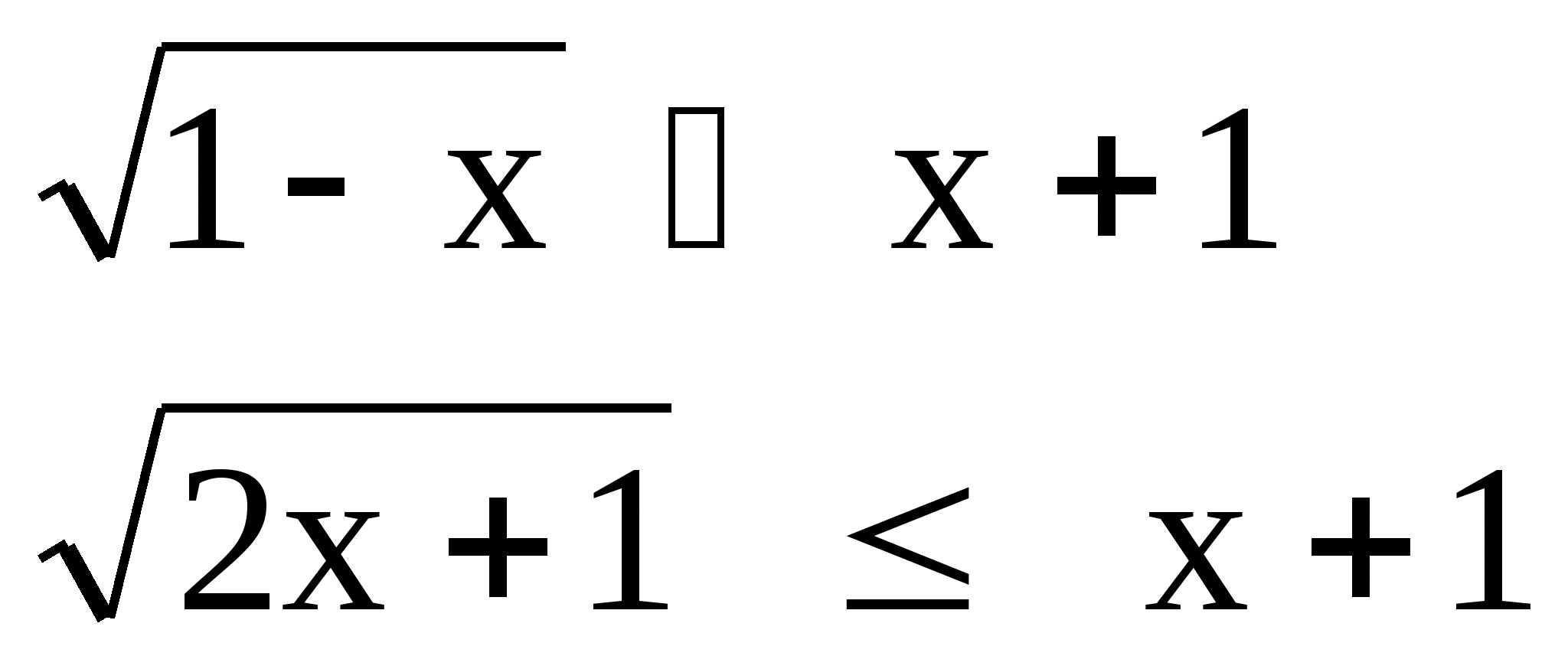
№ 6 сравнить значение выражений:
а) б)
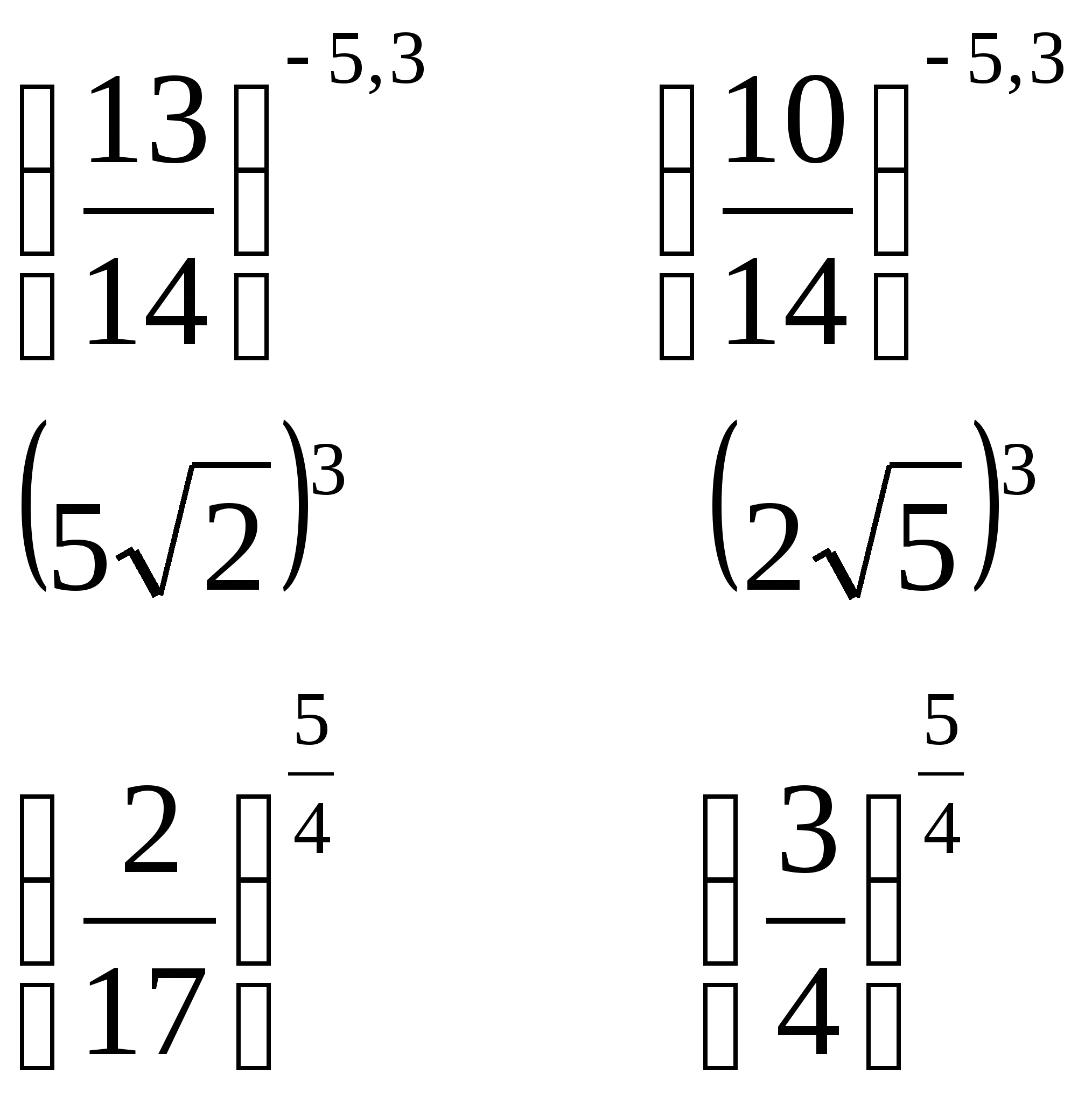
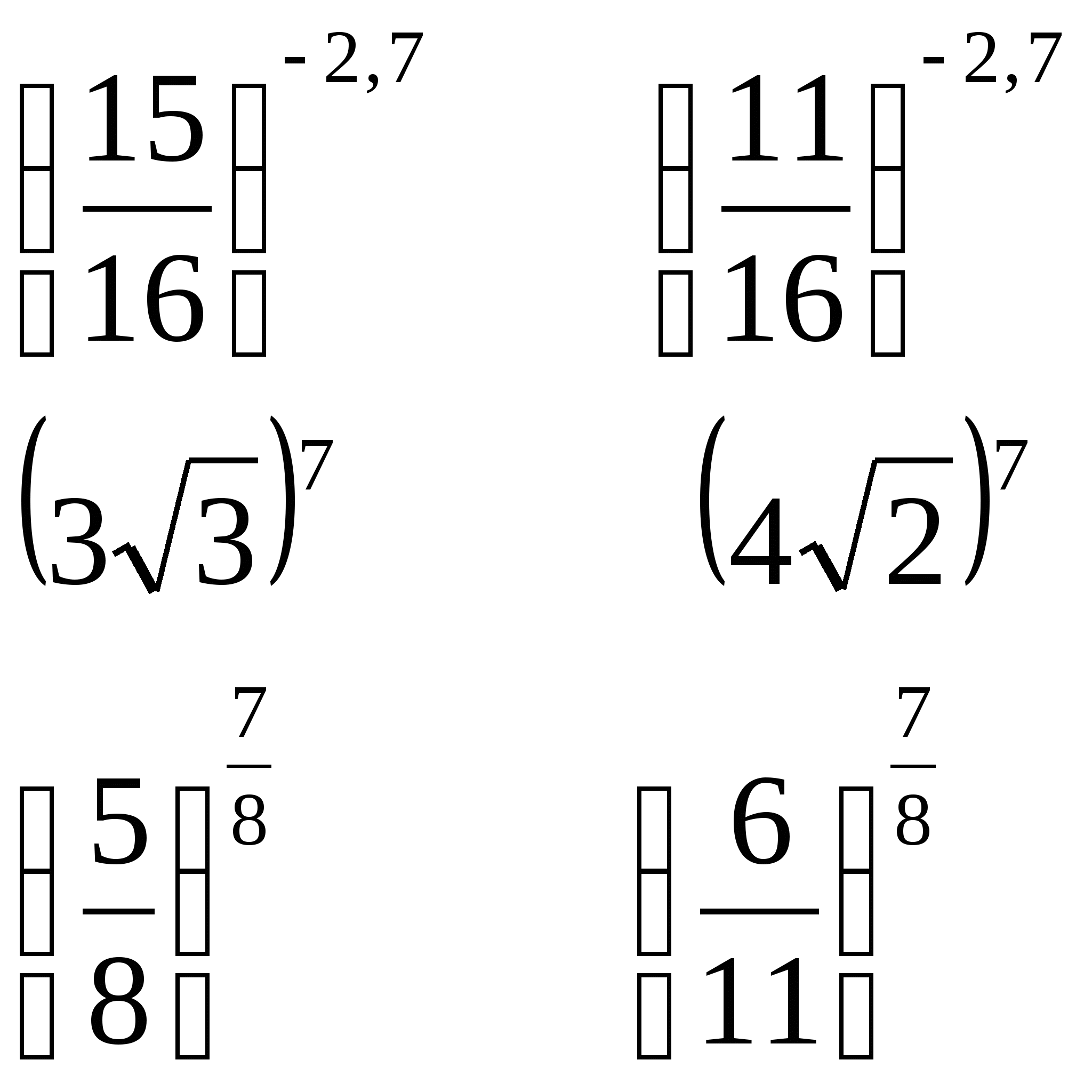
Самостоятельная работа № 1 (10 класс)
Показательная функция
Построить график функции
Самостоятельная работа № 2 (10 класс)
Показательные уравнения
Вариант 1 Вариант 2
1)![]() 1)
1)
![]()
2) 3х-23х-2-7=0 2) 4х-34х-2-13=0
3) 32х-43х=45 3) 4х+2х+3=20
4) 4х5х-1=0,2203-2х 4) 3х+14х=0,25123х-1
5) 2х-82-х=7 5) 3х-93-х=8
6) 4х-5= 5 5-х 6) 3х-2=72-х
7) 3х=11-х (решить графически) 7) (1/3)х=х+1
(решить графически)
Вариант 3 Вариант 4
1) 16-1![]() 2х
1) 8-1
2х
1) 8-1![]() 20,5х
20,5х
2) ![]() 2)
3811/х-1091/х+3=0
2)
3811/х-1091/х+3=0
3) 4х+1+41-х=1 3) 31+х-231-х=7
4) 5х+1-35х-2=122 4) 3х+1-43х-2=69
5) ![]() 5)
5)
![]()
6) 4х+1-6х=232х-2 6) 532х+1552х-1=815х
7) х26-х+![]() 7)
7)
![]()
8) 2х=3-2х-х2 (решить
графически) 8) ![]()
(решить графически)
Самостоятельная работа № 3 (10 класс)
Показательные неравенства
Вариант 1 Вариант 2
1) ![]() 1)
1)
![]()
2) ![]() 2)
2)
![]()
3) 3(х+1)/х 3 3) 2(2х-1)/х 4
4) ![]() 4)
4)
![]()
5) 53х+353х-2 140 5) 7х-7х-1 6
6)![]() 6)
6)
![]()
7) ![]() (графически) 7)
(графически) 7) ![]() (графически)
(графически)
Вариант 3 Вариант 4
1) ![]() 1)
1)
![]()
2) 4х+2х+3 20 2) 9х+1-23х 7
3) ![]() 3)
3)
![]()
4) ![]() 4)
4)
![]()
5) 0,7|х+2|0,7 0,5 5) 0,6|х-3|0,6 0,5
6) 7х-5х+2 27х-1-1185х-1 6) 5х-3х+1 2(5х-1-3х-2)
7) ![]() 7)
7)
![]()
8) ![]() (решить
графически) 8)
(решить
графически) 8) ![]() (решить графически)
(решить графически)
Контрольная работа №3
Тема «Показательная функция»
а) - 1 вариант б) - 2 вариант
1) Построить график функции
а) ![]() и
свойства б)
и
свойства б) ![]() и
свойства
и
свойства
![]()
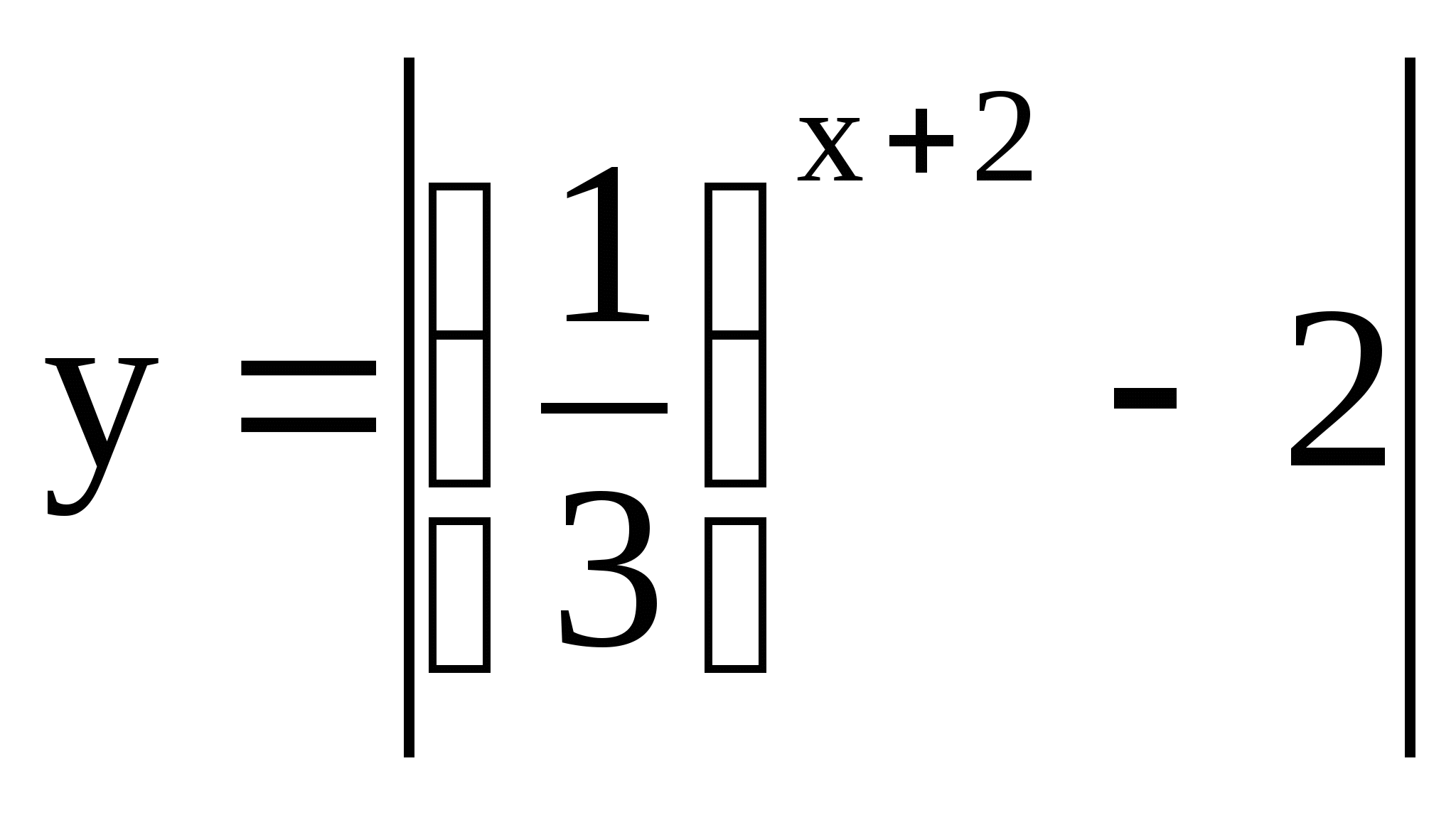
2) Сравнить числа
а) б)
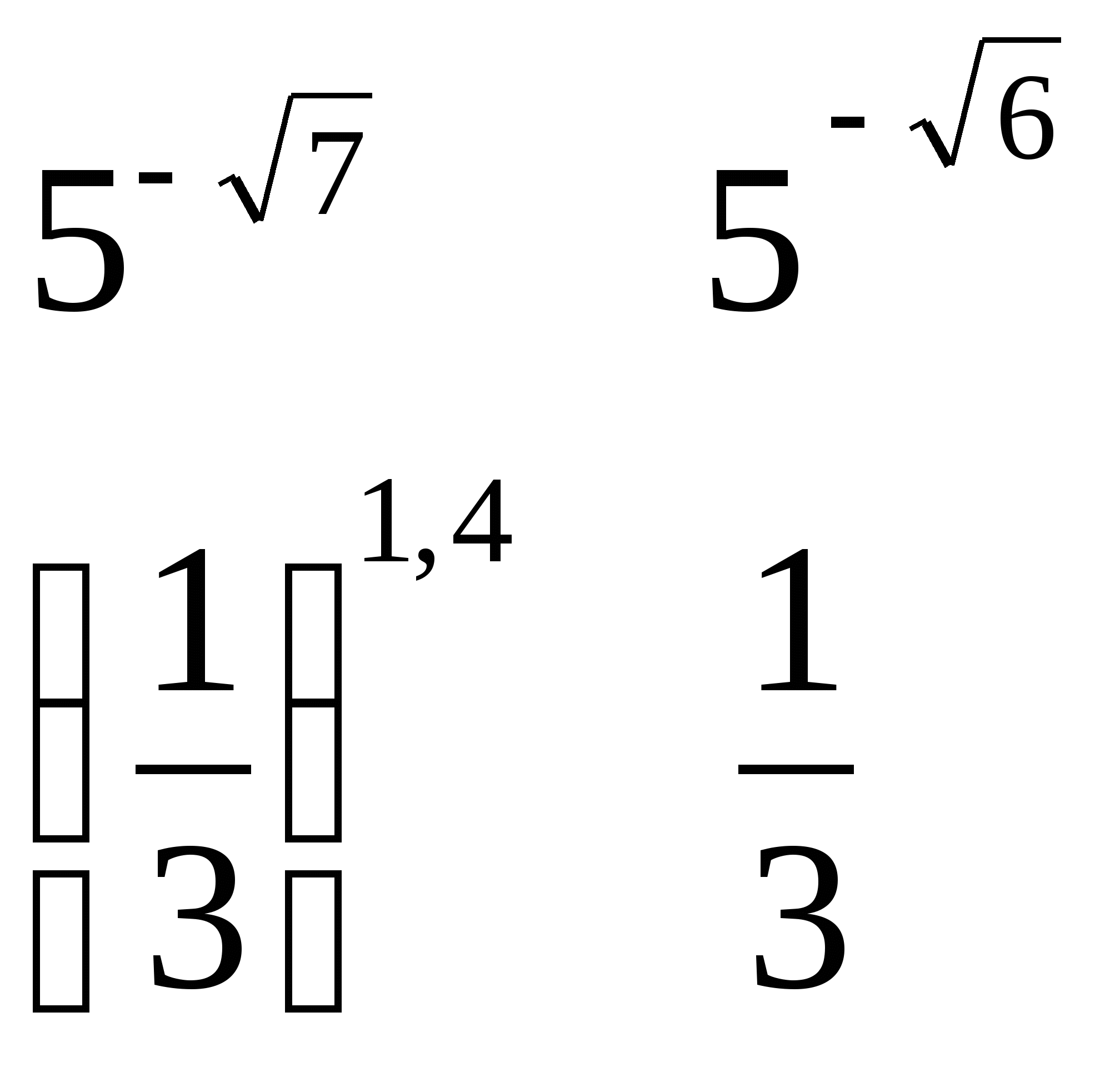
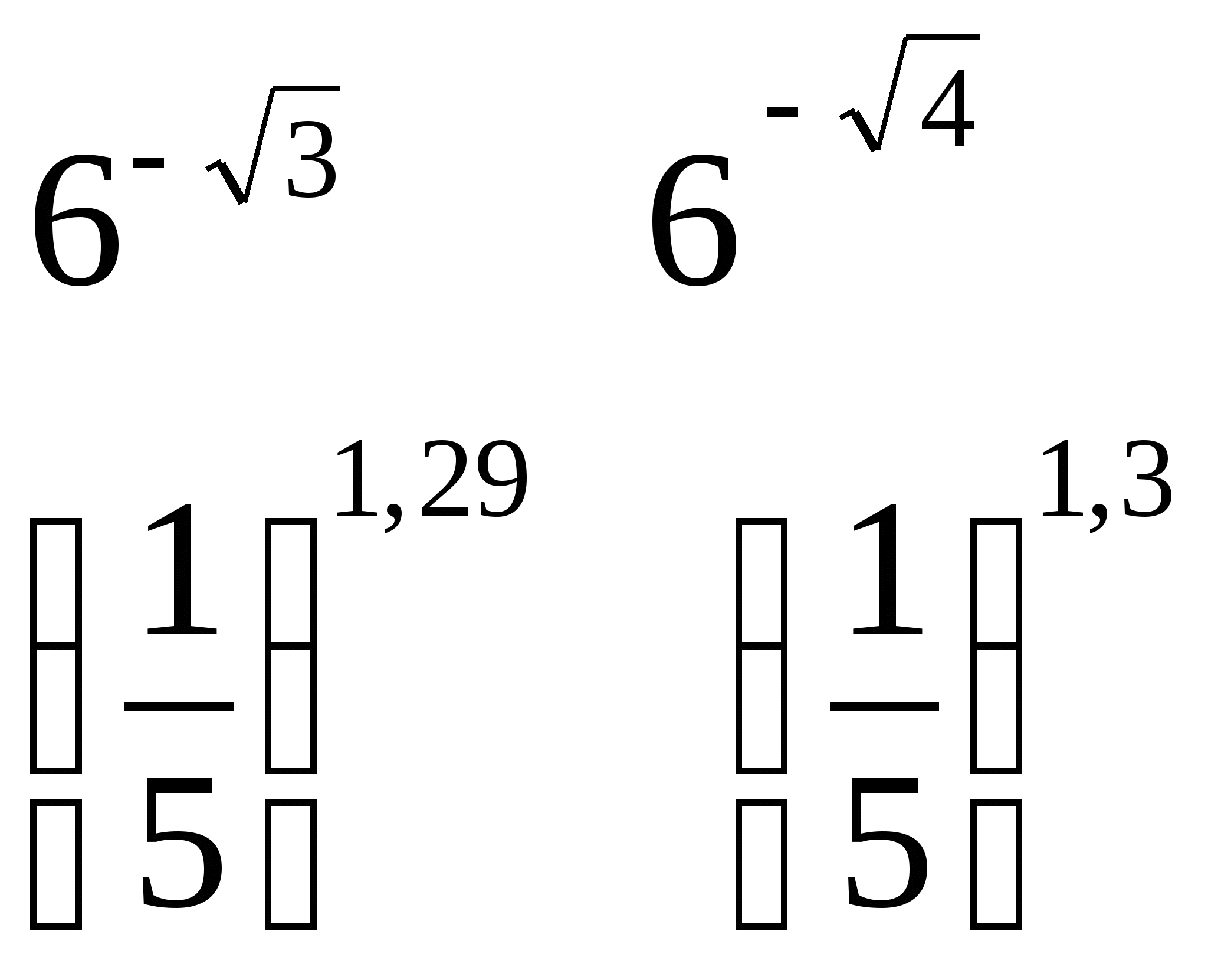
3) Решить уравнение
а) б)
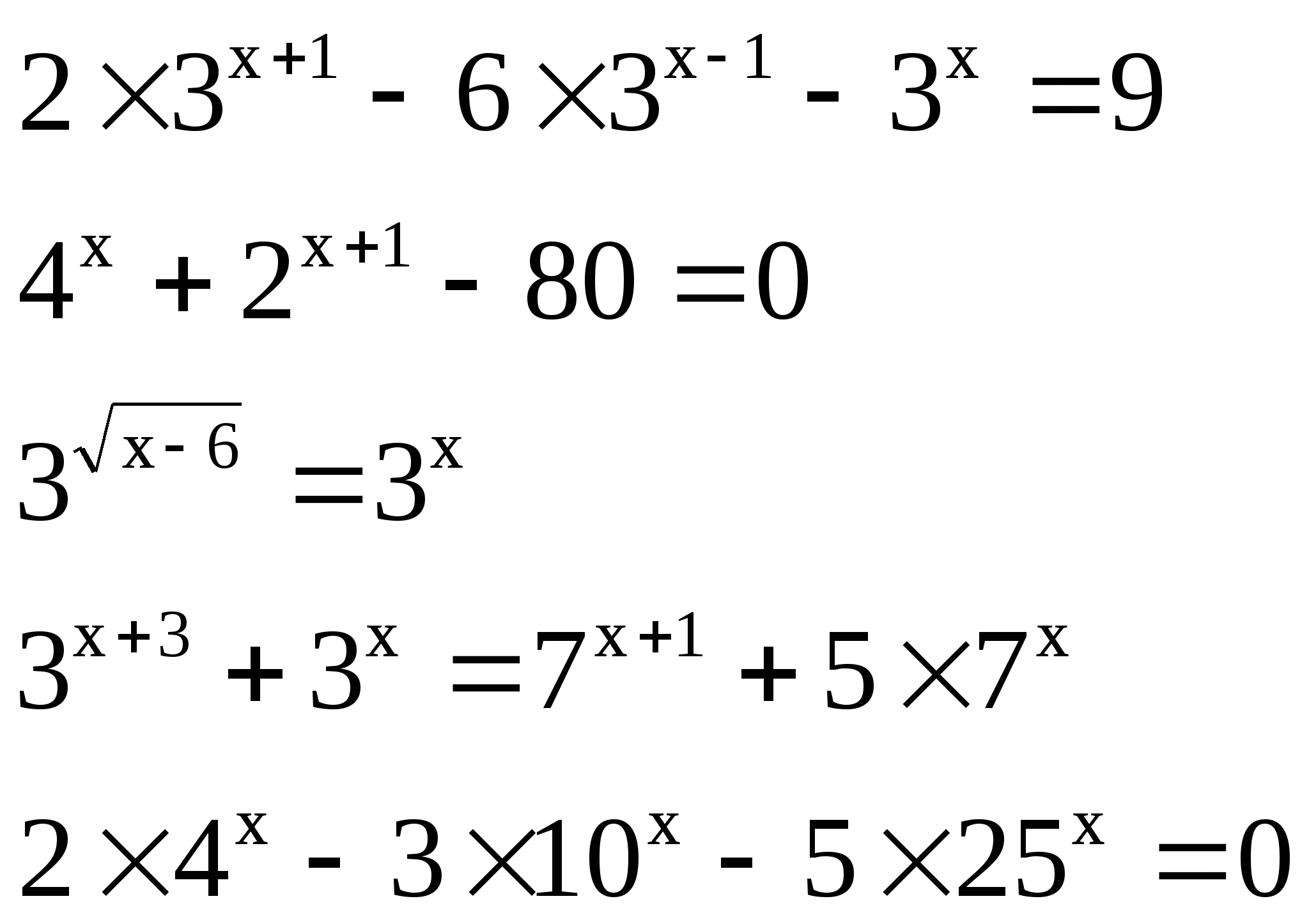
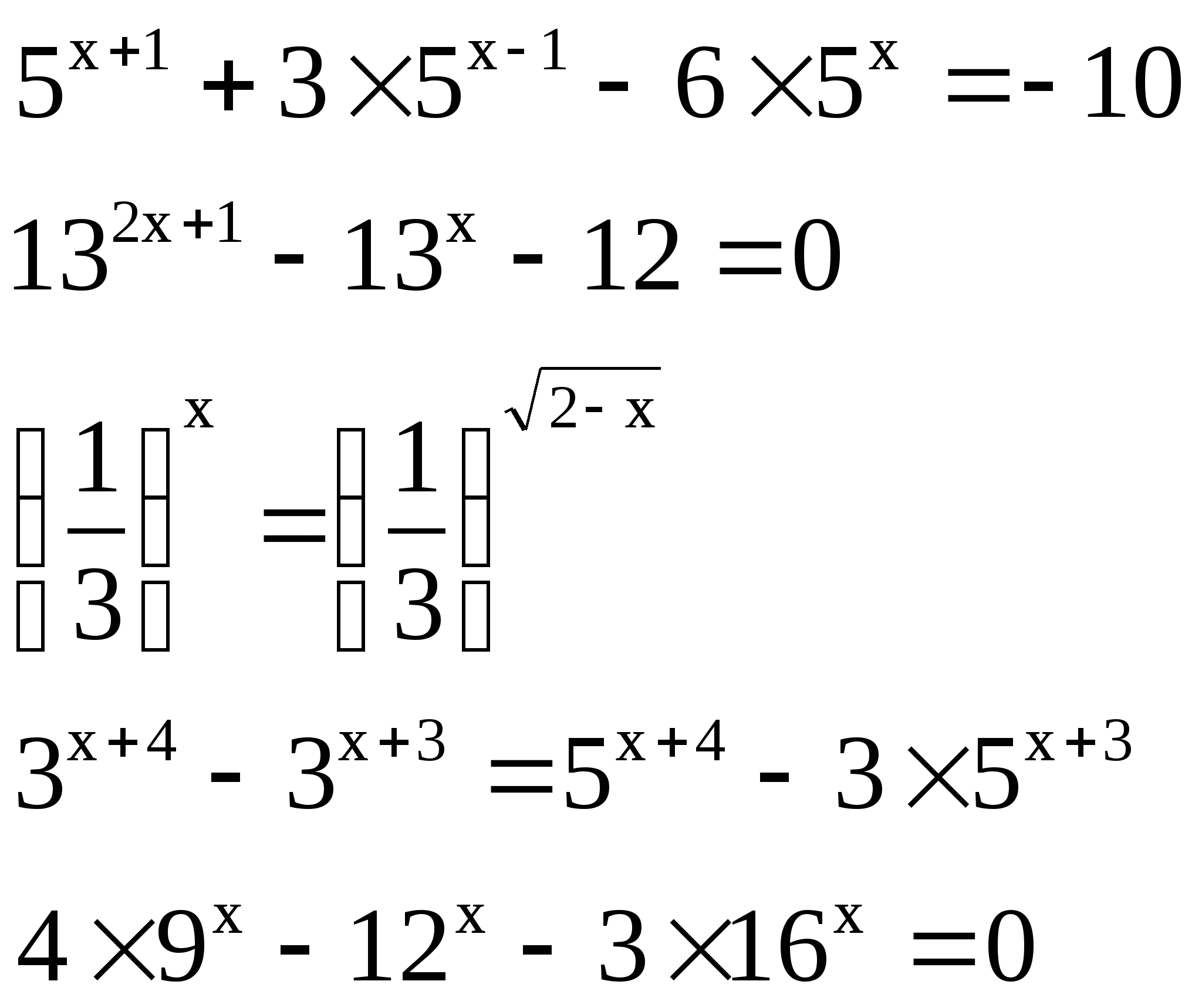
4) Решить неравенство
а) б)
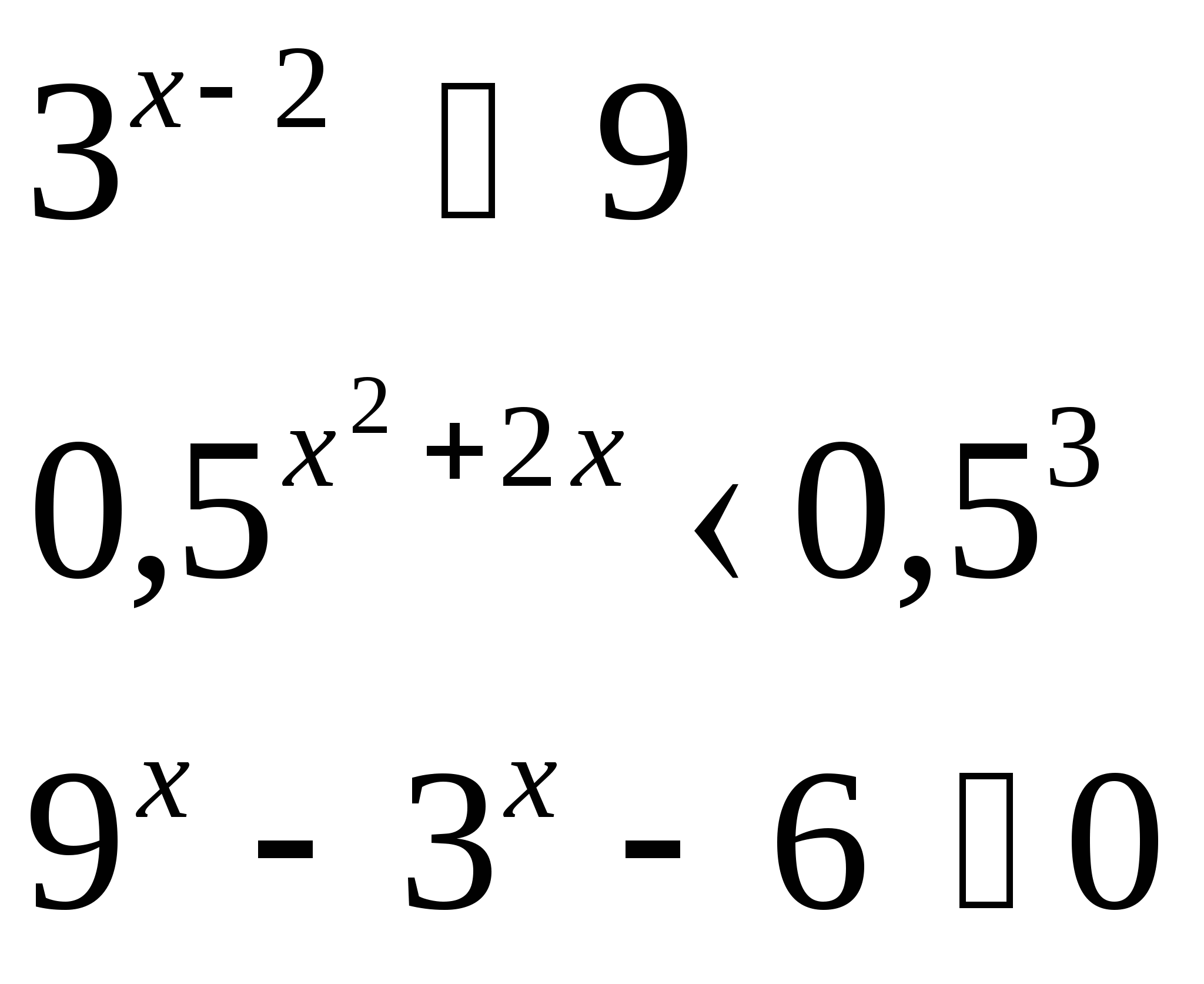
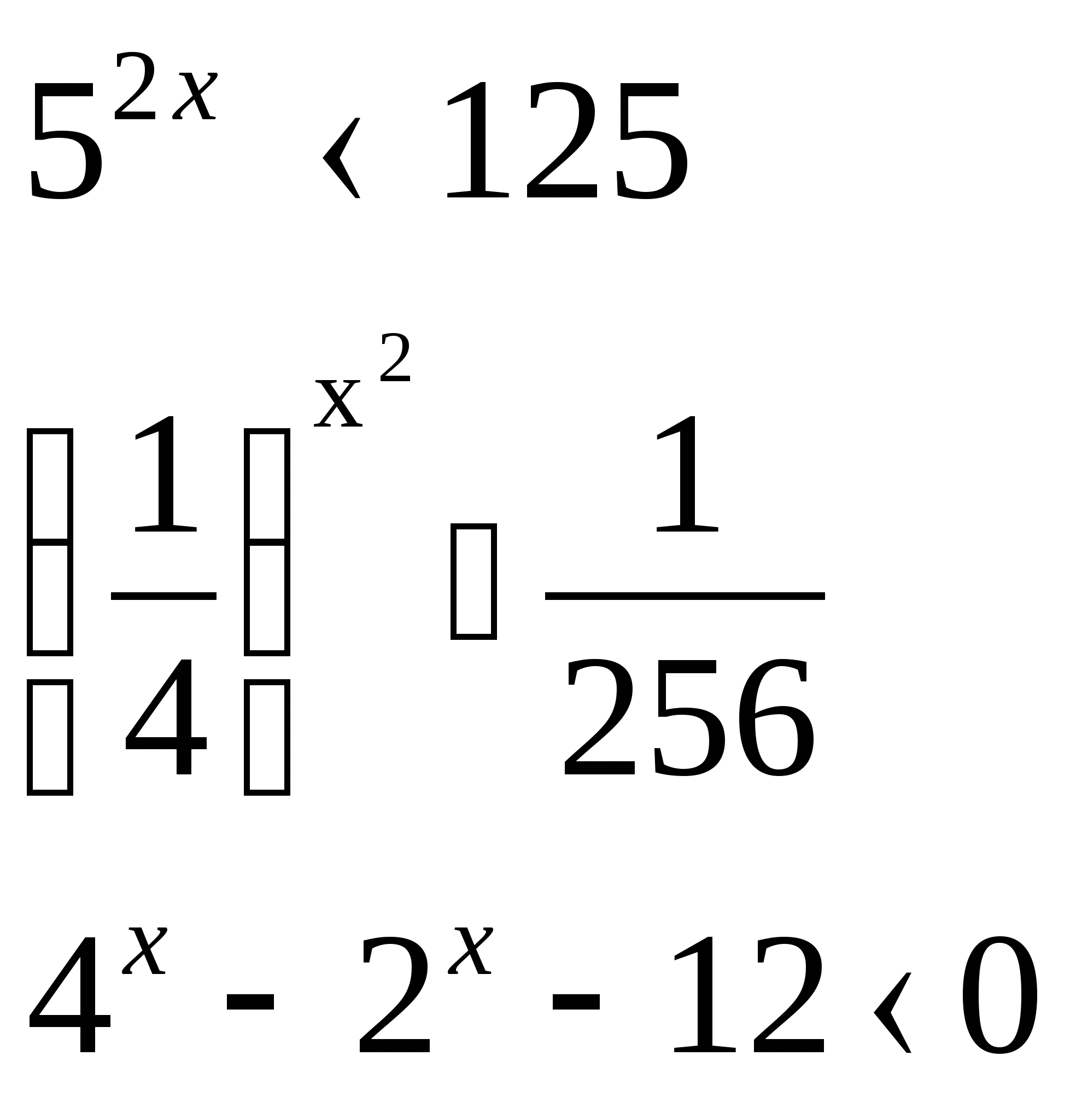
5) Решить неравенство
а) б)
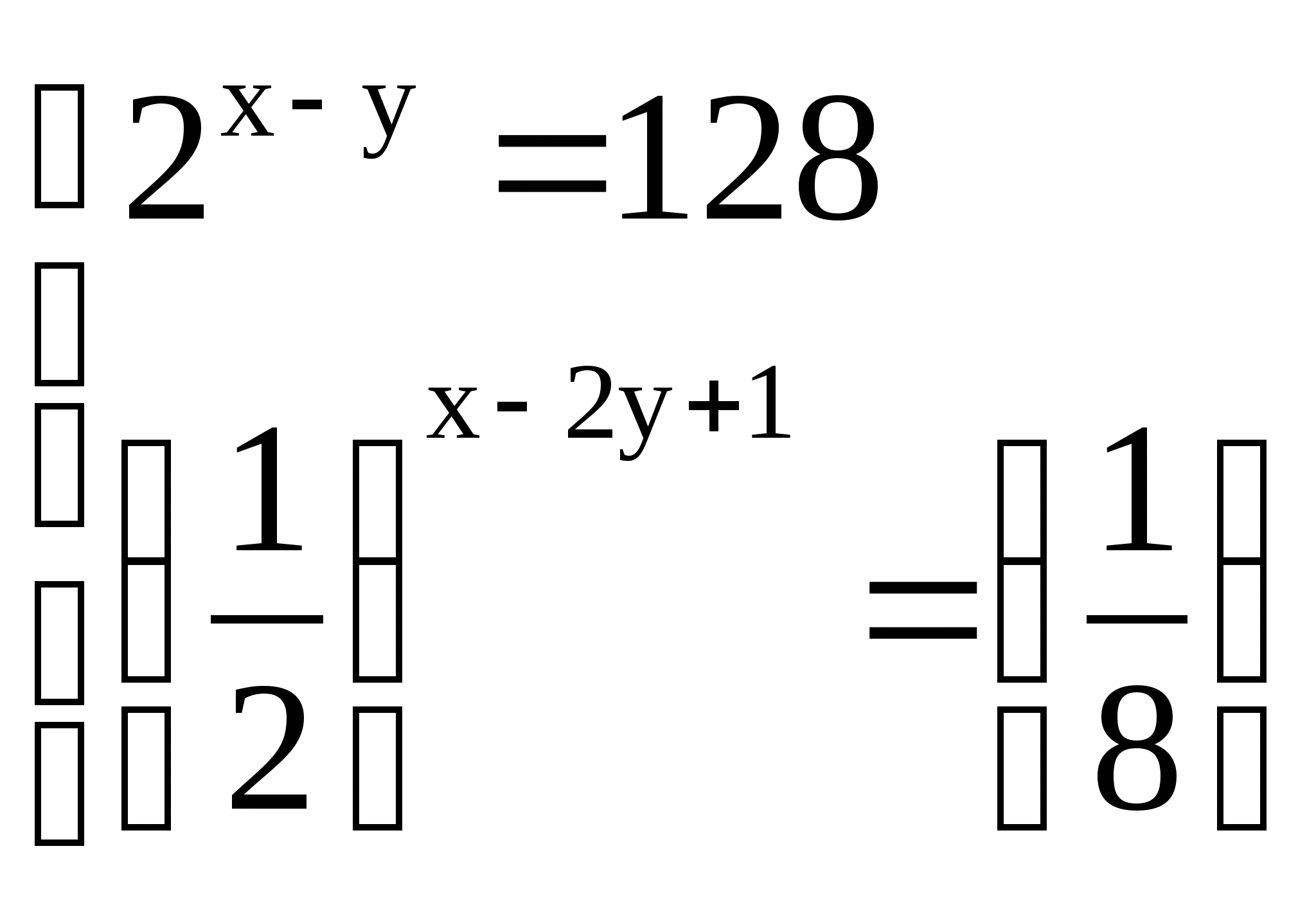
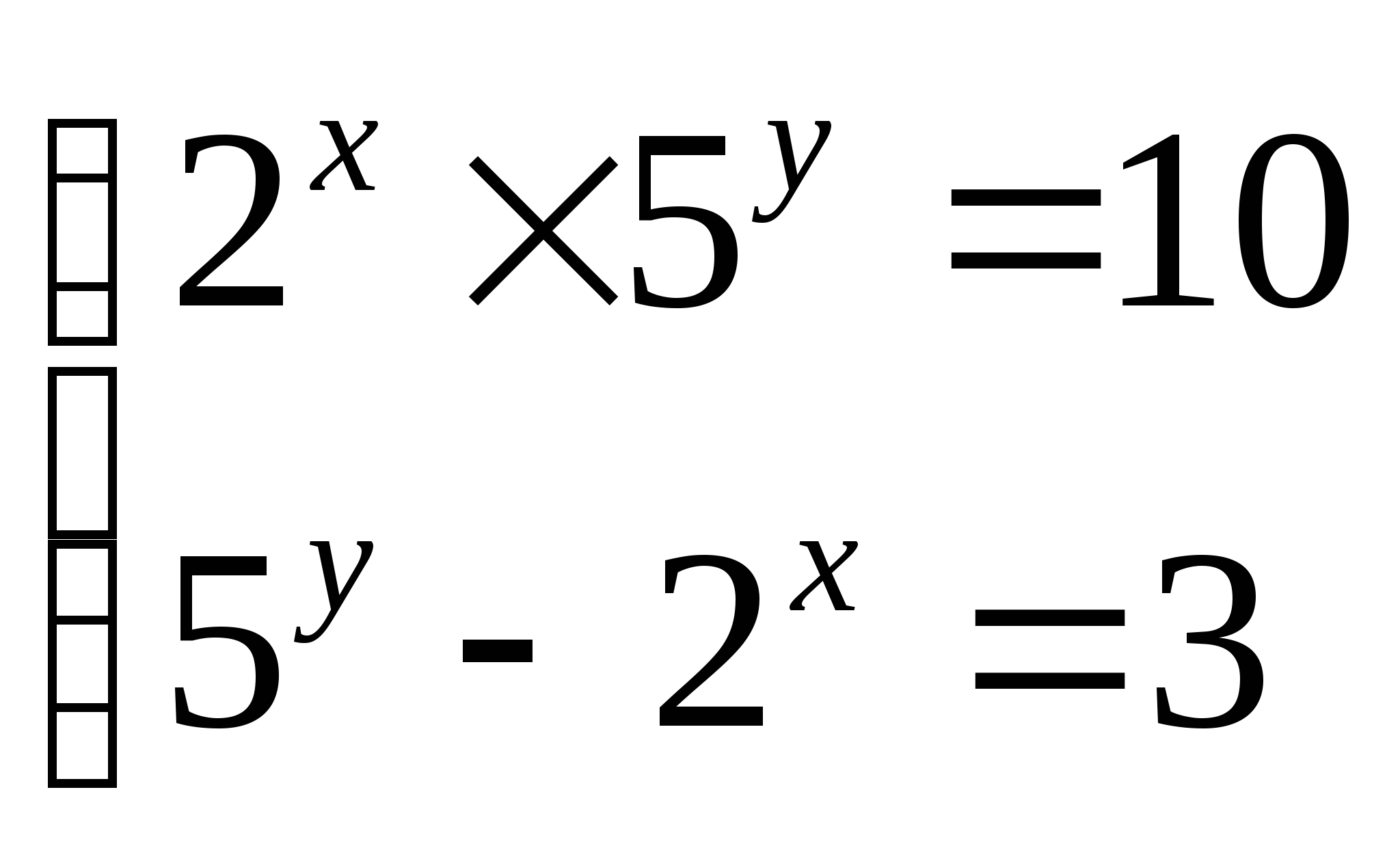
Самостоятельная работа № 4 (10 класс)
Логарифмы и их свойства
Вариант 1 Вариант 2
1) log31/243 1) log71/343
2) ![]() 2)
2)
![]()
3) log 2 log 416 3) log 3 log 20
4) ![]() 4)
(2 + lg 5)(lg 20 + lg 5)
4)
(2 + lg 5)(lg 20 + lg 5)
5) log 915 log 918 log910 5) log 812 log 815 log820
6) Найти их: 6) Найти их
lg х =lg12+lg15-lg18 lg х =lg8+lg20-lg40
Вариант 3
1) ![]()
2) ![]()
3) 6 log 32 log 43 log 54log 65 log 76 log 87
4) ![]()
5) Сравнить числа: ![]() и
и
![]()
6) Найти х: log0,1x=4
log0,13-![]() log0,127-2 log0,16
log0,127-2 log0,16
Вариант 4
1) ![]()
2) ![]()
3) log 57 log 79 log 911log 1123
4)![]()
5) Сравнить числа: ![]() и
и![]()
6) Найти х: log0,1x=2
log0,16-0,5 log0,1100+3 log0,1![]()
Самостоятельная работа № 5 (10 класс)
Логарифмическая функция
Вариант 1 Вариант 2
1) ПГФ: у = log3 x и свойства 1) ПГФ: у = log2 x и свойства
2) ООФ: ![]() 2)
ООФ:
2)
ООФ: ![]()
3) ПГФ: у = log3(x-1)+2 3) ПГФ: у = log2(x+1)-2
4) ООФ: у = log4(x-2)/(х+3) 4) ООФ: у = log2(3-х)/(х+1)
5) ПГФ: ![]()
![]() 5)
ПГФ:
5)
ПГФ: ![]()
![]()
Вариант 3 Вариант 4
1) ПГФ: ![]() и
свойства 1) ПГФ:
и
свойства 1) ПГФ: ![]() и
свойства
и
свойства
2) ООФ: ![]() 2)
ООФ:
2)
ООФ: ![]()
3) ПГФ: ![]() 3)
ПГФ:
3)
ПГФ: 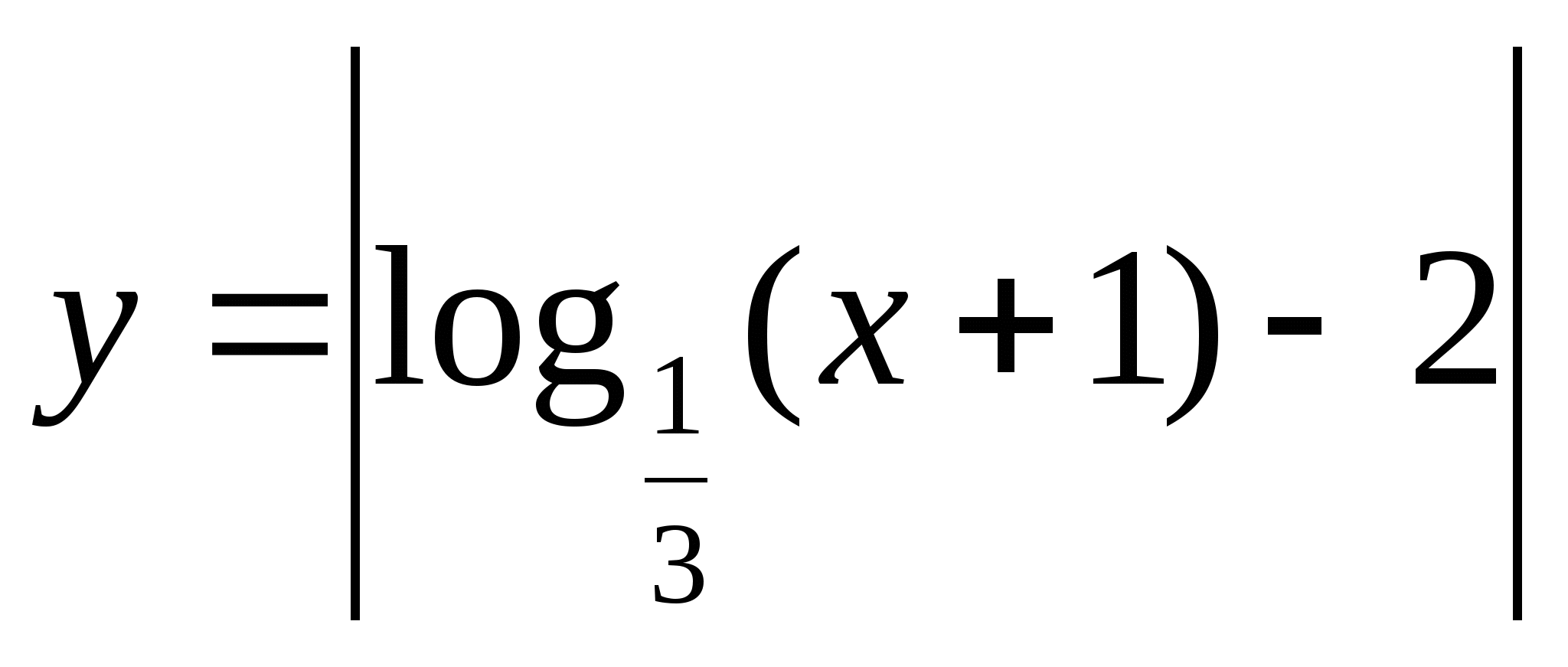
4) ООФ: у = log2log2x 4) ООФ: у = log0,5 log3 x
5) ООФ: ![]() 5)
ООФ:
5)
ООФ: ![]()
Самостоятельная работа № 6 (10 класс)
Логарифмические уравнения
Вариант 1 Вариант 2
1) log3(x2-1)=1 1) log5(x2+1)=1
2) lg(3x-17)-lg(x+1)=0 2) lg(4x+5)-lg(5x+2)=0
3) log 0,5(x2-x)=1 3) log 0,1(x2 +3x)=1
4) ![]() 4)
4)
![]()
5) ![]() 5)
5)
![]()
6) log2 2
X+log2 X2= -1 6)
log24X+log4![]() =
1,5
=
1,5
7) log 4 X + 3log2X =7 7) log 9X + 2log3X =5
Вариант 3 Вариант 4
1) log 20,5(1-X2)=4 1) log 24(1+X2)=0,25
2) ) log3(3-X)+log3(4-X)=1+2log32 2) log0,5(X+2)+log0,5(X+3)=log0,53-1
3) ![]()
![]() 3)
3)
![]()
4) ![]() 4)
4)
![]()
5) logX+2(3x2-12)=2 5) log 2X-1(3,5x2-2,5х)=2
6) |x-3|lg x=2(x-3) 6) |x-5|lg x=x-5
7) log0,5(log22x-3log2x+4)=-1 7) log3(log20,5Х-3log0,5Х+5)=2
8) x2+7=6x log8xlogx16 8) x2 logх27log9 х =x+4
Самостоятельная работа № 7 (10 класс)
Логарифмические неравенства
Вариант 1 Вариант 2
1) log 0,2(4-2x) -1 1) log 0,5(3x-2) -1
2) 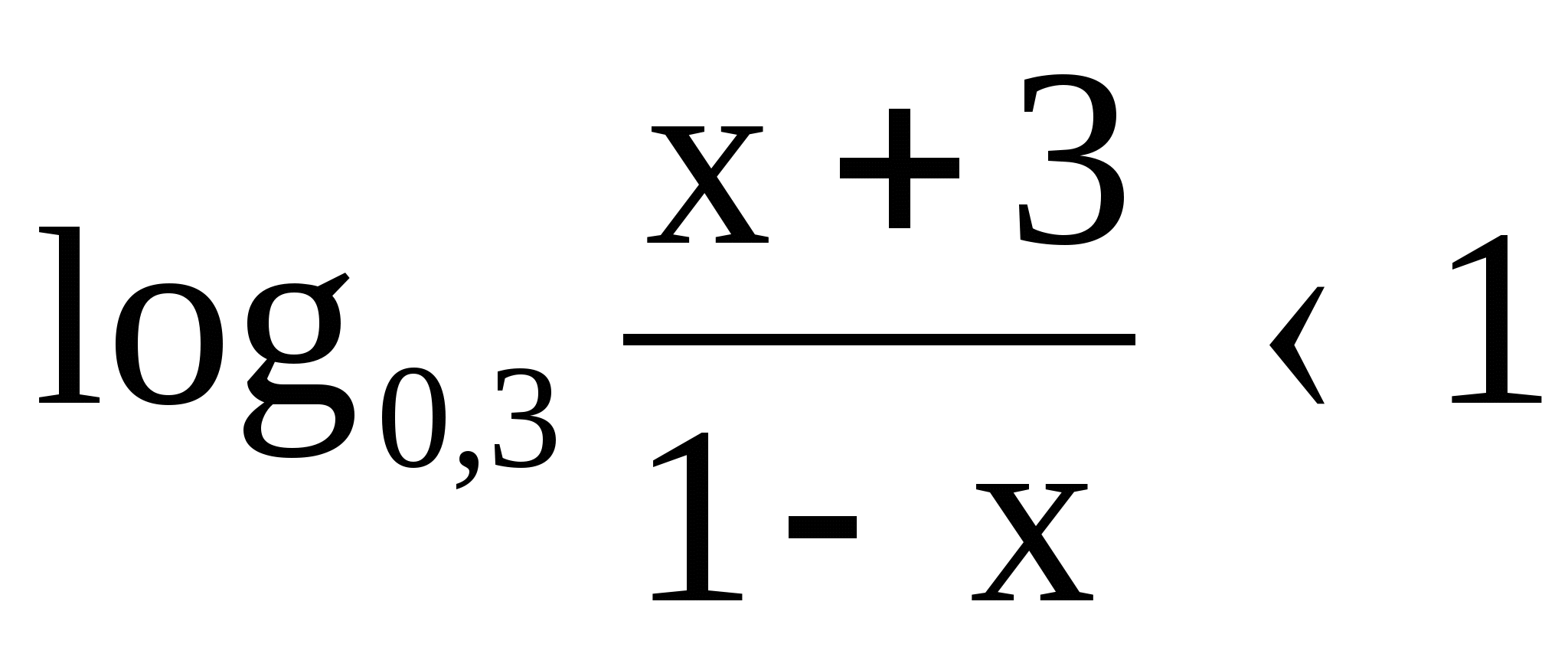 2)
2)
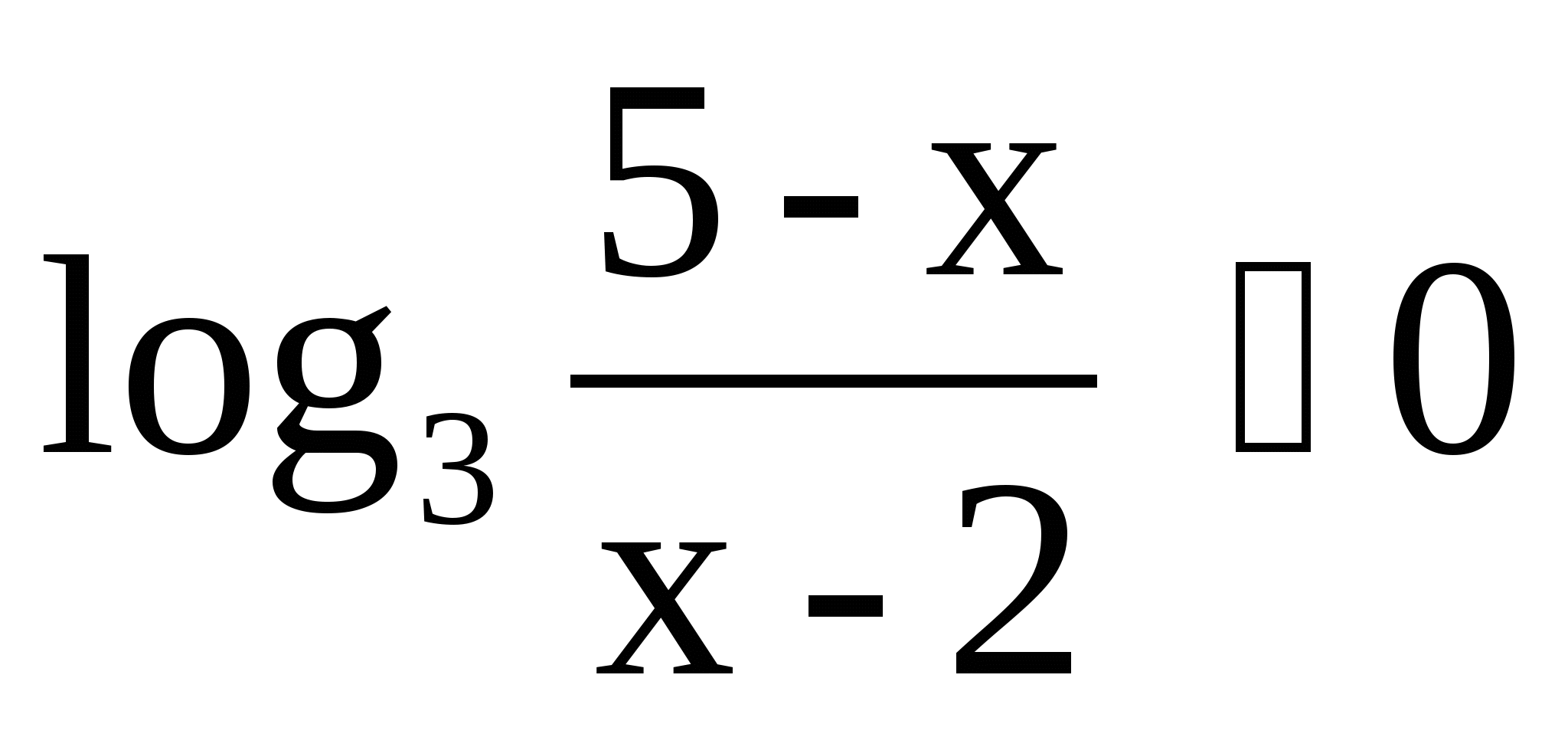
3) log 2(x-1)+log 2 x 1 3) log 3 x+log 3(x-8) 2
4) 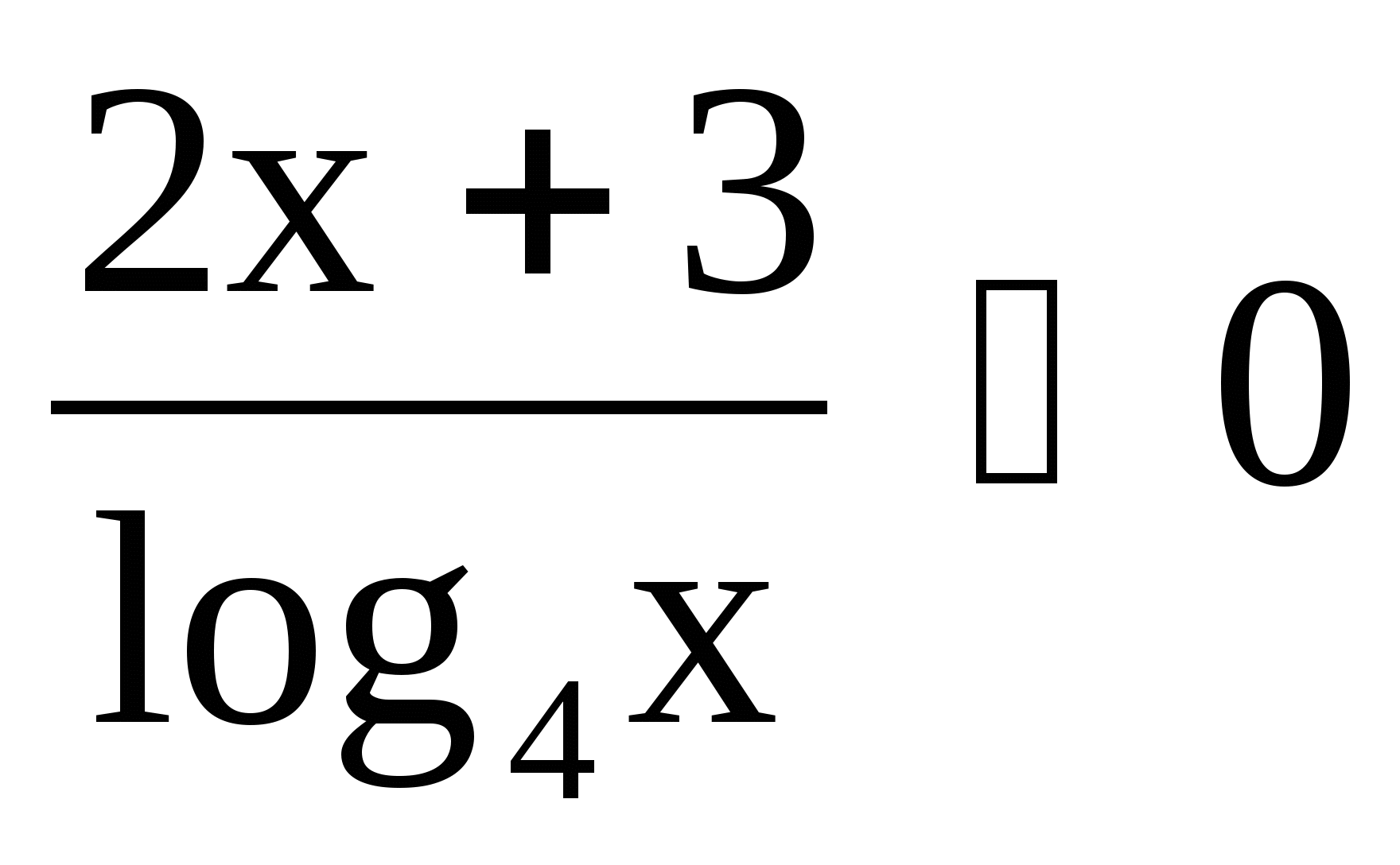 4)
4)
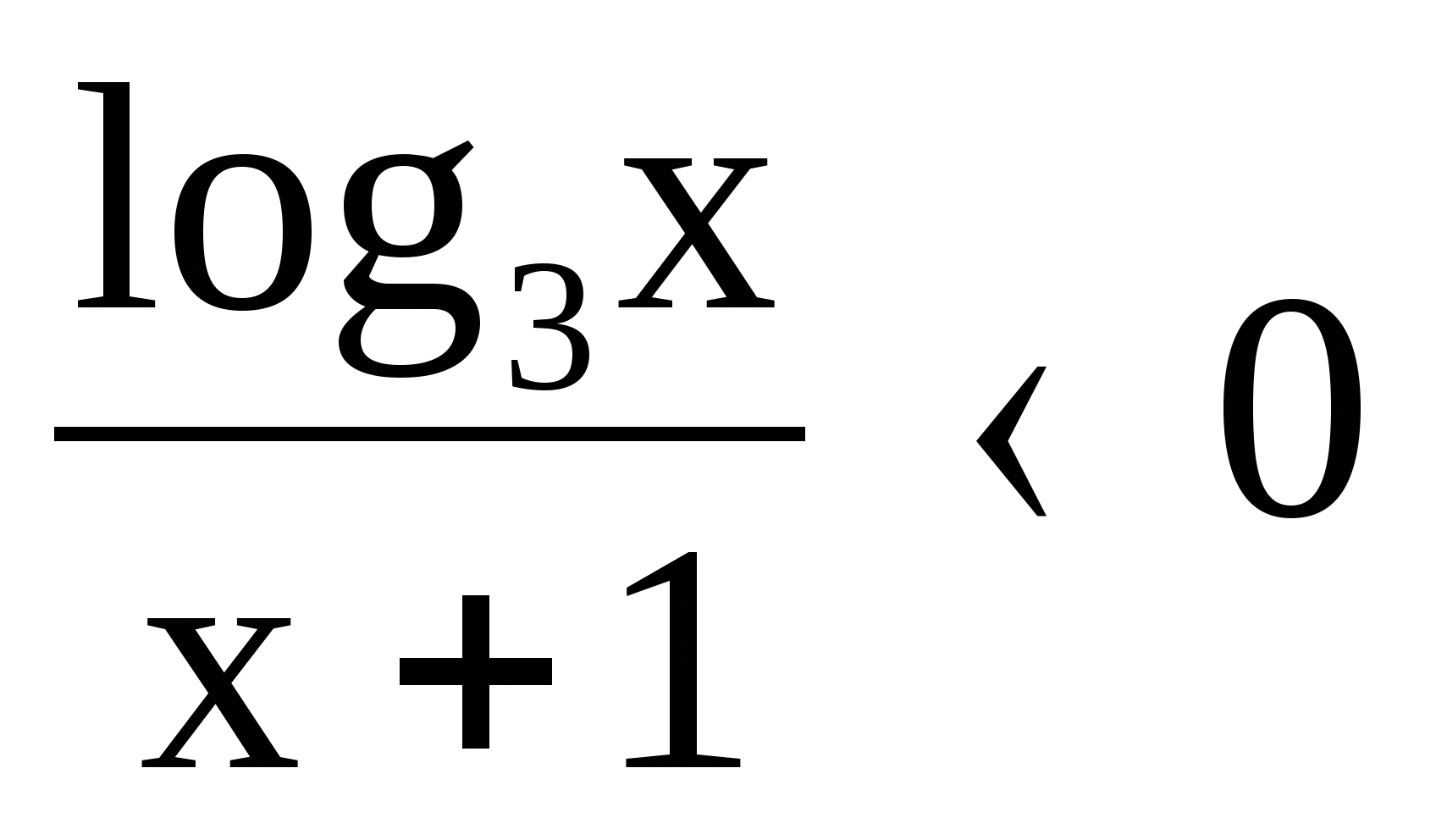
5) lg2x +6 5lgx 5) lg2 x + lg x 2
6) ![]() 6)
6)
![]()
7) 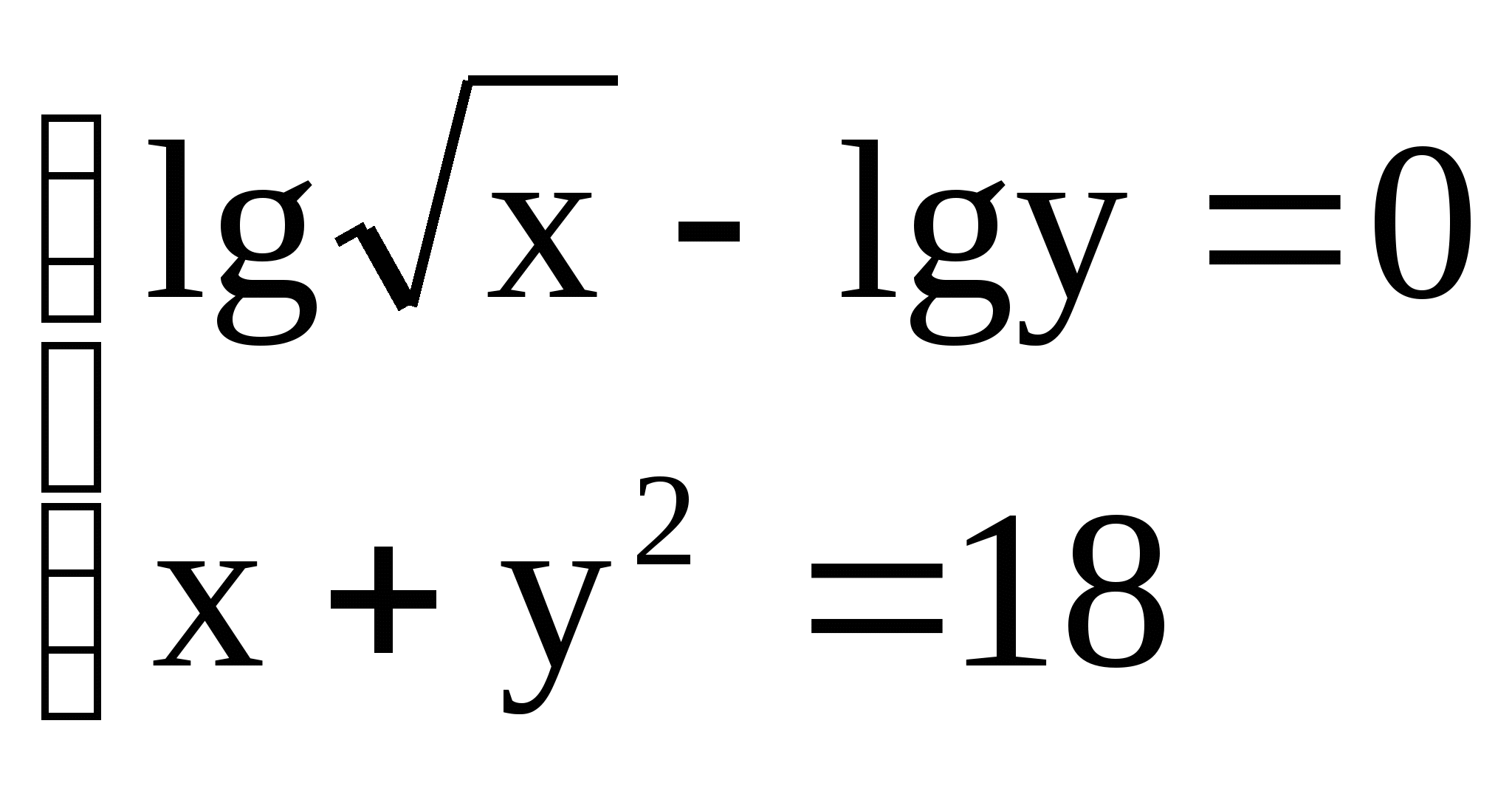 7)
7)
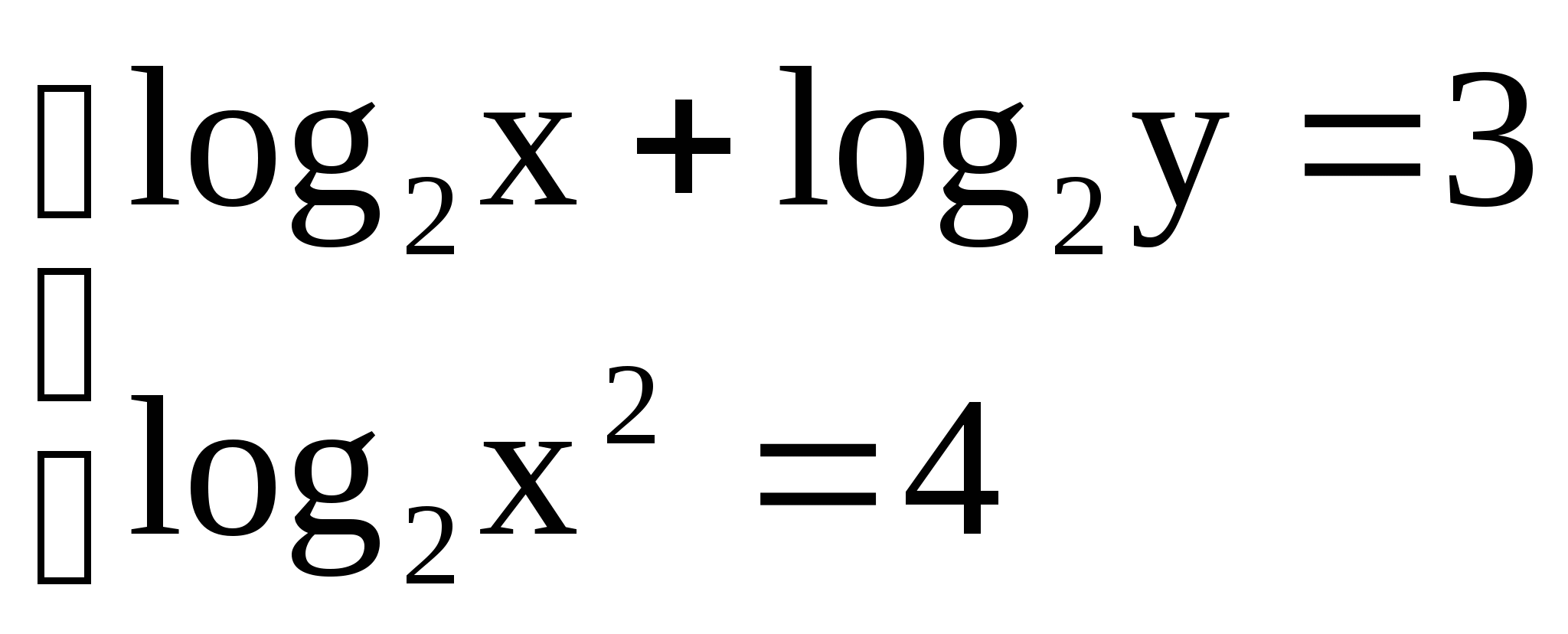
Вариант 3 Вариант 4
1) 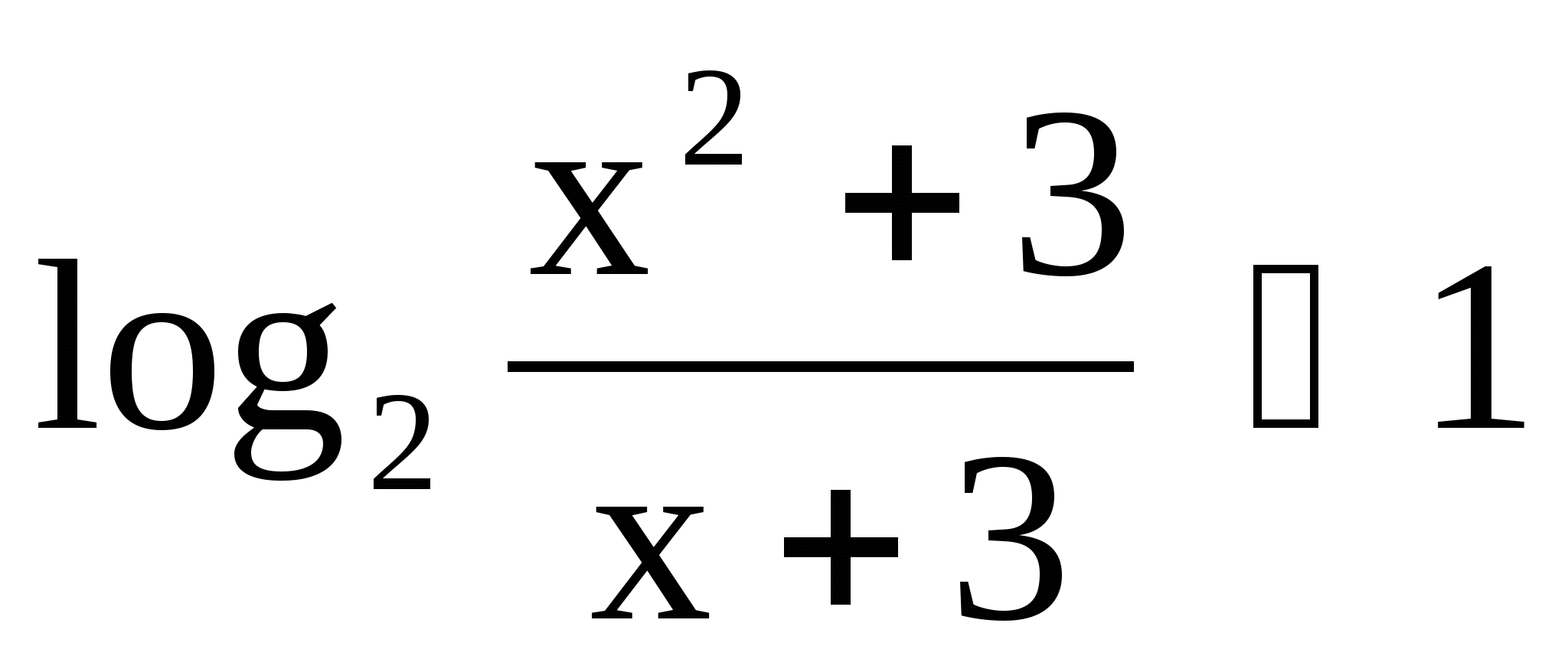 1)
1)
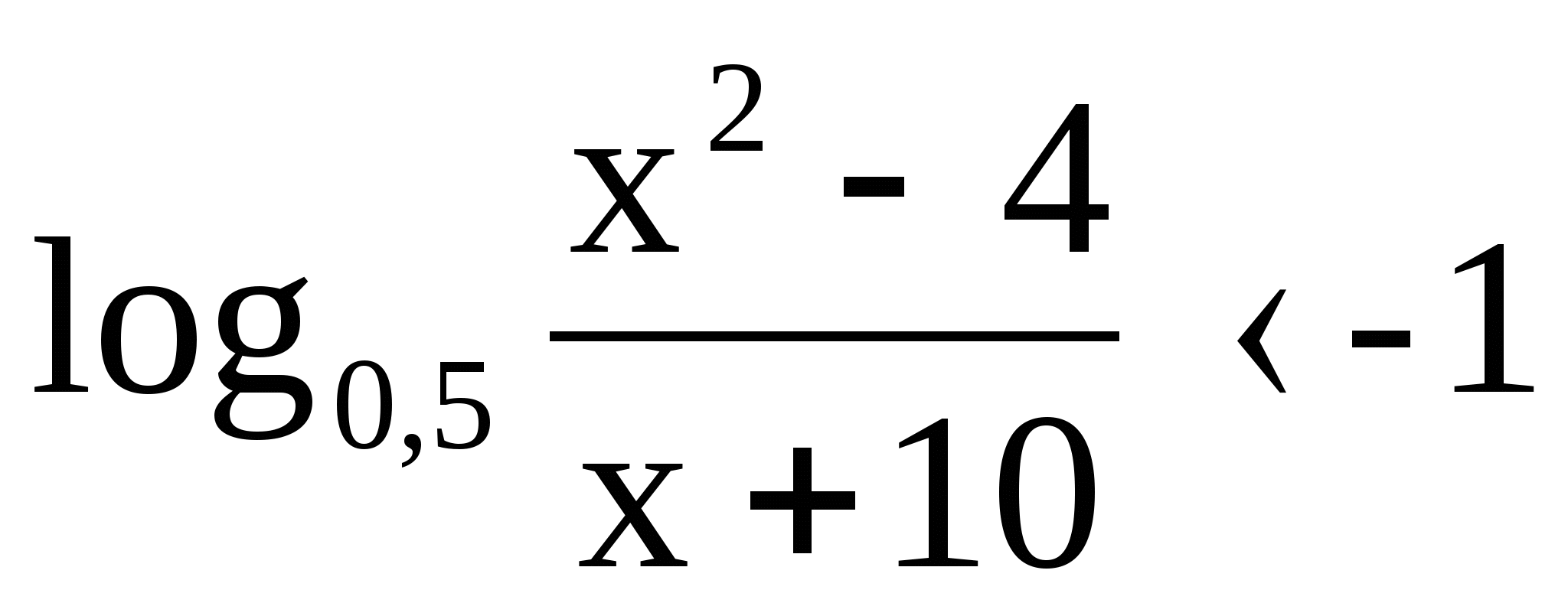
2) log 2 x-2log x 2+1 0 2) lg x+6log x 10 5
3) log 3 x+log 3 (x-1)-1 log 3 2 3) log 0,1 x+log 0,1 (x-2)+1 log 0,1 0,3
4) 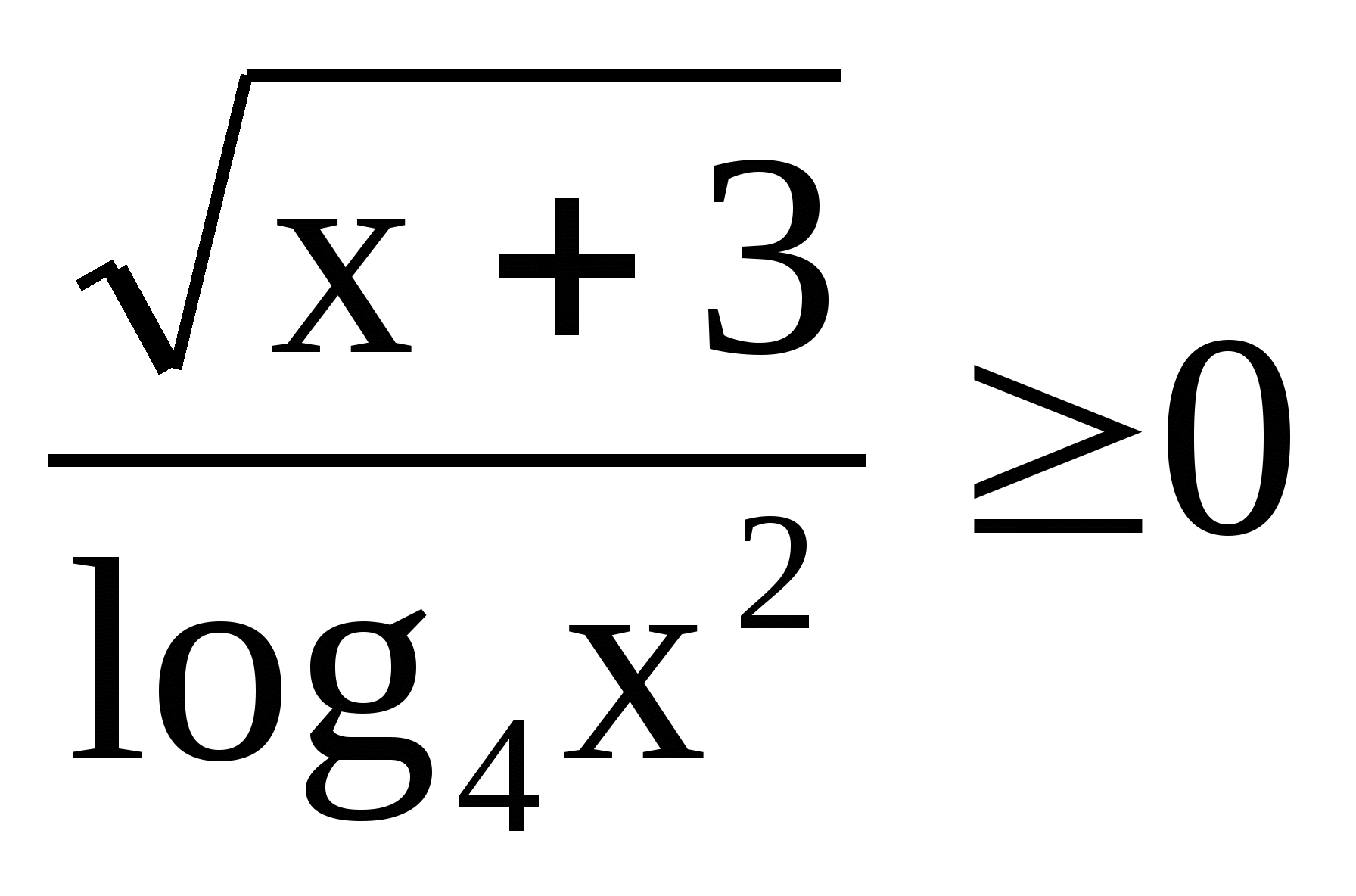 4)
4)
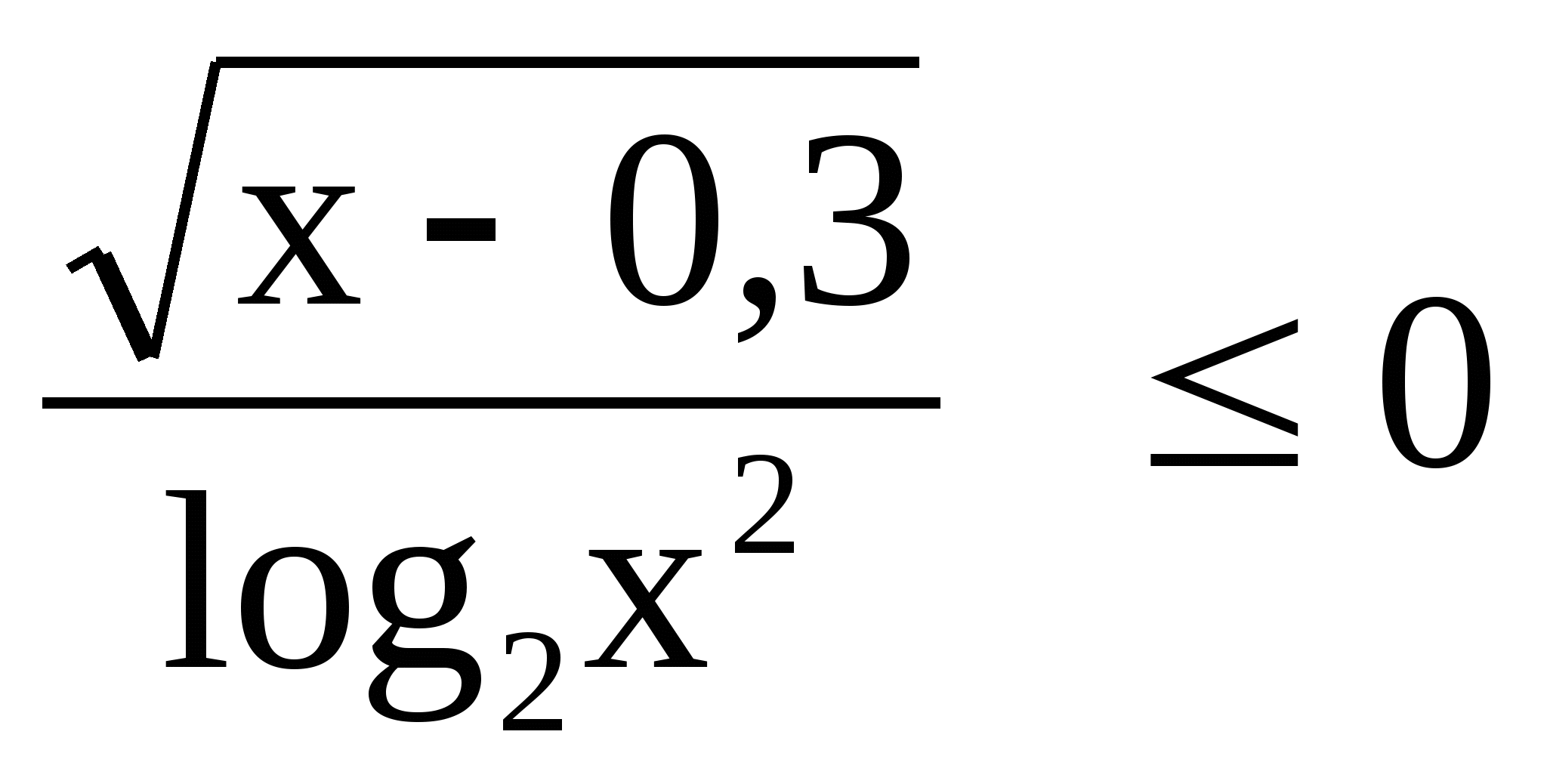
5) ![]() 5)
5)
![]()
6) log 0,5 (x2-x-20)-log 0,5 (x+4) 0 6) log 0,5 (3-x2)+1 log 0,5 (0,5x+0,5)
7) 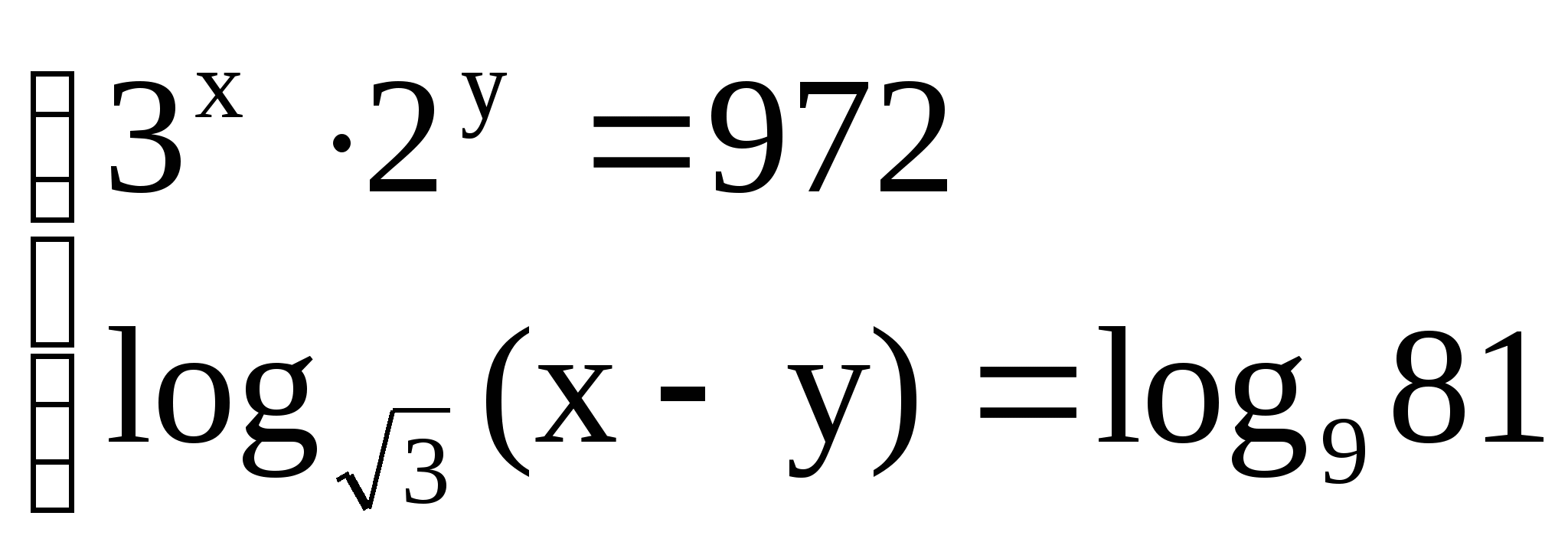 7)
7)
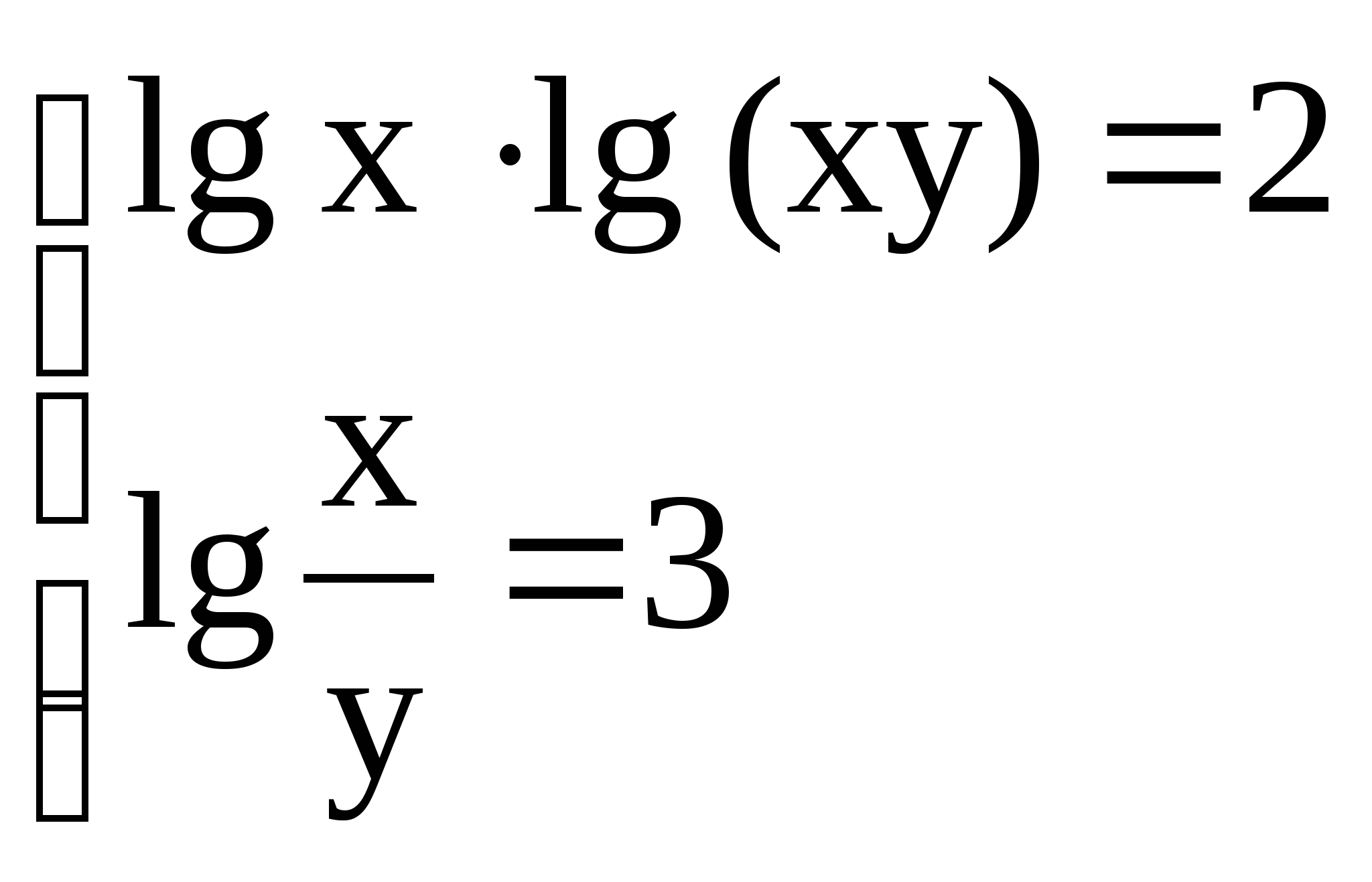
Самостоятельная работа № 8 (10 класс)
Системы уравнений, содержащие показательную и логарифмическую функцию
Вариант 1 Вариант 2
1) 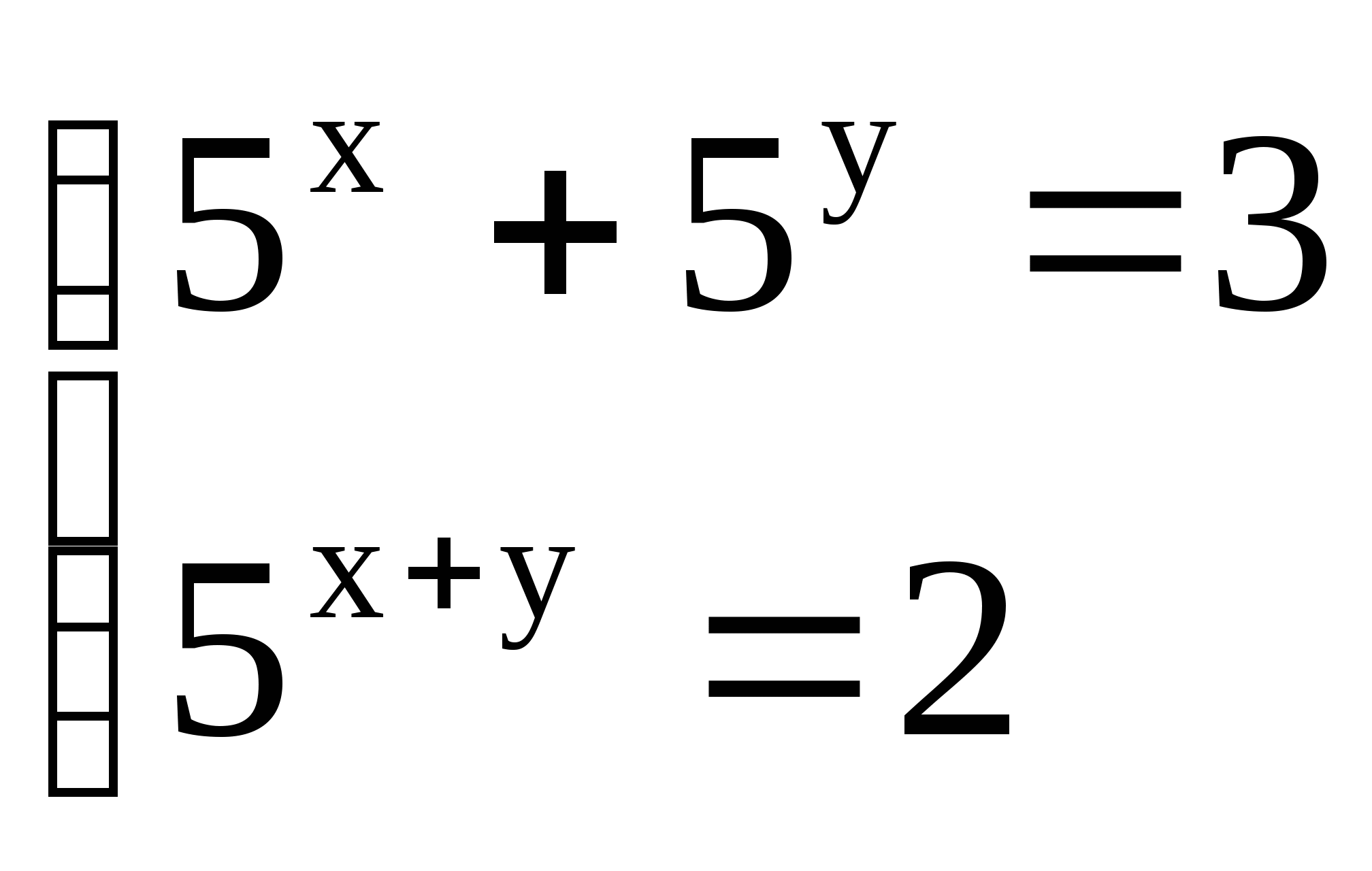 1)
1)
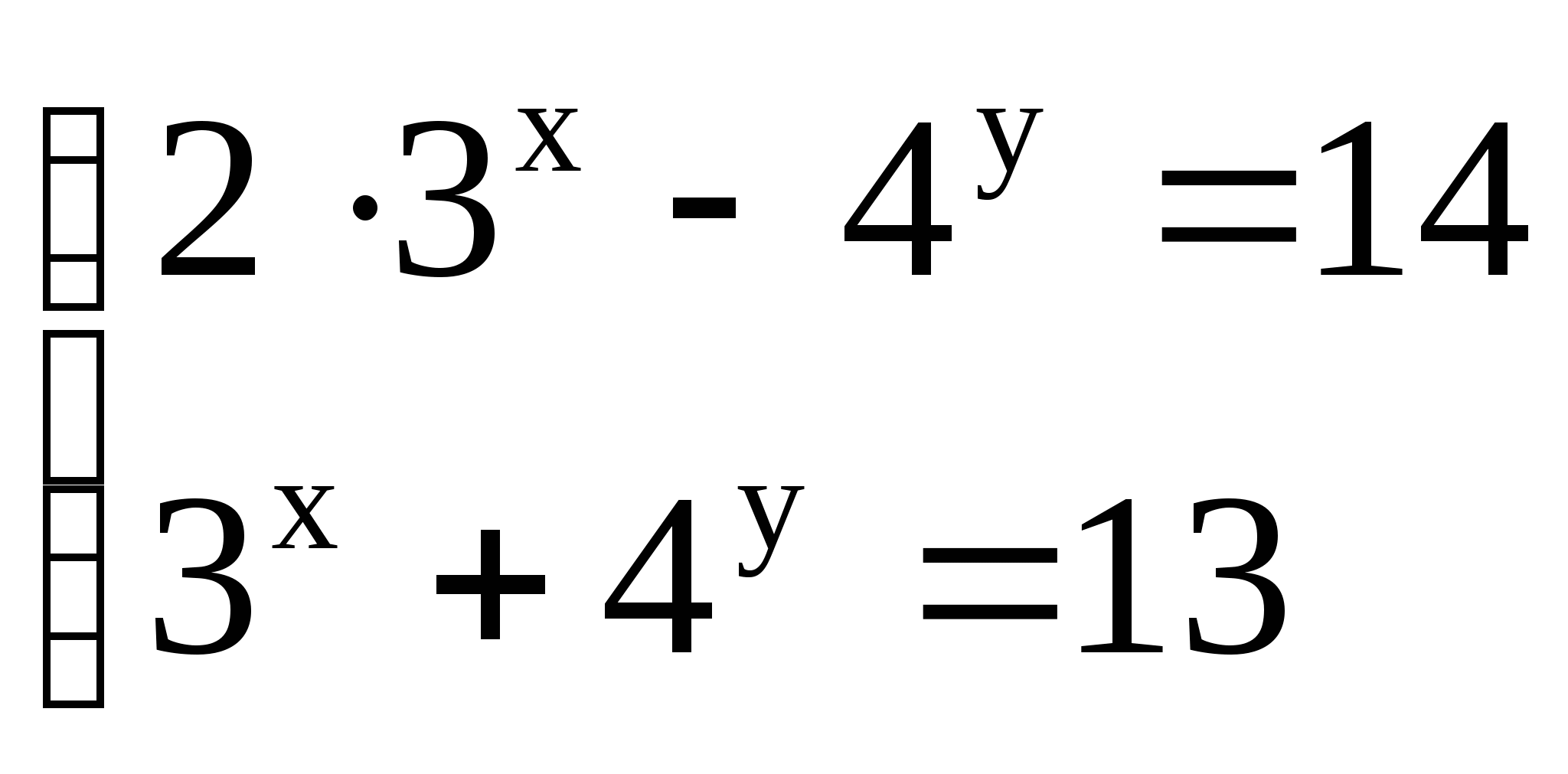
2) 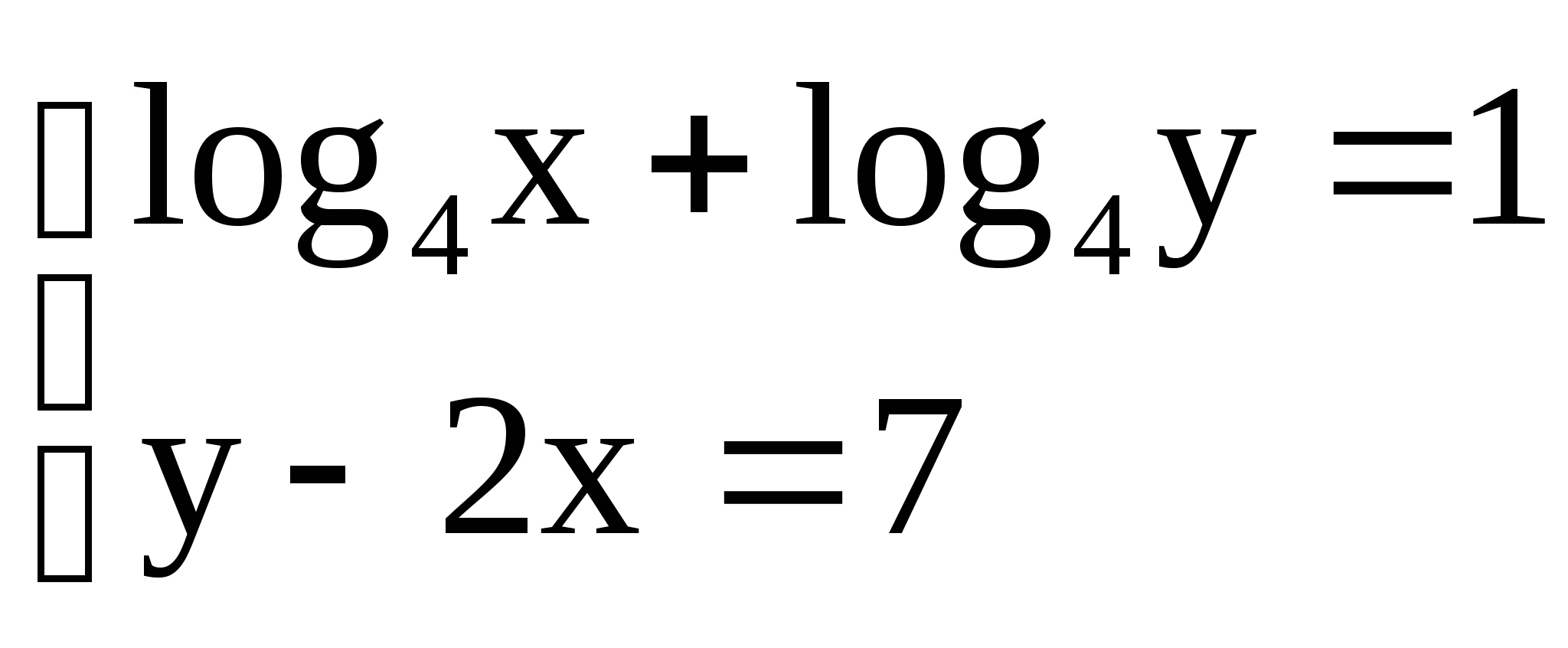 2)
2)
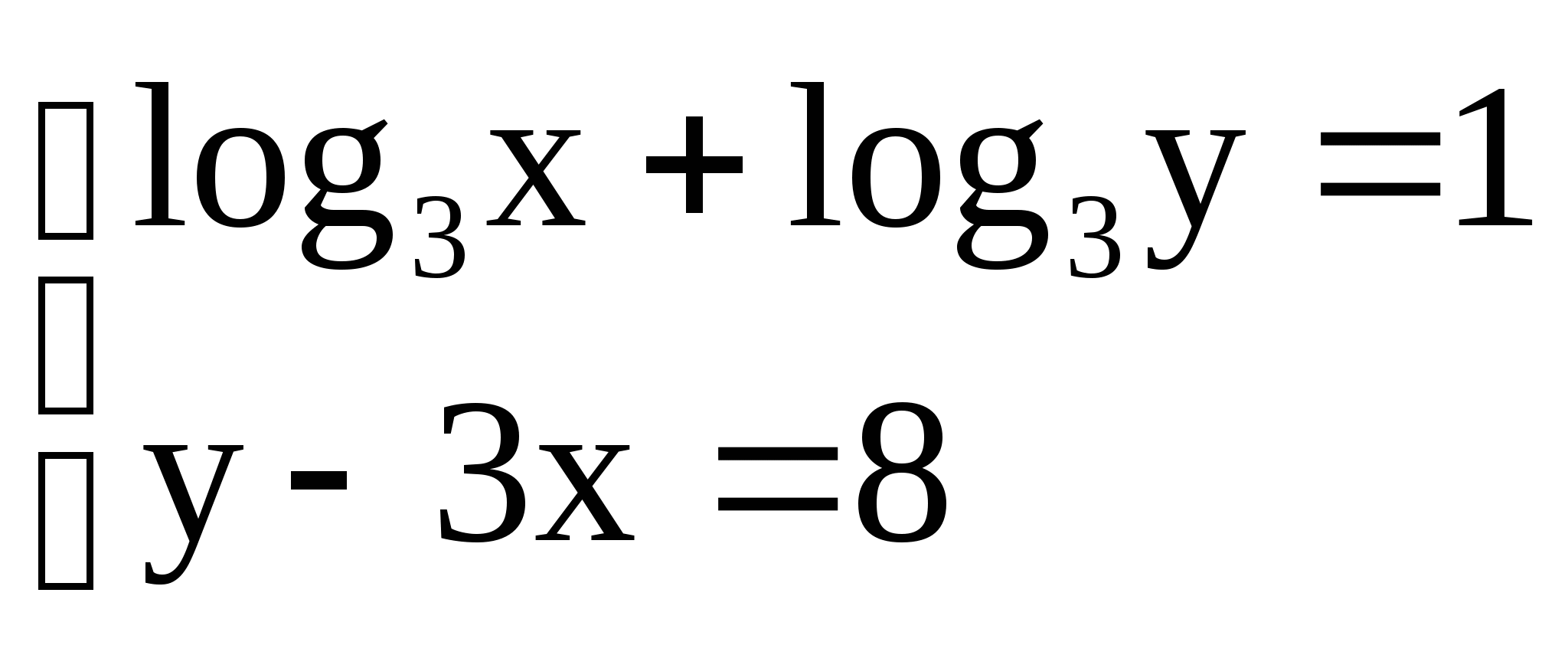
3) 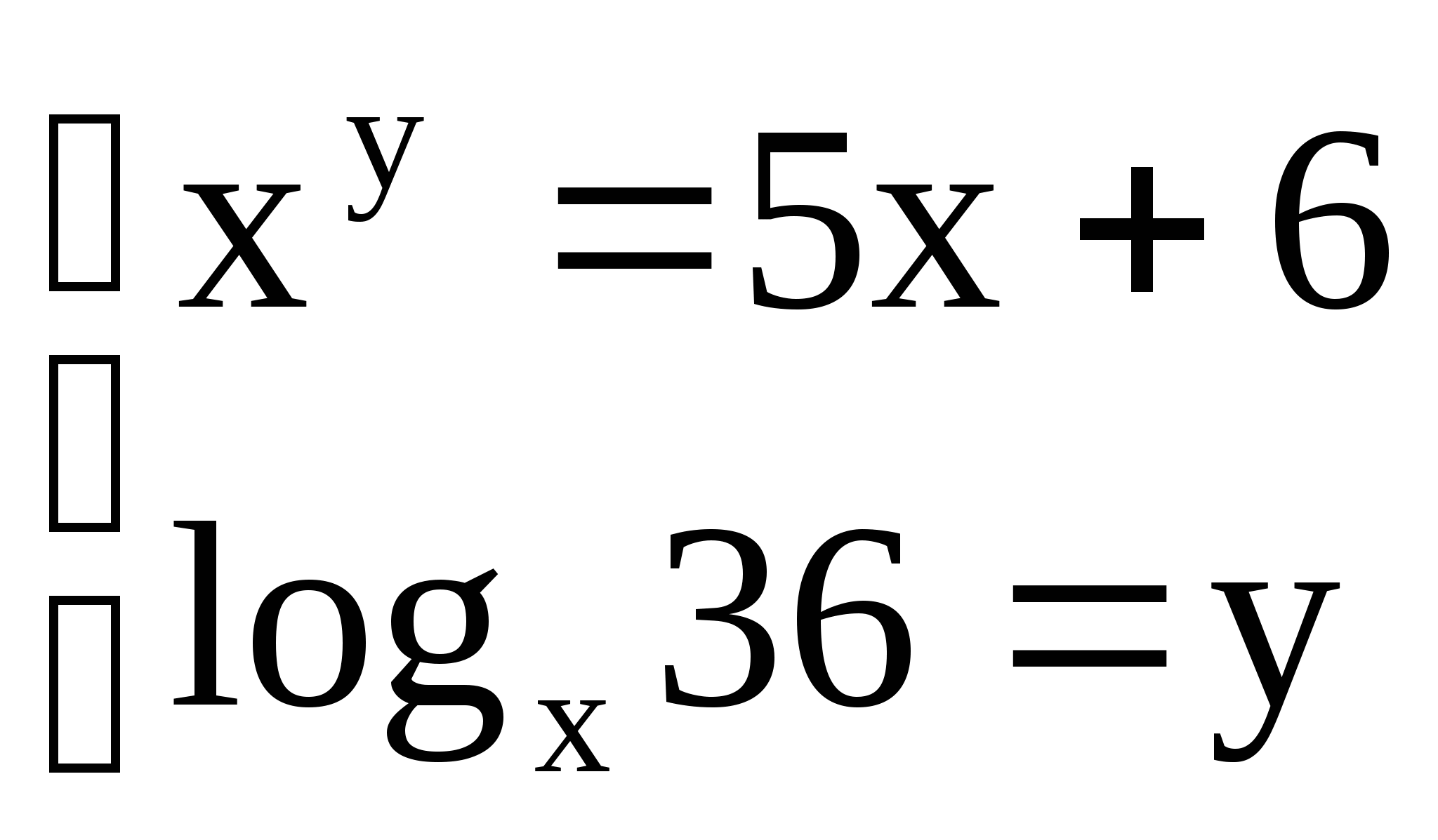 3)
3)
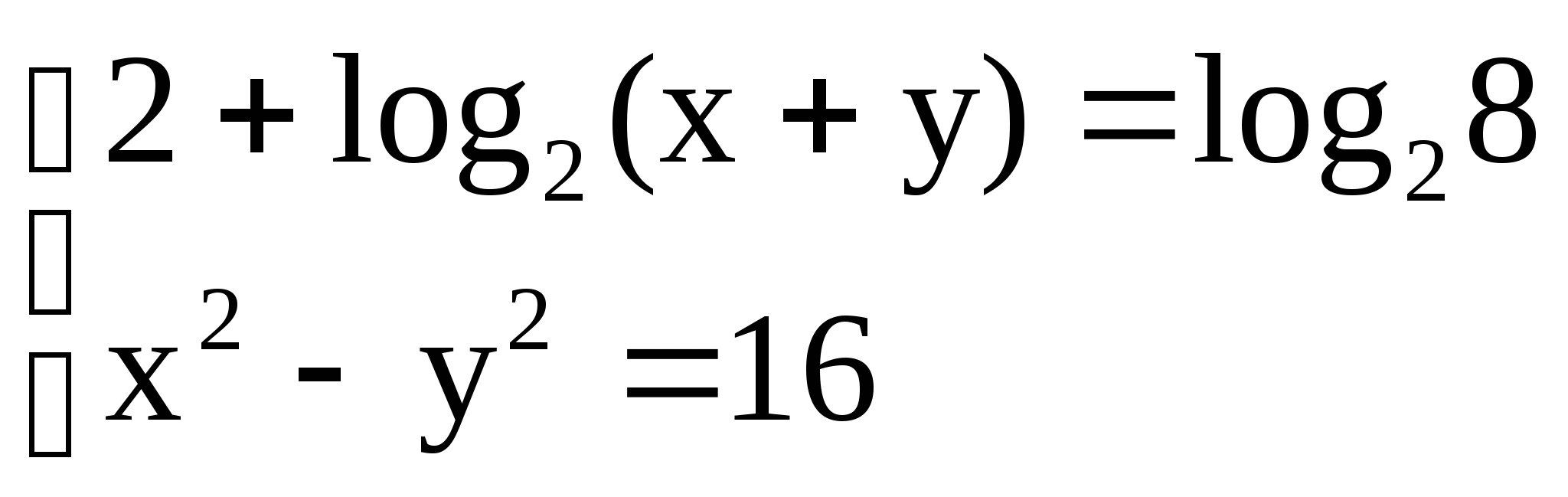
4) 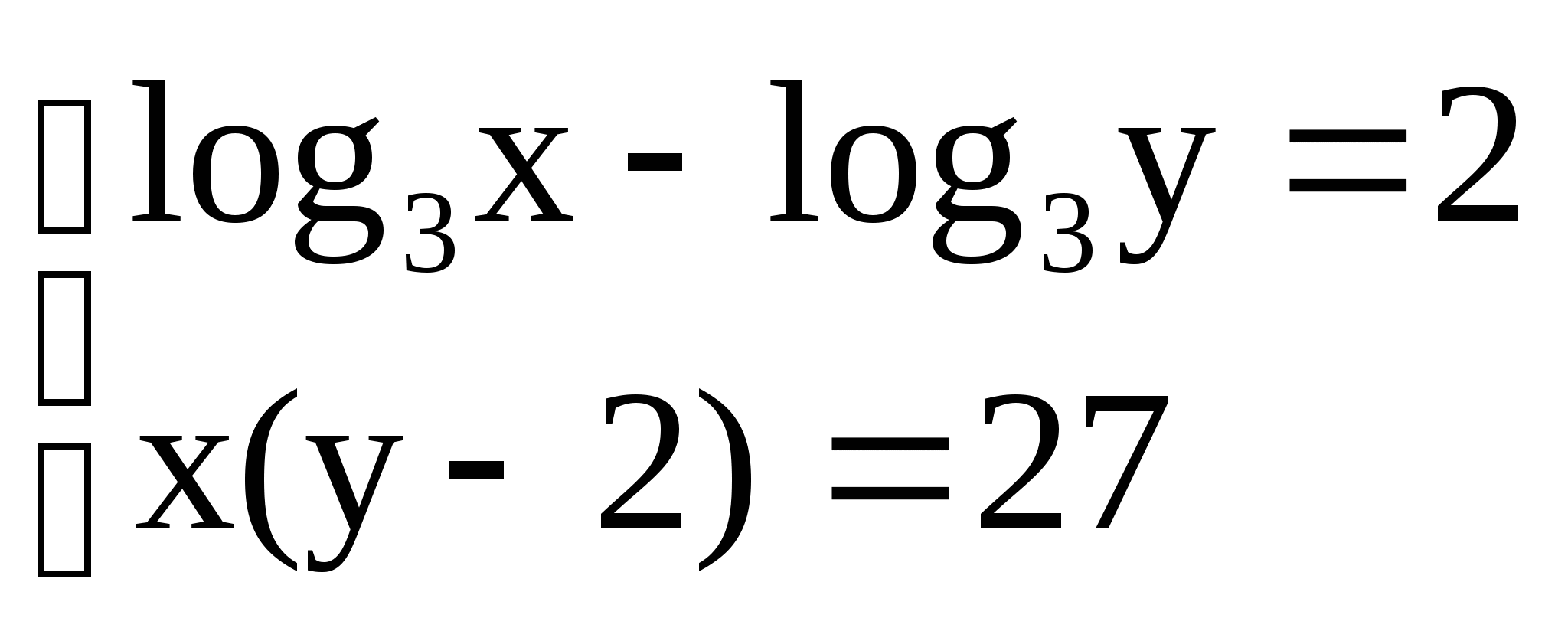 4)
4)
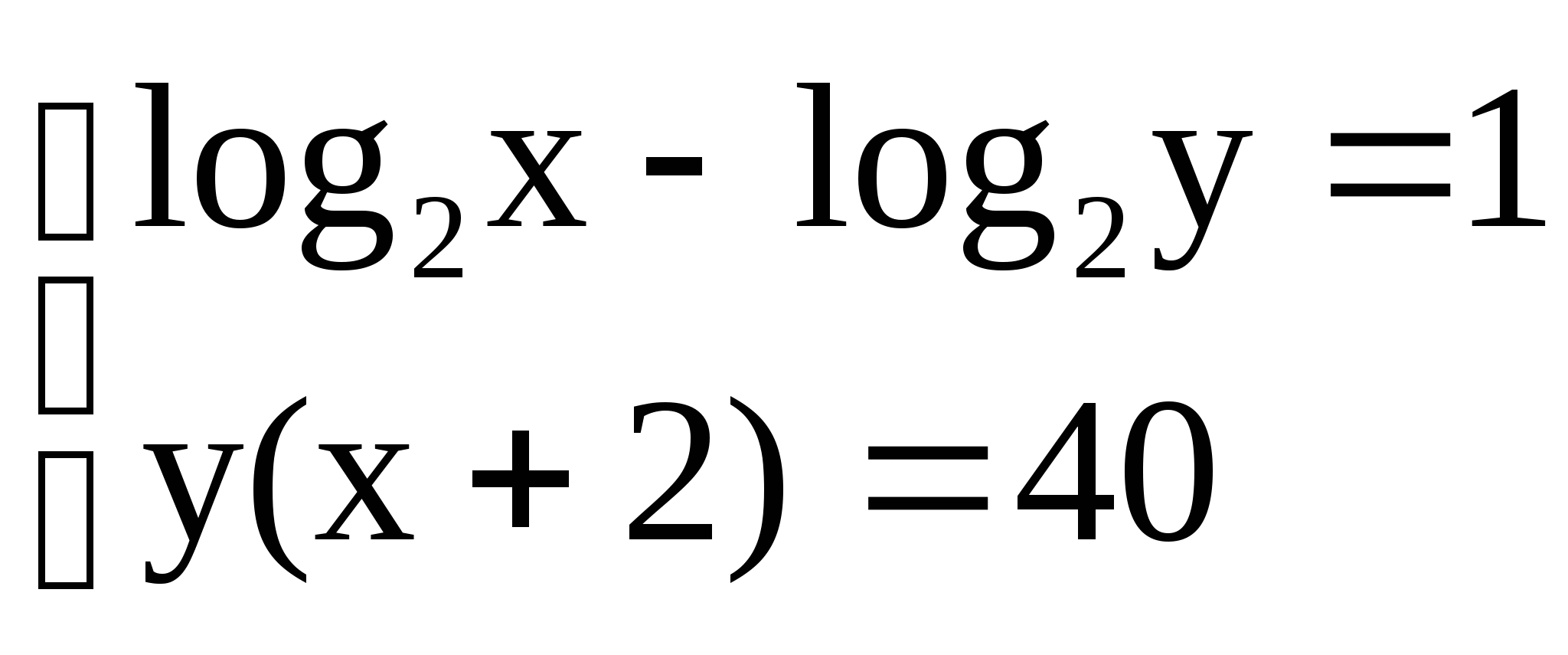
5) 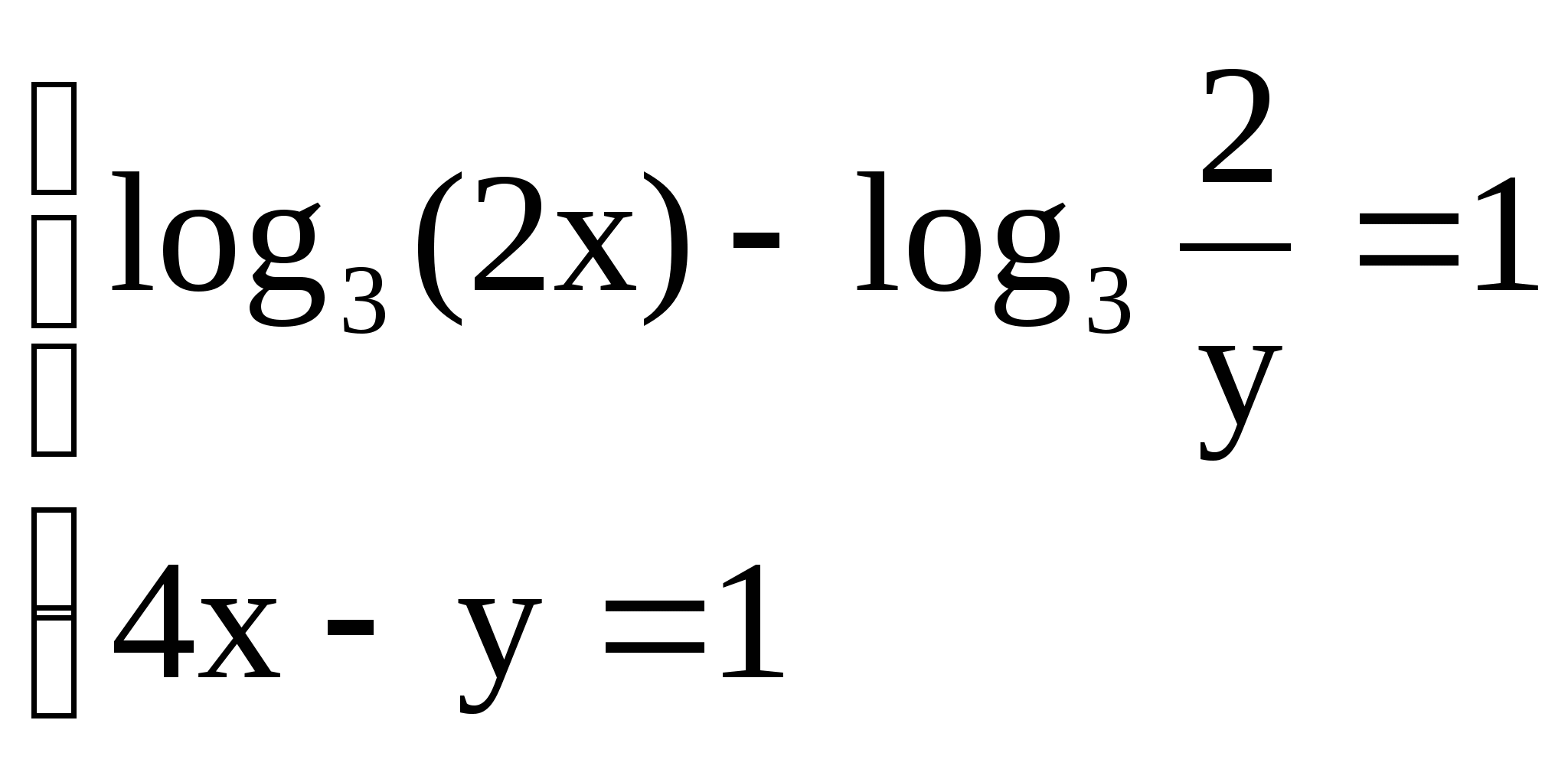 5)
5)
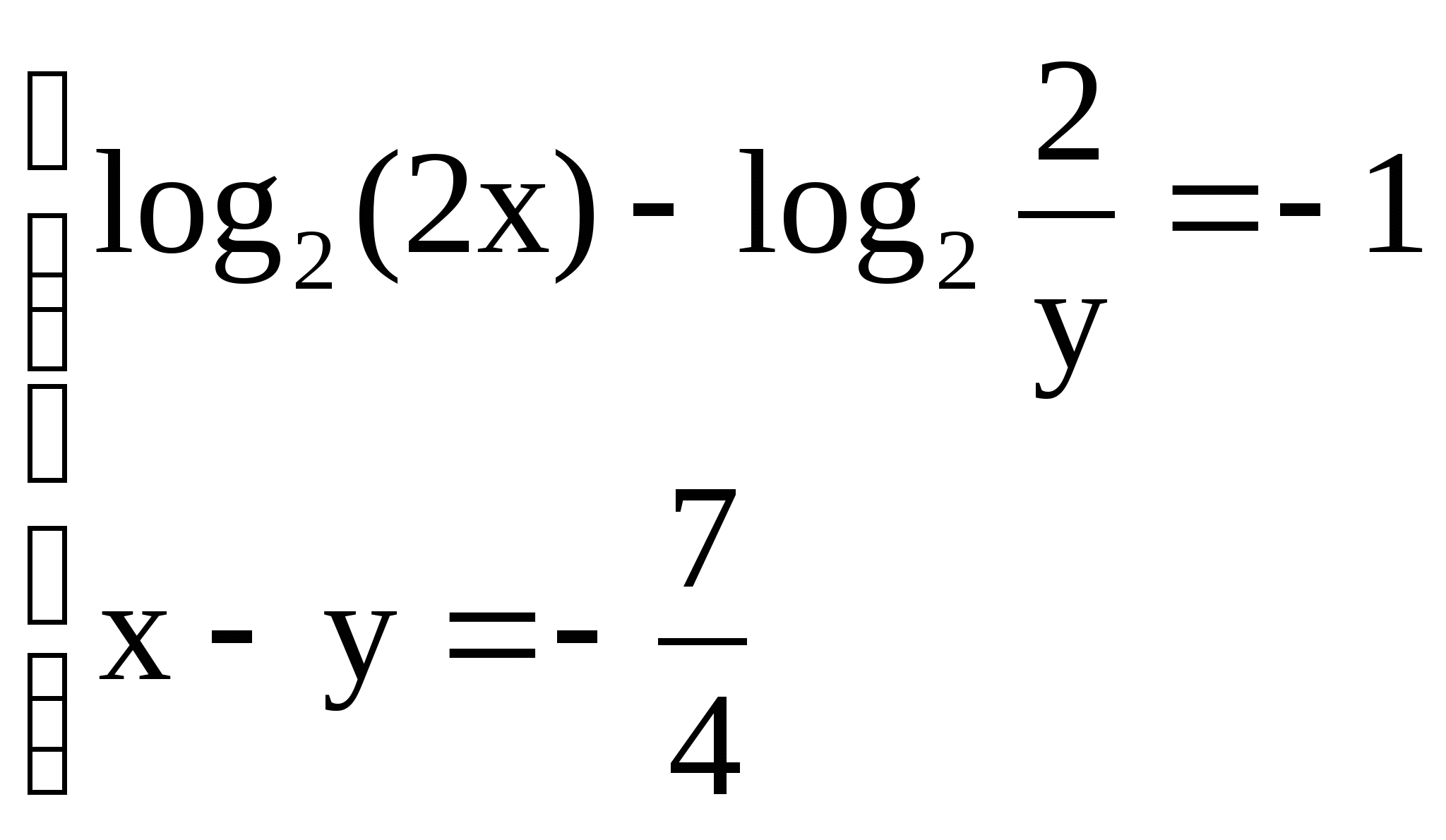
Вариант 3 Вариант 4
1) 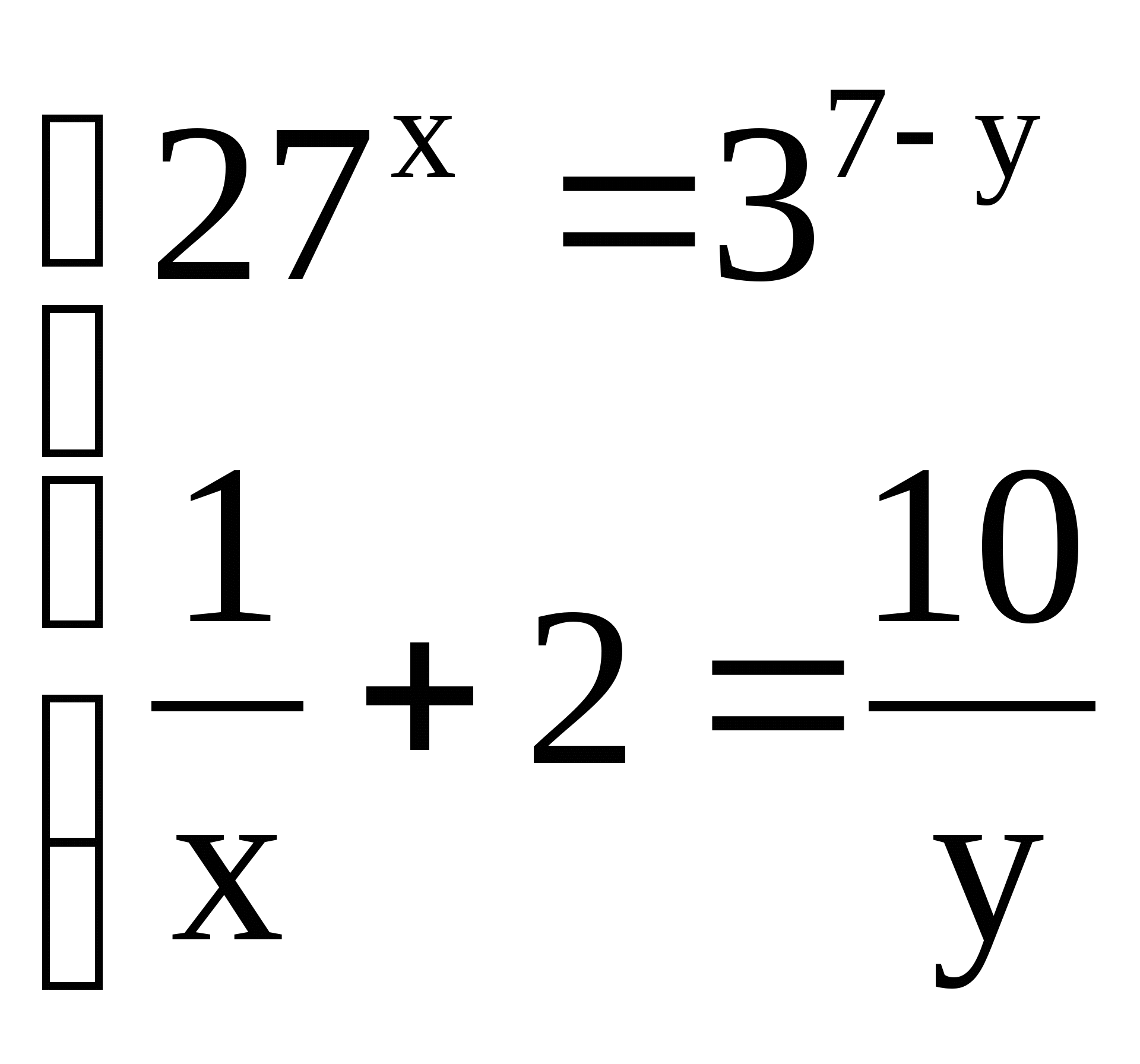 1)
1)
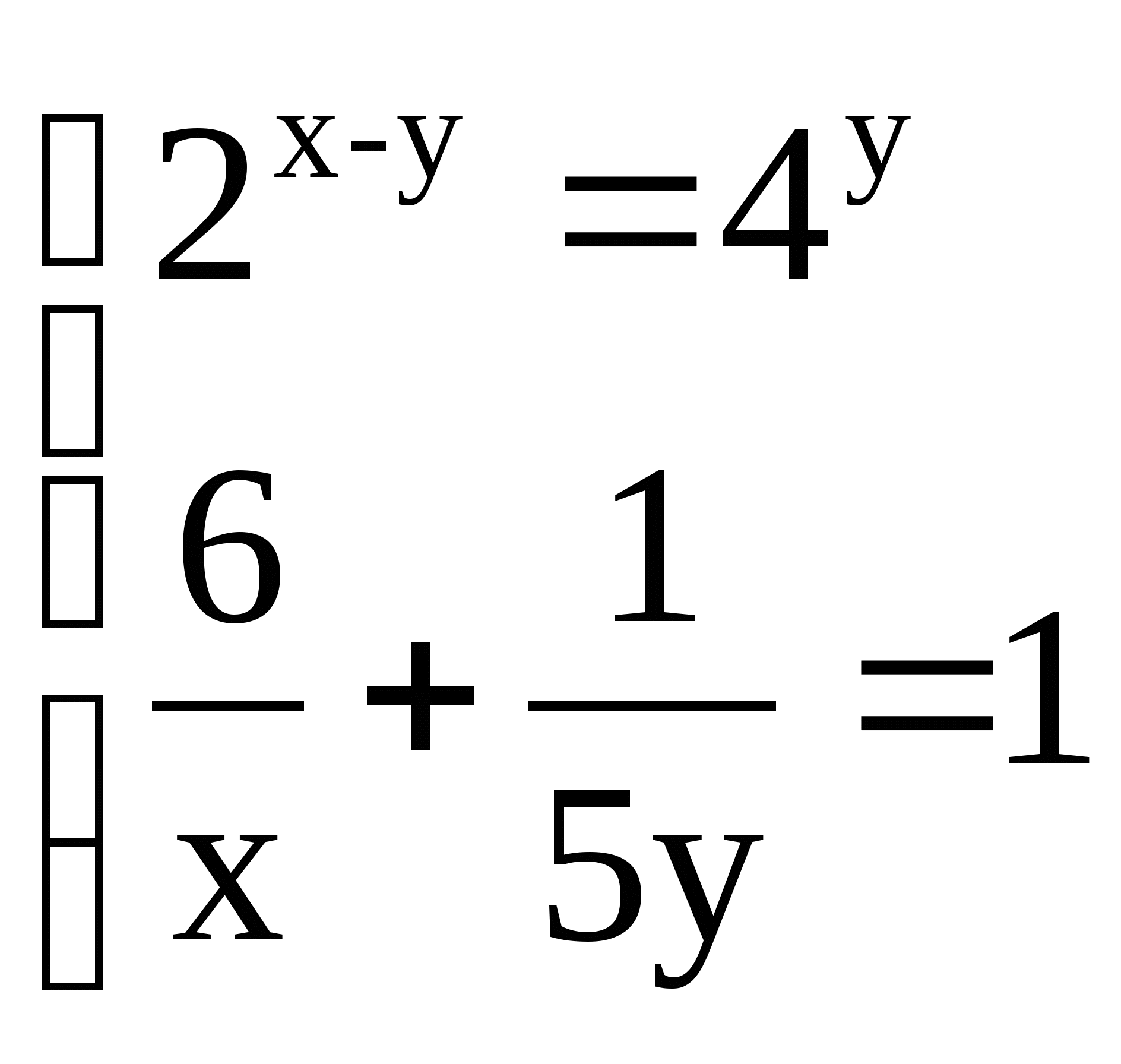
2) 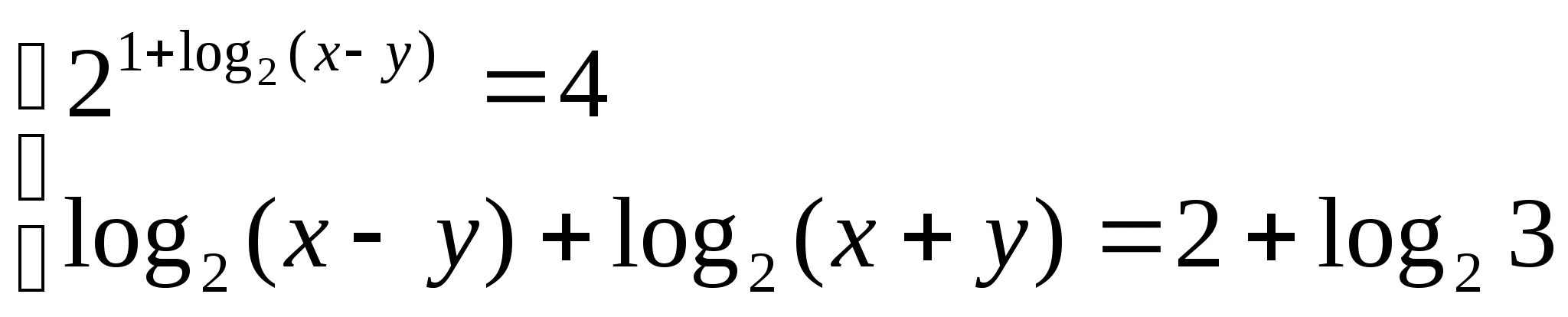 2)
2)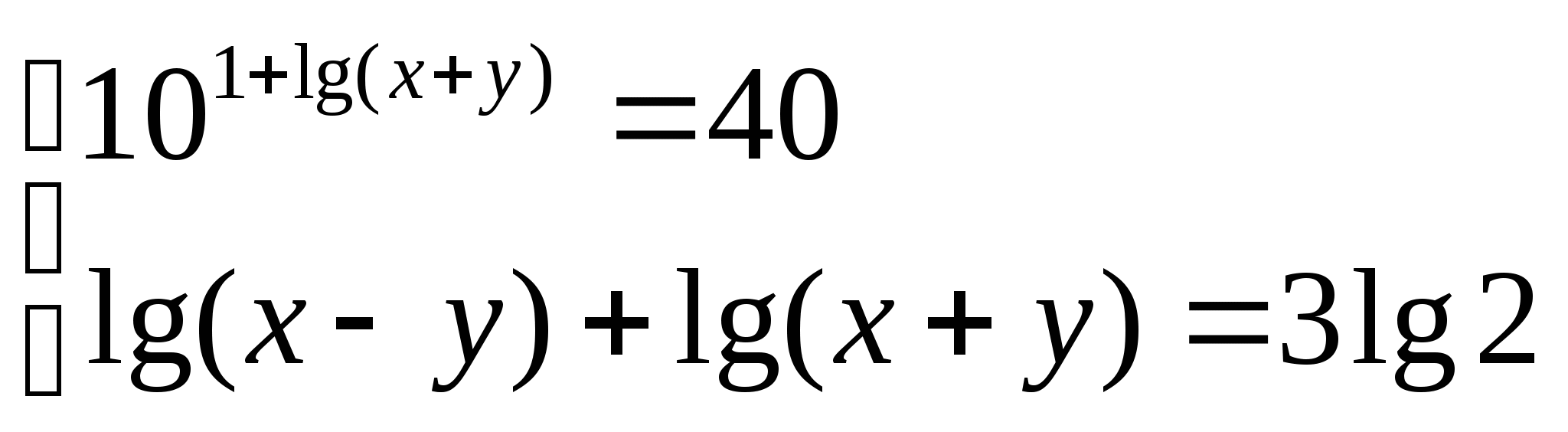
3) 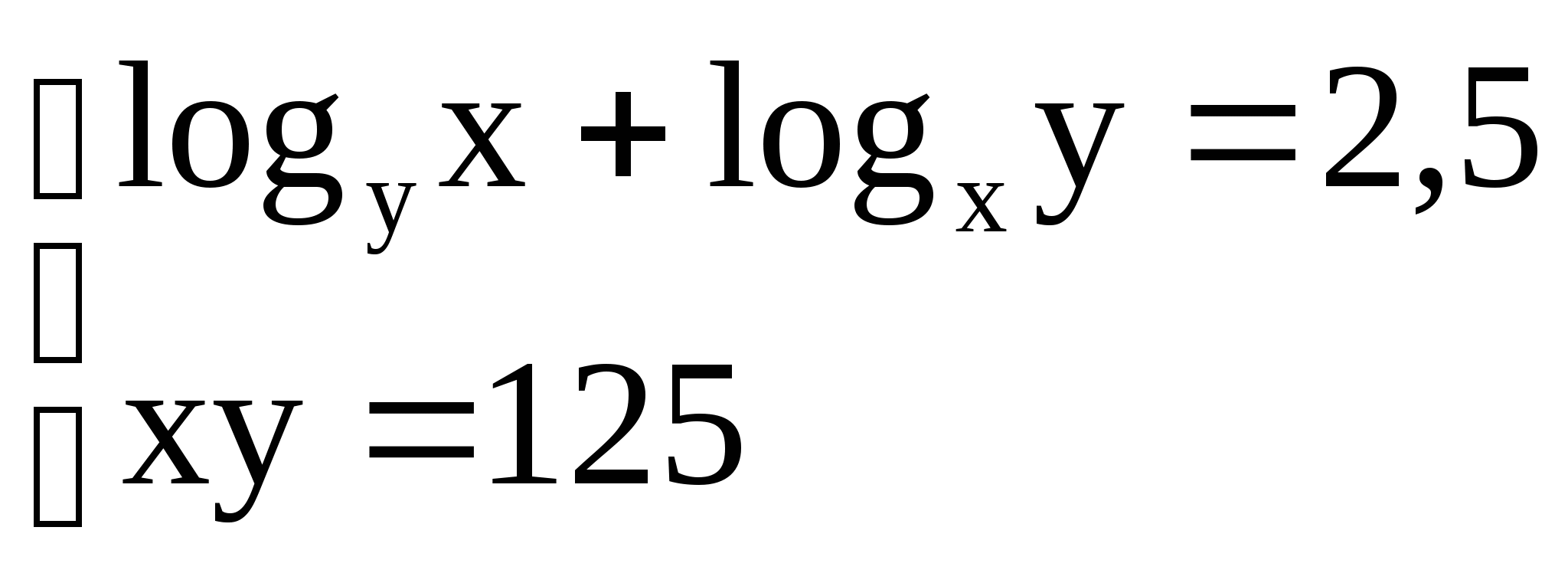 3)
3)
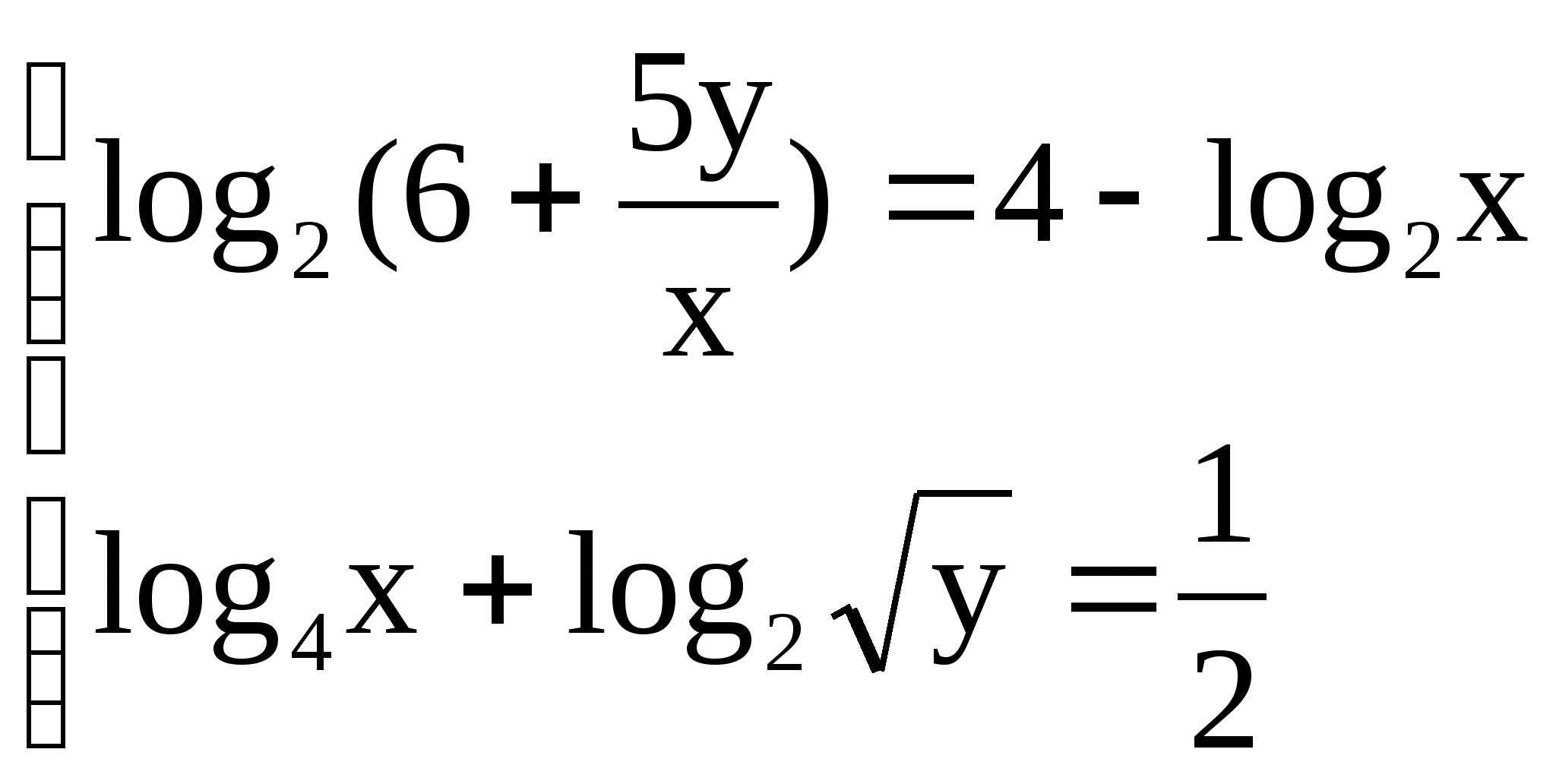
4) 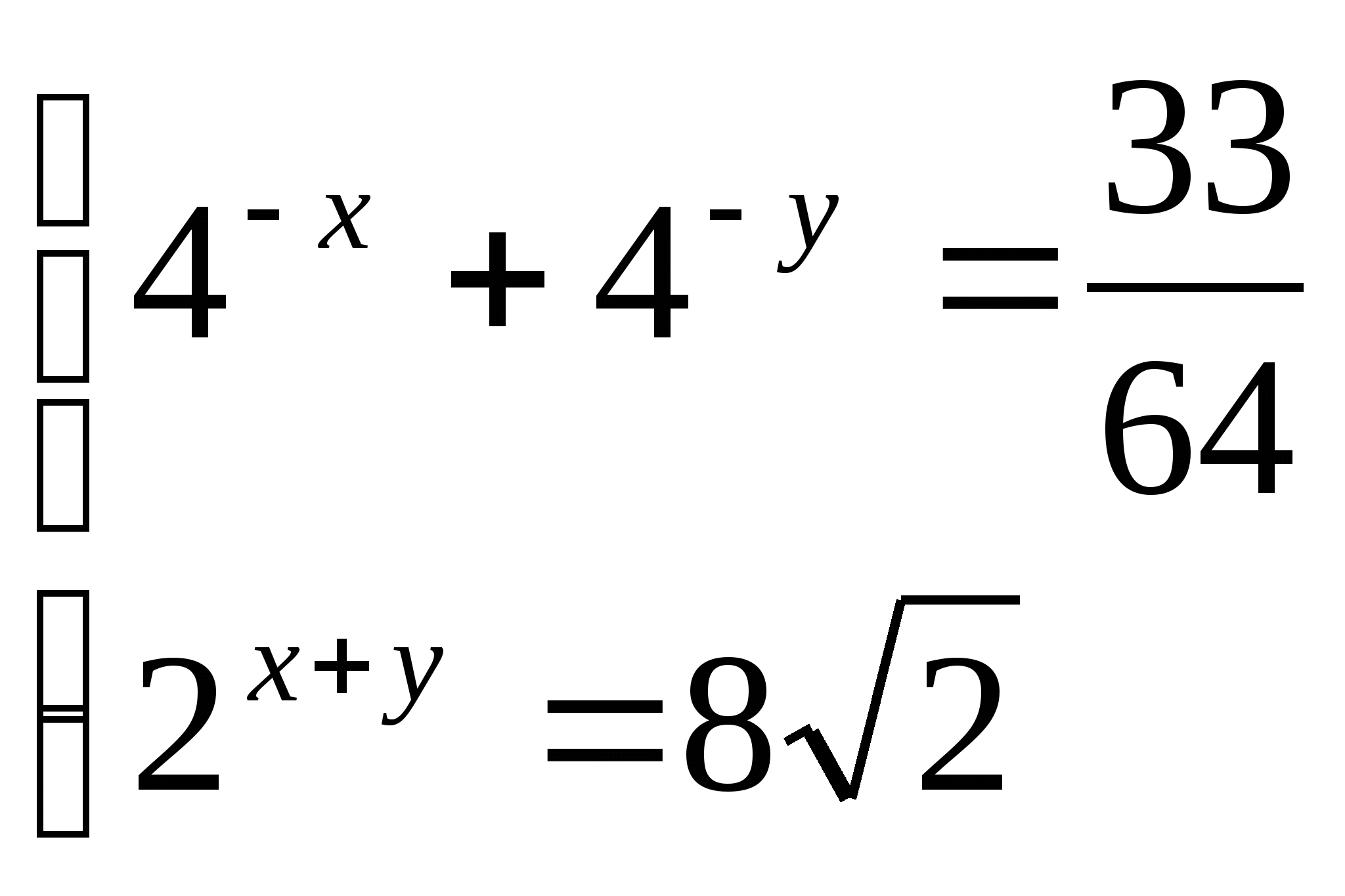 4)
4)
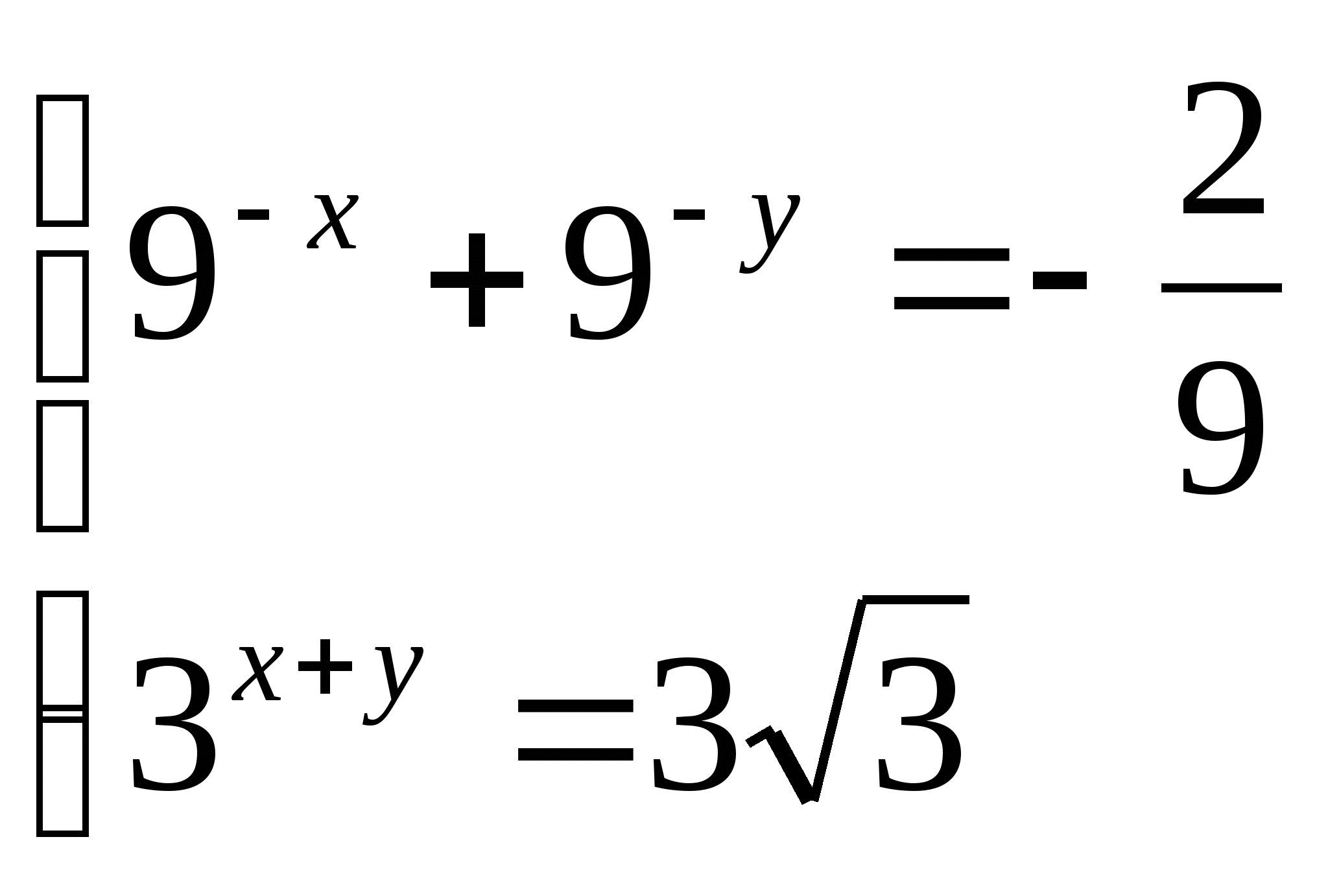
5) 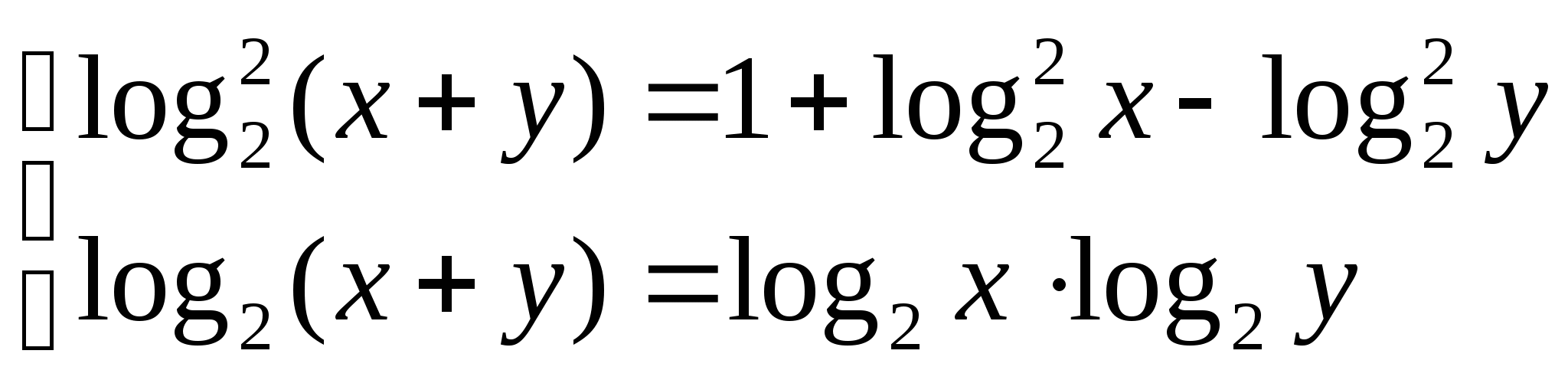 5)
5)
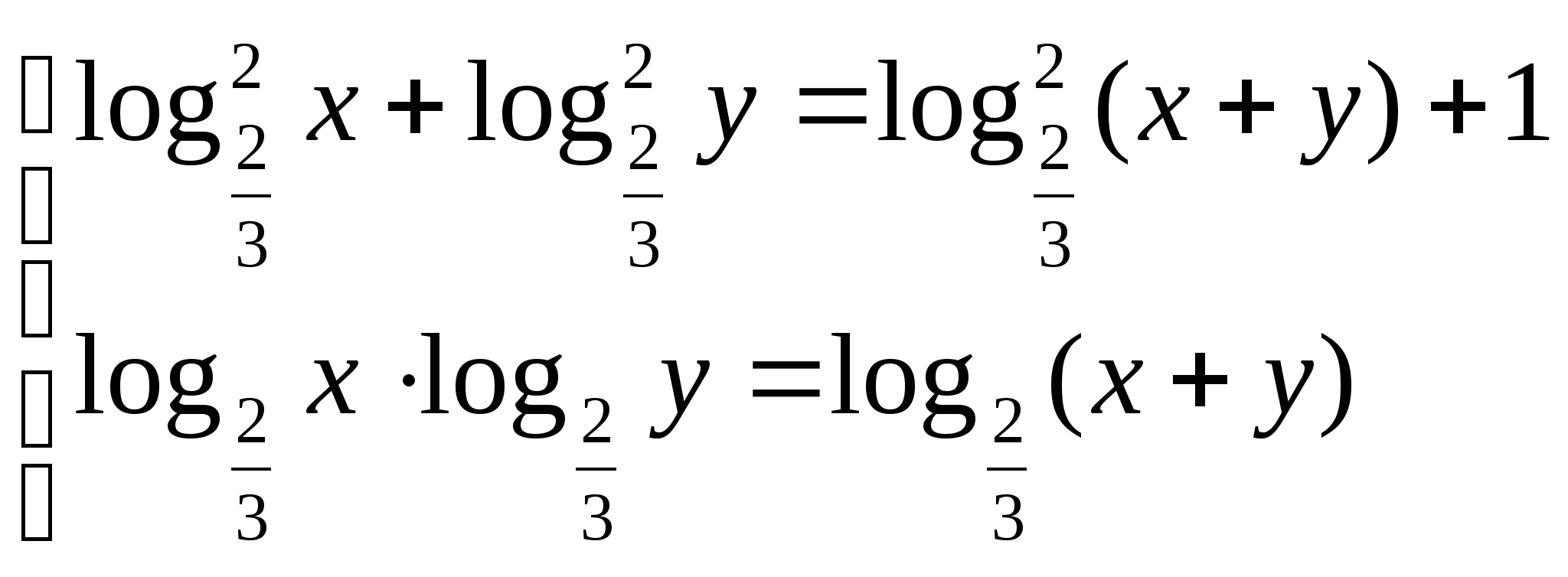
Свойства логарифмов:
![]()
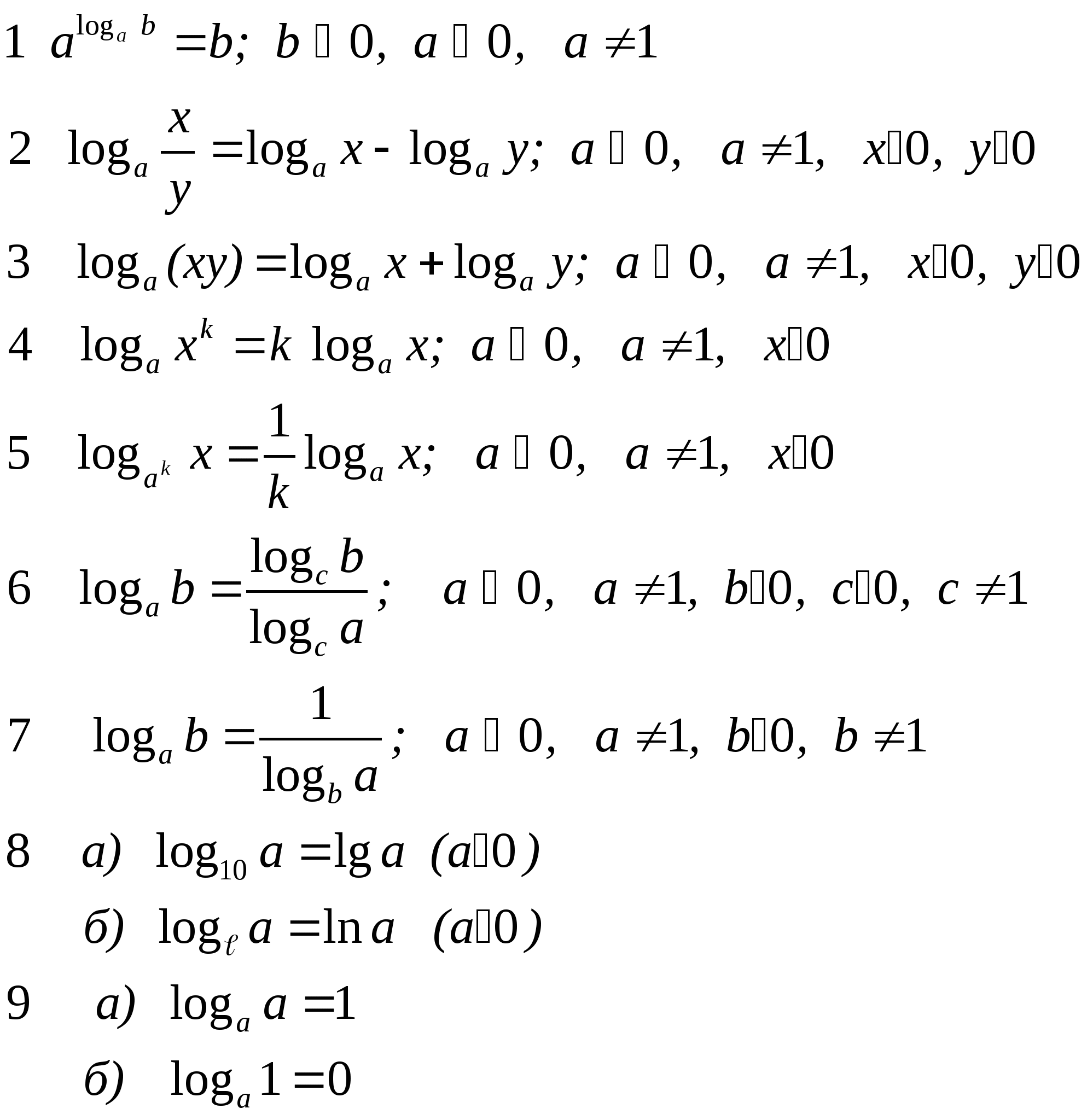
Определения и свойства степени
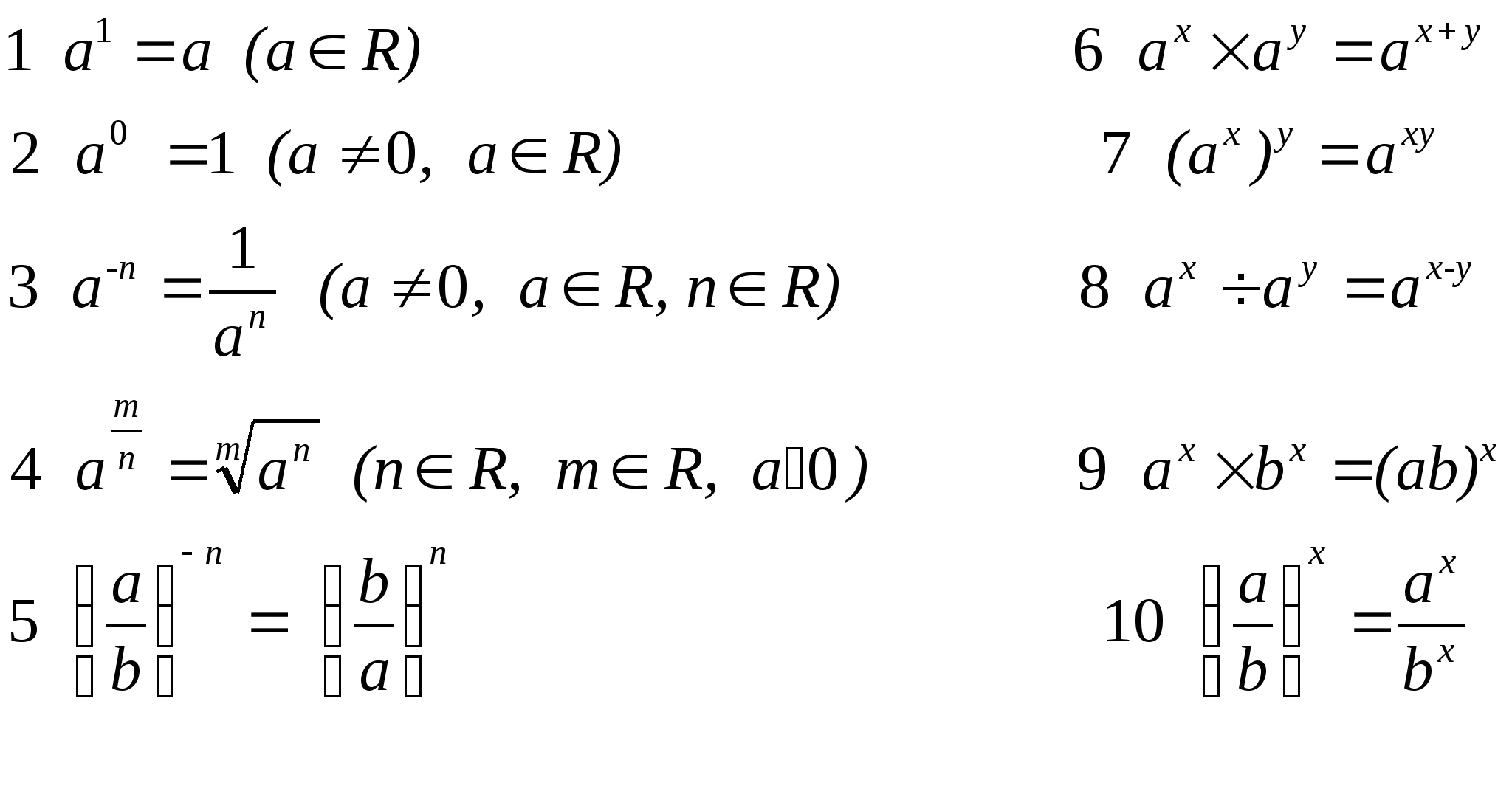
Контрольная работа по алгебре № 2
по теме «Логарифмическая функция » ( 10 класс)
1 урок - 45 минут
а) - 1 вариант б) - 2 вариант
1) ПГФ:
а) у = log2(x+2) - 3 б) y = log2(x - 3) + 2
2) Упростить:
а) ![]() б)
б)
![]()
3) Решите уравнения:
а) 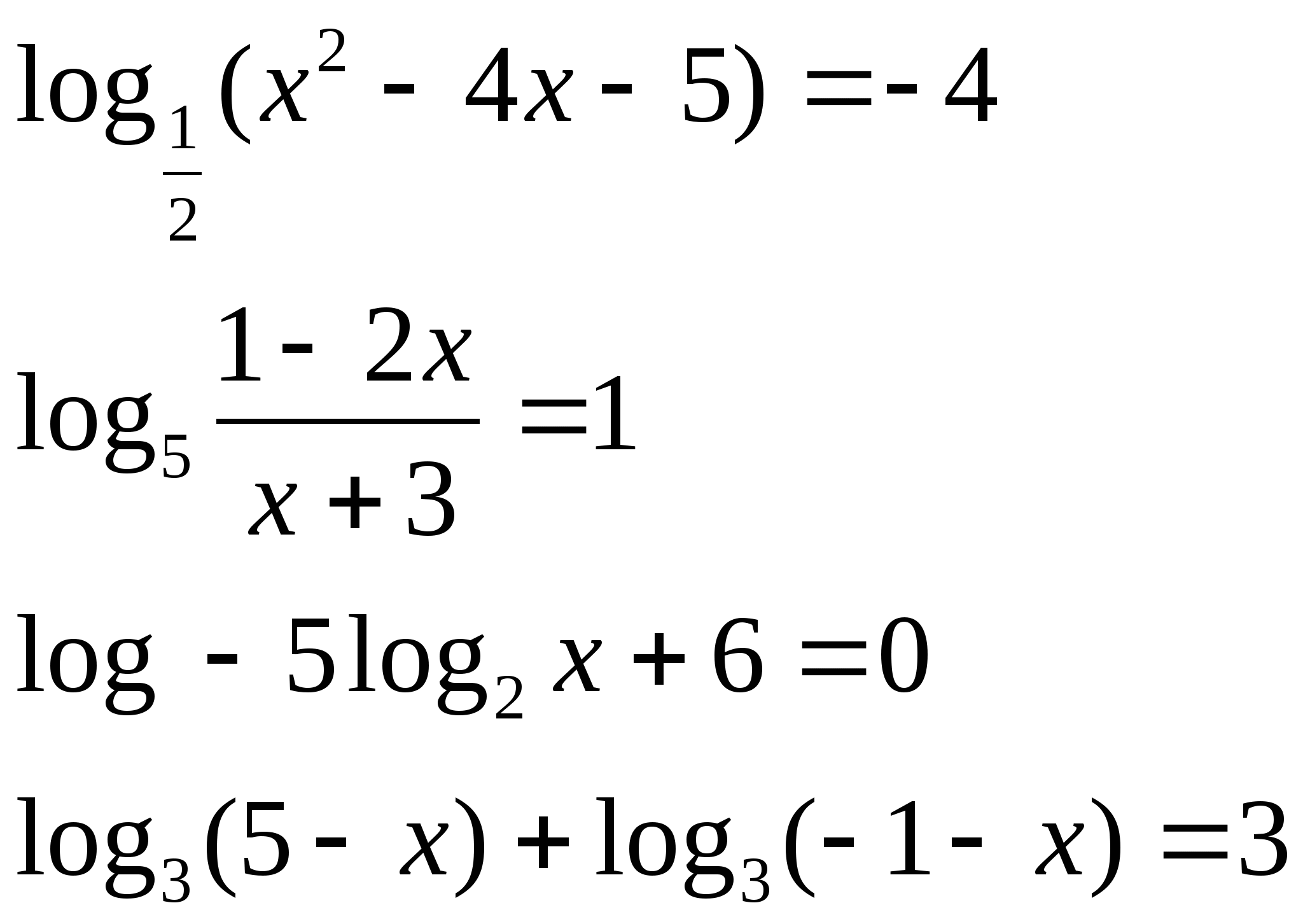 б)
б)
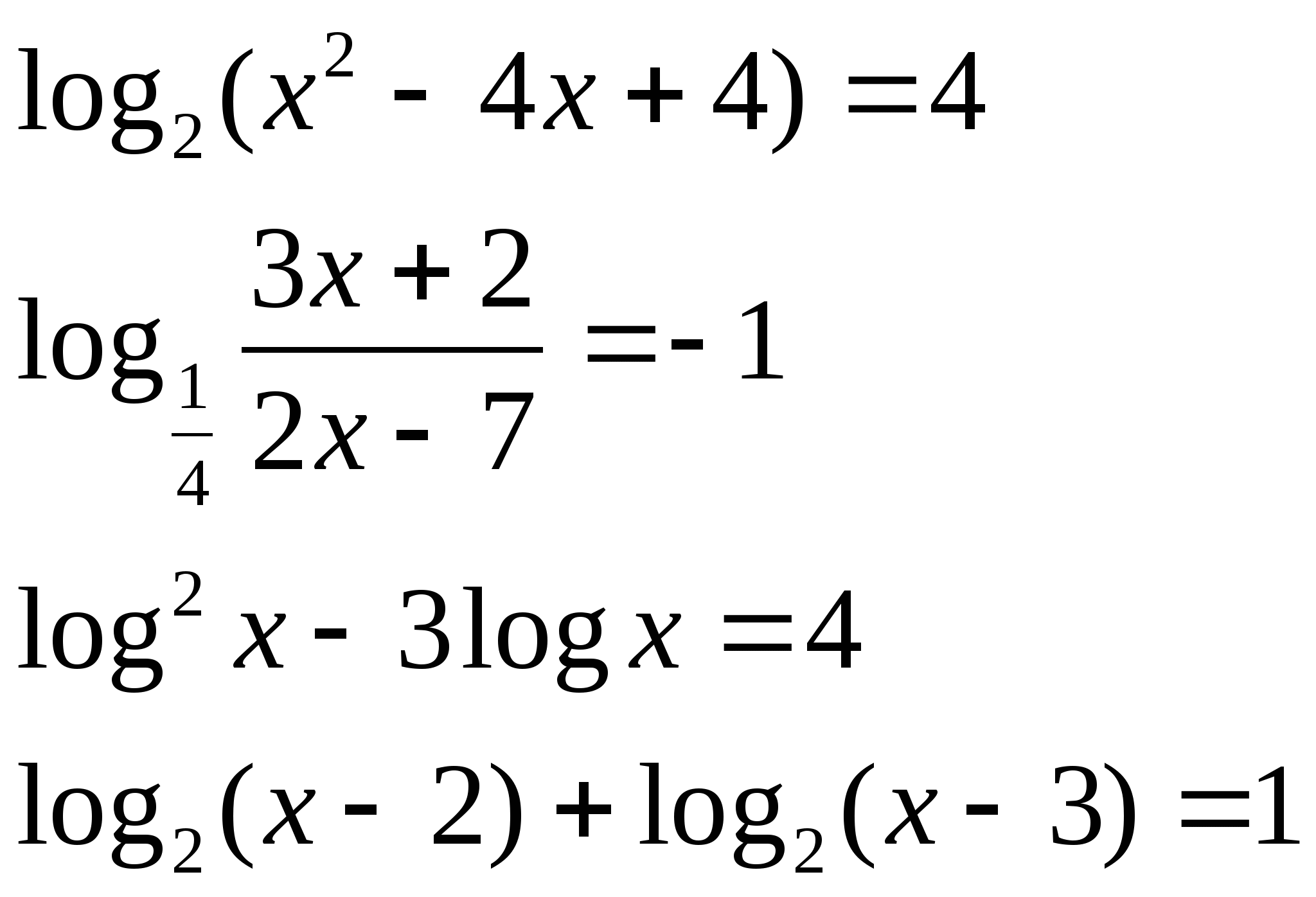
4) Решите неравенство:
а) 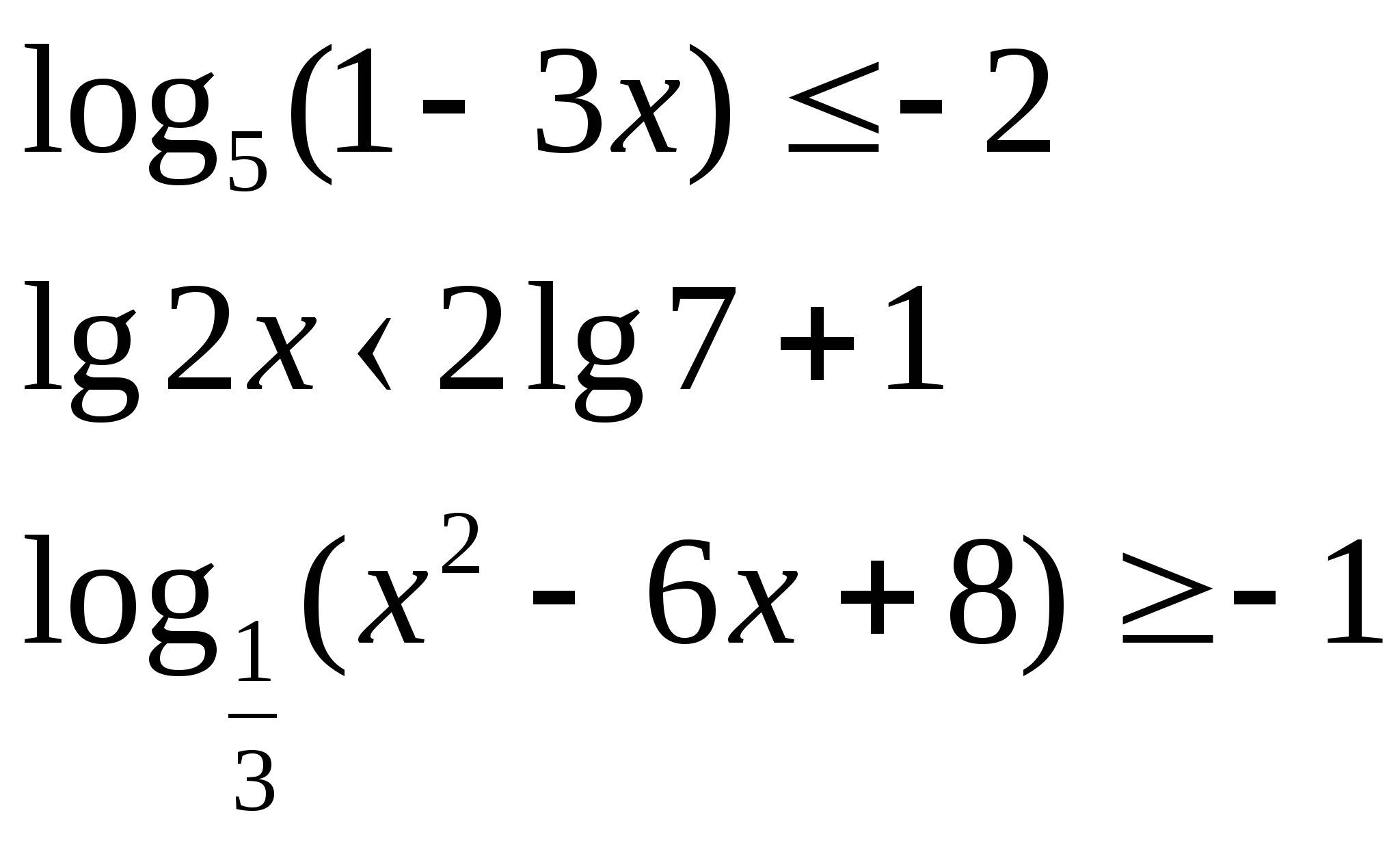 б)
б)
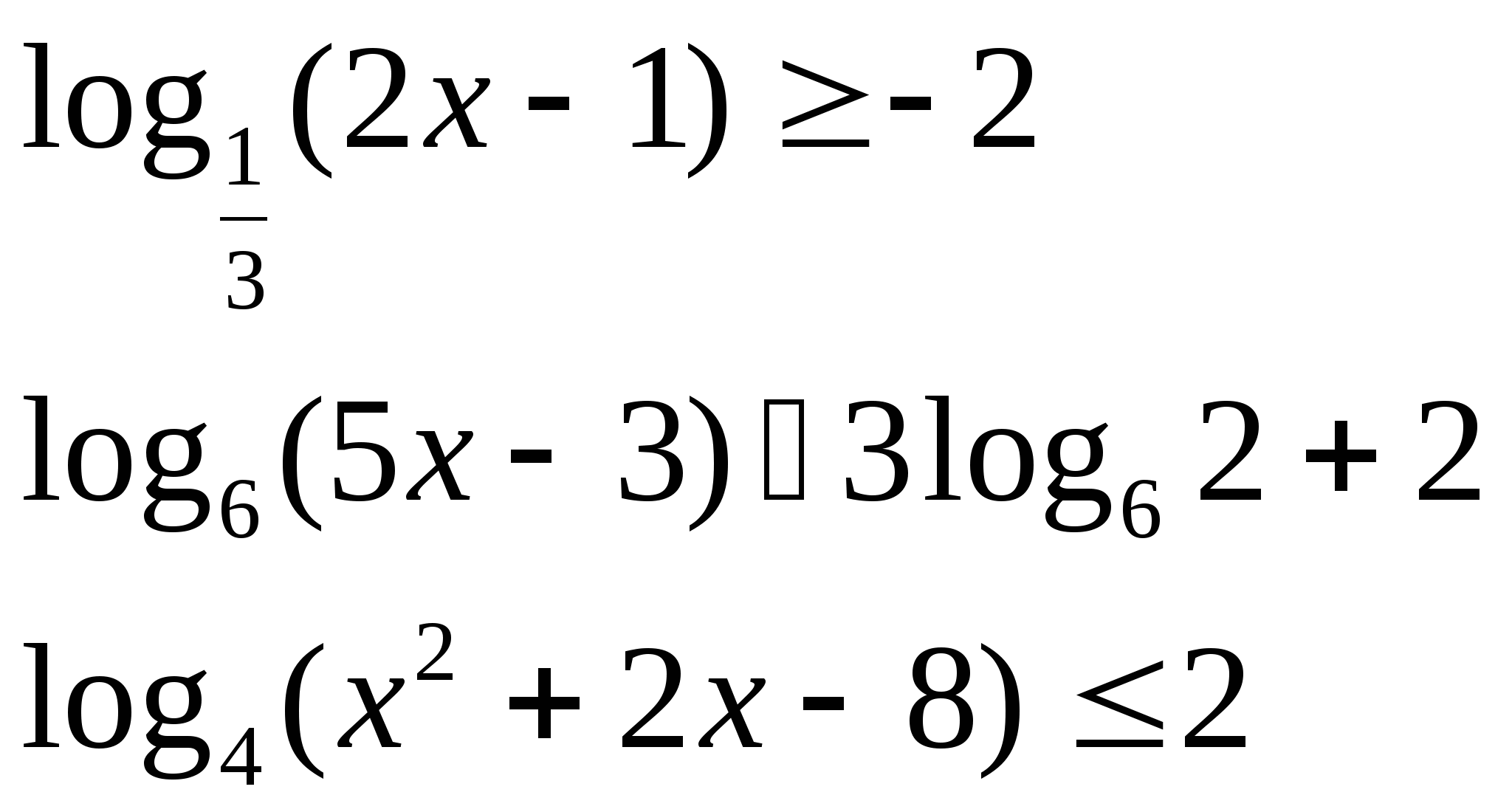
5) ООФ:
а) ![]() б)
б)
![]()
6)* Решите неравенство:
а) 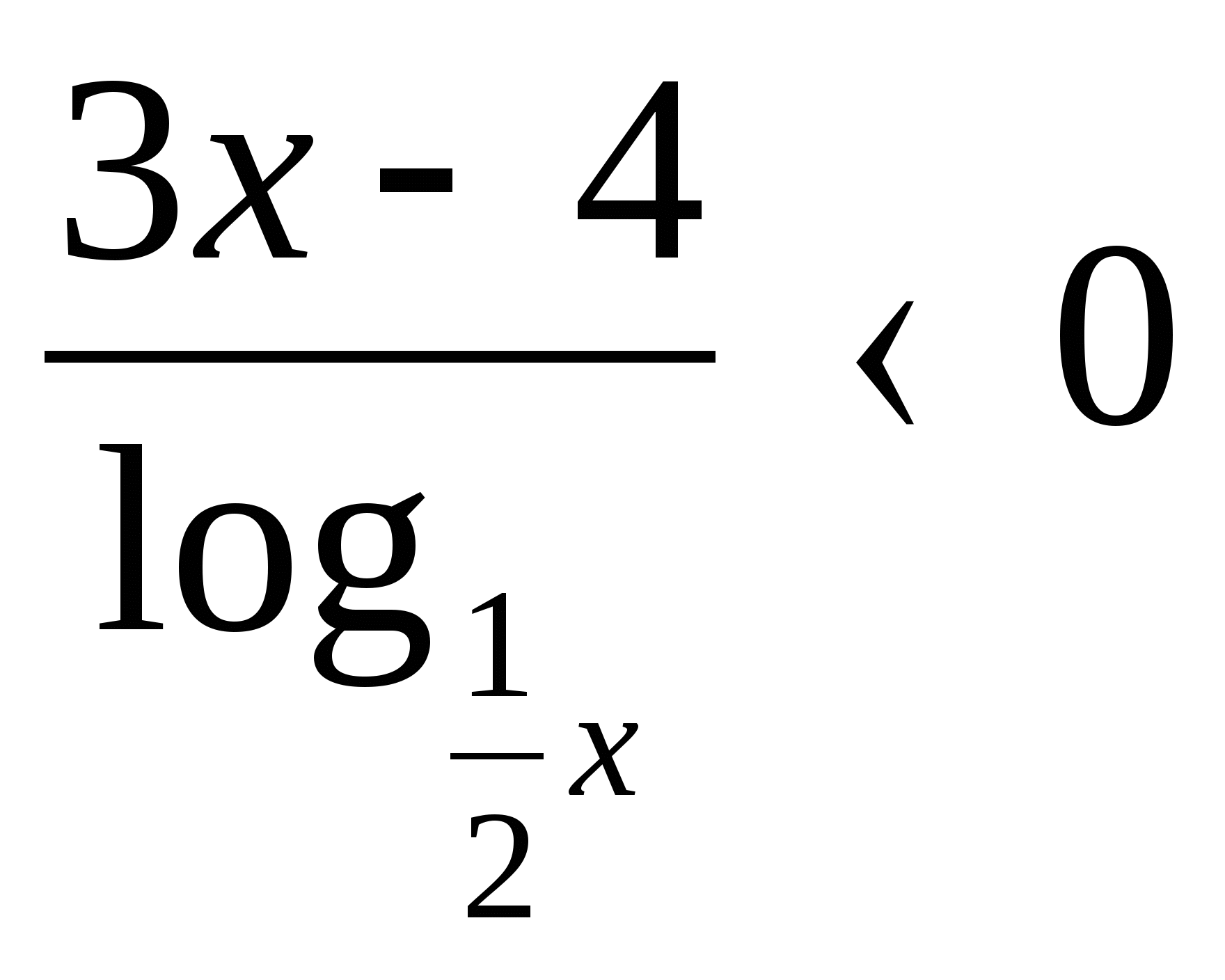 б)
б)
![]()
Контрольная работа по алгебре № 2
по теме «Логарифмическая функция » (10 класс)
![]() 1
урок - 45 минут
1
урок - 45 минут
а) - 1 вариант б) - 2 вариант
1) Вычислите:
а) ![]() б)
б)
![]()
2) Постройте график
а) ![]() б)
б)
![]()
3) Решите уравнения:
а) 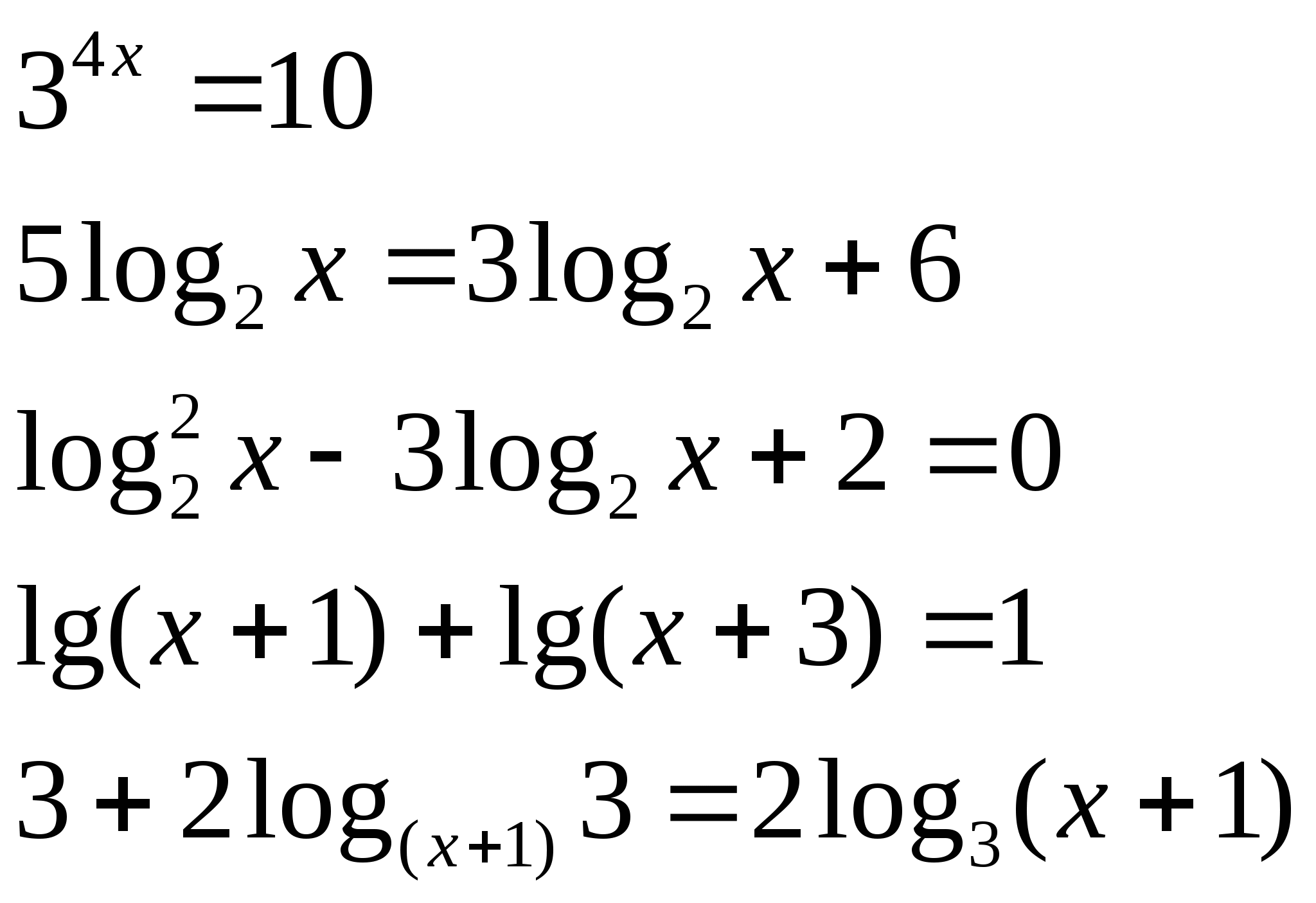 б)
б)
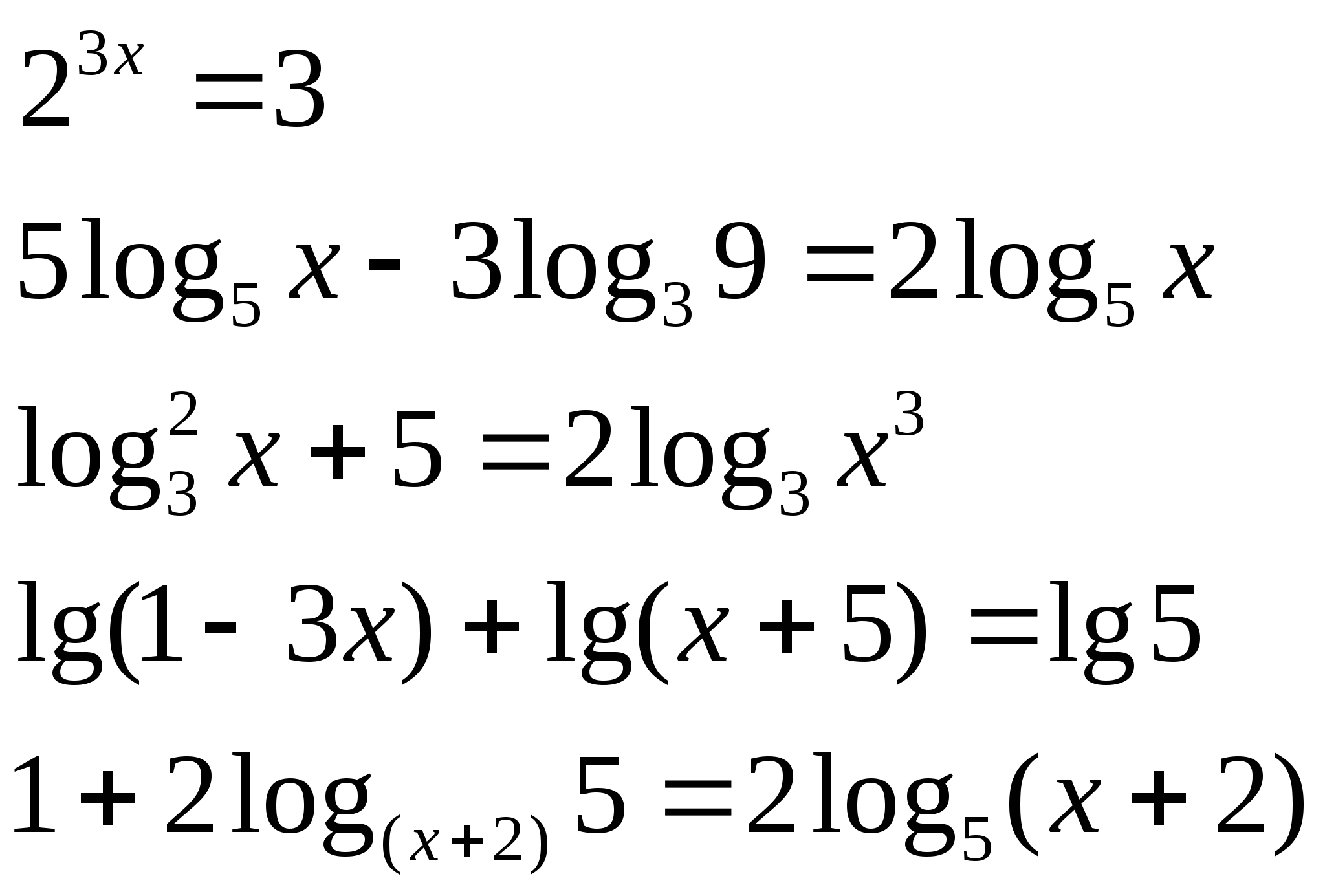
4) Решите неравенства:
а) 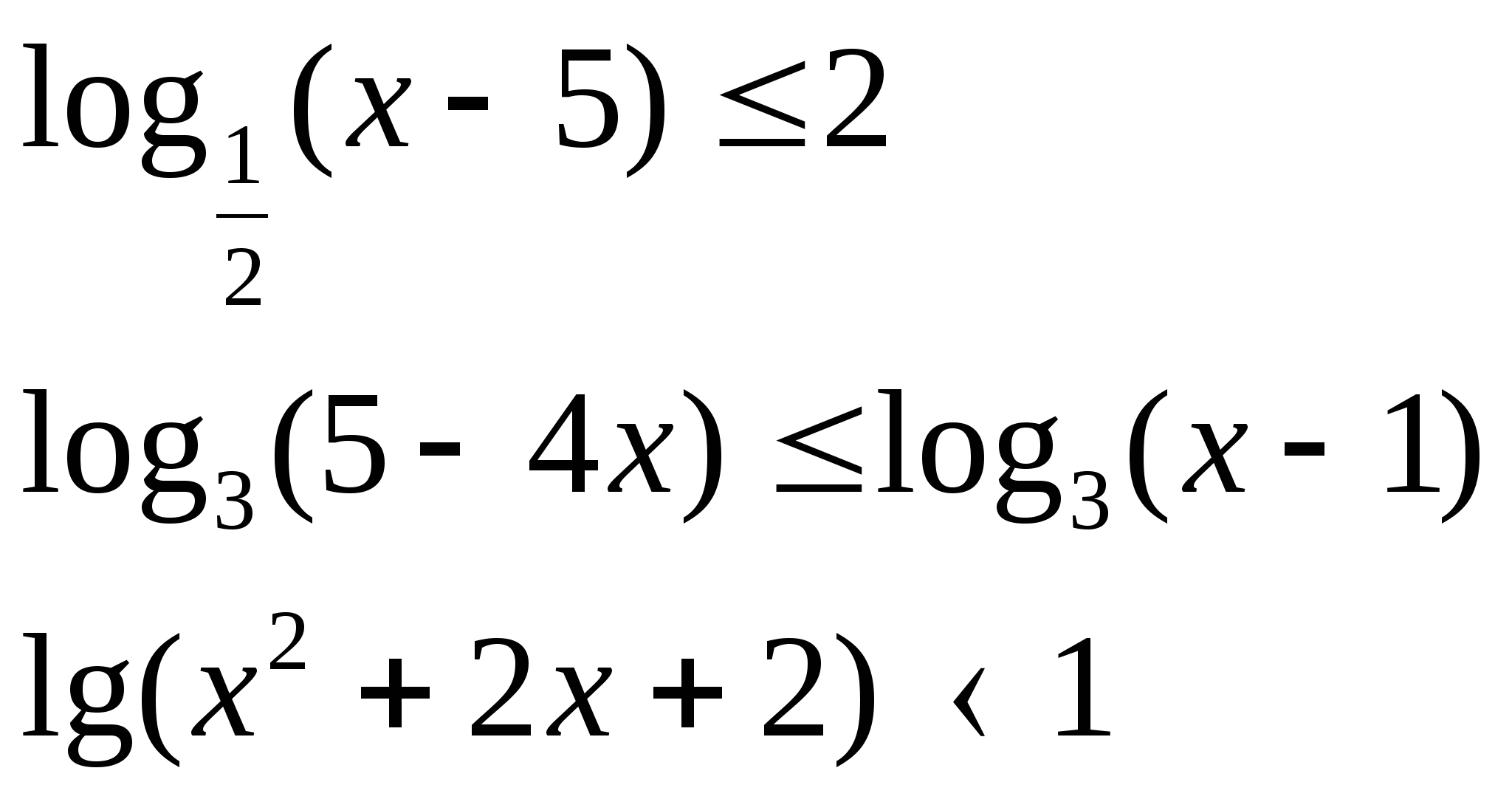 б)
б)
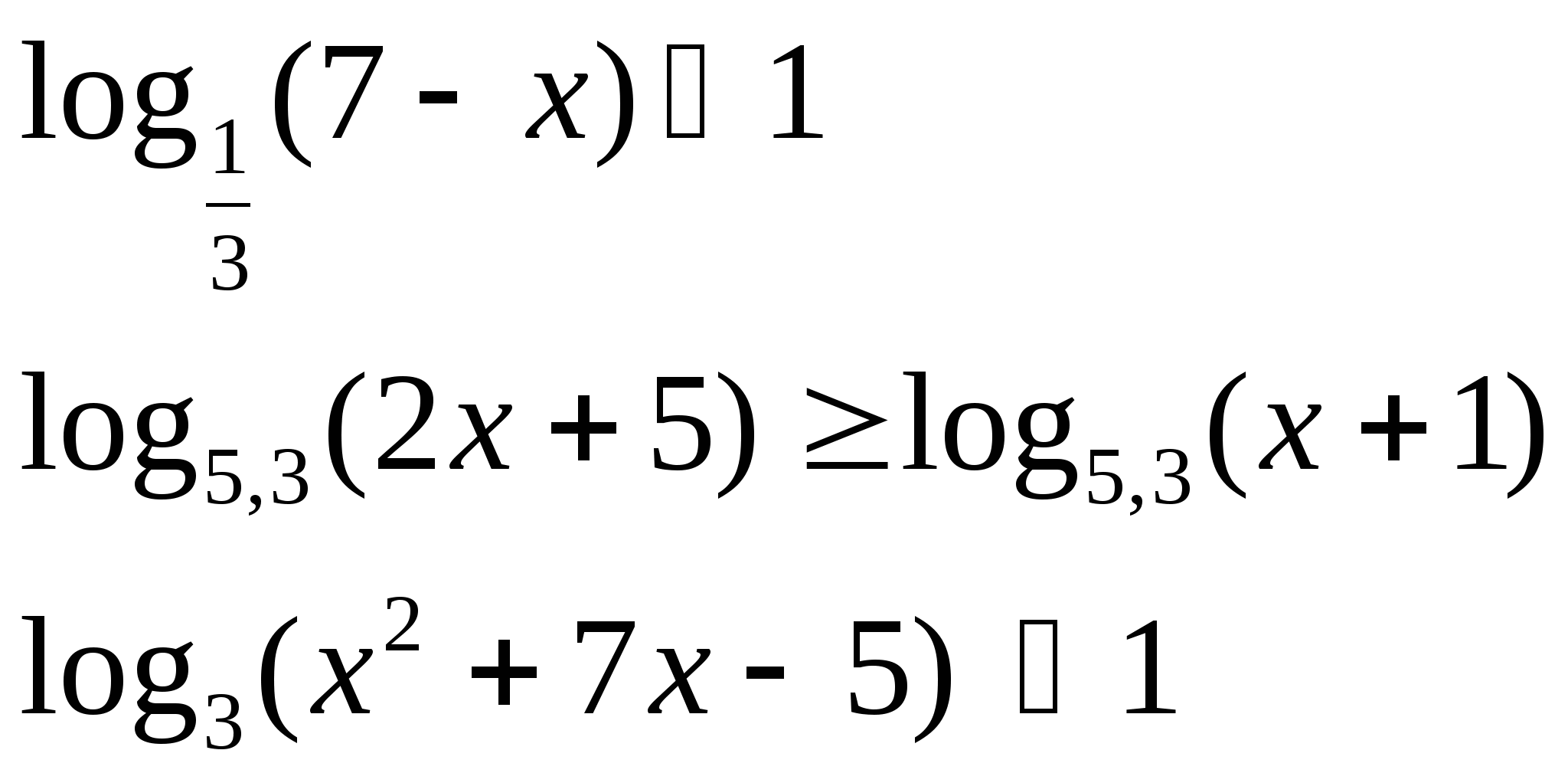
5) ООФ:
а) ![]() б)
б)
![]()
Тренажер № 1
Вычисление логарифмов
1)Вычислите выражение:
1. ![]() 22.
22. ![]()
2. ![]() 23.
23. ![]()
3. ![]() 24.
24. ![]()
4. ![]() 25.
25. ![]()
5. ![]() 26.
26. ![]()
6. ![]() 27.
27. ![]()
7. ![]() 28.
28.![]()
8. ![]() 29.
29. ![]()
9. ![]() 30.
30. ![]()
10. 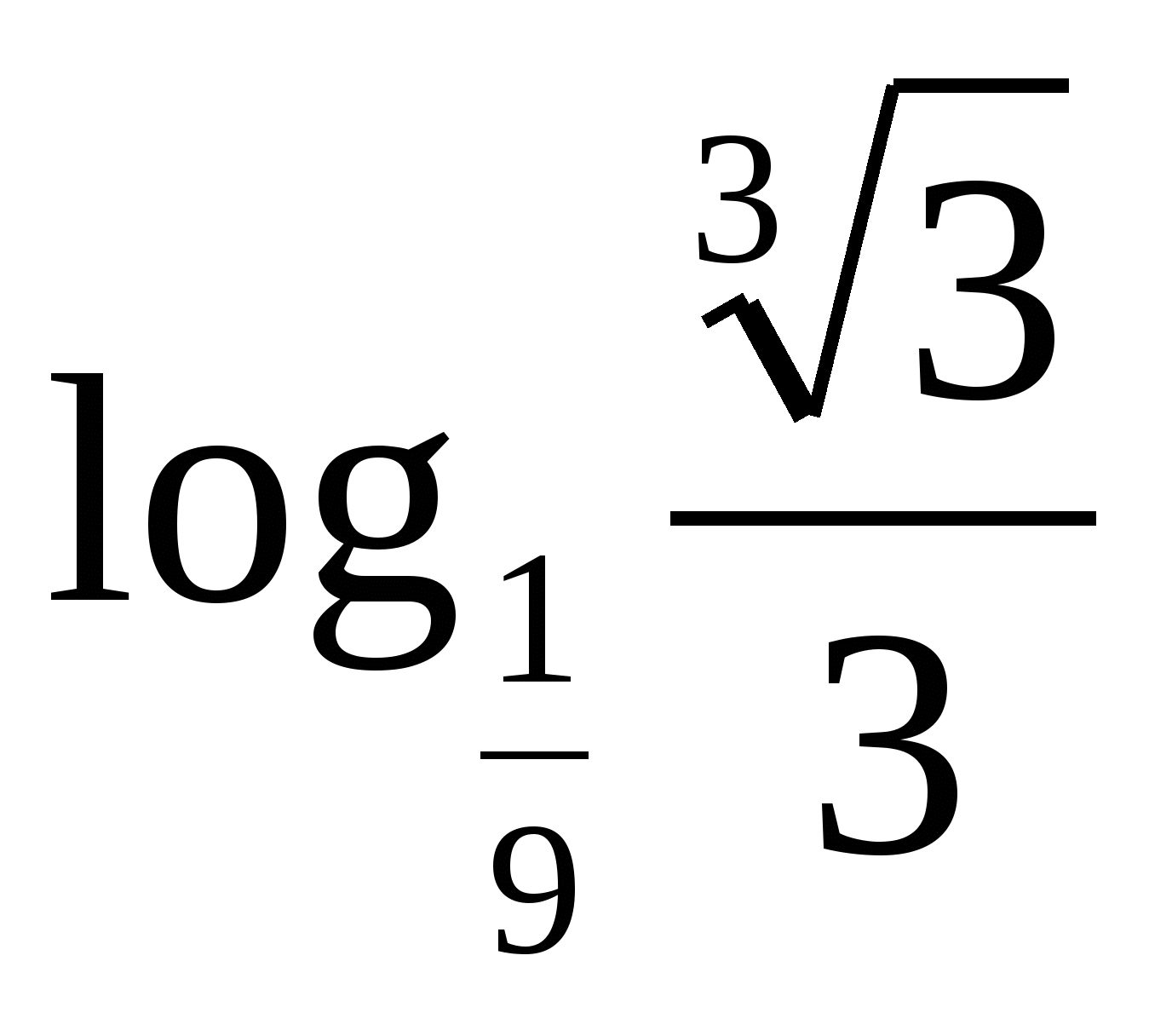 31.
31. ![]()
11. ![]() 31.
31. ![]()
12. ![]() 33.
33. ![]()
13. ![]() 34.
34. ![]()
14. ![]() 35.
35. ![]()
15. ![]() 36.
36. ![]()
16. ![]() 37.
37. ![]()
17. ![]() 38.
38. ![]()
18. ![]() 39.
39. ![]()
19. ![]() 40.
40. 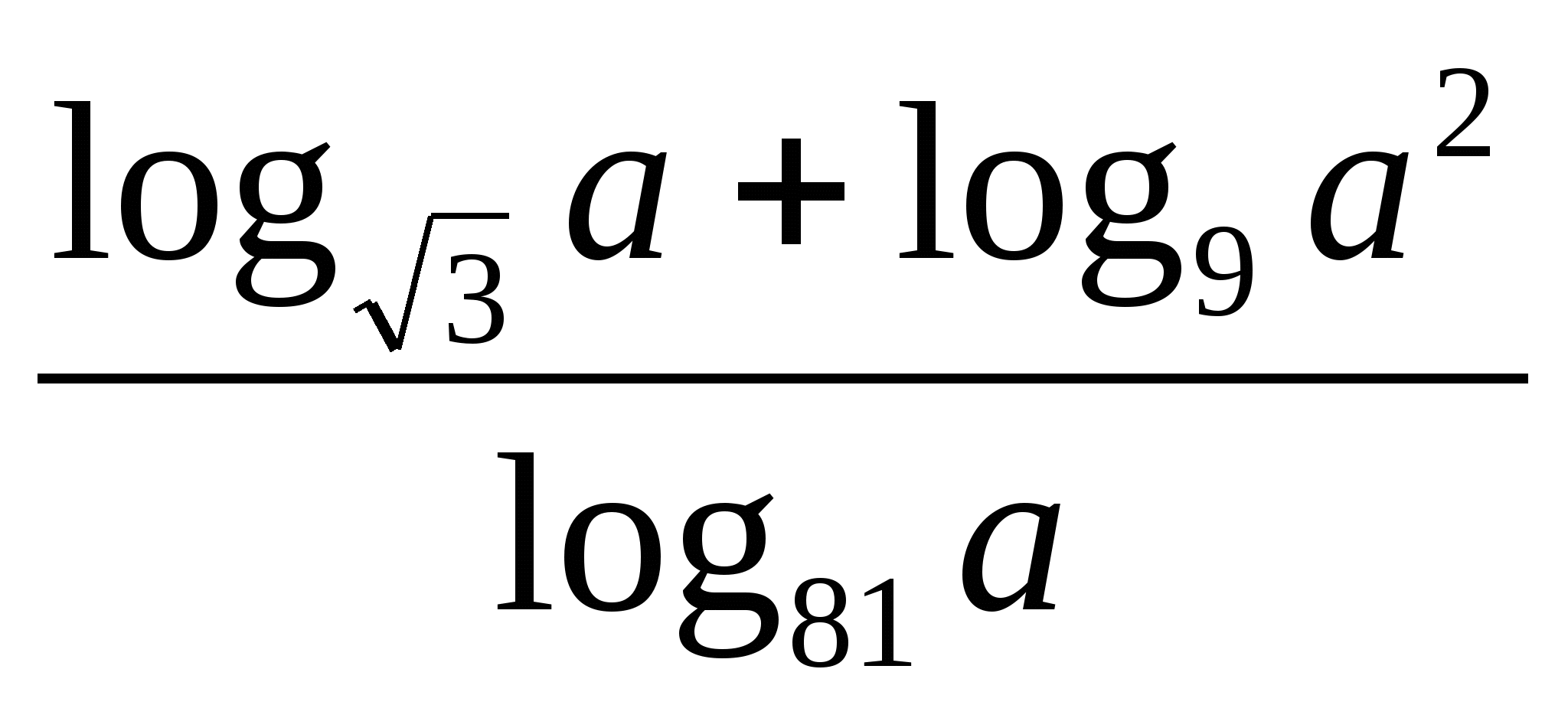
20. ![]()
21. ![]()
2) Выразите lgA через логарифмы простых чисел:
1. А = 720 5. ![]()
2. ![]() 6.
6.
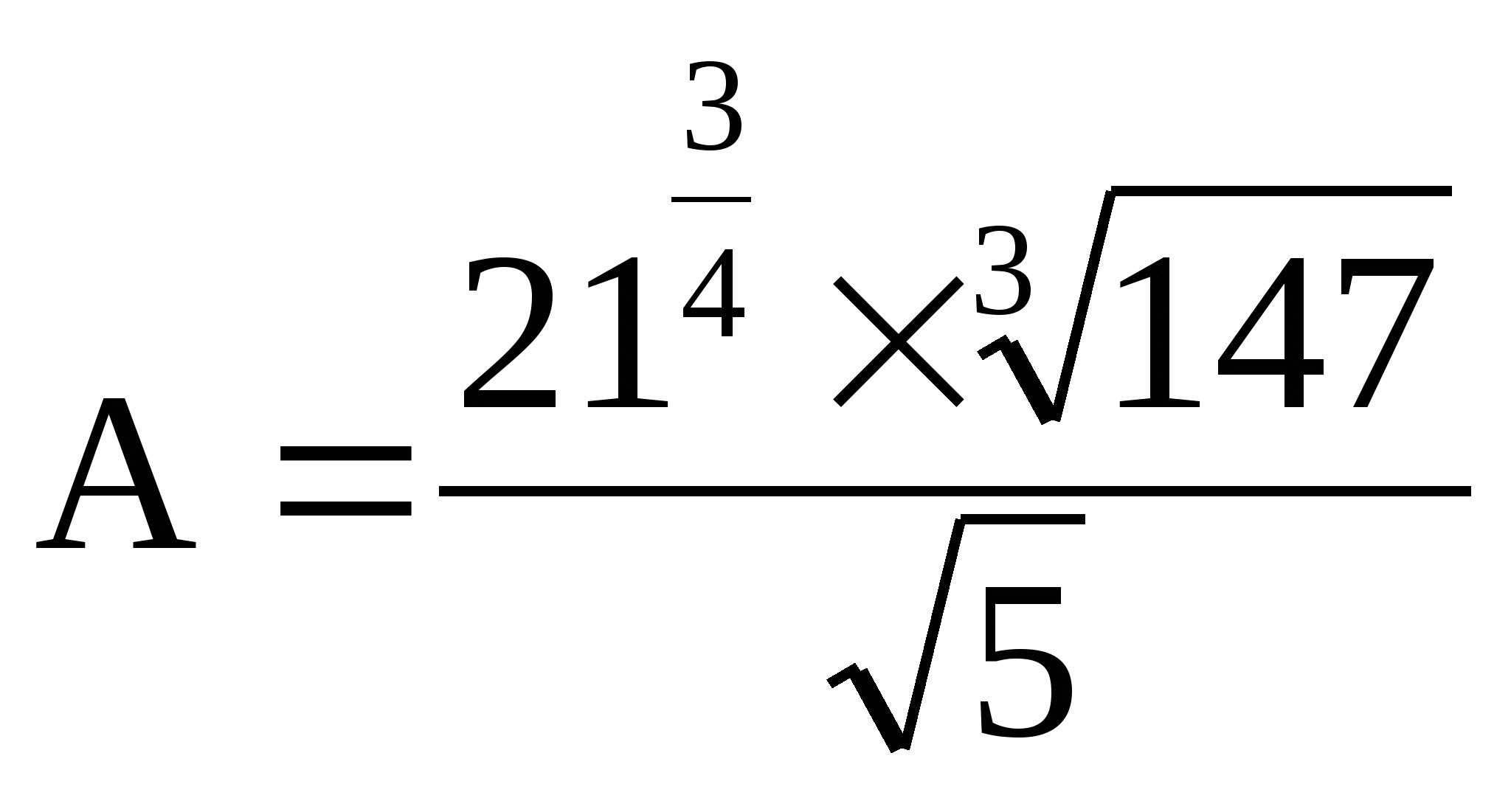
3. ![]() 7.
7.
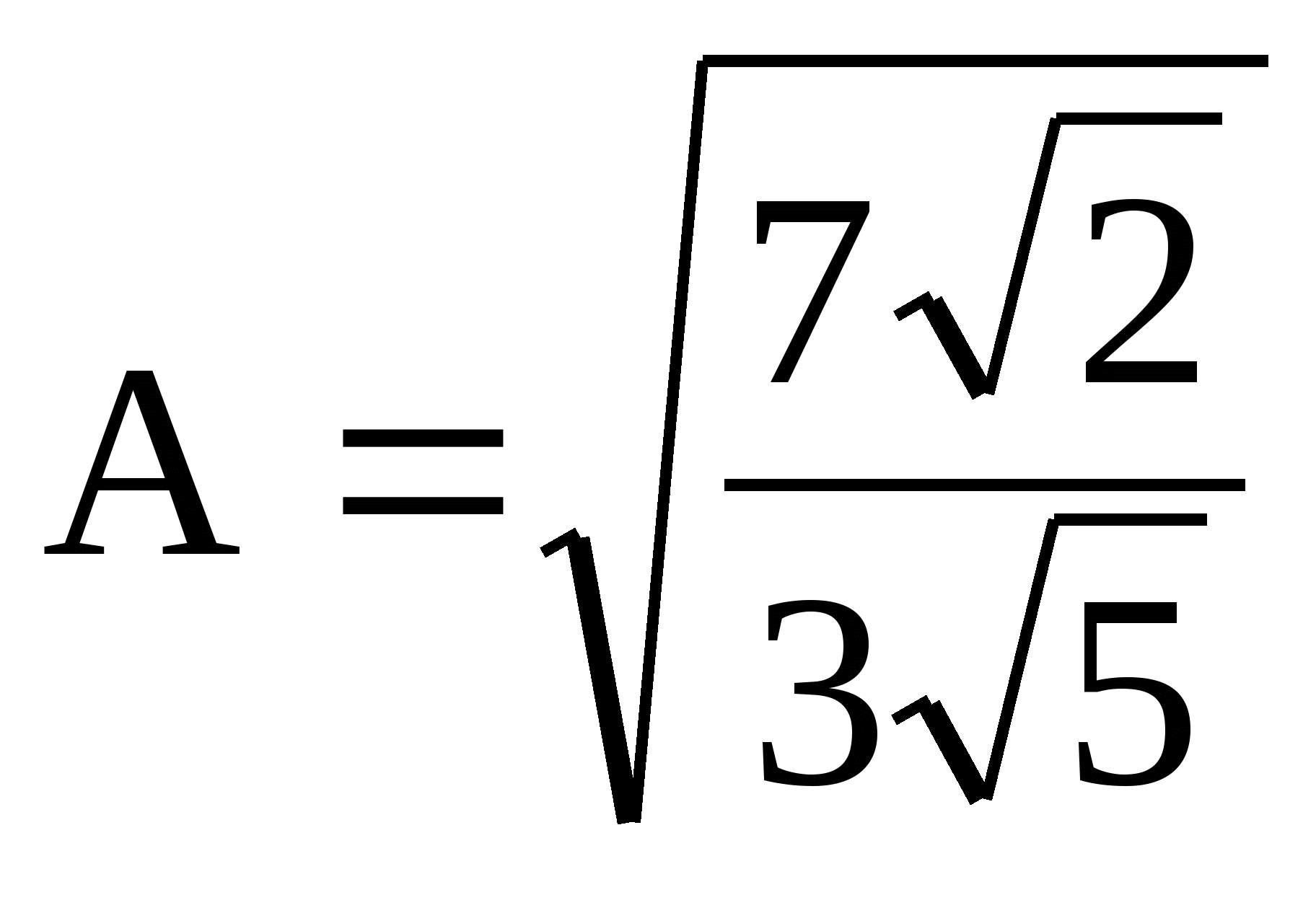
4. ![]() 8.
8.
![]()
3) Вычислите значение выражения, если известно, что logab = 2.
1. ![]()
2. ![]()
3. ![]()
4. 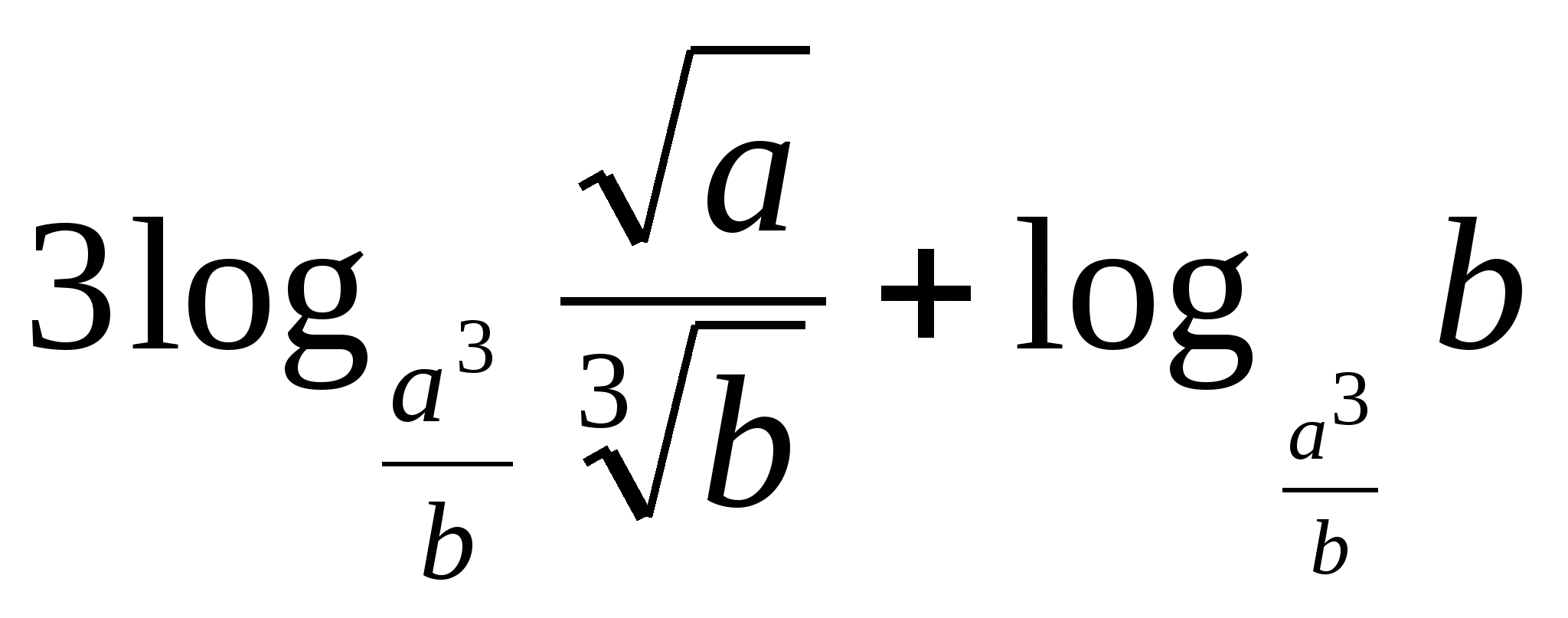
5. ![]()
6. 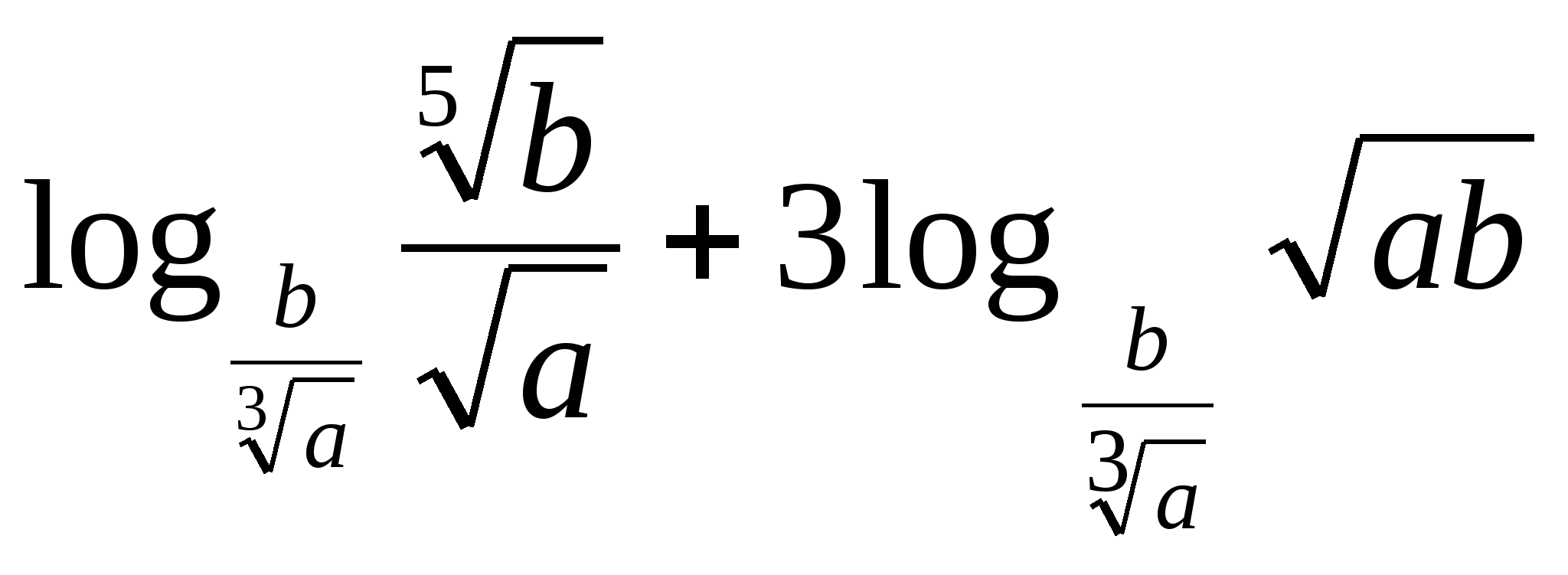
Тренажер № 2
Логарифмические уравнения
Решите уравнение:
1. log2 x = 3 7. log2log3 x = 1
2. log3 x = -1 8. log3log2log2 x = 0
3. log5 (2x) = 1 9. log2log3 x2 = 2
4. log7 x = 0 10. lg x = 2 - lg5
5. log2 (-x) = -3 11. lg x - lg11 = lg19-lg(30-x)
6. lg (x-1)2 = 0
1. ![]() 11.
11. ![]()
2. ![]() 12.
12. ![]()
3. ![]() 13.
13. ![]()
4. ![]() 14.
14. ![]()
5. ![]() 15.
15. ![]()
6. ![]() 16.
16. ![]()
7. ![]() 17.
17. ![]()
8. ![]() 18.
18. ![]()
9. ![]() 19.
19. ![]()
10. ![]() 20.
20. ![]()
21. ![]()
Тренажер № 3
Логарифмические неравенства
Решите неравенства:
1. ![]() 7.
7.
![]()
2. ![]() 8.
8.
![]()
3. ![]() 9.
9.
![]()
4. ![]() 10.
10. ![]()
5. ![]() 11.
11. ![]()
6. ![]() 12.
12. ![]()
13. ![]() 22.
22. ![]()
14. ![]() 23.
23. ![]()
15. 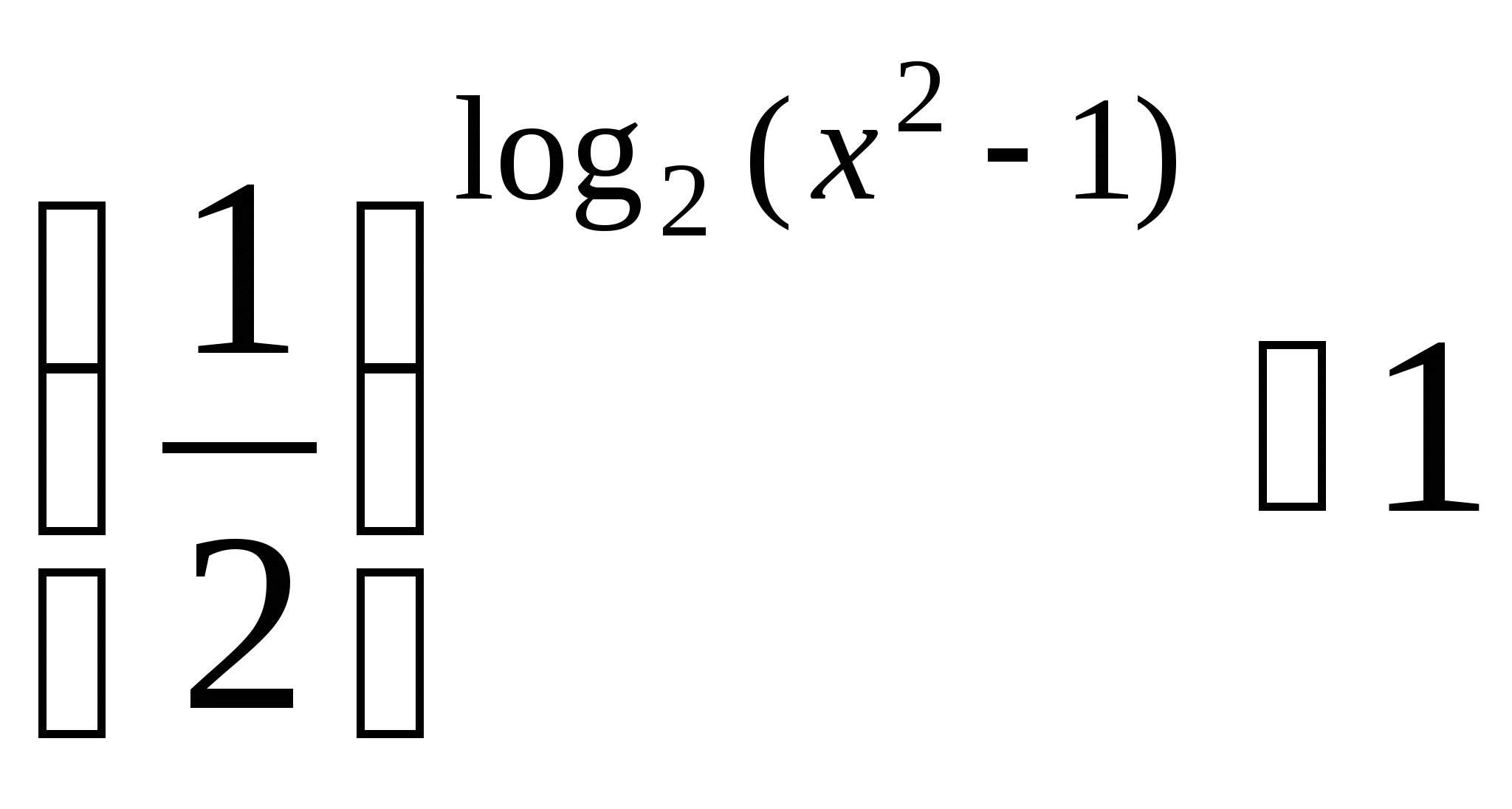 24.
24. ![]()
16. ![]() 25.
25. ![]()
17. ![]() 26.
26. ![]()
18. ![]() 27.
27. ![]()
19. ![]() 28.
28. ![]()
20. ![]() 29.
29. ![]()
21. ![]() 30.
30. ![]()
Cамостоятельная работа № 9 (10 класс)
Тригонометрия. «Зависимость между тригонометрическими функциями одного аргумента. Формулы приведения»
Вариант 1 Вариант 2
1) найти sin и ctg , если 1) найти cos и tg , если
![]()
![]()
2) 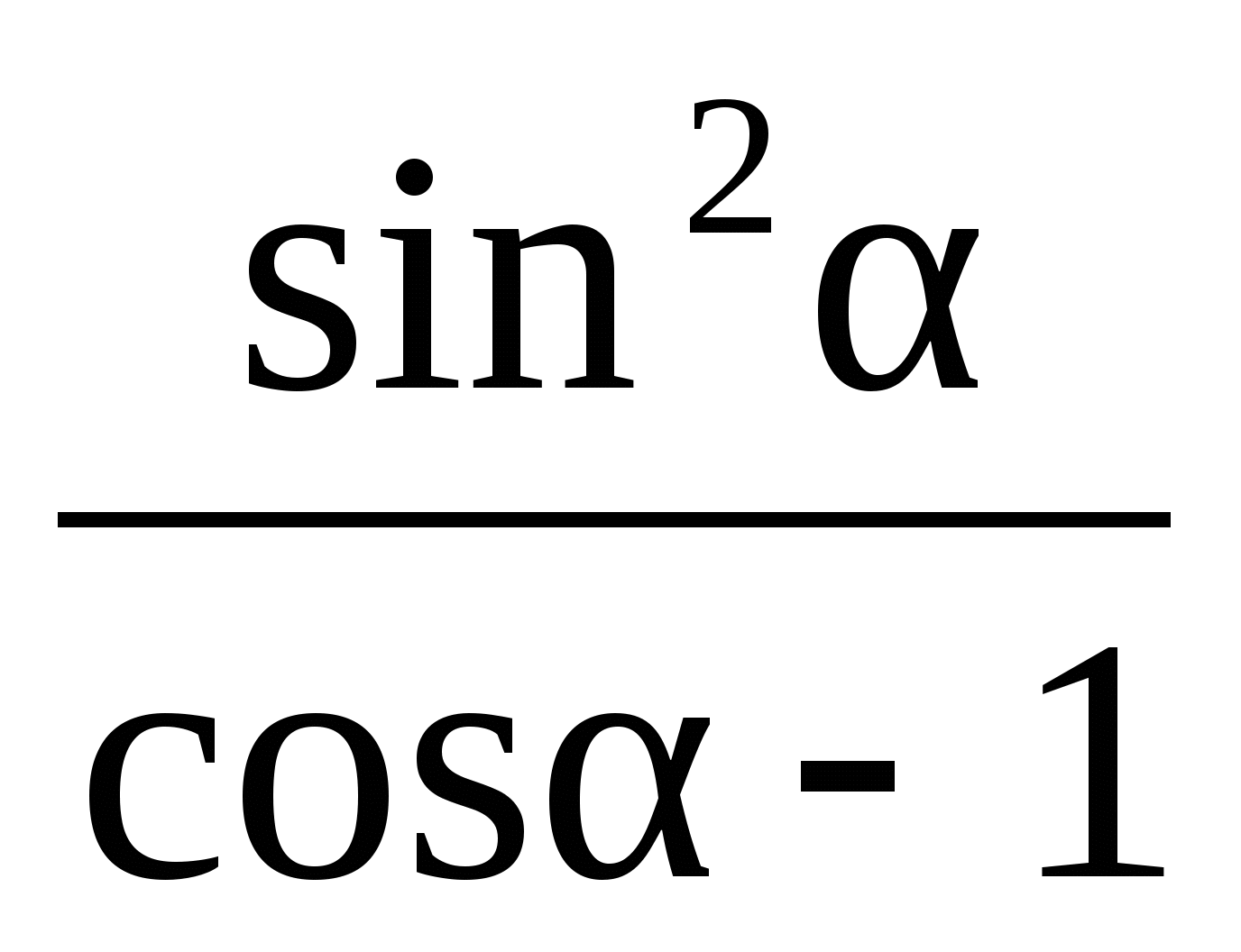 2)
2)
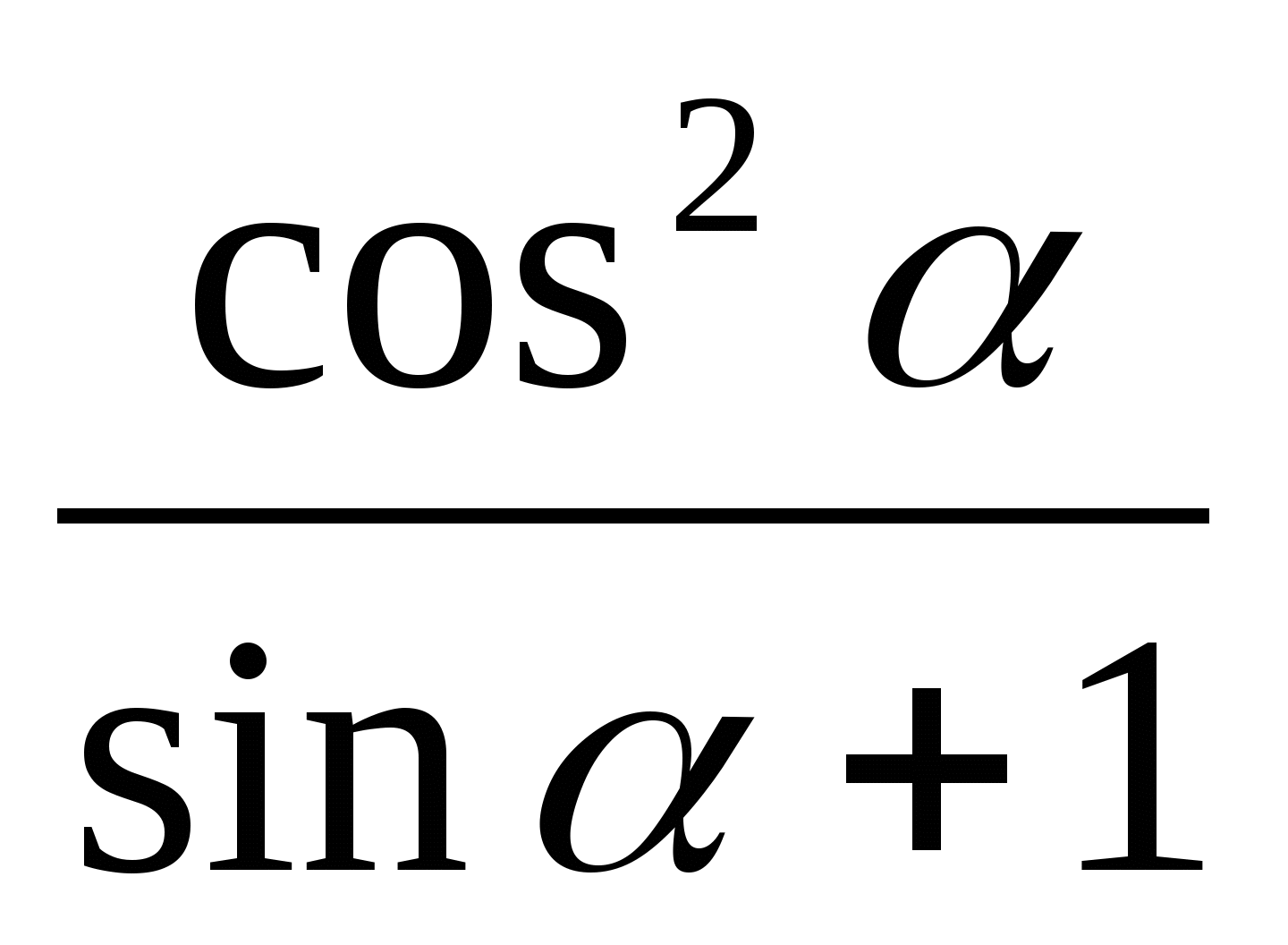
3) 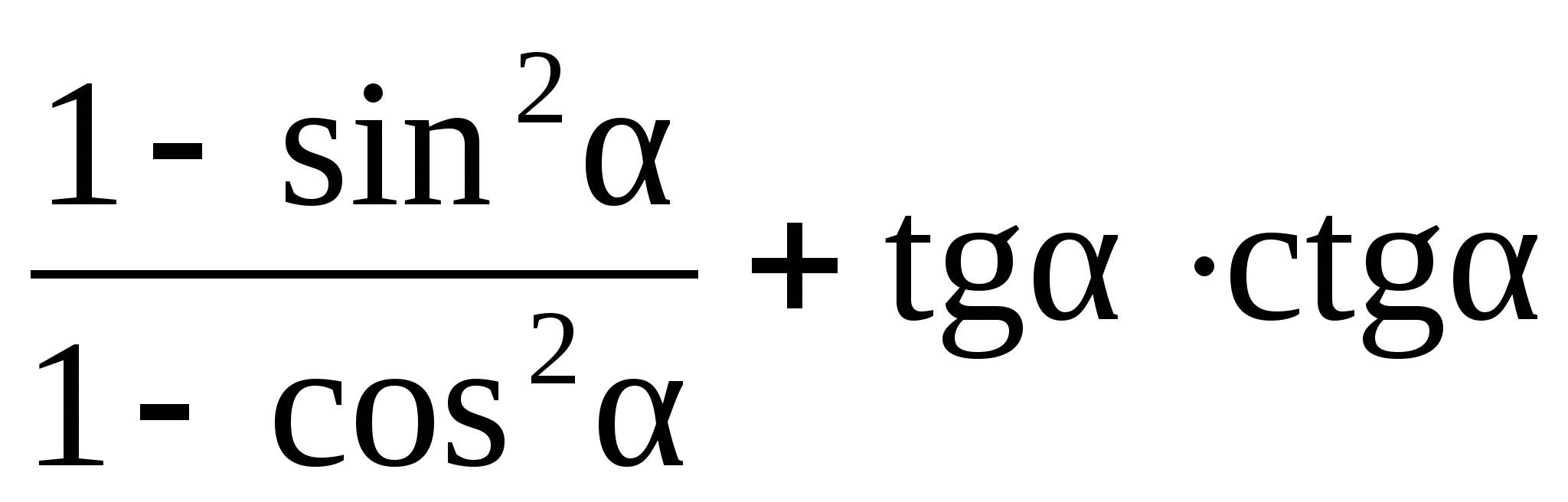 3)
3)
![]()
4) ![]() 4)
4)
![]()
5) tg 225cos330ctg 120sin 240 5) ![]()
![]()
6) 2sin2cos2 +cos4+sin4=1 6) sin4-sin2=cos4-cos2
7) 4 + (ctg-tg)2=(ctg-tg) 7)
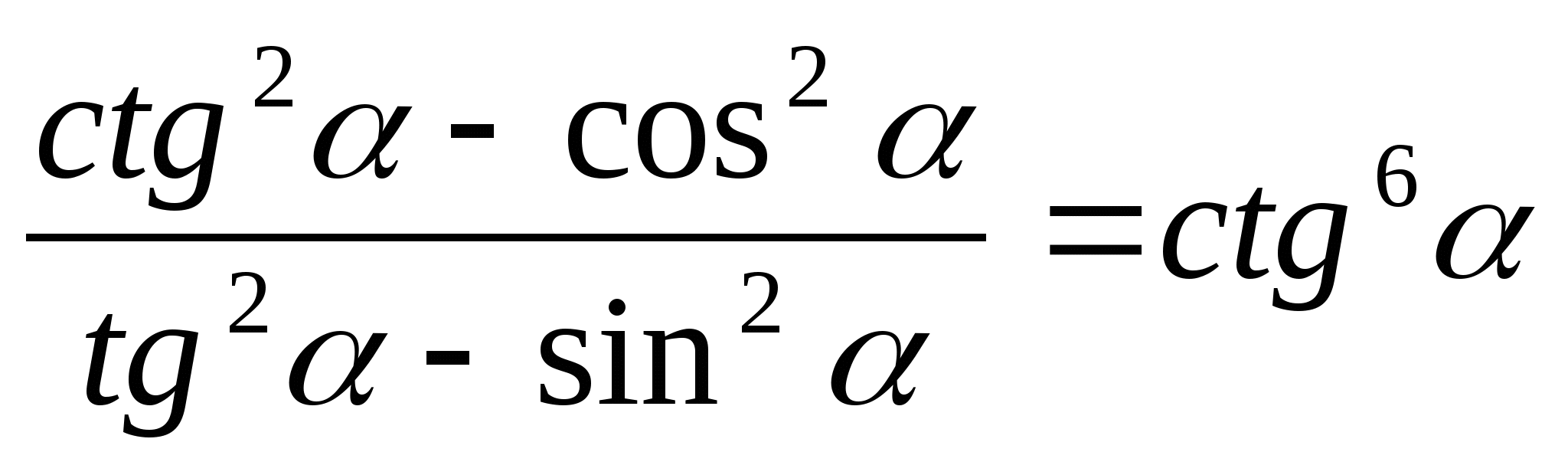
Вариант 3
1) Найти cos и sin , если tg =![]() и
сos 0
и
сos 0
2) 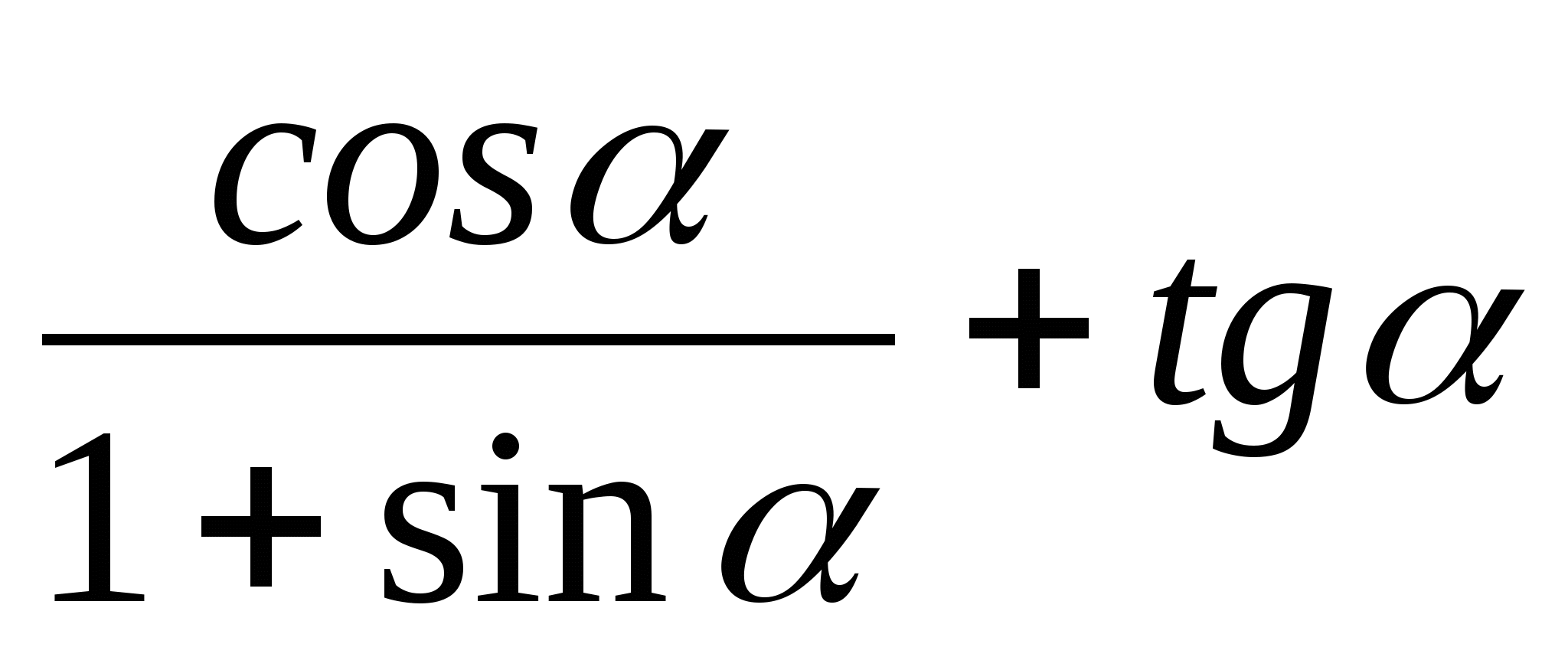
3) 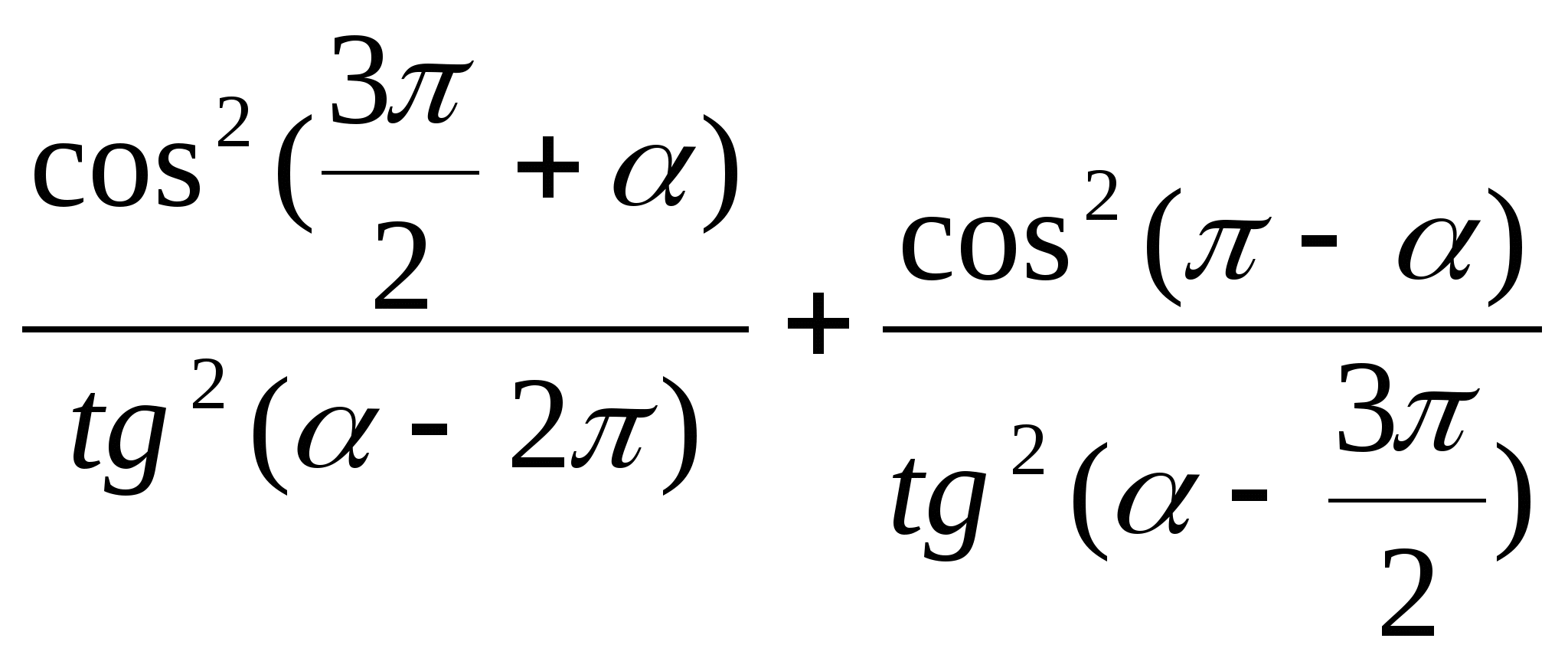
4) ![]()
5) Найти ![]() если
если ![]()
6) tg1tg3tg5…………tg89
7) 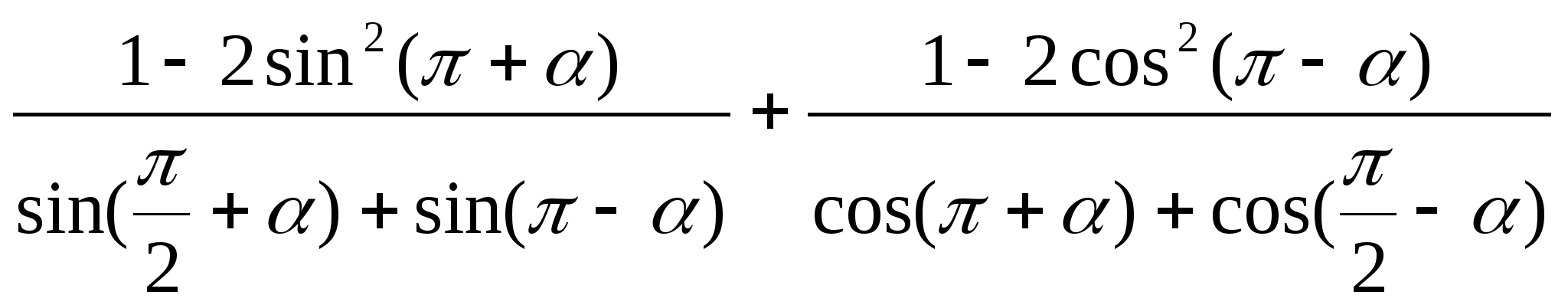
Вариант 4 (продолжение сам работы № 9)
1) Найти sin и сos , если сtg =![]() и
sin 0
и
sin 0
2) 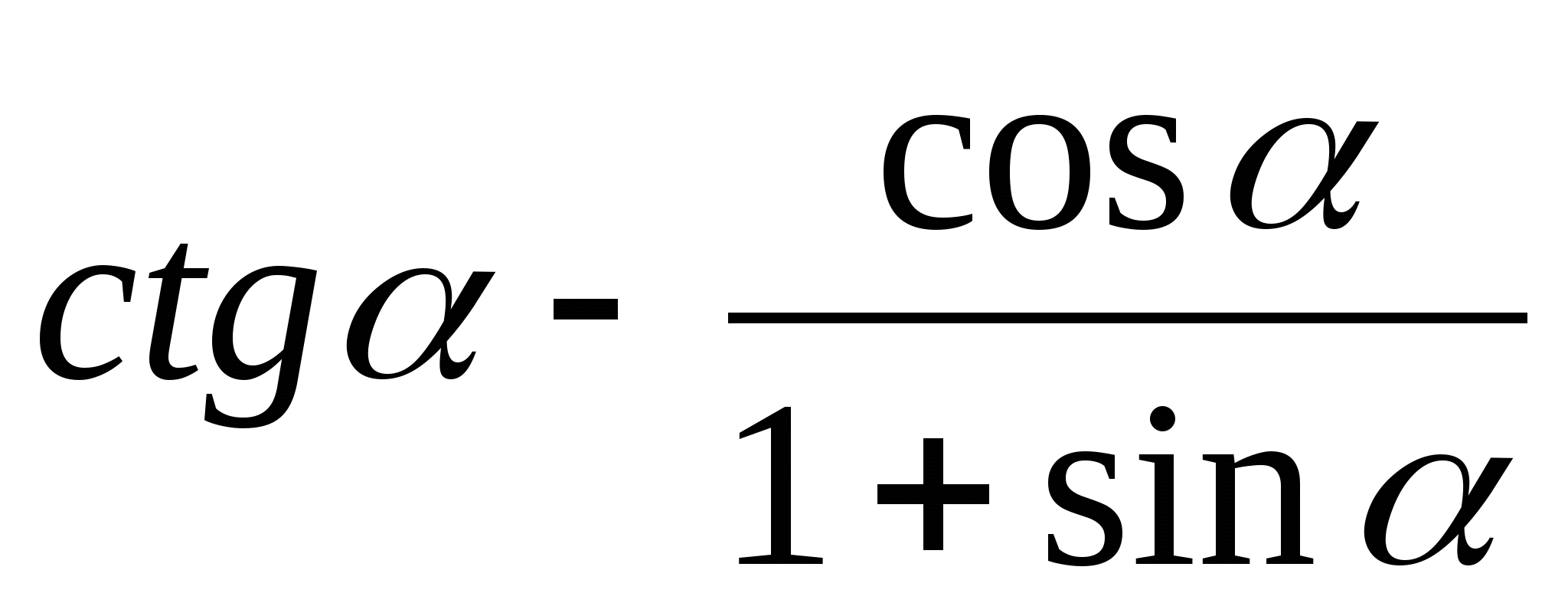
3) 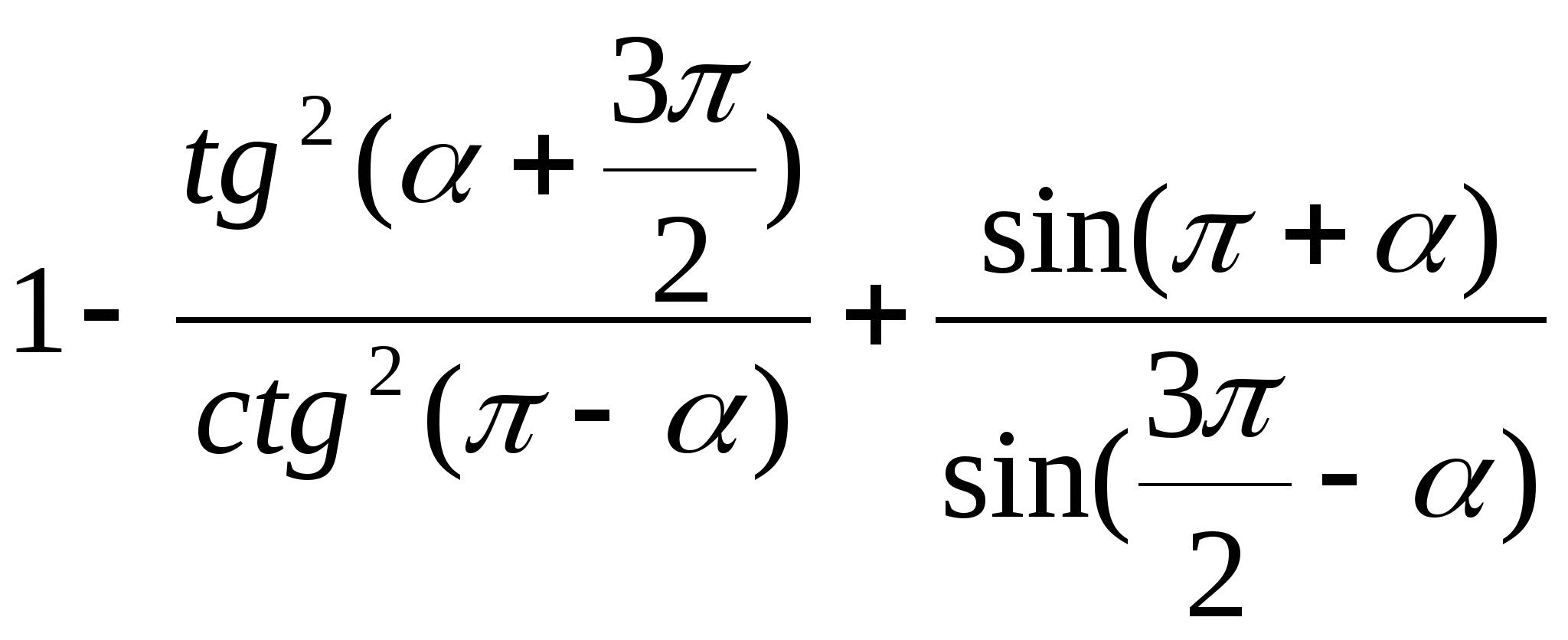
4) ![]()
5) Найти ![]() если
если ![]()
6) tg1tg3tg5…………tg89
7) 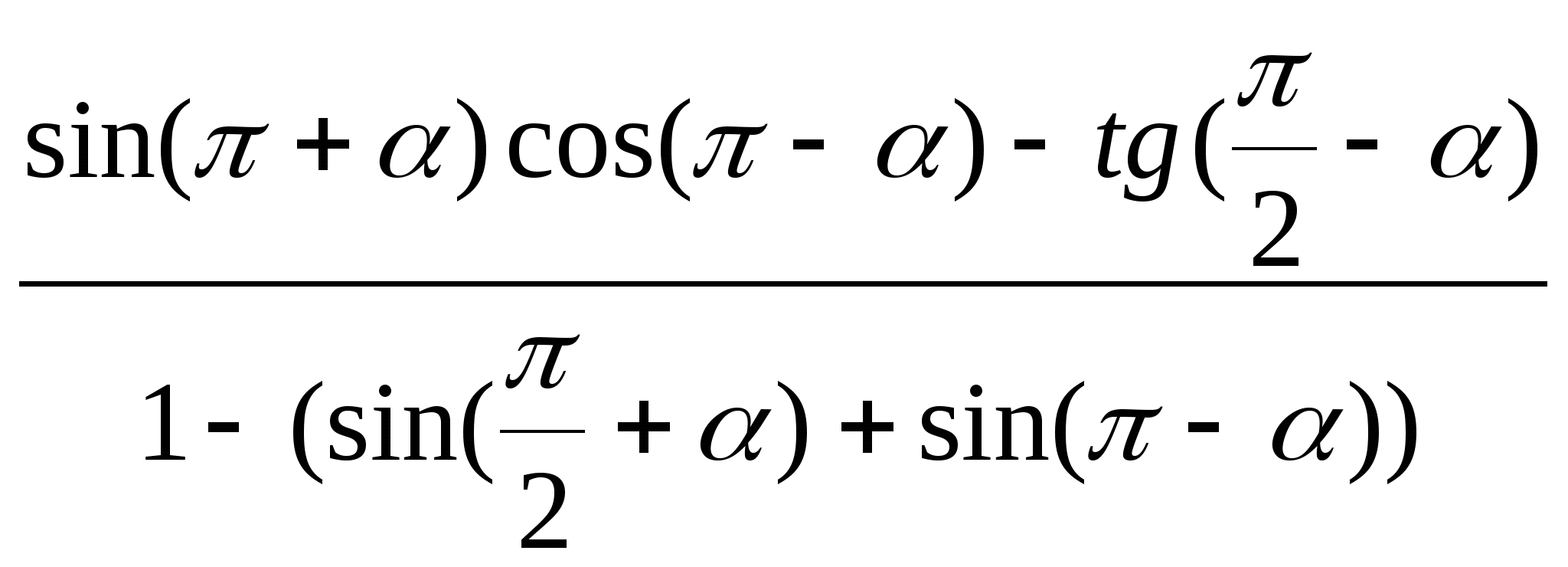
Самостоятельная работа № 11 (10 класс)
Формулы двойного и половинного аргумента
Вариант 1 Вариант 2
1) 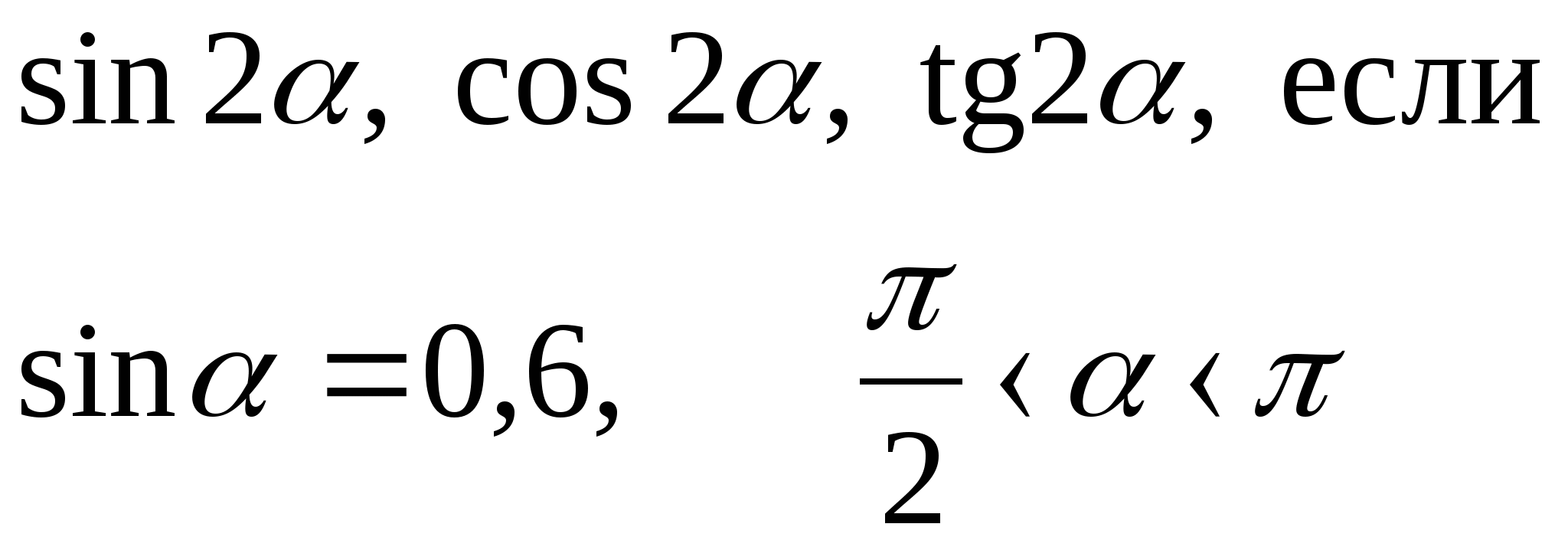 1)
1)
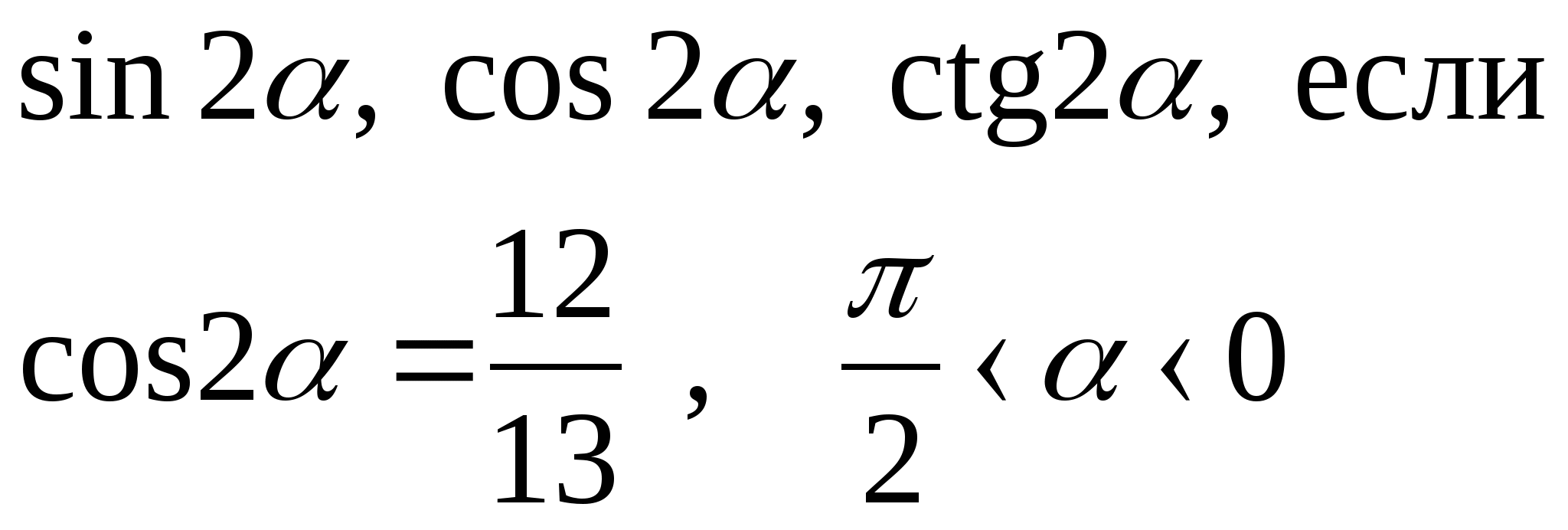
2) ![]() 2)
2)
![]()
3)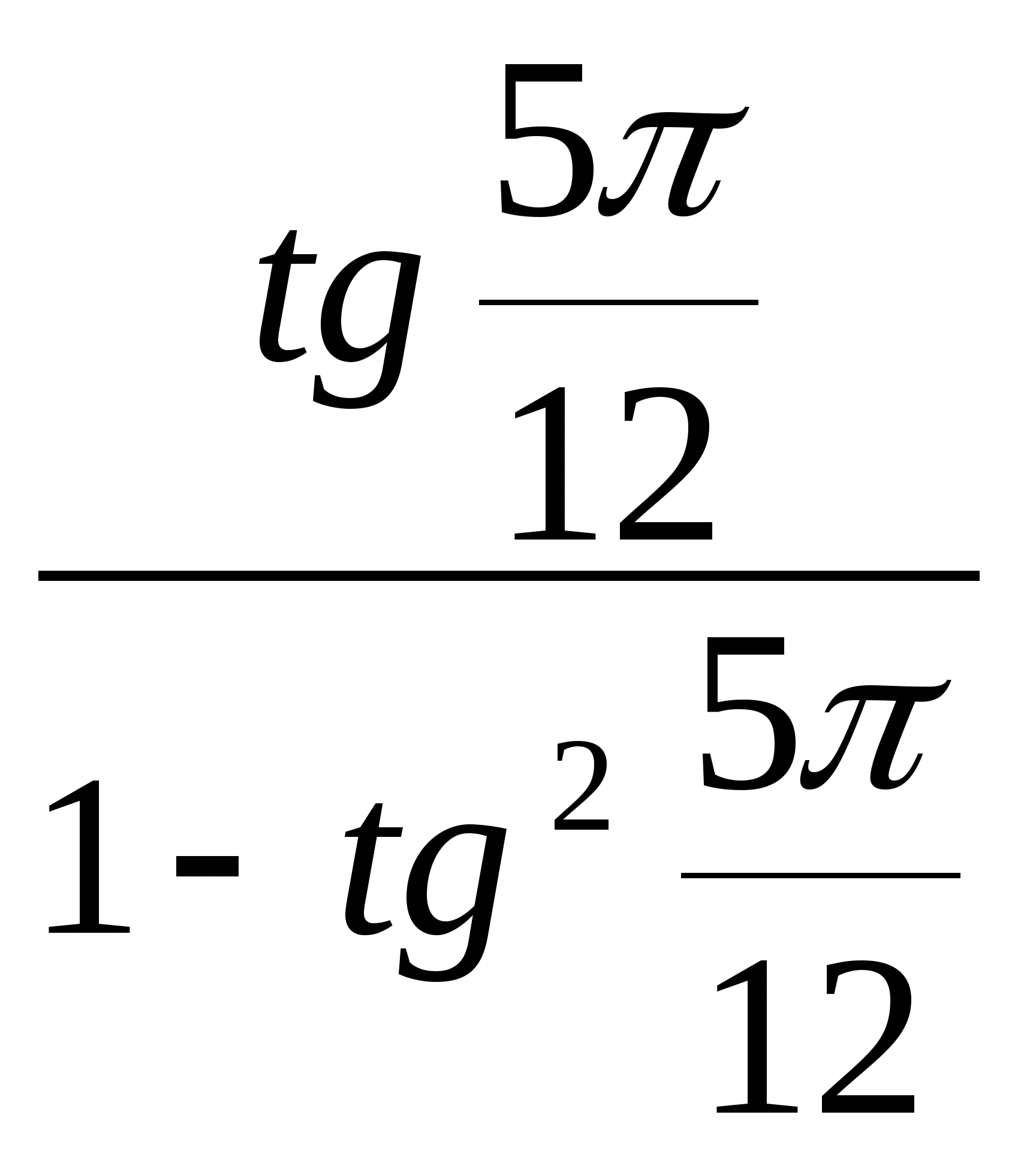 3)
3)
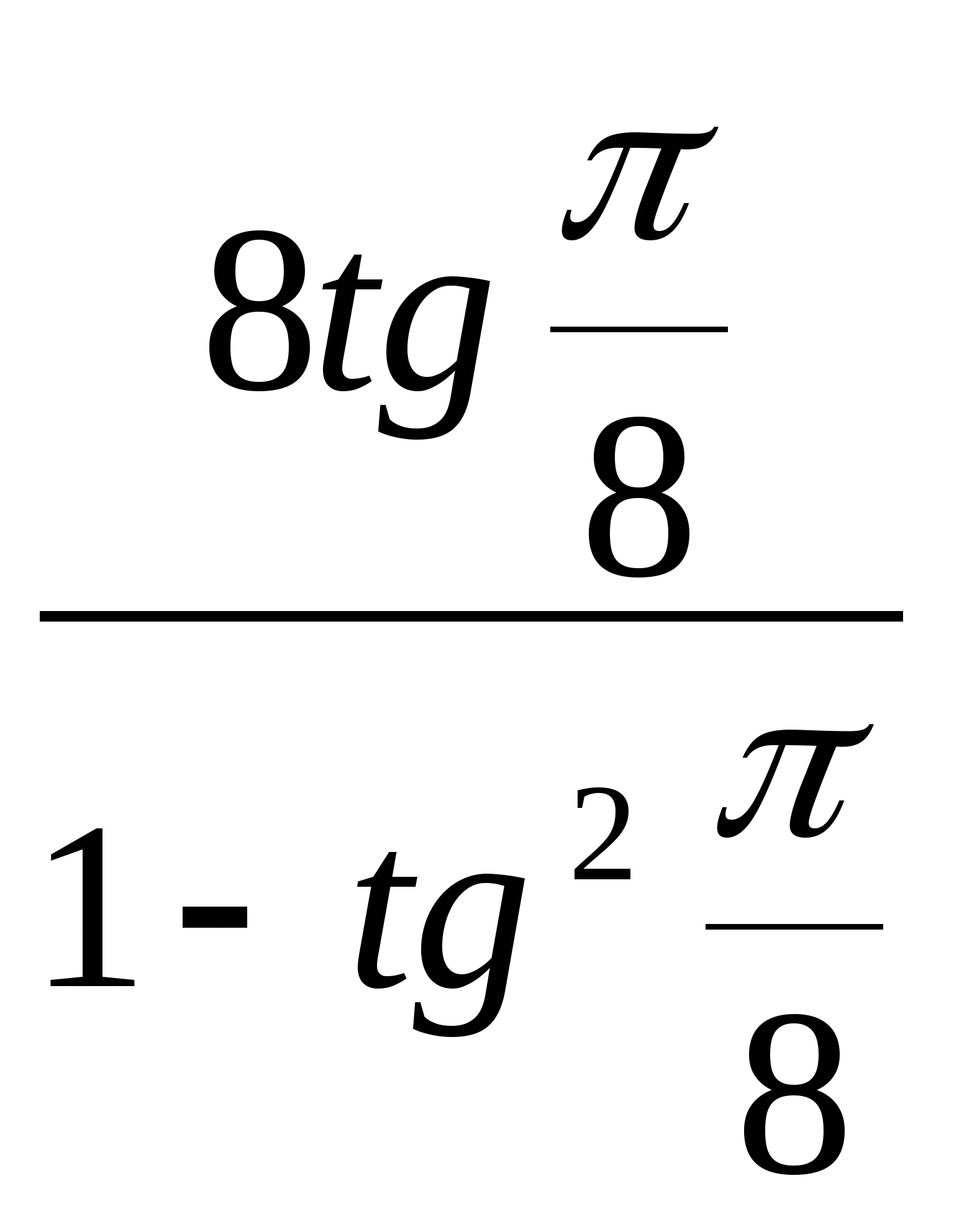
4) 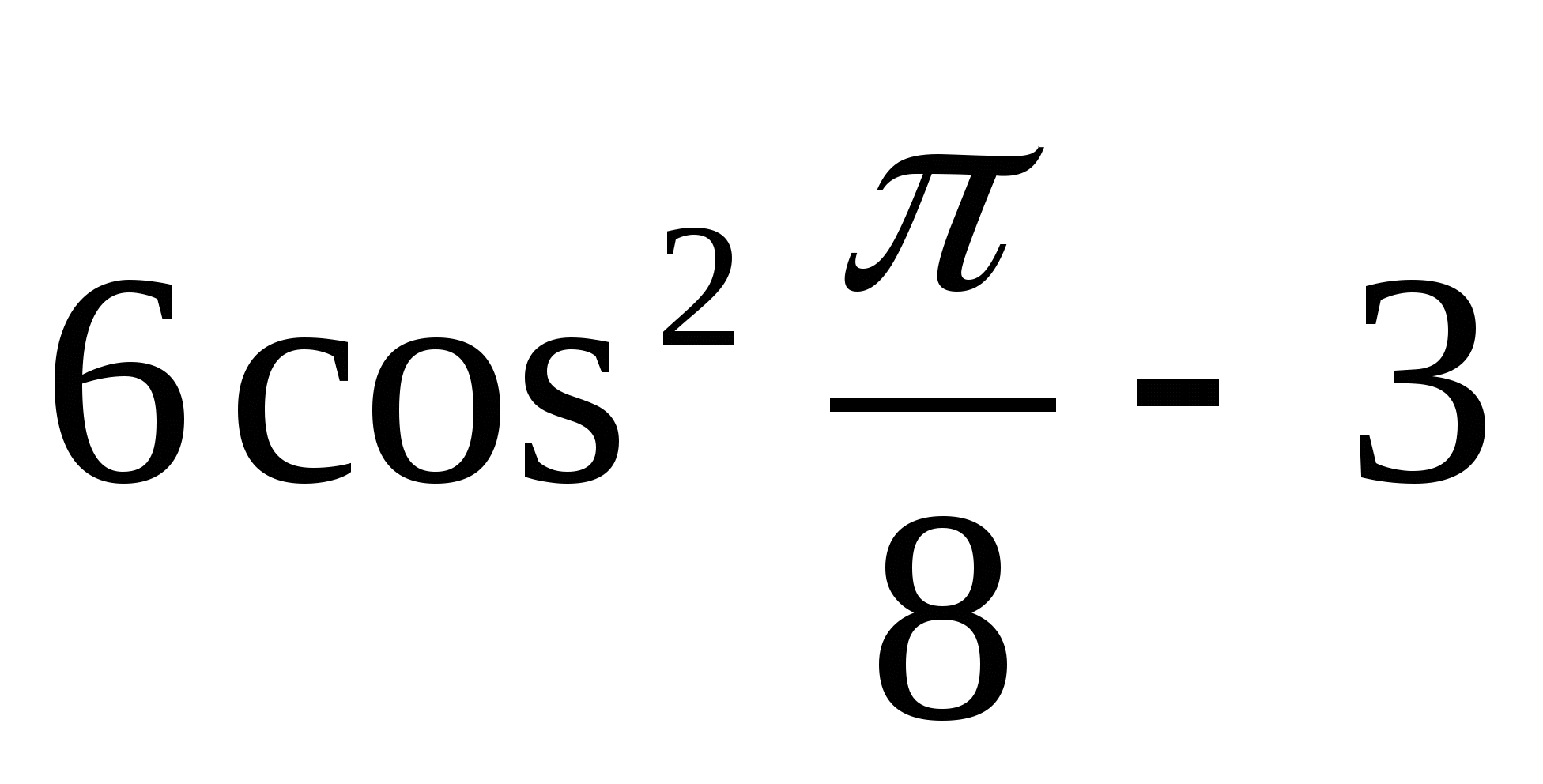 4)
4)
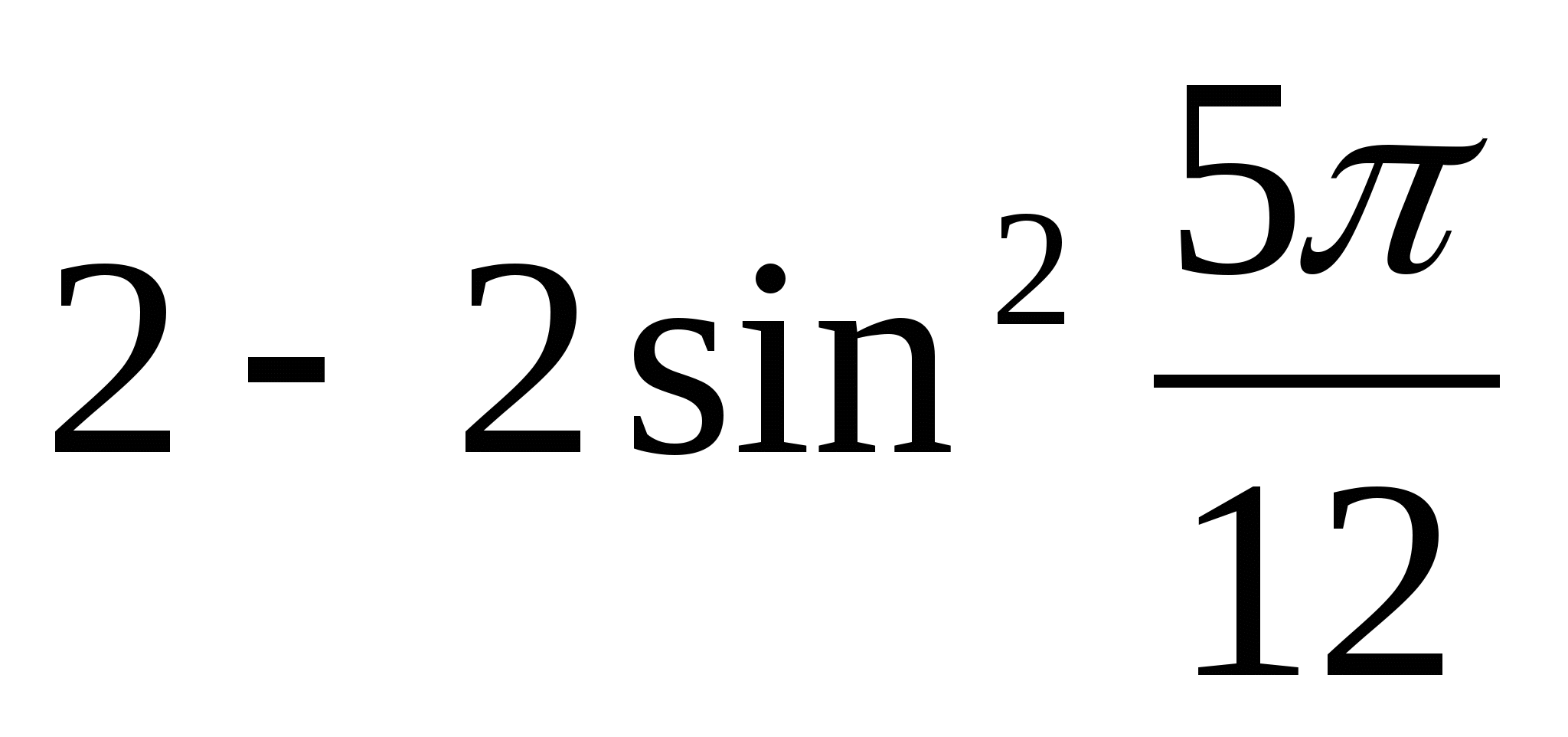
5 )
)
![]() 5)
5)
![]()
Вариант 3 Вариант 4
1) 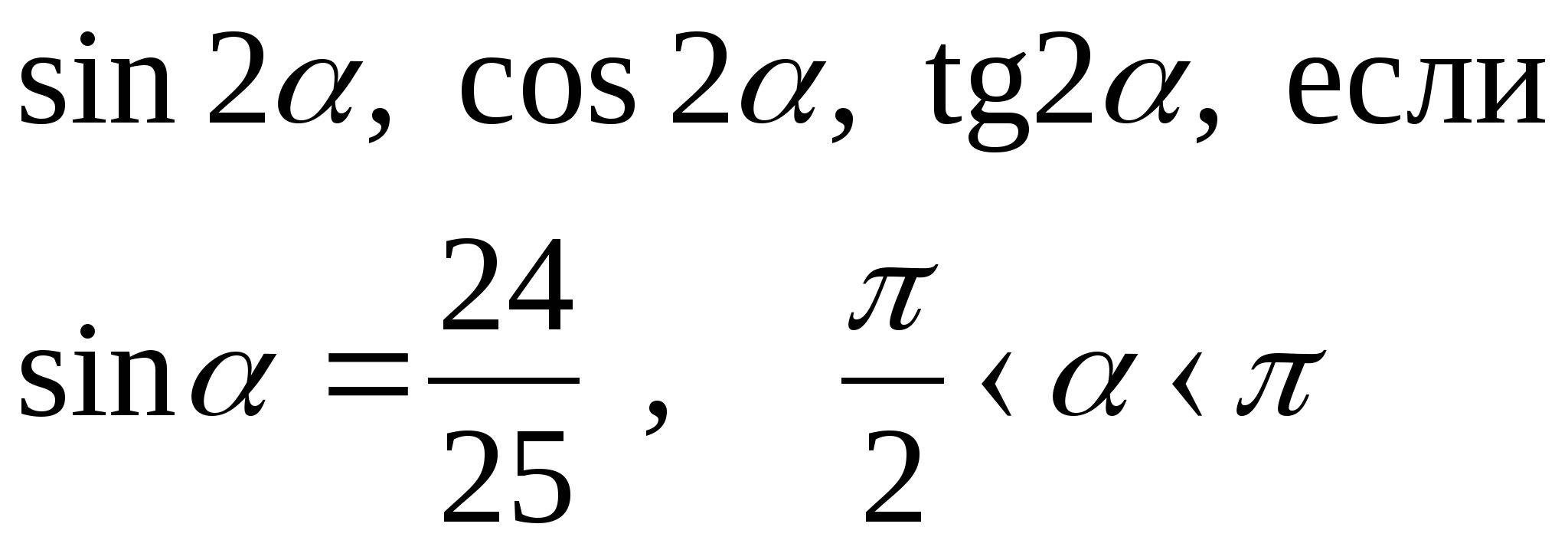 1)
1)
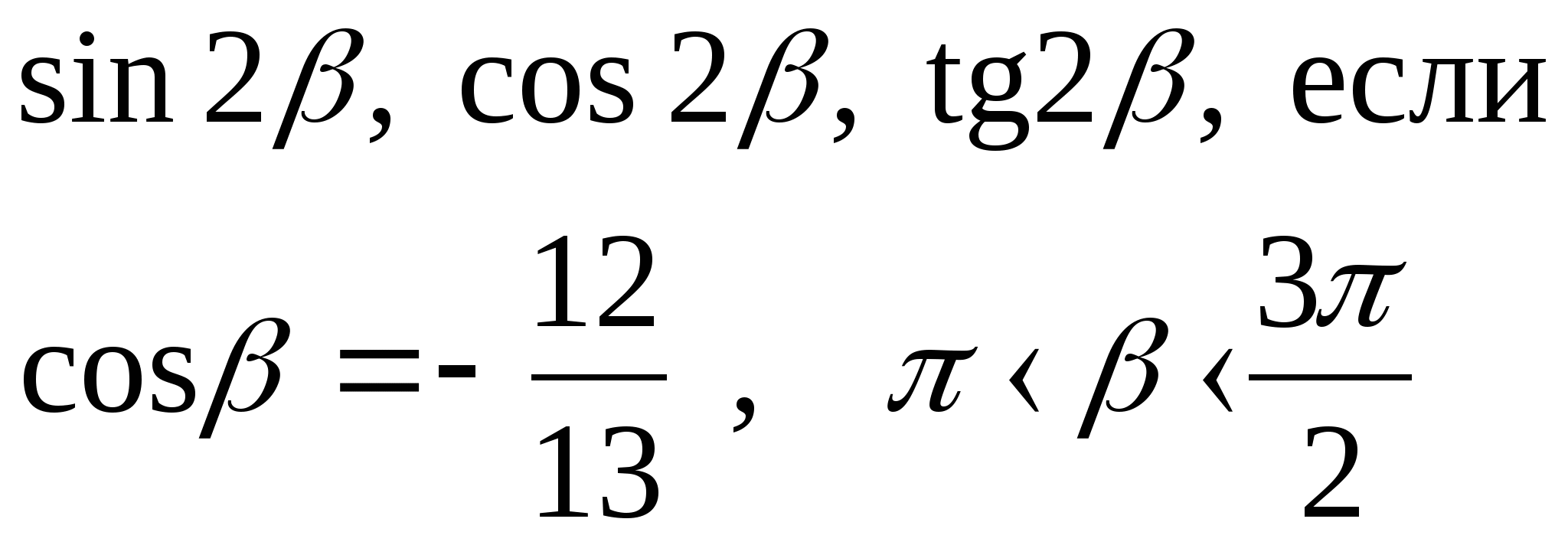
2) ctg-sin2 = ctg cos 2) sin2-tg = tg cos2
3) ![]() 3)
3)
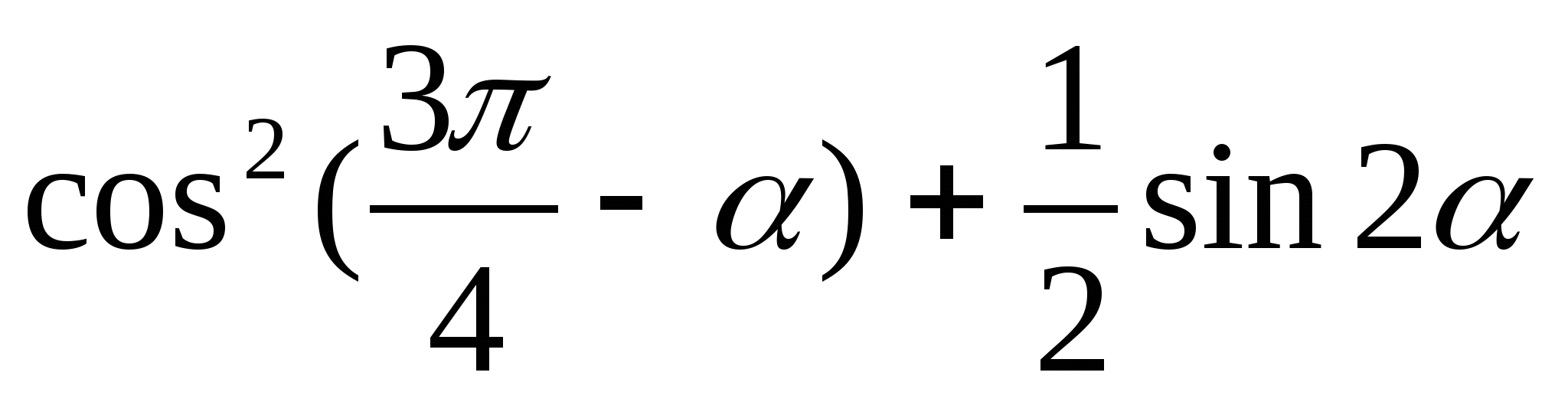
4) ![]() 4)
4)
![]()
5)![]() 5)
20cos40cos80
5)
20cos40cos80
6) sin 2, если 6) cos2, если
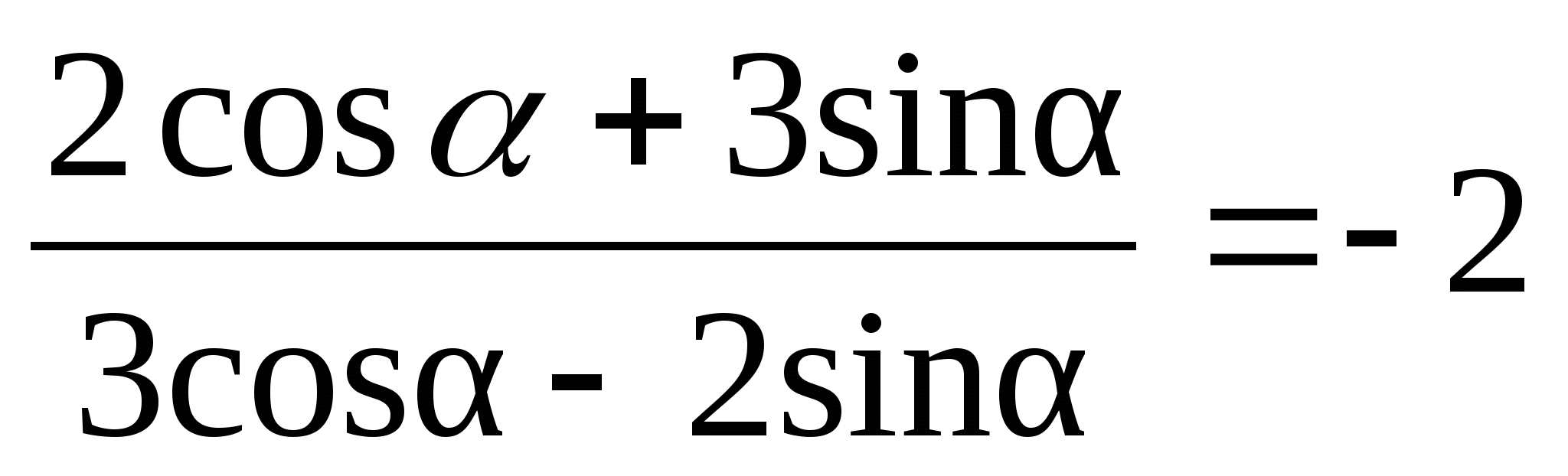
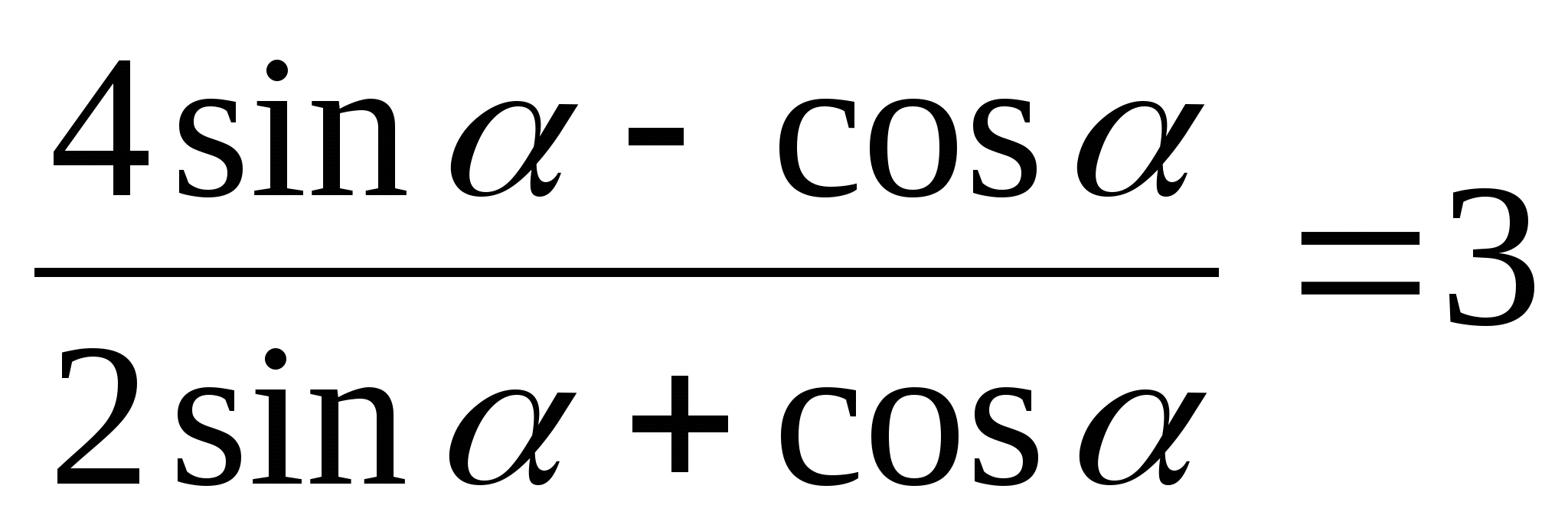
Самостоятельная работа № 12 (10 класс)
«Преобразование суммы тригонометрических функций в произведение»
Вариант 1 Вариант 2
1) 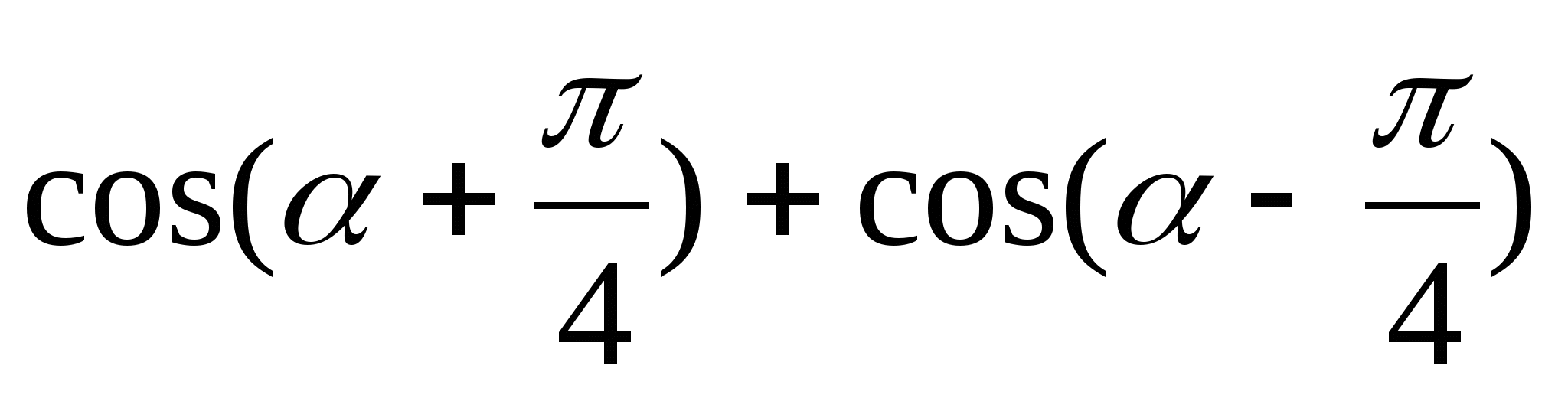 1)
1)
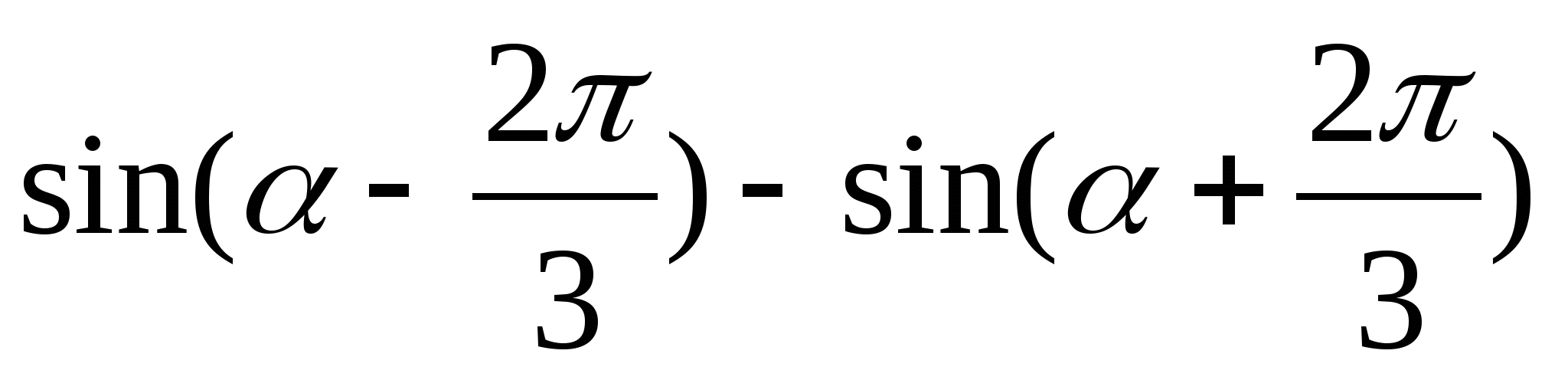
2) 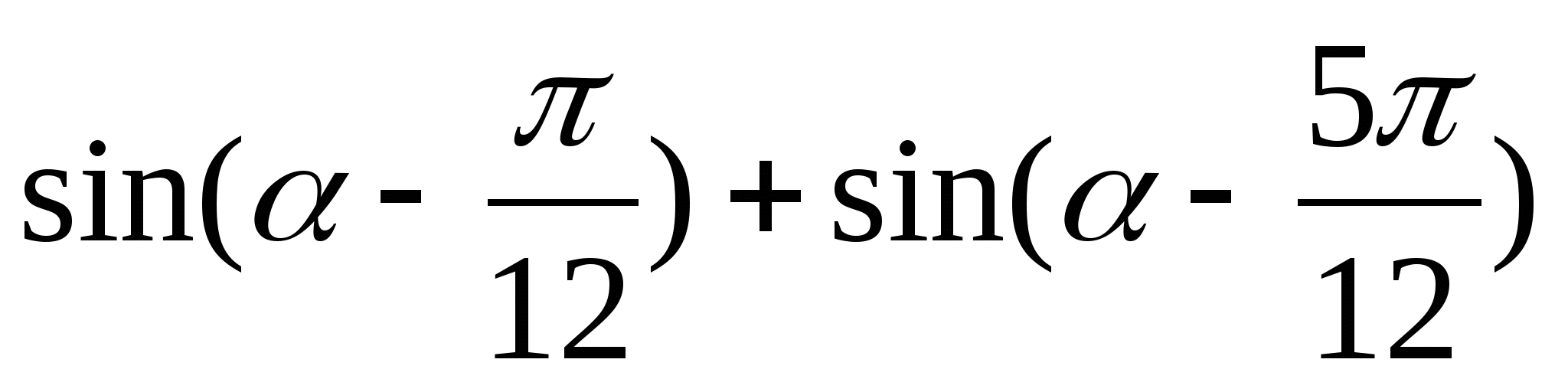 2)
2)
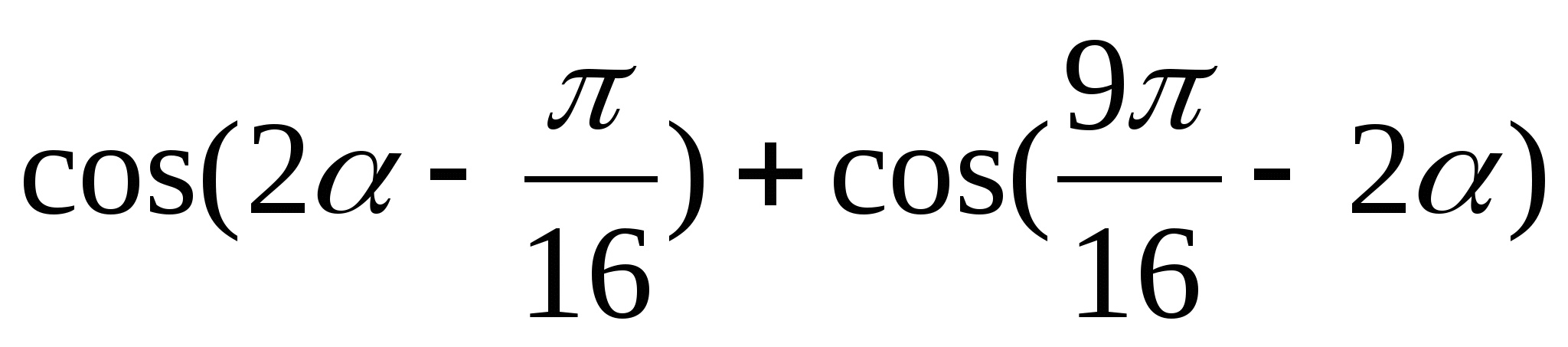
3) ![]() 3)
3)
![]()
4) 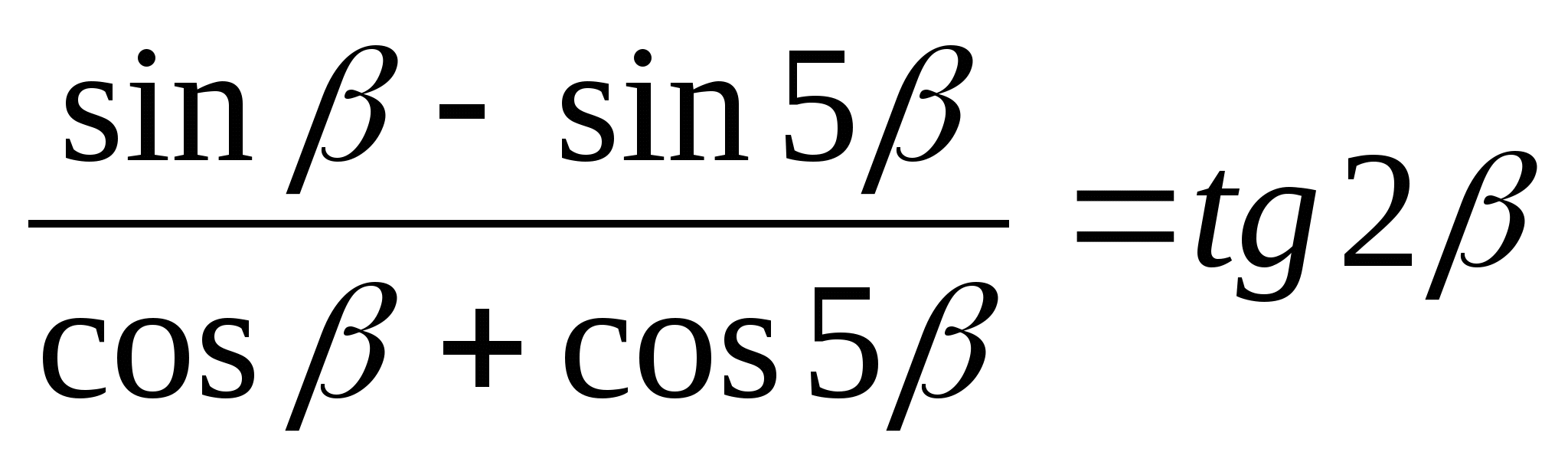 4)
4)
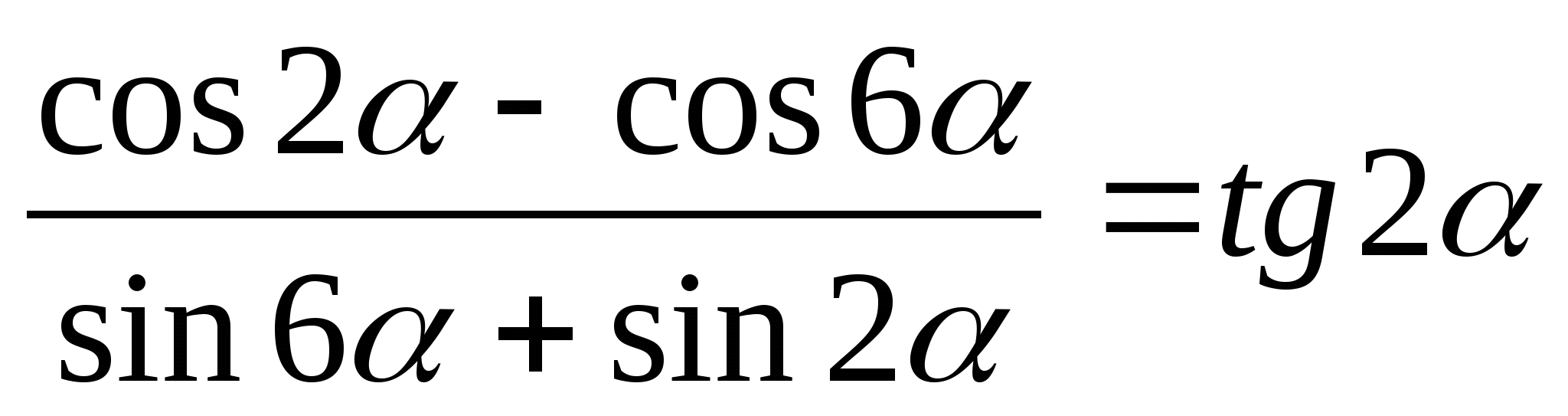
5) Преобразуйте в произведение: 5) Преобразуйте в произведение:
cos2 + cos14 + cos6 + cos10 sin4 + sin10 + sin22 +sin16
Вариант 3 Вариант 4
1) ![]() 1)
1)
![]()
2) 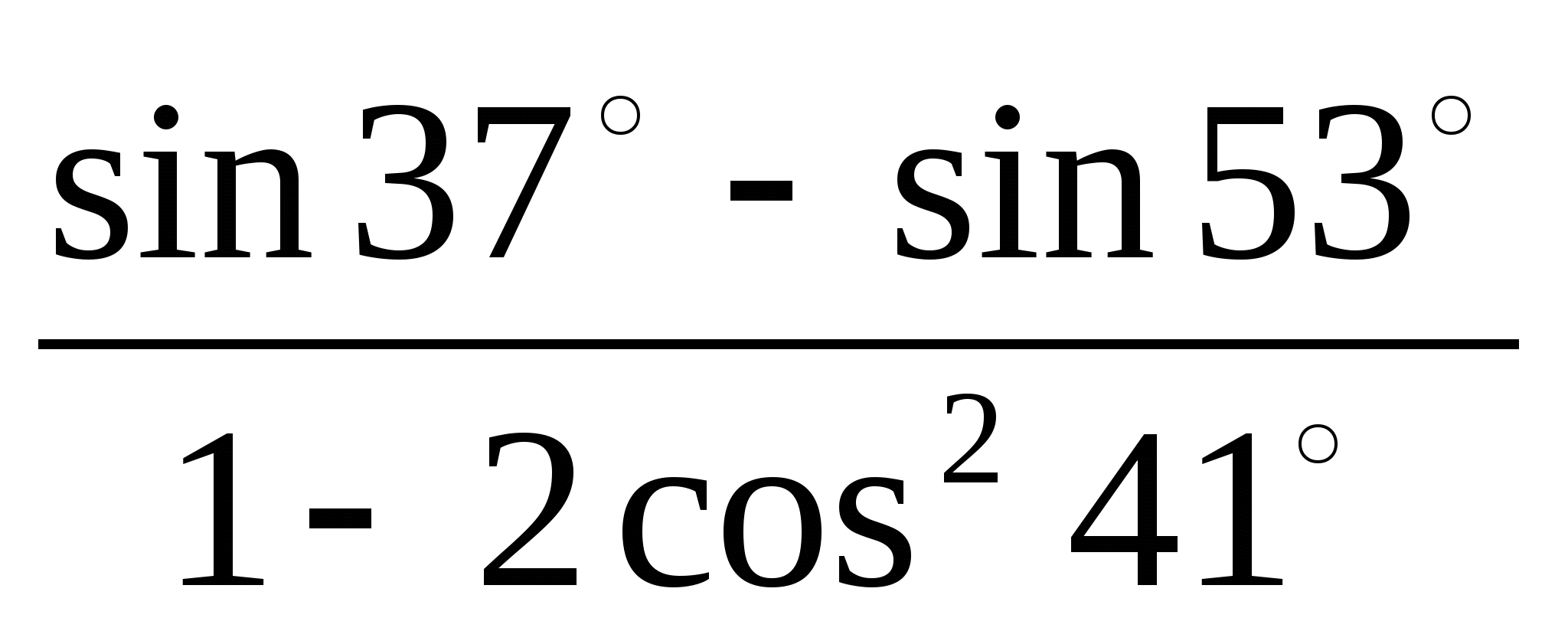 2)
2)
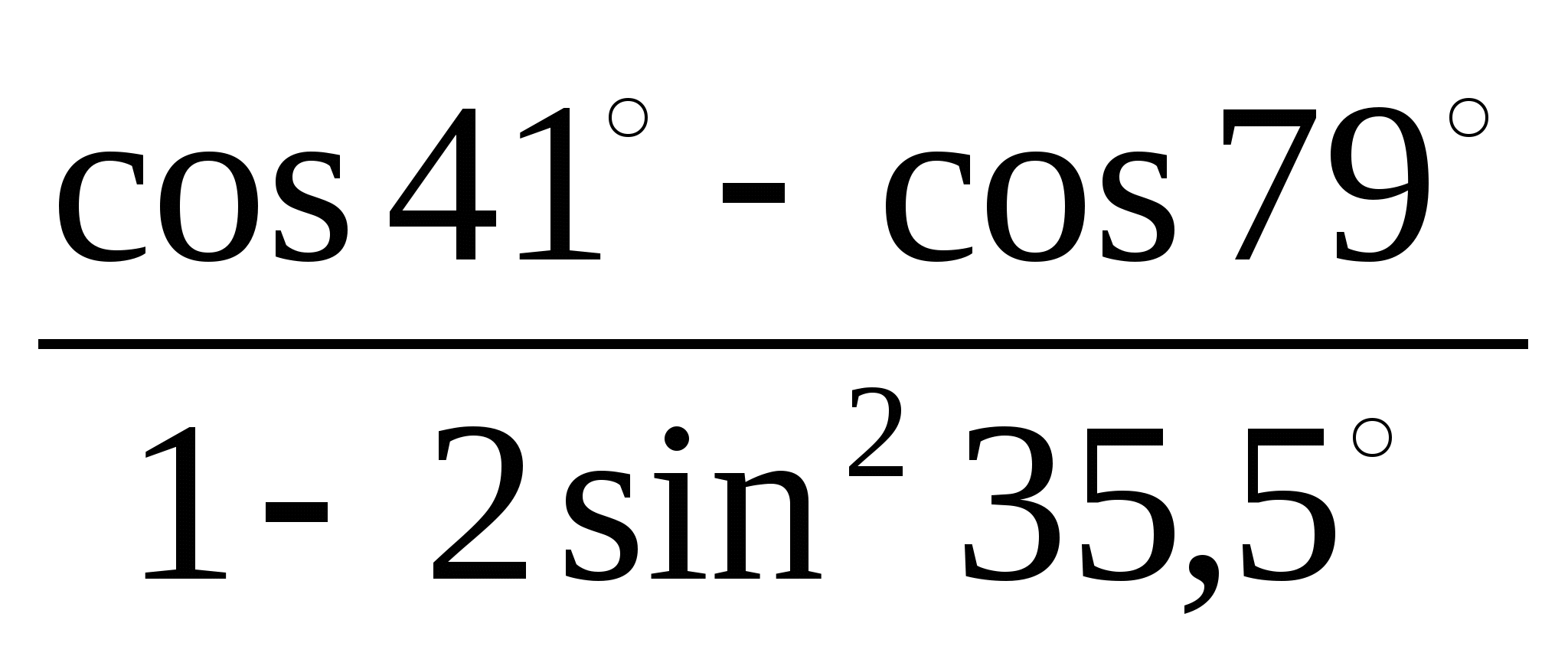
3) ![]() 3)
3)
![]()
4) ![]() 4)
4)
![]()
5) Преобразуйте в произведение: 5) Преобразуйте в произведение:
1-2sin - cos2 1 + 2cos + cos2
Самостоятельная работа № 13 (10 класс)
«Арксинус, арккосинус, арктангенс»
Вариант 1 Вариант 2
1) Может ли arcsin принимать 1) Может ли arccos принимать
значения ![]() значения
значения ![]()
2) При каких имеет смысл 2) При каких имеет смысл
выражение arccos(3-2) выражение arcsin(1-6)
3) Решить уравнение: 3arcsin x = 3) Решить
уравнение: ![]()
4) arctg(-1)-arctg1 4) arcsin0-arccos0
5) ![]() 5)
5)
![]()
6) 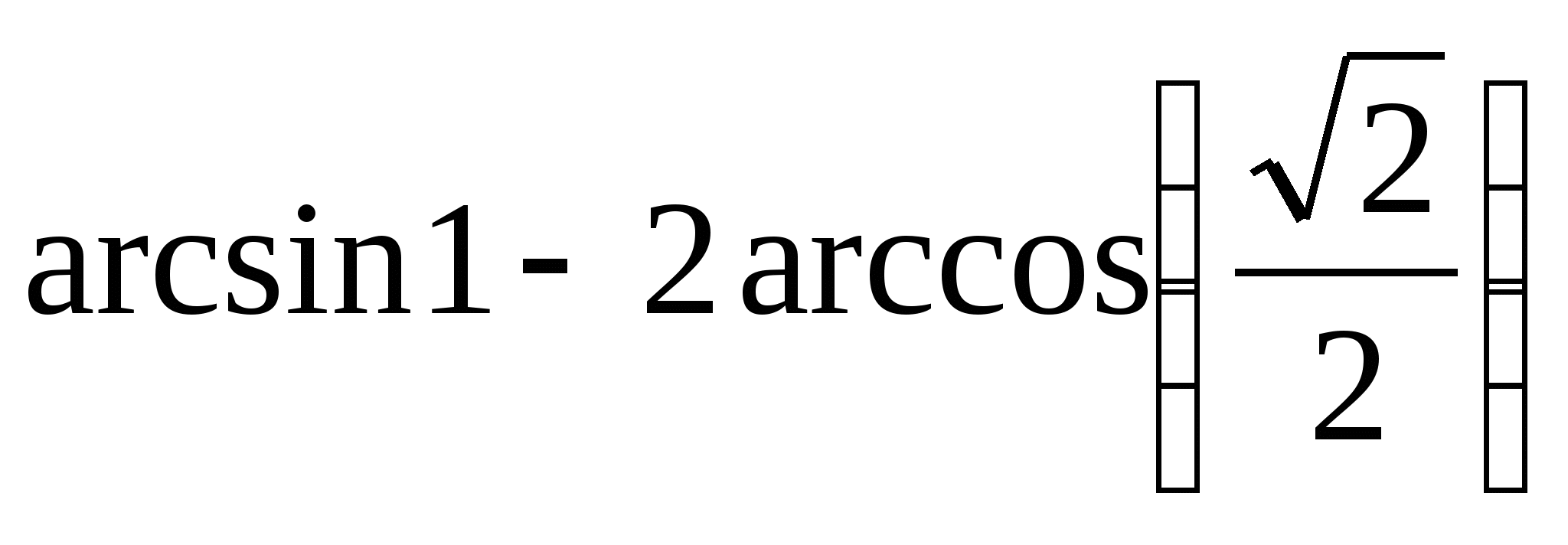 6)
6)
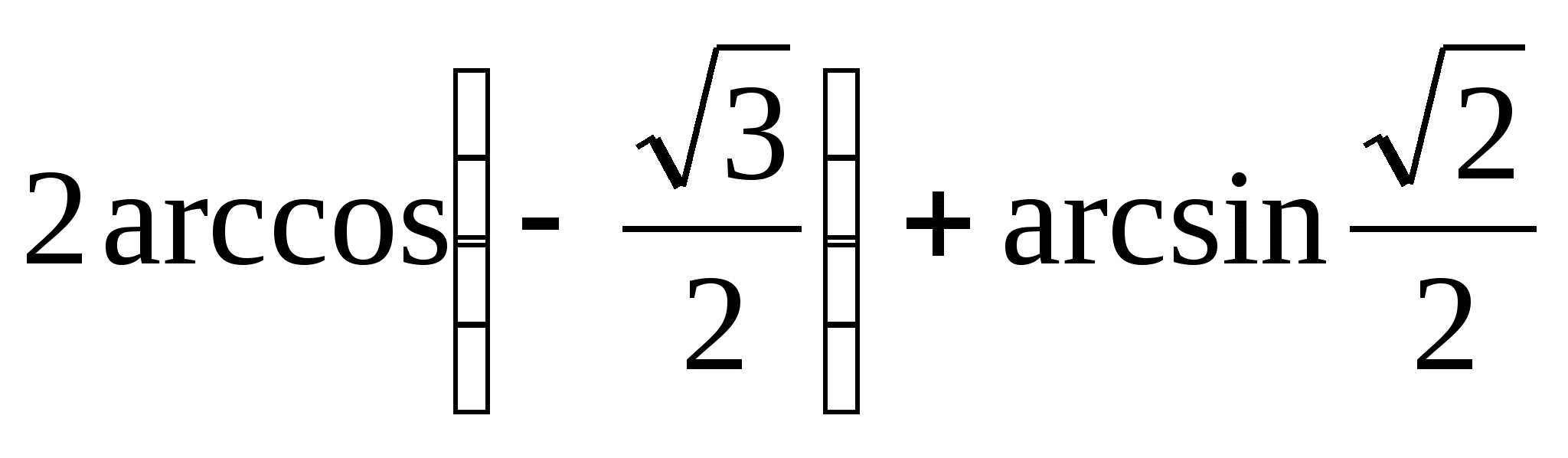
7) ![]() 7)
7)
![]()
8) ![]() 8)
8)
![]()
Вариант 3 Вариант 4
1) ![]() 1)
1)
![]()
2) При каких имеет смысл 2) При каких имеет смысл
выражение arcsin(5-4) выражение arcsin(2+1)
3) Решить уравнение: 3) Решить уравнение:
а) ![]() а)
а)
![]()
б) ![]() б)
б)
![]()
4) ![]() 4)
4)
![]()
5) ![]() 5)
5)
![]()
6) ![]() 6)
6)
![]()
продолжение С/р № 13
7) ![]() 7)
7)
![]()
8) ![]() 8)
8)
![]()
9) ![]() 9)
9)
![]()
Самостоятельная работа № 14 (10 класс)
«Простейшие уравнения»
Вариант 1 Вариант 2
1) ![]() 1)
0,5cos2x = 0
1)
0,5cos2x = 0
2) ![]() 2)
ctg(x-3) = 0
2)
ctg(x-3) = 0
3) ![]() 3)
3)
![]()
4) ![]() 4)
4)
![]()
5) ![]() 5)
5)
![]()
6) sin 3x = -3 6) cos 4x = -4
7) ![]() 7)
7)
![]()
8) ![]() 8)
8)
![]()
Вариант 3 Вариант 4
1) 5sin3x = 1 1) 2cos3x = -1
2) tg (x+5) = 0 2) ctg (x-4) = 0
3) ![]() 3)
3)
![]()
4) ![]() 4)
4)
![]()
5) ![]() 5)
5)
![]()
6) cos 2x = 2 6) cos 3x = -5
7) ![]() 7)
7)
![]()
8) ![]() 8)
8)
![]()
Самостоятельная работа № 15 (10 класс)
«Решение тригонометрических уравнений»
Вариант 1 Вариант 2
1) 3cos2x+10cos x = -3 1) 2 sin2 x+5 sinx + 2 = 0
2) ![]() 2)
2)
![]()
3) 2cos25x - 1 = sin5x 3) ![]()
4) tg x+3ctg x=4 4) tg x - 4ctg x = 3
5) ![]() 5)
5)
![]()
6) sin2 x+14sin x cos x = 15cos2x 6) cos2x-12 sin x cos x = 13 sin2 x
7) ![]() 7)
7)
![]()
8) cos 7x+cos x = 0 8) sin 7x = sin x
9) sin x - cos x = 1 9) sin x + cos x = 1
Вариант 3 Вариант 4
1) 2 + cos2 x = 2sin x 1) 3 - 3cos x =2 sin2 x
2) cos2 2x + 5 cos2x = 2 sin
22x 2) ![]()
3) ![]() 3)
3)
![]()
4) 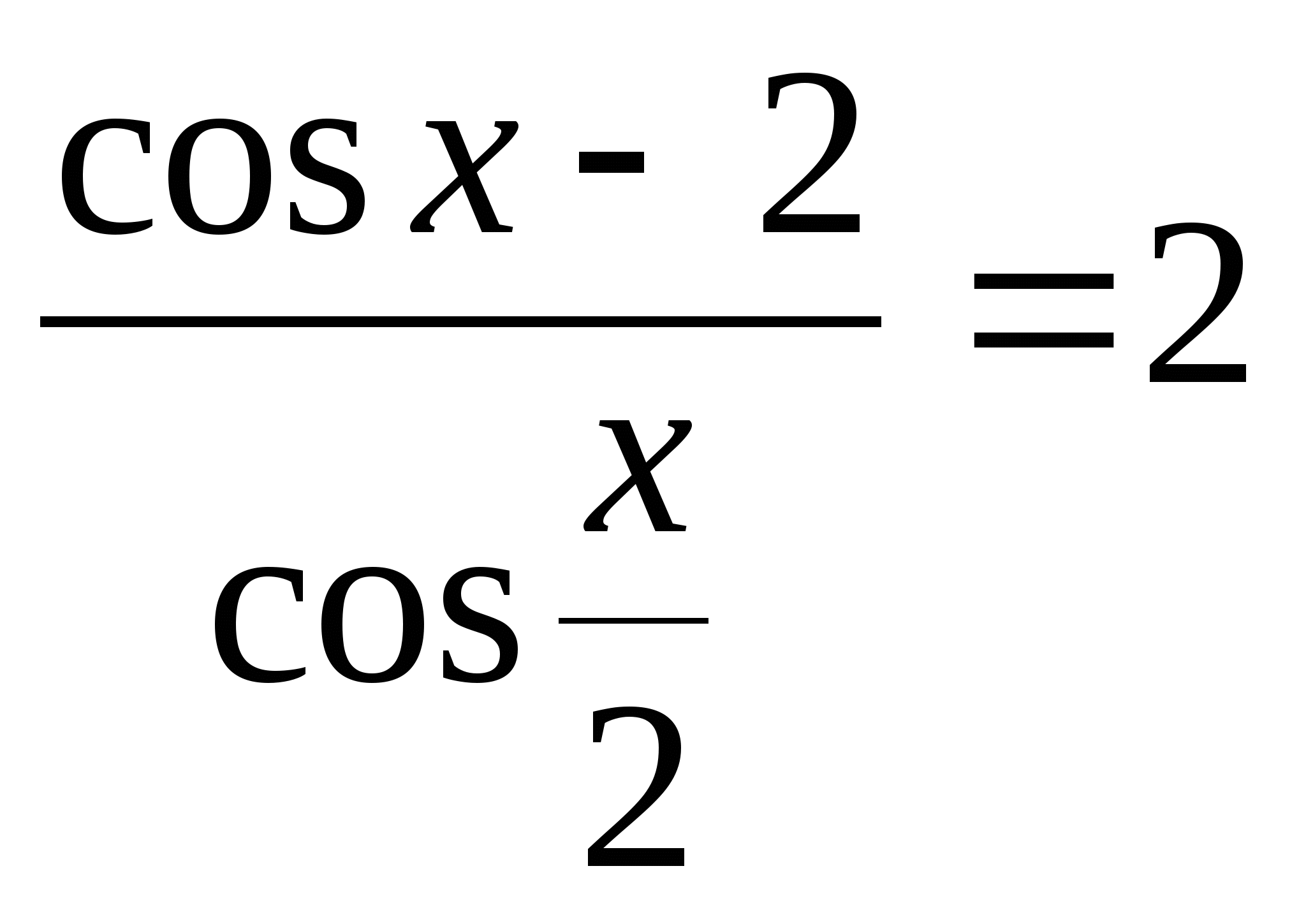 4)
4)
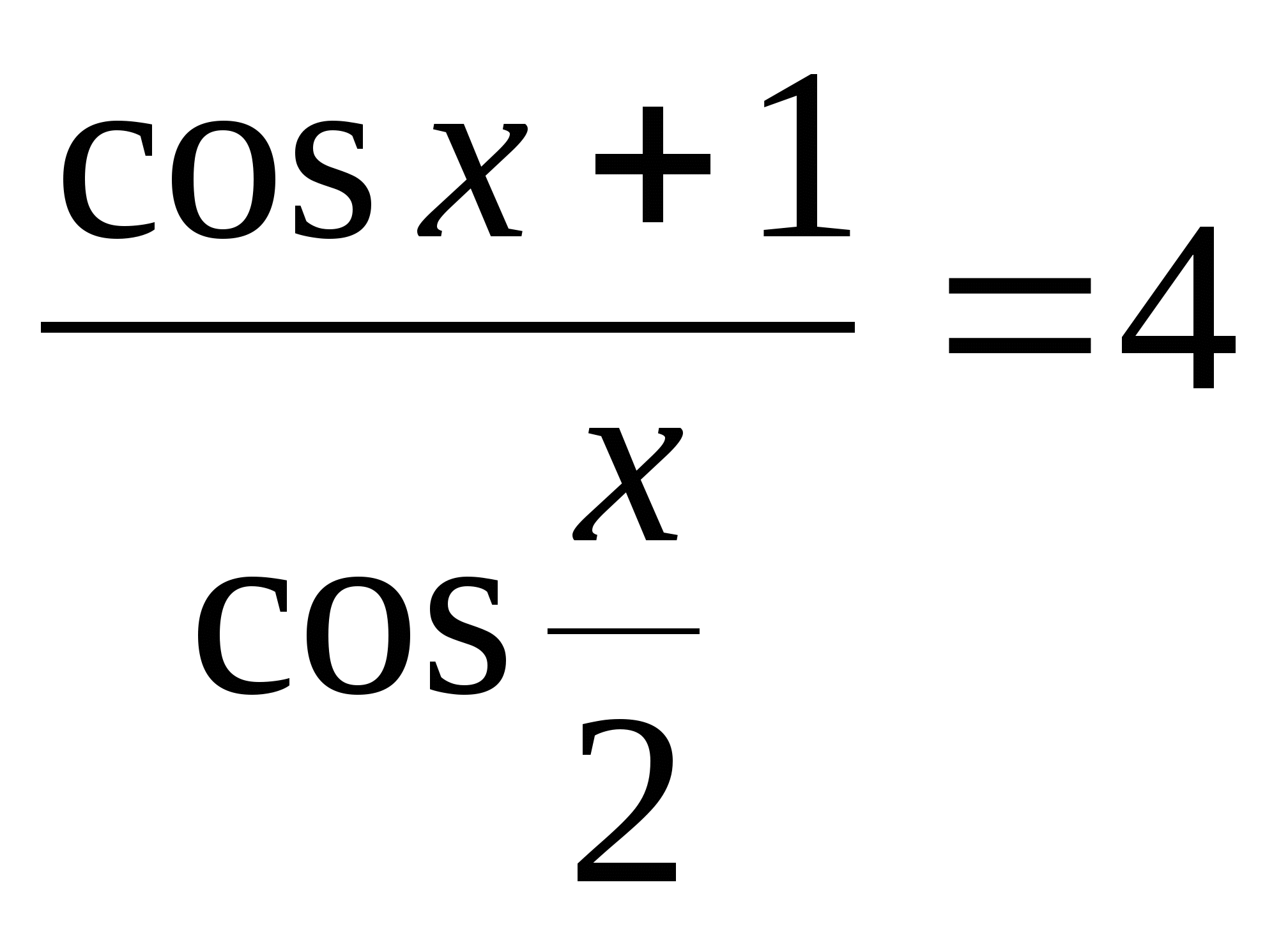
5) 2 sin22x + 3 cos2 2x = 2,5 sin 4x 5) 3sin2x + 8cos2x = 7
6) 6sin2 x = 4 + sin2x 6) 3sin 2x + 8 cos2 x = 0
7) cos x = cos 5x 7) sin x+ sin 5x = 0
8) sin x - 2 cos x = 2 8) sin x + 2 cos x = -2
9) ![]() 9)
9)
![]()
Самостоятельная работа № 15 (10 класс)
«Решение тригонометрических уравнений»
Вариант 1 Вариант 2
1) ![]() 1)
1)
![]()
2) ![]() 2)
2)
![]()
3) ![]() 3)
3)
![]()
4) ![]() 4)
4)
![]()
5) ![]() 5)
5)
![]()
6) ![]() 6)
6)
![]()
7) ![]() 7)
7)
![]()
8) ![]() 8)
8)
![]()
9) ![]() 9)
9)
![]()
Вариант 3 Вариант 4
1) ![]() 1)
1)
![]()
2) ![]() 2)
2)
![]()
3) ![]() 3)
3)
![]()
4) 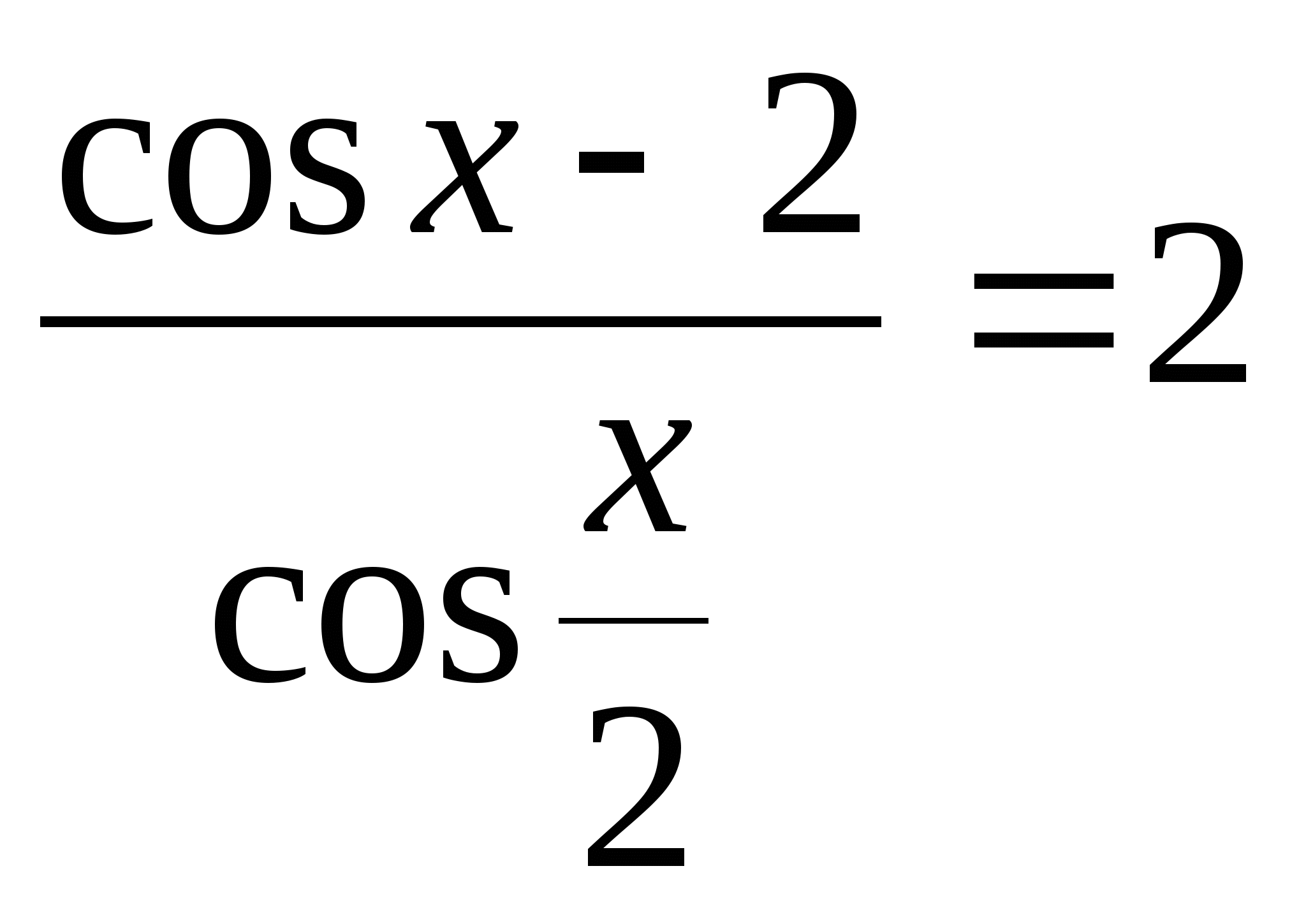 4)
4)
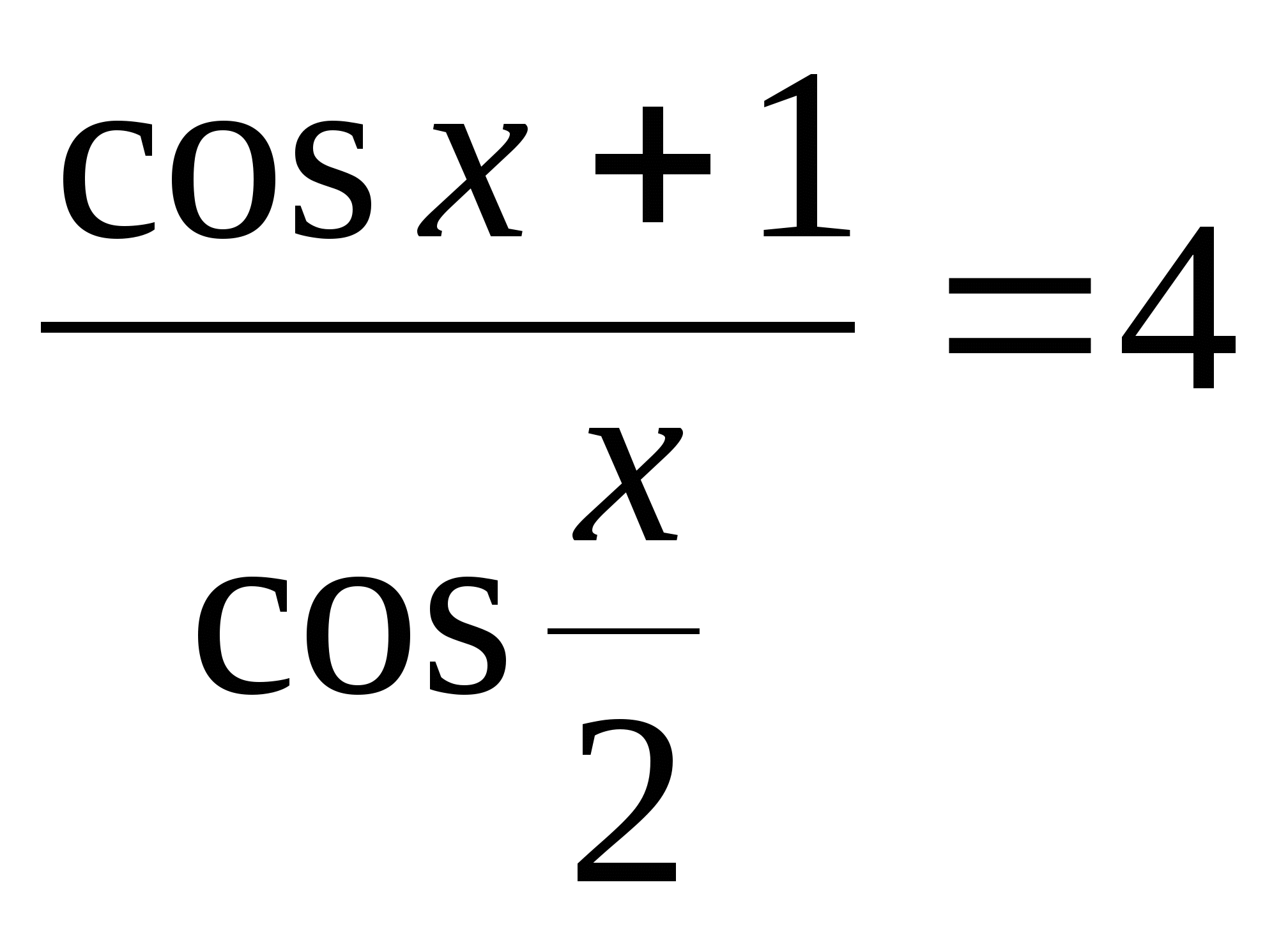
5) ![]() 5)
5)
![]()
6) ![]() 6)
6)
![]()
7) ![]() 7)
7)
![]()
8) ![]() 8)
8)
![]()
9) ![]() 9)
9)
![]()
Самостоятельная работа № 16 ( 10 класс)
«Тригонометрические неравенства»
Вариант 1 Вариант 2
1) 2 sin x -1 1) ![]()
2) 2 cos x 1 2) ![]()
3) ![]() 3)
3)
![]()
4) sin 2x -1 4) cos 2x 1
5) ![]() 5)
5)
![]()
6) ![]() 6)
6)
![]()
Вариант 3 Вариант 4
1) 2 sin x -1 1) ![]()
2) ![]() 2)
2 sin x 1
2)
2 sin x 1
3) ![]() 3)
3)
![]()
4) ![]() 4)
cos 3x -1
4)
cos 3x -1
5) ![]() 5)
5)
![]()
6) ![]() 6)
6)
![]()
Самостоятельная работа № 17 (10 класс)
«Решение тригонометрических систем уравнений»
Вариант 1 Вариант 2
1) 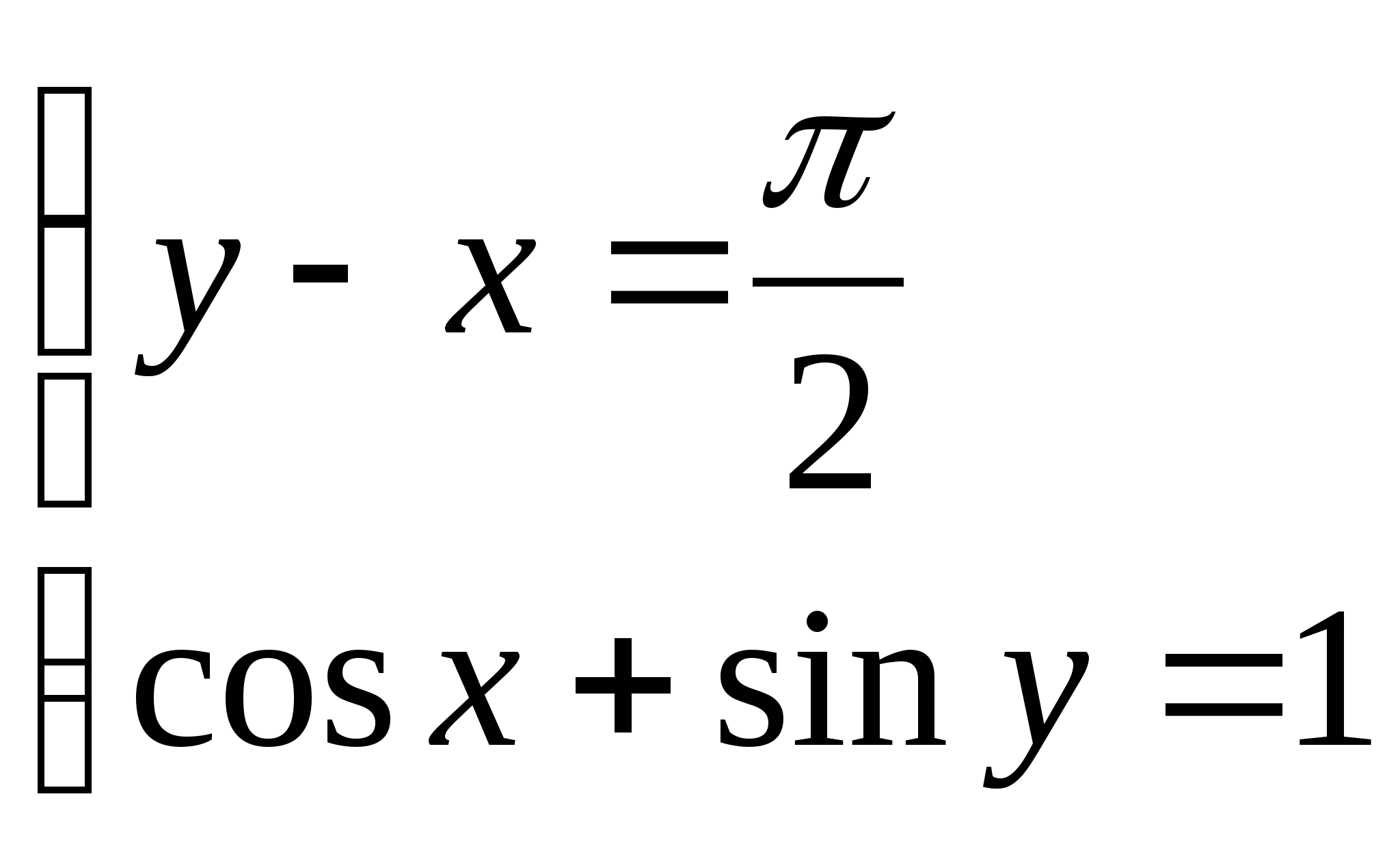 1)
1)
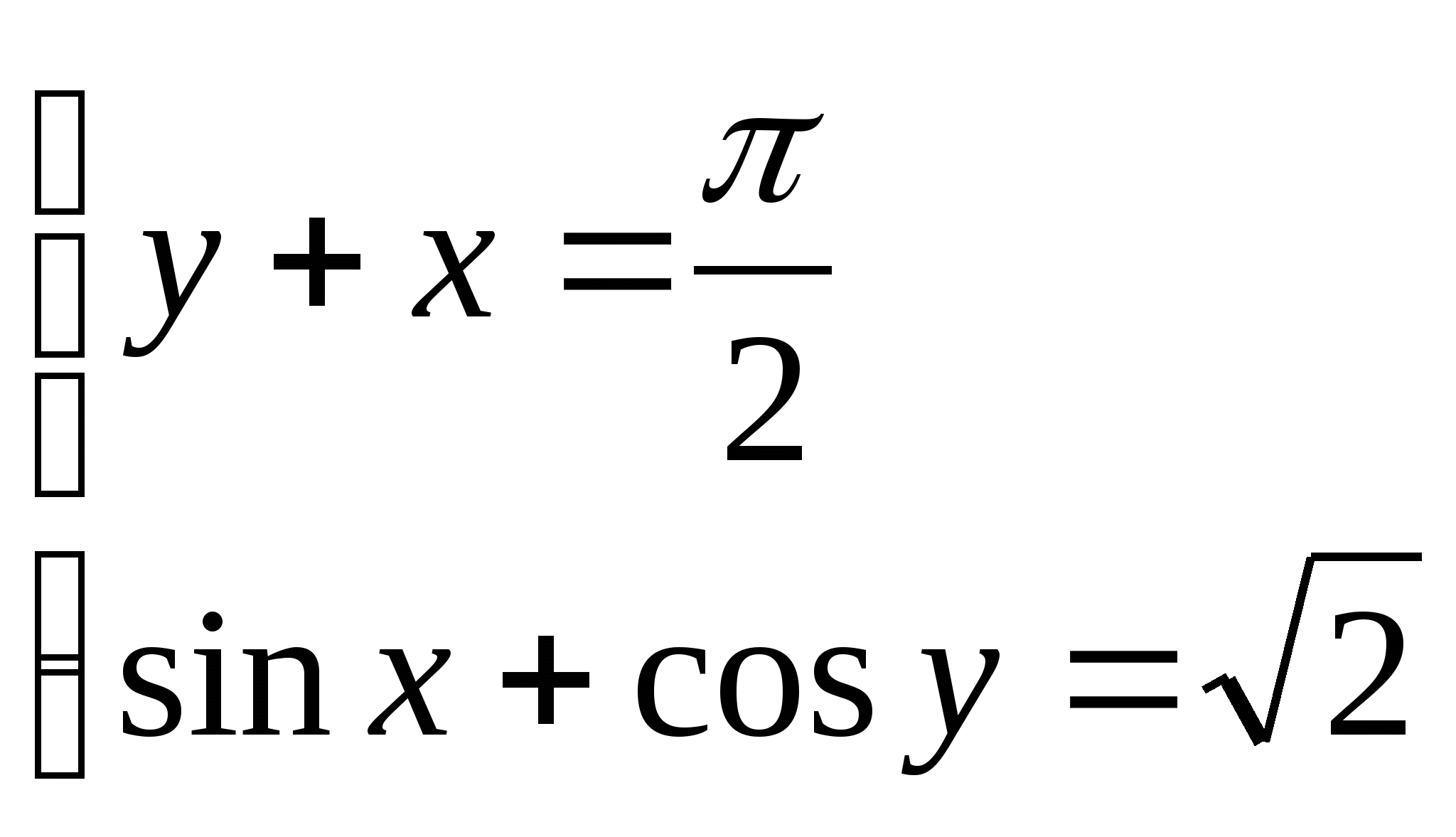
2) 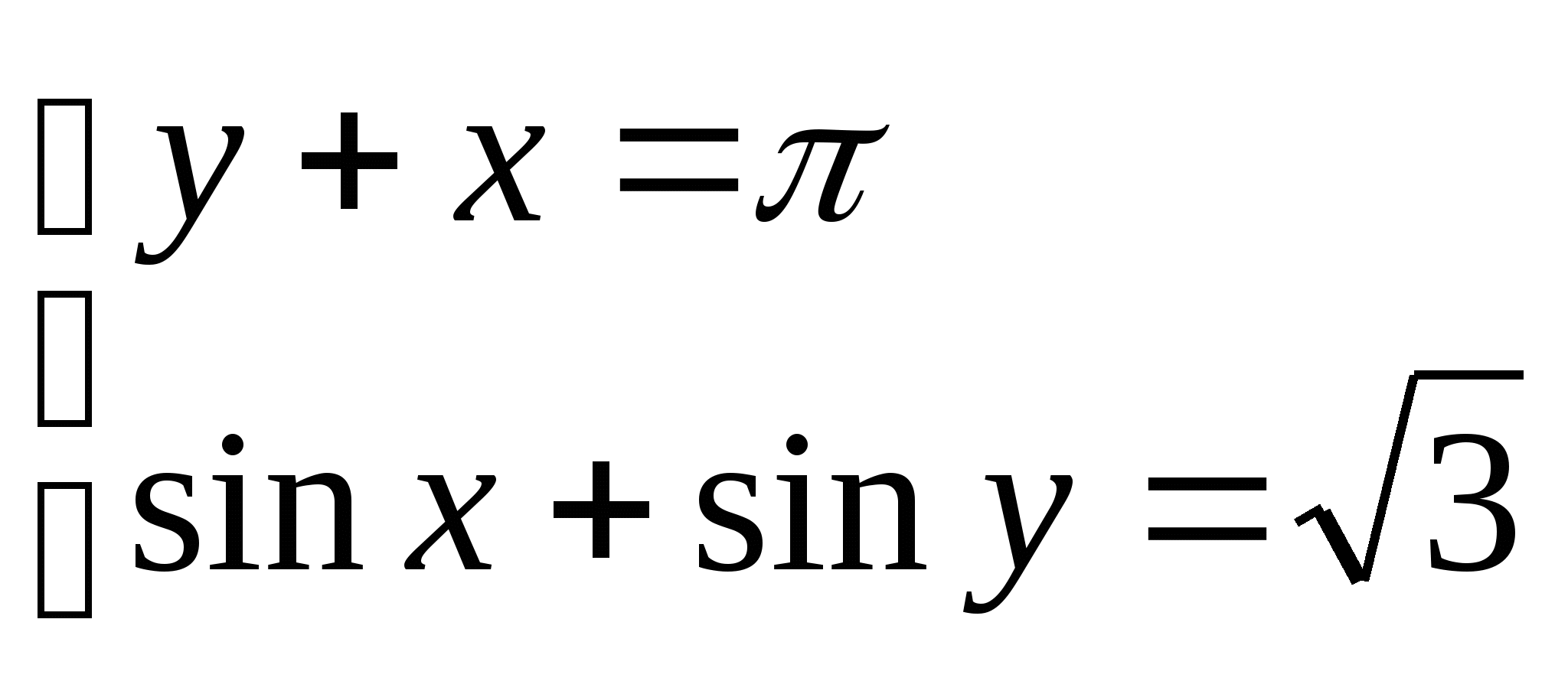 2)
2)
![]()
3) ![]() 3)
3)
![]()
4) 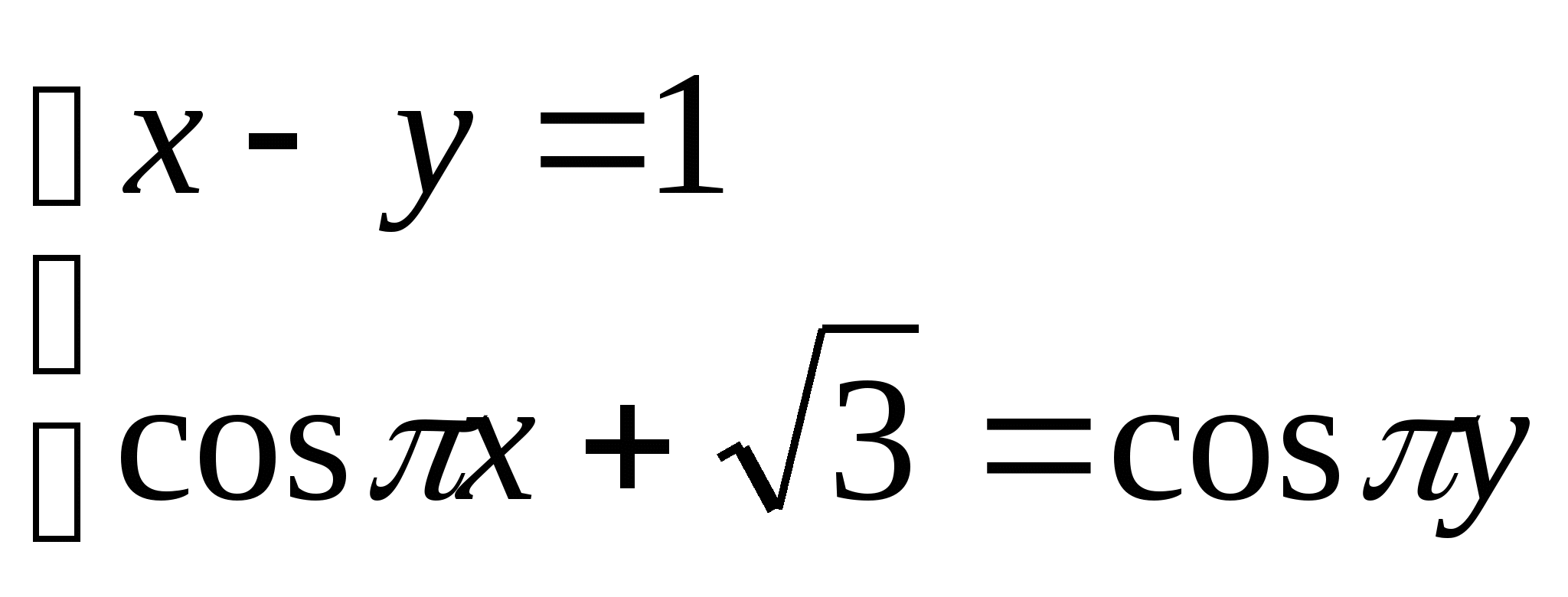 4)
4)
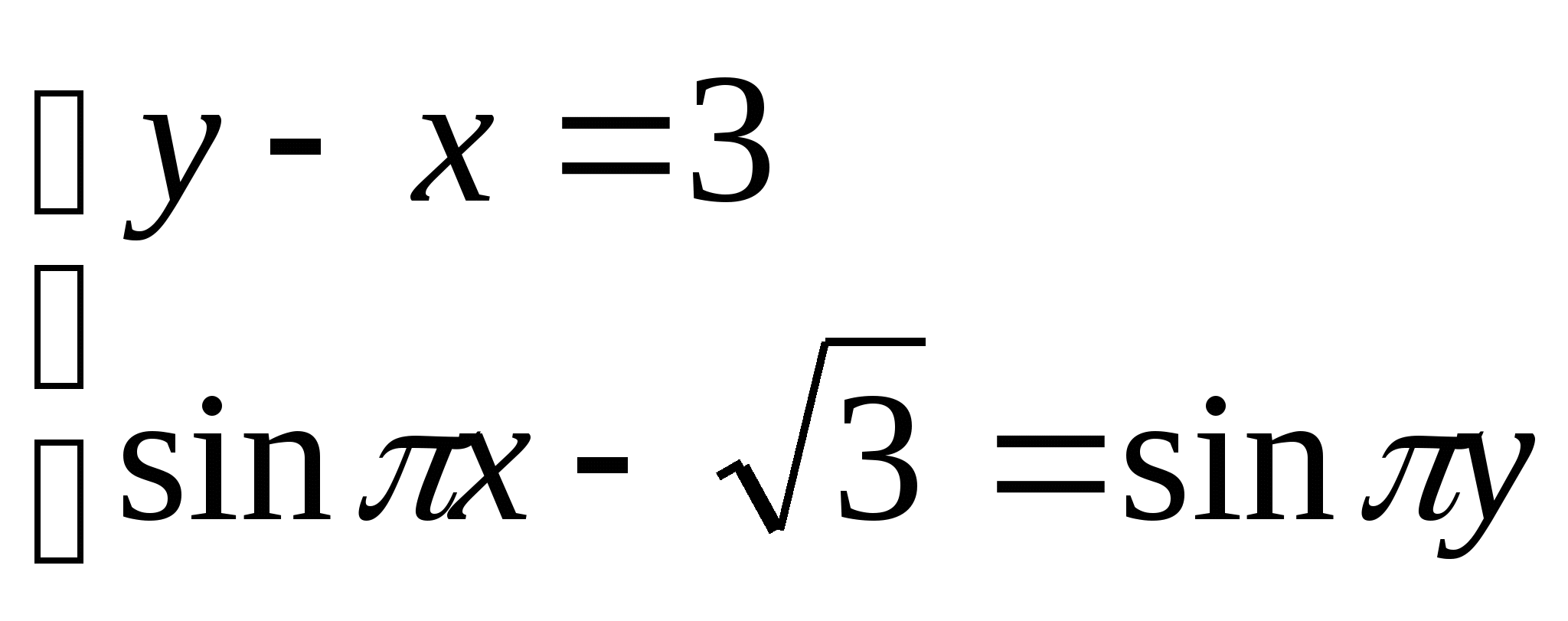
Вариант 3 Вариант 4
1) 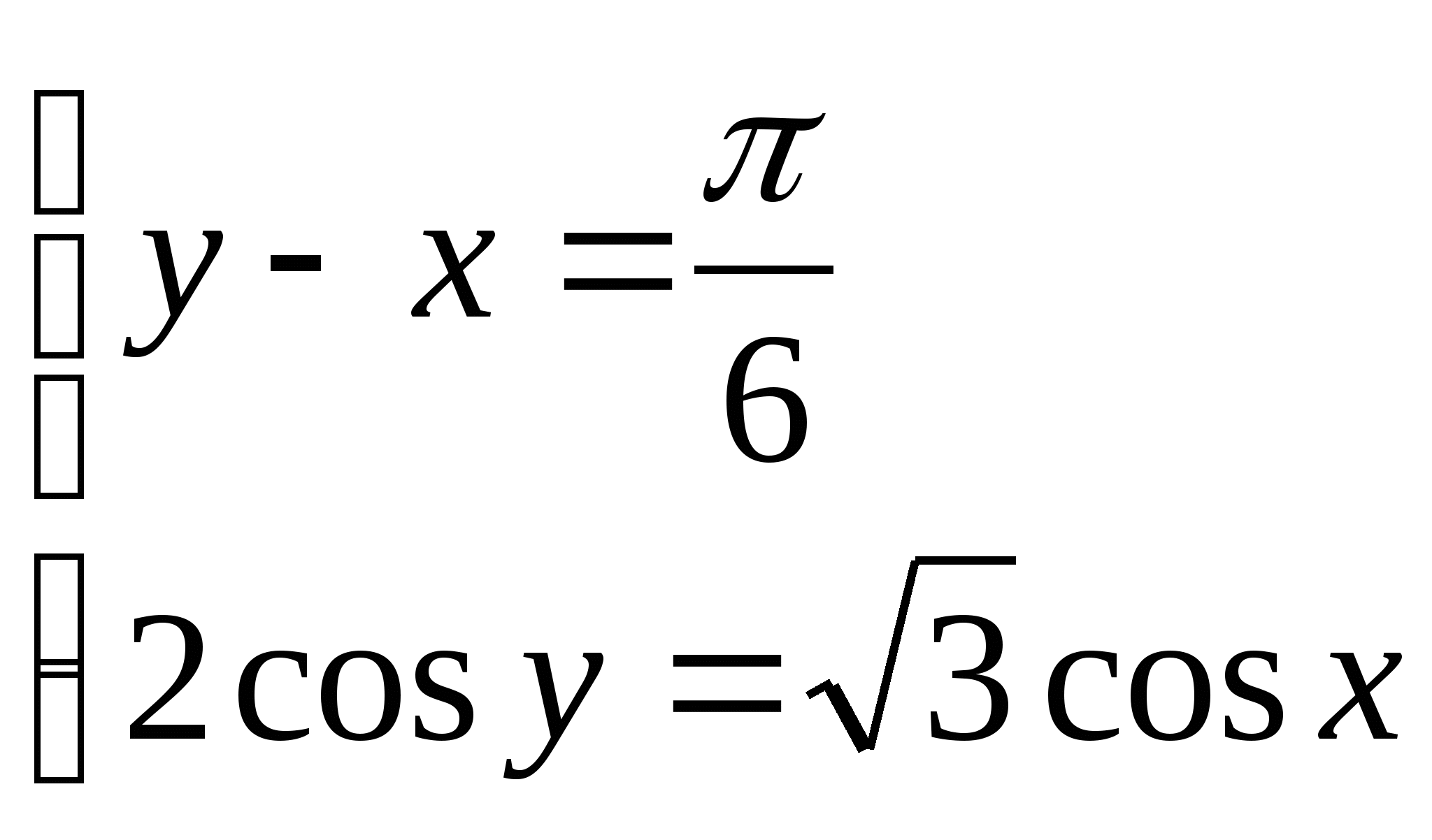 1)
1)
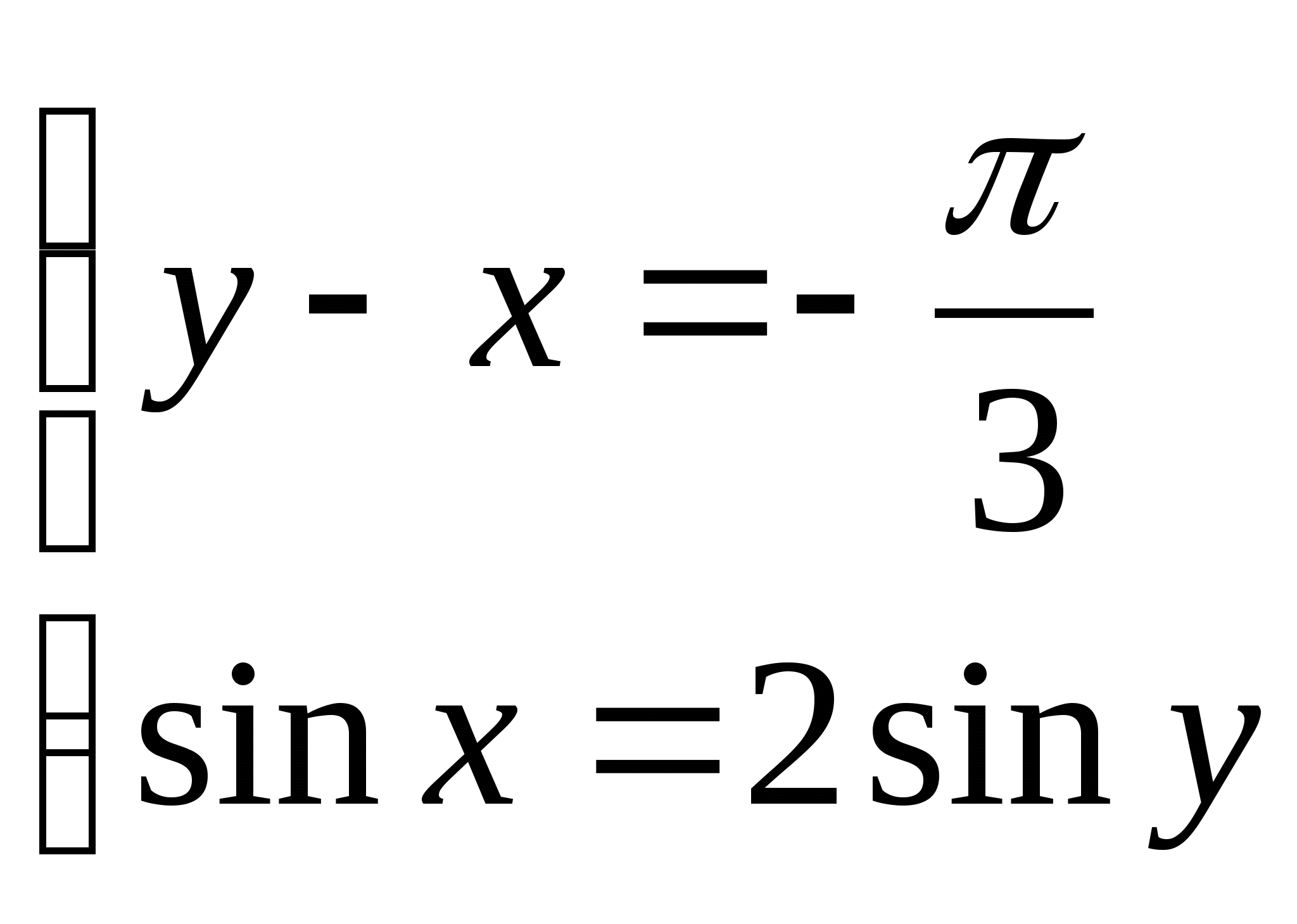
2) 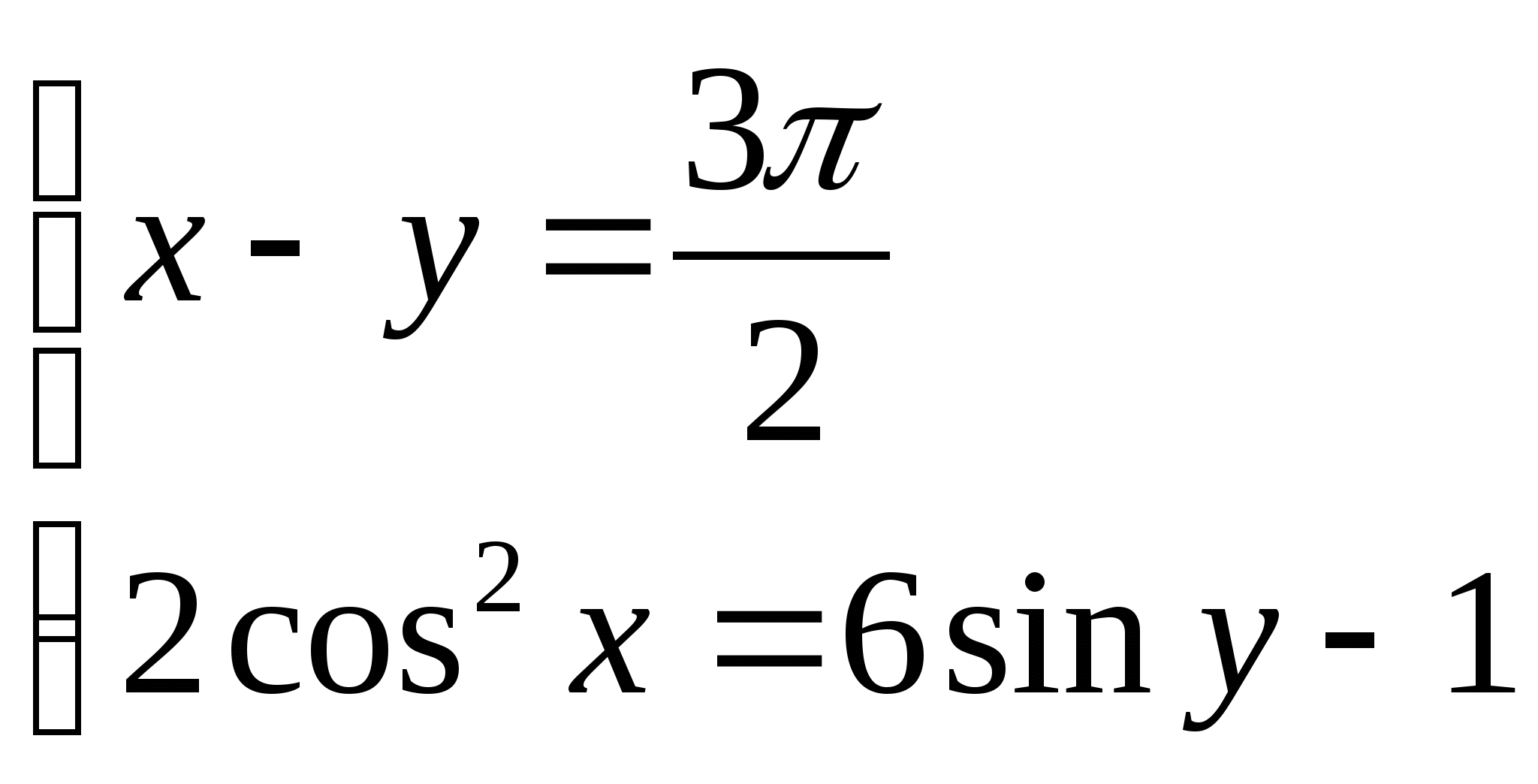 2)
2)
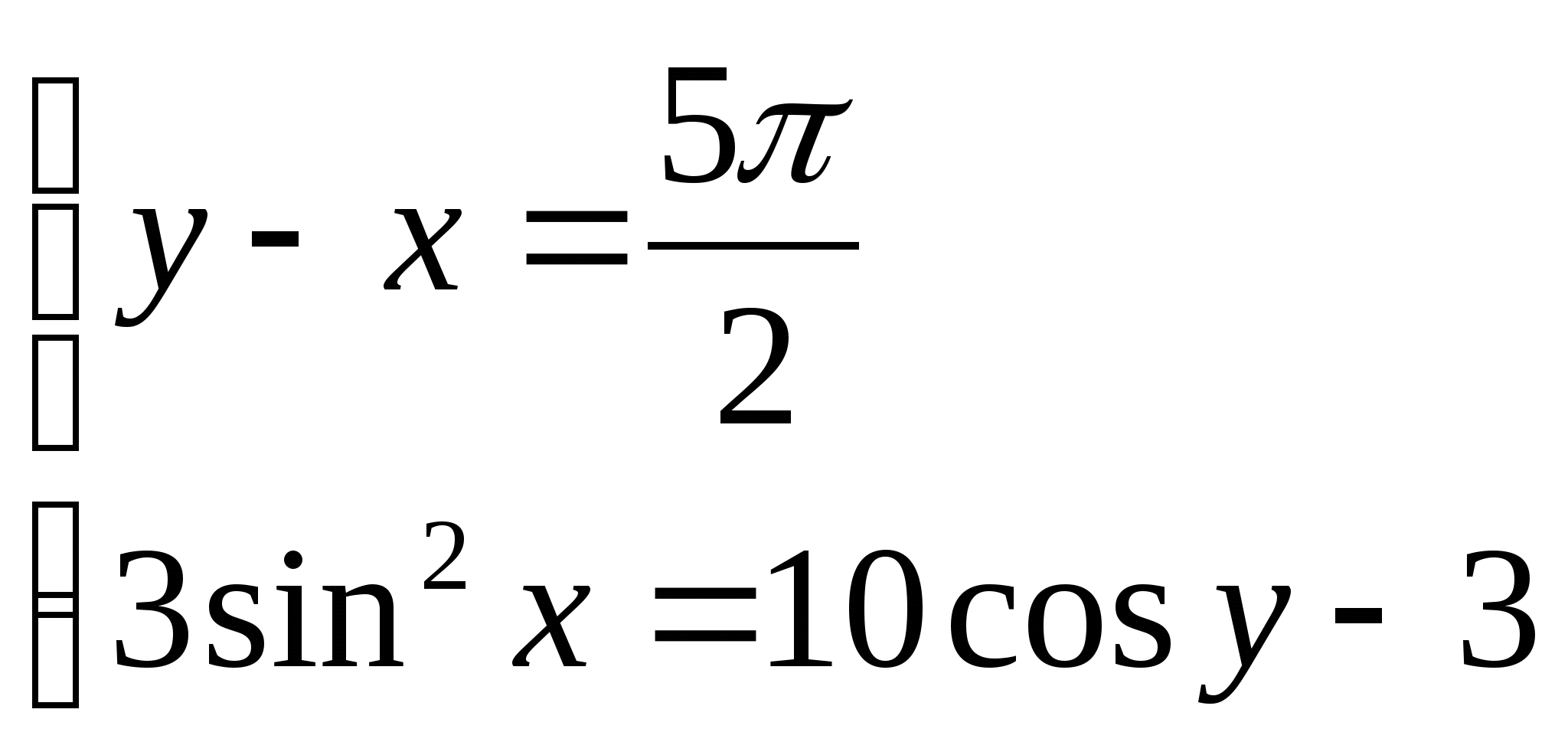
3) 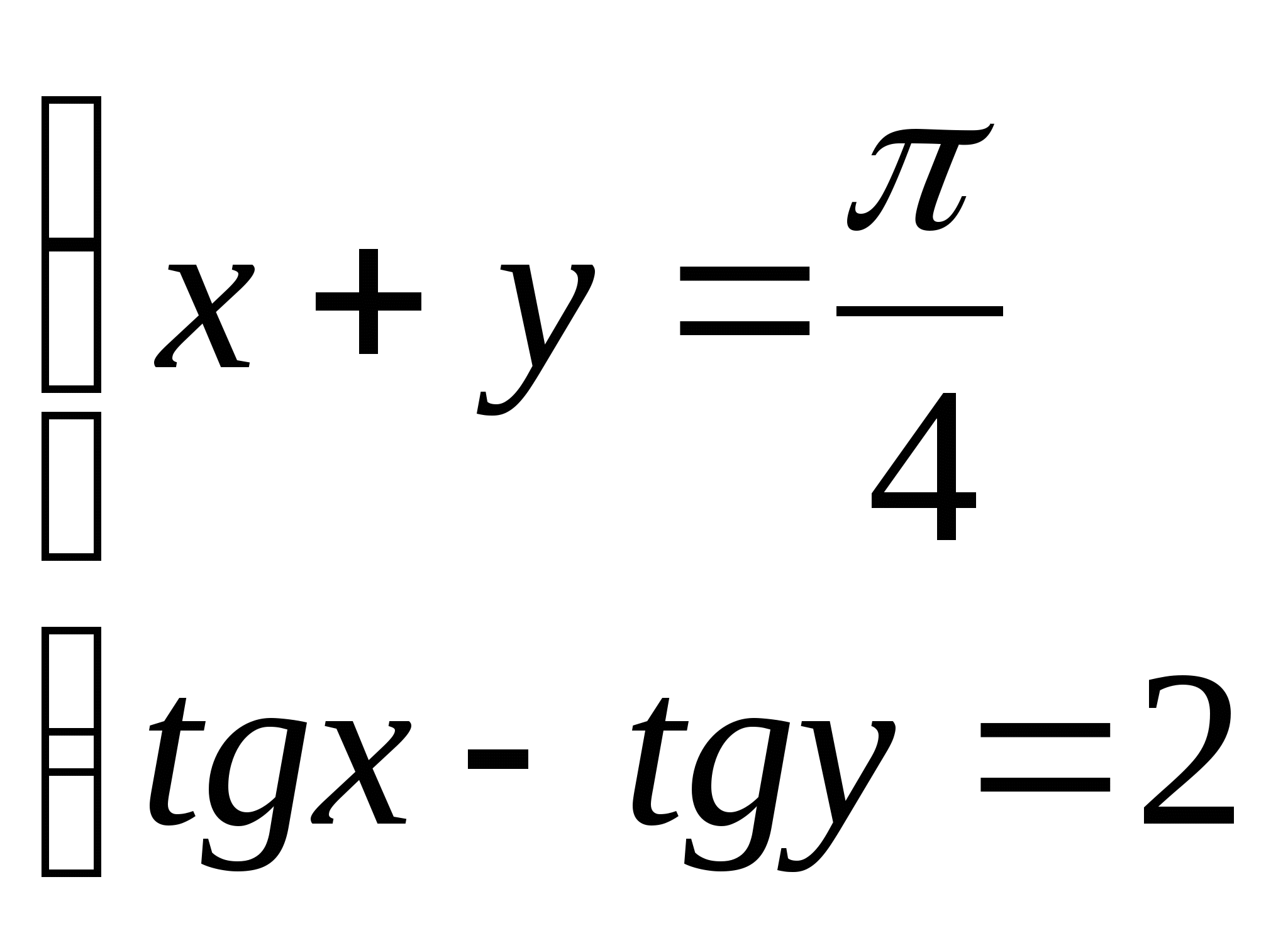 3)
3)
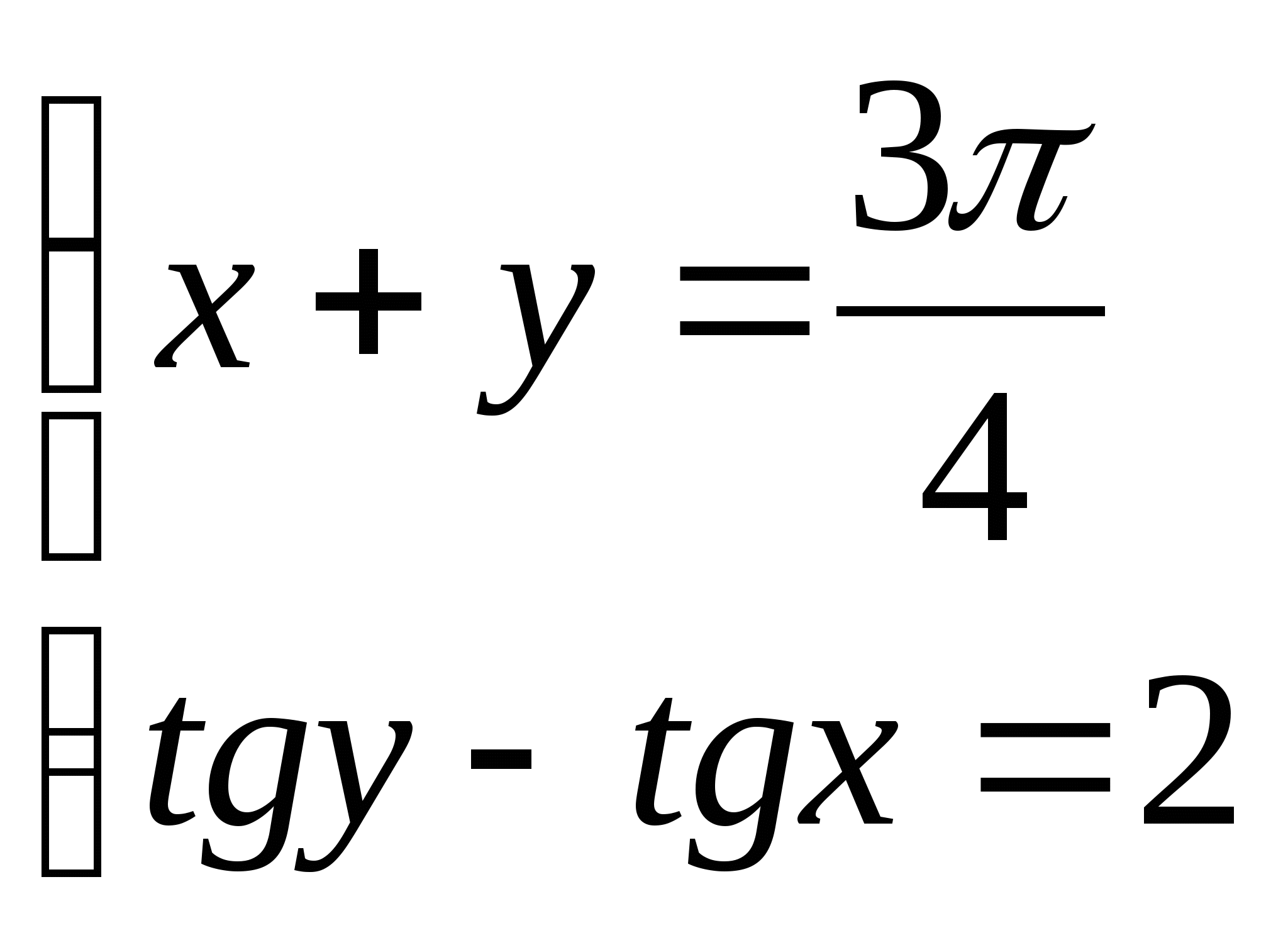
4) 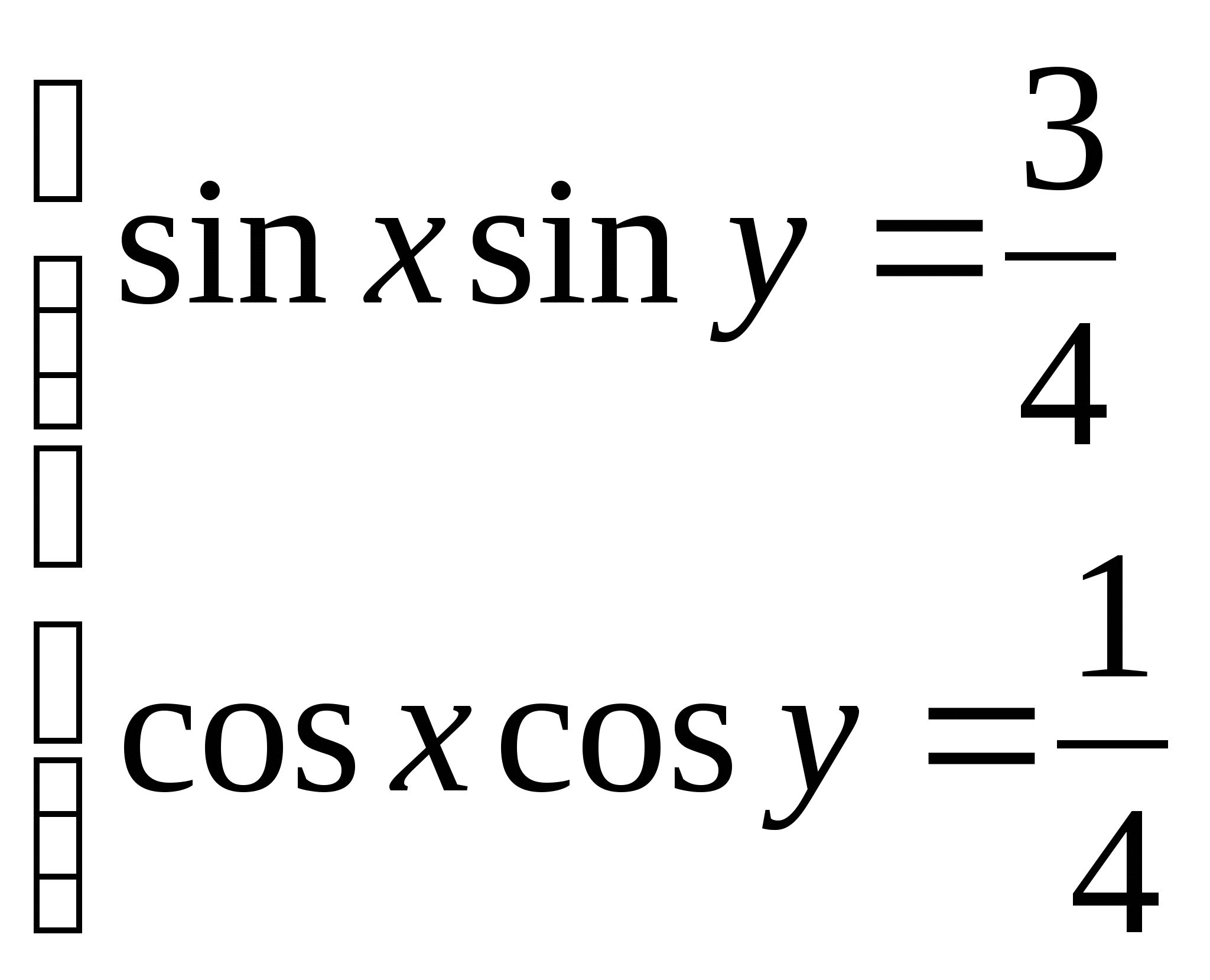 4)
4)
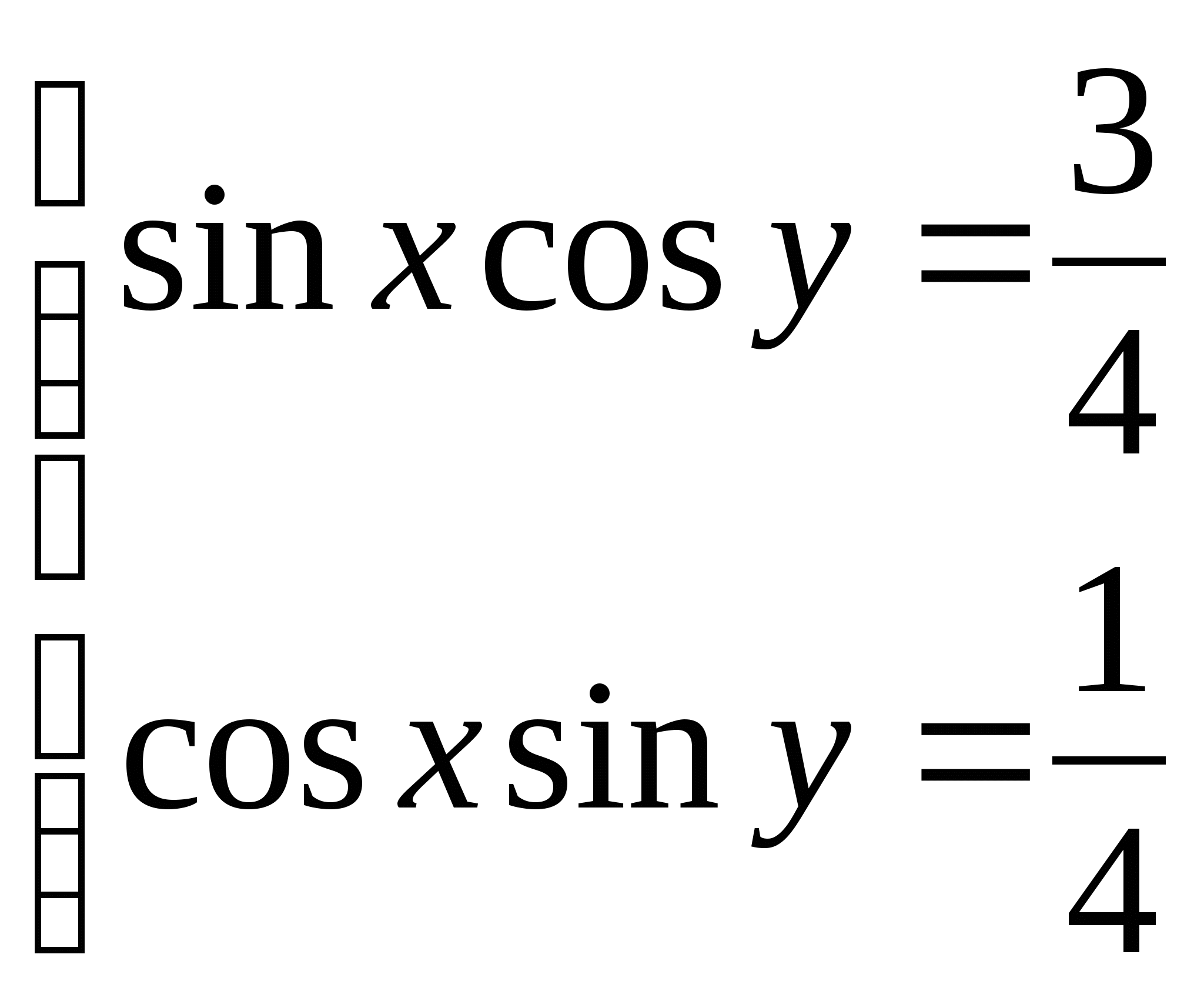
5) 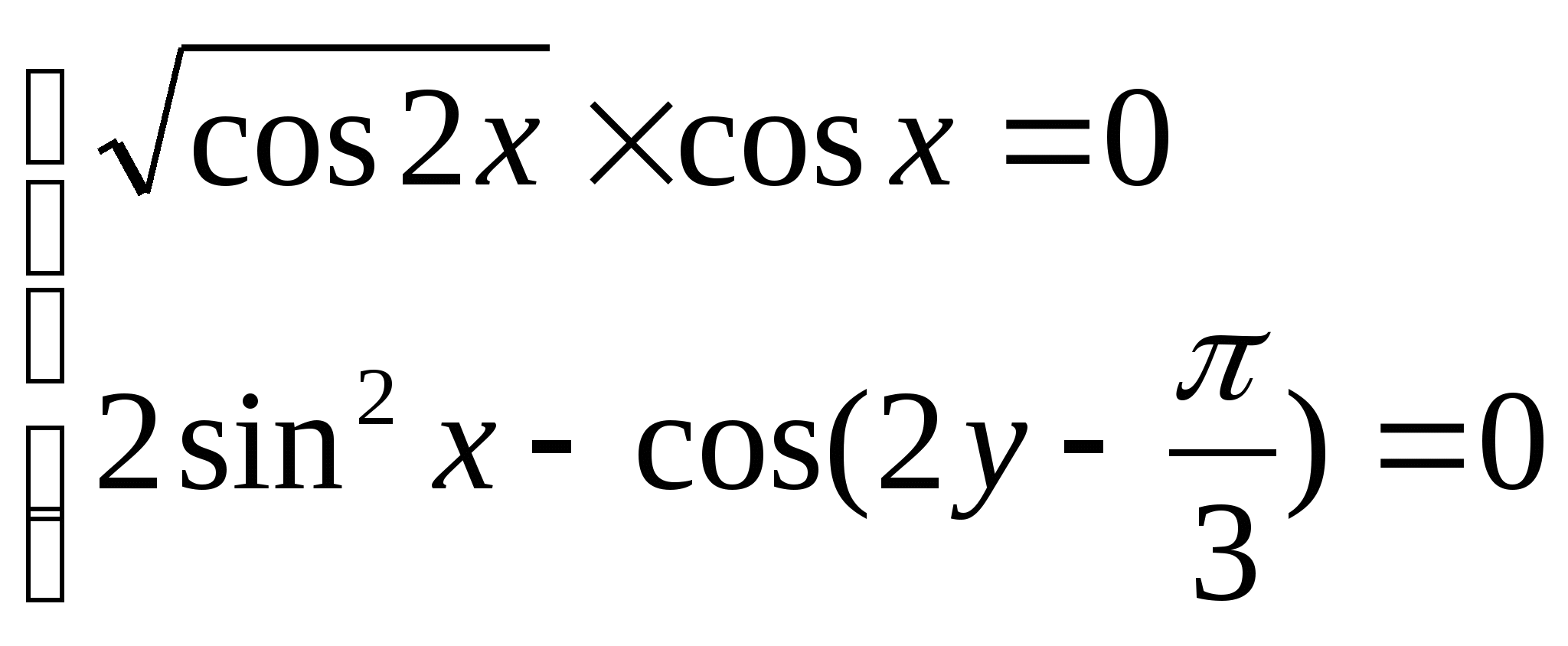 5)
5)
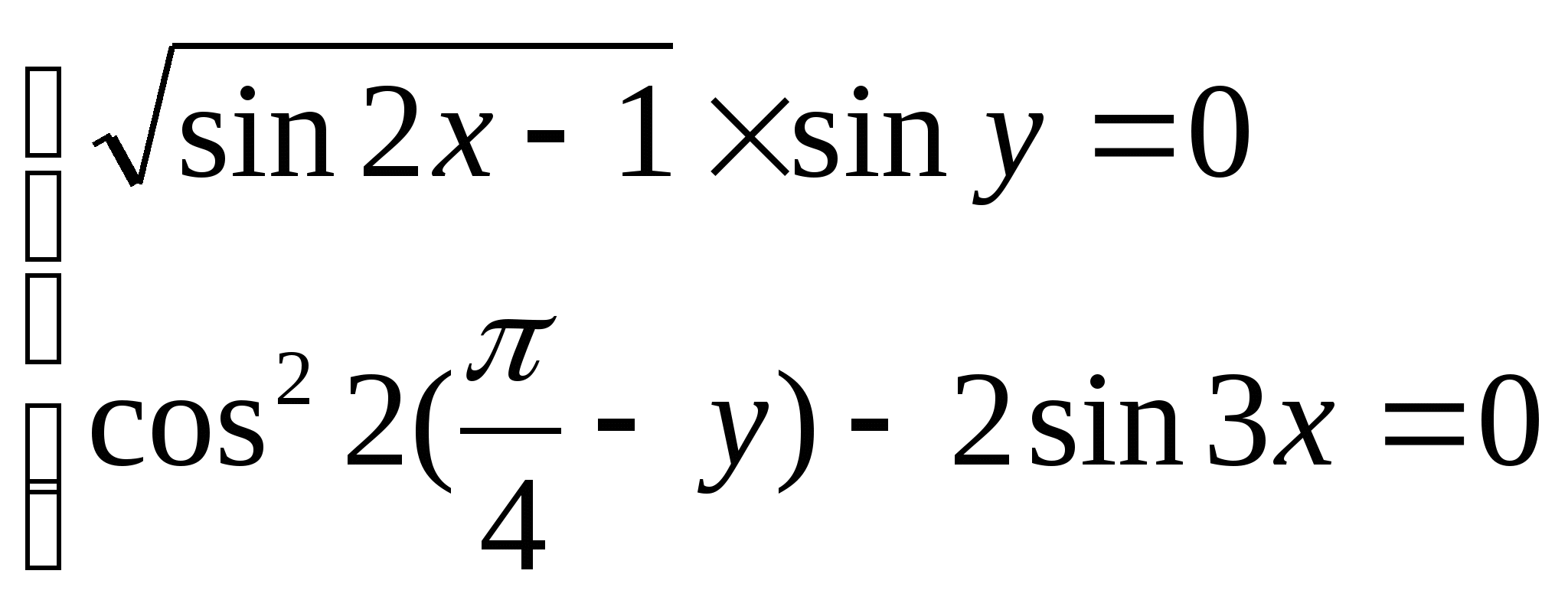
Итоговая контрольная работа (10 класс)
для подготовленных учащихся.
2 часа
а) - 1 вариант б) - 2 вариант
1) Вычислите:
а) ![]() Ответ: 8
Ответ: 8
б) ![]() Ответ: 5
Ответ: 5
2) Пусть (х0;у0) - решение системы. Найти х0 + у0
а) 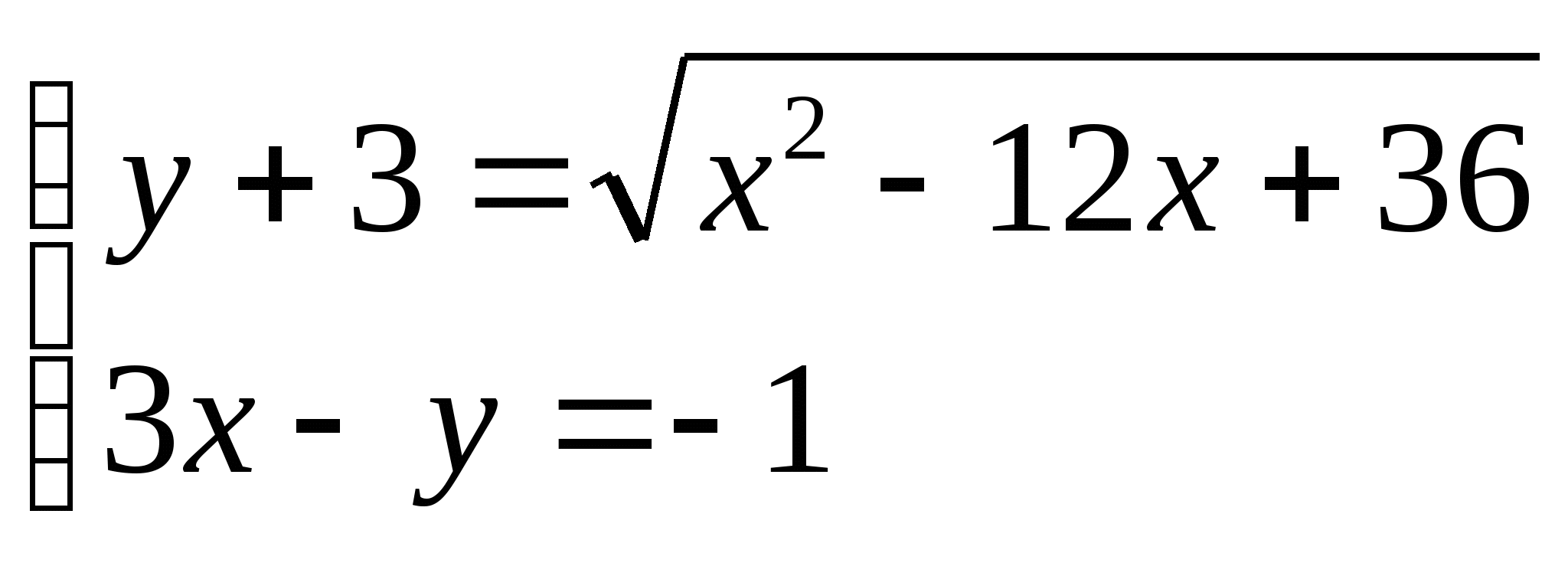 Ответ: 9
Ответ: 9
б) 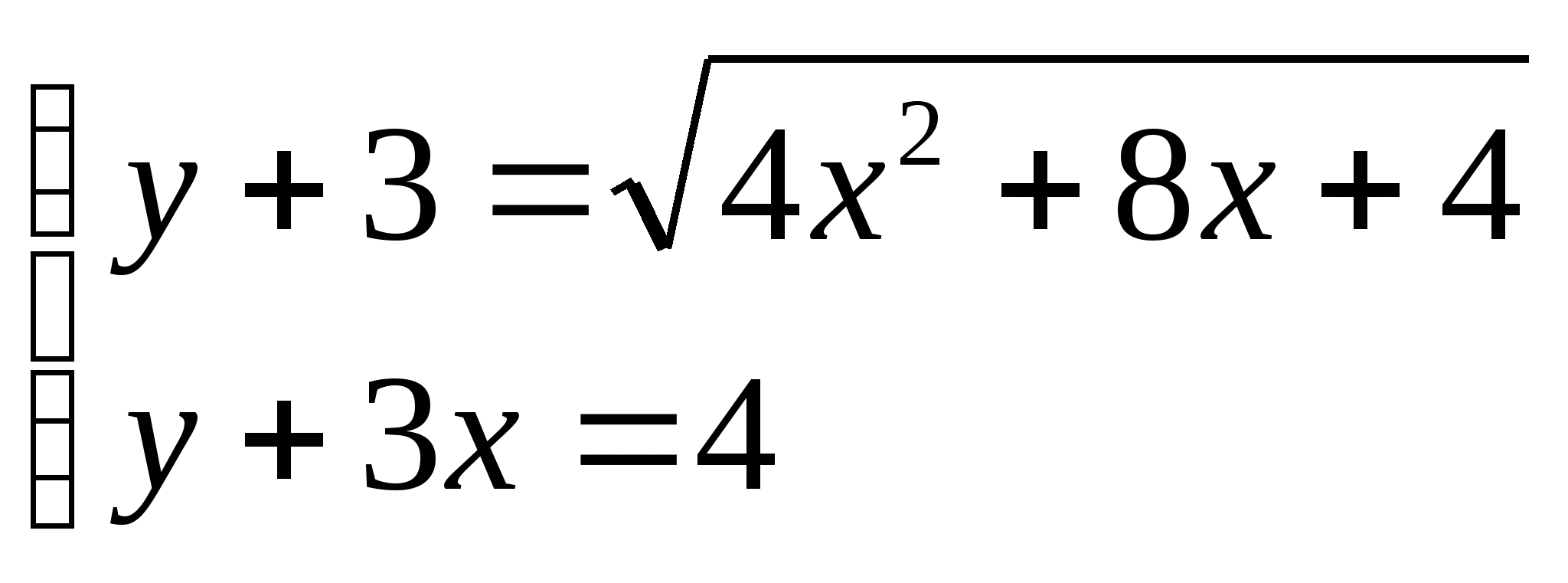 Ответ: 2
Ответ: 2
3) Решить уравнение. В ответе записать число корней уравнения.
а) ![]() Ответ: 5
Ответ: 5
б) ![]() Ответ: 4
Ответ: 4
4) Решить уравнение:
а) 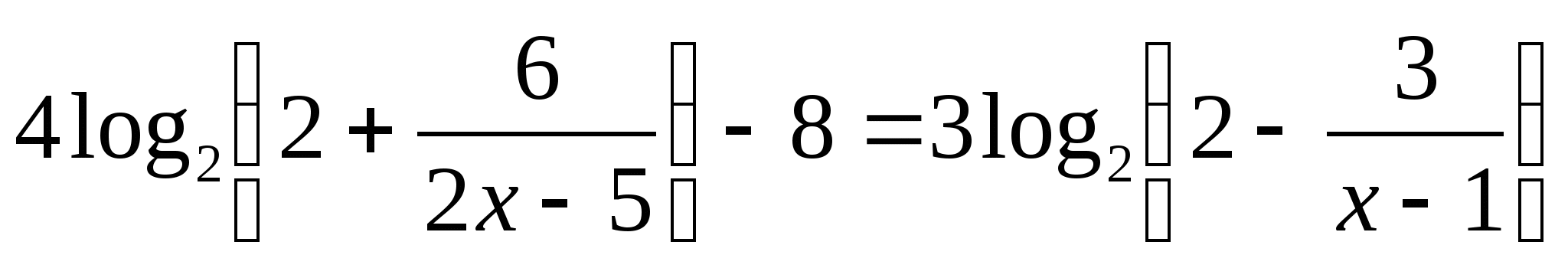 Ответ: 4
Ответ: 4
б) ![]() Ответ: -2
Ответ: -2
5) Решить уравнение:
а) ![]()
б) ![]()
6) Решить неравенство:
а) ![]()
б) ![]()
Контрольная работа по алгебре (10 класс)
«Тригонометрия»
8 из 13 - «3»
меньше 8 - «2»
Вариант 1 Вариант 2
1) Докажите тождество:
а) б)
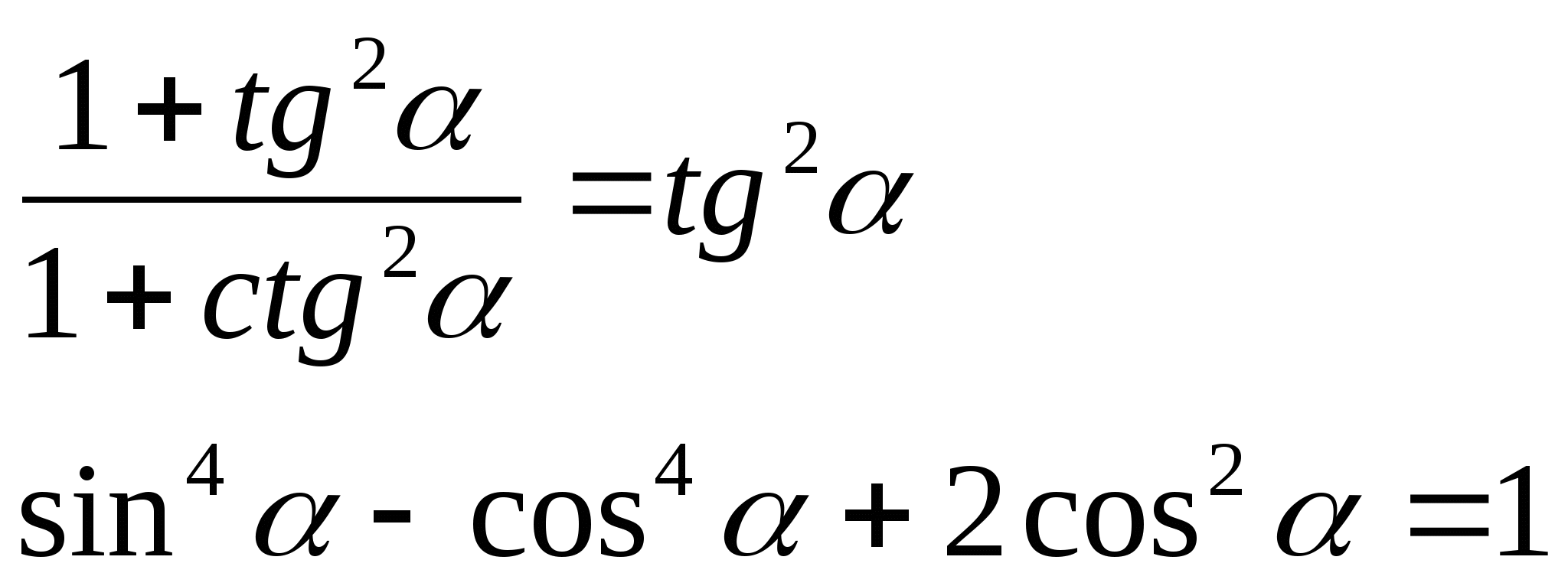
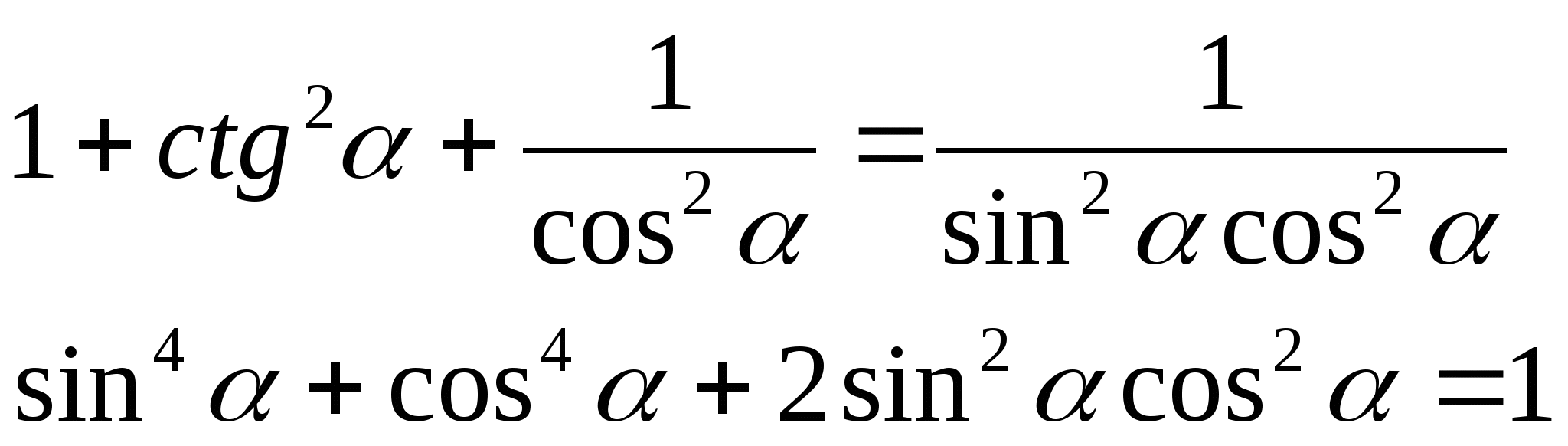
2) Вычислить:
а) б)
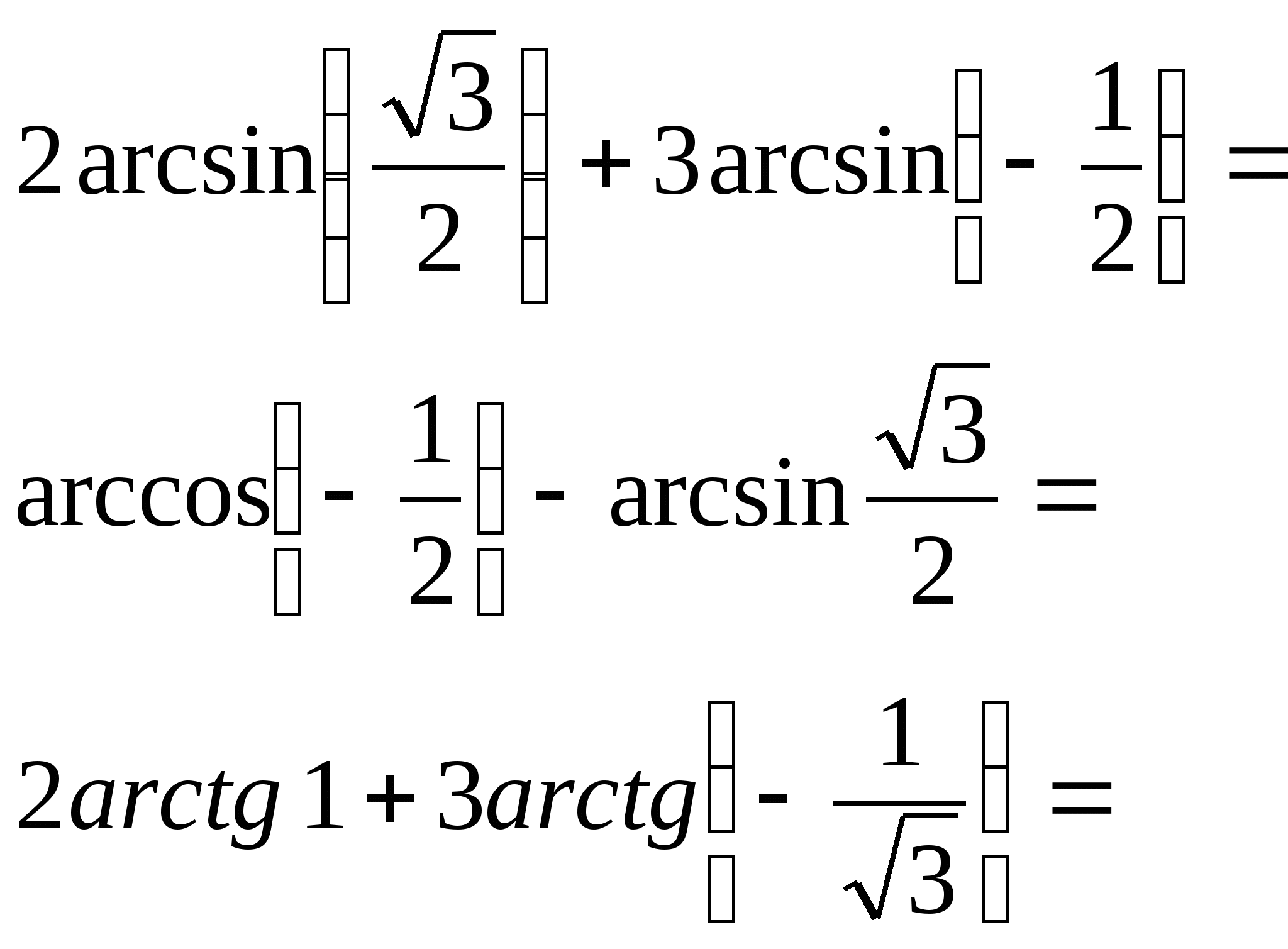
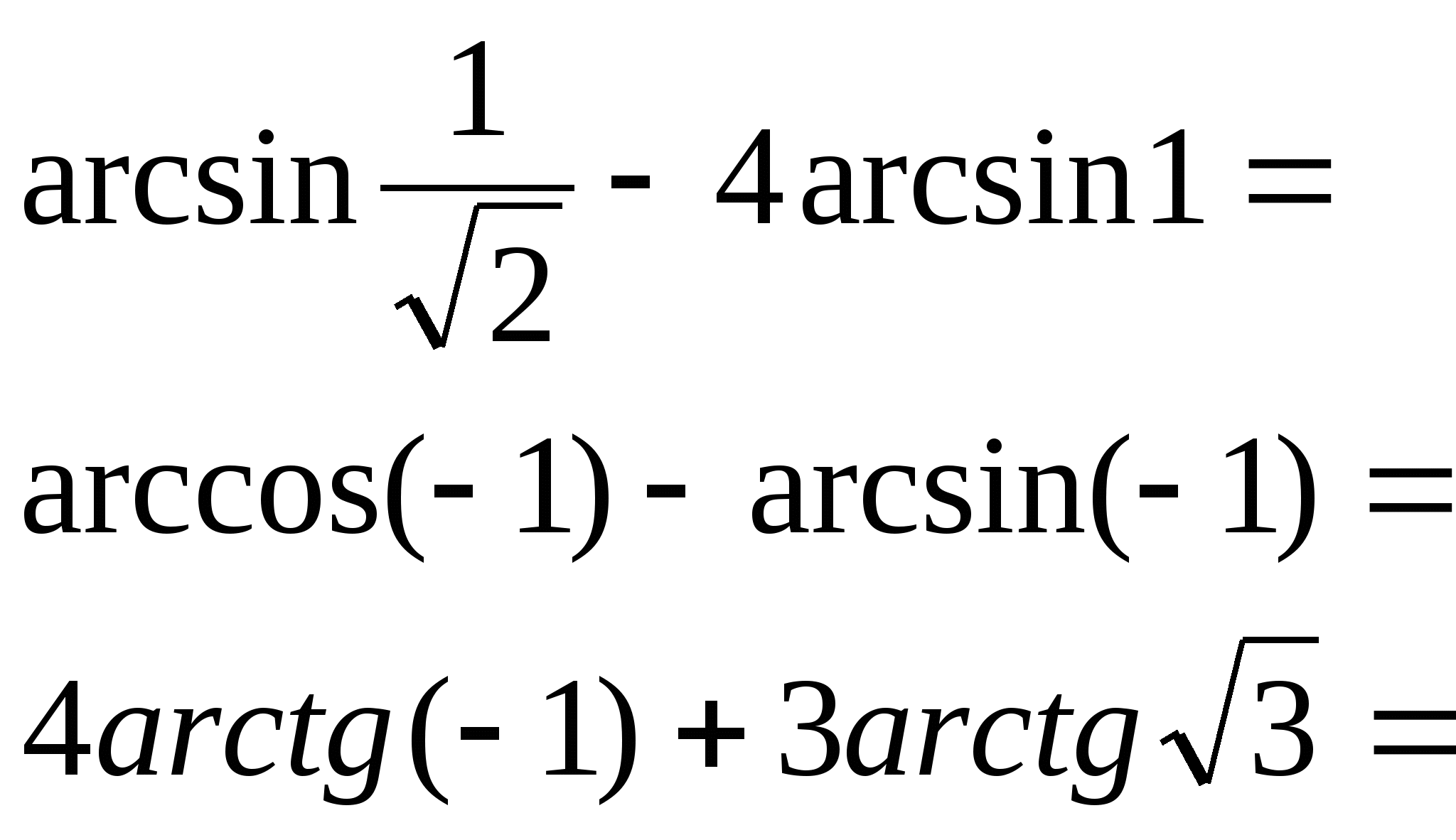
3) Решить уравнения:
а) б)
![]()
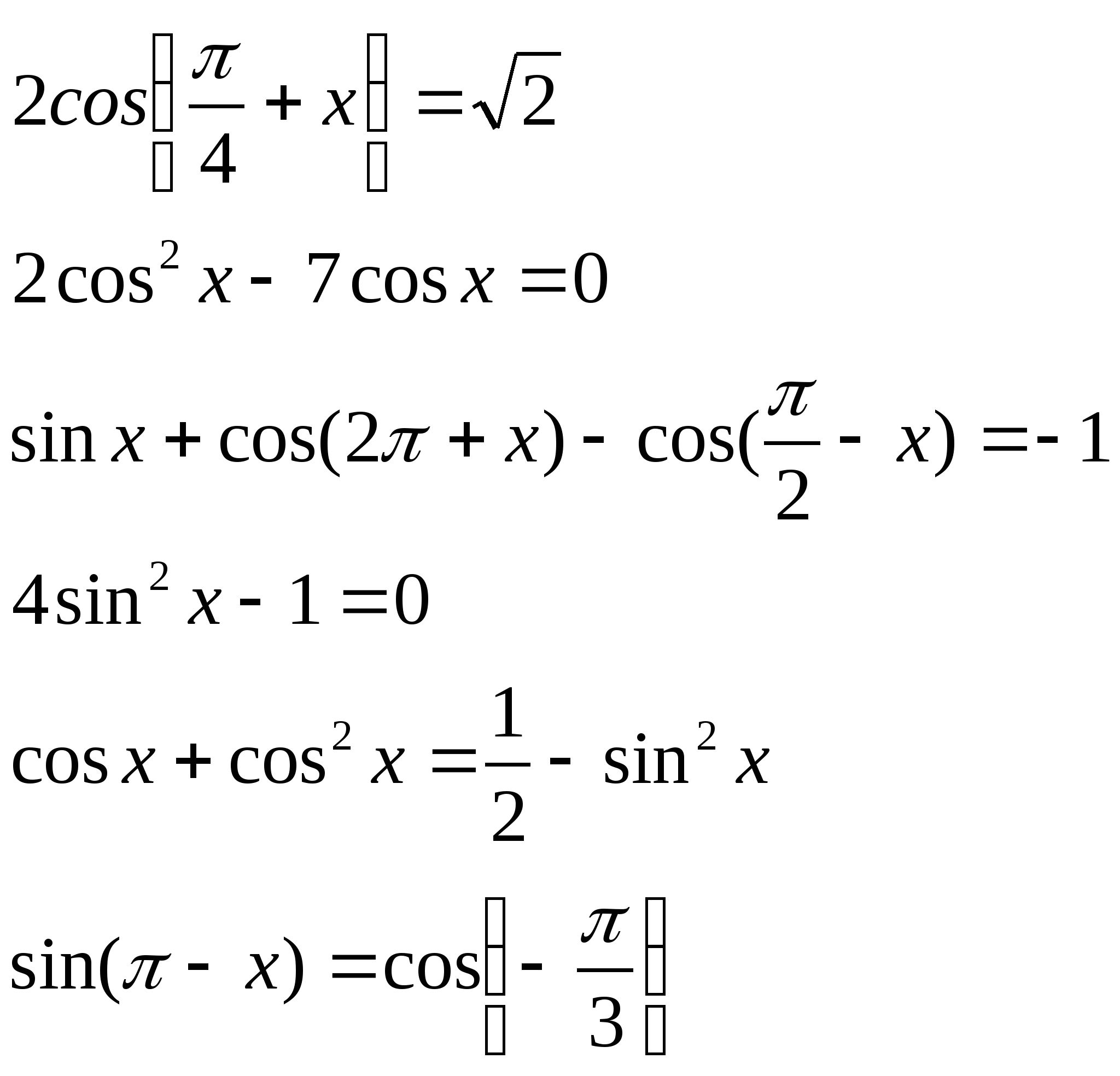
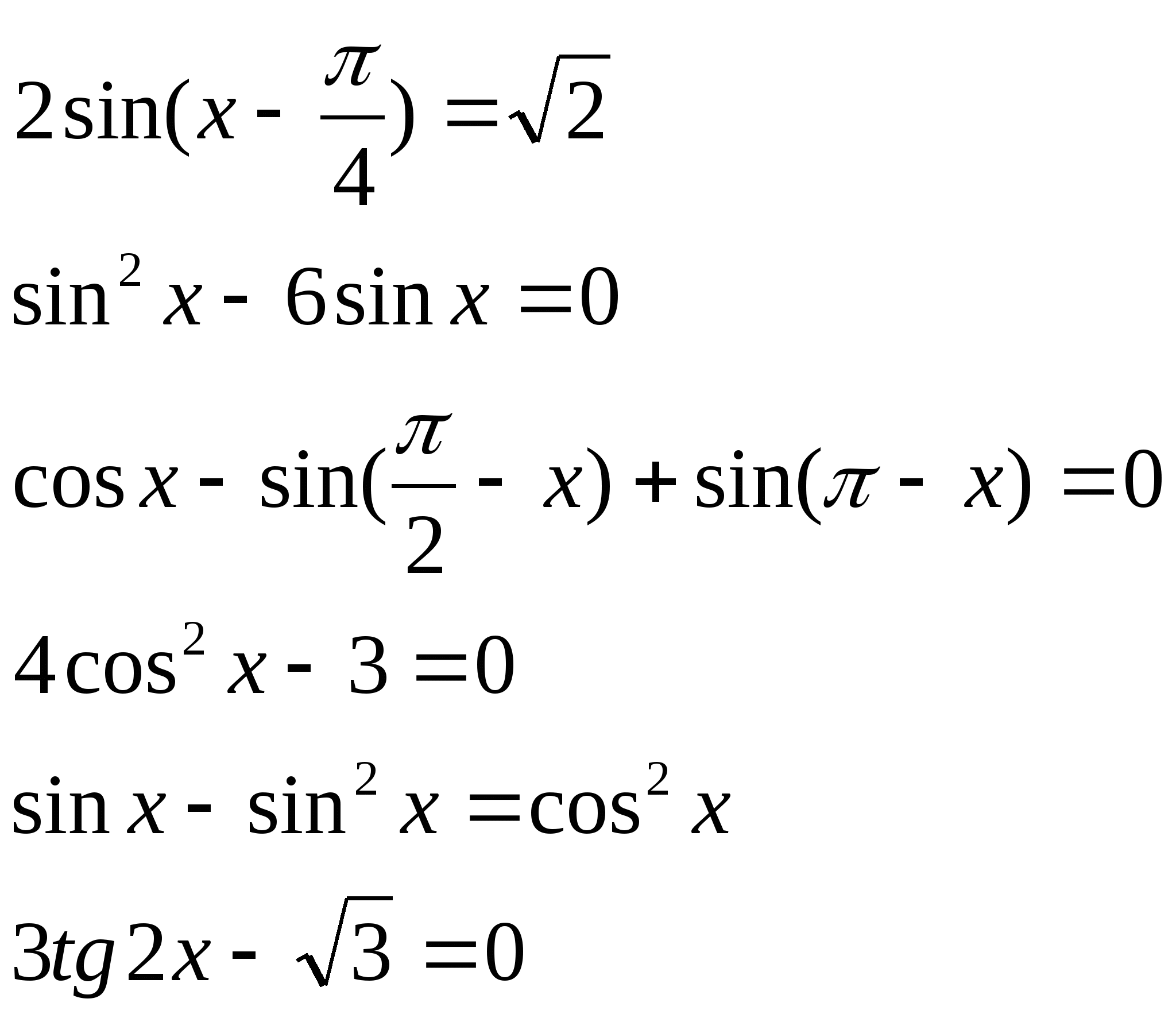
4) Найдите sin или cos, если
а) sin x = ? б) cos x =?
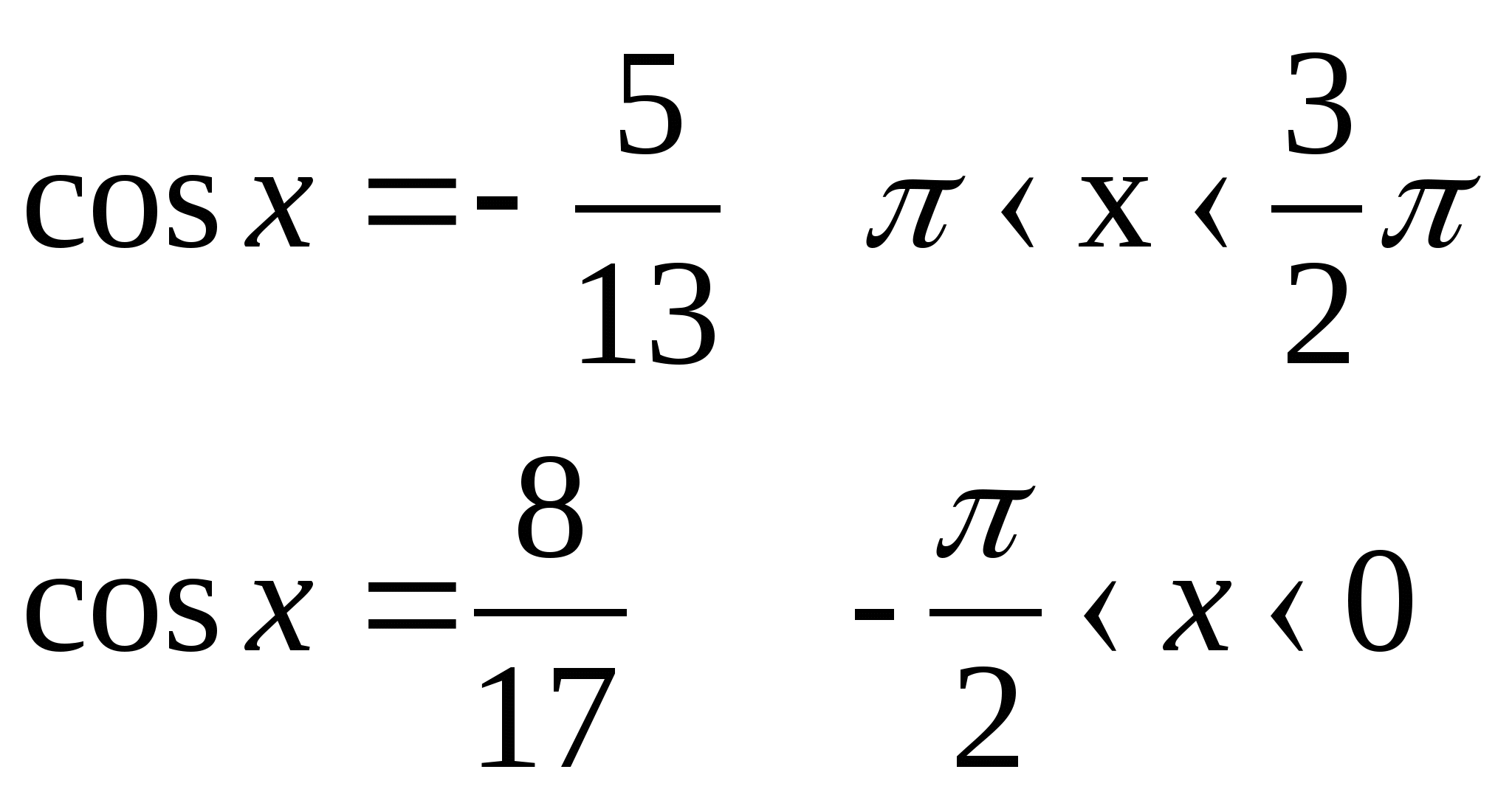
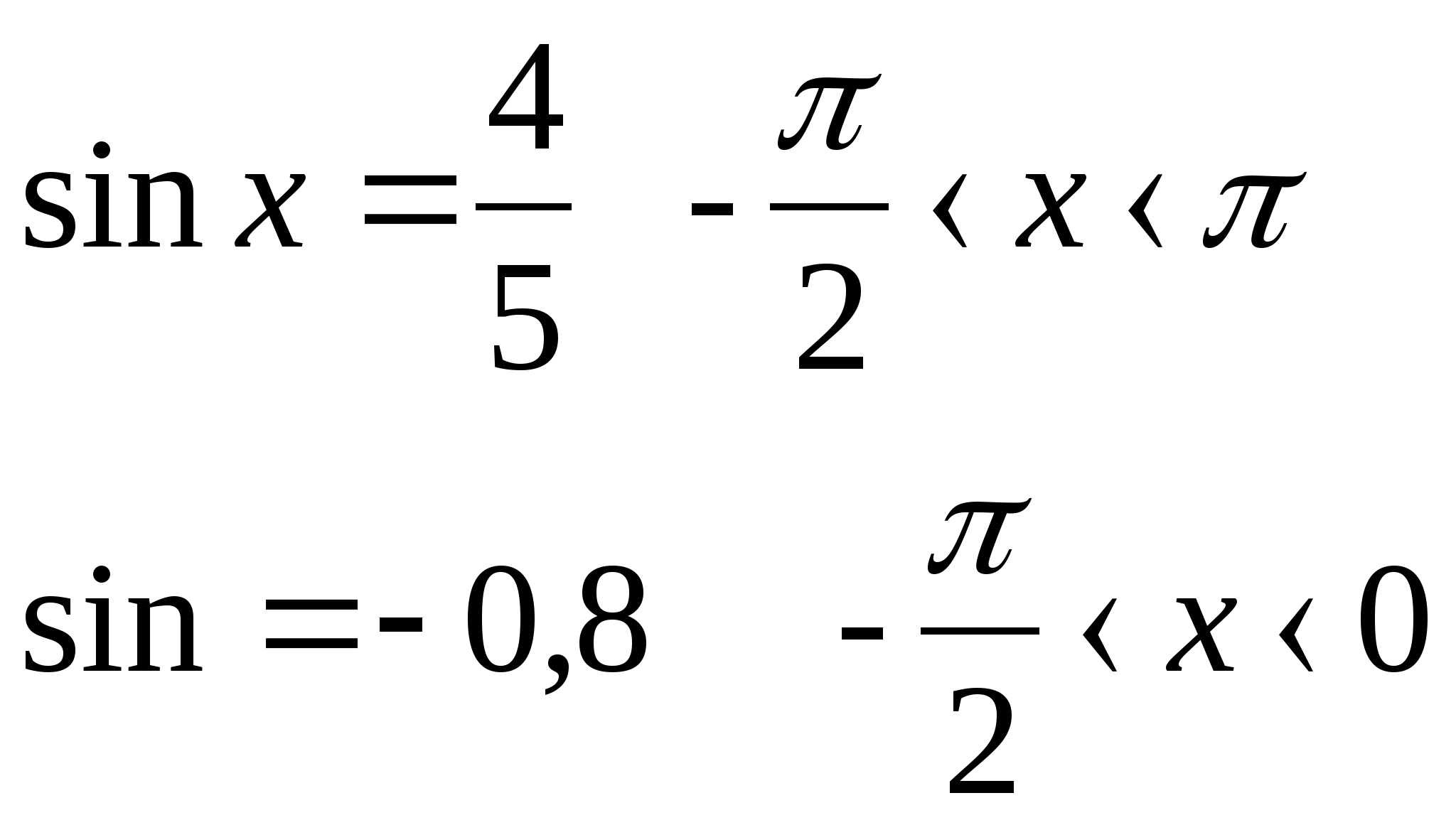
Контрольная работа по алгебре
«Тригонометрические преобразования»
«4 - 5»
Вариант 1 Вариант 2
1) Найти: sin , cos ,sin2, cos2, 1) Найти: sin , cos ,sin2, cos2,
ctg, если ![]() tg, если
tg, если ![]()
2) Упростить выражение: 2) Упростить выражение:
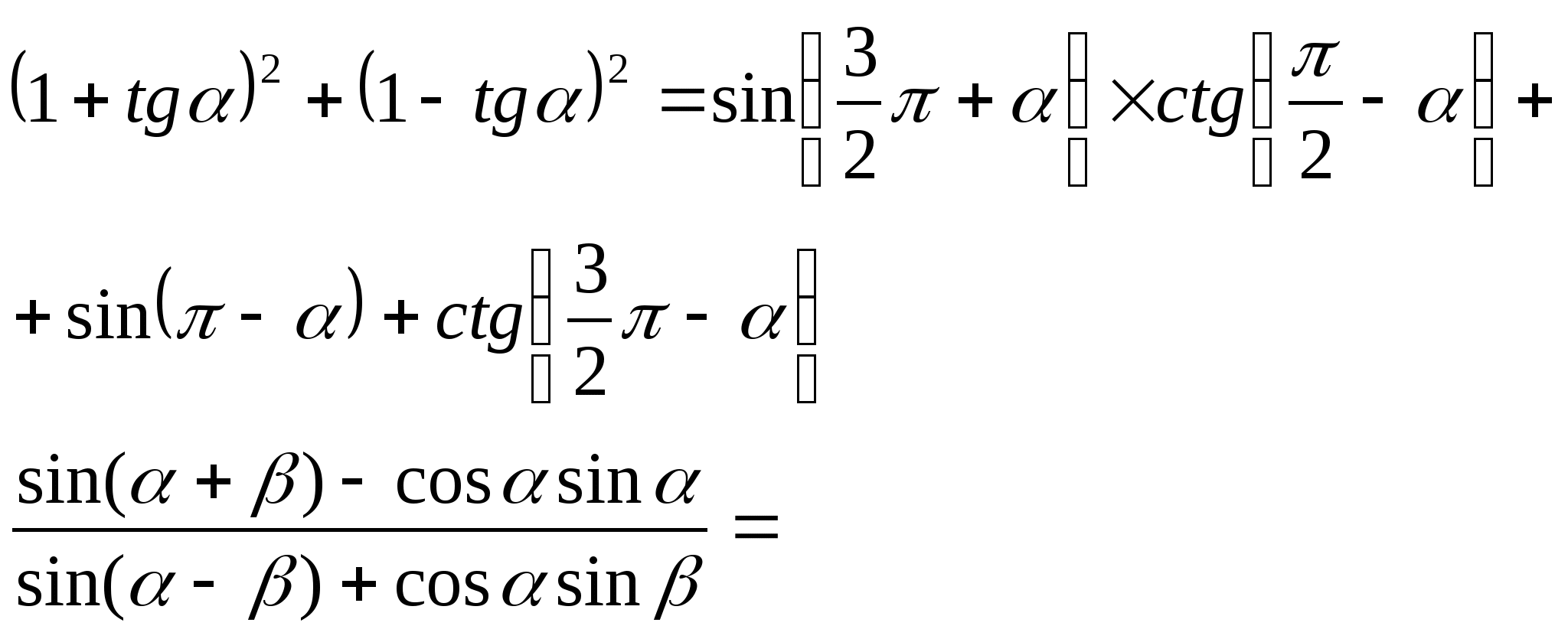
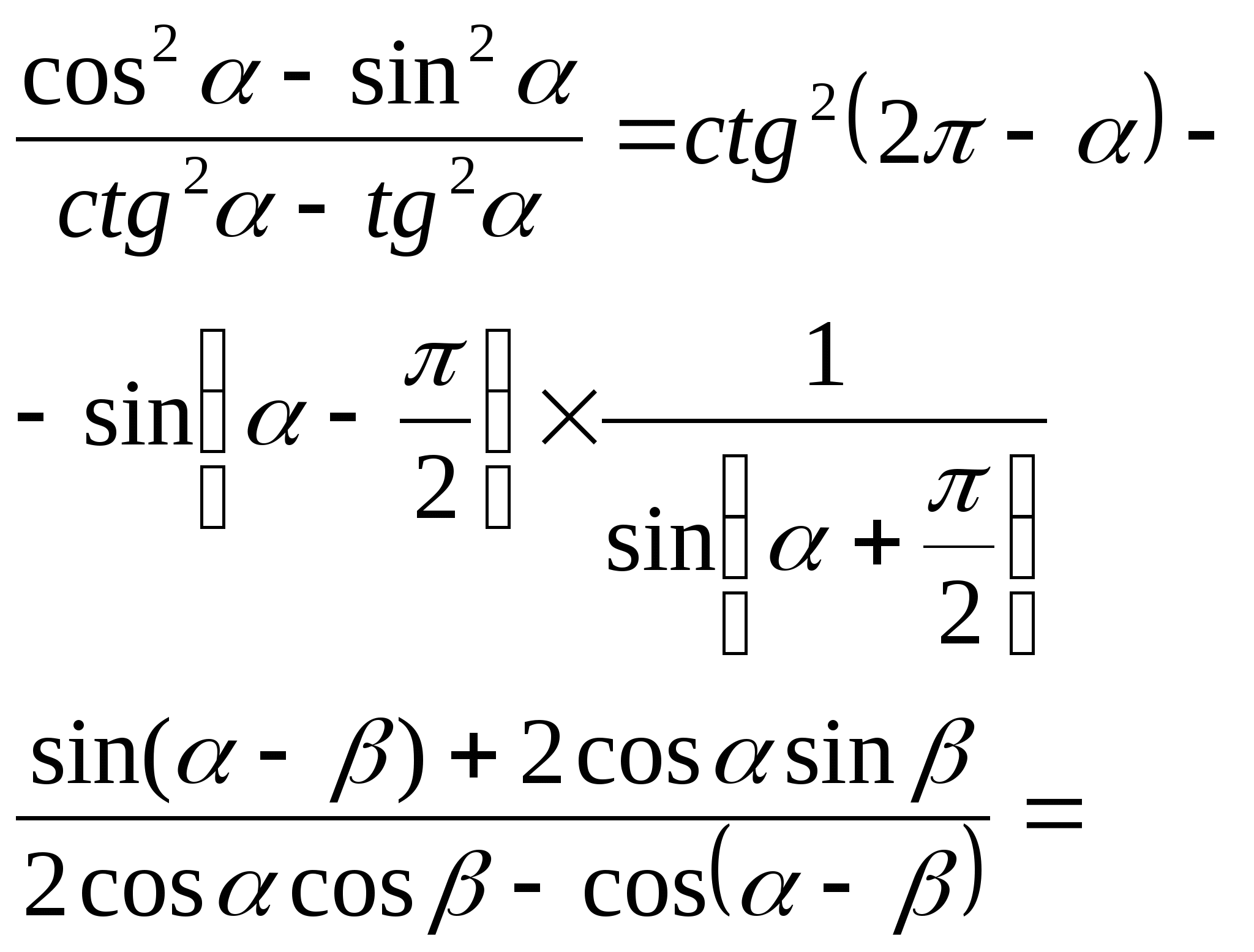
3) Доказать тождество: 3) Доказать тождество:
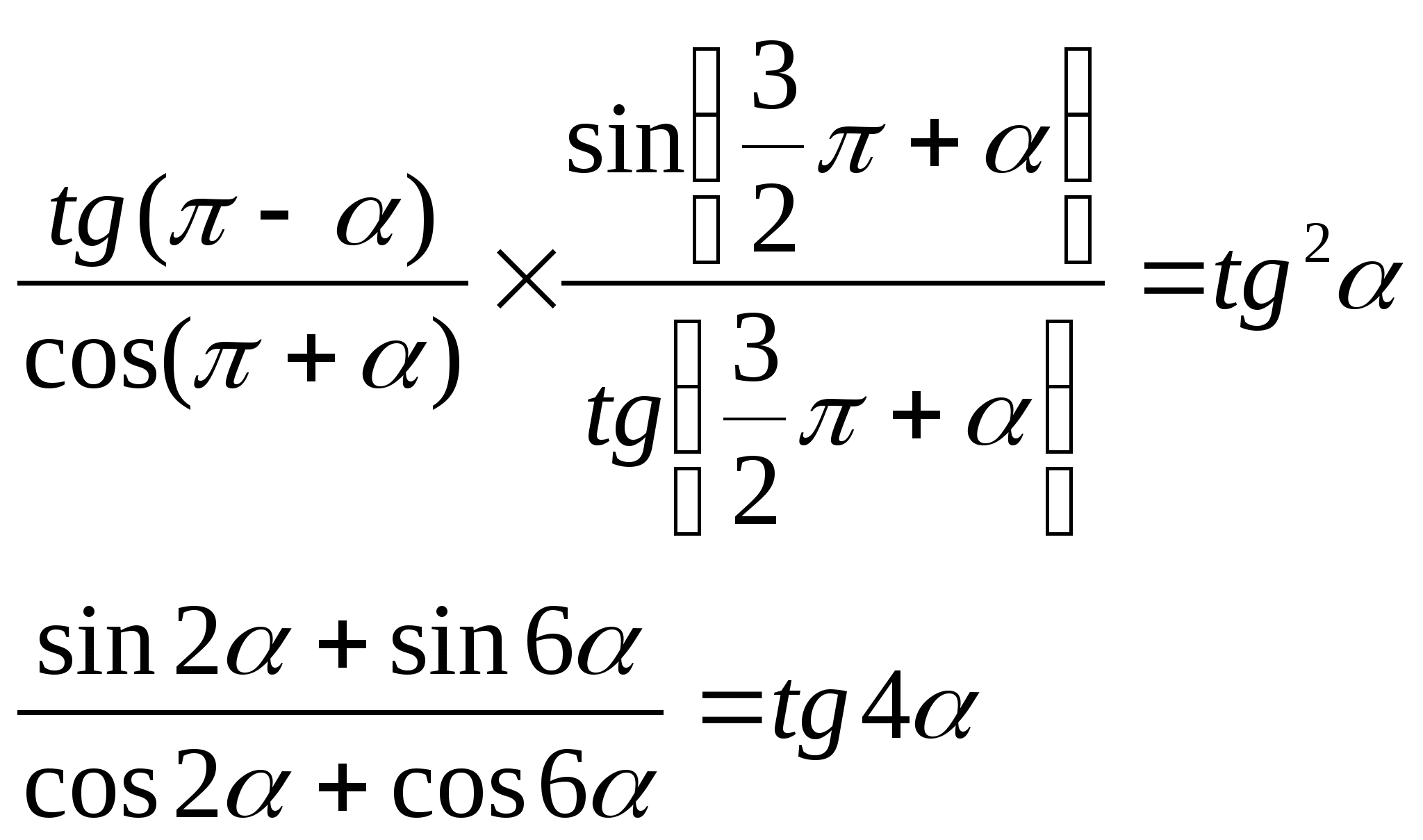
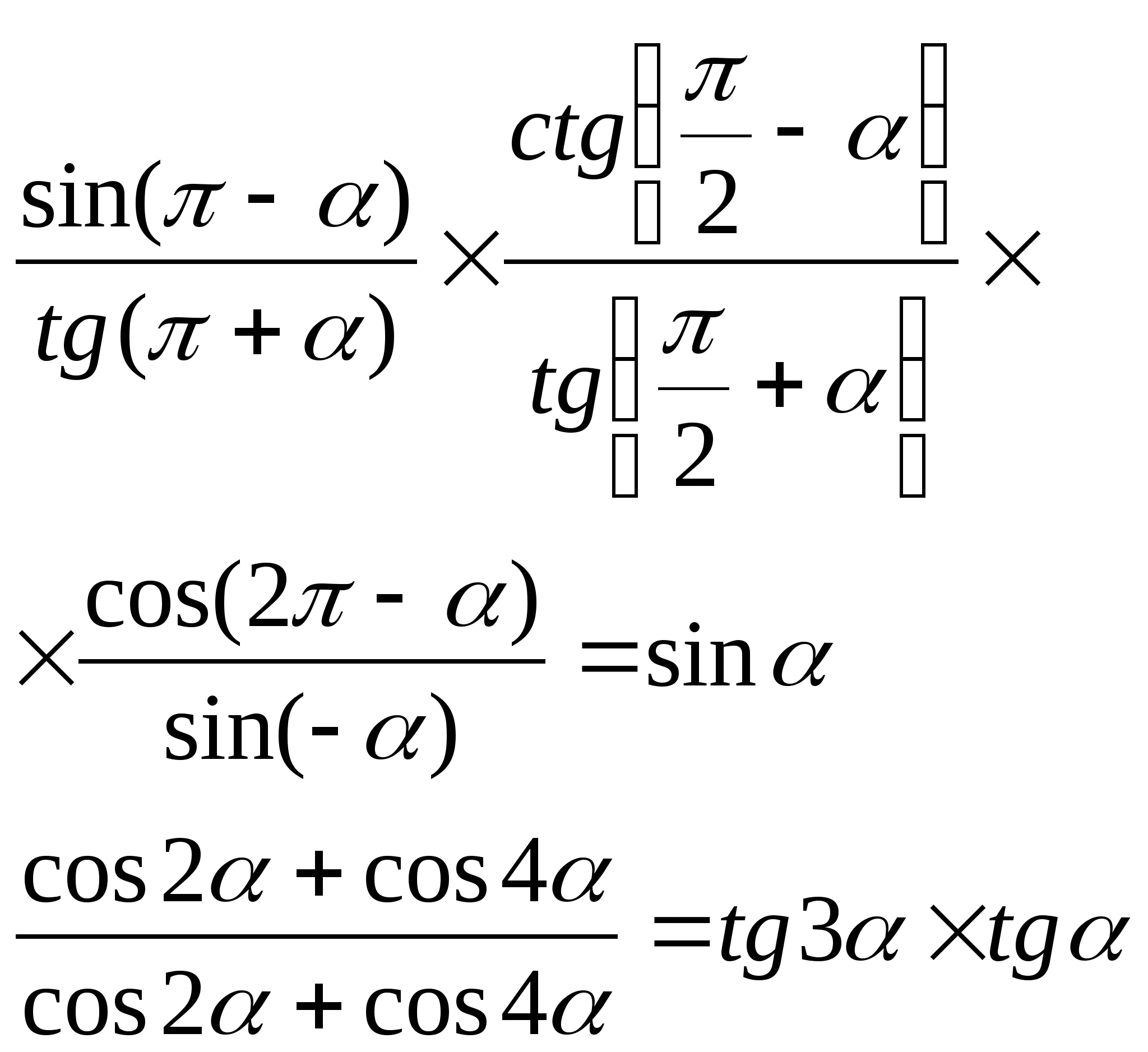
4) Вычислить: 4) Вычислить:
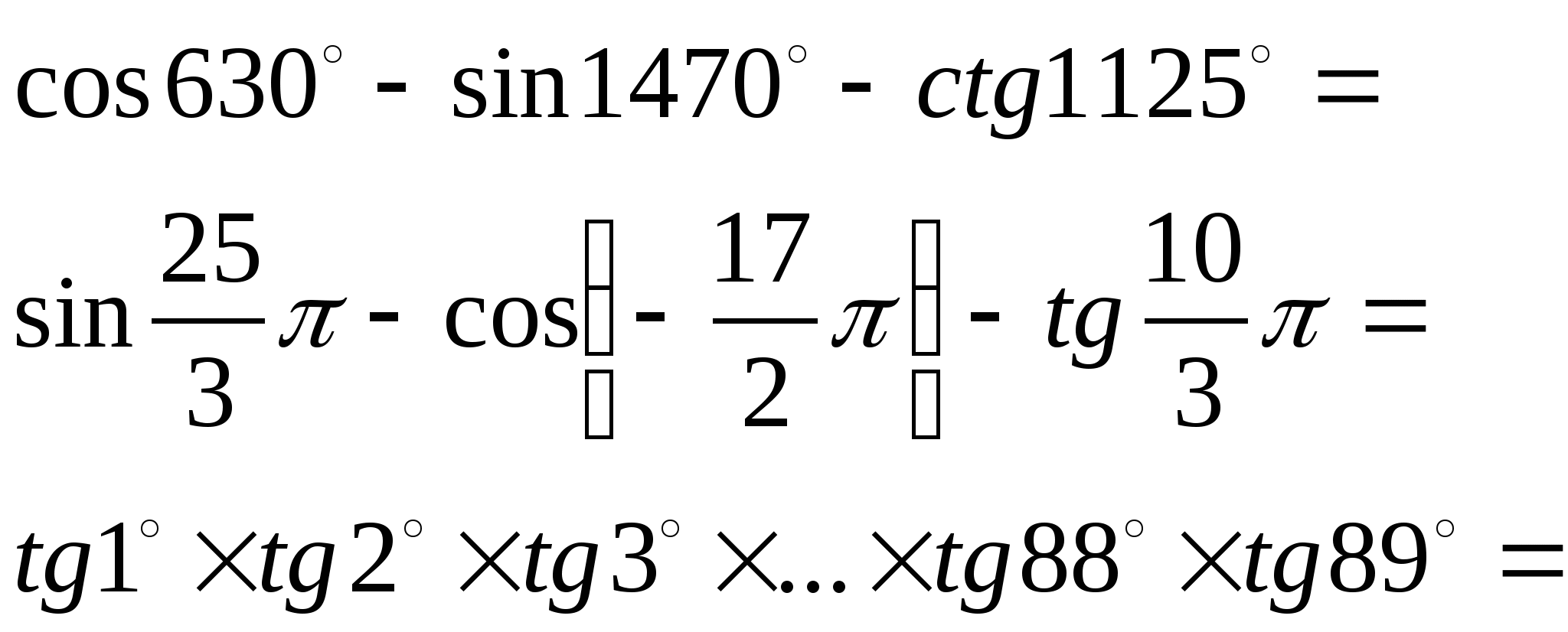
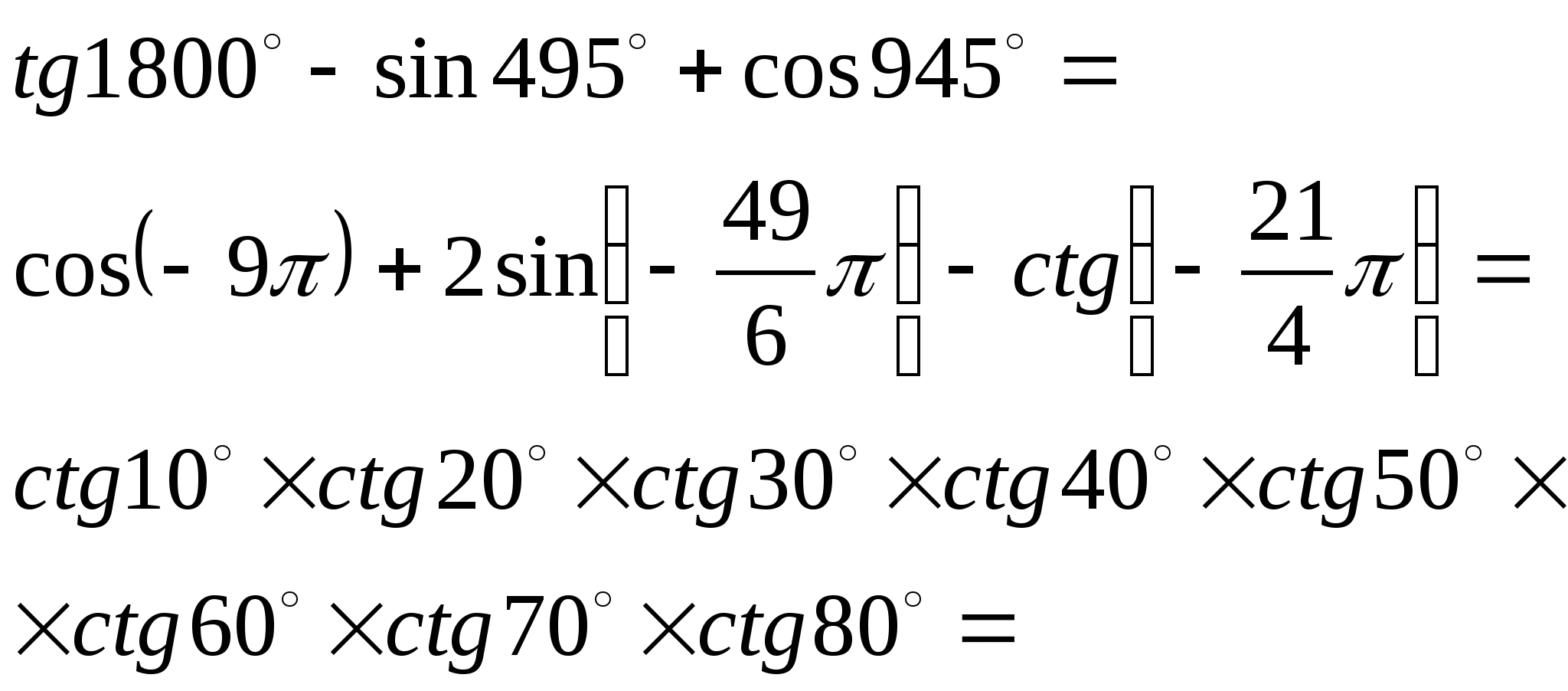
5) Найти: 5) Найти:
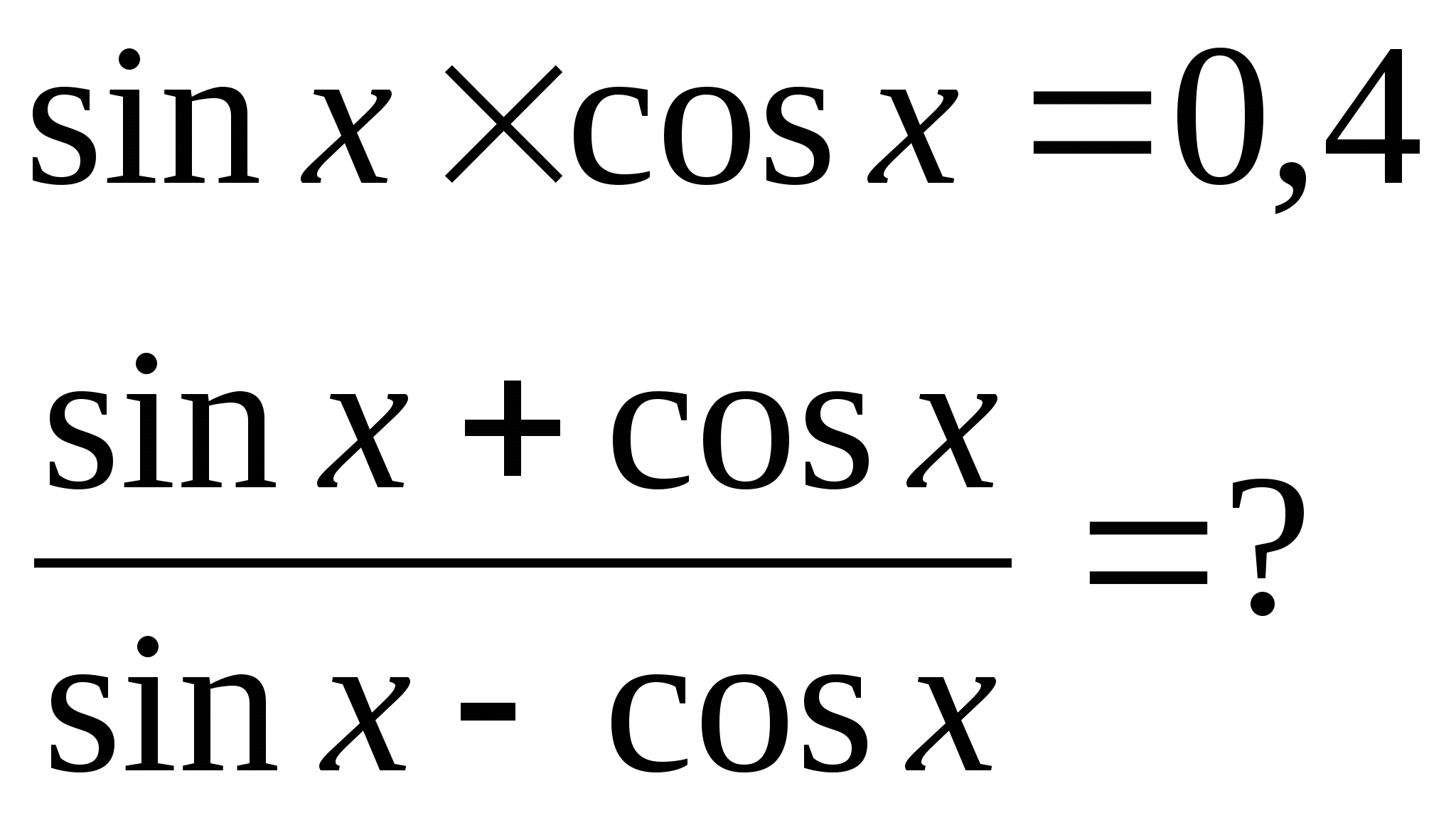
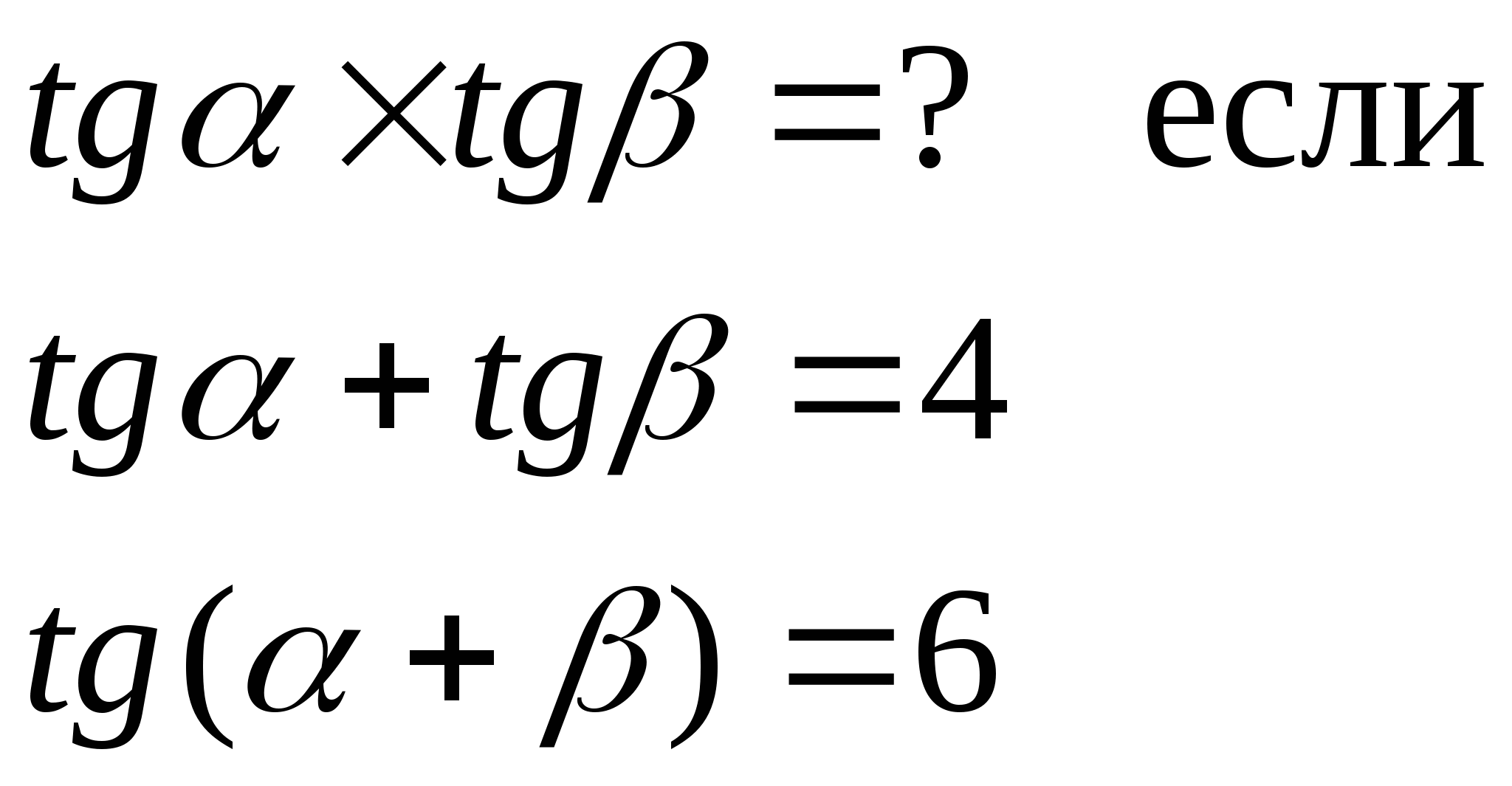
Контрольная работа № 3 (10 класс)
«Тригонометрические уравнения»
1 урок - 45 минут
Вариант 1
1) Из предложенных «х» выберите те, что являются решениями уравнения sin x=1:
![]()
2) Что называется арккосинусом числа «а»
(![]() )
)
3) Реши уравнения:
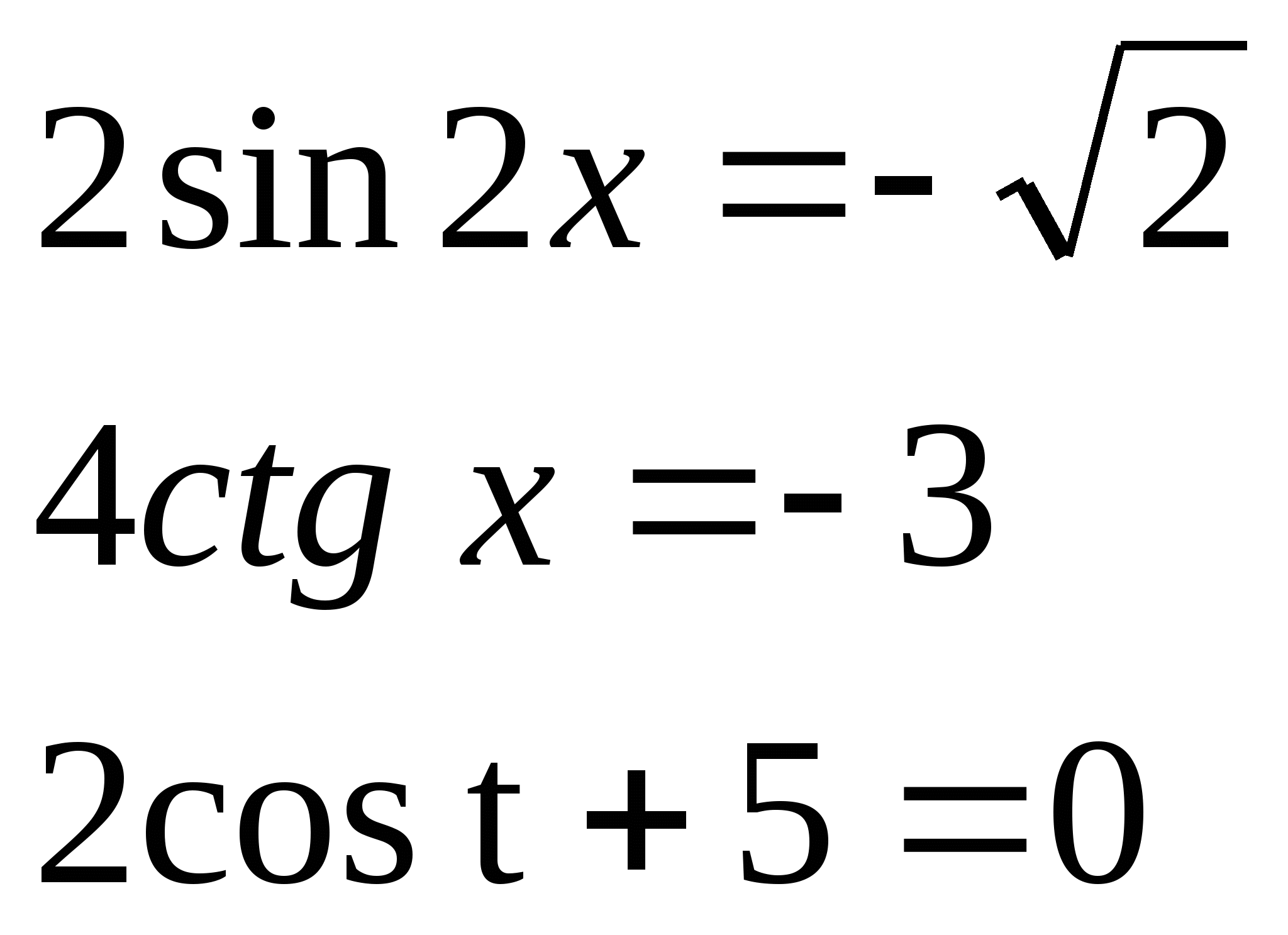
4) Дана f(x) = 2cos22x-2sin2x
Найти ![]()
5) Реши систему:
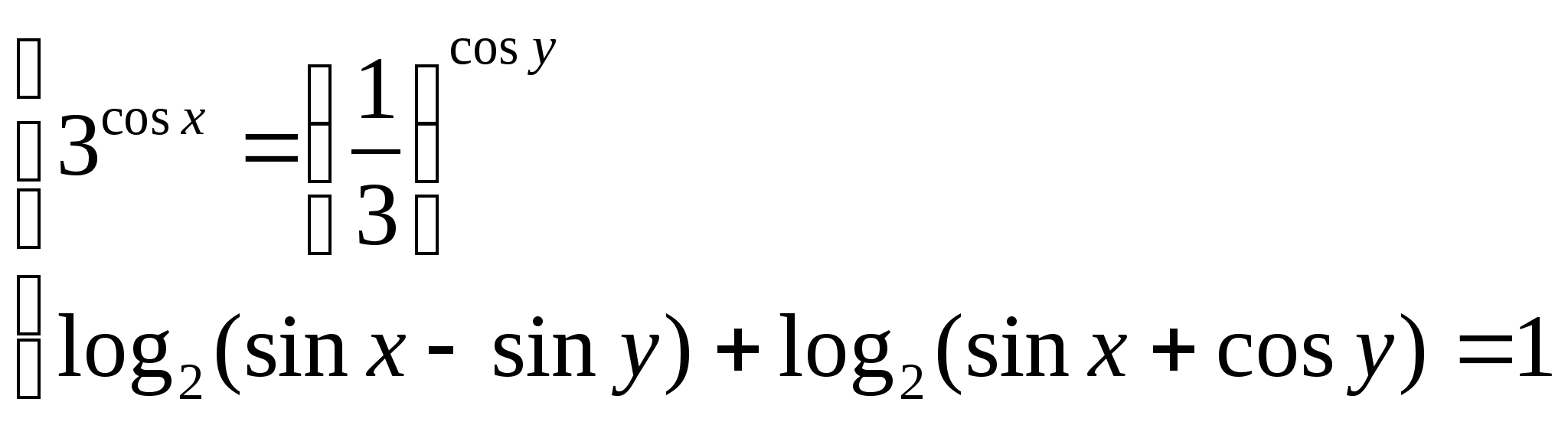
Вариант 2
1) Из предложенных «х» выберите те, что являются решениями уравнения cos x=1:
![]()
2) Что называется арксинусом числа «а»
(![]() )
)
3) Реши уравнения:
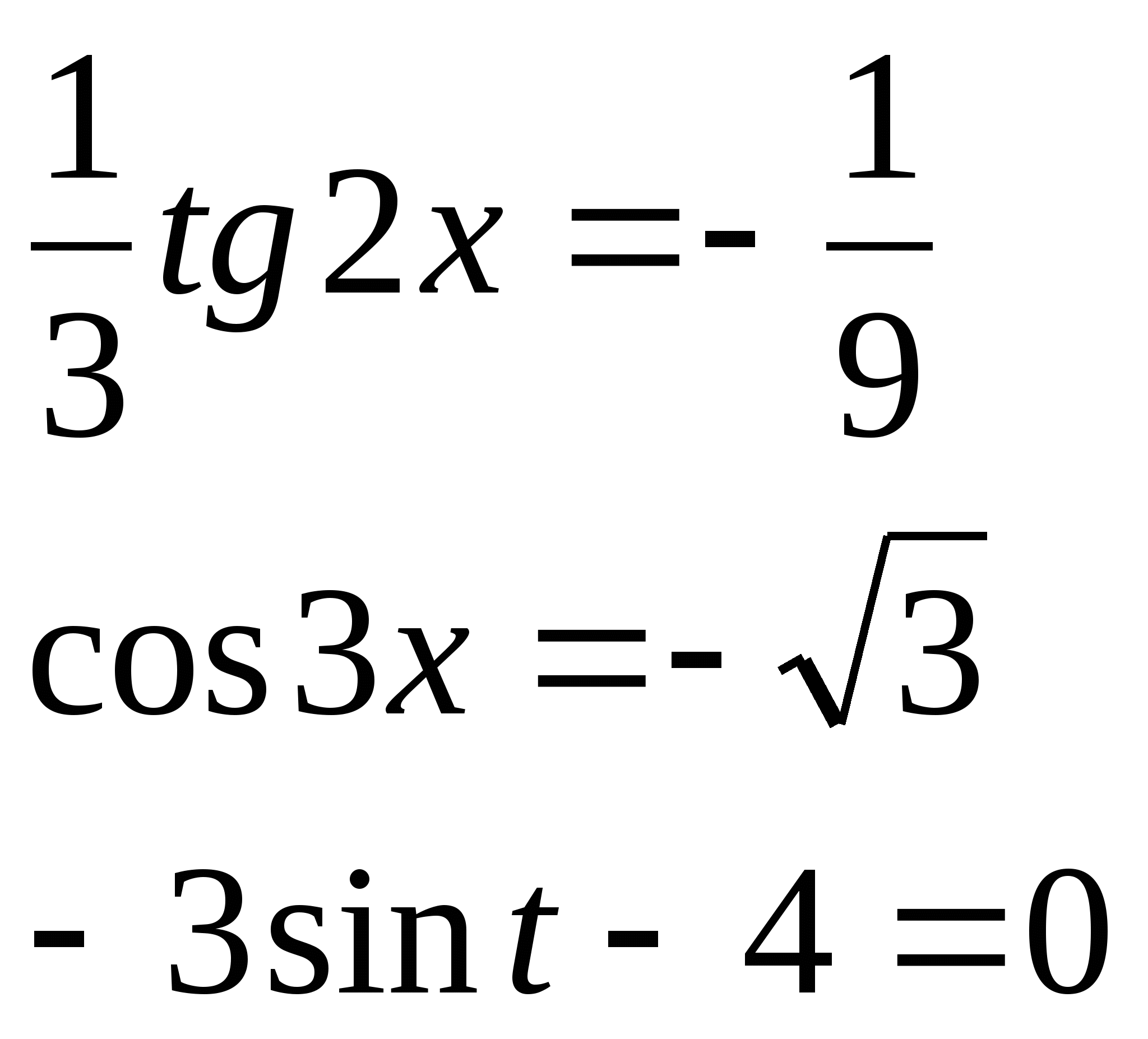
4) Дана f(x) = 2cos2x - 2cos22x
Найти ![]()
5) Реши систему:
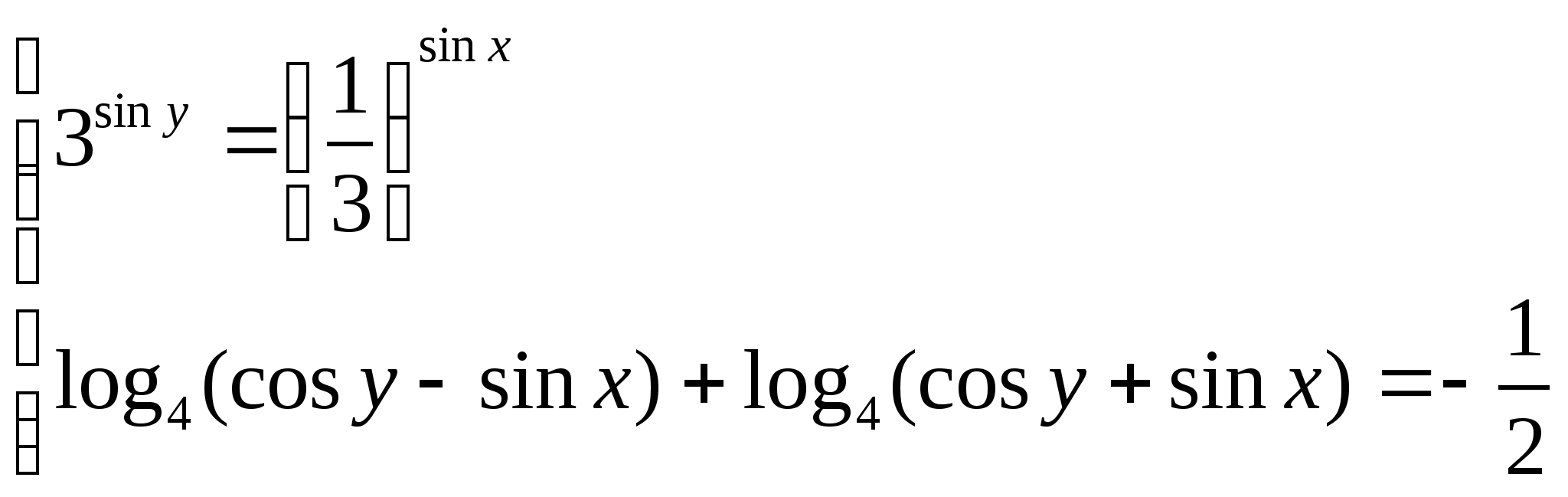
Контрольная работа №3 (10 класс)
«Тригонометрия»
1 урок - 45 минут
а) - 1 вариант б) - 2 вариант
1) Упростить выражение:
а) 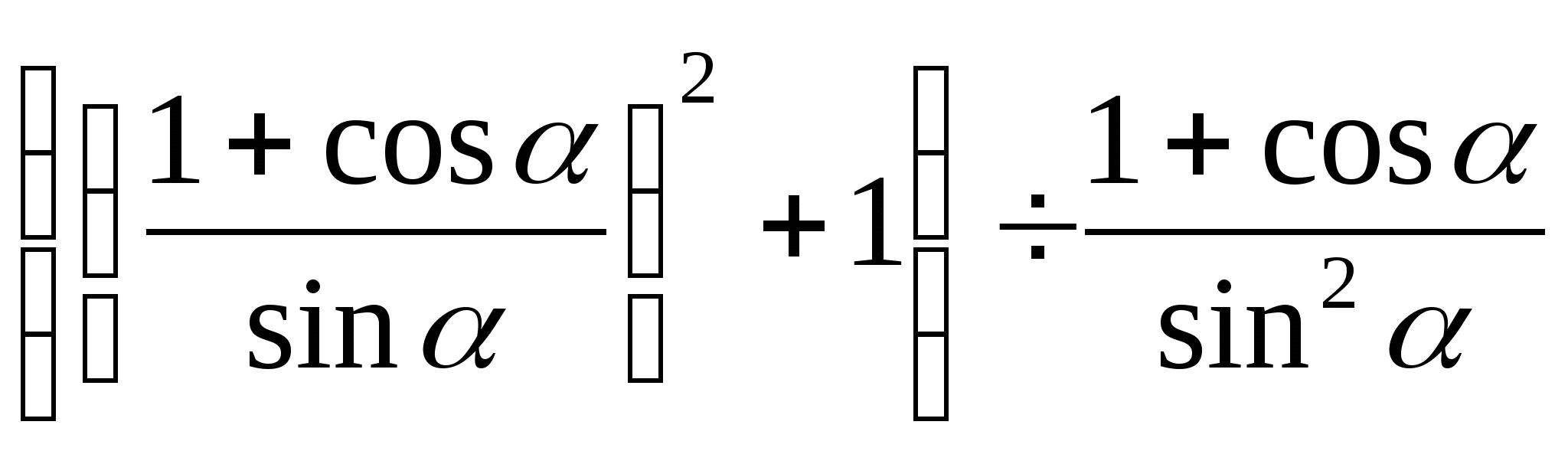 б)
б)
![]()
2) Доказать тождество:
а) 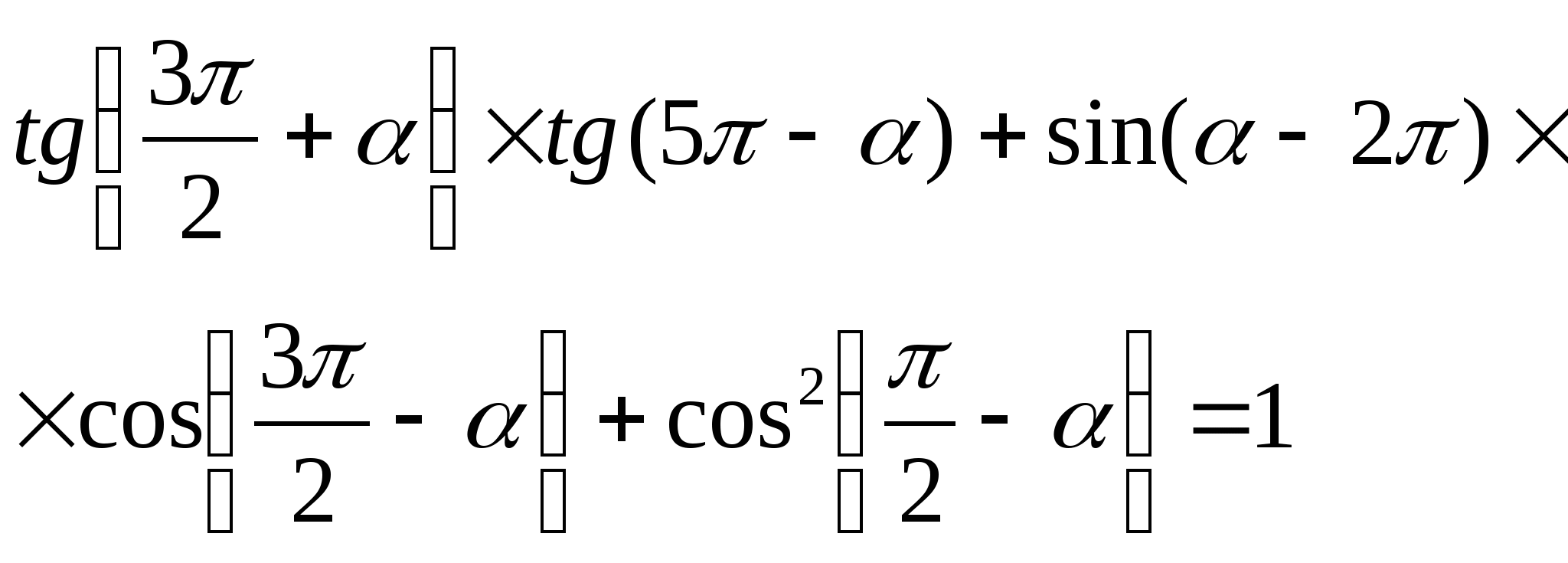 б)
б)
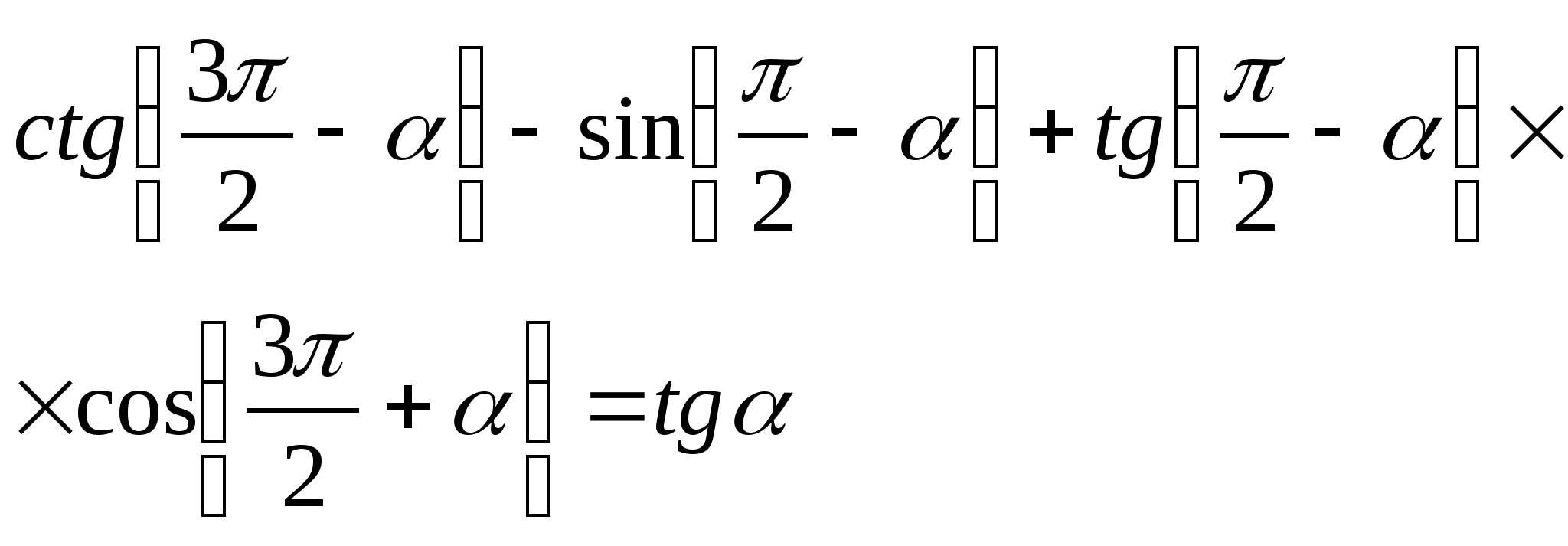
3) Решить уравнения:
а) 15(sin22x + sin x +
cos22x) = 17 + 31sinx б) ![]()
6sin2 x = 4 + sin2x 3sin2x + 8 cos2x = 7
(1-cos6x)cos2x = sin23x ![]()
4) Вычислить:
а) ![]() б)
б)
![]()
5) Решить систему уравнений:
а) 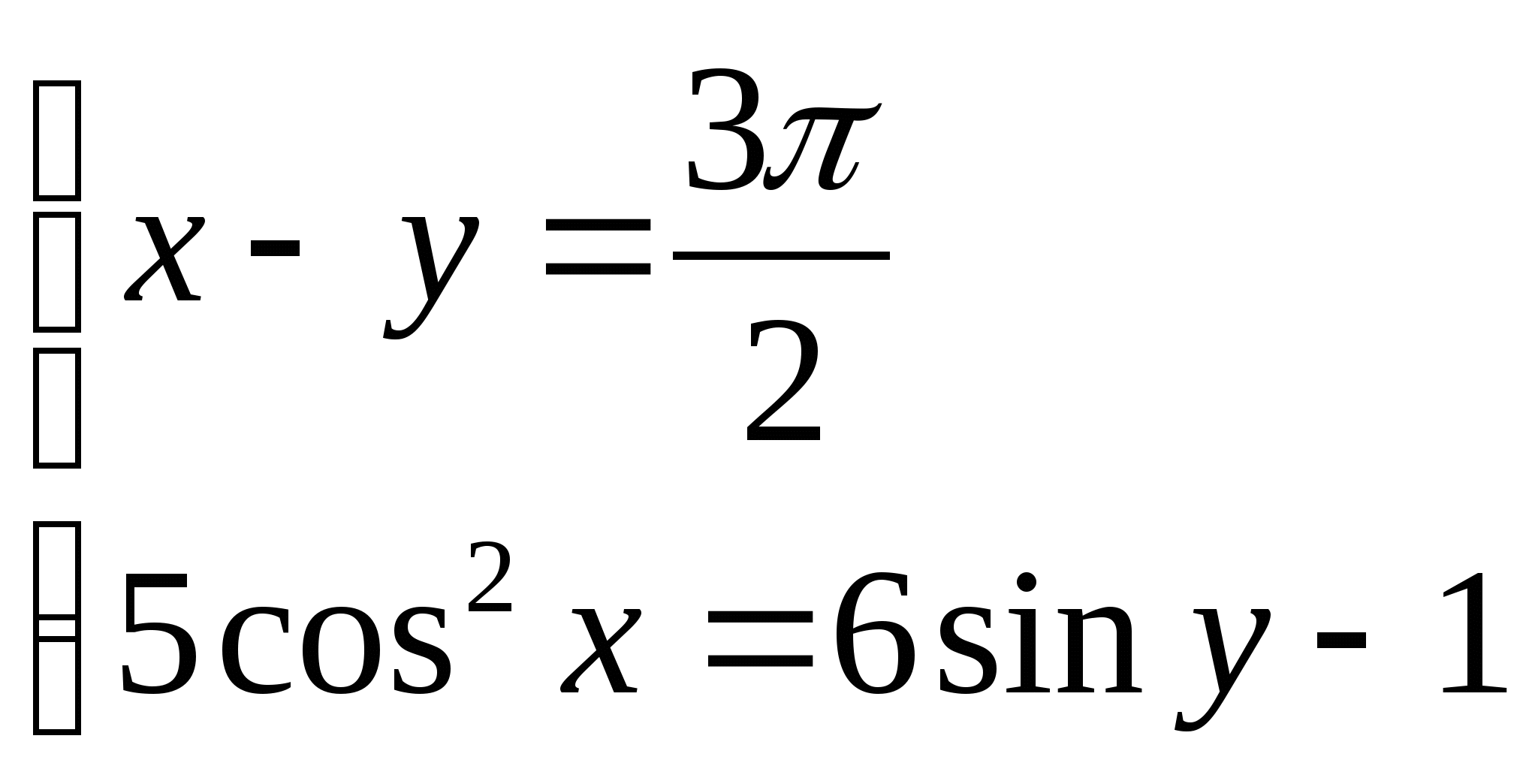 б)
б)
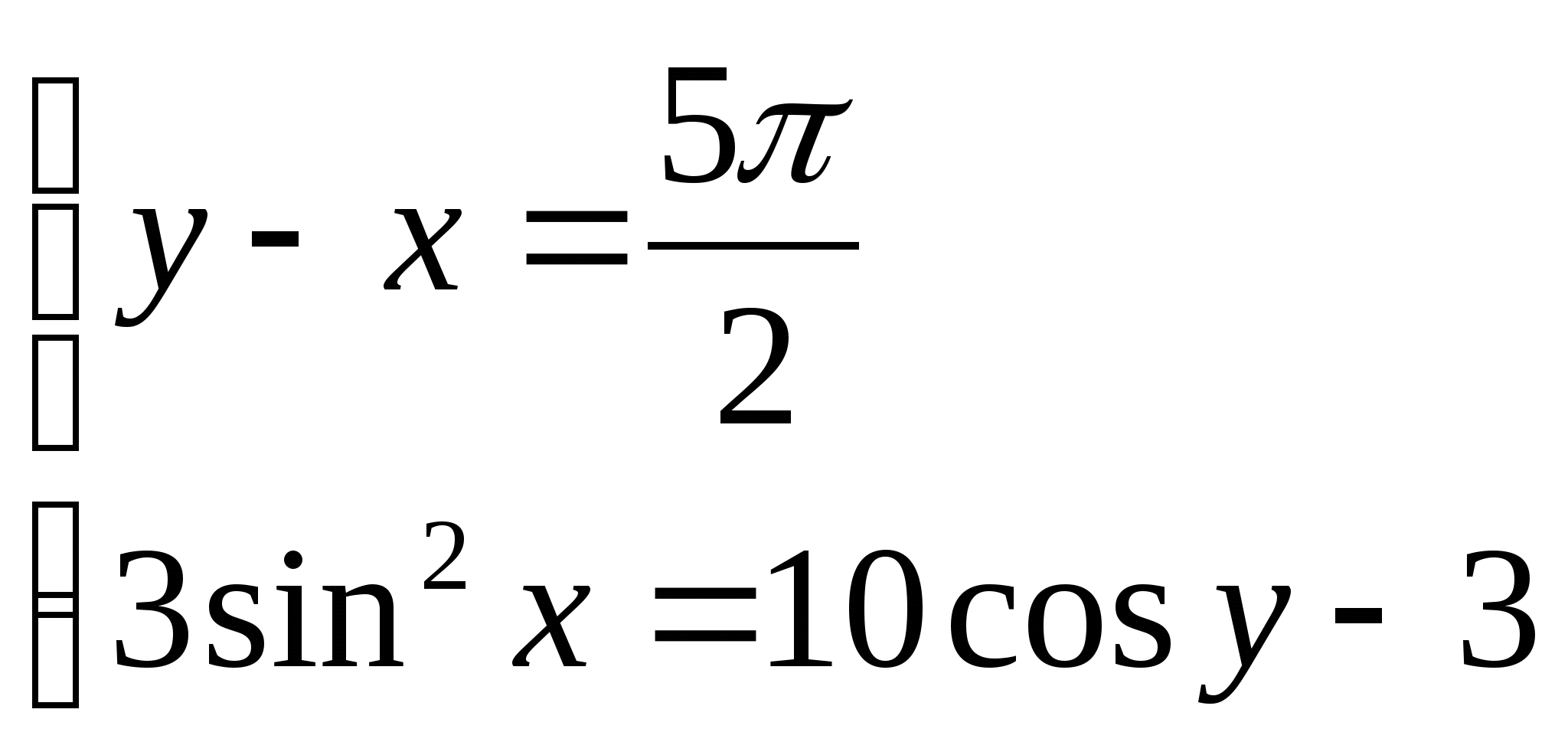
6) Решить неравенство:
а) 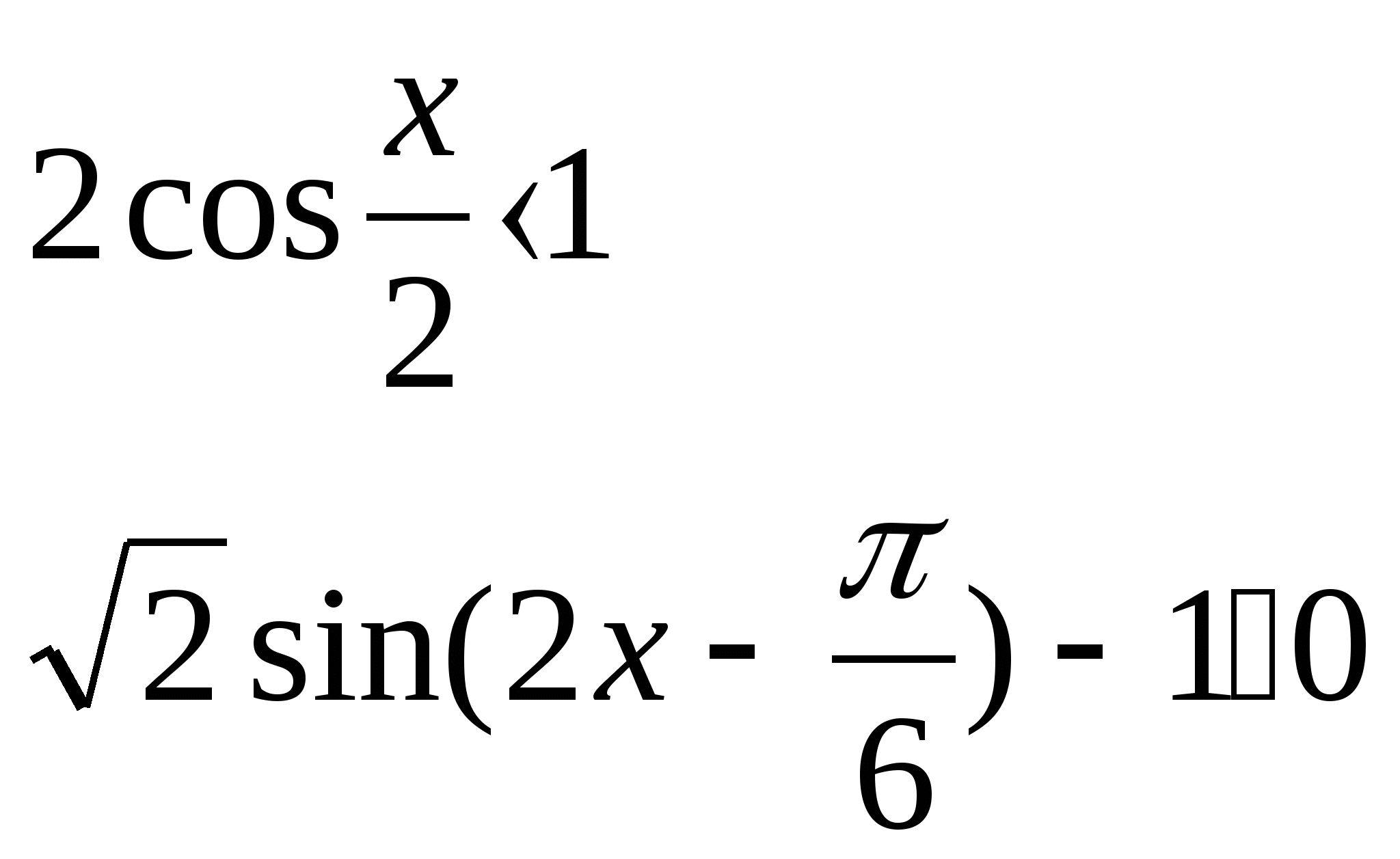 б)
б)
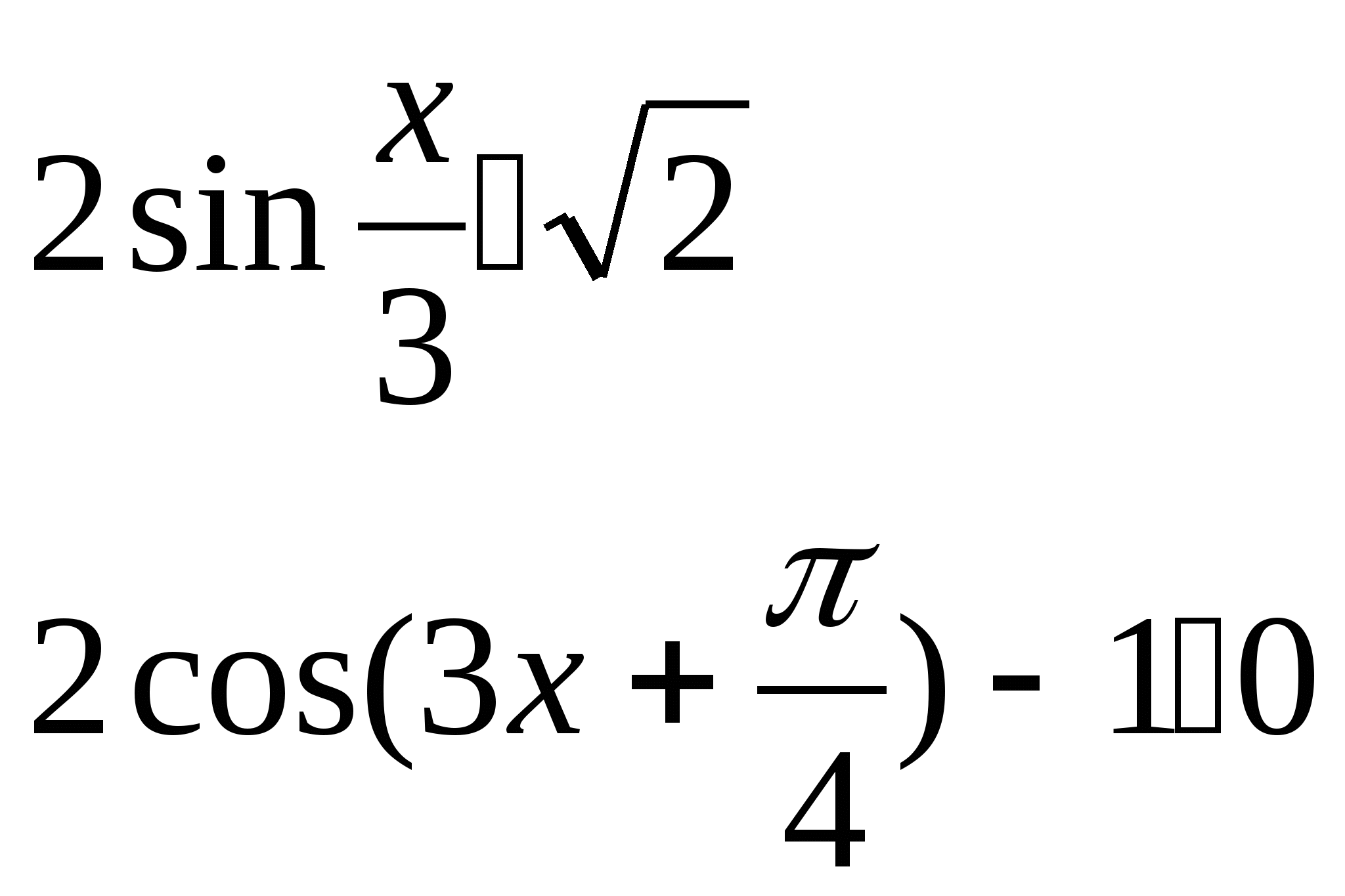
Итоговая контрольная работа
по алгебре и началам анализа (1ое полугодие)
рассчитана на 2 урока, наивысший балл «3»
а) - 1 вариант, б) - 2 вариант
1) Вычислите:
а) ![]() б)
б)![]()
2) Найдите значение выражения, если
а) 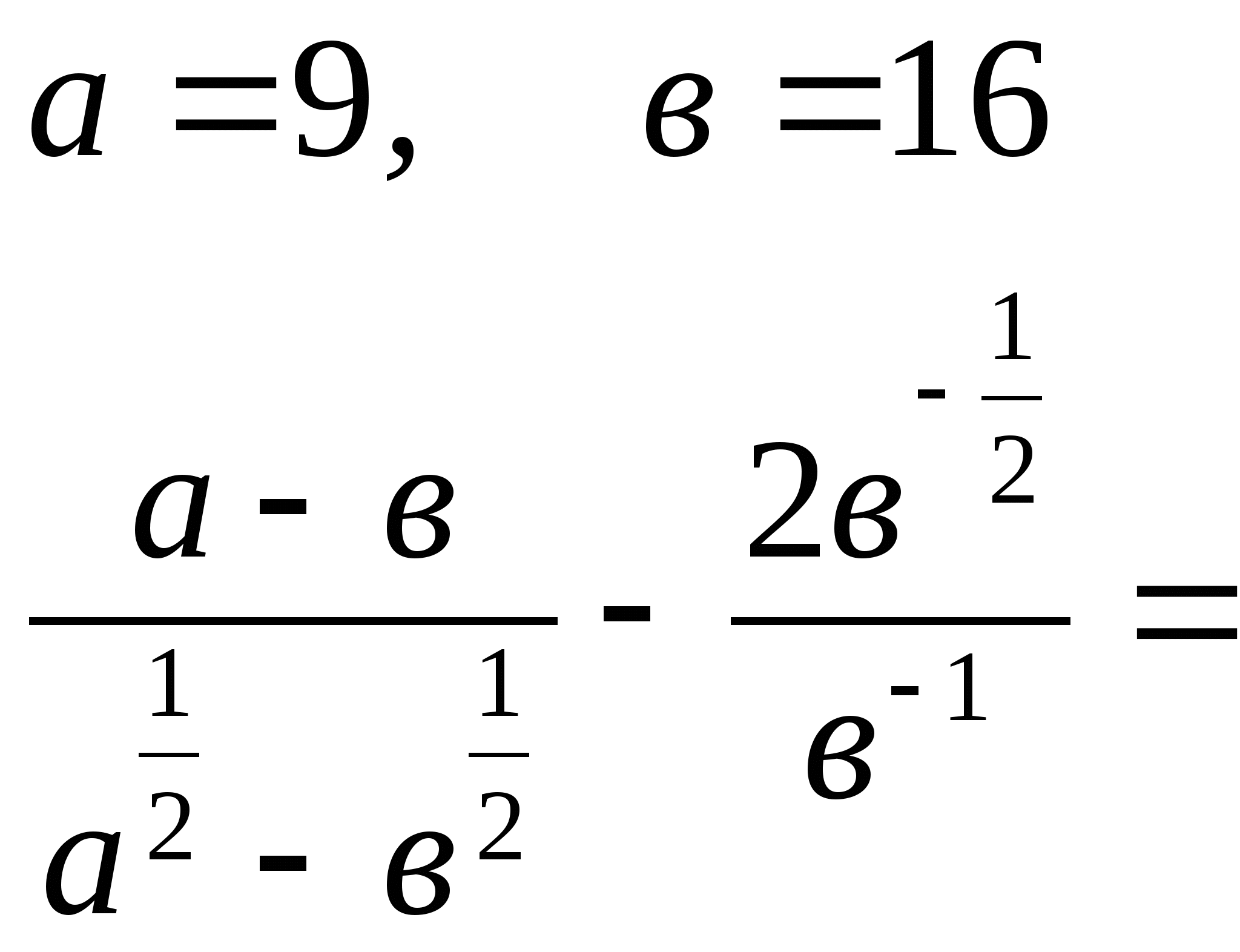 б)
б)
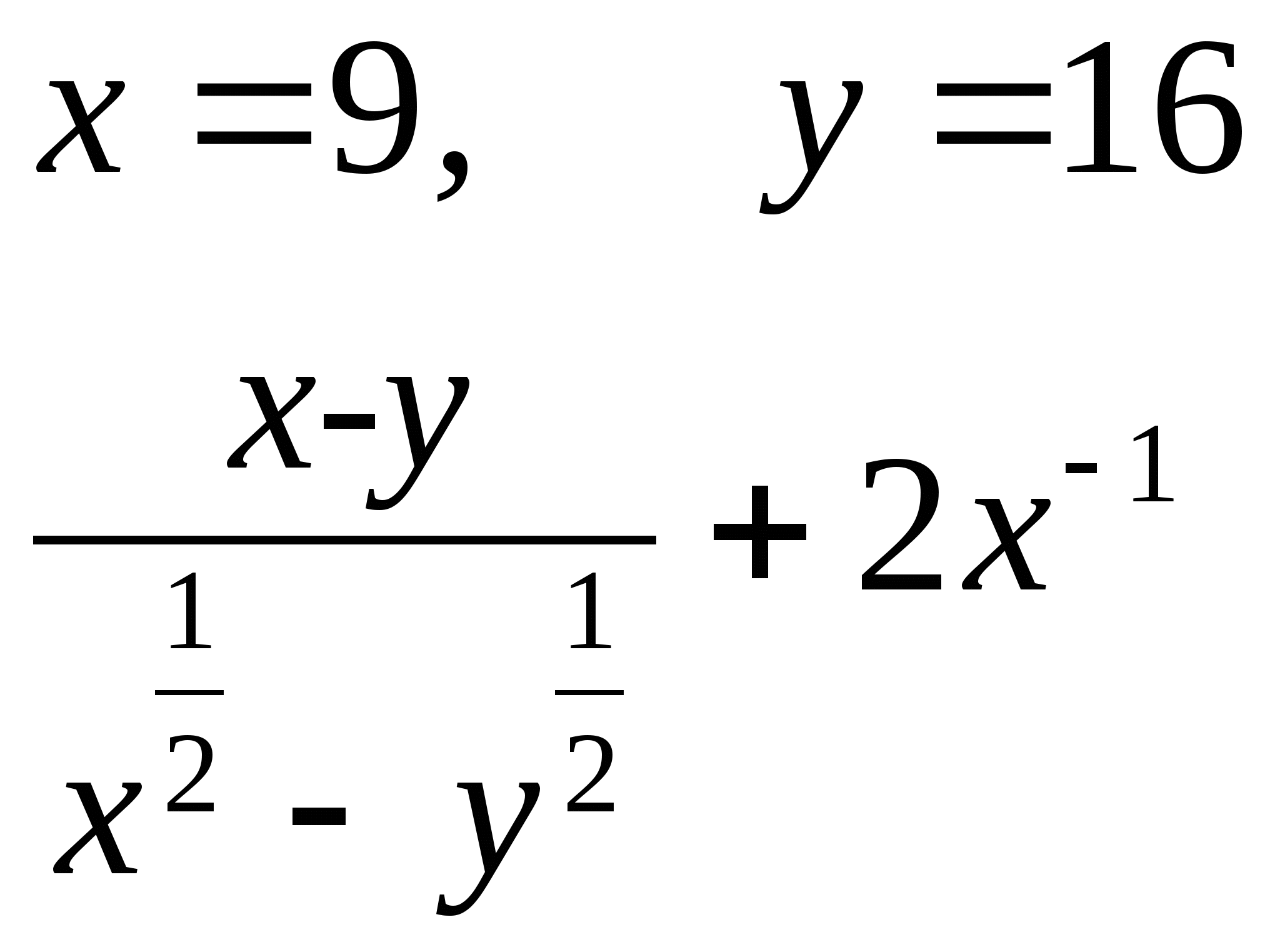
3) Укажите промежуток, которому принадлежит корень уравнения:
а) 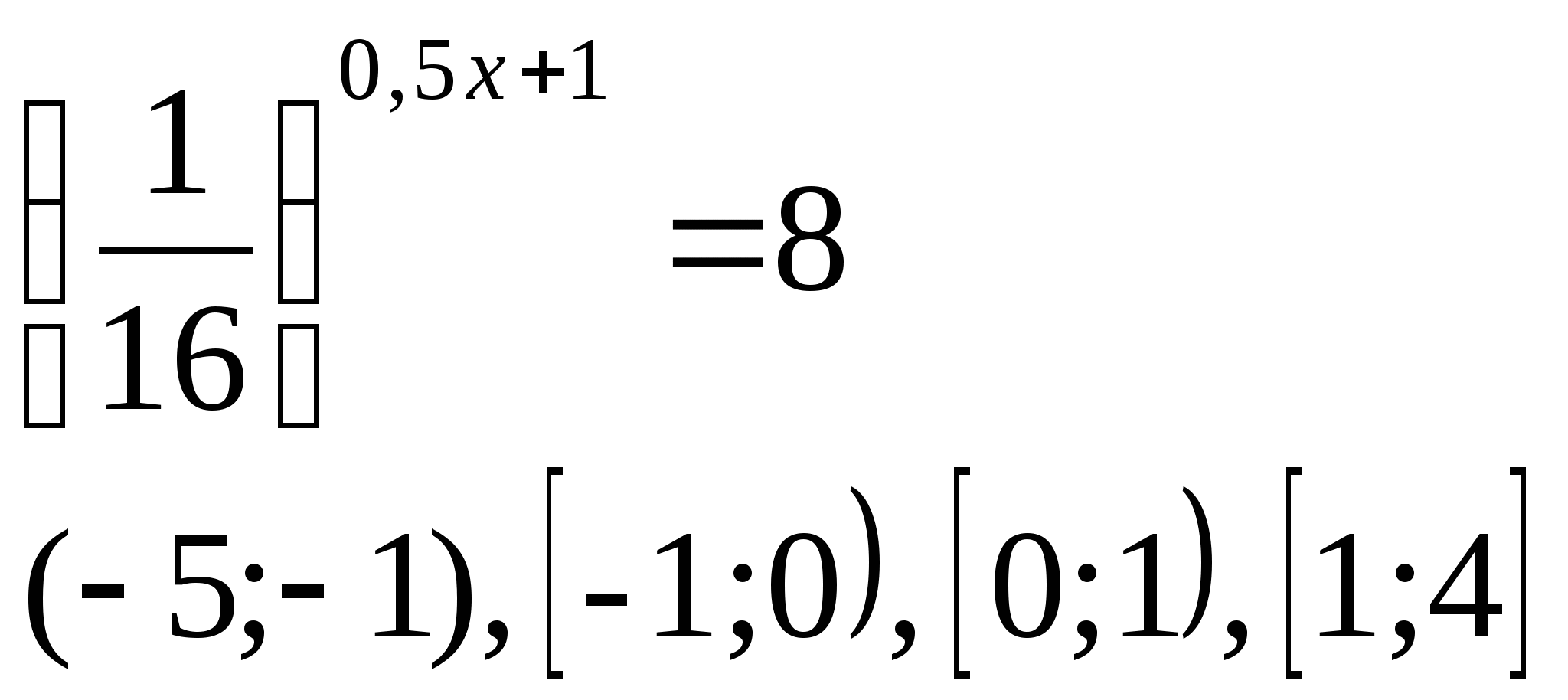 б)
б)
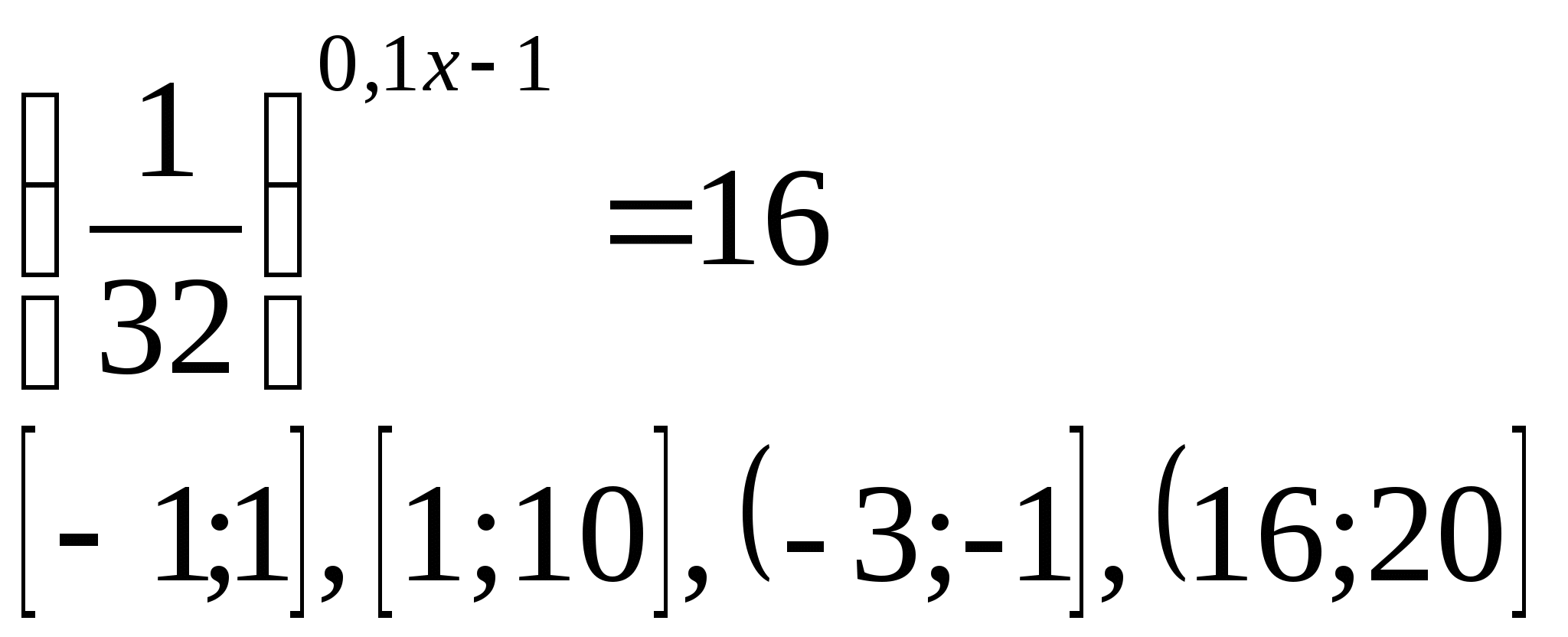
4) Укажите промежуток, которому принадлежат корни уравнения:
а) 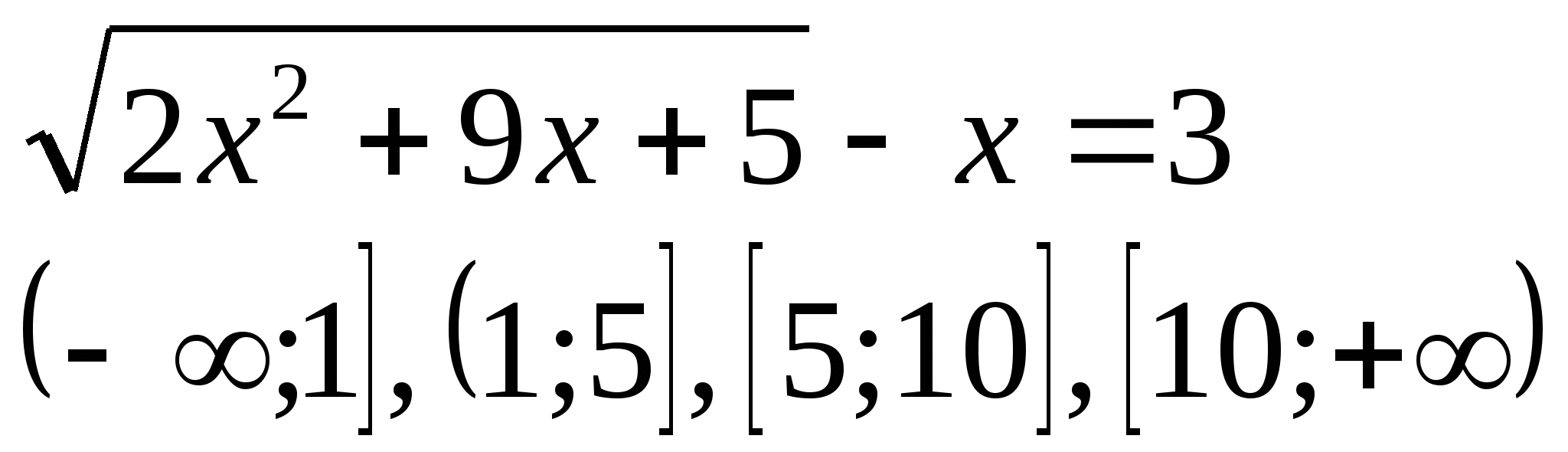 б)
б)
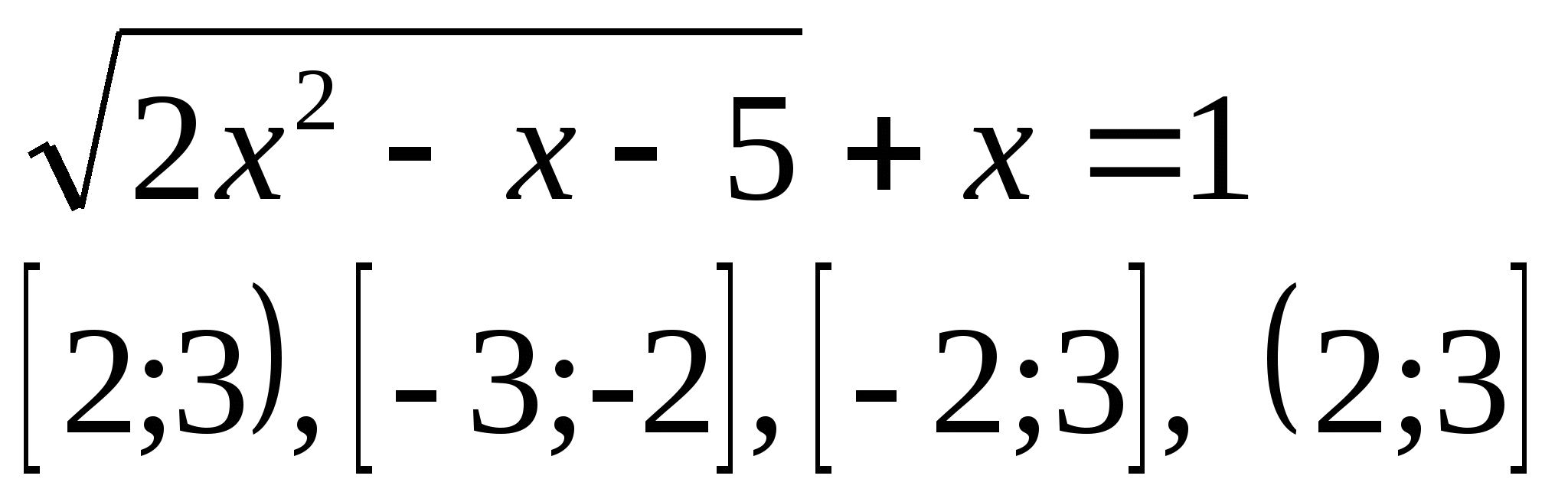
5) Найти ООФ:
а) 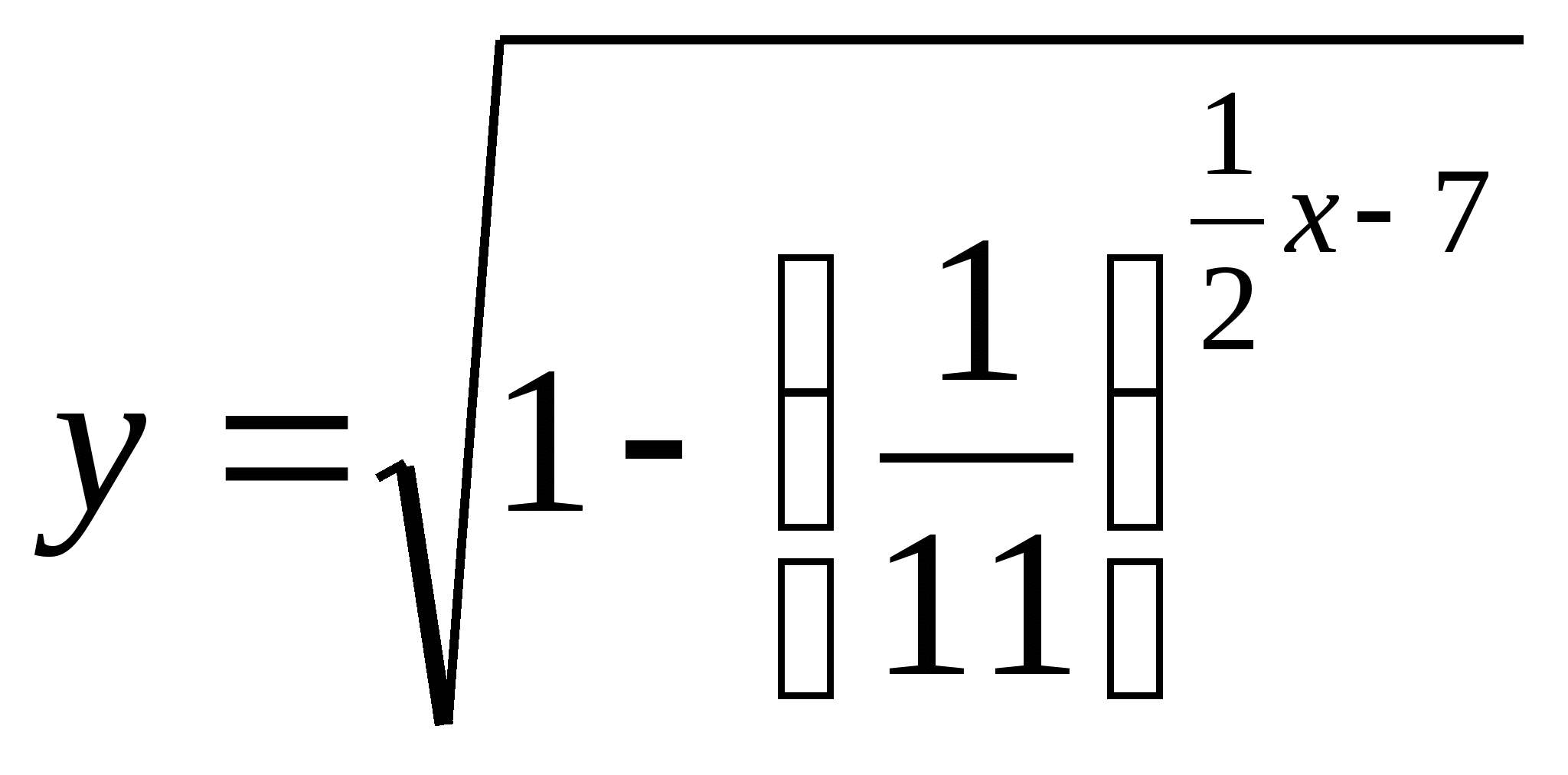 б)
б)
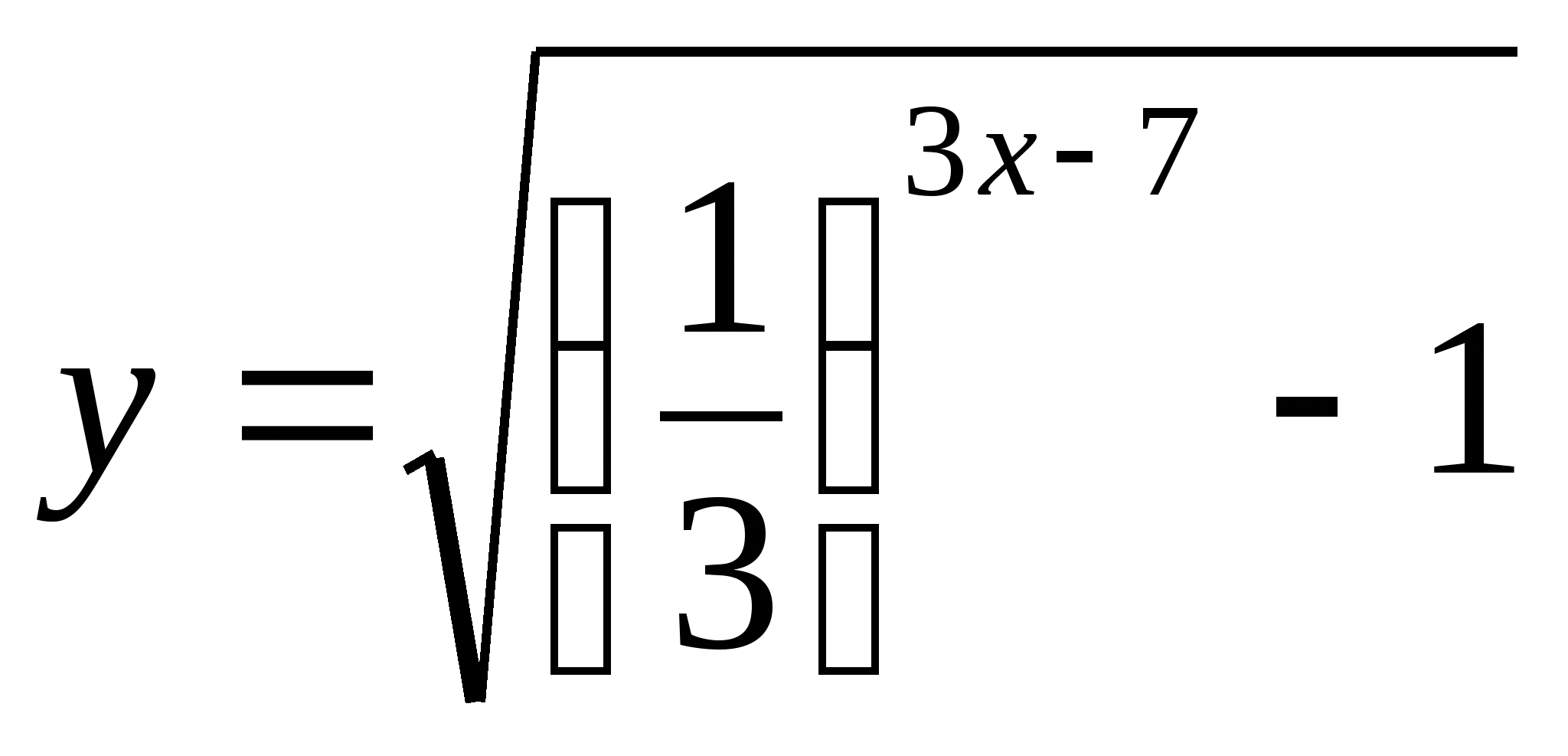
наивысший балл - «5»
1) Пусть (х0;у0) - решение системы
а) Найти х0 - у0 б) Найти х0 + у0
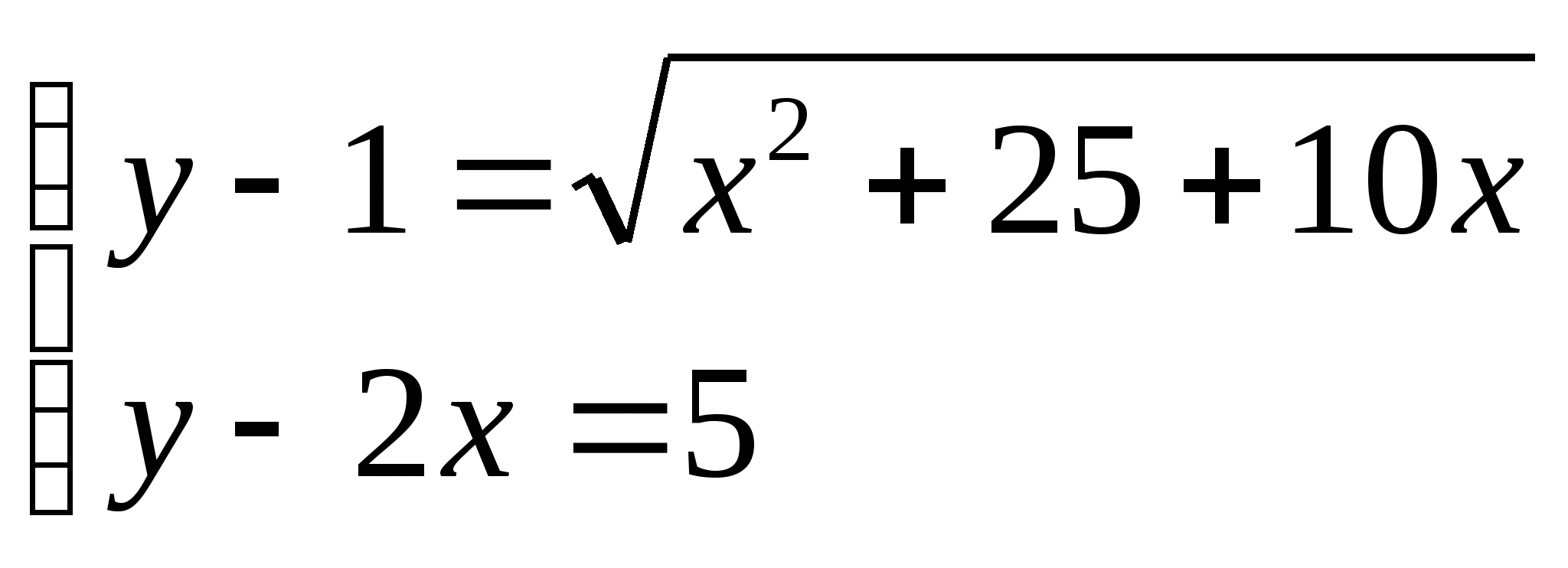
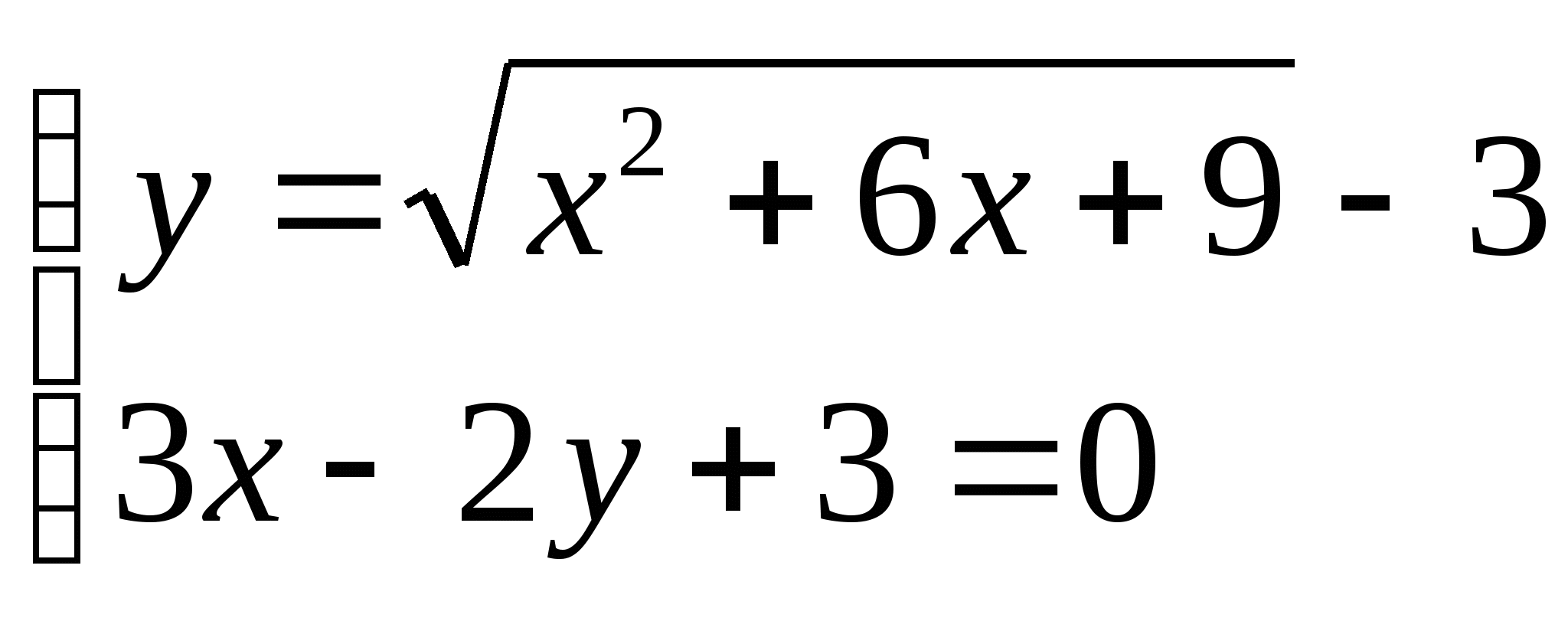
2) Укажите промежуток, которому принадлежит корень уравнения:
а) ![]() б)
б)
![]()
3) Найдите значение выражения при:
а) 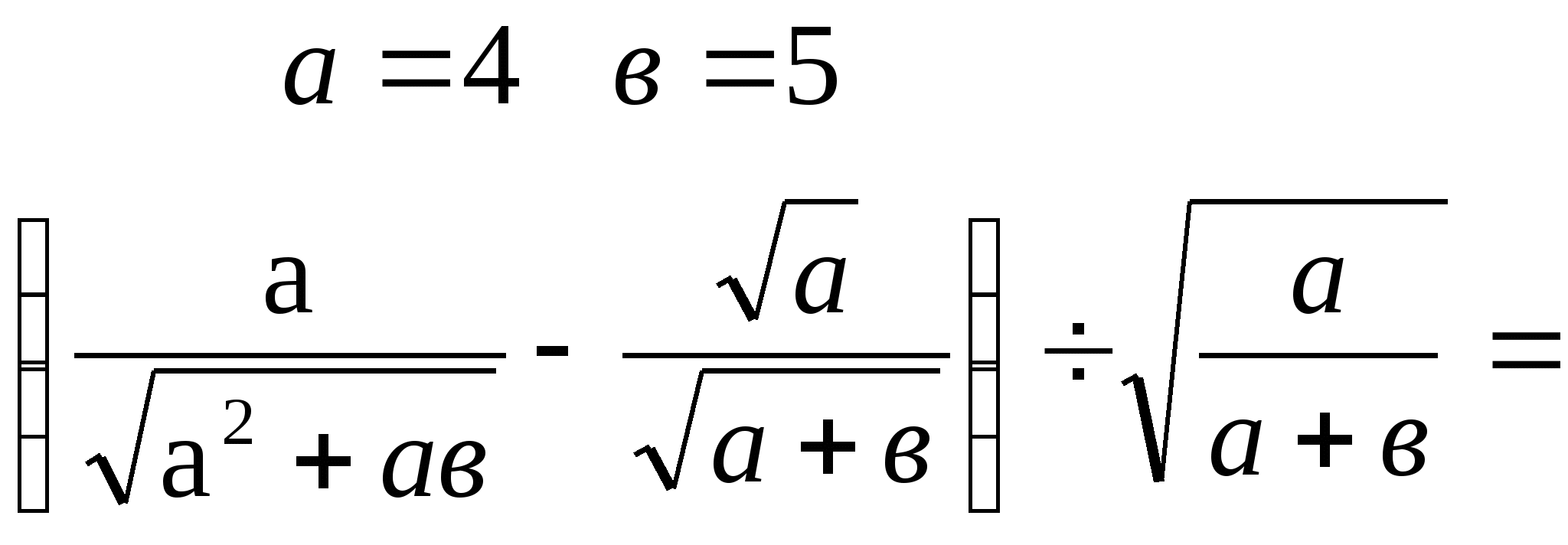 б)
б)
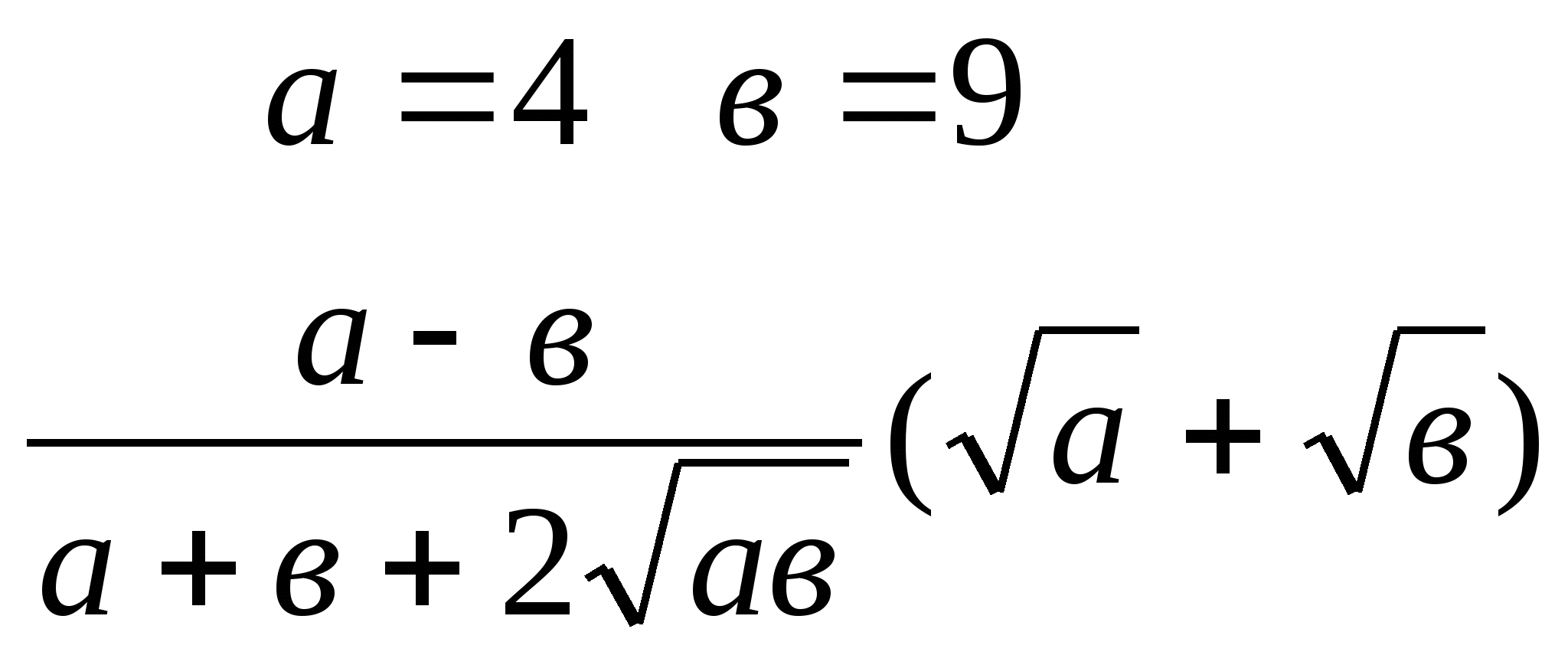
4) Решите уравнение:
а) ![]() б)
б)
![]()
5) Найдите наименьшее х, удовлетворяющего неравенству:
а) ![]() б)
б)
![]()
6) Решите неравенство:
а) ![]() б)
б)
![]()
Контрольная работа № 2
по геометрии «Перпендикулярность прямых и плоскостей в пространстве»
1 урок - 45 минут 10 класс
а) - 1 вариант б) - 2 вариант
1) а) Дан куб ABCDA1B1C1D1. Диагональ куба равна 6 см. Найдите:
-
Р
 ебро
куба.
ебро
куба.
-
Конус угла между диагональю куба и плоскостью основания.
-
Назовите плоскость перпендикулярную плоскости грани СС1DD1 и проходящую через точку В. Ответ обоснуйте.
-
Каково взаимное расположение прямых АА1 и В D. Найдите расстояние между ними.
б) Дан прямоугольный параллелепипед
ABCDA1B1C1D1. Основание
прямоугольного параллелепипеда служит квадрат, диагональ
параллелепипеда равна ![]() см,
а его измерения относятся как 1:1:2. Найдите:
см,
а его измерения относятся как 1:1:2. Найдите:
-
Измерения параллелепипеда.
-
Синус угла между диагональю параллелепипеда и плоскостью его основания.
-
Назовите плоскость, перпендикулярную плоскости грани ВВ1С1С и проходящую через точку Д. Ответ обоснуйте.
2) а) Точка К равноудалена от сторон квадрата
ABCD со стороной а см. Найдите расстояние от точки К до вершины
квадрата, если расстояние от точки К до плоскости квадрата равно
![]() .
.
б) Точка М, равноудаленная от вершин правильного треугольника АВС со стороной в, удалена от плоскости треугольника на расстоянии 2в. Найдите расстояние от точки М до сторон треугольника.
Контрольная работа № 2
по геометрии «Перпендикулярность прямых и плоскостей в пространстве»
1 урок - 45 минут (10 класс гуманитарный класс )
а) - 1 вариант б) - 2 вариант
а) Дан куб ABCDA1B1C1D1. (см рис.)
1 )
Назовите прямые, перпендикулярные прямой АА1;
)
Назовите прямые, перпендикулярные прямой АА1;
2) Назовите прямые, перпендикулярные прямой ВС;
3) Назовите плоскости, перпендикулярные плоскости АА1ВВ1;
4) Назовите плоскости, перпендикулярные прямой В1С1;
5) Назовите прямые, перпендикулярные плоскости А1В1С1D1;
6) Назовите плоскость, перпендикулярную плоскости СС1 D D1 и проходившую через точку В;
7) Каково взаимное расположение прямых АА1 и ВD ? Перпендикулярны ли прямые? Чему равен угол между ними?
8) Ребро куба равно 1. Чему равна диагональ куба?
Ответы:
Назовите прямые, перпендикулярные прямой АА1: АВ, ВС, СD, АD, A1B1, B1C1, C1D1,
A1 D1.
2) Назовите прямые, перпендикулярные прямой ВC: АА1, BB1, D1D, C1C, A1B1, AB1, D1C1, DC.
3) Назовите плоскости, перпендикулярные плоскости АА1ВВ1: A1B1C1D1, ABCD, AA1DD1, BB1CC1.
4) Назовите плоскости, перпендикулярные прямой В1С1: A1B1BA, DD1C1C.
5) Назовите прямые, перпендикулярные плоскости А1В1С1D1: AA1, BB1, CC1, DD1.
6) Назовите плоскость, перпендикулярную плоскости СС1 D D1 и проходившую через точку В: BB1C1C, ABCD.
7) Каково взаимное расположение прямых АА1 и ВD ? Чему равен угол между ними? Перпендикулярные прямые. Да. 900.
8) Ребро куба равно 1. Чему равна диагональ
куба? ![]()
б )
Дан куб ABCDA1B1C1D1.
(см рис.)
)
Дан куб ABCDA1B1C1D1.
(см рис.)
1) Назовите прямые, перпендикулярные прямой DC;
2) Назовите прямые, перпендикулярные прямой A1D1;
3) Назовите плоскости, перпендикулярные плоскости А1В1C1D1;
4) Назовите плоскости, перпендикулярные прямой AB;
5) Назовите прямые, перпендикулярные плоскости DD1C1C;
6) Назовите плоскость, перпендикулярную плоскости BB1C1C и проходившую через точку D;
7) Каково взаимное расположение прямых А1C1 и DD1? Перпендикулярны ли прямые ? Чему равен угол между ними?
8) Ребро куба равно 2. Чему равна диагональ куба?
Ответы:
1) Назовите прямые, перпендикулярные прямой DC: AD, A1D1, BC, B1C1, DD1, BB1, CC1, AA1.
2) Назовите прямые, перпендикулярные прямой A1D1: AA1, DD1, CC1, BB1, A1B1, AB, C1D1, CD.
3) Назовите плоскости, перпендикулярные плоскости А1В1C1D1: AA1DD1, AA1 BB1, BB1C1C, DD1C1C.
4) Назовите плоскости, перпендикулярные прямой AB: AA1D1D, BB1C1C.
5) Назовите прямые, перпендикулярные плоскости DD1C1C: DD1C1C, ABCD.
6) Назовите плоскость, перпендикулярную плоскости BB1C1C и проходившую через точку D:
7) Каково взаимное расположение прямых А1C1 и DD1? Перпендикулярны ли прямые ? Чему равен угол между ними? Скрещивающиеся прямые. Да 900.
8) Ребро куба равно 2. Чему равна диагональ
куба? ![]()
Итоговая контрольная работа
по алгебре и началам анализа (10 класс 2ое полугодие)
Рассчитана на 2 урока, наивысший балл «3».
1) Вычислите:
а) ![]() б)
б)
![]()
2) Найдите значение выражения, если
а) 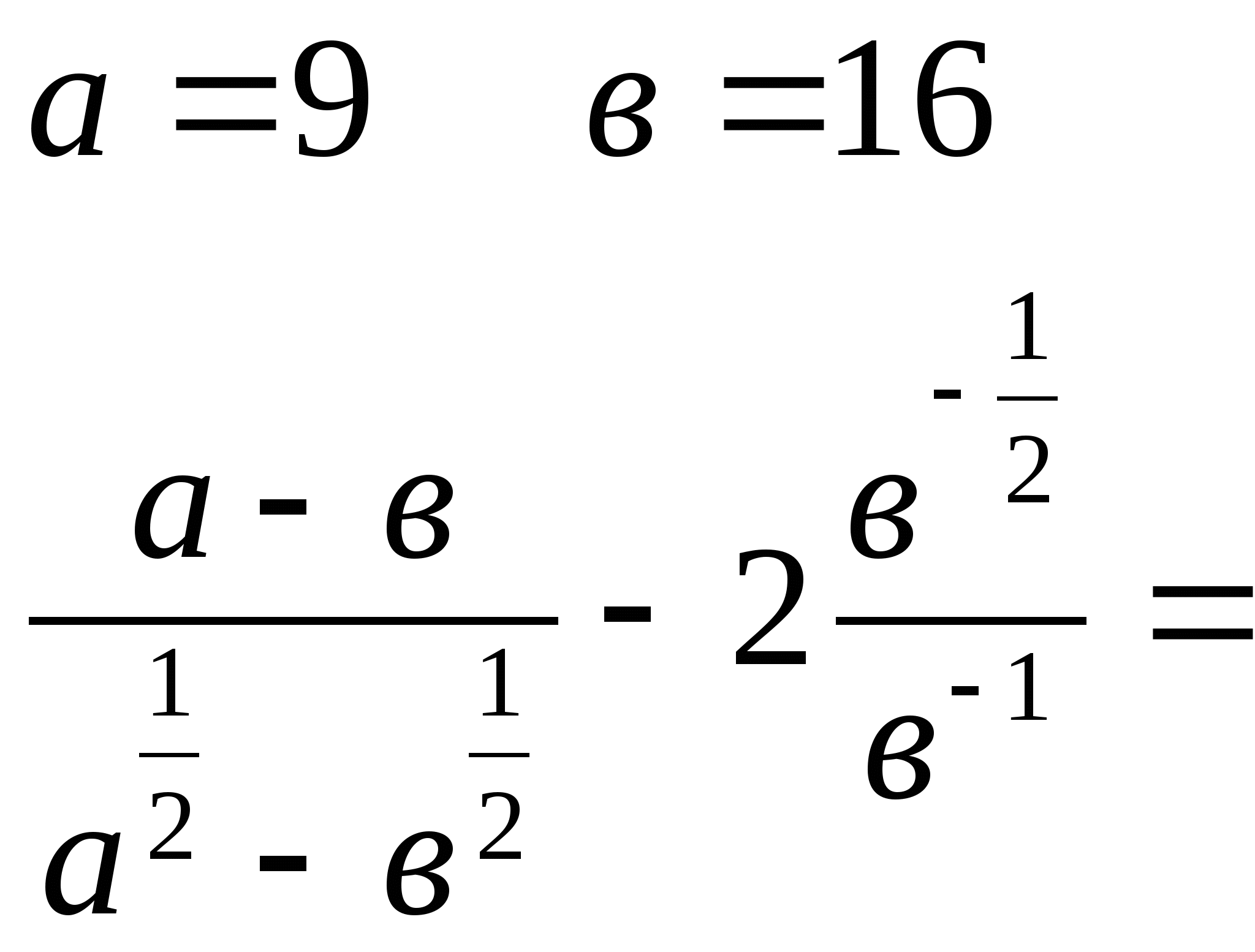 б)
б)
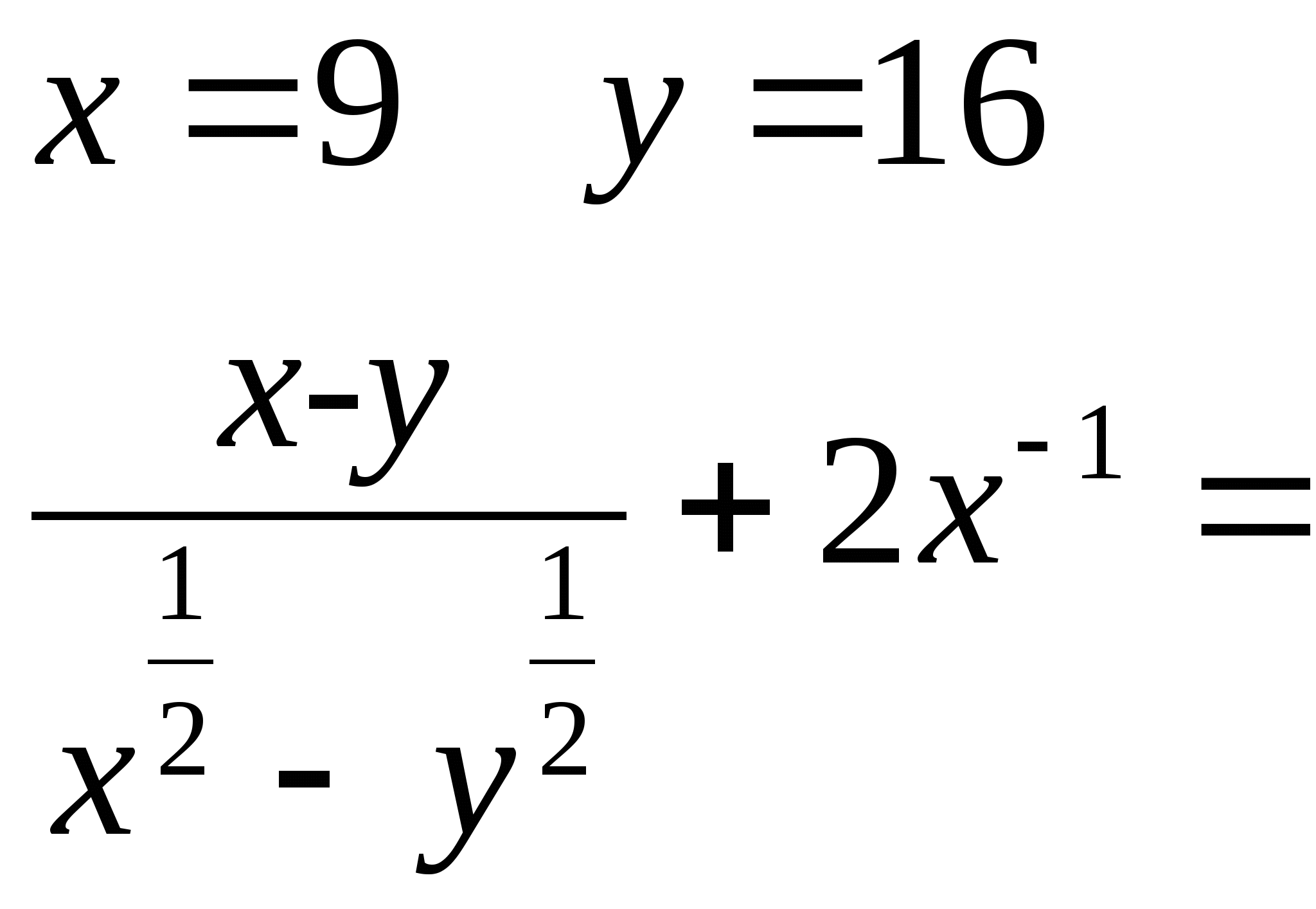
3) Укажите промежуток, которому принадлежит корень уравнения:
а) 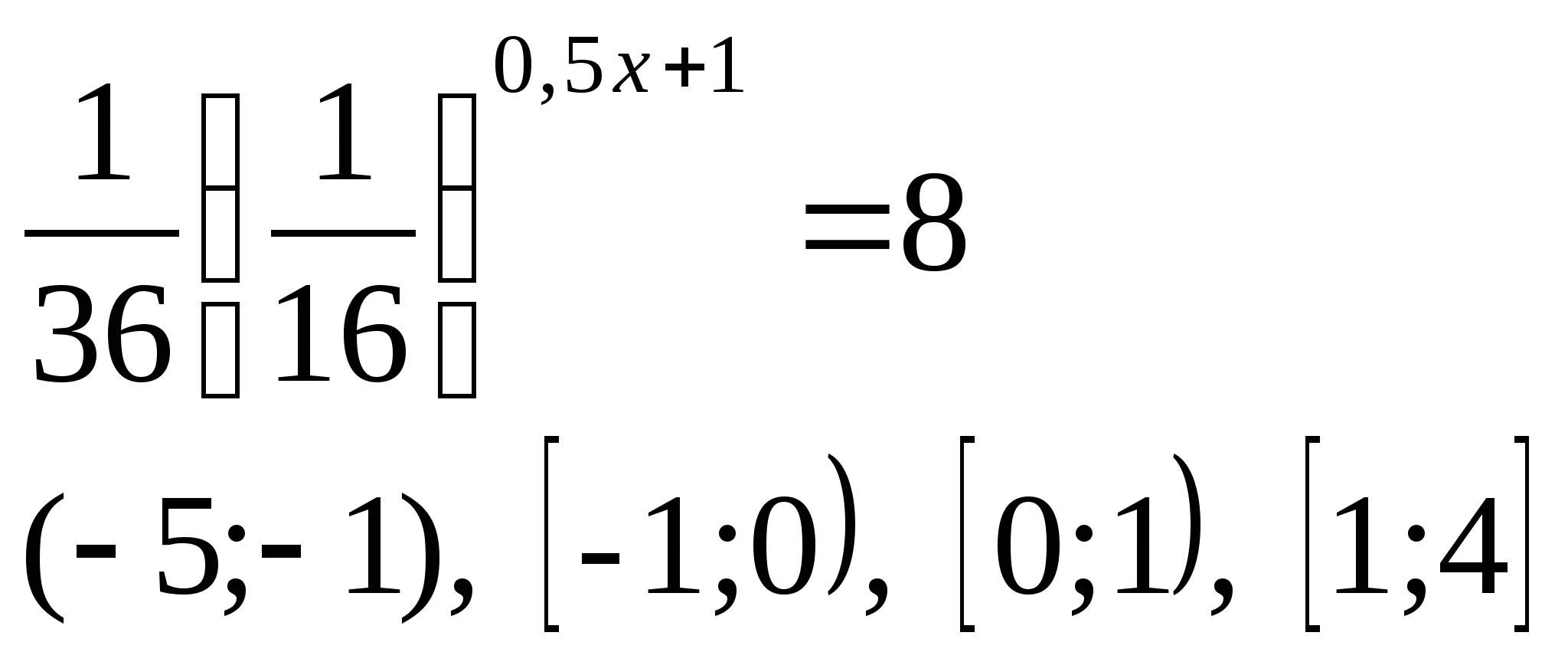 б)
б)
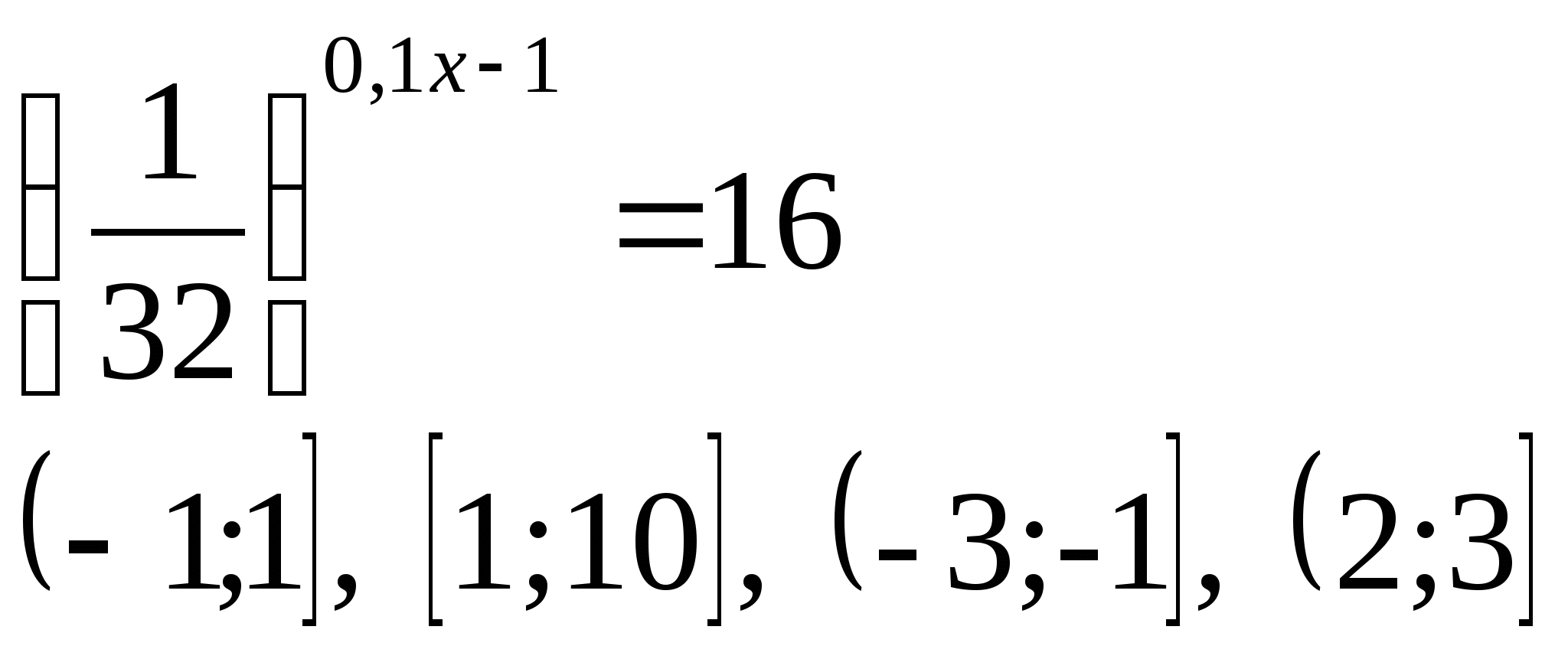
4) Укажите промежуток, которому принадлежат корни уравнения:
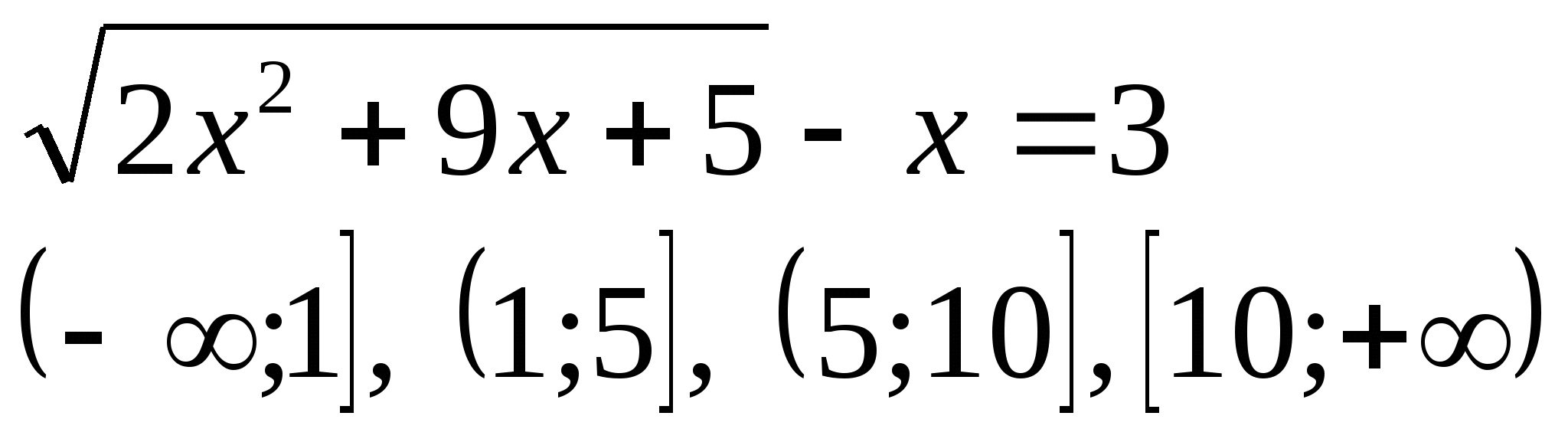 б)
б)
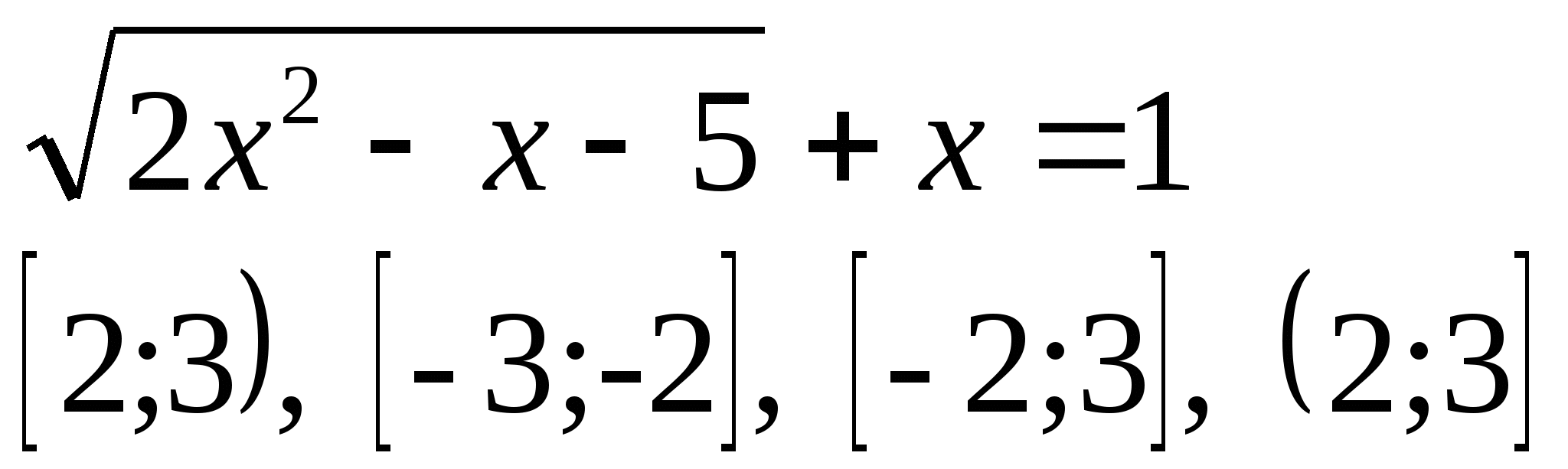
5) Найдите область определения функции:
а) 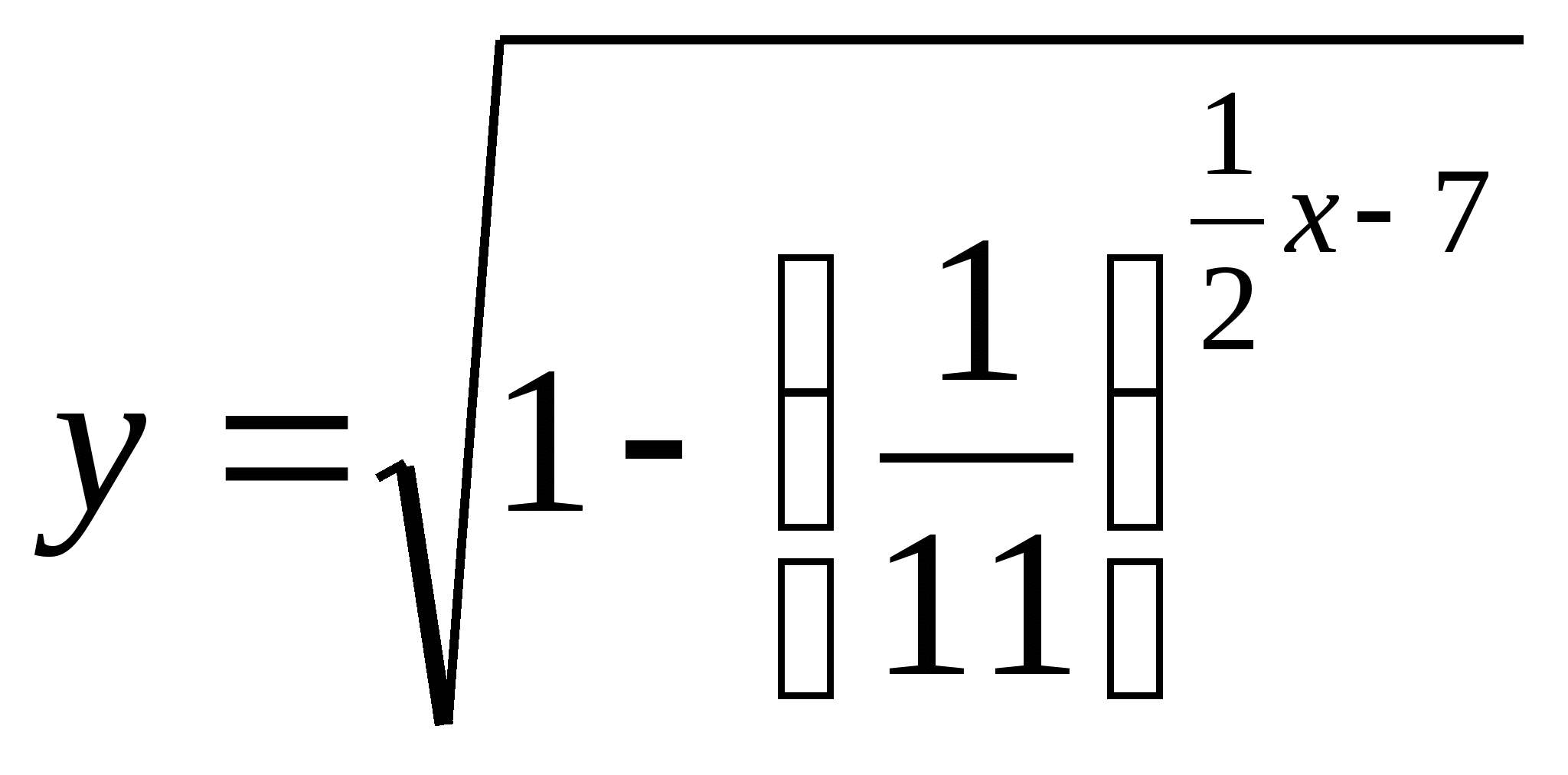 б)
б)