Рабочая тетрадь № 2

Рабочая тетрадь

Тема: «Одночлен и многочлен»

__________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

Данное пособие представляет собой комплект индивидуальных заданий по алгебре для учащихся 7 класса. Оно ориентировано на изучение материала по учебнику «Алгебра 7 класс А.Е.Абылкасымова, В.Е.Корчесвкий, А.Абдиев, З.А.Жумагулова - Алматы: Мектеп, 2012». Представленные здесь задания соответствуют второй главе учебника «Одночлен и многочлен».

Для удобства эти задания напечатаны так, чтобы учащимся можно было работать в данной тетради. Заданий, данных по каждой теме, соответственно больше, чем можно позволить в проверочной работе обычного типа, проводимой в урочное время. Поэтому учителю по своему усмотрению можно давать некоторые задания выполнять дома.

По результатам работы предлагаются два проверочных теста. Данные тестовые задания составлены с целью быстрой проверки усвоения материала темы. Все задания в тесте несложные и, примерно соответствуют обязательному уровню усвоения материала.

§ 5. Одночлен. Стандартный вид одночлена.

Выражения 5а², 2в³(-3)вс², -3а⁷, ху² являются произведениями чисел, переменных и их степеней. Такие выражения называют одночленами.

2в³(-3)вс²=2(-3) в³вс²= - 6в⁴с²

- 6в⁴с² - стандартный вид одночлена

-6 - коэффициент одночлена

например для одночлена - ав⁷ коэффициент равен -1

сумму показателей степеней всех переменных называют степенью одночлена

в одночлене 7ах²у³ сумма показателей степеней всех переменных равна 6

5.1 Выясните, является ли данное выражение одночленом. Если да, то укажите коэффициент и буквенную часть; полученные результаты занесите в таблицу.

выражение

Является ли одночленом?

коэффициент

Буквенная часть

5mn

да

5

mn

-8

5.2 Обведите те одночлены, которые записаны в стандартном виде:

; ; ; ;

; .

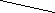5.3 Заполните пустые клетки.

1)

2) .

3) .

4) .

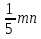5) .

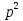6) .

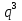5.4 Представьте данный одночлен в виде степени с указанным показателем

(…………………)²

64х¹²у¹⁸ (…………………)³

(…………………)⁶

5.5 Запишите одночлен в стандартном виде.

8bc(0.5)ab=8·0.5·b²ca=4ab²c

………………………………………………………………………………………………………………………

…………………………………………………………………………………………………………………

………………………………………

…………………………………………………………………

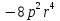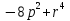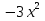5.6 Найдите коэффициент k одночлена

1) ………………………………..

…………………………………………………………………

…………………………………………………………………

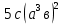2) …………………………………

………………………………………………………………….

…………………………………………………………………..

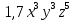Ответ: 1) k=………..; 2) k=……………

5.7 Найдите пары подобных одночленов и вычислите их сумму и разность:

2х 2у х²у 2,9ху² 4х³у⁷ -3х⁵ 6х⁷у³ -9у⁷х³ 5х -7х²у 8,5у 11ху²

…………………………………………………………………

…………………………………………………………………

…………………………………………………………………

…………………………………………………………………

…………………………………………………………………

…………………………………………………………………

5.8 Найдите значение одночлена.

1) 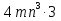, при х=2, у=0,25;

2) 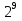, при n=6, p=7, m=2.

……………………………………………………………………………………………………………………………………………………

……………………………………………………………………………………………………………………………………………………

……………………………………………………………………………………………………………………………………………………

……………………………………………………………………………………………………………………………………………………

5.9 Представьте следующие одночлены в виде суммы и разности одночленно

Образец:

+

34s²t

57s²t

-

38s²t

95s²t

57s²t

+

106s²t

-49s²t

+

_____

10 р²k²

-

5 р

21р²k²

+

-8p

-3__

-

+

_____

2.2a²b⁴

-

7.8a

34.2a²b⁴

+

-16.5a

-3__

-27.9

-

5.10 Найдите произведение одночленов. Таблицу заполните по образцу

5.11 Упростите выражение и вычислите его значение при заданных значениях букв

1) (0,8ху²)(0,25ах²у) при а=9, х=-0,75, у=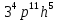

2) 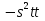при х=0,78, у=4.

……………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………....……………………………………………………………………...............................................................

5.12 Упростите выражение

1) = .……………………………

……………………………………………………………………………………………………………………………………………………

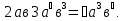2) (-6mn³)(7m³n)+(9m²n²)²=………………………………………

……………………………………………………………………………………………………………………………………………………

3) (-3xy²)²-(2xy²)(-14x²y⁴)=…………………………………………

……………………………………………………………………………………………………………………………………………………

4) (4a²b²)²(3a²b)-(-2ab²)(-3a³b)(8a²b²)=……………………….

……………………………………………………………………………………………………………………………………………………

5.13 Выполните деление одночлена на одночлен:

1) -20m⁴n³: (5m²n²)=…………………………………………………

2) 1.69x³y⁴z⁵:(-1.3x²y³z⁴)=…………………………………………

3) 2583 x³y⁴z⁵:(9x²y):(7y²z³)=………………………………………

…………………………………………………………………………………………………………………………………………………….

5.14 Найдите значение частного при указанных значениях:

1) (-16а⁴в³) : (4а²в²) при а=5, в=0,5;

………………………………………………………………………………………………………………………………………………………………………………………………………………………………

2) (72х⁵у⁴) : (12х⁴у³) при х=-20, у=1/3

……………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………

§ 6. Многочлен и действия над многочленами

Многочленом называется сумма одночленов

выражение 4х²у-5ху+3х-1 - многочлен

в многочлене 5а²в+2+4ав²-3а²в-7

члены 5а²в и -3а²в - подобные члены

если все члены многочлена записать в стандартном виде и выполнить приведение подобных членов, то получится многочлен стандартного вида

5а²в +(-3а²в)=(5-3)·а²в=2а²в

6.1 Подчеркните выражения, которые являются многочленами

2х+2у; 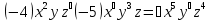; (2х²-5у³)(2х³+5у²);

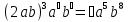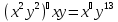; ; 4(2x³-5t³)

6.2 Подчеркните многочлены, записанные в стандартном виде

7x³+5y²-11z; 2x⁴·3x²+8y; 4x³y³-3x+2y-1;

0.6a⁷·a+a⁶+a⁵; 12x⁵+11y⁷+10m⁹; 1.7t⁴b³+t²+0.8b

6.3 Даны одночлены:

5а; - 4аb; 8а²; 2а; - 2,5аb; - а².

Составьте из них еще два многочлена, в котором нет подобных членов:

______________________________________________________________________________________________________

6.4 Запишите слагаемые многочлена в порядке убывания степени переменной:

1. 4а+7а²-5+10а³=…………………………………………………

2. в-3,1в²+2,6в⁴-8,9в³=……………………………………………

3. 11-6с⁸+8с⁵-3с=……………………………………………………

6.5 Выделите многочлен, в котором нет подобных одночленов:

а) 5а + 8а²+12а; б) 5а - 4аb - а²;

в) 8а² + 12а - а².

6.6 Привести подобные члены

1) …………………………

……………………………………………………………………………………………………………………………………

…………………………………………………………………………………………………………………………………….

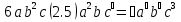2)1,4а³в-3,2ав³+2,1а³в -2,8 ав³-3,5а³в =…………………………

………………………………………………………………………………………………………………………………………………………………………………………………………………………………

6.7 Используя правило отыскания алгебраической суммы многочленов, упростите данное выражение.

а) (7х²+3х)+(5-3х-2х²)=……………………………………………

……………………………………………………………………………………………………………………………………………………

б) (-5х²+2х)-(6+2х-4х²)=…………………………………………

……………………………………………………………………………………………………………………………………………………

6.8 Запишите во втором столбце такой многочлен, чтобы его сумма с первым была равна многочлену, записанному в третьем столбце.

3х + 5

8х - 11

2х + 5а

3х + 6

х² + 2ху + у²

х² - 2ху + у²

7х + 3

х² + 7х - 15

3х + 2а

2х + b

a² - 2ab + b²

a² + 2ab + b²

6.9 Найдите неизвестный множитель:

2а²в

2а·

=

=

4а²

2ав

=

4ав²

=

=

=

3k³

-3k·

-6km²

-3km

6k²m

=

=

6.10 Выполните умножение многочлена на одночлен

(2х+у)·z=………………………………………………………………

b(a-3b)= ………………………………………………………………

(c+2d+a)·a=…………………………………………………………

(-x)(5x+y)=…………………………………………………………

-3a(a-2b+5)=…………………………………………………………

6.11 Выполните умножения многочлена на многочлен:

1. (х+3)(х+2)=………………………………………………………..……..........................................................................................................................................................................................

2. (4n-1)(n+7-m)=……………………………………………………

………………………………………………………………….…………......................................................................................

3. (t3-5t+8)(2t+3)= ……………………………………………

……………………………………………………………….……………………………………………………………….

6.12 Заполните пропуски:

а) (4а - 3) (2а + 5) = 8а² - … + 20а …15 = 8а² … 14а - …;

б) (3х - 5) (5х +4) = 15х² - … + 12х … 20 = 15х² … 13х - …;

в) (2а - 4) (3а + 8) = 6а² - … +16а … 32 = 6а² … 4а - ... .

6.13 Выполните деление

=

12х⁴

=

=

=

-3k·

24х⁵а²

18х³

6х²у²

6.14 Выполните деление двучлена на одночлен:

1. (12х⁴+6х²у²):(6х²)=……………………………………………………………………………………………………………………………………………………………………………………………..

2. (12х⁴-6х²у²):(6х²)=………………………………………………

………………………………………………………………………………………………………………………………………………

3. (18х3+24х5а2) : (6х²)=…………………………………………

………………………………………………………………………

§ 7. Разложение многочлена на множители

1) Вынесение общего множителя за скобку

Это преобразование является следствием распределительного закона ас+вс=с(а+в)

28х³-35х⁴=7х³·4-7х³·5х=7х³(4-5х).

2) Способ группировки

Данный способ основан на том, что переместительный и сочетательный законы сложения позволяют группировать члены многочлена различными способами.

х³-3х²+5х-15 сгруппируем следующим образом

(х³-3х²)+(5х-15)= х²(х-3)+5(х-3)=(х-3)( х²+5)

7.1 Соедините линией соответствующие части определения

представление многочлена в виде суммы двух или нескольких многочленов

Разложение многочлена на множители - это

представление многочлена в виде произведения двух или нескольких одночленов

двух или нескольких многочленов

представление многочлена в виде произведения двух или нескольких многочленов

двух или нескольких многочленов

7.2 Восстановите порядок выполнения действий при разложении многочлена на множители способом группировки.

вынести в каждой группе общий множитель (в виде многочлена) за скобки

1

Чтобы разложить многочлен на множители способом группировки, нужно …

сгруппировать его члены так, чтобы слагаемые в каждой группе имели общий множитель

2

вынести в каждой группе общий множитель в виде одночлена за скобки

3

Ответ:

7.3 Заполните пропуски:

1. cd+c²=c( );

2. xyz-z=z( );

3. k⁴-5k³nb=k³( );

4. 21m³+56mp⁶=7m( );

5. -5ar+15rs=5r( );

6. -n²t-nt³=nt( ).

7.4 Вынесите общий множитель за скобки:

1. ав²+а²в²=____•(а+ав);

2. с³-с⁵=____•(1-с²);

3. -psd-s⁴=____•(pd+s²);

4. -m³n+m f ²=____•(m²n-f ²).

7.5 Заполните пропуски:

1. -а⁷-5…-…=…(а+…а⁵+3);

2. 8х⁴у²-12х²у³+4х²…=…у²(2х²-3у+1);

3. 2ху-3ау+2х²-3ах=(2ху+…)+(-3ау…)=2х(у+х)-3а(у+х)=(у+…)(…-3у).

7.6 Заполните пропуски:

1. k(m-n)+t(m-n)= (m-n)•__________;

2. a(x+y)-b(x+y)= (x+y)•__________;

3. k(m-n)+ (m-n)(m-n)= (m-n)•________.

7.7 Вычислите:

1. 1,08•56-56•0,08=______________________________

_____________________________________________________________________________________________________;

2. 0,3²+0,3•9,7=____________________________________________________________________________________

__________________________________________________.

7.8 Вынесите общий множитель за скобки:

1. 18х³у⁴+12х²у⁵=_______________________________;

2. 12х²у⁵-18х³у⁴=________________________________;

3. -18х³у⁴+12х²у⁵=_______________________________;

4. -12х²у⁵-18х³у⁴=_______________________________.

7.9 Разложите на множители, используя способ введения новых вспомогательных членов:

х²+5ху+4у²=……………………………………………………………………………………………………………………………………

…………………………………………………………………………

х²-6ху+5у²=………………………………………………………….

……………………………………………………………………………………………………………………………………………………

7.10 Вставьте одночлен так, чтобы полученное равенство было верным:

а) 18ab + 16b = . . .(9a + 8);
б) 4ас² + 6а³с³- 2а²с = 2ас (……………………….);
в) ab - ac + b² - bc = (ab - . . .)+(. . . - bc) =

= . . .(b - c) + b(. . . - c) = . . .

7.11 Сгруппируйте попарно члены данного многочлена двумя способами так, чтобы в каждом случае за скобки можно было вынести общий множитель.

1) ac-3bd+ad-3bc=(ac+ad)-(3bd+3bc)=…………………………

………………………………………………………………………….

…………………………………………………………………………..

2) 6ac-3ad+2bc-4bc=(6ac-3ad)+(……………………………….

……………………………………………………………………………………………………………………………………………………

7.13 Разложите на множители:

12а²-18ав+14а-21в=…………………………………………………

…………………………………………………………………………..…………………………………………………………………………..

12х²-4ху-3ху²+у³=……………………………………………………

………………………………………………………………………….…………………………………………………………………………

у+ву+ас-а-ав-су=…………………………………………………..

……………………………………………………………………………………………………………………………………………………

7.14 Найдите значение выражения 3а²-2в+ав-6а при а=2,8 и в=1,6, предварительно разложив его на множители

3а²-2в+ав-6а=………………………………………………………

……………………………………………………………………………………………………………………………………………………

…………………………………………………………………………

7.15 Вычислите:

…………………

…………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………............................................

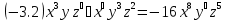ТЕСТЫ

1 вариант

1. Приведите одночлен 2а²вавв³в(-3) к стандартному виду

1. -5а³в⁶;

2. -6а³в⁵;

3. -6а³в⁶;

4. 6а²в⁵.

2. Укажите все подобные среди данных одночленов:

1) а²в; 2) 2а²; 3) -а²в; 4) 2ав²; 5) 5ава.

1. Первый, третий, четвертый;

2. Первый, третий и пятый;

3. Второй, третий и четвертый;

4. Первый и третий.

3. Упростите выражение 3аваа+7а²ва-15ва³:

1. 5а³в;

2. 4а³в;

3. -4а³в;

4. -5а³в.

4. Среди данных равенств укажите все верные:

1. 33а³в⁴=30а³+3в⁴;

2. 33а³в⁴=16 а³в⁴+17в⁴ а³;

3. 33а³в⁴=20а³в⁴+15а³в⁴-2а³в⁴;

4. 33а³в⁴=35а³в⁶-2а³в²;

1. Второе и третье;

2. Второе;

3. Первое и четвертое;

4. Третье.

5. Упростите выражение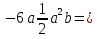

1. -2а²сх⁶;

2. -2а³сх⁵;

3. -2а³х⁵;

4. 2а³сх⁵.

6. Упростите выражение (-а²с)⁵:

1. -а⁷с⁶;

2. а¹⁰с⁵;

3. -а¹⁰с⁵;

4. -а⁷с⁶.

7. Упростите выражение 36а¹²с³d:(-4ac³)

1. -9a¹¹d;

2. -9a¹²;

3. -9a¹¹cd;

4. 9a¹¹d.

8. Какой из указанных ниже одночленов А удовлетворяет равенству 81а⁴в⁶=А²?

1. А=9а²в⁴;

2. А=9а²в³;

3. А=-9ав³;

4. А=27а²в³.

9. Найдите числовое значение выражения 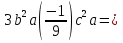, если а=1,5

1. 9;

2. 36;

3. 18;

4. 4,5.

10. Раскройте скобки: -ав(2а-3в²)

1. 2а²в-3ав³;

2. -2а²в+3ав³;

3. -2ав+3ав³;

4. -2а²в-ав³.

11. Раскройте скобки (2а+1)(а-2)

1. 2а²+5а-2;

2. 2а²-3а-2

3. 2а²-3а+2;

4. 2а²+5а+2.

12. Решите уравнение (2х²+5х-3)-2(х²+х+4)=0

1. ;

2. ;

3. ;

4. 

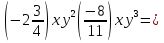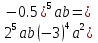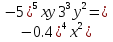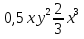
13. Даны равенства:

1) 3а²в-6а³в=3а²в(1-2а);

2) 5х²+10х³+15х⁴=5х²(1+2х+3х²).

Какое их них верно (да), какое неверно (нет)?

1. Да, да;

2. Да, нет;

3. Нет, да;

4. Нет, нет.

14. Разложите многочлен 4-2х на множители

1. 2(2+х);

2. 2(2-х);

3. 4(1-х);

4. 4(1+х)

15. Разложите многочлен а³в²-а⁴в на множители

1. а⁴в(в-а);

2. а³в²(1-а);

3. а³в(в-а);

4. а³в(1-а)

16. Разложите многочлен 15ху²+5ху-20х²у на множители

1. 5ху(3у+1-4х);

2. 5х(3у²+у-2х);

3. 5ху(3у-4х);

4. 5х(3у²+у-4х).

17. Разложите многочлен а(3+в)+в+3 на множители

1. (в+3)(а+1);

2. (3+в)(а-1);

3. (в+3)а;

4. (3+в)(1-а).

18. Разложите многочлен х(у-с)-(с-у) на множители

1. (х-1)(у-с);

2. (х+1)(у-с);

3. (х-1)(с-у);

4. (х+1)(с-у).

19. Разложите многочлен 3х-3у-ах+ау на множители

1. (х-у)(а-3);

2. (х-у)(а+3);

3. (х-у)(3-а);

4. (у-х)(3+а).

20. Решите уравнение 8х(х⁴-2)-2=8х⁵+14

1. 1;

2. -1;

3. 2;

4. -2.

Ответы:

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

2 вариант

1. Приведите одночлен 2а²вав³а(-5) к стандартному виду

1. -10а⁴в³;

2. -10а³в³;

3. -10а⁴в⁴;

4. 10а⁴в⁴.

2. Укажите все подобные среди данных одночленов:

1) 2а²в; 2) а²; 3) -4а²в; 4) 2ав²; 5) 3ваа.

1. Первый, третий, четвертый;

2. Первый, третий и пятый;

3. Второй, третий и четвертый;

4. Первый и пятый.

3. Упростите выражение 2а³ва+7а²ва²-15ава³:

1. -6а⁴в;

2. 6а³в;

3. -6в а⁴;

4. -6а³в.

4. Среди данных равенств укажите все верные:

1. 27а³в⁴=20а³+7в⁴;

2. 27а³в⁴=16 а³в⁴+11в⁴ а³;

3. 27а³в⁴=10а³в⁴+19а³в⁴-2а³в⁴;

4. 27а³в⁴=25а³в⁶+2а³в²;

1. Третье;

2. Второе;

3. Первое и четвертое;

4. Третье и второе.

5. Упростите выражение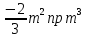

1. -2а⁸вс³;

2. -2а⁶в²с³;

3. -2а⁸в²с³;

4. 2а⁶ в²с³.

6. Упростите выражение (-а³с²)⁴:

1. -а⁷с⁶;

2. а¹²с⁸;

3. -а¹²с⁸;

4. а⁷с⁶.

7. Упростите выражение 48а¹⁰с⁴х:(-6ac³)

1. -8a⁶с;

2. 8a⁹сх;

3. -8a¹⁰cх;

4. -8a⁹сх.

8. Какой из указанных ниже одночленов А удовлетворяет равенству 64у⁴z⁶=А²?

1. А=8у⁶ z ⁴;

2. А=-8у² z ³;

3. А=-8у⁴ z⁴;

4. А=32у⁴ z ³.

9. Найдите числовое значение выражения 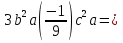, если а=-0,5

1. 2;

2. 4;

3. -2;

4. -4.

10. Раскройте скобки: -ав(3а²-2в)

1. 2ав²-3а³в;

2. -2ав²+3а³в;

3. 2ав-3а³в;

4. -3а²в+2ав².

11. Раскройте скобки (2а-1)(а+2)

1. 2а²+3а-2;

2. 2а²-3а-2;

3. 2а²-3а+2;

4. 2а²+5а+2.

12. Решите уравнение (3х²+5х-3)-3(х²+х+4)=0

1. ;

2. ;

3. ;

4. 

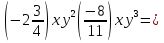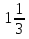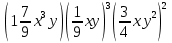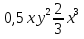
13. Даны равенства:

1) 6ав²-9а³в=3ав(2-3а²);

2) 12с⁵+6с⁴+6с³=6с³(2с²+с).

Какое их них верно (да), какое неверно (нет)?

1. Да, да;

2. Да, нет;

3. Нет, да;

4. Нет, нет.

14. Разложите многочлен 6а-3 на множители

1. 3(2а-1);

2. 3(2а+1);

3. 6(а-1);

4. 3(а-1)

15. Разложите многочлен а²в³-а³в⁴ на множители

1. а²в³ (1-ав);

2. ав³(1-а²в);

3. а³(в³-в⁴);

4. в³(х²-х³)

16. Разложите многочлен 12х²у-6ху-24ху² на множители

1. 6ху(2х-1-4у);

2. 6ху(6х-1-4у);

3. 6ху(2х-4у);

4. 6ху(2х+4у+1).

17. Разложите многочлен х(у+5)+5+у на множители

1. (х-1)(у+5);

2. (у+5)х;

3. (х+1)(у+5);

4. (х-1)(5-у).

18. Разложите многочлен в-с-а(с-в) на множители

1. (а-1)(в+с);

2. (а+1)(с-в);

3. (а-1)(в-с);

4. (а+1)(в-с).

19. Разложите многочлен ав-ас+4с-4в на множители

1. (в+с)(а-4);

2. (в-с)(а+4);

3. (в-с)(4-а);

4. (в-с)(а-4).

20. Решите уравнение 2,5х-5х²=0

1. 0,5;

2. -0,5; 0;

3. 0; 0,5;

4. 0; 2,5.

Ответы:

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

Коды ответов

1 вариант

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

с

в

д

а

в

с

а

в

с

в

в

в

а

в

с

а

а

в

с

в

2 вариант

1

2

3

4

5

6

7

8

9

10

11

12

13

14

15

16

17

18

19

20

с

в

а

д

в

в

д

в

а

а

а

в

д

а

а

а

с

д

д

с

Литература

1. Алгебра 7 класс. Учебник. А.Е.Абылкасымова, В.Е.Корчесвкий, А.Абдиев, З.А.Жумагулова - Алматы: Мектеп, 2012.

2. Рабочая тетрадь. Алгебра 7. И.И.Зубарева, М.С. Мильштейн, «Мнемозина» Москва 2012.

3. Рабочая тетрадь. Алгебра 7. Ю.М.Колягин «Просвещение» 2012.

4. Тесты. Алгебра 7. Мордкович А.Г. 2009

5. Контрольные и проверочные работы по алгебре. Л.И.Звавич, Л.Я.Шляпочник. Москва 2000