Рабочая программа по геометрии 7-9 фгос Атанасян

Краснодарский край

муниципальное образование Кореновский район

муниципальное общеобразовательное бюджетное учреждение

средняя общеобразовательная школа № 9

муниципального образования Кореновский район.

УТВЕРЖДЕНО

решением педагогического совета

от «___» ____________2016 года протокол №__

Председатель педсовета _____________ Т. В. Дорошенко

РАБОЧАЯ ПРОГРАММА

По геометрии 1

Уровень образования (класс) основное общее образование (7 -9 класс)

Количество часов 204 Уровень базовый 1

Учитель Малахова Светлана Николаевна

Программа разработана в соответствии и на основе ФГОС основного общего образования, авторской программы

« Сборник рабочих программ. Геометрия, 7-9 классы», автор/составитель: Т.А. Бурмистрова. - М.: Просвещение, 2011, УМК «Геометрия 7 - 9», авт. Л.С. Атанасян и др. М.: Просвещение

ПЛАНИРУЕМЫЕ РЕЗУЛЬТАТЫ ИЗУЧЕНИЯ КУРСА ГЕОМЕТРИИ.

К концу изучения курса геометрии в основной школе будет обеспечена готовность учащихся к дальнейшему образованию.

Предметные результаты:

• овладение базовым понятийным аппаратом по основным разделам содержания; представление об основных изучаемых понятиях (число, геометрическая фигура) как важнейших математических моделях, позволяющих описывать и изучать реальные процессы и явления;

• умение работать с геометрическим текстом (анализировать, извлекать необходимую информацию), точно и грамотно выражать свои мысли в устной и письменной речи с применением математической терминологии и символики, использовать различные языки математики, проводить классификации, логические обоснования, доказательства математических утверждений;

• овладение навыками устных, письменных, инструментальных вычислений;

• овладение геометрическим языком, умение использовать его для описания предметов окружающего мира, развитие пространственных представлений и изобразительных умений, приобретение навыков геометрических построений; усвоение систематических знаний о плоских фигурах и их свойствах, а также на наглядном уровне - о простейших пространственных телах, умение применять систематические знания о них для решения геометрических и практических задач;

• умение применять систематические знания о них для решения геометрических и практических задач;

• умение измерять длины отрезков, величины углов, использовать формулы для нахождения периметров, площадей и объёмов геометрических фигур;

• умение применять изученные понятия, результаты, методы для решения задач практического характера и задач из смежных дисциплин с использованием при необходимости справочных материалов, калькулятора, компьютера.

Наглядная геометрия

Выпускник научится:

• распознавать на чертежах, рисунках, моделях и в окружающем мире плоские и пространственные геометрические фигуры;

• распознавать развёртки куба, прямоугольного параллелепипеда, правильной пирамиды, цилиндра и конуса;

• определять по линейным размерам развёртки фигуры линейные размеры самой фигуры и наоборот;

• вычислять объём прямоугольного параллелепипеда.

Выпускник получит возможность:

• вычислять объёмы пространственных геометрических фигур, составленных из прямоугольных параллелепипедов;

• углубить и развить представления о пространственных геометрических фигурах;

• применять понятие развёртки для выполнения практических расчётов.

Геометрические фигуры

Выпускник научится:

• пользоваться языком геометрии для описания предметов окружающего мира и их взаимного расположения;

• распознавать и изображать на чертежах и рисунках геометрические фигуры и их конфигурации;

• находить значения длин линейных элементов фигур и их отношения, градусную меру углов от 0 до 180°, применяя определения, свойства и признаки фигур и их элементов, отношения фигур (равенство, подобие, симметрии, поворот, параллельный перенос);

• оперировать с начальными понятиями тригонометрии и выполнять элементарные операции над функциями углов;

• решать задачи на доказательство, опираясь на изученные свойства фигур и отношений между ними и применяя изученные методы доказательств;

• решать несложные задачи на построение, применяя основные алгоритмы построения с помощью циркуля и линейки;

• решать простейшие планиметрические задачи в пространстве.

Выпускник получит возможность:

• овладеть методами решения задан на вычисления и доказательства: методом от противного, методом подобия, методом перебора вариантов и методом геометрических мест точек;

• приобрести опыт применения алгебраического и тригонометрического аппарата и идей движения при решении геометрических задач;

• овладеть традиционной схемой решения задач на построение с помощью циркуля и линейки: анализ, построение, доказательство и исследование;

• научиться решать задачи на построение методом геометрического места точек и методом подобия;

• приобрести опыт исследования свойств планиметрических фигур с помощью компьютерных программ;

• приобрести опыт выполнения проектов по темам: «Гео-метрические преобразования на плоскости», «Построение отрезков по формуле».

Измерение геометрических величин

Выпускник научится:

• использовать свойства измерения длин, площадей и углов при решении задач на нахождение длины отрезка, длины окружности, длины дуги окружности, градусной меры угла;

• вычислять длины линейных элементов фигур и их углы, используя формулы длины окружности и длины дуги окружности, формулы площадей фигур;

• вычислять площади треугольников, прямоугольников, параллелограммов, трапеций, кругов и секторов;

• вычислять длину окружности, длину дуги окружности;

• решать задачи на доказательство с использованием формул длины окружности и длины дуги окружности, формул площадей фигур;

• решать практические задачи, связанные с нахождением геометрических величин (используя при необходимости справочники и технические средства).

• Выпускник получит возможность:

• вычислять площади фигур, составленных из двух или более прямоугольников, параллелограммов, треугольников, круга и сектора;

• вычислять площади многоугольников, используя отношения равновеликости и равносоставленности;

• приобрести опыт применения алгебраического и тригонометрического аппарата и идей движения при решении задач на вычисление площадей многоугольников.

Координаты

Выпускник научится:

вычислять длину отрезка по координатам его концов; вычислять координаты Выпускник получит возможность:

• овладеть координатным методом решения задач на вычисление и доказательство;

• приобрести опыт использования компьютерных программ для анализа частных случаев взаимного расположения окружностей и прямых;

• приобрести опыт выполнения проектов на тему «Применение координатного метода при решении задан на вычисление и доказательство».

Векторы

• середины отрезка;

• использовать координатный метод для изучения свойств прямых и окружностей.

Выпускник научится:

• оперировать с векторами: находить сумму и разность двух векторов, заданных геометрически, находить вектор, равный произведению заданного вектора на число;

• находить для векторов, заданных координатами: длину вектора, координаты суммы и разности двух и более векторов, координаты произведения вектора на число, применяя при необходимости сочетательный, переместительный и распределительный законы;

• вычислять скалярное произведение векторов, находить угол между векторами, устанавливать перпендикулярность прямых.

Выпускник получит возможность:

• овладеть векторным методом для решения задач на вычисление и доказательство;

• приобрести опыт выполнения проектов на тему «Применение векторного метода при решении задач на вычисление и доказательство».

В результате изучения курса геометрии 7 класса ученик научится:

• использовать язык геометрии для описания предметов окружающего мира;

• распознавать и изображать на чертежах и рисунках геометрические фигуры и их отношения;

• использовать свойства измерения длин и углов при решении задач на нахождение длины отрезка и градусной меры угла;

• решать задачи на вычисление градусных мер углов от 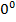до 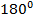с необходимыми теоретическими обоснованиями, опирающимися на изучение свойства фигур и их элементов;

• решать задачи на доказательство, опираясь на изученные свойства фигур и отношения между ними и применяя изученные виды доказательств;

• решать несложные задачи на построение циркуля и линейки;

• решать практические задачи, связанные с нахождением геометрических величин (используя при необходимости справочники и технические средства).

Ученик получит возможность:

• овладеть методами решения задач на вычисления и доказательства: методом от противного;

• овладеть традиционной схемой решения задач на построения с помощью циркуля и линейки: анализ, построение, доказательство и исследование

2. Содержание учебного курса

Наглядная геометрия. Наглядные представления о пространственных фигурах: куб, параллелепипед, призма, пирамида, шар, сфера, конус, цилиндр. Изображение пространственных фигур. Примеры сечений. Многогранники. Правильные многогранники. Примеры разверток многогранников, цилиндра и конуса.

Понятие объема; единицы объема. Объем прямоугольного параллелепипеда, куба

Геометрические фигуры. Прямые и углы. Точка, прямая, плоскость. Отрезок, луч. Угол. Виды углов. Вертикальные и смежные углы. Биссектриса угла.

Параллельные и пересекающееся прямые. Перпендикулярные прямые. Теоремы о параллельности и перпендикулярности прямых. Перпендикуляр и наклонная к прямой. Серединный перпендикуляр к отрезку.

Геометрическое место точек. Свойства биссектрисы угла и серединного перпендикуляра к отрезку.

Треугольник. Высота, медиана, биссектриса, средняя линия треугольника. Равнобедренные и равносторонние треугольники; свойства и признаки равнобедренного треугольника. Признаки равенства треугольников. Неравенство треугольника. Соотношение между сторонами и углами треугольника.

Сумма углов треугольника. Внешние углы треугольника. Теорема Фалеса. Подобие треугольников. Признаки подобия треугольников. Теорема Пифагора. Синус, косинус, тангенс, котангенс, острого угла прямоугольного треугольника и углов от 0 до 180˚; приведение к острому углу. Решение прямоугольных треугольников. Основное тригонометрическое тождество. Формулы, связывающие синус, косинус, тангенс, котангенс одного и того же угла. Решение треугольников: теорема косинусов и теорема синусов. Замечательные точки треугольника.

Четырехугольник. Параллелограмм, его свойства и признаки. Прямоугольник, квадрат, ромб, их свойства и признаки. Трапеция, средняя линия трапеции.

Многоугольник. Выпуклые многоугольники. Сумма углов выпуклого многоугольника. Правильные многоугольники.

Окружность и круг. Дуга, хорда. Сектор, сегмент. Центральный угол, вписанный угол, величина вписанного угла. Взаимное расположение прямой и окружности, двух окружностей. Касательная и секущая к окружности, их свойства. Вписанные и описанные многоугольники. Окружность, вписанная в треугольник, и окружность, описанная около треугольника. Вписанные и описанные окружности правильного многоугольника.

Геометрические преобразования. Понятие о равенстве фигур. Понятие о движении: осевая и центральная симметрия, параллельный перенос, поворот. Понятие о подобии фигур и гомотетии.

Построение с помощью циркуля и линейки. Основные задачи на построение: деление отрезка на пополам; построение угла, равного данному; построение треугольника по трем сторонам; построение перпендикуляра к прямой; построение биссектрисы угла; деление отрезка на n равных частей.

Решение задач на вычисление, доказательство и построение с использованием свойств изученных фигур.

Измерение геометрических величин. Длинна отрезка. Расстояние от точки до прямой. Расстояние между параллельными прямыми.

Периметр многоугольника.

Длинна окружности, число ᴨ; длинна дуги окружности.

Градусная мера угла, соответствие между величиной центрального угла и длинной дуги окружности.

Понятие площади плоских фигур. Равносоставленные и равновеликие фигуры. Площадь прямоугольника. Площади параллелограмма, треугольника и трапеции. Площадь многоугольника. Площадь круга и площадь сектора. Соотношение между площадями подобных фигур.

Решение задач на вычисление и доказательства с использованием изученных формул.

Координаты. Уравнение прямой. Координаты середины отрезка. Формула расстояния между двумя точками плоскости. Уравнение окружности.

Векторы. Длина (модуль) вектора. Равенство векторов. Коллинеарные векторы. Координаты вектора. Умножение вектора на число, сумма векторов, разложение вектора по двум неколлинеарным векторам. Скалярное произведение векторов.

Теоретико-множественные понятия. Множество, элемент множества. Задание множеств перечислением множеств элементов, характеристическим свойством. Подмножество. Объединение и пересечение множеств.

Элементы логики. Определение. Аксиомы и теоремы. Доказательство. Доказательство от противного. Теорема, обратная данной. Пример и контр пример.

Понятия о равносильности, следовании, употребление логических связок если…, то…, в том и только в том случае, логические связки и, или.

Геометрия в историческом развитии. От землемерия к геометрии. Пифагор и его школа. Фалес. Архимед. Построение правильных многоугольников. Трисекция угла. Квадратура круга. Удвоение куба. История числа п. Золотое сечение. «Начала» Эвклида. Л. Эйлер. Н.И. Лобачевский. История пятого постулата.

Изобретение метода координат, позволяющего переводить геометрические объекты на язык алгебры. Р. Декарт и П. Ферма. Примеры различных систем координат на плоскости.

3.1. Тематическое планирование геометрии в 7 классе

Разделы программы

Кол-во часов

Контрольных работ

Характеристика основных видов деятельности ученика

Начальные геометрические сведения

10

1

Объяснять, что такое отрезок, луч, угол, какие фигуры называются равными, как сравниваются и измеряются отрезки и углы, что такое градус и градусная мера угла, какой угол называется прямым, тупым, острым, развёрнутым, что такое середина отрезка и биссектриса угла, какие углы называются смежными и какие вертикальными; формулировать и обосновывать утверждения о свойствах смежных и вертикальных углов; объяснять, какие прямые называются перпендикулярными; формулировать и обосновывать утверждение о свойстве двух прямых, перпендикулярных к третьей; изображать и распознавать указанные простейшие фигуры на чертежах; решать задачи, связанные с этими простейшими фигурами.

Треугольники

17

1

Объяснять, какая фигура называется треугольником, что такое вершины, стороны, углы и периметр треугольника, какой треугольник называется равнобедренным и какой равносторонним, какие треугольники называются равными; изображать и распознавать на чертежах треугольники и их элементы; формулировать и доказывать теоремы о признаках равенства треугольников; объяснять, что называется перпендикуляром, проведённым из данной точки к данной прямой; формулировать и доказывать теорему о перпендикуляре к прямой; объяснять, какие отрезки называются медианой, биссектрисой и высотой треугольника; формулировать и доказывать теоремы о свойствах равнобедренного треугольника; решать задачи, связанные с признаками равенства треугольников и свойствами равнобедренного треугольника; формулировать определение окружности; объяснять, что такое центр, радиус, хорда и диаметр окружности; решать простейшие задачи на построение (построение угла, равного данному, построение биссектрисы угла, построение перпендикулярных прямых, построение середины отрезка) и более сложные задачи, использующие указанные простейшие; сопоставлять полученный результат с условием задачи; анализировать возможные случаи

Параллельные прямые

13

1

Формулировать определение параллельных прямых; объяснять с помощью рисунка, какие углы, образованные при пересечении двух прямых секущей, называются накрест лежащими, какие односторонними и какие соответственными; формулировать и доказывать теоремы, выражающие признаки параллельности двух прямых; объяснять, что такое аксиомы геометрии и какие аксиомы уже использовались ранее; формулировать аксиому параллельных прямых и выводить следствия из неё; формулировать и доказывать теоремы о свойствах параллельных прямых, обратные теоремам о признаках параллельности, связанных с накрест лежащими, соответственными и односторонними углами, в связи с этим объяснять, что такое условие и заключение теоремы, какая теорема называется обратной по отношению к данной теореме; объяснять, в чём заключается метод доказательства от противного: формулировать и доказывать теоремы об углах с соответственно параллельными и перпендикулярными сторонами; приводить примеры использования этого метода; решать задачи на вычисление, доказательство и построение, связанные с параллельными прямыми.

Соотношения между сторонами и углами треугольника

18

2

Формулировать и доказывать теорему о сумме углов треугольника и её следствие о внешнем угле треугольника; проводить классификацию треугольников по углам; формулировать и доказывать теорему о соотношениях между сторонами и углами треугольника (прямое и обратное утверждения) и следствия из неё, теорему о неравенстве треугольника; формулировать и доказывать теоремы о свойствах прямоугольных треугольников (прямоугольный треугольник с углом 30°, признаки равенства прямоугольных треугольников); формулировать определения расстояния от точки до прямой, расстояния между параллельными прямыми; решать задачи на вычисление, доказательство и построение, связанные с соотношениями между сторонами и углами треугольника и расстоянием между параллельными прямыми, при необходимости проводить по ходу решения дополнительные построения, сопоставлять полученный результат с условием задачи, в задачах на построение исследовать возможные случаи.

Повторение. Решение задач.

10

-

Всего уроков

68

Контрольных работ

5

3.2. Тематическое планирование геометрии в 8 классе

СОГЛАСОВАНО

Протокол заседания методического объединения учителей естественно-математического цикла

МОБУ СОШ № 9 МО Кореновский район

от «___» августа 2016 года № 1

________________________________

СОГЛАСОВАНО

Заместитель директора по УВР

_______________/Т.А. Забара/

«___» __________ 2016 года

СОГЛАСОВАНО

Заместитель директора

МОБУ СОШ № 9 по УВР

_______________/Т.А. Забара/

«___» __________ 201 года

Краснодарский край

муниципальное образование Кореновский район

муниципальное общеобразовательное бюджетное учреждение

средняя общеобразовательная школа № 9

муниципального образования Кореновский район.

Календарно-тематическое

планирование

по геометрии 1

Класс 7 1

Учитель Малахова Светлана Николаевна11

Количество часов: всего 68 часов; в неделю 2 часа; 1

Планирование составлено на основе рабочей программы Малаховой Светланы Николаевны, утвержденной решением педагогического совета, протокол №1 от .08. 2016г.

Планирование составлено в соответствии и на основе ФГОС основного общего образования, авторской рабочей программы Т.А. Бурмистровой («Геометрия. Сборник рабочих программ 7 - 9 классы», издательство Москва «Просвещение», 2011), УМК «Геометрия 7-9» Атанасян Л.С.

Учебник: Геометрия. Учебник для 7 - 9 классов общеобразовательных учреждений

Издательство М.: Просвещение 2016 г.

Автор: Л.С. Атанасян