Тетодическая разаботка практичекого занятияТеория Вероятностей

СПб ГБОУ СПО «Медицинский колледж имени В.М. Бехтерева»

Методическая разработка практического занятия

по учебной дисциплине Математика

на тему Элементы теории вероятностей

для специальности среднего профессионального образования

34.02.01 «Сестринское дело»

Санкт - Петербург

2016 г.

Содержание

Пояснительная записка 3

1. Обоснование темы. 3

2. Цель и задачи. 3

3. Материально-техническое и методическое оснащение занятия: 5

4. Схемы интегрированных связей. 5

5. Граф логической структуры проведения занятия: 6

6. План занятия: 7

7. Этапы планирования занятия 8

8. Карта самоподготовки студентов к занятию по теме «Решение задач по комбинаторике.» 9

9. Карта самоподготовки студентов к занятию по теме «Практическое применение статистических показателей для вычисления здоровья населения» 10

10. Термины 11

11. Рекомендованная литература 11

Приложение 1 12

Приложение 2 13

Приложение 3 14

Приложение 4 16

Приложение 5 21

Пояснительная записка

Методическая разработка составлена в соответствии с государственными требованиями к минимуму содержания и уровню подготовки выпускников по специальности для специальности среднего профессионального образования 34.02.01 «Сестринское дело»

1. Обоснование темы.

Вероятность позволяет нам судить о том, как часто можно ожидать появления того или иного события при заданном числе испытаний. . В теории вероятностей исследуются закономерности, относя­щиеся к случайным событиям, величинам, процессам. В биологии и медицине теория вероятностей применялась главным образом для обработки результатов. Методы теории вероятностей и математической статики начинают все больше использоваться в медицине (задачи диагностики и расшифровки ЭКГ, установление эффективности того или иного лекарства).

Овладения основными приемами решения различных математических задач способствует формированию способности выбирать типовые методы и способы выполнения задач, способности к организации собственной деятельности, способности принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность.

а. Тип занятия: Комбинированное занятие.

б. Место проведения занятия по календарно-тематическому плану.

По тематическому планированию учебного материала на изучение темы Элементы теории вероятностей отводится 2 часа

в. Время и место проведения занятия.

г. Метод обучения: репродуктивный

2. Цель и задачи.

а. Цель:

формирование компетенций, необходимых в профессиональной деятельности медицинской сестры.

б. Задачи:

Дидактические:

• Способствовать формированию знаний об основных понятиях теории вероятностей и способах расчета приблизительной вероятности событий, умений применять их для решения задач

Развивающие:

• Способствовать развитию умений наблюдать, сравнивать, применять знания в новой ситуации, выявлять закономерности, обобщать

• способствовать развитию навыков самостоятельной работы, самопроверки, самоконтроля;

Воспитательные:

• способствовать формированию общих компетенций, таких как способность выбирать типовые методы и способы выполнения задач, способность к организации собственной деятельности, способность принимать решения в стандартных и нестандартных ситуациях и нести за них ответственность(ОК 2, ОК 3, ОК 4, ОК 8)

• воспитывать познавательный интерес к математике;

• способствовать формированию профессиональных качеств, таких как аккуратность, внимательность, организованность(ОК 8) при подготовке к занятию и при ведении конспекта, представлять информацию понятном виде(ПК 2.1).

в. Уровень подготовки:

После занятия студенты должны приобрести опыт расчета вероятности событий.

Студенты должны уметь:

• вычислять вероятность случайных событий

Студенты должны знать:

• определение события, виды событий

• определение и виды вероятности

• теоремы вероятности

г. Контролирующая программа занятия:

• Предварительный контроль - фронтальный опрос.

• Заключительный контроль - контрольная работа

3. Материально-техническое и методическое оснащение занятия:

п/п

Наименование

Необходимое количество,шт.

Имеется в наличии, шт.

1

Раздаточный материал

15

15

2

Доска, мел

1

1

3

Групповой журнал

1

1

4

Средства ИКТ

Компьютер(ноутбук), мультимедийный проектор

+

4. Схемы интегрированных связей.

А. Межпредметные связи:

Школьный курс

ПМ.01, ПМ.02, ПМ.03, ПМ.04

ПМ.04

Дисциплина: Математика

Тема: «Элементы теории вероятностей»

Математика

Физика

МДК 04.02 МДК 04.03

Химия

УП

ГИА.00

Б

Проценты и пропорции

Случайные величины и их количественные характеристики.. Внутрипредметные связи

«Элементы теории вероятностей»

Действия с дробями

Элементы теории вероятностей

Предмет математической статистики.

5

«Элементы теории вероятностей»

. Граф логической структуры проведения занятия:

Организационный момент

Цель и задачи занятия

Предварительный контроль

проверка домашнего задания

Актуализация опорных знаний

Объячнение нового материала

Заключительный контроль

Проверочная работа №4

Подведение итогов занятия

Домашнее задание

Выставление оценок

6. План занятия:

1. Организационный момент (2 мин.)

2. Сообщение темы (1 мин.)

3. Цель и задачи занятия (2 мин)

4. Предварительный контроль (8 мин)

5. Объяснение материала (35 минут)

6. Решение примеров (20 мин)

7. Проверочная работа (15мин)

8. Итог урока (5 мин.)

9. Домашнее задание. (2 мин.)

7. Этапы планирования занятия

поясняет алгоритмы решения задач

записывают примеры в тетради

Способствовать формированию навыка решения задач

35 минут

Компьютер, мультимедийный проектор тетради, раздаточный материал.

6

Решение примеров

Контроль за решением примеров

решают задачи, при необходимости ведут конспект

закрепление полученных знаний

20 мин

Тетради, раздаточный материал.

7

Проверочная работа

Дает задания проверочной работы для самостоятельного решения

студенты выполняют задания

контроль

15 мин

раздаточный материал

8

Заключительный контроль. Обобщение и подведение итогов, оценка работы студентов

подводит итог занятия, комментирует работу студентов

выясняют сильные и слабые стороны работы

достижение цели занятия.

5 минут

9

Домашнее задание

задает домашнее задание

записывают домашнее задание

2

минуты

8. Карта самоподготовки студентов к занятию по теме «Решение задач по комбинаторике.»

Конспект

Тема: Основные понятия комбинаторики.

1. Прочитать конспект

2. При чтении обратить внимание на примеры решения задач по теме Основные понятия комбинаторики

3. Подготовить устно ответы на контрольные вопросы

Что такое соединение?

Какое соединение называется перестановкой?

Как рассчитать количество перестановок элементов?

Какое соединение называется размещением?

Как рассчитать количество размещений элементов?

Какое соединение называется сочетанием?

Как рассчитать количество сочетаний элементов?

В чем заключается правило суммы?

В чем заключается правило произведения?

9. Карта самоподготовки студентов к занятию по теме «Практическое применение статистических показателей для вычисления здоровья населения»

Конспект

Тема: Предмет математической статистики. Медицинская статистика.

1. Прочитать конспект

2. Подготовить устно ответы на контрольные вопросы

1. Что такое выборка?

2. Что такое генеральная совокупность?

3. Что такое вариационный ряд?

4. Перечислите количественные характеристики выборки и генеральной совокупности количественной.

5. Как построить полигон частот и гистограмму?

6. Что такое медицинская статистика?

7. Перечислите демографические показатели.

8. Перечислите показатели здоровья населения.

10. Термины

Случайное событие - это всякое явление (факт), которое в результате опыта (испытания) может произойти или не произойти.

Основной количественной характеристикой случайного события является его вероятность Р(А).

Классическое определение вероятности случайного события

Вероятность случайного события Р(А)равна:

где m - число случаев, благоприятствующих появлению события А; n - общее число равновозможных случаев.

Теорема сложения вероятностей

Теорема умножения вероятностей

Формула полной вероятности

Формула Байеса

11. Рекомендованная литература

Литература, рекомендуемая студентам:

основная:

Гилярова М.Г. Математика для медицинских колледжей. Учебное пособие

Издательство: Феникс, Серия: Среднее медицинское образование , 2015

дополнительная:

1. Баврин И.И. Высшая математика - М. : AcademiA, 2008.

2. Габриелян О.С. Химия. 10 класс. Базовый уровень. 3-е изд., перераб. - М.: Дрофа, 2007. - 192 с.

Литература, рекомендуемая преподавателям:

1. Подольский В.А. и др. Сборник задач по математике для техникумов. - М.: Высшая школа, 2009.

Приложение 1

Работа на занятии

Отметка «5» ставится, если:

• студент отвечал самостоятельно без наводящих вопросов учителя.

• в логических рассуждениях и обосновании решения нет пробе лов и ошибок;

• в решении нет математических ошибок

Отметка «4» ставится, если:

• в изложении допущены небольшие пробелы, не исказившие математическое содержание ответа;

• допущены один - два недочета при освещении основного содержания ответа, исправленные по замечанию учителя;

• допущены ошибка или более двух недочетов при освещении второстепенных вопросов или в выкладках, легко исправленные по замечанию учителя.

Отметка «3» ставится, если:

• имелись затруднения или допущены ошибки в определении понятий, использовании математической терминологии, исправленные после нескольких наводящих вопросов учителя;

• ученик не справился с применением теории в новой ситуации при выполнении практического задания, но выполнил задания обязательного уровня сложности по данной теме

• при изложении теоретического материала выявлена недостаточная сформированность основных умений и навыков.

Отметка «2» ставится если:

• допущены существенные ошибки, показавшие, что учащийся не владеет обязательными умениями по данной теме в полной мере

• обнаружено незнание или непонимание учеником большей или наиболее важной части учебного материала;

• допущены ошибки в определении понятий, при использовании математической терминологии, в выкладках, которые не исправлены после нескольких наводящих вопросов учителя.

Приложение 2

Решить задачи

1. В урне 20 шаров с номерами от 1 до 20. Какова вероятность вынуть шар с номером 37?

2. Монета подброшена два раза. Какова вероятность того, что оба раза выпадет герб?

3. Лабораторная крыса помещена в лабиринт, в котором лишь один из четырех возможных путей ведет к поощрению в виде пищи. Определите вероятность выбора крысой такого пути.

4. В урне 20 черных и 80 белых шаров. Из нее наугад вынимается один шар. Определите вероятность того, что этот шар будет черным.

5. В урне находится 50 шаров: 20 белых, 20 черных и 10 красных. Найдите вероятность появления белого (событие А) или красного шара (событие В), когда шар наугад достают из урны.

6. В классе 40 детей. Из них в возрасте от 7 до 7,5 лет 8 мальчиков (А) и 10 девочек (В). Найдите вероятность присутствия в классе детей такого возраста.

7. Есть две урны. В одной находится 2 черных и 8 белых шаров, в другой - 6 черных и 4 белых. Пусть событие А -выбор наугад белого шара из первой урны, В - из второй. Какова вероятность выбрать наугад одновременно из этих урн по белому шару, т.е. чему равна Р (А и В)?

8. В партии из 23 деталей находятся 10 бракованных. Вынимают из партии наудачу две детали. Определить вероятность того, что обе детали окажутся бракованными.

9. В вопросах к зачету имеются 75% вопросов, на которые студенты знают ответы. Преподаватель выбирает из них два вопроса и задает их студенту. Определить вероятность того, что среди полученных студентом вопросов есть хотя бы один, на который он знает ответ.

10. В первом ящике 1 белый, 2 красных и 3 синих шара; во втором ящике 2 белых, 6 красных, 4 синих шара. Из каждого ящика вынули по шару. Какова вероятность, что среди вынутых шаров нет синих?

11. Вероятность того, что в течение дня произойдет неполадка станка, равна 0,03. Какова вероятность того, что в течение четырех дней подряд не произойдет ни одной неполадки?

12. На складе находятся 26 деталей из которых 13 стандартные. Рабочий берет наугад две детали. Пользуясь теоремой умножения вероятностей зависимых событий определить вероятность того, что обе детали окажутся стандартными.

13. В ящике лежат шары: 4 белых, 10 красных, 8 зеленых, 9 коричневых. Из ящика вынимают один шар. Пользуясь теоремой сложения вероятностей определить, какова вероятность, что шар окажется цветным (не белым)?

14. Рацион с пониженным содержанием йода вызывает увеличение щитовидной железы у 60% животных большой популяции. Для эксперимента нужны 4 увеличенных железы. Найдите вероятность того, что у 4 случайно выбранных животных будет увеличенная щитовидная железа.

15. В урне 3 черных шара и 7 белых. Найдите вероятность того, что из этой урны один за другим (причем первый шар не возвращают в урну) будут вынуты 2 белых шара.

16. В двух детских садах, каждый из которых посещает по 100 детей, произошла вспышка инфекционного заболевания. Доли заболевших составляют соответственно 1/5 и 1/4, причем в первом учреждении 70 %, а во втором - 60 % заболевших - дети младше 3-х лет. Случайным образом выбирают одного ребенка. Определите вероятность того, что:

    1. выбранный ребенок относится к первому детскому саду (событие А) и болен (событие В).

    2. выбран ребенок из второго детского сада (событие С), болен (событие D) и старше 3-х лет (событие Е).

17. Имеется три одинаковых по виду ящика. В первом ящике находится 26 белых шаров, во втором 15 белых и 11 черных, в третьем ящике 26 черных шаров. Из выбранного наугад ящика вынули белый шар. Используя формулу Байеса вычислить вероятность того, что белый шар вынут из первого ящика.

18. В сборочный цех поступили детали с трех станков. На первом станке изготовлено 51% деталей от их общего количества, на втором станке 24% и на третьем 25%. При этом на первом станке было изготовлено 90% деталей первого сорта, на втором 80% и на третьем 70%. Используя формулу полной вероятности определить, какова вероятность того, что взятая наугад деталь окажется первого сорта ?

19. При первичном осмотре больного предполагаются 3 диагноза Н₁, Н₂, Н₃. Их вероятности, по мнению врача, распределяются так: Р(Н₁) = 0,5; Р(Н₂) = 0,17; Р(Н₃) = 0,33. Для его уточнения назначается, например, анализ крови, в котором ожидается увеличение СОЭ. Заранее известно (на основании результатов исследований), что вероятности увеличения СОЭ при предполагаемых заболеваниях равны:

Р(А/Н₁) = 0,1; Р(А/Н₂) = 0,2; Р(А/Н₃) = 0,9.

20. В полученном анализе зафиксировано увеличение СОЭ. Какой диагноз наиболее вероятен?

Приложение 4

Контрольная работа

Решение задач по теме «Комбинаторика и теория вероятностей»

Вариант 1

1. В группе 10 юношей и 20 девушек. Сколькими способами можно выбрать из группы двух человек одного пола?

2. Сколько различных перестановок можно образовать изо всех букв слова ИНТЕРВАЛ?

3. Сколько существует различных восьмизначных телефонных номеров (считается, что номер начинаться с нуля не может)?

4. Рота состоит из двух офицеров, пяти сержантов и 50 рядовых. Сколькими способами можно выделить из них отряд, состоящий из офицера, двух сержантов и 20 рядовых?

5. Сколько шести буквенных слов можно образовать из букв слова треугольник?

Сколько среди них таких, которые не содержат буквы р?

6. В ящике 5 белых, 3 черных и 4 синих шаров. Вынули один шар. Вычислить вероятность того, что вынутый шар: 1) бе­лый; 2) черный; 3) синий; 4) белый или черный; 5) белый или синий; 6) черный или синий.

7. В первом ящике 6 белых и 3 черных шаров; во втором ящике 7 белых и 8 черных шаров. Из каждого ящика вынули по шару. Какова вероятность того, что оба шара черные?

8. Вероятность попадания в цель первым стрелком равна 0,8 а вторым стрелком - 0,6. Стрелки выстрелили одновременно. Ка­кова вероятность того, что один из них попадет в цель, а другой не попадет?

9. В классе 12 мальчиков и 18 девочек. Нужно выбрать делегацию из двух человек. Какова вероятность (если считать выбор случайным), что выбраны два мальчика?

10. При первичном осмотре больного предполагаются 3 диагноза Н₁, Н₂, Н₃. Их вероятности, по мнению врача, распределяются так: Р(Н₁) = 0,5; Р(Н₂) = 0,2; Р(Н₃) = 0,3. Для его уточнения назначается, например, анализ крови, в котором ожидается увеличение СОЭ. Заранее известно (на основании результатов исследований), что вероятности увеличения СОЭ при предполагаемых заболеваниях равны 0,4; 0,2 и0,5 соответственно.

В полученном анализе зафиксировано увеличение СОЭ.

Какой диагноз наиболее вероятен?

Решение задач по теме «Комбинаторика и теория вероятностей»

Вариант 2

1. В группе 14 юношей и 25 девушек. Сколькими способами можно выбрать из группы двух человек одного пола?

2. Сколько различных перестановок можно образовать изо всех букв слова ШТОРЫ?

3. Сколько существует различных восьмизначных телефонных номеров (считается, что номер начинаться с нуля не может)?

4. Рота состоит из трех офицеров, пяти сержантов и 100 рядовых. Сколькими способами можно выделить из них отряд, состоящий из офицера, трех сержантов и 30 рядовых?

5. Сколько четырехбуквенных слов можно образовать из букв слова треугольник?

Сколько таких, которые начинаются с буквы е и оканчиваются буквой р?

6. В ящике 5 белых, 7 черных и 4 синих шаров. Вынули один шар. Вычислить вероятность того, что вынутый шар: 1) бе­лый; 2) черный; 3) синий; 4) белый или черный; 5) белый или синий; 6) черный или синий.

7. В первом ящике 7 белых и 2 черных шаров; во втором ящике 3 белых и 2 черных шаров. Из каждого ящика вынули по шару. Какова вероятность того, что оба шара черные?

8. Вероятность попадания в цель первым стрелком равна 0,5, а вторым стрелком - 0,3. Стрелки выстрелили одновременно. Ка­кова вероятность того, что один из них попадет в цель, а другой не попадет?

9. В классе 12 мальчиков и 18 девочек. Нужно выбрать делегацию из двух человек. Какова вероятность (если считать выбор случайным), что выбраны две девоч­ки?

10. При первичном осмотре больного предполагаются 3 диагноза Н₁, Н₂, Н₃. Их вероятности, по мнению врача, распределяются так: Р(Н₁) = 0,2; Р(Н₂) = 0,7; Р(Н₃) = 0,1. Для его уточнения назначается, например, анализ крови, в котором ожидается увеличение СОЭ. Заранее известно (на основании результатов исследований), что вероятности увеличения СОЭ при предполагаемых заболеваниях равны 0,1; 0,2 и 0,3 соответственно.

В полученном анализе зафиксировано увеличение СОЭ.

Какой диагноз наиболее вероятен?

Решение задач по теме «Комбинаторика и теория вероятностей»

Вариант 3

1. В группе 14 юношей и 13 девушек. Сколькими способами можно выбрать из группы двух человек одного пола?

2. Сколько различных перестановок можно образовать изо всех букв слова ПОЕЗД?

3. Сколько существует различных восьмизначных телефонных номеров (считается, что номер начинаться с нуля не может)?

4. Рота состоит из пяти офицеров, шести сержантов и 70 рядовых. Сколькими способами можно выделить из них отряд, состоящий из офицера, двух сержантов и 10 рядовых?

5. Сколько пятибуквенных слов можно образовать из букв слова треугольник?

   1. Сколько таких, которые начинаются с буквы е и оканчиваются буквой р?

6. В ящике 3 белых, 10 черных и 7 синих шаров. Вынули один шар. Вычислить вероятность того, что вынутый шар: 1) бе­лый; 2) черный; 3) синий; 4) белый или черный; 5) белый или синий; 6) черный или синий.

7. В первом ящике 3 белых и 8 черных шаров; во втором ящике 5 белых и 13 черных шаров. Из каждого ящика вынули по шару. Какова вероятность того, что оба шара черные?

8. Вероятность попадания в цель первым стрелком равна 0,5, а вторым стрелком - 0,6. Стрелки выстрелили одновременно. Ка­кова вероятность того, что один из них попадет в цель, а другой не попадет?

9. В классе 12 мальчиков и 18 девочек. Нужно выбрать делегацию из двух человек. Какова вероятность (если считать выбор случайным), что выбраны девочка и мальчик?

10. При первичном осмотре больного предполагаются 3 диагноза Н₁, Н₂, Н₃. Их вероятности, по мнению врача, распределяются так: Р(Н₁) = 0,3; Р(Н₂) = 0,1; Р(Н₃) = 0,6. Для его уточнения назначается, например, анализ крови, в котором ожидается увеличение СОЭ. Заранее известно (на основании результатов исследований), что вероятности увеличения СОЭ при предполагаемых заболеваниях равны 0,1; 0,3 и 0,1 соответственно.

В полученном анализе зафиксировано увеличение СОЭ.

Какой диагноз наиболее вероятен?

Решение задач по теме «Комбинаторика и теория вероятностей»

Вариант 4

1. В группе 16 юношей и 19 девушек. Сколькими способами можно выбрать из группы двух человек одного пола?

2. Сколько различных перестановок можно образовать изо всех букв слова АРТЕЛЬ?

3. Сколько существует различных восьмизначных телефонных номеров (считается, что номер начинаться с нуля не может)?

4. Рота состоит из трех офицеров, двух сержантов и 50 рядовых. Сколькими способами можно выделить из них отряд, состоящий из офицера, двух сержантов и 30 рядовых?

5. Сколько четырехбуквенных слов можно образовать из букв слова треугольник?

Сколько среди них таких, которые не содержат буквы р?

6. В ящике 7 белых, 17 черных и 8 синих шаров. Вынули один шар. Вычислить вероятность того, что вынутый шар: 1) бе­лый; 2) черный; 3) синий; 4) белый или черный; 5) белый или синий; 6) черный или синий.

7. В первом ящике 6 белых и 9 черных шаров; во втором ящике 13 белых и 2 черных шаров. Из каждого ящика вынули по шару. Какова вероятность того, что оба шара черные?

8. Вероятность попадания в цель первым стрелком равна 0,1, а вторым стрелком - 0,3. Стрелки выстрелили одновременно. Ка­кова вероятность того, что один из них попадет в цель, а другой не попадет?

9. В классе 13 мальчиков и 17 девочек. Нужно выбрать делегацию из двух человек. Какова вероятность (если считать выбор случайным), что выбраны девочка и мальчик?

10. При первичном осмотре больного предполагаются 3 диагноза Н₁, Н₂, Н₃. Их вероятности, по мнению врача, распределяются так: Р(Н₁) = 0,5; Р(Н₂) = 0,4; Р(Н₃) = 0,1. Для его уточнения назначается, например, анализ крови, в котором ожидается увеличение СОЭ. Заранее известно (на основании результатов исследований), что вероятности увеличения СОЭ при предполагаемых заболеваниях равны 0,1; 0,1 и 0,9 соответственно.

В полученном анализе зафиксировано увеличение СОЭ.

Какой диагноз наиболее вероятен?

Решение задач по теме «Комбинаторика и теория вероятностей»

Вариант 5

1. В группе 11 юношей и 18 девушек. Сколькими способами можно выбрать из группы двух человек одного пола?

2. Сколько различных перестановок можно образовать изо всех букв слова КНИГА?

3. Сколько существует различных восьмизначных телефонных номеров (считается, что номер начинаться с нуля не может)?

4. Рота состоит из трех офицеров, шести сержантов и 60 рядовых. Сколькими способами можно выделить из них отряд, состоящий из офицера, двух сержантов и 20 рядовых?

5. Сколько трехбуквенных слов можно образовать из букв слова треугольник?

Сколько таких, которые начинаются с буквы е и оканчиваются буквой р?

6. В ящике 7 белых, 14 черных и 23 синих шаров. Вынули один шар. Вычислить вероятность того, что вынутый шар: 1) бе­лый; 2) черный; 3) синий; 4) белый или черный; 5) белый или синий; 6) черный или синий.

7. В первом ящике 12 белых и 8 черных шаров; во втором ящике 16 белых и 5 черных шаров. Из каждого ящика вынули по шару. Какова вероятность того, что оба шара черные?

8. Вероятность попадания в цель первым стрелком равна 0,8, а вторым стрелком - 0,2. Стрелки выстрелили одновременно. Ка­кова вероятность того, что один из них попадет в цель, а другой не попадет?

9. В классе 10 мальчиков и 15 девочек. Нужно выбрать делегацию из двух человек. Какова вероятность (если считать выбор случайным), что выбраны: два мальчика?

10. При первичном осмотре больного предполагаются 3 диагноза Н₁, Н₂, Н₃. Их вероятности, по мнению врача, распределяются так: Р(Н₁) = 0,1; Р(Н₂) = 0,6; Р(Н₃) = 0,3. Для его уточнения назначается, например, анализ крови, в котором ожидается увеличение СОЭ. Заранее известно (на основании результатов исследований), что вероятности увеличения СОЭ при предполагаемых заболеваниях равны 0,9; 0,3 и 0,2 соответственно.

В полученном анализе зафиксировано увеличение СОЭ.

Какой диагноз наиболее вероятен?

</ Приложение 5

Конспект занятия

1. Постановка цели урока

В тетради записать тему занятия: Элементы теории вероятностей

Цель: научиться применять классическое определение вероятности событий и теоремы вероятностей к решению задач.

2. Проверка домашнего задания.

3. Объяснен ие нового материала

(включение презентации. См. комментарии к слайдам)

Теоретический материал

Случайное событие - это всякое явление (факт), которое в результате опыта (испытания) может произойти или не произойти. Случайные события обозначаются буквами А, В, С …

А -выпадение орла (герба) при подбрасывании стандартной монеты;

В - рождение девочки в данной семье;

С -возникновение эпидемического заболевания в данном регионе в определенный период времени и т.д.

Основной количественной характеристикой случайного события является его вероятность Р(А).

Классическое определение вероятности случайного события

Вероятность случайного события Р(А)равна:

где m - число случаев, благоприятствующих появлению события А; n - общее число равновозможных случаев.

Свойства вероятности:

1. Вероятность случайного события - величина безразмерная.

2. Вероятность случайного события всегда положительна и меньше единицы, т.е. 0 < P (A) < 1.

3. Вероятность достоверного события равна единице.

4. Вероятность невозможного события равна нулю.

5. Вероятность любого события - величина не отрицательная и не превышающая единицу:
   
   0  P (A)  1.

Теорема сложения вероятностей

Теорема умножения вероятностей

Формула полной вероятности

Формула Байеса

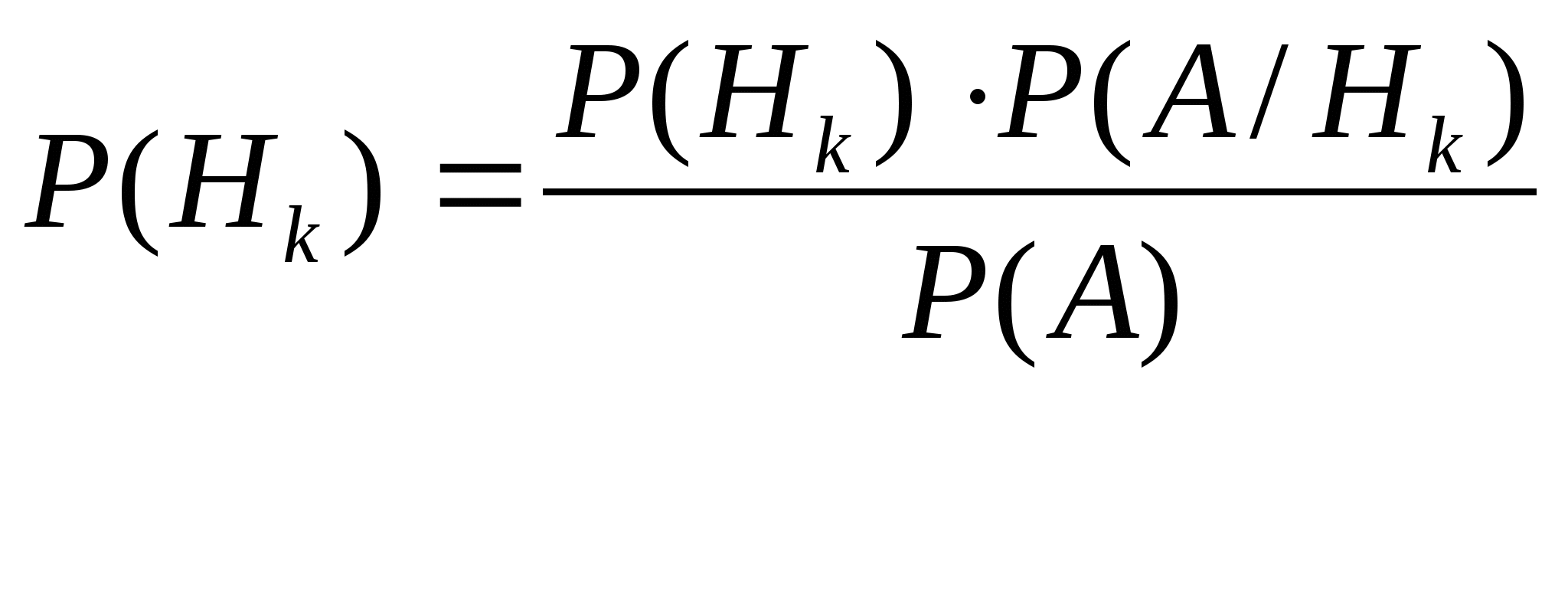
4. Решение примеров

5. Контрольная работа №4 (5 вариантов)

6. Домашнее задание

7. Подведение итогов урока