Открытый урок в 8 классе по теме: "Решение квадратных уравнений"

Цели урока

Образовательные:

• закрепление и обобщение знаний учащихся, полученные при изучении темы;

• отработка способов решения квадратных уравнений, выработка умения выбрать нужный, рациональный способ решения.

• провести диагностику усвоения системы знаний и умений и ее применения для выполнения практических заданий стандартного уровня с переходом на более высокий уровень.

Развивающие:

• развитие логического мышления, памяти, внимания, умений сравнивать и обобщать.

Воспитательные:

• воспитание трудолюбия, взаимопомощи, математической культуры.

Оборудование к уроку:

• Презентация « Квадратные уравнения»

• Интерактивная доска

• Тестовая система с голосованием

Организационные формы общения: групповая, индивидуальная, работа в парах.

Ход урока

1. Организационный момент «Настроимся на урок!»

Добрый день дорогие друзья, гости! Я рада приветствовать Вас на нашем уроке , и прошу всех вас улыбнуться друг другу, а ребят прошу, мысленно пожелать успехов и себе и товарищам. Садитесь.

Сегодняшний урок мы проведем с использованием рейтинговой системы контроля знаний. У вас имеются оценочные листы, в которых вы выставляете баллы, полученные за каждый этап урока. Каждый правильный ответ оценивается в 1 балл .

2. Актуализация знаний учащихся

Учитель: Посмотрите на экран и попробуйте сформулировать тему урока

Предлагаю начать урок со следующего задания: каждой группе решить анаграммы (в словах изменен порядок букв).

Какие слова зашифрованы?

• Таиимдкисрнн (дискриминант)

• Ниваренуе (уравнение)

• Фэкоцинетиф (коэффициент)

• Ерокнь (корень)

Учитель: Тема нашего урока «Решение квадратных уравнений».

Какие основные цели урока вы можете поставить на сегодняшнем уроке?

На этом уроке повторим и закрепим знание и умение решения квадратных уравнений. Каждый из вас должен уметь верно, и рационально решать квадратные уравнения. Эта тема очень важная в курсе математики, она является ступенькой в изучении более сложного материала. В старших классах будем решать логарифмические, показательные, тригонометрические уравнения, приводимые к квадратным. Это будет в 10, 11 классах. А сегодня вы покажете, насколько готовы шагать по ступенькам математики дальше.

Великий, немецкий ученый А. Эйнштейн говорил о себе: «Мне приходится делить своё время между политикой и уравнениями. Однако уравнения, по-моему, гораздо важнее, потому что политика существует только до данного момента, а уравнения будут существовать вечно»

Квадратные уравнения - тема очень важная в курсе математики, она является первой ступенькой в изучении более сложного материала.

Вам дан ключ к решению квадратных уравнений, и если вы научились им пользоваться, вы сможете решить любое квадратное уравнение. А сегодня вы покажете, насколько готовы пользоваться этим ключом.

На доске уравнение: 13х²+2х+2015=0

- Назовите вид данного уравнения. Назовите его коэффициенты.

О каком событии говорят коэффициенты уравнения? (Дата проведения урока)

Итак, откройте тетради и запишите сегодняшнее число, классная работа.

3. Проверка теоретической базы ( За каждый верный ответ 1 балл.)

Начинаем с вопросов теории

1. Определение квадратного уравнения.

2. Виды квадратных уравнений.

3. Что называется дискриминантом квадратного уравнения?

4. От чего зависит количество корней квадратного уравнения?

5. Каковы формулы для нахождения корней квадратного уравнения?

6. Сформулировать теорему Виета

Итак, мы вспомнили теоретический материал данной темы, посмотрим, как вы умеете применять его на практике.

3. 1) Устные упражнения

Устная разминка заполнить таблицу

2. Найти и исправить ошибки

Задание для 1-й группы Задание для 2-й группы Задание для 3 -й группы

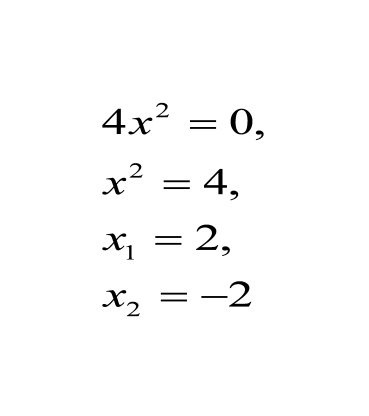
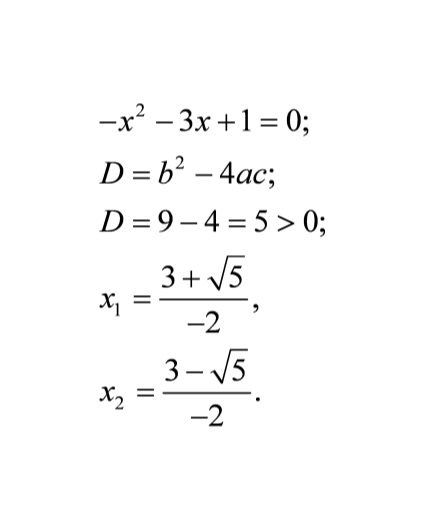
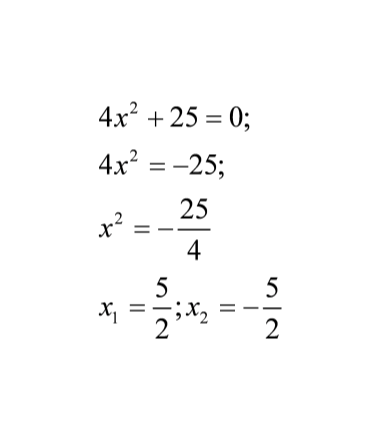
4-я группа работает с кроссвордом с истрическим компонентом:

Группа историков работала по теоретической базе в форме кроссворда /получится ответ на вопрос: В каком древнем городе ещё около 2000 лет до н.э первыми научились решать квадратные уравнения? Вавилон./

1.Как называется уравнение вида ах² +вх+с=0?

2.Название выражения в ²- 4 а с

3.Сколько корней имеет квадратное уравнение, если D > 0 ?

4.Сколько коней имеет квадратное уравнение если D=0 ?

5.Чему равен корень уравнения ах ² = 0 ?

6.Как называется квадратное уравнение, где коэффициенты в или с равны нулю?

7.Как называется квадратное уравнение, в котором первый коэффициент а =1

к

В

а

д

р

а

т

н

о

е

д

и

с

к

р

и

м

и

н

А

н

т

д

В

а

о

д

И

н

н

о

Л

ь

н

е

п

О

л

н

о

е

п

р

и

в

е

д

е

Н

н

о

е

2. Найти лишнее уравнение и объяснить почему?

Каждой группе из предложенных уравнений выбрать «лишнее», объяснить, почему оно является «лишним» и решить его рациональным способом.

3х²+5х-8=0 х²-3х+4=0 4х²-5х+2=0 3х²-х=0

0,3х²-х+7=0 3х²+5х-8=0 -х²+5х-8=0 х²-81=0

Х²-25=0 х²+х-8=0 3,5х²+х+1=0 х²-10х+25=0

(х-2)(х+3)=0 7х+ х²-8=0 х²+2х+8=0 2х²=0

Ответы

1-я группа уравнений

«лишнее» уравнение х²-25=0, так как является неполным квадратным уравнением

2-я группа уравнений

«лишнее» уравнение 3х²+5х-8 =0, так как является полным, не приведенным квадратным уравнением

3-я группа уравнений

«лишнее» уравнение х²+2х+8=0 - приведенное квадратное уравнение

4-я группа уравнений

«лишнее» уравнение х²-10х+25=0 - полное квадратное уравнение.

Учитель. Ребята, здесь вы видите уравнения, определённые по какому-то признаку. Как вы думаете, какое из уравнений группы является лишним?

5. Индивидуальная работа

Уравнения, которые оказались лишними в группе, предлагается решить учащимся самостоятельно на доске. (1-открыто; 2- самостоятельно, (1 ученик-с обратной стороны доски) с последующей проверкой по доске;3- 2 ученика; 4-1 ученик)

Решаются уравнения: (Слайд 10).

1. 4х² - х - 3 = 0,

Ответ: -3/4; 1.

2. 2х² - 7х - 4 = 0, (по формулам корней квадратного уравнения),

Ответ: -1/2; 4.

3. х² + 2х - 35 = 0, (можно использовать 2условия: b = 2k Д = в² - 4ас).

Ответ: -7; 5.

3. х² +ах +1=0 - при каком значении параметра а уравнение имеет 1 корень (-2;+2)

4. Исторический момент

Проверить кроссворд у 4-й группы по ключевому слову «ВАВИЛОН»

Заслушать историческую справку учеников из этой группы.

Формулы решения квадратных уравнений в Европе были впервые изложены в 1202 г. итальянским математиком Леонардом Фибоначчи.

Общее правило решения квадратных уравнений, приведенных к единому каноническому виду х²+вх+с=0 , было сформулировано в Европе лишь в 1544 г. Штифелем.

Вывод формулы решения квадратного уравнения в общем виде имеется у Виета, однако Виет признавал только положительные корни. Лишь в 17 в. благодаря трудам Декарта, Ньютона и других ученых способ решения квадратных уравнений принимает современный ви

3. Решить самостоятельно по группам уравнения

3х² - 7х + 4 =0

5х² -8х +3 =0

Х² -22х - 23 =0

5х² +9х + 4 =0

3х² + 10х + 3 =0

5х² + 26х + 5 =0

Х² -8х -9 = 0

Проверка решение у доски.

Вывод исследовательской группы по коэффициентам.

задание 1 группе задание 2 группе

б) 5 х² - 8х + 3 = 0, б) 15 х² - 22х - 37 = 0,

в) 5 х² - 6х + 1 = 0, в) 5 х² + 9х + 4 = 0,

задание 3 группе задание 4 группе

а) 3 х² + 10х + 3 = 0, Решает все эти уравнения по знакомым формулам.

б) 2 х² + 5х + 2 = 0,

в) 4 х² + 17 х + 4 = 0

Вывод группы № 1:

Сумма коэффициентов равна 0

а + в + с = 0 .

Первый корень: х₁ = 1 .

Второй корень х₂ = с/а.

Вывод группы № 2 :

Если а + с = в.

Первый корень: х₁ = -1.

Второй корень: х₂ = -с/а.

Вывод группы № 3:

а = с, в = а ² + 1

Первый корень: х₁ = -а = - с.

Второй корень: х₂ = -1/а = -1 /с.

Проверка на доске разными способами каждое уравнение.

8. Самостоятельная работа по вариантам (слайд 11).

Проверка 1 группа (по закрытой доске)

2 группа - по экрану

7. Самостоятельная работа «ТЕСТ» по системе голосования.

8.Итог урока

Сегодня на уроке мы с вами повторили и обобщили знания по теме «Квадратные уравнения».

Домашнее задание. Из учебника выбрать квадратные уравнения, которые можно решить по коэффициентам.

Хочется отметить ,что никто из вас не отнеся к работе равнодушно, и если у кого-то не всё получилось не огорчайтесь : «Дорогу осилит идущий»

СПАСИБО, ВСЕМ!