- Учителю
- Урок по геометрии 'Сумма углов треугольников' (7 класс)
Урок по геометрии 'Сумма углов треугольников' (7 класс)
Урок по геометрии в 7 классе.
Составитель:
учитель математики Кидалова Л.Л.
Тема: «Сумма внутренних углов треугольника».
Задача обучения: уметь доказывать теорему о сумме внутренних углов треугольника, применять ее при решении задач, формировать умения анализировать, обобщать, показывать, использовать элементы исследования.
Задача развития: развитие математической речи, логического мышления, навыков построения чертежей по условиям задач.
Задача воспитания: воспитание аккуратности, трудолюбия, самостоятельности, НОТ ученика.
Оборудование: транспортир, линейка, карточки-треугольники разных видов, кодоскоп, выставка творческих работ учащихся.
Наглядно иллюстративный материал
Разносторонний треугольник



Равнобедренный треугольник
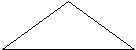
Равносторонний треугольник
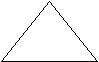
Прямоугольный
треугольник
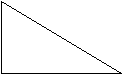

Тупоугольный
треугольник

Остроугольный
треугольник


Треугольник
по сторонам
по углам
Острый угол




 Прямой угол
Прямой угол

 Тупой угол
Тупой угол
Развернутый угол

Накрест лежащие углы
Внутренние, односторонние углы
Соответственные углы
Вертикальные углы
Смежные углы
∠ 1=200∠2=600∠3=?
а) 600; 700; 390
б) 1100; 500; 600
в) 1200; 400; 200

а
2

в
1

с
∠1 = ∠ 2

а

2
в
1

с
∠1 = ∠ 2

а

2
в
1

с
∠1 + ∠2 = 1800

1
2

∠1 + ∠ 2 = 1800

4
1
2
3
∠1 = ∠ 2 ∠3 = ∠ 4

а

в
с

1
2
∠1 = ∠ 2 = 450
1
2

∠1 + ∠ 2 = 900

2
1
3
∠1 = ∠ 2 = ∠ 3
Ход урока.
Предполагаемая деятельность учителя
Предполагаемая деятельность учащихся
1
Организационный момент
Тема урока «Сумма внутренних углов треугольника».
2
На предыдущих уроках мы изучали тему «Треугольники», «Признаки параллельности прямых». Всем было предложено творческое задание. Я благодарю тех, кто принимал участие. Перед вами выставка лучших работ: фигуры, составленные из прямоугольных треугольников.
Все они получают за свою работу оценку «5».
3
Сегодня на уроке мы продолжаем работу с треугольниками. Мы с вами рассмотрим теорему о сумме внутренних углов треугольника и ее практическое применение при решении задач.
4
Открыли тетради, записали число и тему сегодняшнего урока «Сумма внутренних углов треугольника».
Повторение
На доске появляется карточка «Треугольник».
Какая геометрическая фигура называется треугольником?
Треугольник - геометрическая фигура, состоящая из трех точек, не лежащих на одной прямой и попарно соединенных отрезками.
Как мы знаем, треугольники различаются по сторонам и по углам.
На доске выставляются карточки «по сторонам» и « по углам».
Назовите виды треугольников по сторонам.
Разносторонний (все стороны разные).
Равнобедренный (две стороны равны).
Равносторонний (все стороны равны).
На доске выставляются карточки-треугольники, соединяемые в схему.
Треугольник
По сторонам







Прежде чем назвать виды треугольников по углам, давайте с вами вспомним виды углов.
Какая геометрическая фигура называется углом?
По мере ответов учащихся, на доске выставляются карточки-углы.






Угол - это геометрическая фигура, образованная двумя лучами, выходящими из одной точки.
Если величина угла равна 90о, то угол называют прямым.
Если величина угла равна 180о, то угол называют развернутым.
Если величина угла меньше 90о, то угол называют острым.
Если величина угла больше 90о, но меньше 180о, то угол называют тупым.
Назовите виды треугольников по углам.
По мере ответов учащихся на доске дополняется схема треугольников по сторонам и по углам.
Треугольник
по сторонам
По углам














Остроугольный (все углы острые).
Прямоугольный (один угол прямой, а два острых).
Тупоугольный (один угол тупой, а два острых).
На доске изображен чертеж: прямые а и в пересечены прямой с.
Как называется прямая с по отношению к прямым а и в?
Секущая.

а

в
с
При этом образовались углы.
Какие пары углов, образованных прямыми а и в вы знаете?
По мере ответов учащихся, на доске появляются карточки: накрест лежащие углы, соответственные углы, внутренние, односторонние углы, смежные углы, вертикальные углы
Накрест лежащие углы:
∠4 и ∠6; ∠3 и ∠5.
Соответственные углы:
∠1 и ∠5; ∠4 и ∠8; ∠2 и ∠6;
∠ 3 и ∠ 7.
Внутренние, односторонние углы:
∠4 и ∠5; ∠3 и ∠6.
Смежные углы:
∠1и ∠2; ∠2 и∠3; ∠3 и ∠4;
∠4 и ∠1; ∠5 и ∠6; ∠6 и ∠7;
∠7 и ∠8; ∠8 и ∠5.
Вертикальные углы: ∠4 и∠2;
∠1 и ∠3; ∠5 и ∠7; ∠6 и ∠8.
Какими свойствами обладают данные пары углов?
По мере ответов учащихся выставляются карточки, отражающие свойства данных пар углов.
Вертикальные углы равны.
Сумма смежных углов равна 1800.

1
2

∠1 + ∠2 = 1800


3
1
2
4
∠1 = ∠2 ∠3 = ∠4
Пусть прямые а и в параллельны. Какими свойствами при этом будут обладать пары накрест лежащих, соответственных и односторонних углов?
По мере ответов учащихся выставляются карточки, отражающие свойства данных пар углов.
Если две параллельные прямые пересечены секущей, то сумма внутренних, односторонних углов равна 1800.

а

2
в
1

с
∠1 + ∠2 = 1800

а

2
в
1

с
∠1 = ∠2

а
2

в
1

с
∠1 = ∠2
Если две параллельные прямые пересечены секущей, то накрест лежащие углы равны.
Если две параллельные прямые пересечены секущей, то соответственные углы равны.
5
Объяснение нового материала
На предыдущем уроке мы рассмотрели теорему о сумме внутренних углов треугольника и доказали ее опытным путем. Сформулируйте теорему о сумме внутренних углов треугольника.
Домой вам было дано творческое задание: найти различные способы доказательства данной теоремы. Сегодня на уроке мы рассмотрим доказательство данной теоремы, опираясь на ранее изученные свойства, теоремы и аксиомы.
Постройте в тетради произвольный треугольник АВС.
Что в теореме является условием?
Что в теореме является заключением?
Доказательство:
-
Проведем через вершину В треугольника АВС прямую а параллельную стороне АС.
-
Обозначим образовавшиеся углы: ∠1; ∠2; ∠3; ∠4; ∠5; ∠А= ∠ 1; ∠В= ∠ 2; ∠С = ∠3.
-
∠ 1 =∠ 4; ∠3 =∠ 4 как накрест лежащие углы при параллельных прямых а и АС относительно секущей АВ.
-
∠4 + ∠2 + ∠5 = 1800 (части развернутого угла) Заменим ∠ 4 на ∠ 1, ∠5 на ∠3 (из №3)
-
∠1 + ∠2 + ∠3 = 1800
∠А +∠В + ∠С = 1800
Что и требовалось доказать.
Сумма внутренних углов треугольника равна 1800.



4
2
5
1
3
Дано: ΔАВС
Доказать: ∠А+ ∠В+∠С= 1800
6
Закрепление
-
Может ли быть в треугольнике два прямых угла?
-
Может ли быть в треугольнике два тупых угла?
-
Чему равна сумма острых углов прямоугольного треугольника?
-
Чему равны острые углы прямоугольного равнобедренного треугольника?
-
Чему равны углы равностороннего треугольника?
-
Найдите величину третьего угла треугольника, если один из углов равен 200, а другой 600?
-
Существует ли треугольник, у которого углы равны:
А) 600; 700; 390;
Б) 1100; 500; 600;
В) 1200; 400; 200?
Нет, так как сумма двух прямых углов уже равна 1800.
Нет, так как сумма двух тупых углов уже больше 1800.
Величина прямого угла равна 900, значит, на сумму двух острых углов остается 900.
Так как углы при основании равнобедренного треугольника равны, то каждый из них равен 450 (900:2=450).
Так как углы равностороннего треугольника равны, то каждый из них равен 600 (1800:3=600).
Сумма внутренних углов треугольника равна 1800, значит, величина третьего угла треугольника равна 1000 (1800-200-600=1000).
А) Нет, так как сумма углов треугольника равна 1690, что меньше 1800;
б) Нет, так как сумма углов треугольника равна 2200, что больше 1800;
А) Да, так как сумма углов треугольника равна 1800.
7
Помимо всех изученных углов, мы сегодня познакомимся с внешним углом треугольника.
Постройте в тетради произвольный треугольник ДЕР.
Постройте внешний угол треугольника к углу Е. Как это сделать?
Сколько внешних углов можно построить к данному углу треугольника?
Что можно сказать о величинах построенных внешних углов к данному углу треугольника?




Два.
Они равны как вертикальные.
Определение: внешний угол треугольника - угол, смежный с каким-нибудь углом треугольника.
Докажем, что величина внешнего угла равна сумме двух углов треугольника, не смежных с ним.
Обозначим углы: ∠1; ∠2; ∠3; ∠4.
∠1+ ∠2+ ∠3= 1800 (по теореме о сумме внутренних углов треугольника)
∠1 + ∠ 4 = 1800 ( по свойству смежных углов)
очевидно, что ∠ 4 = ∠2 + ∠ 3
Что и требовалось доказать.
Записываем в тетради:
Теорема: внешний угол треугольника равен сумме двух углов, не смежных с ним.
Дано: ΔДЕР
∠Д= ∠2
∠Е = ∠1
∠Р = ∠3
∠4 - внешний к ∠ 1
Доказать:∠ 4 = ∠2 +∠ 3
Доказательство: (впереди)
8
Математическая разминка.
Если ответ «да», то руки поднимаем вверх.
Если ответ «нет», то руки протягиваем перед собой.
Ответ - на счет: раз, два, три.
-
Сумма углов треугольника равна 1800.
-
В треугольнике может быть два тупых угла.
-
В треугольнике может быть один тупой и два острых угла.
-
В треугольнике может быть один тупой, один прямой и один острый угол.
-
В треугольнике может быть один прямой и два острых угла.
-
В треугольнике может быть два прямых угла.
-
Угол равностороннего треугольника равен 600.
-
В треугольнике может быть развернутый угол.
-
Острый угол прямоугольного равнобедренного треугольника равен 450.
-
Сумма острых углов прямоугольного треугольника равна 900.
-
Внешний угол треугольника равен сумме всех углов треугольника.
-
Внешний угол треугольника равен сумме двух углов треугольника, не смежных с ним.
-
Сумма углов треугольника равна 1800.
9
Закрепление
Решаем задачу №224 по учебнику на странице 67,
№234 на странице 68.
Задача №224: Найдите углы треугольника АВС, если
∠А: ∠ В: ∠ С=2:3:5


Дано: ΔАВС
∠А: ∠ В: ∠ С=2:3:5
Найти: ∠А; ∠В; ∠С
Решение:
Пусть х0- 1 часть, тогда
∠А=2х, ∠В=3х; ∠ С=5х
∠А+ ∠В+ ∠С=1800 (по теореме о сумме внутренних углов треугольника)
2х+3х+5х=1800; х=200;
200 - 1 часть, тогда ∠А=400;
∠В=600; ∠С=800.
Ответ: ∠А=400; ∠ В=400;
∠С=800.
Задача №234: Один из внешних углов равнобедренного треугольника равен 1150. Найдите углы треугольника.
Какой треугольник называется равнобедренным?
Каким свойством обладают углы при основании равнобедренного треугольника?
Треугольник называется равнобедренным, если у него две стороны равны. Они называются боковыми, а третья сторона - основание.
Углы при основании равнобедренного треугольника равны.
Построим равнобедренный треугольник АВС.
Построим внешний угол треугольника. Каким должен быть угол треугольника, если внешний угол к нему равен 1150?
Решение:
∠ АСВ+∠ ВСК=1800 (по свойству смежных углов)
∠АСВ+1150=1800; ∠ АСВ=650;
∠А=∠ АСВ (по свойству углов при основании равнобедренного треугольника), значит ∠ А=650;
∠А+ ∠В+ ∠АСВ=1800 (по теореме о сумме внутренних углов треугольника)
650+ ∠В+ 650 = 180); ∠В=500.
Ответ: ∠А= ∠С= 650; ∠В=500.
Острым, 650.


Дано: ΔАВС
АВ=ВС
∠ВСК=1150
Найти: ∠А; ∠В; ∠С
Решение:
Есть ли другое решение задачи?
Рассмотрите это решение самостоятельно.
Да, если внешний угол взять при вершине В Δ АВС.
Проверяем решение 2 случая задачи №224
Дано: ΔАВС
АВ=ВС
∠СВК=1150
Найти: ∠А; ∠В; ∠С
Решение:
∠ АВС+∠ СВК=1800 (по свойству смежных углов)
∠АВС+1150=1800; ∠АВС=650;
∠А= ∠С (по свойству углов при основании равнобедренного треугольника)
∠ А+∠АВС+ ∠С=1800 (по теореме о сумме внутренних углов треугольника), значит
∠А =∠ С = (1800-1150):2
∠ А = ∠С = 32,50 или
∠А = ∠С = 32030
Ответ: ∠А = ∠С = 32,50
∠В = 650
Мы видим, что задача может иметь несколько решений. Все зависит от того, какой угол мы возьмем за данную величину.
Решение второго случая оформить в тетради дома.
10
Домашнее задание
Записываем домашнее задание:
Теорема, №234 (2)
-
№235
11
Итог урока
Подведем итог урока:
что нового мы узнали на уроке?
Оценки за урок.
10