- Учителю
- Конспект и презентация по алгебре для 9 класса 'Квадратичная функция, ее график и свойства'
Конспект и презентация по алгебре для 9 класса 'Квадратичная функция, ее график и свойства'
Разработала учитель математики
МОУ Большечирклейской СОШ
Айбулатова Гюзяль Алиевна
Конспект урока по алгебре.
Класс: 9
Учебник: Ю.Н.Макарычев «Алгебра 9 кл.»
Тема: Функция y=ax2, ее график и свойства.
Тип урока: изучение нового материала.
Цели урока:
-
Ввести определение квадратичной функции.
-
Рассмотреть графики функций y=ax2 (а>0, и а<0) и их свойства.
-
Повторить решение квадратных уравнений.
Оборудование: доска, мел, линейка, презентация (Приложение 1).
Место проведения: Кабинет математики.
Время: 45 минут.
План урока
-
Организационный момент (1 мин).
-
Актуализация знаний (10 мин).
-
Ознакомление с новым материалом (20 мин).
-
Первичное закрепление темы (12 мин).
-
Подведение итогов урока. Домашнее задание (2 мин).
Ход урок
Ход урок
-
Организационный момент. Приветствие. Проверка готовности учащихся к уроку, отметка отсутствующих. Сообщение темы урока и поставка целей урока. (Слайд № 1.)
-
Актуализация знаний.
Учитель: Ребята, сегодня мы будем изучать новую тему. Для этого вспомним ранее изученный материал, в частности повторим определение функции, некоторые понятия, связанные с функциями и вспомним известные нам функции и их некоторые свойства.
Далее задаем вопросы (Слайд № 2 - 5.):
-
Что называется функцией? Дайте определение функции?
Функцией называют такую зависимость переменной y от переменной x, при которой каждому значению переменной x соответствует единственное значение переменной y. Переменную x называют независимой переменной или аргументом, переменную y называют зависимой переменной.
-
Что называется областью определения и областью значений функции?
Все значения независимой переменной образуют область определения функции. Все значения, которые принимает зависимая переменная, образуют область значений функции.
-
Что называется графиком функции?
Графиком функции называется множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты - соответствующим значениям функции.
-
С какими функциями вы уже знакомы?
С линейной функцией, прямой и обратной пропорциональности, функциями, заданными формулами: ![]()
-
Что представляет собой график:
-
Линейной функции?
Прямую
-
Прямой пропорциональности?
Прямую
-
Обратной пропорциональности?
Гиперболу
-
Функции, заданной формулой
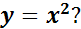
параболу
-
Дайте определение функции, возрастающей в промежутке; убывающей в промежутке?
Функция называется возрастающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует большее значение функции; функция называется убывающей в некотором промежутке, если большему значению аргумента из этого промежутка соответствует меньшее значение функции.
-
Ознакомление с новым материалом.
Введение понятия квадратичной функции осуществляем, используя метод целесообразных задач. Для этого предлагаем учащимся последовательно решить две задачи. (Слайд № 6.).
Задача1.
Выразить площадь поверхности куба через его ребро x. Найти площадь S при x=2; 3; 5.
Решение.
S1=x2, число граней равно 6,
S=6x2 ,
x=2 S=24;
x=3 S=54;
x=5 S=150.
Задача2.
Тело движется с ускорением а=6 м/с2 и к началу отсчета времени t прошло путь S0=20 м, имея в этот момент скорость V0=5 м/с. Найдите пройденный путь S при t=2, 4.
Решение.
Выразим зависимость пути S от времени t.
S=+V0t+S0 , S=3t2+5t+20,
T1=2 S1=3*4+5*2+20=42;
T2=4 S2=3*16+5*4+20=88.
После решения предложенных задач, задаем учащимся следующие вопросы:
-
И в первой, и во второй задаче зависит ли значение переменной S от какой - либо другой переменной?
(Да. В первой задаче S зависит от x; во второй задаче S зависит от t)
-
Значит, S какая переменная? (зависимая переменная)
-
А переменные x и t? (независимые переменные)
-
А сколько значений зависимой переменной соответствует каждому значению независимой переменной в первой задаче? А во второй задаче?
(Каждому значению независимой переменной соответствует единственное значение зависимой переменной и в первой, и во второй задаче)
-
Значит, что мы получили? (Функции)
Теперь, запишем полученную функцию в общем виде. Для этого заменим переменную S на переменную y, переменную t на - x, а числа обозначим через a, b и c. Тогда полученная функция будет иметь следующий вид: y=ax2+bx+c. Ребята, функция вида y=ax2+bx+c называется квадратичной функцией.
-
В этой функции число а - коэффициент при x2 может ли быть равным нулю? Тогда, что мы получаем?
(Число а может быть равным нулю, тогда функция примет вид: y=bx+c)
-
А с функцией y=bx+c мы знакомы? Какая это функция?
(Да. Это линейная функция)
Значит, на число а накладывается ограничение - оно не может быть равным нулю. Теперь, ребята, давайте попробуем дать определение квадратичной функции.
Учащиеся вместе с учителем формулируют определение квадратичной функции. (Слайд №7.)
Определение: Квадратичной функцией называется функция, которую можно задать формулой вида y=ax2+bx+c , где x - независимая переменная, a, b и c - некоторые числа, причем a≠0.
-
Как вы думаете, что является областью определения квадратичной функции?
(Множество всех чисел)
Правильно, областью определения квадратичной функции является множество всех чисел или вся числовая прямая.
Изучение квадратичной функции начнем с частного случая, а именно с функции y=ax2, которая получается из функции y=ax2+bx+c при b=0 и c=0. Примером является функция S=6x2, полученная в первой задаче.
При а=1 формула y=ax2 принимает вид y=x2. С этой функцией вы встречались, ее графиком является парабола.
Теперь давайте построим график функции y=2x2. Для этого составим таблицу значений этой функции.
Учитель на доске составляет таблицу значений функции, а ученики ему помогают и пишут у себя в тетрадях.
X
-2
-1,5
-1
-0,5
0
0,5
1
1,5
2
y
8
4,5
2
0,5
0
0,5
2
4,5
8
Теперь, постройте точки, координаты которых указаны в таблице. Далее соедините их плавной линией. Получаем график функции y=2x2.
Ученики строят график функции y=2x2 в тетрадях, а у учителя на слайде появляется график функции y=2x2, а потом график функции y=x2. (Слайд №8.)
Далее задаем вопросы:
-
Сравнивая графики функций y=2x2 и y=x2, что мы видим?
(Они похожие, при любом x значение функции y=2x2 больше соответствующего значения функции y=x2 в 2 раза)
Правильно, при любом x ≠ 0 значение функции y=2x2 больше соответствующего значения функции y=x2 в 2 раза. Если переместить каждую точку графика функции y=x2 вверх так, чтобы расстояние от этой точки до оси x увеличилось в 2 раза, то она перейдет в точку графика функции y=2x2. При этом каждая точка графика функции y=2x2 может быть получена из некоторой точки графика функции y=x2.
Иными словами, график функции y=2x2 можно получить из параболы y=x2 растяжением от оси x в 2 раза.
Далее предлагаем ученикам построить график функции y=1/2x2. Для этого составляем таблицу значений этой функции.
Учитель на доске составляет таблицу значений функции, а ученики ему помогают и пишут у себя в тетрадях.
X
-4
-3
-2
-1
0
1
2
3
4
y
8
4,5
2
0,5
0
0,5
2
4,5
8
Теперь, постройте точки, координаты которых указаны в таблице. Далее соедините их плавной линией. Получаем график функции y=1/2x2.
Ученики строят график функции y=1/2x2 в тетрадях, а у учителя на этом же слайде появляется график функции y=1/2x2. На данном слайде также для более наглядного сравнения появляются графики всех трех функций на одной координатной плоскости. (Слайд №8.)
Далее задаем вопросы:
-
Сравнивая графики функций y=1/2x2 и y=x2, что мы видим?
(Они похожие, при любом x значение функции y=1/2x2 меньше соответствующего значения функции y=x2 в 2 раза)
Правильно, при любом x ≠ 0 значение функции y=1/2x2 меньше соответствующего значения функции y=x2 в 2 раза. Если переместить каждую точку графика функции y=x2 вниз так, чтобы расстояние от этой точки до оси x уменьшилось в 2 раза, то она перейдет в точку графика функции y=1/2x2, причем каждая точка графика функции y=1/2x2 может быть получена из некоторой точки графика функции y=x2.
Таким образом, график функции y=1/2x2 можно получить из параболы y=x2 сжатием к оси x в 2 раза.
-
Какой вывод из всего выше сказанного можно сделать? Как можно получить график функции y=аx2 из параболы y=x2?
Ученики вместе с учителем делают краткий вывод:
В общем случае, график функции y=аx2 можно получить из параболы y=x2 растяжением от оси x в a раз, если а>1, и сжатием к оси x в 1/а раза, если 0<�������
�����������������������������������������������������������������������������������������������������������������������������������������
-
�������������������������������������������������������������������������
-
����������������������������������������������������������������������������
-
������������������������������������������������������������������������������������������
-
���������������������������������������������
-
�������������������������������������������������������������������������������������������������������������������
����������������������������������������������������������������������������������������������
����������������������������������������������������������������������������
���������
������������������
������������������
������������������
������������������
���������
���������
��������
�������
�������
�������
��������������
���������������
���������
��������������
���
��������������
���������
�����������
������
�����������������������������������������������������������������������������������������������������������������
�������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������
������������������
-
�������������������������������������������������������������������������������������������������������������������
�������������������������������������������
������������������������������������������������������������������������������������������������������������������������������
������������������������������������������������������������������������������������������������������������������������������������������������������������������������
-
�����������������������������������������������������������������������������������������������������������������������
���������������������������������������������
����������������������������������������������������������������������������������������������������������������������
����������������������������������������������������������������������������������������������������������������������������������������
-
�������������������������������������������������������������������������
-
���������������������������������������������������������������������������
-
������������������������������������������������������������������������������������������
-
���������������������������������������������
-
����������������������������������������������������������������������������������������������������������������������������������������
�����������������������������������������������������������������������������������������������������������������������������������������
���������������������������������������������������
����������������������������������������������������������������������������������������������������������������������������������������������������������������������������������������
-
����ное закрепление темы.
Решаем примеры:
№ 90. Постройте график функции y=1/4x2. Найдите:
А) значение y при x= -2,5; -1,5; 3,5
Б) значение x при y= 5, 3, 2
В) промежутки возрастания и промежутки убывания функции.
Решение: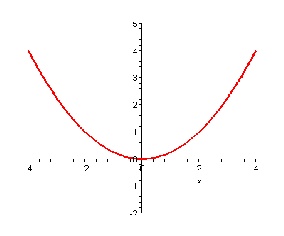
x
y
-4
4
-3
2,25
-2
1
-1
0,25
0
0
1
0,25
2
1
3
2,25
4
4
А) x= -2,5 y=1,5 Б) y=5 x=4,5, x=-4,5 В) (0, ∞) - возрастает.
X= -1,5 y=0,6 y=3 x=3,5, x=-3,5 (-∞, 0) - убывает.
X= 3,5 y=3,1 y=2 x=2,8, x=-2,8
№ 94 (а). Покажите схематически, как расположен в координатной плоскости график функции
а) y=-1,5x2. Перечислите свойства этой функции.
Решение: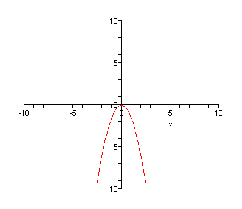
y=-1,5x2
Свойства:
-
График функции проходит через начало координат.
-
График функции расположен в нижней полуплоскости.
-
График функции симметричен относительно оси y.
-
Функция возрастает в промежутке(-∞;0] и убывает в промежутке [0;+∞).
-
Наибольшее значение, равное нулю, функция принимает при x=0, наименьшего значения функция не имеет. Областью значений функции является промежуток [-∞;0).
№ 96 (а, б, в - устно). Пересекаются ли парабола y=2x2 и прямые:
А) y=50, Б) y=100, В) y=-8, Г) y=14x-20. Если точка пересечения существует, то найти их координаты.
Решение:
А) Да. (5, 50), (-5, 50).
Б) Да. (5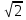 , 100), (-5
, 100), (-5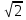 , 100).
, 100).
В) Нет.
Г) 2x2=14x-20
2x2-14x+20=0
x2-7x+10=0
x1=5 x2=2
y1=50 y2=8
(5, 50), (2,8).
-
Подведение итогов урока. Домашнее задание.
-
Что нового вы сегодня узнали на уроке?
-
С какой функцией мы сегодня познакомились?
-
Как она получается из функции y=x2?
-
Что является графиком квадратичной функции?
-
Какие преобразования функций мы сегодня рассмотрели?
Давайте в тетрадях запишем таблицу преобразований функций, на следующих уроках будем ее продолжать. (Слайд №12.)
Функция
Преобразование Y=f(x)
1) y=-f(x)
Симметрично относительно оси x
-
y=a f(x), a›0
y=a f(x), 0‹a‹1
Растяжение по оси x в а раз
Сжатие по оси x в 1/a раз
Теперь запишите в дневниках домашнее задание: п.5, № 91, № 94(б), № 92.
№ 91. Постройте график функции y=-2x2. Найдите:
А) значение y при x= -1,5; 0,6; 1,5
Б) значение x при y= -1, -3, -4,5
В) промежутки возрастания и промежутки убывания функции.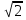
X
y
-4
-32
-3
-18
-2
-8
-1
-2
0
0
1
-2
2
-8
3
-18
4
-32
Решение:
А) x= -1,5 y=-4,5 Б) y=-1 x=0,3, x=-0,3 В) (0, ∞) - убывает.
X= 0,6 y=-0,8 y=-3 x=1,2, x=-1,2 (-∞, 0) - возрастает.
X= 1,5 y=-4,5 y=-4,5 x=1,5, x=-1,5
№ 94 (б). Покажите схематически, как расположен в координатной плоскости график функции
а) y=0,8x2. Перечислите свойства этой функции.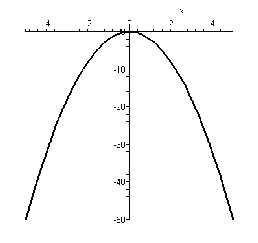
Решение:
y=0,8x2
Свойства:
-
График функции проходит через начало координат.
-
График функции расположен в верхней полуплоскости.
-
График функции симметричен относительно оси y.
-
Функция убывает в промежутке(-∞;0] и возрастает в промежутке [0;+∞).
-
Наименьшее значение, равное нулю, функция принимает при x=0, наибольшего значения функция не имеет. Областью значений функции является промежуток [0;+∞).
№ 92. Постройте в одной координатной плоскости графики функций: y=x2, y=1/8x2, y=1/3x2.
Решение:
y=x2 y=1/8x2
x
y
-4
16
-3
9
-2
4
-1
1
0
0
1
1
2
4
3
9
4
16
x
y
-4
2
-3
1,125
-2
0,5
-1
0,125
0
0
1
0,125
2
0,5
3
1,125
4
2
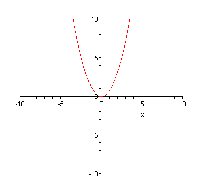
y=1/3x2
x
y
-4
5,333333
-3
3
-2
1,333333
-1
0,333333
0
0
1
0,333333
2
1,333333
3
3
4
5,333333
9