Разработка урока Исследование функции с применением производной 10 класс

Тема занятия: Исследование функции с применением производной

учитель математики и информатики

КУРТАСОВА Л. В.

ГУ СШ №29,

г. АКТОБЕ

Цель: учить применять производную для исследования функций и построения графиков.

Образовательные задачи:

1. Изучение схемы исследования функции;

2. применение полученных теоретических знаний для решения задач;

3. развитие умения анализировать условие задачи с тем, чтобы выбрать оптимальный вариант решения.

Воспитательные задачи:

1. воспитание потребности в знаниях;

2. формирование навыков умственного труда - поиск рациональных путей решения, самообразования, самовоспитания;

3. воспитание культуры общения, взаимопомощи, умения слушать товарища; ответственности.

Развивающие задачи:

1. способствование развитию общеучебных умений;

2. развитие творческой стороны мышления;

3. умение осуществлять исследовательскую деятельность;

4. развитие уверенности в себе, интереса к предмету.

Общая схема исследования функций включает в себя такие элементы, как нахождение промежутков монотонности, точек экстремума, участков выпуклости т.д. Применение производной позволяет значительно упростить эти исследования.

С л е д с т в и е . Если функция разрывна в некоторой точке, то она не имеет производной в этой точке.

П р и м е р .

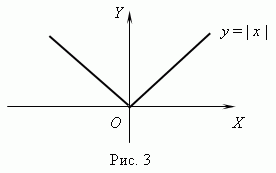
Функция y = | x | ( рис.3 ) всюду непрерывна, но она не имеет производной при x = 0 , так как в этой точке не существует касательной к графику этой функции.

( Подумайте, почему ? )

Достаточные признаки монотонности функции.

Если f '( x ) > 0 в каждой точке интервала ( a, b ), то функция f ( x ) возрастает на этом интервале.

Если f '( x ) < 0 в каждой точке интервала ( a, b ) , то функция f ( x ) убывает на этом интервале.

Теорема Дарбу. Точки, в которых производная функции равна 0 или не существует, делят область определения функции на интервалы, внутри которых производная сохраняет знак.

Используя эти интервалы, можно найти интервалы монотонности функций, что очень важно при их исследовании.

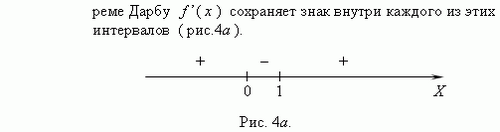
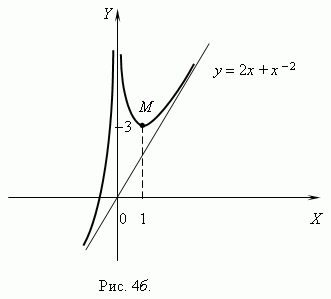
Следовательно, функция возрастает на интервалах (  0 ) и ( 1, + и убывает на интервале ( 0, 1 ). Точка x = 0 не входит в область определения функции, но по мере приближения x к 0 слагаемое x ^2 неограниченно возрастает, поэтому функция также неограниченно возрастает. В точке x = 1 значение функции равно 3. В соответствии с этим анализом мы можем построить график функции ( рис.4б ) .

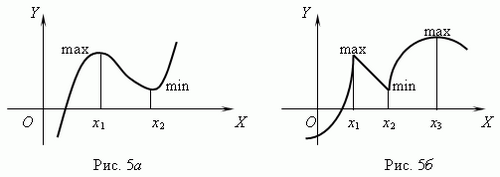
Критические точки. Внутренние точки области определения функции, в которых производная равна нулю или не существует, называются критическими точками этой функции. Эти точки очень важны при анализе функции и построении её графика, потому что только в этих точках функция может иметь экстремум ( минимум или максимум , рис.5а,б).

В точках x₁ , x₂ ( рис.5a ) и x₃ ( рис.5b ) производная равна 0; в точках x₁ , x₂ ( рис.5б ) производная не существует. Но все они точки экстремума.

Необходимое условие экстремума. Если x₀ - точка экстремума функции f(x) и производная f' существует в этой точке, то f'(x₀)=0.

Эта теорема - необходимое условие экстремума. Если производная функции в некоторой точке равна 0, то это не значит, что функция имеет экстремум в этой точке. Например, производная функции f ( x ) = x ³ равна 0 при x = 0, но эта функция не имеет экстремум в этой точке ( рис.6 ).

С другой стороны, функция y = | x | , представленная на рис.3, имеет минимум в точке x = 0 , но в этой точке производной не существует.

Достаточные условия экстремума.

Если производная при переходе через точку x₀ меняет свой знак с плюса на минус, то x₀ - точка максимума.

Если производная при переходе через точку x₀ меняет свой знак с минуса на плюс, то x₀ - точка минимума.

План исследования функции.

Для построения графика функции нужно:

1) найти область определения и область значений функции,

2) установить, является ли функция чётной или нечётной,

3) определить, является ли функция периодической или нет,

4) найти нули функции и её значения при x = 0,

5) найти интервалы знакопостоянства,

6) найти интервалы монотонности,

7) найти точки экстремума и значения функции в этих точках,

8) проанализировать поведение функции вблизи "особых" точек

и при больших значениях модуля x .

П р и м е р . Исследуйте функцию f ( x ) = x ³ + 2x ²  x  2 и постройте график.

Р е ш е н и е . Исследуем функцию по вышеприведенной схеме.

1) область определения x R ( x - любое действительное число);

область значений y R, так как f ( x ) - многочлен нечётной

степени;

2) функция f ( x ) не является ни чётной, ни нечётной

( поясните, пожалуйста );

3) f ( x ) - непериодическая функция ( докажите это сами );

4) график функции пересекается с осью Y в точке ( 0, - 2 ),

так как f ( 0 ) =  2 ; чтобы найти нули функции нужно

решить уравнение: x ³ + 2x ²  x  2 = 0, один из корней

которого ( x = 1 ) очевиден. Другие корни находятся

( если они есть! ) из решения квадратного уравнения:

x ² + 3x + 2 = 0, которое получено делением многочлена

x ³ + 2x ²  x  2 на двучлен ( x - 1 ). Легко проверить,

что два других корня: x₂ = 2 и x₃ = 1. Таким образом,

нулями функции являются: 2, 1 и 1.

5) Это значит, что числовая ось делится этими корнями на

четыре интервала знакопостоянства, внутри которых

функция сохраняет свой знак :

Этот результат может быть получен разложением

многочлена на множители:

x ³ + 2x ²  x  2 = ( x + 2 ) ( x + 1 ( x - 1 )

и оценкой знака произведения .

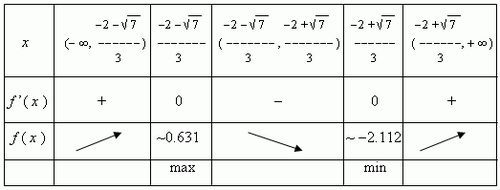
6) Производная f' ( x ) = 3x² + 4x 1 не имеет точек, в которых

она не существует, поэтому её область определения R ( все

действительные числа ); нули f' ( x ) - это корни уравнения:

3x² + 4x  1 = 0 .

Полученные результаты сведены в таблицу:

Механический смысл производной.

Задача 1. Точка движется прямолинейно по закону Найдите среднюю скорость точки на промежутке [1;4]. Найдите скорость лодки в момент времени t = 3 с.

Задача 2. Точка движется прямолинейно по закону В какой момент времени скорость точки окажется равной нулю.

в конце 2 секунды.