Учителю
'Олимпиада по математике', школьный тур для учащихся 5-7 классов

'Олимпиада по математике', школьный тур для учащихся 5-7 классов

Автор публикации: Кузнецова О.Н.

Дата публикации: 02.11.2014

Краткое описание: Олимпиадные задания по математике 5 классЗадача 1. В корзине лежат яблоки, груши и персики – всего 37 плодов. Яблок в корзине в два раза больше, чем персиков, и на 3 штуки больше, чем груш. Сколько в корзине яблок, груш, персиков? Задача 2. Запишите все делители числа 24. Запишите

предварительный просмотр материала

Олимпиадные задания по математике 5 класс

Задача 1. В корзине лежат яблоки, груши и персики - всего 37 плодов. Яблок в корзине в два раза больше, чем персиков, и на 3 штуки больше, чем груш. Сколько в корзине яблок, груш, персиков?

Задача 2. Запишите все делители числа 24. Запишите все числа, меньшие двухсот, которые кратны этому числу.

Задача 3. Из двух городов, расстояние между которыми 100 км, одновременно выехали навстречу друг другу два велосипедиста, скорости которых 12 км/ч и 14 км/ч. Каким будет расстояние между велосипедистами через 3 часа после начала их движения?

Задача 4. Начертите угол, который на 15^о меньше прямого угла. Начертите угол, который на 65^о меньше развёрнутого угла. На сколько градусов первый угол меньше второго?

Задача 5. На стол положили ложки, вилки и ножи - всего 37 приборов. При этом вилок положили в два раза больше, чем ножей и на 2 меньше, чем ложек. Сколько положили на стол ложек, вилок, ножей?

Олимпиадные задания по математике 5 класс

Задача 2. Запишите все делители числа 24. Запишите все числа, меньшие двухсот, которые кратны этому числу.

Олимпиадные задания по математике 5 класс

Задача 2. Запишите все делители числа 24. Запишите все числа, меньшие двухсот, которые кратны этому числу.

Ответы к задачам: 5 класс.

Задача 1.Яблок - 16, груш - 13, персиков - 8.

Задача 2.Делители: 1, 2, 3, 4, 6, 8, 12, 24. Кратные: 24, 48, 72, 96, 120, 144, 168, 192.

Задача 3.Искомое расстояние равно: 100-(12+14)•3=22 (км).

Задача 4.Нужно начертить углы величиной в 75о и 115о. На 40о.

Задача 5.Вилок - 14, ножей - 7, ложек - 16.

Олимпиада по математике. 7 класс.

Что больше: 1234567·1234569 или 1234568² ?
Магазин продал одному покупателю 25% полотна, второму - 30% остатка, а третьему - 40% нового остатка. Сколько процентов полотна осталось?
Учитель математики, проверив контрольные работы у трех друзей: Алексея, Бориса и Василия, сказал им: «Все вы написали работу, причем получили разные отметки («3», «4», 5»). У Василия - не «5», у Бориса - не «4», а у Алексея, по моему, «4». Впоследствии оказалось, что учитель ошибся: одному ученику сказал отметку верно, а другим двум неверно. Какие отметки получил каждый из учеников?
Дворец имеет форму прямоугольника размером 13х15. Каждая клетка, кроме центральной, - комната замка, а в центральной клетке находится бассейн. В каждой стене (стороне клетки), разделяющей две соседние комнаты, есть дверь. Можно ли, не выходя из дворца и не заходя в бассейн, обойти все комнаты, побывав в каждой ровно по одному разу?
Дан угол в 13°. Как получить угол в 11°?

Решения и ответы:

1234568² > 1234567·1234569

1234567·1234569= (1234568-1)·(1234568+1)= 1234568²-1²

1234568² > 1234568²-1²

31,5%.

Пусть было 100% полотна.

После первой продажи осталось 100-25=75% полотна. После второй 100-30=70% остатка, а после третьей 100-40=60% нового остатка. Значит, осталось 100·0,75·0,7·0,6=0,315=31,5%.

Алексей получил «5», Борис - «4», Василий - «3».

Рассмотрим три случая.

1 случай. Пусть учитель сказал верно Алексею. Значит, у Алексея - «4». Т.к. Борису и Василию учитель назвал неверные отметки, то у Бориса - «4», а у Василия - «5». Получилось, что у двух учеников оказались одинаковые отметки, что противоречит условию задачи. Данный случай невозможен.

2 случай. Пусть учитель сказал верно Василию. Тогда у Василия отметка - не «5». Т.к. учитель сказал неверно об отметках Алексея и Бориса, то у Алексея отметка не «4», а у Бориса - «4». Тогда у Алексея - «5», у Василия - «3».

3 случай. Пусть учитель сказал верно Борису. Тогда Борис получил не «4». Т.к. утверждения про отметки Алексея и Василия ложные, то у Алексея - не «4», у Василия - «5». Получается, что отметку «4» никто не получил. Этот случай тоже противоречит условию задачи.

Нельзя.

Раскрасим прямоугольник в шахматном порядке так, чтобы центральная клетка была черная. При этом клеток черного цвета будет на 1 меньше, чем белых клеток. В центральной клетке находится бассейн, поэтому черных комнат на 2 меньше, чем белых. При переходе через дверь мы попадаем в комнату другого цвета, т.е. цвет комнат чередуется. Поэтому разность между количеством пройденных комнат разного цвета не более одного (т.к. путь распадается на пары клеток разного цвета, исключая, может быть, последнюю). Значит, обойти все комнаты, побывав в каждой ровно по одному разу, нельзя.

Отложить 13 раз угол по 13°, получим угол 169°. Тогда разность развернутого угла и 169° даст искомый угол: 180°-169°=11°.

олимпиада

по математике для учащихся 6 классов.

1. Календарь представляет собой два кубика, у каждого кубика на всех гранях написано по цифре. Дату (день месяца) составляют, используя один или два кубика. Придумайте, как написать цифры на кубиках, чтобы можно было получить любую дату от 1 до 31. (В ответе напишите, какие цифры должны быть на одном кубике, а какие - на другом)

2. Одной черепахе 300 лет, а другой 15 лет. Через сколько лет первая черепаха будет вдвое старше второй?

3. Сад разбит на квадраты. Садовник начал обход с верхнего правого квадрата, обошел весь сад и вернулся в тот же угловой квадрат. В закрашенных квадратиках он не был (там располагаются пруды). Во всех остальных квадратиках он побывал по одному разу, причем через вершины квадратов он не проходил. Начертите возможный путь садовника.

4. Прямоугольник разрезали на три прямоугольника, два из которых имеют размеры 5x11 и 4x6. Какие размеры мог иметь третий прямоугольник? (Найдите все возможные варианты.)

5. Винни-Пуху дали полную тарелку манной каши. Он съел половину и положил в тарелку еще столько же меда. Затем он съел треть содержимого тарелки (каши с медом) и снова доложил мед. Потом съел четверть содержимого и опять доложил медом, после чего с аппетитом все съел. Чего в итоге Винни-Пух съел больше: каши или меда?

олимпиада

по математике для учащихся 6 классов.

1. Календарь представляет собой два кубика, у каждого кубика на всех гранях написано по цифре. Дату (день месяца) составляют, используя один или два кубика. Придумайте, как написать цифры на кубиках, чтобы можно было получить любую дату от 1 до 31. (В ответе напишите, какие цифры должны быть на одном кубике, а какие - на другом)

2. Одной черепахе 300 лет, а другой 15 лет. Через сколько лет первая черепаха будет вдвое старше второй?

3. Сад разбит на квадраты. Садовник начал обход с верхнего правого квадрата, обошел весь сад и вернулся в тот же угловой квадрат. В закрашенных квадратиках он не был (там располагаются пруды). Во всех остальных квадратиках он побывал по одному разу, причем через вершины квадратов он не проходил. Начертите возможный путь садовника.

5. Винни-Пуху дали полную тарелку манной каши. Он съел половину и положил в тарелку еще столько же меда. Затем он съел треть содержимого тарелки (каши с медом) и снова доложил мед. Потом съел четверть содержимого и опять доложил медом, после чего с аппетитом все съел. Чего в итоге Винни-Пух съел больше: каши или меда?

Ключи, критерии оценивания олимпиадных заданий

школьного этапа по математике

6 класс

Каждая задача оценивается из 7 баллов. Каждая оценка - целое число от 0 до 7. Ниже приведены некоторые указания к проверке. Естественно, всех случаев жюри предвидеть не может. При оценке решения нужно исходить из того, является ли приведенное решение в целом верным (хотя, может, и с недостатками) - тогда решение оценивается не менее чем в 4 балла. Или оно неверное (хотя, может, и с существенными продвижениями) - в этом случае оценка должна быть не выше 3 баллов.

Задача 1.

Решение. Например, на одном кубике написаны цифры 0, 1, 2, 4, 5, 6, а на другом 1, 2, 3, 7, 8, 9. Замечание. Существуют и другие примеры. Для проверки правильности примера, достаточно проверить, что 1) в каждой группе по 6 цифр, 2) все цифры встречаются, 3) можно составить числа 11, 22 и 30 (т.е. в каждой группе есть цифры 1 и 2, а цифры 0 и 3 находятся в разных группах).

Правильное распределение - 7 баллов. Только неправильный пример - 0 баллов. Сказано, что 1 и 2 должны быть на обоих кубиках т.к. есть числа 11 и 22, а дальше пример неправильный из-за того, что 0 и 3 поместили на один кубик - 2 балла.

Задача 2.

Ответ. Через 270 лет. Решение. Разница между черепахами всегда 300-15=285 лет. Одна будет вдвое старше другой, когда второй будет столько лет, какова разница, т.е. 285. А 285 лет второй черепахе исполнится через 285-15=270 лет.

Только ответ без всяких пояснений - 2 балла. Записаны правильные действия, но без пояснения - 4 балла.

Задача 3. Правильный пример - 7 баллов. Пример незамкнутого пути или пути не по всем клеткам - 0 баллов.

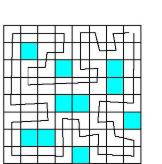
Ответ. Один из возможных примеров обхода приведен на рисунке (возможны и другие пути).

Задача 4.

Ответ. 5x4, 7x6, 1x6, 1x11. Решение. Посмотрим, как могут прилегать прямоугольники друг к другу. Прямоугольник 4x6 может примыкать к стороне 5 или к стороне 11, при этом прилегать он может стороной 4 или стороной 6, т.е. всего 4 варианта. Из них получаем размеры третьего прямоугольника: 5x4, 7x6, 1x6, 1x11.

Найдены все варианты (подтверждены картинками) - 7 баллов. Найдены только три из четырех вариантов - 5 балла. Найдено два варианта - 3 балла. Найден только один вариант - 1 балл.

Задача 5.

Ответ. Меда он съел больше. Решение. Видно, что Пух в итоге съел тарелку каши. Посчитаем, сколько он съел меда: 1/2+1/3+1/4 = 13/12>1.Голый ответ 1 балл. Решение верное, но не доведено до конца - 2 балла. Вычислительная ошибка - минус 1 балл (если вычислительных ошибок несколько, соответственно вычитается больше).

Максимальное количество баллов за работу - 35.

Олимпиадные задания по математике 6 класс

Трехзначное число состоит из возрастающих (слева направо) цифр.
Если это число прочитать, то все слова будут начинаться на одну и туже букву.
Что это за число?

Три курицы за три дня несут три яйца.
Сколько яиц снесут 12 таких же кур за 12 дней?

Пять землекопов за 5 часов выкапывают 5 м канавы.
Сколько потребуется землекопов, для того чтобы выкопать 50 м канавы за 50 часов?

На столе лежат девять монет. Одна из них - фальшивая.
Как при помощи двух взвешиваний можно найти фальшивую монету?
(Фальшивая монета легче настоящих.)

Отец с двумя сыновьями отправился в поход.
На их пути встретилась река, у берега которой находился плот.
Он выдерживает на воде или отца, или двух сыновей.
Как переправиться на другой берег отцу и сыновьям?

На столе лежат две монеты, в сумме они дают 3 рубля.
Одна из них не 1 рубль. Какие это монеты?

Найдите минимальное пятизначное число, все цифры которого различны, и которое делится на 83 без остатка.

Докажите, что при перемножении двух тысяч двенадцати двоек получается число не более, чем из 700 цифр.

Одна дама хвасталась подруге миловидной девушкой, изображенной на фотографии.
Дама сказала, что у нее нет родных сестер и братьев, но мать изображенной девушки была дочерью ее отца.
Кто на фото?

Коробка конфет весит 250 г и еще половина коробки конфет.
Сколько весит коробка конфет?

Арбуз разрезали на четыре части и съели. Получилось пять корок.
Могло ли такое быть?

В классе школьники сидят по одному человеку за партой - в три ряда по пять человек.
Каждый школьник подарил своему соседу (справа, слева, впереди или сзади сидящему) по конфете.
Докажите, что есть школьник, которому подарили по крайне мере две конфеты.

Какие две цифры нужно приписать справа к числу 2012, чтобы получилось число, делящееся на 77?

Докажите, что среди чисел 5х - 3y - 2z, 5y - Зz - 2х, 5z - Зх - 2у найдется хотя бы одно неотрицательное.

Найдите минимальное пятизначное число, которое делится на 79 без остатка.

Олимпиадные задания по математике 8 класс

Задача 1. Какой цифрой оканчивается сумма 9²⁰⁰⁷ + 9²⁰⁰⁶ ?

Ответ: 9²⁰⁰⁷ + 9²⁰⁰⁶ = 9²⁰⁰⁶( 9 + 1) = 9²⁰⁰⁶* 10. Нулем.

Задача 2. В оранжерее было срезано 360 гвоздик. Причем красных на 80 больше, чем белых, а розовых на 160 штук меньше, чем красных.
Какое наибольшее число одинаковых букетов можно составить из этого количества цветов ?
Сколько и каких цветов было в каждом букете?

Ответ: Решая уравнение, получаем 40 розовых гвоздик,120 белых гвоздик, 200 красных гвоздик. НОД (40, 120,200) равен 40, следовательно из 360 гвоздик можно составить 40 букетов, причем каждый букет будет состоять из 1 розовой, 3 белых и 5 красных гвоздик.

Задача 3. Существует ли такой круг, чтобы его площадь и длина окружности выражались одним и тем же числом ?
Ответ: Да, при радиусе равном 2.
Задача 4. После семи стирок измерения куска хозяйственного мыла, имеющего форму прямоугольного параллелепипеда, уменьшились в двое.
На сколько еще стирок хватит оставшегося куска мыла ?

Ответ: Мыла хватит еще на одну стирку, т.к. объем оставшегося мыла составил 1/8 часть первоначального, израсходовано мыла: 1 - 1/8 = 7/8 куска,
значит на каждую стирку расходовалось 1/8 часть куска, именно столько осталось.
Задача 5. Какими двумя цифрами заканчивается число 13! ?
Ответ: В произведении 1*2*3…*13 есть множители 2, 5 и 10, значит число 13!
Заканчивается двумя нулями.
Задача 6. Из 38 учащихся 28 посещают хор и 17 лыжную секцию.
Сколько лыжников посещает хор, если в классе нет учащихся, которые не посещают хор или лыжную секцию ?
Ответ: 7 человек. Хор не посещают 10 человек, все они лыжники.
Лыжников всего 17человек, значит 7 человек надо «взять» из хора.
Задача 7.
Окружность касается квадрата извне и «катится» по нему без скольжения.
Сколько полных оборотов сделает эта окружность около своего центра и какой путь пройдет центр окружности к моменту возвращения в исходную точку, если длина стороны квадрата равна длине окружности и радиус окружности равен а см ?
Те же вопросы, если окружность «катится» по сторонам равностороннего треугольника.

Ответ: В случае квадрата каждая точка окружности сделает 4 оборота около своего центра.
Центр окружности сделает четверть оборота около каждой вершины квадрата.
За один обход центр окружности совершает путь, равный 5*2Па см.
В случае треугольника - соответственно 3 оборота и 8П а см
Олимпиадные задания по математике 8 класс

Олимпиадные задания по математике 8 класс

Задача 1. Какой цифрой оканчивается сумма 9²⁰⁰⁷ + 9²⁰⁰⁶ ?
Задача 2. В оранжерее было срезано 360 гвоздик. Причем красных на 80 больше, чем белых, а розовых на 160 штук меньше, чем красных.
Какое наибольшее число одинаковых букетов можно составить из этого количества цветов? Сколько и каких цветов было в каждом букете?
Задача 3. Существует ли такой круг, чтобы его площадь и длина окружности выражались одним и тем же числом ?
Задача 4. После семи стирок измерения куска хозяйственного мыла, имеющего форму прямоугольного параллелепипеда, уменьшились в двое.На сколько еще стирок хватит оставшегося куска мыла ?
Задача 5. Какими двумя цифрами заканчивается число 13! ?
Задача 6. Из 38 учащихся 28 посещают хор и 17 лыжную секцию.
Сколько лыжников посещает хор, если в классе нет учащихся, которые не посещают хор или лыжную секцию ?
Задача 7. Окружность касается квадрата извне и «катится» по нему без скольжения.
Сколько полных оборотов сделает эта окружность около своего центра и какой путь пройдет центр окружности к моменту возвращения в исходную точку, если длина стороны квадрата равна длине окружности и радиус окружности равен а см ?
Те же вопросы, если окружность «катится» по сторонам равностороннего треугольника.

Задача 8. Во время похода палатки расположились в т. А,В, и С.
В каком месте удобно выбрать площадку для проведения общего костра,
чтобы расстояние от него до палаток было одинаковым ?
Ответ: Точка осей симметрии точек А и В и точек В и С будет искомой.

Задача 9.

Найдите произведение всех целых чисел от (-99) до 99.

Ответ:

0

Задача 10.

Две семьи выехали каждая на машине «Жигули» на прогулку одновременно из одного места.
Обе семьи проехали на машинах одинаковые расстояния и вернулись домой в одно и то же время.
В пути они отдыхали.
Первая семья была в пути в двое больше времени, чем вторая.
Вторая была в пути втрое больше времени. Чем отдыхала первая.
Какая из этих семей двигалась на машине быстрее ?

Ответ:

1-я семья: 2х часов - время на езду, у часов - время на отдых.
2-я семья: 3у часов - время на езду, х часов - время на отдых 2х + у = 3у + х; х = 2у.
Вторая семья отдыхала в два раза больше, чем первая следовательно, она ехала быстрее первой.

Задача 11.

Сосуд имеет форму прямоугольного параллелепипеда.
Как, не делая никаких измерений и не имея других емкостей, наполнить водой ровно половину объема этого сосуда ?

Ответ:

Наклонить параллелепипед так, чтобы уровень воды находился по диагональному сечению параллелепипеда.

Олимпиадные задания по математике 7 класс

Задача 1.

Один из мальчиков испортил выключатель. На вопрос, кто это сделал, получили ответы:
1. Это сделал или Миша, или Коля.
2. Это сделал или Витя, или Коля.
3. Это не могли сделать ни Толя, ни Миша.
4. Это сделал или Витя, или Миша.
Можно ли по этим данным установить, кто виновен в поломке выключателя, если из четырех суждений три истинных?

Задача 2.

Предстоят спортивные соревнования между четырьмя девятыми классами одной школы. В учительской живо обсуждаются возможные результаты, высказываются прогнозы.
- Первое место займет 9А, а второе - 9Б, - сказала учительница математики.
- Да что вы! - сказала учительница географии. - Я недавно ходила с ними в поход и знаю их возможности. 9А - займет второе место, а 9Г - только третье.
- А я думаю, что на втором месте будет 9В, - сказала завуч школы, - а 9Г будет на последнем месте.
Оказалось, что прогнозы их сбылись только на половину.
Какое место занял каждый класс?

Задача 3.

На марафонском беге было сделано два прогноза о местах, которые займут спортсмены Василенко, Левченко и Симченко, реально претендующие на призовое место:
1. "Симченко будет первым, Васильков -вторым, а Левченко - третьим";
2. "Победит Васильков, Левченко придет вторым, а Симченко будет третьим".
После окончания состязания оказалось, что три фаворита действительно заняли три первые места, но оба предсказания оказались ложными.
Ни в одном из предсказаний ни одно из мест не было названо правильно.
Какое место занял каждый спортсмен?

Задача 4.

При составлении расписания уроков на один день учителя истории, математики и литературы высказали следующие предложения:
математик 1 или 2 урок
историк или 1 или 3 урок
литератор или 2 или 3
Составьте расписание.

Задача 5.

Четверо друзей - Алик, Володя, Миша и Юра - собрались в доме у Миши.Мальчики оживленно беседовали о том, как они провели лето.
- Ну, Балашов,ты, наконец, научился плавать? - спросил Володя.
- О, еще как, - ответил Балашов, - могу теперь потягаться в плавании с тобой, Алик.
- Посмотрите, какой я гербарий собрал, - сказал Петров, прерывая разговор друзей, и достал из шкафа большую папку.
Всем, особенно Лунину и Алику, гербарий очень понравился. А Симонов обещал показать товарищам собранную им коллекцию минералов.
Назовите имя и фамилию каждого мальчика.

Задача 6.

В одной школе уроки по биологии, географии, английскому языку, французскому языку, истории и математики вели три учителя: Морозов, Васильев и Токарев. Каждый из них преподавал по два предмета. Учитель географии и учитель французского языка - соседи по дому. Морозов - самый младший из троих. Все трое - Токарев, учитель биологии и учитель французского языка - ездят из школы вместе. Учитель биологии старше учителя математики. В свободное время, если им удается найти четвертого партнера, учитель английского языка, учитель математики и Морозов обычно играют в домино.
Кто какие предметы преподает?

Задача 7.

Пяти летчикам-испытателям - Сергееву, Беляеву, Корниенко, Пугачевскому и Мгеладзе - предстояло испытать пять типов самолетов: ЯК, ИЛ, МИГ, ЛА и ТУ.
В первый день Пугачевский испытал ЯК.
Во второй день Корниенко летал на ЛА.
в третий день Корниенко испытывал самолет ИЛ, а Мгеладзе - Ла
В четвертый день Сергеев поднялся в воздух на самолете ЯК, а Пугачевский на самолете МИГ.
Составьте таблицу испытаний самолетов на все пять дней полетов.

Задача 8.

Кондратьев, Давыдов и Федоров живут на одной улице. Один из них столяр, другой - моряк, третий - водопроводчик.
Федоров и Кондратьев - родственники.
Недавна моряк попросил столяра починить кое-что у него дома за вполне приличную плату. Столяр обещал зайти, но не пришел в условленный час. Моряк сам пошел к нему домой, но домашние столяра сказали, что тот ушел к внезапно заболевшему водопроводчику.
Известно также, что Федоров никогда не слышал о Давыдове.
Кто чем занимается?

Задача 9.

Дина, Жана, Вера, Борис, Дима и Толя вместе учились в школе и институте и три свадьбы эта шестерка решила отпраздновать тоже вместе.
Известно, что:
- Толя - брат Дины;
Вера - старшая из девушек;
- общий возраст каждой четы одинаков, хотя среди них нет ровестников;
- Толя старше Димы;
Диме и Жане вместе столько же лет, как Боре и Диме.
Кто на ком женится?

Олимпиадные задания по математике 10 класс

1. Постройте эскиз графика функции:.
2. Найдите все значения числового параметра а, при которых корни уравнения положительны.

3. М. В. Ломоносов тратил одну денежку на хлеб и квас. Когда цены выросли на 20%, на ту же денежку он приобретал полхлеба и квас. Хватит ли той же денежки ему хотя бы на квас, если цены вырастут еще на 20%?
4. Между числами ⁴/₇ и ⁵/₇ найти натуральное число, являющееся квадратом рационального числа.
5. Разложить многочлен x⁵ + х⁴ +1 в произведение нескольких (не менее двух) многочленов степени не ниже первой.
6. Вершины D, Е и F треугольника DEF лежат на продолжениях сторон АВ, ВС и СА треугольника ABC за вершины В, С и А соответственно. Известно, чти BD=AC, AF=CE=AB и треугольник DEF - равносторонний. Докажите, что и треугольник ABC - равносторонний.
7. Волк и Заяц играют в следующую игру: на доске написано число; ход состоит в том, чтобы вычесть из этого числа какую-либо его ненулевую цифру и записать получившееся число на месте старого. Ходят по очереди. Выигрывает тот, кто первым получает ноль. На доске исходно написано число 1234, первым ходит Волк. Кто выиграет при правильной игре?

Ответы и решения задач по математике 10 класс

1. Постройте эскиз графика функции: .

Решение.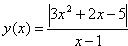

Отсюда график:

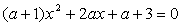
2. Найдите все значения числового параметра а, при которых корни уравнения положительны.
Ответ. .
Решение. Если (а+1)=0, то уравнение будет линейным, и его корнем при а=-1 является х=1. Подходит.
Если а?-1, то уравнение будет квадратным. По теореме Виета его корни положительны тогда и только тогда, когда выполняется

.
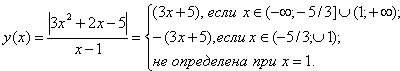С учетом первого случая получаем ответ .
3. М. В. Ломоносов тратил одну денежку на хлеб и квас. Когда цены выросли на 20%, на ту же денежку он приобретал полхлеба и квас. Хватит ли той же денежки ему хотя бы на квас, если цены вырастут еще на 20%?
Ответ. Хватит.
Решение. Пусть первоначально квас стоил х% от денежки, а хлеб - (100-х)%. После подорожания цен на 20%, получим следующий баланс . Отсюда . При двукратном подорожании цен эта величина увеличится в 1,44 разаи достигнет величины 96%, что меньше стоимости денежки.

⇧

⇩