- Учителю
- Модульная программа «Тригонометрические уравнения» (для учащихся 10 класса)
Модульная программа «Тригонометрические уравнения» (для учащихся 10 класса)
Хороших методов существует ровно
столько, сколько существует
хороших учителей.
Д.Пойа
Модульная программа по теме «Тригонометрические уравнения»
(1 часть)
№
УЭ
Учебный материал с указанием заданий
Руководство по освоению учебного материала
УЭ-0
В процессе работы над учебным материалом вы:
-
усвоите понятие тригонометрического уравнения;
-
научитесь решать простейшие тригонометрические уравнения
-
будете развивать умения сравнивать и обобщать
Внимательно прочитайте изложение цели урока.
Алгоритм работы
Найдите УЭ
Работайте с теоретической частью УЭ, выполняйте практическую часть УЭ.
Проверьте практическую работу друг друга.
Работайте по схеме: УЭ-0, УЭ-1, УЭ-2, УЭ-3, УЭ-4,УЭ-5
УЭ-1
Теоретическая часть
Цель: усвоить понятие простейшего тригонометрического уравнения, частный вид уравнения
Ознакомьтесь с п.9 §3
Вопросы и задания для самоконтроля:
1.Какие уравнения называются тригонометрическими?
2.Запишите формулу для решения первого вида уравнений, пример 1; рассмотрите 2 и 3; второго вида уравнений и пример 4; рассмотрите 5 и 6; третьего вида уравнений и пример7; рассмотрите 8 и 9.
3.Приведите свой пример простейшего тригонометрического уравнения.
4.Какие уравнения можно назвать частным случаем простейших т.у.? Запишите формулы для решения таких уравнений.
Работайте по учебнику
Работайте в тетрадях
Работайте в парах
В случае затруднения обратитесь к преподавателю
УЭ-2
Практическая часть
Цель : научиться решать простейшие т.у. и частные уравнения
-
Выполните устно №136 (а,г), №138 (в,г), №140 (а,г).
-
Выполните письменно №137(в,г), №139 (а,б), №141 (в), 142 (б).
Решения записывайте в тетрадь
Проверьте выполненную работу у соседа по парте
Консультируйтесь с преподавателем
УЭ-3
Обобщение
Цель : привести в систему полученные знания, научиться рассуждать при решении задач, делать самостоятельные выводы.
№137 (б), №139(в), №141 (а,г), №142 (а).
Индивидуальная самостоятельная работа в тетрадях
УЭ-4
Самооценка
Цель: оценить свою работу.
«+» - выполнено верно задание; «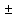 » - допущен недочет
» - допущен недочет
Ответы сверяем с ответами преподавателя
По вопросам оценки консультируйтесь с преподавателем
УЭ-5
Подведение итогов
Цель: выявить степень усвоения материала и получить задания для закрепления.
Проанализируйте, достигли ли вы поставленной цели
УЭ-6
Домашняя самостоятельная работа
Цель: закрепить полученные знания
№139 (г), №141 (б), №142 (в,г)
Выполните работу во внеурочное время
Модульная программа по теме «Тригонометрические уравнения»
(2 часть)
№
УЭ
Учебный материал с указанием заданий
Руководство по освоению учебного материала
УЭ-0
В процессе работы над учебным материалом вы:
-
познакомитесь с различными способами решения т.у.
-
научитесь решать тригонометрические уравнения
-
продолжите развивать умения сравнивать и обобщать
Внимательно прочитайте изложение цели урока.
Алгоритм работы
Найдите УЭ
Работайте с теоретической частью УЭ, выполняйте практическую часть УЭ.
Проверьте практическую работу друг друга.
Работайте по схеме: УЭ-0, УЭ-1, УЭ-2, УЭ-3, УЭ-4,УЭ-5
УЭ-1
Цель: повторить понятие простейшего т.у. и закрепить умение решать простейшие т.у.
Выполните письменно самостоятельную работу
Вариант 1.
1. Какие из данных уравнений не имеют решений:
1) cosx=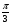 ; 3) sinx=
; 3) sinx=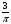 ; 5) tgx=
; 5) tgx=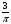 ;
;
2) sinx=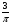 4) cosx=
4) cosx=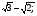 ; 6) ctgx=
; 6) ctgx=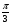 ;
;
а) 1 и 4; б) 1 и 5; в) 1 и 6; г) другой ответ.
2. Найдите сумму корней уравнения cos2x+1=0, принадлежащих промежутку 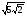 .
.
А) -2,5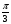 ; б) -4
; б) -4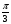 ; в) -
; в) -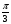 ; г) другой ответ.
; г) другой ответ.
Вариант 2.
1. Какие из данных уравнений имеют корни:
1) cosx=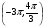 ; 3) sinx=
; 3) sinx= ; 5) tgx=
; 5) tgx=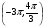 ;
;
2) sinx= ; 4) cosx=0,57; 6) ctg
; 4) cosx=0,57; 6) ctg =8?
=8?
а) 1, 5 и 6; б) 2 и 6; в) 2, 4, 5 и 6; г) другой ответ.
2. Найдите сумму корней уравнения sin2x-1=0, принадлежащих промежутку  .
.
а) 2,5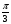 ; б) 3,5
; б) 3,5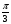 ; в) 3
; в) 3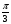 ; г) другой ответ.
; г) другой ответ.
Работайте в парах
За правильными ответами обращайтесь к учителю.
Если все задания выполнены верно, переходите к следующему учебному элементу.
УЭ-2
Практическая часть
Цель : научиться решать т.у. другими способами
-
Рассмотрите пример 1, выполните № 164 (а).
-
Рассмотрите пример 2, выполните № 165 (в,г)
-
Рассмотрите пример 3, выполните №167(г).
Примеры запишите в тетрадь
Работа в группах
УЭ-3
Обобщение
Цель : привести в систему полученные знания, научиться рассуждать при решении задач, делать самостоятельные выводы.
№164(б), №165(а), №167 (а,б).
Индивидуальная самостоятельная работа в тетрадях с последующим обсуждением в группах.
УЭ-4
Самооценка
Цель: оценить свое участи в работе группы.
Примите участие в обсуждении
УЭ-5
Подведение итогов
Цель: выявить степень усвоения материала и получить задания для закрепления.
Проанализируйте, достигли ли вы поставленной цели, какие задания вызвали у вас наибольшее затруднение
УЭ-6
Домашняя самостоятельная работа
Цель: закрепить полученные знания
№164 (г), №165 (б), №167 (в), рассмотрите примеры 4-7.
Выполните работу во внеурочное время
Каждый учащийся - индивидуальный субъект учения. Он имеет возможность обратиться за помощью к преподавателю и к одноклассникам, причем сам указывает, в какой именно помощи он нуждается. При подготовке к урокам по данной технологии следует помнить в первую очередь об учащихся, желающих знать изучаемый материал глубже и желающих заниматься самостоятельно. Специально для этой категории учащихся нужно составить приложение к урокам.
Приложение
Методы решения тригонометрических уравнений
1. Простейшие тригонометрические уравнения.
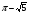
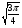
Решаются по соответствующим формулам:
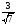
Замечание: 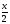
По этим же формулам решаются уравнения вида: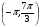
А именно:

Пример 1.

Задания:

Пример 2.

Так как 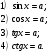 то
то 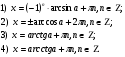 - целое. Тогда
- целое. Тогда
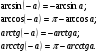
Задания:
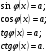
Пример 3.
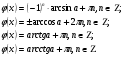
Так как 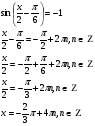 Это верно при n=0,
Это верно при n=0, 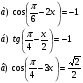
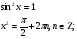
Тогда
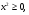
Пример 4.
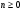
n- не целое. Ответ. Нет решений.
2. ТУ, квадратные относительно тригонометрических функций.
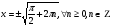
Приводятся к квадратному уравнению методом подстановки.
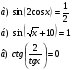
Пример 5.
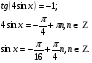
Пусть 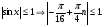 тогда
тогда
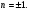
Но 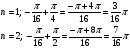 - не подходит.
- не подходит.
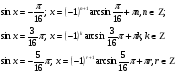
Задания:
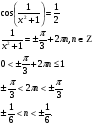
3. ТУ, рациональные относительно тригонометрической функции.
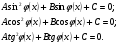
R(t) - рациональная функция аргумента t. Они преобразовываются к рациональному уравнению с помощью подстановок.
Пример 6.
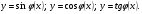
Задания:
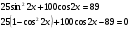
4. Метод вспомогательного угла.
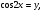
Поделим обе части на 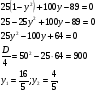 . Коэффициенты при
. Коэффициенты при  и
и 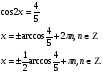 можно считать синусом и косинусом одного и того же угла
можно считать синусом и косинусом одного и того же угла 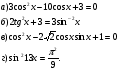 так как
так как
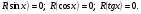
Пусть 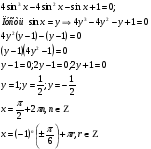
Тогда в качестве 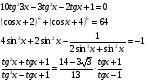 можно взять угол, равный
можно взять угол, равный 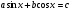

Уравнение привели к простейшему виду.
Пример 7.
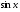
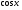
Задания:
5. Преобразование суммы в произведение
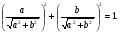
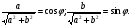
Пример 8.

Задания:
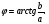
6. Преобразование произведения в сумму.
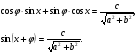
Пример 9.

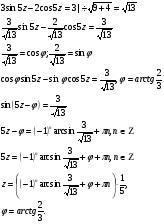
Ответ. 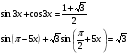
7. Понижение степеней тригонометрических функций.
Задания:
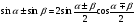
Формулы:
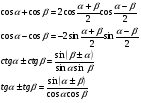
Пример 10. 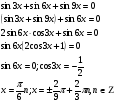
Задания:
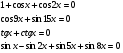
8. Разложение на множители.
Пример 11.
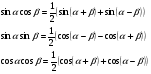
Задания:
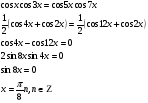
9. Однородные уравнения.
Тригонометрические уравнения 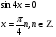 называются однородными, если функция f такова, что
называются однородными, если функция f такова, что
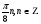 ,
,
где p - некоторое неотрицательное число. Функция f называется однородной функцией степени p.
Пример 12.
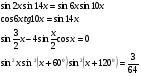
10. Замена переменной.
а) Подстановка 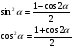
Возведем обе части в квадрат 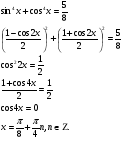
Пример 13.
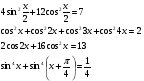
Введем вспомогательный угол: 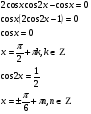
Имеем: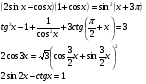
б) Подстановка 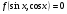 .
.
Выразим 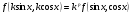 через t. Имеем
через t. Имеем
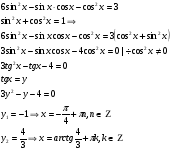
Пример 14. 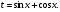
Имеем:
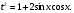
Задания:
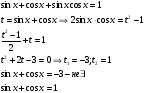
15