Разработка урока по математике в 11 классе. 'Применение интегрального исчисления к решению прикладных задач'

Урок по математике в профильном 11 классе

по теме «Применение интегрального исчисления к решению прикладных задач»

Тема урока: Применение интегрального исчисления к решению прикладных задач

Цели:

Образовательные:

• обобщить и систематизировать знания по теме.

Развивающие:

• развитие интереса к предмету,

• активизация мыслительной деятельности,

• развитие научного мировоззрения, творческого мышления, устной и письменной математической речи.

Воспитательные:

• формирование навыков самостоятельной деятельности,

• выработка внимания.

Оборудование:

• таблица интегралов;

• карточки с заданиями для групп, для парной работы и домашних заданий;

• проектор;

• сборник "Дидактический материал".

Примечание. Класс разбит на три группы А, В, С по принципу заданий тестов.

Ход урока

I. Вводная часть (1 мин.)

Учитель объявляет тему, цель урока.

II. Повторение теоретической части (15-17 мин.)

К доске приглашаются 4 ученика подготовить ответы на следующие вопросы:

1-й вопрос

• понятие первообразной для функции,

• основное свойство F(х),

• геометрический смысл F(х),

• три правила нахождения F(х),

• значение F(х) в точке ХО,

• как найти F(х), график которой проходит через заданную точку (сопровождать примерами).

2-й вопрос

• понятие о криволинейной трапеции, чертеж,

• S кр.тр. через 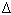F(х) и при каком условии для f(х).

3-й вопрос

• кратко об истории интеграла;

• интеграл;

• определенный, неопределенный интеграл;

• геометрический смысл интеграла;

• как вычислить определенный интеграл;

• может ли значение интеграла быть числом отрицательным или 0, ответ обосновать;

• S кр.тр. = ;

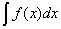• формула Ньютона-Лейбница.

4-й вопрос

• практическое применение интеграла.

(Во время подготовки учащихся к ответам, остальным предлагаются следующие задания).

а) "Сам себе режиссер"

А.

В.

С.

б) "Найти ошибку"

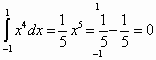
• Проверка заданий.

• Слушаем отвечающих.

• Комментируем ответы.

III. К доске приглашается ученица. Работа вместе с классом (4-5 мин.)

Задание

Используя геометрический смысл интеграла вычислить интеграл.

Решение:

(Алгоритм решение рассказывает ученица).

Примем за D(у) = [8; -8], т.к. 64 - х²0

| x | 8

у² = 64 - х²

у² + х² = 64 - окружность с центром (0; 0) и R= 8

Ответ : 32.

IV. Группе С - дается задание

а) Повышенной трудности. Задания у каждого на карточке. С/р.

б) К доске приглашается ученица (8 мин.). (Алгоритм решения рассказывает ученица).

Задача

Найти площадь фигуры, ограниченной графиком функции у = 3 + 2х - х², касательной к графику в его точке с абсциссой 3 и прямой х = 0

Решение

у = - х² + 2х + 3 - график - парабола.

- х² + 2х + 3 = 0

х² - 2х - 3 = 0

х₁ + х = 2

=> х₁ = -1, х = 3.

х₁ + х = -3

х = (-1 + 3) : 2 = 1; у = у (1) = - 1 + 2 +3 = 4

(0; 3) - точка пересечения параболы с ОY;

(1; 4) - координаты вершин параболы.

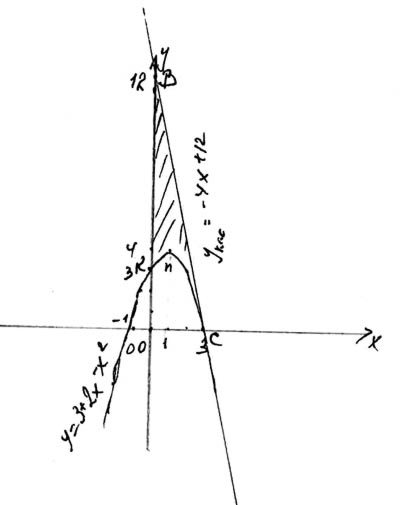
Рис. 1

х = 0 - ось ОY

у кас. = у(х_o) + у'(x_o) (х - х_o) - общий вид уравнения

х_o = 3 касательной

у кас. = -4х + 12

(0; 12) (3; 0)

Строим графики.

Sф = S овс - S кр.тр.ОКnC, SOBC = OC • OB, SOBC = • 3 • 12 = 18

S кр.тр. ОКВС = = ( - х + х² + 3х) / = - 9 + 9 + 9 = 9

Sф = 18 - 9 = 9.

Sф = 9

Ответ: 9

Учащимся группы В дается задание на карточках (10 мин.) решить самостоятельно. (Взаимопроверка)

а) И группа "С" - задания из сборника "Дидактический материал", стр. 60, С-5.

б) Учитель проверяет задание группы "С".

в) К доске приглашаются учащиеся из группы "А". (Каждому предлагается индивидуальное задание).

Работают они под руководством учащихся из группы "С".

V. Подведение итогов (за 4 мин. до окончания урока)

а) Комментирование оценок.

б) Д/з на карточках по группам. (На партах у каждого).

Примечание. Группы А, В, С, названы условно.

По сложности задания распределяются так С, В, А, где С - самое сложное.