- Учителю
- Урок-путешествие «Решение уравнений» в 6 классе
Урок-путешествие «Решение уравнений» в 6 классе
Урок.
Тема : Решение уравнений
Класс: 6
Цели урока:
1) Образовательная
Формировать умение и навыки, способствующие усвоению учащимися основных свойств решения уравнений; учить решать уравнения.
2) Развивающая
Развивать умение логически мыслить, развивать познавательный интерес, смысловую память и аргументированную речь, формирование математической интуиции.
3) Воспитательная
Воспитывать творческое отношение к предмету; расширять математический кругозор; воспитывать культуру речи учащихся; воспитывать чувство ответственности; воспитывать умение контролировать внимание на всех этапах урока.
Методы обучения. Словесный, наглядный, практический; дедуктивный, учебный анализ; репродуктивный, проблемно-поисковый; интерактивный.
Тип урока. Урок ознакомления с новым материалом с использованием интерактивных методов обучения.
Форма проведения: Сказочное путешествие в страну уравнений.
Оборудование к уроку:
-
Видеоматериал с устными упражнениями
-
Плакаты с упражнениями для закрепления
-
Задания для групп: карточки; раздаточный материал.
4) Плакат с рисунком для оформления.
План урока
-
Устный счет
-
Подготовка к изучению нового материала
-
Ознакомление с новым материалом
-
Математический софизм
-
Работа в группах
-
Древнегреческая задача
-
Подведение итогов урока
-
Домашнее задание.
Ход урока
1.Организационный момент. Сообщение темы, цели, задач урока и создание учебной ситуации.
Здравствуйте!
Какая учебная задача решалась вами на протяжении последних уроков?
Ученики: Учились раскрывать скобки и приводить подобные слагаемые.
Учитель: А как вы считаете, для чего нужны все эти операции?
Ученики: Для решения уравнений.
Учитель: А вы хорошо умеете решать уравнения?
Ученики: Конечно, но иногда путаемся.
Учитель: А в чем возникают проблемы?
Ученики: Когда в уравнении есть отрицательные числа.
Учитель: А хотелось бы вам быстрее и легче научиться решать уравнения?
Посмотрите на плакат и скажите: Какие уравнения вы бы сразу решили, а какие бы заставили вас задуматься.
На доске плакат
!. 5х+4=10
2. -6х+8=-10
3. у-7=2
4. -3-5у=-8
5. 11а+3=8
Итак, мы приступаем к изучению новой темы «Решение уравнений». На этом уроке мы должны с вами познакомиться со свойствами уравнений, которые помогут нам намного быстрее справится с их решениями.
А сейчас откройте тетради, запишите число и тему урока.
2. Подготовка к изучению нового материала через повторение и актуализацию опорных знаний.
Учитель: Давайте попробуем разобраться в этой ситуации. Но для этого мы должны попасть в царство уравнений, в эту древнюю, сказочную страну. В царстве уравнений, куда я вас сейчас приглашаю, есть царь - важный и толстый Равно-11, его подданные - числа, Плюсы и минусы, а также встречаются добрые шпионы - неизвестные Иксы , Игреки и другие подозрительные лица, которых все время ищут и находят, но это , кажется, им очень нравится. Жизнь бурлит в царстве Уравнений как и в любом другом государстве.
Итак, вы разбиты на пять групп. Каждая группа сегодня работает сплоченно, дружно и активно. И по количеству полученных каждой группой медалей «Золотая пентаграмма» в конце урока мы оценим каждую группу.
Группы называются: Альфа, Бета, Гамма, Омега и Дельта - буквами греческого алфавита, с которыми вы познакомитесь уже в седьмом классе на уроках геометрии.
Итак, чтобы немного разогреть ваши мысли, необходимо поработать устно. Предлагаю игру, которую применял Пифагор в своей школе к своим ученикам «Развитие мысли».
А как вы думаете, могут ли в царстве уравнений жить Баба Яга и Кощей? Сейчас они предлагают вам свою задачу.
(просмотр видеоматериалов)
3. Ознакомление с новым материалом.
Итак, устно мы поработали. Как вы думаете, по каким законам живут жители царства Уравнений? Назовите их.
Очень хорошо, что вы знаете эти законы. А теперь я расскажу вам историю, которая произошла с жителями этого государства.
В числовом быть может царстве
В уравненье - государстве
Жил-да-был народ честной
Был спокойный он, простой.
Жил по правильным законам
Ничего не нарушая
В этом выгода большая
Для царя того была.
Уравнение делилось на две части - две семьи
И границу между ними пересечь уж не могли
Коль ты правила не знаешь, то сиди ты на печи.
Долго ль коротко ль проходит
Может два, а может год
Взбунтовался весь народ.
Чрез границу уж не хочет проходить он по закону.
Больно уж все долго, нудно
Дайте вы народу волю.
Призадумался тут царь
Стороны той государь
Как же мне народ унять
Славу царскую поднять?
Визы может упразднить?
Иль законы отменить?
А неверное решенье - будет гибелью всему.
За советом к вам пришел он
Помогите вы ему!
Где найти ему спасенье?
Как же обойдя законы
Разрешить им уравненье?
Царь в отчаянье и вот
Осенило вдруг его:
Чтобы перейти границу,
Не открыв загранстраницы
Нужно просто сделать так:
На границе скинь свой знак
И другой взамен возьми
Тогда смело ты иди по ту сторону границы
И свободен будь как птица.
Весь народ возликовал
Сей закон облюбовал.
И с тех пор в стране свободной
Нет запретов обиходных.
Хоть куда теперь иди
Только знак ты свой смени.
На границе сей же час
Выставляет царь Указ:
Стой! При переходе через границу поменяй свой знак на противоположный!
А теперь сформулируем правило: Корни уравнения не изменятся, если перенести слагаемые из одной части уравнения в другую, при этом изменив его знак на противоположный.
Нужно проверить работу этого правила в действии. На плакате записаны уравнения для каждой группы. Представитель группы выходит к доске и показывает перенос слагаемых. За правильное решение группа получает «Золотую пентаграмму».
На плакате:
-
-3х+4=7-х
-
11,5х-13=2х-4
-
2а-11=5а-8
-
15+к=115-2к
-
36-7у=-9у-7.
Вы хорошо справились с заданием. Но вернемся в Царство уравнений. Жителям царства понравились перемены в жизни и они решили не останавливаться на этом. А вот, что еще они придумали, сейчас мы с вами разберемся.
Все вы мыли посуду. А если бы вам предложили автоматизацию труда, например, посудомоечную машину. Это вам бы понравилось. Сейчас я предлагаю автоматизировать процесс решения уравнений. Рассмотрим на примере
4(х+5)=12. По правилу отыскания неизвестного множителя имеем: х+5= 12:4
х+5=3, х=3-5, х=-2. Это же уравнение можно получить, разделив обе части уравнения на 4 или умножить на 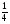 .
.
Итак, корни уравнения не изменятся, если обе части уравнения умножить или разделить на одно и то же число не равное 0.
Мы применим это правило при работе с дробными коэффициентами:
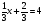 . Умножим обе части уравнения на 3. Почему? (объясняют).
. Умножим обе части уравнения на 3. Почему? (объясняют).
А теперь посмотрим на плакат.
1. 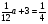
2. 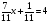
3. 8-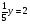
4. 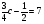
5. 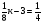
Учащиеся совещаются по группам и представители групп записывают на доске результат.
4. Математический софизм.
Чтобы немного отвлечься от уравнений я предлагаю вам софизм.
Итак, нам даны числа а и b. Пусть число а больше числа b в 1,5 раза, т.е а=1,5 b.
Умножим обе части равенства на 4. Получим: 4а=6 b. Представим 4а=14а-10а, а число b=21 b-15 b. Тогда имеем: 14а-10а=21 b-15 b. Перенесем слагаемые:
14а-21 b=10а-15 b, вынесем за скобки общий множитель 7(2а-3 b)=5(2а-3 b). Разделим обе части равенства на одно и то же выражение и получим, что 7=5. Верно ли это?
Где спрятана ошибка?
Такие, заведомо ложные утверждения называются софизмами.
5. Работа в группах.
Группам даются различные задания, в результате которых они должны получить пословицы. За правильный ответ группа получает медальон, за скорость еще один.
6. Древнегреческая задача.
«Скажи мне, знаменитый Пифагор, сколько человек посещают твою школу?
Половина всех моих учеников изучают математику, четверть занимаются музыкой, седьмая часть находятся в размышлениях, а еще есть три женщины.»
Сколько человек посещают школу Пифагора? Ответ: 28 чел.
Задачу решает один ученик у доски.
7. Подведение итогов урока. Выставление оценок.
Что нового вы узнали сегодня на уроке?
Все группы работали активно, дружно, но та группа, которая набрала больше всех «Золотых пентаграмм" работала лучше всех.
8. Домашнее задание.
-
Дома вы решите номера 1300 и 1302 через один. При решении этих уравнений вы будете использовать правила, которые мы сегодня отработали.
-
Творческое задание: Какие еще новшества могли бы придумать жители Сказочного Царства для более быстрого решения уравнений.