- Учителю
- Программа курса для 8 класса 'Решение задач повышенной сложности'
Программа курса для 8 класса 'Решение задач повышенной сложности'
Пояснительная записка.
Актуальность: курс направлен на расширение знаний учащихся по математике, развитие их теоретического мышления и логической культуры.
Программа ориентирована на учащихся 8 классов, которым интересна как сама математика, так и процесс познания нового.
Новизна: курс дает возможность изучить основные темы школьной программы на углубленном уровне.
Занятия проводятся 1 час в неделю.
Цели : обобщение и систематизация, расширение и углубление знаний по указанным темам, а также обретение практических навыков выполнения заданий, повышение уровня математической подготовки школьников.
Общеобразовательная: овладение системой математических знаний и умений.
Прикладная: формирование принципов математического моделирования каких-либо реальных процессов.
Воспитательная: развитие логического и алгоритмического мышления, формирование трудолюбия, настойчивости, развитие умения ценить красоту мысли.
Задачи :
-
вооружить учащихся системой знаний по указанным темам;
-
сформировать навыки применения данных знаний при решении разнообразных задач различной сложности;
-
сформировать навыки самостоятельной работы, работы в малых группах;
-
сформировать навыки работы со справочной литературой, с компьютером;
-
сформировать умения и навыки исследовательской работы;
-
способствовать развитию алгоритмического мышления учащихся;
-
способствовать формированию познавательного интереса к математике.
Ожидаемые результаты:
Учащиеся раскроют свой творческий потенциал, обогатят себя знанием методов исследовательской деятельности, приобретут прочные знания по основным и дополнительным разделам математики.
Результатом освоения программы курса является представление школьниками творческих индивидуальных и групповых работ на итоговом занятии.
Содержание программы и календарно-тематическое планирование
1.Линейные уравнения и системы линейных алгебраических уравнений:
-
Кусочно-линейные уравнения -1ч
-
Уравнения с параметром-1ч
-
Решение слау методом Крамера -2ч
-
Решение слау методом Гаусса-2ч
-
Решение слау повышенной сложности-1ч
2. Функции и их графики
-
Функции вида у=
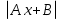 , у=
, у=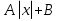 , у=
, у=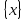 , у=
, у=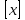 --2ч
--2ч -
Кусочно-заданные функции-1ч
-
Преобразование графиков различных функций -1ч
-
Графики уравнений
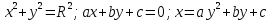 --2ч
--2ч -
Графики неравенств-1ч
-
Чтение графика функции - 1ч
3. Квадратные уравнения
-
Исследование квур. Мнимая единица--1ч
-
Выражения, симметричные относительно корней квур, их связь с коэффициентами-1ч
-
Квур с модулем-1ч
-
Квур с параметром-1ч
-
Введение новой переменной при решении квур-1ч
-
Треугольник Паскаля. Бином Ньютона-1ч
4. Неравенства и системы неравенств
-
Линейные неравенства с модулем-1ч
-
Неравенства с параметром-1ч
-
Решение систем линейных неравенств повышенной сложности - 1ч
5. Элементы комбинаторики и теории вероятностей
-
Элементы комбинаторики. Сочетания с повторениями и сочетания без повторений.-1ч
-
Случайные события и операции над ними-1ч
-
Вероятность случайного события-1ч
-
Вероятность сложных событий-2ч
6. Задачи планиметрии
-
Дополнительные свойства медиан, высот и биссектрис треугольника-1ч
-
Дополнительные свойства четырехугольников и окружности. Площади-1ч
Зачетная работа - 1ч
Итого - 32 часа.
№№
п/п
Тема
Компетентности
Кол-во часов
Дата
пров-я
Приме
чание
1
Линейные уравнения и системы уравнений
Уметь: решать уравнения, содержащие один и несколько модулей; исследовать линейные уравнения с параметром; находить определители и решать с их помощью слау, решать слау методом Крамера и Гаусса; решать системы, содержащие знак модуля.
7
2
Функции и их графики
Уметь: строить графики основных функций и уравнений; преобразовывать графики; строить графики кусочно-заданных функций и неравенств; решать уравнения с модулем графическим способом
8
3
Квадратные уравнения
Уметь: исследовать квур; решать квур, содержащие модуль параметр; определять и решать симметрические и возвратные уравнения
6
4
Неравенства и системы неравенств
Уметь: решать неравенства и системы с модулем, с параметром;
3
5
Элементы комбинаторики и теории вероятностей
Уметь: производить операции над событиями, находить вероятность случайных и сложных событий.
5
6
Задачи планиметрии
Уметь: решать задачи на нахождение площадей плоских фигур; применять дополнительные свойства медиан, высот и биссектрис.
2
Зачетная работа
1
Список литературы
-
С.А.Субханкулова. Задачи с параметрами. Илекса,2010.
-
А.В.Мерлин. Элементарная математика. Чебоксары,1996.
-
Я.И.Перельман. Занимательная алгебра. Наука, 1976
-
Лекции по статистике и теории вероятностей. Преподаватель А.В.Мерлин-профессор физико-математических наук.
-
Функции и их графики, лекции. Преподаватель А.В.Мерлин-профессор физико-математических наук.
-
Я.С.Фельдман, А.Я. Жаржевский. Математика. Решение задач с модулями.Оракул. Санкт-Петербург,1997, 304 с
-
Я.С.Фельдман, А.Я. Жаржевский. Решение задач с параметрами "Агенство ИГРЕК", Санкт-Петербург, 1995, 212 с.