- Учителю
- Урок по теме' Преобразование выражений, содержащих квадратные корни' (урок алгебры в 8 классе)
Урок по теме' Преобразование выражений, содержащих квадратные корни' (урок алгебры в 8 классе)
 Муниципальное общеобразовательное учреждение
Муниципальное общеобразовательное учреждение
«Основная общеобразовательная школа № 4 города Белово»
Преобразование выражений, содержащих квадратные корни
(урок алгебры в 8 классе)
И.Н.Диркс,
учитель математики
2012
Преобразование выражений, содержащих квадратные корни.
Цель урока:
-
Обобщение и систематизация знаний о преобразовании выражений, содержащих квадратные корни.
Задачи урока:
-
выявить уровень сформированности практических умений по тождественным преобразованиям выражений, содержащих квадратные корни
-
продолжить работу над выработкой умений проводить упрощение выражений, сокращение дробей, вынесение и внесение множителя под знак корня;
-
развивать математическую речь, логическое мышление, навыки устного счета, навыки самоконтроля и взаимоконтроля;
-
воспитывать самостоятельность, трудолюбие, стремление к знаниям.
1. Организационный этап
Здравствуйте, ребята. Я надеюсь на то, что урок вам понравится и запомнится. Будьте внимательны, и у нас все получится.
Если в жизни ты хоть на мгновенье
Истину в сердце своем ощутил,
Если луч света сквозь мрак и сомненье
Ярким сияньем твой путь озарил:
Что бы в решенье твоем неизменном
Рок ни назначил тебе впереди,
Память об этом мгновенье священном
Вечно храни, как святыню в груди.
Тучи сберутся громадой нестройной,
Небо покроется черною мглой,
С ясной решимостью, с верой спокойной
Бурю, ты встреть и померься с грозой. (Слайд 1)
Как вы думаете, о чем это стихотворение?
(В этом стихотворении выражено стремление к знаниям, умение преодолевать все преграды, которые встречаются на пути).
Кто может мне назвать автора? (Софья Ковалевская 19 век) (Слайд2)
Сегодня на уроке, мы тоже должны показать свое стремление к знаниям и умение преодолевать преграды по теме «Преобразование выражений, содержащих квадратные корни». (Слайд 3)
Давайте поставим цель нашего урока. (Ответы учащихся)
Итак, цель урока - обобщение знаний по преобразованию выражений, содержащих квадратные корни.
Подвести итоги сегодняшнего урока поможет оценочный лист. Он находится у каждого из вас. Сюда необходимо вносить баллы, полученные за каждый этап урока. В конце урока будет подведен итог и выставлена отметка за усвоение темы.
2. Устная работа (слайд 4)
Учащимся предлагаются задания по нарастанию уровня сложности: «Немного подумайте» - задания базового уровня, «Подумайте лучше» - повышенного, «Хорошенько подумайте» - задания высокого уровня сложности.
Критерии оценивания: каждый, кто правильно ответил на вопрос, ставит в оценочный лист урока соответствующее количество баллов: «Немного подумайте» - 1 балл, «Подумайте лучше» - 2 балла, «Хорошенько подумайте» - 3 балла. (Слайд 5)
Учащиеся, верно ответившие на несколько вопросов, суммируют баллы.
Учащиеся отвечают на вопросы. (Слайд 6-12)
Немного подумайте.
-
Вынесите множитель из-под знака корня:
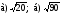
-
Внесите множитель под знак корня:
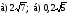
-
Возведите в квадрат:
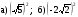
-
Приведите подобные слагаемые:
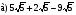
Подумайте лучше.
Найди ошибку:
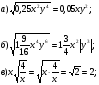
Хорошенько подумайте.
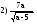
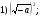 При каких значениях а выражение не имеет смысла:
При каких значениях а выражение не имеет смысла:
Выставляем баллы в оценочный лист за устную работу.
-
Обобщение и систематизация знаний по теме урока.
На этом этапе урока выполняются одновременно два вида деятельности: некоторые учащиеся работают у доски, выполняют дифференцированные задания, а остальные пишут графический диктант.
Переходим к практической работе.
Дифференцированные задания: задания базового уровня, повышенного уровня, высокого уровня. Трое учащихся выходят к доске.
Пока ребята работают у доски, вы пишите графический диктант.
Задания для диктанта находятся у вас на парте.
Графический диктант: думать придется много, писать - мало.
- ДА ^ - НЕТ (Эти обозначения можно записать на доске для учащихся, плохо воспринимающих информацию на слух).
Проверка: -^^-^--^ . (Слайд 13)
Критерии оценивания:
«5» - нет ошибок
«4» - 1 - 2 ошибки
«3» - 3 - 4 ошибки
«2» - более 4-х ошибок
Учащиеся отвечают на вопросы:
1. Корень из произведения неотрицательных множителей равен произведению корней из этих множителей (да).
2. Это верное равенство:
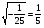 (нет).
(нет).
3. Арифметическим квадратным корнем из числа а называется любое число, квадрат которого равен а (нет).
4. Корень из дроби, числитель которой неотрицательное число, а знаменатель - положительное, равен корню из числителя, деленному на корень из знаменателя (да).
5. Выражение 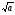 имеет смысл только при отрицательном значении а (нет).
имеет смысл только при отрицательном значении а (нет).
6. Это верное равенство: 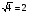 (да).
(да).
7. Чтобы извлечь корень из степени с четным показателем, достаточно представить подкоренное выражение в виде квадрата некоторого выражения и воспользоваться тождеством 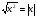 (да).
(да).
8. Равенство 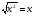 верно при любом значении х (нет).
верно при любом значении х (нет).
Обменялись тетрадями. Осуществляем проверку. Поднимите руку те, кто справился без ошибок. У кого одна ошибка? Есть среди вас те, кто не справился с работой? ( Если есть, то предложить обратиться за помощью к учебнику). Не забываем поставить себе баллы за эту работу.
Во время взаимопроверки, учитель проверяет задания, выполненные на доске с комментированием отметок.
Критерии оценивания: базовый уровень - 3 балла, повышенный - 4 балла, высокий - 5 баллов.
-
Физминутка
Поменяемся рядами,
Поменяемся местами с теми, кто справился с устным счетом.
Сделаем шаг навстречу тому, кто справился с графическим диктантом.
Протянем руки помощи тому, кто допустил ошибки.
Поаплодируем тому, кто был сегодня у доски.
Улыбнемся друг другу и вернемся на свои места.
-
Самостоятельная работа
Отдохнули хорошо, давайте работать дальше. Переходим к самостоятельной работе.
Самостоятельная работа
(Задания 1-4 обязательного уровня, 5-7 повышенного уровня, 8-11 высокого уровня.)
-
Вынесите множитель из-под знака корня:
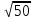
1. 5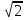 2. 25
2. 25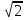 3. 2
3. 2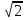 4. 10
4. 10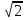
2. Упростите выражение: 3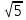 + 6
+ 6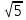 - 7
- 7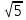
1. -2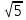 2. 2
2. 2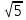 3. 16
3. 16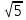 4. 4
4. 4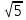
3.Найдите значение выражения: 5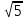 + 3
+ 3 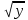
1. 28 2. 82 3. 8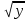 4. 160
4. 160
4. Упростите выражение:
2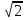 -
- 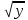 +
+ 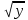
__________________________
5. Упростите выражение: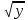 +
+ 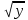 )
)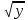 -
- 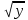 ) + y
) + y
6. Разложите на множители: Х2 - 5
7. Сократите дробь: 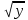
_______________________
8. Найдите значение выражения: 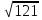 - 3
- 3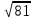 +
+ 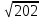
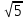 9. Найдите значение выражения:
9. Найдите значение выражения: 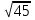 ∙
∙ 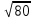
10. Сократите дробь: 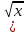
11. Освободитесь от иррациональности в знаменателе: 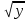
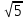
Самопроверка (ответы на слайде) (Слайд 14),критерии (Слайд 15)
Поднимите руки те, кто справился с работой на 5? 4? 3? 2?
Не забываем выставить баллы в свой оценочный лист за самостоятельную работу.
-
Подведение итогов, рефлексия
Учащиеся подсчитывают общее количество баллов, полученных за урок, выставляют отметку согласно критериям. Выставляется итоговая отметка в оценочный лист.
«5» - 12 баллов и более
«4» - 9-11 баллов
«3» - 6-8 баллов
«2» - менее 6 баллов
Кто набрал 12 баллов? А есть среди вас те, кто набрал большее количество баллов? Кто набрал менее 6 баллов?
Кому было на уроке легко? Кому было трудно? Как вы думаете, что нужно сделать, чтобы избежать этих трудностей?
Отметка, полученная вами, это та оценка, которую вы поставили себе за урок. Давайте, узнаем мою оценку вашей работы на уроке. (Слайд 17 - 23)
На экране появляются буквы:
АОВСТЛКРИЧГНМО
Выполняя задания 1 - 7, вычеркните буквы, соответствующие ответам.
Учащиеся устно выполняют задания:
1. 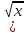 2.
2. 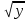 3.
3. 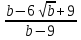 4.
4. 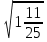 5.
5. 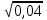
6. 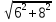 7.
7. 
Шифр: А - 18; В - 4; Г - -2; И - 1; К - 0; М - 0,18; Н - 0,8; О - -5; Р - 0,5; С - 7,3; Т - 25; Ч - 8
Остается слово «Отлично». (Слайд 24)
7. Итог урока
Этого, результата мы достигли, только благодаря вашему трудолюбию, стремлению к знаниям, умению преодолевать трудности. А это дорогого стоит. Надеюсь, знания полученные сегодня на уроке вам помогут при выполнении контрольной работы, которая будет на следующей неделе. Спасибо за урок! (Слайд 25)